Abstract
Quasilongitudinal sound velocities and the second-order elastic moduli of tetragonal hen egg-white lysozyme crystals were determined as a function of relative humidity (RH) by Brillouin scattering. In hydrated crystals the measured sound velocities in the [110] plane vary between 2.12 ± 0.03 km/s along the [001] direction and 2.31 ± 0.08 km/s along the [110] direction. Dehydration from 98% to 67% RH increases the sound velocities and decreases the velocity anisotropy in (110) from 8.2% to 2.0%. A discontinuity in velocity and an inversion of the anisotropy is observed with increasing dehydration providing support for the existence of a structural transition below 88% RH. Brillouin linewidths can be described by a mechanical model in which the phonon is coupled to a relaxation mode of hydration water with a single relaxation time of 55 ± 5 ps. At equilibrium hydration (98% RH) the longitudinal moduli C11 + C12 + 2C66 = 12.81 ± 0.08 GPa, C11 = 5.49 ± 0.03 GPa, and C33 = 5.48 ± 0.05 GPa were directly determined. Inversion of the measured sound velocities in the [110] plane constrains the combination C44 + ½C13 to 2.99 ± 0.05 GPa. Further constraints on the elastic tensor are obtained by combining the Brillouin quasilongitudinal results with axial compressibilities determined from high-pressure x-ray diffraction. We constrain the adiabatic bulk modulus to the range 2.7–5.3 GPa.
INTRODUCTION
The biological activity of proteins is closely connected to their conformational flexibility. The interplay between the chemical properties, mechanical properties, thermal fluctuations, and structural fluctuations plays an essential role in ligand binding, catalysis, and other protein functions in living cells. The relationship between protein structure and mechanical properties is also important, for instance, in the design and application of elastic proteins in biotechnology and materials science (Gosline et al., 2002).
The elastic properties of proteins in solution have been explored by ultrasound velocimetry (Sarvazyan, 1991; Kharakoz, 2000). This technique yields information about the compressibility of protein molecules and their surrounding hydration layer. This in turn indirectly yields information about their hydration state and the amplitude of their structural fluctuations, although separating these contributions is difficult. Since the orientation of the protein molecules in solution is random, this technique yields only the protein's bulk modulus, which is insensitive to intrinsic molecular anisotropy and by itself provides limited information about the protein's physical state (Kharakoz, 2000).
The orientation averaging that occurs in solution studies can be eliminated by studying proteins in crystalline form. Crystal elasticity is determined by the anisotropic elasticity of the individual molecules and of the crystal contacts between molecules. Studies on a wide array of organic and inorganic materials demonstrate that the elastic tensor and associated damping constants can provide detailed information about both static structure and dynamical processes (e.g., Krüger et al., 1989; Lee et al., 1987; Tao et al., 1988). The elastic tensor determines the energetics of cracks, dislocations, vacancies, and other defects responsible for crystal mosaicity. It is essential to understanding how protein crystals respond to mechanical stresses associated with postgrowth treatments such as soaking in solutions containing heavy atom compounds, ligands, drugs, and cryoprotectants, to stresses caused by radiation damage, and to stresses that occur during flash cooling procedures. The elastic tensor is also essential in understanding the structural stability of catalysts based on cross-linked enzyme crystals.
Protein crystal elasticity has been explored using mechanical resonance techniques (Morozov and Morozova, 1981, 1993; Morozov et al., 1988). Young's modulus of selected protein crystals decreases with increasing hydration and with increasing temperature up to the denaturation temperature. Analysis of this data using highly simplified models yields estimates of the molecular and intermolecular elasticity, and of the amplitude of rigid body molecular translations and librations consistent with those obtained by other techniques (Morozov and Morozova, 1986).
The mechanical properties of protein crystals have also been studied using ultrasonic techniques (Edwards et al., 1990; Tachibana et al., 2000), and x-ray diffraction under hydrostatic pressure (Kundrot and Richards, 1987; Katrusiak and Dauter, 1996; Fourme et al., 2001). Both ultrasound and resonance measurements in crystals are very demanding in terms of sample size and preparation requirements. Extensive sample manipulations such as crosslinking, cutting, and gluing can modify crystal properties (Morozov and Morozova, 1981; Edwards et al., 1990). Ultrasound measurements require crystals a few millimeters thick, limiting their applicability to the handful of proteins that yield crystals of such size. The existing results from all of these techniques are fragmentary.
Brillouin spectroscopy (Brillouin, 1922) is a noncontact method that has the potential to give a more complete picture of protein crystal elasticity. It allows direct measurement of the sound velocity along general directions in a transparent medium and hence the determination of the elastic tensor of anisotropic materials. Brillouin spectroscopy has been widely used for the study of inorganic crystals (Zha et al., 1993), polymers (Krüger, 1989) and biological materials (Vaughan and Randall, 1980; Lee et al., 1993).
Here we report results of the first extensive Brillouin scattering study of protein crystal elasticity. Some preliminary results have been published elsewhere (Caylor et al., 2001).
SAMPLES AND EXPERIMENTAL METHODS
Tetragonal hen egg-white lysozyme crystals were grown at 21°C in hanging and sitting drops and in agarose gels (0.1% w/v), using solutions consisting of 40–60 mg/ml lysozyme (Seikagaku, 6× recrystallized) and 0.5 M NaCl in 50 mM acetate buffer at pH = 4.5. All crystals had well-developed {110} and {101} faces, and gel-grown crystals had nearly ideal habits. The equilibrium relative humidity (RH) corresponding to the growth conditions was 98%.
Crystals were dehydrated to different RH by equilibration, at T = 295 ± 1 K, with vapors of saturated salt solutions of KNO3 (93% RH), KCl (86%), KBr (83%), (NH4)2SO4 (79%), NaCl (75%), and CuCl2 (67%). The values of RH are based on those reported in Rockland (1960). A small drop of the appropriate salt solution was placed in the capillary at a distance of ∼1 cm from the crystal. X-ray topography and x-ray diffraction peak shape analysis (Dobrianov et al., 2001) show evidence of fine scale heterogeneities and dislocations in tetragonal lysozyme crystals dehydrated below 88% RH. However, we did not observe any evidence of Brillouin signal degradation even in highly dehydrated crystals.
Using Brillouin scattering, acoustic velocities can be determined in a transparent medium from the frequency shift of laser light inelastically scattered by thermal vibrations. For an optically isotropic medium, conservation of energy and momentum require that the frequency of the scattered light be shifted from that of the incident light by (Brillouin, 1922):
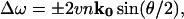 |
(1) |
where v is the phonon velocity in the measured direction, n is the refractive index of the scattering medium, k0 is the wave vector of the incident light, and θ is the angle between the incident and scattered wave vectors. Three Brillouin peaks will in general be produced by the three polarizations (quasilongitudinal, and two quasitransverse) of the scattering phonon along a general direction in crystalline solids. Due to its extremely low bi-refringence (Δn = 0.005; Cervelle et al., 1974), tetragonal lysozyme can be considered as an optically isotropic medium allowing Eq. 1 to be used in the analysis of the Brillouin spectra.
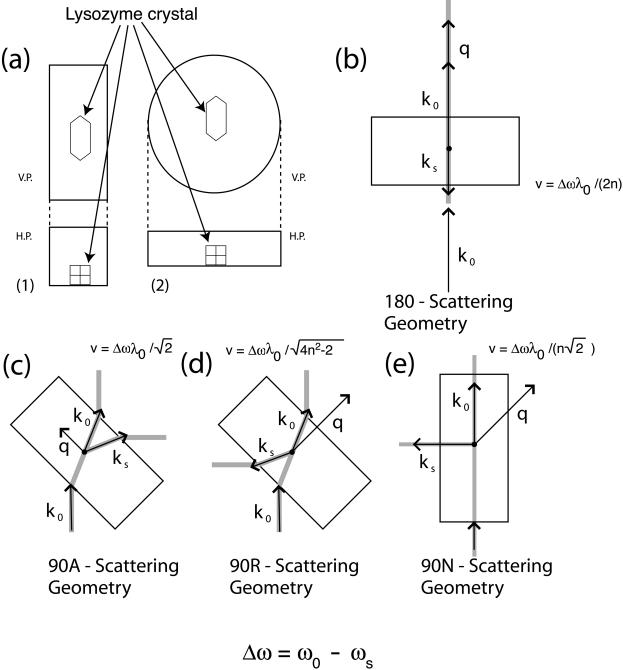
Brillouin scattering is performed using standard scattering geometries characterized by different angles between the directions of the incident and scattered light outside the sample that are shown in Fig. 1, b–d. These geometries prevent overlap of sample scattering with the unshifted incident light and can enhance peak intensities by exploiting selection rules imposed by the elasto-optic coupling in the examined material (e.g., Cummins and Schoen, 1972).
FIGURE 1.
(a) Schematic diagram of the sample holder. (1) square cross-section glass capillary, for measurements in 180 and 90R scattering geometries; and (2) sealed circular glass slides for measurements in the 90A forward geometry, with V.P., vertical plane, and H.P., horizontal plane. (b–e) Diagrams of the scattering geometries in the different experimental configurations used in this study: k0 is the incident wave vector, kS the scattered wave vector, q the phonon wave vector, v the phonon velocity, Δω the Brillouin scattering frequency shift, λ0 the incident laser wavelength, n the refractive index of the scattering medium, ω0 the incident frequency, and ωS the scattered frequency.
The elastic tensor of tetragonal lysozyme (Laue group, 4/mm) has six unique nonzero elements (written in contracted notation as: C11, C12, C13, C33, C44, and C66). The relationship between velocity and polarization of the phonon and the elastic properties of the scattering medium are expressed by Christoffel's equation (Auld, 1973):
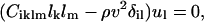 |
(2) |
where Ciklm are the elastic constants, lk and lm are the direction cosines of the phonon, ul is the local displacement vector, ρ is the density of the material, v is the velocity of the phonon, and δil is the Kronecker delta. Eq. 2 is a set of three homogeneous equations, which have nontrivial solutions only if
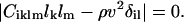 |
(3) |
This is a cubic equation in ρv2 with three real positive roots.
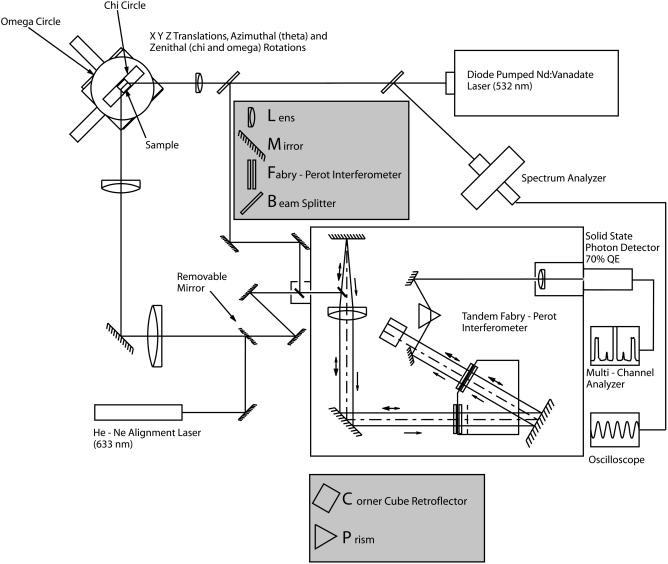
A vertically polarized neodymium vanadate laser (λ = 532.15 nm) operated at 1.59 W and filtered to 1.59 mW was used as an excitation source. X-ray topography and diffraction resolution measurements performed at the Cornell High-Energy Synchrotron Source on crystals after extended laser illumination verified that these small powers caused no heating damage. Brillouin spectra were acquired using a six-pass Sandercock tandem Fabry-Perot interferometer (Lindsay et al., 1981) and a solid-state photon detector with 70% quantum efficiency. Experiments were performed with and without polarization control in the incident and scattered light path. A diagram of the setup of the Brillouin system used in this study is outlined in Fig. 2. Selected crystals were mounted in square cross-section capillaries or sandwiched between parallel glass slides (Fig. 1 a). The typical size of the analyzed crystals was ∼400 × 500 × 100 μm but Brillouin signal was obtained from crystals as small as ∼200 × 300 × 60 μm. The setup that we used is capable of producing intense Brillouin signal from high-quality crystals as small as 60 × 60 × 20 μm.
FIGURE 2.
Schematic diagram of the Brillouin scattering system.
Sound velocities were measured in 90A forward scattering geometry (Fig. 1 c) along 10–18 directions in the (110) plane in crystals at 98%, 79%, and 67% RH. Sound velocities in the [110] and [001] directions were measured using the 90A and 90R scattering geometry (Fig. 1 d) in crystals at 93% and 86% RH. Sound velocities along [110] were measured in the 180 scattering geometry (Fig. 1 b) in crystals at 98% RH. Measurement of sound velocity along the [100] direction were performed in the 90N scattering geometry (Fig. 1 e).
RESULTS
In all experiments only one of the three expected acoustic modes was detected. To identify this mode, we measured the Brillouin shift along the [110] and [001] directions controlling the polarization of the incident and scattered light. A half waveplate was used to rotate the polarization of the incident light, and a polarizer and analyzer with a high extinction ratio were inserted in the incident and scattered light paths, respectively. The Brillouin scattered light intensity, I, can be expressed as (Cummins and Shoen, 1972):
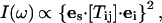 |
(4) |
where es and ei are unit vectors in the direction of the polarization of the scattered and incident light, respectively, and Tij is the Brillouin scattering tensor component, which is related to the elasto-optic coupling tensor. The observed extinction of the Brillouin features in cross-polarized light confirms that the observed acoustic mode has a pure longitudinal polarization in the [110] and [001] directions and a quasilongitudinal character in the intermediate directions. The absence of transverse modes may be due to the low efficiency of the elasto-optic coupling in the examined crystal directions, or to low transverse velocities that cause the corresponding peaks to be obscured by the tails of the elastic scattering peak.
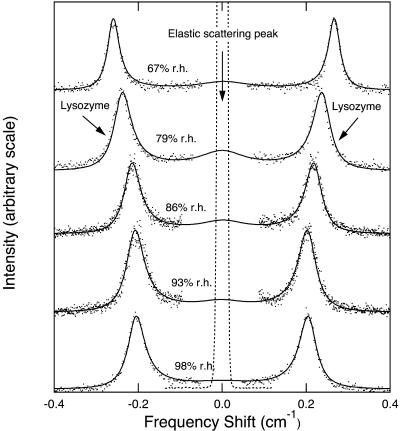
Typical Brillouin spectra are shown in Fig. 3. Comparison of the frequency shift measured in the [110] direction in backscattering (180), forward symmetric (90A), and reflected symmetric (90R) geometries yield a refractive index of 1.51 ± 0.07 in good agreement with the value of 1.56 ± 0.01 obtained by oil immersion and with the value reported by Cervelle et al. (1974) of 1.538–1.575.
FIGURE 3.
Brillouin spectra for phonons propagating in the [110] direction in tetragonal lysozyme crystals at different relative humidities. The dots indicate the raw data. The lines are a fit to a model for the mechanical coupling of the acoustic phonon to a relaxation mode of hydration water.
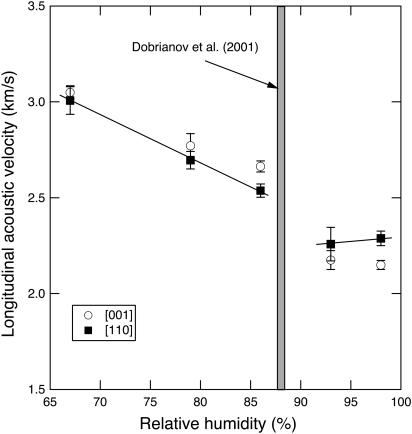
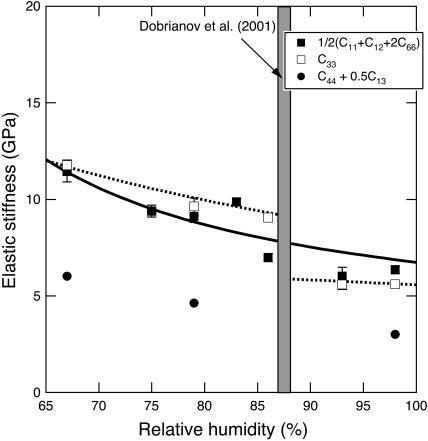
The observed acoustic velocities along the (110) plane of tetragonal lysozyme reveal significant velocity anisotropy, expressed as the absolute value of the difference between the velocity measured along the [110] and [001] directions (Fig. 4). The anisotropy decreases with increasing dehydration from 0.2 km/s at 98% RH to 0.09 km/s at 67% RH. The character of the anisotropy changes between 93% and 86% RH, as indicated by the variation of acoustic mode velocity with crystallographic direction and by a discontinuity in the general trend of increasing acoustic velocity with the degree of dehydration (Fig. 4).
FIGURE 4.
Sound velocity of tetragonal lysozyme along the [110] and [001] directions as a function of RH. There is a discontinuous increase of both velocities and an inversion of the velocity ratio in the 93%–87% RH range.
DISCUSSION
In the [110] direction, Christoffel's equation for the tetragonal system can be factored. The solution for the quasilongitudinal acoustic velocity has the form (e.g., Auld,1973):
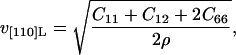 |
(5) |
where ρ is the density of crystalline lysozyme (taken from the isothermal dehydration data of Gevorkyan and Morozov, 1983). The velocity measured along the [001] direction allows us to directly determine the constant C33 from (Auld, 1973):
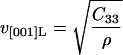 |
(6) |
The effective elastic constants along these two directions show a discontinuity as a function of degree of dehydration in the 93–86% RH range (Fig. 5), in agreement with the direct sound velocity measurements.
FIGURE 5.
Elastic constant C33, and the combinations ½(C11 + C12 + 2C66) and C44 + 0.5C13 (see text) of tetragonal lysozyme crystals plotted as a function of RH. The solid line is the best fit to the structural model for ½(C11 + C12 + 2C66), whereas the dashed line is the best fit for C33.
The velocities of the quasilongitudinal acoustic mode along the [110] and [001] directions at 98% RH are 2.31 ± 0.04 km/s and 2.12 ± 0.03 km/s, respectively. Additional measurements along the [100] direction resulted in a velocity of 2.13 ± 0.01 km/s. These velocities correspond to values for the longitudinal modulus ML[110] = C11 + C12 + 2C66 = 12.81 ± 0.08 GPa, ML[001] = C33 = 5.48 ± 0.05 GPa, and ML[100] = C11 = 5.49 ± 0.03 GPa. The longitudinal acoustic velocity along [110] and the effective stiffness ML[110] is larger than the value determined by ultrasonic measurements performed by Tachibana et al. (2000, 2002) (Table 1). The difference of the measured velocities (25%) and, as a consequence, the difference of the longitudinal modulus (60%), are both much larger than mutual uncertainties.
TABLE 1.
Measured dynamic and static elastic moduli of tetragonal hen egg-white lysozyme crystals
| Longitudinal modulus
|
Bulk modulus
|
Young's modulus
|
|||
|---|---|---|---|---|---|
| Technique | ML[110] (GPa) | ML[001] (GPa) | K (GPa) | E[110] (GPa) | E[001] (GPa) |
| Brillouin scattering (dynamic modulus) | 12.81*–22.2† | 5.48*–11.7† | 4.32*‡ | 3.69*‡ | |
| X-ray diffraction | 4–10§ | ||||
| Resonance method (dynamic modulus) | 1.0*¶–8.0*¶ | ||||
| Microreed bending (static modulus) | 0.18*¶–2.3¶∥** | ||||
| Ultrasonic pulse-echo (dynamic modulus) | 7.99†† | 2.7‡†† | |||
ML[110] = C11 + C12 + 2C66; ML[001] = C33.
98% RH.
67% RH.
Isotropic Young's modulus calculated for Poisson's ratio is 0.33. Velocity is in the specified directions.
Kundrot and Richards (1987), Kharakov (2000), and Fourme et al. (2001); at 98% RH.
Morozov et al. (1988); at 98–0.01% RH.
Average of the values for [001] , [110] , and [100].
0.01% RH.
Tachibana et al. (2000, 2002); at 98% RH.
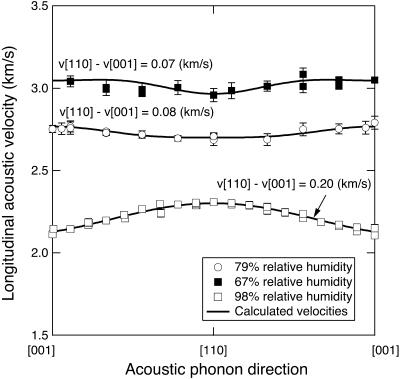
The dependence of the measured acoustic velocity on the phonon direction at 98% RH is anisotropic (Fig. 6). The maximum measured velocity along [110] and the minimum velocity along [001] differ by 0.20 km/s (8.2%). Bounds to the value of Young's modulus, E, can be estimated assuming elastic isotropy, as in Tachibana et al. (2000), using (e.g., Auld, 1973),
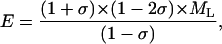 |
(7) |
where ML is the longitudinal modulus, and σ is Poisson's ratio.
FIGURE 6.
Longitudinal sound velocities of tetragonal lysozyme crystals as a function of direction in the (110) plane. The solid lines are model velocities computed from the best-fit elastic constants. Error bars are smaller than the symbols where not shown.
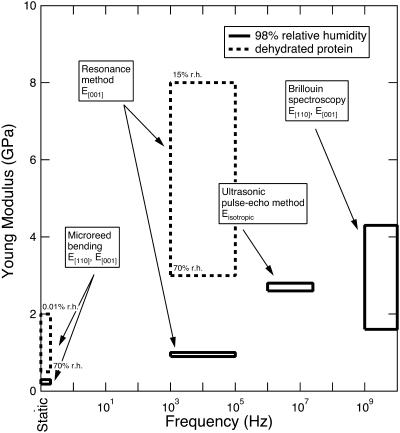
Using the longitudinal moduli along [100] , [001] , and [110] and fixing Poisson's ratio to 0.33, as observed in many polymers, the two “bounds” to the value of the isotropic Young's modulus from data in the [110] and [001] directions are 4.32 ± 0.03 and 3.69 ± 0.02 GPa (Table 1). These values are higher than the dynamic moduli determined with the microreed method (Morozov et al., 1988) and the isotropic value from ultrasonic measurements (Tachibana et al., 2000), and suggest a frequency dependence of Young's modulus (Fig. 7).
FIGURE 7.
Range of values of the Young's moduli of tetragonal lysozyme crystals as determined using different techniques in different frequency ranges. See Table 1 for the data references.
The measurements performed in this study show that dehydration increases the sound velocity in tetragonal lysozyme crystals, consistent with previous measurements of elastic properties of dehydrated triclinic lysozyme crystals (Morozov and Morozova, 1981). Dehydration also decreases the overall velocity anisotropy along the [110] plane from 8.2% at 98% RH, to 2.8% at 79% RH, to 2.0% at 67% RH (Fig. 6). The [110] direction is the fastest direction at elevated RH, but the anisotropy inverts <93% RH, and [001] becomes the fastest direction. The longitudinal acoustic velocities along [110] and [001] directions as a function of dehydration also show a discontinuity in the range from 93% to 86% RH (Fig. 4). These results are in agreement with x-ray diffraction evidence for a structural phase transition in the same humidity range (Salunke et al., 1985, Dobrianov et al., 2001). Sound velocity discontinuities as a function of RH have been interpreted as phase transitions in other organic systems (Lee et al., 1993).
After correction for instrumental broadening, we calculated the normalized attenuation of the quasilongitudinal phonons in the [110] and [001] directions (e.g., Lee et al., 1993),
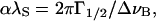 |
(8) |
where α is the phonon's energy decay constant, λS is the phonon wavelength, Γ1/2 is the half-width at half-maximum of the Brillouin peak, and ΔνB is the Brillouin frequency shift.
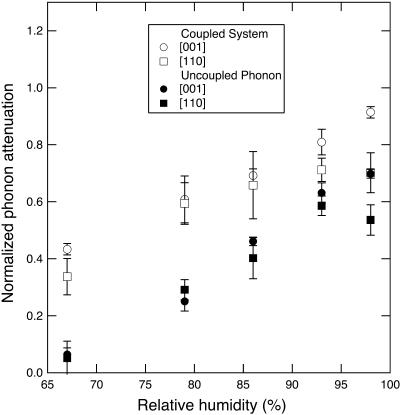
The phonon attenuation decreases with dehydration, and it does not show any discontinuity in the 93–86% RH range (Fig. 8). The value of the phonon attenuation for both the [001] and [110] directions ranges between 0.3 and 0.9, and it is comparable to hypersonic attenuation of plastic crystalline and amorphous organic solids, which ranges between 0.4 and 0.7 (e.g., Folland et al., 1975; Huang and Wang, 1975). However, other factors including static disorder and the effect of coupling with the relaxation mode of the hydration shell (Tao et al., 1988; Lee et al., 1993) could contribute to the observed peak width.
FIGURE 8.
Normalized phonon attenuation αλS as a function of RH, calculated for phonons propagating along the [110] and [001] directions. Both coupled and uncoupled values are shown for comparison.
While the details of hypersonic attenuation in lysozyme and its dependence of dehydration will be the subject of future study, here we briefly outline a simple model to describe the Brillouin linewidths observed in the [001] and [110] directions at different RH. We assume that the dominant source of phonon damping is due to coupling to relaxational modes originating from orientational motions of hydration water surrounding the protein surface inside the crystal (Tao et al., 1988). Our approach closely follows the method developed for DNA by Tominaga et al. (1985) and Lee et al. (1987; 1993). Raman studies have suggested that the dynamics of hydration water are similar for both DNA films and lysozyme crystals (Urabe et al., 1998).
According to the fluctuation-dissipation theorem, the Brillouin spectral profile S(ω) is proportional to the imaginary part of the dynamic susceptibility (Lee et al., 1993),
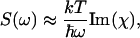 |
(9) |
where k is Boltzmann's constant and T is the temperature (in K). The dynamic susceptibility χ is expressed as
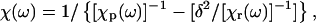 |
(10) |
where χp(ω) = 1/(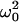 − ω2 − iωγ) is the uncoupled phonon susceptibility; χr(ω) = 1/(1 − iωτ) is the susceptibility of the Debye relaxational mode of the hydration water; δ is the coupling constant, proportional to the coupling strength (Lee et al., 1993); ω0 and γ are the frequency and linewidth of the uncoupled phonon; and τ is the (single) relaxation time of the water of hydration. Twenty Brillouin spectra collected along [110] and [001] at different relative humidities were fit to Eq. 9. Representative results of application of this model are shown in Fig. 8.
− ω2 − iωγ) is the uncoupled phonon susceptibility; χr(ω) = 1/(1 − iωτ) is the susceptibility of the Debye relaxational mode of the hydration water; δ is the coupling constant, proportional to the coupling strength (Lee et al., 1993); ω0 and γ are the frequency and linewidth of the uncoupled phonon; and τ is the (single) relaxation time of the water of hydration. Twenty Brillouin spectra collected along [110] and [001] at different relative humidities were fit to Eq. 9. Representative results of application of this model are shown in Fig. 8.
From Fig. 8, the hydration shell coupling is responsible for 29–85% of the observed acoustic attenuation, but no systematic differences in this coupling along the [110] and [001] directions is observed. The lifetime of the relaxation mode is 55 ± 5 ps, comparable to the value observed in Na-DNA and hyaluronic acids (Tao et al., 1988; Lee et al., 1993). The coupling effect increases with decreasing RH, with a maximum at 79% RH, and δ-ranges between 1.9 and 3.6 GHz. The coupling also slightly affects the apparent Brillouin peak position: the coupled frequency shifts are systematically 1% lower than the uncoupled shifts for both the [110] and [001] phonons at all relative humidities, which translates into a 2% stiffening of the retrieved elastic moduli. The coupling between acoustic phonons and water relaxation in tetragonal lysozyme is unaffected by the structural transition at 88% RH. This suggests that the structural transition is related to processes not involving the hydration shell, either within the protein framework and/or involving water outside the hydration shell.
X-ray diffraction data and our Brillouin data suggest a strong difference between the elastic behavior along [110] and [001] with decreasing dehydration. However, the effect of hydration water appears to be the same in the two directions. Estimates of the stress associated with dehydration from 98% to 70% RH (Morozov et al., 1988) are on the order of 0.04 GPa. Based on available constraints on the intrinsic compressibility of lysozyme in solution (0.1 GPa−1; Gavish et al., 1983; Paci and Marchi, 1996) this stress would correspond to an average 0.4% linear compression of the molecule, which is negligible compared with the observed decrease of unit cell parameters upon dehydration from 98% to 79% RH (Δa/a = 0.03, Δc/c = 0.11; Dobrianov et al., 2001). This suggests that the main effect of dehydration in tetragonal lysozyme is a change in protein packing density associated with loss of water and not with molecular compression. This process is anisotropic because of the relatively loose packing along [001] (e.g., Nadarajah and Pusey, 1996).
The observed longitudinal moduli of tetragonal lysozyme can be modeled as a weighted combination of three independent components: 1), an intramolecular component (the stiffness of the protein molecule itself, which we treat as constant for the entire RH range); 2), a component related to the intermolecular water, equal to the bulk modulus of water; and 3), a separation-dependent intermolecular interaction component that accounts for all the direct and water-mediated interactions (Coulombic, van der Waals, hydrophobic, and hydrogen bonds) between pairs of protein molecules in the crystal. This approach is a variation on that applied by Lee et al. (1987) to DNA films.
We assume that the elastic moduli can be expressed as
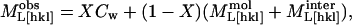 |
(11) |
where 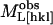 is the measured modulus along [hkl],
is the measured modulus along [hkl], 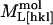 is the intrinsic modulus of the molecule, and
is the intrinsic modulus of the molecule, and 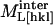 is the component arising from intermolecular interactions. Cw is the elastic modulus of water (2.1 GPa). X is a volumetric weighting factor for water and protein at any degree of hydration,
is the component arising from intermolecular interactions. Cw is the elastic modulus of water (2.1 GPa). X is a volumetric weighting factor for water and protein at any degree of hydration,
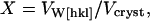 |
(12) |
where VW[hkl] is water's volume fraction along the examined crystallographic direction and Vcryst is the volume of the crystal. This weighting factor accounts for the denser packing of protein molecules in the basal plane compared with the c crystallographic direction. The weighting scheme in Eq. 11 corresponds to an iso-stress (Reuss) boundary condition between the components of the heterogeneous system.
In a preliminary test of this model we have assumed that intermolecular interactions are limited to a combination of repulsive Coulombic and short-range attractive van der Waals forces. Increasing hydration weakens 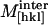 through volume expansion of the crystal. The interaction component of the longitudinal elastic modulus is assumed to have the form (Lee et al., 1987),
through volume expansion of the crystal. The interaction component of the longitudinal elastic modulus is assumed to have the form (Lee et al., 1987),
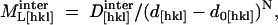 |
(13) |
where 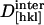 is a constant, d[hkl] is the intermolecular distance determined from crystallographic data, and d0[hkl] is an effective molecular size, fixed to have d[hkl] − d0[hkl] = 3.5 Å at 67% RH. The exponent N is subject to the constraint 3.9 ≤ N ≤ 4.1. Equation 13 is consistent with the form of empirical potentials for lysozyme in moderately dilute salt solutions (NaCl 200 mM; Tardieu et al., 1999). These show an approximately (d − d0)−2 dependence (where d0 in this case is the average molecular diameter) in the d − d0 = 3.5–7 Å range, implying that the corresponding force constant softens approximately as (d − d0)−4.
is a constant, d[hkl] is the intermolecular distance determined from crystallographic data, and d0[hkl] is an effective molecular size, fixed to have d[hkl] − d0[hkl] = 3.5 Å at 67% RH. The exponent N is subject to the constraint 3.9 ≤ N ≤ 4.1. Equation 13 is consistent with the form of empirical potentials for lysozyme in moderately dilute salt solutions (NaCl 200 mM; Tardieu et al., 1999). These show an approximately (d − d0)−2 dependence (where d0 in this case is the average molecular diameter) in the d − d0 = 3.5–7 Å range, implying that the corresponding force constant softens approximately as (d − d0)−4.
For our analysis, packing densities, intermolecular distances and their dependence on dehydration were determined from x-ray structural models (Sauter et al., 2001), from morphological and growth models (Nadarajah and Pusey, 1996), and from dehydration isotherms (Gevorkyan and Morozov, 1983). Values of d0[hkl], N, 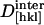 , and
, and 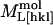 were obtained by requiring the model to agree with experimental data at 67% RH and by adjusting the parameters to obtain a good fit to the data at higher relative humidities (Fig. 5). The best fit parameters are reported in Table 2. Although the model is not unique, it provides a useful starting point for discussing the contribution of different structural components to the observed elasticity and elastic anisotropy. The best fit moduli of the molecule in the [110] and [001] directions are equal within uncertainties (
were obtained by requiring the model to agree with experimental data at 67% RH and by adjusting the parameters to obtain a good fit to the data at higher relative humidities (Fig. 5). The best fit parameters are reported in Table 2. Although the model is not unique, it provides a useful starting point for discussing the contribution of different structural components to the observed elasticity and elastic anisotropy. The best fit moduli of the molecule in the [110] and [001] directions are equal within uncertainties (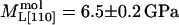 ,
, 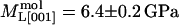 ). At 67% RH the “stiff framework” components of the moduli (
). At 67% RH the “stiff framework” components of the moduli (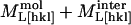 ) along [110] and [001] are 12.3 ± 0.6 and 11.9 ± 0.4 GPa, but at 98% RH they are equal to 7.9 ± 0.6 and 6.5 ± 0.4 GPa, the [110] value decreasing more strongly than the [001] value. By testing a wider range of models using a larger data set, we should be able to better constrain the relative contributions of the different components to the elastic properties of tetragonal lysozyme and other protein crystals.
) along [110] and [001] are 12.3 ± 0.6 and 11.9 ± 0.4 GPa, but at 98% RH they are equal to 7.9 ± 0.6 and 6.5 ± 0.4 GPa, the [110] value decreasing more strongly than the [001] value. By testing a wider range of models using a larger data set, we should be able to better constrain the relative contributions of the different components to the elastic properties of tetragonal lysozyme and other protein crystals.
TABLE 2.
Best fit parameters for the model (Eqs. 11–13) of contributions from molecular and intermolecular elasticity to the longitudinal elastic moduli of tetragonal lysozyme along the [110] and [001] directions
| Modulus (GPa) | [110] Direction | [001] Direction |
|---|---|---|
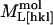 |
6.5 ± 0.2 | 6.4 ± 0.2 |
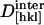 /(d[hkl] − d0[hkl])N /(d[hkl] − d0[hkl])N
|
5.8 ± 0.4* | 5.5 ± 0.2* |
| d0 (Å) | 23.05 ± 0.05 | 29.95 ± 0.05 |
| N | 4.0 | 4.0 |
Calculated at 67% RH.
ADDITIONAL CONSTRAINTS ON THE ELASTIC TENSOR OF LYSOZYME
Christoffel's equation (Eq. 2) can be factored for the (110) plane in the tetragonal system. The phonon velocity is (Fedorov, 1958; Winternheimer and McCurdy, 1978):
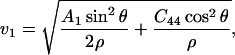 |
(14) |
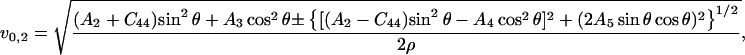 |
(15) |
where θ is the angular direction of the phonon wave vector with respect to the [001] direction, ρ is the crystal density, and
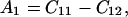 |
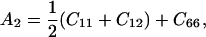 |
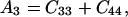 |
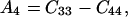 |
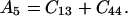 |
Eq. 14 gives velocities of the pure transverse acoustic mode, whereas Eq. 15 gives the velocities of the quasilongitudinal and the quasitransverse modes.
The longitudinal acoustic mode velocities measured along the (110) plane in crystals at 98%, 79%, and 67% RH were fitted to the Christoffel's equation to obtain a subset of the second-order elastic tensor. The absence of observed transverse acoustic phonon velocities restricts our ability to recover the complete elastic tensor (Castagnede et al., 1992), and allows us only to give constraints on the combination of C44 and C13 in addition to the combination C11 + C12 + 2C66 and C33. Additional constraints on the elastic constants derive from the strain energy stability requirement that the elastic tensor is positive definite (Born's criteria), which for a tetragonal crystal translates into (e.g., Fedorov, 1958):
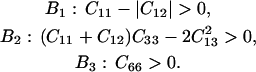 |
(16) |
The procedure used to obtain the elastic constants consisted of two steps: a preliminary parameter search in elastic constant space, and a final nonlinear least-square inversion of the Christoffel's equation performed using the results of the parameter search as a starting model. The inversion routine was based on the Levenberg-Marquardt algorithm.
The same two-stage procedure was also applied to invert the velocity data for the lysozyme crystals at 98%, 79%, and 67% relative humidity. The inversion of the longitudinal velocities allowed us to constrain the combination C44 + 1/2C13. The high linear correlation between these two constants is clearly visible in Fig. 9, which provides an illustration of the “goodness of fit” in the case of 98% RH for a wide range of C13 and C44 values when the other constants are fixed to the best model values. The best solutions are not distinguishable at the 70% confidence level at all the RH conditions. The best-fit constants for the examined degrees of dehydration are reported in Table 3. The calculated and observed sound velocities are compared in Fig. 7.
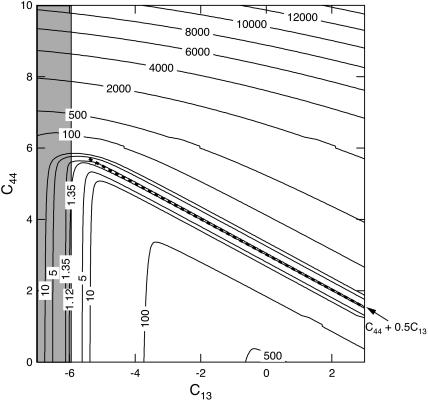
FIGURE 9.
Contour plots of the root mean square (RMS) difference, expressed in km/s, between calculated and observed velocities along directions in the [110] plane of a crystal of tetragonal lysozyme at equilibrium hydration conditions (98% RH). The RMS difference is plotted as a function of the two constants C13 and C44, whereas the values of C11 + C12 + 2C66 and C33 are fixed to their best model values of 12.78 and 5.57, respectively. The shaded area represents a region in the constant space where the stability constraint (C11 + C12) C33 > 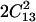 is violated.
is violated.
TABLE 3.
Best-fit elastic constants of tetragonal hen egg-white lysozyme crystals from measurements along the (110) plane
| Constant (GPa) | 98% Relative humidity | 79% Relative humidity | 67% Relative humidity |
|---|---|---|---|
| ρ (106g/m3)* | 1.21 | 1.25 | 1.27 |
| C11 + C12 + 2C66 | 12.81 ± 0.08 | 18.2 ± 0.2 | 22.2 ± 0.4 |
| C33 | 5.48 ± 0.05 | 9.57 ± 0.12 | 11.69 ± 0.08 |
| C44 + 0.5C13 | 2.99 ± 0.05 | 4.57 ± 0.05 | 5.95 ± 0.05 |
| C66 | <6.3† | <9.0† | <11.0† |
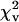 |
1.07–1.12 | 1.30–1.35 | 1.32–1.50 |
| RMS (km/s) | 0.012–0.013 | 0.012–0.014 | 0.016–0.018 |
| KS‡ | 0.12–5.44 | 0.10–9.1 | 0.10–11.0 |
Bounds to C66 are determined from mechanical stability constraints.
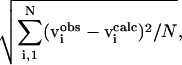
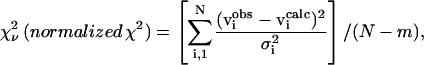 |
Density of tetragonal lysozyme at the appropriate RH.
Maximum value imposed by the mechanical stability requirements: (C11 + C12) C33 − 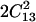 > 0 and C44 > 0.
> 0 and C44 > 0.
Bulk modulus of a polycrystalline aggregate calculated assuming stress continuity through grain boundaries (Reuss bound).
The fit results and the mechanical stability conditions allow us to determine bounds to the values of some elastic moduli (Table 3). The calculated adiabatic bulk modulus, KS = − (dP/d ln V)S, at 98% relative humidity, ranges between 0.12 and 5.44 GPa. Our result marginally overlaps the range of values of the bulk modulus of native proteins in solution and of lysozyme crystals (4–10 GPa; Kundrot and Richards, 1987; Katrusiak and Dauter, 1996; Kharakoz, 2000; Fourme et al., 2001).
In the case of 98% RH, the direct measurement of the longitudinal acoustic velocity along the [100] direction allows us to fix the value of C11 to 5.49 ± 0.01 GPa. The values of the axial compressibilities determined from high-pressure diffraction (Kundrot and Richards, 1987; Fourme et al., 2001) can be used to provide additional constraints on the elastic constants and bulk modulus, if we neglect the difference between the isothermal and isentropic moduli. The logarithmic ratio of the axial compressibilities along the c- and a-axes (Nye, 1985) is
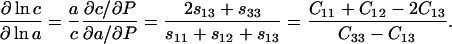 |
(17) |
Combining Brillouin scattering results, axial compressibilities from high-pressure x-ray diffraction by Fourme et al. (2001) (Eq. 17), and the constraints imposed by stability criteria (Eq. 16) we can constrain the value of all the constants for values of C44 between 0.35 and 1.45 GPa (limits fixed by the stability constraints). The range of allowed values of the individual constants and the stability criteria are shown in Fig. 10 a and in Table 4. The range of values of Young's modulus and of selected aggregate elastic moduli are shown in Fig. 10 b. The bulk modulus lies in the range between 5.25 and 2.71 GPa, slightly overlapping, but roughly a factor of 2 below the range obtained from static compression of tetragonal lysozyme (Kundrot and Richards, 1987; Fourme et al., 2001).
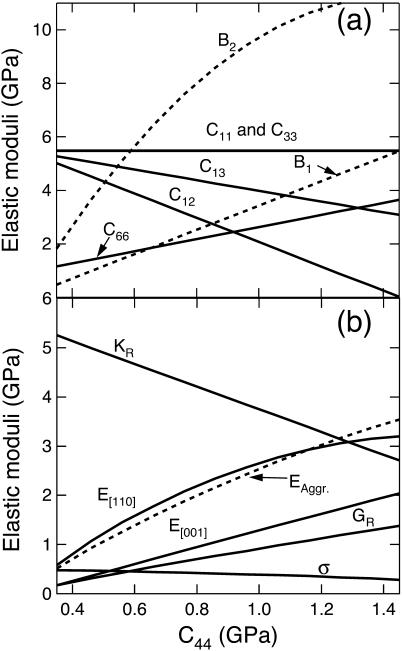
FIGURE 10.
Ranges of possible values of the elastic moduli of tetragonal lysozyme at 98% RH as a function of the value of the constant C44. (a) Elastic constants and mechanical stability criteria (B1, B2). (b) Aggregate of Young's modulus (EAggr.); aggregate of Poisson's ratio (σ); selected directional Young's moduli (E[110], E[001]); and the bulk (KR) and shear (GR) moduli for a polycrystalline aggregate calculated assuming stress continuity across grain boundaries (Reuss bound). B1 = C11 − |C12| and B2 = (C11 + C12) C33 − 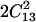 .
.
TABLE 4.
Dynamic elastic constants of tetragonal hen egg-white lysozyme refined using additional Brillouin measurements along the [100] direction and constraints from high-pressure x-ray diffraction
| Constant (GPa) | 98% Relative humidity |
|---|---|
| C11 | 5.49 ± 0.03 |
| C12 | 5.02–0.02 |
| C13 | 5.28–3.08 |
| C33 | 5.48 ± 0.05 |
| C44 | 0.35–1.45* |
| C66 | 1.15–3.65 |
| KS† | 5.25–2.71 |
| G† | 0.17–1.38 |
| E[110] | 0.58–3.20 |
| E[001] | 0.17–2.04 |
Fixed value.
Moduli of a polycrystalline aggregate calculated assuming stress continuity through grain boundaries (Reuss bound).
This discrepancy may in part be due to the difficulty of obtaining a reliable bulk modulus from volume-pressure data over a very limited range of compression. For instance, Fourme et al. (2001) used the ruby fluorescence pressure scale, which is primarily calibrated from measurements made at much higher pressures. While the precision of the ruby fluorescence measurements can be high, the accuracy of the pressure scale is not well-established (Dzwolak et al., 2002). A small absolute inaccuracy, negligible at high pressure, can have a dramatic effect in the comparatively low pressure regimes covered by high-pressure protein crystallography. In addition, systematic errors can result from other factors such as temperature variations (0.02 GPa/K) and internal stresses in ruby grains. The use of Eq. 17 does not require knowledge of the pressure, and thus is not subject to these limitations.
The combined constraints from Brillouin scattering and high-pressure x-ray diffraction measurements restrict the range of values of the shear modulus to 0.17–1.38 G GPa (Fig. 10 b). The “isotropic” Poisson's ratio is not well-constrained, and it can range between the value of 0.48 (for C44 = 0.35 GPa) and 0.28 when C44 = 1.45 GPa. This wide range corresponds to values going from those of rigid polymers to those of soft rubbers. A value similar to our upper bound (0.47) was obtained from ultrasonic measurements for crystals of ribonuclease-A and human hemoglobin (Edwards et al., 1990).
Upper and lower bounds to the Young's moduli along the [110] and [001] directions (see for instance, Nye, 1985, p. 145) are 0.58 and 0.17 GPa (lower bound) and 3.20 and 2.04 GPa (upper bound), respectively (Fig. 9 b, Table 4). The values of the two moduli are constrained to 2.9 ± 0.3 GPa and 1.6 ± 0.3 GPa, respectively, when C44 is >0.8 GPa. These higher bounds of the two moduli are comparable to the Young's moduli calculated assuming elastic isotropy and a Poisson's ratio of 0.33 (Table 1), and support the existence of a frequency dependence of the elastic moduli (Fig. 7). The average logarithmic frequency derivative, ∂E/∂ log ν, calculated by combining the results of this study with the range of the available data from different techniques (see Fig. 7), ranges between 0.2 and 0.4 GPa/decade over the range from 1 Hz to 109 Hz. These values are in good agreement with the available data for the frequency dependence of the bulk modulus in polymers (0.04–0.5 GPa/decade; Lagakos et al., 1986), and indicate that protein crystals exhibit a viscoelastic response.
CONCLUSIONS
Brillouin scattering of tetragonal lysozyme along directions in the (110) plane allowed the determination of the acoustic velocity, the velocity anisotropy, and their dependence on the degree of dehydration. The effect of dehydration is to increase the stiffness and to decrease the elastic anisotropy of tetragonal lysozyme. A velocity discontinuity and a change of the sign of the elastic anisotropy occur at RH in the range between 93% and 86%, consistent with x-ray diffraction measurements of structural changes reported by Dobrianov et al. (2001).
The linewidths of the Brillouin peaks were described using a mechanical model in which the phonon mode couples to a (single) relaxational mode of the hydration water. The relaxation time (55 ps) is similar to that found for DNA films. Another simple model illustrated how information about intermolecular and intramolecular contributions to protein crystal elasticity can be extracted from the humidity dependence of sound velocities. A preliminary test of this model suggests that the anisotropy of tetragonal lysozyme is controlled by crystal packing and not by intrinsic molecular anisotropy.
The dependence of velocity on scattering direction places constraints on the elastic tensor. The inverted elastic moduli provide a more detailed picture of lysozyme elasticity as a function of hydration than has been possible using other techniques.
Our results demonstrate that Brillouin spectroscopy is a powerful probe of elastic and structural properties of protein crystals. It is a nondestructive, noncontact technique, which can be applied to protein crystals of ordinary size. The direct determination of the elastic tensor, when combined with structural data from x-ray crystallography, will allow a more detailed analysis and understanding of protein structure and dynamics.
Acknowledgments
The authors thank R. O. Pohl for initially bringing Brillouin spectroscopy to the attention of R.E.T.
This work was supported by the National Aeronautics and Space Administration (NAG8-1357 and NAG8-1831); the National Science Foundation (EAR-9725395); and the David and Lucille Packard Foundation (to T.S.D.). The Cornell High-Energy Synchrotron Source is supported by the National Science Foundation (DMR 9713424).
References
- Auld, B. 1973. Acoustic Fields and Waves in Solids. Vol. 1. John Wiley and Sons, New York, London, Sidney, Toronto.
- Brillouin, L. 1922. Diffusion de la lumière et des rayons-x par un corps transparent homogène: influence de l'agitation termique. L. Ann. Physique. 17:88–122. [Google Scholar]
- Castagnede, B., A. G. Every, and W. Sachse. 1992. Numerical simulation of the instabilities associated to the recovery of elastic constants of anisotropic solids from quasi-longitudinal velocities alone. C.R. Acad Sci. Paris. 314. Serie. II:865–871. [Google Scholar]
- Caylor, C., S. Speziale, S. Kriminski, T. Duffy, C.-S. Zha, and R. E. Thorne. 2001. Measuring the elastic properties of protein crystals by Brillouin scattering. J. Crystal Growth. 232:498–501. [Google Scholar]
- Cervelle, B., F. Cesbron, and J. Berthou. 1974. Morphologie et propriétés optiques des cristaux de lysozyme de poule de type quadratique et orthorhombique. Acta Crystallogr. A30:645–648. [Google Scholar]
- Cummins, H. Z., and P. E. Schoen. 1972. Linear scattering from thermal fluctuations. In Laser Handbook. F. T. Arecchi, and E. O. Schultz-Dubois, editors. North-Holland, Amsterdam, The Netherlands. 1029–1076.
- Dobrianov, I., S. Kriminski, C. L. Caylor, S. G. Lemay, C. Kimmer, A. Kisselev, K. D. Finkelstein, and R. E. Thorne. 2001. Dynamic response of tetragonal lysozyme crystals to changes in relative humidity: implications for post-growth crystal treatments. Acta Crystallogr. D57:61–68. [DOI] [PubMed] [Google Scholar]
- Dzwolak, W., M. Kato, and Y. Taniguchi. 2002. Fourier transform infrared spectroscopy in high-pressure studies on proteins. Biochim. Biophys. Acta. 1595:131–144. [DOI] [PubMed] [Google Scholar]
- Edwards, C., S. B. Palmer, P. Emsley, J. R. Helliwell, D. Glover, G. W. Harris, and D. S. Moss. 1990. Thermal motion in proteins estimated using laser-generated ultrasound and Young's modulus measurements. Acta Crystallogr. A46:315–320. [Google Scholar]
- Fedorov, F. I. 1958. Theory of Elastic Waves in Crystals. Plenum Press, New York.
- Folland, R., D. A. Jakson, and S. Rajogopal. 1975. Measurement of the elastic constants in the hexagonal plastic crystal of norbornylene. In Light Scattering in Solids. M. Balkanski, R. C. C. Leite, and S. P. S. Porto, editors. John Wiley and Sons, New York, Sidney, Toronto. 694–701.
- Fourme, R., R. Kahn, M. Mezouar, E. Girard, C. Hoerentrup, T. Prangé, and I. Ascone. 2001. High-pressure protein crystallography (HPPX): instrumentation, methodology and results on lysozyme crystals. J. Synchro. Rad. 8:1149–1156. [DOI] [PubMed] [Google Scholar]
- Gavish, B., E. Gratton, and C. J. Hardy. 1983. Adiabatic compressibility of globular proteins. Proc. Natl. Acad. Sci. USA. 80:750–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gevorkyan, S. G., and V. N. Morozov. 1983. Dependence of the hydration isotherm of lysozyme on the packing of the molecules in the solid phase. Biophysics. 28:1002–1007. [Google Scholar]
- Gosline, J., M. Lillie, E. Carrington, P. Guerrette, C. Ortlepp, and K. Savage. 2002. Elastic proteins: biological roles and mechanical properties. Phil. Trans. R. Soc. Lond. B. 357:121–132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, Y. Y., and C. H. Wang. 1975. Brillouin, Rayleigh and depolarized scattering studies of polypropylene glycol. I. J. Chem. Phys. 62:120–126. [Google Scholar]
- Katrusiak, A., and Z. Dauter. 1996. Compressibility of lysozyme protein crystals by x-ray diffraction. Acta Crystallogr. D52:607–608. [DOI] [PubMed] [Google Scholar]
- Kharakov, D. 2000. Protein compressibility, dynamics, and pressure. Biophys. J. 79:511–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krüger, J. K., A. Marx, L. Peetz, R. Roberts, and H.-G. Unruh. 1986. Simultaneous determination of elastic and optical properties of polymers by high performance Brillouin spectroscopy using different scattering geometries. Coll. Polym. Sci. 264:403–414. [Google Scholar]
- Krüger, J. K. 1989. Brillouin spectroscopy and its application to polymers. In Optical Techniques to Characterize Polymer Systems, Studies in Polymer Science, Vol. 5. H. Bässler, editor. Elsevier Science. 429–534.
- Kundrot, C. E., and F. Richards. 1987. Crystal structure of hen egg-white lysozyme at a hydrostatic pressure of 1000 atmospheres. J. Mol. Biol. 193:157–170. [DOI] [PubMed] [Google Scholar]
- Lagakos, N., J. Jarzynski, J. H. Cole, and J. A. Bucaro. 1986. Immersion apparatus for ultrasonic measurements in polymers. J. Acoustic. Soc. Am. 56:1469–1477. [Google Scholar]
- Lee, S. A., S. M. Lindsay, J. W. Powell, T. Weidlich, N. J. Tao, G. D. Lewen, and A. Rupprecht. 1987. A Brillouin scattering study of the hydration of Li- and Na-DNA films. Biopolymers. 26:1637–1665. [DOI] [PubMed] [Google Scholar]
- Lee, S. A., M. R. Flowers, W. F. Oliver, A. Rupprecht, and S. M. Lindsay. 1993. Brillouin-scattering of hyaluronic acid: dynamic coupling with the water of hydration and phase transitions. Phys. Rev. E. 47:667–683. [DOI] [PubMed] [Google Scholar]
- Lindsay, S. M., M. W. Anderson, and J. R. Sandercock. 1981. Construction and alignment of a high performance multipass Vernier tandem Fabry-Perot interferometer. Rev. Sci. Instrum. 52:1478–1486. [Google Scholar]
- Morozov, V. N., and T. Y. Morozova. 1981. Viscoelastic properties of protein crystals: triclinic crystals of hen egg white lysozyme in different conditions. Biopolymers. 20:451–467. [DOI] [PubMed] [Google Scholar]
- Morozov, V. N., and T. Y. Morozova. 1986. Thermal motion of whole protein molecules in protein solids. J. Theor. Biol. 121:73–88. [DOI] [PubMed] [Google Scholar]
- Morozov, V. N., and T. Y. Morozova. 1993. Elasticity of globular proteins. The relation between mechanics, thermodynamics and mobility. J. Biomol. Struct. Dyn. 11:459–481. [DOI] [PubMed] [Google Scholar]
- Morozov, V. N., T. N. Morozova, G. S. Kachalova, and E. T. Myachin. 1988. Interpretation of water desorption isotherms of lysozyme. Int. J. Biol. Macromol. 10:329–336. [Google Scholar]
- Nadarajah, A., and M. L. Pusey. 1996. Growth mechanism and morphology of tetragonal lysozyme crystals. Acta Crystallogr. D52:983–996. [DOI] [PubMed] [Google Scholar]
- Nye, J. F. 1985. Physical Properties of Crystals. Clarendon Press, Oxford, UK.
- Paci, E., and M. Marchi. 1996. Intrinsic compressibility and volume compression in solvated proteins by molecular dynamics at high-pressure. Proc. Natl. Acad. Sci. USA. 93:11609–11614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockland, J. T. 1960. Saturated salt solutions for static control of relative humidity between 5°C and 40°C. Anal. Chem. 32:1375–1376. [Google Scholar]
- Salunke, D. M., B. Veerapandian, R. Kodandapani, and M. Vijayan. 1985. Water-mediated transformations in protein crystals. Acta Crystallogr. B41:431–436. [Google Scholar]
- Sarvazyan, A. P. 1991. Ultrasonic velocimetry of biological compounds. Annu. Rev. Biophys. Biophys. Chem. 20:321–342. [DOI] [PubMed] [Google Scholar]
- Sauter, C., F. Otalora, J.-A. Gaviria, O. Vidal, R. Giege, and J. M. Garcia-Ruiz. Structure of tetragonal hen-egg lysozyme at 0.94 Å from crystals grown by the counter-diffusion method. 2001. Acta Cryst. D57:1119–1126. [DOI] [PubMed] [Google Scholar]
- Tachibana, M., K. Kojima, R. Ikuyama, Y. Kobayashi, and M. Ataka. 2000. Sound velocity and dynamic elastic constants of lysozyme single crystals. Chem. Phys. Lett. 332:259–264. [Google Scholar]
- Tachibana, M., K. Kojima, R. Ikuyama, Y. Kobayashi, and M. Ataka. 2002. Erratum: Sound velocity and dynamic elastic constants of lysozyme single crystals. Chem. Phys. Lett. 354:360. [Google Scholar]
- Tao, N. J., S. M. Lindsay, and A. Rupprecht. 1988. Dynamic coupling between DNA and its primary hydration shell studied by Brillouin scattering. Biopolymers. 27:1655–1671. [DOI] [PubMed] [Google Scholar]
- Tardieu, A., A. Le Verge, M. Malfois, F. Bonnete, S. Finet, M. Ries-Kautt, and L. Belloni. 1999. Proteins in solution: from x-ray scattering intensities to interaction potentials. J. Crystal Growth. 196:193–203. [Google Scholar]
- Tominaga, Y., M. Shida, K. Kubota, H. Urabe, Y. Nishimura, and M. Tsuboi. 1985. Coupled dynamics between DNA double helix and hydrated water by low frequency Raman spectroscopy. J. Chem. Phys. 83:5972–5975. [Google Scholar]
- Urabe, H., Y. Sugawara, M. Ataka, and A. Rupprecht. 1998. Low-frequency Raman spectra of lysozyme crystals and oriented DNA films: dynamics of crystal water. Biophys. J. 74:1533–1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan, J. M., and J. T. Randall. 1980. Brillouin scattering, density and elastic properties of the lens and cornea of the eye. Nature. 284:489–491. [DOI] [PubMed] [Google Scholar]
- Winternheimer, C. G., and A. K. McCurdy. 1978. Phonon focusing and phonon conduction in orthorhombic and tetragonal crystals in the boundary-scattering regime. Phys. Rev. B. 18:6576–6605. [Google Scholar]
- Zha, C.-S., T. S. Duffy, H.-K. Mao, and R. J. Hemley. 1993. Elasticity of hydrogen to 24 GPa from single-crystal Brillouin scattering and synchrotron x-ray diffraction. Phys. Rev. B. 48:9246–9255. [DOI] [PubMed] [Google Scholar]