Abstract
Reduced lattice models of proteins and Monte Carlo dynamics were used to simulate the initial stages of the unfolding of several proteins of various structural types, and the results were compared to experiment. The models semiquantitatively reproduce the approximate order of events of unfolding as well as subtle mutation effects and effects resulting from differences in sequences of similar folds. The short-time mobility of particular residues, observed in simulations, correlates with the crystallographic temperature factor. The main factor controlling unfolding is the native state topology, with sequence playing a less important role. The correlation with various experiments, especially for sequence-specific effects, strongly suggests that properly designed reduced models of proteins can be used for qualitative studies (or prediction) of protein unfolding pathways.
INTRODUCTION
It is believed that during the reversible denaturation of globular proteins the unfolding pathway is, to a large extent, similar to the folding pathway, with a reversed order of events (Creighton, 1990). This notion of pathway reversibility has motivated numerous computational studies of protein unfolding. Protein folding (or unfolding) is a relatively slow process—taking from milliseconds to minutes—depending on the protein type and its molecular mass (Creighton, 1990). Detailed equilibrium molecular dynamics simulations (especially with the explicit treatment of the solvent molecules) of the entire unfolding process are, therefore, not practical (Shea and Brooks III, 2000). Frequently, to overcome this problem, molecular or Brownian dynamics simulations are performed at a very high temperature. It is unclear whether under such conditions the observed mechanism of denaturation is similar to that which takes place at temperatures close to the folding transition temperature.
In this work, we describe a new application of a reduced lattice protein model and Monte Carlo dynamics to equilibrium unfolding simulations. Such models enable a significant reduction of the number of degrees of freedom explicitly treated (Ding et al., 2002; Guo et al., 2002; Irback et al., 2000; Klimov and Thirumalai, 2000; Liwo et al., 2001; Takada et al., 1999). With the solvent as an effective medium, and the time step of the Monte Carlo dynamics being orders-of-magnitude larger than that in molecular or Brownian dynamics simulations, the entire folding/unfolding process could be simulated. However, the cost of having the possibility to simulate such long molecular processes is significant. The reduced models employ knowledge-based potentials, and it is not a trivial task to design a force field that mimics, in a semiquantitative fashion, the real physical interactions within the protein systems. Moreover, application of Monte Carlo dynamics assumes that the very fast relaxation processes can be ignored as they “average out” on longer timescales.
The side-chain-only (SICHO) reduced lattice model of proteins (Kolinski and Skolnick, 1998) employed in this work was previously employed in various studies of protein folding dynamics and thermodynamics (Ilkowski et al., 2000; Kolinski et al., 1999) and was also used as a tool for protein structure prediction (Kihara et al., 2001; Kolinski et al., 2001, 2000; Skolnick et al., 2000). In the latter case, the force field of the model is usually supplemented with predicted tertiary restraints derived from threading. In the present study, we employ only statistical potentials, which are the same for all protein sequences studied here. Additionally (as in previous applications of the SICHO model), secondary structure predicted via the PHD method (Rost and Sander, 1994) was used, providing a bias for some interactions. This is the only place where the evolutionary information enters into the force field in this particular application.
PROTEIN MODEL AND SIMULATION METHOD
The model assumes a single explicit interaction center per residue (SICHO) that corresponds to the center of gravity of the side chain and the corresponding Cα atom. Thus, the interaction center of a glycine residue is located on the Cα, for alanine; it is at the center of Cα-Cβ bond, for valine; it is at the Cβ, and so forth. The bond length connecting consecutive interaction centers is variable and mimics the distribution of distances found in real proteins. The interaction centers are restricted to the vertices of an underlying simple cubic lattice with a lattice spacing equal to 1.45 Å. Given the positions of three consecutive interaction centers, the approximate (off-lattice) position of the Cα of the central amino acid can be easily obtained. The Cα position serves as a reference point for directional interactions that simulate the effect of the main chain hydrogen bonds in proteins.
The force field of the model consists of several types of terms, listed below:
Generic. Independent of sequence, short-range interactions that simulate proteinlike chain stiffness via a bias toward conformations characteristic of either helical or expanded β-type geometry.
Sequence-dependent. Short-range statistical potentials encoding conformational preferences of five residue fragments. Predicted secondary structure imposes a weak bias toward more regular secondary structure geometry for predicted helices or sheets.
Hydrogen-bond model. A model of hydrogen bonds in the form of a directional Cα-Cα potential that mimics the geometrical properties of the main chain hydrogen bonds. The hydrogen bond network is cooperative and moderated by the predicted secondary structure. Hydrogen bonds cannot occur between two amino acids that have helical and β-sheet assignments or two helical residues that are far apart along the sequence.
Pairwise contact interactions of the side chains. These are orientation-dependent, reflecting the tendency toward specific packing arrangements of various side groups in globular proteins.
Burial potentials. These regularize the packing environment propensities and solvent exposure for various amino acids.
The details of the implementation of the force field can be found in our recent publications (Ilkowski et al., 2000; Kihara et al., 2001; Kolinski et al., 2001, 2000; Kolinski and Skolnick, 1998; Skolnick et al., 2000), and the numerical data for the potentials can be extracted from our home page (http://biocomp.chem.uw.edu.pl).
The model of dynamics is based on a random series of small, local conformational transitions, with three types of micro modifications employed. The first is a kink-type of random replacement of a single side-chain unit (with a corresponding change of orientation of the two connecting virtual chain bonds). The portions of the model chain on both sides of the modified fragment (on one side for the chain end fragments) remain fixed. Three-bond and four-bond moves are defined in a similar manner. The random selections of the local micro modifications are biased in a way that ensures frequent jumps over high barriers of conformational energy related to the short-range interactions. The model time unit corresponds to N-2 attempts to perform two bond moves (where N is the chain length), N-3 attempts to perform three bond moves and N-4 attempts to perform four-bond moves. The sequence of moves and their location in the chain are random. Thereby, the simulation algorithm numerically solves a complex stochastic equation of motion.
Simulations were performed using a standard asymmetric Metropolis scheme (Metropolis et al., 1953) for the dynamics of protein-like polymers (Ilkowski et al., 2000; Kolinski and Skolnick, 1996) at a constant temperature. Unfolding experiments started from a lattice representation of the native structure. Several long isothermal runs were executed at various temperatures near the folding transition temperature. In addition to the simulations employing the above-outlined force field of the SICHO model, we performed a parallel set of simulations with the statistical side-chain potential replaced by the Go-type potential (Go et al., 1980). In the model introduced by Go, a constant attractive potential is applied to those pairs of residues in contact in the native structure; other pair interactions are ignored. The native contacts are extracted from analysis of the appropriate PDB files (Bernstein et al., 1977), with a distance cutoff of 4.5 Å between any pair of two atoms of the side chains being in contact. The value of the Go contact potential was set to −0.4 kBT, close to the “average” value of the pairwise amino-acid specific potential, and the temperature of simulations was assumed to be the same as for the complete statistical force field simulations (see below). The purpose of this exercise was to determine the main factor responsible for the observed unfolding mechanism—differences in the side-chain interactions or the overall topology of the native fold (simulations with a Go-type of potential).
RESULTS AND DISCUSSION
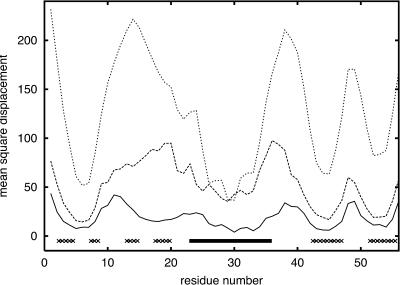
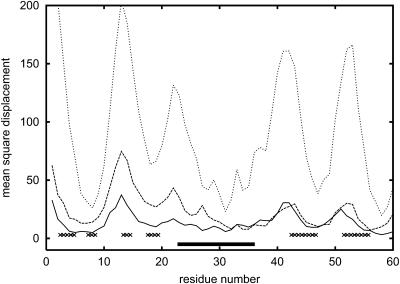
We studied four proteins, the unfolding mechanisms of which were intensively studied experimentally and which represent various secondary structural classes (see Table 1 for details). These are apomyoglobin; leghemoglobin; plastocyanin; and the B-domain of proteins G and L. To measure the mobility of particular segments of the protein, the autocorrelation function (the time-averaged mean-square displacement) is calculated as a function of time lapsed and the position in the sequence,
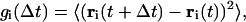 |
(1) |
where ri(t) are Cartesian coordinates of the ith side chain, and 〈 〉 denotes averaging over (long) trajectory.
TABLE 1.
Proteins studied in this work
| Name | Length | PDB code | Type | Resolution (in Å) |
|---|---|---|---|---|
| Apomyoglobin | 153 | 1bvc | α | 1.5 (x-ray) |
| Leghemoglobin | 143 | 1bin | α | 2.2 (x-ray) |
| Plastocyanin | 99 | 2pcy | β | 2.0 (x-ray) |
| Protein G (B1) | 56 | 2gb1 | α/β | 1.2 (NMR) |
| Protein L | 62 | 2ptl | α/β | 1.4 (NMR) |
Performing isothermal simulations at various temperatures near the unfolding temperature, we analyzed mobility of particular residues and structure fragments (as sheets and helices). At low temperatures, we only measure fluctuations around the native state. Under such conditions, the model system is self-bound, and the magnitude of the fluctuations converges rapidly, well within the simulation time. Thus, the measurements at low temperatures (slightly below the estimated unfolding temperature) represent equilibrium fluctuations of the (model) native state, and could be qualitatively compared with the crystallographic temperature factor. In other words, the autocorrelation function gi(Δt) rapidly reaches a plateau, different for all residues, and does not depend on the specific value of Δt, provided it is above a certain critical value (corresponding to the relaxation time of the self-bounded model structure). At higher temperatures, particular elements of protein secondary structure begin to unwrap, and the order of secondary structure disintegration defines an approximate unfolding pathway. At the unfolding temperature and at higher temperatures near the unfolding temperature, the model systems eventually unfold completely. Thus, the simulations are controlled by the average displacement of the chain units, that was kept in the range of the 5–15 Å, and the mobility profiles displayed in this work were obtained by averaging five independent unfolding trajectories. In these cases, the autocorrelation function measures the system dynamics during the fold unwrapping and the value of Δt in the Eq. 1 corresponds to a time which is a fraction of the longest relaxation time of the model chain, and its value is controlled by the superimposed displacement limits. The results of the Monte Carlo simulations could be compared (in a semiquantitative fashion) with known experimental findings.
Plastocyanin
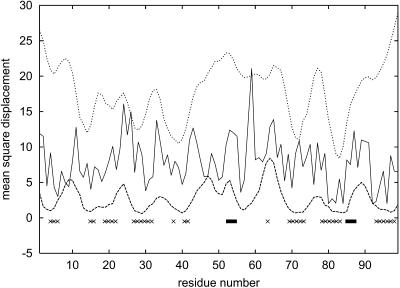
Plastocyanin is a relatively small globular protein containing 99 amino acids. Its secondary structure consists of two four-member β-sheets, arranged in the Greek-key-type topology (Branden and Tooze, 1991), with reversed two-terminal strands. The β-turns and longer loops connecting the extended strands in plastocyanin's three-dimensional structure are very mobile (Dyson et al., 1992). This mobility is critical for its folding mechanism. As demonstrated in Fig. 1, the results of our simulations at low temperatures, near the folding temperature, show that the mobility of particular residues correlates with the crystallographic temperature factor (Blundell and Johnson, 1976). This is true for simulations with the statistical pair potential as well as with the Go potential employed instead of the original pairwise interactions. It is important to note that the Go potential does not correlate well with the statistical potential. The correlations are very similar for various proteins of comparable size and provide an interesting insight into the nature of long-range interactions in proteins. The average value of the side-chain-to-side-chain potentials (for all groups, not necessarily interacting) equals −0.25. For contacting residues, it decreases to −0.66. The correlation coefficient between the N × N (where N is the chain length), statistical potential for this protein and the Go potential is very small and equals 0.10. The N × N matrix was generated by inserting the appropriate (according to the sequence) values of the statistical potential from the 20 × 20 statistical potential tables. For native contacts, a proper orientation of the side chains—which dictates from which of three 20 × 20 tables a specific value has to be extracted—was taken into account in the selection of the pairwise interaction parameters. The correlation coefficient between the Go potential and the statistical potential for interacting residues is much higher and equals 0.75. This leads to an important observation; namely that in the close vicinity of the native state, both potentials should have a similar effect on the local chain mobility; however, after disintegration of a substantial fraction of native contacts, the two potentials become uncorrelated, and their effect on unfolding should be significantly different. Indeed, whereas short-time fluctuations are highly correlated for both potentials, the results of longer time simulations—when real unfolding begins—exhibit much weaker correlations (as shown in Table 2). Correlations of mobility between the results of the simulations with the two types of potential are much higher than the correlation with the crystallographic temperature B-factor curves. Clearly, the B-factor profiles exhibit much more fluctuation, probably reflecting changes in local packing density. On the other hand, the mobility profiles (with both potentials) indicate varying stability of the larger fragments of the structure. At all temperatures studied, the β-turns located between residues 42 and 45 and between residues 65 and 68 dissolve first and the large fragment between residues 42 and 68 becomes the most mobile region of the entire protein, except for the very end fragments of the chain. The somewhat excessive mobility of the chain ends seems to be a common problem of all long-time simulations using reduced models. Most of the residues from the mobile regions are exposed to the solvent and have a smaller-than-average number of side-chain contacts. Also, being rather irregular, they have a small number of main chain hydrogen bonds. Additionally, the secondary propensities for these regions are weak. Thus, it is not surprising that these fragments unfold rapidly. From experimental studies it is known that these β-turns may play an important role in the early stages of protein folding and that their mobility (Dyson et al., 1992) is essential for folding initiation. Mobility of these regions can also play a role in fixing the final secondary structure of the protein. Despite a short helix, located between residues 52 and 55, the relatively long, mostly coil-type region containing this rigid element of secondary structure exhibits high mobility. This fragment of the chain closes an edge of a β-sheet and is most likely one of the first to unfold. These results for plastocyanin show that protein coil regions are very important for the folding/unfolding mechanism and for stability of the entire protein. Even partial unfolding of β-sheets causes a very rapid unfolding of the loop and turn fragments. This is consistent with the picture emerging from nuclear magnetic resonance (NMR) studies of plastocyanin fragments (Dyson et al., 1992); the loop regions are stabilized by the regular fragments of the structure.
FIGURE 1.
Mobility profiles for plastocyanin (2pcy). The upper curve illustrates the results of Monte Carlo simulations near the unfolding temperature (T = 1.4). The lowest curve corresponds to equivalent simulations with Go potential (at the same temperature). Profile of the crystallographic temperature factor (middle solid line) is given for comparison. All data are in Å2. Locations of helices (▪) and β-strands (xxxxx) are marked.
TABLE 2.
Correlation coefficients for the plastocyanin mobility profiles (SICHO and Go potentials) and B-factor profile displayed in Fig. 1
| B-factor | SICHO | Go | |
|---|---|---|---|
| B-factor | 1 | 0.24 | 0.25 |
| SICHO | 0.24 | 1 | 0.44 |
| Go | 0.25 | 0.44 | 1 |
Apomyoglobin
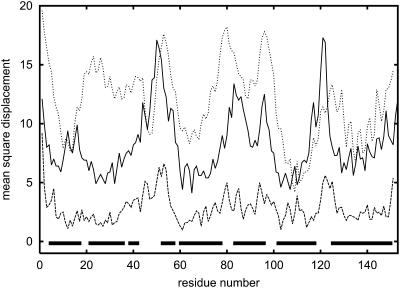
Apomyoglobin is a protein consisting of 153 amino acids that contains eight helices: A, B, C, D, E, F, G, and H. Helices C and D are relatively short; C contains six amino acids and D contains six amino acids (Branden and Tooze, 1991; Wagner et al., 1995). The remaining helices are significantly longer. We compared results obtained from calculations based on SICHO and Go potentials with the crystallographic temperature factor (Blundell and Johnson, 1976). The patterns shown on the graph are very similar for both cases; one exception is for helix B in the SICHO model (Fig. 2). Indeed, the fragment containing helix B in the SICHO model with statistical potential appears significantly less stable than it is suggested by simulations with Go potential or from analysis of the B-factor profiles. Nevertheless, the highest peaks of the mobility along the entire sequence (Fig. 2) coincide nicely for all profiles. In general, the observed mobility of helical proteins (or helical fragments) correlates much better with the crystallographic temperature factor profiles than for other types of protein structure. A similar pattern has been observed by Haliloglu and Bahar (1998) for a much simpler model, where all residues were treated as a single point connected by harmonic springs with neighboring residues. Interestingly, our simulations with the Go potential are also consistent with the crystallographic temperature factor profile of the apomyoglobin structure (see Table 3). This strongly suggests that the topology of the fold is the major factor responsible for mobility of various residues. Experimental data show that only part of B-helix is stable (Reymond et al., 1997)—this is the second part of this helix (staring from residue 29). Very clearly, we can see that helices A, G, and H are the most stable in the entire protein. They are closely packed and have large numbers of interhelical hydrophobic contacts. Also, the helical propensities of the corresponding fragments of polypeptide chains are stronger than average. This is also consistent with experimental results (Eliezer and Wright, 1996; Gilmanshin et al., 1997; Jennings and Wright, 1993; Nishimura et al., 2000; Reymond et al., 1997; Tcherkasskaya and Uversky, 2001; Wright et al., 1988). Thus, it can be concluded that the stability of helices A, G, and H is critical for the folding mechanism for the entire protein. They unfold last during the unfolding process; and they fold first, initiating the entire folding process (Reymond et al., 1997). The critical role of helix H for fold stability has been confirmed by mutation studies (Cavagnero et al., 1999). As shown in Fig. 3, where the mobility of wild-type apomyoglobin is compared with the mobility of the mutant, the effect of mutations (substitution of D132 and E136 by Gly residues) could be reproduced in the simulations. Whereas there are evident differences, the overall correlation coefficient between the two profiles is relatively large and equal to 0.63. Clearly, the mutations increase the mobility of the H-helix due to substitution of helix-forming residues by very flexible Gly residues. Increasing the mobility of helix H simultaneously increases the mobility of helix G. These two helices are parallel to each other and strongly interact in the folded structure. Destabilization of the H-helix causes subsequent destabilization of the G-helix. A similar explanation seems plausible for increased mobility of the portions of the B- and C-helices that are stabilized by the G-helix.
FIGURE 2.
Mobility profiles for apomyoglobin (1bvc). The upper curve illustrates the results of Monte Carlo simulations near the unfolding temperature (T = 1.1). The lowest curve corresponds to equivalent simulations with Go potential (at the same temperature). Profile of crystallographic temperature factor (middle solid line) is given for comparison. All data are in Å2. Locations of helices (▪) are marked.
TABLE 3.
Correlation coefficients for the apomyoglobin mobility profiles (SICHO and Go potentials) and B-factor profile displayed in Fig. 2
| B-factor | SICHO | Go | |
|---|---|---|---|
| B-factor | 1 | 0.52 | 0.52 |
| SICHO | 0.52 | 1 | 0.45 |
| Go | 0.52 | 0.45 | 1 |
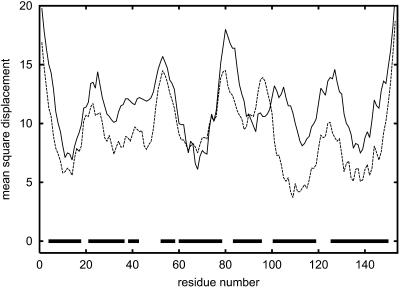
FIGURE 3.
Comparison of mobility profiles for wild-type apomyoglobin (dashed line) and the mutant (solid line). See text for details.
Almost perfect agreement of the short-time mobility patterns seen by Haliloglu and Bahar (1998) with our simulations (especially with the Go potential) strongly suggests that various specific interactions in proteins are not crucial for the mobility of the structure near the native state. Note that Haliloglu and Bahar's model is extremely simplified and based on a three-dimensional harmonic net approximation of protein. Our model, having a relatively accurate approximation of hydrogen bonds, local stiffness of the polypeptide chain, and approximation of the burial (or hydrophobic) interactions, leads to qualitatively similar results. The different average amplitudes of motions should be ascribed to different temperature conditions of the simulations. Thus, the fold topology is the major factor of the local mobility near the native state. Since the later unfolding events follow a similar pattern and agree qualitatively with experimental data, it is safe to say that the fold topology is also a main factor responsible for the unfolding/folding pathway of apomyoglobin. Nevertheless, as shown by comparison of the mutant and the wild-type proteins, sequence details also play an important role. The possibility of studying the sequence effects goes beyond the applicability of a very simple model such as that of Haliloglu and Bahar.
Apomyoglobin versus leghemoglobin
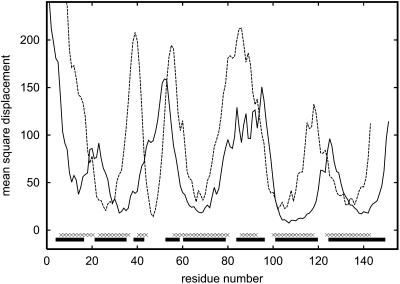
These two proteins are interesting as an example. They belong to the same globin family and have similar tertiary structures (the root-mean-square deviation from native after the best structural superposition is equal to 4.16 Å) despite completely different sequences. Thus, we can check the hypothesis that these two distant evolutionary proteins should have almost the same folding pathways (Nishimura et al., 2000).
If proteins have similar folding pathways, they should also have similar unfolding pathways. Monte Carlo simulations confirm this hypothesis. As shown in Fig. 4, the mobility of the corresponding secondary structure fragments for both proteins is qualitatively similar. The correlation coefficient for the corresponding parts of the two profiles is equal to 0.57. There are, of course, some quantitative differences. Shifts of mobility reflect differences in the location of particular helices along the sequences. Nevertheless, qualitative similarity of unfolding pathways is evident. This means that the folding pathway for these two distant evolutionary proteins is, to a large extent, conserved. Interestingly, Eliezer and Wright (1996) found that the fragments of apomyoglobin—namely, the EF-loop, the F-helix, the FG-loop, and the beginning of the G-helix—exhibit large structural fluctuations at the transition state between the native and unfolded states. This is consistent with our results. We found that the amplitudes of fluctuations of the F-helix and the beginning of the G-helix dramatically increase as the temperature of the system increases from T = 0.9–1.1. A similar effect is observed for B- and D-helices. These helices have a smaller-than-average number of long-range contacts and their secondary structure propensities are lower. From the point of view of the stability of the secondary structure, we found that the most stable fragments of the apomyoglobin are the G-helix (except its beginning) and the H-helix. These fragments exhibit very low fluctuations even at relatively high temperatures. The stability of those helices during the unfolding process suggests that in the reverse phenomenon (folding), these fragments form the first elements of the final fold.
FIGURE 4.
Comparison of mobility profiles for apomyoglobin and leghemoglobin (dashed line) at a temperature slightly higher (T = 1.2) than the unfolding temperature (T = 1.1).
B1-domain of protein G and protein L
The B1 domain of streptococcal protein G is a small, very regular α/β structure consisting of 56 amino acids. The structure (Gronenborn et al., 1991) contains a single helix on top of an antiparallel, four-stranded β-sheet. The folding pathway of this protein was extensively studied experimentally (Blanco et al., 1994; Frank et al., 1995; Gronenborn et al., 1991; Kuszewski et al., 1994; McCallister et al., 2000) and theoretically (Blanco and Serrano, 1995; Ilkowski et al., 2000; Karanicolas and Brooks III, 2002; Munoz et al., 1997; Sheinerman and Brooks III, 1998) via various computer simulation methods. Fig. 5 shows the results of unfolding experiments by the method used in this work. It is clear that the most stable element of the structure is the central helix. This is consistent with experimental findings. The N-terminal β-hairpin is significantly less stable than the C-terminal hairpin and unfolds first. As temperature increases, the second strand (on the edge of the β-sheet) completely dissolves, whereas the C-terminal β-hairpin remains intact. This is the most pronounced in the intermediate temperature curve (but also displays at other close temperatures), where the C-terminal β-strands move very little, although the second N-terminal strand (the edge strand in the protein G fold) is already completely dissolved and detached from the rest of the β-sheet. At the same time, all loop regions and the ends of regular secondary structure elements move a few Ångstroms from the native structure. The mobility of the critical N-terminal strands is of the same magnitude as the mobility of the most flexible loop region. This is also consistent with experimental NMR data (Frank et al., 1995). There are very similar folds that exhibit an opposite behavior (protein L domain) for which the N-terminal part is more stable (Karanicolas and Brooks III, 2002; Wikstrom et al., 1993). The corresponding simulation data for protein L are plotted in Fig. 6. In this case, the N- and C-terminal fragments of the sheet exhibit a similar overall mobility. The experiments and the recent simulations by Clementi et al. (2003) (using the all-atom model with the Go-type potential) show that in protein L the C-terminal hairpin dissolves first. Comparison of our simulations for protein G and protein L show a significant increase of relative stability of N-terminus in protein L; however, the results for protein L are inconclusive with regard to which strands dissolve first. Clementi's simulations strongly suggest that the factors responsible for breaking of symmetry in these proteins are the details of packing of large hydrophobic side chains in the native structures. Our model lacks these details, and this could be a reason why the agreement with experiment is only partial (with a proper prediction for protein G and a more-or-less correct direction of the change of protein L unfolding pattern). Thus, our simulations indicate that the simplified model accounts for simple topological effects (namely, the general similarity of the mobility profiles of the two proteins, with correlation coefficient equal to 0.60 at the lowest temperature displayed) on the unfolding/folding process, and partially for more subtle differences in stability resulting from the sequence of amino acids. The results of simulations with Go potentials are essentially the same with much higher correlation coefficients. Similarity of the results for knowledge-based potential and Go-type potentials of these two proteins suggests that the differences in local interactions (secondary structure propensities) can easily change the details of the unfolding pathways. Indeed, in protein G, the C-terminal hairpin has stronger β-type propensity, whereas for protein L the N-terminal hairpin is better defined with respect to the secondary propensities. The strength of tertiary interactions in these two proteins are of very similar magnitude for C- and N-terminal hairpins, respectively, but subtle details might be missed in the reduced model. Thus the differences in secondary propensities appear to be the main factors responsible for the observed differences in simulations of the unfolding pathways. Nevertheless, a smaller difference of the unfolding profiles of these two proteins with Go potential (higher correlation coefficient) also indicates some (although difficult to quantify) dependency on the tertiary interactions. Consequently, the predictive value of the proposed method goes beyond that for highly simplified models of protein dynamics.
FIGURE 5.
Mobility profiles for protein G at three temperatures T = 0.8, 0.9, and 1.2 (from bottom to top), where T = 1.2 is the estimated unfolding temperature.
FIGURE 6.
Mobility profiles for protein L at T = 0.8, 0.9, and 1.2 (from bottom to top), where T = 1.2 is the estimated unfolding temperature.
CONCLUSIONS
In this work we employed a simplified lattice model and a model of Monte Carlo dynamics to study dynamic behavior of globular proteins near the native state and the mechanisms of protein unfolding. The main conclusions of this work can be formulated as follows:
The model describes the dynamics of the native state and the folding pathways of globular proteins. First, the observed mobility of the reduced models of the native structure qualitatively mimics the very local (short-time) dynamics of the folded proteins, as assessed by the values of the crystallographic temperature factor. More importantly, the order of dissolution of secondary structure elements, at temperatures near the unfolding temperature and slightly higher than the folding temperature, reproduces many of the qualitative features of the unfolding pathways deduced from the experiment (with the salient exception of protein L, where the details are inconclusive). For longer times, the correlation with the crystallographic temperature factor profiles decays.
The earlier and present studies strongly suggest that the main factors controlling mobility of the folded state are the local packing density and overall topology of the native state. To some extent, these factors also dictate very early stages of the unfolding pathways. The later events are more complex and, especially for β-type proteins, do not correlate well with the crystallographic estimation of local mobility. For instance, the different stabilities of the N- and C-terminal fragments of the B1 domain of protein G (and protein L) detected in simulations indicate that the details of molecular interactions may affect the folding pathway. Also, comparison of the unfolding of apomyoglobin and its mutant shows that even small changes of interaction patterns due to two-point mutations leads to a qualitative change of the unfolding pattern. Thus the proposed model, at least on a qualitative level, accounts properly for the sequence effects.
Assuming that the successive events of a folding pathway follow, to some extent, the reverse order of the unfolding events, the proposed methodology may be a very useful tool for qualitative studies of entire folding pathways of large proteins and macromolecular assemblies. Since a technology exists (see the homepage for NIH Research Resource for Multiscale Modeling Tools in Structural Biology, at http://mmtsb.scripps.edu) for bootstrapping the coarse-grained dynamics of the proposed reduced model with the detailed molecular dynamic study of essential short-time events along the folding pathways, the proposed method should also be applicable in more detailed computational studies of long-time dynamics of biomolecular systems. Thus, the present approach goes far beyond simple analytical models such as those developed by Haliloglu and Bahar (1998), enabling study of entire unfolding/folding pathways. Qualitative agreement of the short-time results (where the equilibrium fluctuations of the lattice models of the native state slightly below the estimated unfolding temperature were measured) with the rigorously tractable simple analytical models also suggests that the Monte Carlo dynamics and entire sampling of the lattice model scheme mimics qualitative features of the continuous dynamics of proteins.
Acknowledgments
This research was supported, in part, by National Institutes of Health grant RR1255.
References
- Bernstein, F. C., T. F. Koetzle, G. J. B. Williams, E. F. Meyer, Jr., M. D. Brice, J. R. Rodgers, O. Kennard, T. Simanouchi, and M. Tasumi. 1977. The protein data bank: a computer-based archival file for macromolecular structures. J. Mol. Biol. 112:535–542. [DOI] [PubMed] [Google Scholar]
- Blanco, F., G. Rivas, and L. Serrano. 1994. A short linear peptide that folds into a native stable β-hairpin in aqueous solution. Struct. Biol. 1:584–590. [DOI] [PubMed] [Google Scholar]
- Blanco, J. F., and L. Serrano. 1995. Folding of protein G B1 domain studied by the conformational characterization of fragments comprising its secondary structure elements. Eur. J. Biochem. 230:634–649. [DOI] [PubMed] [Google Scholar]
- Blundell, T. L., and L. N. Johnson. 1976. Protein Crystallography. Academic Press, London, UK.
- Branden, C., and J. Tooze. 1991. Introduction to Protein Structure. Garland Publishing, New York and London.
- Cavagnero, S., H. J. Dyson, and P. E. Wright. 1999. Effect of H-helix destabilizing mutations on the kinetic and equilibrium folding of apomyoglobin. J. Mol. Biol. 285:269–282. [DOI] [PubMed] [Google Scholar]
- Clementi, C., A. Garcia, and J. N. Onuchic. 2003. Interplay among tertiary contacts, secondary structure formation and side-chain packing in the protein folding mechanism: an all-atom representation study. J. Mol. Biol. 326:933–954. [DOI] [PubMed] [Google Scholar]
- Creighton, T. E. 1990. Protein folding. Biochem. J. 270:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding, F., N. V. Dokholyan, S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2002. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 83:3525–3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyson, H. J., J. R. Sayre, H.-C. Shin, G. S. Merutka, R. A. Lerner, and P. E. Wright. 1992. Conformational studies of complete proteins as a series of fragments using proton nuclear magnetic resonance spectroscopy. II. Plastocyanin. J. Mol. Biol. 226:819–835. [DOI] [PubMed] [Google Scholar]
- Eliezer, D., and P. E. Wright. 1996. Is apomyoglobin a molten globule? Structural characterization by NMR. J. Mol. Biol. 263:531–538. [DOI] [PubMed] [Google Scholar]
- Frank, M. K., G. M. Clore, and A. M. Gronenborn. 1995. Structural and dynamic characterization of the urea denatured state of the immunoglobulin binding domain of streptococcal protein G by multidimensional heteronuclear NMR spectroscopy. Protein Sci. 4:2605–2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmanshin, R., S. Williams, H. R. Callender, and W. H. Woodruff. 1997. Fast events in protein folding: relaxation dynamics of secondary and tertiary structure in native apomyoglobin. Biophysics. 94:3709–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Go, N., H. Abe, H. Mizuno, and H. Taketomi (editors). 1980. Protein Folding. Elsevier/North-Holland, Amsterdam, The Netherlands. 167–181.
- Gronenborn, A., D. R. Filpula, N. Z. Essig, A. Achari, M. Whitlow, P. T. Wingfield, and G. M. Clore. 1991. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science. 253:657–660. [DOI] [PubMed] [Google Scholar]
- Guo, C., M. S. Cheung, H. Levine, and D. A. Kessler. 2002. Mechanism underlying sequence-independent beta-sheet formation. J. Chem. Phys. 116:4353–4365. [Google Scholar]
- Haliloglu, T., and I. Bahar. 1998. Coarse-grained simulations of conformational dynamics of proteins: application to apomyoglobin. Proteins. 31:271–281. [PubMed] [Google Scholar]
- Ilkowski, B., J. Skolnick, and A. Kolinski. 2000. Helix-coil and β-sheet-coil transitions in a simplified protein model. Macromol. Theory Simulat. 9:523–533. [Google Scholar]
- Irback, A., F. Sjunnesson, and S. Wallin. 2000. Three-helix-bundle protein in a Ramachandran model. Proc. Natl. Acad. Sci. USA. 97:13614–13618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennings, P. A., and P. E. Wright. 1993. Formation of a molten globule intermediate early in the kinetic folding pathway of apomyoglobin. Science. 262:892–896. [DOI] [PubMed] [Google Scholar]
- Karanicolas, J., and C. L. Brooks III. 2002. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 11:2351–2361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kihara, D., H. Lu, A. Kolinski, and J. Skolnick. 2001. TOUCHSTONE: an ab initio protein structure prediction method that uses threading-based tertiary restraints. Proc. Natl. Acad. Sci. USA. 99:5993–5998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klimov, D. K., and D. Thirumalai. 2000. Mechanisms and kinetics of β-hairpin formation. Proc. Natl. Acad. Sci. USA. 97:2544–2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinski, A., M. Betancourt, D. Kihara, P. Rotkiewicz, and J. Skolnick. 2001. Generalized comparative modeling (GENECOMP): a combination of sequence comparison, threading, lattice and off-lattice modeling for protein structure prediction and refinement. Proteins. 44:133–149. [DOI] [PubMed] [Google Scholar]
- Kolinski, A., B. Ilkowski, and J. Skolnick. 1999. Folding dynamics and thermodynamics of β-hairpin assembly: insight from various simulation techniques. Biophys. J. 77:2942–2952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinski, A., P. Rotkiewicz, B. Ilkowski, and J. Skolnick. 2000. Protein folding: flexible lattice models. Progr. Theor. Phys. (Kyoto). 138:S292–S300. [Google Scholar]
- Kolinski, A., and J. Skolnick. 1996. Lattice Models of Protein Folding, Dynamics and Thermodynamics. R.G. Landes, Austin, TX.
- Kolinski, A., and J. Skolnick. 1998. Assembly of protein structure from sparse experimental data: an efficient Monte Carlo model. Proteins. 32:475–494. [PubMed] [Google Scholar]
- Kuszewski, J., G. M. Clore, and A. M. Gronenborn. 1994. Fast folding of a prototypic polypeptide: the immunoglobin binding domain of streptococcal protein G. Protein Sci. 3:1945–1952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liwo, A., C. Czaplewski, J. Pilardy, and H. A. Scheraga. 2001. Cumulant-based expressions for the multibody terms for the correlation between local and electrostatic interactions in the united-residue force field. J. Chem. Phys. 115:2323–2347. [Google Scholar]
- McCallister, E. L., E. Alm, and D. Baker. 2000. Critical role of β-hairpin formation in protein G folding. Nat. Struct. Biol. 7:669–673. [DOI] [PubMed] [Google Scholar]
- Metropolis, N., A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller. 1953. Equation of state calculations by fast computing machines. J. Chem. Phys. 51:1087–1092. [Google Scholar]
- Munoz, V., P. A. Thompson, J. Hofrichter, and W. A. Eaton. 1997. Folding dynamics and mechanism of β-hairpin formation. Nature. 390:196–197. [DOI] [PubMed] [Google Scholar]
- Nishimura, C., S. Prytulla, H. J. Dyson, and P. E. Wright. 2000. Conservation of folding pathways in evolutionary distant globin sequences. Nat. Struct. Biol. 7:679–686. [DOI] [PubMed] [Google Scholar]
- Reymond, M. T., G. Merutka, H. J. Dyson, and P. E. Wright. 1997. Folding propensities of peptide fragments of myoglobin. Protein Sci. 6:706–716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost, B., and C. Sander. 1994. Combining evolutionary information and neural networks to predict protein secondary structure. Proteins. 19:55–72. [DOI] [PubMed] [Google Scholar]
- Shea, J.-E., and C. L. Brooks III. 2000. From folding theories to folding proteins: a review and assessment of simulation studies of protein folding and unfolding. Annu. Rev. Phys. Chem. 52:499–535. [DOI] [PubMed] [Google Scholar]
- Sheinerman, F. B., and C. L. Brooks III. 1998. Calculations on folding of segment B1 of streptococcal protein G. J. Mol. Biol. 278:439–456. [DOI] [PubMed] [Google Scholar]
- Skolnick, J., A. Kolinski, and A. R. Ortiz. 2000. Derivation of protein-specific pair potentials based on weak sequence fragment similarity. Proteins. 38:3–16. [PubMed] [Google Scholar]
- Takada, S., Z. Luthey-Schulten, and P. G. Wolynes. 1999. Folding dynamics with nonadditive force. A simulation study of designed helical protein and a random heteropolymer. J. Chem. Phys. 110:11616–11629. [Google Scholar]
- Tcherkasskaya, O., and V. N. Uversky. 2001. Denatured collapsed states in protein folding: example of apomyoglobin. Proteins. 44:244–254. [DOI] [PubMed] [Google Scholar]
- Wagner, U. G., N. Moeiler, W. Schmitzberger, H. Falk, and C. Kratky. 1995. Structure determination of the biliverdin apomyoglobin complex: crystal structure analysis of two crystal forms at 1.4 and 1.5 Å resolution. J. Mol. Biol. 247:326–337. [DOI] [PubMed] [Google Scholar]
- Wikstrom, M., U. Sjobring, W. Kastern, L. Bjorck, T. Drakenberg, and S. Forsen. 1993. Proton nuclear magnetic resonance sequential assignments and secondary structure of an immunoglobulin light chain-binding domain of protein L. Biochemistry. 32:3381–3386. [DOI] [PubMed] [Google Scholar]
- Wright, P. E., H. J. Dyson, and R. A. Lerner. 1988. Conformation of peptide fragments of proteins in aqueous solution: implications for initiation of protein folding. Biochemistry. 37:7167–7175. [DOI] [PubMed] [Google Scholar]