Ligand-Receptor Kinetics Measured by Total Internal Reflection with Fluorescence Correlation Spectroscopy

Abstract

Total internal reflection excitation used in combination with fluorescence correlation spectroscopy (TIR-FCS) is a method for characterizing the dynamic behavior and absolute concentrations of fluorescent molecules near or at the interface of a planar substrate and a solution. In this work, we demonstrate for the first time the use of TIR-FCS for examining the interaction kinetics of fluorescent ligands in solution which specifically and reversibly associate with receptors in substrate-supported planar membranes. Fluorescence fluctuation autocorrelation functions were obtained for a fluorescently labeled IgG reversibly associating with the mouse receptor FcγRII, which was purified and reconstituted into substrate-supported planar membranes. Data were obtained as a function of the IgG solution concentration, the Fc receptor surface density, the observation area size, and the incident intensity. Best fits of the autocorrelation functions to appropriate theoretical forms gave measures of the average surface density of bound IgG, the local solution concentration of IgG, the kinetic rate constant for surface dissociation, and the rate of diffusion through the depth of the evanescent field. The average number of observed fluorescent molecules, both in solution and bound to the surface, scaled with the solution concentration of IgG, observation area size, and Fc receptor surface density as expected. The dissociation rate constant and rate of diffusion through the evanescent field agree with previous results, and all measured parameters were independent of the incident intensity.

INTRODUCTION

A variety of cellular signaling processes have been hypothesized to depend not only on the equilibrium strength of the triggering ligand-receptor interactions but also on the average lifetimes, or kinetic dissociation rates, of these interactions. Examples include kinetic proofreading to enhance specificity of signal transduction carried out by T-cell receptors (McKeithan, 1995; Rabinowitz et al., 1996); regulation of signaling complex formation by the dissociation kinetics of IgE (Hlavacek et al., 2001) and tumor necrosis factor (Krippner-Heidenreich et al., 2002) from their receptors; the efficacy of ligands interacting with G-protein coupled receptors (Shea et al., 2000); and effects on synaptic transmission mediated by nicotinic acetylcholine receptors at the neuromuscular junction (Wenningmann and Dilger, 2001). To dissect the mechanisms governing the sensitivity, specificity, and regulation of the initiation of cell signaling, it is necessary to be able to accurately characterize the kinetics of ligand-receptor interactions.

In this work, the usefulness of total internal reflection illumination combined with fluorescence correlation spectroscopy (TIR-FCS) for measuring ligand-receptor kinetic rate constants is demonstrated. In this technique, fluorescent ligands reversibly associate with receptors on a planar transparent surface. A laser beam is internally reflected at the surface/solution interface and a small sample volume is defined by the depth of the evanescent field and a confocal pinhole. The fluorescence fluctuations from the sample volume are monitored and autocorrelated. The autocorrelation function yields information about the ligand-receptor interaction, including the kinetic dissociation rate constant and the average surface density of bound ligand.

Although both evanescent excitation in fluorescence microscopy (Thompson et al., 1993; Thompson and Lagerholm, 1997; Axelrod, 2001) and fluorescence correlation spectroscopy (Rigler and Elson, 2001; Thompson et al., 2002; Haustein and Schwille, 2003) are fairly well-developed methods, the combination of these two techniques has thus far been limited to only a handful of theoretical works (Thompson et al., 1981; Thompson, 1982; Starr and Thompson, 2001) and experimental applications. TIR-FCS has been used previously to examine the nonspecific binding of tetramethylrhodamine-labeled immunoglobulin and insulin to serum albumin-coated fused silica (Thompson and Axelrod, 1983), the reversible adsorption kinetics of rhodamine 6G to C-18-modified silica surfaces (Hansen and Harris, 1998a,b), and the local diffusion coefficients and concentrations of fluorescently labeled, monoclonal IgG in solution very close to substrate-supported phospholipid bilayers (Starr and Thompson, 2002).

In this work, we develop TIR-FCS as a method for examining the specific interaction kinetics between a fluorescently labeled, monoclonal IgG in solution and a cell-surface Fc receptor incorporated into substrate-supported phospholipid bilayers. Average populations of fluorescently labeled IgG molecules, both in solution and bound to the surface within the detection volume, are determined as a function of the IgG solution concentration, the Fc receptor surface density, and the size of the observation area over a range of excitation intensities. The measured dissociation rate constant of the interaction agrees well with results from other methods. This work describes the first application of TIR-FCS to the study of specific ligand-receptor kinetics.

THEORETICAL BACKGROUND

Definitions

Consider a specific binding interaction between molecules in solution and sites on a surface (Fig. 1 a). Fluorescent molecules in solution of concentration A_f are in equilibrium with unoccupied, fixed binding sites on the surface of density B, forming immobile fluorescent complexes on the surface of density C_f. Nonfluorescent molecules in solution of concentration A_n compete for the same surface binding sites to form nonfluorescent complexes on the surface of density C_n. We assume that the kinetic rate constants for association and dissociation, k_a and k_d, as well as the solution diffusion coefficient D, are identical for fluorescent and nonfluorescent molecules. The fraction of surface binding sites that remains unoccupied at equilibrium is given by β = K_d/(K_d + A_t), where K_d = k_d/k_a is the equilibrium dissociation constant for the bimolecular reaction and A_t = A_f + A_n is the total concentration of ligand in solution. The proportion of ligand that is fluorescently labeled is denoted by η = A_f/A_t.

FIGURE 1.

Components of TIR-FCS. (a) Fluorescent molecules in solution of concentration A_f diffuse with coefficient D and bind to surface sites of density B to form fluorescent complexes of surface density C_f. Nonfluorescent molecules in solution of concentration A_n also diffuse with coefficient D and compete for the same surface-binding sites to form nonfluorescent complexes of surface density C_n. Binding rate constants for association and dissociation are given by k_a and k_d, respectively. (b) A laser beam with vacuum wavelength λ₀ traveling from a high refractive index (n₁) medium into a lower refractive index (n₂) medium is totally internally reflected at the interface when its incidence angle α is greater than the critical angle α_c, creating an evanescent field that penetrates a depth d into the lower refractive index medium. A small sample volume is defined by this depth in combination with a circular aperture placed at an intermediate image plane of the microscope that defines an area of radius h in the sample plane. The fluorescence measured from the small sample volume adjacent to the surface fluctuates with time as individual fluorescent ligands diffuse into the volume, bind to surface-associated receptors, dissociate, and diffuse out of the volume. These fluorescence fluctuations are autocorrelated and fit to theoretical expressions to obtain information about the dynamics at or near the surface.

Total internal reflection

A laser beam is internally reflected at the interface of the planar substrate and solution, creating an evanescent field in the solution with an intensity that exponentially decays with distance from the interface (Fig. 1 b). The characteristic depth of penetration is given by

(1)

where λ₀ is the vacuum wavelength of the laser beam, and n₁ and n₂ are the refractive indices of the substrate and solution, respectively. The beam is incident on the interface, from the higher refractive index region, at an angle α which is greater than the critical angle, α_c = sin⁻¹(n₂/n₁). In this work, λ₀ = 488.0 nm, n₁ = 1.467, n₂ = 1.334, α = 70°, and d = 112 nm. The evanescent field selectively excites fluorescent molecules that are bound to, or near, the surface/solution interface. The properties of evanescent fields have been discussed previously in detail (Agudin and Platzeck, 1978; Thompson et al., 1993; Knoll, 1998; Girard et al., 2000).

Total internal reflection fluorescence microscopy (TIR-FM)

To determine the equilibrium dissociation constant for the ligand-receptor interaction, steady-state total internal reflection fluorescence microscopy (TIR-FM) is used to measure the evanescently excited fluorescence from a relatively large elliptical area (1/e² radii ≈ 30 and 100 μm) as a function of the ligand concentration in solution (e.g., Lagerholm et al., 2000). Assuming that the relative fluorescence intensities collected from molecules in solution and bound to the surface are equal, the fluorescence is proportional to the average number of fluorescent molecules in solution, N_Af, plus the average number of fluorescent molecules bound to the surface, N_Cf. In the simplest case, for a given value of η, N_Cf increases to saturation with A_t according to the shape of a standard binding isotherm and N_Af increases linearly with A_t. The average fluorescence intensities as a function of the solution concentration for samples containing (+) or not containing (−) surface binding sites are

(2)

In these expressions, Q is a proportionality constant and S is the total density (occupied and unoccupied) of surface binding sites. Nonlinear curve fitting of the difference data 〈F₊〉−〈F₋〉 as a function of the solution concentration A_t gives a measure of the equilibrium dissociation constant K_d and the product QηS. Fitting matched negative control data 〈F₋〉 to a line gives a measure of the constant Qdη. This quantity, along with the known value of d, can then be used to determine the absolute density of surface binding sites S.

TIR-FCS: General considerations

Information about the kinetics of the ligand-receptor interaction is obtained by using TIR-FCS. A small observation volume is defined by the depth of the evanescent field d, and a circular aperture placed at an intermediate image plane of the microscope that defines an area of radius h ≈ 1.2 μm in the sample plane (Fig. 1 b). As individual molecules diffuse through the observation volume, and bind to or dissociate from sites on the surface, the fluorescence intensity fluctuates with time. These fluctuations are monitored and autocorrelated to obtain information about the concentration, diffusion, and binding characteristics of the molecules. The fluorescence fluctuation autocorrelation function is defined as

(3)

where the fluorescence fluctuation δF(t) = F(t) − 〈F〉 is the difference between the instantaneous fluorescence intensity at time t and the average intensity, the brackets 〈 〉 denote a time average, and τ is the lag time or correlation time. G(τ) decreases monotonically with the correlation time to zero at τ = ∞. Of interest in this work is the manner in which G(τ) depends on the basic kinetic and transport properties of the system. In particular, a theoretical expression describing the autocorrelation data is necessary to extract parameters such as the dissociation rate constant, k_d, and the diffusion coefficient, D.

TIR-FCS: Case of no nonfluorescent molecules

The theoretical form of G(τ) for the case in which fluorescence fluctuations, resulting both from diffusion through the evanescent field and from reversible binding to specific surface sites, contribute to the autocorrelation function has recently been described in detail for η = 1 (Starr and Thompson, 2001). The general expression has four terms and four characteristic rates:

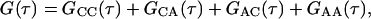(4)

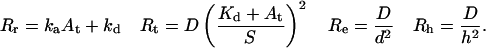(5)

G_CC(τ) and G_AA(τ) are derived from autocorrelations of fluctuations in the densities of surface-bound fluorescent molecules and in the concentrations of fluorescent molecules in solution, respectively. G_CA(τ) and G_AC(τ) result from cross-correlations in the concentration fluctuations of these species. R_r is the relaxation rate for the surface association/dissociation process, R_t describes transport in solution and is related to surface rebinding (Lagerholm and Thompson, 1998), R_h is the rate of diffusion in solution parallel to the surface through the observation area, and R_e is the rate of diffusion in solution through the depth of the evanescent field. For the IgG-FcγRII system described here, A_t ≈ 1 μM, K_d ≈ 2.5 μM, k_a ≈ 0.4 μM⁻¹ s⁻¹, k_d ≈ 1 s⁻¹, D ≈ 5 × 10⁻⁷ cm² s⁻¹, and S ≈ 500 molecules μm⁻² (Poglitsch et al., 1991; Hsieh et al., 1992; Hsieh and Thompson, 1995). Thus, approximate values of the characteristic rates are R_r = 1.4 s⁻¹, R_h = 35 s⁻¹, R_t = 890 s⁻¹, and R_e = 4000 s⁻¹; and R_r ≪ R_h ≪ R_t ≪ R_e.

The relative values of the surface reaction rate R_r and the solution transport rates R_t and R_h determine the nature of G_CC(τ). The faster of the two transport rates determines the rate at which molecules in solution are made available for surface binding. However, it is the slower of the reaction rate and the defining solution transport rate that dominates G_CC(τ) (Thompson et al., 1981; Pearce et al., 1992). Therefore, when R_r ≪ R_h ≪ R_t, diffusion in solution does not play a significant role in G_CC(τ); the shape of this term is a simple exponential that decays with rate R_r. Furthermore, when R_r ≪ R_h ≪ R_t ≪ R_e, the cross-correlation terms are of negligible magnitude. This condition also implies that G_AA(τ) has a simple form depending only on R_e, although it is not exponential (see below). For this case, with η = 1 (Starr and Thompson, 2001),

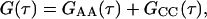(6)

where

(7)

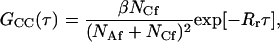(8)

and erfc denotes the complementary error function. In Eqs. 7 and 8, N_Af = πh²dA_f is the average number of fluorescent molecules in solution within the observed volume and N_Cf = πh²C_f is the average number of fluorescent molecules bound to the surface in the observed area. The fraction of surface binding sites remaining unoccupied at equilibrium, β, is defined above.

TIR-FCS: Case of a mixture of fluorescent and nonfluorescent molecules

From Eqs. 7 and 8 one sees that the magnitude of the autocorrelation function increases as the number of observed fluorescent molecules decreases. Therefore, low concentrations of fluorescent molecules are necessary for the fluorescence fluctuations, and thus the magnitude of the autocorrelation function, to be significant. However, to avoid working far below the mid-range of the binding isotherm where rare, tight, nonspecific binding sites might be occupied and dominate the system, a much higher solution concentration of unlabeled ligand was added. The low proportion of fluorescent molecules then acts as a reporter for the whole system (Thompson, 1982).

We have recently generalized our previous theory describing TIR-FCS when both surface kinetics and diffusion in solution contribute to the measured autocorrelation function (Starr and Thompson, 2001) to include the situation in which fluorescent and nonfluorescent molecules compete for the surface binding sites (Lieto and Thompson, unpublished data). In this case, when the kinetic association and dissociation rate constants, as well as the diffusion coefficients in solution, are equivalent for fluorescent and nonfluorescent molecules, the form for G(τ) is similar to but nonetheless more complex than that shown in Eqs. 6–8. The limit for k_d ≪ R_h, R_t, and R_e is given by Eqs. 6, 7, and

(9)

where η is the fraction of ligand that is fluorescently labeled as defined above. This equation agrees with the previously published expression for the case in which fluorescent and nonfluorescent ligands compete for surface binding sites, the kinetic rates for the two species are equivalent, and N_Af ≪ N_Cf (Thompson, 1982). For the experimental conditions used in the work described here, β ∼ ½ and η ≪ 1. Under these conditions, G(τ) is given by Eqs. 6, 7, and the limit of Eq. 9 for η ≪ 1:

(10)

Although in general the autocorrelation function depends on both kinetic rate constants (Eq. 9), for this system one can only determine k_d from G(τ) (Eq. 10).

Autocorrelation function characteristics

Theoretical autocorrelation functions for samples with (pos) and without (neg) binding sites are shown in Fig. 2 a. G_neg(τ), for samples without surface binding sites, is predicted by Eq. 7 with N_Cf = 0. G_pos(τ), for samples with surface binding sites, under the experimental conditions used in this work, is predicted by Eqs. 6, 7, and 10. The shapes of G(τ) for these two situations are readily distinguishable as the surface binding term G_CC(τ) contributes a long-time component. Also shown is the ratio of the magnitudes of the autocorrelation functions for these two cases, G_pos(0)/G_neg(0), as a function of N_Cf/N_Af (Fig. 2 b). The magnitude of G_pos(τ) for samples with binding sites will always be lower than the magnitude of G_neg(τ) for corresponding samples without binding sites. This result follows from the fact that there are more fluorescent molecules observed on average in the samples with surface binding.

FIGURE 2.

Theoretical autocorrelation functions. (a) Theoretically predicted autocorrelation functions are shown for samples with (pos) and without (neg) binding sites. For samples without binding sites, G_neg(τ) is given by Eq. 7 with N_Cf = 0. For samples with surface binding sites, G_pos(τ) is given by Eqs. 6, 7, and 10. In both plots N_Af = 1 and R_e = 4 ms⁻¹, and for G_pos(τ) N_Cf = 1 and k_d⁻¹ = 1 s. (b) The magnitudes of G(τ) are compared as a function of N_Cf/N_Af. The magnitude of G_pos(τ) is always less than that of G_neg(τ), but as N_Cf/N_Af decreases, the ratio of the magnitudes approaches one.

MATERIALS AND METHODS

Antibodies and soluble proteins

Monoclonal anti-dinitrophenyl (DNP) IgG₁ was obtained from the mouse-mouse hybridoma 1B7.11 (American Type Culture Collection, Rockville, MD) (Hsieh et al., 1992). Hybridomas were maintained in DMEM/F12 medium supplemented with 2 mM L-glutamine, 1 mM sodium pyruvate, 100 units ml⁻¹ penicillin G, 100 μg ml⁻¹ streptomycin (GPPS), and 5% fetal calf serum that had been heat-inactivated (30 min, 56°C). 1B7.11 IgG was purified from cell supernatants by affinity chromatography with DNP-conjugated human serum albumin. The IgG was eluted with DNP-glycine, which was later removed by extensive dialysis followed by ion exchange chromatography with Dowex 1X8-200 in a low-pH phosphate buffer (0.01 M sodium phosphate, 0.1 M NaCl, and 0.01% NaN₃, at pH 5.7) (Lagerholm et al., 2000; Schweitzer-Stenner et al., 1992). Each liter of supernatant yielded ∼15–20 mg of antibody as determined spectrophotometrically by assuming that the molar absorptivity at 280 nm was 1.4 ml mg⁻¹ cm⁻¹. Previous work in similar systems has shown that a high percentage of IgG prepared in this manner retains the ability to bind FcγRII (Gesty-Palmer and Thompson, 1997).

1B7.11 IgG was fluorescently labeled (A-) using the Alexa Fluor 488 Protein Labeling Kit (Molecular Probes, Eugene, OR). The solution concentration of A-IgG and the molar ratio of Alexa Fluor 488 to IgG (0.2–0.6 dyes/protein) were estimated spectrophotometrically according to the manufacturer's protocol. To prepare mixtures of labeled and unlabeled IgG, it was assumed that no antibodies were labeled with more than one dye molecule. All antibody solutions were passed through 0.02-μm filters immediately before use.

Monoclonal anti-moFcγRII antibodies were obtained from the rat-mouse hybridoma 2.4G2 (American Type Culture Collection) (Unkeless, 1979). Hybridomas were maintained in RPMI 1640 medium supplemented with GPPS and 5% fetal calf serum (see above). 2.4G2 antibodies were purified from cell supernatants by affinity chromatography with anti-(rat IgG κ light chain) antibodies (Poglitsch et al., 1991). 2.4G2 antibodies were passed through a 0.1-μm filter immediately before use.

Chicken egg albumin (ovalbumin; Sigma, St. Louis, MO) was used to assist with blocking nonspecific binding sites. To reduce background fluorescence levels, ovalbumin dissolved in phosphate-buffered saline (PBS; 0.05 M sodium phosphate, 0.15 M NaCl, and 0.01% NaN₃, at pH 7.4) was passed down a Sephadex G-75 column. Immediately before use, the ovalbumin was passed through a 0.1-μm filter.

Fc receptors

J774A.1, a macrophage-like cell line expressing the cell surface Fc receptor mouse FcγRII, was obtained from the University of North Carolina Tissue Culture Facility. Cells were maintained in DMEM/F12 medium supplemented with GPPS and 5% fetal calf serum (see above). FcγRII was purified from homogenized J774A.1 cells by 2.4G2 Fab affinity chromatography with modifications to a previously developed procedure (Poglitsch et al., 1991). Approximately 10⁹ cells were homogenized in PBS with 0.5% Igepal CA-630 containing Complete Protease Inhibitor Tablets (Roche Diagnostics GmbH, Mannheim, Germany). The homogenate was clarified at 1600 g for 5 min and then twice at 27,000 g for 60 min. The supernatant was carefully removed to minimize contamination by floating lipids and was applied to a 2.4G2 Fab affinity column equilibrated with wash buffer (PBS with 0.5% Igepal CA-630). The column was rinsed with ∼500 ml of wash buffer and then eluted with 0.1 M sodium acetate, and 0.5 M NaCl, at pH 4.0, containing 20 mM n-octyl β-D-glucopyranoside (octylglucoside). The eluate was immediately neutralized with 2 M Tris at pH 7.4 and dialyzed against two 250-ml volumes of buffer A (0.05 M NaCl, 0.165 M sucrose, 10 mM HEPES, and 0.01% NaN₃, at pH 7.4) containing 20 mM octylglucoside. All procedures were carried out at 4°C, and the purity of the product was estimated with SDS-PAGE and silver staining. A bicinchoninic acid assay (Pierce, Rockford, IL) with bovine serum albumin as the standard was used to determine the yield (typically 75–300 μg from 2–5 × 10⁹ cells).

Liposomes

Purified FcγRII was reconstituted into phospholipid liposomes by detergent dialysis (Poglitsch et al., 1991). Egg phosphatidylcholine and cholesterol (Avanti Polar Lipids, Alabaster, AL) were mixed in a ratio of 6:1 (w:w) in chloroform/methanol (2:1, v:v), dried under vacuum for 4–5 h, and solubilized with ∼25 μg ml⁻¹ FcγRII in buffer A with octylglucoside at a protein:lipid ratio of 1:6 (w:w). After treatment in a water-bath sonicator for 2 min on ice, samples were dialyzed against 4 1-L volumes of buffer A. Liposomes were also prepared similarly without FcγRII. Liposome suspensions were clarified by spinning twice for 5 min at 13,600 g immediately before use.

Sample preparation

Supported phospholipid bilayers were formed on planar fused silica surfaces by vesicle adsorption and fusion (Poglitsch et al., 1991). For TIR-FCS measurements, the sample chamber was created between a glass coverslip (24 × 60 mm, No. 0) (Thomas Scientific, Swedesboro, NJ) supported on an aluminum mount and a fused silica substrate (SiO₂; 0.75 in × 1 in × 1 mm) (Quartz Scientific, Fairport Harbor, OH) with double-coated tape (∼100-μm thickness) as a spacer. For TIR-FM measurements, the glass coverslip and aluminum mount were replaced by a glass microscope slide (3 in × 1 in × 1 mm). Fused silica and glass substrates were cleaned by boiling in detergent (ICN, Aurora, OH), bath-sonicating, rinsing extensively with deionized water, and drying at 160°C. Immediately before use, substrates were cleaned in an argon ion plasma cleaner (PDC-3XG, Harrick Scientific, Ossining, NY) for 15 min at 25°C. Planar bilayers were formed by applying ∼45 μl of a liposome suspension to a fused silica substrate (1 h, 25°C), and then rinsing with 3 ml of 0.1-μm filtered PBS. Samples were then treated with 200 μl of 10 mg ml⁻¹ ovalbumin in PBS (30 min, 25°C). Finally, 200 μl of solutions containing various concentrations of unlabeled 1B7.11 and A-1B7.11 with 10 mg ml⁻¹ ovalbumin in PBS, sometimes with 0.25 μM 2.4G2 as a negative control, were applied. Samples were also prepared with approximately one-half the typical receptor surface density by mixing equal volumes of liposomes with and without incorporated FcγRII before application to the substrate. Background samples had unlabeled 1B7.11 in solution adjacent to a planar lipid bilayer (without FcγRII) treated with ovalbumin.

Fluorescence microscopy

All measurements were carried out on an instrument consisting of an argon ion laser (Innova 90-3, Coherent, Palo Alto, CA), an inverted microscope (Zeiss Axiovert 35, Carl Zeiss Microimaging, Thornwood, NY), and a single-photon counting photomultiplier (RCA C31034A, Lancaster, PA). Experiments were carried out at 25°C using the 488-nm laser line. The laser power was typically set at 0.25 W and neutral density filters were inserted in its path giving an incident intensity ≈ 0.03–1.08 μW μm⁻². For TIR-FCS, a pinhole with a radius of 50 μm (or 100 μm) placed at an internal image place of the microscope defined an area with a radius of h ≈ 1.2 μm (or ≈ 2.4 μm) when projected onto the sample plane. On each area of the sample examined, nonspecific, tightly-bound fluorescent molecules were first prebleached with a high power bleach pulse (typically 1 s). The fluorescence arising from the volume defined by the evanescent wave and the pinhole was collected through a 60×, 1.4-NA oil immersion objective (PlanApo, Nikon Instruments, Augusta, GA). The fluorescence signal was autocorrelated by a PC-based correlator board (ALV 5000/E) with collection times ranging from 1 to 10 min. The average fluorescence intensity was approximately constant over the period of each measurement. For TIR-FM, the fluorescence excited by the whole evanescent wave was collected through a much larger image plane aperture and a 40×, 0.75-NA water immersion objective (AchroPlan, Zeiss).

TIR-FCS data analysis

TIR-FCS autocorrelation data measured from negative control samples (no surface binding sites) were fit to Eq. 7 plus an arbitrary constant G_∞, withN_Cf = 0. The free parameters were R_e, N_Af, and G_∞. Autocorrelation data measured from positive samples were fit to the combination of Eqs. 6, 7, and 10, plus an arbitrary constant G_∞. For these fits, R_e was fixed as the average from corresponding negative control samples, and N_Af, N_Cf, k_d, and G_∞ were free parameters. Before fitting, all data were background-corrected by multiplying each data point by the factor 〈S〉²/〈F〉², where 〈F〉 = 〈S〉 − 〈B_g〉 is the average measured fluorescence calculated by subtracting the average measured background signal 〈B_g〉 from the average measured sample signal 〈S〉 (Thompson, 1991). Nonlinear least-squares fits were determined by the Levenberg-Marquardt method using Mathematica 4.1 (Wolfram Research, Champaign, IL). The magnitude of G_∞ was typically ≤0.005.

Consideration was given to calculation of the standard deviation of the autocorrelation function G(τ), at different lag time points τ. Knowledge of the standard deviation is necessary to calculate a value for chi-squared related to the least-squares data fit as well as for weighted data fitting. When considered, an approximate value for the standard deviation is often calculated according to an expression derived for the case of an exponential correlation function, assuming a large number of fluorescent particles in the observation volume, negligible background fluorescence, and sampling times much smaller than the correlation time expected for the process under investigation (Koppel, 1974). This analytical expression has recently been compared to other protocols for determining a measure of the uncertainty in G(τ) (Wohland et al., 2001). The technique thought to yield the most accurate measure of the uncertainty, though also the most time-consuming in terms of data collection, is to collect multiple data sets on a given spot, and then average the correlation data points at each lag time τ. The uncertainty in the correlation is then given by the standard deviation of the data. Thus, the average correlation and the corresponding uncertainty were determined from 4 to 6 measurements per spot for a portion of the data collected, and the uncertainty was used to compare weighted and unweighted data fits. The average correlation data sets were less noisy than the individual sets, but the weighted data fitting did not significantly alter the values of the fit parameters. There was more variation from spot-to-spot on a given sample than between unweighted and weighted data fits; therefore, the fit parameters presented here were determined by unweighted data fitting.

RESULTS

Equilibrium binding

The specificity of the interaction between the Fc portion of A-IgG and FcγRII was confirmed by using steady-state TIR-FM (Hsieh et al., 1992). The evanescently excited fluorescence intensity was measured for a series of samples with increasing IgG concentration (and η ∼ 1) in solution adjacent to supported phospholipid bilayers containing FcγRII (Fig. 3 a). Negative control measurements were made for samples either without FcγRII or with saturating amounts of the monoclonal antibody 2.4G2, which binds specifically and tightly to FcγRII and blocks its interaction with the Fc portion of IgG (Unkeless, 1979). The difference data were fit to the theoretical form for a bimolecular reaction occurring at a surface; i.e., the difference of Eq. 2 (Fig. 3 b). The equilibrium dissociation constant K_d was determined to be 2.4 ± 0.4 μM and the FcγRII surface density was estimated to be S ≈ 800 molecules μm⁻². These values are consistent with those previously measured (Hsieh et al., 1992; Hsieh and Thompson, 1995).

FIGURE 3.

Equilibrium binding. (a) Average surface-associated fluorescence intensity measurements of samples containing A-IgG (η ∼ 1) in solution adjacent to substrate-supported planar membranes containing purified and reconstituted mouse FcγRII were made by TIR-FM. Negative control measurements were carried out by using the monoclonal antibody 2.4G2 to block IgG-FcγRII binding, or on samples not containing FcγRII. Samples also contained 10 mg ml⁻¹ ovalbumin in PBS. (b) The difference data were fit to the theoretical form for a bimolecular reaction occurring at a surface (see Eq. 2) giving a measure of the equilibrium dissociation constant (K_d = 2.4 ± 0.4 μM). The total surface binding site density (S ≈ 800 molecules μm⁻²) was estimated by comparing the fluorescence intensity of samples containing FcγRII (without 2.4G2) with those not containing FcγRII (or also containing 2.4G2) as described in the text. The fluorescence intensities were normalized so that QηS = 1 (see Eq. 2).

TIR-FCS

When viewed with evanescent illumination, a qualitative difference was noticed in the “twinkles” visible on positive and negative samples. Samples without binding sites gave the impression of faster movement. When observing samples with binding sites, individual fluorescent objects were more readily distinguished, and the twinkling appeared to occur at a slower speed.

Representative fluorescence fluctuation autocorrelation functions are shown in Fig. 4. As shown, although the magnitudes of G(τ) were similar for the two sample types, the decay rates were significantly different. In particular, a much more slowly decaying component, consistent with visual observations, was apparent for samples containing FcγRII (Fig. 4 a). The shapes and timescales of the experimental data agree with the theoretically predicted autocorrelation functions (see Fig. 2 a). The values of G(0) are expected to be similar when N_Cf is less than N_Af, and G_pos(0) is always expected to be less than G_neg(0) for the same concentration of fluorescent ligand in solution (see Fig. 2 b) which is seen here.

FIGURE 4.

Representative TIR-FCS autocorrelation data. The data are for 10 nM A-IgG, 1 μM total IgG in PBS with 10 mg ml⁻¹ ovalbumin. A pinhole with a radius of 50 μm was placed at an internal image plane of the microscope (h ≈ 1.2 μm). Each data set is an average of four 130-s measurements of the same observation volume. (a) The planar membrane for the positive sample contained purified and reconstituted mouse FcγRII. The best fit of the data to Eqs. 6, 7, and 10 plus G_∞, with R_e = 5 ms⁻¹, gave N_Af = 2.0, N_Cf = 0.5, and k_d⁻¹ = 430 ms. (b) The planar membrane for the negative control sample contained only lipids. The best fit of the data to Eq. 7 plus G_∞, with N_Cf = 0, gave N_Af = 1.7 and R_e = 4.7 ms⁻¹.

Fluorescence fluctuation autocorrelation data were collected for a series of different conditions, including a range of excitation intensities, various solution concentrations and ratios of A-IgG to total IgG, two FcγRII surface densities, and two pinhole sizes. Positive samples were composed of A-IgG and unlabeled IgG in solution adjacent to supported bilayers containing FcγRII. Negative control samples contained a similar range of solution concentrations of A-IgG and unlabeled IgG, but either did not contain FcγRII in their bilayers, or also contained 2.4G2 in solution to block the binding of IgG to FcγRII.

Negative control data were fit to Eq. 7 plus a constant G_∞, with N_Cf = 0, and values for N_Af and R_e were determined (Table 1). As expected, N_Af increased approximately linearly with the solution concentration of A-IgG for a constant solution concentration of IgG; and N_Af remained approximately constant as the total solution concentration of IgG was varied while the solution concentration of A-IgG remained the same. N_Af also increased with the radius of the observation area h. R_e agreed with previous measurements (Starr and Thompson, 2002) and remained approximately constant under all conditions. N_Af and R_e remained constant, within experimental uncertainty, over a range of excitation intensities (0.22–1.08 μW μm⁻²) (data not shown).

TABLE 1.

Summary of fit parameters: membranes without FcγRII

[A-IgG] (nM)	[IgG] (μM)	h (μm)	NAf	Re(ms−1)
40	1.0	≈1.2	11.6 ± 0.9	5.1 ± 0.2
20	1.0	≈1.2	6.0 ± 0.4	5.0 ± 0.2
10	1.0	≈1.2	2.0 ± 0.2	5.1 ± 0.3
40	2.0	≈1.2	9.5 ± 0.6	4.2 ± 0.2
40	0.5	≈1.2	9.9 ± 0.5	4.6 ± 0.2
20	1.0	≈2.4	14.7 ± 0.8	3.8 ± 0.1

TIR-FCS autocorrelation data collected from samples without specific binding sites were background-corrected and fit to Eq. 7 plus an arbitrary constant G_∞, with N_Cf = 0. Free parameters were R_e, N_Af, and G_∞. Collection times ranged from 1 to 6 min and some data sets were averages over 4–5 measurements on a given spot. For each set of conditions, samples were prepared on two separate occasions and measurements were made on 5–10 different areas of the sample. Fit parameters were averaged over all excitation intensities (0.22–1.08 μW μm⁻²), and uncertainties are standard deviations in the mean.

Positive sample data were fit to Eqs. 6, 7, and 10 plus a constant G_∞, with R_e fixed as the average from corresponding negative control data. Values for N_Af, N_Cf, and k_d were obtained from the fits (Table 2). The values of these parameters did not change, within experimental uncertainty, for a range of excitation intensities (0.03–0.22 μW μm⁻²) (data not shown). In addition, the best-fit values of N_Af agreed roughly with values obtained from corresponding negative control samples (Table 1).

TABLE 2.

Summary of fit parameters: membranes with FcγRII

[A-IgG] (nM)	[IgG] (μM)	FcγRII (molecules μm−2)	h (μm)	NAf	NCf	kd−1(ms)
40	1.0	≈800	≈1.2	14.3 ± 1.1	8.6 ± 1.0	500 ± 30
20	1.0	≈800	≈1.2	7.7 ± 0.6	4.6 ± 0.8	520 ± 30
10	1.0	≈800	≈1.2	2.7 ± 0.2	1.2 ± 0.2	600 ± 40
40	2.0	≈800	≈1.2	14.7 ± 0.8	6.6 ± 0.6	550 ± 50
40	0.5	≈800	≈1.2	14.8 ± 0.8	9.3 ± 1.2	480 ± 20
40	1.0	≈400	≈1.2	12.0 ± 0.4	3.3 ± 0.3	570 ± 40
20	1.0	≈800	≈2.4	23 ± 1	23 ± 2	620 ± 30

TIR-FCS autocorrelation data collected from samples with specific binding sites were background-corrected and fit to Eqs. 6, 7, and 10 plus an arbitrary constant G_∞. R_e was fixed as the average from corresponding negative control fits, and the free parameters were k_d, N_Af, N_Cf, and G_∞. Collection times ranged from 1 to 10 min and some data sets were averages over 4–6 measurements on a given spot. For each set of conditions, samples were prepared on 2–4 separate occasions and measurements were made on 8–17 different areas of the sample. Fit parameters were averaged over all excitation intensities (0.03–0.22 μW μm⁻²), and uncertainties are standard deviations in the mean.

A number of trends are predicted for the behavior of N_Af and N_Cf on positive samples, all of which were observed:

1. For a constant total solution concentration of IgG, both N_Cf and N_Af are expected to increase linearly with the solution concentration of A-IgG.

2. As the total solution concentration of IgG is decreased, while the solution concentration of A-IgG is unchanged, N_Cf is predicted to increase while N_Af should remain constant.

3. As the FcγRII surface density is decreased, N_Cf should decrease whereas N_Af should be unaffected if the solution concentrations of A-IgG and total IgG remain constant.

4. An increase in the observation area size should increase the measured values of both N_Cf and N_Af.

The measured value of the dissociation rate constant k_d remained approximately constant under all conditions, and agrees with previous measurements of this parameter made for IgG and FcγRII by using total internal reflection illumination with fluorescence photobleaching recovery (Hsieh and Thompson, 1995). As described above, transport in solution via rates R_t and R_h is predicted to affect the shape of G_CC(τ) only if the larger of these rates is smaller than or approximately equal to k_d. Thus, because R_t ≫ k_d, changing the observation area size should not change the measured decay rate. This prediction is confirmed since k_d remains approximately constant for both observation area sizes (Table 2).

DISCUSSION

Cellular signaling processes are thought to depend not only on the equilibrium strength of the triggering ligand-receptor interactions but also on the average lifetimes, or kinetic dissociation rates, of these interactions. To understand the mechanisms governing the sensitivity, specificity, and regulation of the initiation of cell signaling, it is therefore necessary to be able to accurately characterize the kinetics of ligand-receptor interactions. Although a large variety of methods have been developed for examining the equilibrium properties of ligand-receptor interactions, techniques for characterizing the kinetic properties are less prevalent.

As shown in this work, combining total internal reflection illumination with fluorescence correlation spectroscopy can be used to measure ligand-receptor kinetic dissociation rate constants. A comprehensive set of fluorescence fluctuation autocorrelation functions were obtained for a fluorescently labeled IgG reversibly associating with the mouse receptor FcγRII in substrate-supported planar membranes, and both theoretical and data analysis methods were developed for extracting the kinetic dissociation rate for this interaction from the measured G(τ). The measured dissociation rate was consistent with that measured previously by combining internal reflection illumination and fluorescence photobleaching recovery.

TIR-FCS is an attractive method for measuring ligand-receptor kinetics because of the small volumes and required amounts of material. In addition, the planar geometry opens the possibility of using this method in combination with microarrays for high throughput screening based on kinetic dissociation rates. Finally, as shown in an accompanying article (Lieto and Thompson, unpublished data), when fluorescent and nonfluorescent molecules compete for the surface binding sites, TIR-FCS autocorrelation functions contain, in general, information about the kinetic rates for both fluorescent and nonfluorescent molecules. Thus, it may be possible to use a single fluorescent ligand to monitor the kinetics of a variety of competitive or potentially competitive nonfluorescent species.