Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Nov;85(5):3310–3318. doi: 10.1016/S0006-3495(03)74750-X

Glucose and Mannitol Diffusion in Human Dura Mater

Alexey N Bashkatov 1, Elina A Genina 1, Yuri P Sinichkin 1, Vyacheslav I Kochubey 1, Nina A Lakodina 1, Valery V Tuchin 1
PMCID: PMC1303608  PMID: 14581232

Abstract

An in vitro experimental study of the control of the human dura mater optical properties at administration of aqueous solutions of glucose and mannitol has been presented. The significant increase of the dura mater optical transmittance under action of immersion liquids has been demonstrated. Diffusion coefficients of glucose and mannitol in the human dura mater tissue at 20°C have been estimated as (1.63 ± 0.29) × 10−6cm2/s and as (1.31 ± 0.41) × 10−6 cm2/s, respectively. Experiments show that administration of immersion liquids allows for the effective control of tissue optical characteristics that make dura mater more transparent, thereby increasing the ability of light penetration through the tissue.

INTRODUCTION

Recent technological advancements in the photonics industry have led to a resurgence of interest in optical imaging technologies and real progress toward the development of noninvasive clinical functional cerebral imaging systems. Interest in using optical methods for physiological-condition monitoring and cancer diagnostics has increased due to their simplicity, low cost, and low risk. The application of cerebral diagnostics, therapy, and surgery is very important for modern laser medicine. One of the problems deals with the transport of the laser beam through the dura mater tissue (Hueber et al., 2001). Dura mater is a typical fibrous tissue similar to sclera or skin dermis (Zyablov et al., 1982; Baron and Mayorova, 1982; Vertel, 2001). The turbidity of most fibrous tissues in visible and NIR (near infrared) spectral ranges is due to their high scattering with low absorption. The turbidity limits spatial resolution and penetration depth for optical methods (Tuchin, 2000).

The optical properties of biological tissues can be effectively controlled by compression, dehydration, coagulation, and other actions (Cilesiz and Welch, 1993; Chan et al., 1996a,b; Demos et al., 1998; Bornhop et al., 2001; Genina et al., 2002; Tuchin, 2000; Zuluaga et al., 2002). Such control means the change of the scattering or absorption properties of a tissue.

It is well-known that the major source of scattering in tissues and cell structures is the refractive index mismatch between cell organelles like mitochondria and cytoplasm, and extracellular media and tissue structural components such as collagen and elastin fibers (Maier et al., 1994; Chance et al., 1995; Liu et al., 1996; Bruulsema et al., 1997; Tuchin, 1999, 2000; Wang, 2000). The scattering properties of fibrous tissues (such as dura mater) can be significantly changed due to action of osmotically active immersion liquids (Beauvoit et al., 1994; Maier et al., 1994; Chance et al., 1995, 1997; Liu et al., 1996; Bruulsema et al., 1997; Tuchin et al., 1997, 2001; Bashkatov et al., 1999, 2000a,b, 2001, 2002a,b; Vargas et al., 1999, 2001, 2003; Wang and Elder, 2002; Yao et al., 2002). Administration of the immersion liquid having a refractive index higher than that of tissue interstitial fluid induces a partial replacement of the interstitial fluids by immersion substance and hence, matching of refractive indices of tissue scatterers and the interstitial fluid. The matching, correspondingly, causes the decrease of scattering.

It has been shown that glucose solution is applicable for the control of tissue scattering properties (Maier et al., 1994; Chance et al., 1995; Liu et al., 1996; Bruulsema et al., 1997; Tuchin et al., 1997, 1999, 2000; Bashkatov et al., 1999, 2000a, 2001, 2002a,b; Wang, 2000; Vargas et al., 2001; Yao et al., 2002). The possibility of application of mannitol solution for optical clearing of membranes surrounding brain has been discussed by Chance et al. (1997). Increase of glucose or mannitol content in a tissue reduces index mismatch and, correspondingly, decreases the scattering coefficient. Measurement of scattering coefficient allows one to monitor the change of glucose concentration in the tissue. It is worth noting that application of osmotically active liquids is accompanied by tissue swelling or shrinkage, which should be taken into account.

Despite numerous investigations related to the control of tissue optical properties, the problem of estimating the diffusion coefficient of immersion liquid in tissues has not been studied in detail. The knowledge of diffusion coefficients is very important for development of mathematical models describing the interaction of osmotically active liquids with tissues in particular, to predict the penetration efficiency of drug and metabolic agents through tissue. Many biophysical techniques for estimating the diffusion coefficients are available (Beck and Schultz, 1972; Deen et al., 1981; Inamori et al., 1994; Peck et al., 1994; Bertram and Pernarowski, 1998; Gribbon and Hardingham, 1998; Papadopoulos et al., 2000; Olmsted et al., 2001), but only a few techniques are applicable for estimating the diffusion coefficient of immersion liquid in a human tissue. The majority of the methods are based on the fluorescence measurements or on the usage of radioactive labels for detecting matter flux. Unfortunately, the fluorescence-based methods cannot be used for determination of diffusion coefficients of nonfluorescent liquids. In the case of in vivo measurements, the methods based on the usage of radioactive labels are invasive. The optical method of estimating the diffusion coefficient of the immersion liquid in a tissue has been suggested by Tuchin et al. (1997). This method is based on the measurements of temporal changes of scattering properties of a tissue caused by dynamic refractive index matching. It can be used both for in vitro and in vivo measurements (Tuchin et al., 1997).

In this article we present the results of in vitro experiments on the human dura mater optical properties control by administration of osmotically active immersion agents such as aqueous glucose and mannitol solutions. The experiments show that such action makes dura mater more transparent. Based on temporal dependencies for tissue scattering coefficients obtained from time-dependent optical transmittance measurements, the diffusion coefficients of glucose and mannitol in human dura mater have been estimated.

MATERIALS AND METHODS

Physical properties and structure of human dura mater

Human dura mater is a protective membrane surrounding the brain. It has a fibrous structure. Typically, with age, the dura mater thickness changes from 0.3 to 0.8 mm. As an object for light propagation, this is a turbid, low-transparent medium in the visible and near-infrared spectral ranges. It consists mainly of conjunctive collagen fibrils packed in lamellar bundles that are immersed in an amorphous ground (interstitial) fluid (Zyablov et al., 1982; Baron and Mayorova, 1982).

Dura mater contains five layers: the external integumentary layer, the external elastin network, the collagen layer, the internal elastin network, and the internal endothelium integumentary layer (Zyablov et al., 1982). The collagen layer is the main layer of human dura mater, having >90% of its thickness. Therefore, its optical properties are mainly defined by the optical properties of the collagen layer. It is worth noting that those abrupt boundaries between upper, middle, and lower layers are absent. Thus, according to its structure, human dura mater is the closest to the sclera and skin dermis. The main difference between the structure of sclera and dura mater is the presence of the branched net of blood vessels in dura mater (Zyablov et al., 1982).

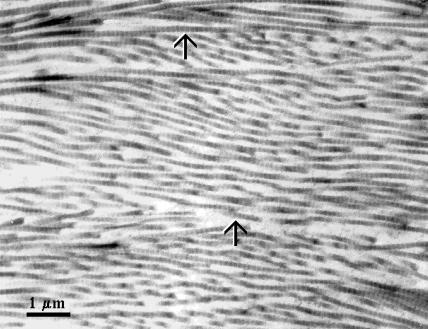
The average diameter of the dura mater collagen fibrils has been estimated using the data of electron microscopy presented by Spacek in the Atlas of Ultrastructural Neurocytology (Spacek, 2000) (see Fig. 1). The figure shows electron microphotography of rat dura mater with layers of densely packed collagen fibrils having an alternating orientation. The diameter of each fibril was measured in pixels and recalculated in nanometers using length of the scale bar presented in the figure. The procedure was made by a standard instrument of computer program Photoshop 6.0. Processing these data, we have found that the average diameter of the dura mater collagen fibrils is 100 ± 5 nm for the total number of 100 fibrils taken for calculations.

FIGURE 1.

FIGURE 1

Open in a new tab

Dura mater with layers of densely packed collagen fibrils having an alternating orientation. (Scale = 1 μm; Rat cerebral dura mater; Spacek, 2000.)

The collagen fibrils of dura mater are arranged in individual bundles in a parallel fashion. Moreover, within each bundle the groups of fibril are separated from each other by the large empty lacunae distributed randomly in space. Collagen bundles of dura mater have a wide range of widths and thicknesses similar to collagen bundles of scleral tissue or skin dermis. These ribbonlike structures are multipally cross-linked. They cross each other in all directions but remain parallel to the dura mater surface (Zyablov et al., 1982).

According to its composition, the dura mater interstitial fluid is very close to the interstitial fluid of skin dermis (Vertel, 2001) and constitutes a clear, colorless liquid containing proteins, proteoglycans, glycoproteins, and hyaluronic acid. Due to their glycosaminoglycan chains, these molecules concentrate negative charges. They are highly hydrophilic and have a propensity to attract ions, creating an osmotic imbalance that results in the glycosaminoglycan absorbing water from surrounding areas. This absorption helps to maintain the hydration of the matrix; the degree of hydration depends on the number of glycosaminoglycan chains and on the restriction placed on proteoglycans swelling by the surrounding collagen fibers (Culav et al., 1999). As the glycosaminoglycan chains attached to the proteoglycan core are negatively charged and extend from the core protein, a high charge density is created. This charge density induces an osmotic swelling pressure, resulting in the movement of water into the matrix. Therefore, the proteoglycans will tend to swell, but the tension-resistant collagen fibers and the bonding of the negatively charged glycosaminoglycan chains to regions of positive charge on collagen fibrils limits the expansion of proteoglycans to ∼20% of their swelling capacity (Wight et al., 1991).

To design the optical model of dura mater, in addition to form, size, and density of the scatterers (collagen fibrils) and the tissue thickness, we are able to have information on the refractive indices of the tissue components. Taking into account the similar structure of dura mater, eye sclera, and skin dermis, we can assume that the refractive index of the collagen fibrils (nc) and interstitial fluid (nI) of dura mater has the same wavelength dependence in the visible spectral range as for skin dermis and sclera (Bashkatov, 2002):

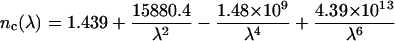graphic file with name M1.gif (1)

and

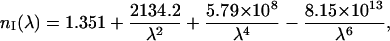graphic file with name M2.gif (2)

where λ is the wavelength, nm.

Method for in vitro estimation of diffusion coefficients of osmotically active immersion liquids in tissues

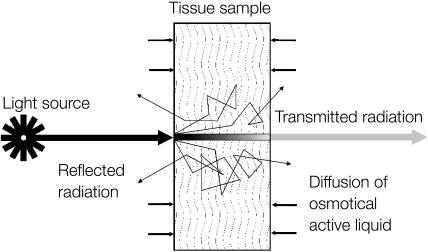
The method is based on the time-dependent measurement of collimated transmittance of tissue samples placed in immersion liquid. Schematic representation of diffusion of the osmotically active immersion liquid into the human dura mater sample and the geometry of light irradiation is presented in Fig. 2. The transport of an immersion liquid within the tissue can be described in the framework of the free diffusion model. We assume that the following approximations are valid for the transport process:

  1. Only concentration diffusion takes place; i.e., the exchange flux of osmotically active solution into the tissue and water from the tissue, at a certain point within the tissue sample, is proportional to the osmotically active substance concentration at this point.

  2. The diffusion coefficient is constant over the entire sample volume.

FIGURE 2.

FIGURE 2

Open in a new tab

Schematic representation of diffusion of the osmotically active immersion liquid into the human dura mater sample and the geometry of light irradiation.

Geometrically the tissue sample is presented as a plane-parallel slab with a finite thickness. Since the cross-section of the experimental samples was 10 × 10 mm, which is >10× bigger than the thickness of the samples, the one-dimensional diffusion problem has been solved.

The one-dimensional diffusion equation of the immersion liquid transport has the form

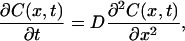graphic file with name M3.gif (3)

where C(x,t) is the immersion liquid concentration, g/ml; D is the diffusion coefficient, cm2/s; t is time, in seconds, s; and x is the spatial coordinate, cm.

We also suppose that penetration of immersion liquid into a tissue sample does not change the immersion liquid concentration in the cuvette. This requirement has been met in the experiments since the immersion liquid volume in the cuvette was ∼3000 mm3 and the volume of the dura mater samples was <100 mm3. The corresponding boundary conditions are

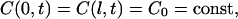graphic file with name M4.gif (4)

where C0 is the concentration of immersion liquid in the external volume (i.e., in the cuvette), g/ml; l is the thickness of the sample, cm.

The initial conditions correspond to the absence of glucose or mannitol inside the dura mater tissue before its incubation in the immersion liquid,

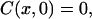graphic file with name M5.gif (5)

for all inner points of the tissue sample.

Solution of Eq. 3 for a slab with a thickness l at the moment t with boundary (Eq. 4) and initial (Eq. 5) conditions has the form (Kotyk and Janacek, 1977)

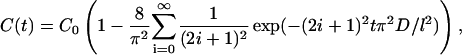graphic file with name M6.gif (6)

where C(t) is the volume-averaged concentration of osmotically active immersion liquid within tissue sample.

In a first-order approximation, Eq. 6 is reduced to the form

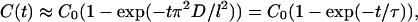graphic file with name M7.gif (7)

where τ = l2/(π2D) is the characteristic diffusion time. This approximation gives results close to the exact solution (Eq. 6) in the limits of experimental errors, but significantly reduces calculation time, especially for inverse problem solving.

The temporal dependence of the refractive index of the interstitial fluid can be derived using the law of Gladstone and Dale, which states that, for a multicomponent system, the resulting value of the refractive index represents an average of the refractive indices of the components related to their volume fractions (Freund et al., 1986; Leonard and Meek, 1997). Such dependence is defined as

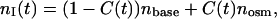graphic file with name M8.gif (8)

where nbase is the refractive index of the dura mater interstitial fluid at the initial moment defined by Eq. 2, and nosm is the refractive index of the glucose or mannitol solutions. Wavelength dependence of aqueous glucose solution can be estimated as nosm(λ) = nw + 0.1515 C, where nw(λ) is the wavelength dependence of the refractive index of water, and C is the glucose concentration, g/ml (Maier et al., 1994). The wavelength dependence of the refractive index of water has been presented by Kohl et al. (1995) as

graphic file with name M9.gif

The optical model of dura mater can be presented as a slab with a thickness l containing scatterers (collagen fibrils)—thin dielectric cylinders with an average diameter of 100 nm, which is considerably smaller than their lengths. The wavelength dependence of the refractive index of these cylinders can be described by Eq. 1. These cylinders are located in planes that are in parallel to the sample surfaces, but within each plane their orientations are random. These simplifications reduce considerably the difficulties in the description of the light scattering by dura mater. For a thin dielectric cylinder in the Rayleigh-Gans approximation of the Mie scattering theory the scattering cross-section σs(t) for unpolarized incident light is given by (Cox et al., 1970; Bohren and Huffman, 1983)

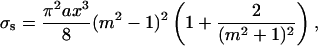graphic file with name M10.gif (9)

where m = nc/nI is the relative refractive index of the scattering particle, i.e., ratio of the refractive indices of the scatterers and the ground materials (i.e., interstitial fluid), and x is the dimensionless relative scatterers size, which is determined as x = 2πanI/λ, where λ is the wavelength and a is the cylinder radius.

As a first approximation, we assume that during the interaction of the immersion liquid with a tissue, the size of the scatterers does not change. This assumption is confirmed by the results presented by Huang and Meek (1999) for scleral and corneal tissue. In this case, all changes in the tissue scattering are connected with the changes of the refractive index of the interstitial fluid described by Eq. 8. The increase of the refractive index of the interstitial fluid provides the decrease of the relative refractive index of the scattering particles and, consequently, the decrease of the scattering coefficient. For noninteracting particles the scattering coefficient of a tissue is defined by the equation

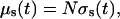graphic file with name M11.gif (10)

where μs(t) is the tissue scattering coefficient, N is number of the scattering particles (fibrils) per unit area, and σs(t) is the time-dependent cross-section of scattering (Eq. 9). The number of the scattering particles per unit area can be estimated as N = φ/(πa2) (Cox et al., 1970), where φ is the volume fraction of the tissue scatterers. For fibrous tissues φ is usually equal to 0.3 (Tuchin et al., 1997; Schmitt and Kumar, 1998; Meglinski and Matcher, 2002).

To take into account interparticle correlation effects which are important for tissues with densely packed scattering particles (such as dura mater), the scattering cross-section has to be corrected by the packing factor of the scattering particles, (1 − φ)3/(1 + φ) (Schmitt and Kumar, 1998). Thus, Eq. 10 has to be rewritten as

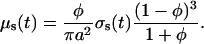graphic file with name M12.gif (11)

Since glucose and mannitol solutions have pH values different from the pH of the interstitial fluid of the native tissue, the immersion of tissue samples into the solutions produces the swelling process. The temporal dependence of the dura mater sample volume can be described assuming that increasing tissue volume is the result of additional absorption of osmotically active liquid (Huang and Meek, 1999). Since we assume that at swelling the size of the tissue scatterers does not change, the increase of tissue volume is associated with increase of the distance between tissue fibrils.

The temporal dependence of the swelling index H(t) of the tissue sample can be calculated from weight measurements as

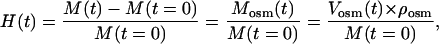graphic file with name M13.gif (12)

where M(t) is mass of the tissue sample in different moments in the swelling process, Mosm(t), Vosm(t), and ρosm(t) are mass, volume, and density of osmotically active liquid absorbed by the tissue sample, respectively. Let V(t) represent the volume of swelling tissue, then

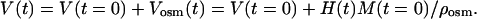graphic file with name M14.gif (13)

Since the tissue swelling is connected with diffusion of osmotically active liquid into the tissue sample, the temporal dependence of swelling index can be approximated by the following phenomenological expression, which is very close to Eq. 7, describing the process of osmotically active liquid penetration into the tissue

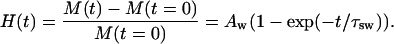graphic file with name M15.gif (14)

Therefore, the temporal dependence of tissue volume during osmotically active liquid action (Eq. 13) can be presented as

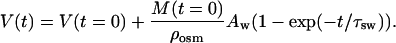graphic file with name M16.gif (15)

At the same time, Eq. 15 can be rewritten in a simpler form, i.e., as

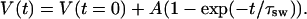graphic file with name M17.gif (16)

In this case, Aw, A, and τsw are some phenomenological constants describing swelling process caused by glucose or mannitol action. Volumetric changes of a tissue sample is mostly due to changes of its thickness l(t), which can be expressed as

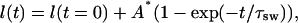graphic file with name M18.gif (17)

where A* = A/S, and S is the tissue sample area. Constants A and τsw can be obtained both from direct measurements of thickness or volume of tissue samples and from time-dependent weight measurements. In this study to estimate these constants, we used the time-dependent weight measurements of the dura mater tissue samples placed into glucose and mannitol solutions.

By changing volume of a tissue the swelling produces the change of the volume fraction of the tissue scatterers, and thus, the change of the scatterers' packing factor and the numerical concentration, i.e., the number of the scattering particles per unit area (see Eqs. 10 and 11). Taking into account Eq. 16, the temporal dependence of the volume fraction of the tissue scatterers can be described as

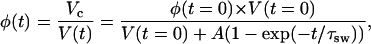graphic file with name M19.gif (18)

where Vc is the volume of the tissue sample scatterers.

The collimated optical transmittance of the dura mater sample impregnated by an immersion solution can be defined as

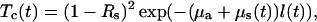graphic file with name M20.gif (19)

where Rs is the specular reflectance and μa is the absorption coefficient. The time-dependent scattering coefficient μs(t) and thickness l(t) are defined by Eqs. 11 and 17, respectively. In the visible spectral range, the absorption coefficient of a tissue is much less than the scattering coefficient except for the blood absorption bands. Since both glucose and mannitol do not have strong absorption bands within the wavelength range investigated, the changes of the dura mater collimated transmittance can be described only by the behavior of the μs.

This set of equations represents the direct problem, i.e., describes the temporal evaluation of the collimated transmittance of a tissue sample dependent on glucose or mannitol concentration in interstitial fluid. On the basis of measurement of the temporal evolution of the collimated transmittance, the reconstruction of the diffusion coefficient of the glucose or mannitol in dura mater has been carried out. The inverse problem solution has been obtained by minimization of the target function as

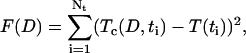graphic file with name M21.gif (20)

where Tc (D,t) and 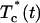Inline graphic are the calculated and experimental values of the time-dependent collimated transmittance, respectively, and Nt is the number of time points obtained at registration of the temporal dynamics of the collimated transmittance. To minimize the target function the Levenberg-Marquardt nonlinear least-squares-fitting algorithm described in detail by Press et al. (1992) has been used. Iteration procedure repeats until experimental and calculated data are matched. As a termination condition of the iteration process, we have used the expression

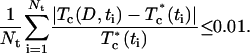graphic file with name M23.gif

Experimental setups

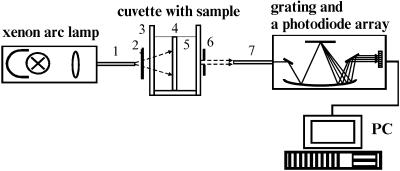
All experiments have been performed in vitro with the human dura mater at room temperature (∼20°C). Measurements of the light collimated transmittance spectra have been performed using multichannel optic spectrometer LESA-6med (BioSpec, Russia). The scheme of the experimental setup is shown in Fig. 3. As a light source, a 250-W xenon arc lamp with filtering of the radiation in the spectral range from 400 to 700 nm has been used in the measurements.

FIGURE 3.

FIGURE 3

Open in a new tab

Experimental setup for measurements of the collimated transmittance spectra: (1) optical irradiating fiber; (2) neutral filter; (3) cuvette; (4) human dura mater sample; (5) aqueous glucose or mannitol solution; (6) the 0.5-mm diaphragm; and (7) optical receiving fiber.

During the light transmission measurements, the glass cuvette with the dura mater sample has been placed between two optical fibers with a core diameter of 400 μm and a numerical aperture of 0.2. One fiber transmitted the excitation radiation to the sample, and another fiber collected the transmitted radiation. The 0.5-mm diaphragm placed 100-mm apart from the tip of the receiving fiber has been used to provide collimated transmittance measurements. Neutral filter has been used to attenuate the incident radiation. The measurements have been performed every 30 s during 15 min for each dura mater sample. Experimental error does not exceed 5% in the spectral range from 500 to 700 nm, or 10% in the spectral range from 400 to 500 nm.

Study of swelling of the dura mater samples has been performed by means of the time-dependent weight measurements; the torsion scales with the precision of 1 mg has been used. The tissue samples have been immersed into a cuvette with aqueous glucose or mannitol solution. Every 2 min during 40 min, each sample has been taken out from the solution and weighed. A careful removal of the solution from the sample surface before weighing has been provided.

The dura mater sample preparation

The human dura mater samples have been obtained by autopsy within 24 h post mortem. The dura mater samples were kept under temperature −12°C. Before experiments dura mater has been unfrozen and cut into pieces with the area ∼10 × 10 mm2. The thickness of each human dura mater sample has been measured at initial moment with a micrometer in 10 points over the sample surface and averaged. The human dura mater samples have been fixed on a plastic plate with a square aperture 5 × 5 mm2 (needed for effective impregnation by glucose or mannitol via both surfaces of the sample) and have been placed in a 5-ml cuvette filled with the glucose or mannitol solution. For the optical clearing measurements, we have used six samples of the human dura mater. Three tissue samples (thickness of the samples was 0.52 ± 0.08 mm, 0.43 ± 0.05 mm, and 0.65 ± 0.09 mm) have been used for optical clearing under action of the mannitol solution and three tissue samples (thickness of the samples was 0.52 ± 0.11 mm, 0.59 ± 0.06 mm, and 0.56 ± 0.07 mm) have been used for optical clearing under action of the glucose solution. Time-dependent weight measurements have been carried out with four tissue samples. Two samples have been used for investigation of dura mater swelling caused by the mannitol solution and two samples were used for investigation of dura mater swelling caused by the solution of glucose. The initial weight of each sample was ∼100 mg.

The osmotically active immersion liquid preparation

As immersion liquids, aqueous glucose solution with concentration 0.2 g/ml and aqueous mannitol solution 0.16 g/ml have been used. Aqueous glucose solution has been prepared using powderlike glucose monohydrate (ChemMed, Russia) and aqueous mannitol solution has been prepared using powderlike D-mannitol (Serva, New York). The densities of the glucose and mannitol solutions have been measured as 1.07 g/ml and 1.06 g/ml, respectively. The refractive indices of the glucose and mannitol solutions have been measured by Abbe refractometer at wavelength 589 nm as 1.363 and 1.357, respectively, and pH of the solutions have been measured by pH-meter HANNA (Portugal) as 6.05 for mannitol solution and as 5.99 for glucose solution.

RESULTS AND DISCUSSION

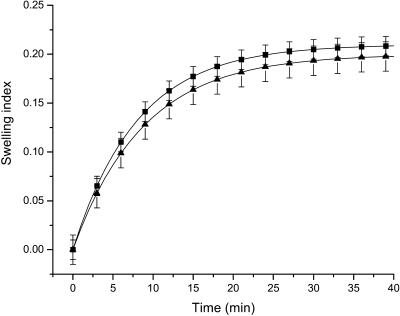
Since the developed algorithm for estimation of diffusion coefficients of osmotically active immersion liquids in tissues requires the knowledge of the tissue volume changes under action of these liquids, we have investigated the temporal dependence of the dura mater swelling index using the time-dependent weight measurements. Fig. 4 shows the temporal dependence of the swelling index of the tissue samples placed in glucose and mannitol solutions. From Fig. 4 it is seen that the mannitol solution produces more swelling of the dura mater sample in comparison with the glucose solution. At the same time, the difference between these dependencies is insignificant, because pH values of these solutions are very close to each other. The difference can be connected with the structural properties of the glucose and mannitol molecules, as the mannitol is a polyhydric alcohol, whereas the glucose is a monosaccharide. For quantitative assessment of the time-dependent weight measurements, the exponential association (Eq. 14) has been used. By least-squares method, the following parameters of the swelling index have been obtained. For the tissue samples immersed in the mannitol solution, we have estimated parameter Aw as 0.21 ± 0.1, and the parameter characterizing the swelling rate, i.e., τsw, as 484 ± 72 s. For the dura mater samples immersed in glucose solution, we have estimated parameter Aw as 0.20 ± 0.2 and τsw as 528 ± 160 s.

FIGURE 4.

FIGURE 4

Open in a new tab

The time-dependent swelling index of different dura mater samples impregnated with the aqueous glucose and mannitol solutions. Symbols correspond to the averaged experimental data and vertical lines correspond to the standard deviation. The squares correspond to the dura mater swelling index under action of the mannitol solution and the triangles correspond to the dura mater swelling index under action of the glucose solution.

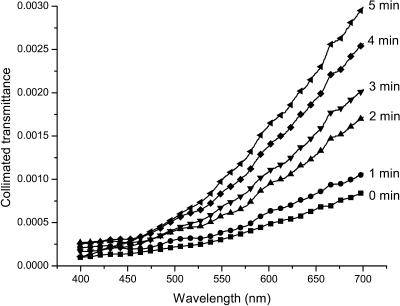
To understand the mechanisms of the optical clearing of dura mater we have measured the collimated transmittance spectra concurrently with administration of the glucose or mannitol solutions. Figs. 5 and 6 illustrate the dynamics of these transmittance spectra. It is easily seen that the untreated dura mater is poorly transparent for the visible light. Glucose and mannitol administration makes this tissue more transparent, increasing the collimated transmittance in the spectral range from 650 to 700 nm, on average, by ∼2.5-fold under action of the mannitol solution (see Fig. 5), and by ∼fivefold under action of the glucose solution (see Fig. 6) at t = 5 min.

FIGURE 5.

FIGURE 5

Open in a new tab

The collimated transmittance spectra of the human dura mater sample measured concurrently with administration of mannitol solution at different time intervals. Experimental error does not exceed 5% in the spectral range from 500 to 700 nm, or 10% in the spectral range from 400 to 500 nm.

FIGURE 6.

FIGURE 6

Open in a new tab

The collimated transmittance spectra of the human dura mater sample measured concurrently with administration of glucose solution at different time intervals. Experimental error does not exceed 5% in the spectral range from 500 to 700 nm, or 10% in the spectral range from 400 to 500 nm.

The blood volume and hemoglobin oxygenation monitoring is very important for cerebral diagnostics and therapy (Koizumi et al., 1999; Benaron et al., 2000; Hueber et al., 2001). The increase of light penetration depth at tissue clearing allows one to acquire more information from blood vessels located in the deep brain layers. In the visible, three spectral bands corresponding to blood absorption can be indicated. There is the Soret band with maximum at 415 nm, the α-band with maximum at 542 nm and the β-band with maximum at 577 nm of oxyhemoglobin absorption (Prahl, 1999). Our experiments have shown (see Figs. 5 and 6) that, in the spectral ranges corresponding to α- and β-bands of the blood absorption, the mannitol solution produces increase of the dura mater collimated transmittance by ∼1.8- and twofold, and the glucose solution by ∼3.5- and fourfold, respectively.

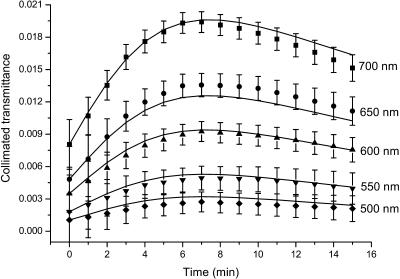
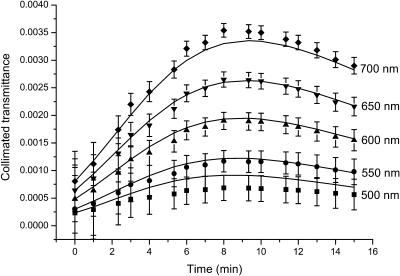
Figs. 7 and 8 present the time-dependent collimated transmittance of the dura mater samples measured at different wavelengths concurrently with administration of the mannitol and glucose solutions, respectively. These temporal dependencies show that osmotically active immersion liquids such as aqueous glucose and mannitol solutions are appropriate for the control of the dura mater optical properties. It is well seen that the action of all solutions produces the increase of the collimated transmittance of the tissue samples. From Figs. 7 and 8, a good matching is seen between experimental data (symbols) and approximating dependencies (solid lines) calculated in the framework of the presented model (Eqs. 3–19). The difference between experimental and calculated data can be explained partially by inaccuracy of the measurements and simplicity of the used model, since the diffusion coefficient can change a little during penetration of the clearing agent in the tissue samples. Moreover, the dura mater samples are volume-inhomogeneous.

FIGURE 7.

FIGURE 7

Open in a new tab

The time-dependent collimated transmittance of the human dura mater sample (initial thickness of sample, 0.043 cm) measured at different wavelengths concurrently with administration of mannitol solution. The symbols correspond to the experimental data. The error bars show the standard deviation values. The solid lines correspond to the data calculated using the developed model (Eqs. 11, 17, and 19).

FIGURE 8.

FIGURE 8

Open in a new tab

The time-dependent collimated transmittance of the human dura mater sample (initial thickness of the sample is 0.059 cm) measured at different wavelengths concurrently with administration of glucose solution. The symbols correspond to the experimental data. The error bars show the standard deviation values. The solid lines correspond to the data calculated using the developed model (Eqs. 11, 17, and 19).

We have to underline that the clearing process has two stages (see Figs. 7 and 8). At the beginning of the process the increase of the transmittance is seen, which is followed by saturation and even the decrease of the transmittance. Two competing processes take place. One of them is optical immersion—the matching of refractive indices of the tissue scatterers and the interstitial fluid that causes the decrease of the tissue scattering and, therefore, the increase of the collimated transmittance. Another one is the tissue swelling that causes the increase of the tissue thickness and, therefore, the decrease of the transmittance. However the present experimental data show that the matching effect prevails, especially at the first stage of the optical clearing. It is well-confirmed by the characteristic time of the swelling (484 ± 72 s and 528 ± 160 s for the mannitol and glucose solutions, respectively) that is longer than the diffusion time. The diffusion time τ = l2/(π2D) has been calculated using glucose and mannitol diffusion coefficient values (see below). The mannitol and glucose diffusion times are 153 ± 29 s and 221 ± 23 s, respectively. It is worth noting that swelling, caused by immersion agent impregnation, is not usually very important for in vivo tissue optical clearing since a living tissue has a high homeostasis degree; however, for in vitro measurements, this stage should be taken into account for the corrected determination of diffusion coefficient. Typically, the saturation of optical transmittance (reflectance) with time for in vivo measurements is caused by immersion liquid diffusion to the surrounding tissues, and it is difficult to provide a continuous supply of immersion liquid to the target tissue (Bashkatov et al., 1999, 2000b, 2001, 2002a,b; Tuchin et al., 2001).

The mannitol and glucose diffusion coefficients in the human dura mater tissue have been estimated using the experimental temporal dependence of the collimated transmittance (see Figs. 7 and 8) and inverse algorithm described by Eqs. 3–20. Calculations have been simultaneously performed for 10 wavelengths, and the obtained values of the diffusion coefficients have been averaged. The diffusion coefficients of both mannitol and glucose have been estimated as (1.31 ± 0.41) × 10−6 cm2/s, and as (1.63 ± 0.29) × 10−6 cm2/s, respectively. It is well-known that diffusion coefficient is increased with the increase of temperature of the solution. The temperature dependence has been presented as 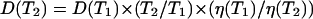Inline graphic (Grigoriev and Meylikhov, 1991), where D(T) is the diffusion coefficient at temperature T, and η(T) is the viscosity of the solution. Extrapolating the obtained values of the diffusion coefficients to the physiological temperature, we have found that the mean values of diffusion coefficient at 37°C are 2.59 ± 10−6 cm2/s and 2.08 × 10−6 cm2/s for glucose and mannitol, respectively. The estimated diffusion coefficient for glucose is very close to the diffusion coefficient measured in vivo for the human skin, which is (2.56 ± 0.13) × 10−6 cm2/s (Tuchin et al., 2001).

It was expected that diffusion coefficients measured for tissues are less than those for solutions (Papadopoulos et al., 2000). For example, Peck et al. (1994), using two-chamber side-by-side diffusion cells, have found DM = (9.03 ± 0.3) × 10−6 cm2/s for mannitol diffusion in phosphate-buffered saline at temperature 37°C, and under the same conditions, for sucrose DS = 7.45 × 10−6 cm2/s (Inamori et al., 1994) and for raffinase DR = (5.72 ± 0.1) × 10−6 cm2/s (Peck et al., 1994). The diffusion coefficients of glucose and mannitol in water are 5.2 × 10−6 cm2/s (at 15°C) and 6.05 × 10−6 cm2/s (at 20°C), respectively (Grigoriev and Meylikhov, 1991). At 37°C the diffusion coefficient of glucose in water is 9.59 × 10−6 cm2/s and the diffusion coefficient of mannitol in water is 9.61 × 10−6 cm2/s; these values are well-matched with the data presented by Peck et al. (1994).

The difference between the diffusion coefficients of these substances in water and in tissue is connected with the structure and composition of dura mater. As it has been shown, the dura mater interstitial fluid (i.e., the interstitial matrix) contains the proteins, proteoglycans, and glycoproteins that constitute the polyelectrolyte gel (Huang and Meek, 1999). The proteins (collagen and elastin fibrils) are the base of the interstitial matrix (Culav et al., 1999). The collagen and elastin fibrils are the hindrance factor for molecules diffusing in the interstitial fluid. Two major mechanisms can hinder rapid diffusion of the molecules through an interstitial matrix. Particles can stick to collagen fibrils or they can be hindered by the size of the mesh spacing between the fibrils (Olmsted et al., 2001). Moreover, since the glucose and mannitol are polar molecules (Peck et al., 1994), their diffusion can be hindered inasmuch as the proteins, glycoproteins, and glycosaminoglycans contained in the interstitial fluid are excellent space filters, which provide selective barriers to the diffusion of the polar molecules. Thus, the penetration of the glucose and mannitol molecules into tissue is restricted.

The difference between the diffusion coefficients obtained in the article and the ones presented by the other authors for solutions is explained mostly by the structural properties of the investigated tissue. The difference can also be due to distinctions in experimental and calculation methods used for estimation of the diffusion coefficients.

CONCLUSIONS

The experimental results presented in this article have shown that controlling the optical properties of tissues is a useful method to increase the ability of light penetration into a tissue and, consequently, to improve the optical probing depth. The results are applicable to numerous laser therapeutic and optical diagnostic and imaging techniques. For example, at laser treatment of brain blood vessels, the rapid attenuation and broadening of the incident beam by light scattering is often a problem. Optical clearing will allow laser light to be focused directly on a blood vessel. Smaller laser spot size will reduce collateral damage. Also, reducing in scattering and subsequent increasing in light penetration depth will affect the precise dosimetry for laser procedures. Changes of the collimated transmittance spectra indicate that administration of the osmotically active immersion liquids into a fibrous tissue allows one to control its optical characteristics effectively, and therefore to get more precise spectroscopic information, which is less disturbed by tissue turbidity. The same is valid for tissue optical imaging, when at reduced scattering of surrounding tissue impregnated by the immersion agent, blood vessels, tumors, and other tissue inhomogeneities can be visualized with a higher contrast.

Based on temporal dependence of the collimated transmittance of the human dura mater samples and the model presented, glucose diffusion coefficient in the dura mater interstitial fluid at 20°C has been estimated as (1.63 ± 0.29) × 10−6 cm2/s and mannitol diffusion coefficient as (1.31 ± 0.41) × 10−6 cm2/s. For physiological temperature, ∼37°C, the diffusion coefficient for glucose may have a value of 2.59 × 10−6 cm2/s, and for mannitol, 2.08 × 10−6 cm2/s. For glucose, this value is very close to that measured, in vivo, in the human skin dermis (Tuchin et al., 2001).

The presented results can be used for developing mathematical models describing the interaction between osmotically active immersion liquids and a living tissue.

Acknowledgments

The authors thank Dr. S. V. Eremina (Department of English and Intercultural Communication of Saratov State University) for the help in manuscript translation to English.

The research described in this publication has been made possible, in part, by award REC-006 of the United States Civilian Research and Development Foundation for the Independent States of the Former Soviet Union; by award of the President of Russian Federation “Leading Scientific Schools” grant 25-2003-2; by contract 40-018-1-1-1314 of the Ministry of Industry, Science and Technologies of the Russian Federation; and by the Ministry of Education of the Russian Federation.

References

  1. Bashkatov, A. N., V. V. Tuchin, E. A. Genina, Yu. P. Sinichkin, N. A. Lakodina, and V. I. Kochubey. 1999. The human sclera dynamic spectra: in vitro and in vivo measurements. Proc. SPIE. 3591:311–319. [Google Scholar]
  2. Bashkatov, A. N., E. A. Genina, V. I. Kochubey, N. A. Lakodina, and V. V. Tuchin. 2000a. Osmotical liquid diffusion within sclera. Proc. SPIE. 3908:266–276. [Google Scholar]
  3. Bashkatov, A. N., E. A. Genina, I. V. Korovina, V. I. Kochubey, Yu. P. Sinichkin, and V. V. Tuchin. 2000b. In vivo and in vitro study of control of rat skin optical properties by acting of osmotical liquid. Proc. SPIE. 4224:300–311. [Google Scholar]
  4. Bashkatov, A. N., E. A. Genina, I. V. Korovina, Yu. P. Sinichkin, O. V. Novikova, and V. V. Tuchin. 2001. In vivo and in vitro study of control of rat skin optical properties by action of 40% glucose solution. Proc. SPIE. 4241:223–230. [Google Scholar]
  5. Bashkatov, A. N., E. A. Genina, Yu. P. Sinichkin, and V. V. Tuchin. 2002a. The influence of glycerol on the transport of light in the skin. Proc. SPIE. 4623:144–152. [Google Scholar]
  6. Bashkatov, A. N., E. A. Genina, and V. V. Tuchin. 2002b. Optical immersion as a tool for tissue scattering properties control. In Perspectives in Engineering Optics. K. Singh, and V. K. Rastogi, editors. Anita Publications, New Delhi, India. 313–334.
  7. Bashkatov, A. N. 2002. Control of tissue optical properties by means of osmotically active immersion liquids. Saratov State University, Saratov, Russia. Ph.D. thesis.
  8. Baron, M. A., and N. A. Mayorova. 1982. Atlas of Functional Stereomorphology of Brain Membranes. Medicine, Moscow.
  9. Beauvoit, B., T. Kitai, and B. Chance. 1994. Contribution of the mitochondrial compartment to the optical properties of rat liver: a theoretical and practical approach. Biophys. J. 67:2501–2510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Beck, R. E., and J. S. Schultz. 1972. Hindrance of solute diffusion within membranes as measured with microporous membranes of known pore geometry. Biochem. Biophys. Acta. 255:272–303. [DOI] [PubMed] [Google Scholar]
  11. Benaron, D. A., S. R. Hintz, A. Villringer, D. Boas, A. Kleinschmidt, J. Frahm, C. Hirth, H. Obrig, J. C. van Houten, E. L. Kermit, W.-F. Cheong, and D. K. Stevenson. 2000. Noninvasive functional imaging of human brain using light. J. Cerebr. Blood Flow Metabol. 20:469–477. [DOI] [PubMed] [Google Scholar]
  12. Bertram, R., and M. Pernarowski. 1998. Glucose diffusion in pancreatic islets of Langerhans. Biophys. J. 74:1722–1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bohren, C. F., and D. R. Huffman. 1983. Absorption and Scattering of Light by Small Particles. Wiley, New York.
  14. Bornhop, D. J., C. H. Contag, K. Licha, and C. J. Murphy. 2001. Advances in contrast agents, reporters, and detection. J. Biomed. Opt. 6:106–110. [DOI] [PubMed] [Google Scholar]
  15. Bruulsema, J. T., J. E. Hayward, T. J. Farrell, M. S. Patterson, L. Heinemann, M. Berger, T. Koschinsky, J. Sandahl-Christiansen, H. Orskov, M. Essenpreis, G. Schmelzeisen-Redeker, and D. Bocker. 1997. Correlation between blood glucose concentration in diabetics and noninvasively measured tissue optical scattering coefficient. Opt. Lett. 22:190–192. [DOI] [PubMed] [Google Scholar]
  16. Chan, E., T. Menovsky, and A. J. Welch. 1996a. Effects of cryogenic grinding on soft-tissue optical properties. Appl. Opt. 35:4526–4532. [DOI] [PubMed] [Google Scholar]
  17. Chan, E. K., B. Sorg, D. Protsenko, M. O'Neil, M. Motamedi, and A. J. Welch. 1996b. Effects of compression on soft tissue optical properties. IEEE J. Quantum Electron. 2:943–950. [Google Scholar]
  18. Chance, B., H. Liu, T. Kitai, and Y. Zhang. 1995. Effects of solutes on optical properties of biological materials: models, cells, and tissues. Anal. Biochem. 227:351–362. [DOI] [PubMed] [Google Scholar]
  19. Chance, B., A. Mayevsky, B. Guan, and Y. Zhang. 1997. Hypoxia/ischemia triggers a light scattering event in rat brain. In Oxygen Transport to Tissue XIX. D. K. Harrison and D. T. Delpy, editors. Plenum Press, New York. 457–467.
  20. Cilesiz, I. F., and A. J. Welch. 1993. Light dosimetry: effects of dehydration and thermal damage on the optical properties of the human aorta. Appl. Opt. 32:477–487. [DOI] [PubMed] [Google Scholar]
  21. Cox, J. L., R. A. Farrell, R. W. Hart, and M. E. Langham. 1970. The transparency of the mammalian cornea. J. Physiol. 210:601–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Culav, E. M., C. H. Clark, and M. J. Merrilees. 1999. Connective tissue: matrix composition and its relevance to physical therapy. Phys. Ther. 79:308–319. [PubMed] [Google Scholar]
  23. Deen, W. M., M. P. Bohrer, and N. B. Epstein. 1981. Effect of molecular size and configuration on diffusion in microporous membranes. Amer. Inst. Chem. Eng. J. 27:952–959. [Google Scholar]
  24. Demos, S. G., W. B. Wang, and R. R. Alfano. 1998. Imaging objects hidden in scattering media with fluorescence polarization preservation of contrast agents. Appl. Opt. 37:792–797. [DOI] [PubMed] [Google Scholar]
  25. Freund, D. E., R. L. McCally, and R. A. Farrell. 1986. Effects of fibril orientations on light scattering in the cornea. J. Opt. Soc. Am. A. 3:1970–1982. [DOI] [PubMed] [Google Scholar]
  26. Genina, E. A., A. N. Bashkatov, Y. P. Sinichkin, V. I. Kochubey, N. A. Lakodina, G. B. Altshuler, and V. V. Tuchin. 2002. In vitro and in vivo study of dye diffusion into the human skin and hair follicles. J. Biomed. Opt. 7:471–477. [DOI] [PubMed] [Google Scholar]
  27. Gribbon, P., and T. E. Hardingham. 1998. Macromolecular diffusion of biological polymers measured by confocal fluorescence recovery after photobleaching. Biophys. J. 75:1032–1039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Grigoriev, I. S., and E. Z. Meylikhov (editors). 1991. Physical Values Handbook. EnergoAtomIzdat, Moscow.
  29. Huang, Y., and K. M. Meek. 1999. Swelling studies on the cornea and sclera: the effects of pH and ionic strength. Biophys. J. 77:1655–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hueber, D. M., M. A. Franceschini, H. Y. Ma, Q. Zhang, J. R. Ballesteros, S. Fantini, D. Wallace, V. Ntziachristos, and B. Chance. 2001. Non-invasive and quantitative near-infrared haemoglobin spectrometry in the piglet brain during hypoxic stress, using a frequency-domain multidistance instrument. Phys. Med. Biol. 46:41–62. [DOI] [PubMed] [Google Scholar]
  31. Inamori, T., A. H. Ghanem, W. I. Higuchi, and V. Srinivasan. 1994. Macromolecule transport in and effective pore size of ethanol pretreated human epidermal membrane. Int. J. Pharmaceut. 105:113–123. [Google Scholar]
  32. Kohl, M., M. Esseupreis, and M. Cope. 1995. The influence of glucose concentration upon the transport of light in tissue-simulating phantoms. Phys. Med. Biol. 40:1267–1287. [DOI] [PubMed] [Google Scholar]
  33. Koizumi, H., Y. Yamashita, A. Maki, T. Yamamoto, Y. Ito, H. Itagaki, and R. Kennan. 1999. Higher-order brain function analysis by trans-cranial dynamic near-infrared spectroscopy imaging. J. Biomed. Opt. 4:403–413. [DOI] [PubMed] [Google Scholar]
  34. Kotyk, A., and K. Janacek. 1977. Membrane Transport: An Interdisciplinary Approach. Plenum Press, New York. [PubMed]
  35. Leonard, D. W., and K. M. Meek. 1997. Refractive indices of the collagen fibrils and extrafibrillar material of the corneal stroma. Biophys. J. 72:1382–1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Liu, H., B. Beauvoit, M. Kimura, and B. Chance. 1996. Dependence of tissue optical properties on solute-induced changes in refractive index and osmolarity. J. Biomed. Opt. 1:200–211. [DOI] [PubMed] [Google Scholar]
  37. Maier, J. S., S. A. Walker, S. Fantini, M. A. Franceschini, and E. Gratton. 1994. Possible correlation between blood glucose concentration and the reduced scattering coefficient of tissues in the near infrared. Opt. Lett. 19:2062–2064. [DOI] [PubMed] [Google Scholar]
  38. Meglinski, I. V., and S. J. Matcher. 2002. Quantitative assessment of skin layers absorption and skin reflectance spectra simulation in visible and near-infrared spectral region. Physiol. Meas. 23:741–753. [DOI] [PubMed] [Google Scholar]
  39. Olmsted, S. S., J. L. Padgett, A. I. Yudin, K. J. Whaley, T. R. Moench, and R. A. Cone. 2001. Diffusion of macromolecules and virus-like particles in human cervical mucus. Biophys. J. 81:1930–1937. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Papadopoulos, S., K. D. Jurgens, and G. Gros. 2000. Protein diffusion in living skeletal muscle fibers: dependence on protein size, fiber type, and contraction. Biophys. J. 79:2084–2094. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Peck, K. D., A. H. Ghanem, and W. I. Higuchi. 1994. Hindered diffusion of polar molecules through and effective pore radii estimates of intact and ethanol treated human epidermal membrane. Pharm. Res. 11:1306–1314. [DOI] [PubMed] [Google Scholar]
  42. Prahl, S. A. 1999. Optical Absorption of Hemoglobin. http://www.omlc.ogi.edu/spectra/.
  43. Press, W. H., S. A. Tuekolsky, W. T. Vettering, and B. P. Flannery. 1992. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
  44. Schmitt, J. M., and G. Kumar. 1998. Optical scattering properties of soft tissue: a discrete particle model. Appl. Opt. 37:2788–2797. [DOI] [PubMed] [Google Scholar]
  45. Spacek, J. 2000. Atlas of Ultrastructural Neurocytology. http://synapses.bu.edu/atlas/.
  46. Tuchin, V. V., I. L. Maksimova, D. A. Zimnyakov, I. L. Kon, A. H. Mavlutov, and A. A. Mishin. 1997. Light propagation in tissues with controlled optical properties. J. Biomed. Opt. 2:401–417. [DOI] [PubMed] [Google Scholar]
  47. Tuchin, V. V. 1999. Coherent optical techniques for the analysis of tissue structure and dynamics. J. Biomed. Opt. 4:106–124. [DOI] [PubMed] [Google Scholar]
  48. Tuchin, V. V. 2000. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis. SPIE Press, Bellingham, WA.
  49. Tuchin, V. V., A. N. Bashkatov, E. A. Genina, Yu. P. Sinichkin, N. A. Lakodina. 2001. In vivo investigation of the immersion-liquid-induced human skin clearing dynamics. Tech. Physics Lett. 27:489–490. [Google Scholar]
  50. Vargas, G., E. K. Chan, J. K. Barton, H. G. Rylander III, and A. J. Welch. 1999. Use of an agent to reduce scattering in skin. Lasers Surg. Med. 24:133–141. [DOI] [PubMed] [Google Scholar]
  51. Vargas, G., K. F. Chan, S. L. Thomsen, and A. J. Welch. 2001. Use of osmotically active agents to alter optical properties of tissue: effects on the detected fluorescence signal measured through skin. Lasers Surg. Med. 29:213–220. [DOI] [PubMed] [Google Scholar]
  52. Vargas, G., A. Readinger, S. S. Dozier, and A. J. Welch. 2003. Morphological changes in blood vessels produced by hyperosmotic agents and measured by optical coherence tomography. Photochem. Photobiol. 77:541–549. [DOI] [PubMed] [Google Scholar]
  53. Vertel, B. M. 2001. Color Textbook of Histology. http://www.finchcms.edu/anatomy/.)
  54. Wang, R. K. 2000. Modelling optical properties of soft tissue by fractal distribution of scatters. J. Mod. Opt. 47:103–120. [Google Scholar]
  55. Wang, R. K., and J. B. Elder. 2002. Propylene glycol as a contrasting agent for optical coherence tomography to image gastrointestinal tissues. Lasers Surg. Med. 30:201–208. [DOI] [PubMed] [Google Scholar]
  56. Wight, T. N., D. K. Heinegard, and V. C. Hascall. 1991. Proteoglycans: structure and function. In Cell Biology of Extracellular Matrix. E. D. Hay, editor. Plenum Press, New York. 45–78.
  57. Yao, L., H. Cheng, Q. Luo, W. Zhang, S. Zeng, and V. V. Tuchin. 2002. Control of rabbit dura mater optical properties with osmotical liquids. Proc. SPIE. 4536:147–152. [Google Scholar]
  58. Zuluaga, A. F., R. Drezek, T. Collier, R. Lotan, M. Follen, and R. Richards-Kortum. 2002. Contrast agents for confocal microscopy: how simple chemicals affect confocal images of normal and cancer cells in suspension. J. Biomed. Opt. 7:398–403. [DOI] [PubMed] [Google Scholar]
  59. Zyablov, V. I., Y. N. Shapovalov, K. D. Toskin, V. V. Tkach, V. V. Zherebovski, and L. S. Georgievskaya. 1982. Structure and physical-mechanical properties of human dura mater concerning aging. Arch. Anat. Histol. Embryol. (Russia). 3:29–36. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES