A Three-Dimensional Viscoelastic Model for Cell Deformation with Experimental Verification

Abstract

A three-dimensional viscoelastic finite element model is developed for cell micromanipulation by magnetocytometry. The model provides a robust tool for analysis of detailed strain/stress fields induced in the cell monolayer produced by forcing one microbead attached atop a single cell or cell monolayer on a basal substrate. Both the membrane/cortex and the cytoskeleton are modeled as Maxwell viscoelastic materials, but the structural effect of the membrane/cortex was found to be negligible on the timescales corresponding to magnetocytometry. Numerical predictions are validated against experiments performed on NIH 3T3 fibroblasts and previous experimental work. The system proved to be linear with respect to cytoskeleton mechanical properties and bead forcing. Stress and strain patterns were highly localized, suggesting that the effects of magnetocytometry are confined to a region extending <10 μm from the bead. Modulation of cell height has little effect on the results, provided the monolayer is >5 μm thick. NIH 3T3 fibroblasts exhibited a viscoelastic timescale of ∼1 s and a shear modulus of ∼1000 Pa.

INTRODUCTION

Cells are exquisitely sensitive to mechanical stimuli, and actively respond through a variety of biological functions including migration, morphological changes, and alterations in gene expression and protein synthesis. Cell-distinct functional (e.g., growth) or dysfunctional phenotypes (e.g., atherosclerosis, Davies, 1995; and asthma, Ressler et al., 2000) involve such mechanisms in response to specific biomechanical stimuli. To understand the cellular response to mechanical stress, numerous experiments have been conducted to apply a quantified mechanical stimulus to a single cell, and study its response. Examples of such experiments are micropipette aspiration, atomic force microscopy, particle tracking laser microrheology, magnetocytometry, and manipulation by optical tweezers (see Brown, 2000 for a review).

Much current work focuses on identifying the mechanism(s) by which cells sense mechanical force and transduce it into a biochemical signal, a process termed “mechanotransduction.” In the case of mechanosensitive ion channels, a signal can be produced when forces acting within the lipid bilayer rise to a level sufficient to produce a conformational change in the protein channel and thereby alter its conductance (Gullingsrud et al., 2001). Forces transmitted via cell surface receptors and the intracellular proteins that connect them to the cytoskeleton can also experience conformational change and, as a result, potentially alter their binding affinity to signaling molecules (Sawada and Sheetz, 2002; Zhu et al., 2000). The extent to which an imposed mechanical perturbation can elicit conformational changes at a particular site therefore depends upon the distribution of forces within the load bearing members of the cell. A need therefore exists to predict how forces are transmitted throughout the cell, as well as the way in which local forces produce conformational change. To the extent that a theoretical model can capture the stress or strain distribution within the cell, it can help us to relate the biological influences of various types of force application, e.g., those due to a fluid dynamic shear stress or produced by magnetocytometry, while at the same time, guide us to a better understanding of cell mechanics.

The specific objective of the present study is to provide insight to the mechanical reaction of the cell during magnetocytometry, experiments in which a paramagnetic bead is tethered to cell surface receptors and a time-varying magnetic force is applied (Bausch et al., 1998; Glogauer and Ferrier, 1998). A computational model is developed based on finite element methods to analyze the forcing of one microbead on a cell monolayer, and determine the internal patterns of mechanical stress/strain distribution. These predictions can then be used to: 1), determine the mechanical properties of the cells by comparison to experimental results; 2), correlate the localized stress/strain patterns to biological responses of the cell; and 3), provide validation for a simple theoretical model that can be used to interpret other experimental observations.

A three-dimensional model is proposed incorporating viscoelastic properties for the cytoskeleton and membrane/cortex composite, and allowing for modulation of cell height and material properties to investigate the behavior of different cell types under mechanical stimuli. Model predictions are compared to experimental results obtained with time-varying force to assess model validity.

METHODS

Model geometry

A computational model was developed to simulate the application of a magnetic force to a bead attached to a cell monolayer (Fig. 1). To simulate a monolayer, we modeled a cylindrical domain (Fig. 1) representing a portion of the continuous monolayer of, for example, endothelium or columnar epithelium. The discrete nature of cytoskeletal filament network—microtubules, actin, and intermediate filaments—was not depicted, based on the observation that the relevant length scale present in the application of force via a tethered bead is considerably larger than the filament network mesh size (∼50–100 nm). The lateral extent of the monolayer was chosen large enough (40 μm) to eliminate any effect of the boundary on the stress or strain distributions in the vicinity of the bead. A reference model with a 10-μm-high and 40-μm-wide cylindrical monolayer was implemented, and its height was modulated to depict different cell types. The cell monolayer consists of two parts: 1), the cytoskeleton, i.e., the main part of the cylinder; and 2), the membrane and the actin cortex, a shell layer atop cytoskeleton.

FIGURE 1.

General model geometry. The cell monolayer is divided into cytoskeleton and membrane/cortex, each of which are assigned different material properties. All elements are drawn to scale, except for the membrane, the thickness of which is exaggerated for clarity. The contact angle between the bead and the cell monolayer is set to 2α = 90°, so that only 3.65 μm of the bead extends from the monolayer.

Beads utilized in magnetocytometry experiments are rigid ferrous spheres of diameter 4.5 μm (Bausch et al., 1998; Huang et al., 2002). Only that portion of the bead that contacts the cell (Figs. 2–7) was modeled here. When using beads coated with an adherent ligand, the contact area between the bead and the cell increases over time, and is not precisely known for each bead at the instant of force application, typically 30–60 min after the beads are introduced (Huang et al., 2002; Laurent et al., 2002; Bausch et al., 2001). Bead immersion angle was measured by Laurent et al. (2002) who used spatial reconstruction of confocal microscopic images on 25 beads attached to epithelial cells and found half-contact angles between the bead and the cell ranging from α = 36° to 86°, with a mean α = 67° (see Fig. 1 for the definition of α). In the majority of the present simulations we used a bead-cell half-angle of α = 45°, corresponding to a contact radius of 1.6 μm (Fig. 1). To probe the effect of varying degrees of bead contact, simulations were also performed at half-angles of α = 60° and 75°.

FIGURE 2.

Cross-sectional view of monolayer (y = 0): displacement field in the forcing (x) direction after 2.0 s. Arrow indicates the force F = 500 pN applied. Only part of the bead (unfilled gray network) is displayed. The displacement field is localized near the bead and exhibits a pulling/squeezing pattern. No significant displacements occur immediately beneath the bead.

FIGURE 7.

Cross-sectional view of the monolayer (y = 0): effective stress after 2.0 s. Arrow indicates the force F = 500 pN applied. Only a part of the bead (unfilled gray network) is displayed. Effective stress is a scalar invariant of the stress tensor excluding the compressive part (see Results).

The model allows for the monolayer surface to adopt a smooth but localized bend beneath the bead, inspired by Transmission Electron Microscopy images (McVittie, 2001; Fabry et al., 2001). The prestress due to bead embedding was neglected, considering that stresses are typically dissipated within seconds, whereas tens of minutes are needed to increase contact area.

Boundary conditions

A zero-displacement boundary condition was imposed at the bottom surface, i.e., the cell monolayer was fixed to a rigid substrate—typically a glass slide in cell cultures or the basal lamina in vivo. A free stress boundary condition was imposed at the perimeter of the cell monolayer.

Mechanical and material properties

Living cells have been shown to exhibit a viscoelastic behavior (Yamada et al., 2000 for epithelial cells; Evans, 1983; Bausch et al., 1998 for other cell types). Therefore, the membrane and the cytoskeleton were represented by either a fluidlike viscoelastic Maxwell model analogous to a spring and a dashpot in series, or a solidlike Voigt model analogous to a spring and a dashpot in parallel. The Voigt model has a solidlike behavior in that, at long timescales (compared with its characteristic time constant), it displaces proportionally to the force applied. In the Maxwell model, on the other hand, the displacement increases with a larger (than linear) dependence on the applied force, i.e., the material flows. To focus on important parameters, models involving more than two parameters were not considered, even though they may be capable of fitting the response curves more closely (Bausch et al., 1998). The bead was modeled as a homogenous, isotropic, elastic material with a Young's modulus large enough to enforce rigidity. All material properties are summarized in Table 1.

TABLE 1.

Material properties introduced in the model

Part of the model	Material	Constants	References	Characteristic time
Membrane and actin cortex	Incompressible homogenous isotropic viscoelastic (Maxwell)	Bending stiffness, Kb = 2.10−18 to 2.10−19 Nm	Hwang and Waugh, 1997,Zhelev et al., 1994	5–100 ms
		Shear viscosity, μ′ = 3.10−7 Pa.m.s (or time constant of 100 ms)	Dimova et al., 1999,Evans, 1989
Cytoskeleton	Incompressible homogenous isotropic viscoelastic (Maxwell)	Shear modulus, G = 100 Pa	Yamada et al., 2000	1 s
		Viscosity, μ = 100 Pa/s	Theret et al., 1998

Cytoskeleton

Several techniques have been utilized to assess the mechanical properties of the cytoskeleton of various cell types (e.g., Brown, 2000; Evans, 1983; Fabry et al., 2001; Glogauer and Ferrier, 1998; Yamada et al., 2000). Micropipette measurements in endothelial cells yield Young's moduli in the range of 10²–10³ Pa (Theret et al., 1998), while measurements performed in epithelial cells using laser tracking microrheology yielded complex moduli of ∼10³ Pa and phase angles ∼30°, corresponding to a shear modulus and viscosity of G_c ∼ 70 Pa and μ_c ∼ 40 Pa.s, respectively (Yamada et al., 2000). Intracellular estimates, inferred from the recording by laser tracking of the Brownian motion of particles embedded in the cytoskeleton (Yamada et al., 2000), are usually one or two orders-of-magnitude smaller than “extracellular” estimates, obtained with other techniques acting on the cell surface. Taking these results into consideration, we chose the baseline viscoelastic parameters of the cytoskeleton as follows: G_c = 100 Pa and μ_c = 100 Pa.s. This yields a characteristic time (μ_c/G_c) of 1 s for the viscoelastic behavior. When the cytoskeletal properties are varied in the results presented below, this characteristic time is assumed constant.

Membrane and cortical layer

The membrane/cortex composite structure, though extremely thin in comparison to the dimensions of the cell, might play an important mechanical role under certain circumstances. Values for the bending stiffness and viscoelastic time constant taken from the literature were utilized to model the membrane/cortex. Bending stiffness has been measured on red blood cells: 2.10⁻¹⁹ N.m (Hwang and Waugh, 1997) and neutrophils: 10⁻¹⁸ to 2.10⁻¹⁸ N.m (Zhelev et al., 1994). We assume here that fibroblasts, endothelial cells, and epithelial cells (for which no cell membrane properties measurements are available, to our knowledge) all exhibit similar values of bending stiffness, and conducted simulations using values for K_b between 2.10⁻¹⁹ and 2.10⁻¹⁸ N.m. The time constant for viscoelastic effects was similarly varied between τ = 5 ms, the value derived from a two-dimensional shear viscosity of 3.10⁻⁷ Pa.m.s (Dimova et al., 1999), and τ = 0.1 s, the characteristic time for viscous dissipation in living red blood cell membrane/cortex after extensional deformations (Evans, 1989). We assumed the membrane/cortex to be incompressible and of constant thickness. It follows from these assumptions that the areal strain is zero for all deformations.

Sensitivity analysis

To quantify the influence of the cytoskeletal properties, its shear modulus was varied, along with its viscosity to maintain the cytoskeletal characteristic time constant (∼1 s). Shear moduli of 200 Pa, 400 Pa, 600 Pa, and 1 kPa were simulated. We assessed the membrane/cortex contribution to the overall response by conducting a simulation with the membrane/cortex shell removed entirely.

Applied load

Cell experiments with the identical forcing in time and magnitude were performed for comparison (see Cell Experiments). The magnitude and time-dependence of the applied force were varied to correspond to the range of typical experimental values. Specifically, the constant rate of force application was varied from 125 pN/s to 2500 pN/s. In addition, a simulation was performed with a force varying sinusoidally between 0 and 250 pN with a frequency of 1 Hz.

During forcing, the bead is tethered to the cell over a part of its circumference (Fig. 1). The displacement at the bead center, directly accessible through experiments, can then be calculated using the finite element model (see below). More generally, the model provides insight into the general response of the cell monolayer to various time-dependent forcing.

Solution techniques

To determine the displacement, strain, and stress fields induced within the cell monolayer, a finite element model was developed using the commercially available software ADINA V. 7.5 (Watertown, MA). A Lagrangian formulation for large stress, large strain was utilized (Bathe, 1996). The cytoskeletal mesh consisted of 17,292 nodes distributed over 15,840 eight-node elements. Since the ratio of membrane/cortex thickness to cell height is ≪1, the membrane/cortex composite was modeled with a single layer of 1440 four-node planar shell elements.

To represent the junction between the membrane/cortex and the cytoskeleton, all finite element nodes associated with the membrane/cortex were shared by the cytoskeleton. Similarly, the bead, the membrane/cortex, and the cytoskeleton shared the same nodes along the bead contact surface, featuring the rigid biological link between them (e.g., fibronectin-integrin-actin filaments).

Running the simulation for the reference model (see above), i.e., with a 17,292-node cellular mesh and a bead forcing rate of 250 pN/s, took ∼200 h on a 4-processor SGI Origin 2000 computer equipped with 6 GB RAM. The maximum RAM required was ∼1 GB. A total of 170 time-steps ranging from 0.005 to 0.04 s were required.

Cell experiments

Magnetic trap calibration

The magnetic trap was calibrated by suspending magnetic beads (Dynal Biotech, Lake Success, NY, Dynabeads M-450) in dimethylpolysiloxane (Sigma Aldrich, St. Louis, MO, DMPS—12 M) and tracking the position of the beads as they are attracted to the magnetic trap over a range of electrical currents (0.3–1.5 Amps). Details on the magnetic trap design and operation are provided in Huang et al. (2002).

Bead coating with extracellular matrix proteins

Magnetic beads were coated with fibronectin (Invitrogen, Carlsbad, CA, 33016-023) according to the manufacturer's protocol with the following modifications: fibronectin was applied at a final concentration of 500 μg/mL in borate buffer (pH 8.5) for 18 h at 37°C.

Cell culture

NIH 3T3 fibroblasts were maintained in Dulbecco's modified Eagle's medium (DMEM, Cambrex, East Rutherford, NJ) supplemented with 10% fetal calf serum and antibiotics.

Experimental procedure

Polystyrene cell culture dishes (Corning, Corning, NY) were coated with 0.1% gelatin in phosphate-buffered saline (PBS, Gibco) overnight at 4°C to facilitate cell attachment. Cells were plated in DMEM supplemented with 10% fetal calf serum (FCS), penicillin/streptomycin, and zeocin (200 μg/mL) at 3 mL per dish on the gelatin-coated dishes at a density of 150,000 cells/dish and incubated at 37°C overnight. Medium was replaced the next day with DMEM containing 5% FCS and 6-μL fibronectin-coated bead suspension (final concentration 1.2 × 10⁶ beads/dish) and incubated at 37°C for 45 min to guarantee sufficient bead attachment to the cells. The cell culture dish was then placed on a temperature-controlled stage. Cells with adherent beads were imaged at 30× magnification using an inverted light microscope (Olympus, Melville, NY, IX-70). Nonconfluent cells with a single bead firmly attached to the flat section of the cell surface were selected for the magnetic trap experiments. The magnetic trap was brought into a parfocal position with the bead at a distance of 115 μm away from the magnetic trap tip. One of the following force profiles was then applied to the bead while recording the bead position with a digital camera (Roper Scientific MASD, San Diego, CA, Megaplus ES310/T) at 60 frames per s:

1. Sine wave: a force-free period of 1 s followed by 8 s of a 1-Hz sine-wave pattern with amplitudes of 0.125 nN or 0.6 nN and an offset of one amplitude, followed by 1 s at zero force to monitor the relaxation of the bead.

2. Step function: a constant force rising in steps of 300 pN every 2 s, so that it reaches 1500 pN after five steps.

3. Force ramp: linearly increasing force from 0 to 500 pN at a rate of 250 pN/s, followed by 2 s at zero force.

A Hall probe was used to simultaneously measure the magnetic field during the force application, and the readout was saved with the video image data.

Subsequent cells were selected at least 5 mm away from any previous force application sites to avoid studying preconditioned cells. Five to fifteen cells were selected in each dish, and the experiments were concluded within 30 min per dish.

Particle tracking and phase lag determination

Custom-written MATLAB (MathWorks, Natick, MA) software that uses a combination of cross-correlation and center-of-mass computation was used to track the bead centroid position from the digitally recorded videos with a spatial resolution of ∼10 nm at 30× magnification. The phase lag between the applied force, represented by the magnetic field strength, and the resulting bead displacement, was computed using cross-correlation analysis. The temporal resolution is one frame, i.e., 1/60 of a second.

The validity of the phase lag measurements was confirmed by applying the technique to beads embedded in purely viscous (dimethylpolysiloxane) or purely elastic media (polyacrylamide gel). Bead displacements in the elastic media exhibited a negligible phase shift of 2.95° ± 3.564°, whereas displacements of beads in viscous media showed a phase lag close to 90°: 86.91° ± 5.94°, i.e., force corresponded to the derivative of the displacement.

For the force step function, maximal displacement was defined as the difference in mean bead position between the last 10 frames (= 0.4 s) of force application at each force level and the initial position, estimated as the mean bead position during the 25 frames (= 1 s) before the application of force.

RESULTS

Model dependence of the results

Simulations with either a viscoelastic Maxwell (fluidlike) or a Voigt (solidlike) cell exhibited similar patterns of deformation and stress. However, the shear modulus values that best fit the data were dependent upon the choice of model. With a time constant of 1 s, the shear modulus was ∼600 Pa for the Maxwell model, whereas the Voigt model yielded 100 Pa. Note that the Voigt model values are ∼6× smaller than those for the Maxwell model, highlighting the difficulty in making direct comparisons between parameters determined using the different viscoelastic models. In separate experiments (results not shown) in which a stepwise force was applied to the bead and held for 4 s, the bead invariably immediately displaced, then continued to creep. In some cases, the creep continued at nearly a constant rate, suggestive of a Maxwell model, whereas in others it approached a constant asymptotic value. Because the Maxwell model seemed somewhat more consistent with experimental observations, all the following comparisons use the Maxwell description in all subsequent simulations.

Self-consistency of the model

A mesh sensitivity study was conducted to ensure the independence of the results from the computational mesh. Three mesh sizes were used. The coarser, medium, and finer meshes consisted, respectively, of 17,292, 22,321, and 27,846 nodes distributed over 15,840, 20,592, and 25,844 eight-node elements in the cytoskeleton and 1440, 1716, and 1988 four-node shell elements in the membrane/cortex.

All three meshes gave similar result patterns. Even in the coarser mesh, the solution patterns did not depend on the patterns of mesh lines. At all time-points, the maximum differences between the three computational meshes were <1% for bead center displacement, 0.9% for monolayer x- and z-displacements, 7% for the stretch components, and 4% for effective stress at all locations. All results presented in the following are therefore obtained with the coarsest mesh (17,292 nodes).

Significant displacements and stresses were localized and confined to the vicinity of the bead. Both decay rapidly with distance from the bead (Figs. 2–8). Consequently, the free stress monolayer boundaries at 20-μm radius experience a negligible displacement; e.g., at 2.0 s (500 pN force), maximum displacement at the edge of the monolayer is <0.05 μm, compared to the maximum displacement of 1.02 μm. Similarly, the zero-displacement boundaries at the bottom of the cell monolayer induced negligible stress therein; at 2.0 s and for radial positions >10 μm, stress <1.5 Pa (Fig. 7), compared to the maximum effective stress of 188.4 Pa. These observations validate the assumption that the monolayer can be considered as infinite in the radial direction.

FIGURE 8.

Membrane displacement in the forcing direction. Enlarged top view after 2.0-s forcing (500 pN). Inset shows the displacement field for the whole model and the region of the enlargement (black rectangle). Bead not shown. Displacements are seen to extend more in the forcing (x) direction than in the transverse (y) direction.

Bead behavior

Magnetic forcing produces both translation in the x-direction and rolling about the y-axis (due to the induced torque around the bottom of the bead fixed to the cell; see Figs. 2–7). After 2.0 s, the bead center translation was 1.67 μm and the bead had rolled ∼θ at ∼20° (Figs. 2–7). This means that, due to the rotation, the cell surface over the region attached to the bead is displaced less than the bead center, by an amount equal to Rθ ∼ 0.8 μm in this case, where R is the radius of the bead. As a consequence, cell surface displacement in the x-direction is also reduced.

Simulations yield bead displacements of ∼1 μm, consistent with experiments (Huang et al., 2002; Bausch et al., 1998). In the force-ramp simulations, the slope of the displacement curve increases with increasing time, consistent with what one would expect for a viscoelastic material. Monolayer thickness has little effect on the observed bead displacement (Fig. 9).

FIGURE 9.

Bead center displacement versus time, resulting from the numerical simulation. Force was imposed at a constant rate of 250 pN/s, so that at 2 s the applied force equals 500 pN. The nonlinearity of the curves stems from the monolayer viscous properties. At a given time, thicker monolayers produce larger bead displacement, as the influence of the cell bottom anchorage to the substrate decreases.

The viscoelastic response of the monolayer was also evident when the bead was forced sinusoidally. Using values in Table 1, we calculated the relaxation timescales: 1 s for the cytoskeleton and 5–100 ms for the membrane/cortex composite. Because the forcing timescale is comparable to the cytoskeleton relaxation timescale and more importantly because it exceeds that of the membrane/cortex, the force-displacement curve is effectively dominated by the characteristics of the cytoskeleton. This was further confirmed by simulations with the membrane/cortex shell removed, for which the bead force-displacement relationship is virtually identical to the complete simulation including the membrane/cortex.

The overall character of the force-displacement curves compare favorably with our measurements performed on NIH 3T3 fibroblasts (Fig. 10). Firstly, the experimental and numerical curves both exhibit the same convex shape. Secondly, the simulation agrees most closely with the experimental data when the cytoskeleton shear modulus are set between 600 Pa and 1 kPa, consistent with reported values for the shear modulus of ∼1 kPa for chick fibroblasts (Thoumine and Ott, 1997). Increasing the cytoskeleton shear modulus does not change the overall trend of the bead force-displacement curve, but significantly decreases the bead displacement for the same force applied (Fig. 10; and see Linear Displacement Studies, below).

FIGURE 10.

Bead center displacement versus time. Numerical results (black curves) are shown for three cytoskeleton shear moduli. The seven gray lines are sample data, each obtained from a different NIH 3T3 fibroblast (see Cell Experiments) within a single experiment. Both numerical and experimental curves were obtained with a force imposed at a constant increasing rate of 250 pN/s.

General cell monolayer movement

Monolayer movement appears to be highly localized in the vicinity of the bead (Figs. 2, 3, and 8), in agreement with the displacements recorded by two-photon images (compare to Fig. 3 of Huang et al., 2002). A cutoff radius—defined here as the radius at which displacement falls to 10% of its maximum—of ∼10 μm is observed, consistent with measurements reported in Huang et al. (2002) and Bausch et al. (1998). More precisely, the cutoff radius is 12.0 μm in the forcing direction and 5.3 μm in the transverse direction. Two distinct regions of large displacement are apparent in all simulations, one in front of the bead and one behind it, so that the overall displacement field exhibits a pulling/squeezing pattern (Figs. 2 and 3). Interestingly, a zero-displacement zone is visible immediately beneath the bead. Consequently, the forces inside the monolayer are expected to be concentrated ahead of and behind the bead and somewhat diminished directly below it.

FIGURE 3.

Cross-sectional view of monolayer (y = 0): displacement in the vertical (z) direction after 2.0 s. Arrow indicates the force F = 500 pN applied. Only a part of the bead (unfilled gray network) is displayed. Vertical displacements are comparable to those in the forcing direction.

In all simulations, the maximum displacement inside the monolayer is in the direction of forcing, located on the membrane, immediately behind the bead, and roughly equal to half of the bead displacement. For example, after 2 s, i.e., when the force applied is 500 pN, the maximum displacement in the monolayer is 1.02 μm in the forcing direction, whereas the bead center displacement is 1.67 μm. The maximum displacement is smaller in other directions: 0.91 μm and 0.21 μm in the vertical and transverse directions, respectively. Predicted displacements are consistent with measured membrane displacements of ∼0.1 μm after 0.2-μm bead displacement a few micrometers away from the bead center (Bausch et al., 1998), and overall displacements under 1 μm (Huang et al., 2002) for forces of 200 pN.

Stretch distribution

To study how the macroscopic monolayer movement is translated into possible microscopic actions, we examined the stretch fields, representing local deformations in the cell. The left stretch tensor was utilized to visualize the strain field within the cell and the membrane. The Eulerian strain tensor and the left stretch tensor 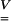are related by Ogden (1984), as

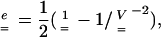(1)

where 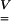is dimensionless—like 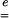—and equal to unity when there is no strain. Values greater than unity correspond to a local lengthening (tensile strains), whereas components smaller than unity correspond to a local shortening.

Maximum components of the stretch tensor 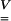were V_xx and V_zz, with x being the bead forcing direction and z the vertical direction (Figs. 2–7). Other components of the stretch tensor were significantly smaller, as expected from the displacement field. The stretch patterns were concentrated in four regions close to the bead (see Figs. 4 and 5 for the V_xx component): two shortening regions (in darker shades) and two lengthening regions (in lighter shades). Shortening was mainly observed at the front of the bead, whereas the higher tensile strain (lengthening) region was located right behind the bead with maximum values on the membrane. Note that despite these large values for individual elements of the strain tensor, the areal strain is zero (i.e., e_x + e_y = 0) as it must be for an incompressible, constant thickness bilayer.

FIGURE 4.

Cross-sectional view of monolayer (y = 0): xx-component of the stretch tensor after 2.0-s forcing. Arrow indicates the force F = 500 pN applied. Only part of the bead (unfilled gray network) is displayed. The stretch tensor is dimensionless and equal to 1 in the absence of strain. The xx-component is the maximum and most relevant term in the stretch tensor.

FIGURE 5.

Membrane xx-stretch. Enlarged top view after 2.0-s forcing (500 pN). Inset shows xx-stress for the whole model and the region of the enlargement (black rectangle). Bead not shown. Stretch-xx exceeds the threshold value of 1.04 (potentially leading to ion channels activation) within a region extending 6.0 μm in the x-direction and 4.9 μm in the y-direction. See text for details.

Stress distribution

The stress field induced in the monolayer was analyzed through two complementary invariants of the stress tensor: pressure and effective stress. The effective (von Mises) stress subtracts out the contribution due to isotropic compression (i.e., pressure) and is defined as

(2)

where σ_ij is the ij-component of Cauchy's stress tensor. The effective stress is, hence, a measure of shear and a sort of modulus of the stress tensor excluding the compressive part.

The pressure field in the cell monolayer is concentrated in the immediate vicinity of the bead (Fig. 6). The two same regions of perturbation mentioned for displacement are observed: one in front and one at the rear of the bead. However, the pressure field is more localized than the displacement field. At the rear of the bead, pressure is negative as a consequence of the pulling exerted by the bead translation and the upward movement imposed on the membrane by the bead rolling. Conversely, pressure is positive in front of the bead due to forward movement of the bead but attenuated by cell spreading. The pressure field is more diffuse in front of the bead compared to the rear, with extrema of 88 Pa and −72 Pa, respectively, at the front and rear regions after 2 s (Fig. 6). Both extrema are located on top of the cytoskeleton. The fluidlike membrane supports little stress by itself; the high-pressure field does not penetrate significantly into the cell cytoskeleton.

FIGURE 6.

Cross-sectional view of the monolayer (y = 0): pressure after 2.0 s. Arrow indicates the force F = 500 pN applied. Only a part of the bead (unfilled gray network) is displayed. The pressure field illustrates the pulling/squeezing pattern.

Effective stresses generally exceed pressure. For example, after 2 s, the maximum effective stress is 188.4 Pa, whereas the maximum pressure is 88 Pa (Fig. 6). Therefore, the stress field is dominated by shear rather than normal stresses. Effective stress rapidly decreases away from the bead (Fig. 6), but remains at the level of a few Pa at distances of >10 μm.

The stress field is more localized at the rear of the bead compared to the front, supporting the interpretation that the monolayer squeezing exerted by the bead spreads stress whereas the pulling only affects a very small region.

Influence of monolayer height

The model was implemented for four different monolayer heights: 5 μm typical of the flat part of a fibroblast or endothelial cells; as well as 10, 15, and 20 μm, representative of epithelial cells. The relationship between bead center displacement and magnetic force applied on the bead has a similar trend for all monolayer heights (Fig. 9), consistent with the observation that displacements are confined to a region extending just a few micrometers from the bead. However, for identical bead forcing, the displacement is slightly smaller for thinner monolayers, confirming that the effect of the basal anchoring is more pronounced for thinner monolayers. As is evident in the figure, the impact of basal anchoring is non-negligible, even in the 20-μm-high monolayer. This is in agreement with results from an elastic model of magnetic twisting cytometry (Mijailovich et al., 2002) for which bead movement increased when the 5-μm-high monolayer was replaced by a semi-infinite space (infinite height).

As one would expect for a viscoelastic medium, the effect of cell height on a bead's force-displacement increases with the applied force, and hence with time. This is due to the progressive relaxation of the viscous elements of the cytoskeleton during the bead-induced deformations. Larger bead displacements yield deeper penetration of the deformations into the cytoskeleton, reminiscent of an elastic component for the monolayer. On the other hand, faster forcing rates lead to smaller penetration depths for the bead-induced perturbations, as manifested by smaller computational gridline deformations deep in the cytoskeleton (data not shown), indicative of the viscous character of the monolayer. Overall, the elastic and viscous aspects of the monolayer dominate its short- and long-term behavior, respectively.

Simulations with these four different monolayer heights exhibited similar patterns and magnitudes for displacement, stretch, pressure, and effective stress. No significant differences were observed between the models, leading to the conclusion that, within this range, cell height has little effect on how the mechanical stimuli are distributed in magnetocytometry experiments.

Influence of the depth of bead embedding

As expected, the magnitude of deformations and stresses decreased significantly with increasing bead embedding. However, the patterns of deformation and stress within the cell were relatively independent of the degree of cell-bead contact. Laurent et al. (2002) studied the effect of bead embedding angle using a linear theory and found that displacements should vary inversely as sin α. Our numerical results for bead displacement exhibited a stronger dependence on contact angle, however, and tended to scale as (sin³ α)⁻¹.

Relative contributions of the membrane/cortex and cytoskeleton to the overall response

Since the viscoelastic time constant of the membrane (5–100 ms) is smaller than that of the cytoskeleton (1 s), we anticipated that the membrane would contribute little to the overall response of the cell to bead forcing with 1-s timescales. To confirm this, we performed similar simulations but with the membrane/cortex shell removed entirely, and found that the results were virtually identical.

Influence of the forcing time dependence

Numerical simulation: influence of the forcing rate

To further assess the implications of the viscoelastic behavior, simulations with various rates of force application on the bead were performed. Faster forcing rates led to smaller bead displacements, consistent with the increasing resistance of the viscoelastic monolayer with the rate of forcing (Fig. 11). For example, a force of 450 pN led to 1.42-μm bead displacement at a 250-pN/s constant forcing rate, but up to 2.00 μm when the forcing rate was reduced by a factor of two (125 pN/s), which is a 30% increase. The response curve was observed to be linear for high forcing rates: with a 2500-pN/s forcing, the displacement is proportional to the force applied with a slope of 1.93 μm/nN.

FIGURE 11.

Bead center displacement versus time for three forcing rates: 125 pN/s, 250 pN/s, and 2500 pN/s. Higher forcing rates led to smaller bead displacements for forcing rates at <∼1000 pN/s. Forcing rates above this value all led to a linear force-displacement relationship (thicker line) of 517.5 pN/s.

As a consequence of the Maxwell model used in these simulations, the force needed to displace the bead by a given amount increases with the forcing rate asymptotically, reaching a constant value for forcing rates higher than ∼1000 pN/s: the monolayer response is then essentially that of a linearly elastic material.

Linear displacement studies

Simulations with monolayers having different cytoskeleton shear moduli led to bead displacements scaling approximately with the inverse of the shear modulus provided the time constant of the material was held fixed (Fig. 10). For example, after 2 s, when the force acting on the bead is 500 pN, bead displacement was 0.86 μm for a cytoskeleton shear modulus of 200 Pa but only 0.46 μm when the shear modulus was increased by a factor of two, to 400 Pa.

Application of a sinusoidal force

Bead displacement under sinusoidal forcing exhibits an oscillatory behavior with a time-varying mean (Fig. 12), indicative of the viscous character of the Maxwell model. For the particular conditions of Fig. 12 with a forcing frequency of 1 Hz and force amplitude of 125 pN, the net bead displacement per cycle was ∼0.21 μm along the forcing direction and the phase lag between the bead displacement and the applied force was 0.05 ± 0.005 s (mean ± SD). Aside from the shift in bead position, the maximum bead displacement decreases slightly from one cycle to the next, from 0.57 μm in the first cycle to 0.50 μm in the fourth cycle.

FIGURE 12.

Bead center displacement (upper graph) as a result of force applied to the bead (lower graph) versus time. Four periods of the numerical simulations (black curve) are represented along with the first four periods of sample data from a single experiment featuring seven beads each attached to a different NIH 3T3 fibroblast (seven gray curves; see also Cell Experiments).

The displacement and stress patterns in the monolayer (data not shown) are similar to those observed in the simulation conducted with a ramp force applied on the bead as shown above.

Cell experiments

Linear displacement studies

To experimentally test the linearity of the force-displacement curves when the force is time-independent, we applied a stepwise increasing force to the beads. The force was increased by 300 pN every 2 s until a maximal force of 1500 pN was reached. For the analysis, only beads that remained attached throughout the entire force application were considered (96 out of 104). Not only was the mean displacement versus force relationship linear, but also almost all beads exhibit a linear force-displacement relationship over the entire range of forces. The linear regression gave

(3)

where a = −0.04492 μm, with a 95% confidence interval between −0.2989 and 0.2091 μm; and b = 0.6497 μm/nN, with a 95% confidence interval between 0.3944 and 0.9049 μm/nN. The departure from linearity in the data was nonsignificant (P = 0.9993) and validated our choice of linear elements to model the cell monolayer material during magnetocytometry. Linear behavior was also observed in experimental sinusoidal forcing, as discussed below.

Application of a sinusoidal force

At 125-pN force amplitude, less than half the cells (8 out of 19) exhibited a detectable response to the force application (Fig. 12). In contrast, almost all cells (18 out of 19) showed a detectable response at 600 pN.

Only cells with detectable sinusoidal displacement pattern were selected for calculation of the phase lag between the displacement and the force. For the lower amplitude (125 pN), the phase lag was 0.0626 ± 0.0414 s, in agreement with our numerical finding of 0.05 s and corresponding to a phase angle of 22.5°. At larger amplitudes (600 pN), the phase lag was 0.0677 ± 0.0401 s, not significantly different than at low amplitudes (P = 0.7783). This lag indicated a significant viscous component in the mechanical cell response. Considering all 19 beads for both experiments, the displacement amplitude at the low force level (125 pN) was 0.0323 ± 0.0429 μm, compared to 0.1184 ± 0.1233 μm at higher forces (600 pN, still applied at 1 Hz). As indicated by the large standard deviation of the displacement amplitudes, the cells exhibit a highly heterogeneous mechanical response due likely to variations in cellular stiffness and/or contact angle of the bead.

The mean displacements, defined as the total bead displacement averaged over one forcing period, increased with time. This viscous creep is consistent with the computational results (Fig. 12). Two distinct patterns are observed in the bead displacement plots versus time. Namely, the beads with low displacement amplitudes seem to maintain a rather constant mean displacement over time, whereas beads with larger displacement amplitudes show an increasing mean displacement over time. These last two observations were consistent in both sets of experiments performed at 125-pN and 600-pN force amplitudes.

Statistical analysis

Multiple regression analysis was used to examine the correlation of phase lag, amplitude, and residual bead displacement (defined as the bead displacement after 1 s of relaxation after the eight-cycle sinusoidal force application) for the 600-pN amplitude experiments. The statistical analysis was performed with 18 cells out of 19, excluding one cell with displacement amplitude lower than the resolution limit (10 nm).

The residual displacement correlated with the phase lag and the displacement amplitude following a linear model,

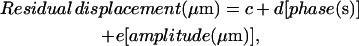(4)

where c = −0.2165 μm, with a 95% confidence interval between −0.3296 and −0.1034 μm; d = 4.627 μm/s, with a 95% confidence interval between 3.404 and 5.849 μm/s; and e = 1.676, with a 95% confidence interval between 1.238 and 2.115. The correlation was significant: R² = 86.71%, with P < 0.0010 for c and P < 0.0001 for d and e.

DISCUSSION

New contributions of the present model

This article presents the first in-depth study of deformation and stresses induced within the cell by magnetic pulling (as opposed to twisting) cytometry. The novelties are primarily found in the finite element model. The experiments reported here largely reproduce what is currently feasible in other laboratories with magnetocytometry facilities; we present them here since these experiments more closely match our simulation conditions, notably with respect to the bead forcing rates, not reported by other research groups. The major contributions of the present work are:

1. Viscoelasticity was used to describe the material properties of the cell. Although measurements of various authors (e.g., Bausch et al., 1998; Yamada et al., 2000) had long noted viscoelastic characteristics, these had not previously been implemented in a spatially distributed cell model for adherent cells. In addition, we conducted a study of the influence of a cell's material properties on its mechanical response, examining both modulation of the viscoelastic parameters of the Maxwell model, and variation of the type of model, considering fluidlike and solidlike viscoelastic models.

2. The effects of the apical cellular membrane and cortex were included. This is the first investigation of their combined mechanical role in magnetocytometry and their relative contribution to the overall response of the cell. The effect of the membrane was found to be small for experiments with large beads and forcing on a timescale of seconds.

3. Inclusion of viscoelasticity allowed us to examine the effects of time-dependent forcing: ramp forcing at various rates and sinusoidal forcing. No previous theoretical or computational studies had considered the effect of loading rate on continuum stress distributions. We found the time-dependence of the force to be critical, with faster loading rates leading to higher stress concentrations within the cell.

We also observed that magnetic pulling induces rotation of the bead (not surprising, yet not previously quantified), that the stress distribution induced within the cell is dominated by shear stress, not by pressure, that the stretch levels on a region of the membrane are above the biologically relevant thresholds previously reported, that an asymmetry exists in the deformation field between the front and the rear of the bead (different from that observed in magnetic twisting), and that bead displacements for a given force vary as the inverse cube of the sine of the half-contact angle.

Bead movement

These simulations demonstrate that a surface-adherent bead undergoes μm-scale translation as well as significant rotation when subjected to time-varying forces on the order of 1 nN. Both the magnitude of displacement and its temporal variation, as observed experimentally, were found to be consistent with the predictions of a linear viscoelastic model for the cell in which both the cytoskeleton and membrane are represented as Maxwell materials. The critical properties that govern this behavior are the cytoskeletal shear modulus (∼1000 Pa) and the time constant for the viscoelastic response (∼1 s).

A pulling/squeezing pattern is observed in the monolayer and a zero-displacement zone directly beneath the bead, both associated with bead rolling. These effects also give rise to significant differences between bead center displacement, as measured in most experiments, and the displacement of the membrane surface. Thus, direct inference of membrane displacement from bead displacement would lead to considerable error and consequent underestimation of cytoskeletal stiffness when used in connection with theories that relate surface displacements to deformations and stress within the (continuum) cell interior (Hertz model, Landau and Lifschitz, 1988; Boulbitch model, Boulbitch, 1999).

Some of these same effects have been previously studied by Mijailovich and co-workers, who used finite element analysis to analyze their magnetic twisting experiments (Mijailovich et al., 2002), in which a torque, but no net force, is applied to the bead. In such cases, the Boulbitch and Hertz models are even less applicable. The twisting field includes all the effects of cell rotation described above, but the translational effects are even further reduced. Unlike the present magnetocytometry experiments, the mean bead rotation angle can be measured during magnetic twisting experiments, using the bead remnant magnetic moment. The rotation angle is large when the bead is bound to nonspecific receptors, but when the bead is bound to the cytoskeleton via integrin receptors, the rotation angles are of the order of 25° (Wang et al., 1993, on endothelial cells).

Model dependence of the results

Since only the Maxwell model would exhibit an immediate displacement after the onset of forcing, it seems a better fit to the data as a whole than the Voigt model. It is important to stress, however, that this is merely a model and provides little insight into the underlying mechanisms that lead to the observed behavior. The model is useful for the purpose of estimating the distribution of stresses and strains throughout the cell and for comparisons between cell types or different cells of the same type, but cannot be more generally applied to experimental protocols that differ significantly in terms of the nature of force application or the timescale of forcing.

More complex models with either multiple, discrete time constants or a continuous spectrum of time constants were not attempted as it was felt that these were not warranted at this time in view of the large standard variability associated with data from different cells, reported for example by Bausch et al. (1998)—“large variability of viscoelastic moduli of individual cells,” Yamada et al. (2000)—“data indicate a high variability of local mechanics,” and quantified by Fabry et al. (2001). While new experimental results are becoming available that help to define cell behavior with greater precision, the currently published data are not yet of sufficient reliability to identify a single model that can be widely generalized. It may therefore be premature to use the results from any single study even though the simplicity of the model is quite appealing.

Still, variability is not a valid excuse for not pursuing more accurate models. We feel, however, that 1), an immediate need exists to model the distributions of stress throughout the cell even if the predictions are restricted to a relatively narrow range of experimental parameters; and 2), that despite some recent encouraging results, no single model exists in which we have sufficient confidence to focus on exclusively. We base this latter comment on the following observations:

• The standard deviation of the mean is large. Fabry et al. (2001) found a geometrical standard deviation of 2.8 for bead displacements in magnetic twisting cytometry (i.e., 68% of the measurements are within a factor of ±2.8 of the mean). Therefore, the cell-to-cell variability is large in a statistically consistent manner.

• The variability was found to be inherent to the behavior of cells. Firstly, the standard deviation of the mean calculated by Fabry et al. (2001) was not significantly reduced (from 2.8 to 2.5) when the statistics were performed on a single measurement from a single well. Secondly, the high variability is not observed in reconstituted gels such as F-actin (Yamada et al., 2000).

Therefore, a model with more parameters (the model of Fabry and co-workers has four adjustable parameters, although only one, the “noise temperature,” was found to vary significantly) would most certainly match the mean value of the experimental data more closely, but the benefits in terms of the depiction and understanding of the behavior of individual cells would be limited.

Influence of depth of bead embedding

Our simulations show that the degree of cell-bead contact strongly influences the magnitude of the mechanical response of the cell to bead forcing, in agreement with computational results from the elastic model of cell behavior under magnetic twisting cytometry (Mijailovich et al., 2002). Theoretical studies of beads partially embedded in purely elastic or purely dissipative media have previously demonstrated that the immersion angle influences the magnitude of the mechanical response of the cell to bead pulling, where bead displacement is found to vary as 1/sinα with both purely elastic and purely viscous cell monolayers (Laurent et al., 2002). Our simulations exhibited a stronger dependence, with bead displacement varying as 1/sin³ α, presumably reflecting nonlinear effects in the solution. This likely explains some of the variability seen in the experimental results (Bausch et al., 1998; Yamada et al., 2000; Fabry et al., 2001), emphasizing the need for some degree of control over contact angle, or direct measurement of it, if accurate estimates of cell viscoelastic properties are to be made.

Comparison to experiments

Under a constant applied force the experiments show that the bead continues to move with time, even under constant force, confirming that the cell response is viscoelastic in nature. In addition, the response of the cell as observed in experiments was largely consistent with the assumption of a linearly elastic material (Landau and Lifschitz, 1988) despite strains as high as 0.18. This observation, though surprising, is consistent with the finding of other groups who have used linear descriptions (Boulbitch, 1999; Mijailovich et al., 2002) and provides some justification for the interpretation of cell behavior using simple, linear models. Breakdown of linearity for bead rotations >15°, predicted by the elastic model of Mijailovich and co-workers for magnetic twisting cytometry (Mijailovich et al., 2002), was not observed in our simulations even though they yielded bead rotations of up to 20°. Note, however, that the present model includes the effects of (linear) viscoelasticity, which has rarely been employed in previous models. Two exceptions are the models used for leukocyte deformation (Dong and Skalak, 1992; Tran-Son-Tay et al., 1991; Dong et al., 1991, 1988; Chien et al., 1987) and the model of Bausch and co-workers for fibroblasts that includes viscoelastic effects in the cytoskeleton (Bausch et al., 1998). Still, one would expect nonlinearity to arise if forces higher yet were applied, or perhaps if a smaller bead was used.

These two observations lend some credence to the choice of a Maxwell model for the cell with a cytoskeletal time constant of ∼1 s. This is particularly relevant since most experiments to date have applied forcing on a timescale of seconds, therefore tending to maximize the combined influence of elastic and viscous behaviors. One should exercise caution, however, in applying this model to interpret experiments at other excitation frequencies either ≫1 Hz or ≪1 Hz. Data from the recent literature, notably the work of Fabry et al. (2001), suggest that cell behavior is unlikely to be captured by a viscoelastic model with a single time constant. In fact, it appears either that a wide range of time constants are relevant, or perhaps that even the notion of representing cellular viscoelasticity with the use of either a discrete or continuous spectrum of time constants might be inappropriate, as suggested by the power-law dependence they observed. We emphasize, therefore, that the present description is intended solely to capture the behavior of the system under the experimental conditions tested, and there is no fundamental or mechanistic reason to expect that it should apply under grossly different conditions. To the extent that the experimental observations of Fabry et al. (2001) are shown to be generally valid, then their results, expressed in terms of a complex shear modulus, might form the basis for a new, more widely applicable approach to continuum modeling. For now, the model presented here should be useful in the prediction of stress and strain deformations, but only for those corresponding to excitation over a relatively narrow range of frequencies in the vicinity of 1 Hz.

Biological significance

This study focuses on the mechanical response of the cell monolayer to bead forcing, hence no active biological response is considered. Implicit is the assumption that whatever remodeling occurs within 2 s, it has minimal effect on the mechanical response of the cell. The characteristic timescale of the mechanical response is of the order of 1 s, whereas the biological response ranges from seconds for calcium release or even focal adhesion remodeling (Balaban et al., 2001) to minutes for cytoskeletal remodeling as reflected by an increase in actin at the site of bead attachment (Glogauer and Ferrier, 1998). Therefore, studying the mechanical effects of the bead on the cell is only the first step to understanding activation of the various pathways after mechanical stimulus. Explicitly, this study aims at identifying the region within which forces or deformations are of sufficient magnitude to potentially elicit a biological response.

The high tensile strains in the membrane, as demonstrated by our simulations, can be correlated to previous experimental observations (Charras and Horton, 2002b). Applying a force by atomic force microscopy (AFM) on the cell membrane and inferring strains from a model, Charras and Horton (2002a) observed that tensile radial strains >0.040 yield a rise in calcium in all osteoblasts, most likely due to stretch-activated ion channels.

Using Eq. 1, the principal values e_i of 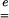can be deduced from the principal values V_i of 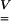as follows:

(5)

Note that and − 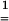are symmetric positive definite second-order tensors. According to Eq. 5, a strain level e_i = 0.04 is equivalent to a stretch level V_i = 1.04.

The numerical simulation led to membrane stretches in excess of 1.04 over a region behind the bead extending 6.0-μm wide in the forcing direction (Fig. 5) and 4.9-μm wide in the transverse direction. Therefore, one might expect that stretch-activated ion channels in this region of the membrane might open due to bead forcing.

The stretches within the monolayer after 2 s at 500 pN range from 0.8 to 1.3, corresponding to strains of up to 20% in extension and 28% in contraction (Fig. 5). These values exceed the threshold of 1–10% strains (Charras et al., 2001; Clark et al., 2002) at which biological responses are elicited, i.e., it is conceivable that mechanotransduction can occur directly by intracellular deformation. Note that these large levels of linear strain occur under the constraint of constant membrane area and are therefore associated with a fluidlike deformation of the bilayer.

Normal stress is predicted to remain <100 Pa in all the simulations reported here. Since no studies demonstrate a biological response to normal stresses this low, it is unlikely that this would initiate biochemical signaling within the cell. Effective stress, in that it provides a measure of shear stress, has a much lower threshold for biological stimulus, on the order of 1 Pa in the case of fluid dynamic shear stress on the cell surface (Resnick and Gimbrone, 1995; Davies, 1995). Effective stresses produced by magnetocytometry are locally far in excess of 1 Pa, and they remain above this threshold over a considerable region extending at least 10 μm from the bead (Fig. 5). Hence, candidate stress-sensitive molecular effectors (integrins, actin-linked proteins, ion channels, G proteins) might potentially be activated as far as 10 μm away from the bead. In addition, regions adjacent to the bead, concentrated just in front of and behind the cell, experience much greater levels of effective stress, approaching 200 Pa, potentially activating pathways with even higher thresholds.

Contribution of the different cell constituents

Simulations conducted with the membrane/cortex shell removed showed that in magnetocytometry experiments at pulling frequencies of ∼1 s⁻¹, the cytoskeleton dominates the overall response of the cell, whereas the membrane/cortex serves simply to transmit the applied force to the cytoskeleton.

Membrane effects may, however, become significant either in the presence of membrane roughness or when the cytometry probe (e.g., AFM probe) size diminishes. In the present simulations, the monolayer surface away from the bead was assumed flat, both for simplification and to enable comparison with the theoretical model of Boulbitch (1999). However, the true membrane contour is more complex. For example, AFM-derived images of the surface of living kidney cells (Le Grimellec et al., 1998) appear granular, with packed particles, whereas epithelial cells typically have cilia, both of which are ignored in the present study.

The membrane may play a more pronounced mechanical role when the probe size decreases, as predicted by the inclusion theory developed by Turner and Sens (1999) for small deformations of an elastic membrane on a purely elastic half-space. According to their predictions, smaller beads or AFM tips with lower applied forces would mainly probe the elastic properties of the membrane, whereas the behavior of larger probes would be influenced predominantly by the cytoskeleton. This might explain why the values of shear modulus obtained by AFM and estimated based on the Hertz theory tend to exceed those reported from other measurement methods.

The smaller characteristic timescale (5–100 ms) of the membrane as compared to the cytoskeleton (1 s) also implies that all stresses in the membrane rapidly relax due to viscous effects, and this would have implications to the stresses that induce conformational changes in ion channels.

Although cell nuclei were not included in our model, on the assumption that nuclear stiffness exceeds that of the cytoskeleton (Guilak et al., 2000), one would expect the nucleus to experience more stress than the surrounding cytoskeleton. Due to the confinement of stresses locally, however, this should have little effect on the present results unless the nucleus is close to the bead. Nevertheless, it has been hypothesized that certain gene transcriptional pathways may be turned on or off in the cell nucleus by direct mechanical stimulus (Ingber, 1997) and the nucleus location with respect to the bead is likely to influence such a response.

Contact between the bead and the cell

Bead attachment to the cell monolayer was modeled using finite element nodes shared by the membrane, the bead, and the cell. However, in reality, the bead is tightly bound via transmembrane receptors (e.g., integrins) directly to the cytoskeleton. These receptors are relatively free to move about in a lipid bilayer composed of laterally mobile phospholipid and protein molecules (Evans, 1983; Lodish et al., 2000). Hence, the membrane is not fixed to the transmembrane receptors, contrary to our depiction in the model, and can flow around them.

The fluidlike, incompressible nature of the membrane is well-rendered by our model utilizing a viscoelastic material with a time constant of 5–100 ms. Indeed, with the forcing rates applied here, the Maxell model for the membrane/cortex essentially reduces to its viscous component, i.e., stress is proportional to strain rate as in a fluid.

The large variation in experimentally recorded bead movement (see Results; also see Fabry et al., 2001)—and the fact that some beads do not show detectable movement at all whereas others in the same experiment move several micrometers—can be attributed to three causes: 1), beads have different contact area with the monolayer, yielding different resistances to the applied force (Laurent et al., 2002); 2), as we have shown, a bead probes only a small cytoskeletal region around it, and hence, different beads probe different parts of a cell with nonuniform stiffness; and 3), cell-to-cell variation.

SUMMARY

The present model is the first in-depth study of deformation and stresses induced within the cell by magnetic force cytometry, features that are essential to gaining a better understanding of force transmission throughout the cell to the various sites where mechanotransduction might occur. Specifically, these simulations address the time-dependent stress/strain distributions induced within the cell by a tethered magnetic bead, using two different continuum viscoelastic models of the cytoskeleton and the membrane/cortex. Although limited in scope, this study provides a framework on which refinements can be made to incorporate the ever-growing body of experimental data on cell mechanics.

Further refinements to the model should address the nature of bead tethering, including the kinetics and thermodynamics of bond formation and rupture, membrane slippage between the bead and the cell, and eventually molecular details. Inclusion of the biological effectors would also help to unravel the mechanisms of mechanotransduction triggered in magnetocytometry.