Interactions of Hydrophobic Peptides with Lipid Bilayers: Monte Carlo Simulations with M2δ

Abstract

We introduce here a novel Monte Carlo simulation method for studying the interactions of hydrophobic peptides with lipid membranes. Each of the peptide's amino acids is represented as two interaction sites: one corresponding to the backbone α-carbon and the other to the side chain, with the membrane represented as a hydrophobic profile. Peptide conformations and locations in the membrane and changes in the membrane width are sampled using the Metropolis criterion, taking into account the underlying energetics. Using this method we investigate the interactions between the hydrophobic peptide M2δ and a model membrane. The simulations show that starting from an extended conformation in the aqueous phase, the peptide first adsorbs onto the membrane surface, while acquiring an ordered helical structure. This is followed by formation of a helical-hairpin and insertion into the membrane. The observed path is in agreement with contemporary understanding of peptide insertion into biological membranes. Two stable orientations of membrane-associated M2δ were obtained: transmembrane (TM) and surface, and the value of the water-to-membrane transfer free energy of each of them is in agreement with calculations and measurements on similar cases. M2δ is most stable in the TM orientation, where it assumes a helical conformation with a tilt of 14° between the helix principal axis and the membrane normal. The peptide conformation agrees well with the experimental data; average root-mean-square deviations of 2.1 Å compared to nuclear magnetic resonance structures obtained in detergent micelles and supported lipid bilayers. The average orientation of the peptide in the membrane in the most stable configurations reported here, and in particular the value of the tilt angle, are in excellent agreement with the ones calculated using the continuum-solvent model and the ones observed in the nuclear magnetic resonance studies. This suggests that the method may be used to predict the three-dimensional structure of TM peptides.

INTRODUCTION

Monte Carlo (MC) simulations have been demonstrated in recent studies to be an important tool in the investigation of peptide-membrane interactions (Milik and Skolnick, 1993, 1995; Baumgartner, 1996; Ducarme et al., 1998; Sintes and Baumgartner, 1998; Efremov et al., 1999a,b, 2002a,b; Lins et al., 2001; Maddox and Longo, 2002). Typically, the MC methods are based on reduced representation of the peptide-membrane system, in contrast to the all-atom representation used in molecular dynamics (MD) simulations. The reduced representation enables comprehensive sampling of peptide conformations and locations in the membrane in an accelerated manner.

The MC methods differ from each other in various aspects. For example, the peptide is represented in atomic resolution in some of them and in residue resolution in others. Similarly, whereas most of these studies are based on approximating the membrane as a hydrophobic profile, in Baumgartner's (1996) study the membrane was represented as a matrix of cylinders, corresponding to the lipid chains. A fundamental difference between the methods is that in some of them the peptide was taken as a rigid helix (e.g., Ducarme et al., 1998), whereas in others it was flexible. The methods also differ from each other in the potential used in the simulations. For example, in the method developed by Efremov et al. (1999a,b), an atomic solvation free-energy term was added to a standard force field. Another free-energy term was recently added to account for effects due to the transmembrane (TM) potential (Efremov et al., 2002a,b). The methods of Milik and Skolnick (1993, 1995) and Maddox and Longo (2002) were based on combining ad hoc potential energy terms that promote α-helix formation, with hydrophobicity scale. Encouragingly, all these methods qualitatively reproduced the relevant experimental data.

We present here a new MC method that can also provide quantitative data, such as the free energy of transfer of the peptide from the aqueous phase into the membrane. A potential was constructed to this effect, and is founded on knowledge-based terms, derived from the proteins of known three-dimensional structure, to govern peptide-conformation changes, in combination with a computationally derived hydrophobicity scale. Each of these terms was first validated separately.

The large electrostatic free energy associated with the transfer of unsatisfied hydrogen bonds from the aqueous phase into the hydrophobic environment of the membrane induces secondary structure formation in TM proteins (Kessel and Ben-Tal, 2002); TM proteins adopt helix bundle or β-barrel folds (White and Wimley, 1999). The hydrophobicity scale mentioned above was derived by calculating the free energy of transfer of the amino acid residues from the aqueous phase into the membrane in the context of a TM polyalanine α-helix. Thus, the model was tailored for short peptides such as M2δ, which are unlikely to form β-barrels, and assume helical structures. (It is noteworthy that recently Efremov and co-workers used their MC method to study the surface adsorption of the β-sheet proteins of the cardiotoxin family; see Efremov et al., 2002a.)

In the work described in the accompanying article, we used continuum-solvent model calculations to characterize key thermodynamic aspects of the interactions between M2δ, a model peptide of 23 residues, corresponding to the second TM segment of the acetylcholine δ-subunit, and lipid bilayers. We determined the most probable peptide-membrane configurations, calculated the free energy of peptide-membrane association, and addressed aspects related to peptide structure and membrane physical properties. In the present study, we used off-lattice MC simulations to study the peptide-membrane association process. We focused on the pathway of M2δ insertion into the lipid bilayer, and the effect of the bilayer and aqueous solution on peptide conformations. Moreover, by describing the lipid bilayer as a polarity profile, we were able to consider effects of the water-membrane interface on M2δ-membrane interactions.

METHODS

The free-energy difference between a peptide in the membrane and in the aqueous phase (ΔG_tot) can be broken down into a sum of differences of the following terms: peptide conformation effects (ΔG_con); solvation free energy (ΔG_sol); peptide immobilization effects (ΔG_imm); lipid perturbation effects (ΔG_lip); and membrane deformation effects (ΔG_def) (Kessel and Ben-Tal, 2002; White and Wimley, 1999), as

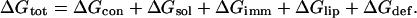(1)

The free-energy terms in Eq. 1 were calculated using the MC method described below, in which the peptide structure was approximated using a reduced representation and the water-membrane environment was represented as a structureless smooth hydrophobicity profile.

Peptide representation

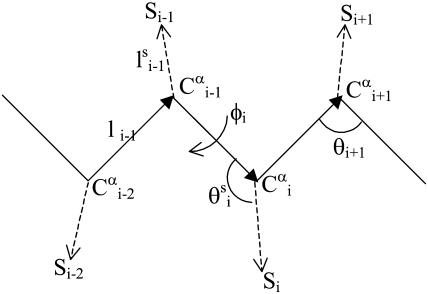
Each residue i was represented by two interaction sites: its α-carbon atom 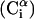and its side chain interaction center S_i (Fig. 1). The latter were selected on the basis of the specific structure and energy characteristics of the amino acids (Bahar and Jernigan, 1996). The peptide backbone was represented by the virtual bond model originally proposed by Flory and collaborators (Flory, 1969). A peptide of n residues has N−1 virtual bonds connecting successive α-carbons. Virtual bonds are highly stiff and were taken here as fixed at their equilibrium values, l_i, all of which are of length 3.81 ± 0.03 Å. Thus, the peptide backbone conformation can be defined by the 2N−5 dimensional vector {θ₂, θ₃, … , θ_n−1, φ₃, φ₄, … ,φ_N−1} corresponding to n−2 virtual bond angles (θ_i) at the i^th carbon, and n−3 dihedral angles (φ_i) at the i^th virtual bond. Similarly, assuming that the distance between S_i and 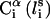is fixed at its equilibrium value, and that the angle between l_i and 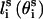is also fixed at its equilibrium value, the conformation of side chain i can be expressed by the torsion angle 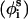, defined by l_i−1, l_i, and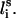

FIGURE 1.

Schematic representation of the virtual bond model. A segment between backbone units 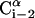and 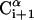is shown. The side chain attached to the i^th α-carbon is marked as S_i. φ_i is the rotational angle of the i^th virtual bond (connecting 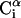and 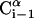). θ_i is the bond angle between virtual bonds i and i + 1. 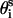(between l_i and 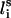, where 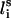is the side-chain virtual bond vector pointing from 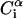to S_i), and 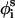(defined by four consecutive atoms 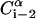, , 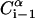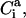and S_i) are the side-chain bonds and torsional angles, respectively.

Internal energy

The internal energy of any conformation Φ = {θ_i, φ_i, and 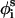) can be decomposed into contributions from short- (E_SR) and long-range (E_LR) interactions, as

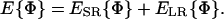(2)

The short-range internal energy was calculated as described in Bahar et al. (1997b) using the formulation of

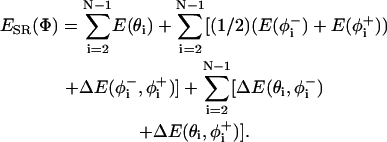(3)

The first summation in Eq. 3 refers to the distortion of bond angles, and the second is for the bond rotational angles, in which φ⁻ and φ⁺ refer to the rotational angles of the virtual bonds preceding and succeeding the i^th α-carbon and the coupling between the latter angles. The last term accounts for the coupling between the rotational and bond angle distortions.

E_LR {Φ} in Eq. 2 was calculated based on Bahar and Jernigan's (1996) knowledge-based potential using the expression

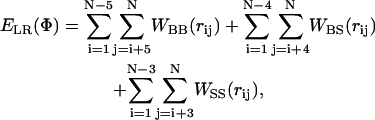(4)

where r_ij is the distance between interaction sites i and j in conformation Φ. The backbone-backbone (BB), backbone-side chain (BS), and side chain-side chain (SS) interactions were taken into account in W_BB, W_BS, and W_SS, respectively.

The functional form of W_BB, W_BS, and W_SS has been derived from data in the Protein Data Bank (PDB); each of them has two minima—characteristics of interactions at the first and second shells in dense systems. Although the suitability of W_BB, W_BS, and W_SS for studies of large and tightly packed proteins has been demonstrated (Bahar et al., 1997a; Haliloglu and Bahar, 1999; Kurt and Haliloglu, 1999, 2001), it is not obvious that this holds for peptides as well. Thus, we carried out MC simulations (of the type described below) of the folding and stability of short polyalanine-like peptides in the aqueous phase (Shental-Bechor, Kirca, Ben-Tal, and Haliloglu, unpublished data). These preliminary studies showed that when all the long-range interactions are included, compact structures such as helical-hairpins are overly stabilized. Our analysis showed that this phenomenon, which is in conflict with the available experimental data, is attributed to a minimum, which corresponds to the second coordination shell in W_BB, W_BS, and W_SS. Thus, we introduced a cutoff distance of 6.8 Å, corresponding to the first coordination shell, into Eq. 4, and included the contributions of the long-range interaction only for interacting sites below this distance.

The exception to this rule is the W_BB term that accounts for generic interactions between the backbone atoms of two closely spaced amino acids independent of their type. Interaction between residues i and i + 5, and between residues i and i + 6, were taken into account in W_BB regardless of the distance cutoff. This means of accounting for the peptide chain's conformational stiffness ensures the incorporation of proteinlike correlations over several consecutive residues (Levy and Karplus, 1979; Hao and Scheraga, 1995; Skolnick and Kolinski, 1999).

Calculation of ΔG_con

The free-energy change due to membrane-induced conformational changes in the peptide (in kT units) can be calculated as

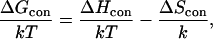(5)

where ΔH_con and ΔS_con are the enthalpy and the entropy changes associated with the transition of the peptide from the aqueous phase into the lipid bilayer, k is the Boltzmann constant, and T is the simulation temperature. A value of T = 1.4 was determined by studying the folding and stability of polyalanine and polyalanine-like peptides of different lengths. Using this value, the experimentally determined Zimm-Bragg parameters and percent helicity were accurately reproduced (Shental-Bechor, Kirca, Ben-Tal, and Haliloglu, unpublished data).

Typically, upon association with the membrane, the peptide assumes a well-defined secondary structure, e.g., an α-helix, to avoid the free-energy penalty due to the transfer of unsatisfied backbone hydrogen bonds from polar to apolar media (Kessel and Ben-Tal, 2002). This affects both ΔH_con and ΔS_con. For example, the confinement of the peptide to the α-helical region in the Ramachandran space leads to negative contributions from the ΔH_con term due to the stable nature of the helical structure, but at the same time it also involves an entropy penalty. This penalty is the difference between S_aq, the entropy in the aqueous phase, and S_mem, the entropy in the membrane; i.e., ΔS_con = S_aq−S_mem.

Both the ΔH_con and the ΔS_con contributions were calculated using the Monte Carlo simulations and the reduced model representation of the peptide. In principle, the free energy itself could have been calculated directly using the internal energies of ample conformations. However, MC (and MD) sampling seeks out lower energy regions, and does not adequately sample the high-energy regions of phase space that make important contributions to the free energy. Thus, the direct calculation of the partition function from the generated conformations may lead to poorly converged and inaccurate results. On the other hand, the free-energy difference between the two equilibrium states is a state function and depends only on the end points. Therefore, we attempted to focus on the properties of the two equilibrium states; the peptide when it interacts with the membrane, and the peptide when it is in the aqueous phase. ΔH_con was approximated as the effective energy difference, ΔE_con, and was calculated by averaging over the internal energy of ample peptide conformations sampled in the latter two states. The ΔS_con term was estimated from the difference between the “volumes” in conformation space that are accessible to the peptide in the respective states.

To this end, the peptide's conformation space was estimated from the local conformation-space volume accessible to its individual bonds. The rotation space of each virtual bond was divided into 72 discrete intervals of 5° each. The entropy was estimated on the premise of independent bond rotations using the familiar “P ln P” relation of

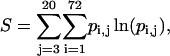(6a)

where p_ij is the probability of virtual bond j to be at interval i. The value of p_ij is estimated as

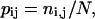(6b)

where n_i,j is the fraction of conformations in which a virtual bond j is at interval i of the total number of conformations N.

Since the termini are in general disordered, we limited the analysis to the helix core, comprised of 18 bond-rotation angles. We estimated the entropy of the peptide in three cases: in water, in TM orientation, and in surface orientation. In simulations around the surface orientation, the peptide is at equilibrium between the water and the membrane. We were interested only in membrane-associated conformations and therefore considered conformations with a negative ΔG_SIL value (see below). This criterion ensures that at least a small portion of the peptide is in the membrane.

ΔG_sol, ΔG_imm, and ΔG_lip

We developed a hydrophobicity scale based on Δg_i, the free energies of transfer of the amino acids from the aqueous phase into lipid bilayers (Kessel and Ben-Tal, 2002). Unlike other hydrophobicity scales (e.g., Kyte and Doolittle, 1982), which assume that the free energies of transfer are proportional to some inherent property (of an individual atom, a chemical group, or an amino acid), this scale was derived using the continuum-solvent model (Honig and Nicholls, 1995), and accounts for the amino acids being located at the center of an α-helix.

The scale, which includes free-energy contributions from peptide solvation and immobilization, and from lipid perturbation effects (Δg__{SIL_i} = Δg_{sol_i} + Δg_{imm_i} + Δg_{lip_i}), is presented in Table 1. Due to the excessive free-energy penalty associated with charge transfer from the aqueous phase into the hydrocarbon region of the bilayer (Honig and Hubbell, 1984), the titratable residues were assumed to be neutral (taking into account the free-energy penalty of neutralizing them in bulk water). Overall, the scale is similar to other hydrophobicity scales in that the hydrophobic and polar/titratable amino acids are at the two extremes. However, it is less hydrophobic than other scales. This is mainly because, unlike other scales, it includes the free-energy penalty of inserting the helix backbone into the bilayer. Our previous studies have indicated that the inclusion of this penalty is crucial for reproducing the experimental values of the free energy of peptide transfer from the aqueous phase into lipid bilayers. Indeed, using this approach, we successfully reproduced the transfer free energy of polyalanine from the aqueous solution to the lipid bilayer (Ben-Tal et al., 1996). Moreover, preliminary tests have shown that the scale is significantly more potent in detecting TM helices in the sequence of membrane proteins compared to other hydrophobicity scales (Chen et al., 2002; Ben-Ami, Honig, and Ben-Tal, unpublished data).

TABLE 1.

Amino acid	ΔGi (kcal/mol)
I	−2.6
L	−2.6
F	−1.5
V	−1.2
A	−0.2
G	0.0
C	+0.4
S	+0.8
T	+1.1
M	+1.3
W	+1.3
P	+2.8
Y	+4.3
Q	+5.4
H	+6.8
K	+7.4
N	+7.7
E	+9.5
D	+11.5
R	+19.8
N–H	+1.8
C=O	+2.5

A hydrophobicity scale representing free energies of transfer of each of the 20 amino acids from water into the center of the hydrocarbon region of a model lipid bilayer (Δg_i). The scale was computationally derived, as described in Kessel and Ben-Tal (2002). The amino acid residues are presented using a single letter code. The values include the free-energy penalty due to the transfer of the backbone hydrogen bond from water into the membrane. The last two rows present an extra free-energy penalty associated with the transfer of unsatisfied backbone N–H and C=O hydrogen bonds from water to the membrane. This penalty was added to the water-to-membrane transfer free energy of amino acids in conformations that are incompatible with hydrogen-bond formation.

Incorporation of the hydrophobicity scale into the reduced model

The free energy (Δg__{SIL_i}(z)) of transferring the i^th residue (at a given conformation) from the aqueous phase to a distance z from the bilayer midplane can be decomposed into contributions from its backbone 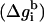and side chain 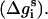We defined ΔG_SIL = ΔG_sol + ΔG_imm + ΔG_lip as the value of the free energy of transferring the whole peptide from the aqueous phase to a distance z from the bilayer midplane as

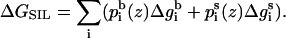(7)

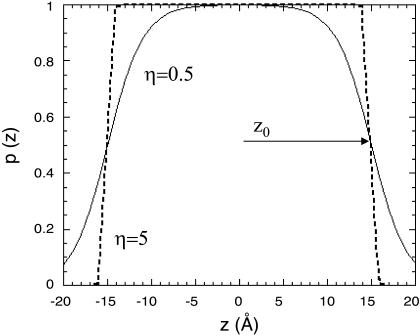
The prefactors in both terms, representing the hydrophobicity of the environment, are proportional to the distance (z) between the interaction site and the bilayer midplane. A sigmoidal function (La Rocca et al., 1999; Milik and Skolnick, 1993; Baumgartner, 1996; Ducarme et al., 1998; Maddox and Longo, 2002; Biggin et al., 1997) of the type (Fig. 2)

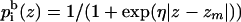(8)

and a similar expression for 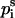were used. In Eq. 8, z_m is the width of a lipid monolayer as defined in the subsection below. The value of η (η > 0) determines the sharpness of the profile, i.e., the characteristic length of the membrane-water interface (Fig. 2); η = 0.5 was used here, whereas η > 5 corresponds to the steep profile of the slab model used in the continuum calculations of the accompanying article.

FIGURE 2.

The hydrophobicity profile. Hydrophobicity, denoted as p, as a function of distance from the bilayer midplane z. The distance between the bilayer midplane and the profile's torque point is marked as z₀. The sharpness of the curve is determined by η. A value of 0.5 (solid line) was used here. At η = 5 (dashed line) the water-membrane interface virtually does not exist.

The free energy of transfer of the peptide backbone from the aqueous phase into the membrane (at a given conformation) was calculated using the set of expressions in Eq. 9,

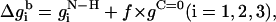(9a)

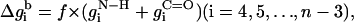(9b)

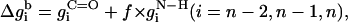(9c)

where the prefactor f is proportional to backbone deviations from the optimal α-helical conformation as observed in Bahar and Jernigan (1996),

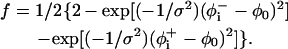(10)

That is, f is assigned a value of zero for residues in their ideal α-helical conformations obtained at φ₀ = −120° (Bahar et al., 1997b); for these residues, the C=O and N–H backbone groups partially neutralize each other. However, the value of f approaches 1 for residues that deviate significantly from the ideal α-helical conformation, e.g., residues that are in extended conformations. For these residues the free-energy penalty due to the transfer of both the C=O and N–H backbone groups is taken into account. Obviously, the presence of Eq. 10 in the potential strongly enhances the formation of helical structures upon membrane association. σ is the standard deviation in the distribution of angles around the optimal α-helical conformation. We estimated a value of σ = 30° based on Fig. 3 in Bahar et al. (1997b) .

FIGURE 3.

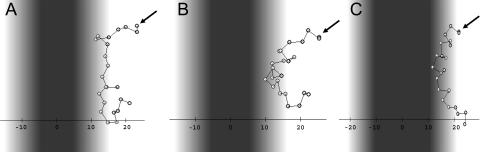
Folding of M2δ on the membrane surface, starting from an extended conformation. The figure presents three snapshots taken at 300 (A), 3300 (B), and 22,500 (C) MC cycles from a representative simulation, carried out using the regular MC sampling protocol. The membrane hydrophobicity profile is color-coded so that dark black represents the most highly hydrophobic region of the lipid chains, gray represents the membrane-water interface, and the aqueous phase is white. The peptide's N-terminus is marked with an arrow. An internal-to-external motion ratio of 10:1 was used.

It is noteworthy that the stretches of three residues at the N- and C-terminals are treated differently than the peptide core (Eq. 9). The free-energy penalty associated with the transfer of the uncompensated hydrogen bonds of the N–H groups of the three residues at the N-terminal is taken into account regardless of the peptide conformation (Eq. 9 a). Likewise, the free-energy penalty due to the transfer of the uncompensated hydrogen bonds of the C=O groups of the three residues at the C-terminal is also taken into account, regardless of the peptide conformation (Eq. 9 c).

Calculation of ΔG_def

Insertion of a rigid hydrophobic inclusion into a lipid bilayer may result in a deformation of the lipid bilayer to match the width of the hydrocarbon region to the hydrophobic length of the inclusion, following the mattress model (Mouritsen and Bloom, 1984). The deformation involves a free-energy penalty, ΔG_def, resulting from the compression or expansion of the lipid chains. ΔG_def has been calculated for lipid bilayers composed of lipids of various types using different methods and yielding similar values (e.g., Mouritsen and Bloom, 1984; Helfrich and Jakobsson, 1990; Fattal and Ben-Shaul, 1993; Ben-Shaul et al., 1996; Dan and Safran, 1998; Nielsen and et al., 1998; May and Ben-Shaul, 1999). We rely on the calculations of Fattal and Ben-Shaul (1993) that are based on a statistical-thermodynamic molecular model of the lipid chains (14-carbon lipids were used), and fitted a harmonic potential of the form

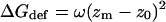(11)

to their calculations. z_m and z₀ are the actual and native widths of a monolayer. We used a value of z₀ = 15 Å based on the available experimental data (White and Wimley, 1999; Nagle and Tristram-Nagle, 2000) and the theoretical studies mentioned above. ω is a harmonic force constant related to the membrane elasticity. A fit to the calculations of Fattal and Ben-Shaul (1993) gives ω = 0.22 kT/Ų.

Generation of conformations

New conformations were generated by simultaneously subjecting the generalized coordinates φ_i, , and θ_i to random perturbations of the type

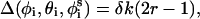(12)

where r is a random number between 0 and 1, and δk is the maximum variation for the respective coordinates. The maximal variation in φ_i was taken as 3°, and a value of 0.5° was used for θ_i and 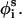Our experience has been that the simulations are not effected by slight changes in the magnitude of δk (Shental-Bechor, Kirca, Ben-Tal, and Haliloglu, unpublished data).

The peptide has a chance of changing its configuration within the membrane mainly by external motions as described below. However, it is noteworthy that a set of randomly chosen conformational changes may eventually lead to slight changes in the orientation of the peptide in the membrane.

Generation of configurations

The external rigid body rotational and translational motions were carried out to allow the peptide to change its configuration, i.e., location in, and orientation with respect to, the membrane. These motions were employed respectively as

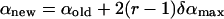(13a)

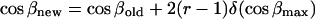(13b)

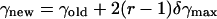(13c)

and

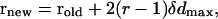(14)

where α, β, and γ are three Euler angles describing the orientation, and r represents the Cartesian coordinates of the peptide's geometric center. δα, δβ, δγ, and δd (=5°, 5°, 5°, and 0.02 Å, respectively) were chosen to be maximum variations (subjected to the adjustment) of the random perturbations of α, β, γ, and d. In general, the maximum variations are adjusted for a reasonable acceptance ratio of the attempted moves. In the current implementation, the proportion of internal versus external moves is also important. These parameters were determined by trial and error, such that the system will have enough time for internal relaxation but will not be trapped too often in local energy minima.

Monte Carlo protocols

We followed a standard MC protocol in sampling the conformational space of the peptide in the aqueous phase; the acceptance of each move, which creates a new conformation from the present conformation, was based on the Metropolis criterion and the internal energy difference (ΔΔE, Eq. 2) between the new and old states (Metropolis et al., 1953). M2δ is a 23-residue peptide. Thus, each MC cycle was composed of N = 23 random perturbations of randomly chosen generalized φ_i, 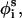and θ_i coordinates.

The equivalent protocol for sampling conformational/configurational space of the M2δ-membrane system would involve using the same criterion and the free-energy difference

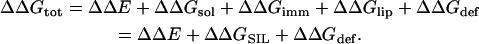(15)

However, although both experimental (Bechinger et al., 1991; Opella et al., 1999) and theoretical (Milik and Skolnick, 1993; Law et al., 2000; Maddox and Longo, 2002) studies indicate that M2δ inserts into lipid bilayers and resides in a TM orientation, it is very well known that membrane insertion involves crossing a large free-energy barrier due to the electrostatic free-energy penalty of transfer of at least one of the peptide's polar termini from the aqueous phase into the hydrocarbon core of the lipid bilayer (Kessel and Ben-Tal, 2002; White and Wimley, 1999). Overcoming this barrier requires a large free-energy fluctuation, and our preliminary simulations indicated that it is very unlikely to occur during the simulation (data not shown).

Thus, for the peptide-membrane system, we used a revised MC protocol composed of two stages, for efficient sampling of the free-energy surface. The first stage was designed for an efficient and rapid sampling of various peptide-membrane configurations, while considering the exact peptide conformation as of secondary importance. The goal at this stage was to detect peptide-membrane configurations of low free energy (e.g., when the peptide is in surface and TM orientations). To this end, we replaced ΔΔG_tot in Eq. 15 with ΔΔG_tot = ΔΔE + ln (ΔΔG_SIL + ΔΔG_def) when applying the Metropolis criterion to the external motions. The use of a logarithmic function for the membrane-related free-energy contributions significantly reduces the barrier of peptide insertion. To further enhance the membrane-insertion probability, we used an internal-to-external-motion ratio of 1:1. Obviously, this crude search is likely to provide only approximated peptide-membrane configurations. (It is noteworthy that utilization of the logarithm of the energy, rather than the energy itself in MC simulations, has been proven to be useful in protein structure predictions as well; see Zhang et al., 2002.)

This crude search provided two main free-energy minima: one corresponded to surface-adsorbed and the other to TM-inserted M2δ. In the following stage, a standard MC sampling with the Metropolis criterion and the free-energy difference of Eq. 15 (without lowering the barrier heights for the external motions) was used in a fine-tuned search in conformation/configuration space in the vicinity of each of these two minima.

Experimental structures used in the study

The structure of M2δ in the simulations was compared to the following structures of the peptide, which have been previously determined using nuclear magnetic resonance (NMR) techniques:

1. The structure of M2δ in dodecylphosphocholine (DPC) micelles (Opella et al., 1999; PDB entry 1A11).

2. The structure of M2δ in dimirystoylphosphatidylcholine (DMPC) bilayers (Opella et al., 1999; PDB entry 1CEK).

3. The molecular model of the AChr M2 channel structure (Opella et al., 1999; PDB entry 1EQ8).

RESULTS

M2δ in water

Starting from an extended conformation, we simulated M2δ in the aqueous phase using the standard Metropolis MC sampling scheme described in Methods. Eight independent runs of 5 million MC cycles each were carried out and the results were averaged over all of them. A very low average helicity of 0.2(±0.05)% was obtained, indicating that M2δ is a random coil in the aqueous phase. This is in agreement with the MD simulations of Law et al. (2000). The average effective conformational energy in the aqueous phase was 〈E_con〉_aq ≈ −49 (±4.9) kT.

The conformational entropy, S_con, of M2δ in the aqueous phase was estimated from the conformation-space volume of its individual bonds, as explained in Methods. In short, the conformation space was divided into discrete intervals of 5° each. The analysis showed that each of these intervals was occasionally occupied by the unstructured peptide bonds during the simulations. We calculated the frequency that an interval of the torsion space was occupied by the peptide. The two bonds at each peptide terminus were flexible both in the aqueous phase and in the membrane so we limited the analysis to the 18 central bonds, and obtained a value of (S_con)_aq = 64.7 ± 2.5 k. (It is noteworthy that the absolute values of (S_con)_aq and (S_con)_mem—i.e., the conformational entropy of the peptide in the aqueous phase and in the membrane, respectively—reflect the sampling procedure and are therefore meaningless; only the entropy change ΔS_con = (S_con)_mem−(S_con)_aq is meaningful.) To check the robustness of the entropy estimate to interval size, we divided the space into 12 intervals of 30°. Although the absolute values of the entropy are different for the two interval sizes, ΔS_con is stable and does not depend on the interval size.

Membrane association

Folding of M2δ on the surface

Simulations of M2δ, starting from a randomly generated conformation near the membrane surface, were carried out with the standard MC sampling procedure described in Methods. The simulations demonstrated the following path of peptide association with the lipid bilayer (Fig. 3). First, the extended chain adsorbed onto the bilayer surface (Fig. 3 A). As a result of its interaction with the lipid bilayer, the chain gradually assumed a highly ordered helical structure (Fig. 3, B and C). M2δ has a hydrophobic core and two polar termini. As a result, it assumed a curved, bridgelike conformation, with both unstructured polar termini anchored in the water-membrane interface, and the helical hydrophobic core slightly immersed in the hydrocarbon region of the membrane (Fig. 3 C). The bananalike helical structure persisted throughout the simulation. A similar adsorption/folding pathway was observed in 13 different runs.

Insertion of M2δ into the membrane

M2δ insertion into the lipid bilayer involves a high free-energy barrier, resulting from the transfer of at least one of the highly polar segments at the peptide termini from the aqueous phase into the hydrophobic core of the bilayer. To facilitate the insertion process, we used the revised MC protocol as described in Methods above, which lowers this free-energy barrier, and allows the system to explore unfavorable configurations with high free energy. In addition, we reduced the desolvation free-energy penalty values of residues E1 and K2 by half. This modification is in accordance with the peptide sequence, which suggests that these two residues may be salt-bridged. The salt-bridge is likely to reduce the polarity of both these residues significantly (Honig and Hubbell, 1984).

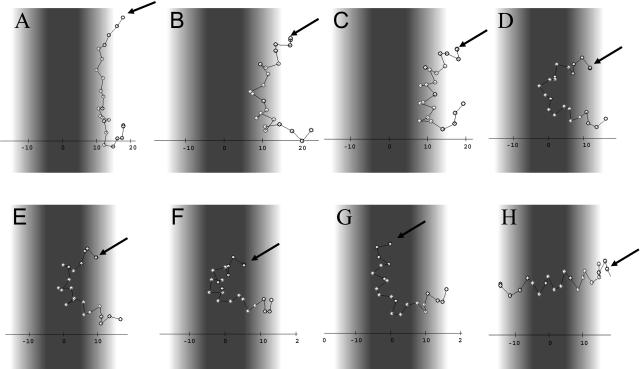
The path of M2δ association with the lipid bilayer, obtained using the revised MC protocol, is shown in Fig. 4. The extended peptide (Fig. 4 A) first adsorbed onto the membrane surface, assuming a helical structure. As the central part of the chain diffused into the hydrocarbon region of the bilayer, the peptide acquired a bridgelike form and its conformation became more ordered (Fig. 4, B and C). As the simulation advanced, the peptide core became more immersed in the hydrocarbon region and its curved conformation turned into a helical-hairpin (Fig. 4, D and E). From this point and on, several attempts to cross the barrier between the surface and TM orientations were made. One of these attempts, involving a translocation of the (modified) N terminus across the membrane, was successful (Fig. 4, F and G) and resulted in TM orientation (Fig. 4 H).

FIGURE 4.

Insertion of M2δ into the membrane. Snapshots from a representative simulation carried out using the revised MC protocol. (A) 0 MC cycles, (B) 240,000 MC cycles, (C) 600,000 MC cycles, (D) 1,100,000 MC cycles, (E) 1,200,000 MC cycles, (F) 1,250,000 MC cycles, (G) 1,280,000 MC cycles, and (H) 1,500,000 MC cycles. The membrane hydrophobicity profile is color-coded as in Fig. 3. The peptide inserts into the membrane with its N-terminus (marked by arrow) first. An internal-to-external motion ratio of 1:1 was used.

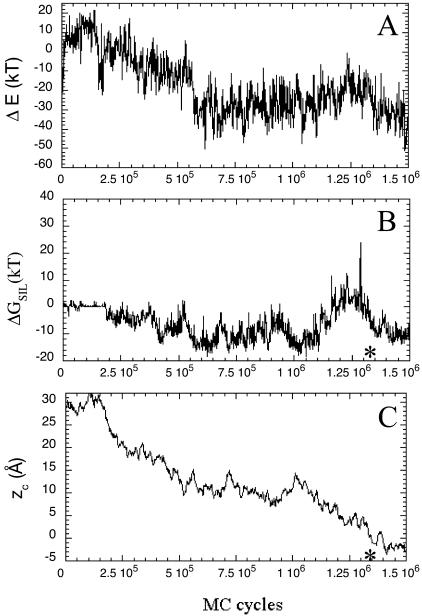
Fig. 5 displays the change in the peptide's internal energy with respect to the value in the aqueous phase, the corresponding solvation free-energy change, and the change in z_c as a function of the number of MC cycles. Peptide folding on the bilayer surface involved a decrease both in the internal energy and in the solvation free energy. At a certain point, the system gained enough solvation free energy to overcome the barrier due to peptide insertion (marked by asterisks in Fig. 5, B and C), and M2δ assumed a TM orientation, with z_c fluctuating around the bilayer midplane. The simulations were carried out using the modified MC protocol described above and the large z_c fluctuations observed for M2δ in the TM orientation are due to the overly smoothed nature of the free-energy surface used.

FIGURE 5.

(A) The internal energy change (ΔE) with respect to aqueous phase (E_aq = 49 kT) vs. the number of MC cycles. (B) The total external free-energy change (ΔG_SIL) vs. the number of MC cycles. (C) The change in z_c (the distance between the peptide's centroid and the membrane midplane) as a function of the number of MC cycles. An internal-to-external motion ratio of 1:1 was used.

Local search around the low energy configurations

The simulations described above show two stable peptide-membrane configurations: surface and TM. These simulations were carried out by the use of the revised MC sampling protocol, which produced a coarse free-energy surface. To derive more accurate free-energy values for the transfer of M2δ from the aqueous phase into the TM and surface orientations in the bilayer, we carried out further simulations around these two orientations using the regular MC sampling. Nine different simulations were carried out around the TM orientation and 13 around the surface orientation. Table 2 shows the thermodynamic characteristics of the average surface and TM orientations, obtained from these simulations. As Table 2 demonstrates, both are stable, with the latter the most stable, in agreement with our continuum-solvent studies (see accompanying article), and the studies mentioned above. The thermodynamic properties of Table 2 are analyzed below in the Discussion.

TABLE 2.

	TM orientation	Surface orientation
ΔGtot* (kT)	−10.2 ± 5.6	−7.4 ± 13.4
ΔGcon† (kT)	−5.4 ± 5.6	−3.3 ± 11.6
ΔE‡ (kT)	−35 ± 5	−14.4 ± 9.6
−TΔScon§ (k)	29.6 ± 2.6	11.1 ± 6.6
ΔGSIL¶ (kT)	−7.6 ± 0.1	−4.3 ± 2.5
ΔGSIL_b‖ (kT)	8.35 ± 0.12	3.5 ± 1.2
ΔGSIL_s** (kT)	−15.91 ± 0.01	−7.8 ± 3.7
ΔGdef†† (kT)	2.8 ± 0.06	0.2 ± 0.2
〈z〉‡‡ (Å)	11.53 ± 0.04	15.4 ± 0.4
abs(zc)§§ (Å)	1.6 ± 0.2	24.6 ± 3.2
〈θ〉¶¶ (°)	13.95 ± 0.3	86 ± 3.2

Thermodynamic parameters for the membrane association of M2δ in TM and surface orientations. The values represent the average obtained after equilibration.

^*Total free energy (ΔG_tot).

^†ΔG_con = ΔE − TΔS_con.

^‡Internal energy, calculated with reference to 〈E_aq〉 = 49 kT.

^§The conformational entropy component.

^¶Total external free energy, including peptide solvation and immobilization and lipid perturbation effects: ΔG_SIL = ΔG_sol + ΔG_imm + ΔG_lip.

^‖Backbone external free energy.

^**Sidechain external free energy.

^††Membrane deformation free energy.

^‡‡The width of a monolayer.

^§§Absolute value of the z-coordinate of the centroid of the chain; midplane of the membrane is at z = 0.

^¶¶The projection angle of the peptide's end-to-end distance vector r and the membrane normal z. The values in parentheses depict the standard deviation of different runs for given case.

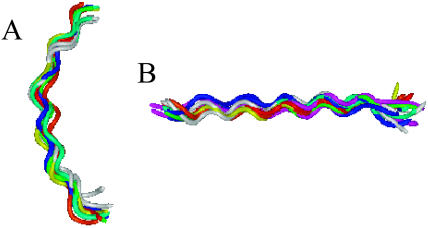
We carried out a clustering analysis of the structures both in the TM and surface orientations. The analysis focused on the peptide core (residues 3–21) alone, since the terminal segments were relatively flexible and it is difficult to tell if this is an inherent property of the peptide or an artifact of the model. The analysis showed that most surface conformations have a helical bananalike core, but they fluctuate significantly at the terminal segments. Approximately one-half of the conformations correspond to a single cluster (Fig. 6 A), whereas the rest are distributed over many other clusters, most of which are singletons.

FIGURE 6.

Clusters of M2δ conformations. Two clusters, corresponding to the peptide in surface, A, and TM, B, orientations, obtained from one simulation. The conformations were clustered according to a similarity measure of RMSD < 2.5 Å. (A) The largest of all the clusters that were obtained in the surface orientation corresponds to a bananalike helix structure. (B) The single cluster that was observed in the TM orientation corresponds to a canonical α-helix structure.

The TM conformations correspond to another cluster of regular helical structures (Fig. 6 B). The 10 NMR structures (1A11) used in the continuum-solvent study (see accompanying article), and the structure of the peptide in the bilayer (1CEK) would also belong to the latter cluster. Our analysis also showed that an ideal α-helix would reside in the same cluster, suggesting that this cluster represents a fluctuating canonical α-helix. A detailed comparison between the average RMSD value of the predicted conformations in the TM and surface orientations and the 10 NMR structures is presented in Table 3. The comparison further emphasizes the similarity between the predicted and experimental structures. The agreement is particularly good for the TM structures, where the average RMSD is typically <2 Å.

TABLE 3.

NMR structure	TM 〈RMSD〉 (Å)	Surface 〈RMSD〉 (Å)
1A11_1	1.93	3.54
1A11_2	2.30	3.91
1A11_3	1.77	3.85
1A11_4	2.20	3.77
1A11_5	1.80	3.91
1A11_6	1.93	3.54
1A11_7	2.09	3.84
1A11_8	1.84	3.81
1A11_9	2.60	3.25
1A11_10	1.76	3.63
1CEK	1.3

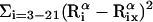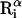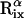Average root-mean-square deviation (〈RMSD〉) of peptide conformations, in the TM and surface orientations, compared to the NMR structures of Opella et al. (1999). The RMSD of each conformation was defined as 1/19 , where and are the position vectors of 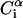in the predicted and NMR structures, respectively, after superimposition.

Solid-state NMR provides information about the orientation of the peptide in oriented lipid bilayer (Opella et al., 1999). With the use of this information we can infer the tilt of the peptide in the lipid bilayer, and the helix rotation about the principal axis. Our simulations show that the average tilt angle about the membrane normal is 14°, which is in good agreement with the value of 12° reported by Opella et al. (1999). In the model of the AchR M2 pentameric channel (PDB 1EQ8), the wide mouth of the funnel is on the N-terminal part of the peptide and the pore lining residues are E1, S8, V15 L18, and Q22. To check the position of these residues in the simulations, we randomly sampled 10 conformations, all of which matched the orientation suggested by Opella et al. (1999).

An estimate of ΔG_con and ΔG_tot

The calculation of ΔS_con, the entropic component of ΔG_con, was carried out using Eq 7. Out of the total of 72 intervals, only a few, corresponding to the rotation angles that are characteristic of helix conformations, were sampled by the membrane-associated peptide bonds in the TM orientation (S_trans = 35.1 (±0.7) k). In the surface orientations, the peptide is less stable and a larger part of the conformational space is accessible (S_surf = 53.7 (±6.1) k). In contrast, all the 72 intervals were accessible to the peptide bonds in the aqueous phase (see above) with high probability (S_aq = 64.7 (±2.5) k). The entropy values of the TM and surface conformations are in accordance with the results of the clustering analysis. The TM conformations are more rigid, and we therefore obtained one cluster of conformations, and a low value of the entropy. The surface conformations are more flexible; hence they are distributed over many clusters, and the entropy value is high.

The average values of the internal energy change (ΔE) due to the transfer of M2δ into the TM and surface orientations are ∼−35 kT and −14 kT, respectively (Table 2). Using Eq. 6 and the estimated ΔS_con, ΔG_con = ∼−5.4 kT and ∼−3.3 kT is obtained for the TM and surface orientations (Table 2). Using these values and Eq. 1, we obtained ΔG_tot values of −10.2 kT and −7.4 kT for the transfer of M2δ from the aqueous phase into the membrane in the TM and surface orientations (Table 2).

DISCUSSION

A novel MC method was used here to study the interactions of M2δ with lipid bilayers. In the following we discuss a few central features of this method and its main limitations in view of the complexity of peptide-membrane systems. We then compare it to other methods and conclude with a discussion of the significance of the results.

Features and limitations of the model

The MC protocol used here involves a rough exploration of the peptide-membrane conformational/configurational space using an approximated potential energy as described above. Peptide-membrane conformations/configurations, which appear to be stable, are then explored further by carrying out more MC sampling using the “exact” potential of mean force of Eq. 15. In the M2δ example presented here, two favorable peptide-membrane configurations were detected: surface (Fig. 4 B) and TM (Fig. 4 H), as anticipated. Less obvious configurations may be discovered by using the same searching protocol to investigate the membrane association of other peptides.

Our approach was similar to that of Efremov et al. (1999a,b, 2002a,b), inasmuch as we verified that, when each of the free-energy terms in Eq. 1 is taken separately, it reproduced the appropriate experimental data. The ΔG_con component, which was essentially derived from the available proteins of known three-dimensional structure, was shown to be potent in reproducing experimental data on the folding and stability of a series of polyalanine-like peptides (Shental-Bechor, Kirca, Ben-Tal, and Haliloglu, unpublished data). Similarly, the membrane-related terms (ΔG_SIL), which were derived from continuum-solvent model calculations of the transfer free energy of each of the amino acids from the aqueous phase into the membrane, were shown to be potent in detecting the TM helices of proteins of known three-dimensional structure (Chen et al., 2002).

The potential we employed favors the formation of the peptide backbone hydrogen bonds in a direct, and an indirect, manner. Hydrogen-bonding is beneficial due to favorable internal energy contributions, and to the fact that by assuming helical conformations, which involve satisfied backbone hydrogen bonds, the system can escape a heavy penalty resulting from the desolvation terms. Indeed, as in similar methods (Milik and Skolnick, 1993, 1995; Baumgartner, 1996; Ducarme et al., 1998; Efremov et al., 1999a,b, 2002b; Lins et al., 2001; Maddox and Longo, 2002) our potential promotes helix formation in the membrane. Nevertheless, differences in the helicity of M2δ between the TM and surface orientations were observed in this study. The hydrophobic environment of the membrane strongly imposed helicity in the TM orientation and significantly limited the conformations accessible to the peptide (Fig. 6 B). In contrast, several conformations with various degrees of helicity were observed in the surface-adsorbed orientation. The fact that stable, nonhelical conformations have been observed in the simulations suggests that the potential of Eq. 1 does not overimpose helicity.

One of the novelties of this study is that peptide-induced membrane deformation effects were included in the MC simulations. This was done by the inclusion of the ΔG_def harmonic component in the potential as described in Methods. The magnitude of this term depends on the values chosen for the unperturbed width of the lipid bilayer and the force constant, reflecting the membrane response to changes in its width. Both of these values may differ, depending on the lipid composition of the membrane. In this study we chose values that are typical for biological membranes (White and Wimley, 1999; Nagle and Tristram-Nagle, 2000). The same approach was successfully used in continuum-solvent model studies of the interactions between different peptides and lipid bilayers (e.g., Kessel et al., 2000a,b; Bransburg-Zabary et al., 2002).

Our simulations suggest the formation of a helical-hairpin structure during peptide insertion into the lipid bilayer (see further discussion below). The insertion of the helical-hairpin into the lipid bilayer is likely to disturb the organization of the latter. In our simulations, membrane perturbation effects were taken into account in the ΔG_SIL term, which is based on the calculated hydrophobicity scale of Kessel and Ben-Tal (2002). However, the values of the scale correspond to the perturbation of a membrane by a single, narrow and rigid α-helix that interacts with the two leaflets, whereas the hairpin, which is wider and most likely less rigid, spans only one leaflet of the bilayer. Since the value of ΔG_lip is small compared to other free-energy terms, even a significant change in its magnitude should not drastically affect the results.

The systematic approach in the construction of the potential in Eq. 1 enabled us to provide an estimate of the total free energy of membrane association as well as an energy breakdown into components. However, it is important to take note that this systematic approach does not fully guarantee that these terms perform well in concert. For example, it may well be that the various free-energy components do not add up to produce a well-balanced, total transfer free energy; that is, unit conversion factors may be missing. In addition there are some cases in which parts of the energy components may be counted several times. For example, in the case of large TM proteins, where residues at the protein core are tightly packed, the hydrophobicity may be accounted for both in the internal side-chain-to-side-chain interaction terms and the external solvation term. Such “overcounting” should have a minor effect in this study, since short peptides such as M2δ are completely surrounded by the solvent.

M2δ is insoluble in water, and tends to aggregate above a certain critical concentration. Our simulations include only one M2δ molecule and hence correspond to infinitely dilute aqueous solutions. This complicates the comparison of our results to experimental data. Experimental studies of M2δ's association with lipid bilayers (e.g., Opella et al., 1999) require its solubilization in organic solvents, which are missing in the simulations. This suggests that the pathway of membrane association and insertion of M2δ in typical experiments is most likely different than the one observed in our simulations.

Comparison with other MC methods

In general, our approach is closest to those of Milik and Skolnick (1993, 1995) and Maddox and Longo (2002). As in these studies, we used a residue-level resolution. However, we used two interaction sites for each amino acid, rather than only one. This is a more realistic representation of the physicochemical nature of the amino acids than single interaction sites. Furthermore, it enables hydrophobic residues, such as Leu, to assume conformations in which the side chain interacts favorably with the hydrocarbon core of the membrane, whereas the polar backbone partitions into the membrane-water interface.

The treatment of backbone hydrogen-bonding in our model is significantly different than that of Milik and Skolnick (1993, 1995) and Maddox and Longo (2002). In contrast to these two methods, the favorable internal energy contribution from hydrogen-bond formation in our model may change depending on the identity of the residue.

Previous MC studies provided only qualitative, rather than quantitative data on the peptide-membrane system (Milik and Skolnick, 1993, 1995; Baumgartner, 1996; Ducarme et al., 1998; Sintes and Baumgartner, 1998; Lins et al., 2001; Maddox and Longo, 2002). The method of Efremov et al. (1999a,b, 2002a,b) is an exception, as the free energy of peptide-membrane association is often provided. However, these values are usually unrealistically large in magnitude. This is presumably an inherent property of the internal energy term used in their potential, since the value reported recently for the membrane adsorption of two cardiotoxins, where only small conformation changes were recorded upon membrane association, appears to be reasonably low in magnitude (Efremov et al., 2002a).

The main advantage of our method over similar MC simulations is that it provides quantitative information. Average values of the free energy of peptide-membrane association were provided, and are comparable to those measured in similar systems. The corresponding standard deviations provide an indication of the stability and convergence of the simulations. The model also accurately reproduced the helical conformation of M2δ and its tilt in the membrane in the TM orientation. A more detailed comparison of our results with the measurements is provided below.

Comparison with continuum-solvent model calculations

In our previous studies (e.g., the accompanying article), we described the lipid bilayer as a low-dielectric slab, embedded in a high dielectric medium (i.e., the aqueous solution). This simplistic model of the bilayer has been shown in our studies with different membrane-spanning peptides to have the capacity to describe the main thermodynamic and kinetic properties of the peptide-membrane system (Kessel et al., 2000a,b; Bransburg-Zabary et al., 2002; Kessel and Ben-Tal, 2002). However, it could not capture various aspects related to the interaction of the peptides with the water-membrane interface. This problem was addressed in the present simulations. Following the approach of Baumgartner (1996), Biggin et al. (1997), Ducarme et al. (1998), La Rocca et al. (1999), Maddox and Longo (2002), and Milik and Skolnick (1993), we described the lipid bilayer using a polarity profile, which allowed a mean field description of the polar headgroup region of the lipid bilayer and its effect on the association of M2δ with the membrane.

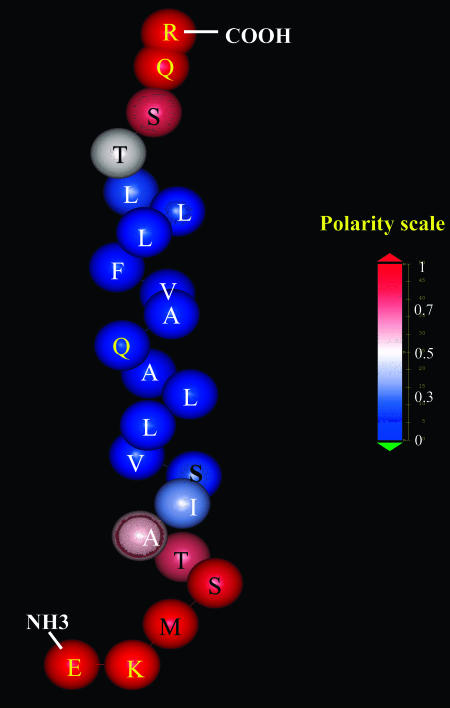
The average TM orientation of M2δ observed in the simulations is such that the polar termini of the peptide reside in the polar headgroup region of the membrane (Fig. 7), which is missing in the slab model used in the accompanying article. This accounts for the difference in the free energy of association with the membrane, as suggested by the two models. That is, the association free energy was less negative when the polarity of the lipid headgroups was considered, as compared to the value obtained from the slab model (Table 2 here versus Table 2 in accompanying article). The reason for the difference is that in the modified model but not in the slab model some of the polar groups at the peptide termini were exposed to regions of intermediate polarity. That is, these regions are more polar than the hydrocarbon region, but not as polar as the aqueous phase. The resulting electrostatic transfer free-energy penalty makes the solvation free energy less negative.

FIGURE 7.

The average position of M2δ in the lipid bilayer in the TM orientation. In the simulations, each residue in the peptide was represented by two interaction centers (backbone and side chain). Here, each residue is presented as a single sphere, for clarity. The spheres are located at the C^α nuclei. The identities of the residues are noted by one letter code. The peptide is colored according to the polarity of the environment of each residue in the average position. The color code appears in the scale at the right side of the figure.

The difference between the two models also accounts for the observed differences in the membrane curvature in the two studies: the continuum-solvent calculations suggested a reduction of ∼10 Å in the width of the lipid bilayer in response to peptide insertion, whereas the MC simulations suggest a more likely value of 7 Å (Table 2). Again, this is most likely due to the fact that the interactions of M2δ's termini with the polar headgroups of membrane lipids are included in the MC, but not in the continuum-solvent model studies.

Our MC simulations use an implicit description of the peptide, where each residue is represented by two interaction sites. The implicit description makes the simulations computationally feasible. However, it involves inaccuracies in the calculations, especially those related to the solvation free energy, which strongly depends on the location of each atom (particularly those that are polar). Conversely, the continuum-solvent model, in which the peptide is described explicitly, emphasizes the consideration of such effects.

Insertion pathway

The simulations show that M2δ association with the lipid bilayer begins with adsorption on the membrane surface (Fig. 3). The following step involves rearrangement into a partially helical structure, which is then inserted into the membrane (Fig. 4). This insertion pathway is in accordance with the model proposed by Jacobs and White (1989). Our continuum-solvent model calculations (see accompanying article), and the studies of Milik and Skolnick (1993, 1995) and Maddox and Longo (2002) give further support to the Jacobs and White model.

In our simulations, M2δ insertion into the lipid bilayer involves the formation of a helical-hairpin intermediate. This intermediate is formed independently of the starting conformation and orientation of the peptide with respect to the bilayer. The helical-hairpin intermediate, first suggested by Engelman and Steitz (1981), is consistent with the amino-acid sequence of M2δ and other membrane-spanning peptides, which are typically composed of a hydrophobic core with polar terminal segments. It was also observed in other MC studies (e.g., Milik and Skolnick, 1993; Maddox and Longo, 2002).

In M2δ, the central region is overall hydrophobic, but includes a few polar residues (e.g., S8, Q13). In the helical-hairpin conformation, these polar residues are transferred into the hydrocarbon region of the bilayer, which is energetically unfavorable. The inherent instability of the hairpin conformation inside the bilayer encourages major structural fluctuations that ultimately lead to membrane translocation of one of the polar termini, such that the peptide resides in a TM orientation. It should be noted that S8 and Q13 are also exposed to the hydrocarbon region of the bilayer in TM orientations. However, in the TM orientations, the destabilizing effect due to the lipid exposure of these two residues is overcompensated by stabilizing internal energy and solvation effects due to α-helix formation.

Recent MC simulations by Maddox and Longo (2002) suggested another insertion pathway. In this alternative pathway, the peptide first assumes a straight helical conformation along the membrane-water interface. One of its termini becomes inserted into the hydrocarbon region of the membrane, and finally sprouts from the other end. Such a pathway was never observed in our simulations and since the potential used in our simulations differs very much from that of Maddox and Longo, it is difficult to suggest a possible reason.

We repeated the simulations with a modified C-terminus; residue R23 was assigned half its desolvation free-energy penalty. Although the peptide structure does not justify this modification, we used it to see whether the simulations were sensitive to the modification. Indeed, the modification led to the insertion of M2δ into the membrane from its C-terminus, in contrast to insertion through the N-terminus, which was observed using the regular protocol (Fig. 4). This is a further demonstration of the dominant effect of the termini on peptide insertion. It also demonstrates that the revised MC scheme, which operates on a much less rough energy surface compared to the regular scheme, is still sensitive enough to distinguish between the energetic modifications at the termini, as in all cases the peptide prefers to insert into membrane from the modified terminus.

Thermodynamic properties

The average free-energy values obtained in our simulations demonstrate the TM orientation to be most favorable for M2δ. This state is favored over the surface orientation by both the solvation (ΔG_sol) and internal (ΔE) components of the total free energies. However, it involves the ΔG_def penalty, since peptide insertion into the membrane introduces local thinning of the membrane to match with the length of the peptide's hydrophobic core, and a high entropy penalty.

The conformation entropy penalty (ΔS_con) of the TM orientation is larger than that of the surface orientation; in the TM orientation the virtual bonds are confined to a much smaller fraction of the conformation space as compared to the surface orientation. The two membrane-associated orientations appear different, both by estimation of the entropy and by cluster analysis of the conformations generated during the simulations (Fig. 6, A and B).

ΔG_con values of −5.4 and −3.3 kT were obtained for membrane association of M2δ in the TM and surface orientations, respectively. These values are very similar to the Zimm-Bragg value of ∼−4 kT (Zimm and Bragg, 1959; Lifson and Roig, 1961; Chakrabartty and Baldwin, 1995; Scholtz and Baldwin, 1992) that was used in the companion article.

On average, the TM orientation is favored over the surface orientation by 3 kT, which is significant in itself, but is smaller in magnitude than the standard deviations in the calculated free-energy values of the two peptide-membrane configurations. In particular, the fluctuations in the total free-energy values of the surface orientation are larger in magnitude than the average value itself: −7.4 (±13.4) kT. The free energy of the TM orientation has a lower variation: −10.2 (±5.6) kT. The large variation in the surface orientation is a result of the high flexibility of the peptide in this orientation, which is reflected in high variability of the internal energy, the conformational entropy, and the solvation components of the total free energy.

Our previous studies of peptide-membrane interactions (e.g., Kessel et al., 2000a,b; Bransburg-Zabary et al., 2002) have demonstrated the dominance of solvation effects in these systems. The free-energy change due to conformation effects (ΔG_con) was assumed to be negligible compared to the solvation free energy, mainly because conformation changes, which accompanied the transfer of the peptide from the aqueous solution into the lipid bilayer, were confined to small regions on the peptide. M2δ is likely to go through significant conformation changes during this transfer, which suggests comparable free-energy changes. Indeed, our simulations suggest that, in the M2δ-membrane system, the value of ΔG_con is similar in magnitude to the value of ΔG_SIL. ΔG_def, which is the only term disfavoring the transfer of the peptide into the membrane, has a significant value as well, resulting from the large deformation observed in this system.

Our simulations demonstrate that, on average, M2δ assumes a TM α-helix conformation with a slight tilt with respect to the membrane normal. The TM conformations produced during the simulations are very close to the NMR structures obtained by Opella et al. (1999), with root-mean-square deviations of <3 Å (usually <2 Å; see Table 3). The observed tilt of 14° (Table 2) compares well with the value of 15° that was calculated using the continuum-solvent model (see accompanying article) and the value of 12°, which was measured in lipid bilayers using solid-state NMR (Opella et al., 1999). The partitioning of M2δ between the aqueous phase and lipid bilayers was not measured, but the calculated water-to-membrane transfer free energy of the peptide (ΔG_tot = −10.2 kT) compared well with values that were measured for similar peptides (White and Wimley, 1999). The overall good agreement between simulations and experiments suggests the potency of the methodology for studying the interactions between hydrophobic peptides and membranes.