Abstract
Valproic acid is a short branched fatty acid used as an anticonvulsant drug whose therapeutic action has been proposed to arise from membrane-disordering properties. Static and kinetic properties of valproic acid interacting with fully hydrated dipalmitoyl phosphatidylcholine lipid bilayers are studied using molecular-dynamics simulations. We calculate spatially resolved free energy profiles and local diffusion coefficients using the distance between the bilayer and valproic acid respective centers-of-mass along the bilayer normal as reaction coordinate. To investigate the pH dependence, we calculate profiles for the neutral valproic acid as well as its water-soluble anionic conjugate base valproate. The local diffusion constants for valproate/valproic acid along the bilayer normal are found to be ∼10−6 to 10−5 cm2 s−1. Assuming protonation of valproic acid upon association with—or insertion into—the lipid bilayer, we calculate the permeation coefficient to be ∼2.0 10−3 cm s−1, consistent with recent experimental estimates of fast fatty acid transport. The ability of the lipid bilayer to sustain local defects such as water intrusions stresses the importance of going beyond mean field and taking into account correlation effects in theoretical descriptions of bilayer translocation processes.
TRANSLOCATION: INTRODUCTION
We study here computationally the permeation of valproic acid across a model lipid bilayer. The translocation of hydrophilic compounds across the semipermeable membranes surrounding biological cells is generally associated with large free energy barriers, roughly corresponding to the transfer from aqueous solution to a hydrocarbon phase and back. This is a fact that may complicate, for example, delivery of candidate drugs to target cells. The relative ease by which a particular compound travels across a membrane does, however, show substantial dependence on both simple properties such as size of the penetrant and width of the bilayer, as well as on more complex properties such as patterns of amphiphilicity (Marrink and Berendsen, 1994, 1996; Kessel et al., 2001; Parsegian, 1969; Powell and Weaver, 1986; van Winkle, 1999). Possible mechanisms of nonprotein-mediated, energetically independent transport across may include: “hopping” peristaltic motion, local chemical modification (i.e., protonation of charged groups), simple diffusion across a mainly unperturbed membrane, spontaneous or induced membrane fluctuations, and polarization of solvent molecules, e.g., water or ions (van Winkle, 1999; Xiang and Anderson, 1994, 1998, 2000).
A rough estimate of ∼50 kcal mol−1 for transport of an single ion such as chlorine across a hydrated phospholipid bilayer is obtained from a simple continuum model (Parsegian, 1969), where the lipid bilayer is represented as a dielectric discontinuity. The dielectric constant of water is ∼80, whereas it is ∼2–10 in the alkyl region of the lipid bilayer. However, many biologically relevant ions contain titratable groups, and may, for instance, become neutralized upon membrane association. In the biological cell, the bilayer composition is also highly heterogeneous (up to ∼75% proteins) and the effect of protein inclusions has been estimated previously to make the bilayer ∼100× more permeable (Powell and Weaver, 1986). In a transition-state-type theory (Schulten et al., 1981) this roughly translates into a free energy barrier difference of 2–3 kcal/mol. Note, however, that recent experiments (Xiang and Anderson, 2002) have shown the importance of taking molecular details into account here.
Most transport processes across biological cell membranes for small neutral molecules are assumed to be of the diffusive type (Xiang and Anderson, 2000), whereas transport of very hydrophilic (e.g., ionic) species is typically protein-mediated (van Winkle, 1999). Phosphatidylcholines are one of the major lipid components in many membranes, and pure phospholipid bilayers are generally accepted to exhibit many of the important properties of real cell membranes. Dipalmitoylphosphatidylcholine (DPPC) is one of the more studied systems, and has been used extensively both experimentally and computationally. Even a pure hydrated phospholipid bilayer is highly complex, and poses challenges for experiments as well as computation. Theoretical approaches have not yet reached the sophistication level that the particularities of the bilayer can be taken into account in any greater detail.
A challenge in current modeling is the lack of detailed experimental data. Molecular-dynamics simulations, where, in principle, all details are available, may fill some gaps. Simulations can be used to identify and characterize important regions and phenomena to serve as a guide for theoretical model building and to evaluate the virtues of existing theories. Earlier simulation studies have highlighted the highly anisotropic nature and importance of correlation effects both for small neutral molecules (Marrink and Berendsen, 1994) and for single atomic ions (Wilson and Pohorille, 1996). At the same time, it is desirable to utilize Occam's Razor frequently, and evaluate predictions from simple theories and models.
Valproic acid is a branched fatty acid (CH3-CH2-CH2-CH(COOH)-CH2-CH2-CH3) that has been routinely used as an anticonvulsant since the 1970s (Dalessio, 1985). Besides treatment of epilepsy it is used as a mood stabilizer for bipolar disorder. It passes the blood-brain barrier and permeates the placenta and it is known to cause skeletal birth defects (Lammer et al., 1987; Dansky and Finnell, 1991). Neither the mechanisms of the developmental effects nor its therapeutic properties are known, but it has been suggested that valproic acid downregulates Pax-1 (Barnes and Mariani, 1996) leading to severe deformations early in the fetal development. Recent studies have also shown that the mechanism of valproate is related to the metabolism of polyunsaturated fatty acids (Chang et al., 2001). Valproic acid has no known specific binding targets and the therapeutic action has been proposed to come from membrane disordering properties (Perlman and Goldstein, 1984; Kessel et al., 2001). Being a (branched) fatty acid, the flip-flop of valproate is also a question of general interest (Abumrad et al., 1998; Hamilton, 1998). Experiments suggest that there are several processes responsible for fatty acid translocation, protein-mediated as well as diffusive (Abumrad et al., 1998), and valproate may utilize facilitated transport to some extent.
As an initial step in investigating phenomena involved in diffusive translocation through lipid bilayers, we have performed molecular-dynamics simulations of model membranes at the atomic level, which allows for detailed analysis of various thermodynamic and dynamic quantities, many of which are not readily accessible experimentally. We present spatially resolved free energy calculations of transport of valproic acid and valproate molecules across hydrated DPPC lipid bilayers. The article is structured as follows: first, we discuss simulation details and the thermodynamic background; then we characterize spatially the thermodynamic quantities for the solute translocating the bilayer. Lastly, we discuss and analyze the data and its implications, and highlight some issues worthy of further study.
SIMULATION METHODS
Liposomes and cell membranes in water are almost free from any external tension except hydrostatic pressure (Fang et al., 1999; Cevc et al., 1981; Cevc and Marsh, 1987; Feller and Pastor, 1999; Lindahl and Edholm, 2000; Shinoda et al., 1997; Shinoda and Okazaki, 1998). The diagonal components of the elastic modulus tensor of the lipid bilayer in the liquid crystal phase are much smaller than those in incompressible fluids (Shinoda et al., 1997), which means that physical properties such as surface area may be greatly affected by small changes in pressure. The small magnitude of the elastic modulus also gives rise to large thermal fluctuations of the area and thickness of the membrane. When inserting molecules into the bilayer, large variations in surface area of the simulated system may occur, due to large stresses as the inserted molecule displaces lipids in the bilayer. A constant stress algorithm, such as the Parrinello-Rahman method (Parrinello and Rahman, 1980), that allows the box shape to change as well as the volume in response to internal stresses, allows a fast pathway to equilibrate the system when subjected to disturbances. Thus we chose the (zero-stress) isothermal-isobaric ensemble for our simulations, to ensure that the system is able to converge to a natural equilibrium structure from an arbitrary initial configuration and that the average hydrodynamic pressure exerted on the system can be set to any desired value, in our case to one atmosphere.
Hydrated lipid bilayers are highly inhomogeneous systems with spatial regions characterized by very different physical properties. This high degree of inhomogeneity also poses special requirements on force-field parameters compared to more standard systems. A drug translocating the membrane will pass through, for example, regions of very different dielectric properties. (When continuum models are applied to lipid bilayer systems, the dielectric constant is typically set to ∼80 in water compared to ∼2–4 in the center of the alkyl region). Ideally, one would like to have a potential that depends on the spatial surroundings—namely, abandon the pair potential approximation and employ a polarizable force field.
Molecular dynamics details
The force field for the hydrated lipid bilayer system is, except for the alkyl chain torsion parameters, the same as the one developed by Smondryev and Berkowitz (1999). The water model employed by them as well as us is TIP3P (Jorgensen et al., 1983). For the hydrocarbon chains we employ the Kuwajima torsion potentials (Fukuda and Kuwajima, 1997), a more modern yet very similar potential to the Ryckaert-Bellemans potential (Ryckaert and Bellemans, 1975) which is the one used by Smondryev and Berkowitz. The same integrator routines and simulation parameters as Smondryev and Berkowitz (1999) were used, and we reproduce the thermodynamic data for the pure lipid bilayer, which is in excellent agreement with experimental data for alkyl chain order parameters or average area per lipid; the average area per lipid is 61.9 ± 0.5 Å2, compared to the experimental value of 62.9 ± 1.3 Å2 (Nagle et al., 1996). For valproic acid and valproate, we employed the CVFF for the partial charges (Dauber-Osguthorpe et al., 1988).
To monitor a proper equilibration of a bilayer requires lengthy calculations. One of the main reasons for this is that average lipid headgroup area typically fluctuates ± 2 Å2 around its mean value where the timescale for the fluctuations can be several hundred picoseconds (Smondryev and Berkowitz, 1999). To further monitor the convergence and lack of hysteresis effects, we also checked that the free energy profile was symmetric near the middle of the bilayer, by calculating points extending 5 Å across the center.
The free energy calculation method (see below) is adopted from the study of water permeation by Marrink and Berendsen (1994). By constraining the center of mass of a particle relative to the center of mass of the bilayer and calculating the average force acting along the bilayer normal, the free energy profile can be estimated. This corresponds to an umbrella sampling with an infinite force constant (Marrink and Berendsen, 1994).
Our starting configuration of the DPPC/water simulations is taken from an earlier equilibrated simulation of a 32 DPPC molecule bilayer (Fang et al., 1999). This simulation was made with a different force field and we smoothly morphed from the old to the new force field during the first 50 ps whereafter the bilayer was allowed to equilibrate for another 600 ps. The 64 DPPC systems are built by duplicating an equilibrated 32 DPPC simulation, and equilibrating for another 500 ps. The lipid bilayers are fully hydrated and the water per lipid ratio is 29:1. After equilibration, in separate calculations valproate and valproic acid were slowly dragged to certain locations perpendicular to the membrane (relative z-values) and further equilibrated. The time needed for equilibrium varies with position. The time needed for the production runs was also heavily dependent on the position in the membrane, but typically between 0.4 and 0.8 ns per position is required. Hence the total production run is ∼15 ns per system.
The system was simulated using the isothermal-isobaric ensemble with the integrator routines taken from the DL_POLY library (Smith and Forester, 1996). Three-dimensional periodic boundary conditions were applied and the smooth particle-mesh Ewald technique (Essmann et al., 1995) was used for the electrostatic calculations. A cutoff at 1 nm was applied for the real space part of the Ewald sum and the dispersion (Lennard-Jones) forces. This setup corresponds to the one used by Smondryev and Berkowitz (1999). The temperature was set to 323 K which is a commonly applied temperature for studies of pure DPPC bilayers (see e.g., Nagle et al., 1996) and the temperature for which the thermodynamic properties of the force field was reported (Smondryev and Berkowitz, 1999). The pressure was set to 1 atm. The barostat and thermostat relaxation times were 0.5 and 0.2 ps, respectively. Bond lengths were constrained using the SHAKE algorithm and the tolerance used was 10−4 and the timestep used was 2 fs. The initial valproic acid structure was built using Insight II (MSI, San Diego, CA). Valproic acid/valproate were subsequently grown into the equilibrated lipid/water systems by slowly switching on the intermolecular interactions (Lennard-Jones 12–6 and electrostatic).
Free energy profiles
The hydrated water/lipid bilayer system exhibits spatial heterogeneity not only in static properties but also in dynamic properties such as local diffusion coefficients. Thus there is no reason to assume that each region of simulation is equally important, and one may sensibly make different approximations when it comes to coarse-graining the description of the lipid/water system. Experimentally, it is of course very difficult to obtain spatially resolved properties across the bilayer, but it is relatively straightforward in our molecular dynamics simulations. An important part of this work is to calculate changes in the free energy of the lipid-ligand-water system for different configurations/conformations of the lipid bilayer and drug molecules. The free energy profiles give one the ability to analyze the contribution of various more or less improbable configurations to the overall transport of molecules across a membrane.
There are several approaches one can take for this type of calculation. Translocation of any molecule, let alone a large hydrophilic one, across a membrane is a rare event on the timescales allowed by present molecular dynamics calculations, so all feasible computational alternatives will impose constraints along some appropriately defined reaction coordinate. Most routine approaches such as umbrella sampling, alchemistic growth, or potential of mean force (Frenkel and Smit, 1996) rely on values calculated at, or near, equilibrium. The Jarzynski equality of nonequilibrium and equilibrium processes (Jarzynski, 1997) has, however, spurred interest in alternative approaches and the number of methods based on this is growing and under evaluation; see e.g., Isralewitz et al. (1997) and Hummer (2001). The approach employed by us does, however, belong to the former category.
We use the method used by Marrink and Berendsen (1994), which is to calculate the spatially resolved free energy difference profile, ΔG(ζ), from the ensemble average of the force, F(ζ), acting along some reaction coordinate, ζ. The quantity ΔG(ζ) is closely related to properties such as the translocation rate and the permeation coefficient. We are interested in translocation across lipid bilayers, and as the reaction coordinate we use the distance z from the center of mass of the transferred solute to the center of mass of the bilayer, bearing in mind that, in reality, we simulate an infinite planar lamellar system. The z-axis is kept normal to the bilayer plane and is used as the measure of reaction coordinate and we have
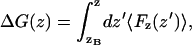 |
(1) |
where zB is a distance deep in bulk water, and the angle brackets, in our case, represent a time average.
Permeation coefficients
We define ΔG to be the difference in free energy between a molecule in the bulk water phase and in the interior of the membrane, and hence this quantity is a free-energy barrier that must be overcome for a molecule to translocate through the membrane. A difference in ΔG between two processes may be related directly to the difference in the rates at which those processes will proceed in nature via an analogy with the elementary kinetic theory of activated processes.
Under standard assumptions (Schulten et al., 1981; Marrink and Berendsen, 1994), the permeability coefficient of the bilayer, P, may be written as
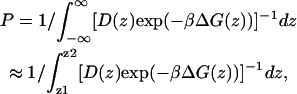 |
(2) |
where β = 1/kBT is the inverse thermal energy, kB is Boltzmann's constant, T is the temperature, and D(z) is the local diffusion coefficient. The limits of the integral z1 and z2 are points deep in the (bulk) water on opposite side of the lipid bilayer. Most often diffusion coefficients are calculated from the asymptotic behavior of the mean square displacement but this is not applicable in the presence of a gradient in the chemical potential. However, when constraining the particle at a particular point in the reaction coordinate, as is the case for the present calculations, the local diffusion coefficient, D(z), along the reaction coordinate is also accessible from the simulations, and may be calculated (Marrink and Berendsen, 1994) according to
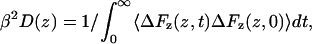 |
(3) |
where F(z, t) is the force in the direction of the reaction coordinate, z, at time t, and
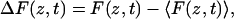 |
(4) |
is the instantaneous fluctuation of the force relative to the average force. Instead of calculating the local diffusion coefficient, one can imagine extrapolating some information from the lateral diffusion, since the particle is only constrained along the bilayer normal. However, the lipid environment is highly anisotropic, and the diffusion coefficient may very well be very different along the interface plane and the bilayer normal.
If one assumes that ΔG(z) is characterized by a large barrier value at some value of z = z*, somewhere, for example, near the midplane of the bilayer, and that D(z) is constant = D in that region, then one may approximate the permeation coefficient in a transition-state-like approximation (Schulten et al., 1981; Wilson and Pohorille, 1996),
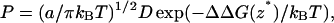 |
(5a) |
where
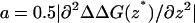 |
(5b) |
is proportional to the curvature at the top of the barrier and ΔΔDG(z*) = ΔG(z*) − ΔG(z′) = G(z*) − G(z′) is the difference between the free energy maximum and minimum values located at z* and z′, respectively. Under this approximation it is thus sufficient to calculate ΔΔDG(s*). Note that one is not restricted to physical reaction coordinates, and the general relationship
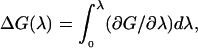 |
(6) |
which also holds for nonphysical reaction coordinates λ, may be used to create any thermodynamic cycle of choice. For example, if we wish to calculate the free energy difference between a system with a solute particle at some position in the bulk water phase and a system with the solute at some position inside the membrane, we may imagine two identical solute molecules, a and b, at these positions. By scaling the interactions of these two solute molecules so that at λ = 0 the interaction of a with the rest of the system is fully turned on and the interaction of b with the system is fully turned off, whereas at λ = 1 the interaction of b with the rest of the system is fully turned on and the interaction of a with the system is fully turned off, we may integrate over λ and get the free energy difference of moving a molecule from outside to inside the membrane.
Setting the parameterization of the interactions to be
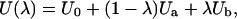 |
(7) |
it is easy to verify that
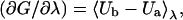 |
(8) |
where U(λ) is the potential energy of the full system when the coupling parameter is λ, U0 is the contribution to the potential energy excluding interactions involving particles a and b, Ua is the potential energy contributed by the interaction of particle a with the other particles in the system, and Ub is similarly defined for particle b. The angle brackets indicate an ensemble average over configurations in which the interactions of particles a and b have been scaled by (1−λ) and λ respectively. In practice, the integrand is calculated at several values of λ, each value of λ requiring a separate simulation. This and Eq. 1 yield two independent paths for calculating the total free energy difference between the water and bilayer center. Initially we performed λ-integrations for water permeation across DPPC and dipalmitoylphosphatidylserine (DPPS), membranes using an eight-point Gauss-Legendre quadrature to verify the calculations using Eq. 1. The values calculated from the two different methods agreed within one standard deviation or 1 kcal mol−1 (data not shown).
TRANSLOCATION RESULTS
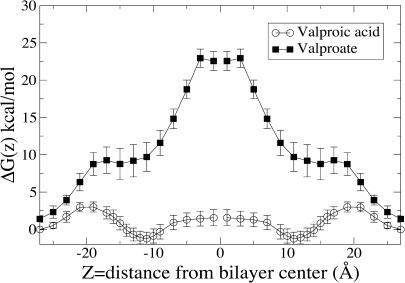
The free energy profile for valproic acid translocating DPPC is shown in Fig. 1. Valproic acid, being a fatty acid with its amphiphilic nature combined with its limited solubility in water, shows—not surprisingly—a minimum at the border between the alkyl region and the headgroups. As valproic acid approaches the water lipid interface from the water phase, the free energy profile shows a barrier hump, the origin of which arises partly from the entropy penalty as it becomes buried. However, in the outermost region a large part of this hump arises from steric collisions with fluctuating lipid headgroups (Israelachvili and Wennerstrom, 1992). Well inside the headgroup region, collisions will, of course still be present—but not only working to push out the drug. Instead, valproic acid experiences a downward fall, largely entropic in nature, governed by the release of water molecules as the alkyl part of valproic acid is desolvated.
FIGURE 1.
Free energy profile for translocating a hydrated DPPC bilayer. Valproic acid (unfilled circles); valproate (solid squares). The middle of the lipid bilayer is centered at ∼z = 0, and the free energy profiles for entering the bilayer to the center are mirrored around the center for clarity.
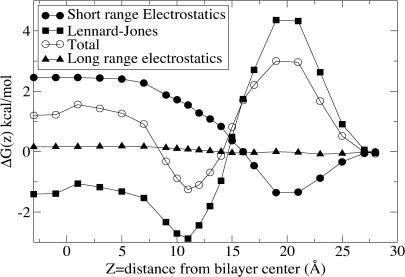
Fig. 2 displays the contributions to the free energy profile of translocation of valproic acid arising from (short- and long-range) electrostatic terms and the Lennard-Jones potentials. It is clear that as the drug enters from the water phase, the largest resistance comes from the LJ-forces whereas the electrostatic term favors insertion/adsorption, partly due to the polar headgroups forming hydrogen bonds with the carboxyl group of valproic acid. Fairly early in its way into the lipid bilayer valproic acid will experience the favorable inclusion of the alkyl chain into the lower dielectric, leading to release of water. There is, however, a large desolvation penalty (∼3.5 kcal mol−1) for the carboxylic group, but its z-profile is not steep, due to the deformation of the bilayer to include water “fingers” that partly solvate the solute far into the bilayer. The favorable electrostatic interactions reach a minimum ∼18 Å from the bilayer center, after which they rise to plateau at ∼7 Å, in the region where valproic acid becomes fully dehydrated. The desolvation is counteracted by favorable nonpolar interactions between the alkyl chains of valproic acid and the lipid tails as the solute translates deeper, and the net result is that the two effects partly counterbalance each other. The free energy profile shown in Fig. 2 is slightly asymmetric at ∼z = 0. The variation needed for perfect symmetry is, however, on the order of 0.1 kcal/mol, which is smaller than our error bars, hence we choose not to give an interpretation of this observation.
FIGURE 2.
Decomposition of the free energy profile of valproic acid translocation (unfilled circles) into long (solid triangles) and short range (solid circles) electrostatic and Lennard-Jones (solid squares) parts. Error bars have been omitted for clarity.
Qualitatively, the picture is similar for the charged species but the details differ. In Fig. 1, we also show the free energy profile of translocation of valproate. Valproate, in contrast to valproic acid, is highly soluble in water, and since it is also charged, it does show a substantial free energy penalty for desolvation, associated with the insertion into the oily tail region of the bilayer. The free energy barrier for inserting a single small ion is expected to be on the order of ∼50 kcal mol−1 (Parsegian, 1969; Wilson and Pohorille, 1996). Although quite high, the free energy barrier is substantially lowered due in part to the favorable interactions with the alkyl chains. The lowering is also due to the fact that the ion never becomes fully desolvated. A plateau region in the free energy profile is found in the alkyl chain/headgroup region of the bilayer, where valproic acid has a minimum. The interaction between the ion and the water is much greater and correlation effects are substantial. Water fingers that reach down to the headgroup may (transiently) extend deep into the tail region and contribute a force that is a truly many body in nature. There is little information to gain in looking only at the first hydration shell, e.g., the hydration number, to characterize the dehydration force. This is most apparent for the ionic form, valproate, which retains its first hydration shell all the way into the center of the bilayer. There is also a slow dynamics related to the solvation/desolvation in this deep region as well as the motion of the headgroups.
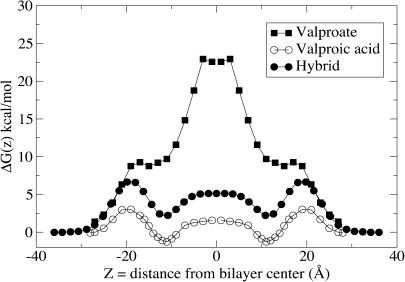
In bulk water valproic acid has a pKa of 4.5, but, as commonly known, the pKa of carboxylic groups are highly dependent on the solvent, and susceptible to local fluctuations and anisotropy in the environment. A particularly strong effect may arise from the presence of charged low-screened groups, such as in the headgroup region. Carboxylic fatty acids are thought to alter the apparent pKa from 4.5 to up to ∼7 upon membrane association (Hamilton, 1998), depending on the particular system. Since valproic acid is not soluble in water whereas valproate is, a natural hypothesis for the translocation is of course protonation of valproate to valproic acid upon association with the membrane. A standard approach is then to match the two free energy profiles to make a path of least effort. Similar to the continuum electrostatics study of Kessel and co-workers (Kessel et al., 2001), we estimate a free energy difference of 3.5 kcal mol−1 upon protonation using the relation
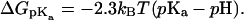 |
(9) |
The resulting free energy profile is shown in Fig. 3.
FIGURE 3.
Hybrid free energy profile (solid circles), assuming protonation of valproate to valproic acid at z ∼ 20 Å from the bilayer center. The curves for valproic acid (unfilled circles) and valproate (solid squares) are the same as in Fig. 1.
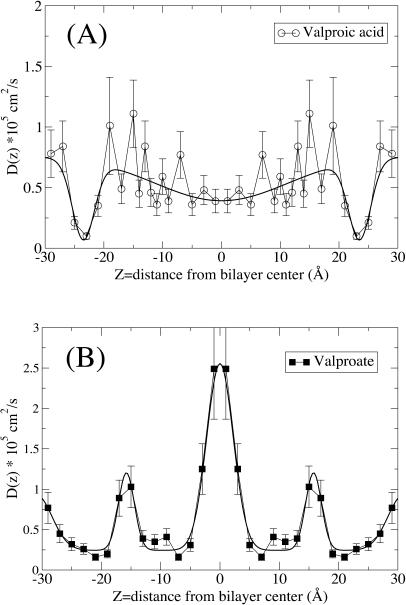
In addition to the free energy profile, ΔG(z), we also need the local diffusion constant, D(z), for the various systems to apply Eq. 2. In Fig. 4 we show D(z) for the two systems calculated via Eq. 3. We observe that the longitudinal diffusion constants are rather small, but on the order of one and two orders-of-magnitude larger than that of the lateral diffusion of the lipids' center of mass (Essmann and Berkowitz, 1999; Moore et al., 2001). The D(z) is calculated from the force autocorrelation functions which near the headgroup region exhibits strong bimodal behavior (data not shown). The fast component has a correlation time <0.02 ps and the slow component has a correlation time almost two orders-of-magnitude higher. The bimodal behavior is a feature also found for smaller molecules (Marrink and Berendsen, 1994) and the area under the curve associated with the slow component is substantial over the whole range in the interior of the bilayer.
FIGURE 4.
Local diffusion coefficient, D(z), for the same systems as in Fig. 1. (A) Valproic acid; (B) valproate.
Using the free energy profiles and the local diffusion coefficient, we thus can calculate the permeation coefficients according to Eq. 2. The integrand of Eq. 2 was fitted to analytical functions with subsequent integration. For the neutral valproic acid we find a value of Pvpa = 4.0 × 10−1 cm s−1, and for the anionic valproate we find a value of Pvp = 9.7 × 10−14 cm s−1. If we use the hybrid profile where we assume protonation of valproate upon membrane association we find a permeation coefficient of Phyb = 2.0 × 10−3 cm s−1.
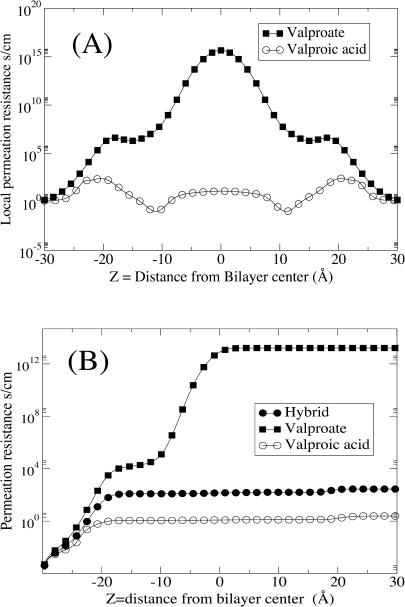
In Fig. 5 we show the local permeation resistance, which is the kernel of the integral of the permeation coefficient, P, Eq. 2. It is clear that for valproate the central region of the bilayer is very dominant whereas the headgroup region is dominant for valproic acid translocation. For smaller hydrogen-bonding penetrants such as water, the local diffusion coefficient, D(z), is substantially higher in the middle and low in the headgroup region. The relatively large size and few hydrogen-bonding groups of valproic acid and valproate counteract this trend. In the case of water permeation, D(z) has a clear minimum in the headgroup region, an effect partly caused by hydrogen bonds with the headgroups. In this region the bimodal behavior of the force autocorrelations is also accentuated and water and valproic acid/valproate diffusion is governed by similar timescales. For water, however, the diffusion coefficient in the middle of the bilayer, D(0), is ∼1 order-of-magnitude higher (Marrink and Berendsen, 1994) whereas D(z) for valproic acid remains in the same order of magnitude throughout the bilayer. Similar to water, D(z) for valproate is enhanced in the middle of the bilayer. For water this enhancement leads to a local minimum of the permeation resistance, but for valproate the permeation resistance is dominated by the large free energy penalty, the exponentially growing Boltzmann factor. Therefore, no such minimum is seen for valproate in the middle of the bilayer.
FIGURE 5.
(A) The local resistance (the integrand of Eq. 2) for translocating from the water phase on one side to the water phase on the other. (B) The integration of the permeation resistance, 1/P, as a function of distance, Eq. 2. Valproic acid (unfilled circles); valproate (solid squares); hybrid path assuming protonation ∼2 nm from the bilayer center (solid circles).
Further insight into the various interactions may be gained from examining the average orientation of valproic acid and valproate as they traverse the bilayer. It is customary to define an order parameter S as
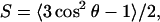 |
(10) |
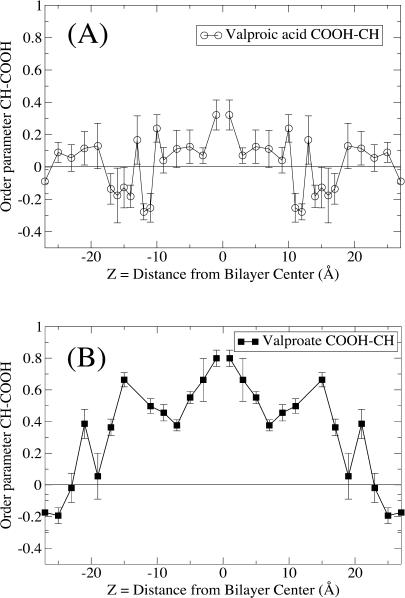
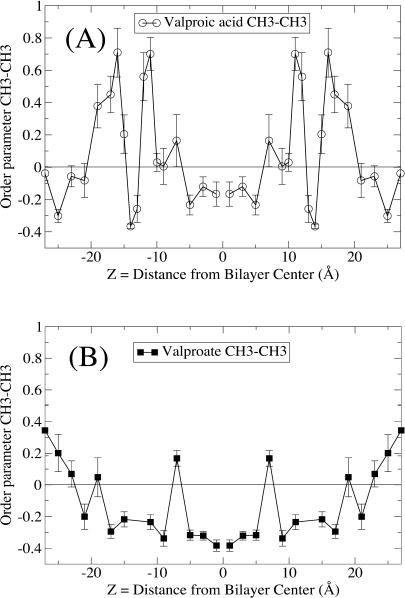
where θ is the angle between an arbitrary vector and the bilayer normal. A vector parallel to the bilayer normal hence gives a value of S = 1, whereas S = −0.5 corresponds to alignment with the bilayer plane. A value of S = 0 is not associated with a particular ordering but can be realized by various distributions as well as a static angle of ∼55°. Fig. 6 shows the order parameter for the C(H)–C(OOH) bond vector, and it also gives us an idea of the level of ordering and average positions of the dipole orientation. The order parameter for the vector joining the methyl endgroups of valproate and valproic acid is shown in Fig. 7 reflecting the mobility and alignment of the alkyl groups. The behavior of valproic acid and valproate is quite different. We find that the strong electrostatic forces align the C(H)–C(OOH) bond of valproate with the headgroups along the bilayer plane, whereas the neutral valproic acid enters the alkyl moiety in a less upright position. A further consequence is that valproate is more restricted in its motion.
FIGURE 6.
Order parameters for the C(H)–C(OOH) bond vector. (A) Valproic acid; (B) valproate. An S-value of −0.5 means perfect ordering along the bilayer plane; S = 1 is perfect ordering along the bilayer normal; same symbols as in Fig. 1.
FIGURE 7.
Order parameter for the vector between the CH3 endpoints of the alkyl chains, same symbols as in Fig. 1. (A) Valproic acid; (B) valproate.
DISCUSSION: POSSIBLE MECHANISMS
The calculations described above support a translocation scenario as follows: as the charged valproate approaches the bilayer, the headgroups polarize, and at the same time permit water fingers protruding into the bilayer to relax the electrostatic penalty from desolvation. This relaxation of the headgroup region causes the free energy profile to be much less steep than suggested by continuum electrostatics calculations (Kessel et al., 2001) which yield very steep profiles, as discussed below. Well inside the headgroup region, valproate may become protonated which leads to a fast flip-flop frequency. On the other side of the bilayer center valproic acid becomes deprotonated, before again being fully solvated. The free energy profile for this path is characterized by a broad peak with pronounced minima at the headgroup/alkyl chain boundary, reflecting the amphiphilic nature of valproic acid.
The flexibility of the bilayer suggests that there may be a substantial dependence on alkyl chain length for charged species, also noted by Wilson and Pohorille (1996). The hydrogen bonds will also be more rigid in the headgroup region (Pandit and Berkowitz, 2002; Marrink and Berendsen, 1994) compared with bulk water. For water, which is a much smaller molecule than valproic acid, the local diffusion coefficient is substantially lowered in the headgroup region. As a consequence, even if the free energy profile of water permeation is characterized by an almost single broad peak, the headgroup region is rate-determining.
Hence the main qualitative picture is that, for neutral polar groups capable of hydrogen bonding, the headgroup region is rate-determining, whereas for ionic groups the center of the bilayer is the main barrier. However, for complex molecules with rich hydrophobic patterns, the correlation effects soon become nonadditive.
Permeation coefficients are often used to rationalize experimental data and do exhibit a straightforward (albeit sometimes forced) relationship with the true processes of translocation (van Winkle, 1999; Marrink and Berendsen, 1994). For many small (uncharged) molecules, permeation coefficients may be correlated fairly well with partition coefficients, for example water/octanol, but the range of applicability remains limited. For large ionic species, one expects a breakdown of homogenous diffusion approximations.
Even though the isothermal-isobaric (NPT) ensemble has many merits, it is far from flawless. For some dynamic properties, or functions such as time-autocorrelation functions, one has to be careful not to pick up signals from the external heat bath (as is true also for the NVT ensemble). For that reason, we validated the results by performing short parallel calculations using the NVE ensemble and the abovementioned calculations of water permeation with the calculated values of Marrink and Berendsen (1994). An alternative approach to ours would be to let the system relax in the isothermal-isobaric ensemble and then run simulations in NVE. When studying inclusions of larger, shape anisotropic molecules, the NVE ensemble may, however, be too restrictive to include the effect of local fluctuations in lipid arrangements.
In the present calculation, the hydrocarbon chains of the lipids are represented using a united-atom model, and moving to full atomic resolution would of course be a natural next step. A consequence of the polarizability implicit to all-atom models on the alkyl chains would likely be a decrease in the enthalpic penalty for inclusion of polar and charged groups in the middle of the bilayer, as well as a decrease in the local diffusion coefficients. Even if the two effects cancelled each other as far as the permeability of polar and charged groups, the decrease in free energy barrier will be large. Quantitative estimates are, however, difficult to obtain, due to all correlation effects discussed earlier. The dielectric constant can be viewed roughly as increasing from 1 to ∼2, and the free energy barrier would be rescaled by roughly a factor of 0.5 (Wilson and Pohorille, 1996). However, this is only applicable in the case where the species would be a fully dehydrated ion in the middle of an infinitely thick bilayer. For an ionic pathway, such an estimate would, however, be a reduction on the order of 10−5 in permeation coefficient (thus leading to P ∼ 10−8 cm s−1). One can picture simulations of ions embedded in an alkyl chain solution, but cooperative effects with water, and perhaps most notably, ion correlations, are likely to be nonadditive. This would affect mainly the free energy barrier of the anionic valproate, and have little effect on the neutral valproic acid. Hence it would not contribute to the hybrid path where valproate gets protonated upon membrane association.
The formation of water fingers induced by ionic inclusions appears to be stable (on the 10-ns timescale accessible for computer simulations). Similar to the study of ion transport by Wilson and Pohorille (1996) we conclude that these water fingers are transient structures, in the sense that when approaching the other side a similar protrusion will take over the solvation of the ionic inclusion at the expense of the first, which will quickly retract. Thus we conjecture that the translocation is mediated by two consecutive water finger formations.
A study of valproic acid translocation of lipid bilayers using mean field theory and a continuum representation of the bilayer has been reported recently (Kessel et al., 2001). The most prominent difference between the free energy profiles obtained by those continuum electrostatic calculations and our simulations arises from the difference in location where desolvation of the solute occurs. This leads to distinctly different free energy profiles, even though the total free energy of inclusion (i.e., the free energy of translocation into the middle) is quite similar. Even though the shape of the free energy profile obtained from the continuum calculations is different, the net permeation coefficients are similar to the present study. Using the free energy profile from the continuum calculations and the local diffusion coefficient obtained from our calculations, one obtains a permeation coefficient P = 1.1 10−1 cm s−1, which is ∼50× higher than our calculation above. By way of comparison, if instead of our calculated value, one adopts the value of D = 10−7 cm2 s−1 (as the authors did) as an approximate value for the lateral diffusion coefficient of the lipid center of mass (Essmann and Berkowitz, 1999; Moore et al., 2001), one arrives at a permeation coefficient of 2.6 10−3 cm2 s−1, which is 1.3× our calculated value. However, this arises from cancellation of two profound differences with the current simulation. If one compares the shape of the free energy profiles, it is clear that our simulations identify the desolvation/resolvation steps as separate from a slightly faster rapid flip-flop in the interior. This is in contrast to the continuum study in which, due to the model of the bilayer, the flip-flop and desolvation are simultaneous. In the high friction limit the mean first passage time, τ, of diffusive motion from point a over a barrier at b can be written as (Kramers, 1940; Schulten et al., 1981; van Kampen, 2001)
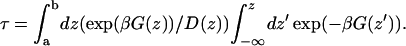 |
(11) |
Using Eq. 11 we get values of 2 μs for the flip-flop time and ∼10 μs for the total translocation time. If we use the free energy profile of Kessel and co-workers (which is calculated at 300 K instead of 323 K as in our case) with our calculated local diffusion constant, D(z), we arrive at a value of 300 μs for the translocation time. Both these studies thus suggest that the flip-flop may take place on a sub-ms timescale. Although no experimental values of valproic acid translocation rates are known, experimental studies of, for example, octanoic acid (Srivastava et al., 1995) yield a t1/2 of 50 μs and the sub-ms timescales found by Hamilton for various fatty acids (Hamilton, 1998) indicate that these values are plausible.
Since the energetics are captured quite reasonably by the simple continuum model, the opportunity still exists for some simple coarse-grained representations of the system to be successful; for example, a simple mean-field theory with responding dielectric boundaries characterized by surface tension or usage of several layers of dielectric properties together with some version of the Poisson-Boltzmann approximation. For some processes such as permeation across ion channels, simple approaches such as the Poisson-Nernst-Planck approximation have indeed been successful (Im and Roux, 2002). Recently the use of effective potentials for McMillan-Mayer level representations of solvent for anisotropic systems such as the electrical double layer has been validated (Kjellander et al., 2001). In the case where the free energy profile is dominated by one barrier in the middle of the bilayer, we believe that continuum models of the lipid bilayer may be quite successful as they stand, particularly in cases when the local diffusion coefficient is fairly uniform. For the cases where one is certain that one knows the rate-determining region (i.e., the region with the highest local permeation resistance; see Fig. 5), the easily implemented thermodynamic integration to morph between different substances may be useful.
The present study is the initial step of a larger program to characterize the thermodynamic and kinetic properties of lipid bilayer translocation. We plan to investigate effects from ion correlations in charged bilayers, by studying the hydrated DPPS/water/Na+ system using the force field of Pandit and Berkowitz (2002). The importance of ion-correlation effects has also been highlighted recently (Ulander et al., 2001b), not only for properties near the surface but also for long-range screening outside electric double layers. The simulation of a fully hydrated membrane is computationally expensive, due principally to the electrostatic forces between water molecules, and approaches that makes it possible to reduce the cost of simulating large systems are highly valued. The simulation of large molecules outside charged bilayers in the presence of an electrolyte, not just counterions outside charged bilayers, may seem prohibitively costly. However, recent efforts have shown the possibility of obtaining correct behavior of correlation functions for charged systems even when simulating very few particles (Ulander and Kjellander, 2001a), also raising the possibility of accurate alternative approaches to rigorous periodic boundary conditions.
CONCLUSIONS
We have used molecular-dynamics simulation to characterize the diffusive translocation of an amphiphilic drug across a model hydrated DPPC bilayer. By assuming protonation of valproic acid upon association with the bilayer, we find a free energy profile of translocation which is characterized by three peaks, each of moderate height (5–8 kcal mol−1). The calculated permeation coefficient of translocation is P = 2.0 × 10−3 cm s−1, and the translocation time is estimated to be on the order of 10−5 s, supporting earlier experimental suggestions (Hamilton, 1998) of fast diffusive translocation for fatty acids. The local diffusion coefficient is on the order of 10−6 to 10−5 cm s−1 throughout the whole bilayer. The ability of lipid bilayers to sustain local defects, induced by the permeating solute, results in “water fingers” for the charged species which greatly facilitates translocation.
These results emphasize the importance of going beyond the mean-field description to obtain an accurate description of transport processes, especially as the solutes become larger or more charged. The presence of groups capable of hydrogen-bond formation not only affects the energetics but also may have great influence on local diffusion coefficients. In accordance with the findings of Wilson and Pohorille (1996), for simple ions we find that water fingers have a profound effect on the permeation properties. For molecules with more complex structure and for charged membranes, we conjecture that the correlation effects will be even more important. In future work, we plan to investigate translocation across charged membranes, and we anticipate that the most important descriptor of charged membranes is not necessarily the average electrostatic potential (in a Gouy-Chapman sense) but rather the polarizability due to mobile charges.
Acknowledgments
We thank the KECK II computational center in San Diego and the Pittsburgh Supercomputer Center for generous allocations of time, and we also thank Dr. G. Papoian for careful reading of the manuscript.
We gratefully acknowledge the University of Houston where this research was started, and computer time from National Partnership for Advanced Computational Infrastructure grant CHE010014P. J.U. gratefully acknowledges the Swedish Research Council and the San Diego Supercomputer Center for financial support.
References
- Abumrad, N., C. H. Harmon, and A. Ibrahimi. 1998. Membrane transport of long-chain fatty acids: evidence for a facilitated process. J. Lipid Res. 39:2309–2318. [PubMed] [Google Scholar]
- Barnes, Jr. G. L., B. D. Mariani, and R. S. Tuan. 1996. Valproic acid-induced somite teratogenesis in the chick embryo: relationship with Pax-1 gene expression. Teratology. 54:93–102. [DOI] [PubMed] [Google Scholar]
- Cevc, G., A. Watts, and D. Marsh. 1981. Titration of the phase transition of phosphatidylserine bilayer membranes. Effect of pH, surface electrostatics, ion binding, and headgroup hydration. Biochemistry. 20:4955–4965. [DOI] [PubMed] [Google Scholar]
- Cevc, G., and D. Marsh. 1987. Phospholipid Bilayers. Wiley-Interscience, New York.
- Chang, M. C., M. A. Contreras, T. A. Rosenberger, J. J. Rintala, J. M. Bell, and S. I. Rapoport. 2001. Chronic valproate treatment decreases the in vivo turnover of arachidonic acid in brain phospholipids: a possible common effect of mood stabilizers. J. Neurochem. 77:796–803. [DOI] [PubMed] [Google Scholar]
- Dalessio, D. J. 1985. Current concepts: seizure disorders and pregnancy. N. Engl. J. Med. 312:559–563. [DOI] [PubMed] [Google Scholar]
- Dansky, L. V., and R. H. Finnell. 1991. Parental epilepsy, anticonvulsant drugs, and reproductive outcome: epidemiological and experimental findings spanning three decades. 2: Human studies. Reprod. Toxicol. 5:301–335. [DOI] [PubMed] [Google Scholar]
- Dauber-Osguthorpe, P., V. A. Roberts, D. J. Osguthorpe, J. Wolff, M. Genest, and A. T. Hagler. 1988. Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system. Proteins. 4:31–47. [DOI] [PubMed] [Google Scholar]
- Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle-mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- Essmann, U., and M. L. Berkowitz. 1999. Dynamical properties of phospholipid bilayers from computer simulation. Biophys. J. 76:2081–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang, Z., A. D. J. Haymet, W. Shinoda, and S. Okazaki. 1999. Parallel molecular dynamics simulation: implementation of PVM for a lipid membrane. Comp. Phys. Comm. 116:295–310. [Google Scholar]
- Feller, S. E., and R. W. Pastor. 1999. Constant surface tension simulations of lipid bilayers: the sensitivity of surface areas and compressibilities. J. Chem. Phys. 111:1281–1287. [Google Scholar]
- Frenkel, D., and B. Smit. 1996. Understanding Molecular Simulation: From Algorithms to Applications. Academic Press, San Diego, CA.
- Fukuda, M., and S. Kuwajima. 1997. Molecular-dynamics simulation of moisture diffusion in polyethylene beyond 10-ns duration. J. Chem. Phys. 107:2149–2159. [Google Scholar]
- Hamilton, J. A. 1998. Fatty acid transport: difficult or easy? J. Lipid Res. 39:467–481. [PubMed] [Google Scholar]
- Hummer, G. 2001. Fast-growth thermodynamic integration: error and efficiency analysis. J. Chem. Phys. 114:7330–7337. [Google Scholar]
- Im, W., and B. Roux. 2002. Ion permeation and selectivity of OmpF porin: a theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 322:851–869. [DOI] [PubMed] [Google Scholar]
- Israelachvili, J. N., and H. Wennerstrom. 1992. Entropic forces between amphiphilic surfaces in liquids. J. Phys. Chem. 96:520–531. [Google Scholar]
- Isralewitz, B., S. Izrailev, and K. Schulten. 1997. Binding pathway of retinal to bacteriorhodopsin: a prediction by molecular dynamics simulations. Biophys. J. 73:2972–2979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarzynski, C. 1997. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78:2690–2693. [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kessel, A., B. Musafia, and N. Ben-Tal. 2001. Continuum solvent model studies of the interactions of an anticonvulsant drug with a lipid bilayer. Biophys. J. 80:2536–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kjellander, R., A. P. Lyubartsev, and S. Marcelja. 2001. McMillan–Mayer theory for solvent effects in inhomogeneous systems: calculation of interaction pressure in aqueous electrical double layers. J. Chem. Phys. 114:9565–9577. [Google Scholar]
- Kramers, H. A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica. 7:284–304. [Google Scholar]
- Lammer, E. J., L. E. Sever, and G. P. Oakley, Jr. 1987. Teratogen update: valproic acid. Teratology. 35:465–473. [DOI] [PubMed] [Google Scholar]
- Lindahl, E., and O. Edholm. 2000. Spatial and energetic-entropic decomposition of surface tension in lipid bilayers from molecular dynamics simulations. J. Chem. Phys. 113:3882–3893. [Google Scholar]
- Marrink, S. J., and H. J. C. Berendsen. 1994. Simulation of water transport through a lipid membrane. J. Phys. Chem. 98:4155–4168. [Google Scholar]
- Marrink, S. J., and H. J. C. Berendsen. 1996. Permeation process of small molecules across lipid membranes studied by molecular dynamics simulations. J. Phys. Chem. 100:16729–16738. [Google Scholar]
- Moore, P. B., C. F. Lopez, and M. L. Klein. 2001. Dynamical properties of a hydrated lipid bilayer from a multinanosecond molecular dynamics simulation. Biophys. J. 81:2484–2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagle, J. F., R. Zhang, S. Tristam-Nagle, W. Sun, H. I. Petrache, and R. M. Suter. 1996. X-ray structure determination of fully hydrated Lα-phase dipalmitoylphosphatidylcholine bilayers. Biophys. J. 70:1419–1431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit, S. A., and M. L. Berkowitz. 2002. Molecular dynamics simulation of dipalmitoylphosphatidylserine bilayer with Na+ counterions. Biophys. J. 82:1818–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parrinello, M., and A. Rahman. 1980. Crystal structure and pair potentials: a molecular-dynamics study. Phys. Rev. Lett. 45:1196–1199. [Google Scholar]
- Parsegian, A. 1969. Energy of an ion crossing a low dielectric membrane: solutions to four relevant electrostatic problems. Nature. 221:844–846. [DOI] [PubMed] [Google Scholar]
- Perlman, B. J., and D. B. Goldstein. 1984. Membrane-disordering potency and anticonvulsant action of valproic acid and other short-chain acids. Mol. Pharmacol. 26:83–89. [PubMed] [Google Scholar]
- Powell, K. T., and J. C. Weaver. 1986. Transient aqueous pore in bilayer membranes: a statistical theory. Bioelectrochem. Bioenerg. 15:211–227. [Google Scholar]
- Ryckaert, J. P., and A. Bellemans. 1975. Molecular dynamics of liquid n-butane near its boiling point. Chem. Phys. Lett. 30:123–125. [Google Scholar]
- Schulten, K., Z. Schulten, and A. Szabo. 1981. Dynamics of reactions involving diffusive barrier crossing. J. Chem. Phys. 74:4426–4432. [Google Scholar]
- Shinoda, W., N. Namiki, and S. Okazaki. 1997. Molecular dynamics study of a lipid bilayer: convergence, structure, and long-time dynamics. J. Chem. Phys. 106:5731–5743. [Google Scholar]
- Shinoda, W., and S. Okazaki. 1998. A Voronoi analysis of lipid area fluctuation in a bilayer. J. Chem. Phys. 109:1517–1521. [Google Scholar]
- Smith, W., and T. R. Forester. 1996. DL_POLY is a package of molecular simulation routines written by W. Smith and T. R. Forester. Copyright by The Council for the Central Laboratory of the Research Councils, Daresbury Laboratory at Daresbury, Nr. Warrington.
- Smondryev, A. M., and M. L. Berkowitz. 1999. United atom force field for phospholipid membranes: constant pressure molecular dynamics simulation of dipalmitoylphosphatidylcholine/water system. J. Comp. Chem. 20:531–545. [Google Scholar]
- Srivastava, A., S. Singh, and G. Krishnamoorthy. 1995. Rapid transport of protons across membranes by aliphatic amines and acids. J. Phys. Chem. 99:11302–11305. [Google Scholar]
- Ulander, J., and R. Kjellander. 2001a. The decay of pair correlation functions in ionic fluids: a dressed ion theory analysis of Monte Carlo simulations. J. Chem. Phys. 114:4893–4904. [Google Scholar]
- Ulander, J., H. Greberg, and R. Kjellander. 2001b. Primary and secondary effective charges for electrical double layer systems with asymmetric electrolytes. J. Chem. Phys. 115:7144–7160. [Google Scholar]
- van Winkle, L. J. 1999. Biomembrane Transport. Academic Press, San Diego, CA.
- van Kampen, N. G. 2001. Stochastic Processes in Physics and Chemistry. Elsevier Science B.V., Amsterdam, The Netherlands.
- Venable, R. M., and R. W. Pastor. 2002. Molecular dynamics simulations of water wires in a lipid bilayer and water/octane model systems. J. Chem. Phys. 116:2663–2664. [Google Scholar]
- Wilson, M. A., and A. Pohorille. 1996. Mechanism of unassisted ion transport across membrane bilayers. J. Am. Chem. Soc. 118:6580–6587. [DOI] [PubMed] [Google Scholar]
- Xiang, T. X., and B. D. Anderson. 1994. Molecular distributions in interfaces: statistical mechanical theory combined with molecular dynamics simulation of a model lipid bilayer. Biophys. J. 66:561–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang, T. X., and B. D. Anderson. 1998. Influence of chain ordering on the selectivity of dipalmitoylphospatidylcholine bilayer membranes for permeant size and shape. Biophys. J. 75:2658–2671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang, T. X., and B. D. Anderson. 2000. Influence of a transmembrane protein on the permeability of small molecules across lipid membranes. J. Membr. Biol. 173:187–201. [DOI] [PubMed] [Google Scholar]
- Xiang, T. X., and B. D. Anderson. 2002. A computer simulation of functional group contributions to free energy in water and a DPPC lipid bilayer. Biophys. J. 82:2052–2066. [DOI] [PMC free article] [PubMed] [Google Scholar]