Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Dec;85(6):3502–3512. doi: 10.1016/S0006-3495(03)74770-5

Interactions of Inertial Cavitation Bubbles with Stratum Corneum Lipid Bilayers during Low-Frequency Sonophoresis

Ahmet Tezel 1, Samir Mitragotri 1
PMCID: PMC1303657  PMID: 14645045

Abstract

Interactions of acoustic cavitation bubbles with biological tissues play an important role in biomedical applications of ultrasound. Acoustic cavitation plays a particularly important role in enhancing transdermal transport of macromolecules, thereby offering a noninvasive mode of drug delivery (sonophoresis). Ultrasound-enhanced transdermal transport is mediated by inertial cavitation, where collapses of cavitation bubbles microscopically disrupt the lipid bilayers of the stratum corneum. In this study, we describe a theoretical analysis of the interactions of cavitation bubbles with the stratum corneum lipid bilayers. Three modes of bubble-stratum corneum interactions including shock wave emission, microjet penetration into the stratum corneum, and impact of microjet on the stratum corneum are considered. By relating the mechanical effects of these events on the stratum corneum structure, the relationship between the number of cavitation events and collapse pressures with experimentally measured increase in skin permeability was established. Theoretical predictions were compared to experimentally measured parameters of cavitation events.

INTRODUCTION

The stratum corneum (SC), the outermost layer of the skin, offers the limiting step in transdermal drug permeation (Bouwastra et al., 1991). The stratum corneum is ∼15 μm thick and is a composite of cornified cells (corneocytes) and lipid bilayers. Application of low-frequency ultrasound enhances SC permeability to a variety of drugs (low-frequency sonophoresis) (Mitragotri et al., 1995a). Since the ordered structure of the SC lipid bilayers is primarily responsible for low skin permeability, the ability of low-frequency ultrasound to increase SC permeability is contingent on disruption of the SC lipid bilayers.

Several studies have conclusively shown that ultrasound-induced SC permeabilization is mediated by acoustic cavitation (Mitragotri et al., 1995b; Tang et al., 2002b; Tezel et al., 2002a, 2001). Interactions of acoustic bubbles with cells and tissues are also important in a variety of other biomedical applications of ultrasound including lithotripsy (Coleman and Saunders, 1993), thrombolysis (Alexandrov, 2002), lipoplasty (Goes and Landecker, 2002), wound healing (Speed, 2001), fracture healing (Hadjiargyrou et al., 1998), and sonoporation (Guzman et al., 2001; Miller and Quddus, 2000; Sundaram et al., 2003; Wu et al., 2002), However, the interactions of cavitation bubbles with biological tissues are not well understood.

Acoustic cavitation can be broadly classified into two categories: stable cavitation, which corresponds to steady oscillations of bubbles, and inertial cavitation, which corresponds to rapid growth followed by a rapid collapse. Two recent studies based on acoustic spectroscopy have shown that inertial (transient) cavitation is primarily responsible for skin permeabilization (Tang et al., 2002b; Tezel et al., 2002a). During low-frequency sonophoresis, inertial cavitation is predominantly induced in the coupling medium (the liquid present between the ultrasound transducer and the skin (Tezel et al., 2002a)). The maximum radius of the cavitation bubbles is related to the frequency and acoustic pressure amplitude (Colussi et al., 1998; Mason and Lorimer, 1989). Under the conditions used for low-frequency sonophoresis (f ∼ 20–100 kHz and pressure amplitudes ∼1–2.4 bar), the maximum bubble radius is estimated to be between 10 and 100 μm. Owing to the large bubble size, cavitation is unlikely to occur within the 15 μm thick SC during low-frequency sonophoresis. Accordingly, cavitation in the coupling medium is of primary concern during low-frequency sonophoresis.

Two important events that occur during inertial cavitation are of particular interest to low-frequency sonophoresis. First, a spherical collapse of bubbles yields high pressure cores that emit shock waves with amplitudes exceeding 10 kbar (Pecha and Gompf, 2000). Second, an aspherical collapse of bubbles near boundaries such as the SC yields microjets with diameters of about one-tenth of the bubble diameter and velocities ∼100 m/s (Popinet and Zaleski, 2002). Based on these two important attributes of collapsing cavities, three possible mechanisms of cavitation-mediated SC permeabilization are analyzed in this study: i), disruption of the SC due to shock waves, ii), disruption of the SC due to impact of microjets on its surface, and iii), penetration of microjets into the SC.

The goal of this study is to analyze the relationship between the number of cavitation collapses in the coupling medium and the enhancement of the SC permeability.

THEORETICAL ANALYSIS

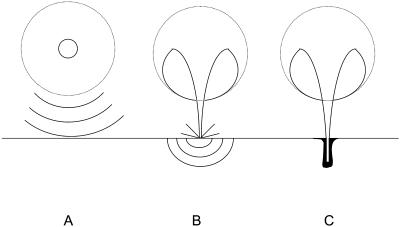
Fig. 1 schematically shows three mechanisms by which inertial cavitation events might enhance the SC permeability. Fig. 1 A shows bubbles that collapse symmetrically and emit a shock wave, which can disrupt the SC lipid bilayers (Lee et al., 1998). Fig. 1 B shows acoustic microjets that might impact the SC without penetration. Impact of microjets may also be responsible for SC lipid bilayer disruption. Fig. 1 C shows microjets resulting from collapsing bubbles near the SC surface that might physically penetrate into the SC and disrupt the structure.

FIGURE 1.

FIGURE 1

Open in a new tab

Three possible modes through which inertial cavitation may enhance SC permeability. (A) Spherical collapse near the SC surface emits shock waves, which can potentially disrupt the SC lipid bilayers. (B) Impact of an acoustic microjet on the SC surface. The microjet possessing a radius about one-tenth of the maximum bubble diameter impacts the SC surface without penetrating into it. The impact pressure of the microjet may enhance SC permeability by disrupting SC lipid bilayers. (C) Microjets may physically penetrate into the SC and enhance the SC permeability.

Symmetric bubble collapses in the coupling medium

Cavitation in the bulk of the coupling medium is clearly visible during low-frequency sonophoresis and is predominant near the face of the transducer. However, the bubbles migrate away from the transducer under the influence of the ultrasonic radiation force and may collapse close to the skin. Cavitation may also originate (nucleate) on the SC surface. The SC possesses a very heterogeneous topography and offers plenty of crevices for nucleation of cavitation bubbles. Cavitation bubbles nucleating and collapsing on the SC surface are likely to make a significant contribution to permeabilization of the SC due to their proximity.

During its growth, a bubble expands to a maximum radius before collapsing adiabatically. At the end of a symmetric collapse, the bubble reaches a minimum radius where it emits a shock wave. Propagation of the shock waves (or pressure waves) through the SC can potentially disrupt its structure (Lee et al., 1998). The disruption of materials exposed to pressure waves may occur through relative particle displacement, compressive failure, tensile loading, or shear strains (Lokhandwalla and Sturtevant, 2000). Though all these mechanisms may potentially be responsible for material damage, linear particle displacement provides the simplest explanation for it.

During the propagation of a pressure pulse through stratum corneum, deformation, Δy, of an element possessing an original dimension of Δx is given by the following equation:

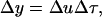graphic file with name M1.gif (1)

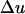where Inline graphic is the difference in the instantaneous particle velocity across the element and Δτ is the time of passage of the pulse through the element. The velocity difference, 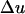Inline graphic, is related to the instantaneous pressure difference between the two ends of the element and is given by the following equation:

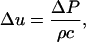graphic file with name M4.gif (2)

where ρ and c are the density of the element and the speed of sound within the element, respectively. Note that Eq. 2 assumes that waves propagate linearly in water and tissues. Propagation of shock waves generated by cavitation bubbles has been studied by several groups using hydrophone measurements (Wenninger et al., 1997; Barber et al., 1997; Wang et al., 1999) and optical methods (Holzfuss et al., 1998). It has been shown that the propagation of cavitation-induced shock waves is nonlinear at the beginning of the emission (that is, near the bubble center) (Pecha and Gompf, 2000). However, propagation of waves away from the bubble (>10 μm) can be described by linear acoustics (Pecha and Gompf, 2000). Since the SC itself is ∼15 μm thick, we assume that linear propagation is a reasonable assumption for most bubbles. Substituting Eq. 2 into Eq. 1 and dividing both sides by Δx, Eq. 1 can be rewritten as follows:

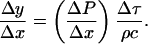graphic file with name M5.gif (3)

The left-hand side of Eq. 3 is the strain induced in the element, ɛ. Equation 3 can also be written in terms of the relationship between the strain rate,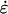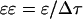Inline graphic (Inline graphic) and spatial pressure gradient (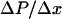Inline graphic) as follows:

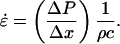graphic file with name M9.gif (4)

The time of propagation of the wave through the element, Δτ, can be related to Δx by 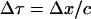Inline graphic. If Δx is chosen to match with the spatial pulse width of the wave, the gradient ΔP is comparable to P, the peak amplitude of the wave. For a typical shock wave emitted by a collapsing cavitation bubble, the spatial width is on the order of 1–10 nm (O(nm)) (Pecha and Gompf, 2000). This length scale is comparable to the thickness of SC lipid bilayers (Glombitza and Muller-Goymann, 2002). Accordingly, the substitution proposed above is justifiable. With the abovementioned approximation, Eq. 4 can be rewritten as follows:

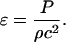graphic file with name M11.gif (5)

Equation 5 provides a direct relationship between the strain, ɛ, and the shock wave amplitude, P. Equation 5 predicts a strain of 0.04 for a typical wave amplitude of 1 kbar in a material with density and sound velocity comparable to that of water (ρ = 1000 kg/m3 and c = 1500 m/s). If the magnitude of the strain exceeds the critical strain, ɛc, disruption of the SC may be observed. The significance of ɛc must be evaluated separately for corneocytes and lipid bilayers, as the critical strains are quite different for the two.

Corneocytes consist of highly cross-linked keratin fibers and are covalently connected by desmosomes (Schneider et al., 1994). Owing to the covalent linkages between keratin fibers and desmosomes, corneocytes possess high elastic moduli and exhibit high tolerance against externally imposed stresses (Leveque et al., 2002, 1988). Thus, corneocytes are unlikely to be irreversibly deformed by the strains induced by the shock/pressure waves. Histological analysis of porcine and human stratum corneum exposed to low-frequency ultrasound also confirms that no gross disruption of the corneocyte structure is observed (Mitragotri et al., 1996; Tang et al., 2002a) (see also data discussed later).

Lipid bilayers on the other hand possess a low structural tolerance against the mechanical strain induced by external stresses (Baumann and Gerebe, 1998). Owing to the noncovalent interactions that determine their structure, lipid bilayers are highly susceptible to mechanical damage. Upon exposure to volumetric or area strains, lipid bilayers exhibit lateral extension and thickness reduction, eventually leading to their disruption. Evans et al. (1976) have shown that critical area strains for disruption of erythrocyte membranes are ∼0.02. Comparable numbers have been reported for other lipid bilayer systems (Koslov and Markin, 1984; Zhelev, 1998). Critical strain may in principle depend on the rate of deformation; however, in the absence of this knowledge, a representative value of 0.02 is used in the analysis presented here. This number is also justified based on the experiments of Lee et al. (2000, 2001) who reported permeabilization of the human SC using a single pressure wave in the presence of sodium lauryl sulfate (SLS). Specifically, they reported that a wave of amplitude in the range of 150–700 bar and temporal widths in the range of 110 ns–10 μs induced permeabilization of the SC. By converting the temporal gradient into a spatial gradient and using Eq. 5, one obtains ɛc in the range of 0.007–0.026, numbers that are comparable to the critical area strains reported by Evans et al. (1976). Note that the sonophoresis data analyzed in this study were also obtained in the presence of SLS (1% w/v).

Disruption of the SC lipid bilayers enhances skin permeability by at least two mechanisms. First, a moderate level of disruption decreases the structural order of lipid bilayers and increases the solute diffusion coefficient (Mitragotri, 2001). At a higher level of disruption, lipid bilayers may loose structural integrity and facilitate penetration of the coupling medium into the SC. Since most sonophoresis experiments considered in this study were performed using coupling media comprising aqueous solutions of surfactants, disruption of the SC lipid bilayers enhances incorporation of surfactants into their structure. Incorporation of excessive water and surfactants further promotes bilayer disruption, thereby opening pathways for solute permeation (Black, 1993; Walters, 1990). In this study, the role of surfactants in the SC permeabilization is assumed to be secondary. In other words, cavitation-induced bilayer disruption plays the key role in sonophoresis by initiating penetration of surfactants into the SC. This assumption is supported by experimental observations that surfactants that are more effective in enhancing the SC permeability by themselves are also more potent in enhancing the SC permeability in combination with ultrasound (Tezel et al., 2002b). This observation suggests that the primary role of ultrasound is to increase penetration of the surfactants into the SC. Since the surfactants themselves are capable of disrupting lipid bilayers, the critical strain for cavitation-induced bilayer disruption may in principle depend on the choice of surfactant. However, based on the assumption that penetration of surfactant into the SC follows cavitation-induced bilayer disruption, it appears reasonable to assume that the critical strain is independent of the surfactant.

Equation 5 can then be used to determine the amplitude of the wave necessary to disrupt the lipid bilayers. While applying Eq. 5 to cavitation-induced shock waves, one modification is necessary to account for the fact that the amplitude of spherical shock waves decreases due to radial propagation by 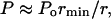Inline graphic where Po is the shock wave amplitude at the origin (that is when the bubble radius is equal to rmin) and r is the distance from the center of the bubble. The final expression to describe the strain induced by the shock waves is given by Eq. 6:

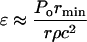graphic file with name M13.gif (6)

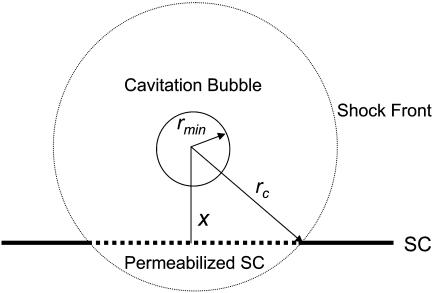
If a spherically symmetric collapse were to occur at a distance, x, from the stratum corneum surface, the area of the stratum corneum, ap, permeabilized by the wave is given by the following (Fig. 2):

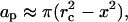graphic file with name M14.gif (7)

where rc is the distance from the bubble center where ɛ drops below the critical value necessary for bilayer disruption, ɛc, and is given (from Eq. 6):

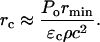graphic file with name M15.gif (8)

If N total collapses occur in a coupling medium of volume V during ultrasound application, the number of collapses occurring in a section of thickness dx located at a distance x from the SC is given by the following:

graphic file with name M16.gif (9)

where As is the surface area of the skin. Equation 9 is written by assuming that the collapses are uniformly distributed throughout the coupling medium. Further assuming that the SC area permeabilized by multiple collapses is mutually exclusive, the area of the SC, dAp, permeabilized by dNx collapses is given by the following:

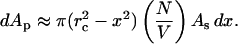graphic file with name M17.gif (10)

The assumption that the SC area permeabilized by two collapses is mutually exclusive is made based on the calculation that the area permeabilized by a single collapse (given by Eq. 7) is O(10−5 cm2). Since a typical SC area used in sonophoresis is O(cm2), the fractional area permeabilized by a single collapse is very low. Accordingly, if the collapses are random, the likelihood that two collapses occur on the same SC area is low. Though proceeding with this assumption, it has to be noted that certain nonrandomness exists in the cavitation collapse density due to inhomogeneities in the SC surface that might localize cavitation to certain skin areas. However, as a first order approximation, we assume that the collapse events in the coupling medium are random. Accordingly, the fractional area of the SC permeabilized by dNx collapses, dα, is given by the following:

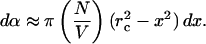graphic file with name M18.gif (11)

The total fraction of the SC permeabilized by N collapses can be obtained by integrating Eq. 11.

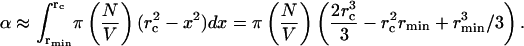graphic file with name M19.gif (12)

The use of a lower limit of rmin allows for the collapses to occur on the SC surface, i.e., at x = rmin. This is particularly relevant for bubbles nucleating on the SC surface that are likely to collapse close to the surface. Note that since rc ≫ rmin (rc ∼ 50 μm and rmin ∼ 1 μm), the last two terms of Eq. 12 could be neglected. By substituting Eq. 8 into Eq. 12, and differentiating with respect to time, the rate at which the SC is permeabilized is given as follows:

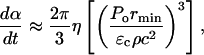graphic file with name M20.gif (13)

where η is the rate of bubble collapse per unit volume of liquid, η = N/(V × t). Equation 13 can be easily modified to account for the heterogeneity of collapse pressures. Assuming that the probability of the occurrence of bubble collapse pressure between Po and Po + dPo is given by γ(Po) such that 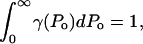Inline graphic Eq. 13 can be modified as follows:

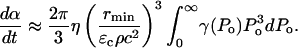graphic file with name M22.gif (14)

FIGURE 2.

FIGURE 2

Open in a new tab

A schematic representation of a spherical shock wave propagating through the SC surface. The bubble collapses symmetrically with the center located at a distance x from the SC surface. The shock wave propagates spherically through the SC and permeabilizes the circular area whose diameter is given by the dotted chord in the figure.

The functionality of γ is difficult to predict from the first principles. However, as shown later, 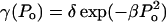Inline graphic appears to describe experimental data reasonably well. Note that δ is the normalization factor, i.e., 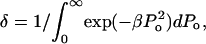Inline graphic and β is a constant. The abovementioned functionality of γ is also understandable since the energy of the collapse wave scales with 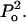Inline graphic Hence, the exponential dependence assumed in the above equation describes the probability distribution of the collapse events based on their energies. Equation 14 can be integrated to arrive at the following equation:

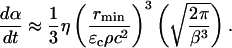graphic file with name M26.gif (15)

Equation 15 offers a relationship between the rate of SC permeabilization and important parameters of cavitation bubble collapse. Of the total six parameters in Eq. 15, values of two parameters including ρ and c are assumed to be the same as that for water (1000 kg/m3 and 1500 m/s, respectively) (Pan et al., 1998; Anderson and Cassidy, 1973). ɛc, the critical strain necessary to disrupt the SC lipid bilayers, was assumed to be 0.02 for the reasons discussed earlier. η, the number of collapse events per unit volume per unit time, depends on the ultrasound intensity and was determined by experimental measurements (described in Experimental Methods). Determination of rmin from the first principles has only been reported through numerical simulations of bubble collapse. Under typical conditions used for sonophoresis (20 kHz, 1 W/cm2) the value of rmin has been reported to be ∼1 μm (Brenner et al., 2002; Hilgenfeldt and Lohse, 1999). The only remaining parameter, β, was determined by fitting Eq. 15 to experimentally measured values of 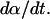Inline graphic

Penetration of acoustic microjets into the stratum corneum

Collapse of cavitation bubbles near solid boundaries induces asphericity and may lead to the formation of microjets (Katz, 1999; Popinet and Zaleski, 2002). The diameter of the microjet is typically about one-tenth of the bubble diameter (Kodama and Tomita, 2000) and the velocity of the jet tip is O(100 m/s) (Popinet and Zaleski, 2002). Kodama and Takayama (1998) reported that collapse-induced microjets penetrated into the rat liver and produced clearly identifiable pits. However, the bubbles and jets used in their study are significantly larger than those encountered during sonophoresis. Accordingly, direct application of their findings to sonophoresis is difficult.

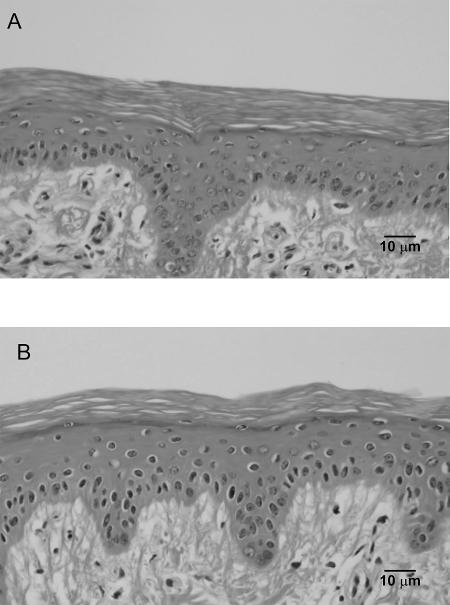
Physical penetration of microjets into the SC, if it did occur, might disrupt the SC in a manner similar to the material damage induced by the liquid jet impact (Jackson and Field, 2000). However, histological studies of porcine skin exposed to low-frequency ultrasound showed no evidence of microjet penetration into the SC. In these studies (Tezel et al., 2001), porcine skin was exposed in vitro to ultrasound (20 kHz, 2.4 W/cm2, 10 min) in the presence of 1% sodium lauryl sulfate. Application of ultrasound under these conditions enhanced skin conductivity by ∼100-fold and permeability to mannitol by ∼50-fold. At the end of ultrasound exposure, skin was fixed in 10% formalin, and histology was performed using the procedures reported in the Experimental Methods section. Fig. 3 shows typical histological images of skin permeabilized by ultrasound. Fig. 3 A shows a cross section of porcine skin not exposed to ultrasound. The SC and the viable epidermis are clearly visible. Fig. 3 B shows a cross section of porcine skin exposed to ultrasound (20 kHz, 2.4 W/cm2, 10 min). No disruption of the stratum corneum is evident. If the microjets had penetrated into the SC, the resulting disruption should have been visible in histological studies. However, the SC of porcine skin was intact and showed no evidence of damage.

FIGURE 3.

FIGURE 3

Open in a new tab

Histological studies of porcine skin exposed to low-frequency ultrasound (20 kHz). (A) Porcine skin not exposed to ultrasound. (B) Porcine skin exposed to low-frequency ultrasound. The scale bar corresponds to 10 μm in both figures. No significant difference can be seen between the two figures. If the 10 μm microjets had penetrated into the SC, a significant disruption of the SC should have been observed.

The lack of penetration of 10 μm jets may be attributed to the small jet diameter, transient existence of the jet, or the use of porcine skin, which is more difficult to penetrate into compared to human skin (Schramm and Mitragotri, 2002). It should be noted that commercial jet injectors used for insulin delivery, possessing diameters of ∼150 μm and velocities in the range of 150–200 m/s, readily penetrate into human skin (Schneider et al., 1994).

Impact of acoustic microjets on the stratum corneum surface

Microjets can enhance skin permeability even without physical penetration into the SC. The mechanics of jet impact on surfaces has been extensively studied experimentally as well as theoretically (Bourne et al., 1997; Field, 1999; Haller et al., 2002; Jackson and Field, 2000). Impact of a jet on a surface induces a high pressure (also known as water hammer pressure), the magnitude of which is given by the following equation (Kodama and Takayama, 1998):

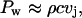graphic file with name M28.gif (16)

where vj is the jet velocity. The water hammer pressure lasts for a short period of time O(ns). According to Bernoulli's equation, this high impact pressure is followed by a more sustained stagnation pressure given by the following:

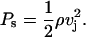graphic file with name M29.gif (17)

The duration of the stagnation pressure is comparable to the duration of the microjet (O(μs)). For a jet impacting at a velocity of ∼100 m/s, the water hammer pressure is ∼1.5 kbar whereas the stagnation pressure is ∼50 bar. Due to its low value, the stagnation pressure is unlikely to induce significant structural alterations. However, the impact pressure of 1.5 kbar is quite capable of disrupting the lipid bilayers of the SC (Eq. 6).

Impact of jets on materials sets up stress waves in the bulk of the target whose magnitudes decrease at least as rapidly as 1/r from the point of jet impact (Jackson and Field, 2000). The jet impact also sets up surface waves (Rayleigh waves) that attenuate more gradually. The effect of bulk stress waves on the structure of the SC can be described using the same principles as those responsible for the enhancement by waves emitted during spherical collapses. The effect of surface waves on the material is not analyzed in this study, although we speculate that their contribution is insignificant since no evidence of surface damage can be found in histological studies (Fig. 3). In the following section, we present an analysis of jet-induced SC permeabilization, assuming that an impact-induced stress wave is primarily responsible for the SC permeabilization.

The radius, rcj, of the hemisphere over which the strain induced by the stress wave exceeds the critical strain is given by the same analysis as discussed while deriving Eq. 6. The resulting equation is given by the following:

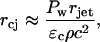graphic file with name M30.gif (18)

where rjet is the jet radius. Hence, the area, a, of the stratum corneum permeabilized by a single jet impact is given by the following equation:

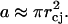graphic file with name M31.gif (19)

Assuming that the jets impact the SC randomly and there is no overlap between the areas impacted by two jets, the area fraction, α, of the SC permeabilized by jet impacts is given as follows:

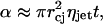graphic file with name M32.gif (20)

where ηjet is the number of jet impacts per unit skin area per unit time. The rate at which the fraction of the SC area is permeabilized is given by the following:

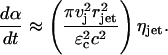graphic file with name M33.gif (21)

The jet velocities have been reported in the range of 50–150 m/s (Brujan et al., 2002; Popinet and Zaleski, 2002). The velocities are likely to depend on various parameters including the maximum bubble radius, ultrasound frequency, and acoustic pressure amplitude (Popinet and Zaleski, 2002). We used two representative jet velocities, 50 m/s and 150 m/s, for calculations. Since utilization of representative values ignores the dependence of jet velocity on ultrasound parameters, the results obtained from this analysis should be considered as order-of-magnitude estimates. The jet radius, rjet, is about one-tenth of the maximum bubble radius (Kodama and Tomita, 2000). Maximum bubble radius is related to ultrasound frequency and acoustic pressure amplitude. In the absence of surfactants, the calculated maximum bubble radii under the conditions used for low-frequency sonophoresis (20–100 kHz, 1–3 W/cm2) are in the range of 10–100 μm (Colussi et al., 1998). Assuming a representative value for maximum bubble radius of ∼50 μm (Sundaram et al., 2003), a representative value for jet radius was chosen as 5 μm.

EXPERIMENTAL METHODS

Ultrasound application and skin conductivity measurements

In vitro experiments were carried out with full-thickness Yorkshire pigskin. Before each experiment, the skin was thawed at room temperature and was mounted on to a Franz diffusion cell (PermeGear, Hellertown, PA). Only skin having an initial resistivity of 30 kΩ-cm2 or more was used to ensure that the skin was intact. A Franz diffusion cell consists of a donor and a receiver compartment. A 4 mm Ag/AgCl disk electrode (E242, Invivo Metrics, Healdsburg, CA) was introduced in both compartments for skin conductivity measurements during the experiment. The receiver compartment was filled with phosphate buffered saline (PBS, NaCl concentration of 0.137 M, pH 7.4) (Sigma-Aldrich, St. Louis, MO). PBS was prepared using deionized water with ∼8 MΩ resistance. The donor compartment was filled with a solution of SLS (1% weight/volume) in PBS. SLS (Sigma-Aldrich) was chosen as the model surfactant. Ultrasound was applied at 20 kHz (Sonics and Materials, Newtown, CT) and the intensity was varied in the range of 0–4 W/cm2. The ultrasound intensity was measured using the methods described by Tezel et al. (2001). A 100% duty cycle was chosen for ultrasound application. Each skin sample was sonicated for a total of 15 min in the presence of SLS.

The average skin conductivity was calculated by applying a 143 mV AC voltage at 10Hz (Agilent 33120A, Palo Alto, CA) and measuring the current. Skin resistance was then calculated using Ohm's law. The same procedure was repeated without mounting the skin. The difference between these two values is the resistance of the skin itself. The skin resistance was then multiplied by the skin area (2.2 cm2) to calculate the skin resistivity. Skin conductivity is the reciprocal of skin resistivity.

Direct comparison of experimental data with model predictions requires a relationship between the skin's electrical conductivity and the area fraction permeabilized, α, of the SC. The simplest relationship is proposed assuming that the fraction of the SC permeabilized is directly proportional to the SC electrical conductivity. The constant of proportionality was experimentally determined by measuring the SC area permeabilized by staining with a colorimetric dye, sulforhodamine B (Molecular Probes, Eugene, OR) (Tezel et al., 2001). We have previously shown that low-frequency ultrasound creates localized transport pathways (LTPs) in the skin that could be successfully stained with sulforhodamine B (Tezel et al., 2001). The dye was added to the donor compartment during the ultrasound application. At the end of ultrasound application, the skin was removed from the diffusion cell, rinsed and was imaged using a digital camera (Optronics, Goleta, CA). The total area of LTPs was quantified to determine the area fraction of the skin permeabilized by ultrasound. The effect of ultrasound on skin conductivity under the same conditions was also measured (Tezel et al., 2001).

Histology

Porcine skin was exposed to ultrasound in vitro using the methods discussed above. Ultrasound was applied until the skin conductivity increased by ∼100-fold. Since the effect of ultrasound on skin is heterogeneous, it leads to the formation of LTPs that occupy ∼5% of skin area. The location of the LTPs was visualized by inclusion of sulforhodamine B in the coupling medium. Since the skin morphology in the LTP is likely to be different from that outside the LTP, skin from LTP and non-LTP regions was collected separately and was fixed in 10% formalin (EMS, Fort Washington, PA) for 5 min. The skin was then sectioned using a microtome and stained with hematoxylin and eosin. Skin sections were observed under a microscope to evaluate the structural effects of ultrasound.

Measurements of aluminum foil pitting

Pitting of aluminum foil was measured to quantify cavitation events near the surface. In these experiments, aluminum foil (20 μm in thickness) was mounted in the diffusion cell and the donor compartment was filled with 1% SLS in PBS. Ultrasound was applied at 20 kHz and intensities in the range of 0–3.6 W/cm2 for 10 s. The number of pits was counted by visual inspection. It is difficult to ascertain whether each pit corresponds to a single cavitation event or whether each cavitation event is recorded by the foil. Accordingly, the number of pits is likely to be an approximate indicator of the number of cavitation events rather than a quantitative determinant.

Measurement of cavitation events in bulk

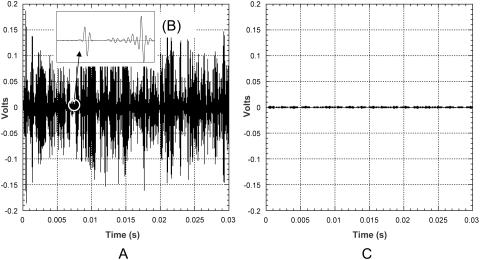
The number of cavitation events in the bulk coupling medium was measured using a hydrophone (model TC 4013, Reson, Goleta, CA). The bandwidth of the hydrophone is 1 Hz–170 kHz (−10dB). The hydrophone diameter is 0.5 cm and the length is ∼2 cm. The hydrophone was mounted in a chamber with dimensions similar to the Franz diffusion cells. The hydrophone was placed directly underneath the transducer and the chamber was filled with 2.6 ml of SLS (1% weight/volume) in PBS. Ultrasound was applied at 20 kHz at six intensities (0.7–3.6 W/cm2). The output of the hydrophone was collected in LabView via a data acquisition board (6052E, National Instruments, Austin, TX). The original signal (voltage in time domain) was passed though a high pass filter (20.5 kHz) to remove the primary frequency wave. A typical resultant waveform is shown in Fig. 4 A. The distribution of collapses was measured with a LabView virtual instrument as follows: First, the virtual instrument divided the voltage spanned by the signal (0–0.6V) into 200 increments, i.e., 0.003 volts per increment. Then the number of peaks between two consecutive voltage thresholds was identified. Finally, to obtain the pressure distribution, the voltage thresholds were converted to pressure amplitudes (PM) using the calibration provided by the hydrophone manufacturer. Fig. 4 B shows an enlarged view of two individual bubble collapses. Fig. 4 C shows the filtered signal in the absence of cavitation (control). The signal presented in Fig. 4 C was collected at an intensity that is below the cavitation threshold, i.e., 0.2 W/cm2. Note that the amplitude of the recorded event, PM, cannot be directly compared to the pressure amplitude of collapsing bubbles, Po, since it decreases at least as rapidly as 1/r from the site of the collapse. Accordingly, the pressure distribution recorded by the hydrophone is a combined result of the true pressure distribution and the distribution generated by the dissipation of the wave. Assuming a spherical propagation of the collapse shock wave, the true collapse pressure can be estimated from the measured pressure using the following equation:

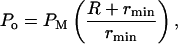graphic file with name M34.gif (22)

where R is the distance between the cavitation event and the hydrophone's acoustic center and rmin is the minimum bubble radius. The precise value of R will be different for different cavitation events. However, the experimental setup was designed such that the thickness of the liquid layer within which cavitation occurs around the transducer was ∼1 mm, thereby allowing determination of R with an uncertainty of 1 mm. The mean value of R is 1 cm. rmin is ∼1 μm. Since the thickness of cavitating liquid around the hydrophone was only 1 mm, it was assumed that the hydrophone recorded the cavitation events very efficiently.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Typical pressure profile of a cavitation event recorded by the hydrophone after the signal is processed through a high pass filter. (B) An enlarged view of two individual bubble collapses. (C) The filtered signal in the absence of cavitation (control).

RESULTS AND DISCUSSION

Analysis of symmetrical collapse events

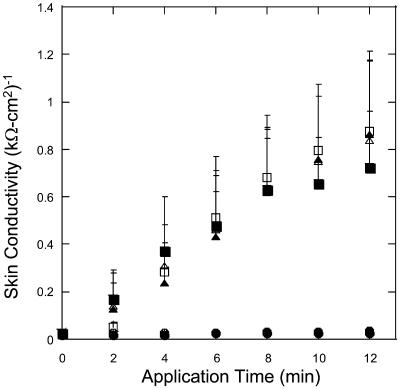
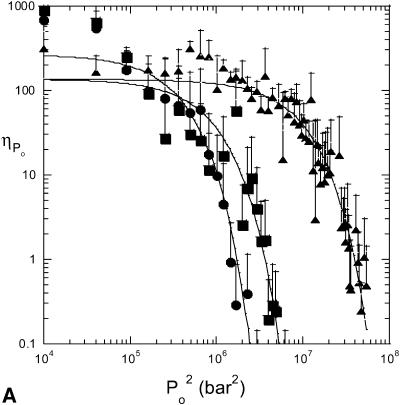
The effect of ultrasound on skin conductivity was measured at six different intensities (0.7, 1.1, 1.6, 2.4, 2.9, and 3.6 W/cm2 at a frequency of 20 kHz) (Fig. 5). To compare these experimental data with Eq. 15, the number of collapse events per unit volume per unit time, η, at the same intensities were measured independently using a hydrophone. Fig. 6 A shows experimentally measured distribution of collapse pressures, Po, at the same ultrasound intensities that were used in conductivity measurements (for clarity only three intensities are presented in Fig. 6 A). These pressures were obtained by correcting the actual measured pressure, Pm, using a correction factor described in Eq. 22. Solid lines show fits of the distribution function 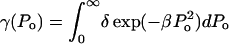Inline graphic that was used to calculate β-values based on direct hydrophone measurements for all six intensities. Since these β-values are based on direct experimental measurements we will denote them as βexp. Also a set of β-values based on the model presented in this article, denoted as βtheory, was determined as follows: the total number of collapse events per unit volume per second, η, at all six ultrasound intensities were measured from data in Fig. 6 A (shown in Fig. 6 B). Using the experimentally measured values of η (Fig. 6 B) along with the experimental measurements of skin conductivity (converted into dα/dt), and Eq. 15, values of βtheory were calculated at each intensity. Using the experimental as well as theory-derived values of β, mean values of Po were separately calculated in each case as follows:

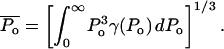graphic file with name M36.gif (23)

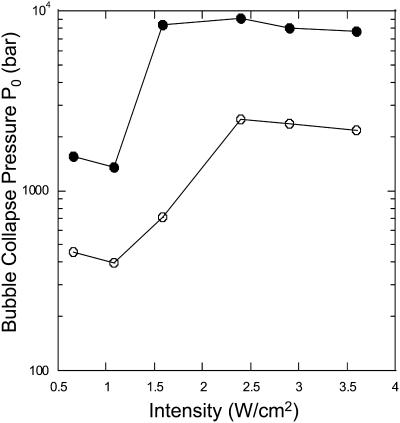
Fig. 7 shows the dependence of 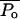Inline graphic determined using theory (calculated using βtheory, filled circles) and experimental data (calculated using βexp, open circles) on ultrasound intensity. The dependence of the model-derived values of collapse pressure on ultrasound intensity is comparable with that of the experimentally measured collapses pressures. However, the absolute values of the collapse pressures in two cases are different. The model-derived collapse pressures are approximately threefold greater than experimentally measured values. This agreement is satisfactory given the uncertainty and variability in the prediction of cavitation events. The error in the model-derived estimation of collapse pressures arises from uncertainty in critical strain, ɛc, and measured values of η. The error in direct measurements of collapse pressures is likely to originate from the correction factor described in Eq. 22. Although the correction factor described in Eq. 22 is routinely used to determine true collapse pressures, recent studies have shown that dissipation of shock waves near the bubble occurs more rapidly than that described in Eq. 22 (Pecha and Gompf, 2000).

FIGURE 5.

FIGURE 5

Open in a new tab

The enhancement of skin conductivity as a function of time at six ultrasound intensities: (•), 0.7 W/cm2; (○), 1.1 W/cm2; (▪), 1.6 W/cm2; (□), 2.4 W/cm2; (▴), 2.9 W/cm2; and (▵), 3.6 W/cm2. The error bars represent the standard deviation values (n = 8).

FIGURE 6.

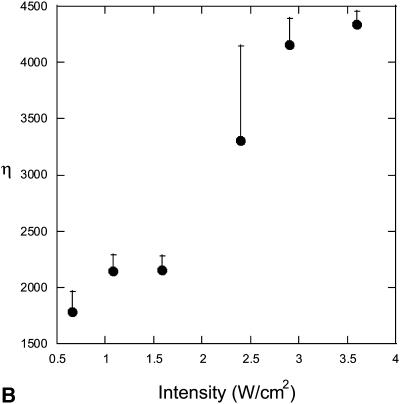
FIGURE 6

FIGURE 6

Open in a new tab

(A) Distribution of collapse pressures at three ultrasound intensities: (•), 0.7 W/cm2; (▪), 1.6 W/cm2; and (▴), 2.9 W/cm2. The plot shows the dependence of the number of collapses (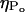Inline graphic) with a collapse pressure between Po and Po + 100 bar. The distribution function fits experimental data well (r2 = 0.87, 0.71, and 0.89 for 0.7 W/cm2, 1.6 W/cm2, and 2.9 W/cm2, respectively). The error bars represent the standard deviation values (n = 4). (B) Dependence of the total number of collapse events (η) on ultrasound intensity. The error bars represent the standard deviation values (n = 4).

FIGURE 7.

FIGURE 7

Open in a new tab

Dependence of collapse pressures (Po) on ultrasound intensity. Filled circles show the collapse pressure determined from the model, i.e., based on βtheory. Open circles show the collapse pressures measured using a hydrophone, i.e., based on βexp.

Values of collapse pressures reported in Fig. 7 can also be compared to independent theoretical calculations and experiments that have been reported in the literature. Theoretical estimates assuming adiabatic collapses of bubbles have yielded pressures of >1 kbar bars inside bubbles at the minimum bubble radius (Vichare et al., 2000). Direct or indirect experimental measurements in collapsing bubbles have also yielded pressures between 1.7 and 40 kbar (Matula et al., 1998; Pecha and Gompf, 2000; Wang et al., 1999). All these numbers are in general agreement with those reported in Fig. 7.

Under a typical condition used for sonophoresis in this study (20 kHz, 2.2 W/cm2), the number of cavitation events in the coupling medium is O(103)/cm3/s (Fig. 6 B). Since the bubbles collapsing only within a distance rc from the SC surface are capable of disrupting the SC surface (Eq. 11), it is informative to calculate the number of bubble collapses within rc from the SC surface. With typical values of Po and rmin, the calculated value of the critical distance of the bubble from the SC, rc, is ∼50 μm (Eq. 8). This value is close to the maximum bubble radius under the conditions used for sonophoresis (Sundaram et al., 2003). Accordingly, it appears that the bubbles collapsing only within one bubble radius away from the SC surface are effective in enhancing skin permeability. With a bubble collapse density of O(103)/cm3/s, the number of collapses within a distance rc from the SC is about O(10) collapses/cm2/s.

Analysis of the role of acoustic microjets

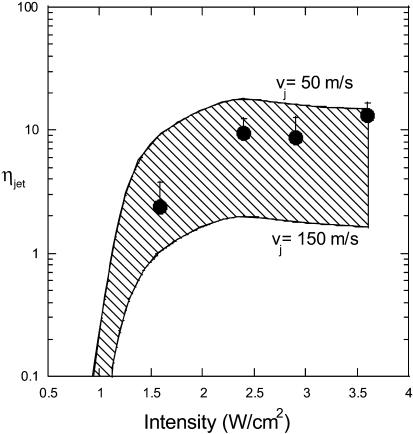
By comparing the predictions of Eq. 21 with experimental data reported in Fig. 5, the number of microjets per cm2 per second was determined (Fig. 8). The shaded region corresponds to the range of predictions where the limits correspond to jet velocities of 50 m/s and 150 m/s. Under typical conditions used for sonophoresis (intensities ∼2 W/cm2), the predicted number of microjets necessary to increase the SC permeability ranges from 1 to 10 microjets/cm2/s. Direct experimental confirmation of the predicted number of microjets is challenging due to the difficulty in observing the microjets. However, indirect confirmation of the number of microjets was obtained by recording pitting of aluminum foil. Pitting of 20 μm thick aluminum was recorded under identical experimental conditions used for sonophoresis. Application of ultrasound induced pits of radii in the range of 20–200 μm. The diameter of the pit is related to the parameters of bubble collapse and was not used in calculations. The number of pits was measured and was used as an indicator of the number of collapse events. It is unclear whether each microjet results in an observable pit and whether each pit is a result of a single event. Accordingly, the number of pits may only be used as an approximate indicator of the number of microjets. This view is further confirmed by the fact that the number of recorded pits is a function of the choice of surface used for the study. The number of pits recorded at various intensities is shown in Fig. 8. The number of pits recorded on aluminum foil is in general agreement with that predicted by the model.

FIGURE 8.

FIGURE 8

Open in a new tab

The number of microjets per cm2 per second (ηjet) necessary to explain the experimental sonophoresis data as a function of ultrasound frequency and intensity. The shaded region corresponds to the area bounded by predictions in limiting cases made by assuming jet velocities of 50 m/s and 150 m/s. Filled circles show the experimental measurements of aluminum foil pits. Error bars correspond to one standard deviation.

Summary of the results

Figs. 7 and 8 show that the spherical collapses as well as microjets are capable of enhancing skin permeability. The model predicts that both microjets and spherical collapses may be responsible for sonophoresis. Regardless of the precise mode of collapse, the model predicts that ∼10 collapses/s/cm2 in the form of spherical collapses or microjets are necessary near the surface of the SC to explain experimentally observed conductivity enhancements. The contribution of spherical collapses may be reconsidered given that collapses only within ∼50 μm from the SC surface are capable of enhancing the SC permeability (that is, rc ∼ 50 μm). A question then arises whether bubbles with maximum radii of ∼50 μm can collapse symmetrically 50 μm away from a solid surface (corresponding to ξ ∼ 0.5, where, ξ is the ratio of distance of the bubble from the surface to maximum bubble diameter). It is generally observed that for ξ < 4, the bubble loses its sphericity during the collapse (Isselin et al., 1998). In light of this discussion, occurrence of spherical collapses within 50 μm from the SC is questionable. However, only direct observations can conclusively address this issue.

The model reported here allows for a direct relationship between the cavitation events and the enhancement of skin permeability. Regardless of the relative role of shock waves and microjets, the model predicts that collapses only close to the SC are responsible for sonophoresis. The model described here is important in understanding the effect of ultrasound on skin permeability. It is also important in understanding the role of ultrasound in a number of other biomedical applications of ultrasound where interactions of cavitation bubbles with surfaces are important. Further studies should focus on direct microscopic observations of cavitation events on the SC surface.

Acknowledgments

Authors acknowledge Sujatha Dokka and Susan Kelly for histological studies.

This work was supported by Whitaker Foundation.

References

  1. Alexandrov, A. V. 2002. Ultrasound-enhanced thrombolysis for stroke: clinical significance. Eur. J. Ultrasound. 16:131–140. [DOI] [PubMed] [Google Scholar]
  2. Anderson, R. L., and J. M. Cassidy. 1973. Variations in physical dimensions and chemical composition of human stratum corneum. J. Invest. Dermatol. 61:30–32. [DOI] [PubMed] [Google Scholar]
  3. Barber, B. P., K. R. Wenninger, and S. J. Puttermann. 1997. Sonoluminescence. Phil. Trans. R. Soc. London. 355:641–648. [Google Scholar]
  4. Baumann, M., and R. Gerebe. 1998. Characteristics of the osmotically induced membrane rupture. Mol. Membr. Biol. 15:193–201. [DOI] [PubMed] [Google Scholar]
  5. Black, G. 1993. Interaction between anionic surfactants and skin. In Pharmaceutical Skin Penetration Enhancement. J. Hadgraft, editor. Marcel Dekker, New York, Basel, and Hong Kong. 145–174.
  6. Bourne, N. K., T. Obara, and J. E. Field. 1997. High-speed photography and stress gauge studies of jet impact upon surfaces. Phil. Trans. R. Soc. Lond. A. 355:607–623. [Google Scholar]
  7. Bouwastra, J. A., M. A. de Vries, G. S. Gooris, W. Bras, J. Brussee, and M. Ponec. 1991. Thermodynamic and structural aspects of the skin barrier. J. Control. Rel. 15:209–220. [Google Scholar]
  8. Brenner, M. P., S. Hilgenfeldt, and D. Lohse. 2002. Single-bubble sonoluminescence. Biophys. J. 74:425–484. [Google Scholar]
  9. Brujan, E. A., G. S. Keen, A. Vogel, and J. R. Blake. 2002. The final stage of the collapse of a cavitation bubble close to a rigid boundary. Phys. of Fluids. 14:85–92. [Google Scholar]
  10. Coleman, A. J., and J. E. Saunders. 1993. A review of the physical properties and biological effects of the high amplitude acoustic field used in extracorporeal lithotripsy. Ultrasonics. 31:75–89. [DOI] [PubMed] [Google Scholar]
  11. Colussi, A. J., L. K. Weavers, and M. R. Hoffmann. 1998. Chemical bubble dynamics and quantitative sonochemistry. J. Phys. Chem. 102:6927–6934. [Google Scholar]
  12. Evans, E. A., R. Waugh, and L. Melnik. 1976. Elastic area compressibility modulus of red cell membrane. Biophys. J. 16:585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Field, J. E. 1999. ELSI conference, invited lecture: Liquid impact—theory, experiment, applications. Wear. 233:1–12. [Google Scholar]
  14. Glombitza, B., and C. C. Muller-Goymann. 2002. Influence of different ceramides on the structure of in vitro model lipid systems of the stratum corneum. Chem. Phys. Lipids. 117:29–44. [DOI] [PubMed] [Google Scholar]
  15. Goes, J. C., and A. Landecker. 2002. Ultrasound-induced lipoplasty (UAL) in breast surgery. Aesthetic Plast. Surg. 26:1–9. [DOI] [PubMed] [Google Scholar]
  16. Guzman, H. R., D. X. Nguyen, S. Khan, and M. R. Prausnitz. 2001. Ultrasound-mediated disruption of cell membranes. I. Quantification of molecular uptake and viability. J. Acoust. Soc. Am. 110:588–596. [DOI] [PubMed] [Google Scholar]
  17. Hadjiargyrou, M., K. McLeod, J. P. Ryaby, and C. Rubin. 1998. Enhancement of fracture healing by low intensity ultrasound. Clin. Orthop. 355(Suppl.):S216–S229. [DOI] [PubMed] [Google Scholar]
  18. Haller, K. K., Y. Ventilkos, D. Poulikakos, and P. Monkewitz. 2002. Computational study of high-speed liquid droplet impact. J. Appl. Phys. 92:2821–2828. [Google Scholar]
  19. Hilgenfeldt, S., and D. Lohse. 1999. Predictions for upscaling sonoluminescence. Phys. Rev. Lett. 82:1036–1039. [Google Scholar]
  20. Holzfuss, J., M. Ruggeberg, and A. Billo. 1998. Shock wave emissions of a sonoluminescing bubble. Phys. Rev. Lett. 81:5434–5437. [Google Scholar]
  21. Isselin, J.-C., A.-P. Alloncle, and M. Autric. 1998. On laser induced single bubble near a solid boundary: contribution to the understanding of erosion phenomena. J. Appl. Phys. 84:5766–5771. [Google Scholar]
  22. Jackson, M. J., and J. E. Field. 2000. Modeling liquid impact fracture threshold in brittle materials. Brit. Ceramic Trans. 99:1–13. [Google Scholar]
  23. Katz, J. I. 1999. Jets from collapsing bubbles. Proc. R. Soc. Lond. A. 455:323–328. [Google Scholar]
  24. Kodama, T., and K. Takayama. 1998. Dynamic behavior of bubbles during extracorporeal shock-wave lithotripsy. Ultrasound Med. Biol. 24:723–738. [DOI] [PubMed] [Google Scholar]
  25. Kodama, T., and Y. Tomita. 2000. Cavitation bubble behavior and bubble-shock wave interaction near a gelatin surface as a study of in vivo bubble dynamics. Appl. Phys. B. 70:139–149. [Google Scholar]
  26. Koslov, M. M., and V. S. Markin. 1984. A theory of osmotic lysis of lipid vesicles. J. Theor. Biol. 109:17–39. [DOI] [PubMed] [Google Scholar]
  27. Lee, S., D. J. McAuliffe, T. Kodama, and A. G. Doukas. 2000. In vivo transdermal delivery using a shock tube. Shock Waves. 10:307–311. [Google Scholar]
  28. Lee, S., D. J. McAuliffe, N. Kollias, T. J. Flotte, and A. G. Doukas. 1998. Photomechanical transcutaneous delivery of macromolecules. J. Invest. Dermatol. 111:925–929. [DOI] [PubMed] [Google Scholar]
  29. Lee, S., D. J. McAuliffe, N. Kollias, T. J. Flotte, and A. G. Doukas. 2001. Permeabilization and recovery of the stratum corneum in vivo: the synergy of photochemical waves and sodium lauryl sulfate. Lasers Surg. Med. 29:145–150. [DOI] [PubMed] [Google Scholar]
  30. Leveque, J. L., P. Hallegot, J. Doucet, and G. Pierard. 2002. Structure and function of human stratum corneum under deformation. Dermatology. 205:353–357. [DOI] [PubMed] [Google Scholar]
  31. Leveque, J. L., M. C. Poelman, J. de Rigal, and A. M. Kligman. 1988. Are corneocytes elastic? Dermatologica. 176:65–69. [DOI] [PubMed] [Google Scholar]
  32. Lokhandwalla, M., and B. Sturtevant. 2000. Fracture mechanics model of stone comminution in ESWL and implications for tissue damage. Phys. Med. Biol. 45:1923–1940. [DOI] [PubMed] [Google Scholar]
  33. Mason, T. J., and J. P. Lorimer. 1989. Sonochemistry: Theory, Applications and Uses of Ultrasound in Chemistry. John Wiley & Sons, New York.
  34. Matula, T., I. M. Hallaj, R. O. Cleveland, and L. A. Crum. 1998. The acoustic emissions from single-bubble sonoluminescence. J. Acoust. Soc. Am. 103:1377–1382. [Google Scholar]
  35. Miller, D., and J. Quddus. 2000. Sonoporation of monolayer cells by diagnostic ultrasound activation of contrast-agent gas bodies. Ultrasound Med. Biol. 26:661–667. [DOI] [PubMed] [Google Scholar]
  36. Mitragotri, S. 2001. Effect of bilayer disruption on transdermal transport of low-molecular weight hydrophobic solutes. Pharm. Res. 18:1022–1028. [DOI] [PubMed] [Google Scholar]
  37. Mitragotri, S., D. Blankschtein, and R. Langer. 1995a. Ultrasound-mediated transdermal protein delivery. Science. 269:850–853. [DOI] [PubMed] [Google Scholar]
  38. Mitragotri, S., D. Blankschtein, and R. Langer. 1996. Transdermal drug delivery using low-frequency sonophoresis. Pharm. Res. 13:411–420. [DOI] [PubMed] [Google Scholar]
  39. Mitragotri, S., D. Edwards, D. Blankschtein, and R. Langer. 1995b. A mechanistic study of ultrasonically enhanced transdermal drug delivery. J. Pharm. Sci. 84:697–706. [DOI] [PubMed] [Google Scholar]
  40. Pan, L., L. Zan, and F. T. Foster. 1998. Ultrasonic and viscoelastic properties of skin under transverse mechanical stress in vitro. Ultrasound Med. Biol. 24:995–1007. [DOI] [PubMed] [Google Scholar]
  41. Pecha, R., and B. Gompf. 2000. Microimplosions: cavitation collapse and shock wave emission on a nanosecond time scale. Phys. Rev. Lett. 84:1328–1330. [DOI] [PubMed] [Google Scholar]
  42. Popinet, S., and S. Zaleski. 2002. Bubble collapse near a solid boundary: a numerical study of the influence viscosity. J. Fluid. Mech. 464:137–163. [Google Scholar]
  43. Schneider, U., R. Birnbacher, and E. Schober. 1994. Painfulness of needle and jet injection in children with diabetes mellitus. Eur. J. Pediatr. 153:409–410. [DOI] [PubMed] [Google Scholar]
  44. Schramm, J., and S. Mitragotri. 2002. Transdermal drug delivery by jet injectors: energetics of jet formation and penetration. Pharm. Res. 19:1673–1679. [DOI] [PubMed] [Google Scholar]
  45. Speed, C. A. 2001. Therapeutic ultrasound in soft tissue lesions. Rheumatology (Oxford). 40:1331–1336. [DOI] [PubMed] [Google Scholar]
  46. Sundaram, J., B. R. Mellein, and S. Mitragotri. 2003. An experimental and theoretical analysis of ultrasound-induced permeabilization of cell membranes. Biophys. J. 84:3087–3101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tang, H., D. Blankschtein, and R. Langer. 2002a. Effects of low-frequency ultrasound on the transdermal penetration of mannitol: comparative studies with in vivo and in vitro studies. J. Pharm. Sci. 91:1776–1794. [DOI] [PubMed] [Google Scholar]
  48. Tang, H., D. Blankschtein, and R. Langer. 2002b. An investigation of the role of cavitation in low-frequency ultrasound-mediated transdermal drug transport. Pharm. Res. 19:1160–1169. [DOI] [PubMed] [Google Scholar]
  49. Tezel, A., A. Sens, and S. Mitragotri. 2002a. Investigations of the role of cavitation in low-frequency sonophoresis using acoustic spectroscopy. J. Pharm. Sci. 91:444–453. [DOI] [PubMed] [Google Scholar]
  50. Tezel, A., A. Sens, J. Tuchscherer, and S. Mitragotri. 2002b. Synergistic effect of low-frequency ultrasound and surfactants on skin permeability. J. Pharm. Sci. 91:91–100. [DOI] [PubMed] [Google Scholar]
  51. Tezel, A., A. Sens, J. Tuchscherer, and S. Mitragotri. 2001. Frequency dependence of sonophoresis. Pharm. Res. 18:1694–1700. [DOI] [PubMed] [Google Scholar]
  52. Vichare, N., P. Senthilkumar, V. Moholkar, P. R. Gogate, and A. B. Pandit. 2000. Energy analysis of acoustic cavitation. Ind. Eng. Chem. Res. 39:1480–1486. [Google Scholar]
  53. Walters, K. A. 1990. Surfactants and percutaneous absorption. In Predictions of Percutaneous Penetration. R. C. Scott, R. H. Guy, and J. Hadgraft, editors. IBC Technical Services, London. 148–162.
  54. Wang, Z. Q., R. Pecha, B. Gompf, and W. Eisenmenger. 1999. Single bubble sonoluminiscence: investigations of the emitted pressure wave with a fiber optic probe hydrophone. Phys. Rev. E. 59:1777–1780. [Google Scholar]
  55. Wenninger, K. R., B. P. Barber, and S. J. Puttermann. 1997. Pulsed mie scattering measurements of the collapse of a sonoluminescing bubble. Phys. Rev. E. 78:1799–1802. [Google Scholar]
  56. Wu, J., J. P. Ross, and J.-F. Chiu. 2002. Reparable sonoporation generated by microstreaming. J. Acoust. Soc. Am. 111:1460–1464. [DOI] [PubMed] [Google Scholar]
  57. Zhelev, D. V. 1998. Material property characteristics for lipid bilayers containing lysolipid. Biophys. J. 75:321–330. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES