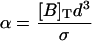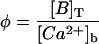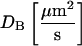Abstract
Calcium waves propagate inside cells due to a regenerative mechanism known as calcium-induced calcium release. Buffer-mediated calcium diffusion in the cytosol plays a crucial role in the process. However, most models of calcium waves either treat buffers phenomenologically or assume that they are in equilibrium with calcium (the rapid buffering approximation). In this article we address the issue of whether this approximation provides a good description of wave propagation. We first compare the timescales present in the problem, and determine the situations in which the equilibrium hypothesis fails. We then present a series of numerical studies based on the simple fire-diffuse-fire model of wave propagation. We find that the differences between the full and reduced descriptions may lead to errors that are above experimental resolution even for relatively fast buffers in the case of saltatory waves. Conversely, in the case of continuous waves, the approximation may give accurate results even for relatively slow buffers.
INTRODUCTION
The Ca2+ ion is the most common signal transduction element in cells (Alberts et al., 2002). However, prolonged high intracellular Ca2+ levels lead to cell death (Berridge et al., 1998). Since Ca2+ cannot be metabolized, cells need to control its concentration very tightly. One way in which cells avoid large intracellular levels is through numerous specialized binding proteins called buffers. The patterns of regulation in which Ca2+ ions are involved are among the most striking examples of intracellular spatio-temporal organization (Berridge et al., 1998), including, among others, various types of Ca2+ waves (Fontanilla and Nuccitelli, 1998; Lechleiter et al., 1991; Jouaville et al., 1995). This supports the idea that vital pieces of information are encoded in the spatio-temporal [Ca2+] distribution, much more than what a static average could ever provide (Lechleiter et al., 1991).
Despite the diversity of mechanisms that underlie Ca2+ signals in different cell types, it is generally accepted that intracellular Ca2+ waves are governed by buffer-mediated Ca2+ diffusion between localized sites of Ca2+ release (the sites with Ca2+ channels) (Sneyd et al., 1998). These channels connect the cytosol and the lumen of intracellular stores, such as the sarcoplasmic reticulum (SR) or endoplasmic reticulum (ER), where the (free) Ca2+ concentration can be two or three orders of magnitude higher than in the cytosol. The open probability of the Ca2+ channels that are located on the membrane of the ER or SR (IP3 and ryanodine receptors, respectively) is modulated by cytosolic Ca2+. Given that Ca2+ itself carries the “opening message”, the release of Ca2+ at one site may eventually induce the release from a channel located further apart. This mechanism is called calcium-induced calcium release (CICR). For CICR to occur, Ca2+ needs to diffuse between release sites. Release and intersite diffusion occur simultaneously with buffering that prevent Ca2+ concentration from building up. Thus, Ca2+ buffers directly affect the spatio-temporal organization of intracellular Ca2+ (Callamaras and Parker, 2000). Realistic models of Ca2+ dynamics must account for their presence.
Though important for their effect on the Ca2+ distribution, the spatio-temporal behavior of buffers themselves is not of interest. For this reason, different ways of simplifying the description of the Ca2+ dynamics in the presence of buffers have been analyzed. In this article, we are interested in the so called rapid buffering approximation (Wagner and Keizer, 1994; Smith et al., 1996), an approximation that can be obtained as a particular example of a systematic perturbative reduction of two-timescale reaction-diffusion systems (Strier and Dawson, 2000). The rapid buffering approximation allows Ca2+ dynamics to be described in a reduced way, namely, in terms of a single evolution equation for [Ca2+]. A necessary condition for this reduced description to hold is the existence of a timescale separation: the reactions with the buffers must occur much faster than all other processes. In this way, it may be assumed that buffers and Ca2+ are locally in chemical equilibrium. In many cases the resulting reduced equation is not of diffusive type (Wagner and Keizer, 1994; Strier et al., 2002), although it can be rewritten as a reaction-diffusion equation with a concentration-dependent diffusion coefficient (Sneyd et al., 1998) (see Model and Methods section). The perturbative approach that underlies the rapid buffering approximation requires that the separation between fast and slow process be uniformly valid in time and space. However, it does not seem likely that such separation will hold in the vicinity of an open Ca2+ channel (Smith et al., 1996, 2001; Naraghi and Neher, 1997; Dawson and Uchitel, 2002). Given the small size of the release sites, it is reasonable to expect the existence of large concentration gradients of Ca2+ that would make diffusion be the fastest process (faster than the reactions with buffers). This is exactly what we investigate in this article. More specifically, we analyze to what extent Ca2+ waves, in which propagation is mediated by Ca2+ release through localized sites, can be accurately described within the rapid buffering approximation.
Some years ago, we introduced the fire-diffuse-fire model (Dawson et al., 1999; Keizer et al., 1998) to study intracellular Ca2+ wave propagation within a simplified setting that yet provided a physical insight into the processes that shape the various signaling modes. Although the fire-diffuse-fire model includes the spacing between release sites, both CICR and the presence of buffers are treated in a simplified manner. The simplicity of the fire-diffuse-fire model allows an easy, but meaningful, identification of the relevant space- and timescales that regulate the transition from saltatory to continuous propagation. Therefore, the fire-diffuse-fire model provides a natural framework within which the limits of applicability of the rapid buffering approximation can be assessed. In the present article we add buffers explicitly to the fire-diffuse-fire model and then perform the standard reduction that leads to the rapid buffering approximation to analyze the limits of applicability of the latter.
MODEL AND METHODS
Full model with explicitly included buffers
The spatio-temporal evolution of the cytosolic Ca2+ concentration, [Ca2+], is the result of various processes. In this article we consider Ca2+ diffusion, the interaction with buffers, and the feeding and re-uptake from internal stores (such as the endoplasmic reticulum), neglecting Ca2+ entrance or removal through the plasma membrane. These processes are thought to be enough to model intracellular Ca2+ waves (see, e.g., De Young and Keizer (1992)). For the interaction with the buffers, we consider the simplest possible model. Namely we include only one type of buffer, B, which interacts with Ca2+ according to the scheme:
 |
(1) |
where C is the buffer with bound Ca2+ . We further assume that the Ca2+ concentration in the stores, [Ca2+]ER, is high enough so that it may be assumed to be constant. In this way, the evolution is described by the following set of reaction-diffusion equations:
 |
(2) |
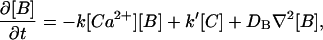 |
(3) |
 |
(4) |
which are to be solved subject to boundary and initial conditions for [Ca2+](x,t), [B](x,t) and [C](x,t). In Eqs. 2–4, [Ca2+](x,t), [B](x,t), [C](x,t), DCa, DB, and DC are the concentrations and diffusion coefficients of the species in the cytosolic medium, respectively; f(x,t) represents the flow of Ca2+ ions through Ca2+ channels (IP3 or ryanodine receptors), whereas g([Ca2+]) represents the re-uptake due to (ATP-operated) pumps and, if present, a permanent leak. For most buffers, it is reasonable to assume that the re-uptake into the stores and the permanent leak always occur more slowly than the binding to the buffers (see De Young and Keizer (1992) and Smith et al. (1996)). Therefore, as done in Dawson et al. (1999), we will take g = 0. By neglecting the effect of pumps, we can study how the “first” front propagates but we cannot describe how [Ca2+] goes back to its basal level or the re-entrance of waves. Thus, our study will focus on whether the dynamics of the front is correctly described by the rapid buffering approximation or not. We have included only one buffer for simplicity. Thus, our analysis is only a first step. More detailed studies including more buffers could be done in the future. Meanwhile, Eq. 2 can be interpreted as being an effective evolution equation for Ca2+ that results from the interactions with the buffers other than B.
For the general discussion that we present at the beginning of the Results section, we do not consider any particular form for f(x,t). In the numerical simulations, we follow Dawson et al. (1999) and consider only plane wave solutions treating CICR very schematically. Namely, we consider that the source term, f, is the following sum of contributions from clusters (or sites) of channels:
 |
(5) |
where δ is the Dirac delta function, the sites are separated by a distance d along the direction of propagation, x (i.e., xi = id), and Θ(x) is the step function, defined by Θ(ξ) = 0 if ξ < 0, and Θ(ξ) = 1 otherwise. Thus, the contribution from the ith site “turns on” or “fires” at time ti (i.e., starts to release Ca2+) when [Ca2+] at the site reaches a threshold, [Ca2+]th, for the first time. This is meant to mimic CICR. The site then remains “on” for a fixed amount of time, τ, releasing a total amount, σ, of Ca2+ ions (Dawson et al., 1999). Note that the values of ti are not known a priori. Instead, it is the evolution of the concentration field that sets those values dynamically. Given an initial condition, a finite value of ti may not exist for some values of i. The nonexistence of such a finite value implies propagation failure.
Equations 2–4 can be simplified if we assume that at t = 0, the total buffer concentration, [B](t = 0) + [C](t = 0), is uniformly distributed over space, [B]T ≡ [B](t = 0) + [C](t = 0) and DB = DC. In such a case, [B] + [C] = [B]T for all times. Thus, we can work with only two variables, [Ca2+](x,t) and [C](x,t), and Eqs. 2–4 (with g = 0) are reduced to:
 |
(6) |
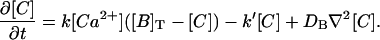 |
(7) |
Reduced model using the rapid buffering approximation
Equations 6 and 7 (with some prescription for f) provide the full description of the problem. By assuming that not all of the processes occur on the same timescales, the slow timescale evolution of the various variables may be described with fewer differential equations. In particular, if the reactions with the buffers are the fastest processes during the whole evolution, Eqs. 6 and 7 may be reduced to (Wagner and Keizer, 1994; Strier and Dawson, 2000):
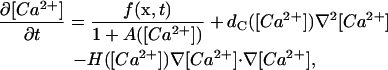 |
(8) |
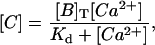 |
(9) |
where
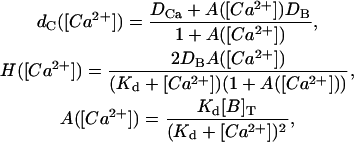 |
(10) |
with Kd = k′/k. This description corresponds to the so-called rapid buffering approximation (Wagner and Keizer, 1994; Smith et al., 1996). As shown in Sneyd et al. (1998), Eq. 8 can be rewritten as:
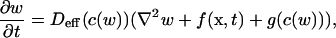 |
(11) |
where
 |
(12) |
[Ca2+] ≡ c(w) is the (positive) inverse of Eq. 12, and
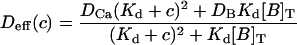 |
(13) |
is an effective (concentration-dependent) diffusion coefficient.
Full model in terms of dimensionless variables
Equations 6 and 7 can be rewritten with fewer free parameters introducing the dimensionless quantities: 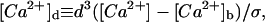 [C]d ≡ ([C] − [C]b)/[B]T, T ≡ t/τ, and x′ ≡ x/d. Taking f as given by Eq. 5, Eqs. 6 and 7 read:
[C]d ≡ ([C] − [C]b)/[B]T, T ≡ t/τ, and x′ ≡ x/d. Taking f as given by Eq. 5, Eqs. 6 and 7 read:
 |
(14) |
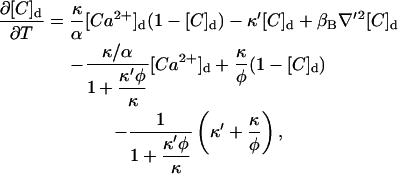 |
(15) |
where ∇′ means that the derivatives are performed with respect to the dimensionless coordinate, x′; t′i is the minimum time, t′, such that [Ca2+]d(i,t′) = d3([Ca2+]th − [Ca2+]b)/σ ≡ 1/Γ, and all other parameters are dimensionless and their definitions are given in Table 1.
TABLE 1.
Dimensionless parameters of the model
| Dimensionless parameters | |
| |
| κ = kτ[B]T | |
| κ′ = k′τ | |
| |
| |
| |
|
Numerical method and parameters of the simulations
We numerically simulate Eqs. 6 and 7 (FDF from now on) and Eq. 8 (RBA from now on) using finite differences both in space and time with grid size Δx = 0.33 μm and time step Δt = 1 μs in most cases. The method is explicit in time and the size of the steps has been checked to provide accurate results by comparing them with those predicted using smaller values. A larger value of Δt is used for the most continuous simulations, but never exceeding Δt = 100 μs. In all cases, the models are simulated in one space dimension, x, (the solutions represent plane waves that propagate in the x direction), using Eq. 5 for the release from Ca2+ channels. The boundary conditions are no-flux and there is only one buffer per simulation. In the simulations it is d = 3.3 μm, σ = 3.5 × 10−12 μmol, DCa = 220 μm2/s (Allbritton et al., 1992), [Ca2+]b = 0.05 μM, [Ca2+]th = 0.25 μM, and [B]T = 100 μM, unless otherwise noted. The buffer parameters are listed in Table 2. We call one of the buffers “parvalbumin-like” since it shares with this protein the values of k′ and DB. For the on-rate constant, k, we picked a particular one among the various that can be found in the literature. The other constants correspond to more or less well-agreed values for the buffers BAPTA, calbindin-D28K, and EGTA. In this way, we have chosen parameters that correspond to both fast and slow and endogenous and exogenous buffers. We have also explored other endogenous buffers, finding similar results to those of the exogenous ones whenever the rate constants were similar. As initial condition, we use step functions for [Ca2+] and [C], such that [Ca2+](x,t = 0) + [C](x,t = 0) = σ/d3 + [Ca2+]b + [C]b for x < x*, and [Ca2+](x,t = 0) = [Ca2+]b, [C](x,t = 0) = [C]b for x > x*, with [Ca2+] and [C] related by the equilibrium condition (Eq. 9) everywhere at t = 0. This initial condition satisfies the boundary conditions of a rightward traveling wave solution for the full model: [Ca2+] → [Ca2+]left as  and [Ca2+] → [Ca2+]b as
and [Ca2+] → [Ca2+]b as  , where [Ca2+]b is the basal Ca2+ level and [Ca2+]left is the solution of [Ca2+]left + [B]T[Ca2+]left/([Ca2+]left + Kd) = σ/d3 + [Ca2+]b + [C]b. The initial condition is not very important, since we are interested in an asymptotic wave solution whose shape and speed should be insensitive to it.
, where [Ca2+]b is the basal Ca2+ level and [Ca2+]left is the solution of [Ca2+]left + [B]T[Ca2+]left/([Ca2+]left + Kd) = σ/d3 + [Ca2+]b + [C]b. The initial condition is not very important, since we are interested in an asymptotic wave solution whose shape and speed should be insensitive to it.
TABLE 2.
Parameters for the endogenous and exogenous Ca2+ buffers used in the simulations and corresponding timescales
| Buffer | k [μM−1s−1] | k′ [s−1] | Kd [μM] |
|
τR[s] | 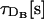 |
|
|---|---|---|---|---|---|---|---|
| EGTA | 1.5 | 0.3 | 0.20 | 113 | 6.7 × 10−3 | 0.096 | |
| Parvalbumin-like | 6 | 1 | 0.17 | 36 | 1.7 × 10−3 | 0.302 | |
| Calbindin-D28K | 20 | 8.6 | 0.43 | 27 | 5.0 × 10−4 | 0.403 | |
| BAPTA | 600 | 100 | 0.17 | 95 | 1.7 × 10−5 | 0.115 |
Tools for the analysis of the numerical simulations
There are two important quantities that characterize the front dynamics. One of them is the velocity of the waves, v, and the other is the number of sites that are simultaneously firing, N. We compute these two quantities for both sets of simulations (FDF and RBA). The front velocity is computed as 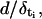 where
where 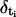 is the difference between the activation times of the sites located at positions i and i − 1, respectively. For a given set of parameters and initial condition, we compute the percentage relative error, (vFDF − vRBA)/vFDF, between the velocities of both models to evaluate the performance of the RBA. To compare the shape of the fronts obtained with both models, we let the systems approach the asymptotic solution. We then pick a time for both types of simulations such that [Ca2+] = [Ca2+]th at a release site. We redefine the time and space origins setting t = 0 at that instant and x = 0 at that particular site in both simulations. This allows us to study how the differences between the two solutions evolve with time.
is the difference between the activation times of the sites located at positions i and i − 1, respectively. For a given set of parameters and initial condition, we compute the percentage relative error, (vFDF − vRBA)/vFDF, between the velocities of both models to evaluate the performance of the RBA. To compare the shape of the fronts obtained with both models, we let the systems approach the asymptotic solution. We then pick a time for both types of simulations such that [Ca2+] = [Ca2+]th at a release site. We redefine the time and space origins setting t = 0 at that instant and x = 0 at that particular site in both simulations. This allows us to study how the differences between the two solutions evolve with time.
RESULTS
Comparison of timescales and preliminary analysis
We discuss here whether the assumptions of the rapid buffering approximation (the ones that underlie the reduction from Eqs. 6 and 7 to Eq. 8) are correct in the case of Ca2+ waves. To do the reduction, we first need to compare the size of the various terms that appear in Eq. 6. The rapid buffering approximation holds if k[Ca2+][B] and k′[C] are much larger than f(x,t) and DCa∇2[Ca2+]. The problem is that all these quantities change with time, and their relative sizes may change during the evolution. Let us assume that initially there is a spatially uniform distribution of buffers and Ca2+, and that at t = 0, the source, f(x,t), is turned on. Let us assume that the source remains “on” for a finite amount of time,  , i.e., f(x,t) = 0 for t < 0 and
, i.e., f(x,t) = 0 for t < 0 and  , and f(x,t) = F(x) for
, and f(x,t) = F(x) for  . Clearly, the initial concentrations must correspond to a spatially uniform equilibrium solution of Eqs. 6 and 7. We will describe the [Ca2+](t = 0) = 0 = [C](t = 0), [B](t = 0) = [B]T case in detail. Other cases can be handled similarly. For the time being, we will not consider a point source, but a source that changes in space over a length scale ℓ.
. Clearly, the initial concentrations must correspond to a spatially uniform equilibrium solution of Eqs. 6 and 7. We will describe the [Ca2+](t = 0) = 0 = [C](t = 0), [B](t = 0) = [B]T case in detail. Other cases can be handled similarly. For the time being, we will not consider a point source, but a source that changes in space over a length scale ℓ.
Immediately after the source is turned on, the only term that is different from zero in the right-hand side of Eq. 6 is f. Therefore, it cannot be neglected in front of the terms related to the binding with the buffers (as done in Wagner and Keizer (1994) and Strier and Dawson (2000)). The Ca2+ concentration will then start to change due to the presence of this source. We may assume that, at least during the earliest stages, [Ca2+] ∼ Ft. Therefore, the term k[Ca2+]([B]T − [C]) in Eq. 6 will be approximately given by kFt[B]T. On the other hand, given that F depends on space, then, the Ca2+ concentration will also depend on space. This means that ∇2[Ca2+] will be different from zero. Considering |∇2F| ∼ F/ℓ2, we may estimate the size of the diffusion term, DCa|∇2[Ca2+]|, as DCaFt/ℓ2. Then, only if the length scale over which the source varies is large enough, we may assume that the binding term becomes larger than the diffusion term after the source is turned on. Namely, 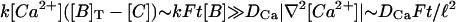 , if the typical length scale of the source, ℓ, satisfies
, if the typical length scale of the source, ℓ, satisfies 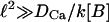 . Taking [B] ∼ 100 μM, we obtain
. Taking [B] ∼ 100 μM, we obtain  for calbindin-D28K and
for calbindin-D28K and  for BAPTA. This condition is never satisfied for a single channel, for which the typical pore width is of the order of some angstroms (Hille, 1992). Now, the elementary events that eventually give rise to global signals may be due to the almost coordinated opening of various channels in a cluster (Yao et al., 1995; Callamaras and Parker, 2000). Thus, if we neglect the small differences in the opening times of the individual channels that open in a cluster, we may consider ℓ as a typical cluster length scale, which has been estimated as 60 nm in Swillens et al. (1999). This number is still too small. Thus, immediately after one such source turns on, diffusion acts on a faster timescale than the binding to the buffers, and the rapid buffering approximation cannot be applied. We then expect the rapid buffering approximation to fail in the case of saltatory waves, in which the release from individual sites is readily observable. In the case of more continuous signals, such as the fertilization wave in the mature egg (Fontanilla and Nuccitelli, 1998), where channels in several clusters are releasing Ca2+ ions into the cytosol simultaneously (Dawson et al., 1999), we may assume that the length scale ℓ is the typical size of the region with simultaneous open channels. In the case of the fertilization wave, this size is given by the width of the wave front that we estimated as 47 μm (Dawson et al., 1999). Thus, for this situation, we may assume that the terms related to the binding and unbinding with the buffers become larger than the diffusion term immediately after the channels open, so that they may be treated as acting on a faster timescale. Now, as mentioned in the Model and Methods section, the resulting equation (Eq. 8) can be rewritten in terms of the effective diffusion coefficient of Eq. 13. This concentration-dependent diffusion coefficient tends to produce steeper fronts (Sneyd et al., 1998), i.e., larger concentration gradients, than the equivalent case with a constant coefficient. Thus, the validity of the rapid-buffering approximation has to be reassessed once the solution is obtained in this case.
for BAPTA. This condition is never satisfied for a single channel, for which the typical pore width is of the order of some angstroms (Hille, 1992). Now, the elementary events that eventually give rise to global signals may be due to the almost coordinated opening of various channels in a cluster (Yao et al., 1995; Callamaras and Parker, 2000). Thus, if we neglect the small differences in the opening times of the individual channels that open in a cluster, we may consider ℓ as a typical cluster length scale, which has been estimated as 60 nm in Swillens et al. (1999). This number is still too small. Thus, immediately after one such source turns on, diffusion acts on a faster timescale than the binding to the buffers, and the rapid buffering approximation cannot be applied. We then expect the rapid buffering approximation to fail in the case of saltatory waves, in which the release from individual sites is readily observable. In the case of more continuous signals, such as the fertilization wave in the mature egg (Fontanilla and Nuccitelli, 1998), where channels in several clusters are releasing Ca2+ ions into the cytosol simultaneously (Dawson et al., 1999), we may assume that the length scale ℓ is the typical size of the region with simultaneous open channels. In the case of the fertilization wave, this size is given by the width of the wave front that we estimated as 47 μm (Dawson et al., 1999). Thus, for this situation, we may assume that the terms related to the binding and unbinding with the buffers become larger than the diffusion term immediately after the channels open, so that they may be treated as acting on a faster timescale. Now, as mentioned in the Model and Methods section, the resulting equation (Eq. 8) can be rewritten in terms of the effective diffusion coefficient of Eq. 13. This concentration-dependent diffusion coefficient tends to produce steeper fronts (Sneyd et al., 1998), i.e., larger concentration gradients, than the equivalent case with a constant coefficient. Thus, the validity of the rapid-buffering approximation has to be reassessed once the solution is obtained in this case.
We then conclude that the rapid buffering approximation may not provide a correct description of intracellular Ca2+ waves, especially in the saltatory case in which the release from very localized regions is noticeable. We present in the following sections the results from various numerical simulations with which we assess the limitations of this approximation.
Numerical results: analysis in terms of dimensional variables
We present here the results obtained with numerical simulations of the FDF and the RBA models as described in the Model and Methods section. We focus first on how the differences between both models depend on the relationships among the relevant timescales of the problem. We can distinguish four timescales in the full description: one associated to the source, τ, one associated to the reactions, τR, and two associated to diffusion,  and
and 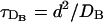 . The definition of a diffusive timescale depends on a choice of length scale. We have chosen that length scale as the intersite distance, d. The limitation of this definition will become evident later. A proper timescale associated to the reaction with the buffer, τR, can be obtained by linearizing the corresponding terms around the equilibrium solution, as done in Wagner and Keizer (1994). Following this procedure, one arrives at τR = 1/(k′ + k([Ca2+] + [B])). Given that the buffer concentration is large compared to [Ca2+], we can neglect the dependence on the Ca2+ concentration and define τR = 1/(k′ + k[B]T). This is good enough for our purposes, and simplifies the analysis. We will limit our analyses to cases in which
. The definition of a diffusive timescale depends on a choice of length scale. We have chosen that length scale as the intersite distance, d. The limitation of this definition will become evident later. A proper timescale associated to the reaction with the buffer, τR, can be obtained by linearizing the corresponding terms around the equilibrium solution, as done in Wagner and Keizer (1994). Following this procedure, one arrives at τR = 1/(k′ + k([Ca2+] + [B])). Given that the buffer concentration is large compared to [Ca2+], we can neglect the dependence on the Ca2+ concentration and define τR = 1/(k′ + k[B]T). This is good enough for our purposes, and simplifies the analysis. We will limit our analyses to cases in which  . The fact that
. The fact that 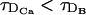 is a consequence of DB < DCa. This condition is physically reasonable since Ca2+ ions are smaller and lighter than buffer molecules. Therefore, by varying τ in the simulations, we can explore the following regimes:
is a consequence of DB < DCa. This condition is physically reasonable since Ca2+ ions are smaller and lighter than buffer molecules. Therefore, by varying τ in the simulations, we can explore the following regimes:
 |
(16) |
The first two cases correspond to saltatory behaviors, and the last two to continuous ones. τR being the smallest timescale of the problem is a necessary condition for the rapid buffering approximation to hold. Thus, we do not expect the approximation to work properly in Case I.
We show in Fig. 1 the percentage relative error, 100 × (vFDF − vRBA)/vFDF, as a function of τ for the four buffers of Table 2. The other characteristic times, τR, 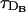 , and
, and 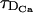 , are indicated in the figures. We may observe that the errors mainly decrease as τ increases, although the curves are not exactly monotone for EGTA or calbindin-D28K. Roughly speaking, we may say that the errors increase as the reaction timescale, τR, increases, although the error for parvalbumin is slightly larger than the one of EGTA for small values of τ. In the case of calbindin-D28K, the error decreases noticeably for some value of τ that is less than an order of magnitude smaller than τR. Despite this drop, it stays relatively high (∼20%) even for
, are indicated in the figures. We may observe that the errors mainly decrease as τ increases, although the curves are not exactly monotone for EGTA or calbindin-D28K. Roughly speaking, we may say that the errors increase as the reaction timescale, τR, increases, although the error for parvalbumin is slightly larger than the one of EGTA for small values of τ. In the case of calbindin-D28K, the error decreases noticeably for some value of τ that is less than an order of magnitude smaller than τR. Despite this drop, it stays relatively high (∼20%) even for 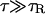 . In Fig. 1, A–C, the error drops abruptly (to a very small value) when τ becomes larger than the intersite diffusion times,
. In Fig. 1, A–C, the error drops abruptly (to a very small value) when τ becomes larger than the intersite diffusion times, 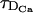 and
and  . For the fastest buffer, BAPTA, the error is ∼30% for τ = τR and drops to below 10% when τ becomes an order of magnitude larger than τR. As in the case of calbindin-D28K, for larger values of τ, the error stays at a level that is relatively insensitive to changes in τ, until τ becomes larger than
. For the fastest buffer, BAPTA, the error is ∼30% for τ = τR and drops to below 10% when τ becomes an order of magnitude larger than τR. As in the case of calbindin-D28K, for larger values of τ, the error stays at a level that is relatively insensitive to changes in τ, until τ becomes larger than  and
and 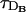 , when the error becomes negligible. As discussed in Dawson et al. (1999), the relationship between τ and the intersite diffusion time rules whether the propagation is saltatory or continuous. Saltatory or continuous waves are characterized by a different number of simultaneously firing sites. The big arrows in Fig. 1 point at the simulations of the FDF model with the smallest value of τ for which there are at least two simultaneously firing sites at the front. We call this value of τ, τ*. We present an analytic estimation of τ* in the Appendix. There is a change of behavior in the error associated to this transition, i.e., when there is a jump from “point source dimension” (ℓ ∼ 0) to intersite distance (ℓ ∼ d). This also shows that, for very saltatory propagation, the diffusion times that need to be compared with τR are smaller than
, when the error becomes negligible. As discussed in Dawson et al. (1999), the relationship between τ and the intersite diffusion time rules whether the propagation is saltatory or continuous. Saltatory or continuous waves are characterized by a different number of simultaneously firing sites. The big arrows in Fig. 1 point at the simulations of the FDF model with the smallest value of τ for which there are at least two simultaneously firing sites at the front. We call this value of τ, τ*. We present an analytic estimation of τ* in the Appendix. There is a change of behavior in the error associated to this transition, i.e., when there is a jump from “point source dimension” (ℓ ∼ 0) to intersite distance (ℓ ∼ d). This also shows that, for very saltatory propagation, the diffusion times that need to be compared with τR are smaller than  and
and 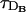 . Thus, even if
. Thus, even if 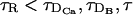 , the RBA may not be good. As the number of simultaneously firing sites increases, the relevant length scale goes from being almost zero to being d, and the diffusion times that need to be compared with τR become
, the RBA may not be good. As the number of simultaneously firing sites increases, the relevant length scale goes from being almost zero to being d, and the diffusion times that need to be compared with τR become 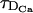 and
and  . From Fig. 1, we may conclude that, unless there is a huge separation between τR and the other timescales (as in the case of BAPTA), the signal needs to become more or less continuous to guarantee a good performance of the RBA. Quite surprisingly, an abrupt drop in the error may also be observed in the case of the slowest buffers (Fig. 1, A and B). However, in the case of EGTA, (Fig. 1 A), it occurs for a larger ratio between τ and the diffusion times than for the other buffers. The front profile in this case shows that even for τ = 0.1 > τ*, the individual release sites are readily distinguishable: the calcium concentration is more or less concentrated around the firing sites and, although there are several active sites, the propagation does not look continuous. The signal is not spread very smoothly in space, and those large gradients are the reason behind the differences between the predictions of both models, as we describe later. Therefore, it is not just the number of simultaneously firing sites that marks the transition to a better performance of the RBA, but the spatial “continuity” or “discreteness” of the signal, which is also determined by
. From Fig. 1, we may conclude that, unless there is a huge separation between τR and the other timescales (as in the case of BAPTA), the signal needs to become more or less continuous to guarantee a good performance of the RBA. Quite surprisingly, an abrupt drop in the error may also be observed in the case of the slowest buffers (Fig. 1, A and B). However, in the case of EGTA, (Fig. 1 A), it occurs for a larger ratio between τ and the diffusion times than for the other buffers. The front profile in this case shows that even for τ = 0.1 > τ*, the individual release sites are readily distinguishable: the calcium concentration is more or less concentrated around the firing sites and, although there are several active sites, the propagation does not look continuous. The signal is not spread very smoothly in space, and those large gradients are the reason behind the differences between the predictions of both models, as we describe later. Therefore, it is not just the number of simultaneously firing sites that marks the transition to a better performance of the RBA, but the spatial “continuity” or “discreteness” of the signal, which is also determined by  and
and 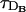 . Comparing the four buffers of Fig. 1, we may conclude that, if τ*≫τR, the value τ = τ* provides a good estimate of the point at which the transition to a more continuous propagation occurs or, equivalently, at which the error of the RBA drops abruptly. For the slower buffers for which the condition τ*≫τR does not hold, the error of the RBA can become very small if τ is much larger than all other timescales, including
. Comparing the four buffers of Fig. 1, we may conclude that, if τ*≫τR, the value τ = τ* provides a good estimate of the point at which the transition to a more continuous propagation occurs or, equivalently, at which the error of the RBA drops abruptly. For the slower buffers for which the condition τ*≫τR does not hold, the error of the RBA can become very small if τ is much larger than all other timescales, including  .
.
FIGURE 1.
Percentage relative error between the FDF and the RBA models as a function of τ for the four buffers of Table 2: EGTA (A), parvalbumin-like (B), calbindin-D28K (C), and BAPTA (D). The relevant timescales, other than τ, are indicated as τR,  , and
, and  . The big arrow points at the simulation of the FDF with the smallest value of τ, τ*, for which there are at least two simultaneously firing sites during the propagation of the wave. Parameter values in the main text.
. The big arrow points at the simulation of the FDF with the smallest value of τ, τ*, for which there are at least two simultaneously firing sites during the propagation of the wave. Parameter values in the main text.
To further explore the reasons behind the improvement in the rapid buffering approximation as the value τ = τ* is crossed, we compare in Fig. 2 the fronts that we obtain with both models for three values of τ. The parameters used for the simulations are the same as in Fig. 1 C (calbindin-D28K), with the exception of [B]T = 170 μM and [Ca2+]th = 0.07 μM for which τ* = 0.06 s. We include in Fig. 2 A a plot of the error as a function of τ where the values used for the simulations in Fig. 2, B–E, are indicated with squares. We show in Fig. 2, B–E, the profiles obtained with the FDF (solid curves) and the RBA models (dashed curves) at three times during the evolution using τ = 0.03 s (B and C), τ = 0.1 s (D), and τ = 10 s (E). The values of τ chosen correspond to decreasing errors of the RBA from B and C to E (see Fig. 2 A). In all cases the dotted lines correspond to the profiles at t = 0, at which [Ca2+](x = 0, t = 0) = [Ca2+]th for both the FDF and the RBA simulations. The two subsequent times are indicated with the labels t1 and t2. We observe in D that at t = 0 the front given by the RBA is steeper than the one given by the FDF. Something similar occurs in B although it cannot be observed within the resolution of the figure. We observe in B and D that at t = t1 (immediately after the source is turned on), the peak concentration is higher for the FDF than for the RBA model. This occurs because of the finite buffering time of the FDF model. Eventually the RBA “catches up” with the FDF. When the site stops releasing Ca2+, the signal is spread over a wider region in the FDF than in the RBA. This is evident at the later time, t2, of Fig. 2 B. This behavior, together with the existence of a steeper front for the RBA at t = 0, can be understood in terms of the effective diffusion coefficient defined in Eq. 13. According to Eq. 13, Ca2+ diffuses faster in regions of higher [Ca2+], which results in steeper fronts than if diffusion were everywhere the same. Thus, the RBA tends to generate steeper fronts than those obtained with the full model. Steeper fronts correspond to larger concentration gradients, making the RBA worse. In the case of a very saltatory propagation (Fig. 2 B), this difference in steepness results in a noticeable difference between the time intervals that separate two subsequent firings in the RBA and the FDF models: whereas at time t2 the site at x ≈ 3 μm is already firing according to the FDF, it has not started yet according to the RBA. This leads to errors in the wave velocity that result in fronts that drift apart with time, as shown in Fig. 2 C, where we plot the fronts predicted by the FDF and the RBA at a much later time. As propagation becomes more continuous, the fronts start to behave more similarly, as can be observed by comparing Fig. 2, B and D. Although in Fig. 2 D at t = t2 the site at x ≈ 3 μm is already firing according to the FDF while it is about to start in the RBA, the peak concentration at x ≈ 3 μm is smaller than in Fig. 2 B. Thus, the difference between both simulations in this case is smaller than in Fig. 2 B. In the example of Fig. 2 D, the second site starts to fire before the first one has stopped, and the gradient at the site that reaches threshold is slightly smaller than in Fig. 2 B. Finally, in the very continuous case, the differences between the RBA and the FDF are unnoticeable, as shown in Fig. 2 E, where the solutions of both models are plotted at three times although it is impossible to distinguish them.
FIGURE 2.
Comparison of the profiles obtained with the FDF (solid curves) and the RBA (dashed curves) models (B–E) for calbindin-D28K with all parameters the same as those in Fig. 1 C, except for [B]T = 170 μM and [Ca2+]th = 0.07 μM, and percentage relative error as a function of τ for the same parameters (A). τ = 0.03 s (B and C), τ = 0.1 s (D), and τ = 10 s (E). In all cases the dotted lines correspond to the profiles at t = 0. The other times shown are: t1 = 0.020 s, t2 = 0.166 s (B); t = 22 s (C); t1 = 0.120 s, t2 = 0.336 s (D), and t1 = 68 s, t2 = 136 s (E). Solid squares in B–E represent the sites of release. Open squares in A correspond to the parameter values of the simulations in B–E.
We may conclude from this discussion that the error of the RBA is most sensitive to the typical length scale over which there is Ca2+ release. There are other parameters besides τ that also affect the way the front is spread in space—among them, the relationship between the effective Ca2+ diffusion coefficient and the rate at which Ca2+ ions are injected in the cytosol, σ/τ. The number of simultaneously firing sites also depends on the threshold value for firing, [Ca2+]th. We analyze the effect of these other parameters in Fig. 3, where we plot the percentage relative error as a function of τ, for simulations done with the reaction rate constants of calbindin-D28K and various values of σ (Fig. 3, A and E), DCa (B), DB (C), [Ca2+]th (D), and [B]T (F). In those figures where the corresponding parameter was not changed, we used σ = 3.5 × 10−12 μmol, DCa = 220 μm2/s, DB = 27 μm2/s, [Ca2+]th = 0.25 μM, and [B]T = 100 μM, with the exception of Fig. 3 D, for which we used σ = 5.5 × 10−12 μmol. The reaction timescales in Fig. 3, A–D, are the same as those of Fig. 1 C.
FIGURE 3.
Percentage relative error between the FDF and the RBA models as a function of various parameters: σ (A), DCa (B), DB (C), [Ca2+]th (D), τ, and σ when σ/τ is constant (E) and [B]T (F). All simulations were done with calbindin-D28K as the only buffer. More details in the main text.
We show in Fig. 3 A how the error is affected by the total number of ions released by a site, σ. In this case, the diffusion timescales are the same as those of Fig. 1 C. We see that, for a given value of τ, the error increases as σ increases. This may be associated to the fact that larger Ca2+ gradients build up near an open source if more ions are released during the same amount of time τ. Larger Ca2+ gradients imply that the diffusive spread of Ca2+ becomes larger as compared to the rate at which Ca2+ is consumed by the reaction with the buffer, breaking the assumption that underlies the rapid buffering approximation. This seems to contradict some of the results reported in Smith et al. (1996). We discuss how to reconcile both observations in the last section. We also observe in Fig. 3 A that τ* decreases as σ increases. This is reasonable since a larger value of σ implies a larger [Ca2+] in the medium which, for a fixed threshold, [Ca2+]th, allows the occurrence of simultaneously firing sites at smaller τ values. Correlated with this behavior, the value of τ at which the error drops abruptly also decreases with increasing σ. We also observe that when τ is bigger than the diffusion times, the error becomes pretty much insensitive to the value of σ.
We show in Fig. 3 B how the error is affected by the rate at which Ca2+ diffuses, DCa. This is not merely a mathematical exercise (which, yet, provides information on the physics of the problem). From a biological point of view, having a different value of DCa could be associated to the effect of other buffers that are not explicitly included in the model. We can observe in Fig. 3 B that, for a given value of τ, the error increases as DCa increases. This is reasonable, since increasing DCa decreases the diffusion timescale, making it closer to the reaction one. However, the error can be pretty large even if  . In this figure,
. In this figure, 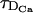 is 0.218 s for the lowest curve, 0.049 s for the middle one, and 0.036 s for the upper one, whereas τR = 5 × 10−4 s. As expected, the value of τ* decreases as DCa increases (since a larger value of DCa favors the occurrence of simultaneously firing sites). Consequently, the value of τ at which the error drops abruptly also decreases with increasing DCa. Thus, increasing DCa plays a dual role: by making the diffusion time smaller and closer to the reaction timescale, it makes the RBA less reliable; however, it facilitates, at the same time, the existence of simultaneously firing sites, a feature that improves the predicting power of the RBA. As in the previous case, when the RBA begins to work, the error becomes insensitive to the value of DCa.
is 0.218 s for the lowest curve, 0.049 s for the middle one, and 0.036 s for the upper one, whereas τR = 5 × 10−4 s. As expected, the value of τ* decreases as DCa increases (since a larger value of DCa favors the occurrence of simultaneously firing sites). Consequently, the value of τ at which the error drops abruptly also decreases with increasing DCa. Thus, increasing DCa plays a dual role: by making the diffusion time smaller and closer to the reaction timescale, it makes the RBA less reliable; however, it facilitates, at the same time, the existence of simultaneously firing sites, a feature that improves the predicting power of the RBA. As in the previous case, when the RBA begins to work, the error becomes insensitive to the value of DCa.
We show in Fig. 3 C how the error is affected by the rate at which the buffer diffuses, DB. Contrary to the case of DCa, given a value of τ, the error decreases as DB increases (whereas DB < DCa). This occurs because increasing DB tends to homogenize the distributions, smoothing large gradients and favoring the existence of spatially spread fronts without affecting the relative size of the various terms that are involved in the evolution equation for [Ca2+] (as DCa does).  is 0.054 s for the lower curve, 0.403 s for the middle one, and goes to infinity for the upper one. Contrary to the previous cases, when the approximation begins to work, the error becomes more sensitive to the value of DB. τ* decreases as DB increases, for the same reasons for which it decreases when DCa increases.
is 0.054 s for the lower curve, 0.403 s for the middle one, and goes to infinity for the upper one. Contrary to the previous cases, when the approximation begins to work, the error becomes more sensitive to the value of DB. τ* decreases as DB increases, for the same reasons for which it decreases when DCa increases.
We show in Fig. 3 D how the error is affected by the threshold concentration for firing, [Ca2+]th (i.e., the excitability of the medium). In this case, for a given value of τ, the error decreases as [Ca2+]th increases. A larger value [Ca2+]th implies that it will take longer for a signal that starts at a particular site to “ignite” the following site. This could result in a smaller [Ca2+] gradient and the accuracy of the RBA would be improved. As shown in the following section, working with dimensionless parameters provides a better understanding of why the error decreases with increasing [Ca2+]th. As expected, the value of τ* increases with [Ca2+]th. As in Fig. 3, A and B, the error becomes insensitive to [Ca2+]th when the approximation works.
The quantity τ is involved in two parameters that have a clear physical meaning: the rate at which Ca2+ ions are injected, σ/τ, and the time during which a site remains open, τ. Increasing the injection rate while leaving the open duration time fixed is equivalent to increasing σ, something that is illustrated in Fig. 3 A. As expected, this makes the RBA less reliable. Now, the fact that the errors of the RBA systematically decrease as τ increases could be related to a smaller injection rate or to a longer duration time. Actually, both changes should improve the approximation: a smaller σ/τ allows the buffer to become in equilibrium with Ca2+ more easily, whereas having a longer duration facilitates the existence of simultaneously firing sites. To distinguish between these two situations, we compare in Fig. 3 E a series of simulations done varying both σ and τ in such a way that σ/τ = 30 × 10−12 μmol/s is the same in all of them. We may observe that the RBA improves as the duration of release is increased, even when there is only one firing site. This agrees with observations reported in Smith et al. (1996) on the performance of the rapid buffering approximation in the presence of a single point source, as discussed in the last section.
Finally, we study in Fig. 3 F how the error is affected by the total buffer concentration, [B]T. We observe here that the error changes nonmonotonically with [B]T: when the propagation is very saltatory, the error is larger for [B]T = 80 μM than for both [B]T = 10 μM and [B]T = 100 μM. We discuss this behavior in the last section. We also observe that τ* increases with [B]T. This can be understood in the following way. Increasing [B]T increases the relative weight of DB to DCa in determining the effective rate at which Ca2+ ions diffuse (see Eq. 13). Since DB < DCa, increasing [B]T decreases the effective Ca2+ diffusion coefficient, favoring in this way saltatory over continuous propagation, which is reflected in a larger value of τ*. Finally, we can observe that, for more continuous propagation (larger values of τ), the error is a monotonically decreasing function of [B]T. As discussed in the last section, this is so because in this regime the way the error behaves with the various parameters is dominated by how they affect the concentration gradient (with the error decreasing as the gradients are smoothed out).
Numerical results: an analysis in terms of dimensionless parameters
Although intuitive, the discussion of the previous section has the complication of the large number of parameters that have an effect on the performance of the RBA. Thus, it is very difficult to explore the parameter space to determine the region of validity of the RBA. On the other hand, the same parameter may have a different effect depending on the other parameter values. To decrease the number of parameters to a minimum, we decided to introduce dimensionless quantities and recast the discussion on the limitations of the RBA in terms of a smaller number of (dimensionless) parameters. This new approach allows us to obtain results that are independent of the particular buffer that is used in the simulation. It also allows us to understand how combinations of parameters, which usually have a physical meaning, affect the accuracy of the RBA. In terms of the dimensionless variables, the wave solutions that travel to the right satisfy  , as
, as 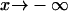 and
and 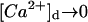 as
as  . Therefore, these solutions are just characterized by the seven parameters of Table 1.
. Therefore, these solutions are just characterized by the seven parameters of Table 1.
Some of the dimensionless parameters are ratios of timescales, or, equivalently, of rate constants, all of them with respect to τ. βCa and βB are dimensionless diffusive rates of Ca2+ and buffer, respectively, whereas κ and κ′ are dimensionless reaction rates, from which a dimensionless reaction timescale, τR′ = 1/(κ + κ′), can be defined as before. By changing two of these dimensionless timescales, we can explore the regimes II–IV defined in Eq. 16, visualizing the errors on a single two-dimensional plot. Given that it is expected that the RBA will not work in regime I, this way of looking at the problem provides a full description of the cases in which the performance of the RBA is not known a priori. We show such a plot in Fig. 4 A, where the percentage relative error is plotted using a color code as a function of βCa and βB. Three curves are superimposed on the figure: βCa = 1, βB = 1, and βCa = βB. These curves divide the βCa − βB plane in regions that correspond to the different regimes of Eq. 16, as indicated in the figure. As explained before, only the regions above the βCa = βB curve are physiologically meaningful. On the other hand, since τR′ = 5 × 10−3 in this figure, the reaction timescale is at least two orders of magnitude smaller than all the other timescales. Since Γ, κ, κ′, α, and φ remain constant in this figure, this βCa − βB plane only allows comparisons between buffers with the same dissociation constant, Kd = k′/k.
FIGURE 4.
(A) Percentage relative error on a βCa − βB plane. The other dimensionless parameters are Γ = 2000, κ = 200, κ′ = 0.86, α = 0.25, and φ = 2000. Three curves are included in the figure: βCa = 1, βB = 1, and βCa = βB, dividing the plane in the regions defined in Eq. 16. (B) Relative error as a function of βB when both βCa and βB are varied along a straight line, βCa = mβB, in A. Curves are labeled by the value of the slope, m.
Moving on Fig. 4 A along a horizontal line from left to right is equivalent to increasing DB, leaving the other parameters fixed. We can observe that the error gets smaller, whereas in the physiological meaningful region, βCa > βB. Moving along a vertical line from bottom to top corresponds to increasing DCa. We can observe that the error gets larger. Thus, if we move along a straight line of the form βCa = mβB, with m > 0, the error can either get larger or smaller depending on the value of m. Furthermore, it can have a nonmonotone behavior depending on m, as shown in Fig. 4 B. Increasing τ while leaving the other parameters fixed is somewhat similar to moving along a straight line with m = DCa/DB > 1. If we take DB equal to the diffusion coefficient of calbindin-D28K, for example, the error does not behave monotonically. We think that the nonmonotone behavior observed in Fig. 1, A and C, is a consequence of the particular ratio of diffusion coefficients that occur for EGTA and calbindin-D28K.
We present in Fig. 5 a similar plot as before, but on the βCa − Γ plane, and as a result of varying three parameters, βCa, Γ, and α in such a way that α = 500/Γ. As in Dawson et al. (1999), Γ is the ratio of the “release concentration”, σ/d3, to the difference between the threshold and the basal concentrations, [Ca2+]th − [Ca2+]b. Therefore, it provides a measure of how hard it is to “ignite” one site with another site. The fact that [Ca2+]th enters into the equations only through the dimensionless parameter Γ means that the threshold concentration affects the accuracy of the RBA depending on how it compares with the release concentration, in particular, with σ. Then, increasing [Ca2+]th while leaving the other parameters fixed is the same as decreasing Γ. We conclude from Fig. 5 that increasing [Ca2+]th reduces the error. Analyzing the problem in terms of dimensionless parameters allows us to relate this behavior with the improvement of the RBA as σ is decreased. Now, σ enters into the equations not only through Γ, but also through α, the ratio of total buffer to release concentrations. So, if α is either very large or very small, and the error is more or less insensitive to changes in its value, then the way the errors behave with Γ together with the definition of Γ imply that increasing [Ca2+]th will have a similar effect to decreasing σ. Decreasing σ results in smaller [Ca2+] gradients and, thus, in smaller errors. Therefore, the improvement as [Ca2+]th is increased is due to the occurrence of smaller [Ca2+] gradients.
FIGURE 5.
Similar to Fig. 4 but on a βCa − Γ plane. The other dimensionless parameters are: α = 500/Γ, βB = 0.24, κ = 200, κ′ = 0.86, and φ = 2000. The arrows correspond to some of the results in Fig. 3. Moving along the solid arrow is equivalent to moving from one curve to another for fixed τ, in Fig. 3 A. Moving along the dashed arrow is equivalent to moving from one curve to another for fixed τ, in Fig. 3 B.
DISCUSSION AND SUMMARY
Intracellular Ca2+ waves propagate regeneratively via the release of Ca2+ ions through the very narrow pores of Ca2+ channels. Although propagation is affected by the presence of buffers, usually buffer dynamics is not of interest. A description of Ca2+ waves in terms of [Ca2+] only is provided by the rapid buffering approximation, which holds when the reactions with the buffers occur much faster than all other processes (Wagner and Keizer, 1994). However, the localized nature of Ca2+ release is likely to break the underlying assumptions of the approximation. In this article we have analyzed the validity of the rapid buffering approximation using an extension of the fire-diffuse-fire model (Dawson et al., 1999) in which the dynamics of one buffer is included explicitly. We have observed that the length scale of the region with Ca2+ release plays a key role, with the approximation becoming more accurate as this length scale increases. This length scale is determined by the number of sites that are simultaneously releasing Ca2+. Thus, the approximation improves when the propagation changes from saltatory to continuous. Increasing the Ca2+ diffusion coefficient, DCa, is not enough to produce this transition. Moreover, the rapid buffering approximation gets worse as DCa is increased since this makes diffusion be a faster process. Increasing the buffer diffusion coefficient, while keeping DB < DCa, favors the transition to continuous propagation and improves the approximation.
Understanding the behavior of the approximation with [B]T, DB, and the Ca2+ current is a little subtle. At [B]T = 0, the error is zero because the FDF and the RBA descriptions are identical. Thus, the error increases with [B]T for [B]T sufficiently small. This agrees with the observation of Smith et al. (1996), where the validity of the rapid buffering approximation near a single point source is studied numerically. Now, the pace at which the buffering reactions occur increases with [B]T and this should result in a smaller error. In fact, we have shown in this article that the error depends nonmonotonically on [B]T. The nonmonotonicity is more noticeable when τ, a parameter that determines both the Ca2+ current and the time during which the channel is open, is small (i.e., with brief but high Ca2+ currents). In Smith et al. (1996), the effect of different Ca2+ currents on the approximation is also studied. In particular, it is shown that the error is greatest at intermediate currents. We do not find this type of behavior. However, the authors of Smith et al. (1996) compute the error mainly in a region around the point source. Buffers may get saturated in that region and this can be the reason behind the nonmonotone behavior of their error with the Ca2+ current. Namely, for small currents the error is small because [Ca2+] gradients are small. When the Ca2+ current is too large, the buffer gets saturated near the source and most Ca2+ is free. In that limit both the rapid buffering approximation and the full model reduce to the “plain” diffusion equation and the error goes again to zero. Although the approximation may get better near the source as the current increases, it may get worse farther away, where the buffer is unsaturated. This is the behavior that we capture with our analysis in the case of saltatory propagation, in which the wave speed is inaccurately predicted by the rapid buffering approximation if the current is too large. The fact that buffer saturation plays a role on the performance of the approximation near a point source is also reflected in the error in that region being larger for mobile than for immobile buffers (Smith et al., 1996). Mobile buffers replenish locally depleted regions, making saturation less favorable. The results of Smith et al. (1996) also show that, on the other hand, the errors are larger away from the source for immobile than for mobile buffers. This agrees with our observation that the error decreases when the buffer diffusivity increases. The different behavior of the approximation close to or far away from the source is also the reason behind the way the errors behave as a function of buffer concentration and diffusion coefficient for parameter values for which propagation is less saltatory. For continuous propagation, the performance is fully dominated by the concentration gradient over the region with simultaneously firing sites. Therefore, increasing the buffer concentration or its diffusion coefficient improves the approximation since it helps smooth out the concentration gradients over that region. In the region with few simultaneous firing sites, the approximation is most sensitive to the values of these parameters exactly for this reason.
Combining the results of Smith et al. (1996) and ours, we may conclude that, near a point source, the rapid-buffering-approximation improves as a “free-diffusion” situation is achieved (i.e., as the Ca2+ current increases and the buffer concentration decreases, the last feature being favored if the buffer is immobile). Farther away from the point source, the approximation improves as the concentration gradients get smaller, something that is achieved for smaller Ca2+ currents and larger concentrations of more mobile buffers. In the case of saltatory waves, it is the way the errors behave away from the source that matters the most to determine the accuracy of the approximation in predicting the wave speed. The approximation improves as the gradients smooth out and the waves become more continuous.
The results presented in this article show that the classification of buffers in slow or fast is somewhat delicate in the case of Ca2+ waves, since the relevant diffusion timescales against which the reaction timescale has to be compared can be arbitrarily small. We have observed that in the case of saltatory propagation, errors in the wave velocity can remain above experimental resolution even when the reaction timescales are much smaller than the intersite diffusion times. Conversely, we have observed that the approximation works pretty well even for slow buffers if the region with active Ca2+ release decays over a sufficiently large length scale. Concentration gradients play a key role in determining the accuracy of the approximation. However, large gradients are induced by the concentration-dependent diffusion coefficient that the rapid buffering approximation gives. In a sense, the approximation has in itself the seed for its own breakup. Therefore it is important to assess a priori the possible sources of error of using the approximation. In the present article we have introduced the relevant distance and timescales that to need be compared for this assessment.
Acknowledgments
We acknowledge useful conversations with J. Pearson.
This work has been funded by Universidad de Buenos Aires, Agencia Nacional de Promoción Científica y Tecnológica-Argentina (PICT 03-08133), and National Institutes of Health (GM65830). S.P.D. is member of Carrera del Investigador Científico (CONICET).
APPENDIX: ANALYTICAL APPROXIMATION TO τ*
The number of sites that are simultaneously firing at the front plays a major role on the accuracy of the RBA. In the original fire-diffuse-fire model, the transition from one to several simultaneously firing sites is ruled by only one ratio of timescales, τ/τD, with D an “effective” diffusion coefficient for Ca2+. In the present case, there are two intersite diffusion timescales and thus two ratios that rule this transition, making it more difficult to estimate the value of τ at which it occurs (τ*). So far, we have calculated τ* numerically but we would like to have an a priori estimate of its value. We present in this Appendix a simple analytic approximation to τ*. To this end we consider Eq. 6 with no pumps or buffers, with an effective diffusion coefficient, D, and with only one site that is turned on at time t = 0 and remains on for the time being:
 |
(17) |
with [Ca2+](x,t = 0) = 0, [Ca2+] → 0 as  . A good approximation to a solution of Eq. 17 is:
. A good approximation to a solution of Eq. 17 is:
 |
(18) |
This approximation has the same spatial dependence as the stationary solution of Eq. 17 and a time dependence that gives the correct number of injected ions (it satisfies 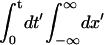 [Ca2+](x′,t′) = σt/(d2τ)). Furthermore, it satisfies [Ca2+] ≥ 0 for all times and space points. With this approximation for [Ca2+](x,t) we can find the time t* at which [Ca2+](d,t*) = [Ca2+]th. If we think of the source as coming from one of the sites of the fire-diffuse-fire model, and assume that there is another such site at x = d, then t* is the instant at which a second source starts to release Ca2+. Thus, by setting the duration during which the first source is on, τ, equal to t*, we obtain the value of τ, τ*, at which the transition from having a single firing site at the front to having two occurs. Proceeding in this way we obtain:
[Ca2+](x′,t′) = σt/(d2τ)). Furthermore, it satisfies [Ca2+] ≥ 0 for all times and space points. With this approximation for [Ca2+](x,t) we can find the time t* at which [Ca2+](d,t*) = [Ca2+]th. If we think of the source as coming from one of the sites of the fire-diffuse-fire model, and assume that there is another such site at x = d, then t* is the instant at which a second source starts to release Ca2+. Thus, by setting the duration during which the first source is on, τ, equal to t*, we obtain the value of τ, τ*, at which the transition from having a single firing site at the front to having two occurs. Proceeding in this way we obtain:
 |
(19) |
This expression depends on the effective diffusion coefficient, D. To include some information on the reaction with the buffer, we compute D as
 |
(20) |
where 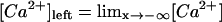 and Deff(c) is given by Eq. 13. We show in Table 3 the values of τ* estimated using Eq. 19 (
and Deff(c) is given by Eq. 13. We show in Table 3 the values of τ* estimated using Eq. 19 (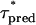 ) and those obtained from the numerical simulations (
) and those obtained from the numerical simulations ( ). The agreement is very good. Therefore, the estimate of τ* can be used to determine a priori whether the RBA may provide a good description of the dynamics or not.
). The agreement is very good. Therefore, the estimate of τ* can be used to determine a priori whether the RBA may provide a good description of the dynamics or not.
TABLE 3.
Prediction and numerical calculation of τ* (smallest value of τ for which there are at least two simultaneously firing sites at the front) for different values of σ and [Ca2+]th
| σ [×10−12μmol] | [Ca2+]th [μM] | Deff [μm2 s−1] |
 [s] [s] |
 [s] [s] |
 [s] [s] |
|---|---|---|---|---|---|
| 5.5 | 0.25 | 190.6 | 0.028 | 0.02 | 0.04 |
| 3.5 | 0.25 | 94.1 | 0.06 | 0.08 | 0.2 |
| 3.0 | 0.25 | 46.2 | 0.12 | 0.1 | 0.2 |
| 5.5 | 0.40 | 190.5 | 0.029 | 0.03 | 0.05 |
The estimated effective diffusion coefficient for [Ca2+], Deff, is also listed.
References
- Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell, 4th ed. Garland Science, New York.
- Allbritton, N. L., T. Meyer, and L. Stryer. 1992. Range of messenger action of calcium ion and inositol 1,4,5-triphosphate. Science. 258:1812–1815. [DOI] [PubMed] [Google Scholar]
- Berridge, M. J., M. D. Bootman, and P. Lipp. 1998. Calcium—a life and death signal. Nature. 395:645–648. [DOI] [PubMed] [Google Scholar]
- Callamaras, N., and I. Parker. 2000. Phasic characteristic of elementary Ca2+ release sites underlying quantal responses to IP3. EMBO J. 19:3608–3617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson, S. P., J. Keizer, and J. E. Pearson. 1999. Fire-diffuse-fire model of dynamics of intracellular calcium waves. Proc. Natl. Acad. Sci. USA. 96:6060–6063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawson, S. P., and O. Uchitel. 2002. The effect of buffered calcium diffusion on neurotransmitter release. Physica D. 168–169:356–364. [Google Scholar]
- De Young, G. W., and J. Keizer. 1992. A single-pool inositol 1,4,5-triphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. USA. 89:9895–9899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontanilla, R. A., and R. Nuccitelli. 1998. Characterization of the sperm-induced calcium wave in Xenopus eggs using confocal microscopy. Biophys. J. 75:2079–2087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille, B. 1992. Ionic channels of excitable membranes. Sinauer, Sunderland, MA.
- Jouaville, L. S., F. Ichas, E. L. Holmuhamedov, P. Camacho, and J. D. Lechleiter. 1995. Synchronization of calcium waves by mitochondrial substrates in Xenopus laevis oocytes. Nature. 377:438–441. [DOI] [PubMed] [Google Scholar]
- Keizer, J., G. Smith, S. Ponce-Dawson, and J. Pearson. 1998. Saltatory propagation of Ca2+ waves by Ca2+ sparks. Biophys. J. 75:595–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lechleiter, J. L., S. Girard, E. G. Peralta, and D. E. Clapham. 1991. Spiral calcium wave propagation and annihilation. Science. 252:123–126. [DOI] [PubMed] [Google Scholar]
- Naraghi, M., and E. Neher. 1997. Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. J. Neurosci. 17:6961–6973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, G. D., J. Wagner, and J. Keizer. 1996. Validity of the rapid buffering approximation near an open Ca2+ channel. Biophys. J. 70:2527–2539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, G. D., L. Dai, R. M. Miura, and A. Sherman. 2001. Asymptotic analysis of buffered calcium diffusion near a point source. SIAM J. Appl. Math. 61:1816–1838. [Google Scholar]
- Sneyd, J., P. Dale, and A. Duffy. 1998. Traveling waves in buffered systems: applications to calcium waves. SIAM J. Appl. Math. 58:1178–1192. [Google Scholar]
- Strier, D. E., and S. P. Dawson. 2000. Rescaling of diffusion coefficients in two-time scale chemical systems. J. Chem. Phys. 112:825–834. [Google Scholar]
- Strier, D. E., A. Chernomoretz, and S. P. Dawson. 2002. Slow time evolution of two-time-scale reaction-diffusion systems: The physical origin of nondiffusive transport. Phys. Rev. E. 65:46233–46247. [DOI] [PubMed] [Google Scholar]
- Swillens, S., G. Dupont, L. Combettes, and P. Champeil. 1999. From calcium blips to calcium puffs: Theoretical analysis of the requirements for interchannel communication. Proc. Natl. Acad. Sci. USA. 96:13750–13755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner, J., and J. Keizer. 1994. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 67:447–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao, Y., J. Choi, and I. Parker. 1995. Quantal puffs of intracellular Ca2+ evoked by inositol trisphosphate in Xenopus oocytes. J. Physiol. 482:533–553. [DOI] [PMC free article] [PubMed] [Google Scholar]