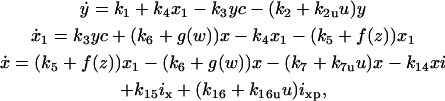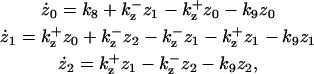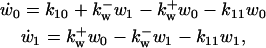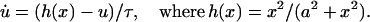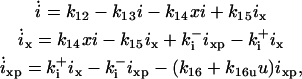Abstract
We have developed a generic mathematical model of a cell cycle signaling network in higher eukaryotes that can be used to simulate both the G1/S and G2/M transitions. In our model, the positive feedback facilitated by CDC25 and wee1 causes bistability in cyclin-dependent kinase activity, whereas the negative feedback facilitated by SKP2 or anaphase-promoting-complex turns this bistable behavior into limit cycle behavior. The cell cycle checkpoint is a Hopf bifurcation point. These behaviors are coordinated by growth and division to maintain normal cell cycle and size homeostasis. This model successfully reproduces sizer, timer, and the restriction point features of the eukaryotic cell cycle, in addition to other experimental findings.
INTRODUCTION
Eukaryotic cells normally reside in a quiescent state, called G0. To replicate, the cell reenters G1 and begins to synthesize the factors necessary for further progression through the cell cycle, as well as increase its mass in preparation for the subsequent division. In late G1, a restriction point (R point) is present. Once the cell passes this point, growth factors are no longer necessary to complete the cycle (Zetterberg and Larsson, 1995). At the G1/S phase transition, cells pass a checkpoint, which controls entry into the S phase. Likewise, in G2, a second checkpoint exists that ensures complete and accurate DNA replication has been completed before progressing to the M phase. At the end of the G2/M transition, the nucleus and cell divide, and the daughter cells start a new cycle. The cycle time between successive cell divisions in higher eukaryotes such as Drosophila and frogs (Masui and Wang, 1998; Montagne et al., 1999) as well as in yeast (Fantes, 1977; Sveiczer et al., 1996), has been shown to depend on cell size, which under normal conditions is divided into two phases, corresponding to a sizer and timer. If the beginning cell size after the previous division is smaller than a critical size, the time required to grow to this critical size is called the sizer phase, which is determined by birth size. When the cell grows to the critical size, or if the birth cell size exceeds it, the time required to complete division is called the timer phase, and is almost constant irrespective of the birth size (Fantes, 1977; Masui and Wang, 1998; Sveiczer et al., 1996).
Checkpoints, cell size, and the sizer and timer phases are regulated by a signaling network of kinases and phosphatases, which is too complex for its underlying mechanisms to be divined by intuition alone. Mathematical modeling and nonlinear dynamics have been essential tools for gaining insight into this most fundamental biological process. A number of mathematical models (Aguda, 1999; Aguda and Tang, 1999; Chen et al., 2000; Gardner et al., 1998; Goldbeter, 1991; Hatzimanikatis et al., 1999; Novak and Tyson, 1997; Obeyesekere et al., 1997; Qu et al., 2003; Sveiczer et al., 2000; Thron, 1997; Tyson, 2002; Tyson et al., 2001; Tyson and Novak, 2001) have been developed to illuminate the workings of the cell cycle, based on various dynamical mechanisms including limit cycle oscillation (Goldbeter, 1991; Hatzimanikatis et al., 1999; Obeyesekere et al., 1997), bistability (Chen et al., 2000; Sveiczer et al., 2000; Thron, 1997; Tyson et al., 2001; Tyson and Novak, 2001), and transient processes (Aguda, 1999; Aguda and Tang, 1999). (See Appendix A for glossary of the nonlinear dynamics terminology used in this article, such as limit cycle, bistability, and various bifurcations.) However, no single dynamical mechanism on its own can account for all features of the cell cycle, including checkpoints, sizers, and timers. For example, as pointed out by Tyson (Tyson and Novak, 2001), a pure limit cycle does not exhibit the checkpoint feature or maintain homeostasis of cell size during successive cycles. A pure bistable system has a clear checkpoint feature, but does not produce repetitive cycles. Therefore, how the cell coordinates its size, checkpoints, and cell cycle progression in terms of these dynamical behaviors is not completely understood, despite its critical importance.
In the past decade, Tyson and colleagues (Chen et al., 2000; Novak and Tyson, 1993, 1997; Sveiczer et al., 2000; Tyson et al., 2001; Tyson and Novak, 2001) developed models for the yeast cell cycle and the Xenopus egg cell cycle which have greatly improved our understanding of cell cycle dynamics. Their models show a saddle-node bifurcation for the G1/S transition checkpoint and a saddle-node-loop bifurcation for the G2/M transition checkpoint (Borisuk and Tyson, 1998; Tyson et al., 2001, 2002). They proposed a cell cycle machine of growth-driven hysteresis in a bistable system, with G1 representing the first, and S-G2-M the second, of the two stable states. In their models, the checkpoint is a saddle-node or saddle-node-loop bifurcation point. Cell growth drives the cell past this point and thus lifts kinase activity from the lower stable steady state to the higher stable steady state (from G1 to S-G2-M). Chromosome alignment drives the cell back to the low kinase activity state from the high state (from S-G2-M to G1), completing the cycle (Tyson et al., 2001, 2002; Tyson and Novak, 2001). In their model, an elegant reconciliation between checkpoints and repetitive cycling has been achieved. However, other features, such as sizers and timers, remain to be explained.
In this article, we formulated a mathematical model to investigate the dynamics of cell cycle in higher eukaryotes, toward the goal of determining whether additional features, such as sizers and timers, could also be explained. To simplify the analysis, we considered a generic signaling module that can be used to represent either the G1/S or G2/M transitions. We show that a Hopf bifurcation, rather than a saddle-node bifurcation, is a natural candidate for checkpoints in the cell cycle. Moreover, in this model, sizers and timers arise naturally as features of this signaling network.
MATHEMATHICAL MODELING AND NUMERICAL METHODS
In the cell cycle of higher eukaryotics, the most important cyclins are cyclin A (CycA), cyclin B (CycB), and cyclin E (CycE), and the major cyclin-dependent kinases (CDKs) are CDK1 and CDK2. Increased CycE:CDK2 activity marks the G1/S transition, whereas increased CycB:CDK1 activity marks the G2/M transition. Although their functions are different, the signaling networks regulating these activities are similar, as illustrated in Fig. 1 and described below. Because of these similarities, we developed a generic model that can be used to represent either the G1/S or G2/M transition.
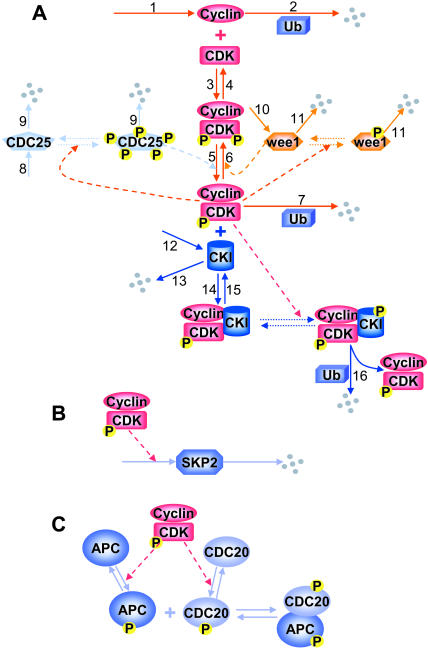
FIGURE 1.
(A) Signaling networks for cyclin and CDK regulation, (B) SKP2 regulation, and (C) APC/CDC20 regulation. The solid lines with arrowheads indicate synthesis or degradation of a protein, or a biochemical reaction step. The dashed lines indicate that the reaction is catalyzed by the protein or protein complex connected to the line. The dotted lines indicate the phosphorylation, and thus dephosphorylation may involve multiple steps, as described in the text. Small gray spheres represent degraded protein molecules.
Modeling cyclin and CDK regulation
Cyclin and CDK bind, forming inactive Cyclin:CDK complex, with CDK phosphorylated at Thr14, Tyr15, and Thr160 (for CDK2) or Thr161 (for CDK1). CDC25 dephosphorylates both Thr14 and Tyr15 to activate the kinase activity of the Cyclin:CDK complex. Wee1 phosphorylates both Thr14 and Tyr15, inactivating this kinase activity. CDC25 must be phosphorylated by active Cyclin:CDK complex to become active (Hoffmann et al., 1994; Solomon et al., 1990; Solomon and Kaldis, 1998), which forms a positive feedback loop in Cyclin:CDK regulation. In contrast, phosphorylation of wee1 inactivates wee1 activity. Wee1 phosphorylation is also catalyzed by active Cyclin:CDK, which forms a double-negative feedback loop, equivalent to a positive feedback loop.
We assume the protein synthesis rates and total CDK are constant (Solomon et al., 1990). The degradation of cell cycle proteins occurs mainly through ubiquitination by the 26S proteasome. At the G1/S transition, the Skp1-CDC53/Cullin-F-box (SCF) complex catalyzes the phosphorylation-dependent ubiquitination of G1 cyclins and other cell cycle proteins (Peters, 1998). Most F-box proteins are constantly synthesized and degraded in a cell cycle-independent manner (Galan and Peter, 1999), but one of them, SKP2, is expressed and phosphorylated in a cell cycle-dependent manner (Bilodeau et al., 1999; Nakayama et al., 2001). At the G2/M transition, a protein called anaphase-promoting-complex (APC) is activated and targets CycB for ubiquitination (Morgan, 1999; Peters, 1998).
Active Cyclin:CDK may be inhibited by binding to CDK inhibitor (CKI). CKI bound to Cyclin:CDK is degradable only after being phosphorylated by active Cyclin:CDK (Montagnoli et al., 1999). Its degradation frees the bound Cyclin:CDK, allowing it to recycle, which forms another positive feedback loop.
The system of differential equations for cyclin and Cyclin:CDK regulation representing the above interactions is presented in Table 1, Eq. 1a. f(z) and g(w) in Eq. 1a represent the kinase activities of CDC25 and wee1, respectively, and will be specified below. The constants ki (i = 1, 16) in Eq. 1a are the rate constants for the corresponding reaction steps shown in Fig. 1.
TABLE 1.
Differential equations, variable definitions, and default parameters
| Differential equations for cyclin and CDK regulation | |||
| |||
| Differential equations for CDC25 regulation | |||
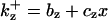 is the rate constant for CDC25 phosphorylation and is the rate constant for CDC25 phosphorylation and 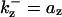 is for dephosphorylation, bz is the rate constant for CDC25 phosphorylation not catalyzed by active Cyclin:CDK, and czx is for phosphorylation catalyzed by active Cyclin:CDK. is for dephosphorylation, bz is the rate constant for CDC25 phosphorylation not catalyzed by active Cyclin:CDK, and czx is for phosphorylation catalyzed by active Cyclin:CDK. | |||
| Differential equations for wee1 regulation | |||
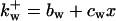 is the rate constant for wee1 phosphorylation and is the rate constant for wee1 phosphorylation and 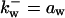 is for dephosphorylation, bw is the rate constant for wee1 phosphorylation not catalyzed by active Cyclin:CDK, and cwx is for phosphorylation catalyzed by active Cyclin:CDK. is for dephosphorylation, bw is the rate constant for wee1 phosphorylation not catalyzed by active Cyclin:CDK, and cwx is for phosphorylation catalyzed by active Cyclin:CDK. | |||
| Differential equations for SKP2 or APC regulation | |||
| |||
| Differential equations for CKI regulation | |||
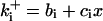 is the rate constant for CKI phosphorylation and is the rate constant for CKI phosphorylation and 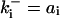 is for dephosphorylation, bi is the rate constant for CKI phosphorylation not catalyzed by active Cyclin:CDK, and cix is for phosphorylation catalyzed by active Cyclin:CDK. is for dephosphorylation, bi is the rate constant for CKI phosphorylation not catalyzed by active Cyclin:CDK, and cix is for phosphorylation catalyzed by active Cyclin:CDK. | |||
| Variable definitions | |||
| y | Free cyclin | ||
| x1 | Inactive Cyclin:CDK complex | ||
| x | Active Cyclin:CDK complex | ||
| c0 | Total CDK | ||
| c | Free CDK (normalized with c0) | ||
| z0 | Unphosphorylated CDC25 | ||
| z1 | One-site phosphorylated CDC25 | ||
| z2 | Two-site phosphorylated CDC25 | ||
| w0 | Unphosphorylated wee1 | ||
| w1 | Phosphorylated wee1 | ||
| u | Active SKP2 or APC | ||
| i | Free CKI | ||
| ix | Cyclin:CDK:CKI complex with CKI unphosphorylated | ||
| ixp | Cyclin:CDK:CKI complex with CKI phosphorylated | ||
| Default parameters | |||
| k1 = 300, k2 = 5, k3 = k4 = 30, k5 = 0.1, k6 = 1, k7 = 10, k8 = 100, k9 = 1, k10 = 10, k11 = 1, k12 = 0, k13 = 1, k14 = 1, k15 = 1, k16 = 2, k2u = 50, k7u = 0, k16u = 25, c0 = 200, a = 4, τ = 25, az = aw = ai = 10, bz = bw = bi = 0.1, and cz = cw = ci = 1. | |||
Modeling CDC25 regulation
CDC25 has many functional phosphorylation sites, a number of which are phosphorylated at the two cell cycle transitions (Hoffmann et al., 1993, 1994; Kumagai and Dunphy, 1992; Morris et al., 2000). To simplify the dynamical analysis, we assume CDC25 has two phosphorylation sites, and is synthesized at a constant rate (k8). All forms of CDC25 have degradation rates proportional to their concentration with a constant coefficient k9. The differential equations are listed in Table 1 as Eq. 1b. We set f(z) = z2 for Eq. 1a, since our previous study (Qu et al., 2003) showed that two-site phosphorylation of CDC25 (i.e., f(z) = z2) was necessary for interesting dynamics to occur. Higher order phosphorylation caused quantitative but not qualitative changes in the dynamics.
Modeling wee1 regulation
We assume wee1 is synthesized at a constant rate (k10), and both unphosphorylated and phosphorylated forms have degradation rates proportional to their concentrations (see reaction step 11 in Fig. 1). The differential equations are listed in Table 1 as Eq. 1c. Since wee1 is inactivated after phosphorylation, we set g(w) = w0 for Eq. 1a, i.e., only the unphosphorylated wee1 is active.
Modeling SKP2 or APC regulation
No detailed information exists on how SKP2 is regulated during the cell cycle. It has been shown SKP2 is expressed and phosphorylated at G1/S transition and throughout the S phase, and its phosphorylation is related to CDK2 not CDK1 (Bilodeau et al., 1999). We assume that SKP2's synthesis or phosphorylation is regulated by CycE:CDK2 (Fig. 1 B). We also assume SKP2 is degraded at a rate proportional to its concentration, so that d[SKP2]/dt = αh(x) − β[SKP2]. Here αh(x) defines the activation rate of SKP2, which is determined by active Cyclin:CDK (x), and β[SKP2] defines the inaction rate of SKP2. α and β are their respective rate constants. APC has to be phosphorylated and bind to phosphorylated CDC20 to be active (Morgan 1999). Both phosphorylation of APC and CDC20 is catalyzed directly or indirectly by active CDK1 (Fig. 1 C). We also assume active APC is inactivated at a rate proportional to its concentration. Therefore, we can use a similar differential equation for APC regulation, i.e., d[APC]/dt = αh(x)-β[APC]. By setting u = β[SKP2]/α or u = β[APC]/α, and τ = 1/β, we obtain a common differential equation (Eq. 1d in Table 1) for both SKP2 and active APC. In Eq. 1d, τ represents the time constant of the reaction, reflecting the time delay in the activation of SKP2 or APC. We use a Hill equation formulation for h(x), with h(x) = x2/(a2 + x2) in Eq. 1d and used a = 4 for all simulations. Other choices of h(x) had quantitative effects, but did not change the qualitative dynamics.
Modeling CKI regulation
The Cyclin:CDK:CKI complex has to be phosphorylated by active Cyclin:CDK for degradation (Montagnoli et al., 1999; Vlach et al., 1997). We assume CKI is synthesized at a constant rate (k12) and degraded at a rate proportional to its concentration. The degradation of phosphorylated CKI complexed with Cyclin:CDK is facilitated by SCF and also by SKP2 (Carrano et al., 1999). The differential equations are listed in Table 1 as Eq. 1e.
Computer simulation
There are 13 differential equations and 31 parameters (see Table 1). We used the fourth-order Runge-Kutta method to integrate Eq. 1 in Table 1 with a timestep smaller than 0.002. Since our purpose is to investigate the dynamics in general rather than to study the cell cycle dynamics for a specific species, we keep all the variables and parameters dimensionless. However, we searched a wide range of parameter spaces to detect different dynamics, and we found only limit cycle and bistability. The parameter set illustrated in Table 1 is typical for giving rise to such dynamics. However, since the dimension of parameter space is very high, we cannot exclude the possibility that other complex dynamics may be generated by this complicated signaling network.
RESULTS
The dynamics of the signaling network
A detailed dynamical analysis of the signaling network outlined schematically in Fig. 1, focusing on the roles of cyclin synthesis and degradation, positive feedback facilitated by CDC25 and wee1, negative feedback facilitated by SKP2 or APC, and CKI, is provided in Appendix B. We summarize the main findings here, which are that the positive feedback facilitated by CDC25 and wee1 causes bistability in Cyclin:CDK complex activity, whereas the negative feedback facilitated by SKP2 or APC turns this bistable behavior into limit cycle behavior. The capability of the negative feedback to turn the bistability into limit cycle depends strongly on the strength of the feedback, whereas the period of limit cycle depends strongly on the time delay of negative feedback. The cell cycle checkpoint in this model is thus a Hopf bifurcation point, rather than a saddle-node bifurcation as in the models by Tyson and colleagues (Tyson et al., 2001, 2002; Tyson and Novak, 2001). At present, there is no decisive experimental evidence to determine which types of bifurcation are responsible for the real cell cycle checkpoint. However, our model also demonstrates features that have not been clearly seen in prior models, including the restriction point, sizer, and timer phases, as well as other experimental findings described below. In our model, these behaviors are coordinated by growth and division to maintain normal cell cycle and size homeostasis.
Checkpoints
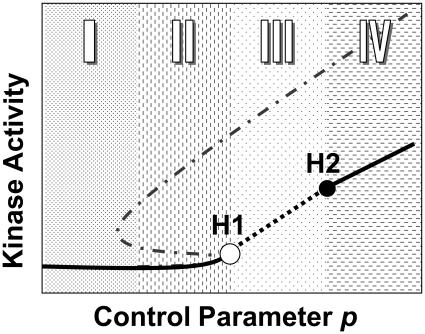
Checkpoint dynamics of the cell cycle arise naturally in the model described above. As noted above, the positive feedback facilitated by CDC25 and wee1 phosphorylation by active Cyclin:CDK causes bistability. However, when the delayed negative feedback is in the system, the bistability may be lost and converted to excitable and limit cycle dynamics (see Figs. 6 and 7, Appendix B). Fig. 2 schematically summarizes the key cell cycle dynamics arising from the mathematical model, as delineated by the detailed analysis provided in the Appendix B. There is a controlling parameter p (which could be cyclin synthesis rate k1, cyclin degradation rate k2, CDK phosphorylation rate, cell size, or combinations thereof, etc.) that controls the dynamics of the system. Without the delayed negative feedback, the system is bistable (dashed-dotted gray line). If p increases from small-to-large, and then from large-to-small, a hysteresis loop occurs. With delayed negative feedback added, however, a key new feature emerges. The steady state of the system is no longer bistable, and becomes monotonic (solid and dashed black lines). At low p, kinase activity is in a low stable steady state (region I). As p increases, kinase activity progresses successively through an excitable region (region II), limit cycle region (region III), and finally a stable high steady state (region IV). At the boundary of regions II and III, a Hopf bifurcation (H1) occurs. Another Hopf bifurcation (H2) occurs at the boundary of regions III and IV. In the limit cycle region, the steady state is unstable (dashed black line).
FIGURE 2.
Schematic plot of cell cycle dynamics. The x-axis represents the controlling parameter p (such as cyclin synthesis rate k1) that controls the dynamics of the cell cycle. The y-axis represents the activated Cyclin:CDK complex driving the cell cycle. The unfilled circle is the first Hopf bifurcation point, which acts as the checkpoint in the cell cycle. See text for further details.
Sizers and timers
Sizer and timer phases of the cell cycle also arise naturally in this model, as follows. The first Hopf bifurcation, H1 (the unfilled circle in Fig. 2), the checkpoint for transitions in the cell cycle, is the starting point of the first phase. Before this point, the kinase activity is low. If p is assumed to represent cell size, then the time to reach H1 will be proportionate to the starting cell size, defining the sizer phase of the cell cycle time. Because of the delay in activation of SKP2 or APC, the cell virtually sees a bistable system (and becomes a true bistable system if cyclin degradation is blocked; see Sha et al., 2003; Solomon et al., 1990). As p increases, however, the cell passes the H1 bifurcation point. Kinase activity increases sharply to the upper branch of the bistable solution (see Fig. 2), after which activation of SKP2 or APC-mediated ubiquitination brings the kinase activity back down. Because the steady state is an unstable focus, the kinase activity will oscillate as a limit cycle. The characteristic period of this limit cycle is the subsequent “timer” phase of the cell cycle. If the cell divides before the second cycle of rising kinase activity, then after division, p is low and the cell returns to G1. This process repeats in the next cycle. If p is even larger (as in the case of cyclin overexpression or impaired cyclin degradation), kinase activity will remain stable at the high level. Thus, in this model, the natural checkpoint feature inherent in bistability is integrated with the natural cycling time inherent in a limit cycle (or excitable regime).
Comparison with experimental observations
Is the dynamical picture depicted in Fig. 2 applicable to the cell cycle machinery? Here we compare our modeling results to experimental observations.
Sizer and timer phases of the cell cycle
A cell must reach a proper size before it begins DNA replication and mitosis. Cell size or nuclear-cytoplasm ratio may influence synthesis rate and concentration of cell cycle proteins. For simplicity, here we assume synthesis of cyclins is proportional to cell size, and that the cell grows exponentially, i.e.,
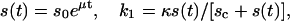 |
(2) |
where s0 is the cell size at beginning of the cycle, and μ, κ, and sc are constants, with values of 0.003, 1000, and 40, respectively, used in the simulation. Here we simulate Eqs. 1 and 2 using the G1/S model, but the same results should apply when G1/S is coupled to G2/M. For simplicity, we define the cell division occurring at the time point T before the second rise in G1/S kinase activity, at which we set s0 = s(T)/2.
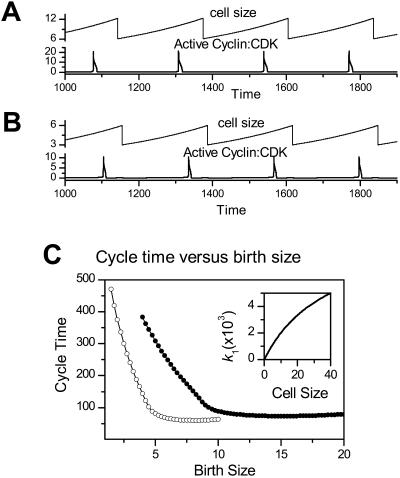
Fig. 3 A shows cell size (s) and G1/S kinase activity (x) versus time (t) during normal cell cycle. The cycle time is ∼230 time units and the cell divides when it reaches a size of 12.4 units. In Fig. 3 B, we simulate a mutation which lowers the synthesis rate of wee1 (decreasing k10 from 10 to 1 in the model). The cell now divides at a smaller cell size of 5.8, but maintains the same cycle time of 230. If we reduce k2 to simulate the case of knocking out Cul1, the cell also divides at a smaller size without changing the cycle time, which may explain the observation that Cul1−/− mouse embryo is smaller than wild-type mouse embryo (Dealy et al., 1999; Wang et al., 1999).
FIGURE 3.
Cell size (above) and active Cyclin:CDK activity (below, both arbitrary units) versus time. (A) Control. (B) The wee1 synthesis rate k10 was reduced from 10 to 1 to simulate the wee1 mutation. Note the smaller cell size. (C) Cycle time versus birth size for the control case with k10 = 10 (unfilled circles) and for the wee1 mutation with k10 = 1 (solid circles). Inset shows how cell size s affects the value of the cyclin synthesis rate k1 at the time of cell division, as in Eq. 2.
In general, cells divide asymmetrically, and since the cycle time depends on the size after division, the purely periodic behavior shown in Fig. 3, A and B, is not observed experimentally. In Fig. 3 C, we show cycle time versus birth size for our cell cycle model in its normal regime (Fig. 3 A) and in the regime simulating the wee1 mutation (Fig. 3 B). Cycle time decreases as birth size increases, and after a critical birth size, the cycle time becomes size-independent. This agrees with the classic observations in yeast (Fantes, 1977; Sveiczer et al., 1996) and frog eggs (Masui and Wang, 1998), showing that the first phase of the cell cycle is a sizer and the second phase is a timer.
The R point at the G1/S transition
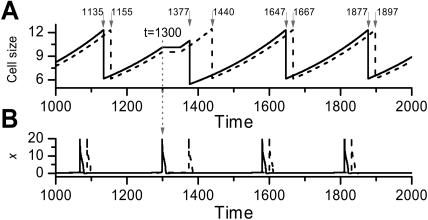
Experimentally, it has been shown that there is a point in the G1/S phase called the R point. If serum is removed for a short period, cells which have already passed the R point still undergo mitosis, whereas cells which have not yet passed the R point have a delay, which equals to the treatment time plus an additional 8 h. Curiously, the cells that have not had a delay in the first mitosis have the same delay in the second mitosis and all cells resume their relative phase after the second mitosis (Cooper, 1998; Zetterberg and Larsson, 1995). It was shown by Zetterberg and Larsson that all cells stopped growing during the delay period in the first mitosis. Here we simulate the R point phenomenon by stopping the cell growth for a certain duration in the first mitosis. In Fig. 4, two cells have a phase difference of 20 time units. At t = 1300, cell 1 has already passed the R point, whereas cell 2 has not. To simulate the effect of brief serum removal, we then stop the cell growth for a duration of 50 time units. Cell 1 divides at t = 1377, 242 time units after the previous division, whereas cell 2 divides at t = 1440, 285 time units after the previous division. The phase difference is 63 time units. At the next cycle, two cells have resumed their phase difference of 20 time units, with the same cycle time of 230 units thereafter. Similar results were obtained using other delays, either shorter or longer in duration.
FIGURE 4.
Simulation of the R point experiment. At t = 1300 (vertical dotted line with arrow), one cell (solid line) passed the R point, but the other (dashed line) had not. Growth for both cells was halted for a time period of 50 time units to simulate growth arrest after brief serum starvation. (A) Cell size (s) versus time (t). Note that the first mitosis is delayed for the cell which did not pass the R point, but the second mitosis is not delayed. (B) Active Cyclin:CDK (x) versus time. Numbers indicate the division times of the two cells.
DNA damage checkpoints
DNA damage at the G1/S transition arrests the cell cycle in G1 by activating the signaling protein chk1, which phosphorylates CDC25A for degradation (Mailand et al., 2000). At the G2/M checkpoint, the analogous signaling protein responding to DNA damage is chk2, which inhibits CDC25C by catalyzing its binding to 14-3-3 (Peng et al., 1997). Our simulation shows (Fig. 7 F) that mimicking the effects of chk1 or chk2 by either reducing the CDC25 synthesis rate (k8) or increasing the degradation rate (k9) moves the H1 point into a much higher k1. Thus, at the same cyclin synthesis rate k1, if there is DNA damage, the cell will remain in G1 or G2.
Cyclin expression and degradation
Insufficient expression of CycE results in cell arrest in G1, whereas overexpression of CycE leads to premature entry into S phase (Ohtsubo et al., 1995), genomic instability (Spruck et al., 1999), and tumorigenesis (Donnellan and Chetty, 1999). Similar to overexpression of cyclin E, failure of destruction of CycE is tumorigenic (Koepp et al., 2001). With either overexpression or low degradation rate, CycE activity became stabilized at a high level (Koepp et al., 2001; Spruck et al., 1999). In our model (Fig. 7, B–D), insufficient expression of cyclin (k1) keeps Cyclin:CDK activity very low, i.e., corresponding to cell arrest in G1, whereas a normal expression rate leads to limit cycle behavior. Overexpression or low degradation (k2 or k2u) of cyclin stabilizes Cyclin:CDK at a high level. This also accounts for the observation that overexpressing CycB or mutating APC arrests cells at mitosis because of the stabilization of high CycB:CDK1 activity.
CKI expression and degradation
Overexpression CKIs such as p27 causes G1 cell cycle arrest (Sherr and Roberts, 1999), but can be rescued by overexpression of cyclin E (Kwon and Nordin, 1997). Fig. 7 H shows that these observations (stable low kinase activity due to high k12, rescued by increasing cyclin synthesis rate k1) are reproduced by our model.
DISCUSSION
We have developed a generic mathematical model of a cell cycle signaling network that can be used to simulate both the G1/S and G2/M transitions. Based on our investigations of the dynamics caused by the positive feedback and the negative feedback loops in this model, we have proposed a mechanism for the cell cycle checkpoint control and cell cycle progression that agrees well with experimental observations. We successfully simulated the R point, the sizer, timer, and their resetting dynamics under simplified conditions. Our major results are: 1), the positive feedback facilitated by CDC25 and wee1 causes bistability in Cyclin:CDK activity; 2), the negative feedback facilitated by SKP2 or APC/CDC20 turns this bistable behavior into limit cycle behavior; and 3), the G1 and G2 checkpoints are thus Hopf bifurcation points, rather than saddle-node or saddle-node-loop bifurcations. This feature thereby elegantly integrates the natural checkpoint feature of bistability with the natural timer feature of the limit cycle. These behaviors are coordinated by growth and division to maintain the normal cell cycle and size homeostasis.
Cell cycle dynamics
In our previous model of the G1/S control (Qu et al., 2003), we showed that dynamics of bistability, limit cycle, and excitable transients arise due to the positive feedback between CDC25A and active CycE:CDK2. In this study, we used a similar signaling network for cyclin and CDK regulation, but added negative feedback. The negative feedback converted a large bistable regime into a limit cycle regime (Fig. 7, B and C). The main dynamical regimes are low stable kinase activity state (which may be excitable), limit cycle oscillation, and high stable kinase activity state. Bistability may occur when the negative feedback is weak. With the present model, we can reproduce many of the experimental observations as they relate to checkpoints, sizers, and timers within the cell cycle. Although we agree with Tyson and colleagues (Tyson, 2002; Tyson and Novak, 2001) that a pure limit cycle cannot explain the dynamics of the somatic cell cycle, we still propose a Hopf bifurcation, rather than a saddle-node bifurcation, as the checkpoint dynamics, which implies that limit cycle dynamics are hidden in the cell cycle.
An immediate question one may ask: what are the major differences in dynamics between the present model and other models, especially the models by Tyson's group? Compared to all the previous limit cycle models (Goldbeter, 1991; Hatzimanikatis et al., 1999; Obeyesekere et al., 1997), our model integrates virtual bistability into the limit cycle so that the system exhibits both checkpoint and oscillatory capabilities. The major differences with the yeast (Chen et al., 2000, Tyson and Novak, 2001; Tyson et al., 2001, 2002) and Xenopus (Borisuk and Tyson, 1998) cell cycle models by Tyson and colleagues is that, from a dynamics perspective, their models propose checkpoint dynamics which are characteristic of bistable systems, namely a saddle-node bifurcation for the G1/S checkpoint and saddle-node-loop bifurcation for the G2/M checkpoint. In our model, we propose Hopf bifurcations, characteristic of limit cycle dynamics, for both checkpoints. In addition, in their models (Tyson and Novak, 2001), the mechanisms of bistability and limit cycle oscillations are realized differently, via APC/CDH1 and APC/CDC20, respectively. In our model, bistability is caused by the positive feedback catalyzed by CDC25 and wee1, and the limit cycle by the negative feedback facilitated by SKP2 or APC/CDC20.
Do these dynamical differences advance our understanding of cell cycle beyond the considerable insights already gained from previous models, particularly those by Tyson and colleagues? Building upon their seminal work, we have shown that the sizer-timer relationships, as well as checkpoint dynamics and other features, arise naturally from the model proposed here. In the models by Tyson and colleagues (Tyson et al., 2001, 2002), the sizer phase ends at the G2/M transition. However, experiments by Sveiczer et al. (1996) showed that the sizer operated until early G2 for wild-type yeast, but moved to G1/S transition for the wee1 mutant, followed in both cases by a timer phase of ∼100 min. Since in their models (Tyson et al., 2001, 2002), the sizer operates until the G2/M transition, it may not be possible to simulate the sizer and timer behaviors shown in Sveiczer et al.'s experiments. However, by proposing both checkpoints in our model as Hopf bifurcations, the sizer can operate in either G1/S or G2/M, which triggers the timer (limit cycle) when the Hopf bifurcation is reached. Thus, either G1/S or G2/M can control the sizer and timer phases. This is an appealing feature of our model, since it allows experimental interventions in yeast known to shift the relationship between the timer/sizer phases relative to G1/S and G2/M (Sveiczer et al., 1996, 1999) to be more flexibly simulated.
Another potential advance in our proposed model is in simulating sequential activation and inactivation of the G1/S cyclins (E and A) followed by G2/M cyclins (A and B) in higher eukaryotes (Pines, 1999), as well as in yeast (Nasmyth, 1996). If each Cyclin:CDK signaling module has the limit cycle dynamics with checkpoint capabilities as we proposed, it is possible to couple them together, similarly to Gonze and Goldbeter (2001), to achieve the sequential activation and inactivation of the individual Cyclin:CDK cascades and recapitulate the dynamics of “dominoes and clocks” (Murray and Kirschner, 1989) and checkpoint capabilities. In the models of Tyson and colleagues, since the inactivation of the CDK activity is after M phase, recreating the sequential activation/inactivation of the individual cascades may be more problematic.
In recent experiments by Sha et al. (2003) and Pomerening et al. (2003), bistability was demonstrated in Xenopus laevis egg extracts when cyclin B was made nondegradable and controlled externally. Similar bistability was also observed in yeast (Cross et al., 2002). These experiments elegantly demonstrate that bistability due to a saddle-node bifurcation can occur in a subsystem of the signaling network. Although these findings were interpreted as key experimental support for the cell cycle dynamics proposed by Tyson and colleagues, it is important to recognize that these findings do not prove that there are saddle-node bifurcations and hysteresis in the normally operating cell cycle. This is because in the normally operating cell cycle, cyclin concentration is not fixed as it was under these experimental conditions, but is both synthesized and degraded, and therefore is a state variable. This can cause the dynamics to change. For example, in Figs. 2 and 6, we showed how bistability was changed to a limit cycle due to cyclin degradation by negative feedback. In other words, in the normally operating cell cycle with the negative feedback present, a Hopf bifurcation instead of a saddle-node bifurcation is at work, whereas in the subsystem without cyclin degradation, corresponding to the experimental conditions in the recent studies mentioned above (Cross et al., 2002; Pomerening et al., 2003; Sha et al., 2003), a saddle-node bifurcation occurs.
Dynamical and biological roles of cell cycle protein regulation
Different cell cycle proteins and their regulatory processes have distinct dynamical and biological roles. In our model, sensitive nonlinear responses are required in the positive feedback circuits between active Cyclin:CDK and CDC25 or wee1 to give rise to bistability, and in the negative feedback to promote excitable transients and limit cycles. We (Qu et al., 2003) have previously suggested that multisite phosphorylation might be the biological mechanism underlying this required sensitive nonlinear response. For simplicity, we assumed here that CDC25 has only two phosphorylation sites and is active only when both sites are phosphorylated directly or indirectly by active Cyclin:CDK. CDC25 may be phosphorylated at many sites and is active in either phosphorylated or unphosphorylated states (Hoffmann et al., 1994; Solomon et al., 1990; Solomon and Kaldis, 1998). In addition, multisite phosphorylation of other proteins, such as CDK, wee1, or CKI, etc., may have similar dynamical consequences (Qu et al., 2003).
Increasing the synthesis rate of cell cycle promoters, such as cyclin and CDC25, promotes the Hopf bifurcation, whereas enhancing their degradation delays the Hopf bifurcation. Conversely, increasing the synthesis rate of the cell cycle inhibitors, such as wee1 and CKI, delays the Hopf bifurcation, whereas enhancing their degradation promotes the Hopf bifurcation. Considering the Hopf bifurcation point, H1, as the cell checkpoint, the dynamical roles of synthesis and degradation generally agree with experimental observations.
The negative feedback facilitated by SKP2 or APC/CDC20 plays a very important role in the cell cycle dynamics in our model, and is critical for cell cycle progression. The positive feedback creates a situation of an all-or-none response (bistability) for the cell, allowing kinase activity to increase rapidly. The delayed negative feedback lets the kinase activity remain high for a certain period of time, and then brings it back to the low level. The delay time τ has a big effect on the period of the limit cycle but little effect on stability (Fig. 7 E). We used a sigmoidal function of Hill coefficient 2 for h(x), but other sigmoidal or linear increasing functions have the same qualitative effect.
Limitations
An important issue is whether the parameter values in a complex model are biologically plausible and in a range consistent with the dynamics proposed to represent the cell cycle. Such validation is complicated, however, by the fact that the cell cycle time in eukaryotes can vary from several minutes to >24 h, suggesting that the kinetic parameters values vary dramatically from species to species. For this reason, we deliberately made our model dimensionless, so it could be adapted to multiple species. From an evolutionary standpoint, an attractive hypothesis is that the nonlinear dynamics of the cell cycle may be relatively simple and generic, so that cells of different species can divide at widely different rates, yet operate using the same proven, reliable dynamics to preserve the fidelity and safeguards of DNA replication despite the complexity of the signaling network. According to this reasoning, cells of different species would use the same common dynamics, but vary the kinetics of key parameters to adapt the cell cycle time appropriately. For a given species, experimentally measured values of most parameters are not available. Nevertheless, from the available data, we can assess the biological plausibility of our model to a limited extent. For example, a previous experimental study (Solomon et al., 1990) has estimated the total CDC2 in Xenopus oocyte cell cycle to be ∼100 nM. In this study, using total CDK of 200 nM (i.e., c0 = 200 in Eq. 1), the threshold of total cyclin which activates CDK activity is ∼60–70 nM (see Fig. 6 B). This threshold is similar to the threshold observed in the recent experiments (Pomerening et al., 2003; Sha et al., 2003) in Xenopus. In addition, according to Felix et al. (1990), the delay of cyclin B degradation in Xenopus is ∼15 min at a sufficiently high active CDC2 concentration. If we set τ = 15 min, the cycle time of limit cycle in our model is ∼40–50 min (see Fig. 7 E), which is roughly the correct cycle time of the Xenopus oocyte in its first 11–12 cycles. Although our dimensionless parameters were set in a range which gave rise to interesting dynamics for the cell cycle machinery, by properly rescaling our model, most parameter values agree well with the parameter values estimated by Marlovits et al. (1998) from experimental data, while preserving the same essential dynamics. Therefore, our model should be applicable to real experimental data.
We have restricted our analysis to the dynamics of a modular generic signaling network of higher eukaryotes representing either G1/S or G2/M, but have yet to couple the two modules together to simulate the complete cell cycle. This may limit the conclusions that we can draw about general cell cycle dynamics, and it is possible that interesting new dynamics will emerge in the complete, coupled network. However, it is interesting that the repertoire of dynamical behaviors exhibited by the network was relatively limited over a wide range of parameter values. That is, we did not observe complex behavior, such as chaos, or even higher-order periodicity. However, the molecular network for cell cycle is much more complex (Kohn, 1999, 2001) than the one we presented in this article, and new dynamics may occur. In addition, we have ignored the high degree of spatial compartmentalization of the signaling network components in the nucleus and cytoplasm of real cells, which adds another layer of complexity to the possible dynamics. Nevertheless, it is encouraging that the analysis of the generic robust signaling module constructed here reproduces so many experimentally observed features of the higher eukaryotic cell cycle.
Acknowledgments
We thank Alan Garfinkel for his encouragement.
This study was supported by funds from the University of California-Los Angeles Department of Medicine, and by the Kawata and Laubisch Endowments.
APPENDIX A: NONLINEAR DYNAMICS GLOSSARY
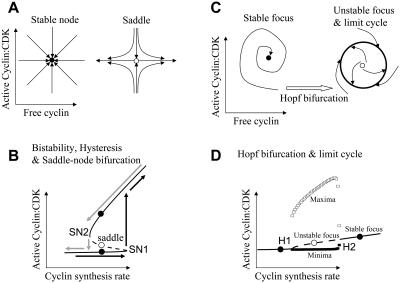
Steady state is a point at which the rate of change of all variables is zero. For example, the steady state of Eq. 1 can be obtained by setting the derivatives of all variables to zero and solving the resulted nonlinear algebra equations. A system exactly positioned at a steady state will stay at this state permanently. If the system returns to its steady state after a slight perturbation, the steady state is stable; otherwise it is unstable. The location and stability of steady states is determined by the parameter values of the system; different types of steady states emerge in different parameter ranges. Fig. 5, A and C, illustrate four types of steady states in a two-dimensional variable space (such as in the active Cyclin:CDK (x) and free cyclin (y) space)—a stable node and a saddle point (Fig. 5 A), and a stable focus and an unstable focus (Fig. 5 C). When the steady state is a stable node, all trajectories on the plane will approach this point. When the steady state is saddle-point, it is unstable. Trajectories from one direction will be attracted, but trajectories from another direction will be repelled, similar to the trajectories of a ball placed on a real horse saddle (which rolls toward the saddle's center in the longitudinal direction, but rolls off the saddle in the perpendicular direction). By changing a parameter, a steady state may change from a stable node to a saddle, called saddle-node bifurcation. Saddle-node bifurcations usually leads to bistability, a property of a nonlinear system that exhibits two different stable steady states (stable nodes, solid circles in Fig. 5 B) with an unstable steady state (saddle, unfilled circle in Fig. 5 B) in between. In a bistable system, when a parameter such as the cyclin synthesis rate k1 is increased, a sudden jump occurs at the saddle-node bifurcation point (SN1 in Fig. 5 B) from one stable node to another stable node (black arrows). However, as the parameter is then decreased, the jump back (gray arrows in Fig. 5 B) occurs at another saddle-node point (SN2) at a much lower parameter value. This behavior is called hysteresis. When the steady state is a stable focus, all trajectories spiral in and finally approach to the steady state. On the contrary, when the steady state is an unstable focus, all trajectories started close to the steady state spiral out. In a nonlinear system, they usually approach an isolated closed trajectory surrounding the steady state, called a stable limit cycle (Fig. 5 C). Trajectories started outside the limit cycle also approach to it. As parameter changes, the steady state may change from a stable focus to an unstable focus, leading to limit cycle oscillation (Fig. 5, C and D). This transition is called Hopf bifurcation. Limit cycle gives rise to clocklike cyclical behavior whereas bistability resembles a toggle switch.
FIGURE 5.
Saddle-node and Hopf bifurcations leading to bistability and limit cycles, respectively. (A) Schematic illustration of a stable node (solid circle) and saddle point (unfilled circle) in a two-variable space, such as a space of active Cyclin:CDK and free cyclin. Arrows represent trajectories. (B) Illustration of bistability and hysteresis in a variable-parameter space. Solid lines and solid circles are for stable nodes. Dashed line and unfilled circle are for saddle points. (C) Schematic illustration of a stable focus (solid circle), unstable focus (unfilled circle), and limit cycle (thick large circle). A Hopf bifurcation occurs when the steady state changes from a stable focus to an unstable focus. (D) Hopf bifurcation and limit cycle in a variable-parameter space. H1 is the first Hopf bifurcation point and H2 is the second. Solid circles and solid lines indicate the stable focus, and unfilled circle and dashed line the unstable focus. Unfilled squares are the maxima of the variable during limit cycle oscillation, and solid squares the minima.
APPENDIX B: DETAILED DYNAMICAL ANALYSIS OF THE CELL CYCLE MODEL
Dynamics caused by the positive feedback of CDC25 and wee1
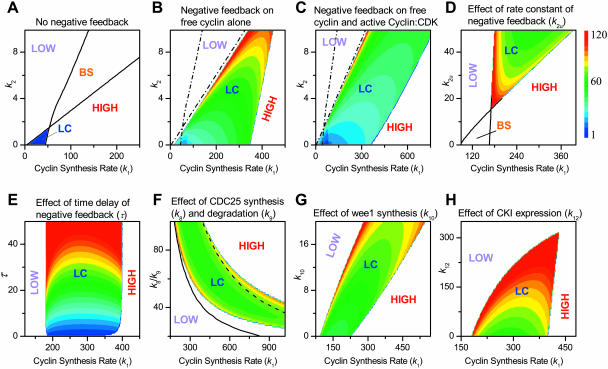
We first characterize the dynamics caused by the positive feedback facilitated by CDC25 and wee1, without the presence of the negative feedback or CKI (by setting k2u = 0, k7u = 0, and k12 = 0 in Eq. 1). Similar to our previous study (Qu et al., 2003), this positive feedback can cause bistable, limit cycle, and excitable behaviors. Fig. 7 A shows that for this signaling network, limit cycle behavior, with an oscillation period typically <10 time units, occurs at low free cyclin degradation rate constant (k2), whereas bistability occurs at high k2. In general, CDK activity is stable at a low level (marked LOW in Fig. 7) when cyclin synthesis rate k1 is small, and is stable at a high level (marked HIGH in Fig. 7) when k1 is large; limit cycle or bistability occurs in the intermediate range depending on the value of k2.
Dynamical role of negative feedback
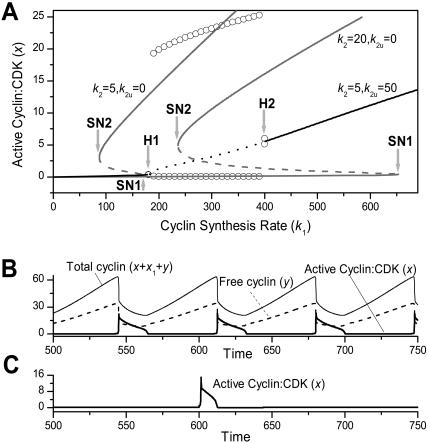
We first add into the network the negative feedback mediated by ubiquitination of free cyclin and/or cyclin complexed with CDK (via SKP2 or APC), as well as by phosphorylation of complexed CDK by wee1, without considering the effects of CKI (by setting k12 = 0 in Eq. 1). The immediate effect of this negative feedback is to convert a large region of the triple steady-state bistability into a large region with a single steady state and limit cycle dynamics. This is illustrated in Fig. 6 A and Fig. 7 B. Without the negative feedback, for high cyclin degradation rate constant (k2 > 2), the steady state is a bistable system with two saddle-node bifurcations (SN1 and SN2 in Fig. 6 A). When the negative feedback is added, the steady state becomes monotonic and two Hopf bifurcations (H1 and H2 in Fig. 6 A) occur, with a limit cycle region between them. Fig. 6 B plots free cyclin, total Cyclin:CDK, and active Cyclin:CDK vs. time for the limit cycle regime showing periodic behavior. At smaller cyclin synthesis rate k1, an excitable region also exists before the limit cycle regime (Fig. 6 C).
FIGURE 6.
(A) Steady states (lines) and limit cycle maxima/minima (circles) of active Cyclin:CDK vs. cyclin synthesis rate k1 without the negative feedback (gray lines) and with the negative feedback (black line and circles). Solid lines are stable steady states; dashed lines are unstable steady states. SN1 and SN2 mark the saddle-node bifurcations without negative feedback present, and H1 and H2 mark the two Hopf bifurcations with negative feedback present. (B) Active Cyclin:CDK (thick solid line), free cyclin (dashed line), and total cyclin (thin solid line) versus time for k1 = 300 in the limit cycle regime shown in A. (C) Active Cyclin:CDK versus time for k1 = 150 in the excitable regime in A. At external stimulus was applied at t = 600 for a duration of 0.5 time units.
FIGURE 7.
Phase diagrams in two parameter planes, with other parameters fixed. LOW is stably low kinase activity, HIGH is stably high kinase activity, LC is limit cycle oscillation, and BS is bistability. The oscillation period of limit cycle is color-coded in the limit cycle region. (A) In the plane of cyclin synthesis rate (k1) and cyclin degradation rate constant (k2) without the negative feedback. (B) In the plane of cyclin synthesis rate (k1) and cyclin degradation rate constant (k2) with negative feedback exerted only on free cyclin; k2u = 50 and k7u = 0. (C) In the plane of cyclin synthesis rate (k1) and cyclin degradation rate constant (k2) with the negative feedback exerted on both free cyclin and active Cyclin:CDK complex; k2u = 25 and k7u = 50. (D) In the plane of cyclin synthesis rate (k1) and rate constant of negative feedback (k2u). (E) In the plane of cyclin synthesis rate (k1) and time delay (τ) for negative feedback. (F) In the plane of cyclin synthesis rate (k1) and CDC25 synthesis and degradation ratio (k8/k9), by either changing CDC25 synthesis rate (k8) (LC in the colored area) or by changing CDC25 degradation rate constant (k9) (LC between the two black lines). (G) In the plane of cyclin synthesis rate (k1) and wee1 synthesis rate (k10). (H) In the plane of cyclin synthesis rate (k1) and CKI synthesis rate (k12). (D–G) With negative feedback exerted only on free cyclin; k2u = 50 and k7u = 0. A–G. No CKI (k12 = 0). (H) With CKI (k12 > 0). The color coding for the period of the limit cycle is shown as the color bar.
Fig. 7 B shows the phase diagram and the oscillation period in the parameter space of cyclin synthesis rate (k1) and degradation rate constant (k2), with negative feedback restricted to free cyclin, illustrating a very large region of limit cycle behavior (for comparison, the stability boundaries from Fig. 7 A are re-plotted as dashed lines in Fig. 7 B). The bistable region has disappeared, and the large limit cycle region occurs right next to it. The oscillation period became shorter as cyclin degradation rate constant (k2) decreased.
When the negative feedback works on both free cyclin and cyclin complexed with CDK, the limit cycle region is even larger (Fig. 7 C). The first Hopf bifurcation (H1, as in Fig. 6) is always close to SN1 and increases to larger cyclin synthesis rates (larger k1 values) as free cyclin degradation rate constant (k2) increases. If the negative feedback is restricted to cyclin complexed with CDK, it also converts bistability to limit cycle behavior. This conversion depends on the strength of the negative feedback, i.e., the values of k2u and k7u. Fig. 7 D shows the phase diagram in k1–k2u space, showing that for a given k2 value, limit cycle behavior occurs above a threshold k2u value.
One interesting feature in this system is the effect of the time constant τ in Eq. 1d. As shown in Fig. 7 E, the time delay τ of the negative feedback has little effect on stability but controls the oscillation period. In contrast, Fig. 7 F shows that increasing CDC25 levels by altering its synthesis or degradation rates has a large effect on stability, although having little effect on the oscillation period. As CDC25 increases (i.e. k8/k9 increases), limit cycle behavior occurs at a smaller cyclin synthesis rate k1. Altering wee1 levels by changing its synthesis rate (k10) has analogous effects, but in the opposite direction, as shown in Fig. 7 G.
Dynamical role of CKI
Finally, we add CKI into the signaling network (Fig. 7 H). The major effect of increasing CKI synthesis rate (k12) is to move the H1 boundary to a higher cyclin synthesis rate k1 regime, until it fuses with the H2 boundary, and the limit cycle disappears. In addition, as CKI increases, the oscillation period also increases. A modeling study by Gardner et al. (1998), who studied the general effects of inhibitory binding of cyclin, showed that it altered the frequency and boundary of the limit cycle, similar to the predicted effects of CKI in our model.
References
- Aguda, B. D. 1999. A quantitative analysis of the kinetics of the G(2) DNA damage checkpoint system. Proc. Natl. Acad. Sci. USA. 96:11352–11357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguda, B. D., and Y. Tang. 1999. The kinetic origins of the restriction point in the mammalian cell cycle. Cell Prolif. 32:321–335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilodeau, M., H. Talarmin, G. Ilyin, C. Rescan, D. Glaise, S. Cariou, P. Loyer, C. Guguen-Guillouzo, and G. Baffet. 1999. SKP2 induction and phosphorylation is associated with the late G1 phase of proliferating fat hepatocytes. FEBS Lett. 452:247–253. [DOI] [PubMed] [Google Scholar]
- Borisuk, M. T., and J. J. Tyson. 1998. Bifurcation analysis of a model of mitotic control in frog eggs. J. Theor. Biol. 195:69–85. [DOI] [PubMed] [Google Scholar]
- Carrano, A. C., E. Eytan, A. Hershko, and M. Pagano. 1999. SKP2 is required for ubiquitin-mediated degradation of the CDK inhibitor p27. Nat. Cell Biol. 1:193–199. [DOI] [PubMed] [Google Scholar]
- Chen, K. C., A. Csikasz-Nagy, B. Gyorffy, J. Val, B. Novak, and J. J. Tyson. 2000. Kinetic analysis of a molecular model of the budding yeast cell cycle. Mol. Biol. Cell. 11:369–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, S. 1998. On the proposal of a G0 phase and the restriction point. FASEB J. 12:367–373. [DOI] [PubMed] [Google Scholar]
- Cross, F. R., V. Archambault, M. Miller, and M. Klovstad. 2002. Testing a mathematical model of the yeast cell cycle. Mol. Biol. Cell. 13:52–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dealy, M. J., K. V. Nguyen, J. Lo, M. Gstaiger, W. Krek, D. Elson, J. Arbeit, E. T. Kipreos, and R. S. Johnson. 1999. Loss of Cul1 results in early embryonic lethality and dysregulation of cyclin E. Nat. Gen. 23:245–248. [DOI] [PubMed] [Google Scholar]
- Donnellan, R., and R. Chetty. 1999. Cyclin E in human cancers. FASEB J. 13:773–780. [DOI] [PubMed] [Google Scholar]
- Fantes, P. A. 1977. Control of cell size and cycle time in Schizosaccharomyces prombe. J. Cell Sci. 24:51–67. [DOI] [PubMed] [Google Scholar]
- Felix, M. A., J. C. Labbe, M. Doree, T. Hunt, and E. Karsenti. 1990. Triggering of cyclin degradation in interphase extracts of amphibian eggs by cdc2 kinase. Nature. 346:379–382. [DOI] [PubMed] [Google Scholar]
- Galan, J. M., and M. Peter. 1999. Ubiquitin-dependent degradation of multiple F-box proteins by an autocatalytic mechanism. Proc. Natl. Acad. Sci. USA. 96:9124–9129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner, T. S., M. Dolnik, and J. J. Collins. 1998. A theory for controlling cell cycle dynamics using a reversibly binding inhibitor. Proc. Natl. Acad. Sci. USA. 95:14190–14195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter, A. 1991. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc. Natl. Acad. Sci. USA. 88:9107–9111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonze, D., and A. Goldbeter. 2001. A model for a network of phosphorylation-dephosphorylation cycles displaying the dynamics of dominoes and clocks. J. Theor. Biol. 210:167–186. [DOI] [PubMed] [Google Scholar]
- Hatzimanikatis, V., K. H. Lee, and J. E. Bailey. 1999. A mathematical description of regulation of the G1-S transition of the mammalian cell cycle. Biotech. Bioeng. 65:631–637. [DOI] [PubMed] [Google Scholar]
- Hoffmann, I., P. R. Clarke, M. J. Marcote, E. Karsenti, and G. Draetta. 1993. Phosphorylation and activation of human cdc25-C by cdc2-cyclin B and its involvement in the self-amplification of MPF at mitosis. EMBO J. 12:53–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann, I., G. Draetta, and E. Karsenti. 1994. Activation of the phosphatase activity of human cdc25A by a cdk2-cyclin E dependent phosphorylation at the G1/S transition. EMBO J. 13:4302–4310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koepp, D. M., L. K. Schaefer, X. Ye, K. Keyomarsi, C. Chu, J. W. Harper, and S. J. Elledge. 2001. Phosphorylation-dependent ubiquitination of cyclin E by the SCFFbw7 ubiquitin ligase. Science. 294:173–177. [DOI] [PubMed] [Google Scholar]
- Kohn, K. W. 1999. Molecular interaction map of the mammalian cell cycle control and DNA repair systems. Mol. Biol. Cell. 10:2703–2734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohn, K. W. 2001. Molecular interaction maps as information organizers and simulation guides. Chaos. 11:84–97. [DOI] [PubMed] [Google Scholar]
- Kumagai, A., and W. G. Dunphy. 1992. Regulation of the cdc25 protein during the cell cycle in Xenopus extracts. Cell. 70:139–151. [DOI] [PubMed] [Google Scholar]
- Kwon, T. K., and A. A. Nordin. 1997. Overexpression of cyclin E and cyclin-dependent kinase inhibitor (p27Kip1): effect on cell cycle regulation in HeLa cells. Biochem. Biophys. Res. Comm. 238:534–538. [DOI] [PubMed] [Google Scholar]
- Mailand, N., J. Falck, C. Lukas, R. G. Syljuâsen, M. Welcker, J. Bartek, and J. Lukas. 2000. Rapid destruction of human Cdc25A in response to DNA damage. Science. 288:1425–1429. [DOI] [PubMed] [Google Scholar]
- Marlovits, G., C. J. Tyson, B. Novak, and J. J. Tyson. 1998. Modeling M-phase control in Xenopus oocyte extracts: the surveillance mechanism for unreplicated DNA. Biophys. Chem. 72:169–184. [DOI] [PubMed] [Google Scholar]
- Masui, Y., and P. Wang. 1998. Cell cycle transition in early embryonic development of Xenopus laevis. Biol. Cell. 90:537–548. [PubMed] [Google Scholar]
- Montagne, J., M. J. Stewart, H. Stocker, E. Hafen, S. C. Kozma, and G. Thomas. 1999. Drosophila S6 kinase: a regulator of cell size. Science. 285:2126–2129. [DOI] [PubMed] [Google Scholar]
- Montagnoli, A., F. Fiore, E. Eytan, A. C. Carrano, G. F. Draetta, A. Hershko, and M. Pagano. 1999. Ubiquitination of p27 is regulated by Cdk-dependent phosphorylation and trimeric complex formation. Gen. Dev. 13:1181–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan, D. O. 1999. Regulation of the APC and the exit from mitosis. Nat. Cell Biol. 1:E47–E53. [DOI] [PubMed] [Google Scholar]
- Morris, M. C., A. Heitz, J. Mery, F. Heitz, and G. Divita. 2000. An essential phosphorylation-site domain of human cdc25C interacts with both 14-3-3 and cyclins. J. Biol. Chem. 275:28849–28857. [DOI] [PubMed] [Google Scholar]
- Murray, A. W., and M. W. Kirschner. 1989. Dominoes and clocks: the union of two views of the cell cycle. Science. 246:614–621. [DOI] [PubMed] [Google Scholar]
- Nakayama, K. I., S. Hatakeyama, and K. Nakayama. 2001. Regulation of the cell cycle at the G1-S transition by proteolysis of cyclin E and p27Kip1. Biochem. Biophys. Res. Comm. 282:853–860. [DOI] [PubMed] [Google Scholar]
- Nasmyth, K. 1996. At the heart of the budding yeast cell cycle. Trends Genet. 12:405–412. [DOI] [PubMed] [Google Scholar]
- Novak, B., and J. J. Tyson. 1993. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J. Cell Sci. 106:1153–1168. [DOI] [PubMed] [Google Scholar]
- Novak, B., and J. J. Tyson. 1997. Modeling the control of DNA replication in fission yeast. Proc. Natl. Acad. Sci. USA. 94:9147–9152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Obeyesekere, M. N., E. S. Knudsen, J. Y. J. Wang, and S. O. Zimmerman. 1997. A mathematical model of the regulation of the G(1) phase of Rb+/+ and Rb−/− mouse embryonic fibroblasts and an osteosarcoma cell line. Cell Prolif. 30:171–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsubo, M., A. M. Theodoras, J. Schumacher, J. M. Roberts, and M. Pagano. 1995. Human cyclin E, a nuclear protein essential for the G1-to-S phase transition. Mol. Cell. Biol. 15:2612–2624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng, C. Y., P. R. Graves, R. S. Thoma, Z. Q. Wu, A. Shaw, A. Piwnica, and H. Worms. 1997. Mitotic and G(2) checkpoint control: regulation of 14–3-3 protein binding by phosphorylation of Cdc25C on serine-216. Science. 277:1501–1505. [DOI] [PubMed] [Google Scholar]
- Peters, J. M. 1998. SCF and APC: the yin and yang of cell cycle regulated proteolysis. Current. Opin. Cell Biol. 10:759–768. [DOI] [PubMed] [Google Scholar]
- Pines, J. 1999. Four-dimensional control of the cell cycle. Nat. Cell Biol. 1:E73–E79. [DOI] [PubMed] [Google Scholar]
- Pomerening, J. R., E. D. Sontag, and J. E. Ferrell, Jr. 2003. Building a cell cycle oscillator: hysteresis and bistability in the activation of cdc2. Nat. Cell Biol. 5:346–351. [DOI] [PubMed] [Google Scholar]
- Qu, Z., J. N. Weiss, and W. R. MacLellan. 2003. Regulation of the mammalian cell cycle: a model of the G1-to-S transition. Am. J. Physiol. Cell Physiol. 284:C349–C364. [DOI] [PubMed] [Google Scholar]
- Sha, W., J. Moore, K. Chen, A. D. Lassaletta, C. S. Yi, J. J. Tyson, and J. C. Sible. 2003. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc. Natl. Acad. Sci. USA. 100:975–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherr, C. J., and J. M. Roberts. 1999. CDK inhibitors: positive and negative regulators of G1-phase progression. Gen. Dev. 13:1501–1512. [DOI] [PubMed] [Google Scholar]
- Solomon, M. J., M. Glotzer, T. H. Lee, M. Philippe, and M. W. Kirschner. 1990. Cyclin activation of p34cdc2. Cell. 63:1013–1024. [DOI] [PubMed] [Google Scholar]
- Solomon, M. J., and P. Kaldis. 1998. Regulation of CDKs by phosphorylation. In Cell Cycle Control. M. Pagano, editor. Springer, Berlin, Germany. 79–109. [DOI] [PubMed]
- Spruck, C. H., K. A. Won, and S. I. Reed. 1999. Deregulated cyclin E induces chromosome instability. Nature. 401:297–300. [DOI] [PubMed] [Google Scholar]
- Sveiczer, A., A. Csikasz-Nagy, B. Gyorffy, J. J. Tyson, and B. Novak. 2000. Modeling the fission yeast cell cycle: quantized cycle times in wee1-cdc25δ mutant cells. Proc. Natl. Acad. Sci. USA. 97:7865–7870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sveiczer, A., B. Novak, and J. M. Mitchison. 1996. The size control of fission yeast revisited. J. Cell Sci. 109:2947–2957. [DOI] [PubMed] [Google Scholar]
- Sveiczer, A., B. Novak, and J. M. Mitchison. 1999. Mitotic control in the absence of cdc25 mitotic inducer in fission yeast. J. Cell Sci. 112:1085–1092. [DOI] [PubMed] [Google Scholar]
- Thron, C. D. 1997. Bistable biochemical switching and the control of the events of the cell cycle. Oncogene. 15:317–325. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J. 2002. Cell cycle controls. In Computational Cell Biology. C. P. Fall, E. S. Marland, J. M. Wagner, and J. J. Tyson, editors. Springer, New York, Berlin. 261–284.
- Tyson, J. J., K. Chen, and B. Novak. 2001. Network dynamics and cell physiology. Nat. Rev. Mol. Cell Biol. 2:908–916. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J., A. Csikasz-Nagy, and B. Novak. 2002. The dynamics of cell cycle regulation. Bioessays. 24:1095–1109. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J., and B. Novak. 2001. Regulation of the eukaryotic cell cycle: molecular antagonism, hysteresis, and irreversible transitions. J. Theor. Biol. 210:249–263. [DOI] [PubMed] [Google Scholar]
- Vlach, J., S. Hennecke, and B. Amati. 1997. Phosphorylation-dependent degradation of the cyclin-dependent kinase inhibitor p27. EMBO J. 16:5334–5344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Y., S. Penfold, X. Tang, N. Hattori, P. Riley, J. W. Harper, J. C. Cross, and M. Tyers. 1999. Deletion of the Cul1 gene in mice causes arrest in early embryogenesis and accumulation of cyclin E. Curr. Biol. 9:1191–1194. [DOI] [PubMed] [Google Scholar]
- Zetterberg, A., and O. Larsson. 1995. Cell cycle progression and cell growth in mammalian cells: kinetic aspects of transition events. In Cell Cycle Control. C. Hutchinson and C. M. Glover, editors. Oxford University Press, Oxford, New York. 206–227.