Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Dec;85(6):3659–3665. doi: 10.1016/S0006-3495(03)74783-3

Stochastic Model of Autocrine and Paracrine Signals in Cell Culture Assays

Lazaros Batsilas *, Alexander M Berezhkovskii †, Stanislav Y Shvartsman *
PMCID: PMC1303670  PMID: 14645058

Abstract

Autocrine signaling systems are commonly studied under cell culture conditions. In a typical cell culture assay, a layer of liquid medium covers a random two-dimensional dispersion of cells, which secrete ligands. In a growing number of experiments, it is important to characterize the spatial range of autocrine and paracrine cell communication. Currently, the spatial distribution of diffusing signals can be analyzed only indirectly, from their effects on the intracellular signaling or physiological responses of autocrine cells. To directly characterize the spatial range of secreted ligands, we propose a stochastic model for autocrine cell cultures and analyze it using a combination of analytical and computational tools. The two main results derived within the framework of this model are 1), an expression for the fraction of autocrine trajectories, i.e., the probability for a ligand to be trapped by the same cell from which it has been secreted; and 2), an expression for the spatial distribution of trapping points of paracrine trajectories. We test these analytical results by stochastic simulations with efficient Brownian dynamics code and apply our model to analyze the spatial operation of autocrine epidermal growth factor receptor systems.

INTRODUCTION

We propose and analyze a stochastic model for autocrine signals in cell culture assays. The two main results of this article are an expression for the autocrine fraction of ligand trajectories, i.e., the probability for a ligand to be captured by the same cell from which it has been secreted; and an expression for the spatial distribution of the trapping points of escaping ligands. These expressions are generalized to account for the effects of ligand-receptor dissociation and receptor-mediated endocytosis. Our approach is based on a combination of computational and analytical tools. First, we develop an efficient Brownian dynamics algorithm for generating the trajectories of secreted ligands. Second, we homogenize the boundary condition on the trap-covered surface that models the cell-covered dish. This homogenization significantly simplifies further analysis of autocrine loops in cell culture assays. Our analytical results capture the dependence of the spatial operation of autocrine loops on parameters of the cell and those of the cell culture assay.

Autocrine signaling accompanies all stages of embryonic development and is important for tissue homeostasis (Sporn and Roberts, 1992; Freeman and Gurdon, 2002). Amplified autocrine signaling is one of the hallmarks of cancer (Sporn and Todaro, 1980; Rozengurt, 1999; Hanahan and Weinberg, 2000; Graeber and Eisenberg, 2001). Understanding the operation of autocrine systems is important for harnessing them in applications such as tissue engineering or targeting the components of autocrine loops in diseases. In vivo, autocrine loops are under control of tissue architecture, cell density, and developmental state of the cell. Although it is next to impossible to control all of these variables in vitro, experiments with cultured cells can be used to ask a number of fundamental questions about the operation of autocrine systems.

A number of recent articles addressed the question of the spatial operation of autocrine loops. Depending on the application, it is important to estimate the fraction of the ligands recaptured by the cell and/or the spatial distribution of trapping points for escaping ligands. The biophysical framework relating these properties to the parameters of the autocrine loop, such as receptor affinity and expression level, and the parameters of the assay, such as cell density and medium height, may guide data analysis and planning of future experiments. The existing approaches to autocrine systems are based on the compartmental models (Forsten and Lauffenburger, 1992; Oehrtman et al., 1998; DeWitt et al., 2001) or on the single-cell or confluent monolayer approximations (Shvartsman et al., 2001, 2002). The compartmental models contain a large number of adjustable parameters, whereas the applicability of the single-cell/confluent monolayer approximations is difficult to evaluate. Here, we go beyond these approximations and develop a stochastic model that is applicable over a wide range of cell densities, medium heights, and molecular/cellular parameters of autocrine systems.

By studying the migration of human mammary epithelial cells equipped with autocrine epidermal growth factor receptor (EGFR) loops and plated at low cell density, Wiley, Lauffenburger and colleagues concluded that autocrine loops could operate already at the level of a single cell (Wiley et al., 1998; Dong et al., 1999; Maheshwari et al., 2001). This conclusion was supported by experiments measuring the rates of ligand release into the medium and its control by the number of cell surface receptors (Lauffenburger et al., 1998; Oehrtman et al., 1998; DeWitt et al., 2001, 2002). These studies naturally lead to the question about the relationship between the efficiency of ligand recapture and parameters of autocrine loops.

The escaping fraction of autocrine ligands can mediate homo- and heterotypic cell-cell interactions. Studying this mode of intercellular signaling, Luttrell and colleagues have prepared co-cultures of autocrine “donor” and “acceptor” cells (Pierce et al., 2001; Ahmed et al., 2003). Autocrine donors could be induced to secrete the ligand (heparin-binding epidermal growth factor) that activated receptors on the donor or acceptor cells. Heterotypic cell-cell interactions could be detected only when the cells where co-cultured at high density. In another area, an increasing number of experiments suggest that secreted growth factors and cytokines contribute to the radiation bystander effect, a phenomenon whereby radiation affects the cells that were not in direct contact with radiation (Barcellos-Hoff and Brooks, 2001; Mothersill and Seymour, 2001; Dainiak, 2002). These studies naturally lead to the question about the spatial range of autocrine signals in cell culture assays, which is the main focus of our analysis in this article.

MODEL

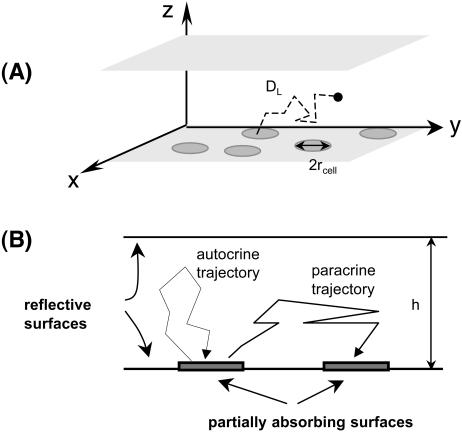
In this section we introduce a stochastic model of autocrine signals in a cell culture assay, Fig. 1, A and B. We consider a random two-dimensional dispersion of cells that secrete ligands uniformly over the cell surface. The secreted ligands diffuse in the medium layer of thickness h; the diffusion coefficient of the ligand is denoted by DL. Ligands can bind to receptors that are uniformly distributed over the cell surface. The cells are modeled by disks of radius rcell, Fig. 1 B. The interaction of diffusing ligands with the receptor-covered cell surface is modeled by imposing a radiation boundary condition on the cell surface. This means that the probability density function for the coordinate of a diffusing ligand, p(x,y,z,t), on the cell surface satisfies

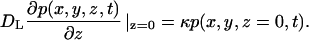graphic file with name M1.gif (1)

The rate constant, κ, is related to the total number of receptors on the cell surface, Rtotal, and ligand-receptor binding rate constant, kon, by the relation κ = konRtotal/(πrcell2NA), where NA is the Avogadro's number (Lauffenburger and Linderman, 1993). A ligand-receptor complex can either dissociate or be internalized by the cell. Both dissociation and internalization are first-order processes characterized by the rate constants koff and ke, respectively.

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Schematic representation of a cell culture assay: a random dispersion of cells is covered by a layer of liquid medium of thickness h. Autocrine and paracrine trajectories: secreted ligand can be captured by the cell surface receptors on the ligand producing cell or its neighbors. (B) Cells are modeled by randomly distributed disklike traps of radius rcell. A reflecting boundary condition is placed at z = h. The boundary condition at z = 0 is partially absorbing on the trap surface and reflecting otherwise.

We trace the “fate” of a ligand that is released at a random point on the cell surface. Specifically, we derive the probability for the ligand to be recaptured by the initial cell, i.e., the fraction of autocrine trajectories. We also find the spatial distribution of the trapping points for the trajectories escaping from the ligand-producing cell; such trajectories are termed paracrine. Finally, we derive an expression for the fraction of the ligand internalized by the initial cell and the spatial distribution of internalization points for ligands internalized outside of the “parent” cell. All of these results are derived as a function of measurable parameters of the cell and parameters of the assay. To illustrate our results, we apply them to the autocrine EGFR system (Oehrtman et al., 1998; Dong et al., 1999; DeWitt et al., 2001, 2002; Maheshwari et al., 2001; Wiley et al., 2003).

ALGORITHM

The size of a single cell is several microns, whereas the height of the medium used in a typical cell culture experiment is several millimeters. This wide separation of length scales, together with the random boundary condition on the trap-covered plane, makes the deterministic numerical methods (e.g., finite elements or finite differences) impractical. We have developed a Brownian dynamics algorithm that efficiently generates the trajectories of ligands in this problem with wide separation of length scales.

Our algorithm combines two techniques from Brownian dynamics simulations of diffusion-limited reactions. Next to the trap-covered surface we use the exact one-dimensional propagator for the partially absorbing boundary condition (Lamm and Schulten, 1981, 1983; Edelstein and Agmon, 1997). Far from the trap-covered plane, we use the first-passage-time technique (Siegel and Langer, 1986; Torquato and Kim, 1989; Zheng and Chiew, 1989). By construction, the algorithm has an adaptive timestep: in the first-passage-time branch of the algorithm, the timestep is chosen based on the distance to the lower (trap-covered) and the upper (reflective) boundary. Next to the trap-covered surface, the timestep is dictated by the lateral distance to the nearest trap or the trap size (to ensure the validity of using a one-dimensional propagator for the vertical displacement). The details of the algorithm implementation can be found in the Appendix.

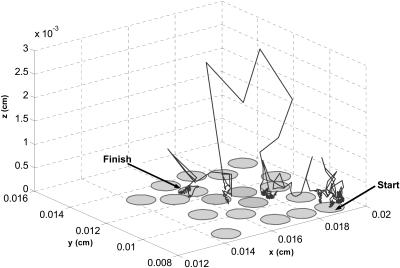
A sample trajectory, shown in Fig. 2, demonstrates the adaptive timestep strategy: the large timesteps away from the trap-covered surface and smaller timesteps next to this surface. After validating the algorithm by comparing its results to the analytical and (deterministic) numerical solutions of a number of problems in simple geometries, we have used it to analyze the statistical properties of autocrine and paracrine trajectories. All the computational results are based on averaging over 20 configurations of 200 randomly placed traps and 105 trajectories for each configuration.

FIGURE 2.

FIGURE 2

Open in a new tab

An adaptive timestep Brownian dynamics algorithm uses the first-passage-time method far from the trap-covered plane and samples from the exact one-dimensional propagators close to the lower boundary. See Appendix for the detailed description of the algorithm.

RESULTS

Autocrine trajectories

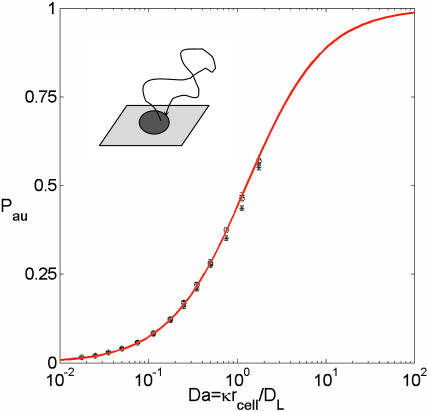
Our Brownian dynamics simulations indicate that the autocrine fraction essentially does not depend on the medium layer height and the trap density. The height was varied from 2 to 3 mm, and the trap density was varied from 1% to 40% of the surface coverage. Dimensional analysis indicates that the dependence on the ligand diffusivity, trap size, and the binding rate constant is reduced to the dependence on a single dimensionless group, the Damköhler number, defined as Da ≡ rcellκDL. The Damköhler-dependence of the fraction of autocrine trajectories, Pau, is shown in Fig. 3. This dependence is well described by

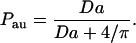graphic file with name M2.gif (2)

The expression in Eq. 2 can be obtained using one of the results from Zwanzig and Szabo (1991). This formula is a generalization of a well-known result for partially absorbing spherical traps (Collins and Kimball, 1949), to the case of a partially absorbing disk on the otherwise reflecting plane. As was shown by Collins and Kimball, the trapping probability for a particle that starts at the surface of a partially absorbing sphere of radius R is given by the ratio k/(k + kSm), where k = 4πR2κ, and kSm = 4πRDL is the Smoluchowski rate constant. To get the result in Eq. 2, we use this ratio with k = πrcell2κ and kSm replaced by the expression for the steady-state rate constant for a perfectly absorbing disk of radius rcell on the otherwise reflecting plane: kdisk = 4rcellDL (Hill, 1975).

FIGURE 3.

FIGURE 3

Open in a new tab

Analysis of autocrine trajectories. The autocrine fraction depends on a single dimensionless group that combines the size of the trap, ligand diffusivity, and the rate constant on the trap surface: Da = κrcell/DL. The results of simulations are shown by symbols; the solid curve is given by Pau = Da/(Da + 4/π) (see text for details). Parameters of the simulations are rcell = 10 μm, kon = 108 M−1 min−1, σ = 0.1, 0.2, 0.4, and Rtotal = 104 − 5 × 106.

To rationalize independence of Pau from the medium layer thickness, h, and the cell surface density, n, one has to compare the average span of autocrine trajectories with h and characteristic length associated with trapping of paracrine trajectories. The span of the autocrine trajectory is defined as the maximal excursion of a secreted ligand before its recapture by a cell surface receptor (Shvartsman et al., 2001, 2002). Using dimensional arguments one can see that the average autocrine excursion length is ∼DL/κ. In our case, DL/κ < 0.1 mm; this is an order-of-magnitude smaller than h, which varies from 2 to 3 mm. To estimate the characteristic length associated with the trapping of the paracrine trajectories, one needs to know the spatial density of the trapping points. We have analyzed this density in Berezhkovskii et al. (2003) and have shown that all moments of the trapping distance diverge as the medium layer thickness tends to infinity. For the case under study, the medium height is large enough and the average trapping length is much greater than DL/κ. Thus, for the relevant range of biophysical parameters, the characteristic length DL/κ is much smaller than both the medium height and the average trapping distance. This is why Pau is independent of both h and the cell surface density.

Paracrine trajectories

In the case under study, the average trapping length is much greater than the average distance between the cells on the surface, given by n−1/2. As a consequence, the inhomogeneous boundary condition on the cell-covered plane can be replaced by the homogeneous one with a trapping rate constant, κeff. This rate constant depends on the parameters rcell and κ of the cell, the fraction of the surface occupied by the traps, σ = πrcell2n, as well as the diffusion constant. For κeff, we use the expression

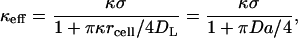graphic file with name M3.gif (3)

which can be obtained from one of the results derived by Zwanzig and Szabo (1991). This is a generalization of the formula for the case when disks are perfectly absorbing (Berg and Purcell, 1977). Indeed, as κ → ∞ the effective rate constant reduces to 4DLσ/(πrcell), which is a well-known Berg-Purcell result. Our Brownian dynamics simulations show that this boundary condition is very accurate for Damkohler numbers ≤1, and over the entire range of medium heights and cell densities considered in this article.

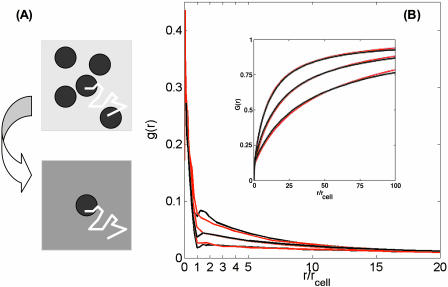
By homogenizing the boundary condition, we replace the initial problem of ligand diffusion above a reflecting plane randomly covered by partially absorbing disks with a much simpler problem, Fig. 4 A. In the homogenized problem, a disk with the initial trapping rate constant κ, from which the ligand starts, is located on a uniformly absorbing plane characterized by the effective trapping rate constant, κeff (Fig. 4 A). Fig. 4 B shows good agreement between the probability densities, g(r), and the cumulative distribution functions of the trapping points, 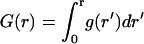Inline graphic, found by simulations of the original and homogenized problems. There are small differences between the two curves for the probability density at 1 < r/rcell < 2, where the homogenization of the boundary condition is not justified.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Schematic representation of the homogenization procedure used to analyze the paracrine trajectories. The trap-covered plane is approximated by the partially absorbing boundary condition. The surface reaction rate constant depends on the trap density and parameters of the trap, Eq. 3. (B) Comparison of the probability density functions and cumulative distribution functions found in simulations of the homogenized and original problems, shown by red and black curves, respectively. Parameters of the simulations are Da = 1.77 and σ = 0.1, 0.2, and 0.4 (bottom to top).

The homogenization of the boundary condition significantly simplifies the numerical analysis of the problem, since it effectively averages the boundary condition outside of the disk, from which the ligand starts, over the trap configurations. In addition, the homogenization enables an analytical treatment of the spatial distribution of the trapping points of the paracrine trajectories. As a consequence of the large average trapping length, one can neglect the disk radius and assume that all trajectories start from the origin. This greatly simplifies the analysis. We have derived an infinite series expression for this distribution at arbitrary values of κeff and h in Berezhkovskii et al. (2003). At large medium heights (h → ∞), the expressions for the density of the trapping points, p(r), is given by

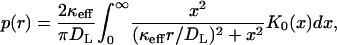graphic file with name M5.gif (4)

where K0(x) is the modified Bessel function (Abramowitz and Stegun, 1964). The corresponding cumulative distribution function is

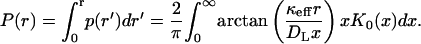graphic file with name M6.gif (5)

This expression works well when hkeff/DL ≥ 1.

The integrals in Eqs. 4 and 5 have to be computed numerically. We have found that the dependence in Eq. 5 is well-approximated by a simple formula,

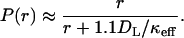graphic file with name M7.gif (6)

This approximate formula predicts the exact r-dependence with a relative error <5%.

The effect of ligand dissociation and endocytosis

A recaptured autocrine ligand can either dissociate from the cell or be internalized by it. Internalization terminates the trajectory of the secreted ligand. The probability of internalization is given by the ratio ν ≡ ke/(koff + ke). The probability that the ligand is not only recaptured but is also internalized by the cell, is given by the sum of the probabilities of internalization during the sequential recapture events as

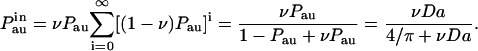graphic file with name M8.gif (7)

Notice that this result can be directly obtained from the expression for the autocrine fraction, given in Eq. 2, with the Damköhler reduced by the factor ν. Similarly, the probability density and cumulative distribution of the internalization distances are given by the same expressions as those in Eqs. 4–6, in which κeff is replaced by νκeff. For example, the analog of Eq. 6 is

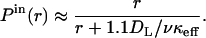graphic file with name M9.gif (8)

Illustrative example

One of the best-studied autocrine systems is that of the EGFR and its ligands (Wiley et al., 2003). The molecular and cellular parameters of this system have been reliably measured. The forward binding rate constant, kon, is ∼108 M−1 min−1, and both the dissociation and endocytosis rate constants, koff and ke, are in the 0.1–0.3 min−1 range. With the typical receptor expression level Rtotal of 104–106 receptors/cell, and the cell radius of ∼10 μm, the rate constant κ in the radiation boundary condition in Eq. 1 is between 0.1 and 10 μm/s. The typical medium height is 2–3 mm and the diffusivity of a ligand is 10−6 cm2/s. In this section, we apply our results to this system.

For the entire range of cell surface receptor densities in this system, DL/κ < h. Therefore, we are in the regime where the statistical properties of secreted trajectories will not depend on the height of the medium and cell density. The Damköhler numbers (Da = κrcell/DL) corresponding to these values of κ lie between Da ≈ 0.01 for 104 receptors/cell and Da ≈ 1 for 106 receptors/cell. Using these values to calculate the probability of autocrine capture by Eq. 2, we get Pau ≈ 0.01 for 104 receptors and Pau ≈ 0.5 for 106 receptors. Thus, 1% and 50% of ligand trajectories will be recaptured by the cell in these two cases. Recent experiments by De Witt and co-workers were done with engineered fibroblasts that expressed ∼104 EGF receptors per cell (DeWitt et al. 2001, 2002). According to our analysis, the fraction of autocrine trajectories is ∼1%. Based on this estimate, we conclude that this experiment was operating in a strongly paracrine regime, i.e. most of the trajectories were “lost” by the cell.

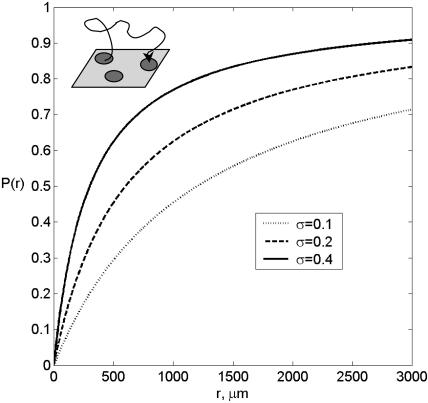
To characterize paracrine trajectories, we first calculate the effective rate constant by Eq. 3 and then use it in Eq. 6. For example, for 105 receptors, κ ≈ 1 μm/s, Da ≈ 0.1, and keff ≈ 0.9 × σ [μm/s]. Substituting these relations into Eq. 6, we get P(r) ≈ r/(r + 120/σ), where r is in microns. The dependence P(r) is shown in Fig. 5 for σ = 0.1, 0.2, and 0.4. From this expression we see that 90% of the paracrine trajectories are captured at the radial distances <1200/σ μm, which is equivalent to 60/σ of cell diameters. For the coverages of 0.1, 0.2, and 0.4, this estimate leads to 600, 300, and 150 cell diameters. This characterizes the “plume” due to ligand secretion from an autocrine cell with 105 receptors. Thus, the spatial range of paracrine signals in a typical cell culture assay is much larger than the size of a single cell. This is an immediate consequence of the fact that the cells are covered by a thick layer of liquid (hkeff/DL ≥ 1). On the other hand, in tissues, e.g., in developing epithelial layers, hkeff/DL ≪ 1, and the spatial range of a diffusible signal can be just a couple of cell diameters (Berezhkovskii et al., 2003). Thus, the extrapolation of the estimates of the ranges of secreted signals from cell culture experiments to tissues must be done with extreme care.

FIGURE 5.

FIGURE 5

Open in a new tab

Spatial distribution of trapping points computed for the parameters corresponding to the autocrine EGFR system is rcell = 10 μm, kon = 108 M−1 min−1, Rtotal = 105, and σ = 0.1, 0.2, and 0.4.

CONCLUSIONS

We have developed a biophysical framework for the analysis of autocrine loops in cell culture assays. Within the framework of our model, we have expressed the autocrine fraction and the spatial distribution of paracrine trajectories as the functions of parameters of the cell and parameters of the assay. Our approach is based on the Brownian dynamics simulations and the homogenization of the boundary condition for the trap-covered surface. For the relevant ranges of biophysical parameters, the autocrine fraction of trajectories is a function of a single dimensionless group that depends on the parameters of a single trap and ligand diffusivity (Eq. 2). The statistical properties of paracrine trajectories can be found by solving the problem where the heterogeneous boundary condition on the trap-covered plane is replaced by the homogeneous partially absorbing boundary condition that depends on parameters of a single trap and the trap-density (Eq. 3).

The ratio DL/κeff defines a dynamic length scale for the analysis of the distances traveled by paracrine ligands. In the relevant regime, the dynamic length scale is less than the height of the extracellular medium and greatly exceeds the size of a single trap. In this case, the distribution functions for the distances traveled to the first capture event can be found analytically (Eqs. 4–6). Thus, both the autocrine fraction and the distribution function for the distance to the first capture are given by analytical expressions. These results were used to analyze the effect of ligand dissociation and receptor-mediated endocytosis (Eqs. 7 and 8). We have tested these results by Brownian dynamics simulations and demonstrated their straightforward application to the autocrine EGFR system.

In this article we have focused on the fate of a single ligand released from the surface of an autocrine cell. In the future, we are planning to characterize autocrine ligand concentrations in cell culture assays. This can be accomplished by incorporating the homogenized boundary condition described in this article into the conventional models of receptor dynamics.

Acknowledgments

The authors thank G. T. Reeves for his critical reading of the manuscript. S.Y.S. is grateful to D. A. Lauffenburger, H. S. Wiley, and J. M. Haugh for many helpful discussions.

This work is supported by grants from the National Science Foundation (DMS-0211864) and the Searle Foundation.

APPENDIX

In the algorithm, we distinguish between the bulk of the “medium” and a “boundary layer” extending a distance δ away from the trap-covered surface. The choice for δ is dictated by running time considerations; we found that a near optimal performance is achieved by using δ = 0.001rcell. When the particle is outside this boundary layer, its next position is chosen to be uniformly distributed on the surface of a sphere that is centered on the current position of a particle and has a radius R = min(z0, h − z0), where z0 is the current position of the particle. The mean time to reach this hypothetical spherical boundary for the first time is

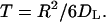graphic file with name M10.gif (A1)

Inside the boundary layer, trajectories are generated using exact one-dimensional propagators. The timestep is fixed and each of the coordinates is sampled separately according to the relevant distributions. In the lateral directions, the particle is advanced according to the Gaussian distribution

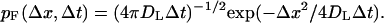graphic file with name M11.gif (A2)

In the vertical direction, different propagators are employed depending on whether the particle is above the reflecting or partially absorbing part boundary. The two propagators are given by Lamm and Schulten (1981, 1983) as

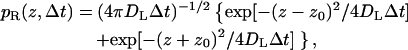graphic file with name M12.gif (A3)
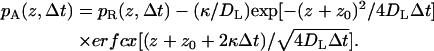graphic file with name M13.gif (A4)

Sampling from the propagator pA (z,Δt) is performed using the rejection method.

Inside the boundary layer and above the trap (or within two trap diameters from it), the timestep corresponds to mean-square displacement 100× smaller than rcell of

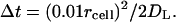graphic file with name M14.gif (A5)

Above the reflective part of the surface, the timestep is chosen according to

graphic file with name M15.gif (A6)

where dnearest is the distance to the nearest trap.

Alexander M. Berezhkovskii's permanent address is Karpov Institute of Physical Chemistry, Vorontsovo Pole 10, Moscow, K-64, 103064, Russia.

References

  1. Abramowitz, M., and I. A. Stegun. 1964. Handbook of Mathematical Tables with Formulas, Graphs, and Mathematical Tables. Dover Publications, Washington, DC.
  2. Ahmed, I., D. Gesty-Palmer, M. K. Drezner, and L. M. Luttrell. 2003. Transactivation of the epidermal growth factor receptor mediates parathyroid hormone and prostaglandin F2 alpha-stimulated mitogen-activated protein kinase activation in cultured transgenic murine osteoblasts. Mol. Endocrinol. 17:1607–1621. [DOI] [PubMed] [Google Scholar]
  3. Barcellos-Hoff, M., and A. Brooks. 2001. Extracellular signaling through the microenvironment: a hypothesis relating carcinogenesis, bystander effects, and genomic instability. Radiat. Res. 156:618–627. [DOI] [PubMed] [Google Scholar]
  4. Berezhkovskii, A. M., L. Batsilas, and S. Y. Shvartsman. 2003. Ligand trapping in cell cultures and epithelial layers. Biophys. Chem. In press. [DOI] [PubMed]
  5. Berg, H. C., and E. M. Purcell. 1977. Physics of chemoreception. Biophys. J. 20:193–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Collins, F. C., and G. E. Kimball. 1949. Diffusion-controlled reaction rates. J. Colloid Sci. 4:425–437. [Google Scholar]
  7. Dainiak, N. 2002. Hematologic consequences of exposure to ionizing radiation. Exp. Hematol. 30:513–528. [DOI] [PubMed] [Google Scholar]
  8. DeWitt, A., J. Dong, H. Wiley, and D. Lauffenburger. 2001. Quantitative analysis of the EGF receptor autocrine system reveals cryptic regulation of cell response by ligand capture. J. Cell Sci. 114:2301–2313. [DOI] [PubMed] [Google Scholar]
  9. DeWitt, A., T. Iida, H. Lam, V. Hill, H. S. Wiley, and D. A. Lauffenburger. 2002. Affinity regulates spatial range of EGF receptor autocrine ligand binding. Dev. Biol. 250:305–316. [PubMed] [Google Scholar]
  10. Dong, J. Y., L. K. Opresko, P. J. Dempsey, D. A. Lauffenburger, R. J. Coffey, and H. S. Wiley. 1999. Metalloprotease-mediated ligand release regulates autocrine signaling through the epidermal growth factor receptor. Proc. Natl. Acad. Sci. USA. 96:6235–6240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Edelstein, A. L., and N. Agmon. 1997. Brownian simulation of many-particle binding to a reversible receptor array. J. Comp. Phys. 132:260–275. [Google Scholar]
  12. Forsten, K. E., and D. A. Lauffenburger. 1992. Autocrine ligand-binding to cell receptors—mathematical analysis of competition by solution decoys. Biophys. J. 61:518–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Freeman, M., and J. B. Gurdon. 2002. Regulatory principles of developmental signaling. Annu. Rev. Cell Dev. Biol. 18:515–539. [DOI] [PubMed] [Google Scholar]
  14. Graeber, T. G., and D. Eisenberg. 2001. Bioinformatic identification of potential autocrine signaling loops in cancers from gene expression profiles. Nat. Genet. 29:295–300. [DOI] [PubMed] [Google Scholar]
  15. Hanahan, D., and R. A. Weinberg. 2000. The hallmarks of cancer. Cell. 100:57–70. [DOI] [PubMed] [Google Scholar]
  16. Hill, T. L. 1975. Effect of rotation on diffusion-controlled rates of ligand-protein association. Proc. Natl. Acad. Sci. USA. 72:4918–4922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lamm, G., and K. Schulten. 1981. Extended Brownian dynamics approach to diffusion-controlled processes. J. Chem. Phys. 75:365–371. [Google Scholar]
  18. Lamm, G., and K. Schulten. 1983. Extended Brownian dynamics. 2. Reactive nonlinear diffusion. J. Chem. Phys. 78:2713–2734. [Google Scholar]
  19. Lauffenburger, D. A., and J. J. Linderman. 1993. Receptors: Models for Binding, Trafficking, and Signaling. Oxford University Press, New York.
  20. Lauffenburger, D. A., G. T. Oehrtman, L. Walker, and H. S. Wiley. 1998. Real-time quantitative measurement of autocrine ligand binding indicates that autocrine loops are spatially localized. Proc. Natl. Acad. Sci. USA. 95:15368–15373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Maheshwari, G., H. S. Wiley, and D. A. Lauffenburger. 2001. Autocrine epidermal growth factor signaling stimulates directionally persistent mammary epithelial cell migration. J. Cell Biol. 155:1123–1128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mothersill, C., and C. Seymour. 2001. Radiation-induced bystander effects: past history and future directions. Radiat. Res. 155:759–767. [DOI] [PubMed] [Google Scholar]
  23. Oehrtman, G. T., H. S. Wiley, and D. A. Lauffenburger. 1998. Escape of autocrine ligands into extracellular medium: experimental test of theoretical model predictions. Biotechnol. Bioeng. 57:571–582. [PubMed] [Google Scholar]
  24. Pierce, K. L., A. Tohgo, S. Ahn, M. E. Field, L. M. Luttrell, and R. J. Lefkowitz. 2001. Epidermal growth factor (EGF) receptor-dependent ERK activation by G protein-coupled receptors: a co-culture system for identifying intermediates upstream and downstream of heparin-binding EGF shedding. J. Biol. Chem. 276:23155–23160. [DOI] [PubMed] [Google Scholar]
  25. Rozengurt, E. 1999. Autocrine loops, signal transduction, and cell cycle abnormalities in the molecular biology of lung cancer. Curr. Opin. Oncol. 11:116–122. [DOI] [PubMed] [Google Scholar]
  26. Shvartsman, S. Y., M. P. Hagan, A. Yacoub, P. Dent, H. S. Wiley, and D. A. Lauffenburger. 2002. Autocrine loops with positive feedback enable context-dependent cell signaling. Am. J. Physiol. Cell Physiol. 282:C545–C559. [DOI] [PubMed] [Google Scholar]
  27. Shvartsman, S. Y., H. S. Wiley, W. M. Deen, and D. A. Lauffenburger. 2001. Spatial range of autocrine signaling: modeling and computational analysis. Biophys. J. 81:1854–1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Siegel, R. A., and R. Langer. 1986. A new Monte Carlo approach to diffusion in constricted porous geometries. J. Coll. Interf. Sci. 109:426–440. [Google Scholar]
  29. Sporn, M. B., and A. B. Roberts. 1992. Autocrine secretion—10 years later. Ann. Intern. Med. 117:408–414. [DOI] [PubMed] [Google Scholar]
  30. Sporn, M. B., and G. J. Todaro. 1980. Autocrine secretion and malignant transformation of cells. N. Engl. J. Med. 303:878–880. [DOI] [PubMed] [Google Scholar]
  31. Torquato, S., and I. C. Kim. 1989. Efficient simulation technique to compute effective properties of heterogeneous media. Appl. Phys. Lett. 55:1847–1849. [Google Scholar]
  32. Wiley, H. S., S. Y. Shvartsman, and D. A. Lauffenburger. 2003. Computational modeling of the EGF-receptor system: a paradigm for systems biology. Trends Cell Biol. 13:43–50. [DOI] [PubMed] [Google Scholar]
  33. Wiley, H. S., M. F. Woolf, L. K. Opresko, P. M. Burke, B. Will, J. R. Morgan, and D. A. Lauffenburger. 1998. Removal of the membrane-anchoring domain of epidermal growth factor leads to intracrine signaling and disruption of mammary epithelial cell organization. J. Cell Biol. 14:1317–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zheng, L. H., and Y. C. Chiew. 1989. Computer-simulation of diffusion-controlled reactions in dispersions of spherical sinks. J. Chem. Phys. 90:322–327. [Google Scholar]
  35. Zwanzig, R., and A. Szabo. 1991. Time-dependent rate of diffusion-influenced ligand-binding to receptors on cell-surfaces. Biophys. J. 60:671–678. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES