Abstract
We present a mathematical model of calcium cycling that takes into account the spatially localized nature of release events that correspond to experimentally observed calcium sparks. This model naturally incorporates graded release by making the rate at which calcium sparks are recruited proportional to the whole cell L-type calcium current, with the total release of calcium from the sarcoplasmic reticulum (SR) being just the sum of local releases. The dynamics of calcium cycling is studied by pacing the model with a clamped action potential waveform. Experimentally observed calcium alternans are obtained at high pacing rates. The results show that the underlying mechanism for this phenomenon is a steep nonlinear dependence of the calcium released from the SR on the diastolic SR calcium concentration (SR load) and/or the diastolic calcium level in the cytosol, where the dependence on diastolic calcium is due to calcium-induced inactivation of the L-type calcium current. In addition, the results reveal that the calcium dynamics can become chaotic even though the voltage pacing is periodic. We reduce the equations of the model to a two-dimensional discrete map that relates the SR and cytosolic concentrations at one beat and the previous beat. From this map, we obtain a condition for the onset of calcium alternans in terms of the slopes of the release-versus-SR load and release-versus-diastolic-calcium curves. From an analysis of this map, we also obtain an understanding of the origin of chaotic dynamics.
INTRODUCTION
The contraction of a cardiac myocyte is triggered by an intracellular rise in calcium concentration that is due to a coordinated release of calcium from the sarcoplasmic reticulum (SR) (Fabiato, 1983). The release of calcium from the SR occurs via ryanodine receptors (RyR), which are in close proximity to L-type calcium channels that are located in the cell surface membrane and T-tubules (Meissner, 1994; Wang et al., 2001). When the cell is depolarized, L-type channels open and allow calcium entry into a confined microdomain. The rise of calcium in this small space is sensed by the nearby cluster of RyR channels that in turn open via calcium-induced calcium release (CICR) (Fabiato, 1983). As the calcium concentration in the cell rises, contractile elements are activated and the cell contracts. An uptake pump, which is activated by the rise in calcium, then pumps calcium back into the SR. This interplay between voltage across the cell membrane and intracellular calcium cycling forms the basis of excitation-contraction (EC) coupling.
During normal beating of the heart, myocardial cells undergo periodic depolarizations of the membrane called action potentials (AP). The shape of the AP waveform is determined by the flux of ions across the membrane. Some of these fluxes, such as those due to the L-type channel current (ICa) and the NaCa exchange current (INaCa), are modulated by intracellular calcium concentration. Thus, the calcium system is driven by an AP waveform that is itself dependent on the dynamics of the calcium system. Recently, Chudin et al. (1999) were able to shed light on this coupling by stimulating a rabbit ventricular myocyte using a clamped AP waveform. They observed that at high stimulation rates the whole cell calcium transients exhibited alternans even when the clamped voltage stimulus was periodic. This result demonstrates that the calcium system could be dynamically unstable independently of the dynamics of the membrane potential. Thus, given the bidirectional coupling between voltage and calcium, this raised the important possibility that abnormalities in calcium cycling could influence the membrane potential and hence promote arrhythmias. For example, ventricular fibrillation is typically preceded by ventricular tachycardia, where the ventricles can be driven at rapid rates by an unstable rotating spiral wave. It is possible that at high rates a dynamical instability of calcium cycling at the single cell level may promote wave break and thus underlie the transition of ventricular tachycardia to ventricular fibrillation. Therefore, a physiologically based model of calcium cycling is necessary to investigate this important bidirectional coupling of voltage and calcium. In particular, it is important that this model reproduces the experimentally observed complex dynamics of the calcium system at high stimulation rates.
There have been many efforts to model intracellular calcium dynamics. Initial modeling attempts were faced with the challenge of explaining the experimentally observed (Wier et al., 1994) linear dependence of calcium release from the SR on the whole cell ICa current (graded release), given that RyR channels are activated by a CICR mechanism that favors an all-or-none response. This issue was resolved by Stern (1992), who pointed out that graded release can be explained by the stochastic recruitment of independent local release fluxes. Stern referred to models of this type as local control models since a small cluster of L-type channels were coupled to a cluster of RyR channels via a local pool of calcium. Stern emphasized that models that couple whole cell ICa to RyR flux via a single pool, which he referred to as common-pool models, would not be able to explain graded release. This hypothesis was later confirmed by high resolution confocal imaging, which showed that the global rise in calcium was due to the summation of many local release events sometimes referred to as calcium sparks (Cannell et al., 1994; Cleemann et al., 1998; Lopez-Lopez et al., 1995; Niggli, 1999; Wier and Balke, 1999).
The local nature of the release has led researchers to explore the detailed calcium dynamics within the dyadic junction, i.e., the space between the L-type channel clusters and the corresponding RyR receptor clusters (Cannell and Soeller, 1997; Greenstein and Winslow, 2002; Rice et al., 1999; Peskoff and Langer, 1998; Sobie et al., 2002; Stern et al., 1999). However, it turns out to be difficult to characterize experimentally the gating kinetics of the RyR clusters and the interaction of these clusters with the L-type channels. As a result, these kinetics are still poorly understood and, in particular, the detailed mechanism by which release from the SR is terminated remains controversial (Bers, 2001; DelPrincipe et al., 1999; Niggli, 1999). Moreover, even if the calcium dynamics at the dyadic junction is precisely known, there are on the order of 104 junctions within a cell (Cleemann et al., 1998). Given that each junction is on a submicron scale, a modeling approach that attempts to resolve the dynamics of each junction is unlikely to be computationally tractable for modeling arrhythmogenesis at the tissue or organ level.
Several authors have proposed tractable phenomenological models of calcium cycling at the whole cell level (Chudin et al., 1999; Fox et al., 2002; Glukhovsky et al., 1998; Jafri et al., 1998; Luo and Rudy, 1994; Snyder et al., 2000; Viswanathan et al., 1999). However, several of these models (Jafri et al., 1998; Glukhovsky et al., 1998; Snyder et al., 2000) are common-pool models and, as Stern (1992) predicted, do not reproduce graded release. Hence, they do not correctly describe the coupling between the L-type calcium current and the release from the SR that is crucial to describe EC coupling. Viswanathan et al. (1999) presented an improved version of a model of release flux from the SR first presented in the Luo-Rudy II model (Luo and Rudy, 1994), which incorporates graded release. This model was able to reproduce calcium alternans in simulations performed in a ring of coupled cells, where the voltage waveform was not clamped (Hund et al., 2000). However, this model does not take into account the fact that the release from the SR is the summation of discrete release events. Consequently, it cannot, for example, describe the influence of the amplitude and duration of these events on the dynamics of calcium cycling and the instability mechanism responsible for alternans.
In this article, we present a new model of EC coupling in ventricular myocytes. This model distinguishes itself from previous models in that it represents release from the SR as a summation of elementary release events that correspond to calcium sparks. Furthermore, the model formulation is based on two experimentally measurable constitutive relations:
The relation between the rate of spark recruitment and the whole cell ICa. This relation describes quantitatively the crucial coupling between ICa and calcium release from the SR. This relation is formulated by introducing a variable, N(t), which corresponds to the total number of sparks recruited at a given time t in the whole cell, and by making the rate of spark recruitment (dN/dt) proportional to the whole cell ICa. This linear relationship between dN/dt and ICa is based on the available experimental data on simultaneous measurements of spark occurrence and whole cell ICa (Collier et al., 1999; Lopez-Lopez et al., 1995) and reproduces graded release.
The relation between the total amount of calcium released form the SR and the SR load. This relation can be built into the model by letting the rate of spark recruitment and/or the average release current of a single spark depend on the junctional SR (JSR) concentration. This dependency is then chosen phenomenologically to reproduce the highly nonlinear relationship between fractional release and load that has been measured experimentally (Bassani et al., 1995).
Another important experimental input into the model is the observation (Cleemann et al., 1998; Niggli, 1999) that the lifetime of sparks is relatively constant and independent of both SR load and diastolic calcium level. Based on this observation, we model termination of release from the SR by assuming that the release current of a single spark decays exponentially in time from its initial peak value, with a time constant that is taken comparable to the observed spark lifetime.
The model includes additional features that are not present in previous models. The first is a phenomenological description of intracellular sodium accumulation. This accumulation is well documented experimentally (Harrison and Boyett, 1995), and was found necessary to reproduce the experimentally observed rise of diastolic calcium at high pacing rates. The second is the compartmentation of the myoplasm into a submembrane space near the sarcolemma and the rest of the myoplasm. This distinction recognizes the fact that the concentration in the submembrane space, which influences both the NaCa exchange current and the calcium-dependent inactivation of ICa, is much larger during release than the average bulk concentration inside the myoplasm, due to the proximity of this space to dyadic junctions. Finally, consistent with the discrete picture of sparking events, the model builds in a diffusional delay between the network SR and the JSR that distinguishes between the average JSR concentration of recruited and unrecruited dyadic junctions. We shall show here that this distinction leads to the interesting effect that this delay can enhance SR release, as opposed to always reducing it, as in previous models where the JSR is treated as a single pool (Jafri et al., 1998; Glukhovsky et al., 1998; Luo and Rudy, 1994).
We explore the dynamics of calcium cycling by pacing the model using a clamped AP waveform that is fitted to those used in the experiments of Chudin et al. (1999). At high pacing rates, the model exhibits sustained calcium alternans, consistent with the experimental findings. Furthermore, we vary parameters of the model to identify which parts of the complex calcium cycling machinery are essential for alternans and which ones have a secondary role. We identify two essential instability mechanisms for alternans. The first is a steep relation between release and SR load, and the second is a steep relation between release and diastolic calcium that is due to calcium-induced inactivation of ICa. In addition, we find that the calcium dynamics can become chaotic even when paced with a periodic AP clamp.
To gain further insight into both alternans and chaotic dynamics, we reduce the ordinary differential equations (ODEs) of the model to a two-dimensional discrete map that relates the SR and cytosolic calcium concentrations at one beat to those at the previous beat. This map allows us to obtain a stability condition for the onset of calcium alternans with AP clamp pacing in terms of the slopes of the relations between release and SR load, and release and diastolic calcium, as well as the strength of the calcium uptake into the SR. In addition, this map allows us to show that the existence of chaos is due to a nonmonotonic relation between the peak calcium transient at one beat to that at the previous beat.
This article is organized as follows. In the next section, we describe the various intracellular compartments used in the model, and define the corresponding calcium concentrations. In the section “SR Release Flux”, we describe a model for the SR release current. The calcium dependent membrane currents are then described in the section, “Calcium Fluxes across the Sarcolemma”. In the section “Dynamics of Calcium Cycling”, we integrate these currents into a set ODEs that are used to study calcium cycling. In the section “Voltage Clamp Pacing”, we present the results of the model when paced under an AP clamp protocol. The reduction of this model to a map is then described in the section “Analysis of Beat-to-Beat Dynamics”, and the results are used to analyze the dynamical behavior of the model. The results are discussed in the “Discussion” section, followed by “Conclusions”.
INTRACELLULAR COMPARTMENTS AND CONCENTRATIONS
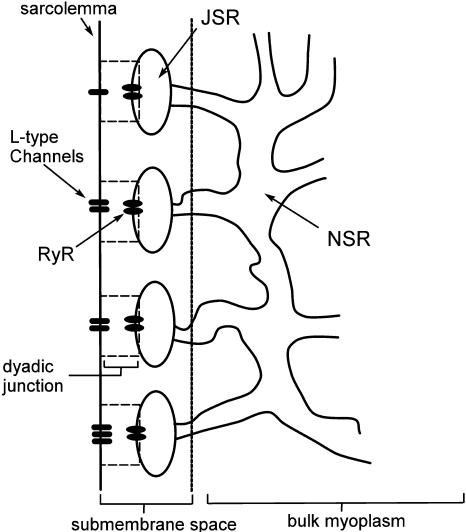
A schematic diagram of the intracellular compartments relevant to calcium cycling is given in Fig. 1. The SR is a spatially diffuse network of tubules and cisternae that is composed of two distinct parts. The first is the network SR (NSR), which is a meshwork of tubules that enwraps the myofilaments. These tubules branch out from the NSR into flattened elliptical sacs, referred to as the junctional SR, that position themselves close to the surface of the cell sarcolemma (Forbes et al., 1985; Franzini-Armstrong et al., 1999). The volume in between the JSR and the sarcolemma is the dyadic junction, wherein RyR channels in the JSR membrane are in close proximity to L-type channels in the sarcolemma. In ventricular myocytes, the sarcolemma forms a uniform array of deep invaginations into the cell, referred to as T-tubules (Soeller and Cannell, 1999), which effectively distribute dyadic junctions uniformly throughout the cell.
FIGURE 1.
Illustration of the intracellular spaces.
The flux of calcium from the SR to the myoplasm, shortly after a voltage depolarization, is due to a summation of several thousand discrete local release events (Cannell et al., 1994; Cleemann et al., 1998). During the release process, calcium in the SR is being drained into the myoplasm via JSR compartments that are being depleted by local calcium release. To describe the calcium concentration within the SR during this release process, we first assume that the SR is composed of Njsr identical JSR compartments, each with a volume, 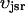 , along with the bulk NSR with volume
, along with the bulk NSR with volume  . This gives a total SR volume of
. This gives a total SR volume of 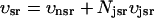 . The total calcium concentration within the kth JSR compartment will be denoted by
. The total calcium concentration within the kth JSR compartment will be denoted by 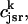 and the concentration in the NSR is cnsr. At any given time, the JSR compartments can be divided into those that are being drained due to a spark in the local dyadic space, and those that are not. The average total calcium concentration within JSR compartments that are not being drained at time t will be denoted by
and the concentration in the NSR is cnsr. At any given time, the JSR compartments can be divided into those that are being drained due to a spark in the local dyadic space, and those that are not. The average total calcium concentration within JSR compartments that are not being drained at time t will be denoted by 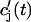 . This average is simply given by
. This average is simply given by
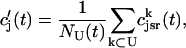 |
(1) |
where the summation is over the set of NU(t) unrecruited JSR compartments. The average total calcium concentration within the entire SR network, which includes all the JSR and the NSR, will be denoted by cj(t) and is given by
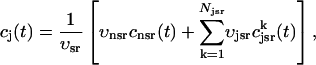 |
(2) |
where the summation is over both recruited and unrecruited JSR volumes. It is important to distinguish between cj and 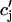 , since in general cj ≠
, since in general cj ≠ 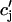 . This is due to the finite time necessary for
. This is due to the finite time necessary for 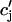 to relax to cj via the diffusion of calcium ions within the SR network. During a local release, at the kth dyadic junction, for instance,
to relax to cj via the diffusion of calcium ions within the SR network. During a local release, at the kth dyadic junction, for instance, 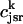 will drop below cj as the JSR compartment is depleted. However,
will drop below cj as the JSR compartment is depleted. However, 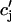 can be larger than cj since the set of unrecruited JSR compartments are not depleted. This feature is quite different from previous models (Jafri et al., 1998; Glukhovsky et al., 1998; Luo and Rudy, 1994), where the entire JSR is treated as a single pool that is being replenished by the NSR. In such models, the JSR concentration is always less than the SR concentration during release.
can be larger than cj since the set of unrecruited JSR compartments are not depleted. This feature is quite different from previous models (Jafri et al., 1998; Glukhovsky et al., 1998; Luo and Rudy, 1994), where the entire JSR is treated as a single pool that is being replenished by the NSR. In such models, the JSR concentration is always less than the SR concentration during release.
To describe the calcium outside of the SR, we first divide this space into the bulk myoplasm (volume 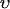 i, average free calcium concentration ci), and a submembrane space (volume
i, average free calcium concentration ci), and a submembrane space (volume 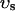 , average free calcium concentration cs), which corresponds to the space in between the bulk myoplasm and the sarcolemma (see Fig. 1). To clarify further, cs is the average concentration that calcium-dependent membrane channels sense. Since membrane currents are delivered into
, average free calcium concentration cs), which corresponds to the space in between the bulk myoplasm and the sarcolemma (see Fig. 1). To clarify further, cs is the average concentration that calcium-dependent membrane channels sense. Since membrane currents are delivered into 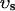 , and since
, and since 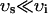 (in this article we use
(in this article we use 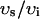 ∼ 10), the concentration changes in the submembrane space are much larger and faster than those in the bulk myoplasm. This effect can potentially influence calcium-dependent ion channels at the sarcolemma. Also, the free calcium concentration within the kth dyadic junction will be denoted by
∼ 10), the concentration changes in the submembrane space are much larger and faster than those in the bulk myoplasm. This effect can potentially influence calcium-dependent ion channels at the sarcolemma. Also, the free calcium concentration within the kth dyadic junction will be denoted by 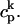 It is important to note that the average volume of a dyadic space is ∼10−9 times smaller than that of the cell volume. Thus, during a calcium spark in the kth dyadic junction the concentration
It is important to note that the average volume of a dyadic space is ∼10−9 times smaller than that of the cell volume. Thus, during a calcium spark in the kth dyadic junction the concentration 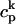 can rise rapidly to levels >100 μM (Peskoff and Langer, 1998), whereas the concentration in the submembrane space will rise to ∼5–10 μM.
can rise rapidly to levels >100 μM (Peskoff and Langer, 1998), whereas the concentration in the submembrane space will rise to ∼5–10 μM.
SR RELEASE FLUX
Spark recruitment rate
To model the release process at the whole cell level, it is first necessary to determine the relationship between the number of release events (sparks) and the corresponding voltage stimulus. Since RyR channels are triggered by nearby L-type channels, it is reasonable to expect that spark recruitment is related to the total calcium current entering the cell via the L-type channels (ICa). Collier et al. (1999) have measured whole cell ICa simultaneously with calcium spark occurrence in rat ventricular myocytes, albeit under experimental conditions of reduced ICa, which allowed for the visualization of individual sparks. They showed that the time course (i.e., time constant of decreasing occurrence) of calcium sparks with sustained depolarization was statistically identical to the time course (i.e., the time constant of inactivation) of the ICa current. This confirmed the conclusions of an earlier study that was similar except that ICa was not measured (Lopez-Lopez, 1995). A more recent article (Sah et al., 2002) again shows in a quantitative manner that the time course of spark occurrence parallels the time course of ICa, using novel voltage clamp protocols, such as triangular and action potential waveforms.
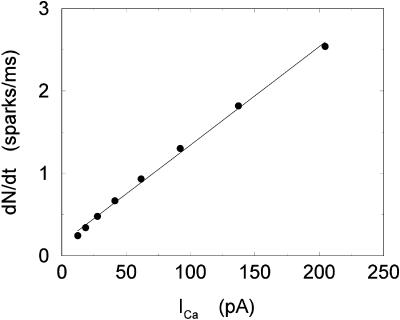
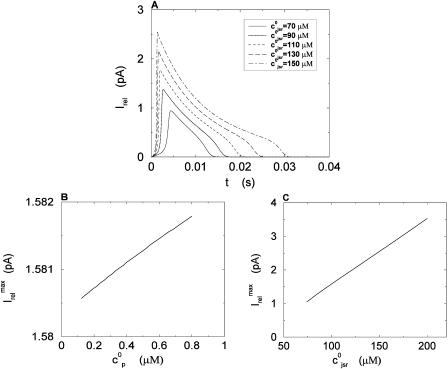
To quantify the relationship between spark occurrence and the ICa current, we will denote the number of sparks recruited at time t to be N(t). Then the rate of spark recruitment is dN(t)/dt, which is the number of sparks recruited in a whole cell per unit time. This rate can be computed directly from experimental measurements of spark occurrence. Using the experimental data presented in the work of Collier et al. (1999), we compared the rate of spark occurrence and the ICa current for a depolarization to a holding potential of 30 mV (see Fig. 4 in their article). In Fig. 2, we plot the computed spark rate as a function of whole cell ICa. It is clear from the plot that, under the physiological conditions of the measurement and for the given depolarization potential, the measured spark rate is to a good approximation proportional to whole cell ICa, i.e., dN(t)/dt ∝ ICa(t).
FIGURE 4.
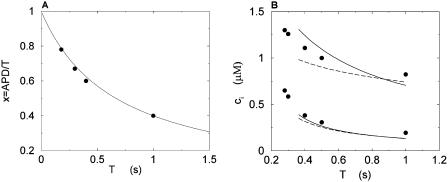
(A) Plot of the ratio x = APD/T versus T. The circles correspond to values of x computed from the experimental AP clamps, and the line is the corresponding fit. (B) Maximum and minimum of bulk myoplasmic calcium concentration during steady state as a function of pacing period T at relatively slow pacing rates. The solid lines are for the case when the internal sodium concentration increases with decreasing period according to Eq. 17. The filled circles correspond to the experimental data points from Chudin et al. (1999). The dashed line corresponds to the case when intracellular sodium is fixed at Nai = 10 mM.
FIGURE 2.
Spark rate versus whole cell ICa using the experimental data of Collier et al. (1999). The straight line corresponds to a linear fit.
It is known experimentally that when the calcium content of the SR is increased, the frequency of spontaneous sparks in a resting myocyte also increases (Cheng et al., 1993; Lukyanenko et al., 1996, 2000). This dependence between spark occurrence and SR content implies that RyR channels are sensitive to the calcium concentration within the local JSR compartment. Now, since JSR compartments, which already have been depleted due to a spark, probably cannot be recruited until they have had enough time to refill, we expect that the rate of spark recruitment should depend on the average calcium concentration within unrecruited JSR compartments (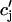 ). Thus, we model the JSR calcium dependence of the whole cell spark rate using
). Thus, we model the JSR calcium dependence of the whole cell spark rate using
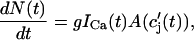 |
(3) |
where the function A(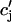 ) gives the JSR load dependence, and where g is a proportionality constant.
) gives the JSR load dependence, and where g is a proportionality constant.
Calcium release during a spark
The local release flux during a spark will be dictated by the gating kinetics of the RyR cluster and the calcium gradients in the dyadic space. However, because the detailed properties of a cluster of RyR channels are not well known, we will describe local release using a simple phenomenological model based on very general considerations. First, we will assume that a spark that is activated at a given time t′, in the kth dyadic junction, is determined primarily by the local JSR concentration at the time of activation 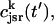 rather than the concentration in the local dyadic space
rather than the concentration in the local dyadic space 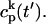 This is a reasonable assumption because the free calcium concentration gradient across the RyR channels is extremely large, and once CICR is induced, the subsequent flux will rise to a value that is determined by the amount of releasable calcium in the JSR. We will also assume that once a spark is recruited it will have a constant lifetime denoted by
This is a reasonable assumption because the free calcium concentration gradient across the RyR channels is extremely large, and once CICR is induced, the subsequent flux will rise to a value that is determined by the amount of releasable calcium in the JSR. We will also assume that once a spark is recruited it will have a constant lifetime denoted by 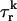 . This assumption is motivated by fluorescence measurements of calcium sparks (Cleemann et al., 1998; Niggli, 1999), which show that sparks have a well defined lifetime around 10–30 ms. Given these simplifying assumptions, the flux at time t, from the kth JSR compartment, during a spark that is activated at time t′ ≤ t, can be written as
. This assumption is motivated by fluorescence measurements of calcium sparks (Cleemann et al., 1998; Niggli, 1999), which show that sparks have a well defined lifetime around 10–30 ms. Given these simplifying assumptions, the flux at time t, from the kth JSR compartment, during a spark that is activated at time t′ ≤ t, can be written as
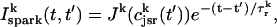 |
(4) |
where the function Jk gives the JSR load dependence of the local flux amplitude at the kth dyadic junction.
Once the whole cell ICa is activated, sparks are stochastically recruited at many dyadic junctions distributed throughout the cell. Thus, at a given time t′, an ensemble of release fluxes given by Eq. 4 is recruited. Here, we will argue that this ensemble of spark fluxes has well-defined averaged properties. This averaging procedure will allow us to drop the superscript k in Eq. 4, and will simplify the subsequent analysis of spark summation. First, we note that 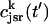 in Eq. 4 denotes the JSR concentration at the time t′ when a spark is just being recruited. Thus, the kth JSR compartment has not yet been depleted and will have a concentration that is roughly the same as the average concentration in unrecruited JSR compartments
in Eq. 4 denotes the JSR concentration at the time t′ when a spark is just being recruited. Thus, the kth JSR compartment has not yet been depleted and will have a concentration that is roughly the same as the average concentration in unrecruited JSR compartments 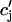 (t′). Hence, we can make the approximation that
(t′). Hence, we can make the approximation that 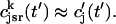 Second, we assume that the lifetime and amplitude of a spark in the kth dyadic junction is roughly the same as the average over the ensemble of recruited sparks. To be more precise, if we define the average
Second, we assume that the lifetime and amplitude of a spark in the kth dyadic junction is roughly the same as the average over the ensemble of recruited sparks. To be more precise, if we define the average 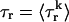 and
and 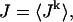 where the brackets denote an average over the ensemble of recruited sparks, then
where the brackets denote an average over the ensemble of recruited sparks, then 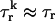 and Jk ≈ J. This claim is equivalent to the statement that the distribution of spark lifetimes and amplitudes is narrowly peaked around their averages. This assumption is motivated by fluorescence images of calcium sparks that show that sparks in different regions of the cell essentially have the same spatial and temporal properties (Cleemann et al., 1998; Niggli, 1999). Thus, the local flux during a spark in the kth junction
and Jk ≈ J. This claim is equivalent to the statement that the distribution of spark lifetimes and amplitudes is narrowly peaked around their averages. This assumption is motivated by fluorescence images of calcium sparks that show that sparks in different regions of the cell essentially have the same spatial and temporal properties (Cleemann et al., 1998; Niggli, 1999). Thus, the local flux during a spark in the kth junction 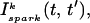 can be represented by an average spark flux
can be represented by an average spark flux 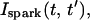 where
where 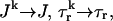 and
and 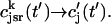
To asses the validity of Eq. 4, we have also developed a set of ODEs that describe the calcium dynamics within a dyadic junction. This model, given in detail in Appendix A, simulates a calcium spark using a simple CICR gating kinetics that is initiated by a short pulse of calcium injected into a simulated dyadic space. Local flux termination is then modeled using a combination of diffusion-driven deactivation and local JSR depletion. In Appendix A, we show that Eq. 4 approximates well the local current due to a simulated local release. However, it is important to note that Eq. 4 does not rely on any specific mechanism underlying the local calcium dynamics, and should hold under more general conditions. Thus, our simple model of the calcium dynamics at the dyadic junction level serves primarily to validate Eq. 4 in a particular case, but is not central to the overall implementation of the model.
Summation of calcium sparks
The total flux draining the SR at time t, which will be denoted by Ir(t), is given by the summation of local fluxes due to sparks recruited at times t′ ≤ t. To compute this sum, we divide the interval of time 0 ≤ t′ ≤ t into M bins of duration Δt′, such that t = MΔt′. Consequently, the flux draining the SR at time t = MΔt′ is given by the discrete sum
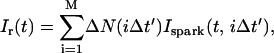 |
(5) |
where ΔN(iΔt′) is the number of sparks recruited during the time interval (i − 1)Δt′ ≤ t′ ≤ iΔt′. If we now take the continuum limit 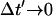 and use the expression for the average spark flux Ispark(t, t′) (Eq. 4 where the superscript k is dropped), the above discrete sum becomes an integral
and use the expression for the average spark flux Ispark(t, t′) (Eq. 4 where the superscript k is dropped), the above discrete sum becomes an integral
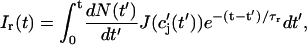 |
(6) |
where t′ = 0 is a time origin when Ir(0) = 0. Finally, differentiating both sides of this equation with respect to t, we obtain
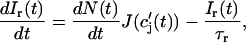 |
(7) |
which will be our basic equation for the release flux Ir(t). Using Eq. 3, the first term on the right-hand side of Eq. 7 can be written as 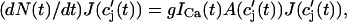 which reveals that the JSR load dependence of release is governed by the function
which reveals that the JSR load dependence of release is governed by the function 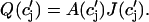
SR load dependence of release
The release of calcium as a function of SR load has been addressed experimentally (Bassani et al., 1995; Shannon et al., 2000b). In the experiment by Bassani et al. (1995), the fraction of SR calcium released as a function of SR load at fixed trigger ICa was measured in ferret ventricular myocytes. The authors found that for low SR loads [Ca]SRT < 50 μmol/l cytosol, almost no calcium is released. At normal loading [Ca]SRT ∼ 90 μmol/l cytosol, about half of the SR is released, whereas for slightly larger loading [Ca]SRT ∼ 100 μmol/l cytosol, almost 70% of the SR is released. Here, [Ca]SRT denotes the total calcium concentration in the SR, which is the quantity measured in the experiment. An important finding of this experiment is that the fraction of calcium released from the SR depends on the initial calcium concentration of the SR in a highly nonlinear fashion. To model this dependence of release on SR load, we will pick a functional form for Q(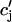 ), which will reproduce the essential features of the experimental results. Since the dependence of release on load only enters through the function Q(
), which will reproduce the essential features of the experimental results. Since the dependence of release on load only enters through the function Q(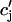 ), it is clear that this function itself should depend on
), it is clear that this function itself should depend on 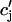 in a nonlinear fashion. There can be several explanations for such a nonlinear dependence of local release on JSR load. One possible scenario is that by virtue of the gating kinetics of the local RyR channels, the amount of calcium released at a single dyad J(
in a nonlinear fashion. There can be several explanations for such a nonlinear dependence of local release on JSR load. One possible scenario is that by virtue of the gating kinetics of the local RyR channels, the amount of calcium released at a single dyad J(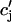 ), may change nonlinearly with JSR load. Another independent possibility is that the sensitivity of the RyR channels may depend on
), may change nonlinearly with JSR load. Another independent possibility is that the sensitivity of the RyR channels may depend on 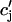 in a nonlinear fashion. In this case, it would be the load dependence of the spark rate A(
in a nonlinear fashion. In this case, it would be the load dependence of the spark rate A(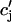 ) that is a nonlinear function. However, the advantage of our phenomenological approach is that the function Q(
) that is a nonlinear function. However, the advantage of our phenomenological approach is that the function Q(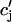 ) can be chosen by appealing directly to experimental data, without a complete model of the SR load dependence of release.
) can be chosen by appealing directly to experimental data, without a complete model of the SR load dependence of release.
JSR-SR diffusional relaxation
To complete the model, we take into account the fact that the average total calcium concentration in the SR (cj) is not the same as the average concentration of unrecruited JSR compartments (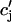 ). This is due to the finite time necessary for calcium to equilibrate, via diffusion, over the entire volume of the SR. This effect can be incorporated into the model by letting
). This is due to the finite time necessary for calcium to equilibrate, via diffusion, over the entire volume of the SR. This effect can be incorporated into the model by letting 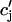 relax to cj using
relax to cj using 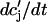 = (cj −
= (cj − 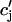 )/τa, where τa is a relaxation time. A rough estimate of τa, which has not yet been measured experimentally, is the average time for a calcium ion to diffuse from a local JSR compartment to the bulk NSR. If we take the effective diffusion coefficient of calcium ions in the SR to be ∼150 (μm)2/s (Stern et al., 1999), then the time for an unobstructed calcium ion to diffuse over a distance 1 μm, (which is roughly the average distance between the NSR and the sarcolemma) is ∼7 ms. However, the calcium ions are confined within the SR, which is a complex tubular network of diameter 25–50 nm (Forbes et al., 1985), and so the diffusion (translocation) time can actually be much longer. Thus, we will consider relaxation times within a fairly wide range of 1–100 ms, and discuss in detail the role of this time constant on the dynamical behavior of the calcium system.
)/τa, where τa is a relaxation time. A rough estimate of τa, which has not yet been measured experimentally, is the average time for a calcium ion to diffuse from a local JSR compartment to the bulk NSR. If we take the effective diffusion coefficient of calcium ions in the SR to be ∼150 (μm)2/s (Stern et al., 1999), then the time for an unobstructed calcium ion to diffuse over a distance 1 μm, (which is roughly the average distance between the NSR and the sarcolemma) is ∼7 ms. However, the calcium ions are confined within the SR, which is a complex tubular network of diameter 25–50 nm (Forbes et al., 1985), and so the diffusion (translocation) time can actually be much longer. Thus, we will consider relaxation times within a fairly wide range of 1–100 ms, and discuss in detail the role of this time constant on the dynamical behavior of the calcium system.
CALCIUM FLUXES ACROSS THE SARCOLEMMA
L-type calcium current
In this model, we have approximated the rate of spark recruitment to be proportional to the whole cell ICa current entering the cell at that time. Hence, a correct formulation of whole cell ICa is an essential component of the model. The whole cell ICa current can be written as ICa = MPoiCa, where M is the number of L-type channels in the cell, Po is the time-dependent open probability of a single channel, and iCa is the single-channel current. We model the open probability of the L-type channel using Po = d∞fq, where d∞ is an instantaneous voltage dependent activation gate, f is a slow voltage dependent inactivation gate variable, and where q describes calcium-induced inactivation. It is important to note that L-type channels, within dyadic junctions where a spark has just been activated, will see a calcium concentration that is much larger than cs. Thus, these channels will have a much lower open probability as compared to the open probability of channels in unrecruited dyadic junctions. Hence, at a given time t, calcium entry into the whole cell via ICa(t) should be dominated by those L-type channels within unrecruited dyadic junctions. Since the average concentration sensed by these channels is roughly the same as cs, then the calcium-dependent gate variable q should depend on cs.
The kinetics of calcium inactivation is modeled using a simple first order scheme that yields
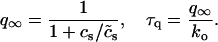 |
(8) |
The detailed parameters of the gate variables are given in Appendix B, and are chosen so that the time course of ICa is qualitatively similar to the most recent experimental measurements in rabbit myocytes (Puglisi et al., 1999).
To explore the role of calcium-induced inactivation on the overall dynamics of the system, it is essential to also investigate more general inactivation schemes. However, we found that simply generalizing Eq. 8 to higher order kinetics led to an ICa time course that was different from experimentally measured currents (Linz and Meyer, 1998; Puglisi et al., 1999). Following an approach similar to Fox et al. (2002), we modeled calcium-induced inactivation using a simple phenomenological scheme with
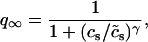 |
(9) |
and with τq a constant in the range 10–50 ms. With this model formulation the exponent γ can be varied, and a steeper cs dependence of calcium-induced inactivation can be explored.
NaCa exchange current
The NaCa exchange current is taken directly from Luo-Rudy II (Eq. 31 in Appendix B). The exchange current is sensitive to the intracellular sodium concentration (Nai). Higher Nai reduces the transmembrane sodium gradient and so reduces the efficiency of the NaCa exchange current at extruding calcium from the cell, which should lead to higher intracellular calcium. An investigation by Harrison and Boyett (1995) used guinea pig ventricular myocytes to study pacing rate dependent increases in twitch shortening. They showed that when the pacing rate was increased from 0.5 to 3 Hz, twitch shortening increased by 34%, whereas if sodium entry (INa) was blocked by tetrodotoxin, twitch shortening increased by only 8%. This result demonstrates that rate dependent changes in Nai could have a substantial effect on intracellular calcium. Thus, we felt it imperative to include a phenomenological description of Nai, where Nai is taken to be an increasing function of the pacing rate.
Role of the submembrane space
As mentioned in “Intracellular Compartments and Concentrations”, we have divided the myoplasm into two spaces: a submembrane space, which is the space in the vicinity of the sarcolemma, and the bulk myoplasm, which is the remainder of the cell volume. This compartmentation of the myoplasm is motivated by the recent experimental and modeling work of Weber et al. (2001). Here, it was shown in particular that the NaCa exchange current INaCa, due to its proximity to dyadic junctions, senses a calcium concentration that is different from the global cytosolic calcium concentration. Consequently, modeling studies showed that the time course of INaCa served as a much more efficient calcium efflux mechanism when it is coupled to the larger and faster concentration changes at the submembrane space (cs) than when it was coupled to the bulk concentration (ci). Likewise, by virtue of calcium-induced inactivation, the time course of ICa should depend on the calcium concentration in the vicinity of the sarcolemma. This effect is particularly important since the calcium released from RyR channels during calcium release is delivered into dyadic junctions that are close to the sarcolemma. Thus, L-type channels sense a much more rapid rise in calcium than that given by the rise of the global cytosolic calcium concentration. To model the effect of a submembrane space, we let the membrane currents ICa and INaCa flow into a compartment of volume 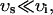 before diffusing to the bulk myoplasm via a simple relaxational current Id = (cs − ci)/τs, with τs a relaxation time that we will take to be in the range 5–10 ms.
before diffusing to the bulk myoplasm via a simple relaxational current Id = (cs − ci)/τs, with τs a relaxation time that we will take to be in the range 5–10 ms.
DYNAMICS OF CALCIUM CYCLING
In this section, we study calcium cycling by incorporating the various currents described in previous sections into a single model. Since our formulation of the SR release flux does not explicitly depend on the calcium concentration gradient between the JSR and the submembrane space, we are free to formulate the dynamics of the SR calcium concentration in terms of the total concentration in the SR, rather than the free calcium concentration. An advantage of using the total SR concentration is that it is the quantity that is measured directly in experiments (Shannon et al., 2000b). Calcium buffering in the cytosol will be taken into account by incorporating the buffering to troponin C, SR, and calmodulin sites, since these are the sites that bind the majority of calcium released from the SR (Shannon et al., 2000a). The buffering to SR and calmodulin sites are fast and will be treated as instantaneous, whereas the time dependent kinetics for the buffering to troponin C will be accounted for.
The equations for calcium cycling can be written as
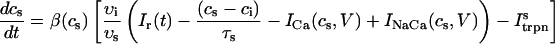 |
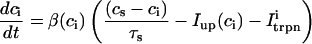 |
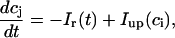 |
(10) |
where the flux out of the SR satisfies
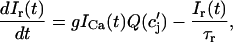 |
(11) |
and where
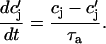 |
(12) |
Here, 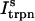 and
and 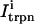 describe the time dependent buffering to troponin C in the submembrane and bulk myoplasm respectively. The functions β(cs) and β(ci) account for the instantaneous buffering to SR and calmodulin sites. The details of the buffering kinetics and parameters are given in Appendix C. Also, V denotes a time-dependent AP waveform.
describe the time dependent buffering to troponin C in the submembrane and bulk myoplasm respectively. The functions β(cs) and β(ci) account for the instantaneous buffering to SR and calmodulin sites. The details of the buffering kinetics and parameters are given in Appendix C. Also, V denotes a time-dependent AP waveform.
The free concentration in the cytosol (ci) and the submembrane space (cs) are in units of μM, whereas the total concentration in the SR and the JSR is scaled by a constant factor 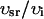 , so that cj is in units of μmol/l cytosol. All fluxes have been divided by the volume of the cytosol
, so that cj is in units of μmol/l cytosol. All fluxes have been divided by the volume of the cytosol 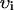 , and have units of μM/s. Thus, currents can be converted to amperes by multiplying by the factor 2
, and have units of μM/s. Thus, currents can be converted to amperes by multiplying by the factor 2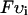 , where F is Faraday's constant. Also, the volume of the cytosol will be taken to be 10 times the volume of the submembrane space (
, where F is Faraday's constant. Also, the volume of the cytosol will be taken to be 10 times the volume of the submembrane space (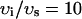 ). The parameters used in the model are given in Tables 1–4. It should be noted that the above equations do not mathematically forbid unphysiological draining of the SR, where cj becomes less than zero. However, for physiologically plausible parameters, such as the ones used in our simulations, cj is always positive.
). The parameters used in the model are given in Tables 1–4. It should be noted that the above equations do not mathematically forbid unphysiological draining of the SR, where cj becomes less than zero. However, for physiologically plausible parameters, such as the ones used in our simulations, cj is always positive.
TABLE 1.
Physical constants and ionic concentrations
| Parameter | Definition | Value |
|---|---|---|
| F | Faraday constant | 9.65 × 104 C/mol |
| R | Universal gas constant | 8.314J mol–1K–1 |
| T | Temperature | 308 K |
| Nao | External sodium concentration | 140 mM |
| Cao | External calcium concentration | 1.8 mM |
| υi | Cell volume | 10−4μl |
| υs | Submembrane volume | 0.1 vi |
TABLE 4.
SR release parameters
| Parameter | Definition | Value |
|---|---|---|
| g | Release current strength | 1.5 × 104 sparks/μM |
| u | Release slope | 11.3 s−1 |
| τr | Spark lifetime | 20 ms |
| τa | Relaxation time of 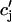 to cj to cj
|
50 ms |
| τs | Submembrane diffusion time constant | 10 ms |
The constant g will be taken to have units of sparks/μM, so that gICa gives the rate, in units of sparks/s, that sparks are recruited in the whole cell. The release function Q(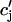 ) is taken to have the simple form
) is taken to have the simple form
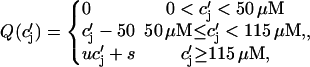 |
(13) |
where u is an adjustable constant, and where s is fixed by the condition that the release function is continuous. Here, the flux Q(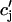 ) is expressed in units of 10−3 μM/s, which, for a typical JSR load of
) is expressed in units of 10−3 μM/s, which, for a typical JSR load of 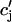 = 100 μM, yields a local release current of ∼1 pA, which is roughly the same as the experimental estimate of local release flux (Cheng et al., 1993). With the above choice of units we will use g = 1.5 × 104 sparks/μM. Thus, for a total calcium entry, during a 1-s cycle, of
= 100 μM, yields a local release current of ∼1 pA, which is roughly the same as the experimental estimate of local release flux (Cheng et al., 1993). With the above choice of units we will use g = 1.5 × 104 sparks/μM. Thus, for a total calcium entry, during a 1-s cycle, of 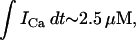 ∼4 × 104 sparks are recruited.
∼4 × 104 sparks are recruited.
The constant u is adjusted so that the fractional release is consistent with the experimental results of Bassani et al. (1995). The fractional release is defined as
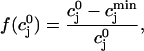 |
(14) |
where 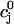 is the total SR concentration just before an AP upstroke, and where
is the total SR concentration just before an AP upstroke, and where 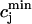 is the minimum total SR concentration shortly after the upstroke. To compute the fractional release, we clamp the voltage from Vmin = −80 mV to Vmax = 30 mV. Under these conditions, ICa quickly peaks and decays during which the SR concentration crosses a minimum value. By computing the minimum value
is the minimum total SR concentration shortly after the upstroke. To compute the fractional release, we clamp the voltage from Vmin = −80 mV to Vmax = 30 mV. Under these conditions, ICa quickly peaks and decays during which the SR concentration crosses a minimum value. By computing the minimum value 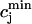 for various initial SR loads, we can compute the function f(
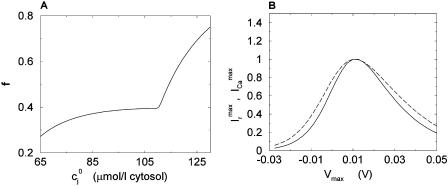
for various initial SR loads, we can compute the function f(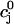 ). In Fig. 3 A we plot the fractional release f versus the initial SR load
). In Fig. 3 A we plot the fractional release f versus the initial SR load 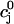 for the parameters given in Tables 1–4.
for the parameters given in Tables 1–4.
FIGURE 3.
(A) Fractional SR release f versus initial SR load 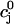 . For all points, the initial conditions are cs(0) = ci(0) = 0.1 μM, f(0) = 1, d(0) = 0, q(0) = 0.8, Ir(0) = 0 μM/s. (B) Relationship between peak ICa and peak SR flux. The solid line is
. For all points, the initial conditions are cs(0) = ci(0) = 0.1 μM, f(0) = 1, d(0) = 0, q(0) = 0.8, Ir(0) = 0 μM/s. (B) Relationship between peak ICa and peak SR flux. The solid line is 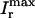 (Vmax), and the dashed line is
(Vmax), and the dashed line is 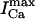 (Vmax). Both curves have been normalized to their peak values. The initial conditions are identical to those given above except that the initial total SR load is fixed at cj(0) = 100 μmol/l cytosol.
(Vmax). Both curves have been normalized to their peak values. The initial conditions are identical to those given above except that the initial total SR load is fixed at cj(0) = 100 μmol/l cytosol.
An important experimental observation that has to be incorporated into any model of EC coupling is graded release. In an important experiment, Wier et al. (1994) measured peak SR flux and peak ICa during depolarizations to various test potentials. In a similar manner, we held the membrane voltage at a V(t) of −80 mV, and depolarized to various test potentials (Vmax). As expected, and similar to Wier's results, peak ICa and peak Ir were bell shaped as a function of Vmax (Fig. 3 B), and peak SR flux was graded with respect to peak ICa. The parameters were adjusted to give a gain 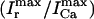 of ∼10 for Vmax in the range 0–30 mV (Wier et al., 1994).
of ∼10 for Vmax in the range 0–30 mV (Wier et al., 1994).
Voltage Clamp Pacing
Pacing protocol
In the experiment of Chudin et al. (1999), intracellular calcium transients were measured as the cell was paced with various AP clamps. The AP clamp used in that experiment can be modeled effectively using
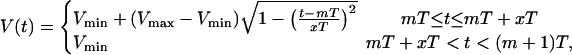 |
(15) |
where T is the period (pacing cycle length), x = APD/T, where APD denotes the action potential duration, and where m denotes the mth beat. The parameter x fixes the shape of the AP, and depends on the pacing period. The action potentials are fitted using Vmin = −80 mV and Vmax = 30 mV. The ratio x = APD/T was fitted to the experimental values using a function of the form
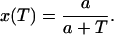 |
(16) |
In Fig. 4 A, we plot the experimental values for x as a function of T, as well as the values given by a fit with a = 2/3.
Intracellular sodium and the rise of the calcium transients
The average whole cell sodium concentration Nai depends on the amount of sodium injected into the cell during pacing, and so depends on the pacing period T. Since our model does not describe intracellular sodium dynamics, we introduce a function Nai(T), which gives the internal sodium concentration at steady state as a function of period T. Faber and Rudy (2000) have suggested that Nai increases from ∼10 mM to close to 15 mM, as the pacing period is decreased from 2 s to 100 ms. Hence, we model the intracellular sodium concentration using a simple function of the form
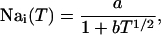 |
(17) |
where the constants a, b are chosen so that Nai(1 s) = 9.6 mM and Nai(.2 s) = 18.5 mM. In Fig. 4 B, we plot  and
and 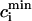 after steady state has been reached for the above set of parameters. On the same graph we include the experimental data of Chudin et al. (1999). As we can see, both quantities rise with decreasing period, as
after steady state has been reached for the above set of parameters. On the same graph we include the experimental data of Chudin et al. (1999). As we can see, both quantities rise with decreasing period, as 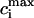 −
− 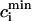 remains fairly constant. On the same graph we plot the same quantities when intracellular sodium concentration is kept constant at Nai = 10 mM. In this case there is only a small rise in
remains fairly constant. On the same graph we plot the same quantities when intracellular sodium concentration is kept constant at Nai = 10 mM. In this case there is only a small rise in 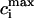 . Hence, in this model, the overall rise in calcium concentration during rapid pacing is primarily due to the accumulation of sodium in the cell.
. Hence, in this model, the overall rise in calcium concentration during rapid pacing is primarily due to the accumulation of sodium in the cell.
Calcium transients and currents during rapid pacing
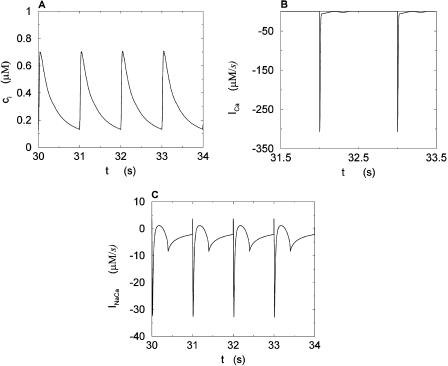
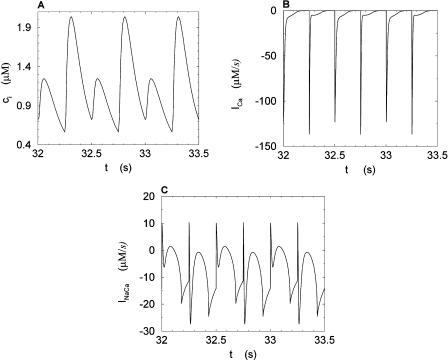
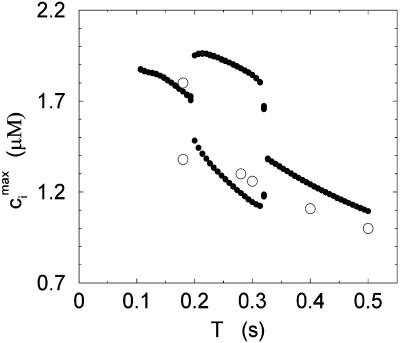
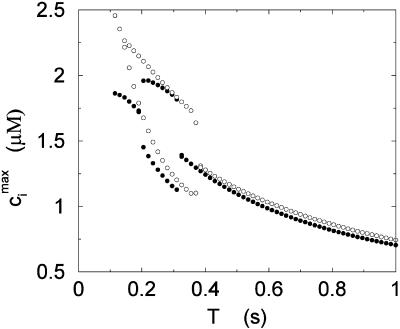
We studied the effects of pacing rate by pacing the calcium system with the clamped AP waveform at different cycle lengths (T). Results of pacing the model at a slow rate, with pacing cycle length of T = 1 s, and a fast rate, with cycle length T = 0.25 s, are shown in Figs. 5 and 6, respectively. Both sets of figures show the steady state values of ci, whole cell ICa, and the NaCa exchange current INaCa. The results of Fig. 6 show clearly that as the whole cell calcium transient alternates, so do the calcium-dependent currents. We explored the dynamics of the model more fully by calculating the peak calcium transient values at different pacing periods (Fig. 7). On the same graph, we plot the experimental data of Chudin et al. (1999). It is clear from the graph that as the period is decreased, the calcium system undergoes a period-doubling bifurcation, qualitatively similar to the experimental findings.
FIGURE 5.
Calcium transients and currents during steady state for a pacing period of T = 1 s. (A) Plot of ci versus t. (B) Plot of ICa versus t. (C) Plot of INaCa versus t.
FIGURE 6.
Calcium transients and currents during steady state for a pacing period of T = 0.250 s. (A) Plot of ci versus t. (B) Plot of ICa versus t. (C) Plot of INaCa versus t.
FIGURE 7.
Peak values of the bulk myoplasmic calcium concentration during steady state as a function of pacing period T at fast pacing rates. The open circles correspond to the experimental results of Chudin et al. (1999). The filled circles correspond to the model predictions.
ANALYSIS OF BEAT-TO-BEAT DYNAMICS
Map reduction with linear instantaneous buffering
To understand the nonlinear dynamics of the calcium system, it is useful to reduce the dynamics of the model ODEs to a system of discrete maps. Using this approach, it is possible to understand the dynamical instability that is responsible for calcium alternans. To make the analysis more tractable, we first focus on the simple case where all cytosolic calcium buffering is linear and instantaneous; in this case, β(cs) = βs, and β(ci) = βi, where βi and βs are constants. This simplification is introduced mainly because it allows us to derive a simple analytical condition for the onset of calcium alternans, which makes transparent the physiological mechanisms that underlie this phenomenon. In the section “Map reduction with instantaneous nonlinear buffering”, we then show that a more elaborate map derived with instantaneous, albeit nonlinear, buffering can yield predictions of calcium dynamics that are in reasonable quantitative agreement with the full model ODEs.
Recall that our basic model (Eqs. 10–12) consists of four variables that represent the average concentrations in the cytosol, ci(t); the submembrane space, cs(t); the JSR, 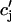 (t); and the SR, cj(t). Furthermore, let us define
(t); and the SR, cj(t). Furthermore, let us define 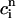 ≡ ci(nT),
≡ ci(nT), 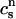 ≡ cs(nT),
≡ cs(nT),  ≡ cj(nT), and
≡ cj(nT), and 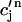 ≡
≡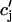 (nT), to be these concentrations at a time t = nT just before the nth AP upstroke. The abruptness of the AP upstroke makes this a natural choice of variables for the discrete map. A mapping between these concentrations at the nth and nth + 1 AP upstrokes can be constructed by integrating the model ODEs from time t = nT to time t = (n + 1)T. A major simplification is that the concentrations in the cytosol and the submembrane space are to a very good approximation equal before an AP upstroke (
(nT), to be these concentrations at a time t = nT just before the nth AP upstroke. The abruptness of the AP upstroke makes this a natural choice of variables for the discrete map. A mapping between these concentrations at the nth and nth + 1 AP upstrokes can be constructed by integrating the model ODEs from time t = nT to time t = (n + 1)T. A major simplification is that the concentrations in the cytosol and the submembrane space are to a very good approximation equal before an AP upstroke (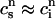 ) and only differ significantly from each other during the upstroke of the calcium transient. This is due to the fact that the volume of the submembrane space is much smaller than the volume of the cytosol
) and only differ significantly from each other during the upstroke of the calcium transient. This is due to the fact that the volume of the submembrane space is much smaller than the volume of the cytosol 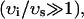 and hence cs relaxes quickly to ci. Hence, the two concentrations are essentially equal except when ci is rapidly varying. Similarly, the concentrations in the SR and in the JSR can be assumed to be equal just before an AP upstroke (
and hence cs relaxes quickly to ci. Hence, the two concentrations are essentially equal except when ci is rapidly varying. Similarly, the concentrations in the SR and in the JSR can be assumed to be equal just before an AP upstroke (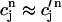 ) as long as the time for calcium to diffuse between these two compartments (τa ∼50 ms) is much smaller than the pacing interval
) as long as the time for calcium to diffuse between these two compartments (τa ∼50 ms) is much smaller than the pacing interval 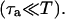 Using the fact that both
Using the fact that both 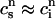 and
and 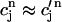 , it is straightforward to obtain from Eq. 10 the map
, it is straightforward to obtain from Eq. 10 the map
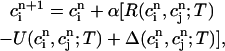 |
(18) |
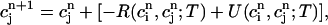 |
(19) |
where α = βi/(1 + βiυs/βsυi), and where we have defined the quantities
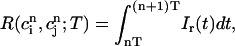 |
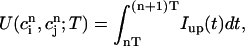 |
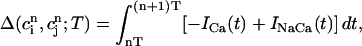 |
(20) |
which represent the total amount of calcium release (R) and uptake (U) in one beat as well as the net total amount of calcium (Δ) that enters the cell. Both R and U are always positive whereas Δ can be either positive or negative depending on whether the amount of calcium that enters the cell through the L-type channels is larger or smaller than the amount of calcium extruded from the cell by the NaCa exchange current in one beat. The currents that appear in the integrals above must be calculated by integrating the full set of ODEs (Eqs. 10–12) for the variables (cs(t), ci(t), cj(t), and 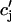 (t)) using as initial conditions cs(nT) = ci(nT) =
(t)) using as initial conditions cs(nT) = ci(nT) = 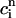 and cj(nT) =
and cj(nT) = 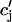 (nT) =
(nT) = 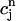 , and values of the gate variables d∞(nT) and f∞(nT) for ICa that are determined by the periodic clamped AP waveform.
, and values of the gate variables d∞(nT) and f∞(nT) for ICa that are determined by the periodic clamped AP waveform.
Calcium alternans
In the rest of this section, we further analyze this map to pinpoint the condition for the onset of alternans. The fixed point of the map 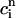 =
= 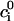 and
and 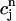 =
= 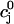 is defined by the conditions R = U and Δ = 0, which implies that at steady state the total uptake during one cycle should be equal to the total release, and the net total flux into the cell over one period should be zero.
is defined by the conditions R = U and Δ = 0, which implies that at steady state the total uptake during one cycle should be equal to the total release, and the net total flux into the cell over one period should be zero.
To obtain a simple analytical condition for the onset of alternans, we assume that the beat-to-beat variation of the net free calcium that enters the cell in one beat is much smaller than the variation of the total amount of calcium pumped into the SR (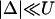 ). This limit is physiologically relevant since the total calcium uptake in one beat is typically 3–4 times larger than the amount of calcium extruded from the cell via the NaCa exchange current (except in diseased states such as heart failure where the uptake and extruded amounts can become comparable). In this limit, the total diastolic amount of calcium in the cell (i.e., including both the myoplasm and the SR) can be assumed to remain approximately constant from beat to beat, or
). This limit is physiologically relevant since the total calcium uptake in one beat is typically 3–4 times larger than the amount of calcium extruded from the cell via the NaCa exchange current (except in diseased states such as heart failure where the uptake and extruded amounts can become comparable). In this limit, the total diastolic amount of calcium in the cell (i.e., including both the myoplasm and the SR) can be assumed to remain approximately constant from beat to beat, or
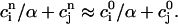 |
(21) |
The above relation allows us to reduce the system of two coupled maps Eqs. 18 and 19 to a single map. One last simplification comes from our numerical finding that the amount of calcium uptake is roughly proportional to the peak concentration of the calcium transient, which is the sum of the diastolic value of ci and the total amount released from the SR, or 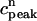 ≡
≡  + αR(
+ αR(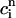 ,
, 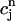 ). This proportionality relation can be written
). This proportionality relation can be written
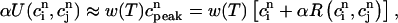 |
(22) |
where the proportionality constant w(T) is cycle length dependent and always less than unity owing to the fact that the amount of calcium uptake cannot exceed the peak calcium concentration. Combining the above, we obtain the one-dimensional map defined by Eq. 19 with U approximated using Eq. 22 and 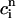 eliminated in favor of
eliminated in favor of 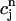 using Eq. 21. A condition for the onset of alternans can now be readily obtained by substituting
using Eq. 21. A condition for the onset of alternans can now be readily obtained by substituting 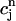 =
= 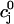 +
+ 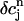 into the map, where
into the map, where 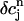 is a small perturbation around the periodic fixed point. Linearizing the map one obtains
is a small perturbation around the periodic fixed point. Linearizing the map one obtains 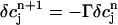 , where
, where
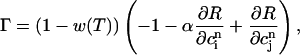 |
(23) |
and where the partial derivatives are evaluated at the fixed point. This fixed point undergoes a period doubling bifurcation when Γ = 1, and is unstable when Γ > 1.
The above analysis shows that calcium alternans under a clamped periodic AP waveform can arise from a sufficiently steep nonlinear dependence of calcium-release R on both SR load (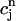 ) and diastolic calcium level (
) and diastolic calcium level (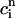 ), with the latter influencing the trigger for release via calcium-induced inactivation of the L-type calcium current. These concentration-dependent restitution properties of the calcium system have a similar destabilizing role as APD-restitution (i.e., dependence of APD on diastolic interval) has for electrical alternans. In particular, the condition Γ > 1 for the onset of calcium alternans is directly analogous to the condition APD-restitution-slope > 1 for the onset of electrical alternans (Nolasco and Dahlen, 1968). Of course, predicting the onset of either calcium or electrical alternans in the more complex case where the AP is unclamped requires a careful consideration of the bidirectional coupling between the voltage and calcium systems.
), with the latter influencing the trigger for release via calcium-induced inactivation of the L-type calcium current. These concentration-dependent restitution properties of the calcium system have a similar destabilizing role as APD-restitution (i.e., dependence of APD on diastolic interval) has for electrical alternans. In particular, the condition Γ > 1 for the onset of calcium alternans is directly analogous to the condition APD-restitution-slope > 1 for the onset of electrical alternans (Nolasco and Dahlen, 1968). Of course, predicting the onset of either calcium or electrical alternans in the more complex case where the AP is unclamped requires a careful consideration of the bidirectional coupling between the voltage and calcium systems.
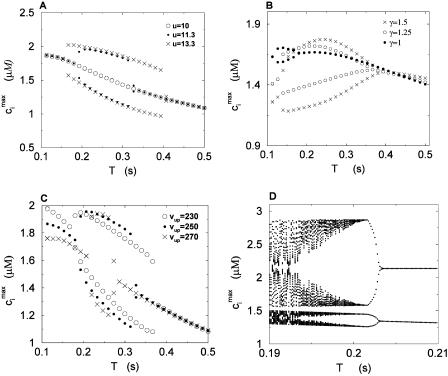
To test the predictions of the stability condition given by Eq. 23 against the full model equations, we study how the onset of alternans depends on various model parameters. The condition for the onset of alternans, given by Eq. 23, predicts that at a given cycle length, an increase in the slope of the SR load dependence of release should promote alternans. In Fig. 8 A, we plot 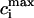 versus T for various values of the release slope u. Recall that u is the slope of the steep part of the release function given in Eq. 13. From the graph, it is clear that the onset of the period doubling bifurcation is sensitive to the release slope u. As u is increased, the period-doubling bifurcation occurs at higher values of T, and the degree of alternans become more pronounced.
versus T for various values of the release slope u. Recall that u is the slope of the steep part of the release function given in Eq. 13. From the graph, it is clear that the onset of the period doubling bifurcation is sensitive to the release slope u. As u is increased, the period-doubling bifurcation occurs at higher values of T, and the degree of alternans become more pronounced.
FIGURE 8.
Peak values of bulk myoplasmic calcium concentration during steady state pacing as predicted by the model ODEs. (A) Peak calcium concentrations for different values of the release slope u. In all cases we fix γ = 1. (B) Peak calcium concentrations for different values of the parameter γ. In all cases the release slope is fixed at u = 11.3 s–1, and τq = 30 ms. (C) Peak calcium concentrations for different values of the strength of the uptake current vup. Here, we fix γ = 1 and u = 11.3 s−1. (D) Peak calcium concentrations for large release slope (u = 43.3 s–1).
A further prediction of Eq. 23 is that the onset of alternans should also depend on the functional relationship between the release and the diastolic calcium level 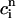 . This functional dependence is primarily due to the calcium-induced inactivation of the L-type calcium channel, i.e., larger diastolic calcium should yield less release. Thus, by varying the steepness of calcium-induced inactivation, which is controlled by the parameter γ, it is possible to probe the effect on dynamics of a steeper
. This functional dependence is primarily due to the calcium-induced inactivation of the L-type calcium channel, i.e., larger diastolic calcium should yield less release. Thus, by varying the steepness of calcium-induced inactivation, which is controlled by the parameter γ, it is possible to probe the effect on dynamics of a steeper 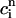 dependence of release. In Fig. 8 B, we plot
dependence of release. In Fig. 8 B, we plot 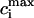 versus T for different exponents γ, while keeping the load dependence of release fixed. From the graph, it is clear that the period of onset and the magnitude of alternans increases with increasing γ. This shows clearly that the dynamical behavior of the model depends crucially on the calcium-induced inactivation of the L-type current.
versus T for different exponents γ, while keeping the load dependence of release fixed. From the graph, it is clear that the period of onset and the magnitude of alternans increases with increasing γ. This shows clearly that the dynamical behavior of the model depends crucially on the calcium-induced inactivation of the L-type current.
The stability condition given by Eq. 23 also reveals that the onset of alternans depends on the strength of the uptake current. The prediction is that a larger uptake current (i.e., larger w(T)) should actually stabilize the periodic fixed point, since Γ decreases with increasing w(T). To check this prediction in the model, in Fig. 8 C we plot the bifurcation diagram for different values of the strength of the uptake current (υup). From the plot, we see that decreasing the strength of the uptake current increases the period at which alternans occurs, which is consistent with the predictions of the stability analysis.
Finally, in Fig. 8 D, we plot the bifurcation diagram for the case when the release slope (u) is very large. Here, we find that the calcium system can undergo a transition to more complex dynamical behavior as the period is decreased. In this particular case, we observe a transition from a period 2 to a period 4, and then a subsequent transition to chaotic (aperiodic) dynamics.
Map reduction with instantaneous nonlinear buffering
Here, we only make the approximation that buffering to troponin C is instantaneous. This approximation is valid since the binding kinetics of troponin C to calcium ions occurs on a time scale of ∼30 ms, which is fast compared to the movement of calcium ions in the cytosol. Thus, buffering to troponin C can be accounted for by simply adding a term BTKT/(ci + KT)2, with KT = 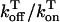 , inside the square brackets of Eq. 34 in Appendix C. In this way the time-dependent kinetics of calcium binding to troponin C can be eliminated from Eqs. 10. Applying the approximations discussed in the section “Map reduction with linear instantaneous buffering”, (cs(nT) ≈
, inside the square brackets of Eq. 34 in Appendix C. In this way the time-dependent kinetics of calcium binding to troponin C can be eliminated from Eqs. 10. Applying the approximations discussed in the section “Map reduction with linear instantaneous buffering”, (cs(nT) ≈ 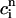 ,
, 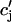 (nT) ≈
(nT) ≈ 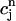 , f(nT) ≈ f∞(V(nT)), q(nT) ≈ q∞(
, f(nT) ≈ f∞(V(nT)), q(nT) ≈ q∞(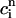 ))), all dynamical variables at times t = nT can be uniquely defined by the concentrations
))), all dynamical variables at times t = nT can be uniquely defined by the concentrations 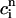 and
and 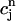 . Thus, integrating the model ODEs from t = nT to t = (n + 1)T defines a unique two-variable mapping
. Thus, integrating the model ODEs from t = nT to t = (n + 1)T defines a unique two-variable mapping 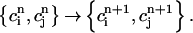
In Fig. 9, we compare the steady-state peak calcium concentration (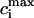 ) versus pacing cycle length (T) obtained with the map and the full model ODEs. The map predicts reasonably well the amplitude of alternans and their existence over a finite range of cycle lengths. It should be noted that the quantitative discrepancy between the map and ODE results is more pronounced for short cycle lengths. This is because the map derivation is based on the assumption that there is sufficient time for the dynamical variables of the ODEs to relax to values that are defined by
) versus pacing cycle length (T) obtained with the map and the full model ODEs. The map predicts reasonably well the amplitude of alternans and their existence over a finite range of cycle lengths. It should be noted that the quantitative discrepancy between the map and ODE results is more pronounced for short cycle lengths. This is because the map derivation is based on the assumption that there is sufficient time for the dynamical variables of the ODEs to relax to values that are defined by  ,
,  , and f∞(V(nT)), just before an AP upstroke. This assumption loses progressively its validity as the pacing cycle decreases. For instance, we assumed that
, and f∞(V(nT)), just before an AP upstroke. This assumption loses progressively its validity as the pacing cycle decreases. For instance, we assumed that 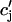 (nT) ≈
(nT) ≈ 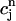 . However, in the model ODEs, the time constant of the exponential relaxation of
. However, in the model ODEs, the time constant of the exponential relaxation of 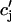 (t) to
(t) to 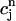 is 50 ms. Thus, for cycle lengths in the range of 100–200 ms,
is 50 ms. Thus, for cycle lengths in the range of 100–200 ms, 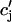 (t) lacks sufficient time to fully relax to
(t) lacks sufficient time to fully relax to 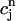 before the next AP upstroke.
before the next AP upstroke.
FIGURE 9.
Peak values of the bulk myoplasmic calcium concentration during steady-state pacing. The filled circles correspond to values predicted by the model ODEs. The open circles are found using the two-dimensional map described in the section “Map reduction with instantaneous nonlinear buffering”.
Chaotic dynamics
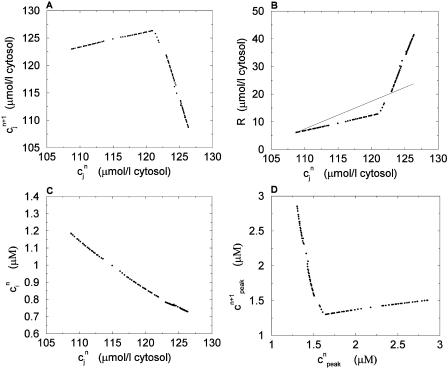
In this section, we analyze in more detail the chaotic dynamics observed in Fig. 8 D. For this, we first plot in Fig. 10A 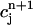 versus
versus 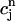 for the same parameters as in Fig. 8 D and for a pacing cycle length where chaotic dynamics is observed (T = 0.19 s). The plot shows that the chaotic attractor can be characterized to a good approximation by a one-dimensional map of
for the same parameters as in Fig. 8 D and for a pacing cycle length where chaotic dynamics is observed (T = 0.19 s). The plot shows that the chaotic attractor can be characterized to a good approximation by a one-dimensional map of 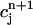 as a function of
as a function of 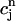 . The one-dimensional character of this map is due to the fact that the net calcium entry into the cell via ICa and INaCa is small in comparison to the total amount of calcium that cycles through the SR in one beat. Therefore, as in our previous analysis of the stability of alternans, we can assume that the total calcium level inside the cell remains constant. Hence, we can use Eq. 21,
. The one-dimensional character of this map is due to the fact that the net calcium entry into the cell via ICa and INaCa is small in comparison to the total amount of calcium that cycles through the SR in one beat. Therefore, as in our previous analysis of the stability of alternans, we can assume that the total calcium level inside the cell remains constant. Hence, we can use Eq. 21, 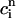 /α +
/α + 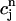 = ctotal, where ctotal is the constant total concentration in the cell, to reduce the two-dimensional map to a one-dimensional map. Substituting this relation into Eq. 19 and making use of Eq. 22 to approximate the uptake with a constant factor w that only depends on period, we find that the diastolic SR load
= ctotal, where ctotal is the constant total concentration in the cell, to reduce the two-dimensional map to a one-dimensional map. Substituting this relation into Eq. 19 and making use of Eq. 22 to approximate the uptake with a constant factor w that only depends on period, we find that the diastolic SR load  satisfies the one-dimensional map
satisfies the one-dimensional map  = F(
= F( ), where
), where
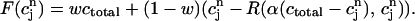 |
(24) |
Next, we make use of the well-known result that one-dimensional maps that exhibit chaos must be nonmonotonic, i.e., must have at least one extremum (Ott, 1993). Thus, the presence of chaos in the present model implies that the map 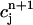 = F(
= F(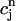 ) should have this property, meaning that the derivative dF/
) should have this property, meaning that the derivative dF/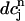 should change sign over a range of
should change sign over a range of 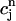 . It follows trivially from Eq. 24 that this condition is equivalent to
. It follows trivially from Eq. 24 that this condition is equivalent to
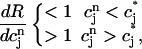 |
(25) |
where 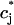 corresponds to a local maximum of F. Therefore, if the total derivative dR/
corresponds to a local maximum of F. Therefore, if the total derivative dR/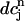 increases rapidly over some range of load, the above condition can be satisfied. To test whether this condition is satisfied directly from the ODEs of the model, we calculate R ≈
increases rapidly over some range of load, the above condition can be satisfied. To test whether this condition is satisfied directly from the ODEs of the model, we calculate R ≈ 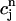 −
− 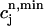 versus
versus 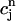 , where
, where 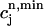 is the minimum SR concentration between times nT and (n + 1)T. The result, which is shown in Fig. 10 B, shows that the slope of R changes from dR/
is the minimum SR concentration between times nT and (n + 1)T. The result, which is shown in Fig. 10 B, shows that the slope of R changes from dR/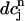 < 1 to dR/
< 1 to dR/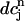 > 1 over the range of SR loads explored by the chaotic trajectory. For the same trajectory, we also check that the conservation condition given by Eq. 21 holds, by plotting, in Fig. 10 C,
> 1 over the range of SR loads explored by the chaotic trajectory. For the same trajectory, we also check that the conservation condition given by Eq. 21 holds, by plotting, in Fig. 10 C, 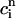 versus
versus 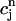 . From the plot, we see that
. From the plot, we see that 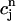 is an approximately linear function of
is an approximately linear function of 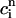 , which confirms our assumption that
, which confirms our assumption that 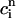 can be eliminated in favor of
can be eliminated in favor of 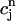 using Eq. 21, and that the dynamical system can be reduced to a one-dimensional discrete map.
using Eq. 21, and that the dynamical system can be reduced to a one-dimensional discrete map.
FIGURE 10.
Plot of the beat-to-beat calcium concentrations during a chaotic calcium transient that is generated using the model ODEs. The parameters are the same as those used in Fig. 8 D with T = 0.19 s. (A) Plot of 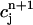 versus
versus 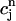 . (B) Plot of the release R versus initial SR load
. (B) Plot of the release R versus initial SR load 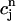 . The straight line corresponds to a line with slope 1. (C) Plot of
. The straight line corresponds to a line with slope 1. (C) Plot of 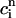 versus
versus 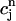 . (D) Plot of peak calcium transients
. (D) Plot of peak calcium transients 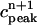 versus
versus 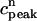 .
.
It is important to emphasize that the total derivative 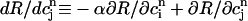 depends both on the steepness of the relations between release and load, and release and diastolic calcium, which is a consequence calcium-induced inactivation of ICa. Hence, the degree of nonlinearity of both relations contribute to the existence of a maximum in the map independent of the strength of the uptake current w. In contrast, the condition for instability (dF/dcj ≥ 1 or, equivalently, Eq. 23) depends on both the steepness of these relations and the strength of uptake. Finally, since the SR concentration is difficult to measure experimentally, we also plot, in Fig. 10 D, the peak cytosolic calcium concentration at one beat versus the next i.e.,
depends both on the steepness of the relations between release and load, and release and diastolic calcium, which is a consequence calcium-induced inactivation of ICa. Hence, the degree of nonlinearity of both relations contribute to the existence of a maximum in the map independent of the strength of the uptake current w. In contrast, the condition for instability (dF/dcj ≥ 1 or, equivalently, Eq. 23) depends on both the steepness of these relations and the strength of uptake. Finally, since the SR concentration is difficult to measure experimentally, we also plot, in Fig. 10 D, the peak cytosolic calcium concentration at one beat versus the next i.e., 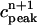 versus
versus 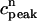 . Here, we find again a nonmonotonic relationship, which is a direct consequence of the condition given in Eq. 25.
. Here, we find again a nonmonotonic relationship, which is a direct consequence of the condition given in Eq. 25.
Role of JSR-SR diffusional relaxation
In this section, we analyze in more detail the role of the JSR-SR relaxation time (τa) on the model behavior. Since there are no experimental measurements of this quantity, we have evaluated the model properties for a wide range of relaxation times (1–100 ms). The primary effect of the relaxation time is to simply change the amount of calcium released from the SR. During release, the SR is drained by the current Ir that depends on the concentration of unrecruited JSR compartments (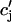 ). However, the average concentration of unrecruited JSR compartments is higher than the average concentration in the SR, i.e.,
). However, the average concentration of unrecruited JSR compartments is higher than the average concentration in the SR, i.e., 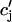 > cj, since these JSR compartments have not been depleted, and are simply relaxing to the average concentration in the SR. Given that Q(
> cj, since these JSR compartments have not been depleted, and are simply relaxing to the average concentration in the SR. Given that Q(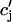 ) is a monotonically increasing function, then a longer delay time will allow more calcium to be drained from the SR since
) is a monotonically increasing function, then a longer delay time will allow more calcium to be drained from the SR since 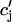 can remain large for a longer time. In Fig. 11, we plot the maximum change in total SR concentration for different initial SR loads (
can remain large for a longer time. In Fig. 11, we plot the maximum change in total SR concentration for different initial SR loads (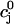 ), and for a relaxation time of 100 ms and 1 ms. It is clear that more calcium is released, for all initial JSR loads, when the relaxation time is large as opposed to when it is small.
), and for a relaxation time of 100 ms and 1 ms. It is clear that more calcium is released, for all initial JSR loads, when the relaxation time is large as opposed to when it is small.
FIGURE 11.
Dependence of the maximum change of total SR calcium concentration on the initial SR load. The dashed line corresponds to a JSR-SR relaxation time of τa = 100 ms, and the solid line corresponds to τa = 1 ms.
Role of spark lifetime
In the remainder of this section, we explore in more detail the dependence of the nonlinearity responsible for calcium alternans on the physiological parameters of the model. In particular, we will focus on the role played by the spark lifetime (τr). Here, we will analyze the simplest case when ICa depends only on time, and where the relaxation time between 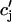 and cj is instantaneous. In this case the release from the SR is given by R ≈
and cj is instantaneous. In this case the release from the SR is given by R ≈ 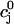 −
− 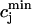 , where
, where 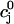 is the concentration before ICa is turned on, and where
is the concentration before ICa is turned on, and where 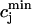 is the minimum concentration in the SR. Also, since we have eliminated the calcium dependence of ICa, the condition for an unstable fixed point can be written as R′ = ∂R/∂cj > 1 + 1/(1 – w(T)), where the partial derivative is evaluated at
is the minimum concentration in the SR. Also, since we have eliminated the calcium dependence of ICa, the condition for an unstable fixed point can be written as R′ = ∂R/∂cj > 1 + 1/(1 – w(T)), where the partial derivative is evaluated at 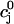 . Since ICa peaks rapidly and decays in a time τm ∼ 30 ms, then most of the release occurs during the time τm. Thus, during the time interval τm after ICa is turned on we can write
. Since ICa peaks rapidly and decays in a time τm ∼ 30 ms, then most of the release occurs during the time τm. Thus, during the time interval τm after ICa is turned on we can write
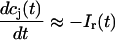 |
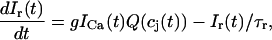 |
(26) |
where we have dropped the uptake current since it is small compared to Ir(t). To explore the dependence of the load dependent nonlinearity on the spark lifetime, we study the behavior of R′ for a range of τr while keeping z = gτr fixed. In Fig. 12 we plot the maximum slope  versus τr for a range of z values. The important feature of the plots is that
versus τr for a range of z values. The important feature of the plots is that  as
as 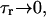 regardless of the value of z. Thus, in this case, a nonzero spark lifetime is essential to destabilize the periodic fixed point, which cannot occur if
regardless of the value of z. Thus, in this case, a nonzero spark lifetime is essential to destabilize the periodic fixed point, which cannot occur if  < 2. This result can be understood analytically by studying Eqs. 26 in the limit
< 2. This result can be understood analytically by studying Eqs. 26 in the limit  In this limit the dynamics of cj is described by
In this limit the dynamics of cj is described by
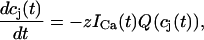 |
(27) |
which is exactly solvable for a given release function Q(x). Furthermore, it can be shown that if Q(x) is any monotonically increasing function, then 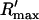 ≤ 1. This result suggests that constructing a model with a steep load dependence that can destabilize the periodic fixed point requires that the release flux at a given time depends on the SR concentration at earlier times. If the release flux depends only on the instantaneous SR concentration, then the periodic fixed point is always stable. Thus, in the model formulation, the finite spark lifetime plays an important role in the dynamical behavior of the model.
≤ 1. This result suggests that constructing a model with a steep load dependence that can destabilize the periodic fixed point requires that the release flux at a given time depends on the SR concentration at earlier times. If the release flux depends only on the instantaneous SR concentration, then the periodic fixed point is always stable. Thus, in the model formulation, the finite spark lifetime plays an important role in the dynamical behavior of the model.
FIGURE 12.
Plot of 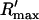 versus spark lifetime τr for different values of the parameter z.
versus spark lifetime τr for different values of the parameter z.
DISCUSSION
An important feature of the model is that the local release flux during a calcium spark is treated phenomenologically using an exponentially decaying time course, with a JSR load-dependent amplitude and a fixed decay time constant. The phenomenological model relies only on two essential properties of the local calcium dynamics. First, a strong dependence of the local release flux on the initial JSR concentration, and secondly, a finite lifetime of local release. The former is an immediate consequence of the regenerative nature of CICR, and the latter depends on the presence of a strong negative feedback mechanism that shuts off release. Thus, the model does not rely on a detailed spark termination mechanism, which still has not been established experimentally. An additional advantage of our approach is that we are able to incorporate into the model experimental measurements of the SR load dependence of release in the whole cell. This is a crucial input into the model, as the steep dependence of whole cell release on SR load has a profound impact on the dynamical behavior. Thus, the model construction takes into account both local properties of experimentally observed calcium sparks, and whole cell measurements of calcium release.
Another important property of the model is that it is able to reproduce the calcium alternans observed by Chudin et al. (1999), when it is paced by a clamped AP waveform that is fitted directly to that used in the experiment. At high pacing rates, calcium accumulates in the cell, and the corresponding increase in SR load and diastolic calcium levels promote a dynamical instability. Furthermore, by reducing the dynamics to a two-variable map, we have shown that the dynamical stability of the calcium system is determined by the functional dependence of the total release (R) on both the SR concentration and the diastolic concentration just before an AP upstroke. To our knowledge, only a steep dependence of total release on SR load has been considered previously as a possible mechanism for calcium transient alternans (Adler et al., 1985; Eisner et al., 2000). The present model shows that the dependence of release on diastolic calcium is also a possible destabilizing mechanism that can act in conjunction with or independently from the dependence of release on SR load. The physiological origin of the dependence of release on diastolic calcium is the calcium-induced inactivation of the L-type calcium current, i.e., a higher diastolic calcium leads to a reduced entry of calcium into the cell and hence to a smaller release.
The nonlinear dependence of release on SR load and diastolic calcium can be viewed as concentration-dependent restitution properties of the calcium system. This view point is analogous to that of electrical restitution, which gives a simplified description of the voltage dynamics by relating the diastolic interval at one beat to the APD at the next. In particular, the stability of the calcium system is determined by the quantity Γ, defined in Eq. 23, in much the same way that the stability of the voltage dynamics is determined by the slope of the electrical restitution curve.
At high pacing rates, and if the SR load dependence of release is made very steep, the calcium system can exhibit chaotic behavior under a periodic voltage clamp. This result can be understood by reducing the dynamics of calcium cycling to a one-dimensional discrete map that is nonmonotonic, and hence can in principle exhibit chaos. In the past, chaotic dynamics has been observed in unclamped voltage measurements in ventricular tissue (Watanabe et al., 1995). In that case, the chaotic voltage dynamics was attributed to a biphasic (nonmonotonic) electrical restitution function. An alternate explanation is that since voltage is coupled to calcium, a chaotic dynamics of calcium cycling can lead to a corresponding chaotic behavior of voltage. Thus, even when the electrical restitution function is stable (slope <1) and monotonic, the coupling between voltage and calcium can lead to unstable voltage dynamics.
In the past, unstable voltage dynamics at the cellular level has been linked to arrhythmias at the level of the whole heart (Chialvo et al., 1990; Garfinkel et al., 1992). Thus, calcium cycling, by having a destabilizing effect on voltage, may promote arrhythmias in the heart. To address this possibility, it is crucial to understand the bidirectional coupling between voltage and calcium under unclamped conditions at a wide range of pacing rates. Moreover, it is crucial to investigate not only the dynamics at the cellular scale but also at the tissue scale. The computational tractability of the phenomenological model presented here should serve as a useful computational tool to begin to address these problems. More detailed mechanistic models of calcium cycling, which attempt to model calcium dynamics at the dyadic junction level, are still far too computationally costly to be useful in this regard. For instance, the most recent computational model of Greenstein and Winslow (2002), requires a run time of ∼40 min on 10 parallel SGI Power Challenge R10,000 processors to simulate a whole cell calcium transient over a 1 s interval. On the other hand, the model ODEs presented here require ∼0.1 s of run time on a single Compaq Alpha EV6.7 667MHz processor, for a simulation over the same time interval. This computational speedup of roughly five orders of magnitude is crucial to begin to investigate, via numerical simulation, the possible link between abnormalities in calcium cycling at the cellular scale and arrhythmias in the whole heart.
The steep load dependence of release, which plays a crucial role in the dynamical instability, is consistent with the experimental work of Bassani et al. (1995). There are several possible reasons why release should increase steeply with SR load at high loads. One interesting possibility is that increasing the SR load may induce regenerative release between neighboring dyads. In other words, at high load, a “spark” may be due to clusters of dyads (macrosparks), rather than a single dyad. As the SR load is increased further, these clusters will grow, and the amount released may increase rapidly with small changes in SR load. This hypothesis is supported by the fact that increasing SR load even slightly more than cj ∼ 100 μmol/l cytosol leads to spontaneous release (Bassani et al., 1995). Thus, the CICR induced cooperativity between neighboring dyads may underlie the nonlinear behavior of release at the whole cell level. To clarify further, it should be noted that this nonlinear load dependence does not describe an arbitrarily defined spontaneous release process, but rather, reflects an inherent instability of the release mechanism.
An important question to consider is whether the JSR-SR relaxation time can be the primary mechanism that underlies calcium alternans at high pacing rates. Based on the available experimental data on calcium alternans, we will argue that this is unlikely to be the case. First, calcium alternans, when induced under rapid pacing, typically occur around cycle lengths of 200 ms. However, the relaxation time between 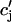 and cj is at most 100 ms, and so there is more than enough time for the JSR to relax to the SR concentration at the rates when calcium alternans are observed. An even stronger argument can be made by noting that alternans can be induced at normal pacing rates (T ∼ 1 s) by application of various external agents such as tetracaine (Diaz et al., 2002). These external agents are known to have a direct effect on the RyR channels, and are unlikely to change the mobility of calcium inside the SR. Moreover, we find in our model simulations that over a wide range of relaxation times (τa), the dynamics of the calcium system does not exhibit alternans at high rates unless a steep load dependence and calcium-induced inactivation is invoked. These findings suggest that the mechanism that underlies alternans is crucially dependent on the RyR release mechanism rather than the JSR-SR relaxation time.
and cj is at most 100 ms, and so there is more than enough time for the JSR to relax to the SR concentration at the rates when calcium alternans are observed. An even stronger argument can be made by noting that alternans can be induced at normal pacing rates (T ∼ 1 s) by application of various external agents such as tetracaine (Diaz et al., 2002). These external agents are known to have a direct effect on the RyR channels, and are unlikely to change the mobility of calcium inside the SR. Moreover, we find in our model simulations that over a wide range of relaxation times (τa), the dynamics of the calcium system does not exhibit alternans at high rates unless a steep load dependence and calcium-induced inactivation is invoked. These findings suggest that the mechanism that underlies alternans is crucially dependent on the RyR release mechanism rather than the JSR-SR relaxation time.
Another possible physiological mechanism that may underlie alternans is nonlinear buffering. The mathematical analysis presented in the section “Map reduction with linear instantaneous buffering” assumed for simplicity linear buffering. Therefore, this analysis does not address the dynamical role of nonlinear buffering. In our model simulations, we find that nonlinear buffering in the cytosol cannot induce alternans without a corresponding steep dependence of release on SR load or on diastolic calcium. However, the onset and amplitude of alternans does depend on the nonlinear buffering kinetics. These results suggest that, with realistic experimentally derived parameters, nonlinear buffering influences, but is not solely responsible for, calcium alternans.
The rise in calcium at high rates depends primarily on the corresponding accumulation of sodium, due to the activity of the NaCa exchange current (Harrison and Boyett, 1995). As the sodium concentration in the cell rises, the Nernst equilibrium potential of the exchange current is shifted such that calcium influx is favored. Another mechanism that promotes calcium loading at high rates is that the AP waveform spends more time per period at plateau potentials, and so the time spent in the calcium efflux mode is reduced. However, we found in our simulations that this effect alone, keeping intracellular sodium fixed, is not enough to account for the large increase of 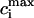 at high rates. Thus, our results suggest that sodium accumulation is essential for calcium loading at high rates, and is probably what underlies the positive force frequency relation that is observed in ventricular myocytes.
at high rates. Thus, our results suggest that sodium accumulation is essential for calcium loading at high rates, and is probably what underlies the positive force frequency relation that is observed in ventricular myocytes.
CONCLUSIONS
In summary, we have presented a physiologically motivated model of calcium cycling under AP clamp conditions. A key feature of this model is to represent the release of calcium from the SR as a sum of spatially localized events that correspond to calcium sparks. The rate at which sparks are recruited is assumed to be directly proportional to the whole cell L-type calcium current (ICa). This assumption is consistent with experiments of simultaneous measurements of spark occurrence and whole cell ICa (Collier et al., 1999). Moreover, this choice naturally yields graded release, consistent with Stern's local control hypothesis (Stern, 1992). An important advantage of this model is that it incorporates known constitutive relationships between experimentally measurable quantities such as fractional release and SR load. Furthermore, it is computationally tractable, and can be used to explore the dynamical behavior of the calcium system under a wide range of pacing rates. At high rates, the model is able to reproduce sustained calcium alternans, consistent with experimental observations (Chudin et al., 1999).
By reducing the dynamics to a two-variable map of the concentrations from one beat to the next, we were able to analyze the nonlinear dynamics of the calcium system in more detail. This analysis revealed that the dynamical instability that underlies calcium alternans is due to the functional dependence of release on both the SR load and the diastolic calcium concentration. We also find that under plausible physiological conditions, the calcium system can exhibit chaos when it is driven by a periodic AP clamp. By further simplifying the discrete map to one variable, we show that the chaotic dynamics can be traced to a nonmonotonic functional relationship between the peak calcium concentration at one beat versus that at the previous beat.
Furthermore, we found that the degree of nonlinearity is sensitive to physiologically measurable quantities such as the spark lifetime and the strength of the uptake current. Hence, the model not only sheds light on the dynamical behavior of the calcium system, but also gives insight on how physiological properties of the calcium cycling machinery influence the dynamics. An interesting future prospect is to pace this model under unclamped conditions to explore the full range of dynamical behavior of the coupled voltage and calcium systems.
TABLE 2.
L-type channel parameters
| Parameter | Definition | Value |
|---|---|---|
| PCa | Constant defined in Luo-Rudy II model | 5.4 × 10−4 cm/s |
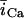 |
Adjustable proportionality constant | 25 μmol C–1 cm–1 |
| τf | Voltage dependent inactivation gate constant | 30 ms |
| ko | Transition rate to open state | 8 s–1 |
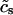 |
Calcium inactivation threshold | 0.5 μM |
TABLE 3.
Exchanger and uptake parameters
| Parameter | Definition | Value |
|---|---|---|
| cup | Uptake threshold | 0.5 μM |
| υup | Uptake strength | 250 μM/s |
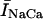 |
Adjustable strength of exchanger | 2 × 104μM/s |
| ksat | Luo-Rudy II constant | 0.1 |
| ξ | Luo-Rudy II constant | 0.35 |
| Km,Na | Luo-Rudy II constant | 87.5 mM |
| Km,Ca | Luo-Rudy II constant | 1.38 mM |
Acknowledgments
The authors acknowledge Professor Godfrey L. Smith, Glasgow University, for reading the manuscript and providing helpful comments. We also thank the referees for several helpful suggestions.
This research was supported in part by National Institutes of Health Special Centers of Research in Sudden Cardiac Death P50-HL52319, and by the Kawata and Laubisch endowments.
APPENDIX A: MODEL OF LOCAL DYNAMICS
In this appendix, we describe a simplified model of calcium dynamics within the dyadic junction. The goal here is to test the assumptions behind our phenomenological description of local calcium release during a spark (Eq. 4), using a plausible model of the local calcium dynamics. The relevant dynamical variables are the free concentration in the local dyadic space cp, and the free concentration 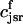 of the local JSR. Here, we have dropped the superscript k, since there is no need to distinguish between different dyadic junctions. We will assume constant linear buffering so that
of the local JSR. Here, we have dropped the superscript k, since there is no need to distinguish between different dyadic junctions. We will assume constant linear buffering so that 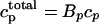 and
and 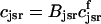 , where Bp and Bjsr are constants. Here, Bjsr will be chosen so that the free JSR concentration before release will be in the range 500–1500 μM.
, where Bp and Bjsr are constants. Here, Bjsr will be chosen so that the free JSR concentration before release will be in the range 500–1500 μM.
The free concentrations obey the ODEs
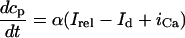 |
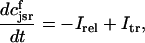 |
(28) |
where Irel is the flux of calcium from the JSR, Id is the diffusion of calcium into the submembrane space, iCa is the current from the local L-type channels, and Itr is the diffusion of calcium from the NSR into the JSR. Here, α = Bjsrυjsr/Bpυp, where υp and υjsr are the volumes of the dyadic space and JSR, respectively. The release current is given by Irel = gsa(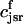 – cp), with gs a constant that denotes the maximum conductance of the RyR cluster, and where a is the open probability. To simulate CICR, the states of the RyR cluster are modeled using a simple reaction scheme, where the transition rate from closed to open states is proportional to the square of cp. This yields da/dt = (a∞ − a)/τa, with a∞ =
– cp), with gs a constant that denotes the maximum conductance of the RyR cluster, and where a is the open probability. To simulate CICR, the states of the RyR cluster are modeled using a simple reaction scheme, where the transition rate from closed to open states is proportional to the square of cp. This yields da/dt = (a∞ − a)/τa, with a∞ = 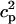 /(
/(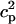 +
+ 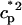 ) and τa = 1/(kd(
) and τa = 1/(kd(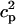 +
+ 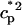 )), where kd is the deactivation rate. The threshold for regenerative release is determined by the concentration
)), where kd is the deactivation rate. The threshold for regenerative release is determined by the concentration 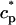 . Given the small volume of the dyadic space, a brief opening of the L-type channels is sufficient to raise cp to levels much higher than in the myoplasm. Thus, to ensure that regenerative release can only be initiated by the local L-type channels, and not by a rise of calcium in the submembrane space, it is crucial that the threshold
. Given the small volume of the dyadic space, a brief opening of the L-type channels is sufficient to raise cp to levels much higher than in the myoplasm. Thus, to ensure that regenerative release can only be initiated by the local L-type channels, and not by a rise of calcium in the submembrane space, it is crucial that the threshold 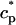 is larger than the peak concentration in the submembrane space (∼10 μM). Thus, in this model we will use a high threshold
is larger than the peak concentration in the submembrane space (∼10 μM). Thus, in this model we will use a high threshold 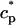 = 65 μM, which is further supported by the fact that, under normal conditions, release from a dyadic junction typically does not trigger release from neighboring junctions.
= 65 μM, which is further supported by the fact that, under normal conditions, release from a dyadic junction typically does not trigger release from neighboring junctions.
The diffusion of calcium away from the dyadic space is modeled using Id = (cp − cs)/τp, where τp is chosen so that cp relaxes to cs in 0.05 ms, which is roughly the same as the time for a calcium ion to diffuse across the 100 nm dyadic cleft. Also, we model diffusion between the NSR and JSR with Itr = (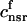 −
− 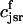 )/τtr, where
)/τtr, where 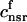 is the free concentration of the bulk NSR, and where τtr is chosen so that
is the free concentration of the bulk NSR, and where τtr is chosen so that 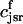 relaxes to
relaxes to 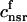 in ∼50 ms. To simulate a spark, we will solve Eqs. 28 with cs and
in ∼50 ms. To simulate a spark, we will solve Eqs. 28 with cs and 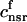 held constant. The initial concentrations in the dyadic space and the JSR are denoted by
held constant. The initial concentrations in the dyadic space and the JSR are denoted by 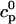 and
and 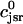 , respectively, with
, respectively, with 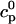 = cs and
= cs and 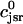 = cnsr. A spark is initiated by the trigger current, which will be a square pulse of 4 ms duration and amplitude 0.05 pA. All parameters of the model are listed in Table 6.
= cnsr. A spark is initiated by the trigger current, which will be a square pulse of 4 ms duration and amplitude 0.05 pA. All parameters of the model are listed in Table 6.
During a simulated spark, cp rises rapidly to ∼200 μM within several milliseconds, and then decays over the next 10–30 ms. The initial rise in cp is due to the positive feedback of CICR, during which the open probability of the RyR rises, and Irel ≫ Id. However, this lasts only for a short time since Irel rapidly decreases as cp approaches 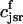 , and Id increases as cp grows much larger than cs. Since the JSR is being replenished in a timescale that is slower than the diffusion away from the dyadic space, then within a few milliseconds we have Id > Irel, in which case cp begins to decline. Since the threshold for activation
, and Id increases as cp grows much larger than cs. Since the JSR is being replenished in a timescale that is slower than the diffusion away from the dyadic space, then within a few milliseconds we have Id > Irel, in which case cp begins to decline. Since the threshold for activation 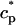 is high, the release flux is robustly terminated as cp drops bellow
is high, the release flux is robustly terminated as cp drops bellow 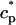 . Thus, in this local model, calcium diffusion away from the dyadic space, in concert with JSR depletion and a high a threshold for local CICR, yields a robust spark termination mechanism.
. Thus, in this local model, calcium diffusion away from the dyadic space, in concert with JSR depletion and a high a threshold for local CICR, yields a robust spark termination mechanism.
In Fig. 13 A, we plot the current flux from a JSR during a spark as a function of time for different initial JSR loads. From the graph, we can see that the duration of the release flux increases from 10 to 30 ms as the total initial JSR concentration is increased from 70 to 150 μM. In Fig. 13 B, we plot the maximum release current during a spark as a function of the dyadic space concentration before CICR is initiated (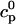 ). It is clear from the plot that the peak flux from the SR remains fairly constant as a function of
). It is clear from the plot that the peak flux from the SR remains fairly constant as a function of 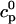 . On the other hand, as seen in Fig. 13 C, if we vary the initial JSR load (
. On the other hand, as seen in Fig. 13 C, if we vary the initial JSR load (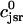 ), the peak release current changes substantially. These results corroborate our initial assumption that the local release flux during a spark can be well approximated by a strong JSR load dependence, and an effectively constant spark lifetime.
), the peak release current changes substantially. These results corroborate our initial assumption that the local release flux during a spark can be well approximated by a strong JSR load dependence, and an effectively constant spark lifetime.
FIGURE 13.
Local release flux Irel during a calcium spark. (A) Plot of Irel versus t for various JSR loads. The initial concentration within the dyadic space is 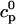 = 0.1 μM for all cases. (B) Plot of the maximum release current
= 0.1 μM for all cases. (B) Plot of the maximum release current 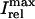 for different initial dyadic concentrations
for different initial dyadic concentrations 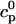 . The initial total JSR concentration
. The initial total JSR concentration 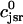 is fixed at 100 μM. (C) Plot of
is fixed at 100 μM. (C) Plot of 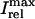 for different initial JSR loads. For all points
for different initial JSR loads. For all points 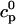 = 0.1 μM.
= 0.1 μM.
APPENDIX B: IONIC CURRENTS
L-type calcium current
We model the L-type calcium current (ICa) based on the most recent experimental measurements in rabbit myocytes at a temperature of 35°C (see Fig. 7 D in Puglisi et al. (1999)). The voltage gates are modeled using
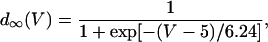 |
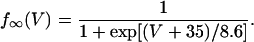 |
(29) |
We have taken the d gate to be instantaneous since τd is the fastest timescale in the model (<5 ms), given that fast sodium currents are not incorporated in the model. We will take the relaxation time of the f gate to be a constant τf in the range 30–50 ms. This is different from the standard formulation in Luo-Rudy II, where τf is taken to have a U-shaped dependence on voltage. However, given that the inactivation properties of the L-type current are both voltage and calcium dependent, it is difficult to measure a purely voltage-dependent quantity such as τf. For a more extensive discussion on this point, see the experimental article of Linz and Meyer (1998). Moreover, we found that we could not reproduce the experimental measurements of Puglisi et al. (1999) using the standard formulation of τf.
To model calcium-induced inactivation, we use 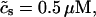 and adjust ko so that τq is in the 10–50 ms range, since experiments (Linz and Meyer (1998); Puglisi et al. (1999)) have shown that calcium-induced inactivation is typically faster than voltage inactivation. The single-channel L-type current is the same as in Luo-Rudy II, and is given by
and adjust ko so that τq is in the 10–50 ms range, since experiments (Linz and Meyer (1998); Puglisi et al. (1999)) have shown that calcium-induced inactivation is typically faster than voltage inactivation. The single-channel L-type current is the same as in Luo-Rudy II, and is given by
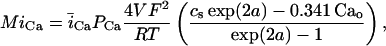 |
(30) |
where 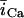 is an adjustable constant. Note that the number of dyadic junctions M, which is constant, is absorbed into
is an adjustable constant. Note that the number of dyadic junctions M, which is constant, is absorbed into 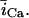 Here,
Here, 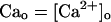 corresponds to the external calcium concentration, and a = VF/RT.
corresponds to the external calcium concentration, and a = VF/RT.
NaCa exchange current
The sodium calcium exchange current as formulated in Luo-Rudy II is given by
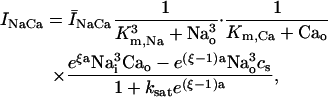 |
(31) |
where the external sodium concentration is 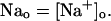 Also,
Also, 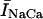 is an adjustable constant that will be used to adjust the strength of the exchanger.
is an adjustable constant that will be used to adjust the strength of the exchanger.
Uptake current
The uptake current is taken to have the simple form
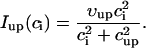 |
(32) |
APPENDIX C: CYTOSOLIC CALCIUM BUFFERING
The amount of calcium in the bulk myoplasm that is bound to troponin C will be denoted by [CaT]i, and satisfies
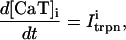 |
(33) |
where 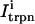 =
=  ci(BT − [CaT]i) −
ci(BT − [CaT]i) −  [CaT]i. The on and off rate constants and the total concentration of troponin C (BT) have been reported previously (Shannon et al., 2000a), and are listed in Table 5. The buffering to SR membrane and calmodulin binding sites are approximated using the rapid buffering approximation (Wagner and Keizer, 1994). This effect is taken into account using
[CaT]i. The on and off rate constants and the total concentration of troponin C (BT) have been reported previously (Shannon et al., 2000a), and are listed in Table 5. The buffering to SR membrane and calmodulin binding sites are approximated using the rapid buffering approximation (Wagner and Keizer, 1994). This effect is taken into account using
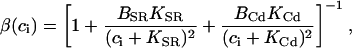 |
(34) |
where KSR and KCd are the buffer dissociation constants for the SR and calmodulin buffers, respectively, and where BSR and BCd denote the total concentration of the respective buffers. The values of these parameters are known experimentally (Shannon et al., 2000a) and are listed in Table 5. Note that for buffering in the submembrane space, we simply replace ci with cs, and [CaT]i with [CaT]s.
TABLE 5.
Cytosolic Buffering parameters
| Parameter | Definition | Value |
|---|---|---|
| BT | Total concentration of troponin C | 70 μmol/l cytosol |
| BSR | Total concentration of SR binding sites | 47 μmol/l cytosol |
| BCd | Total concentration of calmodulin binding sites | 24 μmol/l cytosol |
 |
On rate for troponin C | 32.7/μMs |
 |
Off rate for troponin C | 19.6/s |
| KSR | Dissociation constant for SR binding sites | 0.6 μM |
| KCd | Dissociation constant for calmodulin binding sites | 7 μM |
TABLE 6.
Parameters for local dynamics
| Parameter | Definition | Value |
|---|---|---|
| gs | Maximum RyR cluster conductance | 120 s–1 |
 |
RyR activation threshold | 65 μM |
| τp | Diffusion flux time constant | 0.0025 s |
| τtr | JSR refilling time constant | 0.05 s |
| υjsr | JSR volume | 10−6υi |
| kd | RyR deactivation rate | 0.5 s–1 (μM)–2 |
| α | Buffer and volume ratio | 50 |
References
- Adler, D., A. Y. K. Wong, and Y. Mahler. 1985. Model of mechanical alternans in the mammalian myocardium. J. Theor. Biol. 117:563–577. [DOI] [PubMed] [Google Scholar]
- Bassani, J. W. M., W. Yuan, and D. M. Bers. 1995. Fractional SR Ca release is regulated by trigger Ca and SR Ca content in cardiac myocytes. Am. J. Physiol. Cell Physiol. 268:C1313–C1319. [DOI] [PubMed] [Google Scholar]
- Bers, D. M. 2001. Excitation-Contraction Coupling and Cardiac Contractile Force. Kluwer, Boston.
- Cannell, M. B., H. Cheng, and W. J. Lederer. 1994. Spatial non-uniformities in [Ca2+]i during excitation-contraction coupling in cardiac myocytes. Biophys. J. 67:1942–1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannell, M. B., and C. Soeller. 1997. Numerical analysis of ryanodine receptor activation by L-type channel activity in the cardiac muscle dyad. Biophys. J. 73:112–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng, H., W. J. Lederer, and M. B. Cannell. 1993. Calcium sparks: elementary events underlying excitation-contraction coupling in heart muscle. Science. 262:740–744. [DOI] [PubMed] [Google Scholar]
- Chialvo, D. R., R. F. Gilmour, Jr., and J. Jalife. 1990. Low dimensional chaos in cardiac tissue. Nature. 343:653–657. [DOI] [PubMed] [Google Scholar]
- Chudin, E., J. Goldhaber, A. Garfinkel, J. Weiss, and B. Kogan. 1999. Intracellular Ca2+ dynamics and the stability of ventricular tachycardia. Biophys. J. 77:2930–2941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleemann, L., W. Wang, and M. Morad. 1998. Two-dimensional confocal images of organization, density, and gating of focal Ca2+ release sites in rat cardiac myocytes. Proc. Natl. Acad. Sci. USA. 95:10984–10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collier, M. L., A. P. Thomas, and J. R. Berlin. 1999. Relationship between L-type Ca2+ current and unitary sarcoplasmic reticulum Ca2+ release events in rat ventricular myocytes. J. Physiol. 516:117–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DelPrincipe, F., M. Egger, and E. Niggli. 1999. Calcium signalling in cardiac muscle: refractoriness revealed by coherent activation. Nat. Cell Biol. 1:323–329. [DOI] [PubMed] [Google Scholar]
- Diaz, M. E., D. A. Eisner, and S. C. O'Neill. 2002. Depressed ryanodine receptor activity increases variability and duration of the systolic Ca2+ transient in rat ventricular myocytes. Circ. Res. 91:585–593. [DOI] [PubMed] [Google Scholar]
- Eisner, D. A., H. S. Choi, M. E. Diaz, S. C. O'Neill, and A. W. Trafford. 2000. Integrative analysis of calcium cycling in cardiac muscle. Circ. Res. 87:1087–1094. [DOI] [PubMed] [Google Scholar]
- Faber, G. M., and Y. Rudy. 2000. Action potential and contractility changes in [Na+]i overloaded cardiac myocytes: a simulation study. Biophys. J. 78:2392–2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabiato, A. 1983. Calcium-induced release of calcium from the cardiac sarcoplasmic reticulum. Am. J. Physiol. 245:C1–14. [DOI] [PubMed] [Google Scholar]
- Fox, J. F., J. L. McHarg, and R. F. Gilmour. 2002. Ionic mechanisms of electrical alternans. Am. J. Physiol. Heart Circ. Physiol. 282:H516–H530. [DOI] [PubMed] [Google Scholar]
- Forbes, M. S., L. A. Hawkey, S. K. Jirge, and N. Sperelakis. 1985. The sarcoplasmic reticulum of mouse heart: its divisions, configurations, and distribution. J. Ultrastruct. Res. 93:1–16. [DOI] [PubMed] [Google Scholar]
- Franzini-Armstrong, C., F. Protasi, and V. Ramesh. 1999. Shape, size, and distribution of Ca2+ release units and couplons in skeletal and cardiac muscles. Biophys. J. 77:1528–1539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garfinkel, A., M. L. Spano, W. L. Ditto, and J. N. Weiss. 1992. Controlling cardiac chaos. Science. 257:1230–1235. [DOI] [PubMed] [Google Scholar]
- Glukhovsky, A., D. R. Adam, G. Amitzur, and S. Sideman. 1998. Mechanism of Ca2+ release from the sarcoplasmic reticulum: a computer model. Ann. Biomed. Eng. 26:213–229. [DOI] [PubMed] [Google Scholar]
- Greenstein, J. L., and R. L. Winslow. 2002. An integrative model of the cardiac ventricular myocyte incorporating local control of Ca2+ release. Biophys. J. 83:2918–2945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison, S. M., and M. R. Boyett. 1995. The role of the Na+-Ca2+ exchanger in the rate-dependent increase in contraction in guinea-pig ventricular myocytes. J. Physiol. 482:555–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hund, T. J., N. F. Otani, and Y. Rudy. 2000. Dynamics of action potential head-tail interaction during reentry in cardiac tissue: ionic mechanisms. Am. J. Physiol. Heart Circ. Physiol. 279:H1869–H1879. [DOI] [PubMed] [Google Scholar]
- Jafri, S., J. J. Rice, and R. L. Winslow. 1998. Cardiac Ca2+ dynamics: the roles of ryanodine receptor adaptation and sarcoplasmic reticulum load. Biophys. J. 74:1149–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linz, K. W., and R. Meyer. 1998. Control of L-type current during the action potential of guinea pig ventricular myocytes. J. Physiol. 513:425–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Lopez, J. R., P. S. Shacklock, C. W. Balke, and W. G. Wier. 1995. Local calcium transients triggered by single L-type calcium channel currents in cardiac cells. Science. 268:1042–1045. [DOI] [PubMed] [Google Scholar]
- Lukyanenko, V., I. Gyorke, and S. Gyorke. 1996. Regulation of calcium release by calcium inside the sarcoplasmic reticulum in ventricular myocytes. Pflugers Arch. 432:1047–1054. [DOI] [PubMed] [Google Scholar]
- Lukyanenko, V., S. Viatchenko-Karpinski, A. Smirnov, T. F. Weisner, and S. Gyorke. 2001. Dynamic regulation of sarcoplasmic reticulum Ca2+ content and release by luminal Ca2+-sensitive leak in rat ventricular myocytes. Biophys. J. 81:785–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, C. H., and Y. Rudy. 1994. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 74:1071–1096. [DOI] [PubMed] [Google Scholar]
- Meissner, G. 1994. Ryanodine receptor/Ca2+ release channels and their regulation by endogenous effectors. Annu. Rev. Physiol. 56:485–508. [DOI] [PubMed] [Google Scholar]
- Niggli, E. 1999. Localized intracellular calcium signaling in muscle: calcium sparks and calcium quarks. Annu. Rev. Physiol. 61:311–335. [DOI] [PubMed] [Google Scholar]
- Nolasco, J. B., and R. W. Dahlen. 1968. A graphic method for the study of alternation in cardiac action potential. J. Appl. Physiol. 25:191–196. [DOI] [PubMed] [Google Scholar]
- Ott, E. 1993. Chaos in Dynamical Systems. Cambridge University Press, New York.
- Peskoff, A., and G. A. Langer. 1998. Calcium concentration and movement in the ventricular cardiac cell during an excitation-contraction cycle. Biophys. J. 74:153–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puglisi, J. L., W. Yuan, J. W. M. Bassani, and D. M. Bers. 1999. Ca2+ influx through Ca2+ channels in rabbit ventricular myocytes during action potential clamp: influence of temperature. Circ. Res. 85:e7–e16. [DOI] [PubMed] [Google Scholar]
- Rice, J. J., M. S. Jafri, and R. L. Winslow. 1999. Modeling gain and gradedness of Ca2+ release in the functional unit of the cardiac diadic space. Biophys. J. 77:1871–1884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sah, R., R. J. Ramirez, and P. H. Backx. 2002. Modulation of Ca2+ release in cardiac myocytes by changes in repolarization rate: role of phase-1 action potential repolarization in excitation-contraction coupling. Circ. Res. 90:165–173. [DOI] [PubMed] [Google Scholar]
- Shannon, T. R., K. S. Ginsburg, and D. M. Bers. 2000a. Reverse mode of the sarcoplasmic reticulum calcium pump and load-dependent cytosolic calcium decline in voltage-clamped cardiac myocytes. Biophys. J. 78:322–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon, T. R., K. S. Ginsburg, and D. M. Bers. 2000b. Potentiation of fractional sarcoplasmic reticulum calcium release by total and free intra-sarcoplasmic reticulum calcium concentration. Biophys. J. 78:334–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder, S. M., B. M. Palmer, and R. L. Moore. 2000. A mathematical model of cardiocyte Ca2+ dynamics with a novel representation of sarcoplasmic reticular Ca2+ control. Biophys. J. 79:94–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobie, E. A., K. W. Dilly, J. S. Cruz, W. J. Lederer, and M. S. Jafri. 2002. Termination of cardiac Ca2+ sparks: an investigative mathematical model of calcium-induced calcium release. Biophys. J. 83:59–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soeller, C., and M. B. Cannell. 1999. Examination of the transverse tubular system in living cardiac rat myocytes by 2-photon microscopy and digital image-processing techniques. Circ. Res. 84:266–275. [DOI] [PubMed] [Google Scholar]
- Stern, M. D. 1992. Theory of excitation-contraction coupling in cardiac muscle. Biophys. J. 63:497–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern, M. D., L. S. Song, H. Cheng, J. S. Sham, H. T. Yang, K. R. Boheler, and E. Rios. 1999. Local control models of cardiac excitation-contraction coupling. A possible role of allosteric interactions between ryanodine receptors. J. Gen. Physiol. 113:469–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viswanathan, P. C., R. M. Shaw, and Y. Rudy. 1999. Effects of IKr and IKs heterogeneity on action potential duration and its rate dependence. Circulation. 99:2466–2474. [DOI] [PubMed] [Google Scholar]
- Wagner, J., and J. Keizer. 1994. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 67:447–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, S., L. Song, E. G. Lakatta, and H. Cheng. 2001. Ca2+ signalling between single L-type Ca2+ channels and ryanodine receptors in heart cells. Nature. 410:592–596. [DOI] [PubMed] [Google Scholar]
- Watanabe, M., N. F. Otani, and R. F. Gilmour, Jr. 1995. Biphasic restitution of action potential duration and complex dynamics in ventricular myocardium. Circ. Res. 76:915–921. [DOI] [PubMed] [Google Scholar]
- Weber, C. R., V. Piacentino, III, K. S. Ginsburg, S. R. Houser, and D. M. Bers. 2001. Na+-Ca2+ exchange current and submembrane [Ca2+] during the cardiac action potential. Circ. Res. 90:182–189. [DOI] [PubMed] [Google Scholar]
- Wier, W. G., and C. W. Balke. 1999. Ca2+ release mechanisms, Ca2+ sparks, and local control of excitation-contraction coupling in normal heart muscle. Circ. Res. 85:770–776. [DOI] [PubMed] [Google Scholar]
- Wier, W. G., T. M. Egan, J. R. Lopez-Lopez, and C. W. Balke. 1994. Local control of excitation-contraction coupling in rat heart cells. J. Physiol. 474:463–471. [DOI] [PMC free article] [PubMed] [Google Scholar]