Abstract
M2δ, one of the transmembrane segments of the nicotinic acetylcholine receptor, is a 23-amino-acid peptide, frequently used as a model for peptide-membrane interactions. In this and the companion article we describe studies of M2δ-membrane interactions, using two different computational approaches. In the present work, we used continuum-solvent model calculations to investigate key thermodynamic aspects of its interactions with lipid bilayers. M2δ was represented in atomic detail and the bilayer was represented as a hydrophobic slab embedded in a structureless aqueous phase. Our calculations show that the transmembrane orientation is the most favorable orientation of the peptide in the bilayer, in good agreement with both experimental and computational data. Moreover, our calculations produced the free energy of association of M2δ with the lipid bilayer, which, to our knowledge, has not been reported to date. The calculations included 10 structures of M2δ, determined by nuclear magnetic resonance in dodecylphosphocholine micelles. All the structures were found to be stable inside the lipid bilayer, although their water-to-membrane transfer free energies differed by as much as 12 kT. Although most of the structures were roughly linear, a single structure had a kink in its central region. Interestingly, this structure was found to be the most stable inside the lipid bilayer, in agreement with molecular dynamics simulations of the peptide and with the recently determined structure of the intact receptor. Our analysis showed that the kink reduced the polarity of the peptide in its central region by allowing the electrostatic masking of the Gln13 side chain in that area. Our calculations also showed a tendency for the membrane to deform in response to peptide insertion, as has been previously found for the membrane-active peptides alamethicin and gramicidin. The results are compared to Monte Carlo simulations of the peptide-membrane system, as presented in the accompanying article.
INTRODUCTION
The nicotinic acetylcholine receptor (AChR) is a ligand-gated ion-channel protein that functions in the transmission of neural signals in the central and autonomic nervous systems (Lukas et al., 1999). The structure and function of the AChR have been extensively studied (reviewed by Hucho et al., 1996), and a high resolution cryoelectron microscopy structure of the receptor was recently determined (Miyazawa et al., 2003). The protein is composed of five homologous subunits (α2, β, λ, δ) that are synthesized separately and assemble in the membrane around an aqueous pore (Wang et al., 1996). Each of the subunits is composed of four transmembrane (TM) helices, termed M1–M4. The M2 domain of the protein is an amphipathic helix that lines the lumen of the aqueous pore. This protein segment, which is evolutionarily conserved, is the major component of the pore responsible for the ion channel activities of the protein (Miyazawa et al., 2003). Indeed, the M2 segment of the δ-subunit of AChR (M2δ) has been demonstrated to form a functioning ion-conducting pore in human erythrocyte membranes (Kersh et al., 1989).
M2δ has the sequence
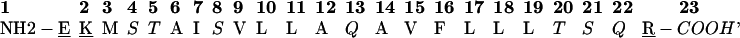 |
where hydrophobic residues are in bold, titratable residues are underlined, and polar residues are in italics.
The peptide is α-helical and amphipathic, as are many membrane-active peptides. It has therefore been used as a model in several experimental and theoretical studies of peptide-membrane interactions. Opella et al. (1997; 1999) studied the structure and orientation of the M2δ monomer in lipid bilayers using solution and solid-state nuclear magnetic resonance (NMR) techniques. M2δ, which was α-helical both in dodecylphosphocholine (DPC) micelles and dimyristoylphosphatidylcholine (DMPC) bilayers, was found to span the bilayer perpendicular to the bilayer plain (Opella et al., 1999). A similar orientation was also found in Monte Carlo (Milik and Skolnick, 1993, 1995; Maddox and Longo, 2002) and molecular dynamics (Law et al., 2000) simulations of M2δ.
In the present study, we used continuum-solvent-model calculations to study different thermodynamic aspects of M2δ-membrane interactions. The continuum-solvent model has been used in our previous studies of polyalanine helices (Ben-Tal et al., 1996), the antibacterial peptide alamethicin (Kessel et al., 2000a,b), and the bacterial channel gramicidin (Bransburg-Zabary et al., 2002), where it successfully reproduced experimental and theoretical data while providing atomic detail interpretation of this data. Several different structures were observed for alamethicin and gramicidin, depending on the experimental conditions, and the calculations suggested the most stable conformation of these two peptides in the membrane.
We used the same method here to screen 10 NMR structures of M2δ (Opella et al., 1997) and to suggest the most favorable one in the membrane. We also explored numerous M2δ-membrane configurations and suggested the most favorable membrane-bound orientation of M2δ, which was in good agreement with the studies mentioned above. Moreover, we addressed other aspects of M2δ-membrane energetics that were not considered by these studies. We report values for the free energy of association of M2δ with the lipid bilayer and analyze the factors that contribute to the stability of different M2δ conformations in the membrane. In addition, we refer to the effect of membrane insertion of M2δ on the curvature of the lipid bilayer, in the light of our previous work with membrane-associated peptides.
In a followup study described in the companion article, we used Monte Carlo simulations to characterize the path of M2δ insertion into the lipid bilayer. We used a model of the lipid bilayer, which allows the consideration of the interactions between the peptide and the bilayer-water interface. The results obtained by both approaches complement each other, as discussed in the articles.
METHODS
The free-energy difference between M2δ in the membrane and in the aqueous phase (ΔGtot) can be broken down into a sum of differences of the following terms: the electrostatic (ΔGelc) and nonpolar (ΔGnp) contributions to the solvation free energy (ΔGsol = ΔGelc + ΔGnp), peptide conformation effects (ΔGcon), peptide immobilization effects (ΔGimm), lipid perturbation effects (ΔGlip), and membrane deformation effects (ΔGdef) (Engelman and Steitz, 1981; Fattal and Ben-Shaul, 1993; Ben-Tal et al., 1996; White and Wimley, 1999; Kessel and Ben-Tal, 2002):
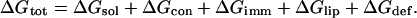 |
(1) |
The methodology for evaluating each of these terms has been described in detail in our recent studies (Kessel et al., 2000a,b). Here we give only a brief overview, with emphasis on the modifications made.
Calculation of ΔGsol
ΔGsol describes the free energy of transfer of M2δ from water to a bulk hydrocarbon phase. It accounts for electrostatic contributions resulting from changes in the polarity of the environment, as well as for van der Waals and solvent structure effects, which together define the classical, hydrophobic effect. We calculated ΔGsol using the continuum-solvent model (Gilson, 1995; Honig and Nicholls, 1995; Nakamura, 1996; Warshel and Papazyan, 1998) as described in Kessel et al. (2000a,b). M2δ was represented in atomic detail, with atomic radii and partial charges defined at the coordinates of each nucleus. The charges and radii were taken from PARSE (Sitkoff et al., 1994, 1996). M2δ and the lipid bilayer were assigned a dielectric constant of 2, whereas bulk water was assigned a dielectric constant of 80. ΔGelc was calculated using a lattice of 1613 points, with a resolution of 3 grid points per Å.
Estimation of ΔGlip, ΔGimm, and ΔGdef
ΔGlip is the free-energy penalty resulting from the interference of the solute with the conformational freedom of the lipid bilayer chains, and ΔGimm is the free-energy penalty which results from the confinement of the external translational and rotational motions of M2δ inside the membrane.
Insertion of M2δ into a lipid bilayer may result in a deformation of the lipid bilayer to match the width of the hydrocarbon region to M2δ's hydrophobic length, following the mattress model (Mouritsen and Bloom, 1984). The deformation involves a free-energy penalty, ΔGdef, that results from the compression or expansion of the lipid chains.
In our previous studies, we used values for ΔGlip, ΔGimm, and ΔGdef based on the estimates of Fattal and Ben-Shaul (1993) and Ben-Shaul et al. (1996). In these studies, statistical thermodynamic calculations were used to estimate the values of ΔGlip and ΔGimm for the insertion of inclusions into a lipid bilayer of hydrophobic widths of 30 Å. However, the membrane insertion of a peptide may involve a deformation of the membrane, as has been demonstrated in our previous work with alamethicin and gramicidin. The deformation of the lipid bilayer results in a change of its width, and the values of ΔGlip and ΔGimm should depend on this change. ΔGlip and ΔGimm values for a lipid bilayer of 22 Å width have been estimated by May and Ben-Shaul (2000). We assumed a linear dependence of ΔGlip and ΔGimm on the width of the lipid bilayer, and interpolated to obtain values for different lipid bilayer widths. A list of these values is presented in Table 1.
TABLE 1.
| Membrane width (Å)* | ΔGlip (kT)† | ΔGimm (kT)‡ | ΔGdef (kT)§ |
|---|---|---|---|
| 30 | 3.95 | 5.45 | 0.00 |
| 29 | 3.88 | 5.43 | 0.02 |
| 28 | 3.81 | 5.40 | 0.14 |
| 27 | 3.76 | 5.37 | 0.35 |
| 26 | 3.70 | 5.35 | 0.69 |
| 25 | 3.63 | 5.32 | 1.15 |
| 24 | 3.56 | 5.28 | 1.70 |
| 23 | 3.49 | 5.27 | 2.38 |
| 22 | 3.43 | 5.23 | 3.16 |
| 21 | 3.36 | 5.20 | 4.03 |
| 20 | 3.29 | 5.18 | 5.05 |
The dependence of ΔGlip, ΔGimm, and ΔGdef on the hydrophobic mismatch between the membrane width and length of the hydrophobic core of a TM α-helix, approximated as a cylinder of 5 Å radius. The width of the unperturbed lipid bilayer was taken as 30 Å, corresponding to the hydrocarbon region of pure phosphatidylcholine bilayer (White and Wimley, 1999).
The width of the hydrocarbon region of the lipid bilayer.
The free-energy change due to lipid perturbation effects.
The free-energy change due to peptide immobilization.
The free-energy change due to membrane deformation effects.
Estimation of ΔGcon
The structure of M2δ is α-helical, both in DPC micelles and DMPC bilayers (Opella et al., 1997, 1999). Sansom and co-workers carried out 2–4-ns molecular dynamics simulations of M2δ in palmitoyloleoylphosphatidylcholine (POPC) bilayers (Law et al., 2000). The simulations confirm that, in the lipid bilayer, the peptide retains the α-helical structure found in DPC micelles. In water, however, the helical structure is retained only in the termini of the peptide, and is completely lost in its center. The central region in the vicinity of Leu-11 of the peptide acts as a molecular hinge, with a kink angle that ranges from 0° to 110°. Thus, the transfer of M2δ from the aqueous solution into the lipid bilayer is likely to involve a major conformational change in the peptide. This change may be accompanied by a free-energy change (ΔGcon), the magnitude of which is currently unknown. Theoretical and experimental studies of the stability of short polyalanine-like α-helices in aqueous solutions indicate that a complete coil-to-helix transition of a polyalanine helix of 23 residues (corresponding to the length of M2δ) involves ΔGcon of ∼−4 kT (Zimm and Bragg, 1959; Lifson and Roig, 1961; Scholtz and Baldwin, 1992; Chakrabartty and Baldwin, 1995). We used this approximated value here.
Models of M2δ
We used three-dimensional structures of M2δ, determined in DPC micelles by NMR spectroscopy (Opella et al., 1997; PDB entry 1A11). We removed the first two residues to make our model peptide compatible with the peptides used in the studies of Milik and Skolnick (1993), Opella et al. (1999), Law et al. (2000), and Maddox and Longo (2002), which are mentioned above.
In the complete structure of the acetylcholine receptor, the termini of M2δ are covalently bonded to other regions of the protein, and we therefore considered the termini of the peptide as polar rather than charged in our calculations.
Residues E1, K2, and R23 are at the termini of M2δ, and therefore may face the aqueous solution even when the peptide spans the entire bilayer width. Accordingly, these titratable residues were taken in their charged state: that is, K2 and R23 were protonated, and E1 was deprotonated.
RESULTS
Association of M2δ with lipid bilayers in surface and TM orientations
Hydrophobic-amphipathic peptides like M2δ may associate with lipid bilayers in two ways (Fig. 1). In the first, the peptide adsorbs onto the bilayer surface. In this orientation, the hydrophilic residues of the peptide face the water-membrane interface, whereas its hydrophobic residues face the hydrocarbon core of the bilayer. In the second, the peptide inserts into the bilayer and assumes a TM orientation. In this orientation, the central region of the peptide faces the hydrocarbon core of the bilayer, and its termini protrude into the polar headgroups region of the bilayer.
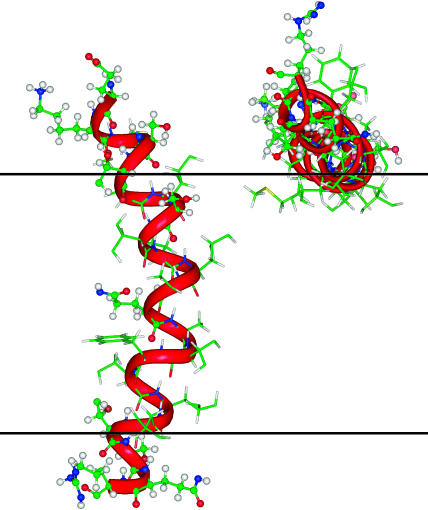
FIGURE 1.
Schematic representation of the most favorable orientations of M2δ in the lipid bilayer. TM (left) and surface (right) orientations of structure 9 (the most stable structure in the bilayer). The peptide is displayed with INSIGHT (Accelrys, San Diego, CA), with carbon atoms (green), hydrogen atoms (white), oxygen atoms (red), and nitrogen atoms (blue). The red ribbon represents the backbone of M2δ. The polar atoms of the peptide are represented as balls and sticks, and the nonpolar atoms as sticks. The two horizontal black lines represent the boundaries of the hydrocarbon region of the lipid bilayer.
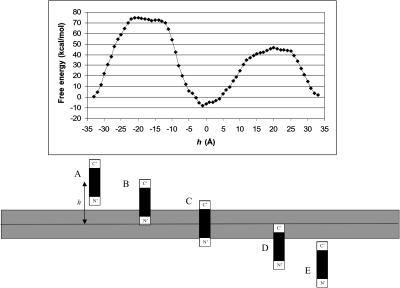
Fig. 2 shows the free energy of transfer of M2δ across the lipid bilayer along the TM insertion path, with the helix principle axis perpendicular to the membrane surface. As the figure demonstrates, insertion of either of the charged terminal segments of the peptide significantly destabilizes the system. This is mainly due to the electrostatic free-energy penalty associated with the water-to-membrane transfer of the charged residues at either ends of M2δ (data not shown). The most stable peptide-membrane configuration was obtained when the central region of the peptide spanned the hydrocarbon core of the lipid bilayer, whereas the charged terminal segments protruded into the aqueous solution (state c in Fig. 2; h = −1 Å).
FIGURE 2.
Insertion of M2δ into a lipid bilayer along a (hypothetical) TM path. (Top) ΔGsol as a function of the distance h between the geometrical center of the peptide and the membrane midplane. The zero of ΔGsol was chosen at h = ∞. Structure 8 of M2δ (Table 2) was used, and the membrane width was set to 22 Å, which is the most stable membrane configuration found for this structure. The calculations were carried out on a lattice of 161 points and a resolution of three grid points per Å as described in Methods. (Bottom) A schematic view of critical M2δ-lipid bilayer configurations corresponding to the ΔGsol curve in A. (A and E) the peptide in aqueous solution; (B) the peptide's N-terminal segment is inserted into the lipid bilayer whereas its C-terminal segment protrudes into the aqueous solution; (C) the hydrophobic core of the peptide is inside the lipid bilayer, whereas both terminal segments protrude into the aqueous solution; and the peptide's C-terminal segment is inserted into the lipid bilayer whereas the N-terminal segment protrudes into the aqueous solution. The large ΔGsol barrier associated with the transfer of each of the terminal segments from the aqueous phase into the lipid bilayer is noticeable.
Adsorption of the peptide onto the surface of the lipid bilayer (not shown) is also favorable, but to a lesser extent. There are two reasons for that. First, in this configuration, the charged terminal segments are partially exposed to the lipid bilayer. Second, the central hydrophobic region of the peptide is only partially immersed inside the bilayer. Thus, only part of the large nonpolar component of the solvation free energy that results from the interaction between this region and the bilayer can be gained.
A third possible configuration, in which the peptide is horizontally immersed inside the lipid bilayer, is highly unlikely, due to the complete exposure of both charged terminal segments to the hydrophobic environment of the bilayer (data not shown).
The free energy of association of M2δ with lipid bilayers and the most favorable M2δ-membrane configuration
To find the most favorable orientation of M2δ in the lipid bilayer, we sampled numerous surface and TM peptide-membrane configurations, and calculated the corresponding association free energy, as described in Kessel et al. (2000a). The results (Table 2) show all the NMR structures of M2δ to be stable in the TM position, in agreement with experimental (Opella et al., 1999) and computational (Milik and Skolnick, 1993; Law et al., 2000; Maddox and Longo, 2002) studies. Most of these structures were also found to be stable (although to a lesser extent) in the surface-adsorbed orientation. Among all the structures, structure 9 represents the most favorable conformation of the peptide both in the TM and surface orientations (Fig. 1), with a free energy of association of −18.9 kT and −13.6 kT, respectively. These values are significantly more negative than the corresponding values obtained for the other NMR structures.
TABLE 2.
| Structure* | TM† (kT) | Surface‡ (kT) |
|---|---|---|
| 1 | −11.8 | −10.1 |
| 2 | −7.2 | |
| 3 | −8.9 | −10.2 |
| 4 | −11.4 | |
| 5 | −13.6 | −1.5 |
| 6 | −12.4 | −10.1 |
| 7 | −14.1 | |
| 8 | −12.8 | −4.8 |
| 9 | −18.9 | −13.6 |
| 10 | −7.5 | −8.1 |
The structures were obtained from Opella et al. (1997). Preliminary electrostatic analysis was carried out for all the structures, and calculations in search for a surface orientation were carried out only for structures that appeared to be significantly amphipathic. The most negative value of ΔGtot was obtained for the TM insertion of M2δ in conformation 9 (in bold).
An index of the structure of M2δ.
The ΔGtot values for the transfer of M2δ from the aqueous phase into the membrane in TM.
The ΔGtot values for the transfer of M2δ from the aqueous phase into the membrane in surface orientations.
The calculations indicate that the energetically most favorable peptide-membrane configuration is obtained when M2δ assumes the conformation of NMR structure 9, and is positioned in a TM orientation with its principle axis tilted ∼15° from the membrane normal. This is in very good agreement with solid-state NMR studies, which determined that the long axis of the peptide is tilted 12° from the membrane normal (Opella et al., 1999).
Structural aspects of M2δ-membrane interactions
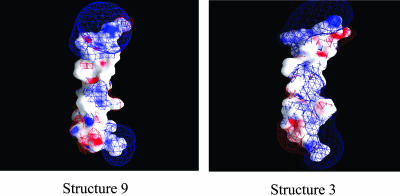
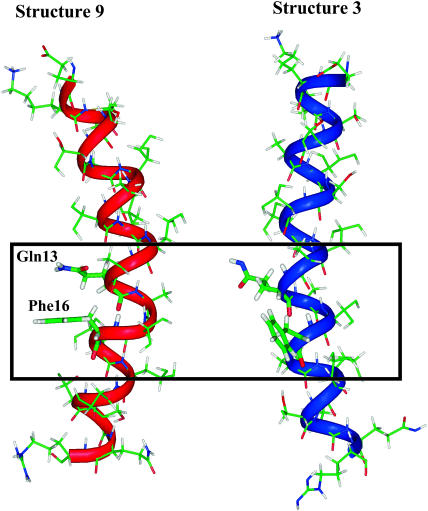
We used 10 different structures of M2δ, determined by NMR spectroscopy in micelles (Opella et al., 1997). As shown in Table 2, the structures, all of which are found to be stable in the lipid bilayer, are characterized by water-to-membrane transfer free energies, which differ by as much as ∼12 kT, both for the TM and surface-adsorbed orientations. The free-energy differences between the structures in the TM orientations are consistent with their electrostatic properties, as demonstrated by surface potential maps of the structures. For example, structure 9, which is suggested by the calculations to be the most stable structure inside the lipid bilayer, has an overall wide hydrophobic area in its lipid-exposed core (Fig. 3). Conversely, structure 3, which is less stable inside the lipid bilayer by 10 kT, has a relatively small hydrophobic area and a large positive potential in its lipid-exposed region. A close inspection of the two conformations (Fig. 4) suggests that the free-energy difference between the two conformations results mainly from their ability to mask the positive potential of the amide group in the Gln13 side chain. In the kinked conformation of structure 9, this group is proximal and parallel to the aromatic ring of the Phe16 side chain. The negative potential at the ring plane of Phe16 should, at least partially, mask the positive potential of the Gln13 side chain. Conversely, in structure 3, which is linear, the side chain of Gln13 is diverted away from that of Phe16, and cannot therefore be electrostatically masked by the latter. We investigated this suggestion by electrostatically neutralizing Phe16 in both structures and calculating the free energy of their transfer from water to the lipid bilayer. Indeed, the results (data not shown) support the suggestion made above: the neutralization of Phe16 destabilized structure 9 by ∼7 kT, whereas structure 3 was not destabilized by the neutralization (in fact, it was stabilized by 1.7 kT).
FIGURE 3.
Surface electrostatic potential of M2δ structures 9 (left) and 3 (right). The electrostatic potential (φ), calculated using DelPhi (Nicholls and Honig, 1991), is color-coded and displayed on the molecular surface using GRASP (Nicholls et al., 1991). Negative potentials (0 kT/e > φ > −20kT/e) are red, positive potentials (0 kT/e < φ < 20 kT/e) are blue, and neutral potentials are white. Three-dimensional equipotential contours are shown at 1 kT/e (blue mesh) and −1 kT/e (red mesh). The peptides are shown with their C-termini pointing down and their N-termini pointing up.
FIGURE 4.
Electrostatic masking of Gln13 by Phe16 in structures 9 (left) and 3 (right). M2δ is represented as in Fig. 3. In the kinked conformation of structure 9, the aromatic ring of Phe16 side chain is close and in parallel to the side chain of Gln13, which in turn allows electrostatic masking of the partially positive charge on the latter. Conversely, in structure 3, the linear conformation does not allow the proximity of the two side chains. This results in insufficient masking of Gln13.
Fig. 4 also demonstrates the partial burial of the carbonyl group of the Gln13 side chain in the kinked (but not in the linear) conformation. The kink-induced burial of the carbonyl group reduces its negative potential at the surface of the peptide (Fig. 3), and therefore further stabilizes the peptide inside the lipid bilayer. However, it should be noted that, in the kinked conformation, the carbonyl group of Gln13 is positioned near the backbone carbonyl group of Val9, which should have some destabilizing effect on the conformation by elevation of the corresponding internal free energy.
Membrane curvature effect
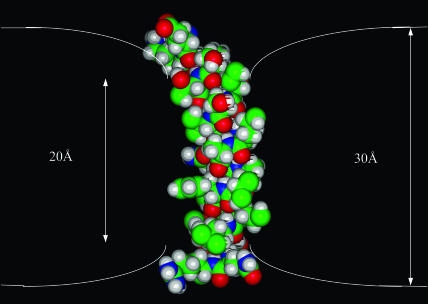
M2δ has a central, overall nonpolar region, flanked by terminal polar residues. The length of the nonpolar region is ∼20 Å, which suggests that the TM insertion of M2δ into a native lipid bilayer of hydrophobic width of 30 Å is likely to lead to membrane deformation, to avoid the exposure of the polar termini of the peptide to the lipid membrane. We calculated the free energy of association of M2δ with lipid bilayers of different widths, and added the free-energy penalty of membrane deformation to approximate insertion into a deformed bilayer. The results confirm that the TM insertion of M2δ is likely to cause an average reduction of 10 Å in the width of the lipid bilayer (Fig. 5).
FIGURE 5.
M2δ-induced deformation of the lipid bilayer. M2δ is presented in a typical TM configuration. The space-filling model of the peptide is displayed with INSIGHT (Accelrys). Carbon atoms are colored green, hydrogen atoms are colored white, oxygen atoms are colored red, and nitrogen atoms are colored blue. The two white lines represent the boundaries of the hydrocarbon region of the lipid bilayer.
Convergence test and error estimate
The error in the ΔGsol value was calculated using a lattice of 1613 grid points and a sequence of focusing runs of increasing resolution (Gilson et al., 1987). The calculation precision was estimated by comparing the values obtained for the resolution used in this study (three grid points per Å) and a higher resolution of four grid points per Å. The difference in free energy was negligible (0.22 kT), indicating that the resolution used in this study is sufficient.
The main source of error in this study probably results from effects due to the other free-energy components in Eq. 1, all of which were estimated. These include the peptide immobilization (ΔGimm), lipid perturbation (ΔGlip), and membrane deformation (ΔGdef) terms. An error could also arise from effects due to the interactions of M2δ with the lipid headgroups, as is referred to in the Discussion below and neglected in this study. We estimate the error of these terms to range between 4 and 5 kT at the most, based on the total magnitude of these free-energy terms. It is important to notice that these values depend on the contact area between the peptide and the lipid bilayer. The latter varies very little between the 10 M2δ structures used in this study. Thus, differences in the total free energy of transfer of these structures from the aqueous phase into the bilayer (ΔΔG) are probably much more accurate than the transfer free energies of individual structures. Thus, we estimate the error of those terms, and of our methodology in whole to be ∼1.5 kT.
It is important to notice that the peptide conformation free-energy (ΔGcon) component, which takes into account, for example, deformation of the peptide structure, introduces another potential source of error. As explained in the Discussion below, the estimated ΔGcon value of −4 kT that was used here is in close agreement with the value that was obtained using the Monte Carlo simulations reported in the adjacent article. We cannot provide an estimate of the error associated with the ΔGcon value, but the small magnitude of this term suggests that the error is probably <2 kT, and that the one in the estimated value of ΔΔGcon (difference between structures) is probably even lower.
DISCUSSION
The limitations of the continuum-solvent model in the study of peptide-membrane interactions have been discussed in detail in Kessel et al. (2000a,b), Bechor and Ben-Tal (2001), Bransburg-Zabary et al. (2002), and Kessel and Ben-Tal (2002). The main uncertainty in the model results from the neglect of the interactions between the peptide and the polar headgroup region of the lipid bilayer. This is presumably of particular importance for peptides in surface orientations (Bechor and Ben-Tal, 2001); the estimated value of the free energy of surface adsorption of M2δ and the favorable orientation of the peptide associated with it should therefore be viewed as rather crude approximations. However, peptides such as M2δ, that contain a hydrophobic core, tend to interact almost exclusively with the hydrocarbon region of the lipid bilayer. It is noticeable that M2δ also contains terminal Glu, Lys, and Arg residues, which may interact with the polar headgroup region of the bilayer. This in turn may affect some of the membrane association determinants of M2δ.
Another uncertainty of the continuum-solvent model approach results from the neglect of peptide conformational changes associated with the transfer of M2δ from water into the lipid bilayer. In the continuum-solvent model calculations, we assumed that M2δ retained an α-helical structure in water. However, molecular dynamics simulations of the peptide in water indicate otherwise (Law et al., 2000). We used an approximated estimate of ΔGcon ≈ −4 kT, corresponding to the Zimm-Bragg value associated with the coil-to-helix transition of (Ala)23. Indeed, the Monte Carlo simulations we carried out on M2δ suggested very close values of −3.3 kT and −5.4 kT for the peptide in surface and TM orientations, respectively (see adjacent article).
Conformational changes in M2δ's structure also affect its interactions with the environment. These effects are taken into account in the continuum-solvent model; the exact same method used here has been successfully employed to differentiate between various experimentally observed conformations of the alamethicin (Kessel et al., 2000a) and gramicidin (Bransburg-Zabary et al., 2002) peptides in membranes. The trace root-mean-square deviations between these conformations were 1–2 Å or even less (smaller than the diameter of a water molecule) and similar to the deviations between the 10 NMR structures of M2δ, which were studied here.
The calculations suggest that the water-to-membrane transfer free energies of the 10 similar M2δ structures may differ by as much as ∼12 kT, which is significantly larger than the estimated calculation error of ∼1.5 kT. This phenomenon has also been observed in our work with the bacterial peptide gramicidin (Bransburg-Zabary et al., 2002), in which a similar free-energy difference was observed for structures with trace root-mean-square deviations of <0.7 Å. Our work with alamethicin (Kessel et al., 2000a) and gramicidin (Bransburg-Zabary et al., 2002) showed that such free-energy differences are often the result of electrostatic effects, attributed to backbone or side-chain groups in the peptide.
This is true for M2δ as well. The results suggest that the free-energy differences between the most (structure 9) and one of the least (structure 3) stable conformations in the membrane are attributed, at least in part, to the ability of the aromatic side chain of Phe16 to electrostatically mask the amide group of the Gln13 side chain. This in turn results from the conformation of the peptide: a kinked conformation (structure 9) permits the correct positioning of the two side chains, thus facilitating the masking, whereas a linear conformation (structure 3) does not. The kink appears to be in the vicinity of Leu11, which is conserved between nicotinic receptors of different species. Based on mutational studies (Revah et al., 1991) it has been suggested that Leu11, which is thought to function as a molecular hinge (Unwin, 1995; Sankararamakrishnan et al., 1996), plays a role in channel gating. Our results suggest that the kink at this region may play an additional role in stabilizing M2δ inside the lipid bilayer. It should be noted that the kink (∼35° in magnitude) only appears in one of the 10 NMR structures. The rest of the structures are roughly linear. However, the newly resolved high resolution cryoelectron microscopy structure of the intact acetylcholine receptor (Miyazawa et al., 2003), and molecular dynamics simulations in POPC bilayers (Law et al., 2000) indicate that the M2 helices of the nicotinic receptor are indeed kinked.
Even though the M2δ peptide is a fragment of the nicotinic acetylcholine receptor, which functions as an autonomous ion channel, it is not straightforward to project from the present study about the in vivo behavior of the entire receptor. For example, in the context of the channel, each of the M2 segments is bound to the other TM helices in its vicinity, and is also partially exposed to the aqueous solution inside and around the pore (Miyazawa et al., 2003). This may affect the peptide conformation. Interestingly, in the 4 Å resolution structure of the membrane-bound acetylcholine receptor, the corresponding M2δ subunit has a conformation similar to that of NMR structure number 9, suggested by our calculations to be the most stable inside the lipid bilayer. That is, the characteristic kink can be observed, although it is less pronounced as compared to the NMR structure. Again, in view of the discussion above, the agreement between the continuum-solvent model calculations and the 4 Å resolution structure of M2δ is probably fortuitous.
The kinetics of membrane insertion is also expected to be different in the two cases (i.e., the isolated segment versus the whole receptor). As any other membrane-embedded protein, the acetylcholine receptor is produced inside cells using membrane-associated ribosomes, and is inserted into the membrane using the complex translocon machinery. The resulting path for the insertion of the M2 peptides into the membrane may be considerably different than the one described in this article.
While keeping these points in mind, we would like to emphasize that the aim of the current study was to use M2δ as a model for membrane-active peptides, which act as independent units, rather than to explore the biological implications of M2δ's behavior on the function of the entire acetylcholine receptor.
M2δ has been studied previously, using different experimental and theoretical methods (e.g., Milik and Skolnick, 1993; Opella et al., 1999; Law et al., 2000; Maddox and Longo, 2002). These studies focused on the association of the peptide with the membrane, and its dynamics in solution and inside the membrane. Using continuum-solvent model calculations, we determined the most favorable orientation of M2δ in the membrane, which was in very good agreement with the studies mentioned above. In addition, the calculations produced water-to-membrane transfer free energies for M2δ (Table 2), which are similar to those measured for similar peptides (White and Wimley, 1999).
The continuum-solvent model calculations suggested that a TM insertion of M2δ into the lipid bilayer is likely to induce bilayer deformation, resulting in a reduction of its width. Peptide-induced deformation of the lipid bilayer has already been observed in our previous work with alamethicin (Kessel et al., 2000a) and gramicidin (Bransburg-Zabary et al., 2002), and in these cases, the deformation was indirectly supported by both experimental and theoretical studies.
The calculations suggested a reduction of ∼10 Å in the width of the lipid bilayer in response to peptide insertion. This value seems exaggerated, considering that it would constitute one-third of the hydrophobic width of the native membrane (i.e., 30 Å). In reality, the deformation is probably smaller in magnitude, due to stabilizing interactions between the polar termini of the peptide and the polar lipid headgroups. Indeed, our Monte Carlo simulations, in which the polar headgroup region was considered, demonstrated that a significant portion of M2δ's termini interacted with the polar headgroup of membrane lipids, which in turn allowed for smaller deformations of the membrane (see companion article).
Jacobs and White (1989) proposed a model for protein insertion into the lipid bilayer, which includes the following steps: 1), Adsorption on the membrane surface; and 2), formation of a secondary structure on the membrane surface, followed by insertion of the protein into a TM configuration. This model was supported by experimental and theoretical studies (e.g., DeGrado et al., 1989; Chung et al., 1992; Bechinger et al., 1993; Matsuzaki et al., 1994; White and Wimley, 1999; Tieleman et al., 1999; Popot and Engelman, 2000). Our continuum-solvent model calculations indicate two plausible association modes of M2δ with the lipid bilayer: surface adsorption and TM insertion, with the latter being more favorable (as explained above). This is consistent with the model presented above, and also with Monte Carlo simulations carried out by Milik and Skolnick (1993) and Maddox and Longo (2002); see also companion article. The free-energy minimum observed for the surface-adsorbed peptide and its capacity to accommodate M2δ in different conformations may facilitate structure rearrangement before membrane insertion (White and Wimley, 1999). In this context, it is important to notice that M2δ is very hydrophobic and experimental studies of its association with lipid bilayers require its solubilization in organic solvents, which are missing in the calculations. The detergent-containing aqueous phase is much less polar than bulk water, and therefore the free-energy barrier of peptide insertion into the membrane is significantly reduced as compared to those of Fig. 2. Moreover, the charged residues at the terminal segments of the peptide are likely to undergo pKa shifts in the aqueous phase to neutralize their charges before their penetration into the hydrocarbon region of the lipid bilayer, thus reducing the barrier height significantly (Honig and Hubbell, 1984; Kessel et al., 2001).
In conclusion, these and our previous studies with membrane-associated peptides suggest that continuum-solvent model calculations may be used for capturing the main thermodynamic features of the peptide-membrane system, such as the free energy of association with the membrane, the relative stability of different conformations inside the membrane, and the physical response of the membrane to peptide insertion. However, one should keep in mind the approximations made by continuum-solvent models and that certain features (e.g., specific peptide-membrane interactions) are neglected in these models. In addition, the kinetic aspects are missing. In the studies of M2δ-membrane interactions, we combined the continuum-solvent model calculations presented here with the Monte Carlo simulations presented in the adjacent article. The results of those studies demonstrate that such integration between thermodynamic- and kinetic-oriented methodologies may lead to a more comprehensive understanding of peptide-membrane interactions.
Acknowledgments
This work was supported by the Magnet “Pharmalogica” Consortium of the Israel Ministry of Industry and Trade and by North Atlantic Treaty Organization grant LAST-CLG 977836. T.H.'s research is supported by State Planning Organization of Turkish Republic grant 01K120280 and Bogazici University research grant 02HA501, Turkish Academy of Sciences, in the framework of the Young Scientist Award Program (EA-TUBA-GEBIP/2001-1-1).
References
- Bechinger, B., M. Zasloff, and S. J. Opella. 1993. Structure and orientation of the antibiotic peptide magainin in membranes by solid-state nuclear magnetic resonance spectroscopy. Protein Sci. 2:2077–2084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bechor, D., and N. Ben-Tal. 2001. Implicit solvent model studies of the interactions of the influenza hemagglutinin fusion peptide with lipid bilayers. Biophys. J. 80:643–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Shaul, A., N. Ben-Tal, and B. Honig. 1996. Statistical thermodynamic analysis of peptide and protein insertion into lipid membranes. Biophys. J. 71:130–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Tal, N., A. Ben-Shaul, A. Nicholls, and B. Honig. 1996. Free-energy determinants of α-helix insertion into lipid bilayers. Biophys. J. 70:1803–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bransburg-Zabary, S., A. Kessel, M. Gutman, and N. Ben-Tal. 2002. Stability of an ion channel in lipid bilayers: implicit solvent model calculations with gramicidin. Biochemistry. 41:6946–6954. [DOI] [PubMed] [Google Scholar]
- Chakrabartty, A., and R. L. Baldwin. 1995. Stability of α-helices. Adv. Protein Chem. 46:141–176. [PubMed] [Google Scholar]
- Chung, L. A., J. D. Lear, and W. F. DeGrado. 1992. Fluorescence studies of the secondary structure and orientation of a model ion channel peptide in phospholipid vesicles. Biochemistry. 31:6608–6616. [DOI] [PubMed] [Google Scholar]
- DeGrado, W. F., Z. R. Wasserman, and J. D. Lear. 1989. Protein design, a minimalist approach. Science. 243:622–628. [DOI] [PubMed] [Google Scholar]
- Engelman, D. M., and T. A. Steitz. 1981. The spontaneous insertion of proteins into and across membranes: the helical-hairpin hypothesis. Cell. 23:411–422. [DOI] [PubMed] [Google Scholar]
- Fattal, D. R., and A. Ben-Shaul. 1993. A molecular model for lipid-protein interaction in membranes: the role of hydrophobic mismatch. Biophys. J. 65:1795–1809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K. 1995. Theory of electrostatic interactions in macromolecules. Curr. Opin. Struct. Biol. 5:216–223. [DOI] [PubMed] [Google Scholar]
- Gilson, M. K., K. A. Sharp, and B. Honig. 1987. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comp. Chem. 9:327–335. [Google Scholar]
- Honig, B. H., and W. L. Hubbell. 1984. Stability of “salt bridges” in membrane proteins. Proc. Natl. Acad. Sci. USA. 81:5412–5416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honig, B., and A. Nicholls. 1995. Classical electrostatics in biology and chemistry. Science. 268:1144–1149. [DOI] [PubMed] [Google Scholar]
- Hucho, F., V. I. Tsetlin, and J. Machold. 1996. The emerging three-dimensional structure of a receptor. The nicotinic acetylcholine receptor. Eur. J. Biochem. 239:539–557. [DOI] [PubMed] [Google Scholar]
- Jacobs, R. E., and S. H. White. 1989. The nature of the hydrophobic binding of small peptides at the bilayer interface: implications for the insertion of transbilayer helices. Biochemistry. 28:3421–3437. [DOI] [PubMed] [Google Scholar]
- Kersh, G. J., J. M. Tomich, and M. Montal. 1989. The M2 δ-transmembrane domain of the nicotinic cholinergic receptor forms ion channels in human erythrocyte membranes. Biochem. Biophys. Res. Commun. 162:352–356. [DOI] [PubMed] [Google Scholar]
- Kessel, A., and N. Ben-Tal. 2002. Free energy determinants of peptide association with lipid bilayers. In Current Topics in Membranes: Peptide-Lipid Interactions. S. Simon and T. McIntosh, editors. Academic Press, San Diego, CA. 205–253.
- Kessel, A., D. S. Cafiso, and N. Ben-Tal. 2000a. Continuum solvent model calculations of alamethicin-membrane interactions: thermodynamic aspects. Biophys. J. 78:571–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessel, A., B. Musafia, and N. Ben-Tal. 2001. Continuum solvent model studies of the interactions of an anticonvulsant drug with a lipid bilayer. Biophys. J. 80:2536–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessel, A., K. Schulten, and N. Ben-Tal. 2000b. Calculations suggest a pathway for the transmembrane migration of a hydrophobic peptide. Biophys. J. 79:2322–2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law, R. J., L. R. Forrest, K. M. Ranatunga, P. La Rocca, D. P. Tieleman, and M. S. Sansom. 2000. Structure and dynamics of the pore-lining helix of the nicotinic receptor: MD simulations in water, lipid bilayers, and transbilayer bundles. Proteins. 39:47–55. [DOI] [PubMed] [Google Scholar]
- Lifson, S., and A. Roig. 1961. On the theory of helix-coil transition in polypeptides. J. Chem. Phys. 34:1963–1974. [Google Scholar]
- Lukas, R. J., J. P. Changeux, N. Le Novere, E. X. Albuquerque, D. J. Balfour, D. K. Berg, D. Bertrand, V. A. Chiappinelli, P. B. Clarke, A. C. Collins, J. A. Dani, S. R. Grady, K. J. Kellar, J. M. Lindstrom, M. J. Marks, M. Quik, P. W. Taylor, and S. Wonnacott. 1999. International Union of Pharmacology. XX. Current status of the nomenclature for nicotinic acetylcholine receptors and their subunits. Pharmacol. Rev. 51:397–401. [PubMed] [Google Scholar]
- Maddox, M. W., and M. L. Longo. 2002. A Monte Carlo study of peptide insertion into lipid bilayers: equilibrium conformations and insertion mechanisms. Biophys. J. 82:244–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki, K., O. Murase, H. Tokuda, S. Funakoshi, N. Fujii, and K. Miyajima. 1994. Orientational and aggregational states of magainin 2 in phospholipid bilayers. Biochemistry. 33:3342–3349. [DOI] [PubMed] [Google Scholar]
- May, S., and A. Ben-Shaul. 2000. A molecular model for lipid-mediated interaction between proteins in membranes. Phys. Chem. Chem. Phys. 2:4494–4502. [Google Scholar]
- Milik, M., and J. Skolnick. 1993. Insertion of peptide chains into lipid membranes: an off-lattice Monte Carlo dynamics model. Proteins. 15:10–25. [DOI] [PubMed] [Google Scholar]
- Milik, M., and J. Skolnick. 1995. A Monte Carlo model of FD and PF1 coat proteins in lipid membranes. Biophys. J. 69:1382–1386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyazawa, A., Y. Fujiyoshi, and N. Unwin. 2003. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 424:949–955. [DOI] [PubMed] [Google Scholar]
- Mouritsen, O. G., and M. Bloom. 1984. Mattress model of lipid-protein interactions in membranes. Biophys. J. 46:141–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura, H. 1996. Roles of electrostatic interaction in proteins. Q. Rev. Biophys. 29:1–90. [DOI] [PubMed] [Google Scholar]
- Nicholls, A., and B. Honig. 1991. A rapid finite difference algorithm, utilizing successive over-relaxation to solve the Poisson-Boltzmann equation. J. Comp. Chem. 12:435–445. [Google Scholar]
- Nicholls, A., K. A. Sharp, and B. Honig. 1991. Protein folding and association: insights from the interfacial and thermodynamic properties of hydrocarbons. Proteins. 11:281–296. [DOI] [PubMed] [Google Scholar]
- Opella, S. J., J. Gesell, A. P. Valente, F. M. Marassi, M. Oblatt-Montal, W. Sun, A. Ferrer-Montiel, and M. Montal. 1997. Structural studies of the pore-lining segments of neurotransmitter-gated channels. Chemtracts Biochem. Mol. Biol. 10:153–167. [Google Scholar]
- Opella, S. J., F. M. Marassi, J. J. Gesell, A. P. Valente, Y. Kim, M. Oblatt-Montal, and M. Montal. 1999. Structures of the M2 channel-lining segments from nicotinic acetylcholine and NMDA receptors by NMR spectroscopy. Nat. Struct. Biol. 6:374–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popot, J. L., and D. M. Engelman. 2000. Helical membrane protein folding, stability, and evolution. Annu. Rev. Biochem. 69:881–922. [DOI] [PubMed] [Google Scholar]
- Revah, F., D. Bertrand, J. L. Galzi, A. Devillers-Thiery, C. Mulle, N. Hussy, S. Bertrand, M. Ballivet, and J. P. Changeux. 1991. Mutations in the channel domain alter desensitization of a neuronal nicotinic receptor. Nature. 353:846–849. [DOI] [PubMed] [Google Scholar]
- Sankararamakrishnan, R., C. Adcock, and M. S. Sansom. 1996. The pore domain of the nicotinic acetylcholine receptor: molecular modeling, pore dimensions, and electrostatics. Biophys. J. 71:1659–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholtz, J. M., and R. L. Baldwin. 1992. The mechanism of α-helix formation by peptides. Annu. Rev. Biophys. Biomol. Struct. 21:95–118. [DOI] [PubMed] [Google Scholar]
- Sitkoff, D., N. Ben-Tal, and B. Honig. 1996. Calculation of alkane to water solvation free energies using continuum solvent models. J. Phys. Chem. 100:2744–2752. [Google Scholar]
- Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculations of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- Tieleman, D. P., H. J. Berendsen, and M. S. Sansom. 1999. Surface binding of alamethicin stabilizes its helical structure: molecular dynamics simulations. Biophys. J. 76:3186–3191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unwin, N. 1995. Acetylcholine receptor channel imaged in the open state. Nature. 373:37–43. [DOI] [PubMed] [Google Scholar]
- Wang, Z. Z., S. F. Hardy, and Z. W. Hall. 1996. Assembly of the nicotinic acetylcholine receptor. The first transmembrane domains of truncated α- and δ-subunits are required for heterodimer formation in vivo. J. Biol. Chem. 271:27575–27584. [DOI] [PubMed] [Google Scholar]
- Warshel, A., and A. Papazyan. 1998. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 8:211–217. [DOI] [PubMed] [Google Scholar]
- White, S. H., and W. C. Wimley. 1999. Membrane protein folding and stability: physical principles. Annu. Rev. Biophys. Biomol. Struct. 28:319–365. [DOI] [PubMed] [Google Scholar]
- Zimm, B. H., and J. K. Bragg. 1959. Theory of the phase transition between helix and random coil in polypeptide chains. J. Phys. Chem. 31:526–535. [Google Scholar]