Electrophysiological Analysis of the Yeast V-Type Proton Pump: Variable Coupling Ratio and Proton Shunt

Abstract

Isolated vacuoles from the yeast Saccharomyces cerevisiae were examined in the whole-vacuole mode of patch recording, to get a detailed functional description of the vacuolar proton pump, the V-ATPase. Functioning of the V-ATPase was characterized by its current-voltage (I-V) relationship, obtained for various levels of vacuolar and cytosolic pH. I-V curves for the V-ATPase were computed as the difference between I-V curves obtained with the pump switched on (ATP, ADP, and P_i present) or off (no ATP). These difference current-voltage relationships usually crossed the voltage axis within the experimental range (from −80 to +80 mV), thus measuring the reversal voltage (E_R) for the V-ATPase, which could be compared with the standing ion gradients and free energy of ATP hydrolysis, to calculate the apparent pump stoichiometry or coupling ratio: the number of protons transported for each ATP molecule hydrolyzed. This ratio was found to depend strongly upon the pH difference (ΔpH) across the vacuolar membrane, being ∼2H⁺/ATP at high ΔpH (4 pH units) and increasing to >4H⁺/ATP for small or zero ΔpH. That result is in quantitative agreement with previous determinations on plant vacuoles. Considerations of purely electrical behavior, together with the physical properties of a recent detailed structural model for V-ATPases, led to a linear equivalent circuit—which quantitatively accounts for all observations of variable coupling ratios in fungal and plant V-ATPases by variations of the conductance for bona fide proton pumping (G_P) through the ATPase relative to independent proton shunting (G_S) through the same protein.

INTRODUCTION

Plant and fungal vacuoles, which can occupy from 10% to 90% of total cell volume in most plant cells, are multifunctional compartments playing a wide range of essential roles in cellular metabolism: long-term and short-term storage, lysosomelike degradation, detoxification, osmoregulation, and ion homeostasis—especially of calcium ions and of protons, namely, cytoplasmic pH regulation. All of these processes involve transport of solutes, ionic or otherwise, across the membrane separating vacuolar contents from other cytoplasmic constituents: i.e., across the vacuolar membrane or tonoplast.

Vacuolar membranes, like most other organellar membranes and all cellular plasma membranes, carry out three types of solute transport: 1), primary active transport, i.e., enzyme-like carriers (or pumps) conduct thermodynamically uphill movement of ions driven by a primary energy source (e.g., light, redox energy, ATP or pyrophosphate); 2), secondary active transport, i.e., uphill movement of one species is directly coupled to the downhill movement of another; and 3), strictly passive transport, i.e., downhill movements only, which are mediated either by pores/channels in the membrane, or by carriers that are not coupled to metabolic free energy.

Within this hierarchy, it is ultimately primary active transport which provides the energy for secondary active transport, and restores the gradients dissipated by strictly passive transport. In plant and fungal vacuolar membranes, there are two types of proton pumps operating via primary active transport mechanisms, one of which extracts energy from the hydrolysis of pyrophosphate (the so-called H⁺-PPase), and the other from hydrolysis of ATP (the so-called V-ATPase). The tonoplast of Saccharomyces cerevisiae does not contain an H⁺-PPase, but only a V-type H⁺-ATPase, which is defined in genetic and molecular terms. This V-ATPase transports only protons, without coupling to other ions, thus transferring one net charge from cytoplasm to vacuolar lumen for each proton pumped into the vacuole (Nishi and Forgac, 2002). Consequently, the yeast V-ATP-ase normally develops both a trans-tonoplast difference of electric potential (cytoplasm negative) and a trans-tonoplast difference of pH (cytoplasm alkaline).

If the pump is tightly coupled and if parallel ionic conductivities are negligible, the relationship among the equilibrium voltage, E_p, i.e., the electromotive force (EMF) of the pump, the proton concentrations on the two sides of the membrane, and the energy from hydrolysis of ATP can be derived from the mass reaction equation for the overall pumping process as

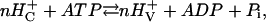(1)

by introducing the respective electrochemical potentials

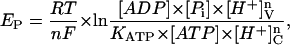(2)

where K_ATP is the apparent equilibrium constant for ATP hydrolysis, R, T, and F have their usual meanings, n is the number of H⁺ translocated per ATP split (the coupling ratio), brackets represent chemical concentrations of the reactants, and v, c denote the vacuolar and cytosolic compartments, respectively.

For a tightly coupled reaction (Eq. 1) and neglecting parallel ionic pathways, E_P should equal the measured reversal voltage, E_R, the voltage at which membrane current is zero. Then, the coupling ratio (n) of the V-ATPase reaction can be calculated from Eq. 2 as

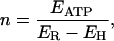(3)

with

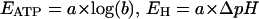and

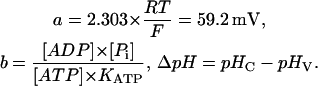The parameter b changes with cytosolic pH, since K_ATP is a function of pH_C (see Table 1). As can be seen from Eq. 3, calculation of n requires that the several concentration terms are known, and that a rational value can be assigned to K_ATP.

TABLE 1.

Estimated standard free energy for ATP hydrolysis

pHC	8.5	7.5	6.0	5.0
Free Mg2+/mM	0.28	0.33	0.94	2.50
Free Mg-ATP/mM	3.2	3.3	2.95	1.85
−ΔG0 (KJ/mol)	45.2	39.8	36.0	36.2
KATP (106 M)	83.8	9.47	2.04	2.21

Values calculated for ATP medium, containing 125 mM KCl, 5 mM MgCl₂, 5 mM K₂-ATP, 5 mM K-ADP, 10 mM KH₂PO₄, 0.5 mM EGTA, and 5 mM MES titrated to the given pH with Tris base; calculated ionic strength was ∼0.2 M. Free Mg²⁺ and Mg-ATP concentrations were obtained via the algorithm calcium.exe (Ver. 2.1), developed by Föhr et al. (1993). ΔG₀ values were extracted from Alberty (1968).

The experiments described below were designed to take advantage of the isolated vacuole preparation from Saccharomyces cerevisiae (Bertl and Slayman, 1990; Kettner et al., 2003), and the patch-clamp technique, to determine the coupling ratio of this particular V-type ATPase/proton pump over a wide range of pH values (cytoplasmic and vacuolar) and under conditions where no competing transport processes are operating. These experiments were prompted by earlier reports that vacuolar ATPases can adjust their coupling ratio according to the magnitude of the hydrogen-ion gradient (pH difference) against which they must work (Davies et al., 1994; Müller and Taiz, 2002; Yabe et al., 1999).

The experimental data from yeast tonoplasts generally confirm the earlier findings on lemon, beet, and other plant vacuolar membranes, but considerations of the nature of the data from which variable coupling ratios are deduced, for the V-ATPases, suggests a straightforward and physically simple interpretation: namely, proton shunting through the pump mechanism, which—because of the usual direction of the electrochemical gradient—would flow predominantly in the reverse direction through the pump. This proton flux would depend upon the presence of ATP, since V-ATPases deprived of ATP do not leak protons (see Grabe et al., 2000), but would not be coupled either to ATP synthesis or to ATP hydrolysis.

MATERIALS AND METHODS

Strains and solutions

The tetraploid strain Y588 (Mirzayan et al., 1992) of Saccharomyces cerevisiae was used for all patch-clamp experiments on isolated vacuoles, and the cells were grown, protoplasted, and treated as previously described (Bertl and Slayman, 1992; Bertl et al., 1998), before gentle osmotic lysis for releasing the vacuoles.

Experiments were started under symmetrical ionic conditions, in which the pipette solution (for the vacuole interior) was the same as the bath solution (replacing cytoplasm), and with continuous perfusion of bath solution through the recording chamber. Starting solution (standard bath medium), contained 150 mM KCl, 5 mM MgCl₂, 0.5 mM EGTA, and 5 mM MES titrated to pH 7.5 with Tris base. ATP, ADP, and P_i (inorganic phosphate) were added to the bath solution as potassium salts, and KCl was diminished to keep the total bath K⁺ concentration constant. Bath solution supplemented with ATP alone (ATP medium) contained 5 mM K₂-ATP and 140 mM KCl plus the other salts, and bath solution supplemented with ATP/ADP/P_i (AAP medium) contained 5 mM K₂-ATP, 5 mM K-ADP, 10 mM KH₂PO₄, and 125 mM KCl plus the other salts.

Recording and analysis

Patch-recording was carried out with an EPC-9/ITC-16 amplifier and data acquisition system (HEKA, Lamprecht, Germany). Data were accumulated at 10 kHz, filtered at 100 Hz, and sampled either at 1 kHz (for I-V analysis) or at 30 Hz (for continuous current recordings), then stored to the computer hard drive. Steady-state current-voltage recordings were made in the whole-vacuole configuration, using linear voltage ramps of 5 s duration running from a membrane voltage (V_m) of −80 mV to +80 mV, and the corresponding whole-vacuole currents were measured.

Current-voltage (I-V) curves describing the characteristics of the V-ATPase were obtained by subtracting each I-V curve for a nonenergized membrane (without ATP) from the corresponding I-V curve for the energized membrane (ATP added); or (as shown previously by Kettner et al., 2003), in the continued presence of ATP by blocking the V-ATPase with bafilomycin, and subtracting the resulting I-V curve from the unblocked control. Under these experimental conditions, Mg-ATP does not induce any spurious ionic currents or conductances in yeast tonoplasts, so the reported difference I-V curves do indeed characterize the yeast V-ATPase itself. Also, Mg-ATP is not a limiting factor in our experiments, since the pump K_M value for Mg-ATP is ∼50 μM (Kettner, 1999) and the experimental free Mg-ATP concentration is between 1.8 and 3.3 mM, depending on the cytosolic pH (see Table 1).

However, to compare I-V data from vacuoles of different sizes and to obtain averaged curves from all of those actually measured under any one condition, the I-V plots shown were scaled to current densities (mA/m²), by dividing each vacuole-membrane area into the corresponding measured currents. Membrane areas were determined from capacitance measurements on each tonoplast, assuming a specific membrane capacitance of 1 μF/cm² (standard for most biological membranes). Measured capacitances ranged from 2 to 7 pF, implying membrane areas of 200–700 μm².

The sign convention proposed by Bertl et al. (1992) for tonoplast voltage and current was used throughout; i.e., the vacuole interior was treated like the cell exterior, and tonoplast voltage was calculated as cytoplasmic potential minus vacuolar potential.

RESULTS

Reversibility of the yeast vacuolar V-ATPase/proton pump

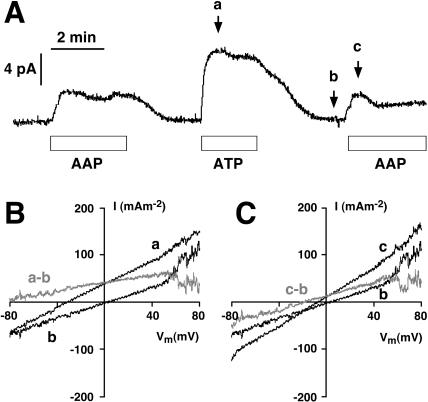
Records from a typical whole-vacuole patch-clamp experiment (from a set of 14 experiments) on an isolated yeast vacuole are shown in Fig. 1, for which a pH difference of 2.5 pH units (pH_C = 7.5; pH_V = 5) was imposed. Recording began ∼5 min before the trace of Fig. 1 A, with the standard bath solution. With the membrane voltage clamped to zero the baseline or reference current (short-circuit current) was neglectable. When AAP medium was flushed through the chamber, current rose to ∼4 pA, then declined to the baseline upon washout with standard bath solution. After 1 min of washing, ATP medium was flushed through the chamber and the same pattern of short-circuit current was repeated, except that the maximal current was ∼9 pA instead of 4 pA. The direction of the current, upward or positive by the standard convention (Bertl et al., 1992), designates a flow of positive charge from the cytosolic side to the vacuolar side of the tonoplast. The smaller peak current (4 pA) obtained in the presence of ADP and P_i along with ATP can be explained by competitive inhibition of the pump by ADP (Kettner et al., 2003).

FIGURE 1.

The basic experiment: ATP activates an outward current (cytoplasm to vacuole) through the short-circuited vacuolar membrane of yeast. (A) Current trace from a yeast vacuole recorded in the whole-vacuole configuration with the membrane voltage-clamped to 0 mV. Symmetrical ionic conditions with pH_C = 7.5 and pH_V = 5. The bars below the traces indicate perfusion of the recording chamber with 5 mM ATP + 5 mM ADP + 10 mM P_i (AAP), or with 5 mM ATP (ATP), respectively. Voltage ramps of 5 s duration were applied at the arrows marked a, b, and c, and the corresponding I-V curves are shown in B and C. (B) I-V curves taken from the vacuole in A, at times indicated by the arrows. Curve a describes the tonoplast I-V characteristics in the presence of 5 mM ATP, and curve b, that of the nonenergized membrane. The difference curve (a–b) characterizes the V-ATPase. With only ATP present at the cytosolic side, the pump curve never intersected the voltage axis; the apparent increase of pump current at positive voltages was due to ion channel activity in the control (curve b). (C) I-V curves from the vacuole in A, describing the membrane energized by 5 mM ATP + 5 mM ADP + 10 mM P_i (curve c), compared with the control (curve b). The pump I-V curve (c–b) clearly intersects the voltage axis at ∼−20 mV, indicating that the pump runs in the reverse direction when the driving force (membrane voltage) is sufficiently large (negative to −20 mV). As in B, the dip at the positive end of the difference I-V trace is due to channel activity in the control curve.

Voltage ramps of 5 s duration from −80 mV to +80 mV were imposed at three times: 1), at the peak of current in ATP medium; 2), at the recovered baseline; and 3), at the peak of current in AAP medium. Current data obtained from these voltage ramps were scaled by the membrane area (the vacuole was ∼9 μm in diameter), and are plotted (black traces) against the clamped voltage. In Fig. 1, B and C, the difference I-V curves, gray traces a–b and c–b, define the current-voltage relationships for the V-ATPase in the two different media, ATP and AAP. It was shown previously (Kettner et al., 2003), that the difference currents become zero in the presence of bafilomycin, a specific inhibitor of V-ATPases. For the medium charged with only ATP, where the free energy of ATP hydrolysis is not well-defined, the reversal voltage (E_R) for the ATPase could not be determined, since it lay in the far negative range of membrane voltage (E_P → −∞ for [ADP] and/or [P_i] = 0; see Eq. 2). But with the ATP/ADP/P_i mixture, E_R fell at ∼−20 mV. Thus, although no attempt was made to measure actual ATP synthesis, it was clear that current could be driven either inward or outward through the V-ATPase, depending upon what voltage was imposed on the tonoplast.

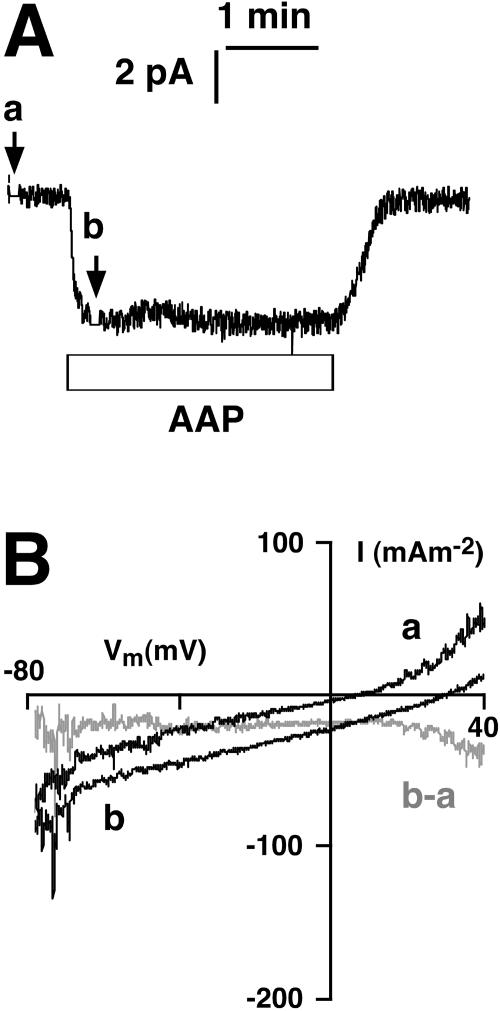
Fig. 2 displays results from one out of three experiments designed explicitly to demonstrate reversed current through the H⁺ pump. Cytoplasmic pH was set at the usual value of 7.5, and vacuolar pH (pipette solution) was set at 3.1, thus exerting a diffusional force (E_H) equivalent to 260 mV directed toward the cytoplasm. With the vacuolar membrane voltage clamped to zero, when cytoplasmic standard medium was replaced by AAP, a current of nearly 5 pA flowed into the cytoplasm—the reverse direction for the pump, as shown by the downward shift of the trace in Fig. 2 A. This inward current was steady for almost 3 min, until AAP was flushed out of the chamber, which brought the pump current back to the baseline.

FIGURE 2.

ADP and P_i activate an inward current (vacuole to cytoplasm) through the short-circuited vacuolar membrane (V_m = 0), when the vacuole is sufficiently acidic. (A) Experiment similar to the left-hand third of Fig. 1 A, except that vacuolar pH was 3.1 compared with cytosolic pH of 7.5. Bar below the trace (AAP) indicates perfusion of the chamber with 5 mM ATP + 5 mM ADP + 10 mM P_i. Again, the arrows a and b indicate times when the 5 s voltage ramps were applied to the tonoplast. The downward current elicited by AAP indicates that the pump runs backward under these experimental conditions. (B) I-V analysis of A, similar to Fig. 1 C, but describing the ATPase reaction to the very acid vacuole (pH_V = 3.1). The difference curve (b–a) is constant over the voltage range −80 mV to +40 mV. Under these conditions, the membrane becomes rather unstable, evidenced by the large current fluctuations at extreme voltages. Under these conditions the reversal voltage for the pump could not be determined.

Standard voltage ramps were imposed at the arrows, and the resultant I-V tracings (a, b), are reproduced in Fig. 2 B, again scaled to the membrane surface area. In this case the difference I-V plot (b–a) was almost flat, but displayed too much fluctuation at the voltage extremes to allow extrapolation to a reliable value for E_R. It is safe to conclude only that the value lay positive to +40 mV.

Coupling ratio versus stoichiometry

The structures of V-ATPases are now sufficiently well-known (see Finbow and Harrison, 1997; Grabe et al., 2000; Grüber et al., 2001; Nishi and Forgac, 2002; Arata et al., 2002) that an ideal stoichiometry of operation can be specified: each 360° turn of the rotor carries six proton-transfer sites past three ATP-hydrolytic sites, so that two protons should be pumped for each ATP molecule split. Several reports in the literature have confirmed a stoichiometry of 2 for the vacuolar ATPase, e.g., in red beet (Bennett and Spanswick, 1984; Schmidt and Briskin, 1993), but more recent reports have appeared of 3, 4, or even more protons being transferred for each ATP hydrolyzed (Davies et al., 1994; Yabe et al., 1999; Müller and Taiz, 2002), depending on membrane voltage and on ion concentrations at both sides of the membrane. These results have forced general use of the operational term coupling ratio, to refer to measurements of H⁺/ATP, rather than to the structural inferences. And indeed, it is the coupling ratio, not the ideal stoichiometry, which reflects the internal dynamics of the pumping process.

From Eq. 3, E_R—the EMF which the V-ATPase can generate—must decline as the ratio of protons transferred per ATP molecule split (n) increases; or else n must increase as the measured reversal voltage approaches E_H.

Obviously, however, the necessary calculation of (n) can be carried out via Eq. 3 only when E_R can be determined experimentally and when all of the chemical concentration terms are known: namely, [ATP], [ADP], [P_i], and [H⁺] at the cytoplasmic surface of the tonoplast (chemically reactive side of the ATPase), and [H⁺] at the vacuolar side: in Fig. 1 A, for the first and third current peaks, obtained in AAP medium; but not for the second current peak, obtained with ATP only.

pH dependence of the I-V characteristic

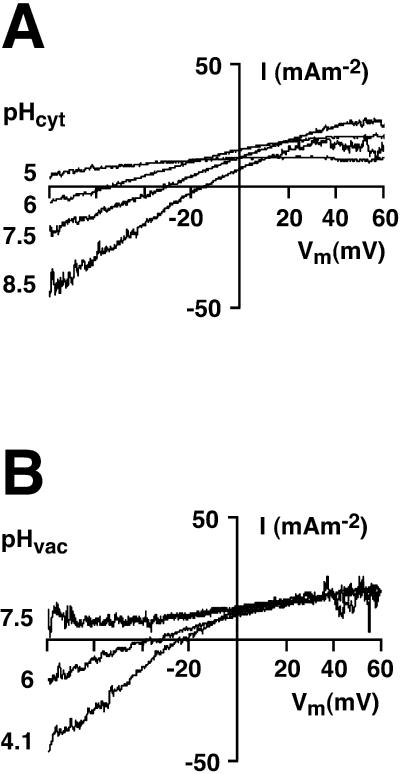
We therefore carried out a series of patch-clamp experiments, analogous to those of Fig. 1, on isolated yeast vacuoles which were specifically energized by fixed concentrations of ATP, ADP, and P_i (see Materials and Methods) and beset with a range of pH values, both cytoplasmic and vacuolar. The resulting averaged difference I-V curves, representing explicitly the behavior of the V-ATPase, are plotted in Fig. 3. For Fig. 3 A, vacuolar pH (pipette solution) was held at 5.0, and cytoplasmic pH (bath solution) was varied from 5.0 to 8.5. Well-determined values of E_R emerged for the three higher cytoplasmic pH values: −59.8 mV, −34.0 mV, and −17.5 mV, respectively, for pH_C = 6.0, 7.5, and 8.5. For Fig. 3 B, cytoplasmic pH was held at 7.5, and vacuolar pH was varied from 7.5 to 4.1. Well-defined values of E_R emerged for the two lower pH values: −38.6 mV and −25.6 mV, respectively, for pH_V = 6.0 and 4.1. In both cases with zero pH difference across the tonoplast (a traces), E_R could not be determined, but clearly lay negative to −80 mV, the largest negative voltage which could reliably be sustained without membrane breakage.

FIGURE 3.

The reversal voltage for the yeast V-ATPase shifts positive with alkalinization of the cytoplasm (A), and negative with alkalinization of the vacuole (B). Averaged difference I-V curves are shown for at least three recordings under each condition; pumping was activated in each case by AAP medium, and the I-V curves were generated as in Fig. 1, B and C, and Fig. 2 B. (A) Vacuolar pH set at 5.0; cytosolic pH varied as indicated from 5 to 8.5. With symmetrical pH (pH_V = pH_C = 5), there is no intersection of the I-V curve with the voltage axis within the applied voltage range of −80 mV to +60 mV. With a pH difference of 1 unit, the reversal voltage (E_R, the intersection of the difference I-V curve with the voltage axis) was roughly −60 mV; and it shifted to more positive voltages as the pH gradient increased. Pump currents saturated at positive membrane voltages. (B) Cytosolic pH set at 7.5; vacuolar pH varied as indicated from 7.5 to 4.1. As in A, the pump I-V curve failed to intersect the voltage axis under symmetrical pH conditions (pH_V = pH_C = 7.5). At a ΔpH of 1.5 the reversal voltage was ∼−40 mV and shifted again toward positive voltages with the pH difference increased.

In summary, only when a definite pH difference was imposed across the vacuolar membrane did a clear intersection of the pump curve with the voltage axis become evident; and that intersection, E_R, shifted in the positive direction as ΔpH increased. The apparent saturation of current at high membrane voltages (+ or −) is most likely the consequence of rate limitation by chemical reactions, such as substrate binding and/or release (i.e., of ATP, ADP, P_i, or protons), rather than by voltage-dependent membrane-transit reactions (Hansen et al., 1981; Davies et al., 1996).

ΔpH dependence of E_R and n

To actually calculate n from the measured E_R it is necessary to know not only the concentrations of protons, ATP, ADP, and P_i, but also K_ATP or the standard free energy for ATP hydrolysis (ΔG₀) under the different conditions of these experiments. Reasonable approximations can be obtained from the classic work of Alberty (1968), along with calculations of the corresponding free Mg²⁺ concentrations and ionic strength (Föhr et al., 1993). The necessary information is set out in Table 1.

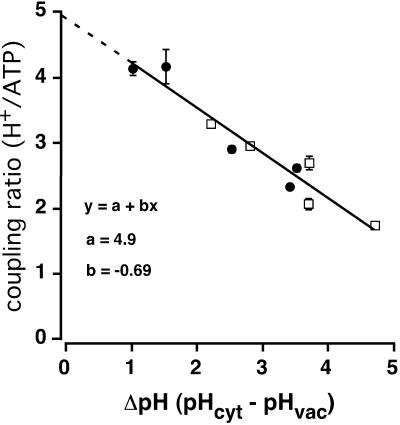
The results in Fig. 3, the experimental concentrations, and the values of K_ATP in Table 1 were applied to Eq. 3 to calculate the corresponding values of n, which are shown in Table 2 and plotted (solid circles) in Fig. 4. These numbers from the yeast vacuole are also compared with the previous results of Davies et al. (1994) from red beet vacuoles (unfilled squares in Fig. 4). The overall plot, which has been fitted by a simple regression line, demonstrates two remarkable facts: 1), the current-voltage behavior of the V-ATPase in yeast tonoplast is essentially identical with that previously described in red beet tonoplast; and 2), the empirical relationship between the coupling ratio (n) and the pH difference across the vacuolar membrane, (pH_C–pH_V), is linear for at least four units of ΔpH, and does not depend on either the vacuolar pH or the cytoplasmic pH, individually.

TABLE 2.

Calculated coupling ratios (n), shunt ratios (n–N), and relative conductance ratios (G_S/G_P) for the yeast V-ATPase

pHC	pHV	ΔpH	EATP/mV	EP/mV N = 2	ER/mV mean ± SE	EH/mV	n (H+/ATP) mean (min, max)	Shunt ratio (n–N)	Relative conductance (GS/GP)
7.5	3.1	4.4	−531.4	−5.2	>+40 (3)	260.5	>2.4	>0.4	>0.20
8.5	5.0	3.5	−587.5	−86.5	−17.5 ± 5 (6)	207.2	2.61 (2.56, 2.67)	0.61	0.307
7.5	4.1	3.4	−531.4	−64.4	−25.6 ± 1 (4)	201.3	2.34 (2.33, 2.35)	0.34	0.171
7.5	5.0	2.5	−531.4	−117.7	−34 ± 4 (14)	148.0	2.92 (2.86, 2.98)	0.92	0.461
7.5	6.0	1.5	−531.4	−176.9	−38.6 ± 9 (3)	88.8	4.17 (3.90, 4.50)	2.17	1.086
6.0	5.0	1.0	−491.9	−186.8	−59.8 ± 3 (9)	59.2	4.13 (4.03, 4.24)	2.13	1.067
5.0	5.0	0.0	−494.0	−247.0	<−80 (5)	0	<6.2	<4.2	<2.09
7.5	7.5	0.0	−531.4	−265.7	<−80 (4)	0	<6.6	<4.6	<2.32

Values of n were calculated, via Eq. 3, using the measured values of E_R (column 6) taken from Fig. 3, and values of E_ATP calculated from K_ATP values in Table 1. Mean values for E_R, are given with the SE of the mean and the number of trials for each experiment in parentheses. Calculated numbers for the coupling ratio n are listed as mean values together with the minimum and maximum values derived from the error limits of E_R by using Eq. 3. The shunt ratio and relative shunt conductance (right two columns) were calculated using an ideal stoichiometry (N) of 2.

FIGURE 4.

For yeast (•) and plant (□) V-ATPases, the coupling ratio declines linearly with increasing ΔpH. Solid circles denote coupling ratios calculated from Fig. 3, above, as described by Eq. 3. Unfilled squares are taken from Davies et al. (1994), for coupling ratios of red beet vacuoles. Error bars of solid circles denote the min and max values of n as shown in Table 2, column 8, and error bars of unfilled squares the min and max values of n as given by Davies et. al. (1994). The solid curve was fitted by least squares to the equation y = a + bx, with y being the coupling ratio and x being ΔpH (a = 4.9; b = −0.69).

The change in coupling ratio for the vacuolar proton pump was ∼0.7 (H⁺/ATP) per ΔpH unit for both preparations, and the excellent agreement between the two indicates a high degree of conservation of V-ATPase function between plants and fungi. At the highest practical ΔpH (4–5 units), n was ∼2 H⁺/ATP, very close to the ideal stoichiometry expected from structural data (Finbow and Harrison, 1997; Grüber et al., 2001; Nishi and Forgac, 2002; Arata et al., 2002). The ratio would increase to, or even perhaps increase beyond, 5 H⁺/ATP, with a ΔpH = 0, as indicated by the extrapolated line (dashed) in Fig. 4.

Interpretation of variable coupling ratios: noncoupled ion movements

As was discussed above, the ideal stoichiometry which can be inferred for V-ATPases, based on structural information, is 2 H⁺ ions transported for each ATP molecule split. The ideal stoichiometry, now represented generally as N, apparently equals the calculated n for large values of ΔpH (∼4), in both the yeast V-ATPase and the red beet V-ATPase, as demonstrated in Fig. 4. Measured deviations from the ideal stoichiometry, for many different pumps and transporters, as well as for V-ATPases, have frequently been referred to as slip, usually meaning that one-half of the implied reaction couple of Eq. 1 can occur without the other half. That definition was explicitly broadened by Grabe et al. (2000), in a detailed physical-chemical model for V-ATPases, to include possible half reactions and total bypass for protons, which they termed proton slip flux. According to Grabe et al. (2000), proton slip flux includes 1), flux of protons that enter the rotor sites from the basic reservoir, make a full 360° turn, and dissociate back into the basic reservoir. This proton slip flux, i.e., J₁, is not associated with a net charge transport; and 2), “a leak flux of protons (J₂) shuttled by rotor sites that fluctuate between the output channel and input channel.” This flux carries a downhill proton current.

Both to avoid confusion with these more complicated ideas, and to associate our elementary model with its electrical properties, we have attached the term proton shunt to the mechanism that seems likely to underlie variable coupling ratios in the V-ATPase.

Referring to Eq. 3 above, it is clear that any process in the vacuolar membrane which moves E_R toward E_H should elevate the calculated value of n. Such a process could, in principle, be unrelated to the V-ATPase, but the design of these experiments implies that such a process must be part of the V-ATPase chemistry, because the difference I-V curve from which E_R was obtained reflects only the pump I-V characteristic. That is, shutdown of the pump by ATP removal gave exactly the same result as shutdown by blockade with the specific inhibitor bafilomycin (Kettner et al., 2003). Then the calculated difference between the coupling ratio (n) and the ideal stoichiometry (N), n–N, would represent the shunted proton flux, or better designated, the shunt ratio, after the general use of the operational term coupling ratio.

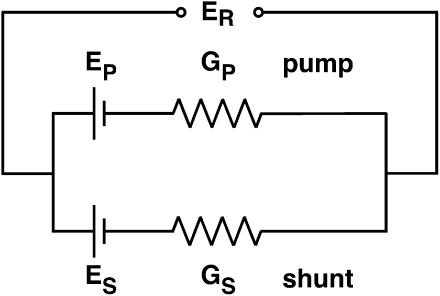
Conceptually, a proton shunt through the enzyme is just the simplest way to displace E_R toward E_H; and the quantitative consequence of such a shunt can readily be derived via a simple linear equivalent circuit, as drawn in Fig. 5. There, one limb represents the coupled pathway through the enzyme, with E_P and G_P designating the EMF and internal conductance of the pump pathway; and the second limb represents the shunt pathway, with E_S and G_S designating its EMF and intrinsic conductance. From the equivalent circuit, E_R is given by

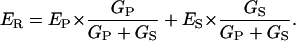(4)

For a tightly coupled V-ATPase, the relationship between the electromotive force E_p and the stoichiometry N of the pump is

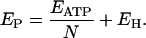(5)

Inserting Eq. 5 into Eq. 4 and letting E_S be equal to E_H (for a proton conductance) gives

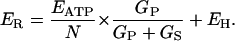(6)

When this result is substituted into Eq. 3, then

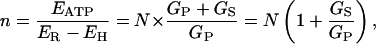(7)

so that, finally, the shunt ratio n–N becomes

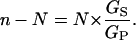(8)

In other words, the shunt ratio for the V-ATPase is simply the product of its design transport stoichiometry (N, for H⁺:ATP) and the relative shunt conductance (or permeability) for protons through the enzyme. As listed in Table 2 (column 9) for the above experiments, values of the shunt ratio varied by a factor of ∼10, from ∼0.4, when the cytoplasmic solution was 4.4 pH units alkaline to the vacuole, to ∼4 when the cytoplasmic and vacuolar solutions were at the same pH. The relative conductance of the shunt, G_S/G_P, varied by the same factor, but reduced by 0.5 (1/N).

FIGURE 5.

Electrical equivalent circuit for V-ATPases, incorporating separate conductances for proton pumping and for proton shunting. E_P and E_S, intrinsic EMF values for the pump and shunt pathways; G_P and G_S, conductance of the two pathways.

DISCUSSION

Mechanistic versus effective stoichiometry (slip)

The question at the heart of observations of variable coupling ratios in ion transporters is whether that variability reflects changes in reaction stoichiometry within the basic transport cycle, or, instead, changes of unrelated or alternative processes within the protein. In a TIBS discussion forum from two decades ago (Konings and Booth, 1981), two viewpoints were argued: 1), that mechanistic stoichiometry does indeed vary; or 2), that only effective stoichiometry varies. The first viewpoint is more interesting, because it would allow transporters to maintain quasiconstant effectiveness in the face of varying transport gradients: in Table 2, for example, hydrolysis of a single ATP molecule appears able to energize the flow of 2.9 protons against a proton concentration difference of 2.5 pH units, but 4.1 protons against a pH difference of 1.5 units. And at that time, at least one case was documented where a switch from N = 1 to N = 2, in a plasma membrane proton pump, would have optimized the pump for maximal ion flux in energy-replete cells (N = 1) and for maximal energetic efficiency in energy-restricted cells (N = 2; Warncke and Slayman, 1980).

With specific respect to V-ATPases, changes in mechanistic stoichiometry can be envisioned, e.g., if the six proton binding sites (one per subunit c of the V₀ domain) differ in their pK_a. Then, binding sites with a high pK_a could be withdrawn from the transport cycle by staying protonated when exposed to an acidic vacuolar lumen, thus reducing the coupling ratio.

Experimental evidence for a possible change in mechanistic stoichiometry has been reported for a closely related F-ATP synthase (Rastogi and Girvin, 1999). The proteolipid subunit c, bearing the proton binding site, has a different conformation at acidic and basic pH values. At pH ∼ 5, the protonated binding site appears to be buried within the rotor, whereas at pH ∼ 8, the deprotonated binding site seems to be at the rotor periphery. If the same circumstance holds for V-ATPases, positioning at low vacuolar pH would expose fewer potential H⁺-transporting sites to surface exchange, so that pump stoichiometry should be low with acidic vacuolar pH and high with alkaline vacuolar pH. This prediction is in rough agreement with our data: at acidic pH (ΔpH = 4), the coupling ratio is near 2.5, whereas at alkaline pH (ΔpH = 0), it rises toward 5. But a stoichiometry of N > 2 would require cryptic proton binding sites not explicitly recognized in structural models of the V-ATPase. Even though three distinct c-subunit homologs compose the rotor of yeast V-ATPase, with a stoichiometry of 4–5:1:1, each subunit bears only a single known H⁺-binding site.

History has come down in favor of the second viewpoint, in part because of intrinsic difficulties like that just discussed for the V-ATPase, but also in part because the second is less demanding and admits a multitude of details, most of which do not involve energy conservation or optimization of efficiency. (Indeed, most actually involve modulation of energy dissipation, as an integral part of transport regulation.) Thus, slip has become a popular redoubt for variable coupling ratios: the execution of only one of a pair of normally coupled steps, during the full reaction cycle of a transport protein. ATP might be hydrolyzed without the normally coupled flux of protons, the transport enzyme nevertheless returning to its initial state; or protons might leak through the enzyme without the hydrolysis of ATP. This kind of mechanism is at heart probabilistic, with experimental circumstances determining the operant probability for each half reaction or the whole reaction to take place. The idea of slip, or uncoupling, has been applied to variable stoichiometries in a wide range of transporters, including V-ATPases, the Na⁺,K⁺-ATPase (Cornelius, 1990; Goldshleger et al, 1990), the SR calcium pump (Sumbilla et al., 2002), the mammalian Na⁺-glucose co-transporter SGLT (Chen et al., 1995), Na⁺-coupled amino acid transport in rabbit intestine (Paterson et al., 1980), and the yeast cytosine transporter (Eddy et al., 1994).

Proton shunt for the yeast V-ATPase

Ion shunting, as postulated here for the yeast V-ATPase, can be viewed as a type of slip, but that is not the only possibility. The overall structural similarities between channels and carriers which have emerged over the past 10 years suggest that under sufficient stress, all carrier-type transporters will occasionally open enough to transmit ions in channel fashion. Such behavior would impact both on the measured or deduced coupling ratios and on the electrical parameters of the transport system; and it could well have been used in evolution to modulate transport processes, albeit at the expense of energetic efficiency. Although coupling ratios inferred from thermodynamic measurements alone (Davies et al., 1994; Yabe et al., 1999) are, in principle, especially vulnerable to errors from ion shunting, V-ATPase coupling ratios inferred from measurements of ion and substrate flux have also shown similar variability (Moriyama and Nelson, 1988; Müller et al., 1999).

An important and frankly paradoxical aspect of the shunt mechanism is that the proton flux that produces apparent variations of coupling ratio always flows downhill—which is in reverse direction to the usual proton pumping. It is the electrical effect of this proton shunting which produces the calculation of variable coupling, because resultant measurements of E_R differ significantly from E_P. Again, as E_R shifts away from E_P toward E_H, the calculated coupling ratio n must increase (see Table 2 and the text introducing Eq. 3, in the Introduction).

A second consequence of the shunt mechanism, as manifest with the yeast and plant V-ATPases, is that the shunt diminishes as the imposed driving force increases (Table 2, columns 9 and 10). Operationally, the apparent coupling ratio approaches the ideal stoichiometry of 2 H⁺:ATP with large proton gradients (vacuole > 4 pH units acid to cytoplasm), and increases as the proton gradient decreases. From an energetic point of view, that is a sensible arrangement, because it embodies negative feedback: reducing the shunt would increase the operating efficiency of ATP-driven forward proton flux (cytoplasm to vacuole), thereby aiding the formation of large gradients.

The conductances G_S and G_P are both functions of voltage and ΔpH (or E_H) which are not explicitly known. Although both could be derived by modeling pump I-V curves obtained under a range of conditions, it is actually only the ratio, G_S/G_P, which determines the deviation of E_R from E_P = E_ATP/N + E_H. In the simplest circumstances, the contribution made by proton leak to variable coupling ratios in the V-ATPase, should be largest when the electrochemical gradient—explicitly, the trans-tonoplast ΔpH or E_H—is largest. This would be true if G_S were fixed, or, more generally, under thermodynamic control. However, in an important recent mechanochemical model of the V-ATPase (Grabe et al., 2000), the leak component of slip (see Interpretation of Variable Coupling Ratios: Noncoupled Ion Movements, above) was argued to increase as conditions approach the stalling point for the enzyme: namely, as the imposed membrane voltage (V_m) approaches the reversal voltage for the whole electrochemical reaction, E_ATP/N + E_H. That prediction arose from the idea that Brownian torque (Oster, 2002) should allow the rotor maximal opportunity to wobble between the input and output proton channels within the stator of the V-ATPase, when the rapid unidirectional rotation normally driven by ATP hydrolysis is not occurring.

If proton shunting through the V-ATPase arises, in the above-discussed fashion, as a Brownian shuttle mechanism, then the per-site leak rates should be compatible with the normal turnover numbers for the enzyme. However, proton shunting could equally arise as transient disruptions of function, allowing individual molecules of the ATPase briefly to behave as bona fide channels. This could be a very rare process, but one which could still have large effects on proton flux, membrane current or voltage (absent the voltage clamp), and computed coupling ratios, because channels usually display much larger unit fluxes than do pumps and co-transporters. Typical carrier turnover numbers are in the range of 10–1000 ions/s, whereas channel turnovers range between 10⁵ and 10⁹ ions/s. Thus, only a few disrupted ATPase molecules could short-circuit the current pumped by a few hundred thousand fully coupled molecules. Obviously, there is more than ample flexibility in such numbers to modulate the conductance ratio, G_S/G_P (Table 2), over the observed 10-fold range. Such disrupted behavior could arise either accidentally, for example during normal protein degradation and recycling, or purposefully, as a component of transport regulation. Indeed, in circumstances where energy conservation is not an essential problem, such as in yeast cells fed on excess glucose (as is customary in the laboratory), channel-like shunting of ions through active transporters could be an extremely sensitive mechanism for regulating net transport.

Fortunately, the hypothesis that variable coupling ratios in the plant and yeast V-ATPases arise primarily from proton shunting is open to experimental testing. For example, with large plant-cell vacuoles, such as those from Characean algae, it should be possible to measure net proton fluxes and ATP hydrolysis associated with V-ATPase pumping, at multiple points along the current-voltage curve. And the corresponding pH measurements should also be feasible with normal-sized plant vacuoles or large fungal vacuoles (e.g., from Neurospora), by means of ion-sensitive microelectrodes. Noise measurements on lemon, sugar-beet, or yeast vacuole might also reveal channel-like events blocked by V-ATPase inhibitors, such as bafilomycin. Finally, in a genetically compliant system such as Saccharomyces, introduction of subunit mutations—especially into the a subunit (stator) and the c subunits (rotor)—could have profound and revealing effects upon measurable properties of the enzyme, including the I-V curve, reversal voltage, coupling ratio, noise characteristics, pH-dependence, salt sensitivity, and thermal sensitivity.