Excessive Counterion Condensation on Immobilized ssDNA in Solutions of High Ionic Strength

Abstract

We present experiments on the bias-induced release of immobilized, single-stranded (ss) 24-mer oligonucleotides from Au-surfaces into electrolyte solutions of varying ionic strength. Desorption is evidenced by fluorescence measurements of dye-labeled ssDNA. Electrostatic interactions between adsorbed ssDNA and the Au-surface are investigated with respect to 1), a variation of the bias potential applied to the Au-electrode; and 2), the screening effect of the electrolyte solution. For the latter, the concentration of monovalent salt in solution is varied from 3 to 1600 mM. We find that the strength of electric interaction is predominantly determined by the effective charge of the ssDNA itself and that the release of DNA mainly occurs before the electrochemical double layer has been established at the electrolyte/Au interface. In agreement with Manning's condensation theory, the measured desorption efficiency (η_rel) stays constant over a wide range of salt concentrations; however, as the Debye length is reduced below a value comparable to the axial charge spacing of the DNA, η_rel decreases substantially. We assign this effect to excessive counterion condensation on the DNA in solutions of high ionic strength. In addition, the relative translational diffusion coefficient of ssDNA in solution is evaluated for different salt concentrations.

INTRODUCTION

Investigations of DNA, immobilized on Au-surfaces, have attracted considerable attention during recent years. The reason for this widespread and interdisciplinary interest is twofold: nowadays, chip-based technology for DNA sequencing and mapping not only constitutes a powerful tool for fundamental research but, moreover, has promising application perspectives in medical treatment. In addition to already successfully employed DNA chips using fluorescently labeled DNAs and optical detection techniques, the development of electrical devices with improved possibilities with respect to miniaturization, costs, and ease of handling is particularly desirable. Besides for analytical applications, the detailed understanding of the immobilization (Herne and Tarlov, 1997; Steel et al., 1998; Huang et al., 2001; Petrovykh et al., 2003) and electrical control of DNA on metal surfaces (Kelley et al., 1998; Zhang et al., 2002; Ge et al., 2003; Edman et al., 1997) could be utilized in many different fields; e.g., site-selective gene delivery where DNA is released from microelectrodes in physiological conditions by electrical triggering (Wang et al., 1999; Takeishi et al., 2003, unpublished results).

However, apart from application-oriented research, oligonucleotides on Au-surfaces also represent a model system to study the interactions of adsorbed, highly charged polyelectrolytes with their supporting metal substrates in electrolyte solution. Recently, great theoretical effort has been undertaken to describe certain aspects of interfacial phenomena related to the adsorption of polyelectrolytes on metal surfaces in aqueous salt solutions (Netz and Andelman, 2003; Mashl et al., 1999; Dobrynin et al., 2000; Crozier and Stevens, 2003), but experimental data is still rare. As a result of the complex adsorption mechanisms (Petrovykh et al. 2003) and possible conformations of even short DNA strands on metal surfaces (Kelley et al. 1998), it is of special interest to gather experimental evidence on the question of which interaction mechanisms play a dominant role at a given parameter set of, e.g., electrolytic conditions, polyelectrolyte charge density, or electrode charge density.

In our contribution, we study the electrolytic screening effect of monovalent aqueous salt solutions on the electrostatic repulsion between single-stranded oligonucleotides and negatively biased Au electrodes. Our method to detect the release of fluorescently labeled oligonucleotides from metal surfaces provides data not only on the desorption process itself, but on the translational diffusion of ssDNAs in electrolyte solution as well.

Our results are discussed within the framework of counterion condensation theory, supporting the notion of a constant effective DNA charge over a wide range of (moderate) salt concentrations. In electrolyte solutions of high ionic strength, our experiments reveal a new regime of excessive counterion condensation on DNA.

EXPERIMENTAL PROCEDURE

Materials

All chemicals were purchased from general suppliers and used without further purification. DNA was obtained from Espec Oligonucleotide Service Corporation (Tsukuba, Japan), and the sequence of the 24-mer single-stranded (ss) oligonucleotides was 5′ Cy3-TAG TCG GAA GCA TCG AAG GCT GAT-(CH₂)₆-SH 3′. For fluorescence detection, the ssDNA was labeled with a cyanine dye, Cy3 (Amersham Life Science, Arlington Heights, IL), at the 5′ end. Au-electrodes of 1.0 or 2.0-mm diameter, respectively, were prepared on 3” single crystalline sapphire wafers, by subsequently depositing Ti(10 nm)/Pt(40)/Au(200) using standard optical lithography and metallization techniques. Before DNA adsorption, the substrates were cleaned in Piranha solution (H₂SO₄:H₂O₂:H₂O = 12:3:2) and DI-water. Immobilization of ssDNA onto the Au-surface was accomplished by exposing the electrodes to aqueous buffer solution ([Tris] = 10 mM, pH = 7.3, [NaCl] = 50 mM) containing oligonucleotides (0.05 mM) for 24 h. After the adsorption process, the electrodes were thoroughly rinsed with pure buffer solution.

Apparatus

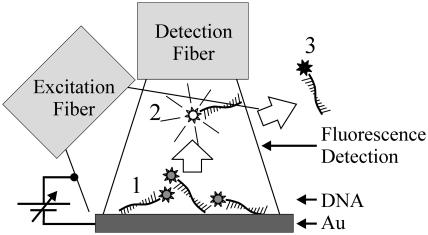
After ssDNA-adsorption onto Au-electrodes, the wafers were installed in an unsealed electrochemical cell which allowed fluorescence measurements using optical fibers. A potentiostat (Autolab PGSTAT30, Eco Chemie, Utrecht, The Netherlands) was utilized for applying bias voltages to the Au-work-electrodes with respect to a Ag/AgCl reference electrode, using a Pt-wire counter electrode, in electrolyte solution. Fluorescence measurements of the immobilized Cy3-labeled ssDNA were conducted by positioning a special fiber mount over the electrode (see Fig. 1). Here, green light from an Ar⁺-Laser (λ = 514 nm) is guided onto the electrode surface at an angle of ∼45°, whereas fluorescence from Cy3 dyes is collected by a second fiber oriented normal to the surface plane. Note that the region of fluorescence detection included not only the electrode surface but also the electrolyte volume above, defined by the intersection of the excitation and detection beams. The spot diameter on the electrode from which light could be coupled into the detection fiber was 0.7 mm, i.e., smaller than the electrode area, and the distance from the electrode surface to the detection fiber was 0.75 mm. Acquisition of Cy3 fluorescence (peak emission wavelength ∼565 nm) was done by coupling light from the detection fiber into a monochromator (using a cutoff filter centered at 530 nm to reduce laser stray light) and measuring its intensity with a cooled photomultiplier operating in single-photon-counting mode. Spectra were routinely taken before and after bias sequences and reference measurements were made on unmodified Au electrodes. For observations of bias-induced effects on the fluorescence intensity, the monochromator was set to the Cy3 peak-emission wavelength.

FIGURE 1.

Sketch of the measurement geometry. (1) Dye-labeled oligonucleotides are adsorbed on Au, but fluorescence is quenched due to the proximity to the metal surface. (2) Upon application of negative bias to the Au-electrode, the nucleotides are released into solution and float within the volume of fluorescence detection; dye fluorescence is no longer quenched. (3) Finally, ssDNA have diffused out of the active volume into a large dark reservoir, where they cannot be detected.

RESULTS AND DISCUSSION

We conducted photoluminescence measurements on dye-labeled 24-mer ssDNA, immobilized on Au-electrodes, and monitored the temporal evolution of the fluorescence signal upon applying negative bias-potential steps to the electrodes. In the following paragraphs, we will at first introduce the observed phenomenon and, by relating it to our measurement geometry, explain how characteristic parameters concerning the DNA-electrode interaction (relative desorption efficiency, time constant of release) as well as the translational diffusion of DNA in electrolyte solution can be extracted from experimental data.

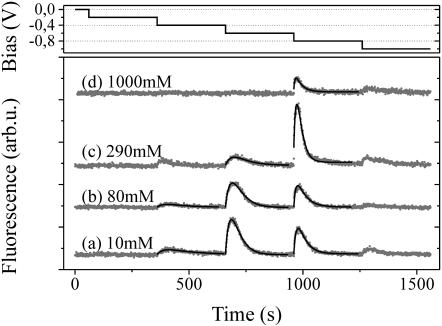
Fig. 2 a depicts the evolution of the fluorescence intensity detected at the Cy3-peak-emission wavelength over time, whereas the topmost graph shows the steplike bias sequence applied to the Au-electrode. We observe a relatively steep increase in fluorescence intensity induced by bias steps in the range from −0.4 to −1.0 V, however, predominantly at −0.6 and −0.8 V, followed by a subsequent decrease. Spectra taken at open-circuit-potential conditions before and after the bias sequence reveal that DNA-Cy3-emission can be detected from the Au-surface before, but not after, applying bias potentials more negative than −1.3 V to the electrodes (data not shown). These observations can be understood by a simple model taking into account the optical measurement geometry, as depicted in Fig. 1: before applying bias potentials to the electrode, ssDNA strands are adsorbed on the Au-surface (state 1). Here, fluorescence from the attached Cy3 dye is substantially quenched due to nonradiative energy transfer to the metal surface (Chance et al., 1978); however, it is not completely suppressed and hence detection of fluorescence emitted by adsorbed Cy3-DNA is still possible. Upon applying negative bias potentials to the DNA-supporting electrodes, electrostatic repulsion causes the negatively charged DNA to be released from the Au-surface and to float in solution underneath the detection fiber (state 2). Because of the increased distance to the metal surface, quenching of fluorescence is no longer effective, and bright Cy3 emission can be observed. Finally, due to translational diffusion, DNA strands will leave the volume of fluorescence detection for a large reservoir, denoted by the dark state 3 in Fig. 1. Supporting evidence for the validity of the suggested desorption hypothesis was obtained by the analysis of solvent relaxation effects in fluorescence spectra from Cy3-DNA subjected to different environments (Lakowicz, 1999). (We observe a distinct blue shift of 4 nm in spectra recorded during periods of high fluorescence intensity, i.e., at times after the electrodes have been subjected to a negative bias step. This behavior corresponds remarkably well to spectra of Cy3-DNA, completely dissolved in aqueous solution, where we find the same blue shift compared to emission from Cy3-DNA adsorbed on Au-surfaces.)

FIGURE 2.

Evolution of the Cy3-fluorescence intensity with time for different electrolyte salt concentrations (a–d) upon application of a steplike bias sequence to the electrode (diameter: 1 mm). Solid lines were fitted according to Eq. 3.

The qualitative understanding of the described desorption process involving three, for nucleotides, accessible states as depicted in Fig. 1, can easily be transferred to a simple rate model involving transitions in a way 1→2, followed by 2→3. Here, N denotes the number of adsorbed nucleotides (state 1) which can be released at a specific bias voltage, and M is the number of DNA molecules in state 2. The release time constant (τ_r) is characteristic for the desorption process, with 1/τ_r being the rate constant for a transition from state 1 to state 2. Similarly, the diffusion time (τ_d) characterizes the efficiency of depopulating M, i.e., a transition from state 2 to state 3.

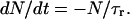(1)

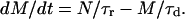(2)

Solving Eqs. 1 and 2 yields an expression for M, the number of nucleotides in state 2, as a function of time t, and N₀, the number of initially adsorbed nucleotides on the Au surface, accessible to desorption at a specific bias step.

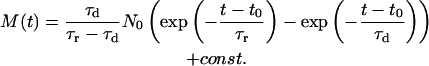(3)

We note that the effect of re-adsorption of nucleotides onto the Au-surface (2→1) was neglected during the deduction of Eq. 3, as well as the possibility that DNA strands might enter the volume of fluorescence detection from other regions in the solution (3→2). The contribution of PL-emission from adsorbed (not completely quenched) Cy3 labels as well as other contributions to background are taken into account by the additive constant. Solid lines in Fig. 2, a–d, were generated using Eq. 3 while fitting the parameters to experimental data. We find good agreement between experiment and the proposed model.

Before proceeding to the discussion of the salt-dependent measurements, we briefly address the observation that desorption of DNA can be induced not only by one distinct, but rather a series, of negative bias steps (see Fig. 2). This indicates the existence of multiple binding mechanisms and reflects the complex adsorption behavior of DNA on Au. We point out that besides a chemisorbed species, grafted to Au via the thiol-linker, a physisorbed species is also likely to be present (Herne and Tarlov, 1997; Netz and Joanny, 1999). In addition, Petrovykh et al. (2003) very recently reported on the chemical binding of thymine bases to the Au-surface. Moreover, owing to the rough microscopic topology of the Au-surface, we also anticipate local variations in the electric field strength at the surface that might affect the interaction with the adsorbed DNA.

In the following, the influence of varying 1:1 salt concentrations in aqueous solutions on the desorption behavior of ss-oligonucleotides from Au-electrodes will be discussed referring to Figs. 2 and 3. Salt in electrolyte solution was composed of 10 mM Tris (simultaneously used for buffering) and an additional amount of NaCl to set the total concentration given in the figures. Very low salt concentrations (3 and 10 mM) consisted of Tris only (at pH = 7.3, [Tris⁺] is ∼90% of the dissolved Tris-base concentration). Changing the salt concentration from 10 to 80 mM does not significantly affect the observed desorption of oligonucleotides in Fig. 2, but as c_s is further increased the threshold of bias-induced release shifts to more negative potentials and, finally, the fluorescence maximum decreases. (Reference measurements were carried out to evaluate the effects of photobleaching and salt-concentration-dependent fluorescence quenching. Characteristic photobleaching time constants of Cy3-DNA adsorbed on Au were >3 h; increasing the salt concentration from 3 mM to 1600 mM resulted in a decrease of Cy3 fluorescence of <15% ([Cy3-DNA] = 0.02 mM in aqueous solution).

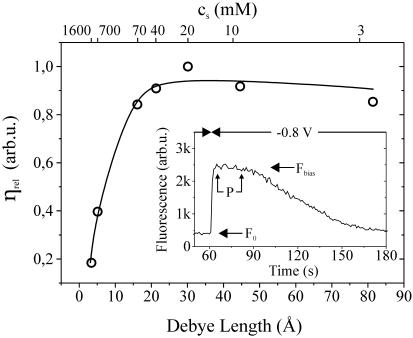
FIGURE 3.

Relative desorption efficiency η_rel for measurements in solutions of varying salt concentrations c_s, characterized by their respective Debye lengths. The inset shows a representative measurement of the fluorescence intensity over time upon switching the Au-electrode from 0 to −0.8 V (l_D = 21 Å, c_s = 40 mM). Arrows indicate the background fluorescence intensity (F₀), bias-induced fluorescence (F_bias), and the plateaulike region (P) that separates the fluorescence onset and decay. η_rel was obtained by extracting F₀ and F_bias from measured data and using Eq. 4. The solid line is a guide to the eye.

In order to quantitatively compare measurements at different salt concentrations, experiments were conducted on electrodes with larger areas (diameter = 2 mm) where only one single bias step (0 to −0.8 V) was applied while monitoring the fluorescence intensity over time. Here, salt concentrations were varied from 3 to 1600 mM, corresponding to Debye screening lengths (l_D) of 78–3.4 Å, respectively. Results of a representative measurement (c_s = 40 mM, l_D = 21 Å) are depicted in the inset of Fig. 3. Note that the altered shape of the fluorescence intensity compared to Fig. 2 is due to the increased electrode size. (Although Eq. 3 can successfully be used to analyze desorption from small electrodes, numerical fitting sometimes becomes unstable and large errors occur in the calculated parameters. Using electrodes with areas considerably larger than the detection fiber spot, on the one hand, prevents the applicability of Eq. 3, inasmuch as the precondition—that state 3 does not contain DNA at all times—is no longer strictly valid; however, on the other hand, it leads to a more straightforward interpretation of measured data, where τ_r and τ_d can be identified easily.) As a consequence thereof, we observe three distinct regions: a relatively rapid onset, an intermediate plateaulike region, and a slow decay of fluorescence intensity. To analyze the characteristic time constants of fluorescence onset and decay, single exponential functions were separately fitted to the distinct regions showing good agreement with experimental data.

As each measurement at a specific salt concentration is carried using an individual electrode, it is useful to normalize the observed fluorescence increase before comparing different measurements relative to each other. Given that the initial surface coverage is proportional to the background fluorescence intensity measured at zero bias (F₀, which is emitted from adsorbed oligonucleotides), we denote the relative bias-induced fluorescence intensity increase by the expression,

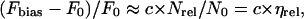(4)

with F_bias being the maximum (plateau) fluorescence intensity observed after switching to negative bias potential (see Fig. 3, inset) and c being a constant. We also note that the first term of Eq. 4 is, to a good approximation, proportional to the relative desorption efficiency (η_rel) given by the number of released nucleotides (N_rel) normalized by the number of originally adsorbed nucleotides (N₀). This proportionality seems justified since the decrease in F₀, and likewise N₀, during a desorption event is negligible, as can be seen in Fig. 2. Although this might appear puzzling at first, it becomes comprehensible when considering the extremely efficient quenching of fluorescence in the case for Cy3-DNA adsorbed on the metal surface compared to Cy3-DNA freely floating in solution. For this reason, a diminutive amount of released Cy3-DNA will cause a large transient fluorescence signal, whereas the relative decrease in background fluorescence stemming from (still) adsorbed Cy3-DNAs is too small to be measured.

A plot of the desorption efficiency versus l_D is presented in Fig. 3, indicating a relatively constant value of η_rel for a Debye length >∼10 Å, whereas for smaller values, i.e., high ionic strength, η_rel decreases considerably.

In the following, we will argue that the desorption of oligonucleotides from the Au-electrodes, after the application of a bias step, is principally occurring before a stationary potential distribution is established within the electrolyte solution adjacent to the electrode surface. The discussion will be based on two distinct experimental results.

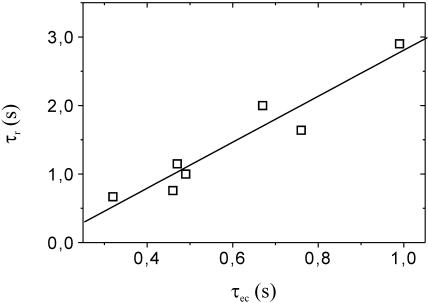
Fig. 4 presents the characteristic time constants of DNA release (τ_r, as determined by optical measurements) versus the capacitive charging time constants (τ_ec) extracted from simultaneous measurements of electrochemical (ec) current. During the charging of the ec-cell, ions within the electrolyte solution redistribute to form the Gouy-Chapman-Stern (GCS) layers at the electrode interface, set to a certain potential. As τ_ec is determined by the product of electrode capacitance and solution resistance, we find varying values of τ_ec for the individual electrodes, corresponding to variations in the respective conducting lead lengths which parasitically contribute to the electrode area that is exposed to electrolyte solution. (This is caused by the design of the electrochemical cell: nonpassivated conducting leads of nonuniform lengths connect the 16 circular Au-electrodes inside the cell to connector pads outside.) Surprisingly, the DNA release time constants correlate remarkably well to the individual charging time constants of the electrochemical double layer. This indicates that the release of oligonucleotides occurs principally before the double-layer formation is completed.

FIGURE 4.

Characteristic time of fluorescence onset τ_r vs. double-layer charging time constant τ_ec. As emphasized by the linear fit line, τ_r correlates to τ_ec.

Another evidence can be obtained by discussing the bias-dependence of the DNA desorption (compare to Fig. 2) within the predictions of the classical GCS theory, describing the screened potential distribution of a charged electrode surface into electrolyte solution. For the electrode potentials used in this study, the GCS theory takes on an “extreme” situation. The main potential drop is found directly at the electrode-solution interface across the Stern layer, whereas the potential drop across the diffuse Gouy-Chapman layer, extending into solution, is comparably small. It can easily be verified and yet is interesting to note that, if the electrode potential is changed from, e.g., −0.4 to −0.8 V, the corresponding additional potential drop in solution is confined to the Stern layer (simply by increasing its counterion density), whereas the potential drop across the Gouy-Chapman layer remains practically unchanged in magnitude for different electrode potentials. At this point, it is illustrative to elucidate the conformation of the oligonucleotides on the Au-surface: Kelley et al. (1998) as well as Zhang et al. (2002) report, in scanning probe microscopy investigations, that immobilized DNA stands straight on Au at surface potentials negative with respect to the potential of zero charge (pzc), which is found to be more positive than +0.3 V (vs. Ag/AgCl). Accordingly, the presented experiments are at all times conducted in a regime where the metal substrates are negatively biased and the DNA strands are expected to extend into solution, thereby susceptible to screening effects.

Hence, given that the localized charge on the DNA is not in direct vicinity to the electrode surface, but rather situated in the Gouy-Chapman layer, one should not expect a variation from −0.4 to −0.8 V of the electrode potential to have an influence on the desorption behavior. However, this is in contradiction to the results of Fig. 2 and the observed range of desorption-inducing potential steps, as well as the shift to higher desorption threshold voltages for increasing salt concentrations. As a consequence, we conclude that the GCS theory is not suited for explaining our desorption-related observations, but, as it describes electrochemical potentials in equilibrium, its inadequacy rather supports the suggestion made in discussing the correlation of τ_r and τ_ec; namely, that the desorption process principally takes place during an unsteady ec-state.

Although so far the discussion has been focused solely on the potential emanating from the electrodes into electrolyte solution, the influence of the DNA's counterion distribution will be the forthcoming subject. According to Manning's condensation theory (Manning, 1978) for polyelectrolytes of high charge density, a fraction θ of the DNA's charge is compensated by cations from the solution which are, in a condensed state, localized on the DNA. Therefore, the net charge of the DNA is reduced. For a 1:1 salt, θ is given by

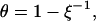(5)

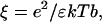(6)

where ξ is a dimensionless structural parameter, proportional to the polyelectrolyte's charge density; b is the axial distance between two elementary charges on the DNA backbone; e is the elementary charge; ɛ is the dielectric constant; k is the Boltzmann constant; and T is the temperature. Evaluating θ for single-stranded DNA (b = 4 Å) in aqueous solution yields θ = 0.44. A principal statement of the condensation concept is that θ is not influenced by the salt concentration of the solution, c_s, but only by the charge density of the polyelectrolyte (∼1/b). More precisely, Manning showed that Eq. 5 holds and θ remains constant for salt concentrations up to values where the (decreasing) Debye length in solution still is appreciably larger than the axial phosphate spacing, b. Hence, the applicability of Eq. 5 to single-stranded DNA would be limited to salt concentrations <∼100 mM (l_D ∼ 10 Å). At critically high salt concentrations, one might anticipate (and Manning circumspectly suggested) that the effective charge of the polyelectrolyte would depart from its constant value and start to decrease for the following reasons: the condensation concept (as derived by Manning, 1978) is based on the consideration that the electrostatic self-energy of the polymer (caused by its like charged units repelling each other) is reduced by counterions condensing on the polymer, which screen electrostatic interactions along the chain. However, condensation of ions from solution to a localized volume around the polymer costs entropic energy, and hence the fraction of compensated ions θ adjusts according to the minimum in free energy, given by the sum of the electrostatic and entropic energy contributions. Due to the special nature of the electrostatic and entropic terms for highly charged linear polyelectrolytes (ξ > 1), θ does not depend on the buffer salt concentration, as long as it is appreciably smaller than the local salt concentration of the condensed layer. Extending these considerations, we can qualitatively depict the onset of excessive counterion condensation in solutions of high ionic strength, as follows.

As the concentration of salt in solution approaches the local concentration of ions in the condensed state, the entropic contribution of the condensed counterions that increases the total free energy declines; however, the tendency to minimize the electrostatic free energy by increasing the number of counterions participating in screening remains. As a consequence, the new minimum of free energy shifts in a way that an increased fraction of the polyelectrolyte charge is compensated by counterions—a state of excessive counterion condensation has developed.

At this point, we will briefly compare our experimental results to recent theoretical simulations of polyelectrolytes with added salt: in a detailed study, Young et al. (1997) performed simulations of a 12-mer double-stranded DNA molecule at (a single) moderate salt concentration using Monte Carlo, nonlinear Poisson Boltzmann, and atomistic molecular dynamics methods confirming the existence of a sharply confined, condensed layer of counterions.

Stevens and Plimpton (1998) investigated the effect of varying salt concentrations by nonatomistic, molecular dynamics simulations. Upon increasing the salt concentration in solution, they find a steadily increasing ion density near the polymer chain, but, as opposed by Manning's classical results and our experimental observations, they do not predict a regime of constant charge compensation.

By merging the discussions on the electrode potential in solution and the DNA's counterion condensation, we suggest the following mechanism of electrostatic interactions between adsorbed ss-oligonucleotides and biased Au-electrodes:

1. At the potentials used in this study (negative to 0 V vs. Ag/AgCl) the DNA strands are susceptible to screening by cations from electrolyte solution, since we observe a dependence of the desorption efficiency on c_s. This is in accordance with the picture of oligonucleotides standing on the Au-surface, as proposed by Kelley et al. (1998) and Zhang et al. (2002).

2. Release of DNA occurs during an unsteady ec-state, i.e., while the electrode potential is not effectively screened by the electrolyte solution. This explains why the magnitude of the applied electrode potential affects the interaction strength—a behavior which is not expected from the GCS theory for the equilibrated case.

3. The fraction of cations θ, condensed on the DNA, adjusts according to c_s before application of bias potentials to the Au-electrode. Hence, the strength of electrostatic interaction directly after a bias step is mainly governed by the effective charge density of the DNA: constant values of θ over a wide range of salt concentrations are reflected by a constant desorption efficiency in that regime (see Fig. 3). The decreasing desorption efficiency for l_D ≲ 10 Å is a direct evidence for excessive condensation of Na⁺ ions on the DNA, thereby reducing its effective charge and weakening the electrostatic repulsion from the Au-electrode. To the best of our knowledge, this is the first experimental observation of excessive counterion condensation on immobilized DNA at high salt concentrations.

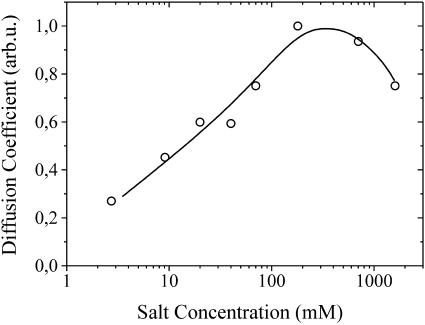
Finally, we discuss the influence of the salt concentration on the diffusion of ssDNA in electrolyte solution. As mentioned earlier, a geometry-specific diffusion time constant can be evaluated from the decay of fluorescence intensity after the desorption process (see Fig. 1 and Fig. 3, inset). Since the formation of the GCS electrical double layer occurs on a short timescale compared to the observed diffusion times (see Fig. 3, inset), the electric field from the Au-electrodes is screened within a few nm from the surface and hence predominantly translational diffusion can be observed. Fig. 5 shows the relative translational diffusion coefficient D_t (∝1/τ_d) versus the salt concentration of the electrolyte solution. As c_s is increased, D_t increases accordingly up to a concentration of ∼200 mM, from which point D_t decreases again. The initial increase of D_t for c_s < 200 mM can be attributed to electrolyte friction, as described by Schurr (1980). Here, the reduced dimensions of the DNA's diffuse counterion cloud in electrolyte solutions of high c_s results in an enhanced translational mobility. We point out that this effect is consistent with the preceding discussion of the desorption mechanism as it is intrinsically related to the counterion distribution of the DNA. However, it is noteworthy that the decrease of D_t at high salt concentrations cannot be attributed to electrolyte friction, as the translational mobility of polyelectrolytes is expected to saturate (at the value of the uncharged molecule) for high c_s. Remarkably, the maximum of D_t coincides with the onset of the regime of excessive counterion condensation on the DNA, at which l_D becomes comparable to b. It is known that effective screening along the chain lowers the electrostatic contribution to the rigidity of oligonucleotides, which in turn might induce conformational changes that affect the mobility of the molecule. Due to the very small persistence length (∼1–7 nm) of single-stranded DNA (Kuznetsov et al., 2001, and references therein), even short oligonucleotides, as being used in this study, could be susceptible to this effect. The capability of ssDNA to form hydrogen bonds with itself, thereby undergoing conformational changes, should also be mentioned here, and one can speculate that a lowered polymer rigidity due to effective screening of the inherent electrostatic repulsion along the chain might enhance this effect. However, we also point out that the viscosity of the aqueous NaCl solution increases by 18% upon increasing the NaCl concentration from 100 to 1600 mM, which could also account for the observed decrease of D_t at high c_s.

FIGURE 5.

Translational diffusion coefficient of 24-mer-ss-oligonucleotides in solutions of varying Tris/NaCl concentrations. The solid line is a guide to the eye.

CONCLUSION

We presented desorption experiments of immobilized ss-oligonucleotides from supporting Au-surfaces at negative electrode potentials, using combined electrochemical and optical measurements to gain insight on the effects of electrolytic screening on electrostatic interactions between DNA and biased metal surfaces. The influences of varying ionic strength of the solution on the electrostatic screening as well as different electrode potentials were studied by means of the desorption efficiency and the characteristic time constants of release and diffusion.

Our results evidence constant strength of electrostatic interaction up to salt concentrations with corresponding Debye lengths of the order of the axial charge spacing on the DNA's backbone. A further increase in salt concentration results in reduced desorption, pointing out the accessibility of adsorbed DNA to cations from electrolyte solution that screen the DNA's intrinsic charge. Moreover, we argue that the desorption process predominantly occurs before formation of the Gouy-Chapman-Stern layers at the electrolyte/Au interface, and hence proceeds during an unsteady electrochemical state. As a consequence, we suggest that electrostatic interaction between DNA and the Au-electrodes mainly depends on the effective charge of the DNA, i.e., the number of charges on the DNA's backbone not compensated by condensed counterions. The observation of a reduced desorption efficiency in solutions of high ionic strength can be attributed to a newly disclosed regime of excessive counterion condensation on the DNA.

Additionally, evaluation of the DNA's relative translational diffusion coefficient yields growing values up to the critical salt concentrations mentioned above, followed by a decrease at higher salt concentrations. The observed monotonic increase can be explained by means of electrolyte friction, i.e., decreasing counterion cloud dimensions of the DNA in electrolyte solutions of higher ionic strength. The origin of the declining diffusion coefficient at high salt concentrations is the subject of ongoing investigations, as the rise in solvent viscosity as well as conformational changes of the ss-oligonucleotides could contribute to this effect.