Bridging the Gap between Structural and Lattice Models: A Parameterization of Energy Transfer and Trapping in Photosystem I

Abstract

In the absence of an accurate structural model, the excited state dynamics of energy-transferring systems are often modeled using lattice models. To demonstrate the validity and other potential merits of such an approach we present the results of the modeling of the energy transfer and trapping in Photosystem I based upon the 2.5 Å structural model, and show that these results can be reproduced in terms of a lattice model with only a few parameters. It has recently been shown that at room temperature the dynamics of a hypothetical Photosystem I particle, not containing any red chlorophylls (chls), are characterized by a longest (trapping) lifetime of 18 ps. The structure-based modeling of the dynamics of this particle yields an almost linear relationship between the possible values of the intrinsic charge-separation time at P700, 1/γ, and the average single-site lifetime in the antenna, τ_ss. Lattice-based modeling, using the approach of a perturbed two-level model, reproduces this linear relation between τ_ss and 1/γ. Moreover, this approach results in a value of the (modified) structure-function corresponding to a structure exhibiting a mixture of the characteristics of both a square and a cubic lattice, consistent with the structural model. These findings demonstrate that the lattice model describes the dynamics of the system appropriately. In the lattice model, the total trapping time is the sum of the delivery time to the reaction center and the time needed to quench the excitation after delivery. For the literature value of τ_ss = 150 fs, both these times contribute almost equally to the total trapping time of 18 ps, indicating that the system is neither transfer- nor trap-limited. The value of ∼9 ps for the delivery time is basically equal to the excitation-transfer time from the bulk chls to the red chls in Synechococcus elongatus, indicating that energy transfer from the bulk to the reaction center and to the red chls are competing processes. These results are consistent with low-temperature time-resolved and steady-state fluorescence measurements. We conclude that lattice models can be used to describe the global energy-transfer properties in complex chromophore networks, with the advantage that such models deal with only a few global, intuitive parameters rather than the many microscopic parameters obtained in structure-based modeling.

INTRODUCTION

The primary processes in all photosynthetic systems involve the absorption of energy from (sun) light by chromophores in a light-harvesting antenna, and the subsequent transfer of this energy to a reaction center (RC) site where the energy is “trapped” by means of a stable charge-separation. Photosystem I (PSI) is one of two such photosystems present in oxygenic photosynthesis. It uses the energy of light to transfer electrons from plastocyanin or soluble cytochrome c₆ to ferredoxin and eventually to NADP⁺. The PSI core is a large pigment-protein complex consisting of 11–13 protein subunits (Scheller et al., 1997), the largest two of which, PsaA and PsaB, form a heterodimer to which the majority of the core antenna pigments and most of the RC co-factors are bound. Spectroscopic data indicate that the core antenna and RC contain ∼90–100 chlorophyll-a (chla) and 10–25 β-carotene molecules in total.

In plants and green algae the PSI core complex binds additional Light-Harvesting Complex I antenna proteins. These accessory chl binding antenna proteins are not present in cyanobacteria. The PSI core complexes of cyanobacteria can be isolated both as monomers and trimers, and probably both aggregation states are native, co-existing in the membrane in a dynamic equilibrium (Kruip et al., 1994).

The structure of the PSI core complex of the cyanobacterium Synechococcus elongatus has been resolved up to 2.5 Å resolution (Jordan et al., 2001). The structural model includes 96 chlorophyll molecules, as well as 22 carotenoids, two phylloquinones, and three Fe₄S₄ clusters.

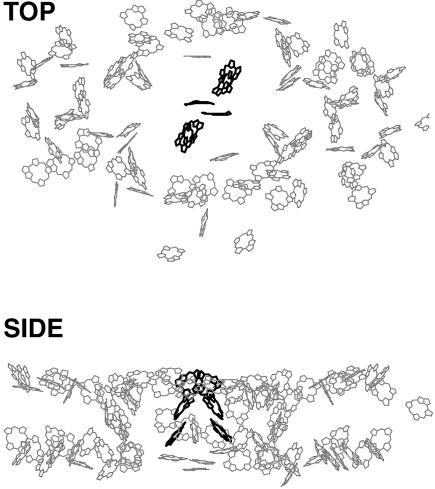
Fig. 1 displays the organization of the chlorophyll molecules in the structural model. For clarity only the porphyrin rings are displayed, although for most chlorophylls (chls) the complete phytol tail was resolved. The top-view clearly shows how the 90 chl molecules that constitute the core antenna (gray) encompass the RC containing the remaining six chls (black). Although located in the middle of the structure, the distance of any of RC chls to most of the antenna chls is larger than 20 Å. The side-view clearly demonstrates that the antenna chls are not distributed homogeneously throughout the whole protein-volume. Whereas the central domain consists of a more or less space-filling three-dimensional chl distribution, the chls in the peripheral domains are concentrated at both the lumenal and stromal side of the protein, with an empty layer in between. The spatial distribution of the chls in the protein is one of the major factors contributing to the energy-transfer characteristics of the system.

FIGURE 1.

Top (upper) and side (lower) view of the spatial arrangement of chla molecules in the PSI core of Synechococcus elongatus, as derived from the 2.5 Å structural model. The gray molecules represent the antenna chls whereas the black molecules represent the chls in the RC. For clarity the phytol tails of the molecules have been omitted.

The dynamics of PSI are determined not only by the structural organization of the antenna, but also by the spectral properties of the chls in the antenna and the RC, in particular since basically all PSI species exhibit a number of low-energy, or “red” chls in their antennae that absorb maximally at wavelengths longer than that of the primary electron donor, P700 (Shubin et al., 1991; Van der Lee et al., 1993; Gobets et al., 1994; Pålsson et al., 1996; Rätsep et al., 2000; Hayes et al., 2000; Gobets and van Grondelle, 2001; Zazubovich et al., 2002). Despite the fact that the number of these low-energy chls is small, <10% of the total chl content of the antenna, it has been shown by both time-resolved and steady-state spectroscopy experiments that their effect upon the energy-transfer and trapping characteristics of the PSI system is considerable (Gobets et al., 2001, 1994; Gobets et al., unpublished data; Gobets and van Grondelle, 2001; Van Grondelle et al., 1994; Pålsson et al., 1998). In PSI cores of cyanobacteria, the amounts and energies of the low-energy chls appear to be highly species-dependent (Gobets et al., 2001; Gobets and van Grondelle, 2001). Moreover, the red chl forms are also affected by the aggregation state of the cyanobacterial core complexes: in monomeric PSI core preparations the number of red chls is generally found to be lower than in trimers. The spectral properties of the various pools of (red) chls in PSI and their location in the protein are important parameters in the modeling of the dynamics in PSI.

Previously, in the absence of a structural model, the modeling of the energy-transfer dynamics in PSI was often based on square or cubic lattices (Owens et al., 1987; Jean et al., 1989; Beauregard et al., 1991; Jia et al., 1992; Trinkunas and Holzwarth, 1994, 1996). The dynamics were calculated either analytically (Owens et al., 1987), using the equations derived by Pearlstein and co-workers (Pearlstein, 1982; Den Hollander et al., 1983), or numerically, by calculating transfer rates between individual pigments using the Förster mechanism for energy transfer (Förster, 1948), and the subsequent solution of the Pauli master equation (Jean et al., 1989; Beauregard et al., 1991; Jia et al., 1992; Trinkunas and Holzwarth, 1994, 1996; Laible et al., 1994). In some cases only energy transfer between the nearest neighboring pigments was taken into account, whereas in other cases all pairwise energy-transfer rates were calculated. Although many of the above-mentioned articles introduced interesting approaches to the modeling of the energy-transfer kinetics in the PSI antenna and lead to new insights, basically all these modeling attempts were hampered by a number of the following problems:

1. The spectral heterogeneity of PSI, and especially the presence of the red chls has to be taken into account for proper modeling of the kinetics of intact PSI particles. The analytical approach is only applicable to a homogeneous antenna (all antenna chls absorb at the same energy). In contrast, the numerical approach does allow for the inclusion of different spectral forms via the overlap integral appearing in the Förster formula. Two problems arise, however. First of all the spectral properties of the different antenna pools need to be known to calculate the overlap integrals. In most cases the overlap integrals are calculated using shifted absorption and emission spectra of chla in organic solvents, which is reasonable for most chl pools, except for the pools of red chls, the spectral properties of which have been shown to differ significantly from those of chls in solution (Gobets et al., 2001, 1994; Pålsson et al., 1996; Rätsep et al., 2000). Another problem is that the dynamics depend strongly upon the locations of the red chl spectral forms in the antenna, which are unknown or at least still a matter of debate (Byrdin et al., 2002; Sener et al., 2002; Damjanovic et al., 2002; Jordan et al., 2001). This leads to an enormous number of possible permutations of the different chl forms, which is quite impossible to sample, both for the reason of computation time as well as for the fact that the problem is underdetermined—that is, the amount and quality of the data do not allow us to select the best configuration. The latter also relates to the next problem.

2. The experimental input for the modeling frequently consisted of single photon counting data (Owens et al., 1987; Trinkunas and Holzwarth, 1994, 1996). This technique is characterized by an instrument response function with a full-width at half-maximum of typically 40–80 ps, allowing for a quite accurate recording of the slowest lifetime component that reflects the overall decay of excitations due to trapping. However, the shorter lifetime components that reflect the energy transfer between the different pools of chls are generally too fast to be recorded by this technique. Even if such a component was recorded it usually did not help to improve the simulations due to the lack of accuracy with which it could be registered. Moreover, the PSI preparations used in some of these experiments were damaged during isolation, due to the use of harsh detergents, resulting in the loss of (most) the red chl forms and possibly a part of the bulk antenna.

3. The main distinguishing feature of most lattice models is that they are two-dimensional with the RC (or P700) occupying one of the sites of the lattice. In these models, for a given spectral composition of the antenna, the dynamics are defined by only two fitting parameters: the rate of charge-separation from P700 and one single distance scaling parameter, the lattice constant. This has led to two limiting cases for the dynamics in PSI. In the transfer-limited case the dynamics are mainly determined by the energy-transfer rate in the antenna, due to relatively slow diffusion of excitations to the RC, whereas in the trap-limited case, a relatively slow intrinsic rate of charge-separation from P700 would govern the dynamics (Pearlstein, 1982; Owens et al., 1987). Structural data now reveal (Fig. 1) that the structure is clearly three-dimensional and, moreover, the RC is not just another site on a lattice. The distance between the RC and the antenna chls is significantly larger as compared to the distance between adjacent antenna chls. Therefore a model describing the energy transfer in PSI should include at least two distinct energy-transfer rates: a larger rate for energy transfer between antenna chls, and a smaller rate for energy transfer from the antenna to the RC. This results in a third limiting case, the transfer-to-the-trap limited case, in which the dynamics are limited by a relatively slow energy-transfer rate from the antenna to the RC (for a review, see Van Grondelle et al., 1994). Already before sufficiently detailed structural data became available, Valkunas and co-workers (Van Grondelle et al., 1994; Valkunas et al., 1995) proposed a model with an organization similar to the bacterial LH1-RC complexes, in which two distinct scaling parameters are present: a short interpigment distance between adjacent antenna chls, and a larger distance between the antenna and the RC.

In this contribution the dynamics of PSI will be modeled using both the analytical (Pearlstein) and the numerical (Förster) approach. Both the experimental input and the nature of the lattice model applied are such that the problems listed above are largely overcome. The experimental input consists of recent room-temperature time-resolved fluorescence data of various PSI particles containing different amounts and types of red chls (Gobets et al., 2001). All the different PSI particles used in this study were isolated using mild detergents and were very well characterized. The experiments were performed using a synchroscan streak camera with an instrument response of ∼3 ps, significantly better than in single photon counting experiments, and allowed for the clear distinction of one or two fast equilibration components (depending on the type of PSI) besides the slowest, trapping component. Target analysis of the dynamics of all PSI particles studied (using a unified compartmental scheme) indicated that in a hypothetical PSI particle, containing no red chls, trapping should occur in 18 ps (Gobets et al., 2001). In the numerical modeling of the energy transfer in such a hypothetical particle, with a homogeneous (or slightly inhomogeneous) antenna, one is relieved from the problems involving the red chl forms (spectral properties and location), thereby greatly reducing the amount of free model-parameters. Since the locations and orientations of the chls can be taken from the structural model, no artificial regular lattice needed to be assumed for the numerical modeling.

For the PSI core “without red chls” the numerical results can be compared with those obtained from an analytical approach. This allows us to formulate a few general concepts that can be intuitively applied to describe the (global) energy-transfer dynamics of a complex system like PSI.

NUMERICAL, STRUCTURE-BASED SIMULATION

To model the kinetics of PSI, not containing red chls, a simulation was performed based upon the recent 2.5 Å structural model of trimeric PSI from Synechococcus elongatus (Jordan et al., 2001). Since most interactions between chls in the PSI core are small the modeling was based on Förster energy-transfer. We note that although the Förster approach may locally not be correct due to the occurrence of some strongly coupled pairs of chls in the PSI core (Sener et al., 2002; Damjanovic et al., 2002; Byrdin et al., 2002), this does not significantly affect the global kinetics resulting from the modeling.

Procedure

We calculated all pairwise energy-transfer rates between the 96 different chls in the system using the Förster equation (Förster, 1948; Struve, 1995; Van Amerongen et al., 2000),

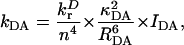(1)

in which k_DA is the rate of transfer of an excitation from a donor chl D to an acceptor chl A in ps⁻¹; 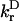is the radiative rate of chla, for which a value 5.4 × 10⁻⁵ ps⁻¹ is used (Kleima et al., 2000); n is the index of refraction of the protein; and R_DA is the distance between donor and acceptor in nm. R_DA was determined by taking the distance between the centers of the four coordinating nitrogen atoms N_A–N_D for each pair of chls in the structure. κ_DA is an orientational factor defined by

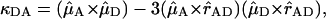(2)

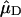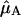in which and represent the Q_y transition dipole moment unit vectors of the donor and the acceptor and 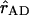represent the unit vector along the line connecting the centers of both transition dipole moments. For each chla molecule in the structure the vector connecting the nitrogen atoms N_B and N_D was taken to represent the direction of the Q_y transition dipole moment vectors. 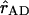was calculated as the unit vector along the line connecting the centers of the four coordinating nitrogen atoms N_A–N_D for each pair of chls in the structure.

The factor I_DA in Eq. 1 represents the overlap integral between the donor emission spectrum and the acceptor absorption spectrum defined by Kleima et al. (2000) and Struve (1995), as

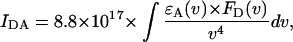(3)

where ɛ_A(ν) represents the acceptor absorption spectrum scaled to the value of the extinction coefficient (in M⁻¹ cm⁻¹) in the absorption maximum and F_D(ν) represents the emission spectrum of the donor, normalized to unit area. Both spectra are recorded on a frequency scale (cm⁻¹).

For all chls, except P700, the overlap integrals I_DA were calculated using shifted absorption and emission spectra of chla in acetone. The absorption spectrum of the two chls constituting P700 was approximated by a Gaussian peaking at 698 nm (Gobets and van Grondelle, 2001), with a full-width at half-maximum of 19 nm (Pålsson et al., 1998). Two different cases were considered: that of a truly homogeneous antenna, with all the antenna chla molecules absorbing maximal at 680 nm, and that of a heterogeneous antenna in which equal amounts of chls absorbing at 670, 680, and 690 nm were randomly distributed over the 90 chl sites in the structural model. In all cases the two chlorophylls at the position of A₀ were chosen to absorb at 686 nm, whereas the two accessory chls were put at 680 nm (Kumazaki et al., 1994; Gobets and van Grondelle, 2001). For the maximum of the extinction coefficient of the bulk pools a value of 7.7 × 10⁴ M⁻¹ cm⁻¹ was used, which is the value reported by Lichtenthaler (1987) for chla in 80% acetone. The absorption spectrum of the P700 pool was scaled to that of the other pools by requiring it to have the same integrated area (total oscillator strength) per monomer.

The energy-transfer rates were calculated using Eq. 1 for downhill energy-transfer only, i.e., pairs of DA, in which the absorption of D peaks at higher or equal energy as compared to the absorption of A. The complementary, uphill rates had to comply with the concept of detailed balance and were thus calculated as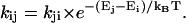

So far this leaves only one free parameter in the simulation, i.e., the index of refraction, n, which effectively scales the average single-site lifetime τ_ss, defined as the time needed for an excitation to hop away from a chl site, averaged over all possible sites. We have to introduce a second free parameter, the trapping parameter γ, the rate at which excitations disappear from the system when they reach one of the two chls constituting P700.

For a particular set of values for n and γ, we can now construct the 96 × 96 matrix of pairwise energy-transfer and decay rates, the eigenvalues of which correspond to the 96 different lifetimes of the system.

Relation between n and 1/γ

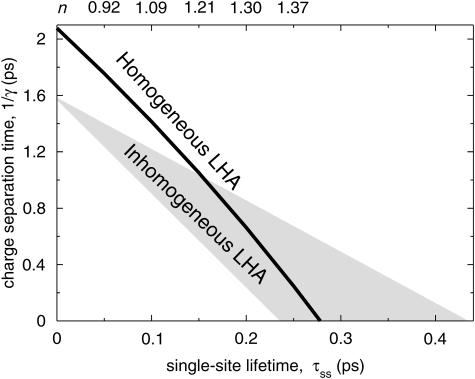
As pointed out above, the simulation only contains two adjustable parameters, n and γ. It has recently been demonstrated that a hypothetical PSI particle void of red chls exhibits a trapping time of 18 ps (Gobets et al., 2001). This slowest lifetime of 18 ps can be modeled using different combinations of n and γ (or τ_ss and 1/γ). The solid line displayed in Fig. 2 represents all the combinations of the intrinsic trapping time 1/γ and τ_ss (which is proportional to n⁻⁴ for a given spectral composition of the antenna) that yield a 18-ps trapping time. The upper axis also shows the actual values of n for the case of the homogeneous antenna. It immediately strikes the eye that the relation between τ_ss and 1/γ is almost (but not perfectly) linear. The line in Fig. 2 readily provides upper limits for both τ_ss and 1/γ, of ∼275 fs and ∼2 ps, respectively. However, these values correspond to infinitely fast trapping (γ = ∞) and transfer (τ_ss = 0), respectively, and therefore are not physically realistic. Time-resolved fluorescence depolarization measurements indicate that τ_ss has a value of 130–180 fs (although these values may be biased by transfer steps leading to a large depolarization; Du et al., 1993; Kennis et al., 2001). These values of τ_ss correspond to a charge-separation time 1/γ of between 0.9 and 1.2 ps, which corresponds well with the 0.9 ps⁻¹ charge separation rate reported by Byrdin et al. (2002). This value of 1/γ is fast, compared, for instance, to the 3-ps charge-separation time reported for the purple-bacterial RC (Parson, 1991), but somewhat slower than the 400-fs charge-separation time as found by Groot et al. (1997) in Photosystem II. For some additional considerations regarding the differences between the rate of charge-separation in plant and bacterial photosynthesis, see Gobets and van Grondelle (2001) and Van Brederode and van Grondelle (1999).

FIGURE 2.

(Solid line) Combinations of the charge-separation time 1/γ and the average single-site lifetime τ_ss that result in a longest lifetime of 18 ps in PSI modeled with a homogeneous antenna. The upper axis shows the values of the index of refraction, n, that correspond to the values of τ_ss on the lower axis (only for homogeneous antenna). The gray area encloses the interval in which similar relationships between 1/γ and τ_ss occurred for 16 random representations of a heterogeneous antenna (see text for details).

Earlier, a figure similar to Fig. 2 was produced based on the “old” 4 Å structure (Gobets and van Grondelle, 2001). In this simulation, the upper limit of the single-site lifetime was found to be ∼150 fs, significantly faster than the 275 fs found for the new structure. The most important difference between both these structures is the fact that in the 2.5 Å structure the orientations of the pigments, and thus the approximate transition dipole moment orientations, could be distinguished—whereas in the 4 Å structure a value of 2/3 was used for the orientation factor κ² (the average value for randomly oriented chromophores in three dimensions). Applying the value of 2/3 to the 2.5 Å structure (ignoring orientational information) leads to an upper limit for τ_ss of 160 fs, very close to that found for the 4 Å structure, indicating that the actual organization of the orientations of the antenna chls has a profound effect on the energy-transfer dynamics in the antenna. If the simulations for the average (not shown) and real orientations are compared for the same values of n and γ, it is found that τ_ss is shorter in the case of an average orientation, but that the trapping time is in fact longer as compared to the case of the real orientations. In reality the antenna chls are apparently organized such that, although τ_ss is decreased with respect to random orientation, the excitations are “guided” such that excitations arrive to the RC faster than in the case of randomly orientated antenna chls.

Erroneously the scaling of the vertical axis in Fig. 8 of Gobets and van Grondelle (2001) is off by a factor 2. Correcting for this factor 2, the upper limit for the trapping time is approximately the same for the 4 Å and the 2.5 Å structure. Since equilibration is infinitely fast in this case, this value of 1/γ simply reflects the relative population of excitations on P700 in a thermally-equilibrated state, × 18 ps. This relative population is slightly lower in the simulation based on the 2.5 Å structure as compared to the simulation based on the 4 Å structure, since in the former structure 96 chls were assigned, whereas in the latter only 89 chls could be distinguished.

In reality the bulk absorption band of the antenna in PSI is not completely homogeneous, but consists of several sub-bands, as evidenced by the absorption spectrum (Gobets and van Grondelle, 2001). To estimate the extent to which inhomogeneity leads to differences with the homogeneous case described above, we also carried out structure-based simulations for which the 90 chls in the antenna were assigned randomly to one of three spectral pools of bulk pigments (with absorption maxima at 670, 680, and 690 nm) such that these pools consisted of equal numbers (30) of chls. The RC chls maintained the specific spectral properties given above. The gray area in Fig. 2 represents the interval containing the relations between 1/γ and τ_ss leading to an 18-ps trapping time, obtained for 16 such different random compositions of the antenna. All antenna compositions result in the same intersection with the vertical axis, demonstrating that for τ_ss = 0 the locations of the various spectral forms do not matter because the system is always in thermal equilibrium. The intersection is at a lower value of 1/γ as compared with the homogeneous antenna, reflecting that the thermal-equilibrium distribution of excitations is shifted toward the antenna in the case of the heterogeneous antenna.

According to Fig. 2, in case of a homogeneous antenna, n would reasonably have a value ∼1.2, with an absolute upper limit of ∼1.4. For all 16 compositions of the heterogeneous antenna a similar upper value of 1.3–1.4 was found. This is consistent with values ranging between 1.22 and 1.34 as found for C-phycocyanin and Allo-phycocyanin, as discussed in van Amerongen et al. (2000), although significantly smaller than the 1.6 ± 0.1 value reported for Peridinin–chlorophyll-a–protein (Kleima et al., 2000), and the value of 1.51 ± 0.04 for CP47 (Renge et al., 1996). Of course the values of and the maximum of the extinction coefficient need not be the same for chla in the PSI protein as compared to chla in solution, which could account for a significant variation of the actual value of n (Knox and van Amerongen, 2002). Also the value of the Stokes' shift may actually be different in the protein.

ANALYTICAL, LATTICE-MODEL SIMULATION

We will now discuss the results of the numerical structure-based analysis in terms of a lattice model in the analytical (Pearlstein) approach. Since this model involves only a limited number of parameters, it represents a simplified view of the system under consideration. However, it is just this kind of simplification that may result in more insight in the global energy-transfer features between the antenna and the RC in PSI than would be obtained by just inspecting the 96 × 95 + 1 individual rates or the 96 eigenvalues present in the structure-based calculation of energy transfer. Moreover, a comparison of the results of the lattice model with the results obtained from structure-based calculations may shed some light on the applicability of lattice models to other, (artificial) photosynthetic systems. (See discussion below.)

Perturbed two-level approach: theory

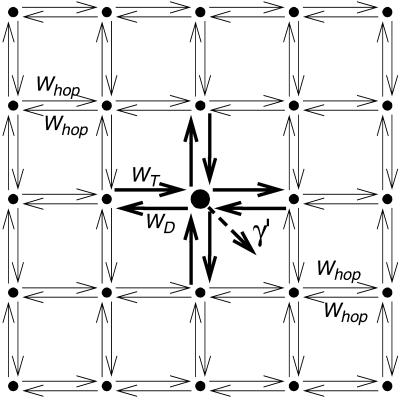
In Fig. 3 a schematic representation is given of the lattice model used to describe PSI. Every lattice site indicated by a dot represents a chl site in the antenna, except for one site, indicated by the larger dot, which represents the whole of the RC. Energy transfer occurs between any of the antenna chls and its nearest neighbors with the rate W_hop. We start out considering a homogeneous antenna for which all antenna chls have the same energy and consequently, W_hop is a constant. In that case the single-site lifetime of an antenna chl site, τ_ss, equals (zW_hop)⁻¹, in which z, the coordination number, represents the number of nearest-neighbors of a lattice site. The energy transfer between the RC and its nearest neighbors occurs with separate rates W_T and W_D, respectively. The RC is the only site in the system where excitations can be quenched, which occurs at a rate of charge-separation γ′. In reality the RC does not consist of only one single chl site, but contains six chla molecules. In the structure-based simulation, charge-separation is presumed only to take place from the two chls constituting P700, at a rate γ. The rates γ′ and γ therefore differ by a factor which accounts for the population of excitations on P700 relative to the other RC chls. By assuming that excitation equilibration among the chls within the RC is very fast, γ′ and γ are related by

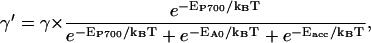(4)

in which E_P700, E_A0, and E_acc represent the energies of the chl dimer constituting P700, the two chls at the position of the primary electron acceptor and the two accessory chls, respectively. k_B is Boltzmann's constant and T is the absolute temperature. The model in Fig. 3 is presented as a square lattice, but we note that no a priori assumptions are made regarding the type of lattice. The specific lattice properties will be accounted for by a structure-function g_d(N), the value of which will be compared to that of known, regular lattices (see below).

FIGURE 3.

Schematic representation of the lattice model. The small dots represent antenna chl sites; the large dot in the middle represents the RC. W_hop is the hopping rate between two “normal” neighbors, W_T and W_D represent the rates of energy-transfer to and from the RC; and γ′ is the rate of charge-separation from the RC.

Since the average interpigment distance in the antenna is significantly shorter than the distance between the RC and the antenna, it seems reasonable to assume that equilibration within the antenna is faster than the transfer of excitations to the RC. Therefore, as a first-order approximation, the energy migration in the antenna is taken to be infinitely fast, and subsequently the finite time of this migration is accounted for in a perturbative way (Somsen et al., 1996; Van Amerongen et al., 2000).

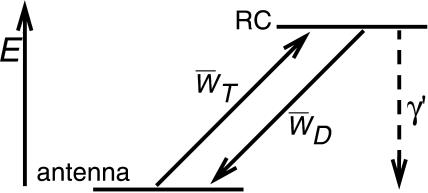
In the case of infinitely fast migration in the antenna, i.e., τ_ss = 0, the lattice model can be treated as the two-level system shown in Fig. 4, with the upper level representing the RC and the lower level representing the antenna. Here and 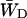are trapping (delivery) and de-trapping (escape) rates of the two level system, which are related to the microscopic trapping and detrapping rates W_T and W_D by Somsen et al. (1996) and Van Amerongen (et al., 2000) as

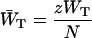(5)

and

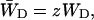(6)

in which N is the total number of antenna chls. In the case of a homogeneous antenna, 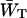can be regarded as the average energy-transfer rate from any chl site in the antenna to the RC, and 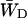as the total rate of energy-transfer from the RC to the antenna.

FIGURE 4.

Energy scheme on which the perturbed two-level model is based. The two levels represent the antenna and the RC. W_T and W_D represent the forward and backward energy-transfer rates between both levels and γ′ is the rate of charge-separation from the RC.

In case τ_ss = 0 the antenna and the RC must be in Boltzmann equilibrium and therefore 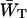and 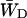are related by

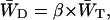(7)

with

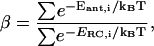(8)

in which E_ant,i and E_RC,i represent the energy levels of the individual antenna and RC chls, and the summations are over all antenna and RC chls, respectively.

The two-level system exhibits two rate constants, the values of which are given by

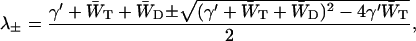(9)

where λ₊ represents the excitation equilibration rate between the antenna and the RC, and λ₋ the excitation decay rate from the equilibrated distribution.

Taking the finite time of excitation migration into account perturbatively results in an additive excitation migration time, τ_mig, for the equilibration (τ₊) and decay (τ₋) times (Somsen et al., 1996; Van Amerongen et al., 2000), of

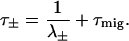(10)

The excitation migration time within the antenna is given by Somsen et al. (1996) and Van Amerongen et al. (2000) as

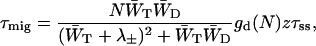(11)

in which g_d(N) is the structure-function of the antenna system which depends on the type of lattice (i.e., linear, square, hexagonal, cubic, etc.; see Somsen et al., 1996 and Van Amerongen et al., 2000).

Combining Eq. 9 with Eq. 7, and replacing the square root by the first two terms of its Taylor expansion (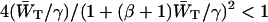 since β > 4), 1/λ₋ can be approximated by

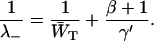(12)

If this expression for λ₋ is substituted into Eq. 11, it is found that the first term in the denominator of Eq. 11 can be neglected, since 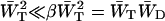, and therefore 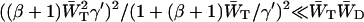. Therefore, τ_mig can be approximated by

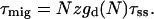(13)

Substitution of Eqs. 12 and 13 into Eq. 10 results in

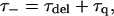(14)

in which

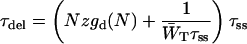(15)

can be regarded as the average time needed to deliver an excitation from the antenna to the RC, analogous to the first passage time, τ_fpt as defined for local trap models (Somsen et al., 1996; Pearlstein, 1982; Van Amerongen et al., 2000). Note that since 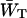and 1/τ_ss are proportional, 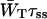is a constant depending on the structure only, and therefore remains unchanged upon variation of τ_ss. The second term in Eq. 14,

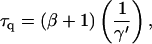(16)

can be regarded as the average time needed to quench the excitation after delivery.

Since the value of τ₋ is fixed to 18 ps, Eqs. 14–16 result in the following linear relationship between τ_ss and 1/γ′:

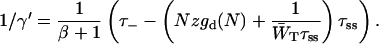(17)

Thus it has been shown that the perturbed two-level approach actually predicts the (almost) linear relation between τ_ss and 1/γ, as obtained from the structure-based numerical simulations, displayed in Fig. 2.

Perturbed two-level approach: results

Homogeneous antenna

The solid curve in Fig. 2, which represents the relation between τ_ss and 1/γ for a homogeneous antennae can be approximated by a straight line which intersects both axes at the coordinates (0, (1/γ)_max) and (τ_ss,max, 0). Using (1/γ′)_max rather than (1/γ)_max yields

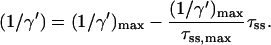(18)

Equating this expression to Eq. 17 yields

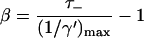(19)

and

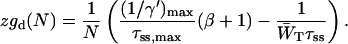(20)

The value of (1/γ)_max for the homogeneous antenna measures 2.08 ps, and using Eq. 4 with values for E_P700, E_A0, and E_acc corresponding to 698 nm, 686 nm, and 680 nm, this yields (1/γ′)_max = 3.03 ps. Inserting this value in Eq. 19, using τ₋ = 18 ps, yields β = 4.94, which is identical to the value found in applying Eq. 8 with E_ant,i corresponding to 680 nm. This confirms that in the limit of τ_ss = 0, both the two-level model and the structure-based simulation result in the same equilibrium between the antenna and the RC.

To make an estimate of zg_d(N) it is necessary to make an estimate of the constant 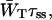that is, estimate 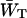for a particular value of τ_ss. As mentioned above, 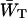for a homogeneous antenna can be regarded as the average energy-transfer rate from any antenna chl to any chl in the RC. The estimate can therefore be obtained from the structure-based simulation by calculating

(21)

in which k_ij represents the transfer rate from antenna chl i to RC chl j, and the summations are over all antenna chls and all RC chls, respectively. For τ_ss = 0.15 ps, this yields 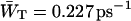, and therefore 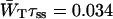andzg_d(N) = 0.39.

Since 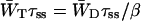, this constant can also be estimated by making an estimation of 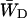based upon the structure-based simulation. According to Eq. 6, 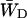is the total transfer rate from the RC to the antenna. Because in the lattice model the RC is treated as a single site rather than the six chls it consists of in reality, 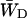is estimated as a weighted sum of the rates from all six RC chls to the antenna. If the equilibration within the RC is assumed to be fast with respect to transfer to the antenna, the weighing factor is just a Boltzmann factor and

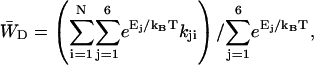(22)

in which E_j represents the energy of RC chl j, k_ji represents the transfer rate from RC chl j to antenna chl i, and the summations are again over all antenna chls and all RC chls, respectively. For τ_ss = 0.15 ps and the RC energies used above, this yields 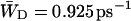and 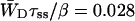. The difference between this value and the value of 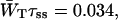estimated above, indicates that our assumption of infinitely fast equilibration within the RC is not fully correct. The value of 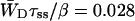corresponds to zg_d(N) = 0.32. Since the estimation of zg_d(N) based upon 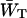did not require any assumptions regarding equilibration in the RC, the first estimation may be considered as more reliable.

Inhomogeneous antenna

The gray triangle in Fig. 2 indicates the variation in the relation between τ_ss and 1/γ that was found for 16 heterogeneous compositions of the antenna, under the condition that τ₋ = 18 ps (see above). All antenna compositions result in the same intersection with the vertical axis, at a value of (1/γ)_max = 1.58, corresponding to β = 6.83, once more identical to the value obtained using Eq. 8. The value of β is larger as compared to the case of a homogeneous antenna, expressing that with this choice of the antenna composition the equilibrium is shifted toward the antenna.

Estimations of zg_d(N) were obtained in a similar way as for the homogeneous antenna, with the exception that for the estimation of the value of 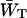, Eq. 21 was modified with a weighing factor to obtain

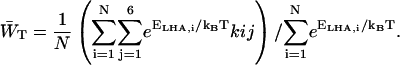(23)

Here the relative occupancies of the antenna chls are accounted for, assuming the antenna to be spectrally equilibrated. For 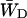, Eq. 22 can be applied. For τ_ss = 0.15 ps, we thus fi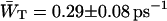nd and 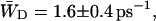corresponding to values of g_d(N)z of 0.33 ± 0.06 and 0.28 ± 0.06.

Perturbed two-level approach: discussion

We have applied the perturbed two-level approach to model the kinetics of PSI. The aim of this study is twofold: first, the comparison with the structural model allows us to judge the applicability of this approach to other systems for which no structural information is available; and second, the perturbed two-level model provides a framework for describing the system in terms of a few global, intuitive parameters, rather than the many microscopic parameters resulting from structure-based modeling. We will discuss some of these global parameters and comment on the application of the perturbed two-level model to other systems.

The delivery and escape times τ_del and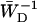

Here we discuss in some detail the value of the delivery time, τ_del, defined in Eq. 15, and how its value relates to other, independent experimental observations. τ_del is the sum of two contributions, Nzg_d(N)τ_ss and 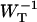. Analogous to definitions used in local-trap models (Van Amerongen et al., 2000) it is tempting to equate these two factors to τ_mig and τ_T. However, in the definition of τ_mig in the local-trap model the structure-function g_d(N) is replaced by a structure-function h_d(N), which is larger. In the perturbed two-level model, therefore, part of the migration through the antenna is accounted for by the factor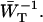

Time-resolved depolarization measurements indicate a value of τ_ss ∼ 0.15 ps (Du et al., 1993; Kennis et al., 2001), and recent modeling of the experimentally observed excitation-wavelength dependence of the fluorescence kinetics in PSI indicates a similar value for τ_ss (Gobets et al., unpublished data). For this value of τ_ss a value of W_T of 0.227 ps⁻¹ is found for the homogeneous antenna, and somewhat faster, ∼0.29 ps⁻¹, for the inhomogeneous antenna. The value of 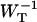therefore amounts to ∼4 ps. The difference between the homogeneous and inhomogeneous antenna reflects that the overlap integrals of the inhomogeneous antenna with the RC are, on the average, 28% better than for the homogeneous antenna.

Using Eq. 13, and applying g_d(N)z ∼ 0.33, it follows that τ_mig ∼ 4.5 ps, and therefore τ_del is of the order of 8.5 ps.

This estimated value of τ_del happens to be basically equal to the effective time needed to transfer energy from the bulk antenna to any of the two pools of red chls in Synechococcus trimeric PSI (Gobets et al., 2001) ((18⁻¹ + 17⁻¹)⁻¹ = 9.2 ps) showing that energy transfer from the bulk to the RC on the one hand, and the red chls on the other hand, are two competing processes. These findings are corroborated by low-temperature steady-state and time-resolved spectroscopy experiments: the 4 K excitation spectrum of Synechococcus trimeric PSI shows that 50% of the excitations are directed to the RC, resulting in a charge-separation, and the remaining 50% of the excitations are transferred to the red chls, where they remain trapped because uphill transfer is blocked at this temperature (Gobets and van Grondelle, 2001), indicating that transfer from the bulk antenna to either the RC or the red chls is equally likely. Also time-resolved streak camera measurements performed at 77 K show an initial 5-ps process, representing energy transfer from the bulk antenna chls to the red chls and photochemical quenching in the RC (Gobets et al., unpublished data), which is the lifetime expected to result from these two competing processes. We do note, however, that the bands of red chls are shifted significantly at low temperatures, as compared to room temperature, and therefore it is not straightforward to assume that all downhill transfer rates remain the same upon cooling.

The escape rate from the RC is given by the rate 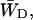which is 0.925 ps⁻¹ for the homogeneous antenna, and ∼1.6 ps⁻¹ for the inhomogeneous antenna—73% faster than for the homogeneous antenna. This demonstrates that the inhomogeneity of the antenna greatly increases the back-transfer from the RC, which must be caused by an enhanced overlap of P700 with the antenna. In any case, the de-trapping occurs in the order of 0.8 ps, and thus competes with charge-separation (1/γ′ ∼1.5 ps).

Obviously the values of 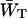and 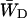should differ between the homogeneous and inhomogeneous antennae, due to the shift of the equilibrium between antenna and RC (i.e., the value of β in Eq. 7). The major difference occurs in the value of 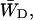since 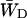depends mainly on the energy difference between the antenna and the RC, whereas 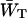to a large extent depends on the migration through the antenna (see above), and not so much on this energy difference.

The structure-function

For regular lattice models (i.e., square, hexagonal, cubic) in which only nearest-neighbor interactions are considered, the value of z, the coordination number, is well defined. However, the real structure of PSI is irregular, and energy transfer is not considered to be limited to nearest-neighbors only. To make an estimation of the value of the structure-function, g_d(N), we attempted to make a definition of z which would also be applicable to an irregular structure. A reasonable proposal would be to regard z as the ratio between the rate from an antenna chl to its nearest neighbor, and the sum of all the rates away from this antenna chl (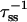), averaged over all antenna chls. This, however, led to a rather low value of z = 1.7 (compare to z = 4 for a square lattice and z = 6 for a cubic lattice), and since g_d(N) is inversely proportional to z, this led to high values of g_d(N). This is caused by the fact that, in contrast to a regular lattice, in an irregular structure for every site there is only one true nearest-neighbor site. The r⁻⁶ dependence of the Förster transfer rate on the average results in a strong preference of transfer to this one nearest-neighbor site, precluding the direct comparison of z and g_d(N) between regular lattices and the real (irregular) structures. This problem is partially solved by considering the value of zg_d(N), rather than the value of g_d(N).

We estimated a value of 0.32 < zg_d(N) < 0.39 for a homogeneous antenna, and a somewhat lower value of 0.28 < zg_d(N) < 0.33 for an inhomogeneous antenna. Comparing this to the values of ∼0.24 for a cubic lattice, and ∼0.64 for a square lattice (Somsen et al., 1996; Van Amerongen et al., 2000), it can be concluded that the PSI structure exhibits a mixture of the characteristics of a two-dimensional, square lattice, and a three-dimensional, cubic lattice. This is in agreement with the structural data, which show that the antenna consists of a central domain which is essential three-dimensional, and a peripheral domain that exhibits a bi-planar architecture.

The validity of model

We have shown that the application of the perturbed two-level model reproduces the linear relation between τ_ss and 1/γ that was found in the structure-based simulation and that the comparison of both models results in a realistic value for the structure-function zg_d(N). Also, the resulting value for τ_fpt = W_T + τ_mig ∼8.5 ps for a realistic value of τ_ss = 0.15 ps is consistent with independent time-resolved and steady-state fluorescence measurements. Since the perturbed two-level model approach works well for PSI, there seems to be no reason why this approach should not be used in other (artificial) antenna-trap systems such as dendrimer systems (Neuwahl et al., 2001; Benites et al., 2002), films of dyes (Yatskou et al., 2001), or systems of dye molecules attached to some kind of substrate, such as, for instance, zeolite crystals (Calzaferri et al., 2002), mesoporous silica (Murata et al., 2001), or polystyrene microbeads (Roberts et al., 1998), for which structures have not been resolved or which are inherently chaotic. It may not be feasible to follow the exact same approach (i.e., varying τ_ss and 1/γ such thatτ₋ remains constant), but we note that Eq. 17 in fact defines a plane in (τ_ss, 1/γ, τ₋)-space, and that sections through that plane, other than shown in Fig. 2, also yield the required parameters. In particular one could consider varying τ_ss by varying the dye concentration and recording the corresponding values of τ₋(1/γ remains unchanged).

CONCLUSIONS

Using a structure-based numerical simulation of energy transfer, it has been shown that in a PSI particle without red chls the possible combinations of τ_ss and 1/γ follow an (almost) linear relationship, and that upper limits of these parameters are ∼400 fs and ∼2 ps, respectively. A realistic value is τ_ss = 150 fs, for which 1/γ measures ∼1 ps. The value of the index of refraction was found to be ∼1.2, with an upper limit of 1.4. Interestingly, the relative orientations of the antenna chls are found to be organized such that excitations are directed to the RC faster than could be achieved for a random orientation of these chls, despite the fact that this organization results in a longer single-site lifetime. Using a lattice-based model, the perturbed two-level model, to describe the energy transfer and trapping in this system, the linear relation between τ_ss and 1/γ could be reproduced. Equating this linear relationship to the one obtained by the structure-based simulation results in a value of the (modified) structure-function zg_d(N) which lies in between that for cubic and square lattices, indicating correctly that the actual structure exhibits characteristics of both these structures. It is concluded that for realistic values of τ_ss and 1/γ, τ_q and τ_del are both ∼9 ps, demonstrating that the system is neither transfer- nor trap-limited. These values have been shown to be consistent both with time-resolved fluorescence measurements and fluorescence excitation measurements at low temperatures. Since the perturbed two-level model appropriately describes the global energy-transfer properties of a complex photosynthetic RC-antenna complex such as PSI, it may be concluded that its application to other (artificial) systems is justified.