Abstract
The energy transfer and charge separation kinetics in core Photosystem I (PSI) particles of Chlamydomonas reinhardtii has been studied using ultrafast transient absorption in the femtosecond-to-nanosecond time range. Although the energy transfer processes in the antenna are found to be generally in good agreement with previous interpretations, we present evidence that the interpretation of the energy trapping and electron transfer processes in terms of both kinetics and mechanisms has to be revised substantially as compared to current interpretations in the literature. We resolved for the first time i), the transient difference spectrum for the excited reaction center state, and ii), the formation and decay of the primary radical pair and its intermediate spectrum directly from measurements on open PSI reaction centers. It is shown that the dominant energy trapping lifetime due to charge separation is only 6–9 ps, i.e., by a factor of 3 shorter than assumed so far. The spectrum of the first radical pair shows the expected strong bleaching band at 680 nm which decays again in the next electron transfer step. We show furthermore that the early electron transfer processes up to ∼100 ps are more complex than assumed so far. Several possibilities are discussed for the intermediate redox states and their sequence which involve oxidation of P700 in the first electron transfer step, as assumed so far, or only in the second electron transfer step, which would represent a fundamental change from the presently assumed mechanism. To explain the data we favor the inclusion of an additional redox state in the electron transfer scheme. Thus we distinguish three different redox intermediates on the timescale up to 100 ps. At this level no final conclusion as to the exact mechanism and the nature of the intermediates can be drawn, however. From comparison of our data with fluorescence kinetics in the literature we also propose a reversible first charge separation step which has been excluded so far for open PSI reaction centers. For the first time an ultrafast 150-fs equilibration process, occurring among exciton states in the reaction center proper, upon direct excitation of the reaction center at 700 nm, has been resolved. Taken together the data call for a fundamental revision of the present understanding of the energy trapping and early electron transfer kinetics in the PSI reaction center. Due to the fact that it shows the fastest trapping time observed so far of any intact PSI particle, the PSI core of C. reinhardtii seems to be best suited to further characterize the electron transfer steps and mechanisms in the reaction center of PSI.
INTRODUCTION
Photosystem I (PSI) is one of the two reaction centers which, by way of two consecutive photodriven electron transfer steps within the well-known Z-scheme, transport electrons from water to NADP+. The recent x-ray structure analysis of cyanobacterial PSI with 2.5 Å resolution (Jordan et al., 2001) in principle opens the possibility for elucidating detailed structure/function relationships for the early events in PSI and should allow us to critically examine existing ideas about the present mechanistic models. The cyanobacterial PSI contains 127 co-factors in total, from which 96 are chlorophylls (Chls). However, as recent simulations have shown, the exact spectral properties of the reaction center pigments and their excited states, the nature of the primary donor state, the energy trapping lifetimes, and the rate of the first electron transfer step in the reaction center (RC) have a profound influence on the outcome of such simulations of the ultrafast energy trapping kinetics (Byrdin et al., 2002; Sener et al., 2002; Damjanovic et al., 2002). For this reason it is important to know those parameters exactly, in advance, to arrive at valid conclusions for the primary steps in detailed calculations based on the structural parameters. Only six Chls make up the reaction center proper, where the electron transfer steps are located (for a review, see Chitnis, 2001). The high ratio of the number of antennae to RC Chls characterizes the difficulties in observing directly the electron transfer processes in the RC, without disturbance by the antenna processes. Due to the presence of the large antennae, the rise and decay of the primary radical pair state and the associated spectral changes have actually never been directly resolved in open PSI RCs but have only been deduced from indirect experiments—i.e., by comparing the kinetics with oxidized and reduced P700 (for reviews, see Brettel and Leibl, 2001; Melkozernov, 2001).
Energy trapping and charge separation kinetics in various PSI particles has been the subject of a large number of ultrafast kinetic studies (see recent reviews by Holzwarth et al., 1998; Karapetyan et al., 1999a; Brettel and Leibl, 2001; Gobets and van Grondelle, 2001; Melkozernov, 2001). The kinetics of isolated Chlamydomonas reinhardtii PSI particles has been studied by several groups using ultrafast transient absorption and fluorescence (Owens et al., 1989; Chan et al., 1989; Du et al., 1993; Hastings et al., 1995a; Melkozernov et al., 1997, 1998, 2000b; Gibasiewicz et al., 2001). At present, agreement seems to exist about the interpretation of the various kinetic components. Ultrafast components in the subpicosecond range and a component in the 2–4-ps range were ascribed to energy equilibration in the antenna and between antenna and RC core (Gibasiewicz et al., 2001), whereas a 20–25 ps-component is ascribed to energy trapping by charge separation in the reaction center (Gibasiewicz et al., 2001). Thus energy equilibration is assumed to be complete after a few picoseconds and longer-lived components are ascribed to charge separation processes.
A very similar situation exists for cyanobacterial PSI particles for which a larger number of studies have been performed. For PSI from Synechocystis and Synechococcus elongatus, sub-ps and a few ps components (2–5 ps) have also been observed in various studies (Holzwarth et al., 1993; Turconi et al., 1993; Hastings et al., 1994a,b, 1995a,b; Turconi et al., 1996; Palsson et al., 1998; Gobets et al., 1998b; Savikhin et al., 1999, 2000; Melkozernov et al., 2000a). However, the ps components were interpreted in cyanobacterial PSI as energy transfer equilibration with special red pigments, i.e., antenna Chls with absorptions significantly longer than the 700-nm absorption of the RC (Karapetyan et al., 1999a; Gobets and van Grondelle, 2001; Melkozernov, 2001), rather than energy transfer only within the core antenna and to the RC. A recent combined femtosecond fluorescence upconversion and fluorescence streak camera study characterized in detail the ultrafast antenna energy transfer steps for Synechococcus PSI which occur mostly in the sub-ps range (Kennis et al., 2001; Gobets et al., 2001a). The presence of a species-dependent, significant amount of red pigments complicates the kinetic picture for cyanobacterial PSI, and the results are not always directly comparable to those of higher plants and green algae.
The energy trapping components for Synechocystis and S. elongatus PSI were found to be in the 25 and 35-ps range, respectively. The overall trapping kinetics for Spirulina platensis PSI is the slowest, at ∼40–50 ps, due to the presence of a particularly large amount of the red pigments in this cyanobacterial PSI complex (Karapetyan et al., 1997, 1998, 1999a,b; Karapetyan, 1998; Gobets and van Grondelle, 2001; Gobets et al., 2001b).
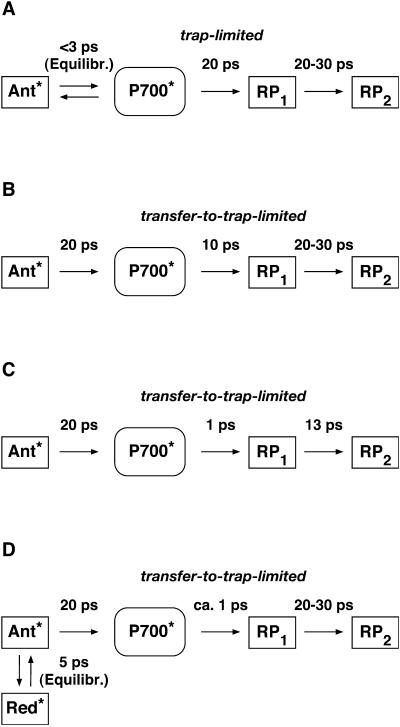
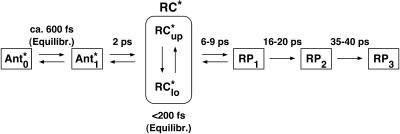
To make the comparison and discussion easier we have summarized in Scheme 1 the different kinetic models presently discussed in the literature for the energy trapping and early electron transfer processes in PSI. Note that some simplifications have been made in these schemes to generalize the models and focus on the most essential processes. Scheme 1 A shows the essentially trap-limited kinetic scheme proposed by Melkozernov et al. for both C. reinhardtii and cyanobacterial PSI (Gibasiewicz et al., 2001; Melkozernov, 2001). (We note that Melkozernov and co-workers did not present a detailed kinetic scheme in their articles; therefore, to make the different models comparable, we have translated the interpretations of Melkozernov et al.'s work into a kinetic scheme. The lifetime for charge separation in Scheme 1 A is an effective lifetime and does not represent an intrinsic lifetime of charge separation.) Scheme 1 B shows a model proposed by Savikhin and co-workers earlier (Savikhin et al., 2000) and Scheme 1 C shows a recently revised interpretation (Savikhin et al., 2001). Scheme 1 D shows the model proposed by Gobets and co-workers for cyanobacterial PSI (Gobets and van Grondelle, 2001; Gobets et al., 2001b). Note that in the latter model we have added the secondary electron transfer step which is missing in their model because the data were based on fluorescence kinetics only. In all the models shown in Scheme 1 the energy trapping and formation of the first radical pair occurs with a lifetime of ∼20–25 ps. This is also the case for Scheme 1 C if the antenna is excited despite the fast intrinsic charge separation step of 1.3 ps. Models 1 A and 1 B are based on both transient absorption and fluorescence kinetic data. Model 1 C is based on transient absorption data alone.
SCHEME 1.
Summary of the presently discussed models in the literature for the energy trapping and early electron transfer steps in PSI RCs. (A) The essentially trap-limited kinetic scheme proposed by Melkozernov and co-workers for both C. reinhardtii and cyanobacterial PSI (Gibasiewicz et al., 2001; Melkozernov, 2001). (B) Transfer-to-trap-limited scheme proposed by Savikhin et al. (2000); (C) revised interpretation by Savikhin et al. (2001); and (D) transfer-to-trap-limited model (simplified) as proposed by Gobets and co-workers for cyanobacterial PSI (Gobets and van Grondelle, 2001; Gobets et al., 2001b). Note that in the latter, the antenna-to-RC transfer of 20 ps (energy trapping) is further slowed down by the red pigments.
The reaction center of PSI consists of six Chls, organized in two branches (Jordan et al., 2001). The two central Chls, believed to form a dimer, upon oxidation are assumed to give rise to the 700-nm absorption difference maximum of what is called the primary donor P700. The primary acceptor is also a Chl termed A0. It is one of those two Chls that are located next to the secondary acceptor A1, which is a phylloquinone (Brettel and Leibl, 2001). An important point is that no details of the early electron transfer steps in the PSI RC have yet been resolved directly in the ultrafast transient absorption measurements on intact PSI particles. Typically in these measurements only the rise of the final radical pair (on the ps timescale), considered to be the P700+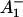 state, has been resolved directly. This state was found to appear with a 25–35-ps rise time in both C. reinhardtii and cyanobacterial PSI (for reviews, see Melkozernov, 2001; Brettel and Leibl, 2001). By comparing transient absorption data obtained with reduced and oxidized P700, respectively, and/or forming the difference spectra at various times after excitation, the difference spectrum
state, has been resolved directly. This state was found to appear with a 25–35-ps rise time in both C. reinhardtii and cyanobacterial PSI (for reviews, see Melkozernov, 2001; Brettel and Leibl, 2001). By comparing transient absorption data obtained with reduced and oxidized P700, respectively, and/or forming the difference spectra at various times after excitation, the difference spectrum 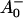 /A0 and the kinetics of what is considered to be the primary acceptor, has been deduced indirectly. This peak in the difference spectrum has a maximum at ∼685 nm (Hastings et al., 1994b, 1995a; Savikhin et al., 2000, 2001) in cyanobacteria, and is somewhat shorter (∼680 nm) in C. reinhardtii (Melkozernov et al., 1997, 1998; Gibasiewicz et al., 2001). According to these works the main bleaching band of the final radical pair (RP) is located at 702 nm for cyanobacteria and at 696 nm for C. reinhardtii in agreement with radical pair spectra on a slower timescale (see review by Brettel and Leibl, 2001). The reason why no such transient and its related difference spectrum have been resolved so far for the primary radical pair from the kinetics of open RCs has usually been explained by the similarity of the trapping time (25–35 ps) and the time for the second electron transfer step (20–50 ps), which would prevent the accumulation of a sizable amount of the first redox intermediate (for a review see Melkozernov, 2001). In a more recent work on cyanobacterial PSI, direct difference spectra of particles with P700 reduced-minus-oxidized have been measured on the ultrafast timescale (Savikhin et al., 2001). The authors concluded that both the charge separation time as well as the secondary electron transfer step from
/A0 and the kinetics of what is considered to be the primary acceptor, has been deduced indirectly. This peak in the difference spectrum has a maximum at ∼685 nm (Hastings et al., 1994b, 1995a; Savikhin et al., 2000, 2001) in cyanobacteria, and is somewhat shorter (∼680 nm) in C. reinhardtii (Melkozernov et al., 1997, 1998; Gibasiewicz et al., 2001). According to these works the main bleaching band of the final radical pair (RP) is located at 702 nm for cyanobacteria and at 696 nm for C. reinhardtii in agreement with radical pair spectra on a slower timescale (see review by Brettel and Leibl, 2001). The reason why no such transient and its related difference spectrum have been resolved so far for the primary radical pair from the kinetics of open RCs has usually been explained by the similarity of the trapping time (25–35 ps) and the time for the second electron transfer step (20–50 ps), which would prevent the accumulation of a sizable amount of the first redox intermediate (for a review see Melkozernov, 2001). In a more recent work on cyanobacterial PSI, direct difference spectra of particles with P700 reduced-minus-oxidized have been measured on the ultrafast timescale (Savikhin et al., 2001). The authors concluded that both the charge separation time as well as the secondary electron transfer step from 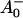 to A1 are, in fact, much faster than believed previously (lifetimes of 1.3 ps for the first and 13 ps for the secondary electron transfer step were deduced; Savikhin et al., 2001). However, the overall trapping kinetics would still be dominated by an ∼20-ps lifetime (see Scheme 1 C).
to A1 are, in fact, much faster than believed previously (lifetimes of 1.3 ps for the first and 13 ps for the secondary electron transfer step were deduced; Savikhin et al., 2001). However, the overall trapping kinetics would still be dominated by an ∼20-ps lifetime (see Scheme 1 C).
The energy transfer and charge separation processes in PSI can be described by a system of coupled differential equations within so-called compartment models (see, e.g., Holzwarth et al., 1987, 1998; Holzwarth, 1996). Even changing only one rate constant in the system, as is certainly done when going from open (P700 reduced) to closed (P700 oxidized) RCs, would have an effect on several, if not all observed lifetimes, albeit to various extents. Although the qualitative insight of forming double difference spectra between kinetics of two different states may be quite useful, such procedures can potentially lead to spurious signals and transients (partly due to the difference formation of kinetics with slightly changed lifetimes) that may lead to erroneous interpretations. It would thus be more desirable to solve the kinetic scheme and the associated transient spectra directly from the transient absorption data. Such kinetic modeling is performed rarely due to the complexities of the kinetic models and/or due to the uncertainties in the data. The insight gained from such modeling is, however, very valuable, and should be free from the problems related to forming difference spectra between transient spectra of different states or of different delay times, as discussed above.
Another problem that needs to be addressed in detail concerns the question of the nature of the primary electron donor and/or the exact redox state of the first intermediate. It is generally assumed that what is usually called P700+ is already formed in the first electron transfer step (all the interpretations of ultrafast data cited above assume such a model; for a review, see Brettel and Leibl, 2001) due to the oxidation of one of the central Chls of the RC—i.e., PA or PB. We note, however, that so far no solid experimental evidence exists to support this assignment. The nature of P700+ has typically been measured and tested only at times much later than the formation and decay of the primary radical pair. A recent electron paramagnetic resonance study showed that the electron hole is most likely located on the Chl PB of the RC, with a partial delocalization on PA (Käss et al., 2001). In principle, however, other initial electron transfer steps and sequences are possible and not excluded by the present data. Thus it may be possible that P700+ forms only in a secondary electron transfer step. Such a scheme was, for example, demonstrated recently for Photosystem II reaction centers (Prokhorenko and Holzwarth, 2000). In contrast to general assumptions that the primary electron donor should be the pseudodimer PD1/PD2 (Zouni et al., 2001), it was shown that, at least at low temperatures, the primary electron donor is the accessory Chl. A similar electron transfer process was observed earlier in bacterial RCs (van Brederode et al., 1999; van Brederode and van Grondelle, 1999), although it plays only a minor role due to the energetically high-lying excited state of the accessory BChl. Similar schemes cannot be excluded at present for PSI either.
The purpose of this work is twofold: 1), to critically re-examine the current interpretations regarding the energy trapping times and mechanism of charge separation; and 2), to test the current models for the secondary electron transfer steps. To this end, we performed ultrafast transient absorption spectroscopy with low excitation intensity and high signal-to-noise (S/N) ratio on open PSI RC core complexes from C. reinhardtii, and then analyzed these kinetic data using kinetic compartment modeling to arrive both at a kinetic scheme and, at the same time, obtain the corresponding transient spectra of the intermediates. Only if both pieces of information, the kinetics and the associated intermediate spectra, yield meaningful results can we be reasonably certain about the validity of the kinetic description of the underlying processes. These data strongly suggest that none of the currently discussed models for the energy trapping and the early electron transfer processes in PSI complexes correctly describes the experimental kinetics. A revised kinetic scheme that describes the early processes up to 100 ps is presented.
MATERIALS AND METHODS
Biochemical preparation and measurement conditions
Cells of C. reinhardtii CC2696 were grown and the PSI complexes prepared as described in Witt et al. (2002). The cells were harvested and thylakoids prepared as in Krabben et al. (2000). Isolation of the PSI complex was performed according to the method of Hippler et al. (1997), with slight modifications. The thylakoid membranes were resuspended in H2O to a Chl concentration of 0.2 mg/ml and were then solubilized once with 0.9% (w/v) n-dodecyl β-d-maltoside (DM) for 20 min at 4°C under stirring. After addition of NaCl to a final concentration of 50 mM, stirring was continued for an additional 10 min before centrifugation. The supernatant was loaded onto a sucrose density gradient and centrifuged for 16 h at 170,000 g. The lowest band was collected to obtain the PSI particles, diluted with 5 mM Tricine-NaOH (pH 7.5), 0.02% DM, and 100 mM NaCl, and concentrated with an Amicon ultrafiltration cell (Millipore, Bedford, MA). Chl concentrations were determined according to the method of Porra et al. (1989).
For the measurements the PSI complexes were diluted to an OD676 = 0.71/mm in 5 mM Tricine-NaOH (pH 7.5), 0.02% DM, 100 mM NaCl, 40 mM Na ascorbate, and 50 μM phenoxy-methosulfate as redox mediator. Integrity of the sample was checked by absorption spectroscopy before and after the measurements. No changes in the spectrum were observed. The measurements were performed at room temperature (22°C).
Femtosecond measurements and analysis
Transient spectra in the femtosecond-to-nanosecond time range have been measured with open (reduced) P700 on these PSI particles at room temperature. The sample was contained in a 1-mm pathlength rotating cuvette which was also shifted sideways. Thus the cycle time to the same volume was ∼1 min, which allowed enough time for reopening of the RCs after a turnover. The fs-transient absorption kinetics were measured as described in Croce et al. (2001) using a Ti-sapphire regenerative amplifier system (Quantronix, model 4810, East Setauket, NY) pumping an optical parametric amplifier (Topas, Light Conversion, Vilnius, Lithuania) for excitation and a homebuilt photodiode array detector system. In short, the pulse width was ∼60 fs with a spectral width (full-width at half-maximum) of ∼8–9 nm. The excitation intensities in the 120–130-μm diameter spot were such that ∼<0.3 photons were absorbed per PSI particle per shot at a 3-kHz repetition rate.
The primary data analysis has been performed by lifetime distribution analysis and is represented as lifetime density maps, as described previously (Croce et al., 2001). For the analysis the data from several measurements, recorded in different time ranges of 5 ps and 300 ps and with different resolutions per point of 13 fs and 0.5 ps, were combined and analyzed globally to calculate a single lifetime density map (Croce et al., 2001). This also involves correction for the minor chirp in the white-light continuum and deconvolution with the excitation pulse. In addition the original spectral resolution in the raw data of 0.5 nm/point (see Fig. 1) was limited to 3 nm by binning several camera pixels, which results in a higher S/N ratio. In summary the lifetime density plots represent the amplitudes of the lifetime components in a quasi-continuous lifetime range. Thus the kinetics is described as
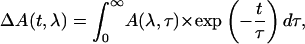 |
which is replaced for analysis by a discrete sum of exponentials,
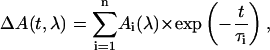 |
where n is a large number (typically 70–100; see Eq. 1 in Croce et al., 2001, for more details). The individual (fixed) lifetimes τi of this distribution themselves have no physical meaning but serve only as a suitable basis function set for the description of the total kinetics. The maxima and shoulders of these lifetime distributions Ai(λ) represent the prevailing physical lifetimes of the system (Holzwarth, 1996). White-yellow spots in the maps represent positive amplitudes Ai and reflect either decay of an absorption or the rise of a bleaching/stimulated emission. Blue-to-black spots represent negative amplitudes and reflect either decay of a bleaching/stimulated emission or the rise of an absorption. The orange background represents the zero amplitude level.
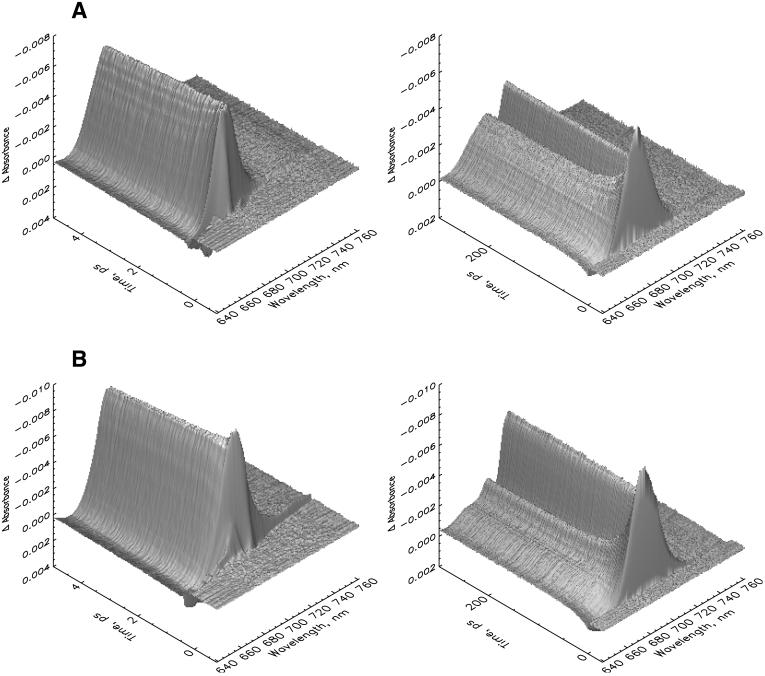
FIGURE 1.
Three-dimensional plot of the femtosecond transient absorption kinetics measured on two different timescales and resolutions (see Materials and Methods for details) for PSI core particles from C. reinhardtii at room temperature. (A) 670-nm excitation with 430 pJ/pulse, and (B) 700-nm excitation with 760 pJ/pulse. Note that the ΔA scale is reversed (negative is up) for better visibility of the surface.
Kinetic compartment modeling was performed with a homewritten program directly on the kinetics obtained from the lifetime density maps (lifetime distributions) and not on a limited set of precalculated decay-associated difference spectra (DADS) and lifetimes, which, a priori, would restrict the number of possible models. Our procedure is essentially identical to performing the kinetic modeling directly on the measured data since the lifetime distribution maps are obtained by a transformation of the original data sets to the lifetime space and represent exactly the total kinetics but with the advantage that the noise and chirp contribution is eliminated. This approach is more useful for various reasons than modeling on a predetermined DADS and lifetime set as discussed before (Holzwarth, 1995, 1996). In the case at hand, the advantage is primarily in the possibility to more reliably distinguish between different kinetic models which yield close-lying lifetime values. The actual procedure used is a semiautomatic fitting procedure that allows immediate graphical inspection of all the important parameters like, e.g., the fit quality, the lifetimes obtained from the model, the rate constant matrix, the time evolution of the population of the intermediates, and the resulting species-associated difference spectra (SADS). The latter represent directly the difference spectra of the various intermediates. The procedure allows us to keep certain rate constants fixed during fitting and/or to control certain rates manually. This model development was found to be much more efficient and less time-consuming than more conventional fully automatic fitting procedures. One of the main advantages is that it allows us to quickly compare different models, start the optimization from different starting parameters for the rate constants, etc., and thus examine efficiently a range of different kinetic models.
RESULTS AND DISCUSSION
Experimental kinetics
Transient absorption spectra have been measured for 670 nm (only antenna excitation) and 700 nm (primarily RC excitation) excitation wavelength for open (P700 reduced) PSI particles from C. reinhardtii CC2696 on the timescale of tens of femtoseconds to hundreds of picoseconds at room temperature. The excitation intensity was low enough to primarily cause single excitations per PSI particle. In fact our excitation intensity was slightly smaller than that used recently for characterization of exciton migration in C. reinhardtii PSI (Gibasiewicz et al., 2001). Detailed calculations show that our excitation conditions on average provide <0.3 excitations per PSI particle. Taking into account the Poissonian distribution, only ∼10% of all excited particles receive a second excitation (for 670-nm excitation; less for 700-nm excitation). Thus our excitation conditions for 670 nm are located close to the onset of exciton annihilation. When decreasing the excitation intensity by a factor of two we did not observe any changes in the kinetics that would significantly change the results. However, our primary aim in this work is the elucidation of the energy trapping and electron transfer processes and not of the precise, very early, antenna equilibration processes. Thus the excitation conditions provide a good compromise between linearity and high S/N ratio, which is important for the resolution of the complex kinetics at longer times.
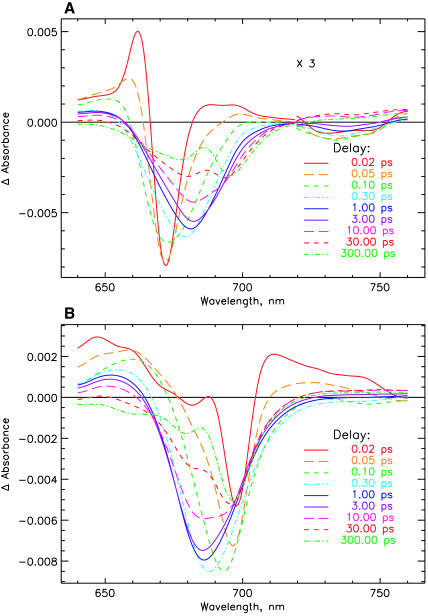
The original transient kinetics of C. reinhardtii PSI cores are shown in Fig. 1 A for 670-nm and Fig. 1 B for 700-nm excitation for two different timescales. The decay of the initial antenna bleaching after excitation and the formation of the P700+ difference spectrum is directly visible. The absorption difference spectra at various delay times are shown in Fig. 2 A, for 670-nm excitation, and Fig. 2 B, for 700-nm excitation. They are calculated from the lifetime density maps of the transient kinetics (Fig. 3) for Fig. 3 A, 670-nm, and Fig. 3 B, 700-nm excitation wavelengths. Inspection of Figs. 1 and 2 indicates that the antenna and antenna/RC core equilibration processes are essentially finished on a timescale of ∼2 ps. The difference spectra at later times show the overall trapping of excitation and the formation/decay of various radical pair states. More detailed analysis of Fig. 2, A and B, reveals that after excitation ultrafast spectral evolution takes ∼100 fs. After that time the initially very narrow bleaching band has broadened and the characteristic stimulated emission (SE) sidebands for the vibronic transitions of excited antenna Chls ∼730–740 nm has developed. For 670-nm excitation the spectrum has been substantially red-shifted at 1-ps delay time, with some minor further development of the spectrum up to 2 ps. At that time the antenna excited-state equilibration seems to be completed. This can be deduced from the absence of further red-shift in the absorption bleaching maximum at longer times (see Fig. 2 A). For 700 nm the initial narrow bleaching band is located at 699 nm and widens up to 100 fs, together with the development of the characteristic SE side band at 745 nm. We believe that this ultrafast time process characterizes the equilibration among the exciton states in the RC core that is directly excited primarily at 700 nm. The RC core comprises at least the six RC Chls and perhaps one or two of the relatively tightly coupled connecting Chls (see the structure of Synechococcus PSI (Jordan et al., 2001)). Most of the spectral development of the excited state distribution is finished already at 1-ps delay in this case, again with some further minor spectral development up to ∼2–4 ps. Thus, as for 670-nm excitation, the excited state equilibration seems to be complete at this time, as judged from the absence of further blue-shift in the absorption bleaching maximum at longer delay times. This provides a first indication that processes on a timescale longer than 3 ps should reflect the energy trapping by charge separation and secondary electron transfer processes. The lifetime density maps in Fig. 3, A and B, present in a condensed form the total kinetics in the system. The exact three-dimensional data sets from which these maps are reproduced are used in the detailed kinetic modeling below.
FIGURE 2.
Transient absorption difference spectra for PSI particles after correction for chirp and deconvolution with the excitation pulse (see the original data in Fig. 1). (A) 670-nm excitation, and (B) 700-nm excitation.
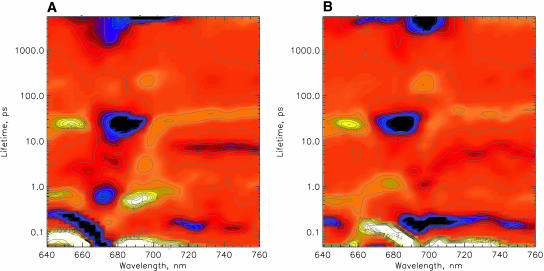
FIGURE 3.
Lifetime density maps (see Materials and Methods for details) of the transient absorption decays of PSI particles as obtained from the data shown in Fig. 1. (A) 670-nm excitation, and (B) 700-nm excitation.
The lifetime maps reveal all the relevant lifetime components: processes on the ultrafast timescale are 1), a spectral evolution with lifetimes below 200 fs; for 670-nm excitation the dominant component(s) of energy transfer comprise lifetimes in the range of 300–800 fs (the corresponding spots on the lifetime density map are rather broad, reflecting a range of underlying lifetimes); 2), a small component (≤5% of the relative amplitude) with a difference spectrum similar to that of the sub-ps components has a lifetime of 2–4 ps; these components show bleaching (negative amplitude, blue) on the short wavelength side and rise of bleaching (positive amplitude, yellow) on the long-wavelength side as is typical for energy transfer components from higher energy to lower energy pigments; and 3), there are several longer lifetime components seen on the lifetime density maps that do not seem to represent energy transfer components—i.e., they do not show the typical pair of negative/positive signals for the same lifetime in the wavelength range of the typical Chl pigment maxima. These are in ascending order: a component of 6–9 ps which is located mainly in the 740–760-nm region but also shows some significant amplitude at shorter wavelengths. A component of 15–30-ps lifetime located below 660 nm and in the range of 680–685 nm (this component of negative amplitude is part of a very broad lifetime distribution indicating that it is composed of at least two lifetime components), and a component of 30–45-ps lifetime (upper end of the distribution) which is best determined and separated from the other components in the 720–760-nm range, but whose amplitude is particularly strong ∼670 and 690 nm (although in that wavelength range it is mixed with the shorter-lived 15–25-ps component. A very small amplitude component of ∼200 ps is located at 695 nm and a very long-lived (nondecaying component) is distributed over the whole detected spectral range, with maxima in the 680–700-nm range. Very similar lifetimes are seen in the lifetime density map for 700-nm excitation, except that the main antenna equilibration component now has a lifetime of ∼1 ps, and the 2–4-ps component is extremely weak and almost undetectable. Instead, a 100–200-fs component shows the dominant amplitudes here. All the longer-lived components described above for 670-nm excitation are also present for 700-nm excitation.
The main difference between 670-nm and 700-nm excitation is the opposite amplitudes of the transient components for the antenna equilibration. For 670-nm excitation there occurs a bleaching decay (negative amplitude) ∼675 nm in the 300–800-fs and the 2–4-ps components, whereas the amplitude of these DADS is positive (rise of a bleaching) at 690 nm. In contrast, for 700-nm excitation the 1-ps component has a negative amplitude at 700 nm (decay of a bleaching) and a positive amplitude (rise of a bleaching) at 675 nm. These reversed amplitudes in the two sets of data simply reflect the antenna equilibrations occurring from different starting distributions, i.e., uphill energy transfer from the pigments excited at 700 nm, as already discussed for the transient absorption spectra at different delay times for Fig. 2, A and B. Also the 100–200-fs component reflects decay of bleaching at 700 nm and rise of bleaching at 665–680 nm, indicating uphill energy equilibration. The absence of the 2–4-ps antenna equilibration component for long-wavelength excitation has also been noted by Gibasiewicz et al. (2001), and their transient absorption data on the short timescale are in fact quite similar to the ones reported here.
The difference spectra at long delay times (300 ps, see Fig. 2, A and B) should reflect the final radical pair state on this timescale (the P700+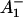 state) and are thus expected to be identical for the two excitations (this is the same component as the so-called nondecaying, i.e., ND, component in the work of other authors; see, e.g., Gibasiewicz et al., 2001). Surprisingly at first glance these final spectra are quite different for the two excitation wavelengths (see Figs. 1 and 2). The same observation has been made by Gibasiewicz et al. (2001) in their transient spectra of the ND component. Inspection of Fig. 3 A in the long lifetime range and comparison to Fig. 3 B indicates that there is a specific difference in the two (ND) lifetime components; i.e., for 670-nm excitation, there occurs an additional 1–2-ns lifetime component showing a bleaching band centered at ∼675 nm which is absent in Fig. 3 B. We have performed steady-state fluorescence experiments on these samples (data not shown) that indicate the presence of a substantial amount of energetically detached light-harvesting complex (LHC I), which emits at ∼740 nm at 77 K. This is responsible for the 1–2-ns component contribution to the long-lived (ND component) bleaching spectrum and thus for the distortion in the 670-nm excitation ND component. It is possible (and necessary) to include this component in the kinetic modeling. It will be demonstrated below that taking into account this energetically detached antenna in the kinetic model completely removes this difference in the long-lived transient spectra of the final radical pair for the two excitation wavelengths.
state) and are thus expected to be identical for the two excitations (this is the same component as the so-called nondecaying, i.e., ND, component in the work of other authors; see, e.g., Gibasiewicz et al., 2001). Surprisingly at first glance these final spectra are quite different for the two excitation wavelengths (see Figs. 1 and 2). The same observation has been made by Gibasiewicz et al. (2001) in their transient spectra of the ND component. Inspection of Fig. 3 A in the long lifetime range and comparison to Fig. 3 B indicates that there is a specific difference in the two (ND) lifetime components; i.e., for 670-nm excitation, there occurs an additional 1–2-ns lifetime component showing a bleaching band centered at ∼675 nm which is absent in Fig. 3 B. We have performed steady-state fluorescence experiments on these samples (data not shown) that indicate the presence of a substantial amount of energetically detached light-harvesting complex (LHC I), which emits at ∼740 nm at 77 K. This is responsible for the 1–2-ns component contribution to the long-lived (ND component) bleaching spectrum and thus for the distortion in the 670-nm excitation ND component. It is possible (and necessary) to include this component in the kinetic modeling. It will be demonstrated below that taking into account this energetically detached antenna in the kinetic model completely removes this difference in the long-lived transient spectra of the final radical pair for the two excitation wavelengths.
For 700-nm excitation no contribution of the uncoupled antenna is present due to the negligible absorption of LHC I at this wavelength in our samples. Thus in this experiment the long-lived (ND) transient spectrum should reflect completely the undistorted P700+–P700 difference spectrum. The main bleaching maximum of this component is located at 697 nm, and the second minor band at 680 nm. The positions of these maxima and the overall shape of this spectrum (ratio of 1/0.3 of the two main bands) are very close to the P700+ absorption difference spectrum measured on the ms-to-s timescale (see the ms-spectrum shown in Gibasiewicz et al., 2001, for a comparison), and thus clearly reflects the P700+ difference spectrum without any significant distortions. In contrast to Gibasiewicz et al. we thus believe that any relaxations of the protein after the radical pair formation have only a minor influence on the shape of this spectrum. A possible protein relaxation step might perhaps be assigned to the very weak 200-ps component, which slightly changes the shape of this difference spectrum on the 200-ps timescale. The most likely reason for the difference of the long-lived (ND) spectrum in our case and that reported in Gibasiewicz et al. (for long wavelength excitation) is the presence of a higher amount of detached LHC I in their samples, such that excitation at 700 nm still partially excited that complex in their experiments. We have tried to eliminate as much of this complex as possible in the isolation procedure, although it does not seem to be possible to remove it entirely without resorting to harsher methods which are prone to remove some of the minor polypeptides as well. We estimate ∼20–25% excitation contribution for LHC I at 670 nm (see below) in our sample. At 700 nm the absorption contribution of such an amount of LHC I to the total sample absorption is expected to be essentially negligible, and our data in fact show that no LHC I component is required to describe the 700-nm experiments. In the following kinetic models we will thus only take into account the excited LHC I for 670-nm excitation and not for 700-nm excitation.
It will be important for the later discussion and interpretations that, entirely independent of any detailed kinetic modeling, it is possible to conclude from the data discussed so far that excited state equilibration is essentially complete after ∼3 ps. (This conclusion is also in good agreement with the data of Gibasiewicz et al., 2001.) Furthermore it follows from these and other data in the literature about excited Chl a difference spectra, that over almost the complete detected wavelength range the processes of energy transfer/equilibration and charge separation/electron transfer show spectral contributions and changes. There exists, however, one wavelength region in our data where there is essentially no contribution from either antenna bleaching (GB) nor excited state absorption (ESA). This is the region of 745–760 nm. Rather, in that region there occurs a weak but characteristic absorption of radical pair states (Nuijs et al., 1986, 1987; van Gorkom and Nuijs, 1987). Thus, it should be possible in that wavelength region to observe and detect, without even resorting to any kinetic models, the time course of the development of the primary radical pair state(s). In that wavelength region we observe in our data a distinct component corresponding to a lifetime of 6–9 ps which has not been resolved in previous work. This component appears both in the 670-nm and in the 700-nm excitation experiments. It has a negative amplitude and thus represents the rise of an absorption. We believe that the only possible explanation for this component is the development of the primary radical pair state, since it cannot be explained by an energy transfer process which would have to show a positive amplitude due to the rise of a bleaching of a long-wavelength SE signal (see Figs. 2 and 3). Inspection of Fig. 2, A and B, shows that the absorption increase in the time range of 10–30 ps at 755–760 nm is highest and that it decays to approximately one-half that value up to 300 ps. Fig. 3 A also shows that the 40–45-ps component has a spectrum quite similar to that of the 6–9-ps component, but with opposite amplitude (positive, reflecting the decay of an absorption). This absorption decrease can thus only reflect a secondary electron transfer step. The most important conclusion from these findings is, however, that the primary radical pair formation does occur with a lifetime of 6–9 ps. This is in contrast to the present interpretation that the energy trapping by charge separation has a 20–25-ps lifetime in C. reinhardtii PSI (Melkozernov et al., 1997, 1998; Gibasiewicz et al., 2001), quite similar to the energy trapping lifetime (20–25-ps lifetime) of Synechocystis PSI (Turconi et al., 1996; Gobets et al., 1998b, 2001b; Savikhin et al., 1999, 2000; Melkozernov et al., 2000a; Gobets and van Grondelle, 2001). If the energy trapping in C. reinhardtii PSI indeed occurs with a lifetime of 6–9 ps this would drastically change the models for energy transfer, trapping, and electron transfer in this RC complex. Although these qualitative observations provide very important and fundamental information for the understanding of the nature and kinetics of the underlying processes, we do not consider this a final proof. Rather this conclusion should be supported by a kinetic model analysis where both the rate constant scheme as well as the corresponding species-associated intermediate difference spectra (SADS) should be in agreement with the conclusions drawn. This is done in the following part.
Kinetic modeling
We now proceed with kinetic modeling of the transient absorption data presented above. C. reinhardtii PSI does not seem to contain any red Chls in its core antenna according to the literature data but seems to contain the red pigments in the peripheral LHC-I complexes (Melkozernov, 2001) which are not attached in our preparation. In the PSI structure of Synechococcus (Jordan et al., 2001) the RC Chls are quite separated from all the antenna Chls (the P700 Chls are separated by 20–30 Å from all other Chls), except for the two so-called connecting Chls, which are closer to the RC Chls. It has been reported, however, that these connecting Chls, contrary to earlier belief, do not play a major role in the energy equilibration between antenna and RC (Byrdin et al., 2002). It thus seems reasonable to expect that the RC complex, comprising at least the six RC Chls, but possibly including the two connecting Chls, represents an entity wherein excitation equilibration occurs quite rapidly, i.e., on the timescale of 100–200 fs (see, e.g., Gibasiewicz et al., 2002). This is even more likely due to the fact that the six RC Chls are fairly strongly coupled excitonically (Beddard, 1998a,b). A similar situation occurs in the PSII RC and it is well known that most of the exciton equilibration among the states in the RC proper (as measured, e.g., in the D1–D2 RC complex) occurs in ∼100 fs, and that only a minor part of the equilibration takes up to 400 fs (Merry et al., 1996; Müller et al., 1996a,b; Prokhorenko and Holzwarth, 2000). A similarly fast equilibration is likely to occur among the exciton states in the PSI RC, as proposed already by Gibasiewicz et al. (2001, 2002), although the exact kinetics of the ultrafast equilibration process was not fully resolved there. This view is in fact well-supported by the data in Fig. 2 B, where the RC is excited directly. If this model is correct, the first electron transfer step would most likely occur from an almost-completely equilibrated RC core, even if we assume that the (intrinsic) rate of the first electron transfer step is very fast, e.g., 2 ps−1. If this is the case, the fast electron transfer step would most likely not be observable with any substantial amplitude in a transient absorption experiment of intact PSI. Rather the observable rate would be slower by a factor of up to 6–8, reflecting the distribution of the excitation over 6–8 Chls in the RC, depending on which Chls should be included in the rapid equilibration process and charge separation from an equilibrated RC core. If correct, the conclusion from this situation would be that we should be able to observe a state (intermediate) in transient absorption (and most likely also in fluorescence) that reflects the absorption difference of the excited but equilibrated RC core proper. This situation would be rather different from the assumptions made in previous models where it was assumed that either 1), the excited RC does not attain any appreciable population due to slow energy transfer from the antenna and faster charge separation (Gobets et al., 1998a, 2001b; Gobets and van Grondelle, 2001; see also this article, Scheme 1 D); or 2), the other popular model, where only P700 (reflecting essentially only the special Chl pair PA PB) is excited and observable in the kinetics (Savikhin et al., 1999, 2000, 2001) (see Scheme 1, B and C). We will test all of these various possibilities in our kinetic modeling. Surprisingly Melkozernov and co-workers (Melkozernov et al., 1997; Gibasiewicz et al., 2001) did not resolve a RC component, although in their model the equilibration of the antenna with the RC is faster than the trapping by charge separation.
We start our kinetic modeling without any assumptions by just taking into account the situation that the model needs to describe at least the four dominant experimentally observed lifetime components (see Fig. 3), which means that there must be at least four different species or intermediates present. In more extended models, five or six components should be present, reflecting the additional 1–2 lifetime components present in the data. The simplest possible model, ignoring for the time-being the energy equilibration processes on a timescale <500 fs, should include at least one antenna pool, the excited RC complex, and two radical pair states. The initial excitation conditions should be such that for 670-nm excitation the antenna is almost exclusively excited (plus the detached LHC I complex which contributes an additional, but unconnected lifetime component), whereas for 700-nm excitation the RC core is excited to ∼70–90% and the core antenna only to a small percentage.
The method used for kinetic modeling is described in the Materials and Methods section. Here only one point needs to be mentioned in addition. Our kinetic modeling does not only aim at a good kinetic description of the data in terms of lifetimes, although such a solution is in fact always possible given enough lifetime components and/or intermediates (in a first-order rate equation model, the number of species is always identical with the number of lifetimes in the system). In every case at least one trivial solution (a sequential model with or without back-reactions) exists. In reality many different kinetic models will satisfy the conditions of merely a good kinetic fitting in terms of lifetimes. Thus, without any further criteria to judge the different formal solutions we cannot differentiate the good from the poor models. These additional criteria required consist in 1), getting the rate constants of the model in a physically meaningful range; 2), obtaining a reasonable probability of initial excitation according to the absorption cross-sections of the different pigment pools; and 3), the most important of these additional criteria, the shape and amplitude of the resulting intermediate spectra (SADS). Kinetic modeling without calculating these intermediate spectra is almost meaningless, since there will always exist a mathematically optimal fitting solution as long as the rate constant scheme yields the correct lifetimes present in the data (Holzwarth, 1995, 1996). Thus, when developing kinetic models, “solutions” will often be obtained where the SADS are clearly meaningless. Such cases can be discarded easily. However, it also happens that some aspects of the spectra appear to be quite reasonable whereas others may be questionable. It is therefore important to further define the criteria by which resulting SADS should be judged in our particular case at hand. The difficulty lies in the problem that these criteria cannot be implemented easily in a quantitative manner into a kinetic fitting program. For this reason we have developed the semiautomatic fitting and kinetic modeling program described above, which allows, at every stage, visual inspection of all important parameters. Even though the criteria for the SADS cannot be defined in such a rigorous quantitative manner as the criteria for a good kinetic fit (like, e.g., the usual χ2-values; see Holzwarth, 1995, 1996), we nevertheless need to define, as clearly as possible, the criteria we used here for judging the SADS, which are given in the following: a difference spectrum of a Chl excited state (or a spectrally broadened inhomogeneous pool of Chls) should typically have only one bleaching maximum, a small SE side band in the range 720–740 nm (appearing as a small bleaching band), and an ESA band starting at wavelengths ∼20–30 nm to the blue from the bleaching maximum. The SE side band is particularly revealing and important. The SADS of radical pairs can have several bleaching maxima but they should have a characteristic small absorption increase above 720 nm (Nuijs et al., 1986, 1987; Holzwarth et al., 1993). Furthermore, the amplitudes of the excited state difference spectra should be fairly similar as long as they reflect mostly nonexcitonically coupled states (or pools of such pigments). Thus, the SADS of antenna pools should have similar amplitudes, whereas the RC* SADS may perhaps have somewhat larger amplitudes due to exciton delocalization which could increase the extinction coefficient as compared to merely monomeric Chls. The reason for this is that the area under the bleaching curves (neglecting excited state absorption) must be proportional to the oscillator strength of the underlying transitions (Holzwarth, 1995, 1996). For the radical pair spectra no such criteria for the amplitudes can be formulated.
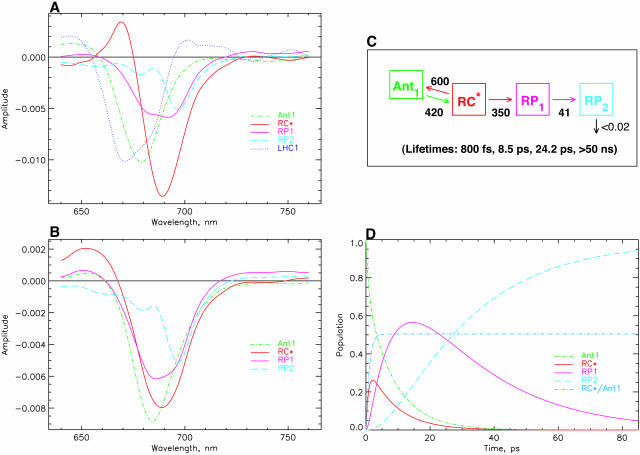
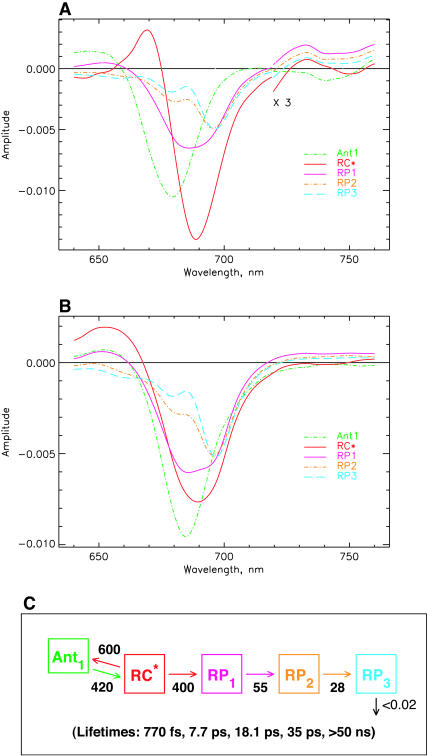
Fig. 4 shows the data for the minimal kinetic model as discussed above. For 670-nm excitation (Fig. 4 A) the additional LHC I antenna with a lifetime in the ∼1.4-ns range was taken into account as a separate component to describe the contribution of this complex to the long-lived bleaching spectrum (called the nondecaying or ND component by other authors; see, e.g., Melkozernov, 2001), which would otherwise distort the resulting RP spectrum. This antenna has no contribution in the models for 700-nm excitation. As shown in Fig. 4 B, it is possible to describe the experiments for the two excitations within the same kinetic model, the same rate constants, and, within the error limits, the same SADS. The only difference between the two sets of spectra is the slightly larger amplitude and the somewhat narrower width of the RC* difference spectrum for 670-nm excitation as compared to 700-nm excitation. Reasons for these small differences will become clear in the further discussion below. Here we simply note that this scheme represents the simplest possible compartment model that describes the main features of the kinetics but still does not reflect all important details of the kinetics. The main reason for these discrepancies can, however, be assigned to the fact that for 700-nm excitation the main part of the excited state equilibration occurs with a lifetime of 100–200 fs, which is not reflected in this kinetic model at all. Also the 400–500-fs energy equilibration component is not reflected properly. Instead, the overall energy equilibration is described by an average ∼800-fs component. Fig. 4 C shows the kinetic scheme and the resulting associated rate constants together with the lifetimes of this model. We note that such a uniform model for drastically different excitation conditions has not been achieved so far for any PSI particle according to our knowledge. The resulting SADS satisfy all the criteria provided above. The antenna SADS and the RC* SADS show the expected SE bands at long wavelength and have only one bleaching band. The two radical pair SADS show an absorption increase above ∼740 nm. The most important result of this simple model is, however, the fact that the first radical pair shows a spectrum with a strong bleaching band at ∼680 nm, in addition to a second bleaching maximum at ∼694 nm. These are the features that have been deduced indirectly previously for the spectrum of the first radical pair, but have never been resolved directly with open RCs in PSI particles. (Note that the RP difference spectra of C. reinhardtii are blue-shifted by 5–7 nm versus those from cyanobacteria; Melkozernov et al., 1997, 2000a,b; Savikhin et al., 2001.) The 680-nm bleaching disappears mostly in the second electron transfer step, resulting in a spectrum for the final radical pair that is essentially identical to the long timescale P700+ difference spectrum, as already mentioned above. Thus all the SADS look very reasonable. Furthermore, this kinetic model resolves, for the first time, the excited states spectrum of the presumably equilibrated RC with a bleaching maximum at 689 nm. Such a feature has neither been resolved in transient absorption nor fluorescence kinetics before.
FIGURE 4.
Results of kinetic modeling. Simplest model with one antenna pool, the RC pool, and two RPs. (A) SADS for 670-nm excitation; (B) SADS for 700-nm excitation; (C) kinetic scheme with optimized rate constants (in units of ns−1) for the model and resulting lifetimes (bottom); and (D) time dependence of relative concentrations of the intermediates in the model for 670-nm excitation (the initial excitation is always 1, corresponding to 100% initial excited state at t = 0). Also given in this figure is the ratio of excitations in the RC to the main antenna pool Ant1. This allows us to judge the timescale of antenna/RC* equilibration. Note that the first RP rises with the dominant lifetime component of 8.5 ps. [General comment for Figs. 4–10: The same type of presentation will be used for the different models in Figs. 5–10 as well. Therefore, please refer to this figure caption for details, while the other captions are provided in short notation. Ant1 denotes the main antenna pool, Ant0 denotes the short wavelength antenna pool, RC* the excited reaction center, and Core* (only used in Fig. 9) an additional exciton state of the RC proper. In general the rate constants (in units of ns−1) in the models have been rounded to the nearest decade, except for the rate constants <50 ns−1. The error in the rate constants is typically in the range of 10% for most rate constants. For the secondary electron transfer rates it is closer to 5%. In some cases the error may be > or < than 10%, which will be indicated in the text specifically. For 670-nm excitation an additional component of 1.4 ns for the disconnected LHC 1 was taken into account (the corresponding SADS for LHC 1 is shown only in Fig. 4 A and is omitted in the other SADS for clarity of presentation). No LHC 1 was taken into account due to negligible excitation for 700-nm excitation experiments (for detailsm see text).]
The trapping lifetime in this kinetic scheme (Fig. 4 C) and thus the formation of the first radical pair RP1 occurs with a lifetime of 8.5 ps and RP1 decays with a lifetime of 24 ps. Thus the main lifetime of the formation of the first radical pair (this can be seen quantitatively from the amplitude matrix provided in the Appendix) coincides with the negative amplitude feature ∼745–760 nm in the lifetime density maps in Fig. 3, A and B. The trapping kinetics is by a factor of ∼3× faster than the 20–25 ps resulting from previous models (see review of Melkozernov, 2001). If, in fact, we would like to prolong the energy trapping to at least a 20-ps lifetime, this can only be achieved in a meaningful way by lowering the rate constant for charge separation from the RC* state. The alternative possibility of actually lowering the rate constants for energy exchange between antenna and RC leads to extremely poor SADS (data not shown). This would actually correspond to the models shown in Scheme 1, B–D. The result of a model with a drastically decreased rate constant for charge separation from the equilibrated RC* from 350 ns−1 to ∼130 ns−1, i.e., by a factor of almost 3, is shown in Fig. 5 (note that this rate constant is not the intrinsic rate constant for electron transfer and is also not the inverse lifetime of the apparent energy trapping, as follows clearly from the kinetic schemes). This situation corresponds roughly to the models in the literature described by Scheme 1 A. This low value of the rate constant (130 ns−1) would most likely imply an intrinsic rate of the first electron transfer step of substantially <1 ps−1, a value which is probably too low in view of numerous higher values deduced from theoretical modeling (Trinkunas and Holzwarth, 1996; Byrdin et al., 2002; Sener et al., 2002) of the kinetics of various PSI particles.
FIGURE 5.
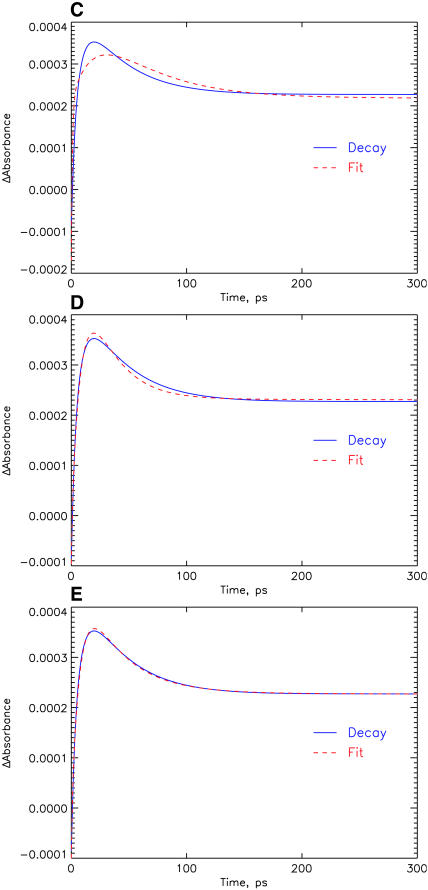
Kinetic model with a hypothetical scheme where charge separation occurs with a lifetime of 20 ps (energy trapping and rise of first RP). This scheme corresponds closely to most current models in the literature for the early processes in PSI from both C. reinhardtii and most cyanobacteria (for details see Results and Discussion). (A) SADS for 670-nm excitation. (B) Kinetic scheme with rate constants (in units of ns−1) and resulting lifetimes. (C–E) Comparison of experimental transient absorption kinetics at 742 nm (solid line) with the fitted curve from the model (dashed line). The three parts show the comparison for different models: (C) for the hypothetical model of Fig. 5 (this model fits the data very poorly, see text); (D) for the model shown in Fig. 4; and (E) for the model shown in Fig. 7. See Note in Fig. 4, legend, for further details.
Reducing the rate constant for charge separation (as done deliberately in the model of Fig. 5) has, however, several adverse consequences: first, the antenna SADS now shows substantial excited state absorption above 710 nm and no SE band; i.e., the antenna SADS now has some characteristics of a radical pair spectrum. Even more drastic is the consequence on the SADS of the first radical pair, wherein we entirely lose the expected strong bleaching band at ∼680 nm. In addition, this model yields quite a poor fit to the experimental kinetics at most wavelengths. We show here only the data in the 740-nm range, which is fitted very poorly by the model with the slower trapping time as compared to the model shown in Fig. 4, due to the lack of a 6–9-ps component (see Fig. 5, C–E). Note, however, that despite the much better fit, the agreement between experiment and fit is not yet perfect for our simple model either. In any case we have to discard the slow trapping scheme on various grounds and conclude that even in the simplest model that can be developed to explain the main features of the present data we get an energy trapping and charge separation with a lifetime in the range of 6–9 ps, i.e., by a factor of three faster than assumed so far by other authors.
More refined kinetic models
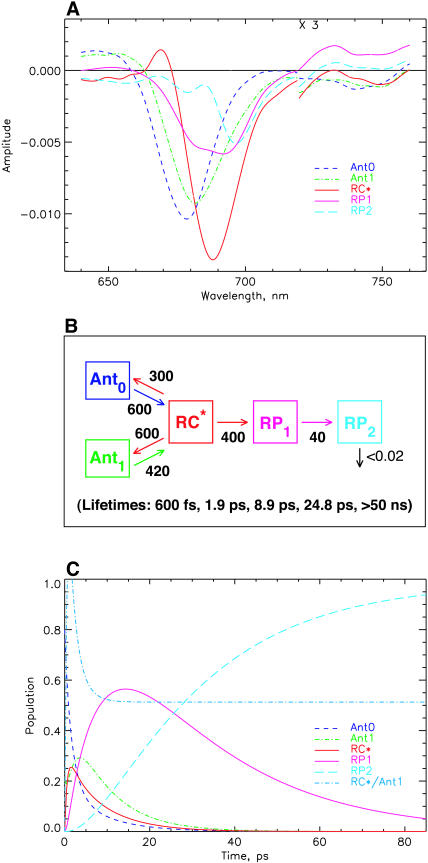
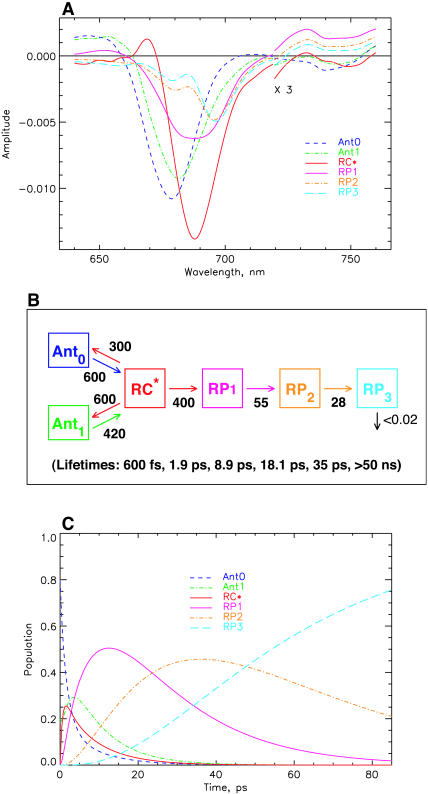
The model shown in Fig. 4 is in various ways too simple and needs extension, although it is well-suited to describe the main features of the kinetics and yield good SADS. First it describes only four lifetimes (including the ND component), whereas the kinetic data (Figs. 1–3) indicate the presence of six major lifetime components, not even including the 100–200-fs component(s). Thus the simple scheme of Fig. 4 averages several kinetic components. The additional components would include at least one more energy equilibration component, thus allowing us to separate the sub-ps and the 1.5–2-ps energy transfer components. One additional lifetime component is required to better describe the lifetime range from 10–45 ps, which shows a very broad distribution ∼680–700 nm and some complexities which are not described by a single 25-ps component (see Figs. 3 and 4). It is easy to include an additional antenna equilibration component as shown in Fig. 6. The two antenna components Ant0 (short wavelength antenna pool) and Ant1 (main core antenna pool) have peak bleaching wavelengths of 678 and 682 nm in their SADS, representing a slightly blue-shifted smaller antenna pool and the major core antenna, respectively. This model extension substantially improves the description of the fast energy equilibration processes, which are now described with two lifetimes of ∼600 fs and 1.9 ps (see kinetic scheme in Fig. 6, B and C). The spectral shapes of the SADS look very reasonable, with smooth band shapes, SE in the long wavelength range for all the excited states, absorption increases for the RPs on the long wavelength side, and ESA in the short wavelength region for the excited states. The amplitude of the RC* SADS is somewhat larger than for the antennae, reflecting probably some increased oscillator strength due to exciton coupling in the RC. The shapes of the radical pair spectra are not affected significantly as compared to those resulting from the simpler model in Fig. 4. This was expected since we have already discussed above that energy transfer and electron transfer/trapping processes occur on different timescales in this PSI particle. The SADS for 700-nm excitation are not shown for this model, inasmuch as the outer antenna Ant0 does not receive any appreciable population upon 700-nm excitation (for a more detailed analysis of the 700-nm experiment, see Fig. 9, below).
FIGURE 6.
Extended kinetic model with two antenna pools, the RC, and two RPs for 670-nm excitation. (A) SADS; (B) kinetic scheme with rate constants and resulting lifetimes (bottom); and (C) time dependence of concentrations of intermediates. The energy trapping and rise of the first RP occurs with a dominant lifetime of 8.9 ps. See Note in Fig. 4, legend, for further details.
FIGURE 9.
Modified scheme (for 700-nm excitation only) where the ultrafast RC equilibration component of ∼150 fs has also been taken into account. The outer antenna pool Ant0 is omitted, since essentially no excitation is returning to that pool upon 700-nm excitation. (A) SADS for 700-nm excitation; (B) Kinetic scheme with rate constants and resulting lifetimes (bottom); and (C) time dependence of concentrations of intermediates. The first RP rises with a dominant lifetime of ∼7 ps. See Note in Fig. 4, legend, for further details.
The energy trapping by charge separation in this model occurs with a lifetime of 8.9 ps, quite similar to the one in the model of Fig. 4. (Note again that this lifetime is not the inverse intrinsic electron transfer rate and also not the inverse apparent charge separation rate from the RC, which is actually 400 ns−1.) In Fig. 6 C the time dependencies of the various intermediates are shown. A 4:1 excitation probability for 670-nm excitation for the two antenna pools best describes the data. The RC* state reaches a maximal concentration of ∼25%, whereas the first radical pair reaches a maximal concentration of nearly 60%. The populations in the inner antenna Ant1 and the RC* are equilibrated within ∼5 ps, i.e., in a time shorter than the effective energy trapping lifetime of 8.9 ps. This points to a kinetics which is considerably more trap-limited than diffusion-limited or transfer-to-trap-limited. In this model the overall trapping lifetime is strongly dependent on the electron transfer rate constant. The model shows that the energy equilibration processes within the antenna on the one hand and between antenna and RC on the other hand can be described very well in a relatively simple way with two antenna pools in this PSI particle. Again the RC* SADS has its maximum at 689 nm, only ∼8 nm longer than the main antenna pool. Although this model describes the energy transfer processes (occurring upon 670-nm excitation) very well, there is still some deviation between experimental and model kinetics for lifetimes in the 10–45-ps range. This will be improved in the next step.
Before going to more complex models it is interesting to compare the excited state equilibration times with the apparent lifetime for energy trapping (6–9 ps). This can be done if we set the rate constant for charge separation in the scheme of Fig. 6 B to zero without changing the other rate constants. The scheme then gives the kinetics that would be observed if by some means the electron transfer could be stopped entirely without any other changes. The data show that the core antenna and the RC* equilibrate with the longest component lifetime of ∼2 ps. This is the actual slow equilibration time between antenna and RC. However, in the intact system with open RC the RC* population is disturbed by the ongoing charge separation and thus the equilibration effectively takes a little longer time.
More complex electron transfer models
In keeping with the main aim of this article we will now try to improve the description of the longer-lived electron transfer processes rather than the energy transfer processes. In order not to complicate the kinetic model too much we will in the following first ignore again the details of the antenna processes, as shown in Fig. 6, and return to a one antenna pool description. This is valid as we have already shown above that the spectra and kinetics related to the components above 3 ps are not influenced significantly by the details of the antenna energy transfer processes. At the end we will introduce again the antenna equilibration and provide a full kinetic model. However, for the time being, things can be kept simpler by just focusing on the radical pair kinetics.
The data in Fig. 3 indicating the qualitative assignment of the effective charge separation (equal to energy trapping) step to a lifetime <10 ps, supported by the models shown in Figs. 4–6, require the inclusion of a further radical pair intermediate to better describe the lifetime range from 10–45 ps which contains more components than described by the models presented so far. With only two radical pair intermediates the broad kinetic feature in Fig. 3, A and B, which spans the lifetime range from ∼10 to ∼40 ps, cannot be described exactly. Note that the inclusion of any back electron transfer reactions in the kinetic scheme, as may be necessary eventually (see below), would not increase the number of lifetime components, but would simply change some lifetimes in the model—which would, in turn, require some changes in the other rates of the kinetic model to arrive again at the correct experimental lifetimes.
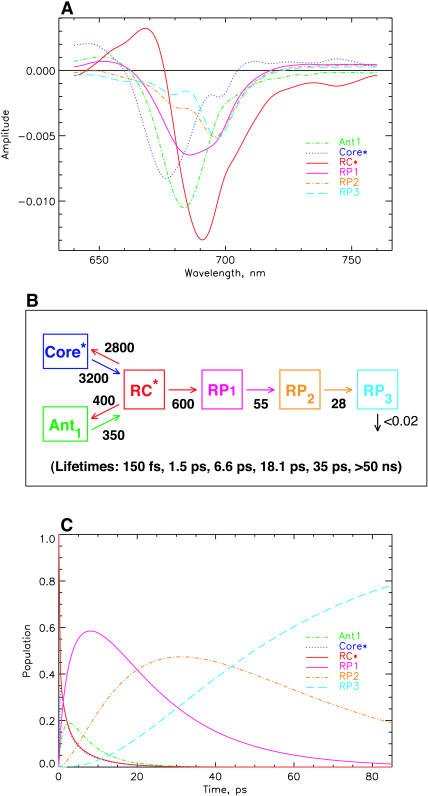
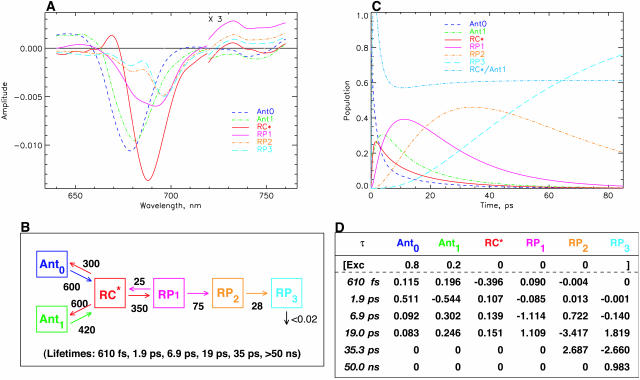
Fig. 7 shows the SADS (Fig. 7, A and B) and the kinetic scheme that best describe the data for both excitation wavelengths with one additional kinetic component in the longer ps lifetime range. The underlying kinetic scheme with the rate constants is shown in Fig. 7 C. In this scheme again the primary RP (RP1) rises with a lifetime of ∼8 ps, as in the more simple models (Figs. 4 and 6) and its SADS is quite similar for this reason. However, there are now two RPs, namely RP2 and RP3, with reduced bleaching in the difference spectrum at 680 nm. The lifetime of RP1 is 18 ps in this model, whereas the lifetime of RP2 is ∼35 ps. The latter corresponds approximately to the upper range of the lifetime distribution ∼685 nm in Fig. 3 and to the weak positive band in the density map in the 740–760-nm range. With this extension of the kinetic scheme the data in Fig. 3 are very well described in the range of 4–100 ps, including the long-lived ND component (which in our models is described by a lifetime of >50 ns).
FIGURE 7.
Kinetic scheme with one antenna pool, the RC, and three RPs. (A) SADS for 670-nm excitation; (B) SADS for 700-nm excitation; and (C) kinetic scheme with rate constants and resulting lifetimes (bottom). The energy trapping and rise of the first RP occur with a dominant lifetime of ∼7.7 ps. See Note in Fig. 4, legend, for further details.
All three RPs show a pronounced and essentially constant bleaching ∼696 nm, although they differ in the amplitudes of the band at 680 nm and in the amount of absorption increase above 720 nm. RP1 shows the well-known two-banded bleaching at 696 nm and 680 nm as we have seen already in the models of Figs. 4 and 6. RP2 and RP3 show a decreased bleaching in the 680-nm band as compared to RP1. The antenna and RC excited state spectra remain more or less unchanged by the inclusion of the additional RP intermediate. Thus all SADS look again quite reasonable according to our criteria. It is worth noting that the RC* spectrum has a somewhat smaller amplitude than the antenna and is also somewhat broader for 700-nm excitation than for 670-nm excitation. This is due to the fact that our model at this point does not provide for a proper description of the very strong 100–200-fs component (Fig. 3 B) which seems to reflect an exciton equilibration process within the RC. We will try to describe this in a further extension of the model after first discussing the general consequences of the present model results. We note in passing that the kinetic scheme in Fig. 7 C brings the kinetics into very good agreement with the data of photovoltage measurements (Hecks et al., 1994). In those data two electrogenic steps with ∼20 and 40–50 ps were obtained, which agrees well with the data of this model.
What are the possible assignments of these three electron transfer intermediates? So far only two RP states have been distinguished in PSI particles in the time range up to ∼100 ps. These were the P700+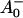 and the P700+
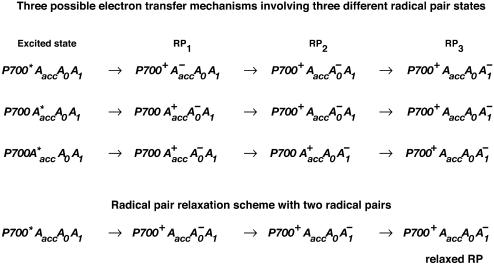
and the P700+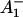 states (see reviews by Melkozernov, 2001, and Brettel and Leibl, 2001). Our data strongly suggest that an additional intermediate is necessary to describe the kinetic data. Several possible assignments, implying different mechanisms for electron transfer, exist a priori to explain these data. The simplest interpretation would result if RP2 and RP3 represent the same redox state but different protein conformations. The possibility of protein relaxation after charge separation has been discussed both for PSI and for PSII. For PSII RCs and intact PSII this process is well-documented (Holzwarth et al., 1994; Gatzen et al., 1996; Konermann et al., 1997). However, it has not been shown to our knowledge so far that such a protein relaxation process is related to a substantial change in the transient difference spectra of the radical pairs for the same redox state. At this level this is a qualitative argument which we cannot substantiate any further, but we doubt that any protein relaxation on the timescale of a few 10 ps could result in a substantial absorption change for the pigments of the RC. The other possibilities are therefore different redox states. The various possibilities are compiled in Scheme 2. One possibility would be that a so-far not-resolved intermediate P700+
states (see reviews by Melkozernov, 2001, and Brettel and Leibl, 2001). Our data strongly suggest that an additional intermediate is necessary to describe the kinetic data. Several possible assignments, implying different mechanisms for electron transfer, exist a priori to explain these data. The simplest interpretation would result if RP2 and RP3 represent the same redox state but different protein conformations. The possibility of protein relaxation after charge separation has been discussed both for PSI and for PSII. For PSII RCs and intact PSII this process is well-documented (Holzwarth et al., 1994; Gatzen et al., 1996; Konermann et al., 1997). However, it has not been shown to our knowledge so far that such a protein relaxation process is related to a substantial change in the transient difference spectra of the radical pairs for the same redox state. At this level this is a qualitative argument which we cannot substantiate any further, but we doubt that any protein relaxation on the timescale of a few 10 ps could result in a substantial absorption change for the pigments of the RC. The other possibilities are therefore different redox states. The various possibilities are compiled in Scheme 2. One possibility would be that a so-far not-resolved intermediate P700+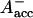 is formed, where Aacc represents the accessory Chl in the active branch. That would be reminiscent of the main electron transfer mechanism in the bacterial RC (Woodbury and Allen, 1995; Zinth et al., 1996; Wachtveitl et al., 1996). Only in the second step, then, would the P700+
is formed, where Aacc represents the accessory Chl in the active branch. That would be reminiscent of the main electron transfer mechanism in the bacterial RC (Woodbury and Allen, 1995; Zinth et al., 1996; Wachtveitl et al., 1996). Only in the second step, then, would the P700+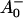 RP be formed. This seems to be a reasonable explanation at present in view of the fact that all the RPs have about the same bleaching in the red 696-nm band, indicating that perhaps P700+ is present in all those redox states. We note, however, that the breaking and reformation of excitonic interactions in the RC during the different electron transfer steps can have quite complicated consequences on the observable spectra of the intermediates that are not transparent without any detailed calculations. Although perhaps more difficult to explain, at least qualitatively, at present we should also not ignore other possibilities. One of them would be electron transfer starting at the accessory Chl, Aacc, in the active branch, thereby reducing first A0. Such a mechanism would necessarily require three different redox intermediates up to the state P700+
RP be formed. This seems to be a reasonable explanation at present in view of the fact that all the RPs have about the same bleaching in the red 696-nm band, indicating that perhaps P700+ is present in all those redox states. We note, however, that the breaking and reformation of excitonic interactions in the RC during the different electron transfer steps can have quite complicated consequences on the observable spectra of the intermediates that are not transparent without any detailed calculations. Although perhaps more difficult to explain, at least qualitatively, at present we should also not ignore other possibilities. One of them would be electron transfer starting at the accessory Chl, Aacc, in the active branch, thereby reducing first A0. Such a mechanism would necessarily require three different redox intermediates up to the state P700+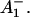 In a second step an electron could be transferred from PA or PB to the oxidized accessory Chl
In a second step an electron could be transferred from PA or PB to the oxidized accessory Chl 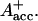 An analogous mechanism is present in PSII RCs (Prokhorenko and Holzwarth, 2000), although, in that case, the first acceptor is a pheophytin. As mentioned above, this possibility may be less likely, given the fact that, in that case, P700 (corresponding to oxidation of PA or PB) is oxidized only in the second RP, which would not allow us to easily explain the initial bleaching at 696 nm. However, we note that the positions of the pigments and the different exciton states in PSI RCs are not known so far. Thus we do not like to exclude that possibility. There is one piece of evidence which in fact would support this model. This is the change in kinetics observed when the His ligating amino acid to the Mg of the PB Chl was mutated to asparagine, which changes the redox potential of P700 and thus changes the electron transfer rate. In that case a drastic reduction in the rate of energy trapping was observed (leading to an increase in lifetime from 25 ps to 50–70 ps; Melkozernov et al., 1998). However, based on our kinetic models presented here, that lifetime component should no longer be assigned to the energy trapping (or first electron transfer step), since we have shown that this process occurs with a lifetime of <10 ps, but rather to the secondary electron transfer process. If that were the case it makes sense to have P700 oxidized only in the second electron transfer step, since this step would be influenced primarily by a change in the redox potential of P700 in such a scheme. Finally, we also cannot entirely rule out a two-branch electron transfer process where the secondary steps could occur with different rates. We have not worked out such a scheme based on our data because we do not have any positive evidence in favor of such a model at present.
An analogous mechanism is present in PSII RCs (Prokhorenko and Holzwarth, 2000), although, in that case, the first acceptor is a pheophytin. As mentioned above, this possibility may be less likely, given the fact that, in that case, P700 (corresponding to oxidation of PA or PB) is oxidized only in the second RP, which would not allow us to easily explain the initial bleaching at 696 nm. However, we note that the positions of the pigments and the different exciton states in PSI RCs are not known so far. Thus we do not like to exclude that possibility. There is one piece of evidence which in fact would support this model. This is the change in kinetics observed when the His ligating amino acid to the Mg of the PB Chl was mutated to asparagine, which changes the redox potential of P700 and thus changes the electron transfer rate. In that case a drastic reduction in the rate of energy trapping was observed (leading to an increase in lifetime from 25 ps to 50–70 ps; Melkozernov et al., 1998). However, based on our kinetic models presented here, that lifetime component should no longer be assigned to the energy trapping (or first electron transfer step), since we have shown that this process occurs with a lifetime of <10 ps, but rather to the secondary electron transfer process. If that were the case it makes sense to have P700 oxidized only in the second electron transfer step, since this step would be influenced primarily by a change in the redox potential of P700 in such a scheme. Finally, we also cannot entirely rule out a two-branch electron transfer process where the secondary steps could occur with different rates. We have not worked out such a scheme based on our data because we do not have any positive evidence in favor of such a model at present.
SCHEME 2.
Three possible redox intermediates corresponding to the three radical pairs as discussed in the text (top), and relaxed radical pair scheme with only three different redox intermediates (bottom).
The fact that the two excitation conditions can be described by the same kinetic model lends important support for its validity. We note that the additional complexities of the electron transfer processes introduced in Fig. 7 did not change the energy equilibration kinetics. Thus, in the more complex scheme as well, the kinetics is closer to trap- rather than diffusion-limited, as already discussed above.
Combined model
A full model, combining the models of Figs. 6 and 7 which contains two antenna pools and three radical pairs, is shown in Fig. 8. The radical pair SADS are essentially the same as in the model in Fig. 7 A and the antenna SADS are the same as in the model in Fig. 6. This model describes all the processes observed in the data of Fig. 3 A for 670-nm excitation, except for the ultrafast RC exciton equilibration present only for 700-nm excitation (Fig. 3 B). All the new features that distinguish our models from previous schemes are combined here: resolution of the RC* spectrum, fast energy trapping with 6–9 ps, and resolution of the first RP with the expected spectral shape. With 700-nm excitation, inclusion of the outer (short-wavelength) antenna is not required, inasmuch as no significant amount of energy returns to that antenna pool. We therefore do not show the 700-nm excitation analysis within this model. Rather, in the latter experiment, the inclusion of the ultrafast RC equilibration (Fig. 9) becomes important.
FIGURE 8.
Full model taking into account two antenna pools, the RC, and three RPs without including effects from charge recombination. (A) SADS for 670-nm excitation; (B) kinetic scheme with rate constants and resulting lifetimes (bottom); and (C) time dependence of concentrations of intermediates. The first RP rises with a dominant lifetime of ∼9 ps. See Note in Fig. 4, legend, for further details.
Ultrafast exciton equilibration in the reaction center
We noted above that the 100–200-fs component, which is very strong for 700-nm excitation (Fig. 3 B), is reflected in none of the models described so far. The inspection of the raw data in Figs. 2 and 3 indicates that this fast process most likely reflects exciton equilibration among the 6–8 Chls forming the RC proper. Thus including a very rapid energy equilibration process involving two RC exciton states should solve this problem. Such a model is shown in Fig. 9. In particular, it results in an RC* SADS that is more similar to that obtained for 670-nm excitation, both in width and location, which is rather gratifying. A new component with a maximum bleaching at 677 nm, denoted as Core*, likely representing a higher energy exciton state of the RC, appears (Fig. 9). There occur essentially no changes in the other SADS. As expected, we have to make some adjustments in the rate constants of charge separation from the equilibrated RC and energy equilibration between RC and core antenna to keep the same longer lifetimes. This model extension essentially leads to the introduction of the 150-fs RC core equilibration process which is strong in the data and provides the corresponding SADS spectrum. What is called the RC* state in this model is actually different now from the other models. This state represents only a low energy subset of all the exciton states in the RC. Since this model assumes that charge separation actually starts from that low energy subset of the exciton state(s), rather than from some averaged exciton state (as in all the other models), the effective rate constant for charge separation must be higher in this model, which is reflected by the increase from 400 to 600 ns−1 (compare to Fig. 8). Actually, the trapping or charge separation time may be somewhat shorter upon direct excitation of the low-lying exciton states of the RC, as is done at 700 nm. This may be reflected by the observation that the small negative amplitude features in the long wavelength range of ∼740–760 nm actually seem to have a somewhat shorter lifetime than the corresponding features for 670-nm excitation (see Fig. 3). Thus in our model for 700-nm excitation that takes into account the ultrafast RC equilibration process, the effective charge separation time is 6.6 ps, i.e., somewhat shorter than in the previous models. Note that ultrafast exciton equilibration in the RC cores has been studied earlier by Gibasiewicz et al. (2001, 2002).
Charge recombination to the excited state
According to the current view, the first electron transfer step is irreversible for any practical purposes in open PSI RCs (see, e.g., Brettel and Leibl, 2001). Only when the quinone acceptor and the Fe-S clusters are reduced does one observe a charge recombination fluorescence (Kleinherenbrink et al., 1994; Polm and Brettel, 1998; Schlodder et al., 1998). In keeping with these so-far accepted ideas that no back electron transfer occurs in a PSI RC with the acceptor side in the open (oxidized) state, we have only included forward electron transfer steps in the models presented up to this point. This assumption, together with the independent qualitative evidence supporting the 6–9-ps energy trapping lifetime, has the important consequence that the longest predicted fluorescence lifetime in all of these models would be <10 ps, corresponding to the observed trapping lifetime of 6–9 ps. Numerous fluorescence kinetic data, however, for both C. reinhardtii PSI and for cyanobacterial PSI, show that longer-lived fluorescence components with large amplitude in the time range of 20–25 ps do exist. Thus our kinetic models so far seem to be at odds with those data. We note, however, that some of these fluorescence kinetic data have been measured with oxidized P700, rather than with reduced RCs (see, e.g., Melkozernov et al., 1997). This constitutes an important difference because we cannot, a priori, assume that the kinetics for open and closed RCs remains the same, although this assumption seems to be more or less fulfilled for some cyanobacterial PSI particles. However, there has never been a good reason to support this hypothesis and it might be just a coincidence for a particular situation or a particular PSI particle. In fact, recent fluorescence data have shown that open and closed PSI do differ in their fluorescence kinetics (Byrdin et al., 2000). In any case, even small kinetic details become very important at this point and we should thus be careful to refer only to data where the fluorescence kinetics has been measured with strictly open RCs. This seems to be clearly the case for several cyanobacterial PSI studies on Synechocystis and Synechococcus (Holzwarth et al., 1993; Turconi et al., 1993, 1996; Hastings et al., 1994a; Kennis et al., 2001; Gobets et al., 2001b), but for C. reinhardtii fewer data with clearly defined measurement conditions exist. The data of Melkozernov et al. (1998) do show the presence of a large 20–25-ps fluorescence component. However, the measurements did not resolve any faster components which makes the overall comparison difficult. In any case, all the present data indicate that with open PSI both in C. reinhardtii as well as in Synechocystis (and with slightly longer lifetime also in Synechococcus) a fluorescence lifetime with large amplitude in the range of 20–30 ps is present. How can this seeming discrepancy between the models presented so far describing the transient absorption data and the experimental fluorescence kinetics be resolved? The most straightforward possibility to get a longer-lived fluorescence component in this range is to include some electron back transfer process in the first electron transfer step. This would, in fact, not be unreasonable, in view of the new redox intermediate that we suggest here. The energy of this intermediate should be between the energy of the P700+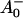 state and the excited state of the RC. Thus it could well be possible to have some contribution of electron back reactions to the excited state in the kinetics. Note that inclusion of such a back transfer step would not increase the number of the lifetime components in the scheme, it would simply change the resulting lifetimes in the scheme (see Figs. 4–9), and would thus require some minor adjustments of some rate constants in the scheme to bring the model again into agreement with the kinetic data (i.e., the lifetimes in the model for the transient absorption data should remain essentially unchanged). However, a 6–9-ps component has not been resolved to our knowledge so far for C. reinhardtii PSI. Nevertheless such a component cannot be excluded at present. One reason is the difficulty to resolve several lifetimes in the 2–4-ps (antenna equilibration) component, a possible 6–9-ps component for charge separation, and a charge recombination lifetime in the range of ∼20 ps. The best time-resolved fluorescence lifetime study for C. reinhardtii core PSI has been measured by fluorescence upconversion (Du et al., 1993) and showed the presence of a 5.5-ps component. Neither in our present transient absorption data nor in the data of other groups has a 5.5-ps component been resolved. The dominant energy transfer component is only ∼2–4 ps. Thus it is very likely that the 5.5-ps component of Du et al. (1993) represents a mixture of the 2–4-ps energy transfer component and the 6–9-ps trapping component. For this reason the transient absorption data could well be in agreement with the fluorescence kinetics if we postulate a charge recombination from the first radical pair. Clearly, more accurate fluorescence kinetics data are needed and we are in the process of acquiring them. However, we note that this is not a trivial task at all to resolve so many close-lying lifetime components. Using the possibility to excite the RC directly, as we have done here at 700 nm, might, however, help to resolve these processes. We note here that charge recombination from the first radical pair back to the excited state is nothing unusual, but actually a well-documented process in both purple bacterial RCs (Schenck et al., 1982; Woodbury and Parson, 1984) and PSII RCs (Schatz and Holzwarth, 1986; Schatz et al., 1987, 1988).
state and the excited state of the RC. Thus it could well be possible to have some contribution of electron back reactions to the excited state in the kinetics. Note that inclusion of such a back transfer step would not increase the number of the lifetime components in the scheme, it would simply change the resulting lifetimes in the scheme (see Figs. 4–9), and would thus require some minor adjustments of some rate constants in the scheme to bring the model again into agreement with the kinetic data (i.e., the lifetimes in the model for the transient absorption data should remain essentially unchanged). However, a 6–9-ps component has not been resolved to our knowledge so far for C. reinhardtii PSI. Nevertheless such a component cannot be excluded at present. One reason is the difficulty to resolve several lifetimes in the 2–4-ps (antenna equilibration) component, a possible 6–9-ps component for charge separation, and a charge recombination lifetime in the range of ∼20 ps. The best time-resolved fluorescence lifetime study for C. reinhardtii core PSI has been measured by fluorescence upconversion (Du et al., 1993) and showed the presence of a 5.5-ps component. Neither in our present transient absorption data nor in the data of other groups has a 5.5-ps component been resolved. The dominant energy transfer component is only ∼2–4 ps. Thus it is very likely that the 5.5-ps component of Du et al. (1993) represents a mixture of the 2–4-ps energy transfer component and the 6–9-ps trapping component. For this reason the transient absorption data could well be in agreement with the fluorescence kinetics if we postulate a charge recombination from the first radical pair. Clearly, more accurate fluorescence kinetics data are needed and we are in the process of acquiring them. However, we note that this is not a trivial task at all to resolve so many close-lying lifetime components. Using the possibility to excite the RC directly, as we have done here at 700 nm, might, however, help to resolve these processes. We note here that charge recombination from the first radical pair back to the excited state is nothing unusual, but actually a well-documented process in both purple bacterial RCs (Schenck et al., 1982; Woodbury and Parson, 1984) and PSII RCs (Schatz and Holzwarth, 1986; Schatz et al., 1987, 1988).
We will now check whether our transient absorption data would, in fact, be in agreement with such a postulated charge recombination mechanism. We can, without any problems, include an electron back transfer step in our kinetic model and still describe the kinetic data very well. As long as the rate constant for back transfer is not very large (i.e., if it remains ≤60 ns−1) this does not lead to any major change or distortion in the SADS of the intermediates as given in Figs. 6–8. Such a model, including two antenna pools, three radical pair states, and including charge recombination from the first radical pair, is shown in Fig. 10 A together with the resulting kinetic scheme (Fig. 10 B) and the time dependence of the intermediate concentrations (Fig. 10 C). This represents the full model which we consider most likely to describe the energy trapping and electron transfer kinetics of C. reinhardtii PSI core particles based on the present transient absorption data and would at the same time be in agreement with existing fluorescence data. The long-lived fluorescence kinetic component in that model is 19 ps. The only uncertainty so far is in the determination of the exact rate of charge recombination. All the principal features of the models developed above, including the proper shapes of the SADS of the intermediates, are maintained if the charge recombination is introduced. The rate constant can be extended at least up to 60 ns−1 without conflicting our present data (see further discussion below). In the model in Fig. 10 we have chosen an intermediate value of 25 ns−1 for the charge recombination rate. Apart from the expected adjustments in some of the other rate constants as compared to the previous models (necessary to obtain a good fitting to the experimentally determined lifetimes) the only difference to the previous models without charge recombination is that the antenna and RC* decays in fluorescence now do show two components of ∼7 ps and 19 ps with about equal amplitude (see the amplitude matrix Fig. 10 D for an exact description). The ratio of amplitudes of the two components depends, of course, on the excitation and detection wavelengths. The amplitude of the longer-lived component can be further increased if the rate constant for charge recombination is increased. One notable consequence of this change in the model is also an increase in the rate constant of the secondary electron transfer from 55 to 75 ns−1. The observable lifetime for this process is, however, ∼20 ps—i.e., the lifetime of the longer-lived fluorescence component. The fluorescence observed from the equilibrated RC* is predicted to have an ∼1:1 amplitude ratio of the longer-lived to the shorter-lived component. Since antenna Ant1 and RC* have quite comparable intermediate concentrations in this model (Fig. 10 C), a substantial part of the fluorescence is actually expected to arise from the RC proper. This would further tend to shift the average observable fluorescence lifetime toward the longer-lived component. Given the fact that the ∼2-ps component also has a significant contribution, it would not be unreasonable to expect that, in the fluorescence kinetic data measured so far, these two shorter-lived components might have remained unresolved (Du et al., 1993).
FIGURE 10.
Full kinetic scheme including the effects of charge recombination from the first RP. Two antenna pools, the RC, and three RPs are taken into account. (A) SADS for 670-nm excitation; (B) kinetic scheme with rate constants and resulting lifetimes (bottom); (C) time dependence of the intermediates; and (D) amplitude matrix Aij for the different lifetimes. The time dependence of concentrations Cj(t) of each intermediate follows the equation 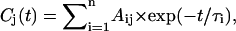 where Aij represents the amplitude matrix and τi are the lifetimes. The excitation conditions are provided in the excitation vector denoted Exc. The radical pair rises with a dominant lifetime of ∼7 ps. See Note in Fig. 4, legend, for further details.
where Aij represents the amplitude matrix and τi are the lifetimes. The excitation conditions are provided in the excitation vector denoted Exc. The radical pair rises with a dominant lifetime of ∼7 ps. See Note in Fig. 4, legend, for further details.
Unfortunately the transient absorption kinetics and SADS are not particularly sensitive to the exact value of the rate constant of the charge recombination step, mainly due to the fact that the lifetimes associated with at least three different processes are overlapping in the 10–50-ps range. Consequently this rate cannot be determined very precisely from the absorption data. The situation should, however, be much more favorable for the fluorescence kinetics. Since transient absorption spectroscopy is clearly not the method of choice for determining this rate constant exactly, we have to wait for improved fluorescence kinetic data to narrow down the uncertainty in this rate. Any value from 0 to 60 ns−1 appears to be consistent with the transient absorption data in principle. The rate constant of 25 ns−1 used in the scheme of Fig. 10 does in our view also satisfy the existing fluorescence kinetic data and would be fully in keeping with the new interpretation of the trapping and electron transfer kinetics as presented here. A rate of <10 ns−1 would most likely not be consistent with the fluorescence data since the contribution of the ∼20-ps component in fluorescence would be too small, and a rate >60 ns−1 would, according to our present modeling, lead to unreasonable SADS for the transient absorption data. Thus the upper and lower limits of this rate seem to be fairly well defined. Since the evidence for a ∼20-ps fluorescence component in PSI is clear, we have to postulate that a charge recombination process occurs from the first radical pair back to the excited state in open PSI reaction centers.
CONCLUSIONS
We have presented ultrafast transient absorption data of PSI core particles from C. reinhardtii that demand a major revision of the present models and mechanisms for the energy trapping and early electron transfer processes. Even without any kinetic models our data qualitatively suggest that energy trapping by charge separation occurs with an effective lifetime of 6–9 ps, i.e., by a factor of 3× faster than assumed so far. Detailed kinetic modeling supports these qualitative interpretations. This has important consequences for the nature of the primary radical pair. Only in models which contain this 6–9-ps component are we able to directly resolve for the first time the rise and decay of the primary radical pair with a spectrum that corresponds closely to what has been deduced so far only indirectly from difference spectra of oxidized and reduced PSI RCs (see Melkozernov, 2001, for a review). In the spectrum of the first radical pair we resolve for the first time the rise and decay of the 680-nm band assigned previously to the formation and decay of the A0 anion radical. The spectra and kinetics of the equilibrated RC* state has been resolved in our data also for the first time. Furthermore, we report the kinetics and intermediate state difference spectra of an ∼150-fs exciton equilibration component at room temperature in the reaction center of PSI upon direct excitation at 700 nm. Evidence for fast exciton equilibration in the RC has been reported earlier also by Gibasiewicz et al. (2001, 2002).
We obtain the best agreement with the data only if we introduce at least two antenna pools, and an additional radical pair intermediate which has not been resolved so far. Various interpretations for the three radical pair intermediates are discussed but no final assignment is possible at present. To obtain agreement with existing fluorescence lifetime data we also have to postulate a charge recombination process to the excited state from the first radical pair. At present this rate constant cannot be determined precisely. All of these points, in essence, represent a fundamental reinterpretation of the energy trapping and electron transfer processes in PSI of C. reinhardtii.
The overall kinetics of trapping seems to be the fastest of all the intact PSI particles known so far, barring the highly antenna depleted PSI particles prepared with solvents (Kumazaki et al., 1998, 2001; Itoh et al., 2001) where some doubts have been expressed as to the intactness of the reaction center structure. The fast kinetics is probably related to the fact that C. reinhardtii PSI likely has a smaller antenna (∼70–80 Chls per P700) than, e.g., cyanobacterial PSI. It furthermore lacks, at least in its core antenna, the extreme red antenna Chls typical of cyanobacterial PSI (Gobets and van Grondelle, 2001; Gibasiewicz et al., 2001). The total kinetics is found closer to trap-limited rather than transfer-to-trap or diffusion-limited. Due to these reasons C. reinhardtii PSI seems to be best suited to study the details of the electron transfer mechanism(s). Due to the fast energy trapping the transient concentration of the first radical pair reaches up to 40% of the initial excited state concentration (Fig. 10, C and D) which helps to resolve directly the radical pair rise and decay processes.
Outlook
At this level several important questions remain unanswered, in particular the exact nature of the early radical pair intermediates, which will require studies on mutants. Such experiments have been started in our laboratory. We finally note that the differences in interpretation to that of previous work do not arise primarily from major differences in our transient absorption data to those of other groups who have measured similar particles (Melkozernov et al., 1998; Gibasiewicz et al., 2001). The need for a revised interpretation of the data originates in part from an improved signal/noise ratio in our data and in part from the use of a more advanced data analysis procedure which together allow a better resolution of the different components. The lifetime density maps which, without any further analysis, directly show the presence of the 6–9-ps component play a central role in that respect. The second important component comes from extensive kinetic modeling on the basis of these lifetime density maps and the development of stringent kinetic models. Clearly conventional global analysis would have hardly resolved the many lifetime components and would in particular not be able to discern the complexities in the 680–700-nm wavelength region for the lifetimes in the range of 10–45 ps. Finally we note that the very small but significant ∼200-ps component present in the data has not been assigned so far. Protein relaxation in the radical pair states is a possible explanation, but we are not ready at this point to make a final interpretation of its origin.
The essentials of the complex models presented here can be summarized in a simplified fashion as drawn in Scheme 3 which shows the most important details. Initial energy equilibration among the antenna pigments occurs on a sub-ps time scale and equilibration of antenna and RC states with lifetimes in the range up to 2–3 ps. Upon direct excitation of the RC, ultrafast exciton equilibration yields a dominant component of 150-fs lifetime due to exciton equilibration among the coupled RC pigments. The trapping kinetics and formation of the first radical pair occurs with a lifetime of 6–9 ps. Three radical pairs are distinguished, the first one decays with a 16–20-ps lifetime and the second one with a 36–40-ps lifetime. Scheme 3 should be compared with the models in the literature presented in Scheme 1. Our data result in an essentially trap-limited model which is similar to Scheme 1 A as far as the energy transfer processes are concerned. The difference to Scheme 1 A is the faster effective trapping lifetime (identical to the effective charge separation lifetime) in our case, i.e., 6–9 ps vs. 20–23 ps. This difference comes due to the fact that Melkozernov and co-workers missed the very fast first electron transfer process and resolved only the second electron transfer step. The models in Scheme 1, B–D, are all transfer-to-trap-limited models. The most important difference of our results to those models is the much faster energy transfer process(es) between core antenna and RC, i.e., a ∼2-ps equilibration in our case (∼3 ps in Scheme 1 A) versus a ∼20-ps equilibration time in the models of Scheme 1, B–D. Since the electron transfer in models Scheme 1, B–D, is faster than the energy transfer to the RC, essentially no back transfer to the antenna occurs in these models. As discussed in the text, none of the models in Scheme 1, B–D, fits our data.
SCHEME 3.
Simplified scheme condensing the essential elements of the findings of this article on the early energy transfer and electron transfer steps in PSI. This scheme condenses the contents of the schemes shown in Figs. 9 and 10 in a simpler fashion in terms of the lifetimes (without giving the detailed rate constants). This scheme should be compared to the current models discussed in the literature as shown in Scheme 1.
Acknowledgments
Note added in proof: We have recently improved slightly the final kinetic scheme (Fig. 10). A connection with two small rate constants has been added between the antenna pools Ant0 and Ant1. The rate constants are 
We acknowledge excellent technical assistance by C. Schulz (Max-Volmer-Institut, Technische Universität, Berlin, Germany) in the preparation of the PSI, and we thank Michael Reus and Andrea Keil (Max-Planck-Institut für Bioanorganische Chemie, Mülheim, Germany) for help with the measurements and characterization of the particles.
APPENDIX 1
In the following we show the amplitude matrices for all the models shown in Figs. 4–10 of this article. The time dependence of concentrations Cj(t) of each intermediate follows the equation
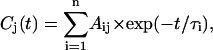 |
where Aij represents the amplitude matrix and τi are the lifetimes. Inspection of these matrices allows us to easily deduce the lifetimes and their amplitudes contributing to the rise (negative amplitude) and decay (positive amplitude) of each of the intermediates in the kinetic model. The row denoted Exc gives the excitation vector characterizing the initial excitation conditions.
APPENDIX 2
Some of the terms used to describe kinetic processes and models in photosynthetic systems have often been used somewhat ambiguously in the past in the literature. To avoid confusion we give here a short definition of the terms used throughout this article.
Energy trapping kinetics (lifetime)
Since the PSI RC is not a deep trap, energy transfer between antenna and RC is reversible and all trapping in PSI occurs actually by charge separation only. Thus the overall antenna trapping lifetime (overall lifetime of antenna excitation) and the appearance time for the first radical pair are essentially identical and the two are used in a synonymous manner in this article. Often this is used in a manner synonymous to the term (overall) charge separation lifetime.
In the models in Figs. 4–10 the rate constants are the fitting parameters obtained by fitting of the specific kinetic model to the data. These rate constants are rate constants for energy transfer or electron transfer between compartments (inasmuch as we use compartment models here; see Holzwarth, 1996). Detailed description of the compartments is given in the text. Note that these rate constants are not the inverse of the experimental lifetimes. Rather, the experimentally observed lifetimes should be compared to the lifetimes calculated from the respective kinetic schemes. The kinetic modeling, by way of finding the optimal set of rate constants in a given scheme, ideally should closely reproduce the experimentally observed lifetimes if the model is correct.
The electron transfer rate constants in Schemes 4–10, in particular for the first electron transfer step, are not the intrinsic electron transfer rate constants for charge separation. Rather, as explained in detail in the article, the rate constant for the first electron transfer step is the effective rate constant for charge separation from the equilibrated excited RC state. The term intrinsic rate constant for electron transfer is reserved exclusively for the electron transfer step from a particular pigment of the RC to the acceptor pigment. The intrinsic rate constant for electron transfer cannot be determined experimentally due to the fact that energy transfer processes in the RC are faster than the electron transfer process. Thus the intrinsic rate constant for the first electron transfer step can only be obtained from a specific model of the energetics and kinetics of the RC.
References
- Beddard, G. S. 1998a. Excitations and excitons in Photosystem I. Phil. Trans. R. Soc. Lond. A. 356:421–448. [Google Scholar]
- Beddard, G. S. 1998b. Exciton coupling in the Photosystem I reaction center. J. Phys. Chem. B. 102:10966–10973. [Google Scholar]
- Brettel, K., and W. Leibl. 2001. Electron transfer in Photosystem I. Review. Biochim. Biophys. Acta. 1507:100–114. [DOI] [PubMed] [Google Scholar]
- Byrdin, M., P. Jordan, N. Krauss, P. Fromme, D. Stehlik, and E. Schlodder. 2002. Light harvesting in Photosystem I: modeling based on the 2.5-Å structure of Photosystem I from Synechococcus elongates. Biophys. J. 83:433–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrdin, M., I. Rimke, E. Schlodder, D. Stehlik, and T. A. Roelofs. 2000. Decay kinetics and quantum yields of fluorescence in Photosystem I from Synechococcus elongatus with P700 in the reduced and oxidized state: are the kinetics of excited state decay trap-limited or transfer-limited? Biophys. J. 79:992–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, C.-K., G. L. Gaines, G. R. Fleming, and L. J. Mets. 1989. Chlorophyll fluorescence lifetime studies of greening in yellow mutants of Chlamydomonas reinhardtii: assembly of the Photosystem I core complex. Biochim. Biophys. Acta. 975:59–65. [Google Scholar]
- Chitnis, P. R. 2001. Photosystem I: function and physiology. Ann. Rev. Plant Physiol. Plant Mol. Biol. 52:593–626. [DOI] [PubMed] [Google Scholar]
- Croce, R., M. G. Müller, R. Bassi, and A. R. Holzwarth. 2001. Carotenoid-to-chlorophyll energy transfer in recombinant major light-harvesting complex (LHC II) of higher plants. I. Femtosecond transient absorption measurements. Biophys. J. 80:901–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damjanovic, A., H. Vaswani, P. Fromme, and G. R. Fleming. 2002. Chlorophyll excitations in Photosystem I of Synechococcus elongates. J. Phys. Chem. B. 106:10251–10262. [Google Scholar]
- Du, M., X. L. Xie, Y. W. Jia, L. Mets, and G. R. Fleming. 1993. Direct observation of ultrafast energy transfer in PSI core antenna. Chem. Phys. Lett. 201:535–542. [Google Scholar]
- Gatzen, G., M. G. Müller, K. Griebenow, and A. R. Holzwarth. 1996. Primary processes and structure of the Photosystem II reaction center. III. Kinetic analysis of picosecond energy transfer and charge separation processes in the D1–D2-cyt-b559 complex measured by time-resolved fluorescence. J. Phys. Chem. 100:7269–7278. [Google Scholar]
- Gibasiewicz, K., V. M. Ramesh, S. Lin, N. W. Woodbury, and A. N. Webber. 2002. Excitation dynamics in eukaryotic PSI from Chlamydomonas reinhardtii CC 2696 at 10 K. Direct detection of the reaction center exciton states. J. Phys. Chem. B. 106:6322–6330. [Google Scholar]
- Gibasiewicz, K., V. M. Ramesh, A. N. Melkozernov, S. Lin, N. W. Woodbury, R. E. Blankenship, and A. N. Webber. 2001. Excitation dynamics in the core antenna of PSI from Chlamydomonas reinhardtii CC 2696 at room temperature. J. Phys. Chem. B. 105:11498–11506. [Google Scholar]
- Gobets, B., and R. van Grondelle. 2001. Energy transfer and trapping in Photosystem I. Review. Biochim. Biophys. Acta. 1507:80–99. [DOI] [PubMed] [Google Scholar]
- Gobets, B., J. P. Dekker, and R. van Grondelle. 1998a. Transfer-to-the-trap limited model of energy transfer in Photosystem 1. In Photosynthesis: Mechanisms and Effects. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 503–508.
- Gobets, B., I. H. M. van Stokkum, F. van Mourik, M. Rögner, J. Kruip, J. P. Dekker, and R. van Grondelle. 1998b. Time-resolved fluorescence measurements of Photosystem I from Synechocystis PCC 6803. In Photosynthesis: Mechanism and Effects. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 571–574.
- Gobets, B., J. T. M. Kennis, J. A. Ihalainen, M. Brazzoli, R. Croce, L. H. M. van Stokkum, R. Bassi, J. P. Dekker, H. van Amerongen, G. R. Fleming, and R. van Grondelle. 2001a. Excitation energy transfer in dimeric Light Harvesting Complex I: a combined streak-camera/fluorescence upconversion study. J. Phys. Chem. B. 105:10132–10139. [Google Scholar]
- Gobets, B., I. H. M. van Stokkum, M. Rogner, J. Kruip, E. Schlodder, N. V. Karapetyan, J. P. Dekker, and R. van Grondelle. 2001b. Time-resolved fluorescence emission measurements of Photosystem I particles of various cyanobacteria: a unified compartmental model. Biophys. J. 81:407–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings, G., F. A. M. Kleinherenbrink, S. Lin, and R. E. Blankenship. 1994a. Time-resolved fluorescence and absorption spectroscopy of Photosystem I. Biochemistry. 33:3185–3192. [DOI] [PubMed] [Google Scholar]
- Hastings, G., F. A. M. Kleinherenbrink, S. Lin, T. J. McHugh, and R. E. Blankenship. 1994b. Observation of the reduction and redoxidation of the primary electron acceptor in Photosystem I. Biochemistry. 33:3193–3200. [DOI] [PubMed] [Google Scholar]
- Hastings, G., S. Hoshina, A. N. Webber, and R. E. Blankenship. 1995a. Universality of energy and electron transfer processes in Photosystem I. Biochemistry. 34:15512–15522. [DOI] [PubMed] [Google Scholar]
- Hastings, G., L. J. Reed, S. Lin, and R. E. Blankenship. 1995b. Excited state dynamics in Photosystem I: effects of detergent and excitation wavelength. Biophys. J. 69:2044–2055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecks, B., K. Wulf, J. Breton, W. Leibl, and H.-W. Trissl. 1994. Primary charge separation in Photosystem I: a two-step electrogenic charge separation connected with P700+ A0- and P700+A1-formation. Biochemistry. 33:8619–8624. [DOI] [PubMed] [Google Scholar]
- Hippler, M., F. Drepper, J. Farah, and J.-D. Rochaix. 1997. Fast electron transfer from cytochrome c6 and plastocyanin to Photosystem I of Chlamydomonas reinhardtii requires PsaF. Biochemistry. 36:6343–6349. [DOI] [PubMed] [Google Scholar]
- Holzwarth, A. R. 1995. Time-resolved fluorescence spectroscopy. In Methods in Enzymology, Vol. 246, Biochemical Spectroscopy. K. Sauer, editor. Academic Press, San Diego, CA. 334–362. [DOI] [PubMed]
- Holzwarth, A. R. 1996. Data analysis of time-resolved measurements. In Biophysical Techniques in Photosynthesis. Advances in Photosynthesis Research. J. Amesz and A. J. Hoff, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 75–92.
- Holzwarth, A. R., J. Wendler, and G. W. Suter. 1987. Studies on chromophore coupling in isolated phycobiliproteins. II. Picosecond energy transfer kinetics and time-resolved fluorescence spectra of C-phycocyanin from Synechococcus 6301 as a function of the aggregation state. Biophys. J. 51:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzwarth, A. R., G. H. Schatz, H. Brock, and E. Bittersmann. 1993. Energy transfer and charge separation kinetics in Photosystem I. 1. Picosecond transient absorption and fluorescence study of cyanobacterial Photosystem I particles. Biophys. J. 64:1813–1826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzwarth, A. R., M. G. Müller, G. Gatzen, M. Hucke, and K. Griebenow. 1994. Ultrafast spectroscopy of the primary electron and energy transfer processes in the reaction center of Photosystem II. J. Luminesc. 61:497–502. [Google Scholar]
- Holzwarth, A. R., D. Dorra, M. G. Müller, and N. V. Karapetyan. 1998. Structure-function relationships and excitation dynamics in Photosystem I. In Photosynthesis: Mechanism and Effects. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 497–502.
- Itoh, S., M. Iwaki, and I. Ikegami. 2001. Modification of Photosystem I reaction center by the extraction and exchange of chlorophylls and quinones. Biochim. Biophys. Acta. 1507:115–138. [DOI] [PubMed] [Google Scholar]
- Jordan, P., P. Fromme, H. T. Witt, O. Klukas, W. Saenger, and N. Krauss. 2001. Three-dimensional structure of cyanobacterial Photosystem I at 2.5 Å resolution. Nature. 411:909–917. [DOI] [PubMed] [Google Scholar]
- Karapetyan, N. V. 1998. Organization and role of the long-wave chlorophylls in the Photosystem I of the cyanobacterium Spirulina. Membr. Cell Biol. 12:571–584. [PubMed] [Google Scholar]
- Karapetyan, N. V., D. Dorra, G. Schweitzer, I. N. Bezsmertnaya, and A. R. Holzwarth. 1997. Fluorescence spectroscopy of the longwave chlorophylls in trimeric and monomeric Photosystem I core complexes from the cyanobacterium Spirulina platensis. Biochemistry. 36:13830–13837. [DOI] [PubMed] [Google Scholar]
- Karapetyan, N. V., D. Dorra, A. R. Holzwarth, J. Kruip, and M. Rögner. 1998. Origin of the extreme longwave chlorophyll form of the Photosystem I trimeric complex of Spirulina. In Photosynthesis: Mechanism and Effects, XI. International Congress on Photosynthesis, Budapest, Hungary, 1998. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, the Netherlands. 583–586.
- Karapetyan, N. V., A. R. Holzwarth, and M. Rögner. 1999a. The Photosystem I trimer of cyanobacteria: molecular organisation, excitation dynamics and physiological significance. FEBS Lett. 460:395–400. [DOI] [PubMed] [Google Scholar]
- Karapetyan, N. V., V. V. Shubin, and R. J. Strasser. 1999b. Energy exchange between the chlorophyll antennae of monomeric subunits within the Photosystem I trimeric complex of the cyanobacterium Spirulina. Photosynth. Res. 61:291–301. [Google Scholar]
- Käss, H., P. Fromme, H. T. Witt, and W. Lubitz. 2001. Orientation and electronic structure of the primary donor radical cation P-700+ in Photosystem I: a single-crystals EPR and ENDOR study. J. Phys. Chem. B. 105:1225–1239. [Google Scholar]
- Kennis, J. T. M., B. Gobets, I. H. M. van Stokkum, J. P. Dekker, R. van Grondelle, and G. R. Fleming. 2001. Light harvesting by chlorophylls and carotenoids in the Photosystem I core complex of Synechococcus elongatus: a fluorescence upconversion study. J. Phys. Chem. B. 105:4485–4494. [Google Scholar]
- Kleinherenbrink, F. A. M., G. Hastings, B. P. Wittmershaus, and R. E. Blankenship. 1994. Delayed fluorescence from Fe-S type photosynthetic reaction centers at low redox potential. Biochemistry. 33:3096–3105. [DOI] [PubMed] [Google Scholar]
- Konermann, L., G. Gatzen, and A. R. Holzwarth. 1997. Primary processes and structure of the Photosystem II reaction center. V. Modeling of the fluorescence kinetics of the D1–D2-Cyt-b559 complex at 77K. J. Phys. Chem. B. 101:2933–2944. [Google Scholar]
- Krabben, L., E. Schlodder, R. Jordan, D. Carbonera, G. Giacometti, H. Lee, A. N. Webber, and W. Lubitz. 2000. Influence of the axial ligands on the spectral properties of P700 of Photosystem I: a study of site-directed mutants. Biochemistry. 39:13012–13025. [DOI] [PubMed] [Google Scholar]
- Kumazaki, S., H. Furusawa, K. Yoshihara, and I. Ikegami. 1998. Excitation wavelength dependence of the excitation transfer in Photosystem I reaction center with reduced number of antenna chlorophylls. In Photosynthesis: Mechanism and Effects, XI. International Congress on Photosynthesis, Budapest, Hungary, 1998. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- Kumazaki, S., I. Ikegami, H. Furusawa, S. Yasuda, and K. Yoshihara. 2001. Observation of the excited state of the primary electron donor chlorophyll (P700) and the ultrafast charge separation in the spinach Photosystem I reaction center. J. Phys. Chem. B. 105:1093–1099. [Google Scholar]
- Melkozernov, A. N. 2001. Excitation energy transfer in Photosystem I from oxygenic organisms. Photosynth. Res. 70:129–153. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N., S. Lin, and R. E. Blankenship. 2000a. Excitation dynamics and heterogeneity of energy equilibration in the core antenna of Photosystem I from the cyanobacterium Synechocystis sp. PCC 6803. Biochemistry. 39:1489–1498. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N., S. Lin, and R. E. Blankenship. 2000b. Femtosecond transient spectroscopy and excitonic interactions in Photosystem I. J. Phys. Chem. B. 104:1651–1656. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N., H. Su, S. Lin, S. Bingham, A. N. Webber, and R. E. Blankenship. 1997. Specific mutation near the primary donor in Photosystem I from Chlamydomonas reinhardtii alters the trapping time and spectroscopic properties of P(700). Biochemistry. 36:2898–2907. [DOI] [PubMed] [Google Scholar]
- Melkozernov, A. N., H. Su, A. N. Webber, and R. E. Blankenship. 1998. Excitation energy transfer in thylakoid membranes from Chlamydomonas reinhardtii lacking chlorophyll b and with mutant Photosystem I. Photosynth. Res. 56:197–207. [Google Scholar]
- Merry, S. A. P., S. Kumazaki, Y. Tachibana, D. M. Joseph, G. Porter, K. Yoshihara, J. Barber, J. R. Durrant, and D. R. Klug. 1996. Sub-picosecond equilibration of excitation energy in isolated Photosystem II reaction centers revisited: time-dependent anisotropy. J. Phys. Chem. 100:10469–10478. [Google Scholar]
- Müller, M. G., M. Hucke, M. Reus, and A. R. Holzwarth. 1996a. Annihilation processes in the isolated D1–D2-cyt-b559 reaction center complex of Photosystem II. An intensity dependence study of femtosecond transient absorption. J. Phys. Chem. 100:9537–9544. [Google Scholar]
- Müller, M. G., M. Hucke, M. Reus, and A. R. Holzwarth. 1996b. Primary processes and structure of the Photosystem II reaction center. IV. Low intensity femtosecond transient absorption spectra of D1–D2 reaction centers. J. Phys. Chem. 100:9527–9536. [Google Scholar]
- Nuijs, A. M., V. A. Shuvalov, H. W. J. Smit, H. J. van Gorkom, and L. N. M. Duysens. 1987. Excited states and primary photochemical reactions in Photosystem I. In Progress in Photosynthesis Research, Vol. 1. J. Biggens, editor. Nijhoff Publishers, Dordrecht, The Netherlands. 229–232.
- Nuijs, A. M., V. A. Shuvalov, H. J. van Gorkom, J. J. Plijter, and L. N. M. Duysens. 1986. Picosecond absorbance difference spectroscopy on the primary reactions and the antenna-excited states in Photosystem I particles. Biochim. Biophys. Acta. 850:310–318. [Google Scholar]
- Owens, T. G., S. P. Webb, L. Mets, R. S. Alberte, and G. R. Fleming. 1989. Antenna structure and excitation dynamics in Photosystem I. II. Studies with photosynthetic mutants of Chlamydomonas reinhardtii lacking Photosystem II. Biophys. J. 56:95–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, L.-O., C. Flemming, B. Gobets, R. van Grondelle, J. P. Dekker, and E. Schlodder. 1998. Energy transfer and charge separation in Photosystem I P700 oxidation upon selective excitation of the long-wavelength antenna chlorophylls of Synechococcus elongates. Biophys. J. 74:2611–2622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polm, M., and K. Brettel. 1998. Secondary pair charge recombination in Photosystem I under strongly reducing conditions: temperature dependence and suggested mechanism. Biophys. J. 74:3173–3181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porra, R. J., W. A. Thompson, and P. E. Kriedemann. 1989. Determination of accurate extinction coefficients and simultaneous equations for assaying chlorophylls a and b extracted with four different solvents: verification of the concentration of chlorophyll standards by atomic absorption spectroscopy. Biochim. Biophys. Acta. 975:384–394. [Google Scholar]
- Prokhorenko, V. I., and A. R. Holzwarth. 2000. Primary process and structure of the Photosystem II reaction center: a photon echo study. J. Phys. Chem. B. 104:11563–11578. [Google Scholar]
- Savikhin, S., W. Xu, P. R. Chitnis, and W. S. Struve. 2000. Ultrafast primary processes in PSI from Synechocystis sp. PCC 6803: Roles of P700 and A0. Biophys. J. 79:1573–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Savikhin, S., W. Xu, P. Martinsson, P. R. Chitnis, and W. S. Struve. 2001. Kinetics of charge separation and
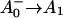 electron transfer in Photosystem I reaction centers. Biochemistry. 40:9282–9290. [DOI] [PubMed] [Google Scholar]
electron transfer in Photosystem I reaction centers. Biochemistry. 40:9282–9290. [DOI] [PubMed] [Google Scholar] - Savikhin, S., W. Xu, V. Soukoulis, P. R. Chitnis, and W. S. Struve. 1999. Ultrafast primary processes in Photosystem I of the cyanobacterium Synechocystis sp. PCC 6803. Biophys. J. 76:3278–3288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schatz, G. H., H. Brock, and A. R. Holzwarth. 1987. Picosecond kinetics of fluorescence and absorbance changes in Photosystem II particles excited at low photon density. Proc. Natl. Acad. Sci. USA. 84:8414–8418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schatz, G. H., H. Brock, and A. R. Holzwarth. 1988. A kinetic and energetic model for the primary processes in Photosystem II. Biophys. J. 54:397–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schatz, G. H., and A. R. Holzwarth. 1986. Mechanisms of chlorophyll fluorescence revisited: prompt or delayed emission from Photosystem II with closed reaction centers? Photosynth. Res. 10:309–318. [DOI] [PubMed] [Google Scholar]
- Schenck, C. C., R. E. Blankenship, and W. W. Parson. 1982. Radical-pair decay kinetics, triplet yields and delayed fluorescence from bacterial reaction centers. Biochim. Biophys. Acta. 680:44–59. [Google Scholar]
-
Schlodder, E., K. Falkenberg, M. Gergeleit, and K. Brettel. 1998. Temperature dependence of forward and reverse electron transfer from
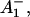 the reduced secondary electron acceptor in Photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar]
the reduced secondary electron acceptor in Photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar] - Sener, M. K., D. Y. Lu, T. Ritz, S. Park, P. Fromme, and K. Schulten. 2002. Robustness and optimality of light harvesting in cyanobacterial Photosystem I. J. Phys. Chem. B. 106:7948–7960. [Google Scholar]
- Trinkunas, G., and A. R. Holzwarth. 1996. Kinetic modeling of exciton migration in photosynthetic systems. 3. Application of genetic algorithms to simulations of excitation dynamics in three-dimensional Photosystem I core antenna/reaction center complexes. Biophys. J. 71:351–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turconi, S., J. Kruip, G. Schweitzer, M. Rögner, and A. R. Holzwarth. 1996. A comparative fluorescence kinetics study of Photosystem I monomers and trimers from Synechocystis PCC 6803. Photosynth. Res. 49:263–268. [DOI] [PubMed] [Google Scholar]
- Turconi, S., G. Schweitzer, and A. R. Holzwarth. 1993. Temperature dependence of picosecond fluorescence kinetics of a cyanobacterial Photosystem I particle. Photochem. Photobiol. 57:113–119. [Google Scholar]
- van Brederode, M. E., and R. van Grondelle. 1999. New and unexpected routes for ultrafast electron transfer in photosynthetic reaction centers. FEBS Lett. 455:1–7. [DOI] [PubMed] [Google Scholar]
- van Brederode, M. E., I. H. M. van Stokkum, E. Katilius, F. van Mourik, M. R. Jones, and R. van Grondelle. 1999. Primary charge separation routes in the BChl: BPhe heterodimer reaction centers of Rhodobacter sphaeroides. Biochemistry. 38:7545–7555. [DOI] [PubMed] [Google Scholar]
- van Gorkom, H. J., and A. M. Nuijs. 1987. The primary photochemical reactions in systems I and II of photosynthesis. In Primary Processes in Photobiology, Springer Proceedings in Physics, Vol. 20. T. Kobayashi, editor. Springer, Berlin, Germany. 61–69.
- Wachtveitl, J., T. Arlt, H. Huber, H. Penzkofer, and W. Zinth. 1996. The primary electron transfer in bacterial reaction centers with altered energetics of the primary acceptor. In Springer Series in Chemical Physics, Vol. 62, Ultrafast Phenomena. X. P. F. Barbara, J. G. Fujimoto, W. H. Knox, and W. Zinth, editors. Springer, Berlin, Germany. 328–329.
- Witt, H., E. Schlodder, C. Teutloff, J. Niklas, E. Bordignon, D. Carbonera, S. Kohler, A. Labahn, and W. Lubitz. 2002. Hydrogen bonding to P700: site-directed mutagenesis of threonine A739 of Photosystem I in Chlamydomonas reinhardtii. Biochemistry. 41:8557–8569. [DOI] [PubMed] [Google Scholar]
- Woodbury, N. W., and J. P. Allen. 1995. The pathway, kinetics and thermodynamics of electron transfer in wild type and mutant reaction centers of purple nonsulfur bacteria. In Anoxygenic Photosynthetic Bacteria. R. E. Blankenship, M. T. Madigan, and C. E. Bauer, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 527–557.
- Woodbury, N. W. T., and W. W. Parson. 1984. Nanosecond fluorescence from isolated photosynthetic reaction centers of Rhodopseudomonas sphaeroides. Biochim. Biophys. Acta. 767:345–361. [DOI] [PubMed] [Google Scholar]
- Zinth, W., K. Dressler, P. Hamm, S. Buchanan, and H. Michel. 1996. Is there a bacteriochlorophyll anion in the primary electron transfer of reaction centers? Femto. React. Dyn. 42:245–253. [Google Scholar]
- Zouni, A., H. T. Witt, J. Kern, P. Fromme, N. Krauss, W. Saenger, and P. Orth. 2001. Crystal structure of Photosystem II from Synechococcus elongatus at 3.8 Å resolution. Nature. 409:739–743. [DOI] [PubMed] [Google Scholar]