The Glass Transition Behavior of the Globular Protein Bovine Serum Albumin

Abstract

The glass-like transition behavior of concentrated aqueous solutions of bovine serum albumin was examined using rheological techniques. At mass fractions >0.4, there was a marked concentration dependence of viscosity with a glass-like kinetic arrest observed at mass fractions in the region of 0.55. At mass fractions >0.6 the material behaved as a solid with a Young's modulus rising from ∼20 MPa at a mass fraction of 0.62–1.1 GPa at 0.86. The solid was viscoelastic and exhibited stress relaxation with relaxation times increasing from 33 to 610 s over the same concentration range. The concentration dependence of the osmotic pressure was measured, at intermediate concentrations, using an osmotic stress technique and could be described using a hard sphere model, indicating that the intermolecular interactions were predominantly repulsive. In summary, a major structural relaxation results from the collective motion of the globules at the supra-globule length scale and, at 20°C, this is arrested at water contents of 40% w/w. This appears to be analogous to the glass transition in colloidal hard spheres.

INTRODUCTION

It is known that on cooling organic molecular liquids below the crystalline melting temperature, providing crystallization does not intervene, there is a progressive slowing of molecular mobility (Angell, 1995; Debenedetti, 1996), and a change from liquid-like to solid-like behavior. Although this change in behavior can occur over a narrow temperature range, it is often considered to be associated with a glass transition temperature, T_g, where the relaxation time for structural rearrangement of the liquid generally exceeds 100 s. This transition temperature is commonly associated with a sharp change in heat capacity and calorimetry is commonly used in the experimental determination of T_g. The glass transition has a large impact on the properties of low water content biopolymeric materials and is relevant to their usefulness in pharmaceuticals (Franks, 1999), foods (Slade and Levine, 1991), and the preservation of biological materials in the dry state (Crowe et al., 1998). It has been proposed that the reduction in molecular mobility, generally associated with vitrification, has a preservative effect through the slowing of the encounter of reactive species involved in deteriorative reactions (Parker et al., 2002).

Water has a strong plasticizing effect on the glass transition of flexible biopolymers. For example, increasing the water content of a cereal protein, a high molecular weight glutenin, from ∼3 to 12% w/w, depresses the calorimetric glass transition from 100°C to 25°C (Noel et al., 1995). Both flexible polysaccharides such as starch (Zeleznak and Hoseney, 1987; Orford et al., 1989), and flexible proteins such as gelatin (Yannas, 1972) and elastin (Lillie and Gosline, 1990), show broadly comparable behavior. For globular proteins the situation is less clear. For lysozyme, a marked change in heat capacity from ∼1.25 Jg⁻¹K⁻¹ to ∼1.55 Jg⁻¹K⁻¹ is observed on increasing water content from 7% to 20% w/w at room temperature (Rupley and Careri, 1991). As the heat capacity change is associated with the onset of enzyme activity and therefore sufficient mobility for enzyme-catalyzed reaction, this transition can be likened to a glass transition. For a concentrated globular protein-water mixture the observed features in heat capacity as a function of temperature are relatively weak, span a comparatively wide temperature range, and are difficult to attribute to a calorimetric glass transition (Sartor et al., 1994). It is generally concluded that associated with the complex tertiary structure of proteins is a correspondingly complex dynamics (McCammon and Harvey, 1987), which cannot be adequately characterized through a single relaxation process. On the denaturation of globular proteins, with the consequent loss of tertiary structure, the calorimetric features associated with the glass transition become more evident and directly comparable with the behavior of flexible proteins (Sochava and Smirnova, 1993; Belopolskaya et al., 2000; Tsereteli et al., 2000).

In addition to consideration of the chain dynamics of the individual protein globule, it is also important to consider the dynamics of a collection of globules, which will have an impact on mechanical and transport behavior. In principle these systems should be analogous to concentrated colloidal suspensions (Trappe et al., 2001; Mason et al., 1997; Mason and Weitz, 1995; Segre et al., 2001) and granular powders that form glassy, “jammed” structures at high volume fractions (Liu and Nagel, 1998; Jaeger and Nagel, 1997).

The viscosity of colloidal suspensions progressively increases with the increasing volume fraction, φ, of particles (Phan et al., 1996; Krieger, 1972). At high volume fractions there is a sufficient slowing of particle dynamics that liquid-like configurations cannot be explored over practical timescales (Mason et al., 1997; Mason and Weitz, 1995). For small applied stresses the material has the solid-like characteristics of a glass with the particles forming jammed structures that are stress bearing. For a random packing of noninteracting monodisperse hard spheres, these structures may form at volume fractions in the vicinity of 0.6 with a random close packing limit, φ_c, of ≈0.644 (Torquato et al., 2000; Rintoul and Torquato, 1998). Although the above phenomena result from repulsive excluded volume interactions when the interaction between particles becomes increasingly attractive (Trappe et al., 2001), three dimensional particle networks, with solid-like characteristics (colloidal gels), will form at lower particle volume fractions (Segre et al., 2001). Recent research has emphasized the similarities between jammed structures that can form with increasing volume fraction of particles, and those, more open structures that form as a result of an increasing attractive interaction between particles (Trappe et al., 2001).

In this article we examine the rheological behavior of concentrated aqueous solutions of the globular protein bovine serum albumin (BSA) to test the proposal that for sufficiently concentrated solutions, glass-like behavior occurs as a consequence of the arrest of particle dynamics. Throughout the composition range examined, the interparticle interaction was probed through the determination of the osmotic pressure as a function of composition.

MATERIALS AND METHODS

Materials

Bovine serum albumin (fraction V) was obtained from Sigma-Aldrich (St. Louis, MO). A polyethylene glycol fraction (PEG 20) with an average MW 20,000 was obtained from BDH. Dialysis tubing (MW cutoff 12,000, Size 0, Medicell, London, UK) was used in the preparation of the more concentrated samples and osmotic stress experiments.

Preparation of protein solutions and hydrated solid bars

Protein solutions (<30% w/w) were prepared by the slow addition of BSA powder to pH 5.4 acetate buffer containing 100 mM sodium chloride, taking care not to foam the solution during stirring. More concentrated solutions (>30% w/w) were prepared by dialyzing these solutions against buffered PEG solutions containing 100 mM sodium chloride. Hydrated solid bars of BSA were prepared through concentrating BSA, firstly by dialysis against concentrated PEG solutions, as above, and then by equilibration over saturated salt solutions of known water activity. During this process the samples were pressed into 30 mm × 6 mm × 2 mm bars. Each sample was then carefully removed from the dialysis bag and immediately immersed in a silicone oil bath to prevent further drying. The extent of aggregation of BSA was checked by size exclusion chromatography using a 60-cm TSK-gel G2000 SW column (Tosoh-Biosep, Montgomeryville, PA) eluted with 150 mM sodium chloride at a flow rate of 1 ml × min⁻¹. For the BSA solutions the majority of the protein eluted in the main peak accounting for ∼97% of the material. A minor, faster eluting peak, ∼3% w/w, indicated a limited aggregation. The extent of aggregation had increased to ∼7% w/w, after concentration to 60% w/w by osmotic stress and storage at room temperature for 24 h.

Photon correlation spectroscopy

The apparatus employed was an ALV/SP-86 spectrogoniometer (ALV, Langen, Germany) equipped with a Coherent Radiation Innova 100-10 vis Argon Ion laser operating at 0.5 W and wavelength of 514 nm. BSA samples with concentrations <36% w/w were placed into the quartz cuvette and maintained at 25°C. The scattered light intensity was monitored using an ALV/PM-15 ODSIII detection system at a fixed scattering angle of 90°. After amplification and discrimination, signals were directed to an ALV/5000E digital multiple-τ correlator and time-intensity correlation functions recorded, typically for 600 s duration. Size distribution functions were computed using the appropriate Windows-based ALV software, which incorporated regularized inverse Laplace transform and ALV-CONTIN packages. Additional analysis was undertaken using Origin V6 (Microcal, Northhampton, MA) proprietary software.

Osmotic stress technique

A buffered 25% w/w BSA solution (2 ml) was dialyzed against buffered PEG solutions at 2°C for 24 h. After further dialysis at 20°C for 24 h the dialysis tube was removed from the PEG solution and the BSA concentration determined in the usual way by spectrophotometry. The osmotic pressure, π, of a w% w/w PEG solution was calculated from the relationship, log π = a + b × (w)^c, using published values of the constants a, b, and c (Parsegian et al., 1986). The suitability of this reference data was confirmed by experiment (Ryden et al., 2000).

Rheometry

A Bohlin CS10 controlled stress rheometer, with a double gap concentric cylinder (capacity 35 ml), was used to measure the dependence of BSA solution viscosity on shear rate, in the range 0.001–100 s⁻¹, for 0–40% w/w BSA solutions at 20°C.

The viscoelasticity of concentrated (40–50% w/w) BSA solutions at 20°C was measured using an Instron 3250 mechanical spectrometer (Canton, MA). Oscillatory measurements were undertaken with a parallel plate geometry (15 mm diameter platens, 0.3 mm gap) in the frequency range 0.01 Hz–10 Hz. The sample was transferred directly from the dialysis bag onto the lower platen and upper platen lowered until the required gap was obtained. While manually adjusting the gap the normal force was constantly monitored and not allowed to exceed 0.2 N and indeed was set to within 0.05 N of zero before testing commenced. Surplus material was quickly removed, and the exposed sample edge coated in silicone oil to prevent sample drying. The viscoelastic behavior was measured as a function of strain at a fixed oscillatory frequency of 1 Hz to determine the region of linearity. The frequency-dependent response was then examined at a strain chosen to lie within the linear region. To check for time-dependent effects such as ageing or of a nonlinear viscoelastic nature, small-strain measurements were periodically repeated at 1 Hz.

The Young's modulus and stress relaxation behavior of the solid-like BSA-water systems (>60% w/w BSA) were measured using a tensile testing machine (Instron 1122) in a three-point bend test with the bar supports 26 mm apart. A load was applied to the bar at the point midway between the supports while maintaining the temperature constant at 20°C. The maximum deflection of the bar at the midpoint of flexure was achieved quickly (within seconds) at a constant but small strain (∼0.02) that fell within the linear stress-strain region. Stress relaxation data were recorded over periods of time commensurate with the viscoelastic properties of the bars.

RESULTS AND DISCUSSION

Photon correlation spectroscopy

The published x-ray crystal structure of serum albumin indicates a heart-shaped molecule that can be approximated to an equilateral triangular prism with sides of 8 nm and a depth of 3 nm. Under conditions of neutral pH BSA has an axial ratio of ∼2.66. The conformation of BSA shows a pH dependence, with the native form being found between pH 4 and 8. In this pH range the equivalent hydrodynamic radius is 3.7 nm. The molecular volume of human serum albumin, calculated from the atomic coordinates of the x-ray structure is 88.25 nm³ (Carter and Ho, 1994; He and Carter, 1992).

Photon correlation spectroscopy was used to characterize both dilute and moderately concentrated solutions of BSA through the determination of a translational diffusion coefficient D_t. For a particle in solution subject to Brownian motion, the translational diffusion coefficient is related to the measured intensity correlation function g⁽²⁾τ by the expression

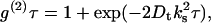(1)

where k_s, the scattering vector, is given by

(2)

where, n is the refractive index of the solution, θ the scattering angle, and λ the wavelength of light (Brown, 1993). For a 1% w/w solution of BSA in 100 mM sodium chloride at pH 5.4 and 20°C, the measured diffusion coefficient was 5.6 × 10⁻¹¹ m²s⁻¹. With increasing concentration of BSA the measured translational diffusion coefficient decreased from 5.6 × 10⁻¹¹ m²s⁻¹ at 10% w/w, to 3.4 × 10⁻¹¹ m²s⁻¹ at 36% w/w (Table 1). For the dilute solutions, the observed intensity correlation functions could be approximated to a single diffusive process. With increasing concentration of BSA, more complex behavior was observed, as indicated by the increasing curvature in plots of −ln g⁽²⁾τ vs. τ. The measurements of the concentration dependence of D_t are consistent with published data (Phillies et al., 1976), and support the view that there is no simple relationship between D_t, measured by photon correlation spectroscopy, and shear viscosity (Tyrrell and Harris, 1984). The photon correlation data on dilute solutions, and the chromatographic data on both dilute solutions and a concentrated solution (60% w/w) that was subsequently diluted indicate that the protein is largely unaggregated (>93%).

TABLE 1.

Diffusion coefficients of BSA in aqueous solution

BSA concentration (% w/w)	DT × 1011 (m2 s−1)	Temperature (°C)
1	5.6	20
10	5.6	20
20	5.5	20
25	5.0	20
36	3.4	20
0.05	6.3*	23

^*Gaigalas et al. (1992).

Rheology

Although moderately concentrated aqueous solutions of BSA behaved as viscous liquids, solid-like behavior was observed at concentrations >∼50% w/w. This concentration-dependent rheological behavior was examined using a range of experimental approaches.

Suspensions of spherical particles such as polymer latices have been the subject of extensive rheological investigation, with the viscosity being determined as a function of particle volume fraction, φ. At intermediate volume fractions (0.2–0.5) these suspensions show two Newtonian plateaus separated by a shear thinning region (Macosko, 1994). For hard sphere suspensions the low shear viscosity, η₀, includes contributions from hydrodynamic forces associated with minimally perturbed equilibrium structures, whereas for the high shear viscosity, η_∞, the structure is substantially perturbed. The shear stress, σ, at which the viscosity is intermediate between η₀ and η_∞, is of the order of

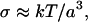(3)

where a is the particle radius, T the temperature and k Boltzmann's constant. For a particle the size of BSA the calculated value of σ is ≈8 × 10⁴ Pa. The dependence of viscosity on shear rate of BSA solutions at concentrations up to 40% w/w was examined using double gap concentric cylinder geometry. Fig. 1 shows a plot of shear viscosity versus shear rate for 30 and 40% w/w BSA at pH 5.4 in 100 mM sodium chloride at 20°C. At these concentrations, Newtonian behavior was observed at shear rates, 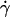, in the range 10–50 s⁻¹. As the associated shear stress was ≪10⁴ Pa we ascribe this behavior to being equivalent to the η₀ of hard sphere colloidal suspensions. Time-dependent deviations from Newtonian behavior, indicative of structure development, were observed at lower shear rates (<1 s⁻¹), for concentrations in the range 10–20% w/w (data not shown). These observations are consistent with reports of the solid-like behavior of relatively dilute BSA solutions (Ikeda and Nishinari, 2000), with the suggestion that at low concentrations a lattice-type structure is formed, the packing of which is disrupted on further addition of BSA. This solid-like behavior was particularly apparent at low shear rates, in the region of 10⁻² s⁻¹, outside the useful range of the instrument for the viscosities tested. At a shear stress of 10 mPa, time-dependent effects could be avoided by completing the experiment in <10³ s. As the time-dependent viscosity effect could be reduced by covering the BSA solution with a layer of silicone oil, it suggests that its cause was a surface drying effect. In this study it was not possible to distinguish between structure development in the bulk, and structure development at the air-liquid interface in the low shear rate (<1 s⁻¹), low concentration (<20% w/w) range.

FIGURE 1.

Viscosity as a function of shear rate under constant rotation for concentrated BSA solutions at pH 5.4 in 10 mM acetate–100 mM sodium chloride buffer.

The viscoelastic behavior of BSA solutions in the concentration range 40–52% w/w was determined by oscillatory rheometry. The variation in the magnitude of the complex modulus, G^*, as a function of applied strain, γ, at a frequency, ω = 1 Hz (2π rad s⁻¹), is shown in Fig. 2 for 47% w/w and 50% w/w BSA solution at 20°C. At small strains, γ < 0.01, both G′ and G″ are independent of γ. At concentrations <50% w/w G″ > G′ i.e., the material is predominantly behaving as a viscous fluid. The small strain behavior was investigated in more detail. The frequency dependence of G′(ω) and G″(ω) is shown in Fig. 3, for 42.5, 47.0, and 50.0% w/w BSA solutions. Over the frequency range examined of 0.01–10 Hz, both G′ and G″ increase with increasing frequency with G′ showing a less marked increase at the higher concentrations. Ultimately, at the highest concentration of 50% w/w BSA, G′ crosses G″ at 10 Hz, indicative of increasing elastic, solid-like behavior. The dynamic viscosity, η′, was calculated from the frequency dependence of G″ (η′ = G″(ω)/ω) (Macosko, 1994). Over the concentration range examined η′ showed a weak dependence on frequency even at 50% w/w BSA. More extensive measurements on the composition dependence of η′, were carried out at a frequency of 1 Hz.

FIGURE 2.

Magnitude of the complex shear modulus (G^*) as a function of oscillatory strain at a frequency of 1 Hz for concentrated BSA solutions at pH 5.4 in 10 mM acetate–100 mM sodium chloride buffer.

FIGURE 3.

Storage shear modulus (G′) and loss shear modulus (G″) as a function of frequency for concentrated BSA solutions at pH 5.4 in 10 mM acetate–100 mM sodium chloride buffer.

Repeated measurements showed no time dependence, indicating that no aging effects were occurring and confirming the absence of any surface drying effects. The composition dependence of viscosity, η, is shown in Fig. 4, which combines the dynamic and steady shear measurements. With increasing concentration the viscosity increases with increasing rapidity, exceeding 10⁴ Pa s at a concentration of 50% w/w.

FIGURE 4.

Shear viscosity, η, as a function of BSA concentration: steady shear (•); oscillatory shear (▴). Solid line is the prediction using Eq. 4, calculated assuming the protein occupies 0.90 ml g⁻¹, φ_max = 0.40 and solvent viscosity = 1 mPa s.

For suspensions of spherical particles the dependence of relative viscosity, η_r, on volume fraction is well described by (Phan et al., 1996)

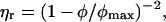(4)

where η_r is the viscosity of the suspension relative to that of the solvent, and φ_max is the maximum packing fraction, which is 0.63 ± 0.02 for low shear rates and 0.70 ± 0.02 for high shear rates. Relationships of the form of Eq. 4 show a marked increase in viscosity over a very small range of volume fraction as φ approaches φ_max. The exponent in Eq. 4 can differ from the value of 2, for example, Krieger (1972) proposed the value of 1.85 though with a correspondingly different value of φ_max. As applied above, Eq. 4 describes the experimental data for hard sphere colloidal dispersions for volume fractions up to 50% and relative viscosities up to ∼50. When particles deviate from spherical shape it is found that the viscosity diverges at a lower maximum packing fraction (Macosko, 1994). Fig. 4 shows the behavior predicted assuming the protein occupies 0.90 ml g⁻¹ (from the osmotic stress results, see later), φ_max = 0.40 and the solvent viscosity = 1 mPa s. The predicted behavior is somewhat similar to the observed viscous behavior of BSA, with the major difference being that the observed increase in viscosity at higher volume fractions is less dramatic, possibly indicating that the BSA particle is soft. This behavior could arise from particle deformability or from the dependence of the interparticle interaction on average particle separation.

At higher concentrations of BSA the material has solid-like characteristics and its mechanical behavior was examined in a three point bend test. For small instantaneous deformations (strain <0.01) there was a linear relationship between stress and strain. This permitted calculation of the tensile modulus, E, the composition dependence of which, over the concentration range 62–86% w/w, is shown in Table 2. Within the solid range the modulus increases by two orders of magnitude from ∼10 MPa to 1.0 GPa. This higher value is characteristic of glassy polymers (Ollett et al., 1991). These stiff materials show stress relaxation behavior at long timescales. Relaxation times (τ_m) characterizing the stress relaxation were obtained by fitting the data to a stretched exponential function of the form

(5)

Fig. 5 shows data for the bar having a concentration of 86% w/w (see Table 2) together with the fitted stretched exponential. The β parameter is a measure of the width of the distribution of relaxation times, β = 1 corresponds to single exponential behavior whereas smaller values of β indicate broader distributions. This behavior is dramatically different to the mechanical behavior of single crystals of BSA (containing similar amounts of water), which fracture at small deformations (Carter and Ho, 1994). For undercooled molecular liquids the mechanical relaxation time is of the order of 100 s at the calorimetric glass transition, T_g, where the viscosity is typically of the order of 10¹² Pa s. The relaxation times obtained for the BSA mixtures, in the region of 100 s, are therefore indicative of glass-like behavior, and the values of the parameter β obtained, in the range 0.38–0.64, are similar to those found in molecular glass formers (Struik, 1978; Hodge, 1994).

TABLE 2.

Mechanical relaxation behavior of concentrated BSA-water mixtures

BSA concentration (% w/w)	E (MPa)	τm (s)	β
62	23	33	0.64
67	80	66	0.45
73	190	95	0.45
86	1100	610	0.38

FIGURE 5.

Stress relaxation data for 86% w/w BSA bar in a three-point bend test: data (•) and the result of a stretched exponential fit to the data (solid line).

Osmotic stress experiments

The osmotic pressure of concentrated solutions of BSA was determined using an osmotic stress approach (Parsegian et al., 1986). Fig. 6 shows a logarithmic plot of the reduced osmotic pressure, π / ρkT, (ρ is the number density) as a function of mass fraction of BSA at pH 5.4 and 25°C throughout the entire composition range. In our experiments, carried out in the presence of 100 mM sodium chloride and 50 mM acetate buffer, the mass fraction ranged from 0.33 to 0.73. Our data are compared with those of Vilker (Vilker et al., 1981) obtained by osmometry, (mass fraction up to ∼0.4, in 150 mM sodium chloride adjusted to pH 5.4) and Bull (1944) determined by water vapor sorption from atmospheres of known water activity (mass fraction range 0.73–0.97). The agreement between the different methodologies employed is satisfactory with the osmotic pressure increasing from 5.4 kPa at a mass fraction of 0.089–400 MPa at a mass fraction of 0.97.

FIGURE 6.

Osmotic pressure as function of mass fraction for BSA: Vilker et al. (1981) (▴); this work (⋄); Bull (1944) (•). Solid line is approximate (Percus-Yevick) hard sphere equation of state (Eq. 6) calculated assuming the protein occupies 0.90 ml g⁻¹.

There have been various physicochemical interpretations of the osmotic pressure data. Previously Minton and co-workers (Minton and Edelhoch, 1982; Minton, 1995) interpreted the variation of osmotic pressure with concentration of BSA as resulting from excluded volume solute-solute interactions and used a hard sphere model to fit the data. More recently, Farrer and Lips (1999) used an adhesive hard sphere model to interpret sodium caseinate osmotic pressure data thus allowing the effects of attractive interactions to be interpreted. The reduced osmotic pressure, π/ρkT, for the present BSA data shows a monotonic increase with concentration indicative of an interaction that is predominantly repulsive. The data only allows a single parameter to be estimated, an apparent volume of the protein. Fig. 6 shows the osmotic pressure calculated using the Percus-Yevick hard sphere equation of state (Eq. 6) (Farrer and Lips, 1999)

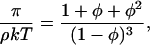(6)

with an apparent protein volume of 0.90 ml g⁻¹ (a least squares fit to our own data). The apparent protein volume is used to relate the mass concentration of the BSA to its volume fraction, φ. This volume depends upon the hydrated volume of the protein and on the intermolecular interactions. The apparent protein volume is larger than the value of 0.67 ml g⁻¹ obtained by Minton (1995) from dilute solution osmotic pressure data (Kanal et al., 1994) and is very much lower than would be predicted from the dilute solution diffusion data (2.13 ml g⁻¹).

GENERAL DISCUSSION

Considering the rheological and osmotic pressure data together and interpreting the results by analogy with the behavior of colloidal dispersions gives a coherent view of the behavior of these concentrated amorphous protein solutions. The ability of the hard sphere equation of state to fit the osmotic pressure data with a plausible effective volume indicates that the system is dominated by repulsive excluded volume interactions. Following from this is the expectation that, at a certain volume fraction, these excluded volume interactions will lead to glass-like arrest. The variation of viscosity with concentration (Fig. 4) shows the divergence that characterizes the approach to the glass transition. In detail the results differ from model hard spheres (Phan et al., 1996). Using the effective volume of the protein, 0.90 ml g⁻¹, the concentration of 50% w/w (highest viscosity point in Fig. 4) converts to a volume fraction of 0.52. Thus, the divergence occurs at a lower volume fraction than for hard spheres that can be ascribed to BSA's known deviation from spherical shape (Carter and Ho, 1994; He and Carter, 1992). Also, the approach to the divergence is relatively slow, which is indicative of softness in the interaction.

At an ionic strength of 100 mM the Debye-Huckel length is 0.92 nm (Kuehner et al., 1997), which is comparable with the size of the molecule. However, estimates of the magnitude of dispersion forces in these systems (Kuehner et al., 1997) mean that the potential of mean force is attractive at all interparticle separations and so the repulsive electrostatic interaction is not predicted to contribute to the apparent size of the molecule. This conclusion depends upon the value of the Hamaker constant. The value used, from a Lifshitz theory calculation, was 5 kT (Kuehner et al., 1997); if the value is dropped to 3.1 kT the repulsive electrostatic interaction starts to predominate. Attempts to predict osmotic pressure of BSA solutions from interparticle potentials have resulted in poor agreement with experiment even for dilute solutions (Vilker et al., 1981). Although this was, in part, due to the use of a virial expansion, it also highlighted the need for improved potentials of mean force. Despite this uncertainty concerning the detailed form of the interparticle forces, considerations of charge balance indicate that electrostatic forces are highly important in these concentrated protein solutions. Titrations (Scatchard et al., 1950; Fogh-Andersen et al., 1993) show that while the isoionic point of BSA is pH ∼5.4, chloride ion binding occurs, which, at 100 mM sodium chloride, leads to a net charge of about −7e. Charge balance calculations show that, in dilute solution, the total negative charge carried by the protein is very much less than that carried by the chloride co-ion, however, at higher concentrations (φ > 0.35) the situation is reversed and the protein is predicted to carry the majority of the charge. The Donnan effect will potentially exert a large effect in these systems.

The colloid analogy suggests that the main structural relaxation results from collective motion over a supra-globule length scale. On the basis of this analogy we would predict that a secondary, more localized, cage-rattling, relaxation would occur at the globule length scale (Mason and Weitz, 1995). Further relaxations, specific to the molecular details of the globule, would be anticipated at subglobule length scale. The conclusion regarding the main structural relaxation and predictions following from it indicate a need for further investigations of dynamics in these systems, including investigation of the effect of ionic environment on observed behavior.

The present behavior is relevant to globular proteins subjected to osmotic stress in biological situations. Typical average protein concentrations in the cytoplasm range from 20 to 35% w/w. If the cytoplasm is subject to a dehydration stress then the current results would suggest that the system would vitrify when the protein content exceeds 60% w/w. This vitrification would have a dramatic effect on transport processes within the cytoplasm. It has been proposed that vitrification, and the consequent arrest of some diffusive processes, is a mechanism that is useful in the preservation of life in the dry state. This is commonly associated with the biosynthesis of polyols and low molecular weight carbohydrates that have the ability to form a glassy matrix (Crowe et al., 1998). The current research on the vitrification of a globular protein suggests that discussion of the vitrification of biological structures should recognize that vitrification can occur on several length scales and can include the vitrification of low molecular weight solutes and the vitrification of larger particles such as globular proteins, which occur at very different water contents. On decreasing water content, particle arrest and vitrification precedes the vitrification of low molecular weight solutes.

CONCLUSIONS

Rheological studies of concentrated solutions of the globular protein BSA show glass-like transition behavior. In detail, the behavior differs from that of hard spherical colloidal particles, which is indicative of the BSA molecule's nonspherical shape and softness of the interaction. Osmotic stress studies, interpreted using a hard sphere model, indicate that the intermolecular forces are predominantly repulsive. Future studies should consider the effect of attractive interactions.