Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Dec;85(6):4134–4145. doi: 10.1016/S0006-3495(03)74825-5

Examination of Optical Depth Effects on Fluorescence Imaging of Cardiac Propagation

Mark-Anthony Bray *, John P Wikswo *,†
PMCID: PMC1303712  PMID: 14645100

Abstract

Optical mapping with voltage-sensitive dyes provides a high-resolution technique to observe cardiac electrodynamic behavior. Although most studies assume that the fluorescent signal is emitted from the surface layer of cells, the effects of signal attenuation with depth on signal interpretation are still unclear. This simulation study examines the effects of a depth-weighted signal on epicardial activation patterns and filament localization. We simulated filament behavior using a detailed cardiac model, and compared the signal obtained from the top (epicardial) layer of the spatial domain with the calculated weighted signal. General observations included a prolongation of the action upstroke duration, early upstroke initiation, and reduction in signal amplitude in the weighted signal. A shallow filament was found to produce a dual-humped action potential morphology consistent with previously reported observations. Simulated scroll wave breakup exhibited effects such as the false appearance of graded potentials, apparent supramaximal conduction velocities, and a spatially blurred signal with the local amplitude dependent upon the immediate subepicardial activity; the combination of these effects produced a corresponding change in the accuracy of filament localization. Our results indicate that the depth-dependent optical signal has significant consequences on the interpretation of epicardial activation dynamics.

INTRODUCTION

Over the past thirty years, optical mapping has been shown to be a powerful tool for discerning cardiac activation patterns, in both isolated single cell (Sharma and Tung, 2001; Knisley et al., 1993) and whole heart preparations (Choi and Salama, 2000; Bray et al., 2000). In such experimental applications, the cell or tissue is stained with a voltage-sensitive fluorescent dye that binds to the cellular membranes and transduces transmembrane potential changes into fluorescent signals. Such methods permit a noncontact eans of recording electrical activity with temporal resolution on the order of microseconds (Salzberg et al., 1993) and spatial resolutions on the scale of 50–100 μm (Grinvald et al., 1986). The generally held view within the cardiac optical mapping literature is that the epifluorescent signal emanates from the superficial layer of cells in a tissue preparation, on the order of a few hundred microns, with an upper limit of 1 mm. Therefore, it is often presumed that the observed optical recordings of dynamic behavior faithfully reproduce the epicardial distribution of the transmembrane potential. Although this approximation may suffice for some preparations, such as those involving cultured cell layers (Entcheva et al., 2000), recently studies involving sections of myocardium of more physiologically realistic thickness are questioning the validity of this assumption (Roth, 2002; Gray, 1999).

The question of the origin of the optically recorded signal is particularly relevant in light of more recent literature attempting to make inferences on the underlying electrical activity on the basis of reentrant activity observed on the surface. The spiral waves associated with reentry rotate around topological defects known as phase singularities (Winfree, 1987). It is believed that the phase singularity is the surface cross-section of a topological line defect known as a filament, which in turn forms the organizing center of a scroll wave, the three-dimensional analog of a spiral wave. Since the myocardium is a three-dimensional excitable substrate, the additional degree of freedom makes the contribution of filaments more complex to discern, yet no less important to the study of arrhythmogenesis (Gray et al., 1995). The extreme technical difficulty of filament observation in situ has made experimental studies of their dynamics limited primarily to examination of oscillatory chemical reactions (Winfree et al., 1996; Pertsov et al., 1993a). Recently, however, the depth effects of the optical signal have been used to infer the existence of underlying filaments based upon the epicardial presence of “dual-humped” action potentials (Efimov et al., 1999, 2000), and others have tailored their imaging technique to pinpoint the location of signals originating from subepicardial tissue (Choi and Salama, 1998).

In this study, we will examine the effects of the inclusion of optical averaging with depth in computational simulations of spiral and scroll wave activity. We will begin with a simple, single filament configuration and progress to the complex case of the behavior of multiple filaments and the corresponding phase singularity localization during fibrillation. Our goal is to gain valuable insight in anticipating potential difficulties in the interpretation of experimentally observed epicardial electrical activity in terms of scroll wave dynamics.

METHODS

For this study, we use the three-variable model implemented by Fenton and Karma for the purpose of reproducing the reentrant wave behavior of more complex ionic models while remaining computationally tractable for three-dimensional applications (Fenton and Karma, 1998). The equations are

graphic file with name M1.gif (1)

where u is the dimensionless transmembrane potential, and v and w are gating variables responsible for inactivation and reactivation of the currents Jfi, Jso, and Jsi, defined by

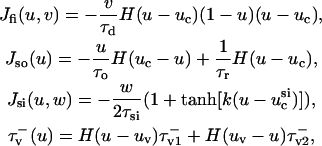graphic file with name M2.gif (2)

and H(x) is the standard Heavyside step function (where H(x) evaluates to 0 for x < 0 and 1 for x ≥ 0). For this article, we employ the parameter values used to fit the model to the modified Luo-Rudy (MLR) and modified Beeler-Reuter (MBR) restitution curves; these values are provided in Fenton and Karma (1998), so we omit them here. Inline graphic is the diffusion tensor defined as

graphic file with name M4.gif (3)

where the zero-elements reflect the fact that the fibers all lie in the (x,y) plane. The remaining elements are defined as

graphic file with name M5.gif (4)
graphic file with name M6.gif (5)
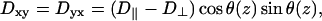graphic file with name M7.gif (6)

where D‖ and D⊥ are the diffusion coefficients for propagation parallel and perpendicular to the local fiber orientation, respectively. θ(z) is the angle between the x-axis and the fiber orientation in plane z and is determined by the formula

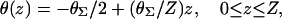graphic file with name M8.gif (7)

where θΣ is the total amount of fiber rotation from epicardium (z = 0) to endocardium (z = Z) as measured from the x-axis. The coefficients D‖ and D⊥ are defined as σ/(SvCm) where σ‖ = 1.863 mS/cm and σ⊥ = 0.186 mS/cm (in accordance with values estimated by Roth, 1997), Sv is the surface-to-volume ratio (3000 cm−1), and Cm is the membrane capacitance (1 μF/cm2). σz was set equal to Inline graphic We imposed no-flux (Neumann) boundary conditions, i.e.,

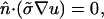graphic file with name M10.gif (8)

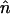where Inline graphic is the normal vector to the boundaries of the spatial domain. Eq. 8 leads to the equations

graphic file with name M12.gif (9)
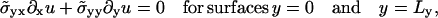graphic file with name M13.gif (10)
graphic file with name M14.gif (11)

The expressions in Eq. 2 are solved explicitly using a finite difference scheme. The spatial discretization steps in all three dimensions were set to 0.133 mm with a timestep of 20 μs.

With this model, the study was conducted in three stages: 1), a two-dimensional cross-section representative of a single straight intramural filament; 2), examination of a rectangular slab with no fiber rotation, i.e., θΣ = 0; and 3), examination of a rectangular slab with rotational anisotropy with θΣ = 120°. Initial conditions were constructed by selecting values for u and w (a recovery variable analogous to the potassium current) by dividing the u field into two adjacent regions, one set to a u value corresponding to excited state, the other corresponding to the resting state; the same procedure was followed for the w field. The border between the two regions in u and that in w were aligned such that they were orthogonal to one another, thereby producing a critical point around which a wavebreak would subsequently form, as might occur as a result of cross-field stimulation (Frazier et al., 1989).

The fluorescent signal corresponding to the depth-weighted transmembrane potential is given as

graphic file with name M15.gif (12)

where the integral is performed from the epicardium (z = 0) to the endocardium (z = Z). w(z) is the epicardial weighting function experimentally determined by Baxter and co-workers in a transillumination study of sheep right ventricle (Baxter et al., 2001),

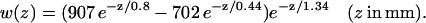graphic file with name M16.gif (13)

Although the Baxter et al. (2001) analysis was primarily focused on transillumination, the values used in Eq. 13 for our study correspond to those provided for epi-illumination. We use u0 to refer to the u-values located at the epicardium (the top layer of grid nodes, z = 0) and 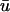Inline graphic to refer to the signal derived from the depth-weighted average of u.

RESULTS

The use of numerical simulations provides an ideal means to catalog the effects of depth-weighting of the optical signal on epicardial propagation activity, since we may create filaments in a variety of configurations and directly observe their evolution with time. We have chosen to develop our study beginning with a simple filament configuration and fiber geometry (two-dimensional filament cross-section, no fiber rotation) and then progress to a more complex filament configuration (L-shaped filament, no fiber rotation) reminiscent of that seen by Efimov et al. (1999). Finally, we conclude with complex filament behavior characteristic of fibrillation as well as physiologically realistic fiber rotation. By progressing in this manner, we may note how the differences between u0 and 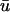Inline graphic present themselves in the simplified cases and observe whether these observations apply to the simulations with more realistic physiological structure.

Cross-section of intramural filament

The initial study observed a single intramural filament, located close and parallel to the epicardium. We model this simple case as a two-dimensional cross-section of tissue in the fiber plane; since the single straight filament is oriented perpendicular to the longitudinal fiber direction, it appears as an isolated singularity in the cross-section with an initial location (x,z) of (2, 0.13) mm. For the model, we have chosen to use the parameter values specific to the MLR restitution curve. The reason for this choice is that the observations of Efimov et al. (1999) indicated the presence of a long, linear core around which the reentrant wave rotated, a property also shared by the MLR model; the core is defined as a region of excitable but unexcited tissue, which in this case is linear (elongated) due to the long action potential duration. For the tissue, we used a 4.8 cm × 0.8 cm section (362 × 62 nodes), with the longer dimension corresponding to the longitudinal fiber direction; the geometry is shown in Fig. 1 a. To localize the phase singularity (the two-dimensional cross-section of the filament), we use the state-space methodology of determining cardiac phase (Gray et al., 1998) in conjunction with the topological charge algorithm developed by Bray et al. (2001). We have shown previously that using the u and v variables in the 3-variable model produces the optimal phase portrait (Bray and Wikswo, 2002). The origin in (u(t),v(t)) state-space was set to (0.175, 0.03).

FIGURE 1.

FIGURE 1

Open in a new tab

(a, Left) A three-dimensional intramural scroll wave and associated filament (black line) at t = 400 ms; double arrow shows longitudinal fiber direction, spatial units are in cm. (Right) Cross-section AA′ showing the position of the scroll wave and associated singularity (unfilled circle, with the subsequent singularity trajectory from t = 400–580 ms shown as a white line), and the two recording locations on the epicardium (1 and 2). Time traces at point (1) are shown in b; time traces at point (2) are shown in c. u0 drawn as dashed line, 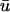Inline graphic drawn as solid line. Panels on the right are insets of an interval from t = 400–580 ms indicated with a box in the left panels.

Fig. 1 b compares the u0 and 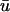Inline graphic signals obtained from a point on the epicardial surface at point 1 (0.13, 0), far from the singularity. We see that although the morphology of 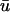Inline graphic is similar to that of u0, there are three noticeable differences between the two signals: 1), the upstroke of 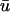Inline graphic starts earlier and its duration is longer than that of u0; 2), Inline graphic is greater in amplitude than u0 during the upstroke until the peak of both signals; and 3), the repolarization trace of 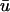Inline graphic is lower in amplitude than that of u0 until the following upstroke. The amount of this decrease varies over the duration of the repolarizing phase, but it reaches a maximum reduction of 0.03 units (recall that u is in the range of [0, 1]). Fig. 1 c shows 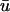Inline graphic and u0 at point 2 (2.33, 0), an epicardial point directly above the transmural reentrant core at the closest point of approach of the scroll wave with the epicardial surface.

Here we observe that 1), the 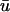Inline graphic signal has a dual-humped morphology, with the first peak much larger in magnitude that the second; 2), both peaks of 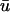Inline graphic are significantly smaller in amplitude than the single peak of u0; and 3), the upstroke of the first depolarization is rapid, as sharp as its u0 counterpart. Calculating the activation time as the difference between the time when u reached its minimum value before activation and the time of du/dtmax of the activation upstroke, we found that from 0 ≤ x ≤ 1.95 cm, the activation time of 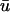Inline graphic could be as much as 15-ms longer than u0. For x > 1.95 cm, the activation time of u0 exceeded that of Inline graphic slightly (maximum activation time: 0.48 ms).

Fig. 2 depicts u0 and 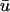Inline graphic in the form of a time-space plot. Time-space plots are a simple means of illustrating the spatiotemporal evolution of the transmembrane potential signal; successive frames of the amplitude of a signal along a line are stacked to form a two-dimensional plot of activation behavior, with time as the y-axis (Pertsov et al., 1993b; Gray et al., 1995). The one-dimensional nature of u0 and Inline graphic in this simulation makes it ideal for this form of visualization. In Fig. 2 a, we see the timecourse of the u0 signal across the length of the tissue. The presence of epicardial breakthroughs, labeled “EB” in the figure, is apparent by the V-shaped patterns of activation in the plot. The corner of the V-pattern of depolarization moves upward with time, indicating that the location of the initial breakthrough is nonstationary. We have used white lines in Fig. 2 a to indicate the slope of activation branches in the vicinity of the breakthrough; the slope of the line is inversely related to the propagation velocity. Also of note is that the slope of the left activation branch is shallower (and hence, the apparent conduction velocity is faster) than that of the right branch (∼74.0 cm/s vs. 43.5 cm/s). In fact, the conduction velocity of the left branch is faster than the maximum conduction velocity for the model in a one-dimensional cable where D is set to D‖ (∼47 cm/s).

FIGURE 2.

FIGURE 2

Open in a new tab

Time-space plots of u from the epicardial surface. (a) Top layer of nodes. Solid white lines show average slope of activation. (b) Weighted average. (c) Difference between a and b. Epicardial breakthroughs labeled as EB, additional secondary depolarizations labeled as AD. Initial transient of 50 ms not shown.

In Fig. 2 b, illustrating the 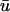Inline graphic signal, we clearly see additional “depolarizations” in between the epicardial breakthrough patterns, lying in the region roughly between x = 1.5 to 3 cm. This behavior resembles a passive response (as opposed to an action potential) since it is transient and is restricted to a local region of tissue. However, the peak magnitude of the depolarization is on the order of 0.42, far above the threshold of activation (u is in the range of [0, 1] ). To highlight the differences between a and b, in Fig. 2 c, we display the result of subtracting the u0 from the 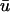Inline graphic images, where the orange and yellow hues indicate the areas where 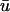Inline graphic is greater than u0, purple is close to zero, and the blue hue indicates where u0 is greater than 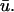Inline graphic We see that the presence of these apparent depolarizations is highlighted by the oval regions of orange. Furthermore, we see adjacent regions of blue color indicating that in these particular areas, the magnitude of the weighted signal in 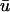Inline graphic significantly underestimates the magnitude of the u0 signal in the epicardial layer.

The reason for both of these phenomena is shown in Fig. 3, where we show the scroll wave cross-section u(x,z) and filament trajectory (bottom panels), along with the corresponding 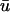Inline graphic and u0 traces as a function of x (top panels); the difference in the two traces over time corresponds to Fig. 2 c. As mentioned above, reentrant waves in the MLR model possess a core trajectory that is approximately linear, in contrast to the highly complex, epi-, or hypocycloidal trajectories seen in other models (Fenton and Karma, 1998). Hence, in Fig. 3 a at t = 262 ms, the wave is rotating clockwise and is in the process of completing the upper arc of its trajectory (as shown by the white line). We see that the trajectory has brought the leading edge of the wave near to the epicardial surface; hence, u0 is still close to maximally depolarized at the region of closest approach. Meanwhile, we see that as the wave completes the turn of its reentrant trajectory (t = 370 ms), the portion of tissue underneath the arc is in the process of repolarization. While the depolarized tissue within the first few epicardial layers plays a substantial role in the magnitude of the weighted signal, the reduced value of u(x,z) in the repolarizing midmyocardial strata contribute as well. The net effect of the summation over depth at this point in time is that 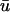Inline graphic is depressed with respect to u0 (see the first peak of the double potential in Fig. 1 b), with the maximum difference located at the point of closest approach, producing the negative blue regions in Fig. 2 c.

FIGURE 3.

FIGURE 3

Open in a new tab

Snapshots of the temporal development of the depth-weighted and top layer signals. (Top panels) 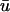Inline graphic (green) and u0 (blue) signals as a function of x. (Bottom panels) Corresponding scroll wave cross-section, with the filament trajectory overlaid as white line. Figure shows wave traversing a above and b below the core, as traced out by the white line.

Likewise, at t = 340 ms in Fig. 3 b, the filament is traversing the lower half of the linear core. Since the closest approach of the filament brings it to within 1.07 mm of the epicardial surface, those repolarizing surface layers experience a slight passive response, corresponding to a very small positive deflection in u0 for those cells. On the other hand, the contribution of the depolarized intramural layers is sufficient to create a significant positive deflection in the weighted 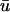Inline graphic signal, as seen in the second peak of the double potential in Fig. 1 b. Again, the location of the peak corresponds to the local maxima in Fig. 2 c (orange regions) at that point in time.

Further examination of scroll wave patterns can provide additional details about the relationship between u0 and 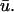Inline graphic The intramural wavefront approaching the epicardium on the upper left of u(x,z) in Fig. 3 b at t = 400 ms, produces the earlier upstroke of 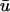Inline graphic (in comparison to u0) as expected, at the point when the wavefront is ∼2 mm from the epicardium, with a clear peak at x = 1.0 cm. This value is in agreement with earlier studies of Baxter et al. (2001). We also observe that 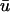Inline graphic is greater than u0 only for the duration of the upstroke in the regions where the wavefront is approaching the epicardium. As the wave progresses, 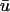Inline graphic is lower in magnitude than u0 due to the decrease in u with depth during repolarization associated with the decreasing fluorescence contribution from the lower tissue strata. However, in the areas where the wavefront is traveling away from the epicardium, such as in the upper right of u(x,z) in Fig. 3 a, t = 362 ms, u0 remains greater than 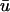Inline graphic for the duration of the upstroke, and the two signals follow almost identical timecourses for x ∈ (0,1.6) and (3.2, 4.8) cm during this rotation. Based upon the trajectory of the scroll wave with respect to the epicardium, we can also see the reason for the apparent supramaximal velocity. The scroll wave approaches the epicardial surface at a shallow oblique angle as can be seen in the upper left corner of the u image at t = 400 ms. This is exhibited in the difference image in Fig. 2 c as a yellow ridge along the left branches indicating that Inline graphic increases rapidly whereas u0 remains at a fairly constant value. This situation continues until the actual moment of breakthrough when the underlying wavefront arrives at the epicardium.

We varied the initial conditions such that the z-coordinate of the closest approach of the filament to the epicardium could be specified, and examined the amplitude of the second peak of 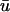Inline graphic as a function of filament depth. In this case, the amplitude of the peak is occluded not only by increased depth of the core itself but also by the fluorescence contribution of the layers overlying the core which are in the process of repolarization during the appearance of the second peak. We found that the second peak is at least 10% of the action potential amplitude for a filament passing within 1.3 mm or less of the epicardium. However, for a scroll wave of this configuration, the filament was unable to pass much closer to the epicardium (<1 mm) without activating it outright and precluding a second peak altogether. Furthermore, the peak is completely unnoticeable for a filament depth of 2 mm or greater.

To summarize, we have noted the following general features in the comparison between u0 and 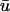Inline graphic for an intramural filament:

  1. As the filament passes above the core, the 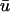Inline graphic potential is typically significantly lower in magnitude than that of u0.

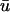  2. The Inline graphic activation often possesses a degree of directional blurring, the magnitude of which is dependent upon the incident angle between the epicardial surface and the incoming scroll wave.

  3. During epicardial breakthroughs, Inline graphic tends to rise before u0 and produces a longer apparent activation time.

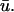
  4. As the filament passes below the core, an additional peak is superimposed on epicardial activity in Inline graphic

L-shaped filament, no fiber rotation

The second study consisted of our observing a shallow L-shaped filament, located close to the epicardium. Such filament comprises one-half of a U-shaped filament, which have been predicted to occur under certain stimulus conditions (Pertsov and Jalife, 1995; Sambelashvili and Efimov, 2002). The filament was initialized as described in Methods, with the addition of an elliptical profile for the u variable; one end terminated on the epicardial z = 0 plane, the other on the y = 0 plane. We model this preparation as a three-dimensional section of tissue. The number of grid points is 362 × 151 × 62, such that the tissue slab has dimensions 4.8 × 2.0 × 0.8 cm3, with the longest dimension corresponding to the longitudinal fiber direction. In this case, the filament has one end located on the upper epicardial surface and the other on a longitudinal face. Again, we use the MLR parameter values for the active kinetic model.

Fig. 4 illustrates the results from this portion of the study. Fig. 4 a shows the filament and its trajectory within the tissue slab at t = 176 ms with u mapped on the bounding surfaces; the orientation of the slab and the fiber direction is the same as that shown in Fig. 1 a. At this point in time, Fig. 4 b (right), depicting 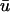Inline graphic − u0 indicates that there is a positive difference between 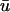Inline graphic and u0 at the region where the underlying scroll wave is closest to the epicardium. Furthermore, the magnitude of (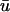Inline graphic − u0) is greatest at the shallowest portion of the scroll wave, adjacent to the linear core, but decreases rapidly in the direction of the filament's major axis (i.e., transverse to the fiber direction as shown by the arrow in Fig. 4 a) due to the short space constant of the weighting function with respect to the increasing filament depth.

FIGURE 4.

FIGURE 4

Open in a new tab

Snapshots of the temporal development of the depth-weighted and epicardial signals for an L-shaped filament. (a) Three-dimensional tissue slab with filament in black. Arrow shows the orientation of the filament as seen from the z = 0 plane. u shown on bounding surfaces. (b) Snapshot of u0 and 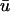Inline graphic and epicardial signals: u0 (left), 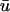Inline graphic (middle), and 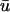Inline graphic − u0 (right). Trajectory of the filament on the bounding surfaces in a and b shown as a white line. (c) Epicardial activation 4-ms isochrone map of 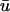Inline graphic for the area outlined in a, showing the linear core of the scroll wave. Arrow is the same as that shown in a. (d) Traces of 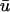Inline graphic (green) and u0 (blue) as a function of time at the locations numbered in c. 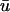Red circles indicate the presence of additional peaks in Inline graphic.

In Fig. 4 c, an epicardial activation map for one period of the scroll wave is constructed from the 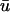Inline graphic signal by locating the maximum of the first derivative of 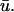Inline graphic The linear core region is clearly demarcated by the convergence of the isochrone contours along a central line, around which the wave rotates. Eleven sites were chosen along the major axis of the filament and the temporal traces of u0 and 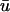Inline graphic are plotted in Fig. 4 d; both c and d are formatted to permit comparison between our simulations and the experimental data in Fig. 5 of Efimov et al. (1999). In this graph, a phase shift between traces 1–5 and traces 7–11 is clearly seen as a result of the time delay of the wave circling the linear core; trace 6 lies on the core itself and possesses a morphology intermediate between 5 and 7—characteristic of signals from the core region (Pertsov et al., 1993b).

FIGURE 5.

FIGURE 5

Open in a new tab

Comparison of 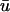Inline graphic and u0 signals during spiral wave breakup. Regions of interest are colored to highlight details. (a) Diminished 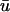Inline graphic magnitude; (b) apparent supramaximal conduction velocity in u0, arrow shows direction of propagation; (c) epicardial breakthrough; and (d) subepicardial graded potentials in 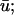Inline graphic arrow shows direction of subepicardial propagation.

An examination of the traces shows the differences produced by the inclusion of optical weighting over the length of the filament. Note that for the activation for traces 1–5 at t ∼ 50 ms, 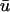Inline graphic exhibits a gradation in the depolarization shape, from an early initiation and prolonged upstroke duration for trace 1, to a significantly reduced peak amplitude and rapid upstroke for trace 5. This transition is a consequence of the increasing z-depth of the initially elliptical filament along its major axis. In addition, circled in red on Fig. 4 d are secondary peaks similar to those observed previously in Fig. 1 c. In contrast, for traces 7–11, the depolarization and repolarization profiles are almost identical, with no associated additional peak during the repolarization phase. This one-sided spatial morphology is consistent with the observations of Efimov et al. (1999).

Three-dimensional scroll wave breakup in presence of fiber rotation

For our final study, we examined a rectangular slab with rotational anisotropy, using θΣ = 120° as a typical value (Streeter et al., 1978); as indicated by Eq. 7, the fibers at the midwall are parallel to the x-axis. The slab has the same dimensions as that of the previous section (4.6 × 2.0 × 0.8 cm). However, it has been shown that a perturbed scroll wave using the MLR model in tissue up to 12-mm thick and at 24°/mm of fiber rotation fails to destabilize (Rappel, 2001). Therefore, we chose to use the MBR parameter values for Eq. 1 for which Rappel (2001) showed that a single filament becomes unstable for the wall thickness and rotation rate values selected for our study (see their Fig. 8).

In Fig. 5, we show the results of scroll wave breakup initiated from a single transmural filament in a more physiologically realistic model. Qualitatively, the optical effects noted in the above sections (particularly those regarding the intramural filament) are present in this simulation as well.

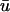  1. The Inline graphic potential is typically significantly lower in magnitude than that of u0. In Fig. 5 a, we observe an epicardial breakthrough activation. In u0, the depolarization is essentially uniform over the region of breakthrough. In contrast, the activation in 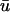Inline graphic is clearly of lower amplitude except in those regions where the action potential is reentering into the transmural epicardium, thereby allowing more layers to contribute to the weighted signal.

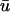  2. The Inline graphic potential often possesses a significant degree of directional blurring. In regions where a scroll wavefront approaches the epicardium at a shallow angle, the encroaching wave exhibits a graded potential over a wide area in the direction of the wavefront in 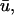Inline graphic producing a subsequent rapid depolarization and an apparent supramaximal velocity in u0. Fig. 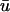5 b illustrates an apparent “finger” of depolarization in Inline graphic directed toward the left (shown by arrows), that the epicardial wave in u0 subsequently follows as it breaks through.

  3. During epicardial breakthroughs, Inline graphic experiences a gradual depolarization. If a filament is oriented parallel to the epicardial surface, the signature of the rising scroll wave is observable at the epicardium in 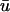Inline graphic before u0. An example is shown in Fig. 5 c, where the u time trace of the point directly over the breakthrough would demonstrate the apparent initiation of depolarization much earlier in 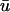Inline graphic than in u0.

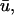  4. Graded potentials from an intramural scroll wave may be superimposed on epicardial activity in Inline graphic In Fig. 5 d, we observe a slender region of repolarization at the top right of the colored region of interest in u0. What is noticeable in Inline graphic but not in u0, is a graded potential extending retrograde to the repolarization tail (shown by arrows). In this intervening region, the wave fails to achieve an epicardial breakthrough, but is sufficiently close to the surface such that it produces an apparent depolarizing deflection in 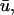Inline graphic but no action potential in u0. This situation is analogous to the double-humped potential observed in the previous section and seen in Efimov et al. (1999).

Singularity detection of filament breakup in presence of fiber rotation

It stands to reason that the combination of the above phenomena would lead to differences in the efficacy of the detection and subsequent tracking of the intersection of the filament with the epicardial surface (i.e., a phase singularity). Given the recent interest in tracking singularities in epifluorescence movies recorded from isolated animal hearts (Gray et al., 1998; Chen et al., 2000; Bray et al., 2001; Samie et al., 2001), we investigated this effect by examining phase singularity localization for both u0 and Inline graphic for the previous fibrillatory computation. Since an experimenter usually has access to only one variable at a time when observing epicardial behavior, rather than use the multivariate state-space phase portrait (u,v) as previously, we use the Takens time-embedding state-space methodology to produce a topologically equivalent time-series phase portrait (Takens, 1981; Gray et al., 1998). This is done by expanding the observed variable u into a vector time series by embedding a time delay τ into u(t) such that the state space in two dimensions is composed of u(t) plotted against u(t − τ). We set the time-embedding delay τ to a value approximately equal to the upstroke duration of the action potential, i.e., 5 ms, to insure the absence of folding in the phase space trajectories (Gray and Jalife, 1999). The origin in (u(t), u(t − τ)) state-space was chosen as (0.21, 0.21) by examining the phase portrait for a two-dimensional spiral wave and selecting a point which was encircled by the smaller phase trajectories. The phase singularities were localized with our topological charge algorithm detailed previously in Bray and Wikswo (2002).

In general, we noted several trends in singularity creation and annihilation which were seen to follow primarily as a consequence of the observations detailed above:

  1. In those regions where the magnitude of 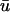Inline graphic is greater than that of u0, the creation of the singularities is generally observed to occur earlier in 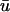Inline graphic than in u0. As mentioned previously, the subepicardial activation causes a premature initiation of the upstroke in 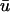Inline graphic as opposed to u0, which leads to an apparent earlier phase resetting when a singularity is produced. 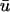Likewise, the annihilation of a singularity pair typically takes place later in Inline graphic than in u0 in these regions since the underlying depolarization also persists longer in Inline graphic than in u0.

  2. In contrast, in those regions where the magnitude of 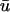Inline graphic is less than that of u0, the singularities are created generally later and annihilate earlier in 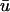Inline graphic than in u0. In this case the activated (whether depolarizing or repolarizing) epicardial tissue is overlying tissue that is close to rest, but the same reasoning in terms of apparent phase resetting applies as in a.

  3. As an extension of a, regions which experience graded potentials in 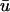Inline graphic are likely to exhibit the appearance of singularities in 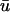Inline graphic which are absent in u0. In such areas, the apparent propagation in 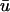Inline graphic is not in fact epicardial at all and hence, although the singularity may be visible in Inline graphic it does not actually represent a filament intersecting with the epicardial surface but instead the trajectory of a filament has brought a section of it just underneath the surface.

  4. Similarly, as an extension of b, regions in which the activation is localized to the epicardial layer and layers immediately beneath it may reveal singularities in u0 which are absent in 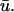Inline graphic This may occur for a very shallow U-shaped filament, for example.

An example of the disparity in detection is illustrated in Fig. 6, which shows eight epicardial singularities in u0 and 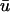Inline graphic tracked during a 20-ms period. In this instance, the error in singularity localization between u0 and 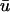Inline graphic over this period is 0.57 ± 0.16 mm. Of note are the false positives represented by trajectories 7 and 8 which were detected in u0 but not in 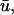Inline graphic corresponding to situation c above. Because the immediately underlying filament activity can produce adjacent areas which are subject to a combination of the above conditions, all of which are reflected in 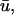Inline graphic it is difficult to generate hard-and-fast rules to determine which of the above scenarios will occur. It should be noted that in many cases the qualitative behavior of the detected phase singularities remained basically the same between 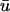Inline graphic and u0. That is, for meandering singularities which persisted for a long time period, even though discrepancies in spatial localization and creation/annihilation times existed, the basic trajectory did not change, such as trajectory 2 in Fig. 6.

FIGURE 6.

FIGURE 6

Open in a new tab

Illustration of phase singularity localization as a function of (x,y,t) during a 20-ms segment of fibrillatory activity in the MBR model. Trajectories from u0 and 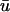Inline graphic shown in blue and green, respectively. The singularities are labeled with numbers.

DISCUSSION

The presence of a depth-dependent optical signal has been well-documented in the literature (Wilson et al., 1985; Preuss et al., 1983) but its effects on the interpretation of the optically mapped cardiac signal have only recently been a topic of investigation (Gray, 1999; Roth, 2002). Generally speaking, investigations which have attempted quantitative measurement of the dependence of emission wavelength upon penetration depth in biological tissue have yielded varying results (Cheong et al., 1990), and unfortunately the same is the case in the cardiac literature. Girouard found decay constants of 0.29 and 0.43 mm for the excitation and emission decay constants using di-4-ANEPPS in guinea pig left ventricle (thickness: 2.25 ± 0.20 mm), with the top 500 μm contributing 95% of the signal and the largest contribution coming from the uppermost 100 μm; however, this value was dependent upon the optical magnification used (Girouard et al., 1996). Knisley estimated that the top 300 μm contributed to the majority of the optical signal for a rabbit ventricular preparation using di-4-ANEPPS (maximum thickness measured: 600 μm; Knisley, 1995). Baxter and co-workers found optical penetration depths of 0.80 and 1.34 mm for the excitation and emission decay constants of di-4-ANEPPS in transmural cross-sections of sheep right ventricle (thickness: 8 mm) with 82% of the signal emanating from the top millimeter (Baxter et al., 2001). A study by Al-Khadra and co-workers observed optically-recorded (di-4-ANEPPS) action potentials from papillary muscles which had a dual-humped morphology (Al-Khadra et al., 2000). Shielding the papillary muscle from the underlying septum yielded action potentials of normal shape, indicating that the optical signal was the sum of the signals from the two tissues. Assuming this is the case, the underlying signal originated from a tissue depth on the order of a millimeter. Similarly, a Monte Carlo simulation by Ding and co-workers using broad field illumination for tissue stained with di-4-ANEPPS calculated that 62% of the collected fluorescence originated within a 1-mm radius block of tissue with a 1-mm depth (Ding et al., 2001). Quantitative measurements on the tissue depth which contributes to the signal have been shown to be dependent on such factors as spectral sensitivity, light absorption, and scattering, among others (Cheong et al., 1990; Baxter, 2001). Recent publications have called increasing attention to the need to be aware of the location of the focal plane with respect to the tissue surface as well as the associated depth-of-field used at a given magnification with the collecting lens; the effect of focus upon the signal becomes an issue if the depth-of-field is smaller than the distance into the tissue from which spatially-resolved light can be detected (Baxter et al., 2001; Efimov, 1998).

In this study, we do not attempt to demonstrate the validity of the numerical estimates of the weighting functions mentioned in the literature. Instead, we report the expected effects of applying the weighting function of Baxter et al. (2001) on observed epicardial activation patterns, allowing inferences to be drawn with other, similar w(z) functions. Using the function in Baxter et al. (2001), Janks and Roth (2002) demonstrated that the inclusion of optical averaging with depth in a simulation of a passive membrane model may provide a partial explanation as to why experiments fail to observe the large transmembrane polarization near the electrode during unipolar stimulation (as predicted theoretically), and surmised that a longer length constant, λ, in w(z) would increase the discrepancy. Likewise, observing active propagation with a larger value of λ would most likely alter the findings in Results (see Cross-Section of Intramural Filament and L-Shaped Filament, No Fiber Rotation) in a quantitative (not qualitative) manner. However, it is doubtful that the effect of a longer λ on fibrillatory tissue, such as that seen in the last section of the Results section, would be as predictable as in Janks and Roth (2002). As noted in Baxter et al. (2001), a subepicardial wave becomes noticeable when the wave approaches 1–2 mm of the surface using their formulation of w(z). For this reason, an intramural filament produced dual-peaked APs in 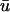Inline graphic only when the trajectory of the filament along the core brought the filament very close to the epicardium without activating it. Obviously, in regard to our observations of a single shallow filament, a longer λ would permit deeper filaments to be observed epicardially, accompanied by even longer upstroke times and larger magnitude second peaks in the filament axis. However, in the case of full fibrillatory activity, the effect of a longer λ is more difficult to estimate due to the decreased relative difference between λ and the scroll wavelength in the z-direction. That is, if more waves are present in those layers which contribute significantly to 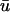Inline graphic (as determined by λ), the activation seen at the surface will seem to become increasingly complex as more of the total filament length (along with the associated twist due to fiber rotation and resultant scroll activity; Rappel, 2001) is represented in w(z).

The presence of a depth-dependent signal adds a new layer of difficulty to the already complex interpretation of cardiac activation patterns. It is well known that since the optical signal is generated from an aggregate of cells, the action potential upstroke can be blurred within a set of pixels and erroneously lead to an artificially long upstroke duration; for charge-coupled device cameras, blurring also increases as a function of the photon integration time required to obtain an adequate signal-to-noise ratio (Girouard et al., 1996; Baxter et al., 1997). These results indicate that even if these technical effects were corrected, blurring would still occur and may be significant depending on the underlying filament orientation. Baxter and co-workers note that their equation for w(z) takes into account scattering losses at the surface and not the effects of lateral scattering within the tissue; fluorophores located deeper within the tissue will appear transversely blurred due to scatter (Hyatt et al., 2003). The effect of the inclusion of this behavior on our results is unknown, but it would most likely exaggerate the effects already reported and further complicate optical data interpretation. The obvious extension of our work would be to incorporate a recently developed optical transfer function that accounts for photon scatter, and repeat the analysis presented here (Hyatt et al., 2003).

The appearance of action potentials with two distinct peaks (“double-humps”) has long been known as a signature of reentrant conduction block (Allessie et al., 1977; Olshansky et al., 1993) and has been used previously for core identification (Jalife et al., 1998). Typically, these double-humped potentials are attributed to electrotonic interaction across the line of block. However, Efimov and co-workers demonstrated double potentials at distances greater than a space constant (up to 12 mm) from the line of block (Efimov et al., 1999). Since this is a longer distance than can be normally accounted for by electrotonics, this led them to consider the possibility that a scroll wave may be rotating sufficiently close to the epicardial surface in such a way that the optical signal experiences two deflections from the wave propagating on either side of the region of conduction block. Our simulations confirm this interpretation as a possibility since a filament is unlikely to elicit a noticeable isolated passive response in u0 unless it passes within a fraction of a millimeter of the epicardium (in which case a minor perturbation in the filament trajectory toward the bounding surface will produce a full active response on the epicardium), whereas the deflection in 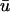Inline graphic can be observed at a tissue depth of an order-of-magnitude larger than the passive length constant. However, while we were able to replicate the double-humped behavior in 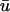Inline graphic in the controlled case of a single L-shaped filament, it required an extremely shallow filament to do so. Also, such multiple peaks were observed to be fairly infrequent in the simulation of filament breakup. This is understandable given that the recordings made by Efimov and co-workers were of sustained polymorphic tachycardia as opposed to full fibrillatory activity, indicating that just a single filament was present (Gray et al., 1995); the dynamic activity of multiple filaments precludes the stability needed to produce the extra peak in our simulations. Also, it is important to note that in the experimental setting, other factors come into play such as motion artifacts and early after-depolarizations associated with some pathological states which may lead to the erroneous presence of multiple peaks in the optical signal.

The detection and tracking of surface phase singularities remains the most straightforward means to discern filament activity, albeit in a limited way (Fenton and Karma, 1998; Gray et al., 1995). Although various methodologies exist to localize singularities (see Bray and Wikswo, 2002, for a short review), all of them assume that the epicardial mapping is in fact an accurate representation of the surface activation dynamics. We have shown here that the inclusion of optical signal depth information can lead to an erroneous characterization of the phase singularity (and hence filament) dynamics, including the occurrence of false-positive and false-negative filament detection under certain conditions. We note again that the basic meander pattern and trajectory is often unaffected, and if the scroll wave is fairly perpendicular to the epicardium (i.e., transmurally) within the length constant λ, then the difference in localization (though probably not the creation/annihilation times) between 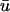Inline graphic and u0 will be small. However, the presence of twist due to rotational anisotropy or other heterogeneities will promote filament bending, thus making such an optimal configuration transient at best, especially once breakup events begin to occur.

In summary, our results indicate that the depth-dependent optical signal has significant consequences on the interpretation of propagation dynamics, in terms of the distortion of the magnitude, spatial extent, and temporal timing of epicardial activation and, as a consequence, phase singularity localization and behavior. As mentioned above, many additional variables clearly play a role in determination of the weighting function but their quantitative values remain unknown or inconsistent thus far; furthermore, it is difficult to reconcile the variability between experiments performed with different protocols. Nevertheless, this study illustrates that accounting for the three-dimensional nature of the optical signal is vital to appropriately bridging the gap between numerical simulations and experimental optical data in understanding cardiac spatiotemporal electrodynamics.

Acknowledgments

We thank Michael Miga for his input into the computational methodology of this manuscript. We are also indebted to the reviewers for their comments and suggestions that provided a larger perspective for this work. We thank Arkady Pertsov for a preprint of the (Hyatt, 2003) paper.

This work was supported in part by a graduate research fellowship from the United Negro College Fund-Merck Science Initiative and a National Institutes of Health National Research Service Award.

References

  1. Al-Khadra, A., V. Nikolski, and I. R. Efimov. 2000. The role of electroporation in defibrillation. Circ. Res. 87:797–804. [DOI] [PubMed] [Google Scholar]
  2. Allessie, M. A., F. I. M. Bonke, and F. J. G. Schopman. 1977. Circus movement in rabbit atrial muscle as a mechanism of tachycardia. III. The “leading circle” concept. A new mode of circus movement in cardiac tissue without the involvement of an anatomical obstacle. Circ. Res. 41:9–18. [DOI] [PubMed] [Google Scholar]
  3. Baxter, W. T. 2001. Optical properties of cardiac tissue. In Optical Mapping of Cardiac Excitation and Arrhythmias. D. S. Rosenbaum, and J. Jalife, editors. Futura Publishing, Armonk, NY. 47–59.
  4. Baxter, W. T., J. M. Davidenko, L. M. Loew, J. P. Wuskell, and J. Jalife. 1997. Technical features of a CCD video camera system to record cardiac fluorescent data. Ann. Biomed. Eng. 25:713–725. [DOI] [PubMed] [Google Scholar]
  5. Baxter, W. T., S. F. Mironov, A. V. Zaitsev, J. Jalife, and A. M. Pertsov. 2001. Visualizing excitation waves inside cardiac muscle using transillumination. Biophys. J. 80:516–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bray, M.-A., S.-F. Lin, R. R. Aliev, B. J. Roth, and J. P. Wikswo, Jr. 2001. Experimental and theoretical analysis of phase singularity dynamics in cardiac tissue. J. Cardiovasc. Electrophysiol. 12:716–722. [DOI] [PubMed] [Google Scholar]
  7. Bray, M.-A., S.-F. Lin, and J. P. Wikswo, Jr. 2000. Three-dimensional surface reconstruction and fluorescent visualization of cardiac activation. IEEE Trans. Biomed. Eng. 47:1382–1391. [DOI] [PubMed] [Google Scholar]
  8. Bray, M.-A., and J. P. Wikswo. 2002. Use of topological charge to determine filament location and dynamics in a numerical model of scroll wave activity. IEEE Trans. Biomed. Eng. 49:1086–1093. [DOI] [PubMed] [Google Scholar]
  9. Chen, J., R. Mandapati, O. Berenfeld, A. C. Skanes, and J. Jalife. 2000. High-frequency periodic sources underlie ventricular fibrillation in the isolated rabbit heart. Circ. Res. 86:86–93. [DOI] [PubMed] [Google Scholar]
  10. Cheong, W. F., S. A. Prahl, and A. J. Welch. 1990. A review of the optical properties of biological tissues. IEEE J. Quant. Elect. 26:2166–2185. [Google Scholar]
  11. Choi, B.-R., and G. Salama. 1998. Optical mapping of atrioventricular node reveals a conduction barrier between atrial and nodal cells. Am. J. Physiol. 274:H829–H845. [DOI] [PubMed] [Google Scholar]
  12. Choi, B.-R., and G. Salama. 2000. Simultaneous maps of optical action potentials and calcium transients in guinea-pig hearts: mechanisms underlying concordant alternans. J. Physiol. (Lond.). 529:171–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ding, L., R. Splinter, and S. B. Knisley. 2001. Quantifying spatial localization of optical mapping using Monte Carlo simulations. IEEE Trans. Biomed. Eng. 48:1098–1107. [DOI] [PubMed] [Google Scholar]
  14. Efimov, I. R. 1998. What is the role of the AV node if the AV delay occurs before it? Am. J. Physiol. 275:H1905–H1906. [DOI] [PubMed] [Google Scholar]
  15. Efimov, I. R., F. Aguel, Y. Cheng, B. Wollenzier, and N. Trayanova. 2000. Virtual electrode polarization in the far field: implications for external defibrillation. Am. J. Physiol. Heart Circ. Physiol. 279:H1055–H1070. [DOI] [PubMed] [Google Scholar]
  16. Efimov, I. R., V. Sidorov, Y. Cheng, and B. Wollenzier. 1999. Evidence of three-dimensional scroll waves with ribbon-shaped filament as a mechanism of ventricular tachycardia in the isolated rabbit heart. J. Cardiovasc. Electrophysiol. 10:1452–1462. [DOI] [PubMed] [Google Scholar]
  17. Entcheva, E., S. N. Lu, R. H. Troppman, V. Sharma, and L. Tung. 2000. Contact fluorescence imaging of reentry in monolayers of cultured neonatal rat ventricular myocytes. J. Cardiovasc. Electrophysiol. 11:665–676. [DOI] [PubMed] [Google Scholar]
  18. Fenton, F., and A. Karma. 1998. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: filament instability and fibrillation. Chaos. 8:20–47. [DOI] [PubMed] [Google Scholar]
  19. Frazier, D. W., P. D. Wolf, J. M. Wharton, A. S. Tang, W. M. Smith, and R. E. Ideker. 1989. Stimulus-induced critical point. Mechanism for electrical initiation of reentry in normal canine myocardium. J. Clin. Invest. 83:1039–1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Girouard, S. D., K. R. Laurita, and D. S. Rosenbaum. 1996. Unique properties of cardiac action potentials recorded with voltage-sensitive dyes. J. Cardiovasc. Electrophysiol. 7:1024–1038. [DOI] [PubMed] [Google Scholar]
  21. Gray, R. A. 1999. What exactly are optically recorded action potentials? J. Cardiovasc. Electrophysiol. 10:1463–1466. [DOI] [PubMed] [Google Scholar]
  22. Gray, R. A., and J. Jalife. 1999. Video imaging of atrial defibrillation. In Cardiac Electrophysiology: From Cell to Bedside. D. P. Zipes, and J. Jalife, editors. W.B. Saunders, Philadelphia, PA. 432–439.
  23. Gray, R. A., J. Jalife, A. Panfilov, W. T. Baxter, C. Cabo, J. M. Davidenko, and A. M. Pertsov. 1995. Nonstationary vortexlike reentrant activity as a mechanism of polymorphic ventricular tachycardia in the isolated rabbit heart. Circulation. 91:2454–2469. [DOI] [PubMed] [Google Scholar]
  24. Gray, R. A., A. M. Pertsov, and J. Jalife. 1998. Spatial and temporal organization during cardiac fibrillation. Nature. 392:75–78. [DOI] [PubMed] [Google Scholar]
  25. Grinvald, A., E. Lieke, R. D. Frostig, C. D. Gilbert, and T. N. Wiesel. 1986. Functional architecture of cortex revealed by optical imaging of intrinsic signals. Nature. 324:361–364. [DOI] [PubMed] [Google Scholar]
  26. Hyatt, C. J., S. F. Mironov, M. Wellner, O. Berenfeld, A. K. Popp, D. A. Weitz, J. Jalife, and A. M. Pertsov. 2003. Reconstruction of voltage-sensitive fluorescence signals from three-dimensional myocardial activation patterns. Biophys. J. 85:2673–2683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Jalife, J., R. A. Gray, G. E. Morley, and J. M. Davidenko. 1998. Self-organization and the dynamical nature of ventricular fibrillation. Chaos. 8:79–93. [DOI] [PubMed] [Google Scholar]
  28. Janks, D. L., and B. J. Roth. 2002. Averaging over depth during optical mapping of unipolar stimulation. IEEE Trans. Biomed. Eng. 49:1051–1054. [DOI] [PubMed] [Google Scholar]
  29. Knisley, S. B. 1995. Transmembrane voltage changes during unipolar stimulation of rabbit ventricle. Circ. Res. 77:1229–1239. [DOI] [PubMed] [Google Scholar]
  30. Knisley, S. B., T. F. Blitchington, B. C. Hill, A. O. Grant, W. M. Smith, T. C. Pilkington, and R. E. Ideker. 1993. Optical measurements of transmembrane potential changes during electric field stimulation of ventricular cells. Circ. Res. 72:255–270. [DOI] [PubMed] [Google Scholar]
  31. Olshansky, B., D. Moreira, and A. L. Waldo. 1993. Characterization of double potentials during ventricular tachycardia. Studies during transient entrainment. Circulation. 87:373–381. [DOI] [PubMed] [Google Scholar]
  32. Pertsov, A., M. Vinson, and S. C. Müller. 1993a. Three-dimensional reconstruction of organizing centers in excitable chemical media. Physica D. 63:233–240. [Google Scholar]
  33. Pertsov, A. M., J. M. Davidenko, R. Salomonsz, W. T. Baxter, and J. Jalife. 1993b. Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ. Res. 72:631–650. [DOI] [PubMed] [Google Scholar]
  34. Pertsov, A. M., and J. Jalife. 1995. Three-dimensional vortex-like reentry. In Cardiac Electrophysiology: From Cell to Bedside. D. P. Zipes, and J. Jalife, editors. W.B. Saunders, Philadelphia, PA. 403–410.
  35. Preuss, L. E., F. P. Bolin, and B. W. Cain. 1983. A comment on spectral transmittance in mammalian skeletal muscle. Photochem. Photobiol. 37:113–116. [DOI] [PubMed] [Google Scholar]
  36. Rappel, W.-J. 2001. Filament instability and rotational tissue anisotropy: a numerical study using detailed cardiac models. Chaos. 11:71–80. [DOI] [PubMed] [Google Scholar]
  37. Roth, B. J. 1997. Electrical conductivity values used with the bi-domain model of cardiac tissue. IEEE Trans. Biomed. Eng. 44:326–328. [DOI] [PubMed] [Google Scholar]
  38. Roth, B. J. 2002. Artifacts, assumptions, and ambiguity: pitfalls in comparing experimental results to numerical simulations when studying electrical stimulation of the heart. Chaos. 12:973–981. [DOI] [PubMed] [Google Scholar]
  39. Salzberg, B. M., A. L. Obaid, and F. Benzanilla. 1993. Microsecond response of a voltage-sensitive merocyanine dye: fast voltage-clamp measurements on squid giant axon. Jpn. J. Physiol. 43 (Suppl 1):S37–S41. [PubMed] [Google Scholar]
  40. Sambelashvili, A., and I. R. Efimov. 2002. The pinwheel experiment re-revisited. J. Theor. Biol. 214:147–153. [DOI] [PubMed] [Google Scholar]
  41. Samie, F. H., O. Berenfeld, J. Anumonwo, S. F. Mironov, S. Udassi, J. Beaumont, S. Taffet, A. M. Pertsov, and J. Jalife. 2001. Rectification of the background potassium current: a determinant of rotor dynamics in ventricular fibrillation. Circ. Res. 89:1216–1223. [DOI] [PubMed] [Google Scholar]
  42. Sharma, V., and L. Tung. 2001. Theoretical and experimental study of sawtooth effect in isolated cardiac cell-pairs. J. Cardiovasc. Electrophysiol. 12:1164–1173. [DOI] [PubMed] [Google Scholar]
  43. Streeter, D. D., W. E. Powers, M. A. Ross, and F. Torrent-Guasp. 1978. Three-dimensional fiber orientation in the mammalian left ventricular wall. In Cardiovascular System Dynamics. J. Baan, A. Noordergraaf, and J. Raines, editors. MIT Press, Cambridge, MA. 73–84.
  44. Takens, F. 1981. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence. D. A. Rand, and L.-S. Young, editors. Springer-Verlag, Berlin. 366–81.
  45. Wilson, B. C., W. P. Jeeves, and D. M. Lowe. 1985. In vivo and post mortem measurements of the attenuation spectra of light in mammalian tissues. Photochem. Photobiol. 42:153–162. [DOI] [PubMed] [Google Scholar]
  46. Winfree, A. T. 1987. When Time Breaks Down: The Three-Dimensional Dynamics Of Electrochemical Waves And Cardiac Arrhythmias. Princeton University Press, Princeton, NJ.
  47. Winfree, A. T., S. Caudle, G. Chen, P. McGuire, and Z. Szilagyi. 1996. Quantitative optical tomography of chemical waves and their organizing centers. Chaos. 6:617–626. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES