Self-Organization of Polarized Cell Signaling via Autocrine Circuits: Computational Model Analysis

Abstract

Recent studies have suggested that autocrine signaling through epidermal growth factor receptor (EGFR) might be involved in generating or maintaining an intrinsic polarity in tissue cells, possibly via spatial localization of EGFR-mediated signaling. The difficulty of experimental investigation of autocrine signaling makes especially valuable an application of computational modeling for critical hypotheses about the dynamic operation of the underlying signaling circuits, both intracellular and extracellular. Toward this end, we develop and analyze here a spatially distributed dynamic computational model of autocrine EGFR signaling. Under certain conditions, the model spontaneously evolves into a state wherein sustained signaling is spatially localized on smaller than cell dimension, conferring a polarity to the otherwise nonpolar model cell. Conditions of a sufficiently large rate of autocrine EGFR ligand release and of a sufficiently small exogenous ligand concentration are qualitatively consistent with experimental observations of EGFR-mediated migration. Thus, computational analysis supports the concept that autocrine EGFR signaling circuits could play a role in helping generate and/or maintain an intrinsic cell spatial polarity, possibly related to migration as well as tissue organization. We additionally offer particular suggestions for critical nodes in the EGFR signaling circuits governing this self-organization capability.

INTRODUCTION

Autocrine cells are capable of both producing signaling molecules and responding to them (Sporn and Todaro, 1980; Sporn and Roberts, 1992). An example of an autocrine system is signaling through epidermal growth factor (EGF) receptor (EGFR) (Lauffenburger et al., 1998; Dong et al., 1999; DeWitt et al., 2001; Maheshwari et al., 2001). A cell releases EGFR ligands into its environment, and a fraction of the released ligand is recaptured by the receptors at the cell surface (Massague and Pandiella, 1993). The activated receptors trigger intracellular signal transduction, whose effects may range from proliferation to migration of the cells (Hackel et al., 1999; Wells et al., 1998). Interestingly, among the effects can be further production of EGFR ligands (Baselga et al., 1996; Diaz Rodriguez et al., 2002; Montero et al., 2002). This positive feedback can result in a sustained activity of the autocrine signaling circuit (Shvartsman et al., 2002). It was hypothesized (Maheshwari et al., 2001; Shvartsman et al., 2001) that the autocrine circuit might be localized and persist in a spatially defined domain of the cell. A significant implication of this hypothesis is that the EGFR signaling dynamics may play a crucial role in helping establish or support intrinsic cell polarity or asymmetry. In particular, spatially localized autocrine signaling may confer directional persistence to cell migration, as suggested by recent experimental observations (Maheshwari et al., 2001). Here we quantitatively test whether key aspects of known topology and physicochemical kinetics of the EGFR signaling network permit the hypothesized spatial self-organization of the autocrine signaling and determine the specific mechanisms that can be responsible for the self-organization. Formulation of quantitatively consistent hypotheses about the complex behavior of a multicomponent signaling network is necessary to guide future experiments, especially given the intrinsically “cryptic” nature of autocrine signaling and the ensuing difficulties of experimentation (Wiley et al., 2003).

There exist two lines of evidence that make the self-organization in this system physically plausible. Firstly, ligand is recaptured by the cell surface receptors close to the point where it was released from the surface into the medium (Lauffenburger et al., 1998; Shvartsman et al., 2001). Secondly, the intracellular signal is propagated by proteins that become inactivated (dephosphorylated) as they diffuse away from the receptors (Brown and Kholodenko, 1999; Kholodenko et al., 2000). Taken together, these two properties would assure that both the extracellular and intracellular segments of the autocrine “loop” are localized in space to a subcellular scale. More precisely, however, they only suggest that if the ligand release is localized, then signaling will also be localized. The remaining questions regarding the hypothesis of spatial localization of autocrine loops are the following. Do the kinetic properties of the autocrine signaling network allow for localization of the ligand release? Due to the extracellular and intracellular diffusion, signaling is always less localized than the ligand release that caused it. Is it then possible that the autocrine loop does not eventually spread over the entire surface of the cell? Does the localized signaling have to be set by an external localized stimulus, or can the autocrine loop localize itself spontaneously? These are the questions to be answered by the quantitative model that we develop here.

Spatial self-organization is known in various physicochemical and biological systems and is usually thought to stipulate two conditions: short-range activation and long-range inhibition (Turing, 1952; Gierer and Meinhardt, 1972). The mechanistic meaning of these conditions differs as much as the nature of the systems in which the self-organization is observed (e.g., Mikhailov, 1990; Li et al., 2001). The principle of short-range activation and long-range inhibition of some process in the cell has been employed to explain the emergence of cell polarity. It has been applied to this problem in abstract terms with a possible molecular interpretation (Meinhardt, 1999), employed to guide model building for a specific molecular network (Narang et al., 2001), and often can be recognized as an implicit principle behind a mechanistic model (Sambeth and Baumgaertner, 2001; Wedlich-Soldner et al., 2003). The approach we take here is to analyze the autocrine EGF signaling system, identifying explicitly its features that can produce short-range activation and long-range inhibition of signaling, and then to build a mechanistic model that incorporates these features.

In the signaling system in question, ligand is shed from the cell surface and binds to transmembrane receptors that initiate an intracellular signaling cascade leading ultimately to stimulation of the ligand release. The first step of the signal transduction in the cytoplasm is recruitment of proteins such as Grb2 and Sos to the cytoplasmic domains of activated receptors (reviewed in Schlessinger, 2000). The resultant protein complexes are capable of stimulating further downstream signaling, most notably the cascade of mitogen-activated protein (MAP) kinases that activate one another sequentially by phosphorylation. Activated extracellular signal-regulated kinase (ERK) at the end of this cascade is responsible for stimulating ligand release from the cell surface (Gechtman et al., 1999; Diaz Rodriguez et al., 2002; Montero et al., 2002). In this system, the receptor complexes possess only a limited mobility because they are imbedded in the membrane (Saxton and Jacobson, 1997), so the signal is propagated in space primarily by ligand outside the cell and by active phosphorylated forms of the MAP kinases in the cytoplasm. As discussed above, signal propagation in space by EGF family ligands and by MAP kinases can be limited kinetically. Hence activation in the entire signaling network can be local, which will constitute one of the requirements for spatial self-organization.

How can the other requirement, global inhibition, be realized in this molecular system? The forms of inhibition of EGFR signaling that are based on inactivation of receptor complexes, such as dephosphorylation of cytoplasmic domains of activated receptors (Östman and Böhmer, 2001) or endocytosis of the receptor complexes (Ceresa and Schmid, 2000), provide only for a local inhibition because they affect only signaling complexes that are already active. Phosphorylation of Sos that is promoted by activated ERK is another element of the network whose function is inhibition of signaling (Langlois et al., 1995). The phosphorylated form of Sos can be considered as a weak participant of the transmembrane signaling complexes, and also as a freely diffusible cytoplasmic protein, like the unphosphorylated form. If the conversion between the two forms is slow relative to diffusion, then the feedback Sos phosphorylation in the cell region where signaling is strong will consume free unphosphorylated Sos in a larger region. The lowered availability of Sos for the signaling complex formation will inhibit signal transduction, potentially throughout the cell. The ERK-Sos negative feedback therefore can provide for global inhibition as the second condition for spatial self-organization.

Another mechanism of inhibition that limits signaling is depletion of inactive forms of signaling proteins. In most components of the EGFR autocrine signaling network, however, conversion into the active form probably does not change diffusivity. Then, for example, a loss of an inactive receptor due to ligand binding is accompanied only by appearance of an activated receptor in the same place, with neither global no local inhibition resulting from the transformation. Similarly, if an ERK molecule diffused in the cytoplasm to the place of its activation, then upon activation it is just as likely to return to where it was. In contrast, a cytoplasmic component of the transmembrane signaling complex changes its mobility significantly upon becoming part of the large, membrane-bound complex. If so, it can arrive to the point of complex formation from distant parts of the cytoplasm but contribute to signal propagation only near that point. Thus, localized signaling will result in lowering the concentrations of such proteins as Grb2 and Sos everywhere in the cell. Depletion of cytoplasmic components of transmembrane signaling complexes is a second possible mechanism of global inhibition as the condition of spatial self-organization that we explore in our model.

MODEL FOR LIGAND, RECEPTOR, AND SIGNALING DYNAMICS

Molecular processes that are explicitly accounted for in the model are shown in the kinetic diagram (Fig. 1). They include ligand shedding, receptor binding, assembly of the receptor signaling complex by recruitment of cytoplasmic Grb2 and Sos, phosphorylation of Raf, and two-site phosphorylation of both MEK and ERK MAP kinases. There are positive and negative feedback loops in the model. The positive feedback is activation of the ligand shedding by ERK. ERK also activates phosphorylation of Sos, which renders the latter incapable to participate in the receptor signaling complex formation and thus constitutes the negative feedback loop.

FIGURE 1.

Components of the autocrine EGFR signaling system and their interactions in the model. Transport, covalent modifications, and protein binding processes are shown by solid arrows. Kinetic acceleration of a process by a species is depicted by a dashed arrow. EGFR is receptor of ligand L; Grb2 is adaptor protein; Sos is activator protein; Raf, MEK, and ERK are protein kinases; p denotes phosphorylated form of a protein, and pp is a double-phosphorylated form.

The molecular processes depicted in Fig. 1 are considered as occurring in three spatial dimensions. EGFR ligand diffuses in the medium beyond the cell membrane, and the intracellular components, namely Grb2, Grb2-Sos, and the different forms of Sos, Raf, MEK, and ERK, diffuse in the cytoplasm. The receptor and its complexes with EGF-family ligand, Grb2, and Sos are considered as fixed in the plasma membrane, because of the relatively low rates of lateral diffusion within the membrane (reviewed in Saxton and Jacobson, 1997). The main simplification of the geometry of the space in which the kinetics of the signaling network is computed is that the model cell is spherical. It is embedded into an infinite volume of the medium, and there is a spherical nucleus in its center, which is impenetrable to the network components. Furthermore, here we will be concerned only with axially symmetric distributions of the molecular species, which are the simplest spatial distributions that can be polarized in the cell-biological sense.

The equations and parameters describing the dynamics of the spatially distributed network are given in the Appendix. The quantitative description is based on integrating select elements from the models of the EGFR complex formation (Kholodenko et al., 1999) and of the MAP kinase cascade (Huang and Ferrell, 1996; Kholodenko, 2000) into the framework of the existing model of EGFR autocrine signaling (Shvartsman et al., 2002). In particular, compared to the latter model, the double phosphorylation of both MEK and ERK is modeled explicitly as a two-step process, and the EGFR activation includes explicitly binding of Grb2 and Sos. In contrast to the previous models we consider all the processes in three spatial dimensions.

The crucial assumptions about the kinetic parameters that enable the reported model properties embody the above-discussed kinetic requirements for self-organization. They are fast phosphorylation and dephosphorylation of MAP kinases, and slow phosphorylation and dephosphorylation of Sos. In addition, the relation between parameters of the MAP cascade that provides for “ultrasensitivity” to the input signal level (Goldbeter and Koshland, 1981, 1984; Huang and Ferrell, 1996; Brown et al., 1997; Ferrell, 1997) needs to be maintained for efficient self-organization. The necessity of high sensitivity also motivates retaining all three levels of the cascade in the parsimonious model. In the rest, the model was found fairly insensitive to variations in parameter values and kinetics laws assumed for the reactions.

RESULTS

Spatial distribution of autocrine signaling

Computational analysis of the behavior of the model under different values of its parameters showed that the model system can adopt three qualitatively different, stable states. The first kind of a stable state is the state with no signaling. The system evolves to this state from any other state when the parameters of the model signify a substantial limitation of the signal transduction potential. For instance, the density of receptors on the cell surface can be so low that stimulation by ligand will cause only a transient excitation of the signaling network. The applied ligand diffuses away from the model cell, and intracellular signaling that it caused is extinguished by constitutive dephosphorylation of the active forms of MAP kinases. The amount of ligand that has been released by the autocrine cell in response to the activation is insufficient in this case to sustain signaling. The behavior of our model in this regime is essentially the same as the behavior of models of EGFR signaling without the autocrine feedback (e.g., Schoeberl et al., 2002), or with a weak feedback that only causes a second transient peak of signaling after an initial external stimulation (see Shvartsman et al., 2002). Our model adopts a qualitatively different kind of a stable state when the parameter values signify a high signaling potential, for instance, when the surface density of receptors is high. This second type of a stable state of signaling is the state wherein autocrine signaling is sustained and distributed uniformly over the cell surface. Ligand is shed from the surface everywhere at an equal rate, causing an equal stimulation of all the receptors. Diffusion of ligand and of activated forms of intracellular proteins from the cell membrane results in this case in a spherically symmetric spatial distribution of signaling (Fig. 2 a). Sustained and spherically symmetric signaling that is achieved in our model under such conditions was also displayed by a previous model of autocrine EGFR signaling (Shvartsman et al., 2002).

FIGURE 2.

Qualitatively different, stable spatial distributions of autocrine signaling. (a) Central section through spherically symmetric distributions of active ERK inside the cell (color coded) and of EGFR ligand outside the cell (grayscale). (b) Central section of axially symmetric, spatially self-organized distributions of the same signaling proteins as in a. (c) Color coding used. ERK activity is measured by the fraction of the double-phosphorylated form of ERK. The boundary between the colored and the grayscale zones is the cell boundary; the nonshaded circle in the center is the cell nucleus. (Other parameter values: R_total = 5 × 10³ μm⁻² in a and 2 × 10⁴ μm⁻² in b; G₁ = 180 μm⁻² min⁻¹; D_L = 10⁻⁸ cm² s⁻¹; V₉ = V₁₀ = 900 nM min⁻¹; k_ps = 0; [Grb]_total = 30 nM; [Sos]_total = 34 nM; L_inf = 0; k₁ = 1.8 min⁻¹.)

Our model also possesses a third kind of a stable state that has not been predicted by the previous models. In this type of a stable state, ligand is released predominantly from one side of the cell, and the receptor activation and intracellular signaling are also stably concentrated at that “active” part of the cell. Near the opposite, “inactive” pole of the cell, ligand shedding, the receptor activation, and intracellular signaling are maintained at stable low levels (Fig. 2 b). This type of a stable spatial distribution of signaling lacks the spherical symmetry of the previously considered spatial distributions of autocrine signaling (Shvartsman et al., 2001, 2002). It possesses only axial symmetry, with the symmetry axis passing through the two emergent poles of the spherical cell, where the levels of signaling are maximal and minimal. Such a polarization of an otherwise spherically symmetric model cell reflects spatial self-organization of the distributed signaling network. It is achieved when the kinetic parameters signify a moderate potential for signal transduction. For instance, the model system self-organizes in space when the surface density of receptors is intermediate between the high and low values that lead respectively to the uniformly high or uniformly zero levels of autocrine signaling.

Bifurcations

The model cell undergoes abrupt transitions (bifurcations) between the different types of stable signaling distributions as parameters reach certain threshold values. For instance, kinetic conditions may be such that autocrine signaling in the model cannot be sustained if the density of receptors at the cell surface is below ∼400 per square micron (Fig. 3). Then a slow, adiabatic increase of the receptor density above this value causes a rapid transition of the model to the spatially self-organized state of polarized signaling. As shown in Fig. 3, this state is characterized, in particular, by greatly different levels of EGF receptor occupancy by ligand at the opposite poles of the cell. At one pole (which emerges on a round cell solely due to self-organization of signaling), most receptors are occupied by ligand and transmit the signal to the underlying cytoplasm. Through the positive feedback loop in the signaling network (Fig. 1), this leads to secretion of more ligand at that pole and so the autocrine signaling is maintained there at a high level. At the opposite emergent pole, only a small fraction of receptors is occupied by ligand (Fig. 3), which results in a locally low level of autocrine signaling as illustrated in Fig. 2 b. Further increase in the receptor density does not result in dramatic changes of the spatial distribution of the receptor occupancy or signaling until another threshold is reached at ∼800 receptors per square micron of plasma membrane. A slow increase of the density beyond this value causes the self-organized state to collapse rapidly, the receptor occupancy dropping at the active pole and sharply rising at the inactive pole until they meet at a relatively high level. Thus, the poles that emerged from signaling now disappear, and the level of autocrine signaling becomes uniform over the entire cell. Above this second threshold, the steady-state occupancy of the receptors is again almost independent of the total receptor density. The model displays a similar three-stage, two-threshold response to slow variations of other control parameters.

FIGURE 3.

Abrupt transitions between qualitatively different stable distributions of autocrine signaling caused by slow variation of a control parameter, here, the surface density of EGF receptors. The solid and dashed curves represent the steady-state fractions of activated, ligand-bound forms of EGFR at the opposite poles of the cell. (Other parameter values: G₁ = 1.25 × 10⁵ μm⁻² min⁻¹, D_L = 10⁻⁸ cm² s⁻¹, V₉ = V₁₀ = 900 nM min⁻¹, k_ps = 0, [Grb]_total = 3 nM, [Sos]_total = 3.4 nM, L_inf = 0; k₁ = 36 min⁻¹.)

Effects of signal propagation range

The sharp separation of the three qualitatively different spatial distributions of signaling allows determination of threshold surfaces that divide the multidimensional parameter space of the model into regions where the combinations of parameter values define the no-signaling, self-organized, and uniform stable states. Some relationships between the control parameters are of particular interest. The receptor density and the rate constant of ligand shedding are two parameters that control the spatial range of autocrine activation. Higher rate of ligand release will increase the ligand concentration not only locally, but also, due to diffusion, at the plasma membrane regions that are distant from the point where the ligand has been released. The effect of diffusion assures that a lower rate of release will increase the ligand concentration mostly locally, as the steady-state profile of concentration drops sharply with the distance from the source in three dimensions (see Shvartsman et al., 2001). A higher density of receptors at the membrane, however, will enable a stronger stimulation of intracellular signaling even by the lower concentration of ligand, thus extending the spatial range of the autocrine activation. A section through the parameter space reveals that when both the receptor density and the rate of shedding are low, the signaling is not sustained, and when they are high, the activation spreads over the entire cell (Fig. 4 a). The spatially self-organized state of signaling requires certain intermediate values of these parameters. A low rate of shedding permits a relatively high receptor density (region 1 in Fig. 4 a), whereas a high shedding rate must be accompanied by a low receptor density for the self-organization to take place (region 2 in Fig. 4 a).

FIGURE 4.

Sections through the multidimensional parameter space of the model that show the domains of the parameter values under which the stable states of the system differ qualitatively. In the blue domain, the stable state is no signaling. In the red domain, the stable state is uniform signaling with a spherically symmetric distribution of protein species. In the green domain, the stable state is spatially self-organized signaling that possesses only axial symmetry. Numbers in the graphs mark locations in the parameter space that are discussed in the text. (a) Receptor density is the total density of receptors and all their complexes at the membrane (R_total). Ligand release rate is the maximum rate (G₁). (b) The phosphatase activity is the maximum rate of ERK dephosphorylation (V₉ = V₁₀). (c) The strength of the negative feedback is measured by the rate constant of Sos phosphorylation, k_ps. The strength of the positive feedback is measured by the rate constant of EGF release, G₁. (The abscissae in a and c refer to the same numerical parameter of the model in its different mechanistic roles.) (d) On the axes, [Grb] and [Sos] are the total concentrations of Grb2 and Sos in the cell, including the Grb2 or Sos components of the different protein complexes. (Other parameter values: L_inf = 0; k₁ = 36 min⁻¹, a; k₁ = 1.8 min⁻¹, b–d.)

The spatial range of the extracellular part of the autocrine circuit is also controlled by the diffusion constant of the secreted ligand. The diffusion constant of growth factors can differ by several orders of magnitude depending on the microstructure of the extracellular medium. So, the ligand mobility can be as high as 10⁻⁶ cm² s⁻¹ in a water environment and as low as 10⁻¹⁰ cm² s⁻¹ in as dense extracellular matrix as basement membrane (Dowd et al., 1999). High extracellular mobility may level the concentration profile of the ligand around the cell, making spatial self-organization impossible. Similarly, the degree of intracellular mobility of such signaling molecules as MAPKs determines the spatial range of the intracellular part of the autocrine circuit and may be critical for self-organization. More precisely, the range will be determined by the characteristic distance an activated MAPK molecule covers by diffusion before it is dephosphorylated (Brown and Kholodenko, 1999). Because diffusion constant of a given intracellular protein is less likely to vary dramatically, the range will be mostly controlled by the activity of phosphatase. A section of the parameter space (Fig. 4 b) reveals that an increase in the phosphatase activity indeed causes transition from uniform to self-organized signaling before it makes sustained signaling altogether impossible, but only does so within a certain intermediate range of the extracellular diffusion constant. The dominant effect of the low ligand diffusivity is accumulation of ligand to higher concentrations around the cell, which enables uniform signaling even though the spatial range of extracellular signaling is short. Conversely, high mobility of ligand leads primarily to its loss to the environment, and thus signaling ceases altogether, even though the long range of the extracellular segment of the autocrine loop could in principle enable uniform signaling.

Effects of positive and negative feedback

The rate constant of ligand shedding that determines, in part, the spatial range of the extracellular signaling, is also a measure of the strength of the positive feedback in the autocrine network, because it determines the steepness of the response of the shedding rate to the level of activation of ERK kinase at the end of the signaling cascade (Fig. 1). As such, its role can be compared with the role of the strength of the negative feedback by ERK-dependent Sos phosphorylation (Fig. 1) for the spatial self-organization of signaling. The correspondent section through the parameter space reveals that a combination of a strong positive and a weak negative feedback leads to the spherically symmetric signaling, whereas the opposite relationship makes sustained signaling impossible (Fig. 4 c). Importantly, increase of the negative feedback strength can abolish signaling altogether (as in region 1 in Fig. 4 c) or cause self-organization of signaling (as in region 3 in Fig. 4 c), depending on the strength of the positive feedback. Although the negative feedback can cause self-organization, it is not required for it, as evidenced by the self-organization predicted for region 2 of the parameter space section in Fig. 4 c, where the negative feedback is weak or absent.

Effect of Grb2 and Sos expression levels

The self-organization in the absence of the negative feedback through the ERK-dependent phosphorylation of Sos can be caused by limited overall amounts of Sos and of another cytoplasmic component of the active receptor complexes, Grb2. The correspondent section through the parameter space shows that high levels of expression of both Sos and Grb2 allow for a uniformly high level of autocrine signaling (Fig. 4 d). A low level of expression of either of these proteins precludes sustained signaling, but at certain intermediate, limited levels of their expression a spatially self-organized state of signaling is achieved (Fig. 4 d). The availability of either one of the proteins can limit signaling to one side of the cell. The diagram in Fig. 4 d demonstrates that at relatively high levels of expression of both proteins simultaneously, their combination that is required for signal transduction (Fig. 1) can still be limiting, and the system is predicted to self-organize spatially. Note that, for example, in the parameter space region marked 1 in Fig. 4 d, Grb2 is limiting whereas the amount of Sos allows for uniform signaling in the nearby region marked 2. Conversely, in region 3, only Sos is limiting, whereas the amount of Grb2 allows for uniform signaling in region 4. In region 5, it is the combination of the two proteins that is limiting, whereas the level of each protein individually is sufficient for uniform signaling in neighboring regions 6 and 7. Together, the sections through the parameter space reveal an extensive multidimensional domain of parameter values that result in the spatial self-organization of autocrine signaling.

Effect of exogenous (or paracrine) ligand stimulation

The predictions of the spatial self-organization of autocrine signaling pose the question about the effect of paracrine stimulation with EGF-family ligand that is either produced by other cells in the tissue or added in the course of an experimental or therapeutic intervention. In our model with autocrine signaling, the concentration of ligand exogenous to the cell is the ligand concentration in the bulk of the medium, far from the cell, where it is not significantly influenced by the autocrine ligand release. We found that increasing the exogenous ligand concentration results in a collapse of the spatially self-organized state of signaling (Fig. 5). Again, there is a threshold, exceeding which causes an abrupt transition, in this case from a “polarized” distribution of signaling species to the spherically symmetric one. One particular prediction about the breakdown of the self-organized state is that the density of activated receptors actually drops at the more active of the two self-organized poles of the autocrine cell when it is subjected to paracrine stimulation (Fig. 5).

FIGURE 5.

Collapse of the spatially self-organized state of the autocrine system of the cell subjected to paracrine stimulation. On the abscissa axis is the concentration of EGFR ligand in the medium far from the autocrine cell. The solid and broken curves are the steady-state fractions of activated, ligand-bound forms of EGFR at the opposite poles of the cell. (Other parameter values: R_total = 1.75 × 10³ μm⁻², G₁ = 3.6 × 10³ μm⁻² min⁻¹, D_L = 10⁻⁸ cm² s⁻¹, V₉ = V₁₀ = 900 nM min⁻¹, k_ps = 0, [Grb]_total = 30 nM, [Sos]_total = 30 nM, k₁ = 1.8 min⁻¹.)

DISCUSSION

Conditions for self-organized cell signaling polarity

Our model of the cellular system of autocrine EGFR signaling predicts that under certain kinetic conditions the system self-organizes in space. The self-organization leads to a stable state in which the cell sheds EGF-family ligand predominantly from a part of its surface, and the intracellular signaling also localizes to that side of the cell. At the opposite, “inactive” pole of the cell the levels of both the ligand release and intracellular signaling are very low. As considered in previous studies (Shvartsman et al., 2001), the localization of signaling requires that the activation loop of the signaling network is localized, which occurs in our model primarily due to a limited rate of autocrine ligand release and a limited receptor density. Our model identifies the complementary conditions of global inhibition in the EGFR autocrine system that are generally required for the stability of the self-organized state (Turing, 1952; Gierer and Meinhardt, 1972). The first condition of the global inhibition in the spatially distributed signaling network is a relatively strong negative feedback in the signaling system, namely the ERK-dependent phosphorylation of Sos. The second one is a relatively low level of expression of the Ras nucleotide exchange factor Sos. The third condition is a relatively low level of expression of the SH2-SH3 domain adaptor protein Grb2 that recruits Sos to receptor complexes at the plasma membrane. The model shows that every one of these conditions of global inhibition can be sufficient, and also that these factors may act synergistically and lead to self-organization even if any one of them is quantitatively insufficient by itself. Remarkably, even though our model is considerably complex (Fig. 1), it suggests only these three conditions of global inhibition. More detailed knowledge of the kinetics of the EGFR autocrine signaling network will likely suggest new candidate mechanisms. All three global inhibition factors that are identified here limit the signaling capacity of the cell, and as such can lead to the cell's inability to sustain autocrine signaling if too strong. Our computations show, however, that as the spatially distributed autocrine EGFR signaling system is inhibited by these factors, the signaling does not diminish monotonically and uniformly throughout the cell. The model predicts rather that as the inhibition exceeds a certain threshold, signaling at one side of the cell drops sharply whereas at the opposite pole of the cell it does not drop, but even increases. Thus, signaling in this system is predicted to differentiate spatially when its level cannot be maintained uniformly high due to the specific kinetic limitations in signal transduction.

A recent paper (Kempiak et al., 2003) has found that active ERK2 appears to spread from the site of activation in cells by EGF-coated beads, though less diffusely than when cells are stimulated by soluble EGF. Thus, there appears to be a spatial decay constant for active ERK2, which is smaller than the cell dimension. This finding is qualitatively consistent with our model, although a quantitative value for the spatial decay constant remains to be determined.

Model limitations

The model is based on a number of simplifications regarding the signaling network involved. Most evidently, a number of processes are omitted from our model. We did not explicitly consider processes whose effect on the spatial organization of the system we believe is secondary. For example, omitted phosphorylation of receptors (reviewed in Schlessinger, 2000) is another step in the receptor activation that occurs locally. The role of adaptor protein Shc (Schlessinger, 2000) is similar to that or Grb2, and therefore Shc is omitted from this model for the sake of clarity. Activation of Raf is represented in our model as a single step, whereas in reality it is a multistep process (Morrison and Cutler, 1997). Omissions such as these fall to those parts of the modeled network that are better known empirically than others. As a result of “leveling” of the depth of detail, for example, phosphorylation of both Raf and Sos is modeled as if it was directly regulated by receptor complex and ERK, respectively. In reality, behind the activation of Raf by receptor complex is the activation of another membrane bound intermediate, Ras (Schlessinger, 2000), whereas it is still unknown how the regulation of Sos phosphorylation by ERK is mediated. Omissions of this kind are not expected to substantially decrease the accuracy of the model, because the overall accuracy is determined primarily by the accuracy of the least certain parts.

The extent to which some of the simplifications affect our results can be assessed on the example of the simplifying assumption of immobility of receptors and their complexes. To do so, we generalized the model and performed computations with the receptors and their complexes diffusing in the membrane with a diffusion constant of 5 × 10⁻² μm² s⁻¹ as an upper bound suggested by experiments (Schlessinger et al., 1978). This changes the results to some extent. For instance, as the receptor density increases with the ligand release constant fixed at 10⁵ μm⁻² s⁻¹ (as in Fig. 4 a), the transition to self-organization is observed at ∼600 receptors per square micron instead of ∼450 without receptor diffusion. We regard such quantitative differences as insignificant, in part because it would be difficult to differentiate between the two threshold densities in an experiment. How to account for the receptor mobility in a model is an important problem. According to the experiments cited, these relatively high values of the diffusion constant are only observed at a low temperature, and at 37°C the receptors are immobilized by clustering.

A potentially more important simplification in the present model is that we only consider diffusion mechanisms of signal propagation in space. Recent experiments and modeling showed that activation of EGF receptors can propagate laterally in the cell membrane by transphosphorylation (Reynolds et al., 2003), and computations suggested that transport of activated receptors within endocytic vesicles may be crucial for spreading of signaling in the cytoplasm (Kholodenko, 2002). The effects of the diverse mechanisms of signal amplification and delivery on spatial organization of signaling networks will likely become important in more detailed models grounded in future quantitative experimental knowledge. Our results emphasize, at the same time, that emergent properties of spatially distributed signaling networks can critically depend on their properties that might so far receive less attention in experiments: restriction of activation and propagation of inhibition.

In our model, the proteins assemble into multicomponent signaling complexes, which results in both a low mobility of these active complexes and depletion of their more mobile components, thus activating the signaling locally and inhibiting it globally. We only considered this effect for the assembly of the EGFR-Grb2-Sos complex, but other components of the EGRF signaling network may also decrease their mobility upon activation. For instance, scaffold proteins and phosphatases may recognize the active forms of the signaling proteins and bind to them. We have neglected the presence of the scaffold proteins and assumed Michaelis-Menten kinetics for the phosphorylation-dephosphorylation reactions. In fact, violation of the Michaelis-Menten conditions in the real system leads to a significant depletion of signaling proteins due to their binding to phosphatases, as suggested by the kinetic analysis (Moehren et al., 2002).

Role of stochastic fluctuations

Technically, the divergence of the levels of signaling at the opposite poles of the cell in our computations is brought about by amplification of asymmetrical numerical errors. The error of the numerical solution to the equations of the model is insignificant due to the high precision of the solvers used, and is practically a random deviation from the true solution that remains small as long as the spherically symmetric solution is stable. This suppressed deviation is, however, amplified when the spherically symmetric solution becomes unstable upon a control parameter, such as the feedback strength, reaching the threshold. The amplification of the numerical defects of the spherical symmetry is followed by convergence of the numerical solution to the new solution, which is stable beyond the threshold of the control parameter. This new solution is axially symmetric by assumption of our model; more complex stable solutions are possible in principle. The change of stability of different solutions in complex dynamic systems is known as bifurcation (see Kuznetsov, 1998; Mikhailov, 1990).

In reality, the sources of the defects of the spherical symmetry that are seeds of the “polarized,” self-organized state of the system may be diverse. For one, it may be stochastic variations about the deterministic spatial distribution of the signaling proteins whose origin is the mere finite number of the molecules in the system. For another, it may be random influences from the cell's environment. Importantly, any such deviation will give rise to the same “polarized” state of the system, provided that the control parameters allow for self-organization, just as any deviation relaxed toward the “nonpolar” state when the control parameters rendered such a state stable. Smaller random asymmetries can require a longer time for the system to attain the self-organized state. The characteristic time of relaxation to either “uniform” or “polarized” states in the model is of the order of tens of minutes, which is the timescale of its slowest reactions. Quantitative estimations (Tranquillo et al., 1988) suggest that the inequality of ligand concentrations perceived by the cell surrounded by a uniform concentration of ligand solely due to the stochastic nature of receptor binding may reach several percent. This inequality would be an orders of magnitude stronger defect of symmetry than the numerical errors that serve as seeds of asymmetry in our deterministic computations.

It must be noted that our model allows for two axially symmetric solutions that are mirror-symmetric to each other: either one of the two opposite poles of the cell can be the “active.” Given the random deviations from the spherically symmetric signaling, it is impossible to predict which one of the two states will be the result of self-organization. Furthermore, the orientation of the axis of symmetry with respect to any external reference cannot be derived from the model either. The model predicts only the shape of the self-organized state, not the direction in which the self-organized autocrine signaling will be the strongest. If the deviations from the spherical symmetry are known, then the deterministic nature of our model will allow one to predict the direction too, after generalizing the coordinate system and the boundary conditions. Still, the orientation of the self-organized state will be defined not by the kinetics and geometry of the system, but by the initial conditions. This means that the orientation is neutrally stable, being subject to change by the continuing stochastic fluctuations within the real system and by variations in its environment. The only prediction that can be made at present about this random walk of the direction of “polarization” under such more realistic conditions is the characteristic time of reorientation of the approximate axis of symmetry. By the order of magnitude, it will be bounded from below by the relaxation time in the deterministic model, tens of minutes, which is the characteristic time of the slowest reactions in the system. Remarkably, the prediction of a model, where the random fluctuations in receptor binding drove the cell reorientation (Tranquillo et al., 1988), does not apply to the present case. It was predicted that the reorientation time is inversely related to the time it takes to erase the intracellular signaling pattern by diffusion and inactivation of signaling species. In the present model, to the contrary, the signaling pattern itself is the basis of polarity, and hence the pattern erasure time will be directly, not inversely, related to the reorientation time.

Implications for cell migration

A number of consequences for cell locomotion can be derived from our model if we assume that the locomotion is guided by EGFR-mediated signaling along the lines examined here. For instance, let us assume specifically that the direction of locomotion is the direction in which signaling is the strongest. Such an assumption will be consistent with a body of experimental evidence that EGFR signaling regulates various processes of cell migration (reviewed in Wells et al., 1998), and particularly with the fact that when the direction of migration is controlled in the experiment, EGFRs concentrate at the leading part of the cell (Zhao et al., 1999). Then, firstly, it will follow from the model that cells can acquire directionality of migration solely by means of the spontaneous self-organization of autocrine signaling. Secondly, in the absence of directional cues in the environment, the direction of migration will change randomly with a characteristic reorientation time of tens of minutes, as discussed above for the reorientation of the polarity axis. Accordingly, in the state of self-organized signal polarity, cell locomotion should exhibit a high degree of directional persistence, whereas in the state of nonpolarized signaling cell locomotion should exhibit a significantly lower degree of persistence. Among the system properties governing the transition from nonpolarity to polarity a prominent parameter is the rate of autocrine ligand release. As the value of this parameter increases beyond a determinable threshold (which depends on the values of other system parameters), directional persistence of cell migration should switch from low to high. Moreover, a further predicted consequence for migration is the abolition of self-organized signaling polarity at sufficiently high concentrations of exogenous EGF, leading to loss of directional persistence in locomotion. Both of these model predictions are consistent with the experimental observations by Maheshwari et al. (2001) for human mammary epithelial cells.

CONCLUSIONS

Our model suggests that an autocrine signaling circuit, possessing a combination of positive and negative feedback loops, can by itself serve as a mechanism for generating or maintaining cell polarity. Of course, other quantitative models and experimentally supported mechanisms have also been proposed to account for origins of cell polarity, considering processes as diverse as intracellular transport, cytoskeleton assembly, or signaling in its basis (e.g., Wedlich-Soldner et al., 2003; Sambeth and Baumgaertner, 2001; Meinhardt, 1999). It is conceivable that in the variety of cell types and states, different mechanisms provide for polarity. It is also possible that the different mechanisms act synergistically or compete to determine the polarity of a cell. In this view, our autocrine model does not only explain and predict some particular phenomena. More generally, the spatial self-organization of autocrine signaling is an addition to the array of complex functional capabilities of cellular systems that emerge from the computational analysis of today's empirical knowledge, and whose relative contributions and interplay are to become the subject of the future integrative research.

APPENDIX

The model is described by reaction-diffusion kinetic equations. The spatial coordinates are r, the distance from the cell center, and θ, the latitude angle of the associated spherical coordinate system. The axially symmetric concentrations of the chemical species that are studied here do not depend on the longitude coordinate. The extracellular concentration of EGFR ligand is denoted as L, the surface density of EGFR as R, and the surface density of ligand-receptor complexes as C. Volume concentrations and surface densities of other species are denoted as [species], using the symbol C for the extracellular ligand-receptor component of the transmembrane complexes, and Grb for Grb2. Nomenclature and values of parameters are given in Table 1.

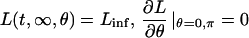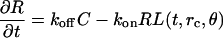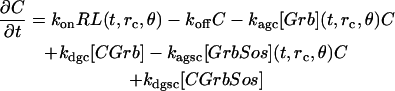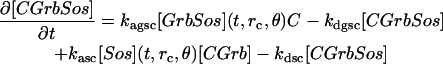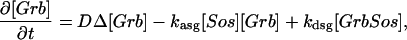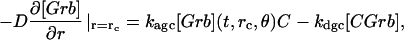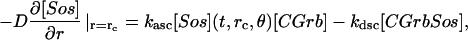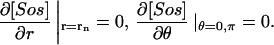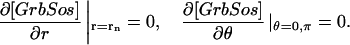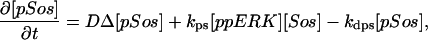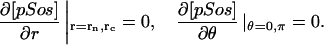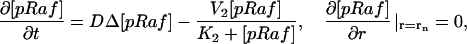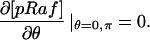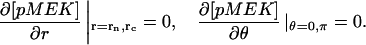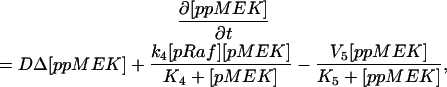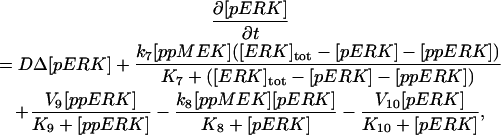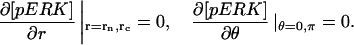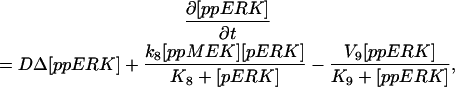TABLE 1.

Kinetic and geometric parameters

Symbol	Parameter	Value
rc	Cell radius	1 × 10−5 m
rn	Radius of nucleus	5 × 10−6 m
DL	Diffusion constant of ligand	10−14–10−10 m2 s−1
koff	Rate constant of dissociation of ligand from EGFR*	1.67 × 10−3 s−1
kon	Rate constant of association of ligand with EGFR*	1.67 × 106 M−1 s−1
Linf	Concentration of ligand in the bulk of the medium	0–1 × 10−9 M
G1	Maximal rate density of ligand shedding	1010–1015 m−2 s−1
D	Diffusion constant of proteins in cytoplasm	10−12 m2 s−1
kagc	Association rate constant of Grb2 with receptor†	3 × 106 M−1 s−1
kdgc	Dissociation rate constant of Grb2 from receptor†	5 × 10−2 s−1
kagsc	Association rate constant of Grb2-Sos with receptor†	4.5 × 106 M−1 s−1
kdgsc	Dissociation rate constant of Grb2-Sos from receptor†	3 × 10−2 s−1
kasc	Association rate constant of Sos with receptor-Grb2†	1 × 107 M−1 s−1
kdsc	Dissociation rate constant of Sos from receptor-Grb2†	6 × 10−2 s−1
kasg	Association rate constant of Sos with Grb2†	1 × 105 M−1 s−1
kdsg	Dissociation rate constant of Sos from Grb2†	1.5 × 10−3 s−1
kps	Phosphorylation rate constant of Sos	0–1 × 109 M−1 s−1
kdps	Dephosphorylation rate constant of pSos	1 × 10−3 s−1
[Raf]tot	Total concentration of all forms of Raf	1 × 10−7 M
[MEK]tot	Total concentration of all forms of MEK	3 × 10−7 M
[ERK]tot	Total concentration of all forms of ERK	3 × 10−7 M
k1	Rate constant of Raf phosphorylation	0.03–0.6 s−1
K1	Michaelis constant of Raf phosphorylation	1 × 10−8 M
V2	Maximal rate of pRaf dephosphorylation	7.5 × 10−9 M s−1
K2	Michaelis constant of pRaf dephosphorylation	8 × 10−9 M
k3	Rate constant of MEK phosphorylation	0.75 s−1
K3	Michaelis constant of MEK phosphorylation	1.5 × 10−8 M
k4	Rate constant of pMEK phosphorylation	0.75 s−1
K4	Michaelis constant of pMEK phosphorylation	1.5 × 10−8 M
V5	Maximal rate of ppMEK dephosphorylation	2.25 × 10−8 M s−1
K5	Michaelis constant of ppMEK dephosphorylation	1.5 × 10−8 M
V6	Maximal rate of pMEK dephosphorylation	2.25 × 10−8 M s−1
K6	Michaelis constant of pMEK dephosphorylation	1.5 × 10−8 M
k7	Rate constant of ERK phosphorylation	0.75 s−1
K7	Michaelis constant of ERK phosphorylation	1.5 × 10−8 M
k8	Rate constant of pERK phosphorylation	0.75 s−1
K8	Michaelis constant of pERK phosphorylation	1.5 × 10−8 M
V9	Maximal rate of ppERK dephosphorylation	10−9–10−6 M s−1
K9	Michaelis constant of ppERK dephosphorylation	1.5 × 10−8 M
V10	Maximal rate of pERK dephosphorylation	10−9–10−6 M s−1
K10	Michaelis constant of pERK dephosphorylation	1.5 × 10−8 M
Rtotal	Total surface density of receptors and complexes	0–2 × 1016 m−2
[Grb]total	Total cellular concentration of Grb2 and complexes	0–5 × 10−8 M
[Sos]total	Total cellular concentration of Sos and complexes	0–5 × 10−8 M

^*Assumed as in Shvartsman et al. (2001).

^†Assumed as in Kholodenko et al. (1999).

The equations were solved using an explicit finite difference method. The model was discretized in space with the step size 1 μm for r and 18° for θ, using the finite difference approximations for the spatial derivatives of variables. The resultant problem was solved with the MATLAB (The MathWorks Inc., Natick, MA) routine ODE15s, a variable-order solver for stiff problems that is based on the numerical differentiation formulas and uses an adaptive time step size. Computations were performed in double precision (15 digits), with relative error tolerance 0.001.

In the initial condition, all variables were set to zero, except [Grb] = [Grb]_total, [Sos] = [Sos]_total, R_θ≠π = R_total, C_θ=π = R_total. Relaxation of an initial condition was followed by an adiabatic change of the control parameters, one at a time. The adiabatic change of the total concentrations of receptors, Grb2 and Sos in the numerical procedure is equivalent to adding very small constant terms to the equations for the dynamics of these species. The asymmetry of the initial condition does not define the asymmetry of the self-organized state. In fact, either of the two poles may become “active,” depending on the path through the parameter space from the same initial condition, and the same asymmetric solution may be obtained if the result of the relaxation of the initial condition is made perfectly spherically symmetric.

The boundary conditions at θ = 0, π are not meant to represent any physical zero-flux conditions, but are consequences of the axial symmetry (see, e.g., Crawford et al., 1991), which is an assumption of the model. This assumption makes the solutions independent of the longitude coordinate ϕ, and allows computing the three-dimensional spatial model on a two-dimensional grid (r, θ). Detection of bifurcations on a three-dimensional grid (r, θ, ϕ) that would be required without this assumption would be too costly computationally. To test whether an axially symmetric solution found on the two-dimensional grid remains stable when the symmetry condition is removed, we represented the solution on the three-dimensional grid with the same step for ϕ as for θ, and computed some eigenvalues of the system Jacobian at the solution using the MATLAB routine eigs. This routine employs ARPACK algorithms used to reliably find eigenvalues of large sparse Jacobians arising in stability analysis of partial-differential-equation problems (see, e.g., Burroughs et al., 2002). The eigenvalues with the largest real part are zeroes followed by negative values, as they should (see, e.g., Nagata et al., 2003) if the solution is neutrally stable with respect to rotations (due to the symmetry of the reaction-diffusion system with only spherical boundaries), and stable with respect to other perturbations.