Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jan;86(1):116–124. doi: 10.1016/S0006-3495(04)74089-8

Refinement of F-Actin Model against Fiber Diffraction Data by Long-Range Normal Modes

Yinghao Wu *, Jianpeng Ma *,†,‡
PMCID: PMC1303775  PMID: 14695255

Abstract

The atomic model of F-actin was refined against fiber diffraction data using long-range normal modes as adjustable parameters to account for the collective long-range filamentous deformations. To determine the effect of long-range deformations on the refinement, each of the four domains of G-actin was treated as a rigid body. It was found that among all modes, the bending modes make the most significant contributions to the improvement of the refinement. Inclusion of only 7–9 bending modes as adjustable parameters yielded a lowest R-factor of 6.3%. These results demonstrate that employing normal modes as refinement parameters has the advantage of using a small number of adjustable parameters to achieve a good fitting efficiency. Such a refinement procedure may therefore prevent the refinement from overfitting the structural model. More importantly, the results of this study demonstrate that, for any fiber diffraction data, a substantial amount of refinement error is due to long-range deformations, especially the bending, of the filaments. The effects of these intrinsic deformations cannot be easily compensated for by adjusting local structural parameters, and must be properly accounted for in the refinement to achieve improved fit of refined models with experimental diffraction data.

INTRODUCTION

Fiber diffraction is a powerful experimental method for determining structures of filamentous systems (Stubbs, 1999) that are abundant in biological organisms. Systems that have been studied by fiber diffraction cover a wide range of forms ranging from simple polypeptides, polynucleotides, and polysaccharides, to cytoskeletal filaments and filamentous viruses.

In fiber diffraction, the fiber specimens align axially, but not azimuthally. Therefore, the diffraction patterns are cylindrically averaged and present characteristic layer lines, the spacing of which are determined by the helical symmetry of the diffracting helical fibers. The cylindrical averaging leads to inevitable loss of diffraction information so that the number of independent diffractions of fibers is considerably smaller than that from a single crystal with a similar size of asymmetric unit. Thus, there are usually not sufficient data to refine the Cartesian coordinates of every atom in the fibers, which imposes a severe challenge to defining a proper set of parameters for effective structural refinement (Wang and Stubbs, 1993).

In fiber diffraction experiments, the fibers are usually flexible and dynamic, and the specimens contain all kinds of deviations from perfectly aligned helical systems. In traditional methods for refining fiber diffraction data, the effects of the cumulative random angular disordering in the calculated intensities are modeled by a convolution of a Gaussian function (Egelman and DeRosier, 1982), as is the disorientation of the fiber axes (Holmes and Leigh, 1974). The fibers themselves are assumed to be straight helices. In reality, however, the fibers undergo all sorts of static and dynamic disordering resulting from deformations such as bending, twisting, and stretching. All these deformations are likely to contribute to the modulation of diffraction patterns and should be taken into account in refinement. Lack of such a consideration in refinement can lead to severe mistreatment of errors.

It has been shown in previous studies (ben-Avraham and Tirion, 1995; Ming et al., 2003a) that collective long-range deformations of a filament, such as bending, twisting, and stretching, can be effectively described by normal modes of the filament. These modes form an orthonormal basis set of the generalized coordinates that theoretically describes collective vibrations of a structure near an energy minimum. With this basis set, a specific molecular deformation can be expressed as a linear combination of the normal modes. In biological macromolecules, only low-frequency modes make dominant contributions to atomic fluctuations (Brooks et al., 1995; Brooks III et al., 1988; Levitt et al., 1985).

Given that they describe molecular deformations in a collective way, normal modes are naturally the adequate choices as refinement parameters when a small set of parameters are allowed to effectively refine the diffraction data. Earlier application of such an idea was to refining the x-ray crystallographic B-factors (Diamond, 1990; Kidera and Go, 1992). In this study, we developed a refinement protocol that employed the long-range normal modes as refinement parameters for fiber diffraction data. As an approximation, we assume that deformations occur within the periodic repeat of the filaments (helical unit cell) with a certain defined length. The straight rigid filament model used in traditional refinement methods is thus substituted by wavelike conformations.

We applied our method to the refinement of the F-actin model against fiber diffraction data. Actins are important filamentous protein complexes that are involved in cell transport, cytoskeletal support, and contractile events in almost all eukaryotic cells (Chen et al., 2000; Oda et al., 2001). They are known to be highly flexible and dynamic (Egelman, 2001; Egelman et al., 1982; Egelman and Orlova, 1995; Galkin et al., 2002; Huxley et al., 1994; Kojima et al., 1994; Orlova et al., 2001; Wakabayashi et al., 1994). The x-ray structures of various states of the monomeric G-actin subunit have been solved (Kabsch et al., 1990; McLaughlin et al., 1993; Otterbein et al., 2001; Robinson et al., 1999; Schutt et al., 1993). The polymeric F-actin filament has the Holmes model (Holmes et al., 1990), established from fiber diffraction data and the x-ray structure of the G-actin subunit (Kabsch et al., 1990). In the standard Holmes model, F-actin filaments appear to be formed by two right-handed long-pitch helical strands that twist around each other with a rise of 27.5 Å and a rotation angle of −166.15° per monomer around the filament axis. The minimum repeat of the double-stranded helix is ∼37.5 nm and contains 13 subunits (the 13-subunit repeat) and the total length of F-actin attains several microns or longer.

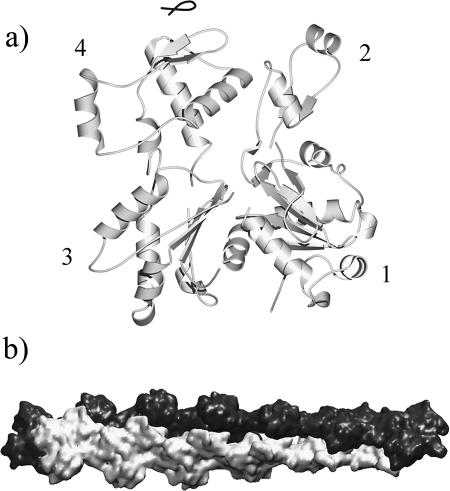
Besides the standard Holmes model, there are several modified versions of the atomic models of F-actin filaments. One model was refined by Tirion and co-workers (Tmodel; Tirion et al., 1995), on the basis of the standard Holmes model, with the deformations of the G-actin subunit modeled by normal modes and all subunits assumed to move in an identical way along the filament. Although the Tmodel used a reduced number of refinement parameters by employing the normal modes calculated on a single G-actin subunit, no effects of long-range filament deformations were included in the refinement. Another model of F-actin was refined by Lorenz and co-workers (Lmodel; Lorenz et al., 1993), using a method called directed mutation algorithm. Although the Lmodel achieved the lowest R-factor reported to date, the refinement utilized too many parameters, which has the potential problem of overfitting (Tirion et al., 1995). A new model was provided by Holmes (nHmodel; Kenneth C. Holmes, private communication), in which each subunit was refined as five rigid bodies; four of them were G-actin domains, and the remaining one was the heptapeptide phalloidin (Fig. 1).

FIGURE 1.

FIGURE 1

Open in a new tab

Structural models of actin. (a) Structure of a monomeric G-actin in the latest F-actin model refined by Holmes (nHmodel; Kenneth C. Holmes, private communication). Four domains are marked (domain 2 carries the DNase I binding loop) and the small heptapeptide phalloidin is drawn in a darker color with a coil representation (at the top of the molecule). (b) A 13-subunit repeat of F-actin filaments established from the helical parameters of the standard Holmes model (Holmes et al., 1990). The two helical strands are colored differently and the atomic coordinates were blurred to 8 Å resolution to illustrate the overall shape.

Our method was tested on the nHmodel, which has an R-factor of 8.7%. It was found that the long-range deformations of the filaments, especially the bending, are the major sources of refinement errors. By incorporating such deformations into the refinement, with only 7–9 low-frequency normal modes as refinement parameters, we achieved the lowest R-factor of 6.3%. The results also demonstrate that errors from long-range filament deformations cannot be easily compensated for by merely adjusting local structural parameters, and that incorporation of such deformations is needed to improve the refinement.

MATERIALS AND METHODS

Fiber diffraction theory

The diffraction pattern from a fiber is characterized by layer lines in reciprocal space due to the repeating nature of helical polymers. These layer lines are perpendicular to the fiber axis in real space. The layer line passing through the origin in reciprocal space is called the zero layer line or equator, whereas the line normal to the equator and passing through the origin is called the meridian.

Conventionally, the helical fiber is described by cylindrical coordinates, (rj, φj, zj) in real space and (R, ψ, Z) in reciprocal space. The layer lines are indexed by l. The separation between layer lines, Z, depends inversely on the length of helical unit cell, c, along the fiber axis (Z = l/c) (Namba and Stubbs, 1985). At the reciprocal space of radius R and lay line l, the intensity of the diffraction pattern (Franklin and Klug, 1955; Waser, 1955) is given by

graphic file with name M1.gif (1)

where 〈…〉ψ stands for cylindrical average and F(R, ψ, l) is the Fourier-Bessel structural factor (Klug et al., 1958) which can be expressed as

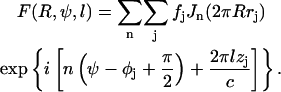graphic file with name M2.gif (2)

In Eq. 2, (rj, φj, zj) are the real-space cylindrical coordinates of atom j in the helical unit cell, fj is the atomic scattering factor of atom j, and Jn is the Bessel function of the first kind of order n. Inside a helical unit cell, there are u asymmetric units in t turns of the helix. The summation over j is over all atoms in the asymmetric unit and the summation over n only includes the terms that satisfy the helical selection rule (Klug et al., 1958),

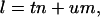graphic file with name M3.gif (3)

where m is any integer. The specific values of t and u describe the symmetry elements of rotation and translation that define the helical structure in real space.

For F-actin filaments, the minimum repeat has 13 G-actin subunits in six turns of the helix. In the conventional refinement of F-actin structures, this 13-subunit repeat is regarded as a helical unit cell and individual G-actin as an asymmetric unit, so t is 6 and u is 13. In this study, however, we are interested in the effects of the intersubunit dynamics on the diffraction pattern; the symmetry within a helical unit cell is completely disregarded so that each unit cell has only one asymmetric unit. Unit cells containing various numbers of G-actin subunits were used in the refinement. Accordingly, the selection rule was adjusted, and the summation over j, which used to be over all atoms in one G-actin subunit (one asymmetric unit), was expanded to include all atoms within one unit cell. For instance, if our calculation uses a 13-subunit repeat as a helical unit cell, t is 6 and u is 1; if our calculation includes a 26-subunit repeat as a helical unit cell, t is 12 and u is 1.

As in the conventional methods for fiber refinement, to take into account the effects of the cumulative angular disordering, the calculated intensities are broadened and convoluted by a Gaussian function (Egelman and DeRosier, 1982). The disorientation of the filaments around fiber axes is also treated as a convolution with a Gaussian function (Holmes and Leigh, 1974).

Long-range normal mode analysis by substructure synthesis method

Due to the size of F-actin filaments and the limitation of the computational capacity, it is impossible for us to do an all-atom calculation for even a single 13-subunit repeat of the F-actin filaments. A Cα-based anisotropy network model (Atilgan et al., 2001) was therefore employed to calculate the coarse-grained normal modes for a 13-subunit repeat. However, with longer F-actin repeats, even the Cα-based method is not applicable to determining the modes anymore. Thus, we employed the newly developed substructure synthesis method (Ming et al., 2003b) to determine the modes for longer F-actin repeats (Ming et al., 2003a) using the modes of the 13-subunit repeat as substructure modes. The algorithmic details of modal synthesis are given in reference (Ming et al., 2003a).

Refinement of F-actin using long-range normal modes

The structural refinement against fiber diffraction data requires adjustments of the coordinates of all atoms in the asymmetric unit, which is the entire helical unit cell of the filament in this study. We generated the coordinates for all atoms after deformation by superimposing the four domains of G-actin subunit, as rigid bodies, onto the Cα trajectories along the eigenvectors of normal modes. Considering that we only used low-frequency modes that describe the long-range collective deformations of the filament in the refinement, this rigid-body assumption for the domains is reasonable. In our study, all the domains were moved collectively along the normal mode trajectories. These motions are stereochemically allowable and can maintain proper interdomain contacts.

Additionally, we also applied interdomain constraints suggested by Holmes in his recent work. These constraints maintain constant distances between two neighboring Cα atoms located at the boundary of different domains. These constraints were added as Lagrangian multipliers in nonlinear least-squares minimization to prevent domains from clashing in adjusting the amplitude of each normal mode.

Nonlinear least-squares refinement

As in previous studies of F-actin refinement (Holmes et al., 1990; Lorenz et al., 1993; Tirion et al., 1995), the error in structural refinement is described by an R-factor defined as residual,

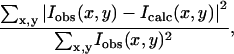graphic file with name M4.gif (4)

where Iobs and Icalc refer to the observed and calculated diffraction intensities at pixel location (x,y), respectively. The summation is over all points in the diffraction pattern.

To refine the model of F-actin filament, one needs to determine the magnitudes of structural parameters by minimizing the error function,

graphic file with name M5.gif (5)

where w is a weighting factor equal to Iobs (x,y) + α. The constant α is chosen to suppress low signal/noise fluctuations. We employed a nonlinear least-squares algorithm (Press et al., 1990) to carry out the minimization. Such a method requires the evaluation of the second derivative matrix of the error function, ξ2, with respect to the structural parameters. This is done numerically by

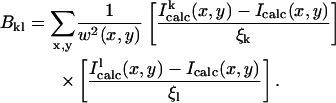graphic file with name M6.gif (6)

Inline graphic is the computed intensity of the current model after a trial shift by a small increment, ξi, of the structural parameters, qi. Here qi are low-frequency normal modes. The set of shifts, Δqi, that minimizes ξ2, is given by the solutions of the set of linear equations,

graphic file with name M8.gif (7)

where Ak is the partial derivative of ξ2 with respect to qk, defined as

graphic file with name M9.gif (8)

The magnitudes of parameters, {Δqi}, are determined repeatedly and iteratively until they converge and produce no change in ξ2 in the error function (Eq. 5).

RESULTS

The starting model of our refinement, nHmodel, has an R-factor of 8.7%. We mainly focused on improving the refinement by taking into account the deformational effects of long filaments. The effects on refinement of long-range deformations are separated from those of local deformations by treating the four domains of G-actin as rigid bodies. The refinement was performed against the fiber diffraction data (Holmes et al., 1990) using various assemblies of G-actin subunits as helical unit cells within which the helical symmetry is completely disregarded, i.e., there is only one asymmetric unit in each helical unit cell and all atoms are treated as unique. As an approximation, the assumption we used throughout this study is that F-actin filaments deform periodically in terms of the helical unit cells.

Improvement of refinement by individual low-frequency modes of a 13-subunit repeat

To start, we used the minimum 13-subunit repeat of F-actin as a helical unit cell for the refinement. The low-frequency normal modes were first calculated on the 13-subunit repeat using a Cα-based anisotropic network model (Atilgan et al., 2001). Then, each individual low-frequency mode was tested on the improvement of the refinement as judged by the reduction of R-factor. Fig. 2 shows the resultant R-factor refined by a single low-frequency mode as a function of the mode index. All first 20 lowest-frequency modes plotted reduced the R-factor to various degrees (the ceiling of the figure is the R-factor of nHmodel, 8.7%). Refinements by the two very lowest-frequency modes (the first and second vibrational modes, after excluding the six zero-modes for overall translation and rotation) resulted in the smallest R-factor (7.4%) among all modes. These two modes belong to two perpendicular bending (transverse) modes. Among the first 11 lowest-frequency modes, except for the third and sixth modes that are twisting (torsional) modes and the ninth that is a stretching (longitudinal) mode, all other modes are various kinds of bending modes with increasing frequency and shortening wavelengths. It is noted that all the bending modes caused larger decreases in R-factor (0.4–1.3%) than nonbending modes (0.2–0.3%), and the decrease of R-factor caused by the bending modes becomes progressively smaller as the mode index increases. From these results, we conclude that bending modes of F-actin filament, especially those with very low frequencies, make the most important contributions to the improvement of structure refinement. After the 11th mode, the trend of changes in R-factor shows less regularity (Fig. 2). These higher-frequency modes do not significantly lower R-factor, and describe more complicated deformations with mixed features of bending, twisting, and stretching modes.

FIGURE 2.

FIGURE 2

Open in a new tab

Refinement results by each of the first 20 lowest-frequency vibrational modes as a function of the mode index. The refinement was based on the normal modes calculated for a 13-subunit repeat using the anisotropic network model. The ceiling of the figure is the value of R-factor of nHmodel (8.7%), the starting point of this study.

Improvement of refinement by individual low-frequency bending modes of longer repeats

In the previous section, the refinement was carried out using 13 G-actin subunits as one helical unit cell, assuming that F-actin filaments deform periodically in terms of the unit cell. Thus, it did not take into account the deformations with wavelengths longer than one 13-subunit repeat. To investigate the effects of those longer-wavelength deformations, we further carried out the refinement using helical unit cells longer than 13 subunits. The normal modes for these longer F-actin repeats were generated by the substructure synthesis method (Ming et al., 2003b), based on the modes calculated on a 13-subunit repeat (Ming et al., 2003a).

Since the bending modes make the dominant contributions, here we explore the effects of individual bending modes at different lengths of repeats (Fig. 3 a). The x axis is calibrated to the multiples of the length of a 13-subunit repeat and the curves are aligned in terms of their approximate half-wavelengths. It is interesting to note that all the curves have a minimum of R-factor converged at a specific point, which corresponds to modes with a half-wavelength of the length of a 26-subunit repeat. They are the first type of bending mode using a 26-subunit repeat, the second type of bending mode using a 52-subunit repeat, and the fourth type of bending mode using a 104-subunit repeat. All of these modes share a similar half-wavelength as schematically illustrated in Fig. 3 b. The shapes of the first four types of bending modes for standing waves and free vibrations with equal lengths are shown in Fig. 3 c. Here, the half-wavelength for a free vibrational mode is approximately defined by comparing its shape with that of the standing wave.

FIGURE 3.

FIGURE 3

FIGURE 3

FIGURE 3

Open in a new tab

(a) Refinement results by individual bending modes with different lengths of repeating units as helical unit cells. For the purpose of illustration, the figure is drawn in a special way to align the modes in terms of their wavelengths. The intervals of the x axis are expressed in terms of multiples of the length of a single 13-subunit repeat. To make the points in the figure spread evenly, all intervals are arranged along the x axis evenly (rather than in terms of the numerical values of the actual multiples). The modes are marked in terms of their half-wavelengths by assuming that the shapes of waves are approximately trigonometric, i.e., those of standing waves. The numbers following the letters at each point are inverted to the types of bending waves in terms of their wavelengths. For example, the first type of bending mode of the 13-subunit repeat has a multiple of 1 and is labeled as a1, and the second type of bending mode has a multiple of 1/2 and is labeled as a2, and so on. All the modes for longer repeating units are aligned correspondingly. For clarity, only one of the two degenerate modes was used in each type of wave. (b) Schematic illustration of the shapes of modes for the first type of bending mode of a 26-subunit repeat (26(1)), the second type of bending mode of a 52-subunit repeat (52(2)), and the fourth type of bending mode of a 104-subunit repeat (104(4)). The curves are made based on the theoretical solutions of bending modes for an elastic homogeneous rod (Meirovitch, 1967). (c) The shapes of the first four types of bending modes for standing waves (left) and for free vibrations with equal lengths (right).

Improvement of refinement by a combination of multiple modes

In addition to the refinements by a single mode in previous sections, we also tested how a combination of multiple modes improves the refinement. The combination of a slightly larger number of modes is expected to provide an increased number of degrees of freedom for a more realistic description of the deformations of the filament without overfitting, and thus yield a lower value of R-factor.

For the refinement with the modes of a 13-subunit repeat, as shown in Fig. 2, the R-factor dropped to 7.4% when only one very-lowest-frequency mode was used. Here, the combination of more low-frequency modes further decreased the R-factor. For instance, the use of nine lowest-frequency modes in the refinement resulted in an R-factor of 7.0% (Fig. 4). The value of R-factor did not decrease significantly when the number of modes exceeded nine. With longer lengths of helical unit cells (26-subunit and 52-subunit repeats), the trends of changes in R-factor are similar, i.e., they monotonically decrease as the number of modes used in refinement increases, and then they level off. The final values of R-factor were 6.8% for the 26-subunits and 6.3% for the 52-subunits using 7–9 lowest-frequency modes.

FIGURE 4.

FIGURE 4

Open in a new tab

Refinement results using various lengths of repeats as helical unit cells with a combination of multiple low-frequency normal modes.

To examine the effects of higher-frequency modes on the refinement, we refined the structure by including more higher-frequency modes of the 13-subunit repeat. It was found that inclusion of these modes only marginally improved R-factor. For example, the use of 28 well-behaved modes selected from the first 50 modes that mainly describe intersubunit or interdomain motions decreases R-factor to 6.9%—only 0.1% better than using nine lowest-frequency modes (7.0%).

Calculation of free R-factors

Free R-factor is widely used in protein crystallography to monitor whether the refined model is overfitted (Brünger, 1997). In doing so, one sets aside a random subset (5–10%) of the diffraction data, and refines the structure with respect to the remaining data. The subset of data excluded from the refinement are then used to calculate the free R-factor so as to cross-validate the refined model. When the number of independent measures is small, as in fiber diffraction, the variations of free R-factors from any single refinement can be very large; therefore, a multiple refinement procedure is adopted (Welsh et al., 1998). The values of free R-factors are then averaged.

In our case, to calculate the values of free R-factor, the original diffraction data were randomly divided into 10 independent groups, with each containing 10% of the data. Then 10 independent refinements were carried out, each with a particular 10% of data excluded from the refinement. The values of free R-factor from all 10 calculations were then averaged to yield a final free R-factor. Table 1 shows the results using the nine lowest-frequency normal modes of a 13-subunit repeat. It is evident that, as the refinement decreased the values of R-factor, the values of free R-factor were simultaneously decreased, suggesting that there is no overfitting problem in this case.

TABLE 1.

Results of free R-factor calculations from 10 independent refinements

Before refinement After refinement
No. refinement R Rfree R Rfree
1 8.8% 8.2% 7.2% 6.6%
2 8.6% 9.9% 7.0% 8.3%
3 8.8% 8.2% 7.1% 6.3%
4 9.0% 6.4% 7.4% 5.4%
5 8.6% 11.4% 7.0% 9.2%
6 8.4% 12.6% 6.8% 10.2%
7 9.1% 5.8% 7.4% 4.4%
8 8.4% 10.5% 6.6% 9.7%
9 8.9% 7.5% 7.2% 6.1%
10 8.8% 8.3% 7.1% 6.8%
Average 8.7% 8.9% 7.1% 7.3%
Open in a new tab

Analysis of the refined structures

As shown in the previous section, the best result for the refinement was obtained using the 52-subunit repeat with at least seven lowest-frequency modes. The shape of the filament after such a refinement is shown in Fig. 5 a together with the nHmodel before the refinement. Compared in Fig. 5 b are the computed (upper-right and lower-left quadrants) and measured (upper-left and lower-right quadrants) diffraction patterns. The nearly-perfect fit of the two diffraction patterns is evident. The root mean-square deviations (RMSD) between G-actin subunits before and after this long-range normal-mode refinement are plotted in Fig. 5 c after a superposition of the 52 subunits of the two models in Fig. 5 a. The deviations between the 52-subunit repeats can be as large as 14–18 Å, indicating a significantly bent conformation of the filament after the refinement. To dissect the contributions of each individual mode, we calculated the Δqi values in Eq. 7 that are plotted in Fig. 5 d as a function of mode index. It is clear that the largest contributions come from the two degenerate second-type bending modes, consistent with the results shown in Fig. 3 a. We also calculated the RMSD for each individual subunit and for each of the four G-actin domains that were treated as rigid bodies and fit along normal mode trajectories step by step in the refinement. The deviations in structures within subunits are expected to derive only from domain rearrangement in our model. As shown in Fig. 5 e, the average value of the RMSD of all the subunits and domains is <0.1 Å, which indicates that all the domains and subunits moved nearly like rigid bodies following the lowest-frequency modes of the filament. The only exception is the smallest domain (domain 2), which has an average RMSD of ∼0.15 Å (Fig. 5 e, bottom). Therefore, the better fit between the model and the diffraction data has been achieved mainly by a more realistic modeling of the long-range deformations rather than through local structural adjustments.

FIGURE 5.

FIGURE 5

FIGURE 5

FIGURE 5

FIGURE 5

FIGURE 5

Open in a new tab

Refinement results using a 52-subunit repeat as a helical unit cell. (a) The structure of the 52-subunit repeat in the initial nHmodel (top) and after refinement by the seven lowest-frequency normal modes (bottom). (b) The comparison of experimental (upper-left and lower-right quadrants) and computed (upper-right and lower-left quadrants) diffraction patterns. A nearly perfect fit between the two diffraction patterns is evident. (c) The RMSD between the 52-subunit repeat in the refined model and the nHmodel shown as a function of G-actin subunit index. The calculations were performed by superimposing all of the 52-subunit repeats. It is apparent that the RMSD has a wavelike distribution, consistent with the predominant contributions of the bending modes to the improvement of the refinement. (d) The contributions of each individual mode, i.e., Δqi in Eq. 7, as a function of mode index. The two second-type of bending modes make the most significant contributions. (e) The values of RMSD of each individual subunit (top) and domain (bottom) as a function of the subunit index. In contrast to the alignment in Fig. 5 c, the calculations were performed by superimposing each individual subunit independently.

It must be pointed out that, in our current refinement procedure, the four domains of G-actin subunit were treated as rigid bodies, so that the local structural adjustment are small—as we observed. This treatment allows the separation of the contributions of long-range deformations to refinement errors from those of local structural motions. However, in doing so, the contributions of modes with wavelengths similar to the physical sizes of the four G-actin domains are diminished. Our future refinement study will be extended to include these modes of shorter wavelengths obtained from normal mode calculations, which is expected to decrease further the R-factor by allowing the adjustment of local structures within domains.

Comparison of refinement results using different F-actin models

To compare the refinement results of using different F-actin models, we also applied our refinement protocol to other atomic models of F-actin filaments: the Tmodel refined by Tirion and co-workers in 1995 (Tirion et al., 1995) and the Lmodel refined by Lorenz and co-workers in 1993 (Lorenz et al., 1993).

As with the nHmodel in previous sections, the Tmodel and Lmodel were refined with nine lowest-frequency modes calculated on a 13-subunit repeat. The starting values of R-factor were 10.9% and 6.7% for Tmodel and Lmodel, respectively. After refinement, the converged R-factor dropped to 9.3% for Tmodel and 5.8% for Lmodel. The decreases of R-factor are 1.6% for Tmodel and 0.9% for Lmodel, in comparison to the 1.7% decrease for nHmodel. The values of RMSD for all the subunits in all models are shown in Fig. 6, calculated from a superposition of all of the 13 subunits before and after the refinement. It is clear that, for all three models of F-actin, the final conformations are also wavelike in shape, indicating the dominating contributions of the bending modes.

FIGURE 6.

FIGURE 6

Open in a new tab

The values of RMSD between 13-subunit repeats before and after the long-range normal-mode refinement using different starting models. All the curves have wavelike shapes, suggesting the predominant contributions of the bending modes.

In short, the results shown here demonstrate that our protocol is efficient for improving the refinement of F-actin models independent of the starting atomic models.

CONCLUDING DISCUSSION

This article reports the results of refining the atomic models of F-actin against the fiber diffraction data by using long-range normal modes as adjustable parameters to realistically describe the collective long-range filament deformations. Each of the four domains of G-actin subunit was treated as a rigid body in the refinement so as to minimize the contributions of local structural deformations. Modes reflecting long-range bending were found to make the most significant contributions to the improvement of the refinement. A combination of a very few of these modes, in most cases, 7–9 modes, was able to lower the R-factor by 1∼2%. Such a result demonstrates that normal-modes-based refinement has the advantage of using a small number of adjustable parameters to achieve a good fitting efficiency, thus avoiding the risk of overfitting the structural model. More importantly, it suggests that, for any fiber diffraction data, a substantial amount of refinement error comes from long-range deformations, especially bending, of the filaments. The effects of these deformations cannot be easily compensated for by adjusting local structural parameters, and must be properly accounted for to achieve an improved fit of refined models with experimental data.

In our refinement protocol, all atoms in a helical unit cell are considered unique and all participate in the calculations. This means the rotational and translational symmetries within a helical unit cell are completely disregarded, and there is only one asymmetric unit in each unit cell. This feature makes such a refinement protocol particularly useful in the final stage of fiber diffraction refinement, once it is possible to determine the normal modes from a refined model obtained from conventional refinement with the perfect helical symmetry imposed. However, one must note that, as the length of the repeat used in normal-mode calculation increases, the number of atoms involved in the calculations quickly increases. This results in a quick increase in the computational costs of the refinement. A way to overcome this weakness will be reported in a forthcoming article.

It is noticed that, although aligned in terms of the wavelengths, the R-factors with different lengths of repeats in Fig. 3 a showed certain degrees of variations at the same wavelength. These variations are probably due to two main factors. One could be the deformations of the two ends of a repeat in normal modes. In our analysis, the modes of the repeats were determined as free vibrational modes, although, in reality, the two ends of the filaments are attached to the neighboring structures. Therefore, using the modes of free vibrations to refine the data is an approximation. If the waves within a single repeat were standing waves, the R-factors refined by modes of equivalent wavelengths are expected to be the same in Fig. 3 a. The other factor affecting the refinement could be the shape-inhomogeneity of F-actin filament that leads to inhomogeneity in different bending modes. That is, since different sections along the filament are not identical, the bending modes along different bending directions are also not identical. The improvement over the approximation of using normal modes computed as free vibrational modes of an isolated F-actin repeat to model the deformations of the filament will be a focus of our future study.

In our study, the four domains of G-actin subunit were assumed to move as rigid bodies. This eliminated the contributions from slightly higher-frequency modes with wavelengths similar to the physical sizes of the domains, which thereby enabled the determination of the contributions of long-range deformations. However, our normal mode calculations, per se, did not have such a restriction. Releasing the restriction of the domains as rigid bodies in refinement would allow local structural adjustments within individual domains, which, in conjunction with the long-range filamentous deformations, are expected to further decrease the R-factor. This will be the focus of our forthcoming article.

Acknowledgments

We thank Professor Kenneth C. Holmes for providing us with the experimental data and an unpublished F-actin atomic model. We also thank Professor Michael F. Schmid for helpful discussions about actin dynamics in general.

J.M.'s research was supported in part by grants from the American Heart Association (AHA-TX0160107Y), the Robert A. Welch Foundation (Q-1512), the National Institutes of Health (R01-GM067801), and the National Science Foundation Career Award (MCB-0237796). J.M. is also a recipient of the Award for Distinguished Young Scholars Abroad from the National Natural Science Foundation of China.

References

  1. Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. ben-Avraham, D., and M. M. Tirion. 1995. Dynamic and elastic properties of F-actin: a normal-modes analysis. Biophys. J. 68:1231–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brooks, B. R., D. Janezic, and M. Karplus. 1995. Harmonic analysis of large systems. I. Methodology. J. Comp. Chem. 16:1522–1542. [Google Scholar]
  4. Brooks III, C. L., M. Karplus, and B. M. Pettitt. 1988. Proteins: a theoretical perspective of dynamics, structure, and thermodynamics. Adv. Chem. Phys. 71:1–249. [Google Scholar]
  5. Brünger, A. T. 1997. Free R-value: cross-validation in crystallography. Methods Enzymol. 277:366–396. [DOI] [PubMed] [Google Scholar]
  6. Chen, H., B. W. Bernstein, and J. R. Bamburg. 2000. Regulating actin-filament dynamics in vivo. TIBS. 25:19–23. [DOI] [PubMed] [Google Scholar]
  7. Diamond, R. 1990. On the use of normal modes in thermal parameters refinement: theory and application to the bovine pancreatic trypsin inhibitor. Acta Crystallogr. A46:425–435. [DOI] [PubMed] [Google Scholar]
  8. Egelman, E. H. 2001. Actin allostery again? Nat. Struct. Biol. 8:735–736. [DOI] [PubMed] [Google Scholar]
  9. Egelman, E. H., and D. J. DeRosier. 1982. The Fourier transform of actin and other helical systems with cumulative random angular disorder. Acta Crystallogr. A. 38:796–799. [Google Scholar]
  10. Egelman, E. H., N. Francis, and D. J. DeRosier. 1982. F-actin is a helix with a random variable twist. Nature. 298:131–135. [DOI] [PubMed] [Google Scholar]
  11. Egelman, E. H., and A. Orlova. 1995. New insights into actin filament dynamics. Curr. Opin. Struct. Biol. 5:172–180. [DOI] [PubMed] [Google Scholar]
  12. Franklin, R. E., and A. Klug. 1955. The splitting of layer lines in x-ray fiber diagrams of helical structures: application to Tobacco Mosaic Virus. Acta Crystallogr. 8:777–780. [Google Scholar]
  13. Galkin, V. E., M. S. VanLoock, A. Orlova, and E. H. Egelman. 2002. A new internal mode in F-actin helps explain the remarkable evolutionary conservation of actin's sequence and structure. Curr. Biol. 12:570–575. [DOI] [PubMed] [Google Scholar]
  14. Holmes, K. C., and J. B. Leigh. 1974. The effect of disorientation on the intensity distribution of non-crystalline fibers. I. Theory. Acta Crystallogr. A. 30:635–638. [Google Scholar]
  15. Holmes, K. C., D. Popp, W. Gebhard, and W. Kabsch. 1990. Atomic model of the actin filament. Nature. 347:44–49. [DOI] [PubMed] [Google Scholar]
  16. Huxley, H. E., A. Stewart, H. Sosa, and T. Irving. 1994. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 67:2411–2421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kabsch, W., H. G. Mannherz, D. Suck, E. F. Pai, and K. C. Holmes. 1990. Atomic structure of the actin:DNase I complex. Nature. 347:37–44. [DOI] [PubMed] [Google Scholar]
  18. Kidera, A., and N. Go. 1992. Normal mode refinement: crystallographic refinement of protein dynamic structure. I. Theory and test by simulated diffraction data. J. Mol. Biol. 225:457–475. [DOI] [PubMed] [Google Scholar]
  19. Klug, A., F. H. C. Crick, and H. W. Wyckoff. 1958. Diffraction of helical structures. Acta Crystallogr. 11:199–213. [Google Scholar]
  20. Kojima, H., A. Ishijima, and T. Yanagida. 1994. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 91:12962–12966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Levitt, M., C. Sander, and P. S. Stern. 1985. Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 181:423–447. [DOI] [PubMed] [Google Scholar]
  22. Lorenz, M., D. Popp, and K. C. Holmes. 1993. Refinement of the F-actin model against x-ray fiber diffraction data by the use of a directed mutation algorithm. J. Mol. Biol. 234:826–836. [DOI] [PubMed] [Google Scholar]
  23. McLaughlin, P. J., J. T. Gooch, H. G. Mannherz, and A. G. Weeds. 1993. Structure of gelsolin segment 1-actin complex and the mechanism of filament severing. Nature. 364:685–692. [DOI] [PubMed] [Google Scholar]
  24. Meirovitch, L. 1967. Analytical Methods in Vibrations. The Macmillan Co., London, UK.
  25. Ming, D., Y. Kong, Y. Wu, and J. Ma. 2003a. Simulation of F-actin filaments of several microns. Biophys. J. 85:27–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Ming, D., Y. Kong, Y. Wu, and J. Ma. 2003b. Substructure synthesis method for simulating large molecular complexes. Proc. Natl. Acad. Sci. USA. 100:104–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Namba, K., and G. Stubbs. 1985. Solving the phase problem in fiber diffraction. Application to Tobacco Mosaic Virus at 3.6 Å resolution. Acta Crystallogr. A41:252–262. [Google Scholar]
  28. Oda, T., K. Makino, I. Yamashita, K. Namba, and Y. Maeda. 2001. Distinct structural changes detected by x-ray fiber diffraction in stabilization of F-actin by lowering pH and increasing ionic strength. Biophys. J. 80:841–851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Orlova, A., V. E. Galkin, M. S. VanLoock, E. Kim, A. Shvetsov, E. Reisler, and E. H. Egelman. 2001. Probing the structure of F-actin: cross-links constrain atomic models and modify actin dynamics. J. Mol. Biol. 312:95–106. [DOI] [PubMed] [Google Scholar]
  30. Otterbein, L. R., P. Graceffa, and R. Dominguez. 2001. The crystal structure of uncomplexed actin in the ADP state. Science. 293:708–711. [DOI] [PubMed] [Google Scholar]
  31. Press, W. H., B. P. Flannery, W. T. Teukolsky, and W. T. Vetterling. 1990. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
  32. Robinson, R. C., M. Mejillano, V. P. Le, L. D. Burtnick, H. L. Yin, and S. Choe. 1999. Domain movement in gelsolin: a calcium-activated switch. Science. 286:1939–1942. [DOI] [PubMed] [Google Scholar]
  33. Schutt, C. E., J. C. Myslik, M. D. Rozycki, N. C. Goonesekere, and U. Lindberg. 1993. The structure of crystalline profilin-β-actin. Nature. 365:810–816. [DOI] [PubMed] [Google Scholar]
  34. Stubbs, G. 1999. Development in fiber diffraction. Curr. Opin. Struct. Biol. 9:615–619. [DOI] [PubMed] [Google Scholar]
  35. Tirion, M. M., D. ben-Avraham, M. Lorenz, and K. C. Holmes. 1995. Normal modes as refinement parameters for the F-actin model. Biophys. J. 68:5–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wakabayashi, K., Y. Sugimoto, H. Tanaka, Y. Ueno, Y. Takezawa, and Y. Amemiya. 1994. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 67:2422–2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Wang, H., and G. Stubbs. 1993. Molecular dynamics in refinement against fiber diffraction data. Acta Crystallogr. A. 49:504–513. [DOI] [PubMed] [Google Scholar]
  38. Waser, J. 1955. Fourier transforms and scattering intensities of tubular objects. Acta Crystallogr. 8:142–150. [Google Scholar]
  39. Welsh, L. C., M. F. Symmons, J. M. Sturtevant, D. A. Marvin, and R. N. Perham. 1998. Structure of the capsid of Pf3 filamentous phase determined from x-ray fiber diffraction data at 3.1 Å resolution. J. Mol. Biol. 283:155–177. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES