Glucose Accumulation Can Account for the Initial Water Flux Triggered by Na⁺/Glucose Cotransport

Abstract

Over the last decade, several cotransport studies have led to the proposal of secondary active transport of water, challenging the dogma that all water transport is passive. The major observation leading to this interpretation was that a Na⁺ influx failed to reproduce the large and rapid cell swelling induced by Na⁺/solute cotransport. We have investigated this phenomenon by comparing a Na⁺/glucose (hSGLT1) induced water flux to water fluxes triggered either by a cationic inward current (using ROMK2 K⁺ channels) or by a glucose influx (using GLUT2, a passive glucose transporter). These proteins were overexpressed in Xenopus oocytes and assayed through volumetric measurements combined with double-electrode electrophysiology or radioactive uptake measurements. The osmotic gradients driving the observed water fluxes were estimated by comparison with the swelling induced by osmotic shocks of known amplitude. We found that, for equivalent cation or glucose uptakes, the combination of substrate accumulations observed with ROMK2 and GLUT2 are sufficient to provide the osmotic gradient necessary to account for a passive water flux through SGLT1. Despite the fact that the Na⁺/glucose stoichiometry of SGLT1 is 2:1, glucose accumulation accounts for two-thirds of the osmotic gradient responsible for the water flux observed at t = 30 s. It is concluded that the different accumulation processes for neutral versus charged solutes can quantitatively account for the fast water flux associated with Na⁺/glucose cotransport activation without having to propose the presence of secondary active water transport.

INTRODUCTION

Understanding water transport through biological membranes has been a subject of continuous interest for the past 50 years. Measurements of activation energies, water permeabilities, and sensitivity to mercurial inhibitors have led to the conclusion that certain proteins are responsible for mediating a significant portion of measured water flux. The first membrane proteins clearly identified to be water permeable were the facilitated glucose transporters (GLUTs); inhibitors of glucose transport significantly reduced the osmotic water permeability of J774 macrophages (Fischbarg et al., 1989), and overexpression of GLUT1, GLUT2, and GLUT4 isoforms in Xenopus oocytes increased their water permeability by approximately fivefold (Fischbarg et al., 1990). Soon after, a first member of the family of water channels was discovered (Preston and Agre, 1991; Zhang et al., 1993), providing a satisfying molecular basis to the contention that water was passing through a specific pathway characterized by a single file of 5–9 water molecules (Macey, 1984).

The dogma that transmembrane water transport is always passive was first challenged in the early 1990s by two studies which suggested that secondary active water transport is mediated by a K⁺/Cl⁻ cotransporter in the choroid plexus epithelium of Necturus maculosus (Zeuthen, 1991, 1994). Later, using overexpression in Xenopus oocytes, the rabbit Na⁺/glucose cotransporter rSGLT1 was proposed to operate as a water pump with a stoichiometry of 260 water molecules per glucose molecule transported (Loo et al., 1996), which was later reevaluated to 390–424 water molecules per glucose. A series of publications then reported observations of water cotransport for several other cotransporters expressed in Xenopus oocytes: the human Na⁺/glucose cotransporter hSGLT1 (Meinild et al., 1998), the Na⁺/glutamate cotransporter EAAT1 (MacAulay et al., 2001), the Na⁺/dicarboxylate cotransporter (Meinild et al., 2000), the Na⁺/iodide cotransporter (mentioned in Loo et al., 1996; Meinild et al., 2000), and the H⁺/amino acid cotransporter (mentioned in Loo et al., 1996; Meinild et al., 2000), with stoichiometries ranging from 50 to 400 water molecules per transport cycle.

The most direct evidence supporting water cotransport is the observation that the initial water flux generated by a pure ionic inward current is much smaller than the water flux induced by a Na⁺/solute cotransport current of similar amplitude. This has been observed for cation pores including gramicidin (Meinild et al., 1998; Zeuthen et al., 2001) and nystatin (Zeuthen et al., 1997), as well as for cation channels such as connexin 50 (Wright and Loo, 2000) and ROMK2 (Duquette et al., 2001). The ∼1-min delay observed between current stimulation and measurable volume increase has been interpreted as an experimental measurement of the time required to build a significant osmotic gradient. Consequently, it was assumed that the early swelling of an oocyte after the start of Na⁺/glucose cotransport was too fast to be osmotically-driven.

Although it is acknowledged that a pure cation influx fails to reproduce the early water flux observed with Na⁺/glucose cotransport, it is not known whether a pure glucose influx would do the same. In fact, the osmotic consequences of an accumulation of ions may not be the same as the effects of cytosolic accumulation of a neutral solute like glucose. The present study is aimed at evaluating the osmotic effect of a glucose influx versus the effect of a cation influx by separately expressing a facilitated glucose transporter and a cation channel in oocytes. Volumetric measurements during transport allow osmolyte local accumulations to be deduced. The accumulations corresponding to K⁺, 2-deoxyglucose (2DG), and Na⁺/glucose are calculated for ROMK2-, GLUT2-, and SGLT1-expressing oocytes, respectively. A comparative analysis of these accumulations demonstrates that glucose accumulates much faster than do ions, which can quantitatively explain the early water flux that accompanies stimulation of Na⁺/glucose cotransport.

MATERIALS AND METHODS

Oocyte injections and incubation

Preparation of the Xenopus laevis oocytes and cRNA injection with human SGLT1 or rat ROMK2 mRNA were done as previously described (Coady et al., 2002; Duquette et al., 2001). For GLUT2 expression, oocytes were injected with 46 nl of solution containing 1 μg/μl of human GLUT2 cRNA. They were then incubated for 4–7 days at 18°C in Barth's solution (in mM: 90 NaCl, 3 KCl, 0.82 MgSO₄, 0.41 CaCl₂, 0.33 Ca(NO₃)₂, and 5 HEPES, pH 7.6) supplemented with 5% horse serum, 2.5 mM Na⁺-pyruvate, 100U/ml penicillin, and 0.1 mg/ml streptomycin.

With hSGLT1-expressing oocytes, the bathing medium (control solution) used for volumetric measurements had the following composition (in mM): 50 NaCl, 3 KCl, 0.82 MgCl₂, 0.74 CaCl₂, 5 HEPES, and 85 mannitol, resulting in a measured osmolality of 197 mOsm/kg of water. Solutions containing α-Methylglucose (αMG) were obtained by replacing 5 mM mannitol with 5 mM αMG. The bathing medium for ROMK2-expressing oocytes was the same as for SGLT1 experiments, except that 20 mM KCl was present rather than 3 mM, and 50 mM mannitol was used rather than 85 mM. In experiments with GLUT2-expressing oocytes, 5 mM 2-deoxyglucose (2DG) was used as a nonmetabolizable substrate in replacement of 5 mM mannitol.

For all experiments, hypotonic solutions were obtained by omitting 20 mM mannitol from the control solutions. Osmolalities were verified within ± 2 mOsm/kg H₂O using a freezing point osmometer (Advanced DigiMatic Osmometer, model 3D2, Advanced Instruments, Needham Heights, MA).

Electrophysiology

The two-electrode voltage clamp technique was used as previously described (Bissonnette et al., 1999; Duquette et al., 2001). Electrode tips were filled with a cushion layer of 1% agarose in 1 M KCl to reduce cell swelling associated with KCl leakage into the cytosol (Schreibmayer et al., 1994).

SGLT1-injected oocytes were clamped at −50 mV before stimulating a cotransport current by superfusing the αMG-containing solution. ROMK2-expressing oocytes were unclamped and a K⁺ current between 0.8 and 1.5 μA was then generated by rapidly clamping to a pre-set potential which was 1–3 mV more negative than the resting potential. GLUT2-injected oocytes were not clamped, but simply held in place by microelectrodes or suction pipettes of ∼150 μm tip diameter.

Optical measurements

The apparatus used for volumetric measurement was a new version of one previously described (Duquette et al., 2001). The perfusion rate was ∼2 ml/min, and solution changes were controlled by an electrical valve and characterized by a total dead space of 50 μl between the solution selector and the experimental chamber. The bath had a volume of ∼120 μl, and 80% of the solution change was achieved within 3 s, as judged by the time required for the cotransport current to reach 80% of its final value after applying a 5 mM concentration of αMG.

The oocyte was illuminated from above, and its cross-section was continuously measured from below using a CCD camera (model CCD72, Dage-MTI, Michigan, IN), through the 3× objective of an inverted microscope. Custom-made software counted the pixels corresponding to the oocyte's cross-section every 0.2 s and the data points were later averaged to obtain 1 point per s. Assuming the oocyte is spherical, and calibrating the system with a steel ball of known diameter, we could then translate the cross-sectional recordings into volume measurements. A noise level of 0.05% of the volume measurement could usually be reached. Before starting the experiments, oocytes were equilibrated for at least 20 min in substrate-free bathing medium to obtain a stable volume measurement. However, a certain endogenous volume change could still be occasionally observed before starting the experiment. This volume change rate averaged 0.14 ± 0.26, 0.17 ± 0.25, and −0.7 ± 0.5 pl/s for SGLT1-, ROMK2-, and GLUT2-expressing oocytes, respectively, and was subtracted from the raw measurements before further analysis.

Isotopic uptakes in oocytes

GLUT2-expressing oocytes were rinsed twice with substrate-free Barth's solution and transport was initiated by exposing a group of 4–6 oocytes to the transport solution containing 5 mM 2-DG (1μCi/ml [1,2] ³H 2DG, PerkinElmer-New England Nuclear, Boston, MA). The nonspecific fraction of uptake was determined by similar incubation of oocytes in media containing 200 μM phloretin. The oocytes were incubated at room temperature for the required incubation time in 1 ml of transport media. The incubation was stopped by rapid removal of transport media followed by addition of 2-ml ice-cold substrate-free media. The oocytes were rinsed a further 3× and individually transferred to scintillation vials. Digestion of the oocytes were performed by addition of 0.2 ml 10% SDS for 2 h before addition of scintillation cocktail (Beta Blend; ICN, Irvine, CA). The vials were counted for tritium activity using an LS6000 SC scintillation counter (Beckman, Fullerton, CA).

Analysis

To determine the osmotic pressure necessary to account for the water fluxes observed during transport, we exposed each oocyte to an osmotic shock of −20 mOsm at the end of each experiment. From the ratio of the slope of swelling during transport to the change in swelling rate induced by the hypotonic shock, we could deduce the osmotic gradient corresponding to any observed swelling rate for that particular oocyte. The hypotonic shock also provided us with the apparent water permeability (L_p, in cm/s) of the oocyte being tested using the equation

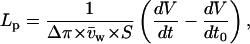(1)

where dV/dt is the initial slope of swelling after the osmotic shock in cm³/s, dV/dt₀ is the baseline swelling observed immediately before the osmotic shock, Δπ is the amplitude of the osmotic shock triggered (20 mOsm in all cases here), 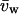is the water-specific molar volume (18.2 cm³/mol), and S is a standard oocyte surface of 0.4 cm² considering a membrane infolding factor of 8.5–9.5-fold (Zampighi et al., 1995).

Spontaneous volume changes of the order of 0.3–0.4 nl are present throughout our volume measurements. As these volume changes occur with characteristic time courses of ∼10 s, they can significantly affect our time to time estimation of cell swelling rate. Consequently, to get an accurate estimation of water flux at any time, a continuous function was fitted to the volume data. For SGLT1 and ROMK2, a function was used where the swelling rate starts from an initial value (m₀) and exponentially reaches a second level (m₀ + dm), as follows,

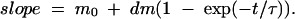(2)

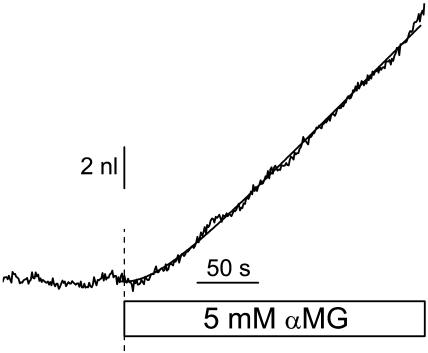
This function was integrated to give a volume-time empirical relation, and the four parameters (m₀, dm, τ, and an initial volume) were numerically adjusted to minimize the chi-squared value. The parameters m₀ and dm were allowed to take any positive or negative value and no restriction was set on τ. Fig. 1 shows an example of the empirical fit for an SGLT1-expressing oocyte exposed to 5 mM αMG. These fitted curves provide a good match to the slightly noisy volume curves, without being influenced by brief (<10 s), spontaneous volume changes.

FIGURE 1.

Volumetric measurement of an SGLT1-expressing oocyte exposed to 5 mM α-methyl-glucose. Empirical fit (smooth line) of this experimental data (jagged line), using Eq. 2 with the following parameters: m₀ = −13 pl/s, dm = 72 pl/s, τ = 31.7 s, and initial volume = 0.901 μl.

For GLUT2-injected oocytes, since 2DG transport decreases over time, the volume curve did not simply accelerate to a steady-state swelling as was the case for channels and electrogenic cotransporters. Hence, we needed to use a different empirical function, where the cell swelling rate starts from an initial value, reaches a maximum, and progressively relaxes to a lower rate corresponding to a reduced, steady-state 2DG influx maintained by its continuous phosphorylation in the cytosol. We chose to describe this cell swelling rate by the addition of two Boltzmann equations as

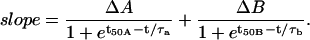(3)

With such an equation, the swelling rate can experience two transitions (ΔA and ΔB) centered at times t_50A and t_50B, and with time constants τ_a and τ_b. The second transition always resulted in a negative ΔB, corresponding to the low steady-state 2DG uptake rate (see Fig. 3). Note that this equation allows for a nonzero initial swelling rate.

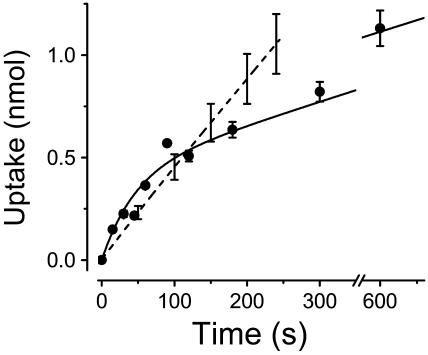
FIGURE 3.

Determination of 2-deoxyglucose (2DG) uptake by GLUT2-expressing oocytes. The solid circles represent the uptake of radio-labeled 2DG into GLUT2-expressing oocytes averaged over up to five different batches of oocytes. Error bars are shown for time points where the uptake represents at least four individual experiments. The smooth curve accompanying the 2DG uptake data is fitted to the data (see Appendix A). For comparison, the dashed line represents αMG transport into SGLT1-injected oocytes (n = 5) as obtained from the cotransport current integration divided by 2.

All numbers are given as mean ± SE with n corresponding to the number of experiments, unless otherwise stated. The experiments were always done using oocytes from at least two different donors.

All of the analysis and calculations were performed using Matlab 5.3.1 software (The Math Works, Natick, MA), except for the empirical volume curve optimizations which were done using Origin 6.1 (OriginLab Corporation, Northampton, MA).

RESULTS

Osmotic gradients generated by cation influx

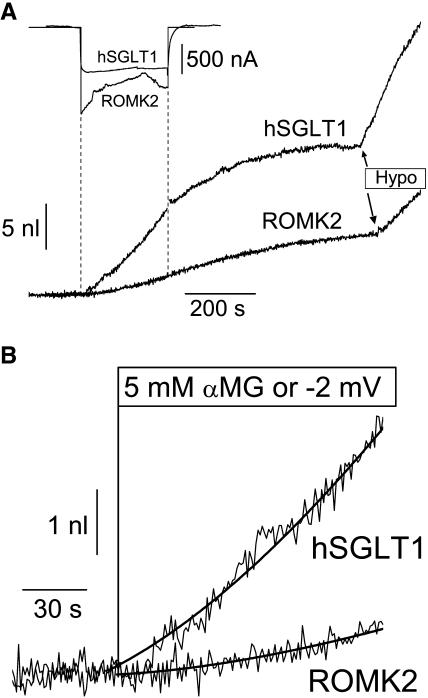
The water flux activated by Na⁺/glucose cotransport was first compared to the osmotic water flux generated by a cationic inward current of similar amplitude using the ROMK2 potassium channel. Fig. 2 A depicts typical experiments with ROMK2- and SGLT1-expressing oocytes. For comparable currents (SGLT1 and ROMK2 currents averaged 880 ± 120 nA and 950 ± 90 nA, respectively), SGLT1 activation clearly generates a much larger initial water flux (Fig. 2 B). As can be seen from the effects of a20-mOsm hypotonic shock (Fig. 2 A), oocytes expressing SGLT1 also display a larger apparent water permeability (L_p, 6.8 ± 0.9 × 10⁻⁴ cm/s, n = 5) versus ROMK2-expressing oocytes (2.5 ± 0.1 × 10⁻⁴ cm/s, n = 5), the L_p values of which are quite similar to the values reported by this laboratory for noninjected oocytes, L_p^control = 2.12 ± 0.14 × 10⁻⁴ cm/s (n = 21, Duquette et al., 2001). This difference in L_p values is taken into account when a local osmolality gradient (Δπ) is calculated by comparing the rate of volume change during current stimulation to the rate of cell swelling induced by a 20 mOsm hypotonic gradient. Normalizing to a standard 1 μA inward current, comparison of the calculated osmotic gradient at t = 30 s indicates that 5.3 ± 1.5 mOsm (n = 5) is required to explain the swelling rate of SGLT1-expressing oocytes whereas the transport-related water influx into ROMK2-expressing oocytes only corresponds to a gradient of 1.5 ± 0.3 mOsm (n = 5). This confirms previous observations used to support the contention that the osmotic gradient generated by a given ionic influx is unable to explain the fast initial cell swelling associated with a similar current through SGLT1. Assuming that the current electrode is not injecting a significant amount of osmolytes (see Discussion), the cation entry would be expected to account for two-thirds of the osmolyte accumulation observed after stimulating a cotransport of 2 Na⁺ ions for one αMG molecule. Analysis of the present series of experiments indicates that the cation uptake can account for only 29 ± 10% of the osmotic gradient needed to explain the water flux observed at 30 s for the SGLT1 cotransporter. This would leave a dominant portion of the cotransport-associated water flux to be explained by either glucose accumulation or water cotransport.

FIGURE 2.

Comparative volumetric analysis between hSGLT1-expressing and ROMK2-expressing oocytes. (A) Comparison of long time-course experiments, including an hypotonic shock of −20 mOsm/kg at the end of each experiment. (B) Enlarged depiction of early events in volume changes. The water flow at 30 s of transport was determined from the slope of the empirical fit. For these specific experiments, the water permeabilities were 6.13 × 10⁻⁴ cm/s for the SGLT1-, and 2.38 × 10⁻⁴ cm/s for the ROMK2-expressing oocyte. The osmotic pressures deduced from their swelling at t = 30 s are, after normalization to a standard 1 μA current, 6.8 mOsm and 1.7 mOsm for SGLT1 and ROMK2, respectively.

Osmotic gradients specifically generated by a glucose influx

A similar approach can be used to compare the water influx generated by activation of either the Na⁺/glucose cotransporter or the facilitated glucose transporter. The hepatic form of the glucose transporter, GLUT2, was chosen for its high expression level in oocytes. To make a significant water fluxes comparison, glucose uptakes through GLUT2 must be similar to those through SGLT1. Since 2-DG transport by GLUT2 is not electrogenic, isotopic uptake measurements were first performed on a large number of GLUT2-expressing oocytes (Fig. 3, solid circles with error bars represent the average and SE of 4–5 individual assays performed as described in the Material and Methods section). The mean 2DG uptake after 30 s is 0.23 ± 0.02 nmol per oocyte (n = 4). This initial uptake rate would be equivalent to a Na⁺/glucose cotransport current of 1500 nA. The uptake rate then relaxes to 0.07 nmol/min after 3–4 min, equivalent to a 225 nA cotransport current in the steady-state period. This period is believed to correspond to the condition where the rate of 2DG entry matches that of intracellular 2DG phosphorylation (Colville et al., 1993; Gould et al., 1991). In comparison, the present series of SGLT1-expressing oocytes averaged a cotransport current of 880 ± 120 nA (n = 5) so that, as shown in Fig. 3, the amount of sugar uptakes through SGLT1 and through GLUT2 are similar at t = 120 s.

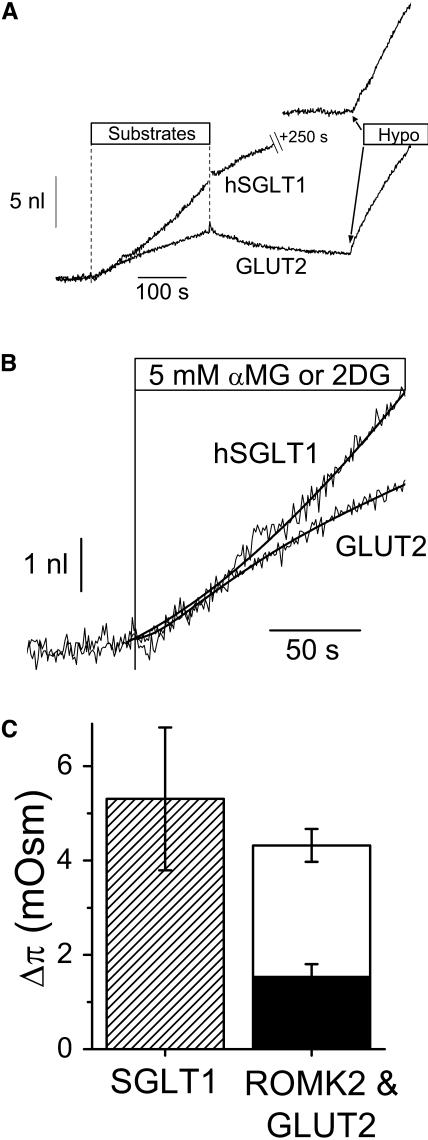
The cell swelling corresponding to 2DG uptake was surprisingly fast (see Fig. 4 A and B). In the first min of transport, the cell swelling observed for GLUT2-expressing oocytes is comparable to that for SGLT1-expressing oocytes and is much larger than the swelling observed in ROMK2-expressing oocytes (Fig. 2 B).

FIGURE 4.

Comparative volumetric analysis between SGLT1- and GLUT2-expressing oocytes. (A) Transport was stimulated for 250 s by the addition of 5 mM αMG or 5 mM 2DG for SGLT1- and GLUT2-expressing oocytes, respectively. An hypotonic shock of −20 mOsm/kg is imposed at the end of each experiment to determine the L_p value. (B) Enlargements of the volume changes presented in A. The water flows after 30 s of transport were determined from the slopes of the empirical fits (smooth lines shown in B) . For these specific experiments, the water permeabilities were 6.13 × 10⁻⁴ cm/s for the SGLT1-, and 6.97 × 10⁻⁴ cm/s for the GLUT2-expressing oocyte; and the osmotic pressures deduced from their swelling at t = 30 s and normalized for the equivalent of a 1 μA cotransport current are 6.8 mOsm and 3.4 mOsm, respectively. (C) Osmotic pressures determined from the ratios between swelling at 30 s and initial slope of the hypotonic shock (n = 5, 5, and 9, for SGLT1, ROMK2, and GLUT2, respectively). The osmotic pressures were normalized for an equivalent 1 μA cotransport current at t = 30 s (which, for GLUT2, corresponds to 2× the 2DG uptake multiplied by the Faraday constant of 96,490 Coul × mol⁻¹). The mean ROMK2 value (solid bar) accounts for 29 ± 10% of the SGLT1 value and the mean GLUT2 value (unfilled bar) accounts for 52 ± 16% of the SGLT1 value.

As described for ROMK2, the size of the transport-generated osmotic gradient can be calculated by using the hypotonic cell swelling recorded in each experiment, followed by normalization for a 1 μA equivalent cotransport current. At 30 s, this calculation yields an effective osmotic pressure of 2.8 ± 0.2 mOsm, compared to 5.3 ± 1.5 mOsm for SGLT1. Glucose accumulation could therefore explain 52 ± 16% of the osmotic pressure observed 30 s after the triggering of Na⁺/glucose cotransport current, which is larger than the one-third proportion expected from the stoichiometry of this cotransport. Fig. 4 C summarizes the comparison between the osmotic gradients estimated at t = 30 s for SGLT1, GLUT2, and ROMK2 after normalizing transport rates to 1 μA (or 5 pmol/s for 2DG uptake using the 2:1 stoichiometry of SGLT1). At t = 30 s, addition of the separate contributions from cations and sugar uptakes can account for 81 ± 19% of the osmotic gradient needed to explain the water flux associated to stimulation of Na⁺/glucose cotransport without having to invoke a secondary active mechanism.

DATA ANALYSIS

The analysis presented so far for a single time point of 30 s takes advantage of the fact that the initial uptake rates for oocytes expressing SGLT1, ROMK2, or GLUT2 were of similar amplitudes. This analysis cannot be carried over time as the time course of 2DG uptake differs somewhat from the rather stable Na⁺/glucose cotransport rate and the slowly declining ROMK2-mediated K⁺ current. An interesting alternative analysis is to compute the effective local concentration reached not as a function of time but as a function of the amount of solute transported for each type of expressing oocyte.

The actual local concentration of a transported solute (i.e., the concentration that is felt by the membrane) is distinct from the effective Δπ inasmuch as the latter also includes a global intracellular dilution due to the measured amount of water uptake. As water fluxes are not identical for ROMK2-, GLUT2-, or SGLT1-expressing oocytes, the diluting effect of each water influx must be separately taken into account to estimate the true amounts of Na⁺, glucose, or K⁺ accumulated. As water enters the oocyte (generating a volume increase of ΔV), it has a predictable diluting effect (Δosm) which is given by Eq. 4 as a function of the initial accessible volume V_acc and the initial internal osmolarity osm_in (assumed to be 197 mOsm). Once this volume is increased to V_acc + ΔV, simple conservation calculations lead to the decrease in osmolarity of

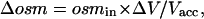(4)

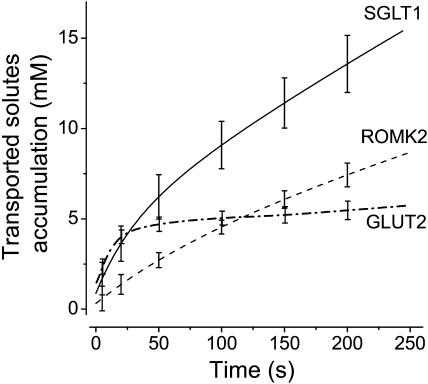
given that ΔV ≪ V_acc. The accessible fraction of the volume was chosen as 0.4, in accordance with the data of Zeuthen et al. (2002) and with data from tritiated water experiments from our own laboratory (data not shown). The volume-time curve from the fitted equations described previously was used to obtain ΔV at any time. For example, at t = 30 s, the correction Δosm is minimal and amounts to 0.27 ± 0.1 mM, 0.05 ± 0.03 mM, and 0.34 ± 0.07 mM for SGLT1, ROMK2, and GLUT2, respectively. At t = 60 s, the correction is more substantial and amounts to 0.75 ± 0.20 mM, 0.14 ± 0.05 mM, and 0.80 ± 0.15 mM for SGLT1, ROMK2, and GLUT2, respectively. When these corrections are incorporated into the results, the real accumulation of transported substrates as a function of time can be calculated (accumulation (t) = Δπ(t) + Δosm (t)) for oocytes expressing the three proteins studied (Fig. 5). It is interesting to see that, in the case of GLUT2, the concentration of transported osmolytes reaches 4 mM within the first 30 s before experiencing a much slower steady-state rate for the remainder of the experiment duration. This is what one would expect from a facilitated transporter exposed to 5 mM external 2DG and presenting an uptake rate that rapidly declines to 15% of its initial rate as seen in Fig. 3. This provides a good support to the assumptions made and to the accuracy of the intracellular concentration calculations based on volume measurements.

FIGURE 5.

Corrected solute accumulation as a function of time for SGLT1 (full line, n = 5), ROMK2 (dashed line, n = 5), and GLUT2 (dash-dotted line, n = 9). The corrections, when added to the osmotic gradients obtained from swelling rates, compensate for the global dilution due to water entry and are applied to each individual experiment before averaging.

Integration of the inward current observed in each experiment yields the uptake-time curves of K⁺ for ROMK2 and of Na⁺ (or αMG) for SGLT1. To compare the accumulations at any time, a continuous estimation of 2DG uptake in GLUT2 oocytes was also needed. The time course of 2DG uptake by GLUT2-expressing oocytes is relatively simple. The initial uptake rate is fast and progressively relaxes to a slower, linear uptake, the slope of which reflects the steady-state phosphorylation rate of intracellular 2DG. The experimental data could be fitted (Fig. 3, smooth curve) to a theoretical equation obtained from the analysis of such an uptake mechanism (see Appendix A). This fit is then used as the uptake/time curve for the volume experiments with GLUT2.

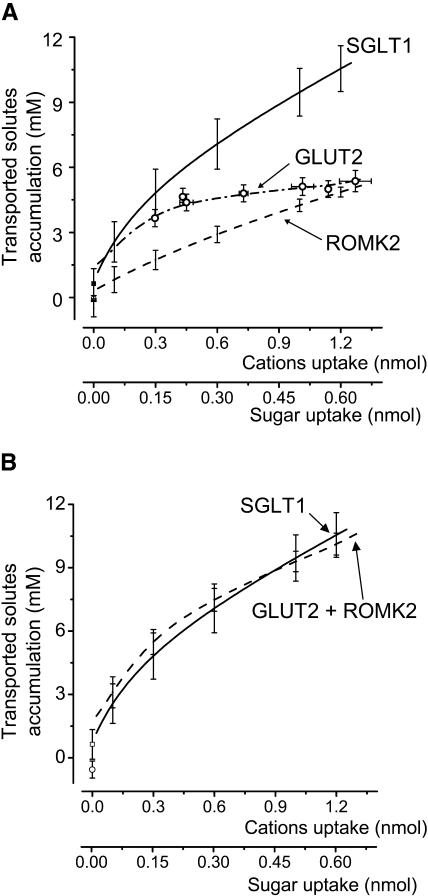
Using the uptake-time curves obtained for SGLT1-, ROMK2-, and GLUT2-expressing oocytes, the time axis of Fig. 5 can be transformed into an uptake axis as shown in Fig. 6 A . Since all oocytes did not express at the same level, this relation was calculated for each experiment and averaged afterwards using predetermined uptake points. It is apparent that 2DG accumulation is ∼2–3× larger than K⁺ accumulation in the initial phase (K⁺ uptake < 0.6 nmol), but becomes progressively similar as uptake continues to increase. Addition of the separate contributions from K⁺ and 2DG (Fig. 6 B) gives rise to a complete reconstruction of the total Na⁺ and αMG accumulation needed to explain the swelling of SGLT1-injected oocytes. It is clear that, throughout the uptake range studied, the effective concentration of the solutes transported by SGLT1 can be accounted for by the ion accumulation predicted by ROMK2-expressing oocytes and the sugar accumulation predicted by GLUT2-expressing oocytes.

FIGURE 6.

(A) Effective transported osmolyte concentrations as a function of the quantity of substrate transported for SGLT1 (n = 5, full line), ROMK2 (n = 5, dashed line), and GLUT2 (n = 9, dotted line and open circles). The values at zero uptake are obtained with linear regressions over the minute preceding the onset of transport. (B) Addition of the substrate accumulations from GLUT2 and ROMK2 (dashed line, open circle) reproduces the substrate accumulation calculated from SGLT1 experiments (continuous line, open square).

DISCUSSION

In 1996, SGLT1 was proposed to generate a secondary active water flux (Loo et al., 1996) as was previously proposed for the KCl cotransporter of the choroid plexus (Zeuthen, 1991, 1994). Water flux through SGLT1 was particularly interesting as the high level of expression in Xenopus oocytes allowed for the simultaneous measurement of cotransport current and of oocyte volume with high sensitivity. The oocyte expression system first revealed that the Na⁺/glucose cotransporter has a significant water permeability. For example, in a precedent series of experiments, L_p = 2 × 10⁻⁴ cm/s was obtained for native oocytes whereas L_p = 4 × 10⁻⁴ cm/s was obtained for hSGLT1-expressing oocytes (Duquette et al., 2001). This water permeability, however, stays much smaller than that of aquaporine-expressing oocytes, which averages 43 ± 2 × 10⁻⁴ cm/s (Zeuthen et al., 2001). Although the L_p of a single AQP molecule is estimated to be 10–40× larger than the L_p of SGLT1 (Duquette et al., 2001; Wright and Loo, 2000), the passive water permeability of SGLT1 may serve an important role if the lower water permeability of SGLT1 can be compensated by a higher density of this cotransporter versus the AQP1 channel. The small intestine is a good example of a tissue presenting a high density of SGLT1 in the virtual absence of aquaporin (Ma and Verkman, 1999). In the original and subsequent publications proposing a water pump activity for SGLT1 (Loo et al., 1996; MacAulay et al., 2001; Meinild et al., 1998; Zeuthen et al., 1997, 2001), the most significant observation supporting the presence of a water cotransport in addition to the osmotically-driven passive water flow was the fact that a pure ionic current of amplitude similar to the cotransport current was completely ineffective in generating any significant water transport within the first minute of transport.

In the present study, we confirm that the cell swelling induced by SGLT1 is much faster than the cell swelling induced by the stimulation of an inward cationic current. By measuring L_p in each experiment, it was possible to show that the difference in swelling rates was not simply due to the larger L_p value of SGLT1 over that of ROMK2. Our analysis has also shown that the accumulation of an osmotic gradient was truly slower for ROMK2- than for SGLT1-expressing oocytes. In the case of ROMK2, a period of at least 30 s is needed to detect a significant osmotic gradient, which is not the case for SGLT1 (see Fig. 2 B). This confirms the original observation that a cationic flux is significantly less efficient than a cotransport current in generating an early water flux. We aimed at completing this observation by comparing the volume increase induced by the transport of a neutral osmolyte to that induced by SGLT1. If water is cotransported through SGLT1, then the onset of SGLT1-dependent water transport should occur sooner than the water flux related to the combined neutral solute and ionic fluxes. Experimental observations showed that the water flux triggered by GLUT2 was fast and comparable in amplitude to the water flux associated with SGLT1 (Fig. 4 B). Further analysis shows that, when added to the water flux expected from a cationic current, the water flux associated with glucose transport through a facilitated transporter can quantitatively explain the entire water flux associated with SGLT1 (Fig. 6).

How could glucose accumulate faster than accompanying cations?

The comparison of the water flux induced by glucose accumulation in GLUT2-expressing oocytes to the flux associated with cation transport in ROMK2-expressing oocytes suggests that, for similar transport rates, glucose can locally accumulate much faster than K⁺. This can be explained by at least two processes. First, in aqueous solutions, glucose has a diffusion coefficient (D = 0.60 × 10⁻⁵ cm²/s) that is 2.3-fold smaller than that for NaCl (D = 1.39 × 10⁻⁵ cm²/s) and ∼2.8-fold smaller than for KCl (D = 1.68 × 10⁻⁵ cm²/s) (Macey, 1980). This implies that, for a given transport rate, Na⁺ should accumulate at the inner face of the plasma membrane much more slowly than would glucose. Second, during ion influx through the plasma membrane, electroneutrality must be respected at all times. If it is assumed that the steady-state cell swelling achieved by an SGLT1-expressing oocyte exposed to αMG for several minutes reflects isotonic water transport, it can be estimated that the cotransport of one glucose molecule corresponds to the net uptake of 2.6–3.3 osmolytes (Table 2 in Zeuthen et al., 2002). This indicates that, for 2 Na⁺ ions entering through the plasma membrane, the current electrode will absorb one cation from the cytosol and inject one anion from the electrode resulting in the net uptake of one glucose and two other osmolytes. As current is injected at the plasma membrane and at the tip of the electrode, it is not straightforward to predict where the osmolality should accumulate. Locally, when a Na⁺ ion (or a K⁺ ion) is transported through the plasma membrane of an oocyte, it will have to either repel another cation or attract an anion. Measurements with ion-selective microelectrodes in Xenopus oocytes yield the following intracellular ionic activities: 9 mM Na⁺, 76 mM K⁺, and 24 mM Cl⁻ (Cougnon et al., 1996). Hence, as the cytosolic ion pool is generally composed of K⁺ and negatively charged proteins, it can be expected that intracellular anions will be less mobile than intracellular cations. The preferential displacement of positive charges (mostly K⁺) away from the plasma membrane should reduce the capacity of cation influx in generating local osmotic gradients. In other words, when a cation influx is generated at the plasma membrane, an equivalent current is injected at the current electrode and “salt” will accumulate either at the plasma membrane or at the current electrode site, depending on the relative mobilities of cytosolic cations and anions. As time progresses during a stimulated cation influx, the osmolyte accumulation generated around the current electrode will reach the plasma membrane and will add its contribution to the local osmotic gradient, which would explain the water flux that can be detected only after 30–60 s. Interestingly, assuming an intracellular diffusion coefficient of 0.2 × 10⁻⁵ cm²/s (see below), half of the osmolytes will have diffused by >150 μm in 60 s (Macey, 1980). If the distance between the electrode tip and the membrane was 150 μm, this simple diffusion process would explain the delay observed between the onset of an ionic current and the detection of its associated water flux.

Why couldn't GLUT2 be considered as a water cotransporter?

GLUT2-activated 2DG transport can reproduce the early cell swelling triggered by Na⁺/glucose cotransport (Fig. 4, A and B). It could be argued that this passive glucose transporter may also function as a molecular water pump. Activation energies of 14.1 ± 1.2 kcal mol⁻¹ and 13–16 kcal mol⁻¹ were reported for glucose transport into human erythrocytes (Hu et al., 2000) and for the passive water permeability through GLUT1, respectively (Iserovich et al., 2002; Zeidel et al., 1992). This would be consistent with important conformational changes associated with these activities. If GLUT2 could act as a water pump, a fixed stoichiometry between sugar uptake and the amount of water accompanying it would be expected. With time, as osmotic gradients are building up, the apparent stoichiometry tends to increase toward isotonicity, which is ∼280 water molecules per osmolyte. If one compares volume flow to 2DG uptake rate (Figs. 3 and 4), the apparent stoichiometry would go from 35 to 310 in the first min of transport and would reach 700 water molecules per 2DG at t = 200 s before slowly relaxing to 280 for a few long experiments lasting up to 900 s (data not shown). As discussed above, this is not consistent with a 2DG/water cotransporter with a fixed stoichiometry. This is, however, expected from a facilitated 2DG transporter which generates a significant osmotic gradient in the first 30–60 s and then continues to stimulate a passive water uptake even after the 2DG transport rate has decreased to a low steady-state level.

Is this consistent with an intracellular diffusion model?

Our lab has recently challenged the water cotransport hypothesis (Duquette et al., 2001; Lapointe et al., 2002a,b), using a simple model where the required osmotic gradient could be generated with a low diffusion coefficient averaging 0.11 ± 0.03 × 10⁻⁵ cm²/s (Duquette et al., 2001) and an oocyte-accessible space of 85%. More recently, new experimental data has indicated that only 40% of the oocyte volume is accessible (Zeuthen et al., 2002). Given that, in our model, a reduced accessible space has the same global effect as a low diffusion coefficient, this new estimate of the accessible space would permit the required diffusion coefficient to be as high as ∼0.23 × 10⁻⁵ cm²/s, which is ∼40% of the diffusion coefficient of glucose in free solution. This number can be considered as a rough estimate of the intracellular diffusion coefficient for an “average” intracellular osmolyte. Given that water entering the cell will dilute not only the transported osmolytes but also all intracellular osmolytes present, concentration gradients will be established for different solutes. The goal of the proposed model was to explain the transport-dependent cell swelling with a minimal number of adjustable parameters. As the accessible space was set and the apparent osmotic permeability of each oocyte was measured, the model was able to explain the glucose-dependent cell swelling for a 600 s experimental period followed by a 600 s recovery using only two adjustable parameters (intracellular diffusion coefficient and number of osmolytes per transported charge). Given the observations in this study, it is clear that a diffusion model should minimally include distinct diffusion coefficients for glucose and for a representative salt composed of Na⁺ or K⁺ and the most abundant and mobile intracellular anion. In addition, the osmolality associated with the cation influx should be distributed between the plasma membrane and the tip of the current electrode located at a certain distance from the membrane. If a diffusion model with two parameters was able to reproduce the cell swelling associated with Na⁺/glucose cotransport, it is clear that a more realistic model involving four or five adjustable parameters should perform even better. But this increased number of parameters would also decrease the relevance and simplicity of the model without changing our conclusions.

CONCLUSION

The observation that activation of Na⁺/glucose cotransport produced an initial rate of cell swelling much larger than did an equivalent cationic influx was one of the strongest pieces of experimental evidence supporting the hypothesis of water cotransport by SGLT1. In the present study, a complete comparison is presented between the cell swelling observed for a cationic flux, a glucose influx, and a Na⁺/glucose cotransport. When analyzed in terms of the capacity of each transport pathway to generate an osmotic gradient at the plasma membrane, it was found that the osmotic gradient required to explain the water flux associated with Na⁺/glucose cotransport can be quantitatively accounted for by adding the effects of a cationic flux to the effect of neutral solute transport. The initial water influx (t < 45s after induction of Na⁺/glucose cotransport) can be largely explained by glucose accumulation whereas the contribution of Na⁺ (and its associated intracellular anion) would become dominant only after ∼100 s of cotransport.

APPENDIX A

Uptake of 2DG by GLUT2-expressing oocytes

The mechanism of 2DG uptake into Xenopus oocytes can be separated into two distinct steps: entry of 2DG molecules through GLUT2 uniporters (rate constant k₁), and their phosphorylation by hexokinase (rate constant k₂). The change in cytosolic, unphosphorylated 2DG is described by the equation

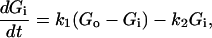(A1)

where G_i and G_o are, respectively, the cytosolic and external unphosphorylated 2DG concentrations. The rate of change in phosphorylated 2DG (concentration P) is simply

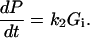(A2)

Assuming that P = 0 initially, solving this pair of equations yields the following result for total 2DG uptake,

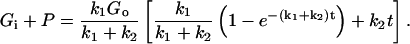(A3)

It is this total quantity of 2DG that is detected in uptake measurements and which is osmotically active in volumetric experiments. Since this type of analysis describes concentration changes after enzymatic reactions without spatial considerations, it cannot be strictly applied to the uptake of the 2DG molecules into a certain intracellular accessible volume which might change with time. Therefore, 2DG uptake (Upt) was fitted using Eq. A4 which contains three parameters (A, τ, and p₂) instead of two, as

(A4)