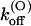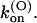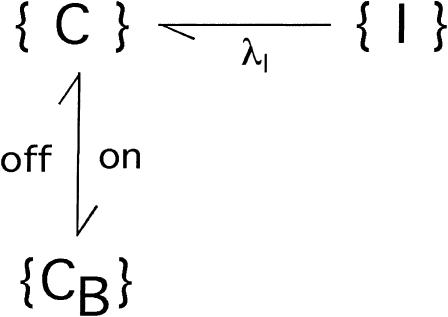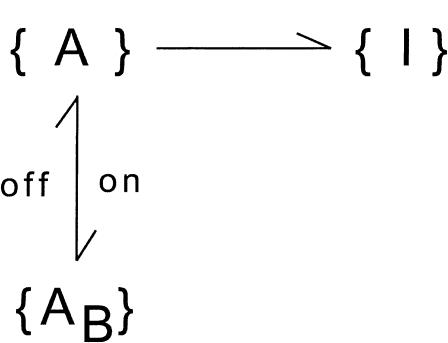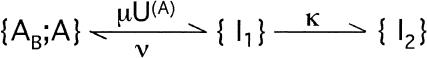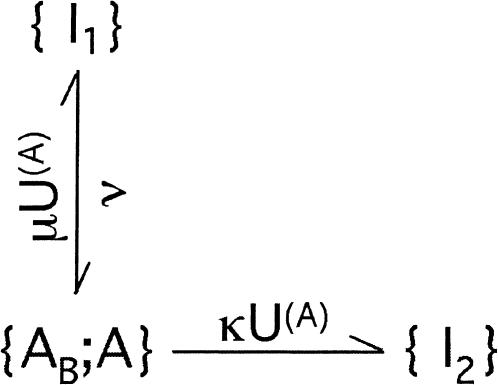Abstract
κ-Conotoxin PVIIA (κ-PVIIA), a 27-amino acid peptide identified from the venom of Conus purpurascens, inhibits the Shaker K+ channel by blocking its outer pore. The toxin appears as a gating modifier because its binding affinity decreases with relatively fast kinetics upon channel opening, but there is no indication that it interferes with the gating transitions of the wild-type channels (WT), including the structural changes of the outer pore that underlie its slow C-type inactivation. In this report we demonstrate that in two outer pore mutants of Shaker-IR (M448K and T449S), that have high toxin sensitivity and fast C-type inactivation, the latter process is instead antagonized by and incompatible with κ-PVIIA binding. Inactivation is slowed by the necessary preliminary unbinding of κ-PVIIA, whereas toxin rebinding must await recovery from inactivation causing a double-exponential relaxation of the second response to double-pulse stimulations. Compared with the lack of similar effects in WT, these results demonstrate the ability of peptide toxins like κ-PVIIA to reveal possibly subtle differences in structural changes of the outer pore of K+ channels; however, they also warn against a naive use of fast inactivating mutants as models for C-type inactivation. Unfolded from the antagonistic effect of inactivation, toxin binding to mutant noninactivated channels shows state- and voltage-dependencies similar to WT: slow and high affinity for closed channels; relatively fast dissociation from open channels at rate increasing with voltage. This supports the idea that these properties depend mainly on interactions with pore-permeation processes that are not affected by the mutations. In mutant channels the state-dependence also greatly enhances the protection of toxin binding against steady-state inactivation at low depolarizations while still allowing large responses to depolarizing pulses that relieve toxin block. Although not obviously applicable to any known combination of natural channel and outer-pore blocker, our biophysical characterization of such highly efficient mechanism of protection from steady-state outer-pore inactivation may be of general interest.
INTRODUCTION
Polypeptide toxins from predatory marine cone snails that interact with ion channels have been a useful tool for investigating channel structure and function. κ-Conotoxin PVIIA (κ-PVIIA), a 27-amino acid peptide from the venom of Conus purpurascens, is the first member of a new family of conotoxins blocking voltage-gated K+ channels. The physiological role of κ-PVIIA in the venom appears to be involved in the extremely rapid immobilization of the fish prey (Terlau et al., 1996). The analysis of the block of Shaker K+ channels by κ-PVIIA showed that it binds to the extracellular mouth of the pore (Shon et al., 1998), and a mutant cycling analysis revealed the amino acids important for this interaction (Jacobsen et al., 2000). It was also shown that toxin binding is strongly dependent on the conductive state of the channel, likely because it is destabilized by the occupancy by K+ of an outer pore site that is favored by channel opening (Terlau et al., 1999). The fairly fast kinetics and the lower affinity of κ-PVIIA binding to open channels can explain in full detail the effects of the toxin on the time course of Shaker-mediated potassium currents without assuming any modification of the existing gating transitions. This is consistent with the idea that activation and fast N-type inactivation involve structural changes of the inner pore (for review see Yellen, 1998) and do not have large allosteric consequences extending to the outer pore region.
“C-type” inactivation, a slow process named after the finding that it proceeds at very different rates in splice variants of the C-terminal third of Shaker proteins (Hoshi et al., 1991), is believed to involve structural changes of the outer vestibule and/or of the outer end of the pore (see Yellen, 1998). Supporting this idea, several single point mutations in the putative outer pore region have been reported to enhance and hasten C-type inactivation and the mutant channels have been used as models for a better understanding of this process (Hoshi et al., 1991; Lopez-Barneo et al., 1993). Another feature consistent with the outer pore location of the C-type inactivation machinery, as opposed to that of N-type process, is that it is antagonized by extracellular tetraethylammonium ions (TEA) (Choi et al., 1991). The antagonism of extracellular TEA for the slow inactivation of the delayed rectifier Kv1.3 in T-lymphocytes provided indeed the first evidence of a distinct outer-pore-related potassium channel inactivation (Grissmer and Cahalan, 1989). Also the fast C-type inactivation of outer-pore mutants can be antagonized by TEA (Yang et al., 1997; Molina et al., 1998). Therefore, expecting the antagonism for outer-pore-related inactivations to be a common feature of strong outer pore blockers, we were surprised to confirm the recent report by Naranjo (2002) that κ-PVIIA has no obvious effect on the C-type inactivation of Shaker channels deprived of the fast inactivation by an N-terminal deletion (Shaker-IR; Hoshi et al., 1990). To gain more insight to this unexpected finding we studied the effects of κ-PVIIA on two Shaker-IR mutants known to have faster and stronger inactivation. M448K and T449S were chosen for this study because, together with fast C-type inactivation (Goldstein et al., 1994; Schlief et al., 1996; Meyer and Heinemann, 1997; Chen et al., 2000), they both exhibit high toxin sensitivity, whereas the affinity of κ-PVIIA to other tested inactivation-modified mutants (D447E, T449Q, T449Y, and T449K) is very low (Shon et al., 1998; Jacobsen et al., 2000). We report here that the inactivation of these mutants is drastically changed by κ-PVIIA binding as if the two processes were mutually exclusive: toxin-liganded channels must lose their ligand before being able to inactivate and, vice versa, inactivated channels cannot bind the toxin. When properly unfolded from the antagonistic effect of inactivation, the properties of toxin binding to noninactivated mutant channels appear otherwise very similar to those of WT channels (Terlau et al., 1999), further supporting the idea that they depend mainly on interactions with pore-permeation processes that are not affected by the mutations.
The different interaction of κ-PVIIA with the inactivating transitions occurring in WT or mutant channels suggest that κ-PVIIA is a very sensitive probe of the outer pore structure of Shaker channels and, if the same basic mechanism is assumed, they impose strong constraints on its possible modeling. As a corollary of our study we show that the antagonism of κ-PVIIA with the inactivation of mutant channels, combined with the state-dependence of toxin binding, afford a particularly strong effect of toxin-protection against steady-state inactivation. Although described here for κ-PVIIA and an artificial channel phenotype, this mechanism may be relevant for the biological effects of other κ-PVIIA-like substances on natural channels with strong outer-pore inactivation.
MATERIALS AND METHODS
The solid-phase peptide synthesis of κ-PVIIA was performed as described in Shon et al. (1998). Point mutations in the pore region of Shaker-Δ6-46 (Hoshi et al., 1990) were introduced by PCR mutagenesis and the amplified sequences were confirmed by sequencing. Capped cRNA was synthesized in vitro after linearizing the plasmid with HindIII and the transcription with T7 RNA polymerase was performed by a standard protocol.
Oocytes from Xenopus laevis were prepared as described previously (Stühmer, 1992). RNA was injected into stage V–VI oocytes and currents were recorded 1–7 days after injection. Whole-cell currents were recorded under two-electrode voltage clamp control using a Turbo-Tec amplifier (NPI Electronic, Tamm, Germany). The intracellular electrodes were filled with 2 M KCl and had a resistance between 0.5 and 1.0 MΩ. Current records were low-pass filtered at 1 or 5 kHz (−3 dB) and sampled at 4 or 20 kHz. The bath solution in the electrophysiological experiments was normal frog Ringer's (NFR) containing (in mM): 115 NaCl, 2.5 KCl, 1.8 CaCl2, and 10 HEPES, at pH 7.2 (NaOH). Leak and capacitive currents were corrected on-line using a P/N method. In all experiments the vitelline membranes of the oocytes were removed mechanically with fine forceps. Toxin solution was added to the bath chamber by using a Gilson tip pipette. The indicated toxin concentrations correspond to the final concentration in the bath chamber.
Off-line analysis of current records was performed using custom-software within IGOR (Wavemetrics). The affinity of κ-PVIIA binding to closed channels was estimated from the reduction of the early currents in response to step depolarizations, and the binding kinetics were unfolded from the recovery of the steady-state features of the second response to a double-pulse stimulation for increasing interpulse durations (see Results). The on and off rates of κ-PVIIA binding to open M448K channels which are in the range of the inactivation kinetics were unfolded from the latter by fitting the double-exponential relaxation of the currents elicited by fully activating voltages under the assumption that the two processes are sequential (see Results). The much faster relaxation rates of κ-PVIIA binding to open T449S channels were estimated from the apparent delay in the activation of blocked channels, whereas the asymptotic probability of open-channel unblock was independently estimated from the slowing of the late phase of inactivation (see Results).
RESULTS
κ-PVIIA appears as a gating-modifier of Shaker mutants with fast C-type inactivation
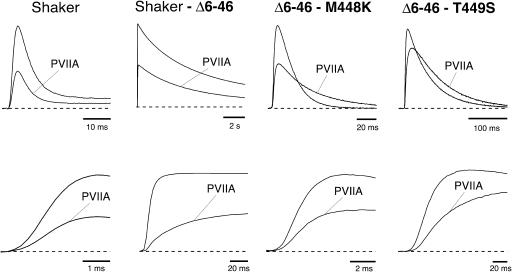
Fig. 1 shows whole cell currents in response to voltage steps to 0 mV recorded from Xenopus oocytes expressing either the wild-type or three different mutants of Shaker channels. The N-terminal deletion (Shaker-Δ6-46, henceforth simply called Shaker-Δ) is known to deprive the channels of the main, fast inactivation process (Hoshi et al., 1990); the other two mutants (Δ6-46-M448K and Δ6-46-T449S, henceforth simply called M448K and T449S) contain additional point mutations in the pore region that confer to these constructs a much faster C-type inactivation (Goldstein et al., 1994; Schlief et al., 1996; Meyer and Heinemann, 1997; Chen et al., 2000). The upper panels display the responses on a timescale appropriate to show the different inactivation processes that occur in the various phenotypes, whereas the early onset of the same responses is shown in the lower panels on expanded timescales. The labeled traces in Fig. 1 show the responses obtained from the same oocytes after the addition to the external bath of either 100 nM κ-PVIIA (Shaker, M448K) or 250 nM κ-PVIIA (Shaker-Δ, T449S). For comparison, all traces are scaled to yield the same peak amplitude of controls.
FIGURE 1.
Effect of κ-PVIIA on the potassium currents mediated by wild-type and mutant Shaker channels. Each panel shows the superposition of responses to 0 mV steps obtained from the same oocyte before and after the external addition of κ-PVIIA at concentrations of 100 nM (panels 1 and 3) or 250 nM (panels 2 and 4). For better comparison currents are adjusted to show control records with similar peak amplitudes at two different timescales. (From left to right) Wild-type Shaker channels (Shaker); channels deprived of fast inactivation by the 6-46 N-terminal deletion (Shaker-Δ6-46); channels with the additional point mutation M448K (Δ6-46-M448K); or with the additional T449S mutation (Δ6-46-T449S). (Upper panel) Notice that the toxin slows drastically the relatively fast C-type inactivation of M448K and T449S, but has no similar effect on either the N-type inactivation of WT-Shaker or the C-type inactivation of Shaker-Δ6-46. (Lower panel) At an expanded timescale it becomes obvious that the apparent effects on the activation are similar for all phenotypes.
By focusing on the rising phase of currents (lower panels) it is seen that the addition of the toxin has qualitatively similar effects on the apparent activation of K+-currents for all phenotypes: there is an early stronger inhibition that decreases at later times, causing a delay in the time to peak that is barely appreciable for WT, more evident for M448K and T449S, and most obvious for Shaker-Δ, where the reversal of toxin block is much slower than channel activation and not blurred by inactivation processes having comparable kinetics. In a previous work (Terlau et al., 1999) it was shown that the delayed rise of Shaker and Shaker-Δ currents is due solely to the state-dependence of κ-PVIIA binding. At normal extracellular K+ concentrations, [K]o = 2.5 mM, κ-PVIIA binds with high affinity (IC50 ∼ 50 nM) to the outer vestibule of the pore (Terlau et al., 1996, 1999; Shon et al., 1998, Garcia et al., 1999; Jacobsen et al., 2000) blocking the early conduction of depolarized channels; however, the block is strongly relieved after channel opening because of the destabilizing action of intracellular potassium ions invading the pore. The similarity of the changes produced by κ-PVIIA on the apparent activation of M448K and T449S points to a same mechanism.
In contrast with the effects on the rising phase, the changes produced by κ-PVIIA on the inactivation of WT or mutant channels are substantially different. The upper panels of Fig. 1 show that neither the rate of N-type inactivation in Shaker nor the slow C-type inactivation of Shaker-Δ are significantly affected, whereas the decay of both M448K and T449S currents is drastically slowed, so that the initial block is reverted at later times in a current increase.
The slowing of M448K and T449S inactivation by κ-PVIIA mimics the effect of extracellular TEA on the slow inactivation of Kv1.3 (Grissmer and Cahalan, 1989) and Shaker-WT (Choi et al., 1991), and on the faster C-type inactivation of these and other outer pore mutants (Yang et al., 1997; Molina et al., 1998). Therefore, its most simple qualitative interpretation is that it arises from the antagonism of κ-PVIIA for conformational changes that affect its binding pocket in the outer vestibule of the K+-channel pore. However, particularly in view of the lack of a similar effect of κ-PVIIA on Shaker-Δ (Naranjo, 2002; and Fig. 1), we must rule out the alternative view that the binding of κ-PVIIA to inactivation-modified channels might cause additional modifications of the inactivation mechanism. This is done in the following by providing several lines of evidence that the binding of κ-PVIIA and the inactivated states of M448K and T449S channels are mutually exclusive. Because of the dependence of toxin binding on the state of channel conductance and of the fact that binding relaxations occur on a timescale comparable to that of channel gating, our analysis must also involve a careful characterization of such state-dependence and an unfolding of binding relaxations from activation and inactivation kinetics.
Equilibrium binding of κ-PVIIA to closed channels
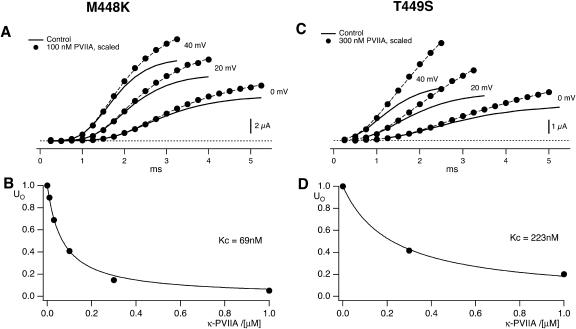
Fig. 2, A and C, show as solid lines the rising phase of the currents elicited by various step depolarizations from a holding potential of −100 mV in oocytes expressing M448K and T449S channels, respectively. Superimposed in the same figures are sample points (solid dots) of the responses to the same steps obtained after toxin addition to the bath (A: M448K, 100 nM κ-PVIIA; C: T449S, 300 nM κ-PVIIA) scaled by a step-independent factor of ∼2.5 that makes them match the early sigmoidal rise of the corresponding control records. An objective estimate of this factor was obtained from the best fit of the toxin currents, ITx, as the sum of two components, respectively proportional to the control currents, ICt, and to their time integral,
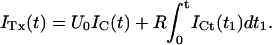 |
(1) |
For step voltages between 0 and 80 mV, the best fits (dashed lines) yielded U0 values scattered by <15% around a mean value of 0.4, whereas the R-values increased with voltage by almost an order of magnitude (from 13 to 100 s−1 for M448K; from 100 to 850 s−1 for T449S). As discussed in Appendix, Eq. 1 describes in first approximation the early currents expected from the fraction U0 of channels that is initially unblocked and yields a normal contribution to the potassium currents (first term in the right member) and from the linear component of the toxin-binding relaxations occuring after channel activation and being characterized by a much higher and steeply voltage-dependent dissociation rate (Terlau et al., 1999).
FIGURE 2.
Steady-state binding of κ-PVIIA to the closed state of M448K and T449S channels. (A) The solid lines show the rising phase of M448K currents elicited by steps to 0, +20, and +40 mV from a holding potential of −100 mV under control conditions; the solid dots are sampled points of similar responses after the addition of 100 nM κ-PVIIA, scaled by a factor of 2.5 to make them match the early rise of the control records. The dashed lines are equally scaled fits of the toxin records with Eq. 1, obtained for a fixed U0 = 0.41 and for R-values increasing from 13 s−1 at 0 mV to 38 s−1 at 40 mV. (B) Dependence of U0 on κ-PVIIA concentration, [T]. The solid line represents a fit using U0([T]) = 1/(1 + [T]/Kc) resulting in a dissociation constant for κ-PVIIA binding of 69 nM (see text). (C) Data of the same type as in A for T449S-mediated currents under control conditions and after addition of 300 nM κ-PVIIA. The dashed lines fitting toxin data to Eq. 1 were obtained for a fixed U0 = 0.42 and for R-values increasing from 95 s−1 at 0 mV to 290 s−1 at 40 mV. (D) Dependence of U0 on toxin concentration. The fit (solid line) corresponds to a dissociation constant for κ-PVIIA binding of 223 nM.
The interpretation of U0 as the fraction of toxin-free channels under resting conditions is further supported by its dependence on toxin concentration, [T]. U0 estimates obtained from the same experiment of Fig. 2 A for different [T] values are plotted in Fig. 2 B; and similar data for the T449S channels of Fig. 2 C are shown in Fig. 2 D. It is seen that in both cases the data are well fitted by binding isotherms containing a single dissociation constant, Kc, that we assume to govern the equilibrium of the 1:1 molecular association of κ-PVIIA with resting (closed) channels, as
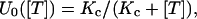 |
where our mean estimate of Kc from n = 43 measurements at [T] values in the range of 0.1 to 10 μM from n = 19 oocytes expressing M448K is Kc = 77 ± 4. From n = 16 measurements with [T] in the range of 0.25 to 10 μM on n = 10 oocytes expressing T449S we estimated Kc = 204 ± 11 nM (see Table 1).
TABLE 1.
Parameters of κ-PVIIA binding to open and closed states of Shaker-D, M448K, and T449S channels
| K(C) (nM) |
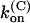 (μM−1 s−1) (μM−1 s−1) |
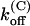 (s−1) (s−1) |
K(O)(0) (nM) |
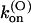 (μM−1 s−1) (μM−1 s−1) |
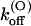 (0) (s−1) (0) (s−1) |
vs (mV) | |
|---|---|---|---|---|---|---|---|
| Sh-Δ | 48 ± 12* | 22 ± 4* | 1.1 ± 0.3* | 207 ± 50* | 132 ± 30* | 26 ± 5* | 41 ± 4* |
| M448K | 77 ± 4 (43) | 5.3 ± 0.2 (21) | 0.41 ± 0.13 (21) | 784 ± 284† | 37 ± 11 (10) | 29 ± 6 (10) | 53 ± 7 (10) |
| T449S | 204 ± 11 (16) | 14.9 ± 5.8 (8) | 3.2 ± 1.3 (8) | 1300 ± 50 (33) | 133 ± 5 (33) | 195 ± 10 (33) | 38 ± 2 (33) |
Kinetics of κ-PVIIA binding to closed M448K channels
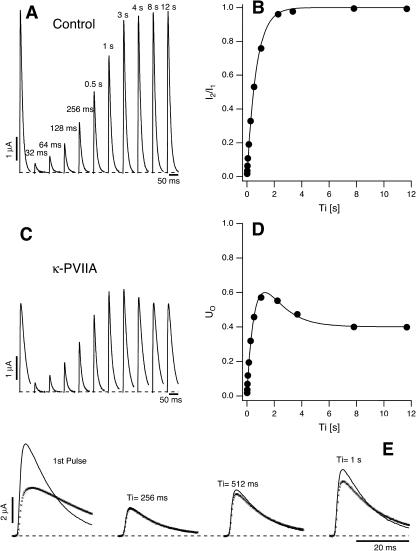
Double-pulse stimulation protocols provide a compelling evidence that the toxin-modified time course of the potassium currents through M448K channels is associated with toxin unbinding. The results of one such measurement are illustrated in Fig. 3. The stimulation protocol consisted of several double pulses, in which pulse P2 was applied after the interval Ti from the end of pulse P1, with Ti increasing from 8 ms to several seconds. Both P1 and P2 were pulses to +40 mV for 320 ms, during which the elicited currents decayed to insignificant levels both in control and under toxin application. Successive stimulations were separated by a pause of 8–12 s at the holding potential of −100 mV to allow full reestablishment of steady-state conditions. Fig. 3 A shows, for control conditions, the P1 record and a sample of P2 records for the indicated Ti values. For convenience of illustration, only the first 50 ms of each record are shown and the P2 records are shifted in time nonproportionally to Ti. Fig. 3 B shows a plot of the relative fraction of P2 currents as a function of Ti, which is well fitted by a single exponential with a rate constant, λI ≈ 1.41 s−1 (smooth line).
FIGURE 3.
Relaxation of κ-PVIIA binding to closed M448K channels revealed by double-pulse stimulation. (A) Currents elicited by double pulses to +40 mV with variable interpulse interval, Ti, from the holding potential of −100 mV under control conditions. The currents elicited by the first pulse, I1, are all superimposed; the responses to the second pulse, I2, for the indicated interpulses, are displayed with an arbitrary horizontal shift. (B) Normalized amplitude of the second response as a function of Ti for the data shown under A (solid circles). The single exponential fit corresponds to a rate constant for recovery from C-type inactivation, λI ≈ 1.41 s−1 (smooth line). (C) Currents measured from the same oocyte as in A using the same pulse protocol after addition of 100 nM κ-PVIIA. Notice the overshoot and the different inactivation kinetics of the currents elicited by the second pulse as compared to the first. (D) The fraction of active and unblocked channels, U0, measured from the second response under toxin by comparison with the first control response as in Fig. 2 A, is plotted as a function of Ti (solid circles). The smooth line is the best fit of the data according to Eq. 2 (see text). (E) Direct comparison of sampled current traces in control (continuous lines) and in 100 nM κ-PVIIA (dotted lines). Notice that after an interpulse period of 256 ms the response elicited by the second pulse in the two different conditions is almost identical; only for longer Ti the second response under toxin acquires progressively the smaller amplitude and the slower inactivation that characterize κ-PVIIA binding to the channels.
Fig. 3 C shows data analogous to those of Fig. 3 A obtained after the addition of 100 nM κ-PVIIA to the bath. In this case the time course of the recovery by the P2 responses of the steady-state P1 properties is more complex, showing in particular a clear overshoot of the amplitude for Ti > 0.5 s. Such nonmonotonic relaxation is more quantitatively described in Fig. 3 D by plotting as a function of Ti the fraction of activatable and unblocked channels estimated from the P2 responses as described for Fig. 2. These data are well fitted by a double-exponential function (smooth line), comprising an early rise with the same rate constant of the normal recovery from inactivation followed by a slower decay. It is obvious to suppose that the latter component reflects mainly the reblock by κ-PVIIA of channels that were freed from toxin binding during the conditioning depolarization: at the holding potential of −100 mV, while an increasing number of channels recovers from inactivation, their block probability increases toward the tonic level (∼60% in this experiment). This is further confirmed by a closer inspection of the P2 responses for relatively small Ti. Fig. 3 E shows that, in contrast with the large difference in amplitude and shape of the P1 responses, the P2 responses before and after toxin application are almost identical for Ti = 256 ms and become clearly distinguishable only for Ti = 0.5 and 1 s. Thus, pulse P1 appears to set all channels in the same initial conditions independently of the presence of κ-PVIIA. This result implies that P1 causes a complete dissociation of the toxin, whose rebinding lags behind the recovery of the channels from inactivation. This provides a sensitive method for studying the kinetics of the binding reaction.
Terlau et al. (1999) showed that in Shaker channels the recovery from N-type inactivation and the rebinding of κ-PVIIA could be simply unfolded by assuming their independence, supporting the view that the toxin does not distinguish between different nonconducting states of the channels if the closed gate is on the intracellular side. Such assumption is clearly not tenable in the case of M448K channels: as shown by Fig. 3 E, the apparent rebinding estimated by normalizing the early P2 responses under toxin to those of control would show a fairly large and unaccountable delay. The double-exponential relaxation of Fig. 3 D can instead be accounted for by a simple kinetic scheme in which toxin binding is incompatible with inactivation and that comprises only three statistically significant states (see Scheme 3 in Appendix): an inactivated state, an unblocked state (activatable for conductance), and a toxin-liganded state (activatable, but unavailable for conductance). If we denote with λI the rate characterizing the single exponential recovery of activatable currents in toxin-free conditions, and with λR=off + on the rate of toxin binding relaxations, such scheme predicts that during repolarizations the fraction U(t) of channels available for conduction follows a double-exponential time course with decaying rates λI and λR, approaching asymptotically a resting value UC = off/(off + on). Even more stringently, for initial conditions in which the channels are all inactivated, it predicts that all four parameters that characterize the expression of U(t) are determined by the sole off and on binding rates according to (see Appendix)
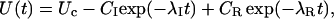 |
(2) |
with
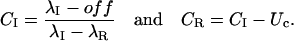 |
Confirming the above predictions, the smooth line in Fig. 3 D was obtained as the best fit of the data with Eq. 2 fixing λI to the value of control and allowing only on and off as free parameters, estimated as off = 0.3 s−1 and on = 0.42 s−1.
The above interpretation of the data of Fig. 3 implies that the inactive conformation of the channels is intrinsically incompatible with toxin binding. Although this assumption accounts in a simple way for the full dissociation of κ-PVIIA at the end of a long depolarizing pulse, the latter observation does not exclude that positive voltages are a major cause for the destabilization of toxin binding to inactivated channels and that inactivated channel-toxin complexes may have a significant probability in different conditions. The results of three experiments in which we tested double-pulse protocols with different pulse duration, Tp, argue against this idea. The P2 relaxations measured on the same oocyte for a fixed toxin concentration and for Tp = 10, 20, 40, or 160 ms were invariably well fitted by the same couple of (λI, λR) estimates, despite the fact that different Tp settings produced very different initial conditions (data not shown). This observation excludes the existence of inactivated and toxin-bound states, because these would produce in some conditions a significant third component in the relaxations.
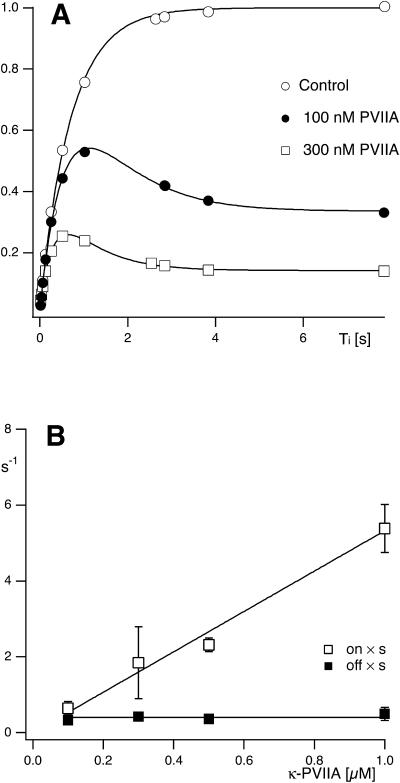
If the off and on estimates obtained from the fit with Eq. 2 according to Scheme 3 do indeed represent the rates of a simple bimolecular binding reaction, they should be more appropriately expressed in terms of the first-order dissociation and second-order association rate constants, koff and kon, respectively, as off = koff and on = kon × [T]. The [T]-dependence of off and on estimates agree with such interpretation. Fig. 4 A shows the results of one experiment in which the same oocyte was tested with double-pulse protocols before, during, and after successive exposures to 100 nM and 300 nM κ-PVIIA. The best fit of the recovery from inactivation in control conditions yielded in this experiment λI = 1.4 s−1; with this same λI value the data at 100 nM κ-PVIIA were best fitted with Eq. 2 for off = 0.35 s−1 and on = 0.69 s−1, whereas the data at 300 nM κ-PVIIA yielded off = 0.42 s−1 and on = 2.5 s−1, in fair agreement with the expectation of the same off and a threefold larger on. Fig. 4 B summarizes the results of several measurements of off and on binding rates as a function of [T] in the range of 100 nM to 1 μm. The overall data show that the on estimates are directly proportional to [T], whereas the off estimates are independent of [T], as expected if these rates do indeed describe a simple bimolecular binding reaction. From this analysis our best characterization of the binding of κ-PVIIA to the closed state of M448K channels estimates the first-order dissociation rate constant as koff = 0.41 s−1, and the second-order association rate constant as kon = 5.33 μM−1 s−1.
FIGURE 4.
The binding relaxation of κ-PVIIA to the closed state of M448K channels during double-pulse stimulations results from a bimolecular binding reaction. (A) Relative fractions of P2 responses as a function of Ti measured in the absence (Control) and in the presence of 100 nM (solid circles) or 300 nM (unfilled squares) κ-PVIIA. The double-pulse protocol consisted of 160-ms pulses with Ti between 16 ms and 8 s from a holding potential of −100 mV. For the control currents the smooth line corresponds to a single exponential fit resulting in a rate constant for recovery from C-type inactivation of λI = 1.4 s−1. The smooth lines for the toxin traces are obtained by using Eq. 2 and correspond to on = 0.69 s−1, and off = 0.35 s−1 for 100 nM κ-PVIIA and on = 2.5 s−1 and off = 0.42 s−1 for 300 nM κ-PVIIA. (B) Concentration dependence of on and off binding-rates of κ-PVIIA to closed M448K channels. The straight lines are fits of the data according to off = koff = 5.33 s−1 and on = kon × T, kon = 0.41 μM−1 s−1.
Kinetics of κ-PVIIA binding to closed T449S channels
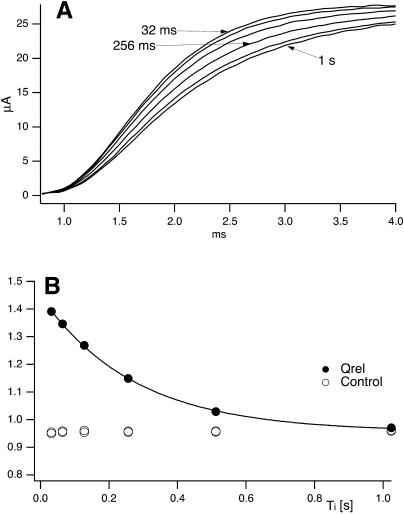
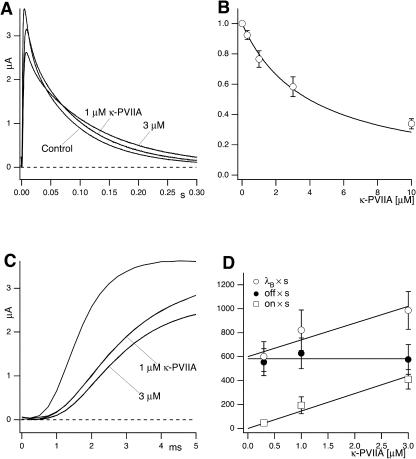
The recovery from inactivation of T449S channels is an extremely slow process that is complete only after >60 s (data not shown), so that for these channels we had to separate routinely any two successive stimulation epochs by 90-s repolarization intervals. This feature, and the fact that the kinetics of κ-PVIIA binding to open T449S channels are much faster than inactivation, spared us the trouble of unfolding the kinetics of κ-PVIIA binding to closed channels from that of recovery from inactivation. Using double-pulse protocols with relatively short pulses that induced a significant unblock but little inactivation we could monitor the recovery of the resting block within times, Ti, in the order of 1 s, during which there was no significant recovery from inactivation. As a monitoring parameter we used the integral, Q(Ti), of the current elicited by the second pulse. The mean charge carried by an initially toxin-free channel, qU, is larger than that carried by an initially blocked channel, qB, whose contribution to conductance is delayed by the open-channel unblock. Therefore, for NA activatable channels, of which NU(Ti) are toxin-free, we expect
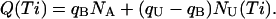 |
Fig. 5 shows the results from a double-pulse protocol with pulse durations of 4 ms and Ti values in the range of 32 ms to 1 s. In toxin-free conditions, the currents elicited by the second pulse for different Ti values were practically indistinguishable (not shown); Q(Ti) values normalized to the first pulse, shown in Fig. 5 B as unfilled symbols, were only slightly smaller than unity, indicating that the first pulse caused an inactivation of ∼4% that was not significantly reversed by repolarizations of <1 s. Quite differently, after addition of 150 nM κ-PVIIA the currents elicited by the second pulse were larger and faster for short Ti values and approached progressively the amplitude and shape of the first response for increasing Ti values (Fig. 5 A). The normalized Q(Ti) was ∼1.45 for a short interpulse and decreased with Ti toward a plateau level of 0.96 (Fig. 5 B, solid symbols); the data are well fitted by a single exponential with a time constant, τ = 260 ms. This behavior is most obviously explained by assuming that a substantial fraction of channels that are tonically blocked lose the toxin during the first pulse and that the effect is progressively reversed at longer repolarizations by the reequilibration of toxin binding to closed channels. Due to the linear relation between Q(Ti) and NU(Ti), the exponential decay of Q(Ti) implies a monoexponential relaxation of NU(Ti) and is consistent with such reequilibration involving a 1:1 molecular binding reaction. Accordingly, we interpret the data of Fig. 5 by relating the estimate of τ to the association and dissociation rate constants of that reaction, kon and koff, according to
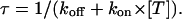 |
The same rates define the tonic probability of closed-channel unblock according to
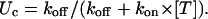 |
In the experiment of Fig. 5, the toxin-induced decrease of the early currents yielded an estimate of Uc = 0.58. Using τ and Uc estimates, the combination of the above two relations yields
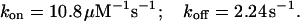 |
Mean values from eight such measurements on four different oocytes and for [T] values between 150 nM and 1 μM are given in Table 1.
FIGURE 5.
Recovery of tonic κ-PVIIA binding to closed T449S channels. (A) Superimposed records of P2 responses from double pulses (Vp = 40 mV, Tp = 4 ms) with variable pulse interval, Ti, in the presence of 150 nM κ-PVIIA. With increasing Ti the current onset of the P2 responses becomes slower, indicating an increasing fraction of initially blocked channels. The P2 response for Ti = 1 s was almost identical to the P1 response (not shown) which showed an early unblock probability, Uc = 0.58 by comparison with control. (B) Relative charge (QP2/QP1) as a function of interpulse interval in the absence of toxin (unfilled circles) and in the presence of 150 nM κ-PVIIA (solid circles). The solid line is a single-exponential decay with τ = 260 ms.
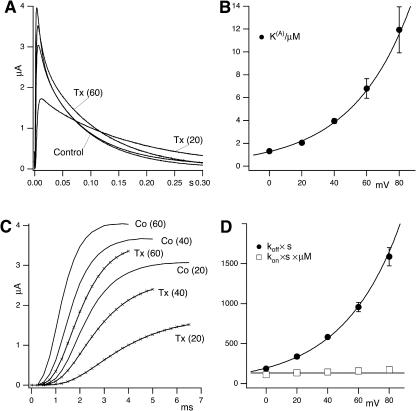
Relaxations of κ-PVIIA binding to open M448K channels
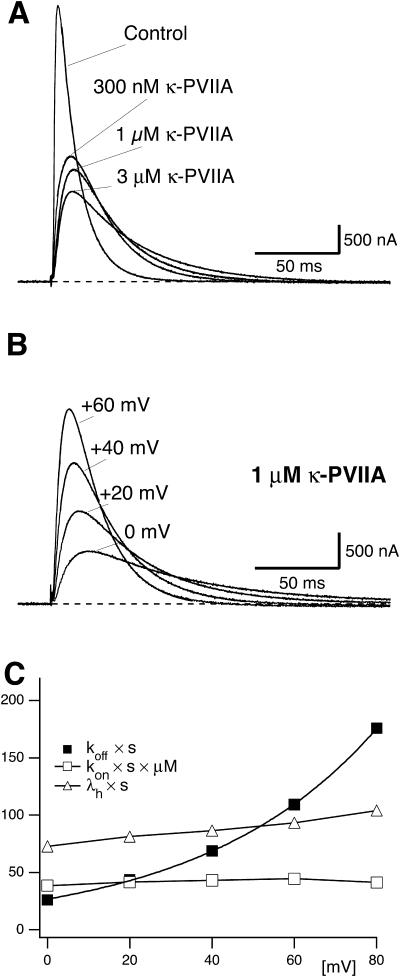
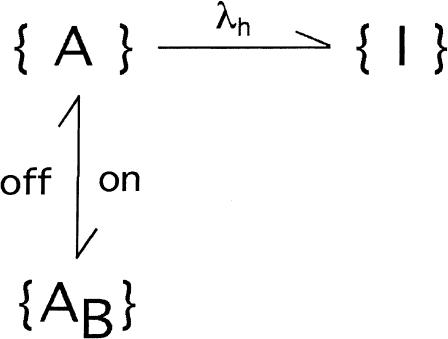
The above results show that a major effect of the gating transitions that occur during depolarizations is a decrease in the percentage of toxin-bound channels. When tested on M448K with long enough pulses this effect is seen to proceed until the complete dissociation of the toxin indicating that κ-PVIIA cannot bind to the inactivated conformation of the channels. However, the reduction of the initial block seen for both mutants soon after a depolarizing step (Fig. 2), and the fact that short pulses that produce very little inactivation cause a very significant unbinding (Fig. 5), also show that the activated conformations of our mutant channels have a much lower affinity for toxin binding, similarly to what has been reported for the WT-Shaker and Shaker-Δ6-46 (Terlau et al., 1999). Characterizing the relaxations of κ-PVIIA binding to open M448K, which are still largely occurring when the activation of these channels is already complete, merely requires unfolding them from the ongoing process of inactivation. Fig. 6 A shows the direct comparison of the currents elicited by a pulse of 40 mV, recorded in the same oocyte-expressing M448K channels, either in NFR (control) or after the addition of three different concentrations of κ-PVIIA, [T] = 300 nM, 1 μM, and 3 μM. It is clear that the changes of the time course of the currents produced by the toxin addition cannot be attributed to a modification of the gating of drug-liganded channels. In particular, the late decays are well fitted by single exponentials with time constants that increase with [T] from 11 ms in control to 40 ms in 3 μM κ-PVIIA, and there is no way to describe them as linear superpositions of “normal” and “modified” responses. The [T]-dependence of the slowing of inactivation is instead simply explained by the antagonism between toxin binding and inactivation, according to a simple three-state kinetic scheme,
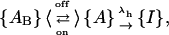 |
which assumes that an activated channel can undergo reversible transitions between toxin-free and toxin-blocked states, {A} and {AB}, before sinking into the inactivated state {I}. If the kinetics of toxin-binding relaxations are comparable to those of inactivation, this scheme predicts a double-exponential time course for the currents carried by channels in state {A}, and the solid lines that fit the records of Fig. 6 A are consistent with such prediction.
FIGURE 6.
Concentration and voltage-dependence of κ-PVIIA binding relaxations to open M448K channels. (A) Effect of κ-PVIIA on M448K currents elicited by +40 mV pulses. Current traces resulting from pulses to +40 mV in the absence (Control) and presence of 300 nM, 1 μM, or 3 μM κ-PVIIA in the external solution. Increasing toxin concentration leads to a reduction in peak currents and to an increased slowing of the inactivation. The solid lines, almost indistinguishable from raw data, are either a monoexponential fit of the inactivation decay for t > 2 × tpeak (Control), or double-exponential fits of the biphasic time course of toxin records in the same time interval. The time constants for the late inactivation are: Control, 11.7 ms; 300 nM κ-PVIIA, 21.3 ms; 1 μM κ-PVIIA, 26.7 ms; and 3 μM κ-PVIIA, 40.3 ms. The dashed line corresponds to 0 currents. (B) M448K-mediated currents upon stimulation to 0, +20, +40, and +60 mV from a holding potential of −100 mV in the presence of 1 μM κ-PVIIA. Notice the increase in the rate of inactivation at higher test voltages. Data are from the same oocyte of Fig. 6 A. The dashed line corresponds to 0 currents. (C) Voltage-dependence of the rate-constants characterizing inactivation and κ-PVIIA binding to open M448K channels. (Unfilled triangles) Inactivation rate of control currents, λh × s. (Unfilled squares) Second-order association rate-constant, kon × μM × s. (Solid squares) First-order dissociation rate-constant, koff × s. The kon and koff estimates were obtained by unfolding toxin-binding relaxations from inactivation as described in the text. λh and kon data are connected by simple line segments. The thicker line through koff data is a least-squares fit with the function koff (V) = koff(0) × exp(V/vs). The kon data do not show any systematic voltage-dependence and have a mean value of 42 μM−1 s−1.
Consistently with this interpretation we can use the values of the rate constants, λf and λs, which describe the double-relaxation of the currents, together with that of the unmodified rate of inactivation, λh, to obtain estimates of the on and off rates according to the relations (see Appendix)
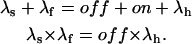 |
A stringent test of the validity of the above interpretation is that these estimates should vary with [T] as the rates of a simple bimolecular association reaction, off coinciding with the [T]-independent first-order dissociation rate-constant, koff, and on being the product of [T] × the second-order association rate-constant, kon. The fits of the toxin traces of Fig. 6 A, spanning a 10-fold range of κ-PVIIA concentrations, were all obtained by a least-squares iterative procedure with the fitting rates, λf and λs, determined by
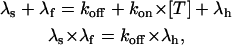 |
and allowing only koff and kon as free kinetic parameters. For the experiment of Fig. 6 A, λh = 85 s−1 was determined by the fit of the control trace (solid line) and the best fit of all the currents recorded for the three toxin concentrations were obtained for koff = 70 s−1 and kon = 38 μM−1 s−1.
As reported for the case of WT channels, the binding of κ-PVIIA to open M448K channels is strongly voltage-dependent. Fig. 6 B shows records of the responses to pulse voltages, V, of 0, 20, 40, and 60 mV, obtained from the same oocyte of Fig. 6 A for [T] = 1 μM. In toxin-free solution the same pulses elicited currents (not shown) with a late rate of inactivation, λh, that increased only little with V (Fig. 6 C, triangles). In contrast, at increasing voltages the records of Fig. 6 B show a much faster decay, with both peak values and inactivation rates approaching control levels (not shown). This indicates that at increasing depolarizations toxin unbinding is both favored and hastened, as expected if both effects arose mainly from an increase in the rate of toxin dissociation. The solid lines fitting the data of Fig. 6 B are least-squares with double-exponentials, from which koff and kon estimates were obtained as described above. Confirming the above qualitative argument, kon estimates (Fig. 6 C, unfilled squares) were found fairly insensitive to voltage, with a mean value of 42 μM−1 s−1 for 0 ≤ V ≤ 80 mV, whereas koff estimates had a strong voltage-dependence, which is well described in the same voltage-range by an exponential increase as
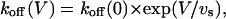 |
(3) |
with koff(0) = 27 s−1 and vs = 43 mV. Therefore, within the accuracy and the range of our present measurements, the most comprehensive description of the binding of κ-PVIIA to open M448K channels involves the specification of only three experimental quantities: kon, koff(0), and vs. Means and standard deviations of the estimates of these quantities obtained from n = 10 experiments are shown in Table 1.
κ-PVIIA binding to open T449S channels
Fig. 7 illustrates the effect of different concentrations of κ-PVIIA on the currents elicited by pulses to +40 mV in oocytes expressing T449S channels. On a timescale of several hundred ms (Fig. 7 A), the toxin appears to decrease by a comparable extent both the peak current and the rate of inactivation, as if it acted as a fast blocker of activated channels that antagonizes at the same time their transition to inactivated states. According to this interpretation, the toxin/control ratio of the late inactivation rates, 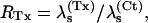 would provide a direct estimate of the open-channel unblock probability, U(A). A slight complication of such analysis arises from the fact that, as reported by others (Meyer and Heinemann, 1997; Chen et al., 2000), the inactivation of T449S channels is double-exponential, with a fast contribution to the total relaxation increasing from 10 to 50% between 0 and 80 mV. Luckily, however, the two most plausible alternative models for the C-type inactivation of T449S, involving two inactivation steps, lead to the same expected relationship between U(A) and RTx (see Appendix),
would provide a direct estimate of the open-channel unblock probability, U(A). A slight complication of such analysis arises from the fact that, as reported by others (Meyer and Heinemann, 1997; Chen et al., 2000), the inactivation of T449S channels is double-exponential, with a fast contribution to the total relaxation increasing from 10 to 50% between 0 and 80 mV. Luckily, however, the two most plausible alternative models for the C-type inactivation of T449S, involving two inactivation steps, lead to the same expected relationship between U(A) and RTx (see Appendix),
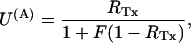 |
where F is a correction factor that depends on the intrinsic properties of T449S inactivation. It also turns out (see Appendix) that the estimates of F, ranging between 0.34 and 0.77 for 0 ≤ V ≤ 80 mV, are independent of the model used for the analysis of control currents.
FIGURE 7.
Dose-dependence of the effect of κ-PVIIA on T449S currents. (A) Current responses elicited by step-depolarizations to +40 mV in toxin-free conditions (Control) and in presence of 1 μM or 3 μM κ-PVIIA in the external solution. Increasing toxin concentration, [T], leads to a progressive reduction in peak currents and slowing of the inactivation. The decay phase of the control record is fitted by a double-exponential function with slow and fast rates, λs = 12.2 s−1 and λf = 111 s−1; the fitted rates of the dominant slow component of the toxin records are 10.6 s−1 for [T] = 1 μM and 8.1 s−1 for [T] = 3 μM. (B) Estimates of the unblock probability of activated channels at 40 mV, U(A), derived from the decrease of λs values (see text), are plotted as a function of [T]. The solid line is the best fit of the data with the function U(A) = K(A)/(K(A) + [T]) with an apparent dissociation constant K(A) = 3.95 μM and n = 14 at 0.3, 10 at 1, 6 at 3, and 3 at 10 M. (C) Comparison of the early phases of the current responses shown in A; the delayed onset of the currents in the presence of 1 and 3 μM κ-PVIIA is fitted by the convolution of control activation and toxin-binding relaxation according to Eq. 4 (see text). The fitted binding-relaxation rates are: 1 μM, λB = 610 s−1 and 3 μM, λB = 820 s−1. (D) [T]-dependence of estimated toxin-binding kinetics at +40 mV. (Unfilled circles) λB estimates from the delay of early currents. (Solid circles) The off rate estimated as the product of λB × the unblock probability, U(A), derived from the slowing of inactivation as in A and B. (Unfilled squares) The on rates estimated as λB × (1 − U(A)). The straight lines are best fits according to λB = koff + kon × [T], with off = koff, on = kon × [T], koff × s = 600 ± 40 s−1, and kon = 140 ± 30 μM−1 s−1. Data is given as mean ± SD; n = 14 at 300 nM, 10 at 1 μM, and 6 at 3 μM.
Fig. 7 B shows a plot of U(A) estimates at 40 mV, obtained from the above relationship in 33 RTx measurements from 19 oocytes at κ-PVIIA-concentrations in the range of 0.3–10 μM. In agreement with the interpretation of U(A) as an unblock probability in a simple 1:1 block-reaction, the data are well fitted by the simple function U(A)([T]) = K(A)/(K(A) + [T]) with an apparent dissociation constant K(A) = 4.0 μM.
An alternative and independent way of assessing the properties of κ-PVIIA binding to activated T449S channels involves the analysis of the toxin effect on the rising phase of the currents mediated by this mutant. As shown in Fig. 7 C, at μM concentrations the toxin inhibits almost completely the early rise of control currents but allows a delayed increase of channel conductance that approaches values comparable to control already at times when there is still little normal inactivation. Interpreting this delayed current rise as the result of channel unblock after activation, we can unfold the two processes without having to cope with the additional process of inactivation. As shown in Appendix, disregarding inactivation and assuming that activation is not affected by toxin binding, the toxin-modified currents, ITx, are expected to be described by
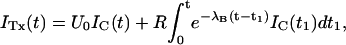 |
(4) |
where IC is the corresponding control current; the first term represents the contribution by channels that are initially unblocked; and the convolution integral represents the fact that the activation of blocked channels is converted into an actual opening through the “filtering” of the toxin-binding relaxation with single-exponential rate λB.
The solid lines through the toxin traces of Fig. 7 C were obtained as least-squares fits according to Eq. 4. The most important parameter of these fits is the binding relaxation rate λB. As expected for a simple 1:1 binding reaction, this rate should be linearly dependent on toxin concentration according to
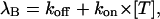 |
where λB estimates at 40 mV are plotted as a function of toxin concentration in Fig. 7 D (unfilled circles). The fair linear fit of these data according to the above relationship yields as kon and koff estimates at 40 mV: koff = 600(±40 s−1 ) and kon= 140(±30) μM−1 s−1.
As a test of the overall validity of our analysis, we verify that the ratio koff/kon yields an estimate for the dissociation constant of κ-PVIIA binding to activated T449S channels, K(A) = 4.3 μM, that is in close agreement with the above K(A) estimate of 4.0 μM, obtained from the slowing of inactivation. Finally, as a further test for consistency, Fig. 7 D also shows plots of direct estimates of on and off rates obtained as off = λB × U(A) and on = λB × (1 − U(A)). It is seen that these off estimates do not depend significantly on [T] and have a mean value very close to the above koff estimate, whereas on estimates are directly proportional to [T] with a slope that is close to the above kon estimate.
As for the case of M448K the binding of κ-PVIIA to open T449S channels is strongly voltage-dependent, which also makes the apparent modification of T449S currents by κ-PVIIA very sensitive to voltage. Fig. 8, A and C, show raw data, for V = 20, 40, and 60 mV, from an experiment testing the effect of 10 μM κ-PVIIA. In Fig. 8 A it is seen that both the slowing of inactivation (whose kinetics are fairly voltage-independent in control) and the decrease of the peak currents are very pronounced at 20 mV but relatively small at 60 mV. Similarly, Fig. 8 C shows also that the delay on the current rise is much smaller at higher voltages. These features are quantitatively described by performing the kind of detailed analysis described in Fig. 7 for different voltages. Fig. 8 B shows a plot of mean K(A) estimates and Fig. 8 D shows plots of koff and kon estimates as a function of voltage. The line through the K(A) data of Fig. 8 B is a least-squares fit with the equation
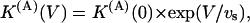 |
with K(A)(0) = 1.3 μM and vs = 36 mV. A similar voltage-dependence fits the koff data of Fig. 8 D,
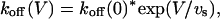 |
with koff(0) = 195 s−1 and a voltage slope factor vs = 38 mV. Finally, kon estimates show no significant voltage-dependence, the line through these data corresponding to a constant kon = 135 μM−1 s−1. Notice again the consistency of koff/kon and K(A) estimates.
FIGURE 8.
Voltage-dependence of κ-PVIIA binding to open T449S channels. (A) T449S-mediated currents upon stimulation to +20 and +60 mV from a holding potential of −100 mV in the absence and presence of 10 μM κ-PVIIA. The inactivation kinetics in control conditions are fairly voltage-independent (20 mV, λs = 11.9 s−1 and 60 mV, λs = 12.2 s−1), whereas the slowing of inactivation by κ-PVIIA is much more pronounced at lower voltages (20 mV, λs = 6, 8 s−1 and 60 mV, λs = 9.7 s−1). (B) Voltage-dependence of the dissociation constant of κ-PVIIA binding to open T449S channels, estimated as in Fig 7 A. The solid line is the best fit of the data to K(A) = K(A)(0) × exp (V/vs) with K(A)(0) = 1.3 (±0.05) μM and vs = 36 (±2) mV (n = 33). (C) Early phase of the currents in A on an expanded timescale. Notice that the delay in the currents elicited in the presence of κ-PVIIA is strongly decreased at higher test potentials, indicating a faster unbinding of the toxin. (D) Estimates of koff and kon, obtained as described in Fig. 7 D, are plotted against test potential. The solid line through koff data is the best fit to koff = koff(0) × exp (V/vs) with koff(0) = 195 (±10) s−1 and vs = 38 (±2) mV. The straight line through kon data corresponds to kon = 133 (±5) μM−1 s−1. Data are given as mean ± SD; the n for the different test voltages was between 15 and 33.
Thus, like for the other phenotypes, we conclude that κ-PVIIA binding to activated T449S channels can be fully described by only three independent parameters: kon = 135 μM−1 s−1; koff(0) = 195 s−1; and a voltage slope factor, vs = 38 mV. Also in this case the voltage-dependence of toxin binding to open channels is entirely afforded by koff.
The blocker κ-PVIIA can act as a conductance enhancer
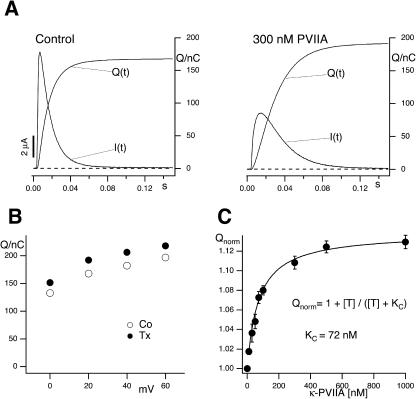
An interesting consequence of the antagonism between κ-PVIIA binding and inactivation is that toxin-blocked channels, by losing the toxin before inactivating, allow the same flow of charge as toxin-free channels. Thus, for long depolarizations that cause full inactivation we expect that the total charge flowing in the presence of the toxin should not be reduced. Fig. 9 shows that this prediction is verified: the integral of the current, Q, passed by M448K channels before being fully inactivated, is not reduced by the presence of the toxin. On the contrary, for Vp ≥ 0 mV the measured value of Q is slightly increased in the presence of κ-PVIIA (Fig. 9 A) by a percentage amount independent of Vp (Fig. 9 B). The mean ratio, QTx/QCt, of toxin to control Q-values for 0 ≤ Vp ≤ +60 mV is plotted as a function of toxin concentration in Fig. 9 C. It is seen that at increasing toxin concentrations the percentage of excess charge, QTx/QCt −1, approaches an upper value of ∼12% following the dose-response curve expected if the effect was correlated to κ-PVIIA binding with a dissociation constant of 72 nM, close to our estimate of the IC50 of κ-PVIIA block of closed channels. Similar results for the mutant T449S showed an asymptotic excess charge of 23% approached at high κ-PVIIA concentrations according to an apparent dissociation constant of ∼300 nM (data not shown). A simple explanation of these observations is that toxin-complexation protects from inactivating transitions that can occur in a toxin-free channel from preopen states. The low rate of κ-PVIIA dissociation from closed states makes toxin-liganded channels avoid such “silent” activation-inactivation because they are subject to inactivation only after losing the toxin in a conductive configuration.
FIGURE 9.
κ-PVIIA does not decrease Shaker-M448K-mediated currents. (A) M448K-mediated currents and the corresponding charge values evoked by stimulations to +40 mV from a holding potential of −100 mV before (Control) and after addition of 300 nM κ-PVIIA. (B) Plot of the charge against test potential for Vp ≥ 0. (C) Ratio of toxin to control charge values for Vp ≥ 0 as a function of toxin concentration. The presence of κ-PVIIA leads to a charge increase of ∼12% at higher toxin concentrations. The solid line corresponds to a dose response curve with an IC50 of 72 nM. Data are given as mean ± SE; the n for the different toxin concentrations was between 10 and 43.
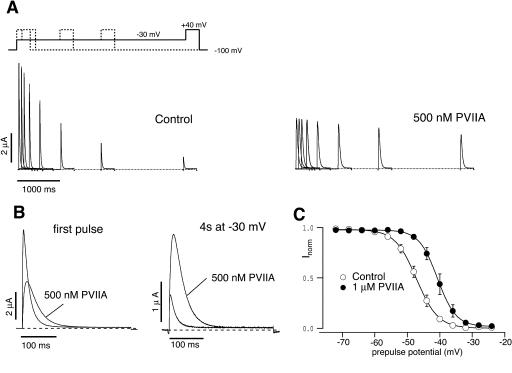
Consistently with its preferential antagonism for silent inactivating transitions, κ-PVIIA exerts a particularly strong protection from inactivation at mild depolarizations during which the channels dwell more in partially activated states. Fig. 10 illustrates such phenomenon for an oocyte expressing M448K channels and exposed to conditioning depolarizations to −30 mV of increasing duration. Although test responses in control conditions show a progressive inactivation with a time constant of ∼1.9 s (Fig. 10 A, left panel), the addition of 500 nM κ-PVIIA slows that process by a factor of ∼7 (Fig. 10 A, right panel), showing a toxin-binding antagonism with an IC50 of ∼80 nM matching that estimated for κ-PVIIA binding to closed channels (Table 1). The peculiar feature of such protection is that, due to κ-PVIIA unbinding from open channels and at variance with the effect of a state-independent blocker, the slowing of inactivation is not accompanied by a comparable reduction of the responses to the test depolarizations. Fig. 10 B shows the direct comparison of control and toxin responses before and after a conditioning period of 4 s. It is seen that the conditioning depolarization reduced the response in control to 12%, whereas it still allowed a response with 33% of the normal peak and 76% of the normal charge in the presence of κ-PVIIA. Fig. 10 C shows that, in addition to slowing the process, κ-PVIIA can also efficiently protect M448K channels from steady-state inactivation. Inactivation curves, plotting the total charge carried by the channels in response to test pulses of 40 mV after conditioning prepulses of 60 s to variable potentials, VPP, are shown for control conditions (unfilled circles) or after application to the bath of 1 μM κ-PVIIA (solid symbols). The data (mean ± SE, n = 3) show that 1 μM κ-PVIIA leads to a positive shift of the inactivation curve by only ∼6 mV (Control: V1/2 = −47.1 mV vs. −40.7 mV in 1 μM κ-PVIIA), but the resulting effect on the relative amplitude of control versus toxin responses in the range of −45 to −30 mV is very large.
FIGURE 10.
κ-PVIIA prevents cumulative C-type inactivation and shifts steady-state inactivation. (A) M448K-mediated currents elicited by a pulse to +40 mV after a variable conditioning period at −30 mV, in the absence (Control) or in the presence of 500 nM κ-PVIIA. The holding potential was −100 mV. (B) Comparison of the currents shown in A for no conditioning (first pulse) and after a conditioning period of 4 s. Notice the increase in current in the presence of toxin. (C) Steady-state inactivation curve of M448K channels without (Control) and with 1 μM κ-PVIIA in the bath solution. Normalized peak currents are plotted against prepulse potential. Cells were depolarized to +40 mV after being held for 60 s at different prepulse potential. Data are given as mean ± SE; n = 3. The solid lines correspond to a Boltzmann fit indicating that the presence of 1 μM κ-PVIIA leads to a shift in the V1/2 for inactivation of 6.4 mV.
DISCUSSION
In this study the binding of κ-PVIIA to pore mutants of the Shaker K+ channel with rapid C-type inactivation in the absence of N-type inactivation (Δ6-46) was investigated. It is shown that the association with κ-PVIIA causes strong modifications of the responses of these mutant channels, including a drastic slowing of their fast and complete inactivation. Our analysis demonstrates that, similarly to what has been described for WT channels by Terlau et al. (1999), the observed effects on the gating of activation are only apparent because they are indirectly caused by the dependence of toxin binding on the state of channel conductance, whereas the effects on inactivation do indeed involve a direct antagonism between this peculiar process of the studied mutants and toxin binding.
As in a previous study of WT- and Δ6-46-Shaker channels (Terlau et al., 1999), we obtained evidence that the delayed increase of toxin-modified currents is due to open-channel unblock from experiments with double-pulse stimulation protocols, showing that the response to the second pulse after relatively short intervals is similar to that of unmodified channels. For increasing interpulse durations, the progressive reestablishment of the toxin-modified properties of the second response was used to study the kinetics of κ-PVIIA binding to the closed state of M448K and T449S channels. The analysis turned out to be very simple for T449S channels, which have very fast κ-PVIIA binding kinetics in the open state and very slow recovery from inactivation. This allowed us to use short, almost noninactivating pulses, to induce a large toxin unblock during the first pulse, and follow by the second response the reestablishment of toxin binding equilibrium without contamination from the process of inactivation recovery. The case of M448K required a more complicated analysis, involving the unfolding of the two kinetically comparable processes of toxin rebinding and inactivation recovery. This analysis also provided evidence of the incompatibility between toxin binding and the inactivated conformation of these channels, a feature that for both mutants is most directly supported by the observation that κ-PVIIA binding protects from inactivation (see later Discussion).
We quantified the parameters of κ-PVIIA binding to the conductive state of our channels by analyzing the modified time course of the activation of K+ currents as a function of toxin concentration. Also for this analysis we had to use different approaches for the two mutants, because we found that the kinetics of open-channel binding to κ-PVIIA are comparable to those of inactivation in the case of M448K and almost as fast as activation for T449S.
As in the previous work with WT channels, the conclusions of our present studies are that:
κ-PVIIA binds to the modified outer pore vestibule of M448K and T449S channels according to a simple 1:1 bimolecular reaction, with reaction parameters that are very different depending on whether or not the channel is in a conductive state;
the binding of κ-PVIIA to closed channels is characterized by higher affinity and slower kinetics; and
the binding of κ-PVIIA to open channels is characterized by a second-order association rate constant,
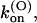 that is fairly voltage-independent and by a first-order dissociation rate constant,
that is fairly voltage-independent and by a first-order dissociation rate constant, 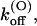 having an e-fold increase for every voltage increase, vs, of ∼40 mV.
having an e-fold increase for every voltage increase, vs, of ∼40 mV.
Thus, the full characterization of κ-PVIIA binding requires the five parameters: 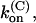
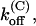
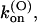
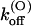 (0), and vs. The comparison between the estimates of these parameters for the mutants of our present study and previous WT estimates is shown in Table 1.
(0), and vs. The comparison between the estimates of these parameters for the mutants of our present study and previous WT estimates is shown in Table 1.
For M448K, 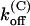 and
and 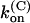 values are smaller than for Shaker-Δ6-46 channels by a factor of 2.7 and 4.2, respectively, yielding only a slightly lower sensitivity of this mutant to κ-PVIIA. Since the M448K mutation introduces four positive charges in the pore region and the toxin is positively charged, the small reduction of both the association and dissociation rates suggests that the side chain of residue M448 does not enter in very close contact with any of the charged toxin groups and likely occupies a water-exposed position in the outer rim of the pore. In the open state the mutant channel appears to offer a similarly increased hindrance to the association of κ-PVIIA, with a
values are smaller than for Shaker-Δ6-46 channels by a factor of 2.7 and 4.2, respectively, yielding only a slightly lower sensitivity of this mutant to κ-PVIIA. Since the M448K mutation introduces four positive charges in the pore region and the toxin is positively charged, the small reduction of both the association and dissociation rates suggests that the side chain of residue M448 does not enter in very close contact with any of the charged toxin groups and likely occupies a water-exposed position in the outer rim of the pore. In the open state the mutant channel appears to offer a similarly increased hindrance to the association of κ-PVIIA, with a 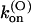 ∼3.6× lower than wild-type, whereas the estimated values of
∼3.6× lower than wild-type, whereas the estimated values of 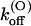 (0) and vs are close to those of wild-type. This is consistent with the model proposed by Terlau et al. (1999), according to which
(0) and vs are close to those of wild-type. This is consistent with the model proposed by Terlau et al. (1999), according to which 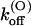 is mainly determined by the interaction of the bound toxin with potassium ions occupying the outermost sites of the permeation pathway. The similarity of the
is mainly determined by the interaction of the bound toxin with potassium ions occupying the outermost sites of the permeation pathway. The similarity of the 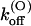 (0) values indicates also that the M448K mutation does not affect the positioning of κ-PVIIA in the channel vestibule relative to the potassium sites at the outer pore.
(0) values indicates also that the M448K mutation does not affect the positioning of κ-PVIIA in the channel vestibule relative to the potassium sites at the outer pore.
The main effect of the T449S mutation on κ-PVIIA binding is a large increase in the rate of toxin dissociation, accounting both for the lower sensitivity and for the faster kinetics of toxin binding to this mutant channel, whereas the rates of association are very close to those of wild-type. The mutation T449S involves the replacement of four threonine residues, putatively exposing their chains to the lumen of the outer pore vestibule (Moran, 2001), with less bulky serine residues of the same polarity. Therefore, it is not surprising that this mutation does not affect kon values appreciably, whereas the increase of koff upon elimination of the threonine methyl groups suggests that the latter contribute to form tight-fitting pockets for some toxin group. Along with this idea, the large increase of 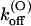 (0) may result from a different positioning of κ-PVIIA that places charged toxin groups in closer interaction with potassium ions occupying the outer pore sites. Consistently with the assumption that such interaction is the major cause of the destabilization of κ-PVIIA binding upon channel opening, we also find that mutant T449S has the same
(0) may result from a different positioning of κ-PVIIA that places charged toxin groups in closer interaction with potassium ions occupying the outer pore sites. Consistently with the assumption that such interaction is the major cause of the destabilization of κ-PVIIA binding upon channel opening, we also find that mutant T449S has the same 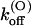 voltage-dependence as M448K and WT. This further supports the general idea proposed for Shaker channels by Terlau et al. (1999) that the state-dependence of κ-PVIIA binding arises almost exclusively from changes in the state of pore occupancy by permeant ions. The state-dependence of binding to K+ channels has also been described for other K+ channel blockers (Avdonin et al., 2000). The question remains if state-dependence of binding could be a general principle for different compounds interacting with K+ channels and if the model proposed by Terlau et al. (1999) may be in all cases appropriate for the underlying mechanism.
voltage-dependence as M448K and WT. This further supports the general idea proposed for Shaker channels by Terlau et al. (1999) that the state-dependence of κ-PVIIA binding arises almost exclusively from changes in the state of pore occupancy by permeant ions. The state-dependence of binding to K+ channels has also been described for other K+ channel blockers (Avdonin et al., 2000). The question remains if state-dependence of binding could be a general principle for different compounds interacting with K+ channels and if the model proposed by Terlau et al. (1999) may be in all cases appropriate for the underlying mechanism.
Our finding that an outer pore blocker like κ-PVIIA antagonizes C-type inactivation processes that involve structural changes in the outer end of the pore (Yellen, 1998) is not, per se, surprising. Extracellular TEA is known to affect likewise the C-type inactivation of both WT (Grissmer and Cahalan, 1989) and mutant channels (Choi et al., 1991; Molina et al., 1997), presumably via the foot-in-the-door effect originally described for intracellular blockers and N-type inactivation (Yeh and Armstrong, 1978). However, in view of the observation that κ-PVIIA has no similar effects on the normal slow inactivation of WT channels (Naranjo, 2002; see also Fig. 1), our present study may have deeper implications for the mechanism of C-type inactivation. Assuming that the point mutations afford the same basic mechanism, our results argue against the hypothesis that C-type inactivation involves only a confined constriction of the outer end of the pore with no major changes of the pore vestibule. In a less conservative perspective we cannot exclude that the inactivated state antagonized by κ-PVIIA corresponds to a substantially different closed conformation of the channels. This view would be in line with suggestions that some of the various processes described as C-type inactivation might actually involve distinct mechanisms (De Biasi et al., 1993; Yang et al., 1997; Olcese et al., 1997; Loots and Isacoff, 1998). The biphasic inactivation of mutant T449S, reported here in agreement with others (Meyer and Heinemann, 1997; Chen et al., 2000), suggests indeed the existence of at least two different inactivated conformations. Biphasic C-type inactivation was also reported for Shaker-Δ6-46-mediated currents measured in outside-out patches (Starkus et al., 1997).
Combined with the state-dependence of its binding affinity, the antagonism of κ-PVIIA against inactivation makes this toxin particularly efficient in protecting mutant channels from inactivation. On one hand, despite their early block, the currents carried by toxin-liganded channels during prolonged depolarizations reach peak values comparable to toxin-free conditions, and even allow a larger charge flow; this is because the toxin unbinds fast from open channels but prevents inactivating transitions that would normally occur before channel opening. On the other hand, due to the high affinity binding of κ-PVIIA to closed channels and to the fact that inactivation from preopen states is predominant at mild depolarizations, the toxin shows in these conditions a most peculiar protective action. At variance with the effect expected from a state-independent blocker, the strong protection of closed channels is only partially counteracted by the weaker block of open channels during large depolarizations.
Although described here for the effect of κ-PVIIA on mutant channels, we believe that the above mechanism, by which a state-dependent blocker may efficiently protect from inactivation without drastically reducing the activation of channel conductance, may turn out to be generally relevant for understanding the effects of κ-PVIIA-like substances on natural channels with strong outer-pore inactivation.
Acknowledgments
This work was supported by grants from the German Research Foundation (TE 137/2-1) and the BioFuture Prize from the German Ministry of Science and Education (0311859/3) to H.T., and by a grant from the Italian Ministry for University and Research to F.C.
APPENDIX
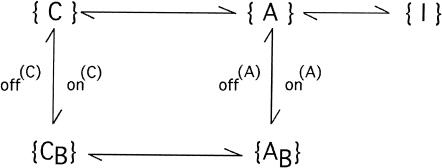
We assume the following general scheme to describe how toxin-channel interactions affect the activation of potassium currents and the availability of activatable channels, where the subscript B indicates a toxin-bound channel; {C} indicates the set of de-activated states; the activated states{A} may comprise preopen configurations in fast equilibrium with the open state; and {I} indicates inactivated states. The main assumption implied by Scheme 1
SCHEME 1.
is that toxin binding is incompatible with channel inactivation. In general, the scheme predicts very complicated multiexponential relaxations that depend on all rate constants for activation, inactivation, and toxin binding, and on initial conditions. However, much simpler relaxations are expected for several particular conditions describing the experiments reported in this article.
Early currents
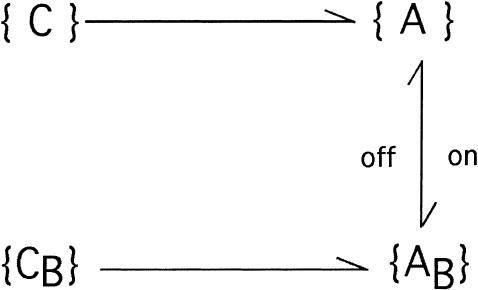
For large depolarizations (V >= 0) the activating transitions {C}→{A} and {CB}→{AB} can be considered irreversible. Furthermore, for times much shorter than those that characterize inactivation, {C}↔{CB} and {A}→{I} transitions can be neglected and Scheme 1 reduces to
SCHEME 2.
where the superscript A in the toxin binding and unbinding rates is omitted for simplicity. Let U0 and 1 − U0 be the initial probabilities of states {C} or {CB}, respectively, and let x(t) and y(t) denote the probabilities of the states {A} and {AB} after the depolarizing step. Denote with xC(t) the time course of P{A} when the same depolarization is applied in the absence of toxin. Then, the rates at which states {A} and {AB} are fed by the activating transitions from states {C} and {CB} are, respectively, 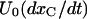 and
and 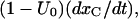 so that the differential equations for x(t) and y(t) are
so that the differential equations for x(t) and y(t) are
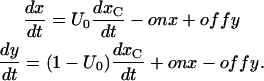 |
Adding the above equations term by term and integrating
 |
substituting this expression of y in the first of the above equations,
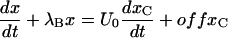 |
where
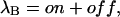 |
is the rate that would characterize the relaxations of toxin binding to the activated state in the absence of gating transitions.
The last equation is of the standard form
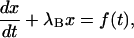 |
and, for the initial conditions x(0) = 0 and f(0) = 0, has the general solution of
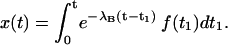 |
Applying this formula to our particular case, we obtain, after some manipulation,
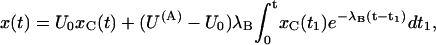 |
(A1) |
where
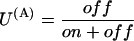 |
is the probability of finding a toxin-free channel that would be achieved at equilibrium and after full activation and in the absence of inactivation. The first term on the right-hand side of Eq. A1 represents the immediate availability for conduction of initially toxin-free channels, whereas the second term accounts for the delayed redistribution of toxin binding to activated channels and vanishes if U(A) = U0, i.e., if the initial distribution of the channels between blocked and unblocked states equals that expected at equilibrium for open-channel binding. For t × λB ≪ 1, the integral in this term is fairly insensitive to the value of λB and Eq. A1 reduces to
 |
(A2) |
Considering that x(t) and xC(t) are proportional to the currents, ITx and ICt, measured respectively in the presence or in the absence of toxin, Eqs. A2 and A1 are equivalent, respectively, to Eqs. 1 and 4 in the text:
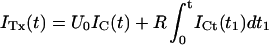 |
(1) |
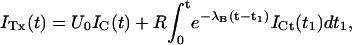 |
(4) |
with
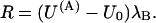 |
Recovery from inactivation and rebinding of κ-PVIIA to closed M448K channels
During large hyperpolarizations the deactivating transitions {A}→{C} and {AB}→{CB} can be considered irreversible and much faster than any other transition, and Scheme 1 reduces to
SCHEME 3.
where λI is the rate of {I}→{A} transitions, characterizing the single exponential recovery of activatable currents in toxin-free conditions, and the superscript C in the toxin binding and unbinding rates is omitted for simplicity. Let U(t) denote the time course of the probability of the unblocked state {C}. Scheme 3 predicts that for any given initial condition, U(t) is a double-exponential function,
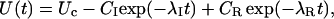 |
(2) |
where recovery from inactivation at the rate λI is transiently counteracted by toxin rebinding to closed channels at the rate of
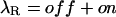 |
and the steady-state value UC is given by
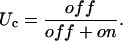 |
In particular, after a conditioning depolarization that causes full inactivation, the initial conditions U(0) = 0 and 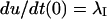 impose
impose
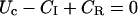 |
and
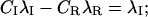 |
or, after simple rearrangements,
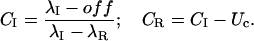 |
Interaction between open-channel binding and inactivation
During large depolarizations (V >= 0) and after activation can be assumed to be complete, the scheme describing the interplay between toxin binding and inactivation is
SCHEME 4.
We distinguish two cases.
1. Inactivation governed by a single rate-limiting step with kinetics comparable to that of toxin binding
This case applies to mutant M448K, described by
SCHEME 5.
where λh is the rate of inactivation in the absence of toxin and the superscript A in the toxin-binding and unbinding rates is omitted for simplicity.
Let x(t) and y(t) denote the probabilities of the states {A} and {AB} after the depolarizing step. The differential equations for x(t) and y(t) are
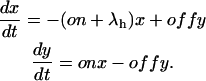 |
According to these equations x(t) is expected to decay as the sum of two exponentials, with rates λf and λs related to the transition rates of Scheme 4 by
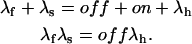 |
Measurements of λf and λs, together with control λh measurements, can be used to obtain from the above relations estimates for the off and on rates of toxin binding at any toxin concentration.
2. Toxin-binding kinetics much faster than inactivation and two inactivated states
We considered this to be the case of mutant T449S, which has κ-PVIIA-binding kinetics comparable to those of activation and whose currents inactivate following a double-exponential decay. The latter observation implies the presence of two inactivated states, only one of which is absorbing. We can model T449S inactivation according to two alternative schemes, in which the inactivated states are either sequential (Scheme 6)
SCHEME 6.
or branch separately from the activated conformation of the channel (Scheme 7), thus
SCHEME 7.
In both schemes the activated states {A} and {AB} are assumed to be in fast equilibrium, with
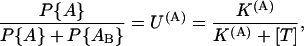 |
(A3) |
with K(A) being the apparent dissociation constant of the toxin from activated channels. Both schemes predict that the probability of the noninactivated states {A, AB} and the associated currents decay as a double-exponential, with rates λf and λs related to the state-transition rates by
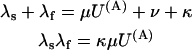 |
(Scheme 6) |
or
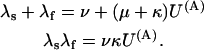 |
(Scheme 7) |
Experimentally, we find that the inactivation of T449S is always characterized by λs ≪ λf, so that it is safe to write
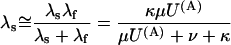 |
(Scheme 6) |
or
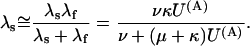 |
(Scheme 7) |
In this approximation, the ratio RTx of the λs values expected under toxin or in control (U(A) = 1) is expressed for both schemes by
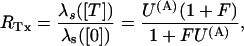 |
(A4) |
where
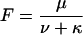 |
(Scheme 6) |
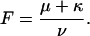 |
(Scheme 7) |
Using Eq. A3 to express the [T]-dependence of U(A) Eq. A4 yields
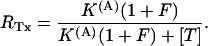 |
(A5) |
Thus, both schemes predict that the addition of κ-PVIIA slows the late phase of T449S inactivation according to the dose-response curve expected for toxin binding to activated states with a dissociation constant larger than the real one by the factor (1 + F). Alternatively, knowing F, Eq. A4 can be used to estimate U(A) from RTx measurements as
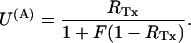 |
Estimates of F can be obtained from the analysis of the inactivation of T449S currents in the absence of κ-PVIIA. Let in this case
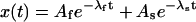 |
describe the time course of the probability of {A} states after the time to peak, defined as t = 0, and when activation can be considered complete. As and Af are proportional to the expected amplitudes of the two components of the decay of the currents, so that their ratio Rfs = Af/As is measurable. If activation is much faster than inactivation, we can assume, as initial conditions in control (U(A) = 1),
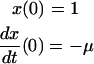 |
(Scheme 6) |
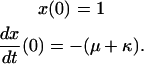 |
(Scheme 7) |
These conditions imply
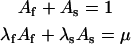 |
(Scheme 6) |
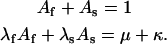 |
(Scheme 7) |
Dividing the above equations term by term we obtain
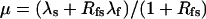 |
(Scheme 6) |
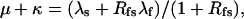 |
(Scheme 7) |
and, since for both schemes μ + ν + κ = λs + λf,
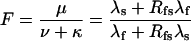 |
(Scheme 6) |
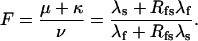 |
(Scheme 7) |
Thus, both schemes yield the same estimate of F in terms of the experimental quantities λs, λf, and Rfs. Mean values (± SE, n ≥ 5) of λs, λf, and Rfs, and consequent estimates of F, are given in Table A1.
TABLE A1.
| Vp | λs | SE | n | λf | SE | n | Rfs | SE | F |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 14.1 | 0.49 | 13 | 79 | 3.3 | 5 | 0.173 | 0.0225 | 0.34 |
| 20 | 13 | 0.544 | 10 | 104 | 8.33 | 10 | 0.273 | 0.0267 | 0.38 |
| 40 | 13.4 | 0.365 | 19 | 124 | 3.64 | 19 | 0.421 | 0.0209 | 0.51 |
| 60 | 12.8 | 0.518 | 10 | 132 | 4.07 | 10 | 0.553 | 0.0327 | 0.62 |
| 80 | 13.3 | 0.617 | 9 | 138 | 4.36 | 9 | 0.724 | 0.0433 | 0.77 |
E. Dietlind Koch's present address: University College London, Dept. of Pharmacology, Gower Street, London WC1E 6BT, UK.
References
- Avdonin, V., B. Nolan, J. M. Sabatier, M. de Waard, and T. Hoshi. 2000. Mechanisms of maurotoxin action on Shaker potassium channels. 2000. Biophys. J. 79:776–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, J., V. Avdonin, M. A. Ciorba, S. H. Heinemann, and T. Hoshi. 2000. Acceleration of P/C-type inactivation in voltage-gated K+ channels by methionine oxidation. Biophys. J. 78:174–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, K. L., R. W. Aldrich, and G. Yellen. 1991. Tetraethylammonium blockade distinguishes two inactivation mechanisms in voltage-activated K+ channels. Proc. Natl. Acad. Sci. USA. 88:5092–5095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Biasi, M., H. A. Hartmann, J. A. Drewe, M. Taglialatela, A. M. Brown, and G. E. Kirsch. 1993. Inactivation determined by a single site in K+ pores. Pflugers Arch. 422:354–363. [DOI] [PubMed] [Google Scholar]
- García, E., M. Scanlon, and D. Naranjo. 1999. A marine snail neurotoxin shares with scorpion toxins a convergent mechanism of blockade on the pore of voltage-gated K channels. J. Gen. Physiol. 114:141–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein, A. N., D. J. Pheasant, and C. Miller. 1994. The charybdotoxin receptor of a Shaker K+ channel: peptide and channel residues mediating molecular recognition. Neuron. 12:1377–1388. [DOI] [PubMed] [Google Scholar]
- Grissmer, S., and M. Cahalan. 1989. TEA prevents inactivation while blocking open K+ channels in human T-lymphocytes. Biophys. J. 55:203–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi, T., W. N. Zagotta, and R. W. Aldrich. 1990. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 250:533–538. [DOI] [PubMed] [Google Scholar]
- Hoshi, T., W. N. Zagotta, and R. W. Aldrich. 1991. Two types of inactivation in Shaker K+ channels: effects of alterations in the carboxy-terminal region. Neuron. 7:547–556. [DOI] [PubMed] [Google Scholar]
- Jacobsen, R. B., E. D. Koch, B. Lange-Malecki, M. Stocker, J. Verhey, R. M. van Wagoner, A. Vyazovkina, B. M. Olivera, and H. Terlau. 2000. Single amino acid substitutions in κ-conotoxin PVIIA disrupt interaction with the Shaker K+ channel. J. Biol. Chem. 275:24639–24644. [DOI] [PubMed] [Google Scholar]
- Loots, E., and E. Y. Isacoff. 1998. Protein rearrangements underlying slow inactivation of the Shaker K+ channel. J. Gen. Physiol. 112:377–389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Barneo, J., T. Hoshi, S. H. Heinemann, and R. W. Aldrich. 1993. Effects of external cations and mutations in the pore region on C-type inactivation of Shaker potassium channels. Receptors Channels. 1:61–71. [PubMed] [Google Scholar]
- Meyer, R., and S. H. Heinemann. 1997. Temperature and pressure dependence of Shaker K+ channel N- and C-type inactivation. Eur. Biophys. J. 26:433–445. [DOI] [PubMed] [Google Scholar]
- Molina, A., A. G. Castellano, and J. López-Barneo. 1997. Pore mutations in Shaker K+ channels distinguish between the sites of tetraethylammonium blockade and C-type inactivation. J. Physiol. 499:361–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molina, A., P. Ortega-Saenz, and J. López-Barneo. 1998. Pore mutations alter closing and opening kinetics in Shaker K+ channels. J. Physiol. 509:327–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran, O. 2001. Molecular simulation of the interaction of κ-conotoxin-PVIIA with the Shaker potassium channel pore. Eur. Biophys. J. 30:528–536. [DOI] [PubMed] [Google Scholar]
- Naranjo, D. 2002. Inhibition of single Shaker K channels by κ-conotoxin-PVIIA. Biophys. J. 82:3003–3011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olcese, R., R. Latorre, L. Toro, F. Bezanilla, and E. Stefani. 1997. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J. Gen. Physiol. 110:579–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlief, T., R. Schönherr, and S. H. Heinemann. 1996. Modification of C-type inactivating Shaker potassium channels by chloramine-T. Pflugers Arch. 431:483–493. [DOI] [PubMed] [Google Scholar]
- Shon, K. J., M. Stocker, H. Terlau, W. Stühmer, R. Jacobsen, G. Walker, M. Grilley, M. Watkins, D. R. Hillyard, W. R. Gray, and B. M. Olivera. 1998. κ-conotoxin PVIIA is a peptide inhibiting the Shaker K+ channel. J. Biol. Chem. 273:33–38. [DOI] [PubMed] [Google Scholar]
- Starkus, J. G., L. Kuschel, M. D. Rayner, and S. H. Heinemann. 1997. Ion conduction through C-type inactivated Shaker channels. J. Gen. Physiol. 110:539–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stühmer, W. 1992. Electrophysiological recordings from Xenopus oocytes. Meth. Enzymol. 207:319–339. [DOI] [PubMed] [Google Scholar]
- Terlau, H., K. Shon, M. Grilley, M. Stocker, W. Stühmer, and B. M. Olivera. 1996. Strategy for rapid immobilization of prey by a fish-hunting marine snail. Nature. 381:148–151. [DOI] [PubMed] [Google Scholar]
- Terlau, H., A. Boccaccio, B. M. Olivera, and F. Conti. 1999. The block of Shaker K+ channels by κ-conotoxin PVIIA is state dependent. J. Gen. Physiol. 114:125–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, Y., Y. Yan, and F. J. Sigworth. 1997. How does the W434F mutation block current in Shaker potassium channels? J. Gen. Physiol. 109:779–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh, J. Z., and C. M. Armstrong. 1978. Immobilisation of gating charge by a substance that simulates inactivation. Nature. 273:387–389. [DOI] [PubMed] [Google Scholar]
- Yellen, G. 1998. The moving parts of voltage-gated ion channels. Q. Rev. Biophys. 31:239–295. [DOI] [PubMed] [Google Scholar]