Water Accessibility, Aggregation, and Motional Features of Polysaccharide-Protein Conjugate Vaccines

Abstract

A relaxometric investigation of a nontoxic mutant of diphtheria toxin and of its conjugates with capsular polysaccharides of different groups of Neisseria meningitidis was performed. The insertion of polysaccharides chains alters dramatically the hydrodynamic properties of the protein. The model-free analysis of the ¹H nuclear magnetic relaxation dispersion profiles of their water solutions shows: i), a reduced protein hydration with respect to the carrier protein alone; ii), a much larger flexibility of the conjugates with respect to a compact macromolecule of the same molecular weight; and iii), a strong tendency to aggregate. The above findings are largely independent on the nature of the polysaccharide and thus provide a fairly general picture of the dynamic properties of glycoconjugate proteins.

INTRODUCTION

The infections caused by Neisseria meningitidis bacteria represent a relevant health problem in the world especially for children. Different serogroups are distinguished by the composition and structure of their capsular polysaccharides and because the virulence is related to them, they are target for vaccine development. However they are not immunogenic in infants and children and the administration of the simple polysaccharides often is not enough to prevent the disease. The conjugation of polysaccharides with immunogenic proteins allows to overcome this problem providing an efficient immunological response also in infants (Costantino et al., 1999; Reingold et al., 1985).

The key feature of glycoconjugate vaccines is a saccharide covalently linked to an appropriate carrier protein, which can give rise to T-cell dependent immune responses against the saccharide (Ravenscroft et al., 1999; Morley and Pollard, 2001). Diphtheria toxin is a very immunogenic protein and a nontoxic mutant, CRM₁₉₇ with 39 lysines has been employed. Capsular polysaccharides of A, C, W135, and Y groups of N. meningitidis (MenA, MenC, MenW, MenY) have been purified from cultivation supernatants of the respective meningococcus serogroups, selected on the basis of their chain length and then activated and conjugated to CRM₁₉₇ through the protein surface lysines (Costantino et al., 1999; Ravenscroft et al., 1999).

Because the immunogenic properties are related to the number of polysaccharide chains linked to the protein surface, to their degree of polymerization (DP) and to their dynamics, it is important to develop new methods to characterize the polysaccharide-protein conjugates (Hsieh, 2000; Egan, 2000). The main problem is actually that at the end of the process the vaccine is formed by a distribution of many glycoforms and only the average properties can be measured. Although the average number of chains and their degree of polymerization can be estimated by analytical measurements, the dynamic properties are not easy to assess.

High resolution NMR provides detailed information on dynamic properties of proteins in solution, whereas for polysaccharides, because they are constituted by many repetitions of the same molecular unit, high resolution NMR studies are less informative. However there is an indirect method to reveal the dynamic properties of macromolecules. Because in solution water molecules interact with solutes, the analysis of the proton relaxation rate of solvent as a function of field (nuclear magnetic relaxation dispersion (NMRD) or relaxometry), can provide information on both hydration and dynamics of the macromolecule (Koenig and Schillinger, 1969; Bertini and Luchinat, 1986, 1996; Schauer et al., 1988; Koenig and Brown, 1990; Banci et al., 1991; Van-Quynh et al., 2003). Relaxometry has been widely used to investigate proteins in solutions (Koenig and Schillinger, 1969; Hallenga and Koenig, 1976; Koenig et al., 1978, 1983; Andersson et al., 1981; Winter and Kimmich, 1982; Bertini et al., 1989, 1995, 1996, 1998, 2000; Koenig and Brown, 1990; Hricovini et al., 1992; Denisov and Halle, 1996; Bryant, 1996; Kroes et al., 1996; Belton, 1997; Banci et al., 1998; Halle et al., 1998). Relaxometry studies on sugars are less common (Hills et al., 1991; Belton, 1997), whereas high resolution relaxation data on some of the sugar moieties investigated here are available (Lindon et al., 1984; Yamasaki and Bacon, 1991), but not when conjugated to proteins. In the present work we show how the NMRD analysis is able to characterize hydration, aggregation, and dynamic properties of a protein conjugated with different polysaccharides. The characterization is based on a model-free analysis of the NMRD profiles and, as such, is of general applicability to any macromolecular system (Halle et al., 1998; Bertini et al., 2000). To our knowledge, this is the first time that an analysis of this type is attempted for glycoconjugate proteins.

MATERIALS AND METHODS

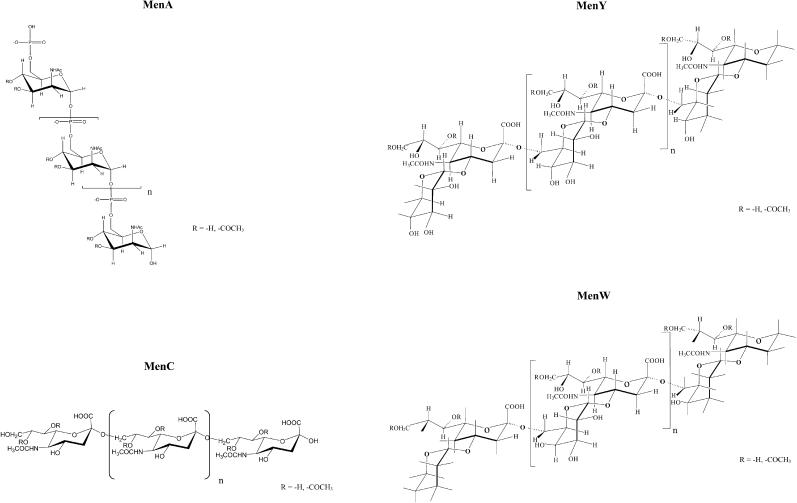
The carrier protein of the meningococcal conjugates is CRM₁₉₇, a 58.4 kDa protein that contains five tryptophans, 18 tyrosines, 18 phenylalanine residues, two disulphide linkages, and 39 lysine residues (Giannini et al., 1984); many of these lysines are available for conjugation to saccharide chains. The serogroup A N. meningitidis capsular polysaccharide is a homopolymer of N-acetyl-mannosamine-phosphate linked α1-6 with partial O-acetylation in C3 and C4. The serogroup C meningococcal polysaccharide capsule is a homopolymer of α2-9-linked N-acetylneuraminic acid (NeupNAc) with partial O-acetylation in C7 and C8 of its sialic acid residues. The serogroup Y and W polysaccharides are constituted by the repeating unit →4)-D-NeupNAc(7/9OAc)-α-(2→6)-D-Gal-α-(1→ and →4)-D-NeupNAc(7/9OAc)-α-(2→6)-D-Glc-α-(1→. The only difference between MenY and MenW is the presence of the epimer Gal instead of Glc. A partial O-acetylation in C7 and C9 of sialic residues appears (Fig. 1).

FIGURE 1.

Structure of MenA, C, Y, W polysaccharides.

The CRM₁₉₇-MenA, CRM₁₉₇-MenC, CRM₁₉₇-MenY, CRM₁₉₇-MenW conjugate vaccines were prepared using the following approach: i), size reduction and fractionation of the polysaccharide by acidic hydrolysis followed by tangential flow ultrafiltration and ion exchange chromatography; ii), activation of the selected oligosaccharides by introduction of an active ester end group; iii), conjugation to the protein carrier through reaction of the activated oligosaccharides with the lysine residues of the protein; and iv), purification of the glycoconjugate molecules by tangential flow ultrafiltration to remove the contamination residues of reaction.

Protein concentration of conjugates was determined by Micro BCA protein assay kit (Pierce Biotechnology, Rockford, IL). Saccharide concentration of conjugates was determined by measuring the sialic acid content of MenC, MenY, and MenW with a modified Svennerholm method (Svennerholm, 1957), and the mannosamine-6-phosphate content of MenA by a highly selective method using the HPAEC-PAD system (Chen et al., 1956; Costantino et al., 1999). The relevant data characterizing the four conjugates are summarized in Table 1.

TABLE 1.

Summary of samples

	avDP	Saccharide concentration (mg/mL)	Protein concentration (mg/mL)	αglyco × 100	Number of saccharide chains for protein
CRM197-MenA	13÷14	0.558	0.970	57.5	8–9
CRM197-MenC	15÷16	0.656	0.969	67.7	8–9
CRM197-MenY	20÷21	0.837	0.583	143.4	9
CRM197-MenW	20÷21	0.940	0.918	102.4	6

avDP: average degree of polymerization; α_glyco: glycosylation degree (saccharide:protein, w/w).

The final samples for NMRD analysis were prepared by diafiltering the glycoconjugates with a 10 kDa membrane against 5 mM phosphate buffer at pH 7.2.

Nuclear magnetic relaxation dispersion experiments

Water ¹H nuclear magnetic relaxation dispersion profiles were obtained by measuring the water proton relaxation rates, R₁, as a function of applied magnetic field. The NMRD profiles have been collected with a Stelar (Pavia, Italy) fast field cycling relaxometer and with a Koenig-Brown field cycling relaxometer in the 0.01–50 MHz proton Larmor frequency range at 300 K. Both instruments provide measurements that are affected by an error of about ±1% (Noack, 1986; Bertini and Luchinat, 1986; Koenig and Brown, 1987).

Water proton NMRD data were analyzed according to model-free analysis (Halle et al., 1998; Bertini et al., 2000).

THEORY

When the water proton relaxation rate is essentially due to the proton-proton dipolar interactions as in solution of diamagnetic macromolecules, its value may be estimated by Eq. 1 (Abragam, 1961; Venu et al., 1997; Bertini et al., 2000):

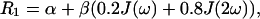(1)

where α and β are constants and J(ω) are spectral density functions.

For diluted solutions of macromolecules and in the absence of aggregation, J(ω) can be considered a Lorentzian function (Denisov and Halle, 1996; Halle et al., 1998; Van-Quynh et al., 2003) with a value given by Eq. 2:

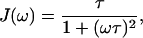(2)

where τ is the time constant, called correlation time, that modulates the dipolar interaction between the protons and ω is equal to 2π times the Larmor frequency.

When the correlation time that modulates the homonuclear dipole-dipole relaxation is the rotational tumbling time, its value can be estimated using a rigid sphere model with the Stokes-Einstein equation:

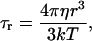(3)

where T is the temperature, k is the Boltzmann constant, r the radius of the protein, assumed spherical, and η the viscosity of the solvent. Deviations from the Stokes-Einstein values can be ascribed to increased protein radius due to the hydration shell (Yguerabide et al., 1970) or, more likely, to protein surface roughness (Garcia de la Torre and Bloomfield, 1981; Denisov and Halle, 1998; Van-Quynh et al., 2003).

However it is often observed (Koenig and Schillinger, 1969; Koenig and Brown, 1990; Hallenga and Koenig, 1976; Koenig et al., 1978, 1983; Andersson et al., 1981; Bertini et al., 1995, 2000; Denisov and Halle, 1996; Kroes et al., 1996; Halle et al., 1998; Halle and Denisov, 2001) that the experimental relaxometric profiles of water solutions of proteins exhibit a quasi-Lorentzian shape that is however somewhat “stretched” over a wide frequency range. Model-free analysis allows to interpret these NMRD profiles of biological macromolecules in terms of multi-Lorentzian functions where the spectral density function is expressed as (Halle et al., 1998):

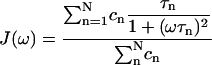(4)

So far, a sum of three Lorentzians turned out to be sufficient to well reproduce any experimental dispersion, providing three τ_n values with their relative weight coefficients c_n (Halle et al., 1998; Bertini et al., 2000).

From the best-fit parameters the average correlation time 〈τ_C〉 can be derived (Halle et al., 1998):

(5)

Although the parameters τ_n and c_n do not have necessarily a physical meaning, the average correlation time 〈τ_C〉 does (Halle et al., 1998).

The α parameter in Eq. 1 represents the fraction of R₁ that remains in the extreme-motional narrowing regime up to the highest sampled frequency, plus the possible contribution of a nondispersive term (Halle et al., 1998). The β parameter in Eq. 1 is related to the integral of the dispersion (Halle et al., 1998). The model-free analysis of NMRD profiles has been successfully applied to proteins allowing to obtain the correlation time 〈τ_C〉. The latter are usually in reasonable agreement with the Brownian rotational times provided by the Stokes-Einstein theory, although the values tend to be somewhat shorter due to the internal motions (Bertini et al., 2000). Indeed the correlation time 〈τ_C〉 provided by the model-free analysis takes into account all collective motions, and its value is a weighted average of the relative correlation times. So when the size of a protein is unknown but the protein is known to be rigid, the value of the average correlation time could provide an estimate of the molecular weight, whereas when the molecular weight is known, the average correlation time provides information on mobility phenomena. The β parameter, that is proportional to the integral of the dispersion profile, reflects the overall proton-proton dipolar coupling strength in solution which, in turn, is a measure of the number of water protons and exchangeable protons attached to the macromolecule with residence times ≥ 〈τ_C〉. Therefore, β, normalized to 1 mM (β/conc) can be taken as a measure of hydration. Because hydration is largely a surface property, β/conc should be roughly proportional to the protein surface area, and thus to the molecular weight raised to 2/3, as experimentally verified (Bertini et al., 2000). Also α, subtracted by bulk water relaxivity (0.3 s⁻¹) and normalized to 1 mM ((α − 0.3)/conc) should be proportional to the surface of the biomolecule (Bertini et al., 2000). The latter parameter actually represents the contribution to relaxation rate due to water molecules in fast exchange with the protein surface and characterized by a correlation time much shorter than the rotational correlation time of the macromolecule, 〈τ_C〉. Besides providing the values of β and α, the model-free analysis provides the value of the parameters τ_n and c_n. Although the latter parameters may not necessarily have a physical meaning, in the presence of independent data they may provide insight on the different proton pools of the protein that contribute to proton relaxation of the bulk solvent, and on their mobility.

RESULTS

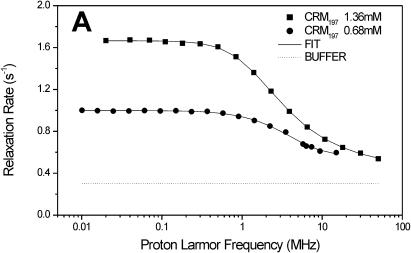
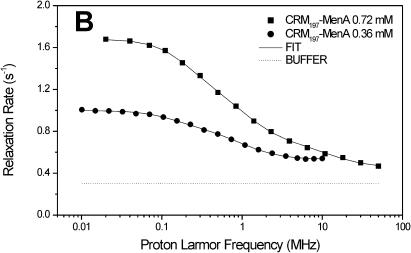
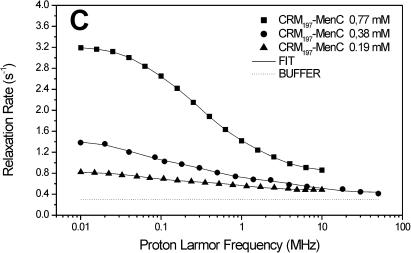
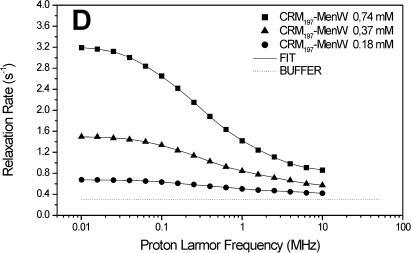
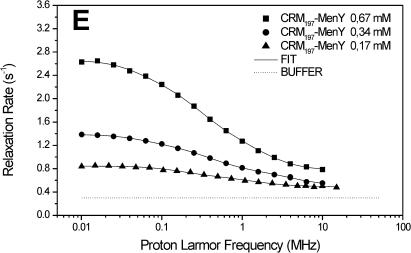
The carrier protein CRM₁₉₇ and four different polysaccharide-protein conjugates (CRM₁₉₇-MenA, C, W, Y; Fig. 1) have been investigated by NMRD. These conjugates have a relevant interest as vaccines considering their ability to fake the surface of the N. meningitidis bacteria and to induce a strong immunologic response. NMRD profiles of water solutions of the carrier protein and of its glycococonjugates at different concentrations have been collected at 300 K in the range between 0.01 and 10 MHz and 0.01 and 50 MHz (Fig. 2). To a first inspection, the profiles of CRM₁₉₇ as such appear somewhat stretched with respect to a Lorentzian behavior, and with a single dispersion of the spectral density function. For all polysaccharide-protein conjugates, the relaxation rate at low field increases with the concentration and the dispersion moves to the left by increasing the concentration. Remarkably, the profiles appear much more stretched than those of CRM₁₉₇ alone. In any case, according to the model-free analysis, all the profiles can be fitted with Eqs. 1 and 2, using a sum of three terms. In Fig. 2, the solid lines represent the fits. The best-fit parameters are reported in Table 2. Protein concentration values are reported in column 1, the rotational correlation times given by the Stokes-Einstein equation in column 2 and the average correlation times values (〈τ_C〉) obtained from model-free fits in column 3. The three τ values and their weights that represent the parameters in Eq. 2 are reported in columns 4–9. In column 10 the values of β normalized to 1 mM of polysaccharide-protein concentration (β/conc) are reported. The values of the α parameter subtracted by bulk water relaxivity contribution and normalized for 1 mM ((α − 0.3)/conc) are reported in column 11.

FIGURE 2.

¹H NMRD profiles of CRM₁₉₇ (A), CRM₁₉₇-MenA (B), CRM₁₉₇-MenC (C), CRM₁₉₇-MenW (D), and CRM₁₉₇-MenY (E). The solid lines represent the best-fit model-free profiles, and the thin line represents the relaxation rate of the buffer as a blank.

TABLE 2.

Best-fit parameters of the carrier protein and of the different polysaccharide-protein conjugates

Protein	Concentration (mM)	〈τStokes〉 (s × 10−8)	〈τC〉 (s × 10−8)	τ1 (s × 10−8)	c1 (%)	τ2 (s × 10−8)	c2 (%)	τ3 (s × 10−8)	c3 (%)	β/concentration (s−2 mM−1 × 107)	(α − 0,3)/concentration (s−1 mM−1)	Molecular weight
CRM197	1.36	2.46	1.53	5.7	14.3	1.87	27.1	0.37	58.6	5.56	0.15	60,000
CRM197	0.68	2.46	1.06	9.6	1.6	2.2	40.6	0.005	57.8	6.16	0.37	60,000
CRM197-MenA	0.72	3.87	3.10	40.4	3.3	7.37	16.4	0.70	80.3	5.47	0.22	94,500
CRM197-MenA	0.36	3.87	1.45	56.5	1.0	8.5	9.5	0.82	89.5	9.30	0.58	94,500
CRM197-MenC	0.77	4.12	18.8	256	3.4	35.6	18.6	4.66	78.0	1.55	0.60	100,500
CRM197-MenC	0.38	4.12	5.54	205	1.2	20.7	9.0	1.47	89.8	4.91	0.37	100,500
CRM197-MenC	0.19	4.12	1.34	150	0.4	8.6	6.3	0.13	93.3	14.3	0.81	100,500
CRM197-MenY	0.67	6.0	13.0	154	2.1	28.2	22.1	4.85	75.8	2.1	0.47	146,000
CRM197-MenY	0.33	6.0	6.26	134	1.1	21.1	14.0	2.08	84.9	4.22	0.61	146,000
CRM197-MenY	0.17	6.0	1.1	49.3	1.0	6.2	6.9	0.18	92.1	22.0	0.78	146,000
CRM197-MenW	0.74	5.0	13.4	129	3.1	25.4	24.1	4.04	72.8	2.46	0.53	121,500
CRM197-MenW	0.37	5.0	8.05	98.7	2.2	23.2	16.2	2.61	81.6	3.21	0.65	121,500
CRM197-MenW	0.18	5.0	1.09	62	0.5	9.4	3.2	0.47	96.3	19.4	0.61	121,500

DISCUSSION

NMRD of CRM₁₉₇

According to the molecular weight of ∼60 kDa and the rigid sphere model, the Stokes-Einstein equation provides for the nontoxic mutant of diphtheria toxin (CRM₁₉₇) as such a rotational correlation time (τ_Stokes) of 2.46 × 10⁻⁸ s. The average correlation times (〈τ_C〉) provided by the model-free analysis performed on profiles at two different concentrations are notably smaller than this value (Table 2). Inspection of the three pairs of model-free parameters (τ_n and c_n) can help in understanding this behavior. The τ₁ values are sizably longer than the τ_Stokes value but their contribution is the smallest, and practically negligible at the lower concentration (0.68 mM). The τ₂ and τ₃ values are the major contributors to the observed stretched profiles, and are of comparable magnitude at the lower concentration. The τ₂ value at this concentration is very close to the Stokes estimate, whereas the τ₃ value is much shorter (its actual value is rather ill-determined). Although τ₂ may essentially reflect the contribution of exchangeable water molecules on the surface of the protein, τ₃ may reflect the contribution of the exchangeable protein protons from protein side chains, which experience much larger mobility. In the case of CRM₁₉₇, the large number of lysine residues (39) justifies the large weight of the τ₃ term. A similar behavior was noticed previously for the lysine-rich protein cytochrome c, where the lysine N_ζ protons provide the main contribution to the NMRD profile (Banci et al., 1998). The small increase of the average correlation time 〈τ_C〉 is usually related to weak a-specific protein-protein interactions that increase upon increasing concentration (Schulz et al., 1989). The τ₁ parameter is the one that may reflect a small degree of protein aggregation (that increases the apparent rotational correlation time). Indeed, on passing from the lower to the higher concentration, τ₁ gains weight essentially at the expenses of τ₂, the weight of τ₃ remaining almost constant.

Importantly, β/conc also remains fairly constant, indicating that the overall hydration is not grossly changed (see Theory section). The overall behavior of CRM₁₉₇ is therefore pretty normal. The NMRD profiles (Fig. 2 A) roughly double their intensity with doubling the concentration, reflecting the essentially constant hydration (β/conc) and the only modest increase of 〈τ_C〉.

NMRD of the conjugates

In light of this analysis, the various polysaccharide-protein conjugates exhibit a completely different behavior. The relaxation rate increases with the concentration like for CRM₁₉₇, but this is accompanied by a marked shift of the dispersion toward low field and by a strong stretching of the profiles (Fig. 2, B–E). The low-field shift of the dispersion is reflected by the average correlation time (〈τ_C〉), which is sizably smaller than the Stokes-Einstein estimate, but increases dramatically with concentration. On the other hand, the value β/conc is higher than for the protein alone, but strongly decreases with increasing concentration (Table 2).

Considering that both 〈τ_C〉 and β/conc are related to the molecular weight of the macromolecule, there is a strong covariance between them; as a matter of fact, the product between 〈τ_C〉 and β/conc remains almost constant. However, fixing β/conc to a constant value, the fits quality falls off, so, even if covariance is present and significant, the qualitative trend of 〈τ_C〉 increasing and β/conc decreasing with increasing concentration is certainly correct.

Deviations from Lorentzian behavior (strongly stretched profiles) can be ascribed to the internal mobility, to the contributions of the different interacting water molecules and to the exchangeable protein protons (Halle and Denisov, 2001). In the case of the glycoconjugates, the overall dipolar interaction among protons should be the sum of i), a protein contribution, and ii), a polysaccharide contribution. The former is expected to be smaller than in the isolated protein due to the loss of free lysines upon conjugation, and possibly to a reduced water accessibility to the protein surface. The polysaccharide contribution apparently more than compensates for the decrease of the protein contribution in diluted solutions. This is expected in light of the presence of many polysaccharide hydroxyl protons that are known to be in fast exchange with water protons (Hills et al., 1991).

Inspection of the three pairs of model-free parameters further corroborates this analysis. In all four conjugates, the shortest τ value, τ₃, has by far the largest weight. At the lowest conjugate concentration, τ₃ is much shorter than the estimated τ_Stokes. This indicates that indeed a large contribution to hydration comes from the exchangeable protons of the sugars, and that the latter are quite mobile. By increasing concentration, the weight of τ₁ and τ₂ increases, again suggesting aggregation. The concomitant large increase of the τ values themselves for all conjugates, except CRM₁₉₇-MenA that has the lowest degree of glycosylation (Table 1), suggests that for these conjugates large aggregates may be present.

In summary, the strong increase in 〈τ_C〉 and the strong decrease in β/conc with the concentration can be easily interpreted in terms of interactions among the polysaccharide-protein conjugates. The formation of aggregates at high concentration would cause both an increase of 〈τ_C〉 and a reduction of the number of accessible (i.e., exchangeable) polysaccharide and protein protons, thereby reducing β/conc. Apparently, the intermolecular interactions among the sugar moieties are much more effective than those between the nonconjugated proteins. This is not unexpected in view of the known ability of polyhydroxylated hydrocarbons, even of the smallest ones like ethyleneglycol or glycerol, to increase dramatically the viscosity of the medium.

The enhancement of 〈τ_C〉 could thus be simply interpreted as an increase of solution viscosity; however, viscosity is a macroscopic phenomenon without a microscopic correspondent, i.e., the glycoconjugates are dissolved in a water medium that exhibits the microviscosity of pure water. In other words, the increase in 〈τ_C〉 depends directly on solute aggregation and not by an increase in macroscopic viscosity, which is only another possible consequence of solute aggregation.

Unlike relaxometric analysis of proteins, the detailed interpretation of the (α − 0.3)/conc parameters, which are related to protons in the extreme motional narrowing regime, is fairly hard in the present case. The presence of apparently highly mobile polysaccharide chains on the macromolecule surface is probably responsible for the higher value, on the average, of the (α − 0.3)/conc parameter in the conjugates with respect to the isolated protein.

CONCLUSIONS

In conclusion, all glycoconjugates investigated here show: 1), a reduced protein hydration with respect to the carrier protein alone. This can be ascribed to both the loss of lysine protons due to conjugation and to a decreased solvent accessibility to the protein surface. 2), A much larger flexibility with respect to a compact macromolecule of the same molecular weight. This is shown by the much more stretched profiles compared to those of proteins, and by the low 〈τ_C〉 values at low concentration. The exchangeable protons of the sugar moieties provide a sizable contribution to the overall proton-proton dipolar interaction, but their contribution to the relaxation is relatively small due to their mobility, which is probably of the same order of that of free sugars. 3), A strong tendency to aggregate, as shown by the dramatic increase in 〈τ_C〉 and decrease in β/conc with increasing conjugate concentration. All these features seem independent of the specific polysaccharide chain conjugated to the protein, although somewhat less marked for one of them, so the above conclusions should provide the first and fairly general picture of the hydration and dynamics of glycoconjugate proteins in solution.