Abstract
Dynamics of sliding were explored in isolated actin and myosin filaments. Sliding occurs in steps. The steps are integer multiples of 2.7 nm, which is equal to the monomeric repeat along the actin filament. When filaments were forced to slide in the reverse direction, the size paradigm was the same. This size paradigm is parallel to that seen in the kinesin-microtubule system, where step size is an integer multiple of the tubulin repeat along the microtubule.
INTRODUCTION
Over the last decade, a large number of experiments have been carried out to investigate the interaction between F-actin and single myosin molecules. Step sizes of 4–25 nm have been reported (Ishijima et al., 1994, 1996; Miyata et al., 1994; Finer et al., 1994, 1995; Simmons et al., 1996). The wide variety of step sizes may be caused in part by the absence of control over myosin-molecule orientation relative to the actin filament in these approaches, leading to diverse step sizes and consequent ambiguity in interpretation.
One way of overcoming this limitation is to use isolated actin and myosin filaments, where molecules are naturally oriented. Up to now, measurement of sliding dynamics in isolated filaments has not been achievable. By using nanofabricated cantilevers, we have succeeded in tracking the time course of sliding of single actin filaments over single thick filaments, with nanometer precision. In this approach, no artificial surface is required; hence the potential for spurious interaction between the myosin molecule and surface on which it is ordinarily mounted is averted. Because actin-myosin interactions are cooperative, molecular steps emerge clearly at the filament level, and are easily detected.
MATERIALS AND METHODS
Experimental arrangement
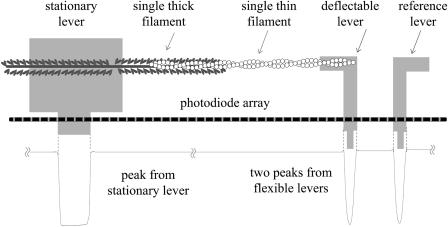
The setup is illustrated in Fig. 1. Briefly, single thick filaments taken from the anterior byssus retractor muscle of the living blue mussel, Mytilus, were rigidly stuck onto a nondeflectable stationary lever. A single F-actin was captured by one of the flexible levers of a pair (Fauver et al., 1998) and then brought to interact with the target thick filament in a well-aligned direction. Deflection of the flexible lever relative to its nondeflectable companion is a direct measure of F-actin translation along the thick filament. The positions of the levers were tracked continuously by a linear photodiode array. The three intensity peaks shown in Fig. 1 are raw data obtained from images of levers on the photodiode array. To optimize the resolution of the displacement measurement, we developed software to analyze the centroids of the lever images, on the basis of a quadratic fit to the lever-intensity peaks. In other words, a quadratic function was adopted to fit to the intensity peaks corresponding to the three levers.
FIGURE 1.
Measurement scheme. Two nanofabricated lever sets were employed, each held by a micromanipulator (Model Ts-5000-150, Burleigh, New York). A stationary lever of one set was used to hold the thick filament, whereas a deflectable lever of the other set was used to catch a single actin filament. Its deflection is a direct measure of F-actin translation along thick filament. Levers were precoated with nitrocellulose. Flexible levers have a stiffness of 0.18 pN/nm. A linear photodiode array was used to detect the positions of the three levers. The three peaks shown are taken from the respective images of the levers projected onto the linear photodiode array.
Apparatus
The measurement apparatus was based on a Zeiss Axiovert 135 TV microscope system (Liu and Pollack, 2002). It could work in either the bright field, differential interference contrast, or fluorescence mode, and was used for displacement measurement and filament visualization and manipulation.
In the bright field mode, the flow cell was illuminated by an intensity-adjustable quartz tungsten halogen light source through a water-immersion condenser (Zeiss Achroplan, 63×/0.9W, Thornwood, NY). The magnified images of the three levers, obtained using a 100× oil immersion objective lens (Zeiss Plan-Neofluar, 100×/1.30 oil) and an intermediate lens, were projected onto a 1024-pixel photodiode array (RL1024K, EG&G, Gaithersburg, MA). By using standard gratings of known period, the calibrated magnification was found to be 99.7 nm/pixel. The nondeflectable lever and each flexible lever cover ∼180 and ∼45 pixels, respectively. The time course of lever position could be recorded continuously at a pixel sampling rate of 50 kHz, which yielded a temporal resolution of 20.5 ms/scan, given the array length of 1024 pixels.
Before attempting to manipulate filaments, the lever pairs' positions and light intensity were adjusted to optimize signal level and shape. The apparatus could then be switched to the fluorescence mode, whose light source was a 100-W mercury arc lamp (HBO 100, Zeiss Attoarc, Thornwood, NY) directed through an optical fiber coupler (Technical Video, Woods Hole, MA). Fluorescence images of levers and filaments were monitored by a silicon intensified camera (ICCD, Sony XC-77 CCD, Sony Electronics, San Jose, CA).
Nanolevers
Nanofabricated cantilevers made of thin silicon nitride film 863 nm thick (Fauver et al., 1998) were used as displacement and tension transducers. One lever “set” consists of two rigid levers and four deflectable lever pairs of different length, any of which can be used for the experiment. One rigid lever was used as the “stationary” lever. The two levers of each pair have identical length and stiffness; one is used as the transducer, the other as a static reference. This design could eliminate the influence of drift because it allows for differential deflection measurements between the two levers of the pair (Fauver et al., 1998). One advantage of the levers over other molecule manipulation methods such as optical traps and glass needles is high stiffness consistency within each batch (±7–16%) because of the precision of the microfabrication technique; hence, stiffness calibrations of several typical samples are sufficient to characterize the entire batch with adequate accuracy. The other advantage is that the cantilevers' wide tension range allowed us to exert tensions as large/small as required.
Proteins
Native thick filaments were isolated from the anterior byssus retractor muscle of the living blue mussel, Mytilus, in thick filament extraction buffer (10 mM PIPES (pH 7.0), 8 mM Na2ATP, 10 mM MgCl2, 4 mM EGTA, 1 mM DTT) as described (Sellers et al., 1991). Rhodamine-phalloidin-labeled F-actin extracted from rabbit skeletal muscles was prepared by the standard method (Pardee and Spudich, 1982), and was provided courtesy of A. M. Gordon and Charles Luo (Department of Physiology and Biophysics, University of Washington). α-Actinin extracted from chicken gizzard (Sigma, St. Louis, MO) at a concentration of ∼4.0 mg/ml was used to increase the affinity of levers for actin filaments. Before use, it was dialyzed against actin buffer (AB): (25 mM imidazole (pH 7.4), 25 mM KCl, 1mM EGTA, 4 mM MgCl2, 1 mM DTT)).
Experimental procedure
The two lever sets were arranged in the flow cell with large (∼10 mm) separation. Near one set, a small quantity (10 μl) of α-actinin was added, and near the other set a similarly small quantity (10 μl) of native thick filaments was pipetted. After ∼5 min, the excess α-actinin and thick filaments were both washed away by a flow of AB perpendicular to the lever shafts. This way, most of the thick filaments would attach at right angles to the stationary lever axis; also the cross contamination of two kinds of protein would be minimized.
Orientation and density of attached thick filaments onto the nondeflectable stationary levers were examined carefully under differential interference contrast microscopy. Only thick filaments with a free segment projecting beyond the lever surface, and with axis at right angle to the lever, were acceptable for experimentation. Hence, myosin orientation was constrained in a natural direction relative to the actin filament, frequently an issue in single molecule experiments (Ishijima et al., 1994, 1996; Miyata et al., 1994; Finer et al., 1994, 1995; Simmons et al., 1996).
To promote visibility of thick filaments under fluorescence microscopy, the following procedure was used. With AB replaced by the solution AB/BSA/GOC (0.5 mg/ml BSA, 3 mg/ml glucose, 0.18 mg/ml glucose oxidase, 0.1 mg/ml catalase, 20 mM DTT in AB), F-actin of short length (1–3 μm) diluted in AB solution was introduced to the chamber in the absence of ATP. The F-actin fragments bound to the thick filaments, making them fluorescently visible. This enabled simultaneous manipulation of F-actin and thick filaments. Next, longer F-actin (5–10 μm) was added to the experimental chamber. A flow stream of AB/BSA/GOC with ATP and calcium perpendicular to the lever shafts was initiated immediately to exchange the chamber buffer. This flow also promoted the capture of single F-actin by the lever coated with α-actinin. When one end of a single F-actin was found attached to the tip of the deflectable lever, it was manipulated into the vicinity of the target thick filament. Once the two filaments interacted, sliding was initiated. Then, the apparatus was immediately switched to the bright-field mode to facilitate displacement measurement.
Stiffness correction
For experiments at the single molecule level, the measured displacements have to be corrected to exclude the influence of connection compliance. Here such a correction is not necessary for the following reasons. First, the F-actin samples were usually shorter than 10 μm, which would result in filament stiffness >4.0 pN/nm (Liu and Pollack, 2002). On the other hand, the connection stiffness between α-actinin and F-actin was ∼8.0 pN/nm according to our previous work on F-actin mechanics (Liu and Pollack, 2002). Therefore, the composite stiffness of F-actin and its connection to the flexible lever was ∼3.0 pN/nm. Compared with the lever stiffness of 0.18 pN/nm, the elongation of the F-actin and connection would have a negligible influence on the measured displacements. Also, interactions of multiple myosin molecules and F-actin give rise to high composite cross-bridge stiffness. Consequently, the overall stiffness of filaments and connections would be an order of magnitude higher than that of the flexible lever.
RESULTS
Nature of sliding
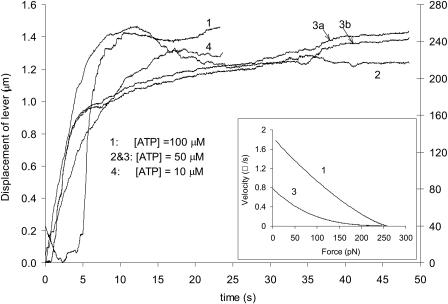
Fig. 2 illustrates representative traces of the time course of lever displacement. All traces except 3b were analyzed by the quadratic-fit method. After the attainment of a plateau, all displacement traces except trace 3 reveal some backward sliding, which may be due to an isometric force that is transiently lower than the load (Edman, 1988).
FIGURE 2.
Time courses of lever displacement at different [ATP]. Inset: Force-velocity curves corresponding to displacement traces. To obtain the force-velocity curves, exponential functions were used to fit the displacement curves, which were then linearly regressed at time segments of five data points with an increment of one data point. For clarity, only two traces are shown, and the dip toward the end of trace 1 was not included.
Generally, displacement from zero load to stall force was in the range of 1.2–1.5 μm, which corresponds to ∼10% of the thick filament length. Given the lever stiffness of 0.18 pN/nm, this displacement is equivalent to a tension of 200–270 pN, consistent with isometric tension of ∼230 pN per thin filament developed in intact whole muscles (Ford et al., 1981). Trace 3b was obtained with a so-called minimum-risk algorithm (Sokolov et al., 2003). This algorithm was used to precisely quantify the intensity-peak movement of each lever between adjacent scans. (Note: one complete scan, including 1024 pixels, takes ∼20.5 ms). The optimal positions of the intensity peaks from each lever are found by minimizing the integrated point-wise product of these positions with the first derivative of its immediate adjacent previous scan. The fact that traces 3a and 3b are similar (3b is shifted upward for clarity) demonstrates that the result is not an artifact of any particular algorithm.
The inset of Fig. 2 shows the force-velocity relation. It illustrates two features: first, the shape is hyperbolic, the same as in single muscle fibers and consistent with the prediction of the single molecular model proposed by Duke et al. (1999, 2000); and, second, maximum velocity depends on [ATP]—as reported in larger preparations (Barany and Barany, 1973) and the in vitro motility assay (Sellers et al., 1991). All of these features imply that actomyosin interaction measured here in single filaments is characteristic of that measured in intact muscle fibers.
Steps
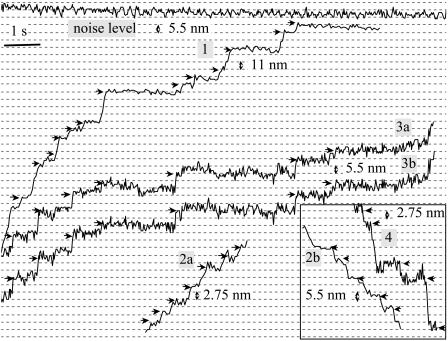
The features of central interest here are shown in Fig. 3, which are magnified images of the traces in Fig. 2, correspondingly labeled. The smooth sliding apparent during the rapid rise eventually gives way to stepwise sliding, which is illustrated. Whether stepwise behavior is also characteristic of earlier portions could not be determined because of time-resolution limitations (data acquisition rate is ∼50 points per second). During the slower rise, however, steps were consistently seen.
FIGURE 3.
Stepwise interaction between single actin and thick filaments. All data are taken from the correspondingly numbered traces of Fig. 2. Note that different traces have different scales. Horizontal line bar represents 1 s, except in traces 1 and 2, where it equals 0.5 s. The two traces in the box show backward steps, whereas traces 1, 2a, and 3 display mainly forward steps. Arrows indicate the positions of each pause. Typical noise level of the reference lever is shown in the top trace, and has the same scale as trace 2.
The minimal detectable step in trace 1 is 11 nm (indicated by arrows), whereas other, larger steps appear as integer multiples of that value, namely 22 nm, 33 nm, and 44 nm. These steps could be easily seen by eye because they were preceded and followed by long pauses. In trace 2a, step size as small as 2.75 nm is also apparent. Also, clear steps ranging from ∼5.5 nm and ∼11.0 nm to nearly 16.5 nm are seen as well in trace 3a (arrows). Trace 3b, which was analyzed with minimum-risk algorithm, reveals the same steps as that of 3a, again implying that the steps are unlikely to have resulted from the artifacts of data analysis.
Steps were not features of forward movement alone. Backward steps (corresponding to sarcomere lengthening) also appeared commonly. In trace 2 of Fig. 2, after the tension had reached a maximum, F-actin transitioned into a backward stepwise movement. Sliding was rapid at first, with short pauses (trace 2b in Fig. 3). Step size was uniformly ∼11 nm. With the increase of backward motion, pauses became considerably longer and step size varied from 11 nm to ∼44 nm (data not shown). Backward steps of 5.5 nm can also be seen in trace 4 of Fig. 2, as depicted in Fig. 3. Occasional backward steps also appeared during periods of largely forward sliding.
Possible artifacts
Several possible artifacts were considered. One possibility is that the steps are generated by the discreteness of the photodiode array—as the lever sweeps across the array, a step is generated for each pixel that is traversed. However, each pixel of the photodiode array corresponds to a movement of ∼100 nm, which is far larger than the size of the steps. A second possibility is that the steps are generated by the software that converts the photodiode-array signal to a length trace. But we have shown above that two independent algorithms generate virtually identical traces. Finally, random noise, when superimposed on a shortening or lengthening ramp, could create step-like signals. To avert this possibility, lever pairs were used instead of single levers, one attached to the actin filament, the other free. Any system noise should appear on both levers. Hence, we could compare each step measured on the deflectable lever with the behavior of the reference lever to determine whether the step arose from noise. Spurious signals were thereby eliminated from consideration.
Sensitivity of the system can be derived from the traces of Fig. 3. The top trace shows typical noise of the reference lever with no filament attached. Root mean-square noise is 3.5 nm. When the system is stiffened by the addition of the actin filament, noise is reduced. In trace 1, for example, during the extended periods of zero translation, root mean-square noise is 1.8 nm, although this figure varies from trace to trace depending on image quality. Hence, the system is easily able to detect steps in the range of several nanometers.
Step analysis
Step size could be easily analyzed from records by eye. For better precision, however, we followed a systematic procedure (Blyakhman et al., 1999, 2001; Yang et al., 1998). In this procedure, the start and end points of each pause are defined by cursors. Then an algorithm computes the best-fit lines for each pause and the best-fit straight line to the segment of the curve between the two pauses (the step). If this line fails to connect the end point of the first pause with the start point of the second one, the step is rejected. If it is accepted, the algorithm computes step size as the vertical displacement between the center of the first pause and the center of the second pause, which gives step size. To qualify as a pause, the dwell time had to be at least 103 ms—in other words, it had to include at least five consecutive data points. Applying slope criteria (i.e., slope of the fitted pause could not deviate from zero by selectable amounts) made no substantive difference in the results, except that the total number of data points was decreased. Sizes obtained from many steps were plotted as a continuous histogram.
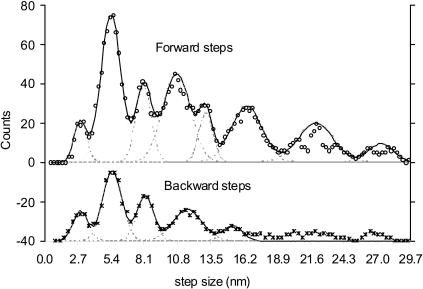
A histogram of forward translation step size is shown as open circles in Fig. 4. The histogram includes 612 steps, at [ATP] of 10–100 μM. A histogram of lengthening or “backward” steps (n = 215), which were generally less distinct than the forward steps, is plotted beneath in a similar way. In both cases, multiple peaks are seen at approximate integer multiples of 2.7 nm, such as 5.4 nm, 8.1 nm, and 10.8 nm. The first peak, at 2.7 nm, may be less reliable than the others because the typical noise level is of similar magnitude. However, peaks also appeared at integer multiples of 2.7 nm, such as 8.1 nm and 13.2 nm, implying that the 2.7-nm peak does not arise from noise.
FIGURE 4.
Continuous histogram of step-size distribution with bin width of 1.0 nm and increments of 0.1 nm. Tick marks on the abscissa are spaced at 2.7-nm increments. See text for details.
To determine the peak positions with precision, Gaussian distributions were fit to each peak (dashed lines). Their sum is depicted as a continuous curve, which gave a good approximation to the experimental data. The fitted peak positions and the corresponding standard deviations are shown in Table 1. Except for the higher orders, for which there were few data, forward and backward peaks were both generally close to their nominal values as integer multiples of 2.7 nm. (The slight rightward shift of the first peak may arise from contributions from the tail of the dominant second peak.) If this consistency is not fortuitous, it implies that, at least to some extent, the contractile process is reversible.
TABLE 1.
Comparison between nominal and Gaussian fit peak positions
| Fitted ± Std (No.) | ||
|---|---|---|
| Nominal | Forward | Backward |
| 2.7 | 2.90 ± 0.50 (26) | 2.90 ± 0.60 (23) |
| 5.4 | 5.40 ± 0.82 (155) | 5.50 ± 0.75 (68) |
| 8.1 | 8.03 ± 0.60 (58) | 8.15 ± 0.65 (47) |
| 10.8 | 10.70 ± 1.10 (125) | 11.6 ± 1.15 (38) |
| 13.5 | 13.10 ± 0.55 (35) | – |
| 16.2 | 16.40 ± 1.23 (89) | – |
| 21.6 | 22.00 ± 1.43 (72) | – |
| 27.0 | 27.30 ± 1.05 (27) | – |
DISCUSSION
Even though this is the first report of steps between single isolated muscle filaments, it is not the first indication of a 2.7-nm paradigm. Stepwise interaction at integer multiples of 2.7 nm has also been reported at the level of the single sarcomere (Blyakhman et al., 1999, 2001; Yang et al., 1998; Yakovenko et al., 2002). Hence, there is some consistency among results obtained at different organizational levels.
The value 2.7 nm is equal to the monomeric repeat along the actin filament. Monomers along each actin strand repeat every 5.4 nm, and, as the two strands making up the filament are axially displaced by half of 5.4 nm, the axial monomeric repeat is 2.7 nm. Steps are an integer multiple of this value. A similar correspondence exists in the kinesin-microtubule system, where steps are integer multiples of the 8-nm tubulin repeat (Svoboda et al., 1993; Malik et al., 1994).
By contrast, steps measured in single molecule experiments using optical traps have yielded many values of step size. Step size was initially reported to be in the range of 10–25 nm (Ishijima et al., 1994, 1996; Miyata et al., 1994; Finer et al. 1994, 1995; Simmons et al., 1996). As the technology improved, step size diminished progressively down to ∼4 nm (Molloy et al., 1995). It may be that the limited signal-to-noise ratio in the optical trap measurements restricts the ability to detect histogram peaks and valleys, and that only the envelope of the peaks is detected; this would explain the rather broad histograms commonly seen. Hence, there may be no real inconsistency between measurements using optical traps and our measurements at the filament and myofibril level. The latter experiments have the advantage not only of higher resolution, but also that molecules are oriented in their natural configuration.
An independent approach to step-size measurement at the molecular level was taken by Kitamura et al. (1999). By employing a very fine glass needle tipped by a single myosin subfragment (S1), translation of the myosin subfragment along bundles of actin filaments fixed onto a glass surface was measured. With good control of myosin orientation, step size of ∼5.4 nm was consistently found. This value is 2 × 2.7 nm, and coincides with the second (and major) peak in our histogram. It appears that the myosin molecule translated from monomer to monomer along a single actin strand in that experiment. By contrast, the physical arrangement in our experiment allowed interactional opportunities with both actin strands, thereby eliciting the occasional smaller step size, although the 5.4-nm peak remained the dominant one. Like ours, the results of Kitamura et al. fit the actin-based paradigm.
The stepwise actomyosin interaction we found here involved perhaps tens of myosin molecules. In other words, this study revealed the collective dynamics of a molecular ensemble. The appearance of steps implies high cooperativity among ensemble members. Single molecules were not studied, and therefore our results do not directly settle the issue of single-molecule step size. They do settle the question of how molecules step collectively in their natural configuration, which, after all, is the major issue of concern: to understand how molecules produce contraction in real muscle. Here, no inferences from smaller-scale specimens need be drawn. Filament dynamics are measured directly, and should be relevant to the dynamics of higher-level muscle systems.
A question is whether the detected step size is necessarily the same as the power stroke. Based on the crystallographic structure of myosin molecules, Rayment et al (1993a,b) predicted a power stroke of ∼6.0 nm by tilting of the myosin-neck region. According to the molecular model of Duke (1999, 2000), step size would decrease to 50–60% of the power stroke size as the tension increased to ∼80% of the isometric value (Fig. 6 in Rayment et al., 1993). Hence, step size of 2.7 nm detected at high load in our experiments might underestimate the power-stroke size, the real value being ∼5.0–6.0 nm, which would be consistent with the lever arm hypothesis (Rayment et al., 1993a,b). Although this is an intriguing idea, it would need to be reconciled with the appearance of steps not only at 2.7 nm but also at integer multiples of this size. Also, the similarity between the backward and forward step paradigm would require explanation. Whether these features are explained by the myosin power-stroke concept remains to be seen. Alternatively, it may be that a more direct fit is obtained by mechanisms based on actin-filament propulsion, which produces a natural fit to the 2.7-nm stepping paradigm (Pollack, 2001).
In summary, the significant result is that stepwise actomyosin interactions of consistent size paradigm are now seen at three levels of organization: single molecule, single filament, and single myofibril. The fact that similar step sizes are found in independent experimental approaches using different methodologies implies that the quantal stepping mechanism is a central feature of the contractile process.
References
- Barany, M., and K. Barany. 1973. The interaction of myosin, actin and ATP in the intact muscle. J. Mechanochem. Cell Motil. 2:51–59. [PubMed] [Google Scholar]
- Blyakhman, F., T. Shklyar, and G. H. Pollack. 1999. Quantal length changes in single contracting sarcomeres. J. Muscle Res. Cell Motil. 20:529–538. [DOI] [PubMed] [Google Scholar]
- Blyakhman, F., A. Tourovskaya, and G. H. Pollack. 2001. Quantal sarcomere-length changes in relaxed single myofibrils. Biophys. J. 81:1093–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duke, T. A. 1999. Molecular model of muscle contraction. Proc. Natl. Acad. Sci. USA. 96:2770–2775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duke, T. A. 2000. Cooperativity of myosin molecules through strain-dependent chemistry. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355:529–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edman, K. A. 1988. Double-hyperbolic force-velocity relation in frog muscle fibres. J. Physiol. 404:301–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fauver, M. E., D. L. Dunaway, D. H. Lilienfeld, H. G. Craighead, and G. H. Pollack. 1998. Microfabricated cantilevers for measurement of subcellular and molecular forces. IEEE Trans. Biomed. Eng. 45:891–898. [DOI] [PubMed] [Google Scholar]
- Finer, J. T., A. D. Mehta, and J. A. Spudich. 1995. Single myosin molecule mechanics: piconewton forces and nanometre steps. Biophys. J. 68(Suppl.):291s–296s; discussion 296s–297s. [DOI] [PubMed] [Google Scholar]
- Finer, J. T., R. M. Simmons, and J. A. Spudich. 1994. Characterization of single actin-myosin interactions. Nature. 368:113–119.8139653 [Google Scholar]
- Ford, L. E., A. F. Huxley, and R. M. Simmons. 1981. The relation between stiffness and filament overlap in stimulated frog muscle fibres. J. Physiol. 311:219–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishijima, A., Y. Harada, H. Kojima, T. Funatsu, H. Higuchi, and T. Yanagida. 1994. Single-molecule analysis of the actomyosin motor using nano-manipulation. Biochem. Biophys. Res. Commun. 199:1057–1063. [DOI] [PubMed] [Google Scholar]
- Ishijima, A., H. Kojima, H. Higuchi, Y. Harada, T. Funatsu, and T. Yanagida. 1996. Multiple- and single-molecule analysis of the actomyosin motor by nanometer-piconewton manipulation with a microneedle: unitary steps and forces. Biophys. J. 10:383–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitamura, K., M. Tokunaga, A. H. Iwane, and T. Yanagida. 1999. A single myosin head moves along an actin filament with regular steps of 5.3 nanometres. Nature. 397:129–134. [DOI] [PubMed] [Google Scholar]
- Liu, X., and G. H. Pollack. 2002. Actin mechanics measured by nanofabricated cantilevers. Biophys. J. 83:2705–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malik, F., D. Brillinger, and R. D. Vale. 1994. High-resolution tracking of microtubule motility driven by a single kinesin motor. Proc. Natl. Acad. Sci. USA. 91:4584–4588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyata, H., H. Hakozaki, H. Yoshikawa, N. Suzuki, K. J. Kinosita, T. Nishizaka, and S. Ishiwata. 1994. Stepwise motion of an actin filament over a small number of heavy meromyosin molecules is revealed in an in vitro motility assay. J. Biochem. (Tokyo). 115:644–647. [DOI] [PubMed] [Google Scholar]
- Molloy, J. E., J. E. Burns, J. Kendrick-Jones, R. T. Tregear, and D. C. White. 1995. Movement and force produced by a single myosin head. Nature. 378:209–212. [DOI] [PubMed] [Google Scholar]
- Pardee, J. D., and J. A. Spudich. 1982. Purification of muscle actin. Methods Enzymol. 85:164–181. [DOI] [PubMed] [Google Scholar]
- Pollack, G. H. 2001. Cells, Gels and the Engines of Life. Ebner & Sons, Seattle.
- Rayment, I., H. M. Holden, M. Whittaker, C. B. Yohn, M. Lorenz, K. C. Holmes, and R. A. Milligan. 1993. Structure of the actin-myosin complex and its implications for muscle contraction. Science. 261:58–65. [DOI] [PubMed] [Google Scholar]
- Rayment, I., W. R. Rypniewski, K. Schmidt-Base, R. Smith, D. R. Tomchick, M. M. Benning, D. A. Winkelmann, G. Wesenberg, and H. M. Holden. 1993. Three-dimensional structure of myosin subfragment-1: a molecular motor. Science. 261:50–58. [DOI] [PubMed] [Google Scholar]
- Sellers, J. R., Y. J. Han, and B. Kachar. 1991. The use of native thick filaments in in vitro motility assays. J. Cell Sci. Suppl. 14:67–71. [DOI] [PubMed] [Google Scholar]
- Simmons, R. M., J. T. Finer, S. Chu, and J. A. Spudich. 1996. Quantitative measurements of force and displacement using an optical trap. Biophys. J. 70:1813–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolov, S. Y., A. A. Grinko, A. V. Tourovskaia, F. B. Reitz, G. H. Pollack, and F. A. Blyakhman. 2003. “Minimum average risk” as a new peak detection algorithm applied to myofibrillar dynamics. Comput Methods Programs Biomed. 72:21–26. [DOI] [PubMed] [Google Scholar]
- Svoboda, K., C. F. Schmidt, B. J. Schnapp, and S. M. Block. 1993. Direct observation of kinesin stepping by optical trapping interferometry. Nature. 365:696–697. [DOI] [PubMed] [Google Scholar]
- Yakovenko, O., F. Blyakhman, and G. H. Pollack. 2002. Fundamental step size in single cardiac and skeletal sarcomeres. Am. J. Physiol. Cell Physiol. 283:C735–C742. [DOI] [PubMed] [Google Scholar]
- Yang, P., T. Tameyasu, and G. H. Pollack. 1998. Stepwise dynamics of connecting filaments measured in single myofibrillar sarcomeres. Biophys. J. 74:1473–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]