Abstract
We discuss the difference between osmotic permeability pf and diffusion permeability pd of single-file water channels and demonstrate that the pf/pd ratio corresponds to the number of effective steps a water molecule needs to take to permeate a channel. While pd can be directly obtained from equilibrium molecular dynamics simulations, pf can be best determined from simulations in which a chemical potential difference of water has been established on the two sides of the channel. In light of this, we suggest a method to induce in molecular dynamics simulations a hydrostatic pressure difference across the membrane, from which pf can be measured. Simulations using this method are performed on aquaporin-1 channels in a lipid bilayer, resulting in a calculated pf of 7.1 × 10−14 cm3/s, which is in close agreement with observation. Using a previously determined pd value, we conclude that pf/pd for aquaporin-1 measures ∼12. This number is explained in terms of channel architecture and conduction mechanism.
INTRODUCTION
Aquaporin-1 (AQP1), a membrane channel protein, is the first characterized member of the aquaporin (AQP) family (Hohmann et al., 2001). The protein is abundantly present in multiple human tissues, such as the kidneys. AQP1 forms homotetramers in cell membranes, each monomer forming a functionally independent water pore, which does not conduct protons, ions, or other charged solutes. A fifth pore is formed in the center of the tetramer. Recent experiments have indicated that the central pore of AQP1 tetramers may conduct ions (Saparov et al., 2001; Yool and Weinstein, 2002). However, the passive transport of water across cell membranes remains to be the major physiological function established for AQP1.
The first atomic structures of AQP1 were obtained by electron microscopy (Murata et al., 2000; Ren et al., 2001). A high-resolution structure of the Escherichia coli glycerol uptake facilitator (GlpF), a bacterial member of the AQP family, was solved by x-ray crystallography at about the same time (Fu et al., 2000). In light of the successful exploration of various membrane ion channels (Bernèche and Roux, 2001; Biggin and Sansom, 2002; Randa et al., 1999; Roux, 2002), molecular dynamics (MD) simulations have also been performed on AQP water channels (de Groot et al., 2001; de Groot and Grubmüller, 2001; Jensen et al., 2001, 2002, 2003; Tajkhorshid et al., 2002; Zhu et al., 2001, 2002) soon after their structures became available. Recently, the structure of AQP1 was also solved by x-ray crystallography at high resolution (Sui et al., 2001), offering a better chance to study the dynamics and function of this water channel in atomic detail.
The key characteristics accounting for transport through water channels such as AQP1 are the osmotic permeability (pf) and the diffusion permeability (pd) (Finkelstein, 1987), which both can be measured experimentally. pf is measured through application of osmotic pressure differences, whereas pd is measured through isotopic labeling, e.g., use of heavy water. In this study, using a continuous-time random-walk model (Berezhkovskii and Hummer, 2002), we will demonstrate that pf and pd of a single-file water channel are related, but differ in value. We will further show that equilibrium MD simulations yield the pd value, and propose a method to induce hydrostatic pressure differences across the membrane in MD simulations, allowing pf of membrane channels to be determined from simulations. We will also describe MD simulations of AQP1 based on the structure reported in (Sui et al., 2001), in which pressure-induced water permeation was used to determine the channel's pf value, which was found to agree well with experimental measurements.
THEORY AND METHODS
In this section, we will define pf and pd for water channels, and, in particular, investigate the relationship between the two for single-file water channels. We will also describe our simulations in which hydrostatic pressure differences across the membrane are established through application of external forces.
Definition of pf and pd
When the solutions on the two sides of a membrane have different concentrations of an impermeable solute, water flows from the low concentration side to the other side. In dilute solutions, the net water flux through a single water channel, jW (mol/s), is linearly proportional to the solute concentration difference ΔCS (mol/cm3):
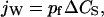 |
(1) |
where pf (cm3/s) is defined as the “osmotic permeability” of the channel (Finkelstein, 1987).
In contrast, no net water flux is expected in equilibrium, i.e., when no solute concentration difference is present. It is, however, still of interest to study water diffusion through the channels for ΔCS = 0. For this purpose, experiments have been designed where a fraction of water molecules is labeled, e.g., by isotopic replacement or by monitoring nuclear spin states, so that they can be traced. Assuming that the interaction of these so-called “tracers” with the membrane and with other water molecules is identical to that of nontracer water molecules, tracers can be used to study diffusion of water molecules through channels.
When the reservoirs on the two sides of a membrane have different concentrations of tracers, a diffusional tracer flux will be established down the concentration gradient, although the average net water flux (consisting of both tracers and other water molecules) remains zero. The tracer flux jtr (mol/s) through a single channel is linearly proportional to the tracer concentration difference ΔCtr (mol/cm3):
 |
(2) |
where pd (cm3/s) is defined as the “diffusion permeability” of the channel (Finkelstein, 1987).
pd quantifies the exchange of individual water molecules between the two reservoirs at equilibrium, as explained below. We define a “permeation event” as a complete transport of a water molecule through the channel from one reservoir to the other. Let q0 be the average number of such permeation events in one direction per unit time; the number of permeation events in either direction should be identical, resulting in a total number of 2q0. q0 is an intrinsic property of a water channel and is independent of tracer concentration.
Let us assume that one reservoir has a tracer concentration of Ctr, and (for the sake of convenience) that the other reservoir has zero tracer concentration. The ratio of tracers to all water molecules in the first reservoir is Ctr/CW, where CW = 1/VW is the concentration of water, and VW (18 cm3/mol) is the molar volume of water, which is usually assumed to be constant. Because according to our assumption tracers move just like normal water molecules, the same proportion (i.e., Ctr/CW) should characterize water molecules permeating the channel. Consequently, the tracer flux can be related to the total number of water molecules permeating the channel (q0) by  , where NA is Avogadro's number. Therefore, pd and q0 are related by a constant factor:
, where NA is Avogadro's number. Therefore, pd and q0 are related by a constant factor:
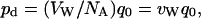 |
(3) |
where vW = VW/NA is the average volume of a single water molecule.
Equilibrium MD simulations provide an ideal tool to study free water diffusion through channels, because all water molecules can be easily traced in the simulations, and q0 counted (de Groot and Grubmüller, 2001; Tajkhorshid et al., 2002). pd can then be calculated according to Eq. 3 from the simulations.
pf and pd of a single-file water channel
Within some narrow channels (AQPs, gramacidins, etc.), water molecules form a single file, and their movement along the channel axis is accordingly highly correlated. Recently, a continuous-time random-walk model (Berezhkovskii and Hummer, 2002) was proposed to describe the transport of single-file water in channels. This model assumes that the channel is always occupied by N water molecules, and the whole water file moves in hops (translocations that shift all water molecules by the distance separating two neighboring water molecules) simultaneously and concertedly, with leftward and rightward hopping rates kl and kr, respectively. In equilibrium, kl and kr have the same value, denoted as k0. Due to strong coupling between the water molecules, local effects (energetic barriers arising from interaction with certain parts of the channel wall, access resistance at channel entrances, etc.) contribute to the hopping rate of the whole water file. Consequently, all factors affecting the kinetics of water movement are effectively integrated into this single parameter (k0). In the following, we will show that both pd and pf can be predicted by this model, in terms of N and k0.
Because the complete permeation of a water molecule from one side of the channel to the other side includes at least N + 1 hops (shifts) of the single file, one expects the rate of permeation events at equilibrium to be smaller than the hopping rate. Indeed, the number of unidirectional permeation events per unit time, q0, is given by
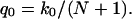 |
(4) |
Equation 4 has been proven from kinetics (Berezhkovskii and Hummer, 2002) as well as using a state diagram (Zhu and Schulten, 2003), and its validity was verified by MD simulations of carbon nanotubes (Hummer et al., 2001; Zhu and Schulten, 2003). Note that p used in Zhu and Schulten (2003) corresponds here to 2q0. Combining Eqs. 3 and 4, pd can be expressed as:
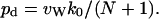 |
(5) |
In contrast, pf is measured when a net water flux is induced by different solute concentrations in the two reservoirs. In this case, the chemical potentials of water in the two reservoirs are different (the difference denoted as Δμ). Consequently, the hopping rates (kr and kl) of the two directions are no longer the same. We note that the yield of a hop is the transfer of one water molecule from one reservoir to the other, resulting in a free energy change of Δμ in the system. In analogy to the forward and backward rates of a chemical reaction, the ratio of kr to kl can be expressed (Kalra et al., 2003) as:
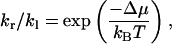 |
(6) |
where kB is the Boltzmann constant and T is the temperature.
We note now that kr and kl are both functions of Δμ/kBT. Because under physiological conditions, Δμ is much smaller than kBT (e.g., Δμ/kBT = 0.0036 for a 200-mM solution of sucrose, according to Eq. 10 below), we can expand kr and kl to first order:
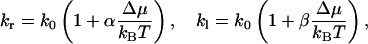 |
(7) |
(for a symmetric channel also holds α = −β). The net water flux can be expressed by the difference between kr and kl:
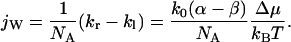 |
(8) |
Substituting Eq. 7 into Eq. 6 and comparing the first order terms in Δμ/kBT leads to β − α = 1. The net water flux is then:
 |
(9) |
For dilute solutions, Δμ is linearly proportional to the solute concentration difference (Finkelstein, 1987):
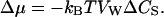 |
(10) |
From Eqs. 1, 9, and 10, we obtain then the expression:
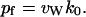 |
(11) |
In a recent study (de Groot et al., 2002), a similar expression for pf was provided, namely, 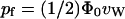 , where Φ0 was defined as the intrinsic flux.
, where Φ0 was defined as the intrinsic flux.
According to Eqs. 5 and 11, the ratio of pf to pd predicted by the continuous-time random-walk model is:
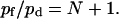 |
(12) |
The difference between pf and pd can be further elaborated as follows. For single-file water transport, a hop results in the net transfer of one water molecule from one side of the channel to the other side. pf is related to the rate of net water transfer under a chemical potential difference and, therefore, is determined by the hopping rate (see Eq. 11). In contrast, pd is determined by the rate of permeation events (see Eq. 3). A permeation event requires an individual water molecule to traverse all the way through the channel, and is not the same as a hop. Actually, the pf/pd ratio is exactly determined by the relative rates of hops and permeation events. Most models proposed for single-file water transport predict this ratio to be N or N + 1 (Finkelstein, 1987).
For AQP1, the average number of water molecules in the single-file region is ∼7, but the experimentally measured ratio of pf/pd is 13.2 (Mathai et al., 1996). To understand the difference, we note that water molecules in an AQP1 channel may occasionally deviate from the single-file configuration due to conformational fluctuation of the protein. Furthermore, the behavior of water in the vestibule regions of the AQP channel (Jensen et al., 2002; Lu et al., 2003; Tajkhorshid et al., 2002) suggests that the single-file model is too simple and that water transport effectively involves vestibular water at the channel entrances, such that the latter water cannot be counted as bulk water. To test these suggestions, one should determine the pf/pd ratio in MD simulations of AQP1. As stated above, for the determination of pf, a chemical potential difference needs to be applied. This can be achieved through application of a hydrostatic pressure difference.
A hydrostatic pressure difference ΔP between the two reservoirs can also give rise to a difference in the chemical potential of water (Finkelstein, 1987):
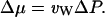 |
(13) |
In fact, the “osmotic pressure” difference between two solutions is defined as the hydrostatic pressure difference that would generate the same Δμ. Therefore, the osmotic pressure difference between two dilute solutions is given by van't Hoff's law (Finkelstein, 1987):
 |
(14) |
where R = kBNA is the gas constant. It is also known experimentally that equal osmotic and hydrostatic pressure differences produce the same water flux through water channels (Sperelakis, 1998). This observation justifies our earlier assumption that the hopping rates and, hence, the water flux are functions of Δμ alone (Eqs. 7 and 9), regardless of whether Δμ arises from osmotic or hydrostatic pressure differences.
Statistics of hops
According to the continuous-time random-walk model, when an osmotic or hydrostatic pressure difference exists, the water file performs a biased random walk, characterized by the hopping rates kr and kl. In this section, we will determine the statistical distribution of hops as a function of time.
Within any infinitesimally small time dt, the probability of the water file to make a rightward hop is krdt, independent of its history, i.e., when and how many rightward hops were made before. Such a process is referred to as a “Poisson process,” and the total number of rightward hops within time t, mr(t), obeys the well-known “Poisson distribution,” whose mean and variance are both krt. The derivation and properties of the Poisson distribution can be found in textbooks of probability theory, e.g., in Larsen and Marx (2001). Similarly, the number of leftward hops, ml(t), also obeys the Poisson distribution, with klt being its mean and variance.
The net number of hops, m(t), is defined as the difference of the numbers of rightward and leftward hops, i.e., m(t) = mr(t) − ml(t). Because the probabilities of making rightward and leftward hops are independent of each other, we obtain
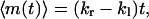 |
(15) |
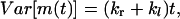 |
(16) |
where  . Equations 15 and 16 show that both the mean and the variance of m(t) increase linearly with time. These expressions show that monitoring the average number of hops and its variance permits one to determine both kr and kl.
. Equations 15 and 16 show that both the mean and the variance of m(t) increase linearly with time. These expressions show that monitoring the average number of hops and its variance permits one to determine both kr and kl.
Methodology for calculating pf from MD simulations
As mentioned earlier, equilibrium MD simulations can be used to calculate pd of a water channel; however, pf is not equal to pd and cannot be directly obtained from equilibrium simulations. To determine pf, one needs to produce different osmotic or hydrostatic pressures on the two sides of the membrane.
Fig. 1 illustrates our scheme to induce a hydrostatic pressure difference in MD simulations, based on a method we proposed recently (Zhu et al., 2002). In a periodic system, the unit cell is replicated in three dimensions; therefore water layers and membranes alternate along the z-direction, defined as the membrane normal. Fig. 1 shows a water layer sandwiched by adjacent membranes. We define three regions (I, II, III) in the water layer, as shown in the figure. Region III is isolated from the two sides of the membrane by regions I and II, respectively. A constant force f along the z-direction is exerted on all water molecules in region III, generating a pressure gradient in this region that, consequently, results in a pressure difference between regions I and II (Zhu et al., 2002):
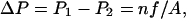 |
(17) |
where n is the number of water molecules in region III, and A is the area of the membrane. Consequently, a net water flux jW through the membrane channels can be induced, and pf calculated from jW and ΔP. We note that the membrane needs to be held in its position, e.g., by constraints, to prevent an overall translation of the whole system along the direction of the applied forces.
FIGURE 1.
Illustration of the method to produce a pressure difference in MD simulations. The two membranes shown in the figure are “images” of each other under periodic boundary conditions. A constant force f is exerted on water molecules in region III.
Assuming that the thickness of region III is d, the number of water molecules in this region is n = Ad/vW. Substituting this into Eq. 17 and the result into Eq. 13, we obtain for the chemical potential difference of water between regions I and II:
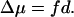 |
(18) |
The external force field generates a mechanical potential difference of fd between regions I and II, which must be exactly balanced by the chemical potential difference Δμ under a stationary population distribution of water, therefore also giving Eq. 18.
In our earlier approach (Zhu et al., 2002), all water molecules in the bulk region, including those adjacent to the entrances of the channels, were subject to external forces, a setup which might artificially affect the number of water molecules permeating the channel. This shortcoming is overcome in our present setup through application of external forces only to water molecules in region III, which leaves regions I and II under uniform hydrostatic pressures, and, hence, represents experimental conditions more closely.
To keep the membrane in place, our earlier method (Zhu et al., 2002) applied constant counter forces on the membrane to balance the effect of different hydrostatic pressures experienced by the membrane on its two sides. In this study, we chose to instead apply constraints on the membrane in the z-direction to prevent an overall translation of the system, mainly because of the following reason: the number of water molecules (n) in region III, and, therefore, the total external force on water (nf), experience slight fluctuations during the simulation, and application of a fixed counter force on the membrane may not always exactly balance nf. Moreover, for very long simulations, applying constraints can also eliminate drifting of the membrane along the z-direction that may happen due to thermal motion. Too strong constraints, however, may restrict the dynamics of the protein, and one must carefully choose the constraints as to minimize this undesired effect.
An interesting method, which we refer to as the “two-chamber setup,” has been used to study osmotically driven water flow in MD simulations (Kalra et al., 2003), where the unit cell consists of two membranes and two water layers containing different concentrations of solutes. In the present study, we chose our proposed method rather than the two-chamber setup for two reasons. Firstly, to observe on the ns timescale a statistically significant water flux through an AQP1 channel, one has to induce in the two-chamber setup a large chemical potential difference (Δμ) of water. However, it is noteworthy that Eq. 10 is valid only for dilute solutions; when the solute concentration is high, Δμ is no longer linearly proportional to the concentration difference. In contrast, in our method, Δμ can be linearly controlled (see Eq. 18). Secondly, the osmotic water flux in the two-chamber setup will decrease with time and eventually stop (Kalra et al., 2003), whereas our method generates a stationary flux, which permits sampling for as long as one can afford.
Simulation setup
The AQP1 (Sui et al., 2001) tetramer was embedded in a palmitoyl-oleoyl-phosphatidyl-ethanolamine (POPE) lipid bilayer and solvated by adding layers of water molecules on both sides of the membrane. The whole system (shown in Fig.2) contains 81,065 atoms. The system was first equilibrated for 500 ps with the protein fixed, under constant temperature (310 K) and constant pressure (1 atm) conditions. Then the protein was released and another 450 ps equilibration performed.
FIGURE 2.
Side view of the unit cell including the AQP1 tetramer, POPE lipid molecules, and water molecules. The protein is shown in tube representation; lipids in line representation (hydrogen atoms not shown); phosphorus atoms of lipids are drawn as vdW spheres; water molecules are shown in line representation, with those in region III (see Fig. 1) colored blue.
Starting from the last frame of the equilibration, four simulations were initiated. In these simulations (to which we refer as sim1, sim2, sim3, and sim4), a constant force (f) was applied on the oxygen atoms of the water molecules in region III, defined as a 7.7-Å thick layer (shown in Fig. 2) in our system, to induce a pressure difference across the membrane. In principle, the position and thickness of region III can be arbitrarily defined and should not affect the results, as long as the induced pressure difference is set to the same value (by choosing a proper f); in practice, one would partition the bulk water in such a way that each of the three regions (I, II, III) has a sufficiently large thickness (relative to the diameter of a water molecule). The constant forces used in the four simulations differ in their direction or magnitude, generating four pressure differences, as summarized in Table 1. The simulations were performed under constant temperature (310 K) and constant volume conditions.
TABLE 1.
Summary of the four simulations reported in this study
| f (pN) | ΔP (MPa) | Δμ (kcal/mol) | |
|---|---|---|---|
| sim1 | −7.36 | −195 | −0.814 |
| sim2 | −3.68 | −97 | −0.407 |
| sim3 | 3.68 | 97 | 0.407 |
| sim4 | 7.36 | 195 | 0.814 |
The thickness of region III is d = 7.68 Å, containing on average n = 2.47 × 103 water molecules. f is the constant force applied on individual water molecules. The area of the membrane in the unit cell is A = 9.35 × 10−17 m2. The induced pressure difference ΔP and chemical potential difference Δμ of water are calculated according to Eqs. 17 and 18, respectively.
As mentioned earlier, the membrane needs to be constrained to prevent the overall movement of the system under the external forces. This is done by applying harmonic constraints to the Cα atoms of the protein and the phosphorus atoms of the lipid molecules, with spring constants of 0.12 kcal/mol/Å2 and 0.8 kcal/mol/Å2, respectively. These spring constants are chosen to fully balance the external forces when the whole membrane is displaced by ∼1 Å along z from its reference position under a pressure difference of 200 MPa (as in sim1 and sim4). The constraints are applied only in the z-direction, and all atoms are free to move in the x- and y-directions. Note that the constraints on the protein are fairly weak and act only on the backbone Cα atoms; therefore, significant flexibility of the protein (especially its side chains) is still realized during the simulations.
During preliminary simulations, the side chain of ARG197 (PDB entry 1J4N) was found to deviate from its original position (and in some cases even blocked the channel) due to the breaking of an H-bond between its guanidinium group and its backbone oxygen. A similar behavior of this ARG residue was observed in simulations of GlpF with induced pressure differences (Zhu et al., 2002), but not in equilibrium simulations of AQP1 or GlpF (de Groot and Grubmüller, 2001; Tajkhorshid et al., 2002). Therefore, the inward motion of the ARG appears to arise from the application of large pressure differences in the present study. We constrained the above mentioned H-bond in our present simulations to avoid blockage of the channel, a measure also applied in our earlier simulations (Zhu et al., 2002). In the crystal structure of AQP1 (1J4N), a water molecule (HOH:383) is buried inside the protein, at a position close to an intrinsic H-bond of an α-helix. In our preliminary simulations, this water molecule was usually squeezed out of the protein; however, occasionally it attracted other water molecules from the outside into this region and made the protein unstable. To avoid the instability, the stated water molecule was deleted for the simulations reported in this article.
All simulations were performed using the CHARMM27 force field (MacKerell et al., 1998; Schlenkrich et al., 1996), the TIP3P (Jorgensen et al., 1983) water model, and the MD program NAMD2 (Kalé et al., 1999). Full electrostatics was employed using the particle mesh Ewald (PME) method (Essmann et al., 1995). Simulations sim1, sim2, sim3, and sim4 were each run for 5 ns, with the first 1 ns discarded and the remaining 4 ns used for analysis. One nanosecond of simulation took 22.4 h on 128 1-GHz Alpha processors.
RESULTS
During the simulations, the water density distribution in regions I, II, and III exhibited different patterns, as shown in Fig. 3, where the dashed lines are the boundaries separating these regions. In region III, where the external forces are applied, a gradient of water density is observed; in regions I and II, the density of water is roughly constant, indicating that the hydrostatic pressure in these regions is uniform. The water density gradient in region III and, hence, the density difference between regions I and II, differ in the four simulations. From the observed water density difference and the calculated pressure difference (see Table 1) in these simulations, the compressibility of water is estimated to be 4.9 × 10−5 atm−1, which is in satisfactory agreement with its experimental value of 4.5 × 10−5 atm−1 (Sperelakis, 1998).
FIGURE 3.
Water density distribution along the z-direction in region III (within the dashed lines) and part of regions I and II. Data points marked by circles, diamonds, stars, and squares represent sim1, sim2, sim3, and sim4, respectively. The density is measured by averaging the number of water molecules within a 1-Å thick slab over the last 4 ns of each trajectory.
Water molecules in the channels were usually found in the single-file configuration (as shown in Fig. 4 a) and moved concertedly during the simulations (as shown in Fig. 4 b), despite occasional exceptions when more water molecules were accommodated in the channel, or when the water file appeared broken in a part of the channel. Nevertheless, the continuous-time random-walk model can be used to provide a simplified quantitative description of water movement in AQP1 channels. According to the model, the parameters characterizing the water movement are the hopping rates kr and kl. In the following, we suggest a method to determine these rates from MD trajectories.
FIGURE 4.
(a) An AQP1 monomer with channel water and nearby bulk water. Water molecules in the constriction (single-file) region, the vestibules of the channel, and in the bulk are rendered in vdW, CPK, and line representations, respectively. The two bars indicate the 15-Å long region in which water movement is analyzed as described in the text. (b) Trajectories (from sim1) of seven water molecules in the constriction region during 500 ps.
We define a region that spans the constriction region of an AQP1 channel, with length L = 15 Å (as indicated by the two bars in Fig. 4 a), and only look at water movement in this region. We also define a coordinate, X, by cumulating the sum of one-dimensional displacements of all water molecules in the mentioned region every picosecond. If a water molecule enters or exits the defined region within a picosecond, only the portion of its displacement within the region contributes to the sum. In this way, the actual many-body water movement is reduced to a single-particle trajectory (see Fig. 5), which represents the collective water movement inside the channel.
FIGURE 5.
Trajectories of the collective coordinate X for water molecules in the defined region in an AQP1 monomer, determined as described in the text. The four curves were obtained from simulations sim1, sim2, sim3, and sim4, respectively.
When a hop, as defined in the continuous-time random-walk model, occurs, X will have a displacement of +L or −L. Therefore, the total displacement of X during time t is determined by: ΔX(t) = m(t)L, where m(t) is the net number of hops defined earlier. According to Eqs. 15 and 16, we have:
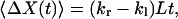 |
(19) |
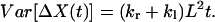 |
(20) |
The values of kr − kl and kr + kl can be calculated from the mean and variance of ΔX(t).
The estimated hopping rates for each simulation are provided in Table 2. To obtain Var[ΔX(t)] and (kr + kl), the 4-ns trajectory of X was divided into M = 20 subtrajectories, each l = 200 ps long, and Var[ΔX(t)] was calculated from the 20 displacements in different subtrajectories at t. Because the results may depend on how we split the trajectory, we checked two alternative dividing schemes, i.e., (M = 10, l = 400 ps) and (M = 40, l = 100 ps), respectively, but in both cases obtained (kr + kl) values close to those listed in Table 2. Note that it is not feasible to choose very large l and very small M, because that would result in a large uncertainty in the variance.
TABLE 2.
Hopping rates estimated from the simulations
| kr − kl (#/ns) | kr + kl (#/ns) | kl (#/ns) | kr (#/ns) | kr/kl | 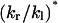 |
|
|---|---|---|---|---|---|---|
| sim1 | −3.9 ± 0.3 | 5.7 ± 1.4 | 4.8 ± 0.7 | 0.9 ± 0.7 | 0.19 | 0.27 |
| sim2 | −1.9 ± 0.6 | 5.1 ± 1.4 | 3.5 ± 0.8 | 1.6 ± 0.8 | 0.46 | 0.52 |
| sim3 | 2.0 ± 0.3 | 4.0 ± 0.4 | 1.0 ± 0.3 | 3.0 ± 0.3 | 3.1 | 1.9 |
| sim4 | 2.3 ± 0.3 | 4.6 ± 0.4 | 1.1 ± 0.2 | 3.5 ± 0.2 | 3.1 | 3.7 |
For each channel, the trajectory of the collective coordinate X for water molecules in the defined region (length L = 15 Å) was obtained as described in the text. kr − kl was calculated from the total displacement of X in 4 ns, according to Eq. 19. To calculate kr + kl, the 4-ns trajectory of X was divided into 20 subtrajectories, each of 200 ps duration. For each t, the variance of the displacements in the 20 subtrajectories during time t was computed, and kr + kl was calculated from the slope of the variance-t curve, according to Eq. 20. kr, kl, and kr/kl were obtained from kr − kl and kr + kl. The last column ( * of the table is the predicted value of kr/kl, calculated from exp(−Δμ/kBT) (Eq. 6), using T = 310 K and Δμ taken from Table 1.
* of the table is the predicted value of kr/kl, calculated from exp(−Δμ/kBT) (Eq. 6), using T = 310 K and Δμ taken from Table 1.
The obtained kr and kl values are in the range of 1–5/ns. In contrast, the equilibrium hopping rate (k0) for a narrow carbon nanotube was determined to be ∼14–38/ns (Berezhkovskii and Hummer, 2002; Zhu and Schulten, 2003), indicating much faster water movement than in AQP1. The slow kinetics in AQP1 and the relatively short sampling time introduce large statistical errors to the resulting kr and kl values. According to Eq. 6, the ratio kr/kl can be predicted from the chemical potential difference (Δμ) of water. Indeed, one can see from Table 2 that the obtained ratio for each simulation is of the same order of magnitude as the prediction (compare the last two columns of the table).
The net water fluxes, directly determined from the simulations, are given in Table 3. These values are plotted versus the applied pressure difference in Fig. 6. From their best-fit slope, and according to Eqs. 1 and 14, the osmotic permeability was determined to be pf = (7.1 ± 0.9) × 10−14 cm3/s. Different experiments have reported pf values for AQP1 monomers in the range of 1–16 × 10−14 cm3/s, the variation being probably due to uncertainties in the number of channels per unit membrane area (Heymann and Engel, 1999); typically referenced pf values range from 5.43 × 10−14 cm3/s (Walz et al., 1994) to 11.7 × 10−14 cm3/s (Zeidel et al., 1992). In light of this, the pf value calculated from our simulations agrees satisfactorily with experiments. According to Eq. 11, the equilibrium hopping rate in the continuous-time random-walk model for AQP1 is then k0 = 2.4/ns. Assuming that the AQP1 channel is symmetric, and according to Eq. 7, this corresponds to a (kr + kl = 2k0) value of 4.8/ns. This value is indeed consistent with the (kr + kl) values (4–6/ns) in Table 2, determined from monitoring Var[ΔX(t)] in our simulations.
TABLE 3.
Water flux observed in the four simulations
| Water count
|
Flux (#/ns)
|
|||||
|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M4 | Mean | SD | |
| sim1 | −13.5 | −14.5 | −15 | −17.5 | −3.8 | 0.4 |
| sim2 | −9.5 | −6 | −1 | −12.5 | −1.8 | 1.2 |
| sim3 | 11.5 | 8.5 | 5 | 8 | 2.1 | 0.7 |
| sim4 | 11.5 | 9 | 10.5 | 7 | 2.4 | 0.5 |
To obtain the net water transfer through a channel, a plane normal to its axis is defined, and when a water molecule crosses the plane, a count of +1 or −1 is accumulated, depending on its crossing direction. Two such planes were defined in the central part of the channel, and the average of their net counts is listed as the water count of the channel. The mean and standard deviation (SD) of the flux were calculated from the water counts of the four monomers (M1–M4) during 4 ns.
FIGURE 6.
The dependence of water flux on the applied pressure difference. Values of pressure differences and water fluxes are taken from Tables 1 and 3, respectively. A line with the best-fit slope for the four data points is also shown in the figure.
Equilibrium MD simulations of AQP1 were performed by other researchers, where a total of 16 permeation events (in four AQP1 monomers in either direction) were observed in 10 ns (de Groot and Grubmüller, 2001). Therefore the rate of unidirectional permeation events in a monomer is q0 = 0.2 H2O/ns. According to Eq. 3, this q0 value translates into a diffusion permeability of pd = 6.0 × 10−15 cm3/s. Using this pd value and the calculated pf value of this study, one obtains a pf/pd ratio of 11.9, in good agreement with the experimentally measured ratio of 13.2 for AQP1 (Mathai et al., 1996). The ratio corresponds to the number of effective steps in which a water molecule needs to participate to cross AQP1.
The number (∼12) of effective steps in a complete permeation event should be interpreted as follows. In the bulk, water conduction is essentially uncorrelated, i.e., the bulk phase does not contribute to the pf/pd ratio. In the constriction region of the channel, however, (average) N = 7 water molecules move essentially in single file, i.e., in a correlated and concerted fashion, such that N + 1 = 8 steps are needed to transport a water molecule through. Water molecules in the vestibules (also shown in Fig. 4 a) at the termini of the channel are not forming a single file, but nevertheless move in a somewhat concerted fashion, contributing the remainder of the pf/pd ratio.
DISCUSSION
We have discussed the difference between osmotic and diffusion permeabilities through theoretical analysis of single-file water transport and computational investigation of AQP1. Understanding this difference is important for the correct interpretation of simulations studying water transport. In particular, although it is a common practice to count permeation events in equilibrium simulations, one should note that it is not correct to use this count to calculate pf. Although the present study focuses on single-file water transport in channels, the issue is even more critical for larger water pores, in which the pf/pd ratio can be even larger (Finkelstein, 1987) and improper comparison between simulations and experiments would lead to a more serious discrepancy.
It is noteworthy that the magnitudes of the chemical potential difference (Δμ) of water in our simulations are 1.32 kBT and 0.66 kBT. In this case, because Δμ is not much smaller than kBT, it may not be safe to keep only the linear terms of Δμ/kBT in Eq. 7. Consequently, the net water flux is not guaranteed to be linear in Δμ. However, the water flux was not found to significantly deviate from linearity in the present study. In earlier simulations where even higher pressure differences were induced (Zhu et al., 2002), nonlinear behavior was not observed either. For single-file water channels, breaking of the single-file configuration at high pressure differences poses an upper limit for the validity of the continuous-time random-walk model, and probably also for the linear range of the flux-pressure relationship. However, nonlinear effects may already arise before the pressure difference reaches this upper limit. It is desirable to know when and how the water flux deviates from linearity at high pressure differences, and to even develop a nonlinear model to describe the general behavior. For this purpose, one could first study the flux-pressure relationship for some simpler water channels, e.g., carbon nanotubes (Hummer et al., 2001; Zhu and Schulten, 2003) or other nanopores (Beckstein and Sansom, 2003), because due to their stability and small size, they can be more easily simulated for both high and low pressure differences.
In this study, we have demonstrated that the major experimental quantity for AQP1 channels, pf, can be reproduced in MD simulations with induced hydrostatic pressure difference. We expect that our method of inducing pressure differences can be used also to determine the permeability of other water channels. In light of ever increasing computing power, the accuracy of such computational measurements will be further improved when longer simulations, in which the induced pressure difference can be lower and closer to experimental conditions, become affordable. Consequently, the presented method may serve as a complementary technique to experiments for quantitative characterizations of water channels.
Acknowledgments
Molecular images in this paper were generated with the molecular graphics program VMD (Humphrey et al., 1996).
This work was supported by grants from the National Institutes of Health (NIH PHS 5 P41 RR05969 and R01 7M067887) and from the National Science Foundation (NSF CCR 02-10843). The authors also acknowledge computer time provided at the NSF centers by the grant NRAC MCA93S028. F.Z. acknowledges a graduate fellowship awarded by the UIUC Beckman Institute.
References
- Beckstein, O., and M. S. P. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berezhkovskii, A., and G. Hummer. 2002. Single-file transport of water molecules through a carbon nanotube. Phys. Rev. Lett. 89:064503. [DOI] [PubMed] [Google Scholar]
- Bernèche, S., and B. Roux. 2001. Energetics of ion conduction through the K+ channel. Nature. 414:73–77. [DOI] [PubMed] [Google Scholar]
- Biggin, P. C., and M. S. P. Sansom. 2002. Open-state models of a potassium channel. Biophys. J. 83:1867–1876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Groot, B. L., A. Engel, and H. Grubmüller. 2001. A refined structure of human aquaporin-1. FEBS Lett. 504:206–211. [DOI] [PubMed] [Google Scholar]
- de Groot, B. L., and H. Grubmüller. 2001. Water permeation across biological membranes: mechanism and dynamics of aquaporin-1 and GlpF. Science. 294:2353–2357. [DOI] [PubMed] [Google Scholar]
- de Groot, B. L., D. P. Tieleman, P. Pohl, and H. Grubmüller. 2002. Water permeation through gramicidin A: desformylation and the double helix: a molecular dynamics study. Biophys. J. 82:2934–2942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- Finkelstein, A. 1987. Water Movement through Lipid Bilayers, Pores, and Plasma Membranes. John Wiley & Sons, New York.
- Fu, D., A. Libson, L. J. W. Miercke, C. Weitzman, P. Nollert, J. Krucinski, and R. M. Stroud. 2000. Structure of a glycerol conducting channel and the basis for its selectivity. Science. 290:481–486. [DOI] [PubMed] [Google Scholar]
- Heymann, J. B., and A. Engel. 1999. Aquaporins: phylogeny, structure, and physiology of water channels. News Physiol. Sci. 14:187–193. [DOI] [PubMed] [Google Scholar]
- Hohmann, S., S. Nielsen, and P. Agre. 2001. Aquaporins. Academic Press, San Diego, CA.
- Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—Visual Molecular Dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Jensen, M. Ø., S. Park, E. Tajkhorshid, and K. Schulten. 2002. Energetics of glycerol conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. USA. 99:6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen, M. Ø., E. Tajkhorshid, and K. Schulten. 2001. The mechanism of glycerol conduction in aquaglyceroporins. Structure. 9:1083–1093. [DOI] [PubMed] [Google Scholar]
- Jensen, M. Ø., E. Tajkhorshid, and K. Schulten. 2003. Electrostatic tuning of permeation and selectivity in aquaporin water channels. Biophys. J. 85:2884–2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: Greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
- Kalra, A., S. Garde, and G. Hummer. 2003. Osmotic water transport through carbon nanotube membranes. Proc. Natl. Acad. Sci. USA. 100:10175–10180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen, R. J., and M. L. Marx. 2001. An Introduction to Mathematical Statistics and its Applications. Prentice-Hall, Upper Saddle River, NJ. 246–262.
- Lu, D., P. Grayson, and K. Schulten. 2003. Glycerol conductance and physical asymmetry of the Escherichia coli glycerol facilitator GlpF. Biophys. J. 85:2977–2987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-hydrogen empirical potential for molecular modeling and dynamics studies of proteins using the CHARMM22 force field. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Mathai, J. C., S. Mori, B. L. Smith, G. M. Preston, N. Mohandas, M. Collins, P. C. M. van Zijl, M. L. Zeidel, and P. Agre. 1996. Functional analysis of aquaporin-1 deficient red cells. J. Biol. Chem. 271:1309–1313. [DOI] [PubMed] [Google Scholar]
- Murata, K., K. Mitsuoka, T. Hirai, T. Walz, P. Agre, J. B. Heymann, A. Engel, and Y. Fujiyoshi. 2000. Structural determinants of water permeation through aquaporin-1. Nature. 407:599–605. [DOI] [PubMed] [Google Scholar]
- Randa, H. S., L. R. Forrest, G. A. Voth, and M. S. P. Sansom. 1999. Molecular dynamics of synthetic leucine-serine ion channels in a phospholipid membrane. Biophys. J. 77:2400–2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren, G., V. S. Reddy, A. Cheng, P. Melnyk, and A. K. Mitra. 2001. Visualization of a water-selective pore by electron crystallography in vitreous ice. Proc. Natl. Acad. Sci. USA. 98:1398–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux, B. 2002. Computational studies of the gramicidin channel. Acc. Chem. Res. 35:366–375. [DOI] [PubMed] [Google Scholar]
- Saparov, S. M., D. Kozono, U. Rothe, P. Agre, and P. Pohl. 2001. Water and ion permeation of aquaporin-1 in planar lipid bilayers. J. Biol. Chem. 276:31515–31520. [DOI] [PubMed] [Google Scholar]
- Schlenkrich, M., J. Brickmann, A. D. MacKerell, Jr., and M. Karplus. 1996. Empirical potential energy function for phospholipids: criteria for parameter optimization and applications. In Biological Membranes: A Molecular Perspective from Computation and Experiment. K. M. Merz and B. Roux, editors. Birkhauser, Boston, MA. 31–81.
- Sperelakis, N. 1998. Cell Physiology Source Book. Academic Press, San Diego, CA.
- Sui, H., B.-G. Han, J. K. Lee, P. Walian, and B. K. Jap. 2001. Structural basis of water-specific transport through the AQP1 water channel. Nature. 414:872–878. [DOI] [PubMed] [Google Scholar]
- Tajkhorshid, E., P. Nollert, M. Ø. Jensen, L. J. W. Miercke, J. O'Connell, R. M. Stroud, and K. Schulten. 2002. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 296:525–530. [DOI] [PubMed] [Google Scholar]
- Walz, T., B. L. Smith, M. L. Zeidel, A. Engel, and P. Agre. 1994. Biologically active two-dimensional crystals of aquaporin chip. J. Biol. Chem. 269:1583–1586. [PubMed] [Google Scholar]
- Yool, A. J., and A. M. Weinstein. 2002. New roles for old holes: ion channel function in aquaporin-1. News Physiol. Sci. 17:68–72. [DOI] [PubMed] [Google Scholar]
- Zeidel, M. L., S. V. Ambudkar, B. L. Smith, and P. Agre. 1992. Reconstitution of functional water channels in liposomes containing purified red cell CHIP28 protein. Biochemistry. 31:7436–7440. [DOI] [PubMed] [Google Scholar]
- Zhu, F., and K. Schulten. 2003. Water and proton conduction through carbon nanotubes as models for biological channels. Biophys. J. 85:236–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, F., E. Tajkhorshid, and K. Schulten. 2001. Molecular dynamics study of aquaporin-1 water channel in a lipid bilayer. FEBS Lett. 504:212–218. [DOI] [PubMed] [Google Scholar]
- Zhu, F., E. Tajkhorshid, and K. Schulten. 2002. Pressure-induced water transport in membrane channels studied by molecular dynamics. Biophys. J. 83:154–160. [DOI] [PMC free article] [PubMed] [Google Scholar]








