Sensitivity of O_R in Phage λ

Abstract

We investigate the sensitivity of the right operator in bacteriophage lambda. In particular, the system is probed in the three different regulatory protein concentration-regimes: 1), lysogen (CI dominates); 2), during induction (CI and Cro at comparable concentrations); and 3), after induction (Cro dominates). Systematic perturbations of the protein-operator binding energies show in a lysogen that the activity (production rate) at promoter P_RM is robust to variations, in contrast to P_R, where the sensitivity is high. Both promoters, however, show large sensitivity in regimes 2 and 3. In all regimes we identify several suppressors, meaning that for a given large perturbation (±2 kcal/mol) of one binding energy, there exist compensating perturbation(s) that restore the wild-type activity.

INTRODUCTION

A genetic switch is a system made up of a sequence of DNA and a number of regulatory proteins that decides which of a set of genes will be transcribed under given intracellular and extracellular physical and chemical conditions (Alberts et al., 1994). In other words, genetic switches regulate the cell and become the key elements in the synthesis of certain proteins. To understand the performance of a genetic switch, it turns out to be important to obtain detailed knowledge about the physical and chemical properties of the system (Alberts, 1998). A well-studied regulatory system is the bacteriophage lambda (phage λ) in the bacterium Escherichia coli, which under physiological conditions exhibits an extremely high stability (Brooks and Clark, 1967; Little et al., 1999).

Upon phage λ infection of E. coli, either one phage λ genome (prophage) is introduced into the host genome and silently replicated for generations, which is called the lysogenic track; or it becomes massively replicated by use of the host cell chemistry and the E. coli cell bursts (lyses), called the lytic track. The latter is also the outcome when a lysogen (E. coli cell on the lysogenic track) becomes irradiated with ultraviolet light (DNA becomes damaged) (Ptashne, 1992).

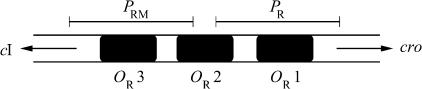
The right operator (O_R) is playing an important role in the fate of the bacterium after infection. As shown in Fig. 1, O_R consists of three operator sites, each potential binding sites for dimers of the regulatory proteins CI (commonly called repressor) and Cro. RNA polymerase (RNAP) is able to bind either to a region including O_R1 and parts of O_R2 (promoter P_R in Fig. 1), and thereby initiates cro transcription, or it can bind to a region including O_R3 and parts of O_R2 (promoter P_RM in Fig. 1), initiating cI transcription. (Nomenclature: genes are denoted with italicized letters and their protein products with Roman letters where the first letter is capitalized.) In a lysogen, O_R1 and O_R2 are usually occupied by one CI dimer each, exhibiting a cooperative interaction, and P_RM is occupied by RNAP such that CI is continuously expressed that maintains repression of cro.

FIGURE 1.

Schematic illustration of the O_R of the phage λ genome. Three operator (binding) sites are shown, O_R1, O_R2, and O_R3, where CI and Cro dimers are able to bind. P_RM and P_R indicate the promoter regions where RNA polymerase binds to initiate transcription of cI and cro genes. The arrows associated with cI and cro indicate the transcription direction of these genes, respectively.

For the past three decades, there has been reported an increasing amount of quantitative experimental data on protein-operator interactions at O_R of the phage λ genome (Johnson et al., 1979; Takeda et al., 1992; Darling et al., 2000b). We will use experimental data of the affinities (protein-operator binding energies) of CI, Cro, and RNAP within a statistical-mechanical approach similar to Ackers et al. (1982). This provides us with the probabilities for RNAP occupancy of the promoters that are proportional to the activities that in turn are proportional to the production rates of CI and Cro, respectively. We study the sensitivity of the activities of P_RM and P_R to variations of the operator affinities within their experimental uncertainty. Furthermore, from experiments it is known that a single point mutation of operator DNA typically corresponds to a shift of ±2 kcal/mol in the binding affinity (Burz and Ackers, 1996; Little et al., 1999). One mutation may in principle be compensated through another mutation corresponding to a shift of another affinity (suppression).

Below, we systematically perturb the affinities ±2 kcal/mol, one by one, to mimic mutations. Thus, such (large) perturbations may be regarded as hypothetical mutations and in the following we for simplicity term these ±2 kcal/mol perturbations as mutations. Note that these mutations are not directly linked to experimental data, but serve us to assess the stability of the λ-switch. In our analysis, we check for possible suppressors for the affinities where the mutations correspond to a significant change in activity (>25% in absolute value relative to wild-type activity). We study the system in three different regimes: 1), lysogen, where CI dominates; 2), during induction, where CI and Cro are at comparable concentrations; and 3), after induction, where Cro dominates.

We find that the activity is not very sensitive within the experimental error in the lysogenic regime at P_RM; however, in regimes 2 and 3, the activities turn out to be more sensitive at both promoters. The strength of the RNAP affinities appears to be important to maintain the activity. Interestingly, we find a number of suppressors in all regimes.

In the following, we first introduce the thermodynamics and the models involved, whereupon the sensitivity in three different concentration regimes is investigated before drawing our conclusions.

MODELING THE SYSTEM

Timescales

Let us first recall the typical timescales in the system. The messenger RNA (mRNA) production rate per RNAP-DNA complex is typically of the order 10⁻² s⁻¹, i.e., one mRNA is synthesized per minute if the corresponding gene is constantly occupied by one RNAP (Hawley and McClure, 1982). This means that mRNAs (and proteins) are produced on a timescale of minutes. Furthermore, Aurell et al. (2002) estimate that protein association typically occurs in fractions of a second. Thus, with regard to the production of mRNAs in a cell, it is a reasonable assumption that the protein association with DNA is in equilibrium.

Thermodynamics

As mentioned, we apply the statistical-mechanical (equilibrium) approach presented by Ackers et al. (1982). Binding of CI dimers (CI₂), Cro dimers (Cro₂), and RNAP to O_R of phage λ can occur in 40 different combinations s as listed in Table 1. The associated probability f_s for finding the system in one of these 40 states s is (Hill, 1960; Ackers et al., 1982)

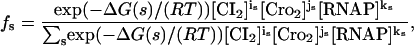(1)

where R = 8.31 J/(mol K) is the gas constant, T = 310 K is the absolute temperature, and ΔG(s) is the Gibbs free energy difference (binding energy) between state s and the unoccupied state (s = 1). [CI₂], [Cro₂], and [RNAP] are the free (unbound) concentrations of CI dimers, Cro dimers, and RNAP, respectively. i_s ∈ {0, 1, 2, 3}, j_s ∈ {0, 1, 2, 3}, and k_s ∈ {0, 1, 2} are the number of CI dimers, Cro dimers, and RNAP bound to O_R in the state s. For instance, from Table 1 the state s = 23 corresponds to i₂₃ = 1, j₂₃ = 0, k₂₃ = 1, and ΔG(23) = −22.0 kcal/mol.

TABLE 1.

Gibbs free energies (GFEs), associated with protein binding to O_R, in the different binding states (s) of CI dimers (R) Cro dimers (C), and RNAP

s	OR3		OR2		OR1	Terms	GFE
1	0		0		0	Reference state	0
2	0		0		R	ΔG1	−12.5
3	0		R		0	ΔG2	−10.5
4	R*		0		0	ΔG3	−9.5
5	0		0		C	ΔG1′	−10.8
6	0		C		0	ΔG2′	−10.8
7	C†		0		0	ΔG3′	−12.1
8	RNAP†		0		0	ΔGRM	−11.5
9	0			RNAP		ΔGR	−12.5
10	0		R	←→	R	ΔG1 + ΔG2 + ΔG12	−25.7
11	R		0		R	ΔG1 + ΔG3	−22.0
12	R	←→	R		0	ΔG2 + ΔG3 + ΔG23	−22.9
13	0		C	←→	C	ΔG1′ + ΔG2′ + ΔG12′	−21.6
14	C		0		C	ΔG1′ + ΔG3′	−22.9
15	C	←→	C		0	ΔG2′ + ΔG3′ + ΔG23′	−22.9
16	RNAP			RNAP		ΔGRM + ΔGR	−24.0
17	0		C		R	ΔG1 + ΔG2′	−23.3
18	0		R		C	ΔG1′ + ΔG2	−21.3
19	R		0		C	ΔG1′ + ΔG3	−20.3
20	C		0		R	ΔG1 + ΔG3′	−24.6
21	R		C		0	ΔG2′ + ΔG3	−20.3
22	C		R		0	ΔG2 + ΔG3′	−22.6
23	R			RNAP		ΔGR + ΔG3	−22.0
24	RNAP		R		0	ΔG2 + ΔGRM	−22.0
25	RNAP		0		R	ΔG1 + ΔGRM	−24.0
26	C			RNAP		ΔGR + ΔG3′	−24.6
27	RNAP		C		0	ΔG2′ + ΔGRM	−22.3
28	RNAP		0		C	ΔG1′ + ΔGRM	−22.3
29	R		R	←→	R	ΔG1 + ΔG2 + ΔG3 + ΔG12	−35.2
30	C	←→	C	←→	C	ΔG1′ + ΔG2′ + ΔG3′ + ΔG123′	−33.7
31	C		R	←→	R	ΔG1 + ΔG2 + ΔG3′ + ΔG12	−37.8
32	R		C		R	ΔG1 + ΔG2′ + ΔG3	−32.8
33	R	←→	R		C	ΔG1′ + ΔG2 + ΔG3 + ΔG23	−33.7
34	R		C	←→	C	ΔG1′ + ΔG2′ + ΔG3 + ΔG12′	−31.1
35	C		R		C	ΔG1′ + ΔG2 + ΔG3′	−33.4
36	C	←→	C		R	ΔG1 + ΔG2′ + ΔG3′ + ΔG23′	−35.4
37	RNAP		R	←→	R	ΔG1 + ΔG2 + ΔGRM + ΔG12	−37.2
38	RNAP		C	←→	C	ΔG1′ + ΔG2′ + ΔGRM + ΔG12′	−33.1
39	RNAP		C		R	ΔG1 + ΔG2′ + ΔGRM	−34.8
40	RNAP		R		C	ΔG1′ + ΔG2 + ΔGRM	−32.8

0, empty site; ←→, cooperative interaction; Terms, GFE terms due to Table 2.

GFEs are measured relative to the unbound state of zero GFE (reference state, s = 1). All energies are measured at 37°C in units of kcal/mol. Note that we have indicated Cro cooperative interaction terms, because these are (one by one) set to a nonzero value in the perturbation scheme performed in this work (although being zero without perturbation).

^*Koblan and Ackers (1992).

^†Shea and Ackers (1985).

Following the notation of Shea and Ackers (1985), ΔG₁ = ΔG(2) is the free energy associated with the binding of CI₂ to O_R1, etc., and ΔG_1′ = ΔG(5) is the free energy associated with the binding of Cro₂ to O_R1, etc. (Table 2). Furthermore, two CI dimers at neighboring operator sites are supposed to obtain an additional cooperative free energy (see Fig. 2 in Shea and Ackers (1985) for a more detailed explanation). Thus, ΔG₁₂ is the cooperative free energy associated with the binding of CI₂ to both O_R1 and O_R2, and ΔG₂₃ is the cooperative free energy associated with the binding of CI₂ to both O_R2 and O_R3, provided that no repressor is bound to O_R1. The data in Table 1 are all obtained in vitro in 200 mM KCl, resembling “physiological” conditions (Kao-Huang et al., 1977; Ackers et al., 1982).

TABLE 2.

Gibbs free energies for protein binding to O_R

CI	ΔG1	ΔG2	ΔG3	ΔG12	ΔG23
	−12.5	−10.5	−9.5	−2.7	−2.9
Cro	ΔG1′	ΔG2′	ΔG3′	ΔG12′	ΔG23′	ΔG123′
	−10.8	−10.8	−12.1	0	0	0

CI binding (affinity) data from Koblan and Ackers (1992) and Cro binding data from Shea and Ackers (1985). All energies measured at 37°C in kcal/mol. Note that we have included Cro cooperative interaction terms, because these are (one by one) set to a nonzero value in the perturbation scheme performed in this work.

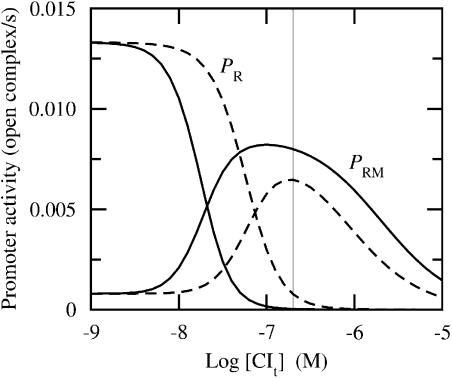
FIGURE 2.

Promoter activity versus total CI concentration for two different data sets ([Cro] ≈ 0 in both sets). Fully drawn curves correspond to CI affinity data from Koblan and Ackers (1992) (applied throughout this work) and dashed lines correspond to CI affinity data from Shea and Ackers (1985). Cro affinity data are from Shea and Ackers (1985) in all simulations (applied throughout this work). P_R corresponds to cro activity and P_RM corresponds to cI activity. Thin vertical line indicates lysogenic concentration (≈200 nM). Unit “open complex/s” corresponds to the number of RNAP-DNA complexes that are being transformed from the closed to open form (isomerizations) per second. Abscissa is drawn on logarithmic (decadic) scale.

The Cro affinity data from Shea and Ackers (1985) assume no cooperativity between Cro dimers bound to vicinal operator sites. The more recent results reported by Darling et al. (2000b) state that Cro exhibits cooperativity as well. However, as these experiments are performed at 20°C, we prefer in this work to apply the Cro data from Shea and Ackers (1985) measured at 37°C. To check for possible implications of such cooperative interactions between Cro dimers in our perturbations, we introduce the tetrameric interactions, i.e., dimer-dimer interactions, ΔG_12′ and ΔG_23′, and the hexameric Gibbs free energy term ΔG_123′ (see Table 1). The latter term takes into account the additional Gibbs free energy when all three operators are occupied by Cro₂ (Darling et al., 2000b). Let us stress again that such Cro cooperativity is not assumed in the wild-type data (unperturbed), as stated in Table 2.

The Gibbs free energy of RNAP association at P_R and P_RM is ΔG_R = −12.5 kcal/mol and ΔG_RM = −11.5 kcal/mol, respectively. The latter values have an accuracy of ±0.5 kcal/mol (Shea and Ackers, 1985). Even though more details on RNAP have recently been obtained from in vivo experiments (Ptashne and Gann, 2002), to our knowledge there do not exist more accurate data of RNAP affinities. The overall resulting Gibbs free energies associated with the 40 states of the DNA associations of CI, Cro, and RNAP are listed in Table 1. Throughout this work we have for simplicity assumed a constant free RNAP concentration of 30 nM, as applied by Shea and Ackers (1985).

The free concentrations of CI monomers and dimers ([CI₁] and [CI₂]) are supposed to be in equilibrium, with a dissociation constant K_d = [CI₁]²/[CI₂] = 18 nM (Koblan and Ackers, 1991). Furthermore, Cro is in this work only supposed to occur in the dimeric form; this was also the assumption of Shea and Ackers (1985) during their analysis of the Cro affinity data (which we apply in this work). However, introduction of a nonzero dissociation constant of Cro does not modify our main results.

The total concentration of CI molecules, in monomeric equivalents, yields

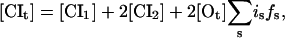(2)

where the first and second term on the right-hand side count the free monomeric and dimeric concentration, respectively, and the last term is the average concentration of operator-bound dimers. Usually this term can be neglected for large concentrations; however, for completeness, this term and the corresponding last term in Eq. 3 are included in our simulations. f_s is given by Eq. 1 and [O_t] = 1 nM is the total concentration of operators, where the latter value corresponds to one operator in an average cellular volume of 1.7 × 10⁻¹⁵ dm³. The corresponding equation for Cro yields

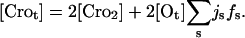(3)

Activity

The main purpose of this article is to estimate the effects of perturbations of the protein-operator and RNAP-operator affinities on the production rates (activities) of the regulatory proteins CI and Cro. Ptashne et al. (1980) point out that transcription initiation is the rate-limiting step in protein synthesis. More specifically, it is apparently the step taking the RNAP-DNA complex from the closed to the open form (isomerization step) that is limiting the rate with respect to repressor and Cro synthesis in a lysogen, and during induction of lysis (McClure, 1980). Thus, activity may be defined as the product of isomerization rate times the probability of RNAP occupancy of the promoter. In what follows, we use the same rate constants as Shea and Ackers (1985) in enumerating the activities. Thus, the rate constant we apply for cro isomerization is k_R = 0.014 s⁻¹, whereas the rate constant for cI isomerization is split into two terms: one stimulated rate when O_R2 is occupied by CI₂, k_RM1 = 0.011 s⁻¹, and one unstimulated rate when O_R2 is not occupied by CI₂, k_RM2 = 0.001 s⁻¹. The ratio k_RM1/k_RM2 = 11 is according to Hawley and McClure (1982).

One should note that the origin of the stimulated transcription is unresolved, e.g., it is argued that the increased cooperativity transcription is due to higher promoter affinity of RNAP because the CI dimer at O_R2 touches the polymerase and thereby enhances cI transcription (pages 21–22 in Ptashne (1992)). We will in this work use the traditional approach of Hawley and McClure, as mentioned above.

The promoter activities are

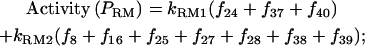(4)

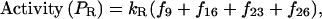(5)

with probabilities (f_s) given by Eq. 1.

Since we are using a different data set for the CI affinities in this work compared with Shea and Ackers (1985), it is interesting to compare the promoter activities emerging from the two data sets, as shown in Fig. 2. Although both sets have the same qualitative behavior, they differ quantitatively. Employing the CI data from Shea and Ackers (1985) instead of the CI data of Koblan and Ackers (1992), Cro activity (P_R) at lysogenic level ([CI_t] ≈ 200 nM and [Cro_t] ≈ 0) is elevated to a nonzero value, whereas the CI activity (P_RM) is reduced by a factor 0.8 at the same protein level. However, given this observation, it is not straightforwardly possible to conclude what effect the changes of the individual CI affinities have on the total activity. We therefore systematically perturb the wild-type affinities in the following.

Dynamics

The dynamics of the system is quantified by the promoter activity and through subsequent intracellular production and degradation of CI and Cro versus time. From this, we obtain a rough estimate of the protein levels around the induction point, where the total CI and Cro levels are comparable. We use the dynamical equations and parameters of Shea and Ackers (1985). CI and Cro production rates are proportional to the promoter activities in Eqs. 4 and 5 above. In the rate equation for CI production, we also introduce a degradation term that is introduced to model RecA-mediated cleavage of repressor monomers, which causes that the repressors are unable to dimerize and thereby bind to the operator (Ptashne, 1992). We ignore cell growth in our simulations, but as the determination of the induction point is not crucial, this approximation will not significantly influence on our main results.

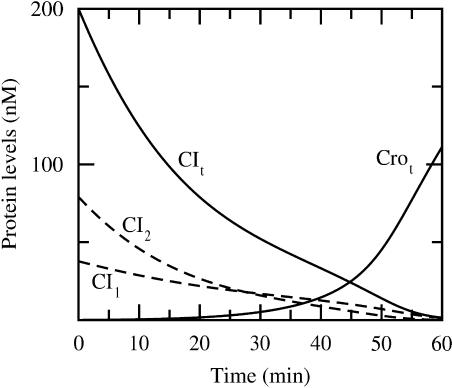
The two dynamical rate equations we obtain for CI and Cro (both of the form d([CI] or [Cro])/dt ∼ probability for RNAP occupancy of P_RM or P_R), which are equivalent to Eqs. 2 and 3 of Shea and Ackers (1985) and therein described in detail, are solved simultaneously by means of the fourth order Runge-Kutta method (numerical time step algorithm) (Dahlquist and Björk, 1974). This simulation yields the curves in Fig. 3. The initial conditions (time = 0) are [CI_t] = 200 nM and zero Cro concentration, which may be regarded as typical concentrations for a lysogen. It is the protease- (RecA) mediated cleavage of repressor monomers that reduces the repressor concentration and makes it possible for Cro concentration to increase and eventually dominate as shown in Fig. 3.

FIGURE 3.

Total protein concentration versus time (fully drawn lines) (simulated as described in Dynamics). RecA mediated cleavage introduced at time = 0. CI monomeric (CI₁) and dimeric (CI₂) free concentrations are also provided (dashed lines). Induction occurs around 45 min where the total protein concentrations are comparable (≈24 nM), corresponding to free concentrations [CI₂] = 5.6 nM and [Cro₂] = 12 nM.

RESULTS AND DISCUSSION

Perturbations

All affinities in Table 2 and the two affinities ΔG_RM and ΔG_R (associated with RNAP) are systematically perturbed ±1 kcal/mol in the three different concentration regimes: lysogeny (1), around induction (2), and after induction (3). We note that with the footprint titration technique Koblan and Ackers (1992) applied to determine the CI affinities, the deviations of the affinities range up to 0.7 kcal/mol with ±67% confidence intervals. Thus, a perturbation of ±1 kcal/mol is reasonable to take into account experimental uncertainties and to probe for their potential effects.

We also study the effect of large perturbations by systematically changing each individual affinity ±2 kcal/mol, representing a typical operator mutation (Burz and Ackers, 1996; Little et al., 1999). Finally, we check for possible suppressors counteracting these large perturbations (termed mutations for simplicity) in all three different concentration regimes. We stress that the ±2 kcal/mol mutations (and their suppressors) are not directly linked to experimental data, but may rather be regarded as a prediction or indication of the effect such perturbations (mutations) have upon the activity.

Regime 1

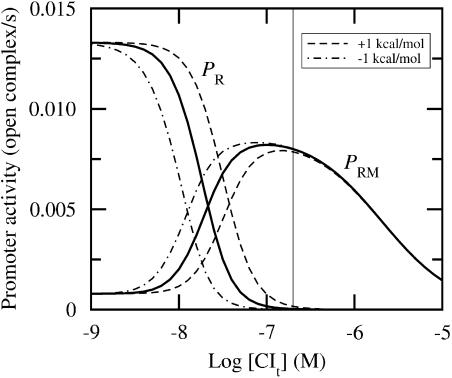
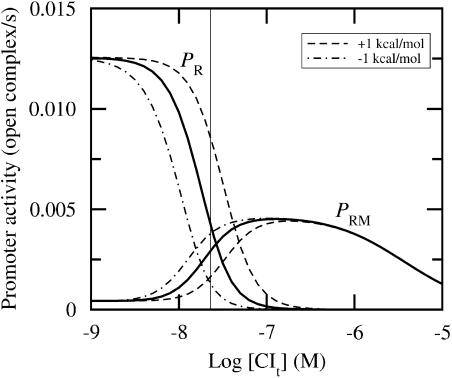
We first consider the lysogenic regime. This state is characterized by a negligible Cro concentration and [CI_t] ≈ 200 nM in monomeric equivalents. Fig. 4 illustrates that a perturbation of ΔG₁ has hardly any effect on the activity in a lysogen. Table 3 presents the results of systematic perturbations.

FIGURE 4.

Promoter activity versus total CI concentration for [Cro_t] ≈ 0. Fully drawn lines correspond to wild-type data, whereas the other lines correspond to ΔG₁ perturbed ±1 kcal/mol, as indicated in the graph. CI affinity data from Koblan and Ackers (1992) and Cro affinity data from Shea and Ackers (1985). Thin vertical line indicates lysogenic concentration (≈200 nM). Abscissa is drawn on logarithmic (decadic) scale.

TABLE 3.

Relative change in activity at lysogenic concentrations ([CI_t] ≈ 200 nM and [Cro_t] ≈ 0) compared with wild-type activity at promoters P_RM and P_R due to perturbations of ±1 kcal/mol of the different affinities of CI; e.g., −0.2 corresponds to a 20% reduction of the activity

	+1 kcal/mol		−1 kcal/mol
	PRM	PR	PRM	PR
ΔG1	0	4.0	0	−0.8
ΔG2	0	3.9	0	−0.8
ΔG3	0.1	0	−0.2	0
ΔG12	0	3.9	0	−0.8
ΔG23	0	0	0	0
ΔGRM	−0.5	0	0.3	0
ΔGR	0	−0.8	0	4.0

A zero means that the relative change is <±5%. Wild-type activity in regime 1 is 8.0 × 10⁻³ s⁻¹ at P_RM and 3.3 × 10⁻⁵ s⁻¹ at P_R.

As a general result, the activity associated with P_RM in a lysogen is not sensitive to perturbations of the regulatory protein affinities, within experimental error and typical protein fluctuations. In contrast, P_R is sensitive to perturbations. However, one should note that the ratio between the activities at P_RM and P_R is of order 10². Thus, we will in this section mainly focus on P_RM activity.

The perturbation of ΔG₃ has the largest effect on the activity at P_RM among the CI affinities. This is reasonable because a more negative ΔG₃ makes CI repress its own synthesis (Ptashne, 1992) (a decrease in Gibbs free energy is equivalent to a stronger binding). Similarly, an increase in ΔG_RM leads to a decreased activity because RNAP then visits, and thereby transcribes, P_RM less frequently. Naturally, the activities at P_RM and P_R are expected to be sensitive upon perturbations of ΔG_RM and ΔG_R, respectively.

By perturbing the affinities systematically ±2 kcal/mol, which we term as (hypothetical) mutations, we find in regime 1 that it is only the +2 kcal/mol mutation of ΔG_RM and the −2 kcal/mol mutation of ΔG₃ and ΔG_RM that leads to >25% change of the activity at P_RM. Perturbations of the Cro affinities do not change the activity due to zero Cro concentration in this regime.

Regarding a mutation of +2 kcal/mol, ΔG_RM has no suppressors, i.e., this mutation cannot be compensated by another mutation (of another affinity), such that wild-type activity is restored. Conversely, all CI affinities and ΔG_R are suppressors for a mutation of −2 kcal/mol of ΔG_RM. Consequently, the binding strength of RNAP at P_RM seems to be crucial for maintenance of wild-type activity.

Even though the impact of the perturbations of ΔG₁ at P_RM under lysogenic conditions is negligible, we see in Fig. 4 that the effect is more pronounced at lower CI concentrations. In other words, the impact of perturbations will strongly depend on the respective concentrations, and thus motivates us to consider perturbations at other protein concentrations.

Regime 2

To estimate typical protein concentrations at the transition when the switch turns over such that CI production is replaced by Cro production, we perform a simulation as described in Dynamics. In Fig. 3, we display the dynamics after the introduction at time = 0 of CI monomer degradation mediated by protease RecA. At 45 min the total protein concentrations of CI and Cro are comparable (24 nM). At this concentration the Cro level starts to rise substantially, indicating that the system is committed to the lytic pathway. We call this crossover the induction point, but note that this definition of the induction point is somewhat arbitrary.

The induction point in the simulations of Shea and Ackers (with other CI affinity data), in comparison, occurs at 22 min corresponding to total concentrations of 43 nM. Thus, the numerical values of the simulated protein levels during induction are sensitive with respect to the affinity data. Furthermore, in our simulations (Fig. 3), we see that the repressor level has to be substantially lower compared with the lysogenic level (∼20%) to induce derepression at P_R and thereby enhance Cro production. This behavior is also reported on in vivo experiments by Bailone et al. (1979).

In Fig. 5, we plot the promoter activities versus repressor level. Around induction both activities associated with P_RM and P_R are significant, and both activities are influenced by the perturbation of ΔG₁. In Table 4, we present the results from a systematic perturbation scheme. We find that the changes in both activities are relatively large for perturbations of ΔG₁, ΔG₂, ΔG₁₂, and ΔG_R. We also note that the activity of P_RM changes considerably due to the perturbations of ΔG_3′ and ΔG_RM. This is interesting, because the perturbations of the affinities around induction then have different effects on the corresponding activities compared with the perturbations in the lysogenic regime, in particular at P_RM. Except for the high sensitivity of ΔG_3′ at P_RM, sensitivity of Cro is low in this regime.

FIGURE 5.

Promoter activity versus total CI concentration for [Cro_t] ≈ 24 nM. Perturbations performed as in Fig. 4. Thin vertical line indicates a typical concentration around induction (≈24 nM). Abscissa is drawn on logarithmic (decadic) scale.

TABLE 4.

Relative change in activity at concentrations around induction ([CI_t] ≈ [Cro_t] ≈ 24 nM) at P_RM and P_R corresponding to perturbations as performed in Table 3

	+1 kcal/mol		−1 kcal/mol
	PRM	PR	PRM	PR
ΔG1	−0.5	1.2	0.3	−0.7
ΔG2	−0.5	1.0	0.4	−0.7
ΔG3	0	0	0	0
ΔG12	−0.5	0.9	0.4	−0.7
ΔG23	0	0	0	0
ΔG1′	0	0	0	0
ΔG2′	0	0	−0.1	−0.1
ΔG3′	0.6	0	−0.6	0
ΔG12′	0	0	0	0
ΔG23′	0	0	−0.1	−0.1
ΔG123′	0	0	0	0
ΔGRM	−0.7	0	0.8	0
ΔGR	0.3	−0.7	−0.5	1.4

Wild-type activity in regime 2 is 3.0 × 10⁻³ s⁻¹ at P_RM and 4.0 × 10⁻³ s⁻¹ at P_R.

In regime 2 the ±2 kcal/mol mutations of ΔG₁, ΔG₂, and ΔG_R, and the +2 kcal/mol mutation of ΔG_23′ change the activities at both promoters more than 25%. Interestingly, in regime 2 we find common suppressors that restore both wild-type activities within 5% for all these latter mentioned affinities. The only exception is the +2 kcal/mol mutation of ΔG_R. This means, for instance, that a +2 kcal/mol mutation of ΔG₂ can be compensated by a −2 kcal/mol mutation of ΔG₁₂, whereupon the wild-type activity is restored (within 5%) at both promoters.

As mentioned above, the induction point is sensitive upon affinity data. To check possible implications we choose another induction point that is equivalent of Shea and Ackers (1985) at total protein concentrations 43 nM, which is about twice the value previously discussed (24 nM). With this shift of induction point, P_RM activity is reduced by a factor two and P_R activity is reduced by a factor four, because the increased CI and Cro concentrations repress P_RM and P_R, respectively. Regarding the ±1 kcal/mol perturbations, with the new induction point, most of the activities change in a similar manner as listed in Table 4 (within 20%); however, for a few activities, the change in the activities is increased by a factor two, presumably due to the reduced wild-type activity that leads to an increased sensitivity upon perturbations of the affinities. We also find the same pattern of suppressors in this new situation with the induction point moved to total protein concentration of 43 nM. The only difference in this respect is that two new suppressors occur in the latter case (43 nM) compared to the original case (24 nM).

Regime 3

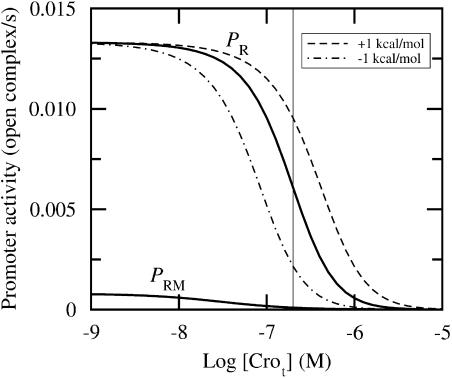
Finally, we introduce perturbations in the lytic regime. Here, the protein levels after induction are not known in vivo. However, as seen in Fig. 4, the repressor level is approximately zero for [Cro_t] above 100 nM, and we choose [Cro_t] ≈ 200 nM as a typical protein concentration after induction. Fig. 6 shows for large Cro levels that the activity at P_RM is negligible. The ratio between P_R and P_RM is of order 10². Table 5 shows that the sensitivity of Cro affinities is in general high in this regime at both promoters.

FIGURE 6.

Promoter activity versus total Cro concentration for [CI_t] ≈ 0 (fully drawn line). Dashed lines correspond to ΔG_1′ perturbed ±1 kcal/mol. Perturbations have negligible impact on the activity at P_RM. Thin vertical line indicates 200 nM. Abscissa is drawn on logarithmic (decadic) scale.

TABLE 5.

Relative change in activity at lytic concentrations ([CI_t] ≈ 0 and [Cro_t] ≈ 200 nM) corresponding to perturbations as performed in Table 3

	+1 kcal/mol		−1 kcal/mol
	PRM	PR	PRM	PR
ΔG1′	0	0.6	0	−0.6
ΔG2′	0	0.6	0	−0.6
ΔG3′	2.3	0	−0.8	0
ΔG12′	−0.3	0	1.1	−0.2
ΔG23′	0.1	0.1	−0.2	−0.2
ΔG123′	0.3	0.3	−0.6	−0.6
ΔGRM	−0.8	0	2.6	0
ΔGR	0	−0.7	0	0.8

Wild-type activity in regime 3 is 1.0 × 10⁻⁴ s⁻¹ at P_RM and 6.1 × 10⁻³ s⁻¹ at P_R.

In regime 3, perturbations of CI affinities have no effect upon the activities, due to zero repressor concentration. Also note that all affinities, apart from ΔG_R, have suppressors. The latter observation shows the uniqueness of ΔG_R in this regime.

The recent data of Darling et al. (2000a) show that Cro has a nonzero dissociation constant at 20°C. We are not aware of any corresponding Cro affinity data measured at 37°C. Nevertheless, it is important to probe for the impact of such a monomer-dimer equilibrium. We find that at a given free Cro concentration, a nonzero Cro dissociation constant has no impact on the activity at any concentration. However, for a given total Cro concentration, a nonzero dissociation constant leads to less free Cro dimers, implying an effectively weaker Cro affinity associated with O_R.

As previously mentioned (in Thermodynamics section), Darling et al. (2000b) measured nonzero Cro cooperative affinity terms—ΔG_12′, ΔG_23′, and ΔG_123′ in Table 2. However, these data were measured at 20°C. In this work we study the system at 37°C and apply Cro data from Shea and Ackers (1985) without Cro cooperative terms. Nevertheless, we want to check implications of such Cro cooperative terms. Thus, these are given nonzero values, one by one, in our perturbation analysis. The ±1 kcal/mol perturbations in regime 1 and 2 of Cro cooperative terms lead to negligible changes of the activity. This is interesting in light of the size of the Cro cooperative affinities that are in the range 0.5–1 kcal/mol (Darling et al., 2000b). However, in regime 3, as shown in Table 5, Cro cooperativity has a nonnegligible effect upon both activities.

DNA binding of CI and Cro outside O_R (nonspecific binding) may have impact on the free intracellular protein concentrations (Reinitz and Vaisnys, 1990; Johnson et al., 1981). Nonspecific binding leads to a larger effective cellular volume (Aurell et al., 2002). We test our simulation with regards to the perturbations performed at a volume increased by a factor 2. For a lysogen, the effect is negligible compared to original data, and in regime 3 the sensitivity is slightly reduced. However, our main conclusions about sensitivity remain unchanged. In regime 2, the situation is more complex, because nonspecific binding leads to another induction point and comparison to the original data is not obvious.

Another source of error, with regards to the relevance of our results in vivo, is the possibility for DNA loops formed by a more or less stable repressor octamer between the left operator and O_R of phage λ that effectively reduces P_RM activity (Dodd et al., 2001). Due to the fact that such mechanism is a recent finding and sufficient experimental details remain to be established, we do not here discuss the influence of such DNA looping.

SUMMARY AND CONCLUSION

We have studied the right operator (O_R) of phage λ genome. Experimental values of the protein-operator interactions are applied in a statistical-mechanical approach, with a probability for the different binding states given in Eq. 1. This is used to predict the activity (proportional to the rate of protein production) of the two competing promoters P_RM and P_R associated with O_R.

Systematic perturbations (±1 kcal/mol) of the affinities in three different concentration regimes (lysogenic, around induction, and lytic) show that a lysogen at P_RM is not very sensitive with respect to the activity, in contrast to inductive and lytic regimes. Thus, within experimental error of the affinities (±(0.5–1) kcal/mol), which may also reflect typical fluctuations of the cellular protein concentrations, lysogenic activity at P_RM remains stable. The fact that the sensitivity is significant in the late lytic regime may not be a “problem” for the system to make lysis efficient, because at this stage other genes are important (Ptashne, 1992). In this respect, the sensitivity of regime 2 may turn out to be the most notable one.

In regime 1, at P_RM, only perturbations of ΔG_RM (RNAP at P_RM) significantly change the activity. In regime 3, at P_R, the corresponding changes are linked to perturbations of P_R-associated Cro affinities and ΔG_R (RNAP at P_R). Around induction, where both promoters are active, the sensitivity of the activity is large upon perturbations of three CI affinities and one Cro affinity, and both RNAP affinities.

We also look at large perturbations of order ±2 kcal/mol that may resemble a typical shift in the binding energy upon a mutation (Burz and Ackers, 1996; Little et al., 1999). Thus, for simplicity, such large perturbations are here called mutations, but we stress that these are not linked to specific experimental data and should therefore be regarded as hypothetical ones. In particular we study mutations that alter the activity >25%.

Most affinities (in all three regimes) have one or more suppressors defined as a perturbation that compensates for a mutation (±2 kcal/mol) such that wild-type activity is restored. However, it is notable that a +2 kcal/mol mutation of ΔG_RM in regime 1, ΔG_RM and ΔG_R in regime 2, and ΔG_R in regime 3 have no suppressors. In other words the RNAP affinities cannot be weakened much without destroying the function of the λ-switch. Furthermore, in regime 2 there are several affinities that change the activity >25% at both promoters. Surprisingly, it is only the +2 kcal/mol perturbation of ΔG_R that cannot be suppressed, by the same compensating mutation, such that wild-type activity is restored at both promoters.

It is also interesting that our perturbations may to some extent incorporate intracellular (time) fluctuations and cell-to-cell (ensemble) variations, i.e., noise (Metzler, 2001; Aurell and Sneppen, 2002; Elowitz et al., 2002), because these variations may effectively be regarded as uncertainties of the affinities. Thus in regime 1, within this approximation, it is only noise that effectively influences RNAP affinity that has significant effect upon P_RM activity. Following this argumentation, noise will in general influence the activities mostly around induction and in the lytic regime.

To our knowledge, we have for the first time presented a systematic study of the sensitivity of the regulatory system associated with O_R in phage λ. The identification of a small number of affinities that have a high sensitivity is expected to shed new light on the operating principle of genetic switches, similarly the findings of suppressors.