Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jan;86(1):599–608. doi: 10.1016/S0006-3495(04)74138-7

Spatial Analysis of 3′ Phosphoinositide Signaling in Living Fibroblasts: II. Parameter Estimates for Individual Cells from Experiments

Ian C Schneider 1, Jason M Haugh 1
PMCID: PMC1303829  PMID: 14695304

Abstract

Fibroblast migration is directed by gradients of platelet-derived growth factor (PDGF) during wound healing. As in other chemotactic systems, it has been shown recently that localized stimulation of intracellular phosphoinositide (PI) 3-kinase activity and production of 3′ PI lipids in the plasma membrane are important events in the signaling of spatially biased motility processes. In turn, 3′ PI localization depends on the effective diffusion coefficient, D, and turnover rate constant, k, of these lipids. Here we present a systematic and direct comparison of mathematical model calculations and experimental measurements to estimate the values of the effective 3′ PI diffusion coefficient, D, turnover rate constant, k, and other parameters in individual fibroblasts stimulated uniformly with PDGF. In the context of our uniform stimulation model, the values of D and k in each cell were typically estimated within 10–20% or less, and the mean values across all of the cells analyzed were D = 0.37 ± 0.25 μm2/s and k = 1.18 ± 0.54 min−1. In addition, we report that 3′ PI turnover is not affected by PDGF receptor signaling in our cells, allowing us to focus our attention on the regulation of 3′ PI production as this system is studied further.

INTRODUCTION

Fibroblasts in tissue respond to a host of growth factors, including forms of platelet-derived growth factor (PDGF), fibroblast growth factor, insulin-like growth factor, and heparin-binding epidermal growth factor. These factors act through specific cell surface receptors of the receptor tyrosine kinase family, which activate a common set of intracellular signal transduction pathways to elicit cell proliferation (van der Geer et al., 1994; Schlessinger, 2000). PDGF is also a chemoattractant, stimulating directed migration (chemotaxis) of fibroblasts and other cell types toward a PDGF gradient (Heldin and Westermark, 1999). Such gradients are formed in tissue during wound healing, through secretion of PDGF by activated platelets, and are important for recruitment of fibroblasts as well as macrophages to the wound site (Martin, 1997).

One requirement for stimulating directed cell motility is the coupling of receptor signaling to regulation of the actin cytoskeleton, and in this respect the PDGF receptor-mediated chemotactic pathway has largely been elucidated. Activated PDGF receptors recruit type IA phosphoinositide (PI) 3-kinases to the inner leaflet of the plasma membrane, where these enzymes phosphorylate the lipid substrate phosphatidylinositol (4,5)-bisphosphate (PtdIns(4,5)P2), producing the 3′ PI lipid second messenger PtdIns(3,4,5)P3 (Vanhaesebroeck and Waterfield, 1999). Another 3′ PI, PtdIns(3,4)P2, is subsequently formed from PtdIns(3,4,5)P3 (Hawkins et al., 1992). 3′ PIs and other phosphoinositides function by recruiting signaling proteins to the plasma membrane through interactions with pleckstrin homology (PH) domains and other protein motifs (Cullen et al., 2001; McLaughlin et al., 2002). The importance of 3′ PI-dependent signaling pathways in PDGF-stimulated chemotaxis was established in a number of studies, in which blocking PI 3-kinase recruitment or activity abolished cell migration toward PDGF (Kundra et al., 1994; Wennström et al., 1994a,b; Wymann and Arcaro, 1994). One of the important molecular players that couple PDGF-stimulated 3′ PI production to actin rearrangements and cell movement is the small GTPase Rac, which mediates membrane ruffling and formation of the lammellipod, the leading membrane edge in a migrating cell (Ridley et al., 1992; Hawkins et al., 1995; Hooshmand-Rad et al., 1997).

Eukaryotic cells respond to chemoattractant gradients by distinguishing the levels of receptor-ligand binding in different cellular locations, a process called spatial sensing. Thus, another aspect of chemotactic signaling is the polarized spatial localization of the pathway components, which biases membrane protrusion in the direction of the chemoattractant gradient (Weiner, 2002). Indeed, it has been shown recently that intracellular gradients of 3′ PIs are generated in the plasma membranes of fibroblasts exposed to a PDGF gradient (Haugh et al., 2000). Interestingly, fibroblasts uniformly stimulated with PDGF also showed intracellular 3′ PI membrane gradients, increasing radially from the center to the periphery of the contact area. The radial gradients were consistent with a restriction of PDGF receptor-mediated 3′ PI production to the top of the cell, and the evolution of the gradient in a representative cell was used in conjunction with a mathematical model to give rough estimates of the 3′ PI diffusion coefficient and turnover rate constant (Haugh et al., 2000). The ratio of these two parameters defines the spatial range of a second messenger, providing a biophysical basis for the ability of an intracellular molecule to transduce a localized signal for spatial sensing and chemotaxis.

Although many of the molecular requirements in PDGF-stimulated cell motility have been established, the PI 3-kinase-mediated spatial sensing mechanism is still in the process of being characterized. Lingering questions surround the ability of the mechanism to be robust yet sensitive to shallow gradients (Weiner, 2002). It is also unclear to what extent spatial sensing mechanisms are conserved across cell and receptor types. We are working toward a unified model that explains the 3′ PI signaling responses of fibroblasts to both uniform and gradient PDGF stimulation. In such a model, it is important to establish which processes depend on the mode of PDGF presentation and which do not. For those processes not regulated by receptor signaling, parameter values obtained under uniform stimulation conditions, which are easier to implement, analyze, and reproduce, are expected to translate to the more complicated gradient stimulation case. Whereas it is established that production of 3′ PIs is regulated through PDGF receptor modulation of PI 3-kinase activity, the possible regulation of 3′ PI turnover, through the action of PI 3-phosphatase activities, has not been studied in detail.

In the preceding companion article, a generalized uniform stimulation model was presented, and it was shown that fluorescence measurements could be used to delineate constraints on the parameter values. Here, a systematic series of experiments were performed, and the model was found to be generally suitable for capturing the observed 3′ PI dynamics in individual fibroblasts. An important qualitative finding is that 3′ PI turnover is not regulated by PDGF receptor signaling, suggesting fundamental differences in the spatial sensing mechanisms utilized by different classes of chemoattractant receptors. Quantitative results include rigorous estimates of the effective 3′ PI diffusion coefficient, D, the 3′ PI turnover rate constant, k, and other parameters in individual cells. Our approach allowed the precision of these single-cell parameter estimates as well as the cell-to-cell variability of the parameter values to be evaluated. The minimum and maximum estimated values of D and k in each cell typically showed a difference of <20%, whereas the values from cell to cell were typically within a factor of 2 of the mean.

MATERIALS AND METHODS

cDNA constructs, cell culture, and transfection

The GFP-AktPH construct consists of the PH domain of human Akt1 attached with a short linker to the C-terminus of enhanced green fluorescent protein (EGFP), made by cloning into BamHI/XbaI of pEGFP-C1 (Clontech, Palo Alto, CA). This insert was also cloned into the same sites of pEYFP-C1 and pECFP-C1, yielding YFP-AktPH and CFP-AktPH, respectively. Membrane-targeted lyn-CFP contains the palmitoylation sequence from Lyn (Teruel et al., 1999) cloned into pECFP-N1. Unless otherwise noted, all tissue culture reagents were from Invitrogen (Carlsbad, CA) or Sigma (St. Louis, MO). NIH 3T3 fibroblasts (American Type Culture Collection, Manassas, VA) were subcultured in 10 cm tissue culture dishes with Dulbecco's modified Eagle's medium containing 10% fetal bovine serum, 2 mM l-glutamine, and the antibiotics penicillin and streptomycin. Cells were seeded onto 25 mm square glass coverslips, pre-coated with poly-d-lysine, and were later transfected with the vector(s) indicated using Lipofectamine Plus (Invitrogen). After 24 h, transfected cells were incubated in serum-free Dulbecco's modified Eagle's medium with 2 mM l-glutamine, penicillin, and streptomycin, and 1 mg/ml fatty acid-free bovine serum albumin for 4 h before imaging.

Total internal reflection fluorescence microscopy

Total internal reflection fluorescence (TIRF) microscopy was performed essentially as described (Haugh et al., 2000). In this technique, an evanescent wave is produced with energy that decays exponentially with distance into the sample (characteristic space constant ∼100 nm), selectively exciting fluorophores in close proximity to the membrane-substratum contact area (Axelrod, 2001; Steyer and Almers, 2001; Toomre and Manstein, 2001). Our TIRF excitation source was from a Melles Griot (Irvine, CA) tunable wavelength laser head, emitting lines of 457 nm (enhanced cyan fluorescent protein (ECFP), 15 mW), 488 nm (EGFP, 60 mW), or 514 nm (enhanced yellow fluorescent protein (EYFP), 60 mW); each line was used at maximum power. A shutter with controller was from Vincent Associates (Rochester, NY). Other components included a base stand and water immersion objectives (Zeiss, Thornwood, NY), emission filter wheel with controller (Ludl, Hawthorne, NY), and band pass emission filters (480/30 nm for ECFP, 515/30 nm for EGFP, and 535/30 nm for EYFP; Chroma, Brattleboro, VT). Digital images were acquired using a Hamamatsu ORCA ER cooled CCD (Hamamatsu, Bridgewater, NJ) and later analyzed with Metamorph software (Universal Imaging, West Chester, PA). The imaging buffer was composed of 20 mM HEPES pH 7.4, 125 mM NaCl, 5 mM KCl, 1.5 mM MgCl2, 1.5 mM CaCl2, 10 mM glucose, and 2 mg/ml fatty acid-free bovine serum albumin. Fields of cells were visualized at a combined magnification of 25× over a 20 min time course, acquiring TIRF images with 2 × 2 binning every 10 s, with each image integrated over an exposure time of ∼500 ms.

Association-dissociation experiments and analysis of radial fluorescence profiles

Our time course experiments consisted of two distinct phases, as shown in Fig. 1. After recording the basal, unstimulated fluorescence for 1 min, cells were first stimulated with a uniform concentration of human recombinant PDGF-BB (PeproTech, Rocky Hill, NJ) to activate generation of 3′ PIs and recruitment of GFP-AktPH. In the second phase of the time course, a high concentration of wortmannin (5 μM; Sigma) was added to halt 3′ PI production, allowing the kinetics of 3′ PI consumption to be isolated. To signify these two treatments and the changes they elicit, such time courses are termed association-dissociation experiments (Fig. 1 a).

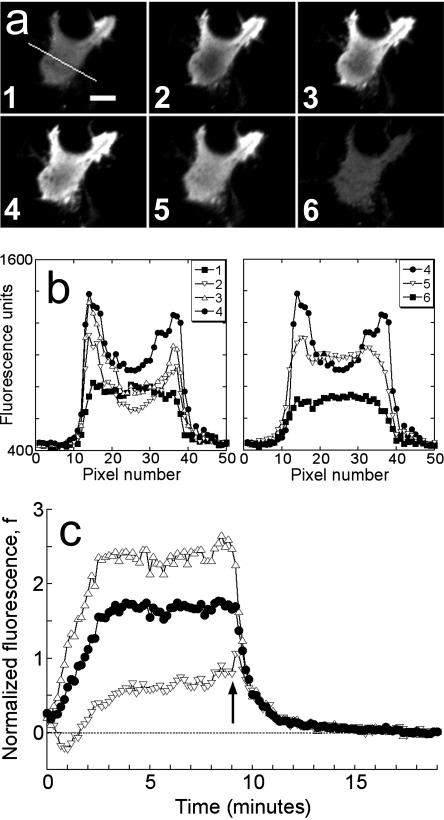
FIGURE 1.

FIGURE 1

Open in a new tab

Association-dissociation experiments with TIRF excitation. (a) Total internal reflection fluorescence (TIRF) images of a representative GFP-AktPH-transfected NIH 3T3 fibroblast. Panel 1 shows the cell before treatment (scale bar = 10 μm); the line scan used to generate the data is also shown. Panels 2, 3, and 4 were acquired 1, 2, and 7 min after addition of 10 nM PDGF-BB, over which time the fluorescence profile achieved a steady state. Panels 5 and 6 were acquired 0.5 and 10 min after addition of wortmannin, which rapidly blocks 3′ PI production. (b) Raw fluorescence profiles across the line scan are shown for each of the six images in a. (c) The line scan profiles at all time points, acquired every 10 s, were converted into normalized kinetic traces as described in Materials and Methods: open triangles, contact area periphery f(1,t); open inverted triangles, contact area center f(0,t); closed circles, contact area average 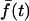Inline graphic. Time zero corresponds to the addition of PDGF, and the arrow signifies the addition of wortmannin.

The spatial fluorescence profile for each cell was processed in the following manner. A line was drawn through the shortest distance across the contact area to include the center (which exhibits the lowest intensity once the radial gradient is established), and at each time point the pixel intensities along this line were imported into Excel (Fig. 1 b). The background intensity, averaged over several pixels in acellular areas adjacent to the cell, was subtracted from each value. The fluorescence intensities at the center of the contact area and each of the two endpoints at the contact area periphery (exhibiting the maximum intensities in the radial gradient) were each averaged with their two adjacent pixel values, and the two resulting periphery values were then averaged. The fluorescence intensity averaged over the length of the line scan was calculated by taking sums over all pixels i between and including the endpoints:

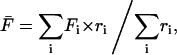graphic file with name M1.gif (1)

where Fi and ri are the fluorescence intensity and absolute distance from the center, respectively, for pixel i. Thus, the line is effectively extrapolated to a circular area, over which the average is taken. Finally, the center, periphery, and average intensities were normalized using the cytosolic fluorescence intensity, Fcyt, taken as the mean of the intensities at the last six time points (after the wortmannin treatment has dissociated all GFP-AktPH molecules from the membrane); the normalized intensity, f, is defined as

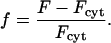graphic file with name M2.gif (2)

By plotting as a function of time the normalized fluorescence at the center of, at the periphery of, and averaged over a line scan through the contact area, one can effectively visualize the kinetics of 3′ PI accumulation as well as the development of a radial 3′ PI gradient in the contact area (Fig. 1 c).

The intensity of TIRF emission is a function of distance from the glass-buffer interface as well as the fluorophore concentration. Therefore it is important to ensure that the separation distance of the cell does not change significantly during the time course. This was confirmed in a number of control experiments, each subjected to the association-dissociation procedure (results not shown). These involved cells transfected with soluble GFP variants and membrane targeted lyn-CFP, untransfected cells with fluorescein isothiocyanate-labeled dextran added to the medium, and cells cotransfected with YFP-AktPH and lyn-CFP. In all cases, neither PDGF nor wortmannin prompted significant changes in the apparent membrane-substratum separation distance. These experiments also allowed us to rule out the influence of significant photobleaching, as did a series of experiments in which the duration of PDGF stimulation, before wortmannin addition, was varied. Finally, the dissociation responses were carried out with various doses of wortmannin to address the specificity of this treatment. Concentrations of 100 nM and above brought the fluorescence to similar values relative to the unstimulated level. However, a dose above 1 μM was required to block PI 3-kinase most rapidly; i.e., lower concentrations yielded fluorescence decay rates limited by the rate of wortmannin interaction with PI 3-kinase. Another PI 3-kinase inhibitor, LY294002, yielded similar kinetics and extent of fluorescence decrease when added at high concentration (250 μM; data not shown).

RESULTS

Fibroblasts exhibit distinct spatiotemporal features in association-dissociation experiments

As exemplified in Fig. 1 c, GFP-AktPH-transfected cells consistently showed a number of reproducible characteristics in our association-dissociation experiments. Each displayed a detectable 3′ PI level before stimulation, as judged by the offset between the fluorescence intensities at the beginning and end of the experiment, defined as f0. In response to stimulation with PDGF-BB concentrations above ∼0.01 nM, a fluorescence increase was detected with a radial gradient from the center to the periphery of the contact area. Finally, in the dissociation phase of the time course, the fluorescence intensities at the center and periphery rapidly merged and decayed exponentially. When PI 3-kinase was activated maximally, as in Fig. 1 with PDGF-BB at 0.5 nM or above, the association kinetics were generally marked by two additional features. First, the normalized fluorescence at the center exhibits a transient dip, passing through a minimum defined as fmin(0); based on the definition of f (Eq. 2), this value can be negative if a significant amount of cytosolic GFP-AktPH is recruited to the top of the cell before significant diffusion of 3′ PIs to the bottom domain can occur. Second, the fluorescence profile approaches a steady state within 5 min, characterized by center, periphery, and average fluorescence values denoted fss(0), fss(1), and 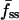Inline graphic, respectively.

Consumption of 3′ phosphoinositides is not modulated by PDGF receptor signaling

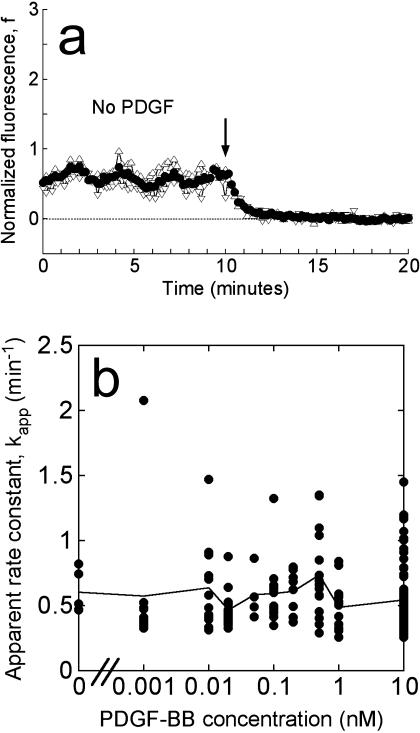
The dissociation phase in our experiments allowed us to focus on the processes that consume 3′ PIs in the plasma membrane. Given the apparent prelocalization of GFP-AktPH before stimulation in our cells, we were thus able to address whether 3′ PI consumption is under control of the PDGF receptor (Fig. 2). In 97 experiments performed on 20 different days, the concentration of PDGF-BB added during the association phase was systematically varied over a range of 0–10 nM. Even in the absence of PDGF stimulation, the consumption of the basal 3′ PI level could be detected after addition of wortmannin (Fig. 2 a).

FIGURE 2.

FIGURE 2

Open in a new tab

The apparent 3′ PI turnover rate constant is not altered by PDGF signaling. (a) Representative association-dissociation experiment with no PDGF added during the association phase, demonstrating that the decay of the basal 3′ PI level could be detected in our assay. Symbols are as in Fig. 1 c, and the arrow signifies the addition of wortmannin. (b) For each of 197 cells stimulated with various concentrations of PDGF-BB, the time course of the average fluorescence was fit to Eq. 3, and the apparent 3′ PI turnover rate constant, kapp, was accepted if the fit exhibited an R2 value exceeding 0.95. Circle symbols are kapp values for 168 individual cells, plotted as a function of the PDGF-BB concentration used in the association phase. The solid line connects the means at each PDGF-BB dose.

Kinetic traces were analyzed for all fluorescent regions of interest that met the following objective criteria: 1), a continuous contact area >300 μm2, completely in the field of view and not obscured by other fluorescent cells; 2), an average fluorescence 150 intensity units above the acellular background at the end of the dissociation; and 3), fluorescence below the saturation level of the CCD at all times. A significant fraction of the regions of interest were too dim to satisfy the second criterion, and such cells tended to exhibit noisy kinetic traces in the normalized data. Thus, applying these criteria to a total of more than 700 regions of interest yielded 197 cells for further analysis.

The average fluorescence for each of these cells was fit to a single exponential:

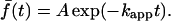graphic file with name M4.gif (3)

Cells were judged to have adequately fit this simple expression with R2 values exceeding 0.95; 168 out of 197 cells, or 85%, met this standard. Fig. 2 b shows the values of the apparent 3′ PI turnover rate constant, kapp, as a function of the PDGF concentration during the association period, for each of the 168 cells. The mean value at each concentration, representing multiple fields and days of experiments, is also shown. Cell-to-cell variability was observed as expected, but 89% of the cells exhibited kapp values within a factor of 2 of the overall average (0.57 ± 0.29 min−1, mean ± SD.). Importantly, no significant trend is apparent as the PDGF dose is increased from zero to a saturating dose of 10 nM, indicating that the consumption of 3′ PIs is not modulated positively or negatively by the level of PDGF receptor signaling. The 3′ PI level stimulated by PDGF is apparently regulated through activation of PI 3-kinases only, and 3′ PI consumption may be described mathematically with a pseudo first-order rate constant.

Direct comparison of normalized fluorescence traces and the uniform stimulation model

We have shown that TIRF measurements can be used to calculate ranges of the dimensionless parameters in our uniform stimulation model. Here we wish to apply this strategy to experimental data and obtain the dimensional values of the effective 3′ PI diffusion coefficient and turnover rate constant. When the concentration of PDGF-BB is 0.5 nM or above, neither the magnitude nor the kinetics of the GFP-AktPH association response is sensitive to PDGF concentration (Haugh et al., 2000, and results not shown). This suggests that PI 3-kinase is rapidly activated under these conditions, such that the model assumption of a step increase in 3′ PI production rate is justified. Of the 168 cells discussed in the previous section, 98 saw sufficiently high concentrations of PDGF. To objectively select the best of these cells with which to perform a direct comparison to the uniform stimulation model, additional criteria were imposed. First, a more stringent fluorescence above background cutoff was used (250 intensity units). Of the 71 cells that met that standard, 5 cells were classified as nonresponders (with 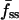Inline graphic not greater than f0), and others exhibited no detectable gradient (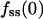Inline graphic not less than 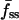Inline graphic, 9 cells) and/or no dip in the center (fmin(0) not less than both f0 and fss(0), 27 cells; 6 of these were also among the no gradient cells). With these cells eliminated, 36 cells were identified for the full analysis, of which 32 cells successfully yielded parameter estimates consistent with the uniform stimulation model.

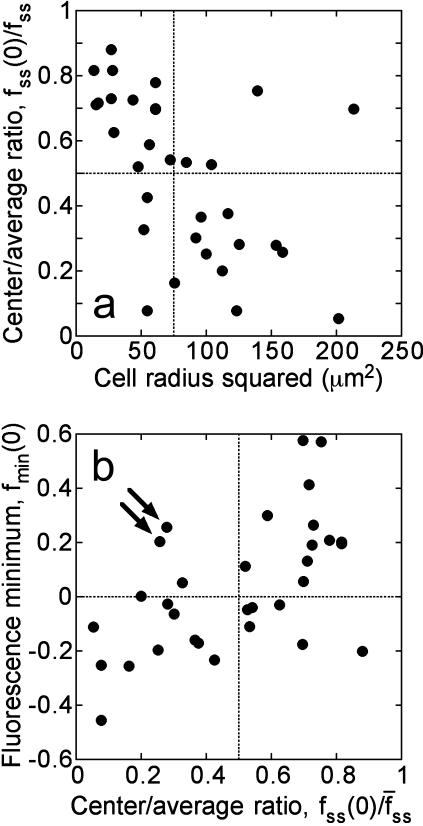
These cells exhibited a range of responses with respect to the depth of the radial gradient that developed during the association phase, as shown in Fig. 3. In the context of our uniform stimulation model, the depth of the gradient is a strong function of the dimensionless parameter Da, which compares the rates of 3′ PI consumption and diffusion:

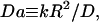graphic file with name M8.gif (4)

where D and k are the effective diffusion coefficient and turnover rate constant of 3′ PIs, and R is the radius of the contact area; thus, the depth of the gradient should be sensitive to contact area size. Indeed, the cells with shallower gradients in our experiments (higher 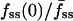Inline graphic) tended to have the smaller effective contact areas and vice versa (Fig. 3 a). In the model, the value of Da also affects the initial dip in fluorescence at the center of the contact area, and indeed a positive correlation between the values of 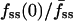Inline graphic and fmin(0) was observed in our cells (Fig. 3 b).

FIGURE 3.

FIGURE 3

Open in a new tab

Fluorescence characteristics of individual cells subjected to the full model analysis. Of the cells imaged in association-dissociation experiments, 32 satisfied all criteria for comparison with model calculations. (a) The gradient depth of each cell, assessed through the steady-state center/average fluorescence ratio, 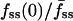Inline graphic, is a function of cell size, measured as the radius of the line scan squared. (b) Correlation of the fluorescence dip at the center of the contact area, fmin(0) (y axis), and the steady-state center/average fluorescence ratio, 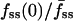Inline graphic (x axis). Two cells with relatively low 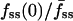Inline graphic yet high fmin(0) are indicated with arrows; these are referred to again in Fig. 5.

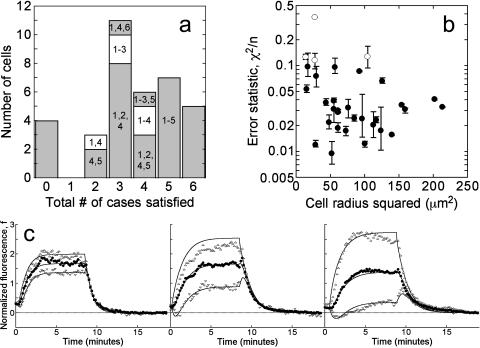
The model was fit to a cell's fluorescence tracks using the following procedure. First, the values of f0, fmin(0), 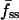Inline graphic, and fss(0) were estimated from the data. With this information alone, sets of dimensionless parameters (Da, σ, x0, and pss) that yield the observed fluorescence characteristics in up to six limiting cases of the uniform stimulation model were identified, as described in the companion article. This approach constrains the parameter space and thus delineates the precision of the parameter estimates. Each of the six limiting cases, listed in Table 1, was satisfied in a fraction of the cells, and typically a cell satisfied at least three of the cases (Fig. 4 a); however, as mentioned above, 4 out of the 36 cells selected failed to satisfy any of the cases. With the dimensionless parameters specified, the uniform stimulation model was used to simulate the corresponding association-dissociation experiment for each limiting case in dimensionless time, τ = k*t. Finally, the simulated kinetics for each case were optimally mapped to real time by least-squares regression of the kinetic traces associated with the center and average fluorescence. Here we allowed the 3′ PI production to lag behind the addition of PDGF, and thus the fit yields two parameter values: the 3′ PI consumption rate constant k and the lag time tlag. The sum of the squared residuals, χ2, divided by the number of data points considered, n, serves as a measure of the quality of fit. The fluorescence at the periphery of the contact area was not included in the fit because small but not insignificant differences between the values at the endpoints of the line scan were typically observed (as in Fig. 1 b), perhaps suggesting that the periphery is susceptible to subtle edge effects. All but 4 of the 32 cells exhibited average χ2/n values <0.10, and more than two-thirds gave average χ2/n values <0.05 (Fig. 4 b). Although cells with the smallest contact areas were among those giving the poorest fits, the uniform stimulation model performed well on cells exhibiting various depths of the 3′ PI gradient (Fig. 4 c). With k determined by this method for each limiting case, the 3′ PI diffusion coefficient D (μm2/s) was estimated from the associated value of Da (Eq. 4), taking the half-width of the line scan as the effective radius of the contact area.

TABLE 1.

Limiting cases of the uniform stimulation model

Case Description* Cells Score†
1 No 3′ PI production in contact area, 3′ PI in excess 30 0.96
2 No 3′ PI production in contact area, moderate affinity 28 1
3 No 3′ PI production in contact area, high affinity 17 0.73
4 Basal 3′ PI production in contact area, 3′ PI in excess 29 0.83
5 Basal 3′ PI production in contact area, moderate affinity 18 0.74
6 Basal 3′ PI production in contact area, high affinity 6 0.32
Open in a new tab
*

In terms of the model parameters, no 3′ PI production in the contact area means that ν = 0; basal 3′ PI production in the contact area means that ν = x0.3′ PI in excess over the probe refers to μ = 5; moderate or high probe affinity refers to κ = 1 − pss or κ = 10−3, respectively.

†

The relative score is calculated by summing (χ2/n)−1 values of the model fits for that limiting case, and then normalizing by the maximum score (case 2). This score thus rewards a case for the number of cells in which a parameter set was obtained as well as for quality of fit.

FIGURE 4.

FIGURE 4

Open in a new tab

Model fits to individual cell fluorescence tracks. (a) Limiting cases of the model were used to constrain the parameter space. A histogram for the number of cases (up to 6) satisfied is shown, and the identities of the cases are indicated (see also Table 1). (b) The quantity χ2/n is used to assess quality of fit, where n is the number of data points considered. The χ2/n value for each cell, averaged over the applicable limiting cases, is plotted versus cell size, taken as the square of the line scan radius (μm2); the error bars signify the range of χ2/n values obtained. The four cells indicated with open symbols yielded the least ideal model fits, with average χ2/n > 0.10. (c) Representative cell tracks exhibiting radial gradients of varying depth. The values of Inline graphic are (left) 0.82, (middle) 0.53, and (right) 0.25. Symbols signify fluorescence measurements as in Fig. 1 c, and solid curves are the best-fit model calculations.

An implicit assumption here is that the effective diffusion coefficient and turnover rate constant in the nonadherent portion of the membrane are the same as in the contact area. The observation that the fluorescence values at the center and periphery of the contact area rapidly merge during the dissociation phase (Fig. 1 c) indicates that the turnover rate constants in the two domains must indeed be approximately equal.

Model analysis defines narrow ranges for the 3′ PI diffusion coefficient, turnover rate constant, and other parameters in individual cells

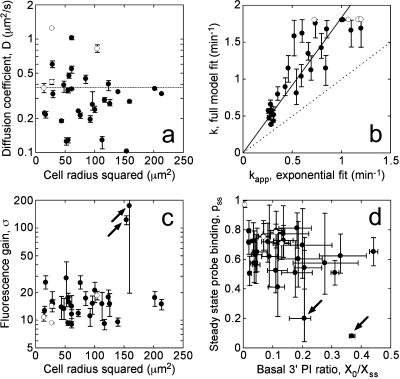
Whereas the depth of the radial 3′ PI gradient is apparently sensitive to the width of the contact area (Fig. 3 a), the estimated value of the diffusion coefficient, D, is expected to be independent of the contact area size. This was confirmed by plotting the D value for each of the 32 cells as a function of the line scan radius squared in Fig. 5 a; each value is reported as the average of the D values obtained for the applicable limiting cases of the model, and the range of possible D values for each cell and the overall mean (0.37 μm2/s) are also indicated on the plot. No apparent correlation was observed over the range of cell sizes. As expected, some cell-to-cell variability in the estimated value of D was observed, yet ∼80% of the cells were within a factor of 2 of the overall mean (Fig. 5 a). One factor that could influence the degree of variability in the apparent D values is deviation of actual contact area morphologies from that of the model; if a cell is long and slender, its D value estimated by our method would tend to be underestimated, by as much as a factor of 2 or so. However, the fluorescence pattern emanating from the center of the contact area was reasonably symmetrical in most cells, and the apparent D values did not correlate with morphometric quantities such as shape factor or elliptical form factor (results not shown).

FIGURE 5.

FIGURE 5

Open in a new tab

Estimates of the 3′ PI diffusion coefficient, turnover rate constant, and other parameters in individual cells. Circle symbols mark the mean parameter value averaged over the limiting model fits, and the error bars signify the range of parameter values for each cell. Open symbols signify the four cells that yielded less ideal model fits as described under Fig. 4. (a) The estimated diffusion coefficient D (μm2/s) in each cell is plotted versus the square of the line scan radius (μm2), demonstrating that the apparent lipid mobility is independent of cell size. The dotted line indicates the mean of the 32 cells (0.374 μm2/s). (b) The average turnover rate constant, k, is correlated versus the associated kapp, from a fit to Eq. 3, for each cell. The solid line is the best fit of the data to y = m*x, with m = 1.75; the dashed line is the y = x line. (c) The fluorescence gain, σ, the ratio of the cytosolic volume to the effective volume of TIRF excitation, is plotted versus the square of the line scan radius (μm2). (d) The estimated values of basal/steady-state 3′ PI ratio, X0/Xss (x axis), and the steady-state probe-binding fraction, pss (y axis), are shown.

Fig. 5 b shows the estimated average value and range of the 3′ PI consumption rate constant, k, in each of the 32 cells, as correlated with the apparent value of this rate constant, kapp, estimated from the single exponential fit (Eq. 3). The single exponential fit is strongly indicative of the rate constant determined from the more refined model analysis; i.e., low kapp values correspond to low k values and vice versa. However, kapp was always significantly lower than k (Fig. 5 b). This relationship was also observed when simulated dissociation kinetics, rather than experimental data, were fit to Eq. 3 (results not shown), and it is attributed to two distinct factors. First, Eq. 3 assumes a homogeneous 3′ PI profile in the contact area, i.e., that the gradient rapidly disappears; this is only approximately true. More significantly, the decay in fluorescence is slower than the decay in 3′ PI level when the bound fraction of the probe is appreciable. The fit is affected most by the higher fluorescence values, corresponding to higher fractions of bound probe.

Another parameter is the fluorescence gain σ, which characterizes the physics of TIRF microscopy; its inverse is the fraction of a cell's volume excited by TIRF. Although 2 of the 32 cells exhibited very high apparent σ values (above 100), the remaining cells showed a relatively narrow distribution (15 ± 5, mean ± SD) (Fig. 5 c). As explained in the companion article, an arbitrarily high σ value can be obtained when the steady-state gradient is moderately steep yet the fmin(0) is shallow, and indeed this was the case for the two outlier cells (Fig. 3 b). A method for estimating σ independently was also devised, as described in the Appendix. Applying this method yielded an estimated σ value of 17.5 ± 5.5 (mean ± SD), in approximate agreement with the range of values estimated from our model analysis.

The two remaining parameters are X0/Xss, the basal 3′ PI level relative to the maximum, steady-state level (in the context of the model, X0/Xss = 3x0/(2 + ν)), and pss, the fraction of GFP-AktPH associated with the membrane at steady state (Fig. 5 d). The value of X0/Xss was relatively difficult to determine precisely in each cell, and its estimated value varied widely among cells (0.14 ± 0.11). With that said, the values of X0/Xss are in rough agreement with biochemical measurements with PDGF-stimulated Swiss 3T3 fibroblasts, in which the levels of PtdIns(3,4,5)P3 and PtdIns(3,4)P2 were found to increase ∼8- and 4-fold, respectively (Jackson et al., 1992). The value of pss was also difficult to estimate precisely, yet the analysis consistently predicted that at least 40% of the probe was recruited to the membrane at steady state (Fig. 5 d). The two exceptions were the cells that also yielded the arbitrarily high σ values (Fig. 5 c). The estimated parameter values from the model analysis are summarized in Table 2. Each parameter showed varying degrees of cell-to-cell variability, as assessed by the standard deviation of the value, and precision, as judged by the percent difference between the minimum and maximum values estimated for each cell (reported as the median of all cells).

TABLE 2.

Summary of parameter values estimated from model analysis

Parameter Description Value* % Difference†
D 3′ PI diffusion coefficient 0.37 ± 0.25 μm2/s 11%
k 3′ PI turnover rate constant 1.18 ± 0.54 min−1 18%
tlag Lag in PI 3-kinase activation 42 ± 35 s 47%
X0/Xss Basal/steady-state 3′ PI ratio 0.14 ± 0.11 53%
σ Fluorescence gain parameter 15.3 ± 5.0‡ 30%‡
pss Fraction of probe bound 0.67 ± 0.12‡ 37%‡
Open in a new tab
*

Parameter values obtained with the applicable limiting constraints (up to six) for each cell were averaged, and the value reported is the average over all cells analyzed (mean ± SD). The standard deviation of this value is thus a measure of cell-to-cell variability.

†

The percent difference between the maximum and minimum parameter values obtained from the applicable limiting cases was calculated for each cell. Given is the median percent difference for the cells analyzed, a measure of the precision in the parameter value.

‡

Two out of 32 cells, yielding both arbitrarily high average σ values (175 and 123) and arbitrarily low pss values (0.20 and 0.082), were excluded from these statistics; the next highest average σ value was 29, and the next lowest average pss was 0.41.

DISCUSSION

The use of fluorescent protein fusion constructs to probe the spatial regulation and kinetics of intracellular processes is now commonplace (Lippincott-Schwartz et al., 2001; Tavaré et al., 2001; Wouters et al., 2001; Meyer and Teruel, 2003; Weijer, 2003). Quantitative modeling can be applied to directly interpret such experiments and evaluate the roles of various intracellular processes (Slepchenko et al., 2002), and here we have presented a systematic modeling and experimental approach to the analysis of radial 3′ PI gradients, typically observed in response to PDGF stimulation of GFP-AktPH-transfected NIH 3T3 fibroblasts (Haugh et al., 2000). Why is the modeling component so important? One major reason is that the fluorescence intensity at a location, indicative of the number of probe-target molecule complexes, very rarely changes in direct proportion to the total number of target molecules. Such proportionality is approximately true only when the fraction of probe molecules bound is small, in which case changes in probe recruitment would be difficult to measure. Indeed, in the majority of the cells we analyzed, it was estimated that >50% of the GFP-AktPH was recruited from the cytosol at steady state (Fig. 5 d). The model was successful in identifying narrow ranges for the 3′ PI diffusion coefficient (D) and turnover rate constant (k); had a simpler analysis been performed, e.g., using a single exponential fit to estimate k, and obtaining Da directly from the depth of the steady-state gradient (assuming infinite σ), both k and D would have been grossly underestimated.

Other parameters such as X0/Xss and pss were difficult to evaluate precisely in each cell, as their estimated values depend greatly on the limiting case of the model. We observed that cases 1 and 2 outperformed the others based on their applicability and quality of fit (Table 1); these cases assume that the PI 3-kinase activity acting at the contact area vanishes upon maximal PDGF stimulation, and that at least half of the 3′ PI is not bound by the GFP-AktPH probe. These assumptions are plausible on two grounds. First, 3′ PI production is maximal at 0.5 nM PDGF-BB, yet this concentration elicits only half-maximal PDGF receptor phosphorylation in our cells; this suggests that PI 3-kinase molecules are limiting (Park et al., 2003). Second, if a significant fraction of the 3′ PI was bound by the probe, one would expect the probe to exert a dominant-negative effect on 3′ PI-dependent processes. We presume then that the probe would be toxic to cells expressing very high levels of GFP-AktPH. Indeed, the brightest cells we observed tended to exhibit altered contact area morphology (results not shown), although we cannot say conclusively that this was caused by 3′ PI buffering. When the individual cell parameter estimates were restricted to cases 1 and 2, the range for each parameter value was predictably much smaller (median of 20% difference or less for all parameters), whereas the means and standard deviations of the parameter values were not grossly altered from those listed in Table 2.

An intriguing although not unexpected finding from our quantitative analysis is that individual cells can vary significantly with respect to their estimated parameter values. Insofar as these parameters affect the ability of a cell to sense a PDGF gradient and migrate toward, certain cells in the population may be more sensitive than others to gradient stimulation. Variability in the values of D, k, and X0/Xss may reflect intrinsic differences in the apparent membrane fluidity of cells as well as their relative expression levels of PDGF receptors, PI 3-kinases, and PI 3-phosphatases. The size and morphology of the cell contact area, relative to the orientation of the gradient, also affects the ability of a cell to localize 3′ PIs, but this situation can change dynamically on the timescale of minutes as cells actively spread in response to PDGF. It is therefore tempting to speculate that individual fibroblasts may be selectively screened to determine which are recruited to sites of PDGF secretion, such as clotted wounds.

Recently, the spatial sensing problem has been the subject of a number of elegant theoretical investigations (Meinhardt, 1999; Narang et al., 2001; Postma and Van Haastert, 2001; Levchenko and Iglesias, 2002), in which it has been important to compare the cellular responses to uniform and gradient stimulation. However, it should be noted that these modeling studies were not based on a direct comparison with experiment. Our work is a departure from those studies in another major way: the previous models have sought to explain specific phenomenological features of spatial sensing mediated by certain G-protein-coupled receptors, as classically observed in neutrophils and in the slime mold Dictyostelium discoideum (Devreotes and Zigmond, 1988). In those systems, as in PDGF-stimulated fibroblasts, it is now well-established that 3′ PIs are responsible for coupling the presence of an extracellular gradient to polarized cytoskeletal activity (Chung et al., 2001; Wang et al., 2002; Weiner, 2002), but it would be premature to expect all aspects of spatial sensing mechanisms to be conserved.

Whereas gradient stimulation elicits persistently localized 3′ PI production in all cases, the cell responses to uniform stimulation with PDGF and chemoattractants that act through G-protein-coupled receptors are markedly different. The latter stimulate very rapid, transient responses with nearly complete adaptation (Stephens et al., 1991; Parent et al., 1998; Servant et al., 2000). In contrast, biochemical measurements have shown that both PtdIns(3,4,5)P3 and PtdIns(3,4)P2 levels in PDGF-stimulated fibroblasts achieve a steady state that is maintained for several minutes (Hawkins et al., 1992; Jackson et al., 1992), in accord with our fluorescence measurements. A proposed mechanism that can simultaneously account for the desensitization of the uniform response and the persistence of the gradient response in neutrophils and Dictyostelium is the parallel receptor-mediated activation of both 3′ PI production and consumption (Levchenko and Iglesias, 2002). In apparent support of the regulation of 3′ PI consumption, at least in Dictyostelium, it was recently shown that localization of the PI 3-phosphatase PTEN is altered in response to gradient versus uniform stimulation (Funamoto et al., 2002; Iijima and Devreotes, 2002).

If this localization indeed signifies receptor regulation of 3′ PI consumption rates, then in this respect the PDGF sensing mechanism differs. By applying a sensitive fluorescence technique, we detected, for the first time, the consumption of the basal 3′ PI level in response to PI 3-kinase inhibition. The apparent turnover rate constant exhibited the same range of values regardless of the concentration of PDGF in our association-dissociation experiments, indicating that 3′ PI turnover is not regulated by PDGF receptor signaling (Fig. 2). The values obtained were similar to the rate constant previously obtained in a PDGF-stimulated fibroblast line by biochemical measurements (Whiteford et al., 1996). Based on our observation that the radial gradient rapidly disappears after PI 3-kinase inhibition, we may also conclude that the 3′ PIs in the nonadherent portion of the membrane also experience the same turnover rate constant. Together with the lack of rapid adaptation in response to uniform PDGF stimulation, this suggests that the spatial regulation of 3′ PI distribution in our cells is governed simply by the modulation of PI 3-kinase activity. Thus, as we now characterize the response to gradient PDGF stimulation, we do not necessarily expect the same mechanisms and assumptions that have been attributed to spatial sensing in other systems to hold.

Acknowledgments

Members of the Haugh laboratory, especially Jodee Lewis and Michael Weiger, are gratefully acknowledged for technical assistance. The authors also thank Kyle Grant and Jorge Pikunic for their efforts on earlier parameter fitting algorithms. The lyn-ECFP-N1 vector was a kind gift from the laboratory of Tobias Meyer (Stanford University).

This work was supported by the Whitaker Foundation (RG-01-0150) and from an award to J.M.H. from the Henry & Camille Dreyfus Foundation. I.C.S. was also supported by a Graduate Assistance in Areas of National Need Biotechnology Fellowship from the U.S. Department of Education.

APPENDIX: Independent determination of σ

The parameter σ is defined as the volume of the cytosol over the effective excitation volume of the evanescent wave:

graphic file with name M17.gif (A1)

where Vcyt is the volume of the cytosol, Ac is the surface area of the membrane contact zone, and dcell is the effective penetration depth of the evanescent wave into the cell (∼100 nm). Our approach is to sequentially image the same cell using epifluorescence (entire volume) and TIRF excitation of EYFP and ECFP probes. To acquire epifluorescence, our Zeiss stand was also equipped with an HBO 50 lamp and optics train, and excitation dichroics for ECFP and EYFP were from Chroma. The experiments described here were all performed on the same day.

The first experiment is used to calibrate the power densities of the excitation sources. Cells are cotransfected with soluble YFP and CFP. The average fluorescence intensities for epifluorescence and TIRF excitation in the YFP channel are given by:

graphic file with name M18.gif (A2)

The constants qEpi,Y and qTIRF,Y are the fluorescence emission detected in the YFP channel per mole YFP in the excitation region for epifluorescence and TIRF excitation modes, respectively. They account for the power density of excitation, absorbance and quantum yield by the fluorophore, and quantum efficiency of the light collection and detection setup. CY is the concentration of YFP in the cytosol, Aepi is the area of the region of interest in epifluorescence mode, dbuff,Y is the space constant of evanescent wave decay in the extracellular buffer, and hgap is the average height of the gap between the glass surface and the inner face of the plasma membrane. With corresponding measurements in the CFP channel, and noting that dcell is proportional to excitation wavelength, we obtain the cytosolic ratioρc/c:

graphic file with name M19.gif (A3)

where λex,C/λex,Y is the ratio of the excitation wavelengths used to excite CFP and YFP in TIRF mode. Technically, the ratio βC/βY varies among cells with different hgap, but the variation is expected to be small. For example, we estimate that a difference in hgap of 50 nm yields a difference in βC/βY of only 8%. Applying this methodology to different cells imaged in multiple fields, we observed a ρc/c value of 4.259 ± 0.925 × 10−3 (mean ± SD, n = 14).

In the second experiment, cells are cotransfected with soluble YFP and a plasma membrane-targeted CFP construct containing the myristoylation sequence of Lyn. Assuming that the confinement distance of lyn-CFP at the plasma membrane (<10 nm) is much less than dcell,C (∼100 nm), the average fluorescence intensities for epifluorescence and TIRF excitation in the CFP channel would be

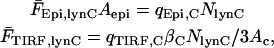graphic file with name M20.gif (A4)

where NlynC is the moles of lyn-CFP expressed in the cell. Thus, we may define the membrane/cytosol ratio, ρm/c, as

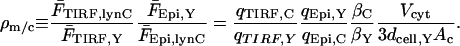graphic file with name M21.gif (A5)

Measurements in multiple fields yielded ρm/c = 26.51 ± 6.02 × 10−3 (mean ± SD, n = 16).

Combining the results of these two experiments gives the value of σ. For example, to obtain the value for GFP excitation, σG,

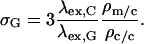graphic file with name M22.gif (A6)

With λex,C = 457 nm and λex,G = 488 nm, and applying standard propagation of error, one obtains a σG value of 17.5 ± 5.5.

References

  1. Axelrod, D. 2001. Total internal reflection fluorescence microscopy in cell biology. Traffic. 2:764–774. [DOI] [PubMed] [Google Scholar]
  2. Chung, C. Y., S. Funamoto, and R. A. Firtel. 2001. Signaling pathways controlling cell polarity and chemotaxis. Trends Biochem. Sci. 26:557–566. [DOI] [PubMed] [Google Scholar]
  3. Cullen, P. J., G. E. Cozier, G. Banting, and H. Mellor. 2001. Modular phosphoinositide-binding domains: their role in signalling and membrane trafficking. Curr. Biol. 11:R882–R893. [DOI] [PubMed] [Google Scholar]
  4. Devreotes, P. N., and S. H. Zigmond. 1988. Chemotaxis in eukaryotic cells: a focus on leukocytes and Dictyostelium. Annu. Rev. Cell Biol. 4:649–686. [DOI] [PubMed] [Google Scholar]
  5. Funamoto, S., R. Meili, S. Lee, L. Parry, and R. A. Firtel. 2002. Spatial and temporal regulation of 3-phosphoinositides by PI 3-kinase and PTEN mediates chemotaxis. Cell. 109:611–623. [DOI] [PubMed] [Google Scholar]
  6. Haugh, J. M., F. Codazzi, M. Teruel, and T. Meyer. 2000. Spatial sensing in fibroblasts mediated by 3′ phosphoinositides. J. Cell Biol. 151:1269–1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hawkins, P. T., A. Eguinoa, R. G. Qiu, D. Stokoe, F. T. Cooke, R. Walters, S. Wennstrom, L. Claesson-Welsh, T. Evans, M. Symons, and L. Stephens. 1995. PDGF stimulates an increase in GTP-Rac via activation of phosphoinositide 3-kinase. Curr. Biol. 5:393–403. [DOI] [PubMed] [Google Scholar]
  8. Hawkins, P. T., T. R. Jackson, and L. R. Stephens. 1992. Platelet-derived growth factor stimulates synthesis of PtdIns(3,4,5)P3 by activating a PtdIns(4,5)P2 3-OH kinase. Nature. 358:157–159. [DOI] [PubMed] [Google Scholar]
  9. Heldin, C. H., and B. Westermark. 1999. Mechanism of action and in vivo role of platelet-derived growth factor. Physiol. Rev. 79:1283–1316. [DOI] [PubMed] [Google Scholar]
  10. Hooshmand-Rad, R., L. Claesson-Welsh, S. Wennström, K. Yokote, A. Siegbahn, and C. H. Heldin. 1997. Involvement of phosphatidylinositide 3′-kinase and Rac in platelet-derived growth factor-induced actin reorganization and chemotaxis. Exp. Cell Res. 234:434–441. [DOI] [PubMed] [Google Scholar]
  11. Iijima, M., and P. Devreotes. 2002. Tumor suppressor PTEN mediates sensing of chemoattractant gradients. Cell. 109:599–610. [DOI] [PubMed] [Google Scholar]
  12. Jackson, T. R., L. R. Stephens, and P. T. Hawkins. 1992. Receptor specificity of growth factor-stimulated synthesis of 3-phosphorylated inositol lipids in Swiss 3T3 cells. J. Biol. Chem. 267:16627–16636. [PubMed] [Google Scholar]
  13. Kundra, V., J. A. Escobedo, A. Kazlauskas, H. K. Kim, S. G. Rhee, L. T. Williams, and B. R. Zetter. 1994. Regulation of chemotaxis by the platelet-derived growth factor receptor-β. Nature. 367:474–476. [DOI] [PubMed] [Google Scholar]
  14. Levchenko, A., and P. A. Iglesias. 2002. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys. J. 82:50–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lippincott-Schwartz, J., E. Snapp, and A. Kenworthy. 2001. Studying protein dynamics in living cells. Nat. Rev. Mol. Cell Biol. 2:444–456. [DOI] [PubMed] [Google Scholar]
  16. Martin, P. 1997. Wound healing—aiming for perfect skin regeneration. Science. 276:75–81. [DOI] [PubMed] [Google Scholar]
  17. McLaughlin, S., J. Y. Wang, A. Gambhir, and D. Murray. 2002. PIP2 and proteins: interactions, organization, and information flow. Annu. Rev. Biophys. Biomol. Struct. 31:151–175. [DOI] [PubMed] [Google Scholar]
  18. Meinhardt, H. 1999. Orientation of chemotactic cells and growth cones: models and mechanisms. J. Cell Sci. 112:2867–2874. [DOI] [PubMed] [Google Scholar]
  19. Meyer, T., and M. N. Teruel. 2003. Fluorescence imaging of signaling networks. Trends Cell Biol. 13:101–106. [DOI] [PubMed] [Google Scholar]
  20. Narang, A., K. K. Subramanian, and D. A. Lauffenburger. 2001. A mathematical model for chemoattractant gradient sensing based on receptor-regulated membrane phospholipid signaling dynamics. Ann. Biomed. Eng. 29:677–691. [DOI] [PubMed] [Google Scholar]
  21. Parent, C. A., B. J. Blacklock, W. M. Froehlich, D. B. Murphy, and P. N. Devreotes. 1998. G protein signaling events are activated at the leading edge of chemotactic cells. Cell. 95:81–91. [DOI] [PubMed] [Google Scholar]
  22. Park, C. S., I. C. Schneider, and J. M. Haugh. 2003. Kinetic analysis of platelet-derived growth factor receptor/phosphoinositide 3-kinase/Akt signaling in fibroblasts. J. Biol. Chem. 278:37064–37072. [DOI] [PubMed] [Google Scholar]
  23. Postma, M., and P. J. M. Van Haastert. 2001. A diffusion-translocation model for gradient sensing by chemotactic cells. Biophys. J. 81:1314–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Ridley, A. J., H. F. Paterson, C. L. Johnston, D. Diekmann, and A. Hall. 1992. The small GTP-binding protein rac regulates growth factor-induced membrane ruffling. Cell. 70:401–410. [DOI] [PubMed] [Google Scholar]
  25. Schlessinger, J. 2000. Cell signaling by receptor tyrosine kinases. Cell. 103:211–225. [DOI] [PubMed] [Google Scholar]
  26. Servant, G., O. D. Weiner, P. Herzmark, T. Balla, J. W. Sedat, and H. R. Bourne. 2000. Polarization of chemoattractant receptor signaling during neutrophil chemotaxis. Science. 287:1037–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Slepchenko, B. M., J. C. Schaff, J. H. Carson, and L. M. Loew. 2002. Computational cell biology: spatiotemporal simulation of cellular events. Annu. Rev. Biophys. Biomol. Struct. 31:423–441. [DOI] [PubMed] [Google Scholar]
  28. Stephens, L. R., K. T. Hughes, and R. F. Irvine. 1991. Pathway of phosphatidylinositol(3,4,5)-trisphosphate synthesis in activated neutrophils. Nature. 351:33–39. [DOI] [PubMed] [Google Scholar]
  29. Steyer, J. A., and W. Almers. 2001. A real-time view of life within 100 nm of the plasma membrane. Nat. Rev. Mol. Cell Biol. 2:268–275. [DOI] [PubMed] [Google Scholar]
  30. Tavaré, J. M., L. M. Fletcher, and G. I. Welsh. 2001. Using green fluorescent protein to study intracellular signalling. J. Endocrinol. 170:297–306. [DOI] [PubMed] [Google Scholar]
  31. Teruel, M. N., T. A. Blanpied, K. Shen, G. J. Augustine, and T. Meyer. 1999. A versatile microporation technique for the transfection of cultured CNS neurons. J. Neurosci. Methods. 93:37–48. [DOI] [PubMed] [Google Scholar]
  32. Toomre, D., and D. J. Manstein. 2001. Lighting up the cell surface with evanescent wave microscopy. Trends Cell Biol. 11:298–303. [DOI] [PubMed] [Google Scholar]
  33. van der Geer, P., T. Hunter, and R. A. Lindberg. 1994. Receptor protein-tyrosine kinases and their signal transduction pathways. Annu. Rev. Cell Biol. 10:251–337. [DOI] [PubMed] [Google Scholar]
  34. Vanhaesebroeck, B., and M. D. Waterfield. 1999. Signaling by distinct classes of phosphoinositide 3-kinases. Exp. Cell Res. 253:239–254. [DOI] [PubMed] [Google Scholar]
  35. Wang, F., P. Herzmark, O. D. Weiner, S. Srinivasan, G. Servant, and H. R. Bourne. 2002. Lipid products of PI(3)Ks maintain persistent cell polarity and directed motility in neutrophils. Nat. Cell Biol. 4:513–518. [DOI] [PubMed] [Google Scholar]
  36. Weijer, C. J. 2003. Visualizing signals moving in cells. Science. 300:96–100. [DOI] [PubMed] [Google Scholar]
  37. Weiner, O. D. 2002. Regulation of cell polarity during eukaryotic chemotaxis: the chemotactic compass. Curr. Opin. Cell Biol. 14:196–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wennström, S., P. Hawkins, F. Cooke, K. Hara, K. Yonezawa, M. Kasuga, T. Jackson, L. Claesson-Welsh, and L. Stephens. 1994a. Activation of phosphoinositide 3-kinase is required for PDGF-stimulated membrane ruffling. Curr. Biol. 4:385–393. [DOI] [PubMed] [Google Scholar]
  39. Wennström, S., A. Siegbahn, K. Yokote, A. Arvidsson, C. H. Heldin, S. Mori, and L. Claesson-Welsh. 1994b. Membrane ruffling and chemotaxis transduced by the PDGF β-receptor require the binding site for phosphatidylinositol 3′ kinase. Oncogene. 9:651–660. [PubMed] [Google Scholar]
  40. Whiteford, C. C., C. Best, A. Kazlauskas, and E. T. Ulug. 1996. D-3 phosphoinositide metabolism in cells treated with platelet-derived growth factor. Biochem. J. 319:851–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wouters, F. S., P. J. Verveer, and P. I. H. Bastiaens. 2001. Imaging biochemistry inside cells. Trends Cell Biol. 11:203–211. [DOI] [PubMed] [Google Scholar]
  42. Wymann, M., and A. Arcaro. 1994. Platelet-derived growth factor-induced phosphatidylinositol 3-kinase activation mediates actin rearrangements in fibroblasts. Biochem. J. 298:517–520. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES