Abstract
The prediction of absolute ligand-receptor binding affinities is essential in a wide range of biophysical queries, from the study of protein-protein interactions to structure-based drug design. End-point free energy methods, such as the Molecular Mechanics Poisson-Boltzmann Surface Area (MM/PBSA) model, have received much attention and widespread application in recent literature. These methods benefit from computational efficiency as only the initial and final states of the system are evaluated, yet there remains a need for strengthening their theoretical foundation. Here a clear connection between statistical thermodynamics and end-point free energy models is presented. The importance of the association free energy, arising from one molecule's loss of translational and rotational freedom from the standard state concentration, is addressed. A novel method for calculating this quantity directly from a molecular dynamics simulation is described. The challenges of accounting for changes in the protein conformation and its fluctuations from separate simulations are discussed. A simple first-order approximation of the configuration integral is presented to lay the groundwork for future efforts. This model has been applied to FKBP12, a small immunophilin that has been widely studied in the drug industry for its potential immunosuppressive and neuroregenerative effects.
INTRODUCTION
The theoretical prediction of binding affinities is one of the most important problems in computational biochemistry. It complements experimental analysis and adds molecular insight to the macroscopic properties measured therein. It serves as a cornerstone in disease research and rational drug design where accurate scoring functions remain a challenge. It is no wonder, then, that computational models aimed at the prediction of binding affinities have been highly sought after for over half a century and are the subject of frequent reviews (Ajay and Murcko, 1995; Gilson et al., 1997; McCammon, 1998; Simonson et al., 2002).
The theory underlying binding affinities has been well described by many, yet the complexity and accuracy of its application has varied. The most rigorous methods involve alchemical or structural transformations such as free energy perturbation and thermodynamic integration (Beveridge and DiCapua, 1989; Straatsma and McCammon, 1992). The accuracy of these methods relies on equilibrium sampling of the entire transformation path, from an initial to a final state. The computational demand of adequate sampling makes relative binding affinities between similar ligands the most amenable targets of free energy perturbation and thermodynamic integration. Relative binding affinities between diverse ligands and absolute binding affinities pose more of a challenge.
End-point free energy models, wherein only the initial and final states of the system are evaluated, present a desirable alternative to perturbation simulations. They are less computationally expensive making them suitable for a greater variety of systems and problems. They are typically based on partitioning the free energy into a sum of enthalpic and entropic contributions (Aqvist et al., 2002; Srinivasan et al., 1998; Vorobjev and Hermans, 1999). Frameworks that use implicit solvent approximations reduce computational demands even further. Although all such models are founded in statistical mechanics, there is a need for strengthening the theoretical framework of many to account for standard state dependence and entropic considerations. Other implicit solvent, end-point models have thorough theoretical descriptions (Lazaridis et al., 2002; Luo and Sharp, 2002; Luo and Gilson, 2000), yet there remains a need for further analyses regarding which contributions to include, how to measure them, and which approximations are appropriate to make.
This work focuses on providing a clear theoretical foundation for end-point free energy models. Two issues that have been inconsistently applied in previous analyses are highlighted; the association free energy, which results from one molecule's loss of translational and rotational freedom from the standard state, and the conformational free energy due to changes in both molecules' intramolecular motions. An implicit solvent approximation is used to evaluate the initial and final equilibrium ensembles generated during explicit solvent MD simulations. The association free energy is thoroughly discussed and measured from the simulation. Determining the conformational free energy represents the most challenging aspect of this work and of all such methods as it is tied to the evaluation of the internal configuration integral of the bound and free systems. A first-order approximation assumes that the changes in conformational freedom are minimal and that the energy landscape can be characterized from a sufficiently long MD simulation. This simplification serves as a necessary stepping stone for more advanced evaluations of the configuration integral.
To illustrate our method, a small, fairly rigid protein-ligand system, FK506 binding protein (FKBP12) and the ligand 4-hydroxy-2-butanone (BUT), was chosen. FKBP12 is an immunophilin that, when bound by the immunosuppressant drug FK506, blocks early T-cell activation via calcineurin inhibition. Smaller ligands that mimic FK506 as potential immunosuppressive drugs have been highly sought after. In an attempt to characterize its binding properties, the crystal structure of FKBP12 bound by several small molecules including BUT was determined (Burkhard et al., 2000). With only six heavy atoms and four rotatable bonds, BUT was one of the smallest ligands to bind FKBP12 with a measured binding affinity, Ki, of 500 μM. Despite the current method's exclusion of the changes in conformational free energy, which is expected to be positive, the calculated change in free energy was only 10 kJ/mol lower than that measured in experiment. The small magnitude of this discrepancy is consistent with the low binding affinity of the ligand, which is unlikely to substantially perturb the protein's conformation or fluctuations.
First, the theoretical framework will be described. Some of the foundation from previous publications (Gilson et al., 1997) will be reviewed for a complete description. The simulation methods and numerical results will then be presented. Evaluation of the association free energy will be compared to previously published methods and deviations from experimental results will be discussed. Finally we will summarize the groundwork for future efforts.
THEORY
We are interested in calculating the standard change in free energy upon noncovalent molecular association. Consider the following reaction,
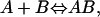 |
(1) |
where A represents the protein, B the ligand, and AB the protein-ligand complex. Each molecule can be described by a sum of translational, rotational, and internal modes of freedom. Upon binding, the ligand's external translational and rotational motions become internal motions of the complex. According to classical statistical mechanics, after the kinetic contributions of each species have cancelled (Gilson et al., 1997), the standard change in free energy can be expressed as a ratio of configuration integrals,
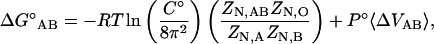 |
(2) |
where R is the gas constant, T is the absolute temperature, C° is the standard state concentration (typically 1 M or 1 molecule/1660 Å3), N is the number of solvent molecules, and P°Δ〈VAB〉 is the pressure-volume work associated with changing the system size from the replacement of two free molecules by one bound species. The last term is generally considered to be negligibly small in water at 1 atm. It is important to note that all mass dependent terms have cancelled in Eq. 2. This is a direct result of the equal kinetic contribution to the partition function of the bound and the free species. The configuration integral of the protein, A, in solution is
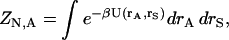 |
(3) |
where U(rA,rS) is the potential energy as a function of all solute coordinates, rA, and solvent coordinates, rS, and β is the reciprocal of the product of the Boltzmann constant and temperature. A similar equation gives ZN,B for the ligand. The configuration integral of the solvent alone is
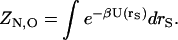 |
(4) |
The ratio of configuration integrals in Eq. 2 can be simplified with an implicit solvent approximation, as
 |
(5) |
where
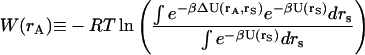 |
(6) |
represents the solvation free energy of species A, and the quantity ΔU(rA,rS) is U(rA, rS) − U(rA) − U(rS). Analogous equations hold for the complex and ligand. The complex, however, contains six degrees of freedom that represent the residual translational and rotational motions of the bound ligand. To account for these modes of motion, it is helpful to introduce a set of coordinates, δB ≡ (x1,x2,x3,ξ1,ξ2,ξ3), which define the bound ligand's position and orientation with respect to the protein. The complete complex configuration integral is
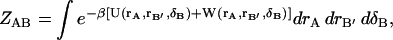 |
(7) |
where rB′ represents the bound ligand's remaining internal coordinates and δB spans conformations where A and B form a complex. As will be seen below, the displacements of δB in the dynamics of the complex are very small. It is therefore reasonable to assume that the higher order coupling terms in the potential energy function due to the effect of the ligand's translational/rotational motions on either species' internal vibrational motions are very small. Thus, the potential and solvation energies in Eq. 7 are separable:
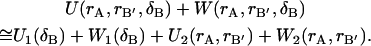 |
(8) |
One can define a potential of mean force (Go and Scheraga, 1969) for a particular ligand position and orientation, δB,
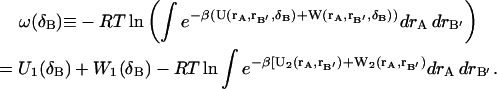 |
(9) |
Eq. 9 shows that the ligand's potential and solvation energies are equal to within a constant of the potential of mean force.
A similar assumption about the correlation between translational and rotational motions, permits further decomposition of 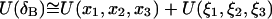 and
and 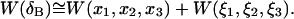 These separate contributions can be directly measured from a MD simulation as described in Methods. Substituting Eqs. 5 and 9 into Eq. 2 we have
These separate contributions can be directly measured from a MD simulation as described in Methods. Substituting Eqs. 5 and 9 into Eq. 2 we have
 |
(10) |
where  ,
,  and
and  Eq. 10 holds the most challenging aspect of this work, the evaluation of many-dimensional configuration integrals. As a first-order approximation, one can assume that the energetic landscape of each species has an energy and a volume that can be determined from a sufficiently long MD simulation,
Eq. 10 holds the most challenging aspect of this work, the evaluation of many-dimensional configuration integrals. As a first-order approximation, one can assume that the energetic landscape of each species has an energy and a volume that can be determined from a sufficiently long MD simulation,
 |
(11) |
〈EA〉 ≡ 〈U(rA) + W(rA)〉 represents the average molecular mechanics plus solvation energy over the simulation and  is the internal configuration integral. Equivalent equations hold for the ligand, ZB, and the complex ZAB′. If one assumes that the volumes of configuration space occupied by the ligand and protein change negligibly upon association, that is,
is the internal configuration integral. Equivalent equations hold for the ligand, ZB, and the complex ZAB′. If one assumes that the volumes of configuration space occupied by the ligand and protein change negligibly upon association, that is,  , then all internal configuration integrals cancel in the ratio, leaving
, then all internal configuration integrals cancel in the ratio, leaving
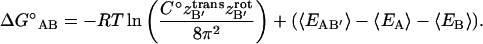 |
(12) |
Alternatively, the volume of configuration space occupied by each species can be approximated and the changes in conformational entropy can be included, as described in Discussion.
METHODS
Molecular dynamics protocol
The coordinates of the ligand, the protein, and the complex were taken from the 1.85 Å resolution complex crystal structure in the Brookhaven Protein Data Bank (PDB code 1D7J) (Burkhard et al., 2000). The free ligand was optimized with Gaussian 98 (Frisch et al., 1998) at the Hartree-Fock level with the 6–31G* basis set. It was assigned RESP charges as implemented in the ANTECHAMBER module from AMBER 7.0 (Wang et al., 2001). The complex was prepared in three steps. First, the program GRID (Goodford, 1985) was used to add 142 buried and first shell water molecules to the 126 crystal waters already present. WHAT IF (Vriend, 1990) was then used to place hydrogens and to assign favorable protonation states of histidine residues, as well as the favorable orientations of glutamine and asparagine side chains. Finally, the system was placed in a 80.2 Å × 78.9 Å × 78.9 Å TIP3 water box with the LEAP module from AMBER 7.0 (Case et al., 2002). One of the bulk water molecules was replaced with a chloride ion to neutralize the system.
Simulations of the complex, protein, and ligand were run under constant N,P,T conditions with the Sander module from AMBER 7.0. Periodic boundary conditions, particle-mesh Ewald treatment of the electrostatics, and SHAKE-enabled 2-fs time steps were employed. The protein and ligand heavy atoms were restrained during a 500-step minimization. Restraints were maintained through a 40-ps gradual warming from 0 to 300 K under constant volume and temperature conditions (N,V,T). Ten picoseconds of constant pressure and temperature (N,P,T) allowed the system to reach the proper density. A minor modification of the Sander module allowed a linear release of the heavy atom restraints over 30 ps. Unrestrained N,P,T completed the equilibration phase, and 3 ns of production phase was collected.
Energetic analysis
The binding affinity was approximated from both a single simulation, in which the protein and ligand structures were taken from the complex simulation, and from separate simulations. Snapshots taken every 2 ps from the 3 ns of production phase simulation were evaluated for a total of 1500 structures. The molecular mechanics energy, UMM, was evaluated in a single MD step in the Sander module using an infinite cutoff for nonbonded interactions. The solvation free energy can be decomposed into electrostatic and nonelectrostatic components, 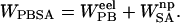 The electrostatic contribution to the solvation free energy,
The electrostatic contribution to the solvation free energy, 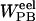 , was calculated with the Adaptive Poisson-Boltzmann Solver (Baker et al., 2001). The interior of the protein was given a dielectric constant of 1, in agreement with simulation conditions. The reference system had a solvent dielectric of 1 and 0 M salt concentration. The solvated system had a solvent dielectric of 78.4 and 100 mM salt concentration. The electrostatic energy of the reference system was subtracted from that of the solvated system to yield the solvation energy. Harmonic smoothing was used to define the protein boundary. Finally, the nonpolar contribution to the solvation free energy,
, was calculated with the Adaptive Poisson-Boltzmann Solver (Baker et al., 2001). The interior of the protein was given a dielectric constant of 1, in agreement with simulation conditions. The reference system had a solvent dielectric of 1 and 0 M salt concentration. The solvated system had a solvent dielectric of 78.4 and 100 mM salt concentration. The electrostatic energy of the reference system was subtracted from that of the solvated system to yield the solvation energy. Harmonic smoothing was used to define the protein boundary. Finally, the nonpolar contribution to the solvation free energy, 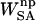 , was approximated with the commonly used solvent-accessible surface area (SASA) model,
, was approximated with the commonly used solvent-accessible surface area (SASA) model, 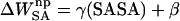 , where γ = 0.00542 kcal/mol Å2 and β = 0.92 kcal/mol (Sanner et al., 1996). The SASA was estimated with a 1.4 Å solvent-probe radius as implemented in Sander.
, where γ = 0.00542 kcal/mol Å2 and β = 0.92 kcal/mol (Sanner et al., 1996). The SASA was estimated with a 1.4 Å solvent-probe radius as implemented in Sander.
Ligand translational freedom
The bound ligand's translational configuration integral, 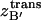 , can be conceptually linked to the volume of space that its center of mass occupies through the simulation. As previously mentioned, δB′ in Eq. 7 spans conformations where A and B form a complex. Thus, this analysis is only valid for simulations where the ligand remains bound to the protein. The effective volume was measured with the quasiharmonic model, which relies on the assumption that the translational motion can be described by a multivariate Gaussian probability distribution. Superimposition of every snapshot according to protein C-α atoms defined a static protein reference system and an average ligand structure. Centered at the origin, the ligand's center of mass covariance matrix was then evaluated, accounting for the possible coupling of motions along different axes. The resulting eigenvalues, λi, describe the variance
, can be conceptually linked to the volume of space that its center of mass occupies through the simulation. As previously mentioned, δB′ in Eq. 7 spans conformations where A and B form a complex. Thus, this analysis is only valid for simulations where the ligand remains bound to the protein. The effective volume was measured with the quasiharmonic model, which relies on the assumption that the translational motion can be described by a multivariate Gaussian probability distribution. Superimposition of every snapshot according to protein C-α atoms defined a static protein reference system and an average ligand structure. Centered at the origin, the ligand's center of mass covariance matrix was then evaluated, accounting for the possible coupling of motions along different axes. The resulting eigenvalues, λi, describe the variance  along each principal axis by λi =
along each principal axis by λi =  The equipartition theorem allows one to relate the variance to the force constant of the classical harmonic oscillator as the average potential energy for one dimension is 〈U(x) + W(x)〉 = (1/2) κ 〈Δx2〉 ≅ (1/2)kBT, such that κ ≅ kBT/〈Δx2〉. Thus,
The equipartition theorem allows one to relate the variance to the force constant of the classical harmonic oscillator as the average potential energy for one dimension is 〈U(x) + W(x)〉 = (1/2) κ 〈Δx2〉 ≅ (1/2)kBT, such that κ ≅ kBT/〈Δx2〉. Thus, 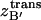 can be calculated as
can be calculated as
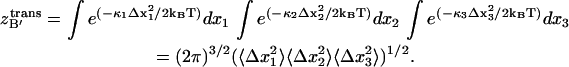 |
(13) |
Ligand rotational freedom
The ligand's rotational freedom,  , was accounted for in a similar manner. Quaternions, an elegant alternative to Euler angles, were used to represent the ligand's rotational motion. The transformation of each ligand snapshot, within the protein reference binding pocket, was described by the product of three quaternions, each defining the rotation about one axis. A small angle approximation (see Appendix A for details) reduces this product to a single quaternion which is sinusoidally related to three angles of rotation. The covariance matrix was evaluated to account for coupling between axes. The resulting eigenvalues were related to a spring force constant assuming a Gaussian distribution, and
, was accounted for in a similar manner. Quaternions, an elegant alternative to Euler angles, were used to represent the ligand's rotational motion. The transformation of each ligand snapshot, within the protein reference binding pocket, was described by the product of three quaternions, each defining the rotation about one axis. A small angle approximation (see Appendix A for details) reduces this product to a single quaternion which is sinusoidally related to three angles of rotation. The covariance matrix was evaluated to account for coupling between axes. The resulting eigenvalues were related to a spring force constant assuming a Gaussian distribution, and 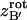 was evaluated according to Eq. 13, replacing (Δx1, Δx2, Δx3) with (Δξ1, Δξ2, Δξ3). Although the present analysis assumes that the bound ligand's translational and rotational motions are dominated by a single minimum energy well, it is easily extendible to multiple minima.
was evaluated according to Eq. 13, replacing (Δx1, Δx2, Δx3) with (Δξ1, Δξ2, Δξ3). Although the present analysis assumes that the bound ligand's translational and rotational motions are dominated by a single minimum energy well, it is easily extendible to multiple minima.
RESULTS AND DISCUSSION
Energetic convergence
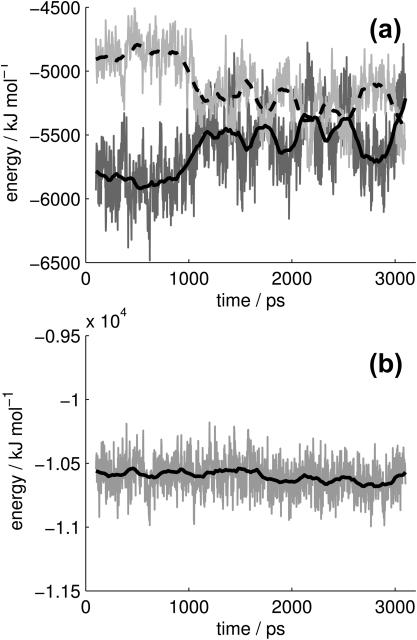
Each simulation reached a satisfactory equilibrium after 100 ps as indicated by the total system energy. The protein's energetic contributions as a function of time in the simulation of the complex are shown in Fig. 1. Similar plots were obtained for the complex and ligand from the complex simulation as well as the protein and ligand from the separate simulations. The variation in the solvation energy and the molecular mechanics energy (Fig. 1 a) are anticorrelated, yielding a fairly stable total energy (Fig. 1 b). This is further supported by the average energetic contributions and standard deviations of the complex simulation evaluations, shown in Table 1. The standard deviations of the molecular mechanics and solvation energies are consistently 4–5% whereas that of the total energy is <1%.
FIGURE 1.
(a) The protein's solvation energy (light gray) and molecular mechanics energy (dark gray) across 3 ns of simulation. The darker solid and dashed lines represent a 100 ps running average. (b) The protein's total energy, ETOT = UMM + WPBSA, and running average.
TABLE 1.
Energetic averages (kJ/mol)
| Simulation | 〈UMM〉* | 〈WPB〉† | 〈WSA〉‡ | 〈GMM/PBSA〉§ |
|---|---|---|---|---|
| Complex | −5759 (281) | −5123 (247) | 134.0 (2.9) | −10,748 (130) |
| Protein | −5605 (273) | −5134 (241) | 135.1 (2.8) | −10,604 (130) |
| Ligand | −50 (11) | −46 (3) | 8.5 (0.1) | −88 (10) |
| Com-Pro-Lig | −103 (26) | 57 (15) | −9.6 (0.5) | −56 (15) |
Energetic averages (kJ/mol) is the average of 1500 snapshots from 100 to 3100 ps with standard deviations in parentheses.
Molecular mechanical energy.
Electrostatic solvation energy.
Nonpolar solvation energy.
Molecular mechanics Poisson-Boltzmann surface area energy: 〈GMM/PBSA〉 = 〈UMM〉 + 〈WPB〉 + 〈WSA〉.
Relaxation energies and protein flexibility
The ideal mimicry of an in vitro binding event would be to run three separate simulations and calculate the energetic components of each. This would include the effects of the conformational changes upon binding, e.g., protein flexibility. The relaxation energy would be captured in the molecular mechanics and solvation energy, and the conformational free energy would be captured by a complete evaluation of the configuration integral. This evaluation relies on sufficient sampling of configuration space, which remains a major challenge on the timescale of MD simulations.
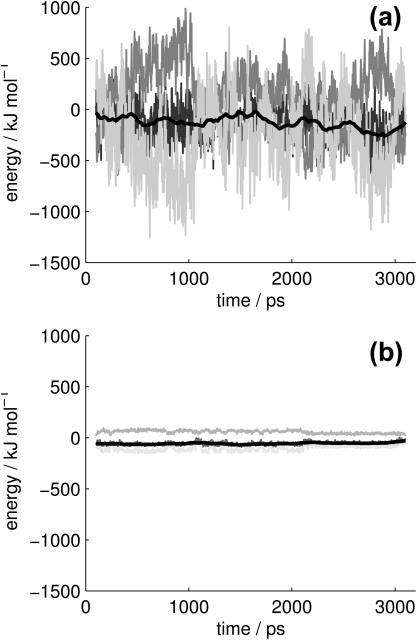
In an approximate single simulation evaluation, the protein and ligand structures are taken from the complex simulation. This, in theory, assumes that the structures and conformational freedom of the protein and ligand change negligibly upon binding. In practice, taking all structures from a single simulation cancels the noise that would result from sampling inconsistencies and the error inherent in force-field and implicit solvation energies. Although the analysis based on simulations of separate species (results not shown) generated similar trends to the single simulation analysis, it was clearly dependent on simulation length and dominated by noise. A striking representation of this phenomenon is shown in Fig. 2, where the differences in energetic contributions are given as a function of time for both the single and the separate simulations. It should be noted that the corresponding structures from the free and bound simulations cannot be equated for any given timeframe. Thus plot A is a nonphysical measurement. Given the commutative nature of averages, however, the total energies, shown as the smoothed dark line, are the quantitative results of the molecular mechanic and solvation free energies. The same axis scales are used to emphasize the noise of the separate simulations compared to the single simulation.
FIGURE 2.
The change in free energy (EAB − EA − EB) of each snapshot for (a) the separate and (b) the single simulation evaluations. The lightest shade is the molecular mechanics energy, the middle is the solvation energy, the darkest is the total, and the smooth black line is a 100-frame running average of the total energy.
While it was clear that the protein sampling was insufficient, the small ligand sampling was extensive. It was possible, therefore, to capture the ligand's relaxation energy, ΔELR, which is the difference between the total energy of the ligand from the complex simulation and that from the free simulation. The final calculated binding free energy and its components, including the ligand relaxation energy of 1.7 kJ/mol, are shown in Table 2.
TABLE 2.
Contributions to the free energy (kJ/mol)
Molecular mechanics Poisson-Boltzmann surface area energy.
Association free energy.
Ligand relaxation energy.
Total calculated free energy.
Experimental free energy.
Association free energy: the change in the ligand's translational and rotational free energy
At 1-M standard concentration, a free molecule has 1660 Å3 (C° = 1/1660 Å3 in Eq. 12) of translational freedom and 8π2 of rotational freedom. Upon association, one solute molecule loses translational and rotational freedom whereas released solvent molecules gain translational and rotational freedom. As previously described, the solvent's enthalpic and entropic contributions are accounted for in the implicit approximation of the solvation free energy. The solute's contribution, which we describe as the association free energy, was directly measured from the simulation (see Methods). To provide some context for this evaluation, a brief, and therefore incomplete, historical account of comparable theoretical studies on the association free energy is helpful.
The free energy change, and particularly the entropic cost, due to one molecule's loss of translational and rotational freedom has been well recognized for over 40 years (Steinberg and Scheraga, 1963). These degrees of freedom do not disappear but are transformed into internal motions within the complex. The range of these motions determines the magnitude of the entropic cost. More tightly bound ligands will have a higher entropic cost than loosely bound ligands. Quantifying the ligand's residual translational and rotational motions, however, is not an easy task. Many authors have estimated them with cubic box translational and isotropic rotational approximations, such that TΔStrans = RT ln(Δx3/1660 Å3) and TΔSrot = RT ln(Δθ3/8π2).
Finkelstein and Janin (1989) assumed that the atomic motions in crystals were representative of any bound ligand's motion. Using Debye-Waller temperature factors, they estimated a standard deviation of 0.25 Å along three principal axes, resulting in a translational entropic cost of −15 kcal/mol. Since the magnitudes of rotational oscillations in crystals were unknown at the time, they assumed a similar angular displacement from δθ = 2δx/d, where d is the distance to the ligand interface. This resulted in a rotational entropic cost of −7.2 kcal/mol and a total association entropy of −22.2 kcal/mol.
Tidor and Karplus (1994) took a different approach. Using normal mode analysis to study insulin dimerization, they found the internal vibrational modes of the complex increased, contributing −7.2 kcal/mol to the binding free energy. Although the six introduced modes of motion are included in this estimate, it is impossible to separate them to account for the range of the bound ligand's motion or the exact association entropy. Assuming no change in internal vibrational modes and estimating the free energy change due to complete loss of rotational and translational motion from gas phase (TΔS = −27.3 kcal/mol), they reported an association entropy ∼−20 kcal/mol.
Hermans and Wang (1997) presented the first complete evaluation of an absolute binding free energy with free energy pertubation. In this study they evaluated the effective volume of the bound ligand in two independent ways. First, they applied translational restraints to the ligand in the standard state gas phase. Releasing the restraints in the protein environment and taking the difference in free energies for the two processes, they measured the association entropy (−7 kcal/mol). Second, they estimated the ligand's positional and orientational root mean-square displacement (RMSD) directly from the simulation. It should be emphasized that these two methods of obtaining the effective volume, using RMSD values versus the energetically measured volume, are very different. The point, in this case, is a methodological one as the two are similarly small. The calculated RMSD volume, 0.184 Å3, and the energetically measured volume, 0.4 Å3, result in −5.0 kcal/mol and −5.4 kcal/mol entropic contributions, respectively.
Lazaridis et al. (2002) evaluated the ranges of deviation in the ligand's center of mass and orientation, described with Euler angles, from a dynamics simulation. They weighted these ranges according to their probability distributions. It is not clear whether they evaluated these deviations along the principal axes or along an arbitrary reference frame. Our results indicated that similar range assumptions resulted in significantly larger translational and rotational motions that were sensitive to simulation length. This could explain the smaller translational and rotational entropic contributions measured in this study.
Luo and Sharp (2002) used quasiharmonic analysis of short simulations to account for the ligand's translational, rotational, as well as internal vibrational motions. They assumed that the rotational motion was isotropic and divided by a factor of 33/2 to yield TΔSrot = RT ln(σ3/(6π)1/2). They measured association entropies between −1.5 kcal/mol and −7.5 kcal/mol for four different ligands.
As described in Methods, we have proposed a similar evaluation of the association free energy using the quasiharmonic model. The covariance matrix accounts for coupled motions in different dimensions and defines the principal components, capturing a more accurate variation than an arbitrary reference frame. Quaternions were found to be a desirable alternative description of angular motions, eliminating the cumbersome conversion to Euler angles. They smoothly converted into a covariance matrix and produced three different eigenvalues. This finding discourages the assumption that rotational motion is isotropic. As summarized in Table 3, the ligand experienced 1.72 Å3 of translational motion and 6.57 radians of rotational motion. This correlates to a free energy change of 17.1 kJ/mol and 6.2 kJ/mol, respectively. Thus, the total association free energy was 23.3 kJ/mol. If we assume that the translational and orientational motions of the ligand within the complex can in fact be described as classical harmonic oscillator displacements, we can separate this total free energy of association into enthalpic and entropic components. The six configurational degrees of freedom would contribute an equipartition enthalpy of 3RT ≈ 7.5 kJ/mol. The remainder, ∼15.8 kJ/mol, then represents the entropic cost of limiting the ranges of translational and rotational motion.
TABLE 3.
Contributions to the association free energy
Translational configuration integral (Å3).
All energies reported in kJ/mol.
Rotational configuration integral.
Association free energy.
Conformational free energy
Detailed evaluations of the configuration integrals in Eq. 10 would inherently capture the exact changes in conformational free energy upon binding. This remains, to date, computationally infeasible. Changes in intramolecular conformational free energy have traditionally been approximated with quasiharmonic analysis, normal mode analysis, or side-chain rotational analysis. Yet the validity and accuracy of these methods remain questionable. In the current study, quasiharmonic analysis was extensively explored (data not shown). Although the results followed the expected trends, making the calculated free energy of binding less favorable, they were clearly sensitive to simulation length. Similar to the separate simulation analysis, this lack of convergence indicates inadequate sampling. This is likely compounded by a large noise/signal ratio due to the weak binding nature of this ligand. A system with stronger interactions may prove more amenable to analysis. Given the challenges of a weak binding system and the excluded protein relaxation energy and configurational free energy, both of which are expected to be slightly positive, it is encouraging to find the calculated binding free energy (Table 2) only 10 kJ/mol lower than that measured in experiment.
CONCLUSIONS
Although the theory of binding affinity calculations has been discussed by many previous authors, it remains an ongoing topic of research. The implementation of end-point free energy models has improved with increasing computational resources and thoughtful design. A connection between theory and implementation was the focus of this article. We have discussed the statistical mechanical basis for the change in free energy upon binding and its link to obtaining this quantity from a molecular dynamics trajectory. We have emphasized the importance of the standard state dependence. We have presented a novel method for evaluating a bound ligand's residual translational and rotational motion from an MD simulation and used these quantities to calculate the association free energy. Finally, we hope to have established the proper groundwork for end-point free energy calculations such that future efforts can focus on the inclusion of protein relaxation energies and changes in conformational free energy.
Acknowledgments
We thank Dr. Gennady Verkhivker for helpful insights on the FKBP12 system, Dr. Jung-Hsing Lin for help with the molecular dynamics simulations, and Dr. Steve Bond for mathematical accumen.
This work was supported by grants from National Science Foundation, National Institutes of Health, National Biomedical Computation Resource at the University of California at San Diego, the W.M. Keck Foundation, and Accelrys, Inc. J.M.J.S. has been supported by the University of California at San Diego Molecular Biophysics Training Grant and by a predoctoral fellowship from the Center for Theoretical Biological Physics.
Appendix A
Quaternions are hypercomplex numbers that can be represented as a linear combination of a scalar (a1) and a vector ( ):
):
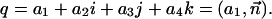 |
The rotation of point p through angle φ about a normalized axis 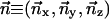 can be computed with the quaternion q and its complex conjugate q*:
can be computed with the quaternion q and its complex conjugate q*:
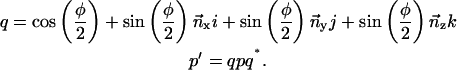 |
The rotational transformation of any point about three axes is the product of three quaternions. When the angles of rotation are small, the cross-terms of this product will be negligibly small:
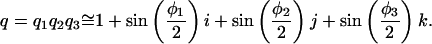 |
We evaluated the quaternion of each snapshot, i, yielding the rotation about each of the axes, x,y,z. The variance was then measured:
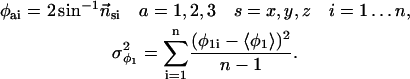 |
References
- Ajay, A., and M. A. Murcko. 1995. Computational methods to predict binding free energy in ligand-receptor complexes. J. Med. Chem. 38:4953–4967. [DOI] [PubMed] [Google Scholar]
- Aqvist, J., V. B. Luzhkov, and B. O. Brandsdal. 2002. Ligand binding affinities from MD simulations. Acct. Chem. Res. 35:358–365. [DOI] [PubMed] [Google Scholar]
- Baker, N. A., D. Sept, S. Joseph, M. J. Holst, and J. A. McCammon. 2001. Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. USA. 98:10037–10041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beveridge, D. L., and F. M. DiCapua. 1989. Free-energy via molecular simulation—applications to chemical and biomolecular systems. Annu. Rev. Biophys. Bio. 18:431–492. [DOI] [PubMed] [Google Scholar]
- Burkhard, P., P. Taylor, and M. D. Walkinshaw. 2000. X-ray structures of small ligand-FKBP complexes provide an estimate for hydrophobic interaction energies. J. Mol. Biol. 295:953–962. [DOI] [PubMed] [Google Scholar]
- Case, D. A., D. Pearlman, J. Caldwell, T. Cheatham III, J. Wang, W. Ross, C. Simmerling, T. Darden, T. Merz, R. Stanton, A. Cheng, J. Vincent, M. Crowley, V. Tsui, H. Gohlke, R. Radmer, Y. Duan, J. Pitera, I. Massova, G. Seibel, U. C. Singh, P. Weiner, and P. A. Kollman. 2002. AMBER 7. University of California, San Francisco, CA.
- Finkelstein, A. V., and J. Janin. 1989. The price of lost freedom—entropy of biomolecular complex-formation. Prot. Eng. 3:1–3. [DOI] [PubMed] [Google Scholar]
- Frisch, M. J., G. Trucks, H. Schlegel, G. Scuseria, J. R. C. M. A. Robb, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle, and J. A. Pople. 1998. Gaussian 98. Gaussian, Inc., Pittsburgh, PA.
- Gilson, M. K., J. A. Given, B. L. Bush, and J. A. McCammon. 1997. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 72:1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Go, N., and H. Scheraga. 1969. Analysis of the contribution of internal vibrations to the statistical weights of equilibrium conformations of macromolecules. J. Chem. Phys. 51:4751–4767. [Google Scholar]
- Goodford, P. J. 1985. A computational procedure for determining energetically favorable binding sites on biologically important macromolecules. J. Med. Chem. 28:849–857. [DOI] [PubMed] [Google Scholar]
- Hermans, J., and L. Wang. 1997. Inclusion of loss of translational and rotational freedom in theoretical estimates of free energies of binding. Application to a complex of benzene and mutant T4 lysozyme. J. Am. Chem. Soc. 119:2707–2714. [Google Scholar]
- Lazaridis, T., A. Masunov, and F. Gandolfo. 2002. Contributions to the binding free energy of ligands to avidin and streptavidin. Proteins. 47:194–208. [DOI] [PubMed] [Google Scholar]
- Luo, H. B., and K. Sharp. 2002. On the calculation of absolute macromolecular binding free energies. Proc. Natl. Acad. Sci. USA. 99:10399–10404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo, R., and M. K. Gilson. 2000. Synthetic adenine receptors: direct calculation of binding affinity and entropy. J. Am. Chem. Soc. 122:2934–2937. [Google Scholar]
- McCammon, J. A. 1998. Theory of biomolecular recognition. Curr. Opin. Struct. Biol. 8:245–249. [DOI] [PubMed] [Google Scholar]
- Sanner, M. F., A. J. Olson, and J. C. Spehner. 1996. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 38:305–320. [DOI] [PubMed] [Google Scholar]
- Simonson, T., G. Archontis, and M. Karplus. 2002. Free energy simulations come of age: protein-ligand recognition. Acct. Chem. Res. 35:430–437. [DOI] [PubMed] [Google Scholar]
- Srinivasan, J., T. E. Cheatham, P. Cieplak, P. A. Kollman, and D. A. Case. 1998. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 120:9401–9409. [Google Scholar]
- Steinberg, I., and H. Scheraga. 1963. Entropy changes accompanying association reactions of proteins. J. Biol. Chem. 238:172–181. [PubMed] [Google Scholar]
- Straatsma, T. P., and J. A. McCammon. 1992. Computational alchemy. Annu. Rev. Phys. Chem. 43:407–435. [Google Scholar]
- Tidor, B., and M. Karplus. 1994. The contribution of vibrational entropy to molecular association—the dimerization of insulin. J. Mol. Biol. 238:405–414. [DOI] [PubMed] [Google Scholar]
- Vorobjev, Y. N., and J. Hermans. 1999. ES/IS: estimation of conformational free energy by combining dynamics simulations with explicit solvent with an implicit solvent continuum model. Biophys. Chem. 78:195–205. [DOI] [PubMed] [Google Scholar]
- Vriend, G. 1990. WHAT IF: a molecular modeling and drug design program. J. Mol. Graph. 8:29,52–56. [DOI] [PubMed] [Google Scholar]
- Wang, J. M., W. Wang, and P. A. Kollman. 2001. ANTECHAMBER: an accessory software package for molecular mechanical calculations. Abstr. Pap. Am. Chem. S. 222:U403. [Google Scholar]