Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Feb;86(2):1082–1088. doi: 10.1016/S0006-3495(04)74183-1

Determination of the Topological Shape of Integral Membrane Protein Light-Harvesting Complex LH2 from Photosynthetic Bacteria in the Detergent Solution by Small-Angle X-Ray Scattering

Xinguo Hong *,†, Yu-Xiang Weng *, Ming Li *
PMCID: PMC1303901  PMID: 14747343

Abstract

The topological shape of the integral membrane protein light-harvesting complex LH2 from photosynthetic bacteria Rhodobacter spheroides 2.4.1 in detergent solution has been determined from synchrotron small-angle X-ray scattering data using direct curve-fitting by the ellipsoid, ab initio shape determination methods of simulated annealing algorithm and multipole expansion, respectively. The results indicate that the LH2 protein in aqueous solution is encapsulated by a monolayered detergent shell. The detergent-stabilized structure has the shape of an oblate plate, with a thickness of 40 Å, a long axis of 110 Å, and a short axis of 85 Å . After correction for the detergent shell, the shape of the LH2 core is also an oblate plate with a height of 40 Å, a long axis of 80 Å, and a short axis of 55 Å. In contrast to the cylindrical crystal structure with a height of 40 Å and a diameter of 68 Å, the molecular shape of the LH2 complex in detergent solution clearly deviates from the ringlike crystal structure, with an eccentricity found to be 0.59—consistent with the result of single molecular spectroscopy study of the isolated single LH2 molecules.

INTRODUCTION

The primary process in photosynthesis is the absorption of a photon by the light-harvesting antenna system, followed by the rapid and efficient energy transfer to the reaction center where the charge separation takes place and the energy becomes available as chemical energy. Compared to the other photosynthetic organisms, purple bacteria are relatively simple. In most purple bacteria species such as Rhodobacter spheroides, Rhodopseudomonas acidophila, and Rhodospirillum molischianum, the photosynthetic membrane contains two types of antenna complexes, light-harvesting complexes 1 and 2 (LH1 and LH2, respectively). LH1 is known as the core complex surrounding the reaction center (RC), whereas LH2 is the peripheral complex which transfers energy to LH1 and finally to RC for charge separation (van Grondelle et al., 1994; Pullerits and Sundström, 1996; Fleming and van Grondelle, 1997). The crystal structure of LH2 from the purple bacteria Rps. acidophila strain 10050 has been solved by Richard Cogdell and co-workers (McDermott et al., 1995; Freer et al., 1996). The structure of the LH2 complex of the purple bacterium Rps. acidophila demonstrates a high symmetry with a ninefold rotational axis defined by nine αβ-dipeptides. The basic building block is the protein αβ heteromer which binds three BChl a molecules and one carotenoid molecule. The total 27 BChl a form two concentric rings supported by the αβ-dipeptides. One ring with nine BChl a of a larger interpigment separation is known as B800, and another with 18 BChl a with a shorter interpigment separation is known as B850. A similar crystal structure of LH2, but with eightfold symmetry containing 16 B850 molecules and eight B800 molecules, was found in Rs. molischianum (Koepke et al., 1996). Although a high diversity is found among the photosynthetic bacteria with respect to the growth conditions, habitats, and cellular shape, the photosynthetic apparatus of all species is quite similar. There are indications that only the LH2 complex of Rs. molischianum has an octamer of αβ-dimers, whereas many other species including Rb. spheroides consist of nine dimers (Georgakopoulou et al., 2002). With the knowledge of the high-resolution structure and the advent of ultrafast laser spectroscopy, primary photosynthetic process in the light-harvesting systems becomes one of the most studied subjects in current photosynthetic research, as has been reviewed recently (Sundström et al., 1999).

In recent years, various spectroscopic means including ultrafast laser spectroscopy, and single molecular spectroscopy, have been employed to elucidate the function of efficient energy transfer in view of its unique molecular geometry for the LH2 complex. Ultrafast laser spectroscopy reveals a distinct feature for the excited state of BChl a in the B850 ring, which shows that the excitation can be delocalized on the whole ring known as the exciton state, although the lowest excited state is optically forbidden and does not fluoresce. The B850 ring acts as an energy storage, preserving excitation energy until it is forwarded to other rings and ultimately to the RCs, with an overall quantum efficiency as high as ∼95% (Hu and Schulten, 1997). Although single molecular spectroscopy is noteworthy for its unique property of elimination of the average effect of an ensemble, it can also explore some important photoproperties of a single molecule which otherwise cannot be observed in the bulk (Xie and Trautman, 1998). Single molecular polarization-dependent fluorescence study has been performed on LH2 (Rps. acidophila) immobilized on a mica surface at 300 K, which reveals that the LH2 is an elliptic absorber and emitter, indicating that the high symmetry found in LH2 crystal is not present in the isolated molecules (Bopp et al., 1999). Polarization-dependent fluorescence-excitation spectra have been performed on the single LH2 molecules (Rps. acidophila) immobilized in polyvinyl alcohol matrix at cryogenic temperature (1.2 K), the results of which unambiguously show that the B850 ring structurally deforms in their isolated form. Further simulation reveals that the isolated LH2 molecule deforms from a ring of C9 symmetry to an elliptical shape of C2 symmetry with an eccentricity of 0.52 (van Oijen et al., 1999; Ketelaars et al., 2001; Matsushita et al., 2001). Thus, the question of whether the elliptical shape is representative of the structure for LH2 in the detergent solution or in the membranes remains a question deserving further study (Ketelaars et al., 2001). Up until now all the evidence for the deformed ringlike shape of LH2 complex in the isolated form comes from the single molecular spectroscopic study, so further direct structural evidence is obviously necessary.

Solution X-ray and neutron scattering has proven to be a very useful technique for obtaining low-resolution molecular shape of proteins and their complexes in solution (Mayor et al., 2003; Wall et al., 2000; Sardet et al., 1976; Osborne et al., 1978). Recently, there has been significant progress in the development of ab initio methods for low-resolution shape restoration by using dummy atom models (Svergun et al., 1987; Svergun, 1999) and in terms of spherical harmonics (Svergun, 2000; Svergun and Stuhrmann, 1991; Svergun et al., 1996) and simulation. The spatial parameters of a molecular envelope or configuration models can be determined in a model-independent manner which does not, for example, require the use of crystal structure coordinates for interpretation. This method has been successfully used to provide a stable and unique shape restoration for several proteins (Grossmann and Hasnain, 1997; Ockwell et al., 2000; Hao, 2001). In this work we report, for the first time, the results of a small-angle X-ray scattering (SAXS) study of LH2 molecules of Rb. spheroides 2.4.1 in the detergent solutions, wherein the low-resolution topological shape of LH2 protein in aqueous solution is determined and the topological structure compared with the LH2 crystal structure from Rps. acidophila of ninefold symmetry, which provides direct evidence for the elliptical structure of LH2 complex in the detergent solution.

MATERIALS AND METHODS

The LH2 complex was obtained by solubilization of the chromatophores of Rb. spheroides 2.4.1 with 1% LDAO (n,n dimethyldodecylamine n-oxide) and by subsequent purification using DE52 ion-exchange column chromatography using stepwise elution with sodium chloride (Ohashi et al., 1996). The SAXS experiments were carried out at Beamline 4B9A at the Beijing Synchrotron Radiation Facility, using a SAXS apparatus constructed at the station. A detailed description of the spectrometer has been given elsewhere (Dong et al., 1997). Briefly, the wavelength of the incident monochromatic X-ray beam in the present experiment is λ = 1.54 Å. The scattered X-ray intensities were recorded using image plate technology, as a function of the modulus of the scattering vector h = 4 πsinθ/λ, where 2θ is the scattering angle. The detector for SAXS data collection is an image plate system, BAS-2500 of FUJIFILM, Japan, with an active area of 400 mm × 200 mm and a minimum pixel size of 50 μm. The sample-to-detector distance of 1550.0 mm and the X-ray wavelength of λ = 1.54 Å allows the coverage of scattering vector interval of 0.01 < h < 0.25 Å−1. The background scattering was subtracted from the total measured SAXS intensity, and the absorption of the samples was corrected. The samples were encapsulated inside a cell between two thin parallel windows. The data accumulation time was typically 5–10 min, depending on the scattering intensity. The concentration of LH2 was adjusted by making the optical density of LH2 at 850 nm equal to 3.0 at 1.0-cm optical pathlength by diluting with distilled water, and the concentration of LH2 samples for the SAXS experiment were further diluted in twice-distilled water at ratios of 1:1, 1:5, 1:10, and 1:50. All the samples of different concentrations produced almost the same scattering profiles, except that the lower concentration samples had a larger noise. Therefore at the selected concentration range, the contribution from the interparticle scattering can be safely excluded.

RESULTS AND DISCUSSION

Molecular-shape determination

The average radius of gyration of LH2 molecule in water can be calculated by Guinier and Fournet (1955) as

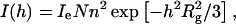graphic file with name M1.gif (1)

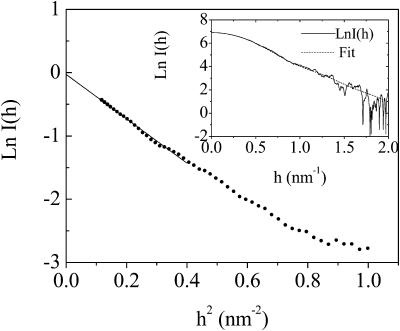
where Ie is the scattering intensity per electron, N is the number of the scatterers, and n is the number of electrons. In practice, a linearized representation will be used, by plotting ln[I(h)] vs. h2 (Guinier plot). Simple linear regression yields the radius of gyration from the slope, as shown in Fig. 1, which leads to Rg of LH2 protein in detergent solution being 33 Å. The radius of gyration Rg is related to the size of a particle in the solution (Glatter and Kratky, 1982).

FIGURE 1.

FIGURE 1

Open in a new tab

Guinier plot of ln[I(h)] vs. h2 of the scattering intensity curve for LH2 complex in water. The inset shows the experimental data (solid line) and the theoretical fitting (dashed line) using an ellipsoid of rotation axes 33.2 Å and ω = 0.31.

To obtain some a priori structural knowledge for the shape restoration, we fit the scattering curves at first by directly using an ellipsoid to find out if the overall shape is similar to a prolate rod or an oblate plate. In the case of a monodisperse system, the scattered intensity I(h) for the ellipsoidal molecules defined by the semiaxes a, a, and ωa is given by Guinier and Fournet (1955) as

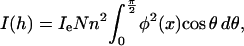graphic file with name M2.gif (2)

where ω is the ratio of major to minor semiaxes, φ(x) = 3(sin(x) − x cos(x))/x3, and 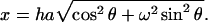Inline graphic The prolate or rodlike scatterer can be viewed as a prolate ellipsoid with ω > 1, for a spherical scatterer with ω = 1, and for the oblate plate (oblate ellipsoid) with ω < 1. The shape of the scatterers can be determined by directly fitting to the experimental data using Eq. 2. The experimental curve was fitted up to 0.17 Å−1 to avoid the obvious noise at higher angle. We got the semiaxes of ellipsoid a = 51.3 Å and ω = 0.31, indicating the scatterer has a shape of the oblate ellipsoid. These parameters can be taken as a priori information for further shape restoration.

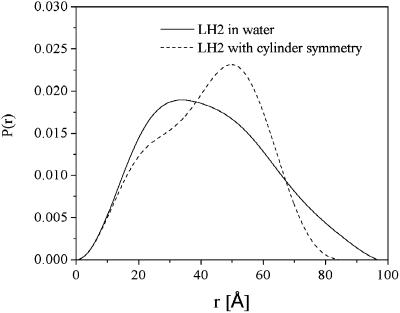
The intraparticle distance distribution function, P(r), is a measure of the frequency of interatomic vector lengths within the protein. This function is very sensitive to the overall asymmetry and domain structure within the protein. P(r) can be calculated using a direct Fourier transform method,

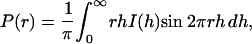graphic file with name M4.gif (3)

where I(h) is the experimental scattering data. Fig. 2 shows the calculated P(r) of LH2 complex in detergent solution (solid line) based on the experimental data and that of the presumed LH2 complex with a cylindrical symmetry (dashed line) in water for the purpose of comparison. The presumed scattering intensity is modeled by a cylindrically symmetrical LH2 protein using the program CRYSOL by taking the influence of the hydration shell into account (Svergun et al., 1995). The coordinates of the model structure (Rps. acidophila) is obtained from the Protein Data Bank (PDB 1KZU). It can be seen that the P(r) of LH2 complex in detergent solution is considerably different from that of the presumed cylindrical one. In solution, the main peak of P(r) becomes broad, with an asymmetric shape toward a larger r until 95 Å. This value can be employed as an input parameter of the maximum dimension, which is needed in an indirect Fourier transform method as implemented in the program GNOM (Semenyuk and Svergun, 1991; Svergun, 1992). An inappropriate value of maximum dimension could produce rather strange P(r). By using GNOM, we obtained the structural parameters: Rg = 32.2 Å ± 1%, Dmax (maximum particle dimension) = 95 Å ± 4%, and V (particle volume) = 37,000 Å3 ± 5%.

FIGURE 2.

FIGURE 2

Open in a new tab

Distance distribution function P(r) of LH2 complex in water (solid line), and the calculated P(r) with a cylindrical model of ninefold symmetry (dashed line), revealing that the ring-shaped model does not fit the experimental data properly.

The topological shape of LH2 complex is restored from the experimental data using an ab initio method of simulated annealing algorithm as implemented in DAMMIN (Grossmann and Hasnain, 1997; Ockwell et al., 2000). In this method, a dummy atom model (DAM) is generated by filling a sphere of diameter equal to the maximum particle size by a number of M densely packed small spheres (dummy atoms) M ≈ (Dmax/r0)3 ≈ 103. Each dummy atom should be ascribed either to particle or to solvent (Positionj = 1 or 0). DAMMIN searches for a compact dummy atom configuration in such a way as to minimize the discrepancy between the calculated scattering curve from the model and the experimental data. The minimization is performed using a simulated annealing process (Press et al., 1992; Ingber, 1993), i.e.: first, start from a random configuration at a high temperature, T0, for example, T0 = f (X0); second, select an atom at random and calculate Δ = f (X′) − f (X); third, if Δ < 0, move to X′, if Δ > 0, do this with a probability exp(−Δ/T); and finally, hold T constant for 100 N reconfigurations or 10 N successful reconfigurations, whichever comes first, then cool the system (T′ = 0.9 T). Continue cooling until no improvement in f (X) is observed.

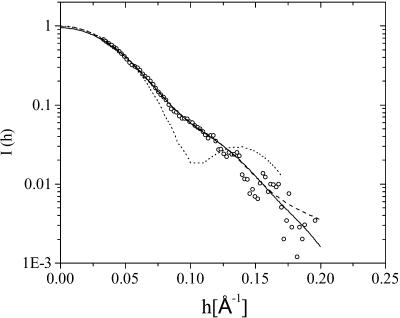
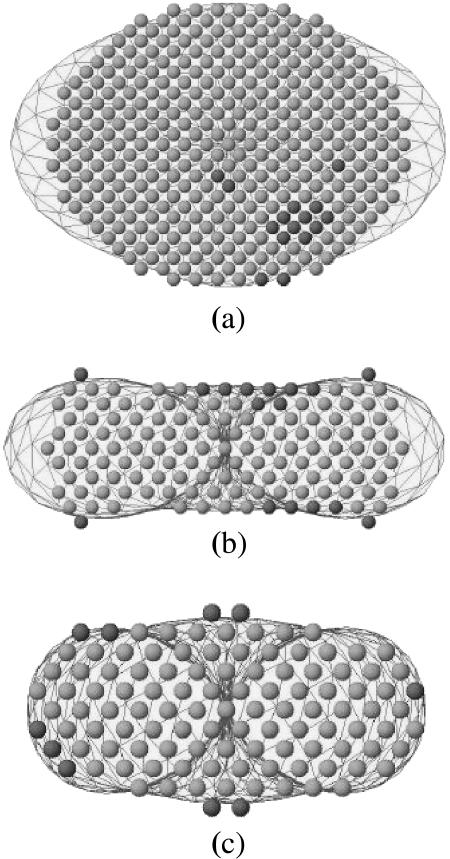
Several runs of ab initio shape determination with different starting conditions lead to consistent results as judged by the structural similarity of the output models, yielding nearly identical scattering patterns and statistical discrepancy in a stable and self-consistent process. It should be noted that no symmetrical constraint is applied to the DAM model in the simulation. The protein models have been generated up to 10 times yielding similar results. The fitting curve from the restored DAM configuration is represented by a solid line in Fig. 3. Two of the restored DAM configurations of LH2 complex are superimposed and illustrated in Fig. 4.

FIGURE 3.

FIGURE 3

Open in a new tab

Experimental SAXS results for LH2 in water (open circle) and fitting of the experimental data (a) by the simulated annealing algorithm (solid line) and (b) by the restored envelope (dashed line) and the calculated scattering curve (dotted line) from the LH2 model by CRYSOL (Svergun et al., 1995).

FIGURE 4.

FIGURE 4

Open in a new tab

Topological shape of LH2 complex in water solution for (a) top view, (b) front view, and (c) lateral view. The envelope of the molecular shape found from solution scattering by the restored envelope is represented by the dashed curve. The superimposed balls show two sets of restored DAM configurations by the simulated annealing algorithm.

Fig. 5 shows the crystallographic structural model of LH2 complex (Rps. acidophila), whose coordinate sets for LH2 were obtained from the Protein Data Bank (PDB 1KZU), superimposed by the restored shape envelope for comparison. The simulated annealing algorithm indicates that the ellipsoidal plate has a shorter semiaxis of a = 38 Å, a longer one of b = 46 Å, and a height of 40 Å. From Fig. 5, it can be seen that the shape of the protein reproduces most of the molecular features when compared with the overall details of the LH2 crystal structure (Rps. acidophila).

FIGURE 5.

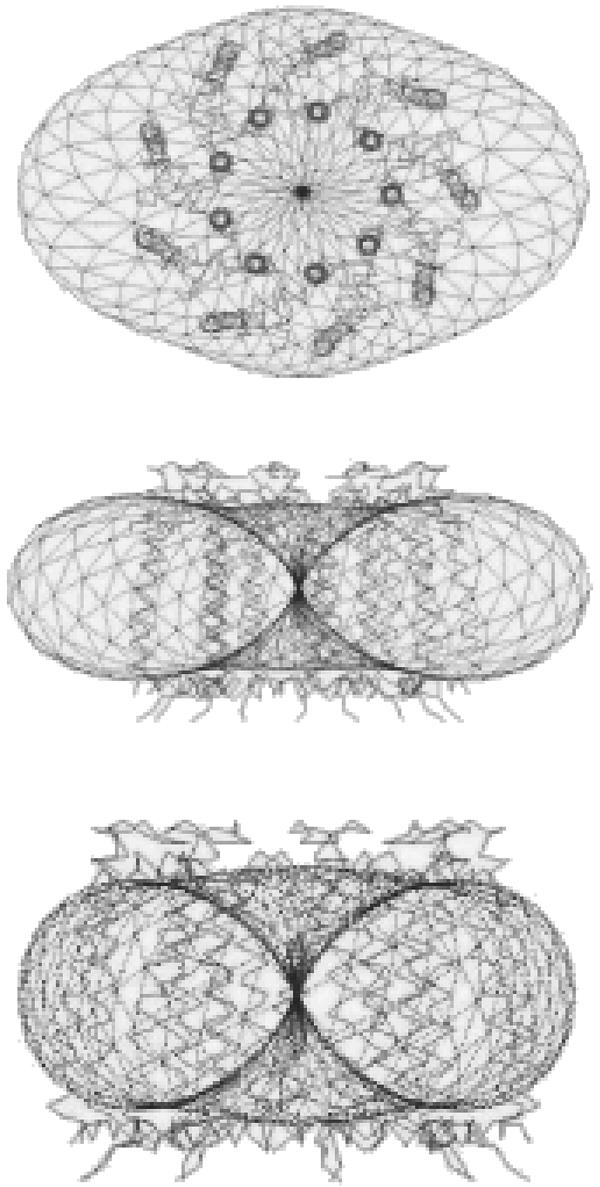
FIGURE 5

Open in a new tab

The restored shape envelope of LH2 complex (dashed lines) in water together with the corresponding structural model in crystal represented by chains (displayed in three different orientations).

To further confirm the resolved topological structure of LH2 complex in solution, a different ab initio method is employed to restore the molecular shape from the experimental scattering data. In this method, the shape is represented by an envelope angular function, parameterized in terms of spherical harmonics using a multipole expansion method proposed by Stuhrmann (1970) and developed by Svergun and co-workers (Svergun et al., 1987, 1996; Svergun and Stuhrmann, 1991). In the case of a monodisperse system consisting of randomly orientated particles, it is possible to obtain structural information of the particles from small-angle scattering data. From the measured one-dimensional scattering profile, the three-dimensional shape of the particles can be characterized in terms of a series of multipole coefficients. Knowledge of these multipole coefficients allows one to generate an approximate model of the shape of the macromolecules being examined (Svergun et al., 1996; Stuhrmann, 1970).

Assuming that the scattering is caused by a globular homogeneous molecule, one can define its molecular envelope by a two-dimensional angular function, F(θ,ϕ), describing the molecular boundary such that the particle density ρ(r) is unity inside and vanishes elsewhere. The function F(θ,ϕ) can be conveniently expanded into a series of spherical harmonics, Ylm(θ,ϕ), according to Press et al. (1992),

graphic file with name M5.gif (4)

with flm being complex multipole coefficients and L representing the multipole order. R0 is a scale factor of ∼(3V/4π)1/3, where V is the volume of the particle, and the ratio of quadrupolar term over the zero-order term, 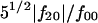Inline graphic, is a good indication of the deviation of the molecular shape from sphericity. A computational procedure to evaluate the multipole coefficients from the experimental scattering curve by minimizing the residual of fitting the experimental curve was developed by Svergun and Stuhrmann (1991). Details of the algorithm can be found in examples in Svergun et al. (1996).

The range of experimentally available scattering data generally allows the determination of 15–20 variables in the shape description. This imposes an upper limit for the multipole order L, since the number of independent parameters in the above series is equal to (L + 1)2−6 (Svergun et al., 1996). Consequently, in general, unique shape calculations with the multipole order of L = 4 are possible. In addition, molecular symmetry imposes restrictions on the multipole coefficients, flm, which can improve the reliability of the shape restoration by reducing the number of parameters to be calculated. The higher the symmetry, the fewer the multipole coefficients necessary, which results in an enhanced resolution. The smoothed scattering profile was fitted ab initio by the scattering from an envelope function starting from an ellipsoidal initial approximation. The molecular shape was characterized with spherical harmonics up to fourth order, assuming a C2 symmetry axis. The ratio 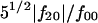Inline graphic is ∼1.0, indicating that the molecular shape has a severe deviation from the sphericity. The topological structure of LH2 complex obtained by the restored envelope is shown in Fig. 4 (net curve) and the calculated scattering curve by the restored structural envelope model is given in Fig. 3 (dashed line). The elliptical plate obtained by envelope determination has a rough dimension of ∼40 Å thick, 85 Å wide, and 110 Å long. Although it is found that the solution of this method is not quite stable because of the obvious noise at higher angle, the obtained topological structure is quite consistent with that produced by the method of simulated annealing algorithm, thus providing additional evidence for the elliptical shape of LH2 complex in the detergent solution.

Comparing the calculated scattering intensity curves with the experimental data shown in Fig. 3, it is found that the calculated curve for the restored structure from the simulated annealing algorithm can best fit the experimental data, and that for the restored envelope fits fairly well; however, the calculated curve for the presumed ring structure, as in the crystal, deviates much from the experimental data. The molecular shape viewed at three orthogonal orientations is shown in Fig. 5, together with the crystal structure (Rps. acidophila) for comparison.

The molecular shape of the LH2 complex

LH2 molecule is an integral membrane protein (IMP) complex. It is isolated from the lipid membrane by a suitable detergent extraction. In the detergent solution, it is generally regarded that the protein is surrounded by a “belt” of detergent molecules that cover the hydrophobic region originally embedded in the membrane (Roth et al., 1991). Early work of SAXS and small-angle neutron scattering studies on some other IMPs in the detergent solution support this view (Sardet et al., 1976; Osborne et al., 1978). After purification, the micelle-encapsulated IMP can be crystallized; the detergent phase assumed in the solution has been found in the crystals of a number of IMPs. Recent studies of neutron diffraction of the IMPs crystals reveal the low-resolution structure and distribution of the detergents in the crystals (Roth et al., 1989, 1991).

The crystal structure of LH2 complex (Rps. acidophila) determined by X-ray diffraction at atomic solution can be described briefly as a two-walled concentric hollow cylinder. The outer wall consists of nine β-apoprotein helices with a diameter of 68 Å, the inner wall consists of nine α-apoprotein helices with a diameter of 36 Å, and the height of the cylinder is 40 Å. However, the detergent phase in crystal cannot be seen in the X-ray crystal structure due to its disordered character. Recently the detergent shell of β-octyl-glucoside (βOG) in LH2 crystal (Rps. acidophila) has been determined by means of neutron diffraction (Prince et al., 2003). From this experiment, the maximum thickness of the detergent belt surrounding the outer wall of hydrophobic β-polypeptides is 15 Å. For a fully extended βOG molecule, the total length is ∼15.4 Å. The detergent belt is consistent with the fact that the hydrophobic surfaces of LH2 are in contact with a monolayer of detergent with the hydrophilic head orientating outward. The fact also supports the proposed detergent configuration of IMPs in the solution where the detergent is located in a monolayer around the hydrophobic domain (Le Maire et al., 1983). The extended molecular length for the two detergents, βOG and LDAO, is quite similar; the former is 15.4 Å in length (Prince et al., 2003), whereas the latter is ∼15–16 Å (Roth et al., 1989). Therefore the expected LDAO-surrounded LH2 ring in the solution would have a maximum diameter of 98 Å, with the inner hollow filled with detergent extended to 40 Å, the full height of the LH2 cylinder. Although an X-ray crystal structure of LH2 complex from Rb. spheroides at atomic resolution is not available, an electron micrograph of a two-dimensional crystal reconstructed structure at 6 Å resolution of LH2 from Rb. spheroides shows that the LH2 complex has nine αβ-dipeptides, with a diameter of 62 Å for the outer ring and 35 Å for the inner ring, comparable to the X-ray structure of LH2 from Rps. acidophila (Walz et al., 1998). The fact justifies the direct comparison of the topological structure of LH2 from Rb. spheroides determined by SAXS to the X-ray crystal structure of LH2 from Rps. acidophila.

Compared to the detergent-surrounded structure of LH2 in crystal (Rps. acidophila), the detergent-encapsulated LH2 ring determined by SAXS deforms to an ellipsoid with a long axis of 110 Å and a short axis of 85 Å for the model restored by the multipole expansion, and a long axis of 92 Å and a short axis of 76 Å for the dummy atom model. Both of the models give a height of 40 Å, the same as that for the LH2 cylinder in the crystal. Considering that the thickness of the detergent monolayer shell is homogeneous around the LH2 complex, such a deformation can be caused only by the distortion of the protein frame. Based on the underlying principle in the calculation, the multipole expansion method could possibly better define the interface between the solution and the hydrophilic head of the detergent phase, so we therefore take oblate plate of the envelope model as the molecular shape of LH2 complex in solution. By peeling off the detergent monolayer, an elliptical frame of 80 Å in long axis and 55 Å in the short axis is obtained for the LH2 complex in the detergent solution. The eccentricity, ɛ, of the deformed ring, defined by (1 − a2/b2)1/2, where a and b are the length of the short and long axes, respectively, can be calculated in the model of restored envelope as 0.59. This result is well-consistent with the experiment of single-molecule spectroscopy, by which it has been found that the elliptic deformation of the individual LH2 molecule from Rps. acidophila has an eccentricity of ɛ = 0.52 (van Oijen et al., 1999). It is interesting to note that other experimental evidence also points to an elliptical deformation in LH2 complexes. An earlier evidence comes from the electron micrograph of two-dimensional crystals of LH2 from Rb. spheroides, which provided low-resolution data that suggests a breakdown of circular symmetry into elliptical symmetry. It was attributed to a tilt of the LH2 rings of ∼5° of the β-helices relative to the membrane normal. However, if we ascribe such a symmetry breaking to the elliptical deformation of LH2 complexes, it would result in an ɛ of 0.09. A recent evidence is the high-resolution AFM topograph of reconstituted arrays of LH2 complexes from Rubrivivax gelatinosus in which LH2 complex is loosely compact; unlike the circular symmetry found in the crystal, the data show a small elliptical deformation of LH2 complexes with an eccentricity of ɛ = 0.31 for cytoplasmic side and ɛ = 0.41 for the periplasmic side (Scheuring et al., 2001). Summarizing the elliptical deformations of LH2 complexes at different conditions, the following order can be obtained as LH2 molecule from Rb. spheroides in solution (ɛ = 0.59, determined by SAXS, this work); that single LH2 molecule from Rps. acidophila in polyvinyl alcohol matrix at 1.2 K can be viewed as a frozen liquid state (ɛ = 0.52, determined by single molecular spectroscopy, van Oijen et al., 1999); reconstituted arrays of LH2 complexes from Rubrivivax gelatinosus of loosely compact (ɛ = 0.31, 0.41, Scheuring et al., 2001); two-dimensional crystals of LH2 from Rb. spheroides (ɛ = 0.09, Walz et al., 1998); and three-dimensional crystals of LH2 from Rps. acidophila (ɛ = 0, McDermott et al., 1995). An obvious tendency is that the more freedom for LH2 complexes to move, the larger deformation the LH2 complexes suffer. This might also explain the discrepancy of elliptical deformations observed by different groups.

It is noteworthy that the thickness of the micelle-encapsulated LH2 has almost the same height as that of the crystal structure, which indicates that there is almost no detergent monolayer formed on the two planes of the N- and C-terminal ends in the solution. This may be accounted for by the hydrophilic feature of the residual amino acids in the two end planes of the oblate plate exposed to the solvent. It is known that the C-terminal end of α-apoprotein consists of a hydrophilic Glu residue, whereas the N-terminal contains two hydrophilic residues, Thr and Asn; for β-apoprotein, the N-terminal contains a hydrophilic sequence, TDD, whereas the C-terminal consists of a hydrophobic sequence, GLWP (Hunter, 1995). Except for the C-terminal of β-apoprotein, it is expected that the ends of the apoproteins can be directly solvated without the help of the detergent.

CONCLUSIONS

The results of SAXS study in this work unambiguously reveal that the structure of LH2 complex from Rb. spheroides is different from that of Rps. acidophila in the crystal phase in that it deforms from a ring structure in crystal to an ellipsoid in the detergent solution with an eccentricity of 0.59, consistent with the result of single molecular spectroscopy study of the isolated single LH2 molecules from Rps. acidophila. The cylindrical wall of LH2, consisting of hydrophobic β-apoprotein helices, is encapsulated by a monolayered detergent shell, while the two bottom planes of the LH2 cylinder are almost directly exposed to the solvent medium because of the hydrophilic property of the residual amino acids at the C- and N- terminals. An account for such a symmetry-lowering deformation, as already suggested by van Oijen et al. (1999), is that the LH2 molecules are densely packed in the crystals, causing a stabilization of the structure, whereas such a stabilizing force is absent in the solution.

Acknowledgments

We thank Prof. Y. Koyama and Dr. R. Fujii for help in sample preparation, and Profs. D. C. Xian, Z. H. Mai, and T. D. Hu for their support to this research. Assistance in the experiments from Dr. Z. H. Wu and Z. J. Chen is gratefully acknowledged.

This work was supported by the Chinese National Key Basic Research and Development Plan under grant G1998010102, and the Chinese National Natural Science Fund for International Cooperation.

References

  1. Bopp, M. A., A. Sytnik, T. D. Howard, R. J. Cogdell, and R. M. Hochstrasser. 1999. The dynamics of structural deformations of immobilized single light-harvesting complexes. Proc. Natl. Acad. Sci. USA. 96:11271–11276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Dong, B. Z., W. J. Sheng, H. L. Yang, and Z. J. Zhang. 1997. Status of the small-angle scattering station at the Beijing Synchrotron Radiation Facility. J. Appl. Crystallogr. 30:877–879. [Google Scholar]
  3. Fleming, G. R., and R. van Grondelle. 1997. Femtosecond spectroscopy of photosynthetic light-harvesting systems. Curr. Opin. Struct. Biol. 7:738–748. [DOI] [PubMed] [Google Scholar]
  4. Freer, A., S. Prince, K. Sauer, M. Papiz, A. Hawthornthwaite-Lawless, G. McDermott, R. Cogdell, and N. W. Isaacs. 1996. Pigment-pigment interactions and energy transfer in the antenna complex of the photosynthetic bacterium Rhodopseudomonas acidophila. Structure. 4:449–462. [DOI] [PubMed] [Google Scholar]
  5. Georgakopoulou, S., R. N. Frese, E. Johnson, C. Koolhaas, R. J. Cogdell, R. van Grondelle, and G. van der Zwan. 2002. Absorption and CD spectroscopy and modeling of various LH2 complexes from purple bacteria. Biophys. J. 82:2184–2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Glatter, O., and O. Kratky. 1982. Small Angle X-Ray Scattering. Academic Press, New York.
  7. Grossmann, J. G., and S. S. Hasnain. 1997. X-ray scattering studies of metalloproteins in solution: a quantitative approach for studying molecular conformations. J. Appl. Crystallogr. 30:770–775. [Google Scholar]
  8. Guinier, A., and G. Fournet. 1955. Small-Angle Scattering of X-Rays. John Wiley & Sons, London, UK.
  9. Hao, Q. 2001. Phasing from an envelope. Acta Crystallogr. D57:1410–1414. [DOI] [PubMed] [Google Scholar]
  10. Hu, X., and K. Schulten. 1997. How nature harvests sunlight. Phys. Today. 50:28–34. [Google Scholar]
  11. Hunter, C. N. 1995. Genetic manipulation of the antenna complexes of purple bacteria. In Anoxygenic Photosynthetic Bacteria. R. E. Blankenship, M. T. Madigan, and C. E. Bauer, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 473–501.
  12. Ingber, L. 1993. Simulated annealing: practice versus theory. Math. Comput. Model. 18:29–57. [Google Scholar]
  13. Ketelaars, M., A. M. van Oijen, M. Matsushita, J. Köhler, J. Schmidt, and T. J. Aartsma. 2001. Spectroscopy on the B850 band of individual light-harvesting II complexes of Rhodopseudomonas acidophila. I. Experiments and Monte Carlo simulations. Biophys. J. 80:1591–1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Koepke, J., X. Hu, C. Muencke, K. Schulten, and H. Michel. 1996. The crystal structure of the light-harvesting complex II (B800–850) from Rhodospirillum molischianum. Structure. 4:581–597. [DOI] [PubMed] [Google Scholar]
  15. Le Maire, M., S. Kwee, J. P. Andersen, and J. V. Moller. 1983. Mode of interaction of polyoxyethyleneglycol detergents with membrane proteins. Eur. J. Biochem. 129:525–532. [DOI] [PubMed] [Google Scholar]
  16. Matsushita, M., M. Ketelaars, A. M. van Oijen, J. Köhler, T. J. Aartsma, and J. Schmidt. 2001. Spectroscopy on the B850 band of individual light-harvesting 2 complexes of Rhodopseudomonas acidophila. II. Exciton states of an elliptically deformed ring aggregate. Biophys. J. 80:1604–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mayor, U., N. R. Guydosh, C. M. Johnson, J. G. Grossmann, S. Sato, G. S. Jas, S. M. V. Freund, D. O. V. Alonso, V. Daggett, and A. R. Fersht. 2003. The complete folding pathway of a protein from nanoseconds to microseconds. Nature. 421:863–867. [DOI] [PubMed] [Google Scholar]
  18. McDermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
  19. Ockwell, D. M., M. A. Hough, J. G. Grossmann, S. S. Hasnain, and Q. Hao. 2000. Implementation of cluster analysis for ab initio phasing using the molecular envelope from solution X-ray scattering. Acta Cryst. D56:1002–1006. [DOI] [PubMed] [Google Scholar]
  20. Ohashi, N., N. Ko-Chi, M. Kuki, T. Shimamura, R. J. Cogdell, and Y. Koyama. 1996. The structures of S0 spheroidene in the light-harvesting (LH2) complex and S0 and T1 spheroidene in the reaction center of Rhodobacter spheroides 2.4.1 as revealed by Raman spectroscopy. Biospectroscopy. 2:59–69. [Google Scholar]
  21. Osborne, H. B., C. Sardet, M. Michel-Villaz, and M. Chabre. 1978. Structural study of rhodopsin in detergent micelles by small-angle neutron scattering. J. Mol. Biol. 123:177–206. [DOI] [PubMed] [Google Scholar]
  22. Press, W. H., S. A. Teukolsky, W. T. Wetterling, and B. P. Flannery. 1992. Numerical Recipes. University Press, Cambridge, MA.
  23. Prince, S. M., T. D. Howard, D. A. A. Myles, C. Wilkinson, M. Z. Papiz, A. A. Freer, R. J. Cogdell, and N. W. Isaacs. 2003. Detergent structure in crystals of the integral membrane light-harvesting complex LH2 from Rhodopseudomonas acidophila strain 10050. J. Mol. Biol. 326:307–315. [DOI] [PubMed] [Google Scholar]
  24. Pullerits, T., and V. Sundström. 1996. Photosynthetic light-harvesting pigment-protein complexes: toward understanding how and why. Acc. Chem. Res. 29:381–389. [Google Scholar]
  25. Roth, M., B. Arnoux, A. Ducruix, and F. Reiss-Husson. 1991. Structure of the detergent phase and protein-detergent interactions in crystals of the wild-type (strain Y) Rhodobacter spheroides photochemical reaction center. Biochemistry. 30:9403–9413. [DOI] [PubMed] [Google Scholar]
  26. Roth, M., M. Lewitt-Bentley, H. Michel, J. Deisenhofer, R. Huber, and D. Oesterhelt. 1989. Detergent structure in crystals of a bacterial photosynthetic reaction centre. Nature. 340:659–662. [Google Scholar]
  27. Sardet, C., A. Tardieu, and V. Luzzatti. 1976. Shape and size of bovine rhodopsin: a small-angle X-ray scattering study of a rhodopsin-detergent complex. J. Mol. Biol. 105:383–407. [DOI] [PubMed] [Google Scholar]
  28. Scheuring, S., F. Reiss-Husson, A. Engel, J.-L. Rigaud, and J.-L. Ranck. 2001. High resolution AFM topographs of Rubrivivax gelatinosus light-harvesting complex LH2. EMBO J. 20:3029–3035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Semenyuk, A. V., and D. I. Svergun. 1991. GNOM—a program package for small-angle scattering data processing. J. Appl. Crystallogr. 24:537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Stuhrmann, H. B. 1970. Interpretation of small-angle scattering functions of dilute solutions and gases: a representation of the structures related to a one-particle scattering function. Acta Crystallogr. A26:297–306. [Google Scholar]
  31. Sundström, V., T. Pullerits, and R. van Grondelle. 1999. Photosynthetic light-harvesting: reconciling dynamics and structure of purple bacterial LH2 reveals function of photosynthetic unit. J. Phys. Chem. B. 103:2327–2346. [Google Scholar]
  32. Svergun, D. I., V. V. Volkov, M. B. Kozin, H. B. Sturmann, C. Barberato, and M. H. J. Koch. 1987. Shape determination from solution scattering of biopolymers. J. Appl. Crystallogr. 30:798–802. [Google Scholar]
  33. Svergun, D. I., and H. B. Stuhrmann. 1991. New developments in direct shape determination from small-angle scatter. 1. Theory and model calculations. Acta Crystallogr. A47:736–744. [Google Scholar]
  34. Svergun, D. I. 1992. Determination of the regularization parameter in indirect-transform methods using perceptual criteria. J. Appl. Crystallogr. 25:495–503. [Google Scholar]
  35. Svergun, D. I., C. Barberato, and M. H. Koch. 1995. CRYSOL—a program to evaluate X-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Crystallogr. 28:768–773. [Google Scholar]
  36. Svergun, D. I., V. V. Volkov, M. B. Kozin, and H. B. Stuhrmann. 1996. New developments in direct shape determination from small-angle scattering. 2. Uniqueness. Acta Crystallogr. A52:419–426. [Google Scholar]
  37. Svergun, D. I. 1999. Restoring low resolution structure of biological macromolecules from solution scattering using simulated annealing. Biophys. J. 76:2879–2886. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Svergun, D. I. 2000. Advanced solution scattering data analysis methods and their applications. J. Appl. Crystallogr. 33:530–534. [Google Scholar]
  39. van Grondelle, R., J. P. Dekker, T. Gillbro, and V. Sundström. 1994. Energy-transfer and trapping in photosynthesis. Biochim. Biophys. Acta. 1187:1–65. [Google Scholar]
  40. van Oijen, A. M., M. Ketelaars, J. Köhler, T. J. Aartsma, and J. Schmidt. 1999. Unravelling the electronic structure of individual photosynthetic pigment-protein complexes. Science. 285:400–402. [DOI] [PubMed] [Google Scholar]
  41. Wall, M. E., S. C. Gallagher, and J. Trewhella. 2000. Large-scale shape changes in proteins and macromolecular complexes. Annu. Rev. Phys. Chem. 51:355–380. [DOI] [PubMed] [Google Scholar]
  42. Walz, T., S. J. Jamieson, C. M. Bowers, P. A. Bullough, and C. N. Hunter. 1998. Projection structures of three photosynthetic complexes from Rhodobacter spheroides: LH2 at 6 Å, LH1 and RC-LH1 at 25 Å. J. Mol. Biol. 282:833–845. [DOI] [PubMed] [Google Scholar]
  43. Xie, X. S., and J. K. Trautman. 1998. Optical studies of single molecules at room temperature. Annu. Rev. Phys. Chem. 49:441–480. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES