Localization Accuracy in Single-Molecule Microscopy

Abstract

One of the most basic questions in single-molecule microscopy concerns the accuracy with which the location of a single molecule can be determined. Using the Fisher information matrix it is shown that the limit of the localization accuracy for a single molecule is given by 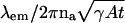, where λ_em, n_a, γ, A, and t denote the emission wavelength of the single molecule, the numerical aperture of the objective, the efficiency of the optical system, the emission rate of the single molecule and the acquisition time, respectively. Using Monte Carlo simulations it is shown that estimation algorithms can come close to attaining the limit given in the expression. Explicit quantitative results are also provided to show how the limit of the localization accuracy is reduced by factors such as pixelation of the detector and noise sources in the detection system. The results demonstrate what is achievable by single-molecule microscopy and provide guidelines for experimental design.

INTRODUCTION

In recent years, advances in imaging technology, computer control of experiments, and fluorescent labeling methodology, including green fluorescent protein based methods, have made it possible to detect single molecules even in a cellular environment; see, e.g., Chalfie et al. (1994), Schmidt et al. (1995), Vale et al. (1996), Schütz et al. (1997a, 2000a,b), Pierce et al. (1997), Weiss (1999), Smith et al. (1999), Kubitscheck et al. (2000), Harms et al. (2001), Kues et al. (2001), Yildiz et al. (2003). The possibility to study the behavior of individual molecules holds the promise to provide significant new insights into biological and biophysical processes. In single-molecule microscopy, the quantitative analysis of experimental data plays a crucial role in the interpretation of the results. For example, by mapping the trajectory of a fluorescently tagged protein and calculating its diffusion coefficient, the behavior of a membrane protein can be characterized; see, e.g., Saxton and Jacobson (1997).

One of the most fundamental issues in the quantitative analysis of single-molecule microscopy data concerns the accuracy with which the position of a single molecule can be determined. Specifying the accuracy with which the location of a single molecule can be established is not only of importance to be able to characterize the level of accuracy that is achievable in single-molecule microscopy. The accuracy with which a single molecule can be localized has significant influence on the type of studies that can be carried out using single molecule microscopy. It is also of significance in the analysis of single-molecule data. For example, it has recently been shown in Martin et al. (2002) that the accuracy of the location estimates has to be taken into account when analyzing the diffusion behavior of single molecules. Otherwise noisy measurements of the single-molecule locations could lead to the erroneous interpretation that subdiffusional behavior is present even though this is not the case.

Earlier approaches to the characterization of the localization accuracy mainly relied on an approach by Bobroff (1986) in which the localization accuracy problem was examined using the least-squares criterion; see, e.g., Schütz et al. (1997b), Kubitscheck et al. (2000), Ghosh and Webb (1994), Thompson et al. (2002), and Cheezum et al. (2001). The use of the least-squares criterion is problematic if applied to probability distributions that are not compatible with this criterion. This criterion is ideally suited to estimate parameters from data that has a Gaussian probability distribution because in that case the least-squares estimate is a maximum likelihood estimate; see, e.g., Kay (1993). It does, however, appear problematic to assume that single-molecule data is in fact Gaussian distributed.

Aside from the reliance on the least-squares algorithm other approximations are made in Bobroff (1986) in the derivation of the result that are often difficult to verify. Moreover, in the application of those results to single-molecule microscopy the image profile of a single molecule predicted by standard diffraction theory is often replaced by a Gaussian profile; see Santos and Young (2000) for a numerical comparison concerning the localization accuracy for both situations. Our results and approaches do not rely on this approximation.

Here we present a novel approach to determine the localization accuracy that can be achieved in single-molecule microscopy. This approach is based on the well-established statistical theory concerning the Fisher information matrix; see, e.g., Kay (1993). We obtain an explicit analytical expression that establishes a fundamental limit of the localization accuracy for single molecules. The importance of this result lies in the fact that it shows with an unexpectedly simple expression how fundamental properties of the photon-emission process of the single molecule (emission wavelength, photon-emission rate) and of the detection system (numerical aperture of the objective lens, optical efficiency of the setup, acquisition time) influence the localization accuracy of the single molecule.

It is of importance that the limit of the localization accuracy that is derived here does not depend on a specific estimation algorithm. In fact, the very idea of the approach presented here is that a limit be given that cannot be surpassed by a specific estimation procedure that produces a reasonable estimate of the location of a single molecule. Analytical expressions are also given to show how the fundamental limit of the localization accuracy is reduced by experimental conditions such as pixelation of the detector and noise sources in the detection process. As expected, the fundamental limit decreases with the inverse of the square root of the number of detected photons. If the point-spread function of the optical system is described by the classical Airy profile we will show that the numerator of the fundamental limit depends on the physical properties of the optical-detection system and the wavelength of the emitted photons. If the point-spread function is modeled to be a Gaussian profile the numerator of the fundamental limit will be the standard deviation of the Gaussian distribution. However, we also show that the numerator of the fundamental limit cannot, in general, be expected to be the standard deviation of the distribution that describes the point-spread function of the optical system.

As will be shown here our approach can be applied, for example, to Poisson distributed data without having to rely on potentially problematic approximations. In fact we demonstrate with a concrete result that relatively intricate distributions can be analyzed. We also present a limit of the localization accuracy for single molecule data that is the sum of a Poisson and Gaussian random variable. Such data arises, for example, when the photon counts are distorted by measurement noise in the CCD camera.

The results presented here are not restricted to single molecule microscopy. They have applications to localization problems in all areas of optical detection of objects, in particular point sources. The expectation is that the results and approaches presented here will give the single molecule microscopist novel tools to analyze the localization accuracy of single-molecule experiments without having to rely on approaches whose assumptions may not be appropriate for single molecule microscopy.

METHODS

Simulations and parameter values

All simulations and calculations were carried out in the Matlab (Mathworks, Natick, MA) programming environment (Coleman et al., 2000). We assume the fluorescent single molecule to have an emission wavelength of 520 nm. For all calculations, unless explicitly stated, the numerical aperture is set to be n_a = 1.4, the magnification is set to be M = 100, and the acquisition time is in the range from t = 0.01 s to t = 1 s. We set the photon-emission rate to be A = 2 × 10⁶ photons/s and the optical efficiency to be γ = 0.033. These values of A and γ are in the range of values typically observed in single-molecule experiments (Schmidt et al., 1995; Schütz et al., 1997b; Kubitscheck et al., 2000; Kues et al., 2001). In Figs. 2–6 we assume square pixels with no dead space between adjacent pixels and unless otherwise stated, the single molecule is positioned at the center of the pixel array.

FIGURE 2.

Fundamental limit (solid line) of the localization accuracy (see Eq. 2) for the u coordinate of a single molecule with experimental parameters similar to those for a GFP molecule as a function of the expected number of detected photons γAt = 66,000 photons/s t. The x axis range corresponds to an acquisition time range from t = 0.01 s to t = 1 s. The figure also shows the standard deviation of the maximum likelihood estimates of the single-molecule position as a function of the expected number γAt of detected photons (+) and as a function of the total number of detected photons (⋄). The standard deviations of both the estimates approach the fundamental limit as the expected (total) number of detected photons increases. Note that the standard deviation for the latter case is uniformly closer to the fundamental limit than for the former case.

FIGURE 6.

Limit of the localization accuracy of the u coordinate of a single molecule with experimental parameters similar to those for a GFP molecule for a pixelated detector as a function of the single-molecule position for different noise levels and pixel sizes. Panel a (triangles) shows results in the presence of noise with a scattering rate (b_k) of 6600 photons/pixel/s and a readout noise (σ_k) of 57 e⁻/pixel (rms) for a 5 × 5 pixel array with a pixel size of 20 μm × 20 μm. Panel b shows the same for a scattering rate (b_k) of 660 photons/pixel/s and a readout noise (σ_k) of 7 e⁻/pixel (rms) (triangles). Panel c shows results in the noise-free case for a 10 × 10 pixel array with 10 μm × 10 μm pixels (⋄) and for a 50 × 50 pixel array with 2 μm × 2 μm pixels (○). The fundamental limit (solid line) is also shown for reference. In all three plots the acquisition time is t = 0.01 s, the pixel array size is 100 μm × 100 μm, and • shows the limit of the localization accuracy in the noise-free case for a 5 × 5 pixel array with 20-μm × 20-μm pixels. The x axis of the plots denotes the position of the single molecule with respect to the center of the pixel array (in the detector plane). The single molecule is moved in steps of 10 nm in the specimen plane, which corresponds to 1-μm steps in the detector plane. All movements are parallel to the pixel edges. For a 20 μm × 20 μm pixel this corresponds to moving the single molecule from one edge of the central pixel to the opposite edge of the pixel, whereas for a 10 μm × 10 μm pixel this corresponds to moving the single molecule over a pair of pixels that are centrally located on the detector and for a 5 μm × 5 μm pixel this corresponds to moving the single molecule over a set of four pixels centrally located on the detector.

Maximum likelihood estimation

In the nonpixelated case, maximum likelihood estimation was carried out for two different acquisition methods, one when the acquisition time was fixed and the other when the total number of detected photons was fixed. In the former case, due to the stochastic nature of photon emission, the total number of detected photons varied for every image, whereas in the latter case, the number of detected photons remained the same.

For the first acquisition method, a Poisson random number N₁ with mean γAt (denoting the expected number of detected photons) was generated and N₁ random vectors were generated (see “Random number generation”) that describe the spatial coordinates of the detected photons. The maximum likelihood estimation was carried out using a gradient-based search algorithm (Optimization Toolbox of Matlab; Coleman et al., 1999). For every value of γAt, 300 estimates of position were computed from which the standard deviation was calculated. For the second acquisition method the same procedure was followed except that no Poisson random number was generated because the number of detected photons was fixed.

In the pixelated case, the maximum likelihood estimation was performed for the fixed acquisition time method. For a given pixel array size, pixel dimensions, single-molecule location, and γAt, 300 images were simulated by first generating a noise-free pixelated image and then adding Poisson and Gaussian noise to the pixel values. Using the simulated data, maximum likelihood estimation was carried out using an algorithm analogous to the one that was mentioned above. The standard deviation of the estimates of the single-molecule location was then calculated.

Random number generation

The simulation of the two-dimensional distribution corresponding to the point spread function can be carried out by reducing the simulation to that of two one-dimensional distributions. Let Φ denote a uniform random variable with density function f_Φ(φ) = 1/2π, 0 ≤ φ ≤ 2π and let R denote a one-dimensional continuous random variable with density function r ≥ 0, where a = (2πn_a)/(λ_emM). Let R and Φ be independent of each other. Define X ≔ R cos Φ + Mu and Y ≔ R sin Φ + Mv, where u, v denote the coordinates of location of the single molecule and M denotes the magnification of the objective lens. Then the joint density function of X and Y is given by

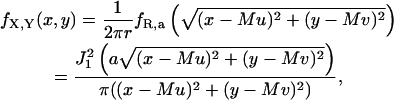where −∞ < x, y < ∞. To generate a random vector (x, y) that describes the spatial coordinates of the detected photons on the detector, we first generate a uniform random number φ between 0 and 2π, then generate a random number r with density function f_R,a and set x ≔ r cos φ + Mu, y ≔ r sin φ + Mv. The uniform random number φ is generated using a standard random number generator (Coleman et al., 2000). The random number r is generated by the transformation method (Ross, 2000) in conjunction with a numerical inversion of the distribution function corresponding to f_R,a using a look-up table.

RESULTS AND DISCUSSION

Fundamental limit of the localization accuracy

We consider a basic setup of an optical system (see Fig. 1) where a single molecule in the specimen plane is at the focus of an objective lens and its image is captured by a planar detector. The time points of the photon emission process of the single molecule are modeled as a Poisson process and the single molecule that is imaged through the optical system is modeled as a point source (Born and Wolf, 1999). We assume that the detector captures the spatial coordinates of the detected photons. Since the photon emission process is inherently a stochastic phenomenon the acquired data is stochastic in nature. Therefore the coordinates on the detector of the detected photons are assumed to be independent and identically distributed random variables with a density function

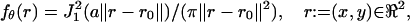(1)

where θ = (u, v) ∈ ℜ² denotes the position of the single molecule/point source in the specimen plane, r₀ = Mθ denotes the center of the image of the single molecule/point source in the detector plane, , a = 2πn_a/(λ_emM), n_a, M denotes the numerical aperture and the magnification of the objective lens respectively, λ_em denotes the emission wavelength of the single molecule, and J₁ denotes the first order Bessel function of the first kind.

FIGURE 1.

Schematic setup of the optical system used to capture the image of a single molecule. Here θ ≔ (u, v) denotes the position of the single molecule on the specimen plane and r₀ = (x₀, y₀) = Mθ denotes the position of the center of the image of the single molecule on the detector plane where M denotes the magnification of the lens.

The experimental data from which the location of the single molecule has to be inferred are the coordinates on the detector at which the emitted photons are recorded. Due to the random nature of the acquired data the determination of the location of the single molecule is a statistical problem. We therefore define the localization accuracy of a specific estimation method as the standard deviation of the estimated locations of the single molecule assuming repeated experiments; see also Bobroff (1986), Schütz et al. (1998), and Thompson et al. (2002). However, there are several methods by which the location of a single molecule can be estimated; see, e.g., Cheezum et al. (2001). Hence the question arises as to what is the best possible localization accuracy that can be achieved.

To answer this question, we calculate the Fisher information matrix for the underlying stochastic data generation process; see, e.g., Zacks (1971) and Kay (1993). The Fisher information matrix I(θ) plays a central role in the analysis of estimation algorithms. Its inverse provides, through the classical Cramer-Rao lower bound (see, e.g., Zacks, 1971, and Kay, 1993), a lower bound for the variance of any unbiased estimator (i.e., any estimation procedure whose mean produces the correct result), specifically

Moreover, fundamental results in large sample statistics show that any “reasonable” estimator (including the maximum likelihood estimator) has an asymptotic variance that equals the inverse of the Fisher information matrix; see, e.g., Rao (1965), Zacks (1971), and Kay (1993). If this methodology is applied to the problem at hand the Cramer Rao lower bound shows that the variance for any unbiased estimation procedure for the coordinates of the single molecule will be larger than the inverse of the Fisher information matrix. Therefore we interpret the inverse of the Fisher information matrix as a lower limit to the variances of the estimation procedures that might be used in the detection of single molecules. It is important to note that the inverse I⁻¹(θ) of the Fisher information matrix is independent of a particular estimation procedure and therefore serves as a uniform bound for any reasonable estimation method. We are interested in obtaining a limit for the standard deviation rather than for the variance of the estimation procedures. We therefore consider the square root of the inverse of the Fisher information matrix as a limit of the localization accuracy for a single molecule.

To obtain a bound on the localization accuracy it is therefore necessary to calculate the Fisher information matrix and its inverse based on the general form of the Fisher information matrix (see Eq. 7 in the Appendix). The Fisher information matrix only depends on the statistical model of the data generation process. Here we consider three different scenarios. In the first case, which we introduced above, we analyze the situation in which the stochastic data generation is described by the photon emission process and the distribution of the detected photons in the detector plane is given by the Airy point-spread function profile. In the second scenario (subsequent section) we also consider pixelation of the detector and Poisson noise sources due to, for example, the dark current in a CCD detector, scattered photons, or background fluorescence. In the third case (subsequent section) we expand on the second scenario by allowing for additional Gaussian noise sources that arise for example in the readout process of a CCD camera (Janesick, 2000). Each of these stochastic models leads to a different Fisher information matrix (see Appendix for the calculations), which in turn leads to a different bound.

Within the first stochastic framework laid out above the fundamental limit δ_u (δ_v) of the localization accuracy for the u (v) coordinate of the single molecule is given by (see Appendix for the derivation)

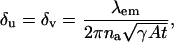(2)

where A denotes the photon emission rate of the single molecule, 0 ≤ γ ≤ 1 denotes the optical efficiency of the detection system, i.e., the probability that a photon, which is emitted by the single molecule is detected by the detector and t denotes the acquisition time. For example, the fundamental limit of the localization accuracy for a green fluorescent protein (GFP) single molecule is 2.3010 nm for an acquisition time of t = 0.01 s and 0.7277 nm for an acquisition time of t = 0.1 s. Here we have assumed typical experimental conditions, i.e., A = 2 × 10⁶ photons/s, λ_em = 520 nm, γ = 0.033, n_a = 1.4; see also Kues et al. (2001) where similar values for experimental parameters are reported for a GFP molecule. Fig. 2 shows the dependence of the fundamental limit on the expected number of detected photons for these experimental settings.

We use the term fundamental here to describe the fact that the model that underlies this expression does not take into account any deteriorating effects in the acquisition system such as pixelation of the detector and the various noise sources that typically occur in experimental settings. This expression only takes into consideration the basic optical and stochastic phenomena that are inherent in any single-molecule experiment. The effects that experimental conditions have on the limit of the localization accuracy are analyzed in subsequent sections.

This result provides a simple analytical expression that quantitatively exhibits the dependence of the limit of the localization accuracy on the optical properties of the microscope and the photophysical properties of the single molecule. The fundamental limit exhibits an inverse square root dependence on the expected number of detected photons, which is in agreement with previously published results; see, e.g., Ghosh and Webb (1994) and Thompson et al. (2002). The result, in particular, implies that to improve the limit of the localization accuracy by a factor of two (i.e., halve the value of δ_u), we either need to double the numerical aperture of the objective lens, or increase the photon-emission rate or the optical efficiency by a factor of four, or halve the emission wavelength of the single molecule. This means that the location of a single molecule emitting blue light can be more accurately determined than one that is emitting red light, provided all other factors remain the same. It should be noted that the fundamental limit is independent of the magnification M of the optical system.

The above result provides a limit for the smallest possible value of the standard deviation of a reasonable estimator of the location of a single molecule. It is therefore important to know whether an estimator exists whose standard deviation comes close to this limit. It is well known from large sample statistics that the variance of a large class of estimators asymptotically approaches the inverse of the Fisher information matrix (Zacks, 1971; Rao, 1965). We therefore consider one such estimator, namely the maximum likelihood estimator. Fig. 2 shows the standard deviations of the maximum likelihood estimates of the single-molecule location for two different acquisition methods, one when the acquisition time is fixed and the other when the total number of detected photons is fixed. In both cases the standard deviation of the maximum likelihood estimates approaches the fundamental limit as the expected (total) number of detected photons increases.

We have assumed that the measured data consists of the spatial coordinates of the detected photons. If we additionally assume that the time points of detection of the photons are also available, not surprisingly, the statistical analysis of the problem (see Appendix for details) shows that the expression for the fundamental limit is independent of this additional information and that only the (expected) total number of detected photons and their spatial coordinates are of significance.

Effects of pixelation and noise

The derivation of the fundamental limit of the localization accuracy assumes the best case scenario for the acquisition system. This was done to obtain an expression for the best possible localization accuracy in the absence of deteriorating factors due to specific experimental settings. For example, it was assumed that the precise coordinates of each detected photon can be recorded. Current imaging detectors have pixels and can therefore record the coordinates of the detected photons only up to the size of the pixel. In addition to pixelation we also consider two main categories of noise that are encountered in practical experimentation. Poisson noise can be used to model, for example, the effect of scattered photons on the measured data and Gaussian noise characterizes, for example, measurement noise in the CCD detector (Snyder et al., 1993, 1995). To obtain an expression for the limit of the localization accuracy for a pixelated detector, we assume that the detector has K pixels denoted by . No specific assumptions are made on the sizes, shapes, or positions of the pixels. 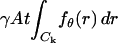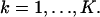The number of photons detected by a pixel C_k during the exposure time t is assumed to be Poisson distributed with mean for We also assume that the collected data in the k^th pixel is corrupted by additive noise that is Poisson distributed with mean b_kt, 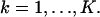For this setting the limit of the localization accuracy for the estimation of the u coordinate (the expression for the v coordinate is analogous) of the single molecule is given by (see Appendix)

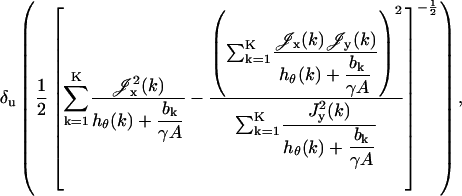(3)

where 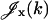, 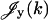are given by

and J₂ denotes the second order Bessel function of the first kind and 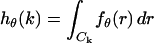denotes the integral of the point-spread function (Eq. 1) over the k^th pixel for 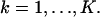Note that setting b_k = 0 in Eq. 3 leads to a straightforward modification of Eq. 3 to provide an expression for the limit of the localization accuracy for a pixelated finite-sized detector in the absence of any noise sources.

The expression for the limit of the localization accuracy for a pixelated detector is a modification of the fundamental limit δ_u given in Eq. 2. In fact, the expression involves the fundamental limit δ_u and a correction term (given in parentheses) that expresses the deterioration of the limit due to pixelation and noise.

We next consider the case when the acquired data in each pixel is further corrupted by Gaussian noise of mean η_k and variance 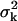for Gaussian noise arises in the CCD circuitry and becomes a component of the signal measured in a pixel (Snyder et al., 1993, 1995). The limit of the localization accuracy for the u coordinate (the expression for the v coordinate is analogous) is then given by (see Appendix)

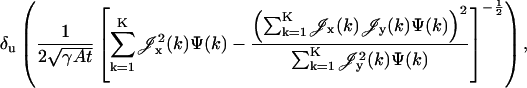(4)

where

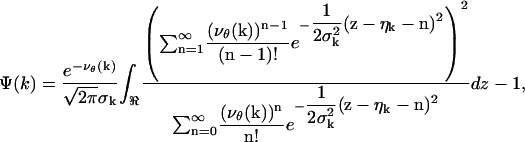with ν_θ(k) ≔ γAth_θ(k) + b_kt, k = 1,…,K.

We now illustrate the above expressions by showing how various experimental aspects such as magnification, pixel array size, pixel dimensions, and noise levels influence the accuracy with which the location of a single molecule can be determined. The fundamental limit (Eq. 2) serves as an important reference point to establish how closely the specific experimental implementation approaches the best possible localization accuracy.

For the numerical illustrations we chose parameters that are typical values for single molecule experiments with GFP molecules; see also Kues et al. (2001) where similar values were used. In all figures, unless otherwise specified, the photon emission rate of the single molecule is assumed to be A = 2 × 10⁶ photons/s and the optical efficiency is assumed to be γ = 0.033. This implies that the expected value for the number of photons that can be detected in the detector plane is 66,000 per second. The emission wavelength is set to be λ_em = 520 nm corresponding to a GFP molecule, the numerical aperture is set to be n_a = 1.4 and the magnification is set to be M = 100. The single molecule is assumed to be located at the center of the pixel array. We also assume that the detector consists of square pixels with no dead space region between adjacent pixels.

We first consider the effect of pixelation on the localization accuracy in the absence of noise. Fig. 3, a and c, illustrate the limit of the localization accuracy for a 11 × 11 pixel array as a function of different magnification values for t = 0.01 s and t = 1 s, respectively. For very low magnification values the image of the single molecule is to a large extent concentrated on one pixel. Therefore there is little information in the data about the location of the single molecule on the pixel. By increasing the magnification, the image of the single molecule spreads out over the pixel array and the localization accuracy improves. However, due to the finite size of the pixel array, for larger magnification values only a small fraction of the image of the single molecule is detected by the pixel array that results in a deterioration of the localization accuracy. This shows that if data is only acquired or analyzed for a fixed pixel array, care has to be taken to match the pixel array and magnification. With an appropriate choice of magnification it is, however, possible to come close to the fundamental limit.

FIGURE 3.

Limit of the localization accuracy for the u coordinate of a single molecule with experimental parameters similar to those for a GFP molecule for an 11 × 11 pixel array (5 μm × 5 μm pixel size) as a function of magnification for different acquisition times and noise levels. Panels a and c, respectively, show results in the noise-free case for t = 0.01 s (⋄) and t = 1 s (○). In both figures, the fundamental limit (solid line) is also shown for reference. Panel b shows results for two different sets of noise parameter values. Here, × corresponds to a scattering rate (b_k) of 6600 photons/pixel/s and a readout noise (σ_k) of 57 e⁻/pixel (rms), and • corresponds to a scattering rate of 660 photon/pixel/s and a readout noise of 7 e⁻/pixel (rms). In both cases the acquisition time is 10 ms.

We next consider the effect of pixel array size on the limit of the localization accuracy. Fig. 4 a shows the effect of the number of pixels on the limit of the localization accuracy in the noise-free case for a 5 × 5 array and for a 21 × 21 array. In both cases the pixel size is fixed to 6.8 μm × 6.8 μm. By increasing the pixel array size from a 5 × 5 array to a 21 × 21 array the limit of the localization accuracy comes closer to the fundamental limit. As is to be expected, increasing the size of the pixel array improves the localization accuracy by increasing the amount of data that is available for analysis. However, in practical situations it is not always possible to arbitrarily increase the size of the pixel array as often other elements are present in the image. This limits the number of pixels that can be used to determine the location of the single molecule unless a significant effort is made to model these other elements in the image.

FIGURE 4.

Limit of the localization accuracy of the u coordinate of a single molecule with experimental parameters similar to those for a GFP molecule as a function of the expected number of detected photons for a pixelated detector in the presence of different noise levels. Panel a shows the results in the noise-free case for a 5 × 5 pixel array (•) and for a 21 × 21 pixel array (triangles). The fundamental limit (solid line) is also shown for reference. Panel b shows the limit of the localization accuracy (○) in the presence of noise with a scattering rate (b_k) of 660 photons/pixel/s and a readout noise (σ_k) of 7 e⁻/pixel (rms) for a 5 × 5 pixel array. Similarly, panel c shows the limit of the localization accuracy (⋄) with a scattering rate (b_k) of 6600 photons/pixel/s and a readout noise (σ_k) of 57 e⁻/pixel (rms). For all the plots the pixel size is fixed to 6.8 μm × 6.8 μm and the x axis range corresponds to an acquisition time range from t = 0.01 s to t = 1 s. In panels b and c, the limit of the localization accuracy in the noise-free case (•) for a 5 × 5 pixel array is also shown for reference.

The expression for the limit of the localization accuracy in the presence of noise sources allows for two noise sources, Gaussian noise as it arises, for example, in the readout process of the CCD camera and Poisson noise, which can be used, for example, to model dark current in the CCD chip, scattered photons, and autofluorescence. To study the effect of noise sources on the limit of the localization accuracy, we consider two sets of noise parameter values. In one, we set the standard deviation (σ_k) of the Gaussian noise, e.g., the readout noise, to be 7 e⁻/pixel (rms). In our simulations we assume that the mean of the Gaussian noise is zero. This value for the readout noise is on the lower level of reported noise levels for current CCD cameras. For the low noise simulations we assume that the Poisson noise has a rate b_k of 0.01γA = 660 photons/pixel/s. This means, for example, that we assume that in each pixel scattered photons are collected at a rate that is 1% of the rate at which the photons emitted by the single molecule arrive in the detector plane. In the second set of noise parameters we consider parameters that correspond to high noise levels, in particular for the readout noise. In this case we set the standard deviation of the readout noise to be 57 e⁻/pixel (rms) and the scattering rate to be 0.1γA = 6600 photons/pixel/s. This level of readout noise is toward the high end on the scale of readout noise levels for current CCD cameras. The smaller value for the scattering rate is typically observed when imaging single molecules in solution (Schmidt et al., 1995), whereas the larger value is observed when imaging single molecules in a cellular environment (Kues et al., 2001). In all figures we assume that the noise statistics are the same for all pixels.

The dramatic effect that noise can have on the limit of the localization accuracy is shown in Fig. 4 b, where the limit of the localization accuracy is plotted as a function of the expected number of detected photons for low scattering and measurement noise levels for a 5 × 5 pixel array with 6.8 μm × 6.8 μm pixel size. Fig. 4 c shows the same for high scattering and measurement noise levels. The effect is especially pronounced for low photon count numbers where the limit of the localization accuracy can be an order of magnitude larger than in the noise free case (see Fig. 4 c). However, by increasing the total number of detected photons it is possible to come close to the fundamental limit even at high noise levels.

A similar effect of the noise sources on the limit of the localization accuracy is shown in Fig. 3 b, where the limit of the localization accuracy is plotted as a function of magnification for different measurement and scattering noise levels and for the noise-free case for a 11 × 11 pixel array with a pixel size of 5 μm × 5 μm. For a given magnification value, the presence of high noise levels can deteriorate the best possible localization accuracy by an order of magnitude when compared to the noise-free case. Also, at high noise levels the limit of the localization accuracy deteriorates by a factor of four when the magnification varies from 50× to 200×. For example, consider the image of a GFP single molecule centered on a 11 × 11 pixel array with a pixel size of 5 μm × 5 μm. At 50× magnification (n_a = 1.4), the image of the GFP single molecule in the pixel array will contain 93% of the expected number of detected photons. At 100× magnification (n_a = 1.4), the image of the GFP single molecule in the pixel array will contain 87% of the expected number of detected photons. Although by increasing the magnification from 50× to 100× we only lose ∼6% of the total number of detected photons, the limit of the localization accuracy significantly deteriorates from 38 nm at 50× magnification to 60 nm at 100× magnification at high noise levels.

As mentioned earlier, it is important to determine whether an estimation algorithm can attain the limit of the localization accuracy. In Table 1 we list the standard deviations of the maximum likelihood estimates of the single-molecule location for different experimental conditions typically reported in the single-molecule microscopy literature. The table also lists the limit of the localization accuracy that is calculated using Eq. 4. From the table we see that the standard deviations of the maximum likelihood estimates come reasonably close to the limit of the localization accuracy under the various experimental conditions. However, there are differences and in some cases the standard deviation of the estimates is even lower than the limit of the localization accuracy. This points to an important aspect of the theory that underlies the approach presented here. Whereas the theoretical derivations are based on considerations of the standard deviations of random variables, the simulations in Table 1 report estimates of those standard deviations, which can differ from the actual values.

TABLE 1.

Limit of the localization accuracy for the u coordinate of a single molecule

Parameter set No.	Pixel dimensions (μm × μm)	Readout noise e−/pixel (rms)	Scattering noise photons/pixel/s	Pixel array size	Acquisition time (ms)	Fundamental limit (nm)	Limit of the localization accuracy in the pixelated case in the absence of noise sources (nm)	Limit of the localization accuracy in the pixelated case with readout and scattering noise (nm)	Standard deviation of the maximum likelihood estimator (nm)
1	6.45 × 6.45	6	660	13 × 13	10	2.3010	2.9152	6.6469	6.6903
2	6.8 × 6.8	18	660	12 × 12	10	2.3010	2.9377	14.8733	14.8175
3	13 × 13	4	660	7 × 7	10	2.3010	3.4338	4.4387	4.6287
4	15 × 15	32	660	6 × 6	10	2.3010	3.9379	13.5599	13.0138
5	6.45 × 6.45	6	6600	13 × 13	100	0.7277	0.9219	2.5138	2.6835
6	6.45 × 6.45	6	660	13 × 13	100	0.7277	0.9219	1.4241	1.4059
7	6.45 × 6.45	6	0	13 × 13	100	0.7277	0.9219	1.1951	1.4174
8	6.8 × 6.8	18	660	12 × 12	100	0.7277	0.9290	1.9855	1.8245
9	13 × 13	4	660	7 × 7	100	0.7277	1.0859	1.2319	1.3837
10	15 × 15	32	660	6 × 6	100	0.7277	1.2453	1.9365	1.7012

The table shows the limit of the localization accuracy for the u coordinate of a single molecule with parameters similar to those of a GFP molecule under typical experimental conditions. The pixel dimensions and readout noise correspond to CCD cameras often used to image single molecules. For all calculations we set the photon emission rate to be A = 2 × 10⁶ photons/s, the optical efficiency to be γ = 0.033, the magnification to be M = 100, the numerical aperture to be n_a = 1.4, the emission wavelength to be λ_em = 520 nm, and the mean of the measurement noise to be zero. For a given pixel dimension, the pixel array is chosen such that 92% of the photons that reach the image plane are collected. For all calculations and simulations we assume that all pixels have the same noise statistics and the single molecule is positioned at the center of the pixel array. The standard deviation of the maximum likelihood estimator for each parameter set was calculated based on maximum likelihood estimates of the single molecule location in 300 simulated images.

In Table 1, for a given pixel size, the pixel array was chosen such that ∼92% of the photons that reach the detector plane are collected by the pixel array. Despite this, we see that the limit of the localization accuracy varies widely for different experimental conditions, especially for short acquisition times (t = 10 ms, parameter sets 1–4). If the acquisition time is increased (t = 100 ms, parameter sets 6, 8–10), we see that the variation of the limits of the localization accuracy diminishes for the different experimental conditions. In addition, the limits of the localization accuracy also come close to the fundamental limit.

So far we have shown that noise sources can significantly deteriorate the limit of the localization accuracy. It is instructive to investigate the contribution of the different noise types to the deterioration of the localization accuracy. In parameter sets 5–7 of Table 1, we show that when the scattering noise parameter is decreased from 6600 photons/pixel/s to 0 photons/pixel/s with measurement noise fixed to 6 e⁻/pixel (rms), the limit of the localization accuracy decreases from 2.5138 nm to 1.1951 nm. However, in parameter set 7 we see that if the measurement noise is also set to 0, then the limit of the localization accuracy in the noise-free case reduces to 0.9219 nm, which is significantly closer to the fundamental limit of 0.7277 nm.

Fig. 5 shows the effect of pixel size on the limit of the localization accuracy for a 1000 μm × 1000 μm pixel array at different measurement noise levels with the scattering noise parameters set to zero, i.e., b_k = 0. The figure also shows the results in the noise-free case and the fundamental limit. We consider a 1000 μm × 1000 μm pixel array to ensure that a sufficient number of photons are detected in the case of large pixels. We note that the measurement noise is independent of the number of detected photons and only depends on the readout process of the CCD camera. Hence it is kept fixed when the pixel size is varied. However, because the number of pixels decreases as the pixel size increases, less noise is added to the total accumulated data. In the noise-free case the limit of the localization accuracy decreases with decreasing pixel size, because with reduced pixel sizes the effect of pixelation diminishes and the limit of the localization accuracy approaches the fundamental limit. However, in the presence of measurement noise the limit of the localization accuracy first decreases but then increases with decreasing pixel size, because by decreasing the pixel size the number of detected photons in each pixel decreases, whereas the measurement noise remains the same.

FIGURE 5.

Limit of the localization accuracy of the u coordinate of a single molecule with experimental parameters similar to those for a GFP molecule as a function of pixel size for a pixelated detector in the presence of measurement noise. ⋄ corresponds to a readout noise (σ_k) of 57 e⁻/pixel (rms), ○ corresponds to a readout noise (σ_k) of 7 e⁻/pixel (rms), and the scattering rate (b_k) is set to 0 in both the cases. The limit of the localization accuracy in the noise-free case (•) and the fundamental limit (solid line) are also shown for reference. For all the plots the acquisition time is set to be t = 0.05 s and the pixel array size is 1000 μm × 1000 μm. The pixel sizes were chosen such that the pixel array consists of an odd number of rows and columns.

We recall that a similar behavior was observed in Fig. 3 due to the variation in magnification. However, the present effect is different from that shown in Fig. 3, because by varying the magnification the size of the single molecule image was varied and this in turn affected the number of photons captured by the pixel array. In the present case, the pixel array is fixed to 1000 μm × 1000 μm ensuring that the same number of photons are captured by the pixel array for all pixel sizes. From this we deduce that for a given experimental setup, the limit of the localization accuracy depends not only on the total number of detected photons but also on the number of photons captured in each pixel in the pixel array. We note that an analogous behavior was reported in Thompson et al. (2002), where the effect of pixel size on the localization accuracy was discussed for a specific estimation procedure.

We next consider the effect of the location of the single molecule with respect to the pixel array on the limit of the localization accuracy. Fig. 6 a shows the variation of the limit of the localization accuracy as a function of the single molecule position for a 5 × 5 pixel array with a pixel size of 20 μm × 20 μm for high measurement and scattering noise levels. Fig. 6 b shows the same for low measurement and scattering noise levels. In both figures, the result for the noise-free case is also shown for reference. From Fig. 6, a and b, we observe that the localization accuracy varies periodically as the single molecule is moved along the x direction. The best, i.e., the smallest, values for the limit of the localization accuracy are achieved when the image of the single molecule is centered on the edge of a pixel. This is due to the fact that small changes in the location of the single molecule at the edge of a pixel lead to significant changes in the collected data. The worst, i.e., largest, values for the limit of the localization accuracy are achieved when the image of the single molecule is located at the center of a pixel. From Fig. 6, a and b, we see that the worst case value can be anywhere between 10%–80% higher than the best case value depending on the noise level. Note that the variation of the limit of the localization accuracy is particularly pronounced for large pixel sizes. This periodicity for a pixelated detector is in contrast to the fundamental limit (Eq. 2), which is independent of the location of the single molecule. As shown in Fig. 6 c, by reducing the pixel size the effect of pixelation is diminished and hence the periodic variation in the localization accuracy also decreases. An immediate implication of the above result is that moderate variations in the single-molecule position within a pixel can lead to substantially different localization accuracy values in the presence of high noise levels. This analysis also provides an explanation of the phenomenon that was reported in Cheezum et al. (2001), where it was observed using numerical investigations that the localization accuracy depends on the location of the single molecule with respect to the pixels. It should be noted that other published expressions for the localization accuracy (Kubitscheck et al., 2000; Thompson et al., 2002) do not show a dependence on the magnification and on the location of the single molecule. This is due to approximations that were used in the model for the acquired signal in the pixels.

The results presented in this section give an indication as to the type of phenomena that can be investigated with our approach. Further applications are easily conceivable such as the evaluation of the effect of pixel shape or the presence of dead space regions on the detector (e.g., due to the presence of antiblooming gates) on the limit of the localization accuracy. Although the expressions for the limit of the localization accuracy in the pixelated case are not as straightforward to analyze as the expression for the fundamental limit they can be numerically evaluated in a relatively straightforward way.

Generalization of the fundamental limit

In deriving the fundamental limit of the localization accuracy we assumed that the time points of the photon emission process are Poisson distributed and that the image of a single molecule is described by the classical description of the point-spread function. We now generalize this result and present an expression for the limit of the localization accuracy for the detection of an object whose time points of the emitted photons are described by a general counting process N(t), t ≥ 0, and whose image is described by a profile f_θ(r) ≔ (1/M²)q(r/M − θ), r ∈ ℜ², where q is a general image function. An image function describes the image of an object on the detector that is located at the center of the coordinate system and is imaged through a lens with unit magnification (i.e., M = 1). The limit of the localization accuracy for the general setting for the u coordinate of the object (the expression for the v coordinate is analogous) is where I⁻¹(θ) is the inverse of the Fisher information matrix given by (see Appendix for the derivation)

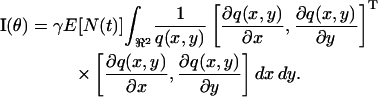(5)

If the image function q is symmetric (i.e., q(x, y) = q(−x, y) = q(x, −y), x, y ∈ ℜ) the off-diagonal entries of the Fisher information matrix will be zero and the generalized localization accuracy for the u coordinate is given by (see Appendix for the derivation)

(6)

From the above expressions we note that the generalized limit of the localization accuracy depends only on the expectation value of the photon-emission process and on an integral involving the image function and its derivative. This explains the occurrence of the term γAt in the fundamental limit (Eq. 2) as γAt is the expected number of detected photons assuming a Poisson emission process with rate A. Based on the results in Bobroff (1986) an expression was given in Betzig (1995) that has a formal resemblance to the expression in Eq. 6. Despite this formal similarity it appears that the expressions cannot be reconciled, for example, due to the fact that the constants and the domain of integration do not match.

The general expressions (Eqs. 5 and 6) presented above can be used to calculate the limit of the localization accuracy for specific image functions such as the Gaussian profile. The two-dimensional Gaussian profile has been widely used to approximate the point-spread function (Schütz et al., 1997b; Kubitscheck et al., 2000; Kues et al., 2001; Cheezum et al., 2001; Thompson et al., 2002). A normalized two-dimensional Gaussian image function is given by 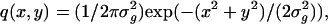x, y ∈ ℜ, σ_g > 0. Using Eq. 6 the limit of the localization accuracy is given by (see Appendix for the derivation)

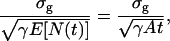where in the last equality we assumed that the time points of the emitted photons are Poisson distributed. The typical approximation of the point-spread function (with parameters n_a = 1.4 and λ_em = 520 nm) by a Gaussian profile using least-squares approximation (with the Marquardt-Levenberg Algorithm; Coleman et al., 1999) yields a value of σ_g = 81.73 nm. For an acquisition time of 10 ms and γA = 66,000 photons/s, the fundamental limit of the localization accuracy for the point-spread function is 2.30 nm, whereas for the Gaussian profile it is 3.18 nm. This shows a significant difference between the expressions for the localization accuracies of the two image functions despite one being the best approximant of the other in a least-squares sense. It should be noted, however, that both the Airy profile and the Gaussian profile are normalized to have an integral of one. Therefore the approximation of an Airy profile by a Gaussian is not as good as would be the case if the prefactor of the Gaussian was not constrained.

However, if an image profile is in fact Gaussian, significant advantages exist (see Appendix). The center of gravity estimator can be computed in a straightforward manner by calculating the mean (adjusted for the magnification of the lens) of the coordinates of the detected photons (Cheezum et al., 2001; Ghosh and Webb, 1994; Goulian and Simon, 2000). In our stochastic setting, if the image profile is Gaussian the center of gravity estimator is a maximum likelihood estimator. Therefore it has the generally good statistical properties of a maximum likelihood estimator, while at the same time being straightforward to calculate, which is typically not the case for a maximum likelihood estimator. Moreover, this estimator is unbiased (i.e., its mean attains the correct result) and its variance is equal to the inverse of the Fisher information matrix if the total number of detected photons is assumed to be known (see Appendix). This implies that in this case the center of gravity estimator perfectly attains the limit of the localization accuracy, even for small photon count numbers, i.e., it has the best possible properties according to our criteria. Note that here we have considered the pixel-free case. Others (Cheezum et al., 2001) have shown that the center of gravity estimator can be biased due to the potentially nonsymmetric averaging and sampling of the profile that occurs due to pixelation.

Assuming that the number of detected photons is known also leads to an improvement of the maximum likelihood estimator when the image profile is the point-spread function. This is shown in Fig. 2 where the maximum likelihood estimator is calculated for two different acquisition methods, one when the acquisition time is fixed and the other when the total number of detected photons is fixed. From the figure we see that the standard deviation in the latter case is smaller than in the former case, because by fixing the total number of detected photons in every image we reduce the stochasticity of the experimental data and hence gain in terms of the performance of the estimator.

It is occasionally suggested that the localization accuracy is given by 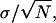where N is the number of detected photons and σ is the standard deviation corresponding to the point spread function profile. The above results show that this is indeed correct if the profile is Gaussian. However, in general this may not be correct for other profiles because the integral expression in Eq. 6 does not necessarily reduce to the variance of the distribution.

Although we will not state explicit expressions, it should, however, be noted that expressions analogous to Eq. 5 can be derived for the effects of pixelation and noise on the limit of the localization accuracy for a general image function. The corresponding expressions for the Fisher information matrix are stated in the Appendix.

The results given in this paper can be employed in several ways in the context of single molecule microscopy. For instance, a concrete experimental setting can be evaluated to see how close it can come to achieving the fundamental limit of the localization accuracy. Moreover, these expressions can be used as a standard against which algorithms can be evaluated that are used to estimate the location of single molecules from images. The discussion concerning a general image profile is not only of importance in the analysis of the localization accuracy in single-molecule microscopy. In fact, these expressions can be used to determine the localization accuracy for any object with a known image function that is imaged by a lens.

APPENDIX

Fundamental limit of the localization accuracy

In this section we discuss the technical details of the stochastic data-generation process and the derivation of the results on the fundamental limit of the localization accuracy. The counting process that describes the time points of photon emission from the single molecule is denoted by N(t), t ≥ 0. The spatial coordinates of the detected photons are independent and identically distributed random variables with density function where r ∈ ℜ², q is an image function, M denotes the magnification of the lens, and θ denotes the position of the single molecule in the specimen plane. Due to the finite transmission efficiencies of the optical components in the light path, some of the photons emitted from the single molecule are randomly deleted with probability 1 − γ and only the remaining fraction of emitted photons are detected by the detector, where γ denotes the overall efficiency of the detection system (i.e., microscope optics and detector).

We assume that the counting process and the random variables that describe the spatial coordinates are mutually independent. Given the observed data, i.e., the spatial coordinates and the time points of the detected photons, the location θ of the single molecule in the specimen plane is to be estimated. For this data-generation process, we first derive a general expression for the Fisher information matrix and then give the results for the specific cases of the point-spread function and the Gaussian profile.

The general expression for the Fisher information matrix is given by (Rao, 1965; Zacks, 1971; Kay, 1993)

(7)

where E[·] denotes the expectation operation with respect to the underlying density function f_θ and the log-likelihood function is given by

Here denotes the observed data with z_k ≔ (r_k, t_k), where r_k ≔ (x_k, y_k) denotes the spatial coordinates of the k^th detected photon and t_k, denotes the arrival time of the k^th detected photon, 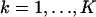. In the above expression Z(·) denotes the counting process that describes the times at which the photons are detected.

For the present discussion, it is assumed that the density function f_θ satisfies the regularity conditions (Rao, 1965; Zacks, 1971) that are necessary for the calculation of the Fisher information matrix. It can easily be verified that for the specific special cases of the Gaussian profile and the point-spread function, the regularity conditions are satisfied. A straightforward calculation shows that the Fisher information matrix I(θ) is given by

(8)

If we further assume that the image function is symmetric (i.e., q(x, y) = q(−x, y) = q(x, −y), x, y ∈ ℜ) it can be easily verified that the off-diagonal terms of the Fisher information matrix are zero.

Using Eq. 8 we now derive the fundamental limit of the localization accuracy for the point-spread function and the Gaussian profile. We assume that the counting process N(·) is a Poisson process with rate A (i.e., E[N(t)] = At). We first consider the point-spread function given by 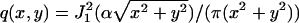, (x, y) ∈ ℜ², where α = (2πn_a)/λ_em. Since q is symmetric [I(θ)]₁₂ = [I(θ)]₂₁ = 0. The derivative of q with respect to x is given by

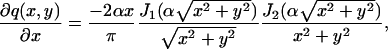where we used the recurrence relations for Bessel functions given in Watson (1958). Using an integral identity for Bessel functions (Watson, 1958) we have

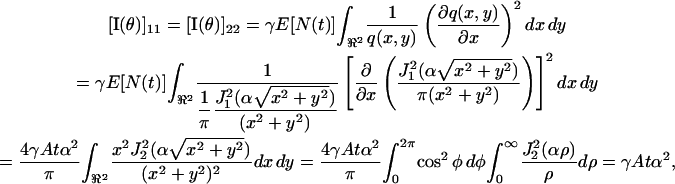where x = ρ cos φ and y = ρ sin φ. Similarly we show that [I(θ)]₂₂ = γAtα². Then the fundamental limit of the localization accuracy of the single molecule is given by the square root of the diagonal elements of the inverse Fisher information matrix, i.e.,

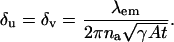Next we consider the Gaussian profile given by 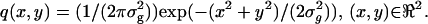Due to symmetry, the off-diagonal terms of the Fisher information matrix are zero and we have

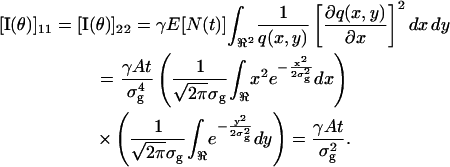Therefore the limit of the localization accuracy for a Gaussian profile is given by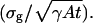

In the previous result we had assumed that the observed data was acquired for a fixed time t. Because the photon detection process is a random process, the number of detected photons for every image will vary in repeated experiments. We now show that if the detector can be set to acquire a fixed number of photons several advantages exist in case the image function is a Gaussian profile. A derivation that is analogous to the above shows that the corresponding expressions for the Fisher information matrix and the limits of the localization accuracy can easily be obtained from the earlier expressions by replacing the terms γE[N(t)] and γAt, respectively, by N₀, the number of detected photons.

In the remainder of this derivation we assume the image function q to be a Gaussian profile. The log-likelihood function for the underlying data generation process is given by 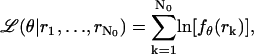where 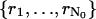, r_k ≔ (x_k, y_k) ∈ ℜ² for 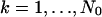denotes the observed data. The maximum likelihood estimator 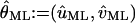of θ = (u, v) is obtained by solving the equation

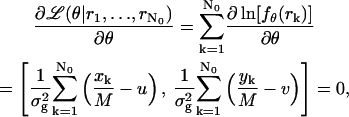and is given by

which is nothing but the center of gravity estimator.

We can easily verify that is an unbiased estimator of θ, i.e., 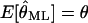and that the (co-)variance of is given by

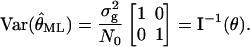This shows that in the case of a Gaussian profile, the variance of the center of gravity estimator is equal to the inverse of the Fisher information matrix (i.e., it is an efficient estimator). This means that the center of gravity estimator has the best possible properties according to our criteria. See also Snyder and Miller (1991) where an analogous derivation was carried out for a laser tracking problem in the context of optical communications.

Effects of pixelation and noise

Imaging detectors have pixels and the experimental data are often corrupted by various noise sources. These experimental effects lead to a modification of the description of the stochastic data-generation process. We assume that the detector is made up of a set of pixels 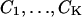and that the noise sources that are considered are additive Poisson noise and additive Gaussian noise. The acquired image is denoted by 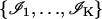where denotes data acquired in the k^th pixel, θ denotes the unknown position of the single molecule, S_θ, _k is a Poisson random variable with mean 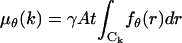with f_θ is given in Eq. 1, B_k is a Poisson random variable with mean b_kt, t denotes the acquisition time, and W_k is a Gaussian random variable with mean η_k and variance . We further assume that S_θ, _k, W_k, and B_k are independent random variables for .

We consider three scenarios, namely the noise-free case, the presence of Poisson noise and the presence of both Gaussian and Poisson noise. The limit of the localization accuracy for each of the above cases is obtained by calculating the square root of the inverse of the Fisher information matrix (Eq. 7). To calculate the latter, the log-likelihood function ℒ needs to be specified. This is given in terms of the logarithm of the joint probability density function of the observed data. In the following results we set θ₁ ≔ u, θ₂ ≔ v and the Fisher information matrix I(θ) is a 2 × 2 matrix.

Fisher information matrix for the noise-free case

The following expression for the Fisher information matrix in the noise-free case follows from the application of a well-known result for the Fisher information matrix for Poisson random variables (see, e.g., Snyder and Miller, 1991, and Kay, 1993) to our situation.

(9)

Similar to Eq. 8 the Fisher information matrix depends on the integral of the density function f_θ(r) that characterizes the image profile.

Fisher information matrix for the Poisson noise case

This next expression gives the Fisher information matrix for the situation when the data in each pixel is corrupted by Poisson noise of mean b_kt, 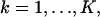such as due to scattered photons or cellular autofluorescence. Because this noise component is assumed to be stochastically independent of the data due to the photon emission of the single molecule, the number of photons collected in the k^th pixel is Poisson distributed with mean μ_θ(k) + b_kt for 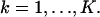We also assume that the noise component is independent of the location of the single molecule. Analogously to the way the Fisher information matrix was obtained in the noise-free case we therefore have that

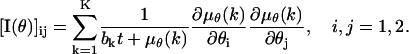Note that by setting b_k = 0, 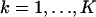, we obtain the Fisher information matrix for the noise-free case. The resulting expression for the limit of the localization accuracy is given in Eq. 3.

Fisher information matrix for the Poisson and Gaussian noise case

The Fisher information matrix for a pixelated dectector in the presence of independent Poisson noise with mean b_kt and independent Gaussian noise with mean η_k and variance , is given by

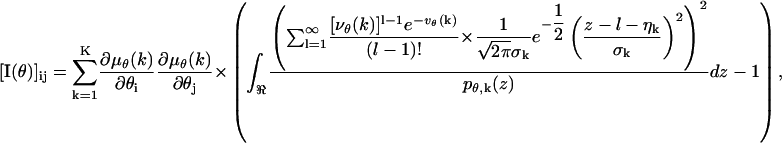where i, j = 1, 2 and

(10)

with ν_θ(k) ≔ μ_θ(k) + b_kt for 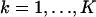. The derivation of this expression is based on the fact that the probability density function of a sum of a Poisson and independent Gaussian random variable is given by Eq. 10 (Snyder et al., 1995). The log-likelihood function ℒ can then be calculated. Substituting for ℒ in Eq. 7 we obtain the above result. The resulting expressions for the limit of the localization accuracy are given in Eq. 4.