Abstract
Interest centers here on whether a polyproline II helix can propagate through adjacent non-proline residues, and on shedding light on recent experimental observations suggesting the presence of significant PPII structure in a short alanine-based peptide with no proline in the sequence. For this purpose, we explored the formation of polyproline II helices in proline-rich peptides with the sequences Ac-(Pro)3-X-(Pro)3-Gly-Tyr-NH2, with X = Pro (PPP), Ala (PAP), Gln (PQP), Gly (PGP), and Val (PVP), and Ac-(Pro)3-Ala-Ala-(Pro)3-Gly-Tyr-NH2 (PAAP), by using a theoretical approach that includes a solvent effect as well as cis ↔ trans isomerization of the peptide groups and puckering conformations of the pyrrolidine ring of the proline residues. Since 13C chemical shifts have proven to be useful for identifying secondary-structure preferences in proteins and peptides, and because values of the dihedral angles (φ,ψ) are the main determinants of their magnitudes, we have, therefore, computed the Boltzmann-averaged 13C chemical shifts for the guest residues in the PXP peptide (X = Pro, Ala, Gln, Gly, and Val) with a combination of approaches, involving molecular mechanics, statistical mechanics, and quantum mechanics. In addition, an improved procedure was used to carry out the conformational searches and to compute the solvent polarization effects faster and more accurately than in previous work. The current theoretical work and additional experimental evidence show that, in short proline-rich peptides, alanine decreases the polyproline II helix content. In particular, the theoretical evidence accumulated in this work calls into question the proposal that alanine has a strong preference to adopt conformations in the polyproline II region of the Ramachandran map.
INTRODUCTION
A nonstructured conformation of a polypeptide, the so-called statistical-coil state, corresponds to an energy-weighted ensemble of conformations in which a single residue can occupy any of the regions of the Ramachandran map (Ramachandran et al., 1963) with a certain probability specified by the Boltzmann distribution (Vila et al., 2002). This definition at the residue level is no longer valid for oligopeptides or polypeptides in which interresidue interactions introduce additional energetic contributions. Long-range and sequence-dependent interactions render the statistical-coil definition inapplicable for a polypeptide, i.e., a nonstructured state of an oligopeptide or polypeptide is then a collective property, and corresponds to an energy-weighted ensemble of conformations in which the sequence can occupy any accessible region in the conformational space.
Whether or not the most populated region occupied by oligopeptides or polypeptides in a nonstructured state is the left-handed polyproline II (PPII) conformation has been the object of much discussion, as in an early review by Woody (1992), and in numerous recent articles and reviews (Creamer, 1998; Sreerama and Woody, 1999; Stapley and Creamer, 1999; Kelly et al., 2001; Rucker and Creamer, 2002; Shi et al., 2002a,b; Pappu and Rose, 2002). Among the experimental studies, Kelly et al. (2001) examined the conformational preferences of some naturally occurring amino acids and used circular dichroism (CD) to study the left-handed PPII-helix. In particular, Kelly and co-workers used a host-guest technique based on the sequences Ac-(Pro)3-X-(Pro)3-Gly-Tyr-NH2, with X = Pro (PPP), Ala (PAP), Gln (PQP), Gly (PGP), Leu (PLP), Met (PMP), Ile (PIP), Val (PVP), Asn (PNP), and Ac-(Pro)3-Ala-Ala-(Pro)3-Gly-Tyr-NH2 (PAAP) to derive an intrinsic propensity scale for the PPII-helical conformation, and to examine whether the helix is propagated through two adjacent alanines. Their experiments showed that the decrease of the PPII helix content in going from PPP to PAP to PAAP is nonlinear with respect to the number of alanines, i.e., the difference between PAP and PAAP (9%) was greater than that between PPP and PAP (3%). Despite this nonlinearity, Kelly and co-workers suggested possible reasons that could influence the conformational preferences of alanine residues when they are flanked by prolines; based on these possible reasons, they suggest that 1), PAAP still possesses significant PPII character; 2), alanine has a relatively high intrinsic propensity to adopt this structure; and 3), the PPII helix can propagate through two adjacent non-proline residues.
Theoretical studies of proline-rich peptides were carried out recently by Creamer (1998), who simulated a series of peptides with the sequences Ac-Ala-(Pro)3-X-(Pro)3-Ala-NMe (with X = Ala, Val, Leu, Phe, and Gly). These simulations employed the following approximations: 1), a hard sphere potential with a united-atom approximation, i.e., the hydrogens attached to carbon atoms were not treated explicitly; 2), excluded-volume effects with no attractive components, i.e., a hard-sphere potential with only two possible energy states—zero when there are no atomic overlaps, or infinite energy when atoms overlap; 3), no solvent was included in the calculations; 4), only the trans-conformation of proline was considered, i.e., neither proline cis ↔ trans isomerization nor ring puckering were considered. The amino acid sequence used by Creamer (1998) was similar, but not identical, to the one studied by Kelly et al (2001). Of all the approximations used by Creamer (1998), the neglect of both solvent effects and cis ↔ trans isomerization should be emphasized, since it is well known that 1), solvent effects play an important role in conformational transitions in polypeptides and proteins, in particular in polyprolines; i.e., there is both theoretical (Tanaka and Scheraga, 1975a,b) and experimental (Steinberg, et al., 1960; Gornick et al., 1964; Mandelkern 1967; Strassmair et al., 1969) evidence that solvent effects plays a dominant role influencing the form I → form II transition in poly(L-proline) and 2), that the cis ↔ trans isomerization around the X-Pro peptide groups plays a key role in the rate-determining steps of protein folding (Brandts et al., 1975). The cis and trans forms of proline peptide groups are almost isoenergetic, with the trans form being slightly more favorable, and small peptides exhibit a mixture of cis and trans forms (Wüthrich, et al., 1974; Zimmerman and Scheraga, 1976); hence, consideration of the cis-trans conversion cannot be neglected in any theoretical analysis of proline-rich peptides. Moreover, these properties of the peptide group are important not only in oligopeptides and globular proteins but also in homopolymers of proline, i.e., polyproline I is all cis in a right-handed helical conformation whereas PPII is all trans in a left-handed helical conformation, depending on the solvent (Steinberg, et al., 1960).
The all-trans conformation lies near φ = −78°, ψ = 146° (Cowan and McGavin, 1955), which falls in the F region defined by Zimmerman et al. (1977) as −110° ≤ φ ≤ −40° and 130° ≤ ψ ≤ 180° in the map of Ramachandran et al. (1963). The nearby E region encompasses the β-pleated-sheet structure (Arnott et al., 1967). We assign a PPII conformation to any residue in the F region. The CD spectrum of the PPP peptide exhibits a maximum at 228 nm and a minimum at 205 nm (Kelly et al., 2001), characteristic of a PPII helix formed by a polyproline peptide in aqueous solution (Woody, 1992). Significantly smaller molar ellipticity may indicate shorter helices and/or larger deviations from the long PPII helix conformation (Ma et al., 2001). The corresponding CD spectrum of a β-sheet structure typically has positive and negative bands at ∼195 and 218 nm, respectively (Sreerama and Woody, 2003).
In this article, we have carried out a detailed theoretical study of the oligopeptides studied by Kelly et al. (2001) to 1), understand whether a polyproline II helix can propagate through adjacent non-proline residues and 2), shed light on the recent experimental observations by Shi et al. (2002a,b), showing the presence of significant PPII structure in a short alanine-based peptide in a non-prolyl environment.
METHODS
The general procedure
In this work, we generated ensembles of conformations of the oligopeptides studied by Kelly et al. (2001), and computed their Boltzmann-averaged chemical shifts to provide a test of the conformational preferences predicted in our simulations. The conformations were generated at pH 7 with the electrostatically driven Monte Carlo (EDMC) method (Ripoll and Scheraga, 1988; Ripoll et al., 1996). An all-atom representation of the chain was used with the ECEPP/3 force field (Momany et al., 1975; Némethy et al., 1983, 1992; Sippl et al., 1984) and explicit consideration of 1), cis ↔ trans isomerization of the peptide group for proline residues; 2), both up (U) and down (D) puckering conformations of the pyrrolidine ring, which pertain to the (φ = −53.0° and χ1 = −28.1°) and (φ = −68.8° and χ1 = 27.4°) positions, respectively, of the Cγ atom of the proline residue; and 3), conformational entropy, by following the approach of Gō and Scheraga (1969) and Zimmerman et al. (1977) as implemented in EDMC.
To investigate the role of the solvent in the conformational preference for the helical PPII conformation, alternative forms of the potential energy function were used to evaluate the total free energy. Gas-phase (GP) representations, i.e., the ECEPP/3 potential, with omission of solvent effects, were used. These gas-phase simulations provide a basis for comparison with the two solvation models used here, namely, a gas-phase potential represented by ECEPP/3 with a solvent-accessible surface area model, or GPSAS (Vila et al., 1991) to represent the interaction with the solvent; and a gas-phase potential represented by ECEPP/3 combined with a fast multigrid boundary element (MBE), i.e., GPSP, method to account for the solvation free energy and solvent polarization effects as well as the equilibrium binding of protons and its dependence on environmental conditions (Vorobjev et al., 1994, 1995; Vorobjev and Scheraga, 1997). These approaches provide a solution to the problem of ionization equilibria (Bashford and Karplus, 1990; Yang et al., 1993; Yang and Honig, 1993; Gilson, 1993; Beroza et al., 1995; Vila et al., 1998).
Evaluation of the total free energy
Three alternative forms were used to compute the total free energy as a function of the coordinates rp; viz., a gas phase potential (GP),
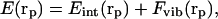 |
(1) |
where Eint(rp) is the internal conformational energy of the molecule in the absence of solvent, assumed to correspond to the ECEPP/3 energy (Némethy et al., 1992) of the neutral molecule, and Fvib(rp) is the conformational entropy contribution. The contribution from Fvib(rp) to the total free energy has been treated by a harmonic vibrational approximation (Gō and Scheraga, 1969; Zimmerman et al., 1977) for each conformation obtained by using the ECEPP/3 potential function.
The next form is a gas phase potential plus a solvent-accessible surface area model (GPSAS),
 |
(2) |
where Fsas(rp) represents the solvation free energy as defined by Vila et al. (1991), and the third form is a gas phase potential combined with the MBE method (GPSP),
 |
(3) |
where Fcav(rp) is the free energy associated with the process of cavity creation when transferring the molecule from the gas phase into the aqueous solution; Fsolv(rp) is the free energy associated with the polarization of the aqueous solution; and Finz(rp, pH) is the free energy associated with the change in the state of ionization of the ionizable groups due to the transfer of the molecule from the gas phase to the solvent, at a fixed pH value.
Fcav(rp) describes the free energy of creation of a cavity to accommodate a zero-charge peptide molecule, i.e., with all partial atomic charges set to zero. As shown previously (Sitkoff et al., 1994; Simonson and Brünger, 1994), Fcav(rp) can be considered as the free energy of transfer of a nonpolar molecule from the gas phase to water. This free energy is proportional to the solvent-accessible surface area of the molecule. The term Fsolv(rp) is obtained by using the fast MBE method, and Finz(rp, pH) is calculated by using general multisite titration formalism (Bashford and Karplus, 1990; Yang et al., 1993; Vorobjev et al., 1994).
Conformational search
A full search for the global minimum of the function represented by Eq. 3 requires the energy minimization of thousands of conformations, which is beyond current computational capabilities. For this reason, a protocol that produces a reasonable sampling of the conformational space, defined by E(rp, pH) without minimizing this particular function, is used (Vila et al., 2003). The protocol that we previously used (Ripoll et al., 1996; Vila et al., 2002, 2003) involved energy minimization of an approximate form of E(rp, pH), viz., (Eapprox(rp)), given by Eint(rp), by using the secant unconstrained minimization solver algorithm (Gay, 1983). In this work, Eapprox(rp) is represented by
 |
(4) |
where FGB(rp) represents the pairwise Generalized Born (GB) solvation model of Hawkins et al. (1996), from the laboratory of D. A. Case, as implemented by Ghosh et al. (2002). This implementation of the pairwise GB solvation model includes analytical derivatives with respect to atomic coordinates, keeping the effective Born radii fixed.
The term FGB(rp) is a good representation of the free energy of solvation Fsolv(rp) used in Eq. 3, since this approximate solution of the Poisson-Boltzmann, as given by the GB model, has been shown to give results that are close to the exact solution (Tsui and Case, 2001; Onufriev et al., 2002). Consequently, the new protocol is expected to provide better results than the procedure used previously (Vila et al., 1998, 2001, 2002), i.e., when Eapprox(rp) = Eint(rp).
It should be pointed out that, during the calculation with the GPSP approach, the total free energy, E(rp, pH), of the conformations is always computed by Eq. 3, i.e., by computing the solvent polarization effects with the fast MBE method, even though the conformational search was carried out with Eq. 4, i.e., with the GB potential.
Clustering analysis
Classification of the accepted conformations listed in Table 1 was carried out with the clustering procedure used by Vila et al. (2003) to study statistical-coil peptides in solution, i.e., through a minimal tree (the minimal spanning tree method described by Ripoll et al., 1999), and then the minimal tree was partitioned in terms of a specified root mean-square deviation (RMSD) cutoff, leading to a given number of families. The families resulting from the RMSD clustering procedure were ranked in increasing order according to their total free energy, given by Eq. 1. For each family, we evaluated both the number of conformations belonging to that family and the set of dihedral angles of the lowest-energy conformation. We refer to the lowest-energy conformation of a family as the leading member. The Boltzmann averages over all the families for a given peptide were computed by using only the leading member of each family. A cutoff of 2 Å RMSD between all heavy atoms in the peptides PXP and PAAP, with no cutoff in the energy, was used during the clustering procedure. As shown previously (Vila et al., 2003), higher-number clusters, i.e., these with higher energy, will not make any significant contribution to the Boltzmann average because the leading members of such families are much higher in energy than the leading members of lower-number clustered families. For this reason, we chose a cutoff in the total number of cluster families for each amino acid X; i.e., we considered only those families that represent >95% of the total number of accepted conformations. The reduced number of ensembles of conformations that meet this criterion are listed in parentheses in the last column of Table 1.
TABLE 1.
Summary of the EDMC runs
| Peptide sequence* | Number of energy-minimized conformations† | Number of accepted conformations‡ | Zimmerman code of the lowest energy conformation§ | Number of cluster families¶ |
|---|---|---|---|---|
| PPP∥ | 135,222 | 2049 | FFFFFFADD | 77 |
| PPP** | 35,360 | 1000 | FFFFFFADA | 16 |
| PPP†† | 54,871 | 1091 | FFFFFFAAD | 23 (8) |
| PAP∥ | 129,533 | 1798 | FFCDFFADD | 80 |
| PAP** | 124,383 | 2000 | FFADFFADA | 26 |
| PAP†† | 53,675 | 1243 | FFFF*FFAAF | 45 (4) |
| PAAP∥ | 154,277 | 1875 | FFAAFFFCD*D | 99 |
| PAAP** | 147,092 | 2000 | FFAADFFADA | 46 |
| PAAP†† | 107,148 | 2363 | FFAA*A*FFACG | 74 (3) |
| PQP∥ | 178,308 | 2154 | FFAEFFAA*D | 90 |
| PQP** | 122,601 | 2078 | FFADFFADA | 23 |
| PQP†† | 66,747 | 1774 | FFAA*FFFAF | 72 (7) |
| PGP∥ | 162,930 | 2345 | FFFD*FFAGF | 105 |
| PGP** | 145,665 | 3000 | FFADFFADA | 30 |
| PGP†† | 64,634 | 1478 | FFADFFAAA | 46 (5) |
| PVP∥ | 184,106 | 1921 | FFCDFFADD | 86 |
| PVP** | 127,073 | 2629 | FFADFFADA | 29 |
| PVP†† | 114,613 | 3128 | FFAAFFACA | 45 (9) |
PXP and PXXP represent the X residue in the sequence Ac-PPPXPPPGY-NH2 (for X = Pro, Ala, Gln, Gly, and Val) and Ac-PPPXXPPPGY-NH2 (for XX = AlaAla), respectively.
These values correspond to the total number of generated conformations for the runs with three different force fields as explained in Methods and footnotes ∥, **, and ††, using the procedure described in Methods.
According to the Metropolis criterion.
For the leading member of family 1. Conformations are classified in terms of the regions of the φ−ψ Ramachandran (Ramachandran et al., 1963) map in which they occur (Zimmerman et al., 1977). On the left-hand half of the map (φ < 0°), the regions are defined as A–G; on the right-hand half of the map (φ ≥ 0°), the regions are defined by inversion of the left-hand half around the center of the map, and an asterisk is appended to the letters. The conformation of the guest residues are underlined. One of the alanines of PAAP in the PPII region (Zimmerman code F) is shown in boldface.
Total number of families after a minimal-tree cluster analysis of all accepted conformations, i.e., those listed in column 3 within a cutoff of 2 Å RMSD over all heavy atoms in the PXP and PAAP peptides, with no cutoff in energy. The number of cluster families containing >95% of the total accepted conformations is given in parentheses only for those peptides for which the Boltzmann-averaged 13C chemical shifts were computed as explained in Methods.
The calculations were carried out by using a GP potential, as explained in Methods.
The calculations were carried out by using a GPSAS potential, as explained in Methods.
The calculations were carried out at pH 7 at t = 25°C by using the GPSP potential, as described in Methods. The value of 10.10 was adopted as the 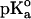 for the ionizable group of the Tyr residue, as an average from the data of Perrin (1972).
for the ionizable group of the Tyr residue, as an average from the data of Perrin (1972).
As can be seen from Table 1 (column 5), the number of families for each amino acid ranges from 105 (glycine) to 16 (proline). These upper and lower limits in the number of family clusters found for the peptides PXP indicate that the presence of proline as a guest residue, i.e., X = Pro, results in a much more extremely rigid conformation than the one that corresponds to X = Gly, no doubt because glycine is the more conformationally unrestricted residue of the 20 naturally occurring amino acids.
Quantum-chemical calculations of the 13C chemical shift
The conformations of the PXP and PAAP molecules, employed for calculating the 13C shielding, corresponded to the leading members of each family. These conformations were not energy-minimized at the quantum chemical level of theory because such geometry-optimized structures lead only to very small additional effects on the computed shielding (Sun et al., 2002; Vila et al., 2002). However, these conformations represent energy-minimized structures obtained with the geometries defined by the ECCEP/3 force field.
All 13C shielding calculations were carried out by using a hybrid density functional level of theory (Parr and Yang, 1989) with the gauge-independent atomic orbitals procedure (Wolinski et al., 1990) as implemented in the Gaussian 98 program (Frisch et al., 1998). The selected (hybrid density functional level of theory) B3LYP methods employed two different exchange-correlation functionals—Becke's three-parameter functional (Becke, 1993) in combination with nonlocal correlation provided by the Lee-Yang-Parr expression (Lee et al., 1988), which contains both local and nonlocal terms. This functional has proven to be a very good choice to predict 13C magnetic shielding tensors as proposed by Cheeseman et al. (1996).
Since NMR shielding tensors are predominantly local properties, it is possible to obtain theoretical shielding values of good quality by using large basis sets located only on the atoms whose shifts are of interest, whereas the rest of the atoms in the molecule are given more modest bases (Chesnut and Moore, 1989). This is called the locally dense basis approach, and its use enables us to minimize the length of the chemical-shift calculations while maintaining the accuracy of the results. This approach has been revised by Laws et al. (1995), who concluded that the results correlate very well with calculations using a very large basis set, although the time is significantly reduced. In the present work, the X and the Ala residues in the PXP and PAAP peptides, respectively, were treated with a 6−311+G(2d,p) locally dense basis set, whereas the remaining residues in the molecule were described by a 3−21G basis set. These basis-set notations refer to those of Pople and co-workers (Hehre et al., 1986), as implemented in the Gaussian 98 program (Frisch et al., 1998). Recently, by using the locally dense approximation, Sun et al. (2002) found good agreement between theory and experiment, making its use very attractive for treating large systems such as the peptides studied in this work. The reason for such good agreement between theory and experiment, by using the locally dense approximation, resides in the physical basis of the chemical shift effect, i.e., as noted by Chesnut and Moore (1989): “the chemical shift is sensitive to the electron distribution near the resonant nucleus and therefore requires a good description of that distribution in the vicinity of the resonant nucleus and a lesser description further away…”.
To enable us to compare calculated and experimental values of chemical shifts (δ), the calculated 13C chemical shielding isotropic tensors (σiso) were converted to a tetramethylsilane (TMS) shift scale by using the equation δ = 182.48 − σiso, where the 182.48 value represents the 13C shielding of TMS obtained by using B3LYP/6-311 + G(2d,p)//B3LYP/6 − 31G(d) geometry. The corresponding experimental value for the 13C shielding of TMS is σTMS,exp = 188.1 ppm (Jameson and Jameson, 1987).
To test the locally dense approach used here, we compared 13C chemical shifts calculated recently (Vila et al., 2002) for the unblocked tetrapeptide GGXA by using a uniform basis set, i.e., 6−311+G(2d,p) over all residues, with the ones obtained using the locally dense approximation, i.e., in which the X residue is treated with a 6−311+G(2d,p) locally dense basis set, whereas the remaining residues in the unblocked tetrapeptide were described by a 3−21G basis set. Fig. 1 shows the statistical correlation of the 13C chemical shifts when the guest residue X in the GGXA peptide is alanine. The nine 13C chemical shifts plotted in Fig. 1 for the GGAA peptide correspond to the leading members of each family obtained after clustering the statistical-coil ensemble as described by Vila et al. (2002). Fig. 1, a and b, shows good agreement between both basis sets with a correlation coefficient of R = 0.990 and 0.997 for the 13Cα and 13Cβ chemical shifts, respectively. These results provide strong support for the hypothesis of Chesnut and Moore (1989) that the 13C chemical shifts are predominantly a local property.
FIGURE 1.
(a) Correlation between the 13Cα chemical shifts for the guest alanine residue in the GGAA peptide computed by using a uniform basis set (Vila et al., 2002) and those computed by using the locally dense basis set approach (Chesnut and Moore, 1989) as explained in Methods. R = 0.990; slope of 0.95 for the correlation line. (b) Same as a for the 13Cβ chemical shifts. R = 0.997; slope of 1.09 for the correlation line.
RESULTS AND DISCUSSION
Taking into account the experimental helix contents of PPII reported by Kelly et al. (2001), and their corresponding experimental error, i.e., ±2% for the PPP, PAP, PQP, PGP, PLP, PMP, and PNP peptides, and ±1% for the PIP and PVP peptides, we arranged these sequences in three different groups, viz.: 1), PPP, PAP, and PQP with an ∼66% helix content of PPII; 2), PGP, PLP, PMP, and PNP with an ∼57% helix content of PPII; and 3), PIP and PVP with an ∼50% helix content of PPII. Peptide PAAP, with an ∼54 ± 2% helix content of PPII, cannot be included in any of these groups because it contains a different number of residues.
We are particularly interested in the residues with higher PPII propensity and, hence, simulations were carried out for PPP, PAP, PQP, and one representative sequence of each of the remaining two groups, viz., PGP and PVP, respectively. In addition, simulations were carried out for PAAP because 1), this represents a sequence with a different alanine content from that of PAP; 2), the sequence containing two alanines will better reflect the possibility of propagation of the PPII helix conformation through more than one alanine; and 3), there is experimental evidence (Kelly et al., 2001) showing that the decrease of helix content from PPP to PAP to PAAP is nonlinear with respect to the number of alanines.
In this study, we carried out EDMC runs for the six different polypeptides sequences shown in Table 1. In all the sequences, the end groups were acetyl (CH3CO-) and amino (-NH2). For each of the runs described in Table 1, >35,000 conformations were generated, following the procedure described in the Methods section. For each sequence, three different runs were carried out, viz., 1), without consideration of solvent effects by using a gas-phase potential as described by ECEPP/3; 2), with explicit consideration of solvent effects with a solvent-accessible surface area model (using the SRFOPT set of solvation parameters described by Vila et al., 1991); and 3), by explicit consideration of solvent polarization effects from a solution of the Poisson-Boltzmann equation by using the fast MBE method developed by Vorobjev and Scheraga (1997).
Conformational analysis of PPP
Rucker and Creamer (2002) considered that PPII is an energetically favorable option for oligopeptides because all backbone polar groups are well-solvated in this conformation in water, thus compensating for the lack of intramolecular hydrogen bonds. The implicit assumption in this statement is that a polyproline peptide must be all trans and, of course, any non-proline residue in this conformation must be trans. Therefore, the characteristic ratio (C) should be ≈20 at 30°C, according to the experimentally determined value for polyproline in an organic solvent in which the polypeptide is in the all-trans conformation (Mattice and Mandelkern, 1971). However, as shown by Mattice and Mandelkern, the characteristic ratio is C ≈ 14 in an aqueous solvent at 30°C. In water, the polyproline II (all-trans) conformation is favored over the polyproline I (all-cis) conformation (Steinberg, et al., 1960). Based on these observations, and by using a statistical analysis of randomly-coiled poly(L-proline), Tanaka and Scheraga (1975c) concluded that such a significant change in the characteristic ratio is due to a mixture of trans and cis conformations in a PPII helix. These authors found that close agreement with the experimental results of Mattice and Mandelkern (1971) is obtained when the characteristic ratio is computed by assuming that 5% of the proline peptide bonds are in the cis conformation. In other words, the introduction of a small amount of cis peptide groups into a predominantly trans chain in poly(L-proline) can influence its characteristic ratio considerably. In line with this finding, the lowest-energy conformation (−235 Kcal/mol) computed for the PPP peptide with the GPSP potential at pH 7, shown in Fig. 2, has an end-to-end distance of ∼8 Å, which is shorter than a conformation that is higher in energy (−226 Kcal/mol) with all its peptide bonds in the trans state and with an end-to-end distance of ∼24 Å, as shown in Fig. 3. Nevertheless, the computed Boltzmann-averaged PPII helix content for the PPP peptide, by using all the accepted conformations listed in the third column of Table 1, computed with GP and GPSP (66.7%) or with the GPSAS (68.0%) potentials, respectively, are in agreement with the 66.0 ± 2% determined experimentally by Kelly et al. (2001), as shown in Table 2. To test the adequacy of our approach for computing averages, we recomputed the Boltzmann-averaged PPII helix content in the PXP and PAAP peptide by using both: all the accepted conformations listed in the third column of Table 1 and only the leading members, weighted by the population, of the corresponding cluster listed in the fifth column of Table 1, respectively. The values obtained are included in the fifth column of Table 2, with and without brackets, respectively. Very good agreement exists between both approaches with a correlation coefficient of R = 0.96 and a slope of 1.02 for the correlation line.
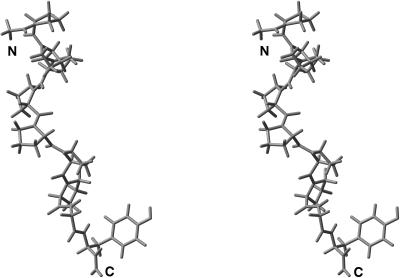
FIGURE 2.
Stereo view of the leading member of family 1 of the peptide PPP, after clustering the accepted conformations shown in Table 1. The conformations of the peptide bonds for the proline residues of this structure are CTCTCTT, computed with the GPSP potential, as shown in Table 2.
FIGURE 3.
Stereo view of the leading member of family 2 of the peptide PPP, after clustering the accepted conformations shown in Table 1. The conformations of the peptide bonds for the proline residues of this structure are TTTTTTT, computed with the GPSP potential.
TABLE 2.
Conformational analysis
| Peptide sequence* | Zimmerman code of the lowest energy conformation† | Conformation of pyrrolidine ring‡ | Peptide bond conformation§ | PPII content¶ (%) |
|---|---|---|---|---|
| PPP∥ | FFFFFFADD | DDD D DDD | TTC C TCT | 66.7 [66.7] (66.0 ± 2) |
| PPP** | FFFFFFADA | DDD D DDD | TTT T TTT | 68.0 [66.7] (66.0 ± 2) |
| PPP†† | FFFFFFAAD | DDD D DDU | CTC T CTT | 66.7 [66.7] (66.0 ± 2) |
| PAP∥ | FFCDFFADD | UUD - DDD | TTT - TCT | 44.4 [44.4] (63.0 ± 2) |
| PAP** | FFADFFADA | DUD - DDD | TTT - TTT | 46.2 [44.4] (63.0 ± 2) |
| PAP†† | FFFF*FFAAF | DDU - DDU | CTT - TTT | 66.7 [66.7] (63.0 ± 2) |
| PAAP∥ | FFAAFFFCD*D | DDD - - DDU | TTT - - CTT | 50.6 [50.0] (54.0 ± 2) |
| PAAP** | FFAADFFADA | DDD - - DDD | TTT - - TTT | 40.5 [40.0] (54.0 ± 2) |
| PAAP†† | FFAA*A*FFACG | DUD - - DDU | CTT - - CTT | 40.0 [40.0] (54.0 ± 2) |
| PQP∥ | FFAEFFAA*D | DUD - DDD | TTT - TCT | 44.4 [44.5] (65.0 ± 2) |
| PQP** | FFADFFADA | DUD - DDD | TTT - TTT | 46.6 [44.4] (65.0 ± 2) |
| PQP†† | FFAA*FFFAF | DDU - UUU | TTT - CTT | 66.7 [66.7] (65.0 ± 2) |
| PGP∥ | FFFD*FFAGF | DDU - DDD | TTT - TCT | 54.3 [66.5] (58.0 ± 2) |
| PGP** | FFADFFADA | DUD - DDD | TTT - TTT | 46.6 [44.4] (58.0 ± 2) |
| PGP†† | FFADFFAAA | UUU - DDU | TTT - CTT | 44.4 [44.4] (58.0 ± 2) |
| PVP∥ | FFCDFFADD | DUD - DDD | TTT - TCT | 44.8 [44.6] (49.0 ± 1) |
| PVP** | FFADFFADA | DUD - DDU | TTT - TTT | 46.0 [44.4] (49.0 ± 1) |
| PVP†† | FFAAFFACA | UDU - UDD | TTT - TCT | 33.3 [33.3] (49.0 ± 1) |
PXP and PXXP represent the X residue in the sequence Ac-PPPXPPPGY-NH2 (for X = Pro, Ala, Gln, Gly, and Val) and Ac-PPPXXPPPGY-NH2 (for XX = AlaAla), respectively. A dash is used in columns 3 and 4 to denote that the guest residue is not proline, and hence no results are displayed for this residue in these columns.
Conformations are classified in terms of the regions of the φ−ψ Ramachandran (Ramachandran et al., 1963) map in which they occur (Zimmerman et al., 1977). On the left-hand half of the map (φ < 0°), the regions are defined as A–G; on the right-hand half of the map (φ ≥ 0°), the regions are defined by inversion of the left-hand half around the center of the map, and an asterisk is appended to the letters.
The designation of U (up) and D (down) pertain to the (φ = −53.0° and χ1 = −28.1°) and (φ = −68.8° and χ1 = 27.4°) positions, respectively, of the Cγ atom.
C and T are used to designate the cis and trans states of the peptide bond only for prolines. All the non-prolines are trans.
For each peptide in this table, we show 1), the Boltzmann-averaged PPII helix content computed using all accepted conformations listed in the third column of Table 1; 2), within brackets, the Boltzmann-averaged PPII helix content computed by using only the leading members, weighted by the population, of the corresponding cluster listed in the fifth column of Table 1; and 3), in parentheses, the corresponding experimental values (Kelly et al., 2001). Very good agreement for the computed Boltzmann-averaged PPII helix content exists between both procedures 1 and 2, i.e., with a correlation coefficient of R = 0.96 and slope of 1.02 for the correlation line. In these calculations, it is assumed that only residues in the F region contribute to the PPII helix content.
The calculations were carried out by using a GP potential, as explained in Methods.
The calculations were carried by using a GPSAS potential, as explained in Methods.
The calculations were carried out at pH 7 at t = 25°C by using the GPSP potential, as described in Methods. The value of 10.10 was adopted as the 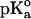 for the ionizable group of the Tyr residue, as an average from the data of Perrin (1972).
for the ionizable group of the Tyr residue, as an average from the data of Perrin (1972).
Inspection of the lowest-energy conformation of the PPP peptide obtained from the simulations, carried out using the GP potential, shows that this conformation is similar to that displayed in Fig. 2. The lowest-energy conformations for the simulations with the GP and GPSP potentials have in common a mixture of trans and cis isomeric states of the peptide bonds, as shown in Table 2. The mixture of cis and trans peptide bonds, obtained with both the GP and GPSP potential functions, is consistent with the results obtained by Tanaka and Scheraga (1974), showing that nucleation of cis ↔ trans isomerization may occur not only at the termini but also in the middle of the chain, and also that cis residues may occur randomly within the poly(L-proline) chain. The existence of mixed conformations of trans and cis peptide bonds in oligomers of L-proline has been observed in NMR experiments (Deber et al., 1970). According to all the accumulated theoretical and experimental evidence, the view that the optimal conformation of a polyproline-rich peptide is an ideal or canonical PPII helix in water is an oversimplification that results from lack of consideration of the cis ↔ trans isomerization of the peptide group for proline residues.
Polyproline helix content of PXP and PAAP
In Table 3, we have listed all the Boltzmann-averaged values for the 13C chemical shifts for residues X and Ala in the peptides PXP and PAAP, respectively. Since the main factor determining 13Cα and 13Cβ chemical shifts is the set of backbone dihedral angles (φ,ψ), with minor influence from the side-chain dihedral angles χ (Spera and Bax, 1991; Iwadate et al., 1999; Wishart and Case, 2001; Vila, et al., 2003), comparison between the predicted and measured values for the 13C chemical shifts will provide a test of the conformational preferences predicted in our simulations.
TABLE 3.
Boltzmann-averaged values of the 13C chemical shifts for the peptides PXP
| Residue name (X)* | Chemical shift (ppm) | |||||
|---|---|---|---|---|---|---|
|
|
13Cα
|
13Cβ
|
13Cγ
|
13Cδ
|
||
| Pro† | 59.0 | 30.2 | 21.3 | 48.4 | ||
| Ala† | 52.9 | 19.8 | ||||
| Gln† | 55.3 | 27.0 | 37.7 | 175.5 | ||
| Gly† | 46.8 | |||||
| Val† | 67.5 | 35.3 | 22.7 | 19.8 | ||
| Ala‡ | 53.6 | 15.9 | ||||
| Ala§ | 51.8 | 19.2 | ||||
For each residue in this table, we show the Boltzmann-averaged 13C chemical shifts with respect to tetramethylsilane (TMS), by using the leading member of each family obtained by the clustering procedure and the locally dense quantum chemical approximation, as described in Methods.
Values in this row belong to the residue X in the peptide PXP.
Values in this row belong to the boldface Alanine in the peptide PAAP.
Values in this row belong to the boldface Alanine in the peptide PAAP.
The 13C chemical shifts have been used to distinguish between cis and trans X-Pro peptide bonds in small peptides (Dorman and Bovey, 1973). For this reason, we compared the Boltzmann-averaged 13Cβ and 13Cγ chemical shifts of residue X = PRO in the PXP peptide with the maximum and minimum values, obtained from an analysis of the 13Cβ and 13Cγ chemical shifts of 1033 proline residues from 304 proteins for the X-Pro peptide bond in the cis and trans conformations by Schubert et al. (2002). Our calculated 13Cβ and 13Cγ Boltzmann-averaged chemical shift values (30.2 ppm and 21.3 ppm, respectively) for proline in the PPP peptide are consistent with a peptide bond in the trans conformation since 1), they are greater than the minimum observed values (26.3 ppm and 19.3 ppm, respectively) for a peptide bond in the trans conformation, but 2), they are lower than the minimum observed values (30.7 ppm and 22.1 ppm, respectively) for a peptide bond in the cis conformation (Schubert et al., 2002). From this comparison between the computed Boltzmann-averaged values for the 13Cβ and 13Cγ chemical shifts for the PPP peptide and the maximum and minimum experimental values observed by Schubert et al. (2002), we can conclude that the guest (proline) residue is in the trans conformation in the PPP peptide. This result is consistent with the peptide-bond conformation shown in Table 2, for the simulations carried out with the GPSP potential.
As shown in Table 2 for simulations carried out in water, all guest residues in the PXP peptide, when X is not proline, do not show a conformational preference for the F region of the Zimmermann map. We can conclude that, in the presence of water, there is no propagation of the PPII conformational preference into the preceding (guest) residue for all the PXP sequences, when X is not proline, contrary to the proposal of Kelly et al. (2001). The lack of propagation through non-proline residues, observed in our simulations, is due to the low propensity for the PPII conformation of any of the tested residues, arising (among others) from consideration of hydration effects. In other words, the strong tendency attributed to some amino acids for the PPII region, and the widely-held belief that such residues in proline-rich regions will adopt this structure predominantly, will have to be revised.
As shown for the underlined and boldfaced conformations in Table 1, column 4, a proline residue of PAAP seems to have a significant influence only on the preceding member (alanine) in the sequence (in forcing such a non-proline residue to adopt the PPII conformation) in the simulations carried out for this peptide using the GP potential energy function. However, this influence disappears when water is included in the simulation. Alanine does not seem to propagate the PPII helix conformation when it is surrounded by a proline-rich environment, in disagreement with the suggestion of Kelly et al. (2001).
Does Ala prefer the PPII conformation?
The PPII helix gives rise to a CD spectrum that is remarkably similar to that of unfolded proteins. This similarity has been used to justify the hypothesis that unfolded proteins possess considerable PPII helix, rather than β, content. Since the original observation of Tiffany and Krimm (1968), a plethora of experiments on proline-rich sequences have been reported, attempting to validate this hypothesis. However, many of these experimental results involve contradictions that have not been properly addressed. As an example, Shi et al. (2002a) studied the oligopeptide Ac-ZZ-(Ala)7-OO-NH2 [ZAO] (where Z denotes diaminobutyric acid and O is ornithine), with no proline in the sequence, by using CD and NMR experiments. Based mainly on J-vicinal coupling constants (and the corresponding φ-values) derived from the NMR experiments, the data were interpreted as placing all seven alanine residues in the PPII region, even at high temperature. If this were the case, the CD spectra of Shi et al. (2002a) should be similar to those obtained by Rucker and Creamer (2002) for the peptide Ac-(Pro)7-Gly-Tyr-NH2 (P7). However, they are not (see Fig. 5 of Shi et al., 2002a, and Fig. 1 of Rucker and Creamer, 2002). On the other hand, the CD spectrum obtained by Shi et al. (2002a) is remarkably similar to the one obtained by Rucker and Creamer (2002) for the peptide Ac-(Lys)7-Gly-Tyr-NH2 (K7) at pH 12, which, according to the latter authors, has lost some PPII helix character with an increase in the population of disordered states and/or the appearance of some small amount of β-sheet.
Since Shi et al. (2002a) did not report the vicinal coupling constants for the whole 11-residue peptide, but only for the seven alanine residues, it is not possible to make an accurate estimate of the overall PPII helix content based on their NMR analysis; hence, we cannot compare the PPII helix content for the whole peptide with our estimation of ∼35% based on their CD spectrum. It should be noted that the CD spectrum published by Shi et al. (2002b) is shifted on the y axis when compared with the one published by Shi et al. (2002a); such a shift could easily lead to a wrong (90%) estimate of the PPII helix content. According to N. R. Kallenbach (private communication, 2002), the correct spectrum is the one published by Shi et al. (2002a), which shows no sizeable positive shoulder in the 215–230 nm, the which, if present, would have implied a high PPII content.
Our estimated value of ∼35% of PPII helix content is in disagreement with the ∼90% PPII conformation reported by Shi et al. (2002b) for the Ala7 sequence. The suggested ∼90% PPII content for the Ala7 sequence, based on their NMR analysis, means that the PPII helix content for the whole ZAO peptide should be at least ∼60%, i.e., with ∼7 out of 11 residues in the PPII region. This lower value for the PPII helix content is obtained under the assumption that neither the diaminobutyric acid nor the ornithine residues occupy the PPII conformational region. However, the ornithine and diaminobutyric acid residues could also contribute to the PPII helix content. For example, diaminobutyric acid has one less side-chain methylene group than ornithine and two less than lysine. A comparison of α-helix stabilities of poly-L-lysine, poly-L-ornithine, and poly-L-diaminobutyric acid) shows that, in water at pH < 8, they all belong to a nonstructured state, i.e., not to an α-helical structure (Grourke and Gibbs, 1971). A homopolymer of poly-L-lysine at low pH, ionic strength, and temperature exhibits a CD spectrum consistent with a PPII helix (Woody, 1992). Recently, Rucker and Creamer (2002) suggested that the CD spectra collected at pH 7 for a lysine-rich peptide (K7) indicate a high PPII helix content. According to Rucker and Creamer (2002), this conformational preference for the PPII helical structure appears as the result of the nature of the backbone rather than as a consequence of electrostatic interaction between side chains. Based on this hypothesis, it is conceivable that similar behavior could be displayed by residues related to lysine, such as ornithine or diaminobutyric acid, and hence, the possibility that ornithine or diaminobutyric acid populate the PPII region at pH 7 cannot be ruled out. In other words, there is reason to believe that such discrepancy between the NMR-determined (∼60%) and CD-determined (∼35%) PPII helix content in the experiment of Shi et al. (2002a) could be greater than these estimates.
Consider, further, the disagreement between the estimated PPII helix content derived from CD (∼35%) and NMR (60%) data, respectively, by Shi et al. (2002a). The observation made by Pappu and Rose (2002) that a seven-residue alanine-based peptide can be dominated by fluctuations around the left-handed PPII helix (φ = −78°, ψ = 146°) and a nearby conformation (φ = −147°, ψ = 81°), i.e., populating the F and D regions, respectively, of the Zimmerman et al. (1977) map, may account for the disagreement. Because of the degeneracy of the Karplus relation between coupling constant and φ-value, the coupling constants are similar in the F and D regions. Thus, the assumption of such fluctuations may explain the low CD signal, although still being consistent with the observed value for the NMR-determined vicinal coupling constant. In other words, residues in the F and D regions of the Zimmerman et al. (1977) map could each display a vicinal coupling (3JNHα) constant <6.0 Hz, which is consistent with the results of Shi et al. (2002a) at 2°C. From the degenerate Karplus relation, a coupling constant <6 Hz could correspond to many values of φ, viz., those in whole range of −180° ≤ φ ≤ 180°. Therefore, one cannot identify a particular value of φ based only on a coupling constant of <6 Hz. Table 4 shows that non-proline residues can populate A, A*, D, D*, C, and F regions with coupling constants <6 Hz. It is conceivable that experimental values for 〈3JNHα〉 observed by Shi et al. (2002a) could represent a Boltzmann-averaged distribution of residues displaying preferences for many regions of the Ramachandran map, because residues in these regions could also display a backbone dihedral angle φ consistent with a coupling constant <6.0 Hz, without displaying any particular regular structure such as α- or PPII-helices.
TABLE 4.
Computation of the 〈3JNHα〉 coupling constant
| Peptide sequence* | Boltzmann-averaged† value of the vicinal coupling constant 〈3JNHα〉‡ | Zimmerman code of the lowest energy conformation§ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PPP¶ | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 4.6 | 8.6 | FFFFFFADD | |
| PPP∥ | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.1 | 4.9 | 8.8 | 6.6 | FFFFFFADA | |
| PPP** | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 | 3.4 | 3.7 | 6.9 | FFFFFFAAD | |
| PAP¶ | 3.4 | 3.4 | 5.3 | 6.6 | 5.2 | 5.3 | 5.3 | 4.7 | 8.6 | FFCDFFADD | |
| PAP∥ | 5.3 | 3.7 | 5.2 | 8.0 | 5.3 | 5.3 | 4.8 | 9.5 | 6.6 | FFADFFADA | |
| PAP** | 5.3 | 5.3 | 3.4 | 6.8 | 5.3 | 5.3 | 3.4 | 4.1 | 4.3 | FFFF*FFAAF | |
| PAAP¶ | 5.1 | 5.3 | 5.3 | 4.9 | 6.8 | 5.3 | 5.3 | 3.5 | 4.4 | 6.5 | FFAAFFFCD*D |
| PAAP∥ | 5.2 | 5.3 | 5.3 | 6.8 | 8.0 | 5.2 | 5.3 | 5.1 | 8.6 | 6.3 | FFAADFFADA |
| PAAP** | 5.3 | 3.4 | 5.3 | 6.8 | 6.8 | 5.3 | 5.3 | 3.4 | 4.2 | 6.2 | FFAA*A*FFACG |
| PQP¶ | 5.3 | 4.0 | 5.3 | 8.5 | 4.7 | 4.7 | 5.3 | 4.8 | 7.4 | FFAEFFAA*D | |
| PQP∥ | 5.3 | 3.7 | 5.0 | 8.6 | 5.3 | 5.3 | 5.0 | 9.1 | 6.6 | FFADFFADA | |
| PQP** | 5.3 | 5.3 | 3.4 | 6.8 | 3.4 | 3.4 | 3.4 | 5.1 | 4.4 | FFAA*FFFAF | |
| PGP¶ | 4.7 | 5.2 | 4.7 | 2.9 | 5.1 | 5.1 | 5.3 | 5.3 | 8.3 | FFFD*FFAGF | |
| PGP∥ | 5.1 | 4.3 | 4.9 | 7.5 | 5.2 | 5.2 | 4.7 | 9.4 | 6.8 | FFADFFADA | |
| PGP** | 3.4 | 3.4 | 3.4 | 6.2 | 5.3 | 5.3 | 3.4 | 2.9 | 7.9 | FFADFFAAA | |
| PVP¶ | 5.3 | 3.5 | 5.3 | 8.7 | 5.3 | 5.3 | 5.3 | 5.0 | 9.1 | FFCDFFADD | |
| PVP∥ | 5.2 | 4.8 | 4.3 | 9.6 | 4.7 | 5.3 | 4.4 | 7.9 | 6.3 | FFADFFADA | |
| PVP** | 3.4 | 5.3 | 3.4 | 5.4 | 3.4 | 5.3 | 5.3 | 6.0 | 7.6 | FFAAFFACA | |
PXP and PXXP represent the X residue in the sequence Ac-PPPXPPPGY-NH2 (for X = Pro, Ala, Gln, Gly, and Val) and Ac-PPPXXPPPGY-NH2 (for XX = AlaAla), respectively.
Values computed by using all the accepted conformations listed in Table 1. The values of the coupling constants of all the non-proline residues in the sequence are in boldface. The values for the X residue in the sequence PXP and PAAP are underlined.
The theoretical values of the coupling constants were computed from the calculated values of the dihedral angle φ by using the Karplus relation (Karplus, 1959, 1963): 3JNHα = A cos2ϕ − B cos ϕ + C, with ϕ = |φ − 60.0| and A = 6.4, B = 1.4, and C = 1.9, as parameterized by Pardi et al. (1984).
Conformations are classified in terms of the regions of the φ–ψ Ramachandran (Ramachandran et al., 1963) map in which they occur (Zimmerman et al., 1977). On the left-hand half of the map (φ < 0°), the regions are defined as A–G; on the right-hand half of the map (φ ≥ 0°), the regions are defined by inversion of the left-hand half around the center of the map and an asterisk is appended to the letters. The conformations of all non-proline residues in the sequence are in boldface. The X residue in the sequence PXP and PAAP is underlined.
The calculations were carried out by using a GP potential, as explained in Methods.
The calculations were carried out by using a GPSAS potential, as explained in Methods.
The calculations were carried out at pH 7 at t = 25°C by using the GPSP potential, as described in Methods. The value of 10.10 was adopted as the 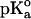 for the ionizable group of the residue Tyr, as an average from the data of Perrin (1972).
for the ionizable group of the residue Tyr, as an average from the data of Perrin (1972).
Shi et al. (2002a) also suggested that the dihedral angle ψ for all alanine residues are likely to be +145° ± 20°, based on the ratio of nuclear Overhauser effects between nearest-neighbor β-protons. In such a case, only the F region of the Zimmerman et al. (1977) map is compatible with the observed values for the coupling constant (<6 Hz at 2°C). If this were the case, the existence of fluctuations around two noncooperative structures, as proposed by Pappu and Rose (2002), or a Boltzmann-averaged distribution of residues displaying preferences for different regions of the Ramachandran map, as we proposed above, should be ruled out because this ψ-dihedral angle is consistent only with the possibility of the existence of residues in the PPII (or F) region of the Ramachandran map. A possible clarification of this problem could be obtained by an experimental determination of the 13Cα and 13Cβ chemical shifts for all the alanine residues because, as was already noted (Spera and Bax, 1991; Iwadate et al., 1999; Wishart and Case, 2001; Vila, et al., 2003), both of the backbone dihedral angles (φ,ψ) seem to be the largest individual factors controlling 13Cα and 13Cβ chemical shifts. In other words, determination of the 13Cα and 13Cβ chemical shifts would avoid the uncertainties about an accurate ψ-dihedral angle and the existence of degenerate values for the φ-dihedral angle, as happens with an analysis based only on a vicinal coupling constant such as 3JNHα.
CONCLUSIONS
Our theoretical results and analysis for the PXP and PAAP peptides are in qualitative agreement with 1), experimental CD spectroscopic evidence for proline-containing undecamers with alanine and glycine substituted in the central position (Petrella et al., 1996), showing that the PPII helix content is reduced compared with the all-proline peptide; 2), experimental results of Kelly et al. (2001) on PAP and PAAP peptides; and 3), recent experimental evidence using isothermal titration calorimetry (Ferreon and Hilser, 2003) showing that the probability of the PPII conformation in the denatured states of Ala is ∼30%. As Ferreon and Hilser noted, their (∼30%) PPII content, estimated for Ala, differs considerably from that determined by Shi et al. (2002a), viz., ∼90%. The prediction of Ferreon and Hilser for Ala is in agreement with the ∼35% PPII helix content that we have estimated from the CD spectrum published by Shi et al. (2002a).
Our simulations show that water affects the conformational properties of polyproline but, instead of stabilizing the extended PPII helical form, a less extended structure is found (involving some cis residues), in good agreement with experimental observations made by Mattice and Mandelkern (1971). In addition, we find that, in the presence of water, there is no propagation of the PPII conformational preference into the guest residues for all the PXP sequences, when X is not proline.
Finally, using two approaches, namely the reduction of the total number of conformations by the clustering procedure and the quantum chemical computation of the chemical shifts of the resulting leading members of each family by using a locally dense basis set, we have been able to treat the quantum chemical computation of Boltzmann-averaged chemical shifts of 13C carbons in the PXP and PAAP peptides.
Acknowledgments
This research was supported by grants from the National Institutes of Health (GM-14312 and TW00857) and the National Science Foundation (MCB00-03722). Support was also received from the National Foundation for Cancer Research, the National Research Council of Argentina (Consejo Nacional de Investigaciones Científicas y Técnicas), and Project No P-328402 of the Universidad Nacional de San Luis, Argentina. Part of this research was conducted using the resources of the Cornell Theory Center (which receives funding from Cornell University, the State of New York, federal agencies, foundations, and corporate partners), and the National Partnership for Advanced Computational Infrastructure at the Pittsburgh Supercomputing Center (which is supported in part by the National Science Foundation, MCA99S007P).
Avijit Ghosh's present address is Drexel University, Dept. of Physics, 3141 Chestnut St., Philadelphia, PA 19104.
References
- Arnott, S., S. D. Dover, and A. Elliott. 1967. Structure of β-poly-L-alanine: refined atomic coordinates for an antiparallel β-pleated sheet. J. Mol. Biol. 30:201–208. [DOI] [PubMed] [Google Scholar]
- Bashford, D., and M. Karplus. 1990. pKas of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
- Becke, A. D. 1993. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98:5648–5652. [Google Scholar]
-
Beroza, P., D. R. Fredkin, M. Y. Okamura, and G. Feher. 1995. Electrostatic calculations of amino acid titration and electron transfer,
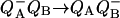 , in the reaction center. Biophys. J. 68:2233–2250. [DOI] [PMC free article] [PubMed] [Google Scholar]
, in the reaction center. Biophys. J. 68:2233–2250. [DOI] [PMC free article] [PubMed] [Google Scholar] - Brandts, J. F., H. R. Halvorson, and M. Brennan. 1975. Consideration of the possibility that the slow step in protein denaturation reactions is due to cis-trans isomerism of proline residues. Biochemistry. 14:4953–4963. [DOI] [PubMed] [Google Scholar]
- Cheeseman, J. R., G. W. Trucks, T. A. Keith, and M. J. Frisch. 1996. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J. Chem. Phys. 104:5497–5509. [Google Scholar]
- Chesnut, D. B., and K. D. Moore. 1989. Locally dense basis sets for chemical shift calculations. J. Comp. Chem. 10:648–659. [Google Scholar]
- Cowan, P. M., and S. McGavin. 1955. Structure of poly-L-proline. Nature. 176:501–503. [Google Scholar]
- Creamer, T. P. 1998. Left-handed polyproline II helix formation is (very) locally driven. Prot. Struct. Funct. Genet. 33:218–226. [PubMed] [Google Scholar]
- Deber, C. M., F. A. Bovey, J. P. Carver, and E. R. Blout. 1970. Nuclear magnetic resonance evidence for cis-peptide bonds in proline oligomers. J. Am. Chem. Soc. 92:6191–6198. [DOI] [PubMed] [Google Scholar]
- Dorman, D. E., and F. A. Bovey. 1973. Carbon-13 magnetic resonance spectroscopy. The spectrum of proline in oligopeptides. J. Org. Chem. 38:2379–2383. [Google Scholar]
- Ferreon, J. C., and V. J. Hilser. 2003. The effect of the polyproline II (PPII) conformation on the denatured state entropy. Protein Sci. 12:447–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle, and J. A. Pople. 1998. Gaussian 98, Rev. A7. Gaussian, Inc., Pittsburgh, PA.
- Gay, D. M. 1983. Algorithm 611: subroutines for unconstrained minimization using a model/trust-region approach. ACM Trans. Math. Software. 9:503–524. [Google Scholar]
- Ghosh, A., R. Elber, and H. A. Scheraga. 2002. An atomically detailed study of the folding pathways of protein A with the stochastic difference equation. Proc. Natl. Acad. Sci. USA. 99:10394–10398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K. 1993. Multiple-site titration and molecular modeling: two rapid methods for computing energies and forces for ionizable groups in proteins. Prot. Struct. Funct. Genet. 15:266–282. [DOI] [PubMed] [Google Scholar]
- Gō, N., and H. A. Scheraga. 1969. Analysis of the contribution of internal vibrations to the statistical weights of equilibrium conformations of macromolecules. J. Chem. Phys. 51:4751–4767. [Google Scholar]
- Gornick, F., L. Mandelkern, A. F. Diorio, and D. E. Roberts. 1964. Evidence for a cooperative intramolecular transition in poly-L-proline. J. Am. Chem. Soc. 86:2549–2555. [Google Scholar]
- Grourke, M. J., and J. H. Gibbs. 1971. Comparison of helix stabilities of poly-L-lysine, poly-L-ornithine, and poly-L-diaminobutyric acid. Biopolymers. 10:795–808. [DOI] [PubMed] [Google Scholar]
- Hawkins, G. D., C. J. Cramer, and D. G. Truhlar. 1996. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 100:19824–19839. [Google Scholar]
- Hehre, W. J., L. Radom, P. Schleyer, and J. A. Pople. 1986. Ab Initio Molecular Orbital Theory. John Wiley and Sons, New York.
- Iwadate, M., T. Asakura, and M. P. Williamson. 1999. Cα and Cβ carbon-13 chemical shifts in proteins from an empirical database. J. Biomol. NMR. 13:199–211. [DOI] [PubMed] [Google Scholar]
- Jameson, A. K., and C. J. Jameson. 1987. Gas-phase 13C chemical shifts in the zero-pressure limit: refinements to the absolute shielding scale for 13C. Phys. Lett. 134:461–466. [Google Scholar]
- Karplus, M. 1959. Contact electron-spin coupling of nuclear magnetic moments. J. Chem. Phys. 30:11–15. [Google Scholar]
- Karplus, M. 1963. Vicinal proton coupling in nuclear magnetic resonance. J. Am. Chem. Soc. 85:2870–2871. [Google Scholar]
- Kelly, M. A., B. W. Chellgren, A. L. Rucker, J. M. Troutman, M. G. Fried, A.-F. Miller, and T. P. Creamer. 2001. Host-Guest study of left-handed polyproline II helix formation. Biochemistry. 40:14376–14383. [DOI] [PubMed] [Google Scholar]
- Laws, D. D., H. Le, A. C. de Dios, R. H. Havlin, and E. Oldfield. 1995. A basis size dependence study of carbon-13 nuclear magnetic resonance spectroscopic shielding in alanyl and valyl fragments: toward protein shielding hypersurfaces. J. Am. Chem. Soc. 117:9542–9546. [Google Scholar]
- Lee, C., W. Yang, and R. G. Parr. 1988. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 37:785–789. [DOI] [PubMed] [Google Scholar]
- Ma, K., L.-S. Kan, and K. Wang. 2001. Polyproline II helix is a key structural motif of the elastic PEVK segment of titin. Biochemistry. 40:3427–3438. [DOI] [PubMed] [Google Scholar]
- Mandelkern, L. 1967. Poly-L-proline. In Poly-α-Amino Acids. G. D. Fasman, editor. Marcel Dekker, New York. 675–724.
- Mattice, W. L., and L. Mandelkern. 1971. Conformational properties of poly-L-proline form II in dilute solution. J. Am. Chem. Soc. 93:1769–1777. [DOI] [PubMed] [Google Scholar]
- Momany, F. A., R. F. McGuire, A. W. Burgess, and H. A. Scheraga. 1975. Energy parameters in polypeptides. VII. Geometric parameters, partial atomic charges, nonbonded interactions, hydrogen bond interactions, and intrinsic torsional potentials for the naturally occurring amino acids. J. Phys. Chem. 79:2361–2381. [Google Scholar]
- Némethy, G., K. D. Gibson, K. A. Palmer, C. N. Yoon, G. Paterlini, A. Zagari, S. Rumsey, and H. A. Scheraga. 1992. Energy parameters in polypeptides. 10. Improved geometrical parameters and nonbonded interactions for use in the ECEPP/3 algorithm, with application to proline-containing peptides. J. Phys. Chem. 96:6472–6484. [Google Scholar]
- Némethy, G., M. S. Pottle, and H. A. Scheraga. 1983. Energy parameters in polypeptides. 9. Updating of geometrical parameters, nonbonded interactions, and hydrogen bond interactions for the naturally occurring amino acids. J. Phys. Chem. 87:1883–1887. [Google Scholar]
- Onufriev, A., D. A. Case, and D. Bashford. 2002. Effective Born radii in the generalized Born approximation: the importance of being perfect. J. Comp. Chem. 23:1297–1304. [DOI] [PubMed] [Google Scholar]
- Pappu, R. V., and G. D. Rose. 2002. A simple model for polyproline II structure in unfolded states of alanine-based peptides. Protein Sci. 11:2437–2455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardi, A., M. Billeter, and K. Wüthrich. 1984. Calibration of the angular dependence of the amide proton-Cα proton coupling constants, 3JHNα, in a globular protein. J. Mol. Biol. 180:741–751. [DOI] [PubMed] [Google Scholar]
- Parr, R. G., and W. Yang. 1989. Density Functional Theory of Atoms and Molecules. Oxford University Press, New York.
- Perrin, D. D. 1972. Dissociation Constants of Organic Bases in Aqueous Solution. 402. Butterworths, London.
- Petrella, E. C., L. M. Machesky, D. A. Kaiser, and T. D. Pollard. 1996. Structural requirements and thermodynamics of the interaction of proline peptides with profilin. Biochemistry. 35:16535–16543. [DOI] [PubMed] [Google Scholar]
- Ramachandran, G. N., C. Ramakrishnan, and V. Sasisekharan. 1963. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 7:95–99. [DOI] [PubMed] [Google Scholar]
- Ripoll, D. R., and H. A. Scheraga. 1988. On the multiple-minima problem in the conformational analysis of polypeptides. II. An electrostatically driven Monte Carlo method-tests on poly(L-alanine). Biopolymers. 27:1283–1303. [DOI] [PubMed] [Google Scholar]
- Ripoll, D. R., Y. N. Vorobjev, A. Liwo, J. A. Vila, and H. A. Scheraga. 1996. Coupling between folding and ionization equilibria: effects of pH on the conformational preferences of polypeptide. J. Mol. Biol. 264:770–783. [DOI] [PubMed] [Google Scholar]
- Ripoll, D. R., A. Liwo, and C. Czaplewski. 1999. The ECEPP package for conformational analysis of polypeptides. T.A.S.K. Quart. 3:313–331. [Google Scholar]
- Rucker, A. L., and T. P. Creamer. 2002. Polyproline II helical structure in protein unfolded states: lysine peptides revisited. Protein Sci. 11:980–985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert, M., D. Labudde, H. Oschkinat, and P. Schmieder. 2002. A software tool for the prediction of Xaa-Pro peptide bond conformations in proteins based on 13C chemical shift statistics. J. Biomol. NMR. 24:149–154. [DOI] [PubMed] [Google Scholar]
- Shi, Z., C. A. Olson, G. D. Rose, R. L. Baldwin, and N. R. Kallenbach. 2002a. Polyproline II structure in a sequence of seven alanine residues. Proc. Natl. Acad. Sci. USA. 99:9190–9195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi, Z., R. W. Woody, and N. R. Kallenbach. 2002b. Is polyproline II a major backbone conformation in unfolded proteins? Adv. Protein Chem. 62:163–240. [DOI] [PubMed] [Google Scholar]
- Simonson, T., and A. T. Brünger. 1994. Solvation free energies estimated from macroscopic continuum theory: an accuracy assessment. J. Phys. Chem. 98:4683–4694. [Google Scholar]
- Sippl, M. J., G. Némethy, and H. A. Scheraga. 1984. Intermolecular potentials from crystal data. 6. Determination of empirical potentials for O-H···O=C hydrogen bonds from packing configurations. J. Phys. Chem. 88:6231–6233. [Google Scholar]
- Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- Spera, S., and A. Bax. 1991. Empirical correlation between protein backbone conformation and Cα and Cβ and 13C nuclear magnetic resonance chemical shifts. J. Am. Chem. Soc. 113:5490–5492. [Google Scholar]
- Sreerama, N., and R. W. Woody. 1999. Molecular dynamics simulations of polypeptide conformations in water: a comparison of α, β and poly(Pro)II conformations. Prot. Struct. Funct. Genet. 36:400–406. [PubMed] [Google Scholar]
- Sreerama, N., and R. W. Woody. 2003. Structural composition of βI- and βII-proteins. Protein Sci. 12:384–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stapley, B. J., and T. P. Creamer. 1999. A survey of left-handed polyproline II helices. Protein Sci. 8:587–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinberg, I. Z., W. F. Harrington, A. Berger, M. Sela, and E. Katchalski. 1960. The configurational changes of poly-L-proline in solution. J. Am. Chem. Soc. 82:5263–5279. [Google Scholar]
- Strassmair, H., J. Engel, and G. Zundel. 1969. Binding of alcohols to the peptide CO-group of poly-L-proline in the I and II conformation. I. Demonstration of the binding by infrared spectroscopy and optical rotatory dispersion. Biopolymers. 8:237–246. [Google Scholar]
- Sun, H., L. K. Sanders, and E. Oldfield. 2002. Carbon-13 NMR shielding in the twenty common amino acids: comparisons with experimental results in proteins. J. Am. Chem. Soc. 124:5486–5495. [DOI] [PubMed] [Google Scholar]
- Tanaka, S., and H. A. Scheraga. 1974. Calculation of conformational properties of oligomers of L-proline. Macromolecules. 7:698–705. [DOI] [PubMed] [Google Scholar]
- Tanaka, S., and H. A. Scheraga. 1975a. Theory of the cooperative transition between two ordered conformations of poly(L-proline). II. Molecular theory in the absence of solvent. Macromolecules. 8:504–516. [DOI] [PubMed] [Google Scholar]
- Tanaka, S., and H. A. Scheraga. 1975b. Theory of the cooperative transition between two ordered conformations of poly(L-proline). III. Molecular theory in the presence of solvent. Macromolecules. 8:516–521. [DOI] [PubMed] [Google Scholar]
- Tanaka, S., and H. A. Scheraga. 1975c. Calculation of the characteristic ratio of randomly coiled poly(L-proline). Macromolecules. 8:623–631. [DOI] [PubMed] [Google Scholar]
- Tiffany, M. L., and S. Krimm. 1968. New chain conformations of poly(glutamic acid) and polylysine. Biopolymers. 6:1379–1382. [DOI] [PubMed] [Google Scholar]
- Tsui, V., and D. A. Case. 2001. Theory and applications of the generalized Born solvation model in macromolecular simulations. Biopolymers. 56:275–291. [DOI] [PubMed] [Google Scholar]
- Vila, J., R. L. Williams, M. Vásquez, and H. A. Scheraga. 1991. Empirical solvation models can be used to differentiate native from near-native conformations of bovine pancreatic trypsin inhibitor. Prot. Struct. Funct. Genet. 10:199–218. [DOI] [PubMed] [Google Scholar]
- Vila, J. A., D. R. Ripoll, M. E. Villegas, Y. N. Vorobjev, and H. A. Scheraga. 1998. Role of hydrophobicity and solvent-mediated charge-charge interactions in stabilizing α-helices. Biophys. J. 75:2637–2646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vila, J. A., D. R. Ripoll, and H. A. Scheraga. 2001. Influence of lysine content and pH on the stability of alanine-based co-polypeptides. Biopolymers. 58:235–246. [DOI] [PubMed] [Google Scholar]
- Vila, J. A., D. R. Ripoll, H. A. Baldoni, and H. A. Scheraga. 2002. Unblocked statistical-coil tetrapeptides and pentapeptides in aqueous solution: a theoretical study. J. Biomol. NMR. 24:245–262. [DOI] [PubMed] [Google Scholar]
- Vila, J. A., H. A. Baldoni, D. R. Ripoll, and H. A. Scheraga. 2003. Unblocked statistical-coil tetrapeptides in aqueous solution: quantum-chemical computation of the carbon-13 NMR chemical shifts. J. Biomol. NMR. 26:113–130. [DOI] [PubMed] [Google Scholar]
- Vorobjev, Y. N., H. A. Scheraga, B. Hitz, and B. Honig. 1994. Theoretical modeling of electrostatic effects of titratable side-chain groups on protein conformation in a polar ionic solution. 1. Potential of mean force between charged lysine residues and titration of poly-(L-lysine) in 95% methanol solution. J. Phys. Chem. 98:10940–10948. [Google Scholar]
- Vorobjev, Y. N., H. A. Scheraga, and B. Honig. 1995. Theoretical modeling of electrostatic effects of titratable side-chain groups on protein conformation in a polar ionic solution. 2. pH-induced helix-coil transition of poly-(L-lysine) in water and methanol ionic solutions. J. Phys. Chem. 99:7180–7187. [Google Scholar]
- Vorobjev, Y. N., and H. A. Scheraga. 1997. A fast adaptive multigrid boundary element method for macromolecular electrostatic computations in a solvent. J. Comput. Chem. 18:569–583. [Google Scholar]
- Wishart, D. S., and D. A. Case. 2001. Use of chemical shifts in macromolecular structure determination. Methods Enzymol. 338:3–34. [DOI] [PubMed] [Google Scholar]
- Wolinski, K., J. F. Hinton, and P. Pulay. 1990. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 112:8251–8260. [Google Scholar]
- Woody, R. W. 1992. Circular dichroism and conformation of unordered polypeptides. Adv. Biophys. Chem. 2:37–39. [Google Scholar]
- Wüthrich, K., C. Grathwohl, and R. Schwyzer. 1974. Cis, trans, and nonplanar peptide bonds in oligopeptides: 13C-NMR studies. In Peptides, Polypeptides and Proteins. E. R. Blout, F. A. Bovey, M. Goodman, and N. Lotan, editors. Wiley, New York. 300–307.
- Yang, A.-S., M. R. Gunner, R. Sampogna, K. Sharp, and B. Honig. 1993. On the calculation of PKas in proteins. Prot. Struct. Funct. Genet. 15:252–265. [DOI] [PubMed] [Google Scholar]
- Yang, A.-S., and B. Honig. 1993. On the pH dependence of protein stability. J. Mol. Biol. 231:459–474. [DOI] [PubMed] [Google Scholar]
- Zimmerman, S. S., and H. A. Scheraga. 1976. Stability of cis, trans, and nonplanar peptide groups. Macromolecules. 9:408–416. [DOI] [PubMed] [Google Scholar]
- Zimmerman, S. S., M. S. Pottle, G. Némethy, and H. A. Scheraga. 1977. Conformational analysis of the 20 naturally occurring amino acid residues using ECEPP. Macromolecules. 10:1–9. [DOI] [PubMed] [Google Scholar]