Activation Kinetics of Skinned Cardiac Muscle by Laser Photolysis of Nitrophenyl-EGTA

Abstract

The kinetics of Ca²⁺-induced contractions of chemically skinned guinea pig trabeculae was studied using laser photolysis of NP-EGTA. The amount of free Ca²⁺ released was altered by varying the output from a frequency-doubled ruby laser focused on the trabeculae, while maintaining constant total [NP-EGTA] and [Ca²⁺]. The time courses of the rise in stiffness and tension were biexponential at 23°C, pH 7.1, and 200 mM ionic strength. At full activation (pCa < 5.0), the rates of the rapid phase of the stiffness and tension rise were 56 ± 7 s⁻¹ (n = 7) and 48 ± 6 s⁻¹ (n = 11) while the amplitudes were 21 ± 2 and 23 ± 3%, respectively. These rates had similar dependencies on final [Ca²⁺] achieved by photolysis: 43 and 50 s⁻¹ per pCa unit, respectively, over a range of [Ca²⁺] producing from 15% to 90% of maximal isometric tension. At all [Ca²⁺], the rise in stiffness initially was faster than that of tension. The maximal rates for the slower components of the rise in stiffness and tension were 4.1 ± 0.8 and 6.2 ± 1.0 s⁻¹. The rate of this slower phase exhibited significantly less Ca²⁺ sensitivity, 1 and 4 s⁻¹ per pCa unit for stiffness and tension, respectively. These data, along with previous studies indicating that the force-generating step in the cross-bridge cycle of cardiac muscle is marginally sensitive to [Ca²⁺], suggest a mechanism of regulation in which Ca²⁺ controls the attachment step in the cross-bridge cycle via a rapid equilibrium with the thin filament activation state. Myosin kinetics sets the time course for the rise in stiffness and force generation with the biexponential nature of the mechanical responses to steps in [Ca²⁺] arising from a shift to slower cross-bridge kinetics as the number of strongly bound cross-bridges increases.

INTRODUCTION

In striated muscle, the thin filament regulatory system is composed of three troponin subunits—troponin C (TnC), troponin I (TnI), and troponin T (TnT)—and tropomyosin (Tm), an α-helical coiled coil protein that spans seven actin monomers. There is general agreement that the primary regulation of striated muscle contraction involves the interaction of calcium ions with TnC which in turn induces a structural change in the regulatory system, leading to increased cross-bridge formation, force generation, and cross-bridge cycling (reviewed by Gordon et al., 2000). Despite significant progress, a precise description of this process remains elusive. In particular, how does Ca²⁺ binding to the thin filament regulatory system control the time course of contraction?

H. E. Huxley and others proposed a two-state steric model of muscle regulation in which tropomyosin, under the control of troponin and Ca²⁺, is thought to block myosin binding sites on the actin filament in an on-off switch-like fashion (Bremel and Weber, 1972; Huxley, 1972; Kress et al., 1986). Subsequent studies of muscle activation kinetics in vitro have led to a three-state model of muscle activation (Lehrer and Morris, 1982; McKillop and Geeves, 1993). These data, along with those from structural studies (e.g., Craig and Lehman, 2001), suggest that the regulatory protein tropomyosin can be located in three positions on the thin filament. In the absence of Ca²⁺, troponin induces an “off” state, which constrains tropomyosin in a position on the outer domain of actin that sterically hinders strong cross-bridge binding. Ca²⁺ binding to TnC causes tropomyosin to move toward the inner domain of actin, bringing it closer to the groove between the two actin strands that comprise the thin filaments, and thereby exposes myosin-binding sites. A second tropomyosin shift, further toward the groove, is promoted by myosin binding and required for full thin filament activation. In all these models, Ca²⁺ regulation occurs at the step of cross-bridge formation or the transition from a weakly to strongly bound state. However, the role of these thin filament states in governing other rate constants in the cross-bridge chemomechanical cycle at intermediate [Ca²⁺] is not yet known, nor have the full effects of the thin filament kinetics been discerned in situ.

Other approaches to determine the mechanism of thin-filament control of striated muscle contraction involved mechanical perturbations to alter the distribution of cross-bridge states under steady [Ca²⁺], thus bypassing the kinetics of thin filament activation brought about by changes in [Ca²⁺]. The protocol was designed to detach cross-bridges in Ca²⁺-activated skinned rabbit psoas fibers by allowing shortening under zero load, followed by a rapid stretch back to the original fiber length. The resultant force after the restretch was low and redeveloped with a single exponential time course defined by a rate constant for tension redevelopment, k_tr (Brenner, 1988). This rate constant was found to be Ca²⁺-dependent, varying approximately 10-fold from submaximal to maximal activation levels in fast muscle types. These data, along with biochemical studies showing that whereas ATP hydrolysis of myosin subfragment 1 is increased 20-fold with Ca²⁺, the association constant for regulated actin is virtually the same in the presence and absence of Ca²⁺ (Chalovich and Eisenberg, 1982), led Brenner and co-workers to conclude that the force-generating step in the cross-bridge cycle was Ca²⁺-dependent. They proposed a kinetic model of regulation of skeletal muscle contraction, in which the thin filament regulatory complex controls the rate of cross-bridge transition from weakly attached to strongly attached states.

Studies have consistently confirmed the dependence of k_tr on [Ca²⁺] in fast (Metzger and Moss, 1990; Millar and Homsher, 1990; Regnier et al., 1995) and slow skeletal muscle (Metzger and Moss, 1990; Millar and Homsher, 1992). Studies of cardiac muscle have also shown that k_tr was Ca²⁺-dependent in skinned cardiac muscle (Araujo and Walker, 1994; Wolff et al., 1995; Vannier et al., 1996; Palmer and Kentish, 1998; Brandt et al., 1998), in cardiac myofibrils (Stehle et al., 2002), and in intact cardiac preparations (Baker et al., 1998), with one exception. Hancock and colleagues found that k_tr was independent of [Ca²⁺] in both intact ferret papillary and skinned rat trabeculae (Hancock et al., 1993, 1996, 1997), results that directly refute the kinetic model of regulation.

In skeletal muscle, it is well established that phosphate (Pi) release is coupled to the force-generating transition in the cross-bridge cycle. Studies of skinned fibers using photolysis of caged inorganic phosphate (caged P_i) have shown that a rapid increase of [P_i] inside an isometrically contracting fiber resulted in a brief delay before force dropped with an observed rate (k_Pi) proportional to the post-photolysis [P_i] at lower [Pi] but saturated at high [Pi] (Millar and Homsher, 1990; Walker et al., 1992; Dantzig et al., 1992). These results indicate that force is generated during an isomerization of a strongly attached, Pi-bound cross-bridge state: AM.ADP.Pi to AM*. ADP.Pi. This is followed by P_i release, which stabilizes a second strongly bound force bearing state, AM.ADP. Studies of both skeletal (Millar and Homsher, 1990; Walker et al., 1992) and cardiac muscle (Araujo and Walker, 1996; Martin et al., 2003) have reported k_Pi to be either slightly or not affected by [Ca²⁺], and when compared to k_tr in the same preparation, two times faster (Millar and Homsher, 1990; Regnier et al., 1995; Tesi et al., 2000). These results indicate that the tension-generating step is not directly Ca-regulated but suggest a step before force generation is able to sense the steady [Ca²⁺] via the activation level of the thin filament. However these studies do not address the question whether the time course of thin filament activation kinetics governs the time course of contraction.

To more directly assess the Ca²⁺ dependence of the transition to force-producing conformations, some studies have used laser photolysis of NP-EGTA (Ellis-Davies and Kaplan, 1994) or rapid solution changes (Stehle et al., 2002) to activate relaxed cross-bridges in skinned cardiac preparations. Thus, unlike k_tr studies in which [Ca²⁺] and presumably the level of thin filament activation is constant, the stiffness/tension time course after Ca²⁺ activation results from the coupling of two kinetic processes: 1), Ca²⁺ binding and thin filament activation and 2), cross-bridges binding and their transition to force producing states. In addition, there is mounting evidence that in cardiac tissue, these pathways interact, with strong cross-bridge binding enhancing the state of thin filament activation (Fitzsimons et al., 2001). Previous studies using caged Ca²⁺photolysis to activate skinned cardiac muscle have reported a monoexponential tension time course with a rate, k_Ca proportional to [Ca²⁺] (Araujo and Walker, 1994; Palmer and Kentish, 1998). Stehle and co-workers reported that k_tr and k_Ca declined to a similar extent with [Ca²⁺], but Kentish and co-workers reported that at [Ca²⁺] resulting in less than 60% tension, k_tr remained constant while k_Ca declined with [Ca²⁺], suggesting thin filament kinetics become rate limiting for tension generation at lower [Ca²⁺]. If thin filament activation kinetics were rate-limiting, e.g., at low [Ca²⁺] as suggested by Kentish's work, stiffness and tension should rise in near unison. In the work reported here, the Ca²⁺ dependence of skinned cardiac muscle activation was studied by monitoring simultaneously the time course of the change in stiffness and tension after laser photolysis of NP-EGTA in skinned trabeculae of the guinea pig. Upon activation, the stiffness time course led that of tension, suggesting that cross-bridge activation occurs in discrete steps with attachment or a strong cross-bridge binding state preceding tension production, consistent with the steric model. In addition, at all [Ca²⁺] the time course of stiffness led that of tension. Both time courses were biexponential and exhibited Ca²⁺ dependence. The results are discussed within the context of a simplified model of Ca²⁺ activation and cross-bridge cycling in which regulation is mediated by altering a rapid equilibrium between [Ca²⁺] and the thin filament activation state that, in turn, controls the number of myosin binding sites.

METHODS

Tissue preparation and solutions

Two types of chemically skinned guinea pig trabeculae were prepared as described previously (Smith and Barsotti, 1993). Briefly, trabeculae less than 300 μm in diameter were dissected from the ventricles of Dunkin-Hartley guinea pigs, weighing 350–400 grams. The animals were sacrificed by CO₂ inhalation in accordance with a protocol approved by Thomas Jefferson University's Animal Care and Use Committee. The hearts were excised; quickly immersed in ice-cold, Ca²⁺-free, modified Krebs solution; and gently massaged to expel the remaining blood. The trabeculae were then dissected under this cold Krebs solution, pinned slightly taut in a sylgard-coated petri dish, and then skinned in 0.5% Triton X-100 or 500 μg ml⁻¹ saponin (Matsubara et al., 1989) in relaxing solution at 21°C for one hour. The skinned tissue was transferred into relaxing solution containing 50% glycerol and stored at −20°C for up to one week. For some preparations, we attempted to minimize tissue compliance and improve stability both by maintaining cell-to-cell connections through skinning with saponin and by fixing the ends of the trabeculae with glutaraldehyde before clipping. These procedures did not affect significantly either the amplitude or the rate of the fast or slow phases of contraction. Therefore, these data were combined with those from Triton-skinned trabeculae with unfixed ends.

Unless otherwise stated, all solutions contained 100 mM TES (pH 7.1), 5 mM MgATP, 1 mM free Mg²⁺, 15 mM creatine phosphate, 1 mg/ml (∼250 units/ml) creatine kinase, and the ionic strength was adjusted to 200 mM using 1,6-diaminohexane-N,N,N′,N′-tetraacetic acid (HDTA, Aldrich Chemical Co., Milwaukee, WI). Nitrophenyl-EGTA (NP-EGTA) was synthesized as described in Ellis-Davies and Kaplan (1994). Relaxing and activating solutions contained 30 mM EGTA (pCa > 8) and 30 mM Ca²⁺-EGTA (pCa 4.5), respectively. To lower the free EGTA concentration before transfer into either activating or NP-EGTA containing solutions, the tissue was bathed in a “preactivating” solution that was identical to the relaxing solution, except that HDTA replaced all but 0.1 mM of the EGTA. The NP-EGTA solutions contained 100 mM TES, 37 mM HDTA, 15 mM creatine phosphate, 1 mg/ml creatine kinase, 10 mM glutathione, 5.5 mM ATP, 6.8 mM MgCl₂, 2 mM NP-EGTA, and ∼1.7 mM CaCl₂. The free [Ca²⁺] was adjusted for each trabecula to produce 1%–2% P_max before photolysis to ensure maximal Ca²⁺ loading of NP-EGTA.

Apparatus

The apparatus used in the experiments was described in detail in Martin and Barsotti (1994a,b). Briefly, the fibers were attached at one end to an Akers (model 801, SensoNor, Horten, Norway) silicon strain gauge mounted in a similar fashion to that described in Smith and Barsotti (1993). The resonance frequency of the transducer with connections was >3 kHz. Small (<0.5% of total length) sinusoidal length changes were made using a piezoelectric device (P-840.40, Physik Instrumente, Polytec Optronics, Costa Mesa, CA) driven by a custom-built low voltage amplifier. A two-phase lock-in amplifier equipped with a sine wave oscillator (Model 3961B, Ithaco, Ithaca, NY) supplied the sine wave reference and performed real-time demodulation of the sinusoidal tension oscillation into components in-phase and 90° out of phase with the imposed length change. Only the in-phase component was analyzed in these experiments to provide the stiffness of the fiber, an estimate of the number of attached cross-bridges. In some experiments, a PC-based program that emulates a lock-in amplifier was used to demodulate the sinusoidal oscillation in the tension recordings. The signal from the strain gauge was preamplified and distributed to a four-channel digital oscilloscope (Model 4094C, Nicolet, Madison, WI), the lock-in amplifier, and a custom built notch filter, which removed the small sinusoidal signal for some of the tension recordings. Length and tension data were collected at 5 kHz and stored digitally by the oscilloscope or a data acquisition board (MetraByte, DAS-16f, Taunton, MA) installed in a PC.

NP-EGTA was photolyzed by a 50 ns pulse of 347-nm light produced using a frequency doubled, Q-switched ruby laser (Laser Applications, Winter Park, FL). The system employed an angle-tuned, temperature-stabilized potassium dideuterium phosphate (KDP) crystal to frequency-double the output from 694 to 347 nm. The primary beam (λ = 694 nm) was separated from the 347 nm pulse by a Brewster stack polarizer and a UG-11 filter placed between the KDP crystal and the tissue. The 0.5-inch-diameter beam was compressed to 1.5 mm wide and focused onto the trabeculae using a quartz cylindrical lens. An adjustable slit assembly mounted immediately in front of the preparation masked the hooks extending from the tension transducer and the piezo. The laser energy striking the fiber was varied between ∼30 to 250 mJ by placing glass plates in the beam. The sequence of charging, firing the laser, and triggering of data collection were controlled by a custom-built programmable timer.

Protocol

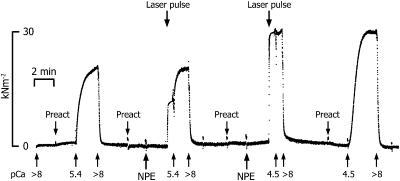
T-shaped aluminum foil clips were wrapped around each end of the trabeculae, which was then mounted in the mechanical apparatus while bathed in relaxing solution. The tissue was stretched ∼1.2 times its slack length to set the initial sarcomere spacing. Fiber dimensions, length, width, and sarcomere length were measured optically. The mean diameter and sarcomere length were 188 ± 8 μm and 2.18 ± 0.02 μm (mean ± SE, n = 25). Sarcomere length was checked several times during the experiment. All experiments were carried out at 23°C, 200 mM ionic strength, and pH 7.1. The averaged force developed in pCa 4.5 was 33 ± 2.4 kN/m². The tissue was transferred from relaxing solution to a preactivating solution and incubated for two minutes to lower the EGTA concentration in the tissue before transfer into solutions containing either various concentrations of free [Ca²⁺] or containing NP-EGTA. To estimate the final [Ca²⁺] photoreleased, the following protocol was used to determine the pCa-tension relationship in each trabecula. The tissue then served as a bioassay for the free [Ca²⁺] produced upon photolysis of NP-EGTA, based on the amount of tension developed after activation. The trabeculae were activated first using solutions containing various known free [Ca²⁺]. Subsequent control activations at different [Ca²⁺] bracketed contractions induced by photolysis of NP-EGTA. In addition, after a level of steady tension was reached after NP-EGTA photolysis (see the middle two contractions in Fig. 1), the trabeculae were transferred into solution containing known concentrations of free Ca²⁺ before eventual transfer into relaxing solution. In the procedure illustrated in Fig. 1, after an initial contraction in pCa 5.4, the tissue was relaxed and then activated by photolysis of NP-EGTA at attenuated pulse energy. When a relatively steady tension level was achieved, the tissue was transferred to a pCa 5.4 solution and then relaxed in a pCa > 8 solution. The tissue was activated again by the photorelease of Ca²⁺, using higher laser energy, transferred immediately into activating solution (pCa 4.5). The steady-state pCa-tension relationship for each trabecula was determined at four pCas. The level of steady tension reached after NP-EGTA photolysis was then compared to the steady-state pCa-tension relationship to estimate the [Ca²⁺] released in that photolysis trial. In Fig. 1, the free [Ca²⁺] produced in the photolysis trials was ∼pCa 5.5 and 4.8 by light pulses of 100 and 161 mJ, respectively.

FIGURE 1.

A slow time base recording of tension produced by a single trabecula during four successive relax-contract-relax cycles, illustrating the protocol used to estimate the free [Ca²⁺] produced after the photolysis of NP-EGTA. The contractions induced by photolysis (middle two activations) were bracketed by relaxations and then contractions in solutions containing known [Ca²⁺], in this experiment pCa 5.4 and 4.5. In addition, when peak tension was reached in the contractions evoked by NP-EGTA photolysis, the tissue was transferred immediately into activating solutions containing known free [Ca²⁺]. The goal was to establish the pCa-tension relationship for each trabecula and then to use this relation in estimating the free [Ca²⁺] produced after NP-EGTA photolysis based on the amount of tension produced. Laser energy: 100 mJ (first trial), 161 mJ (second trial). Trabecula dimensions: 1115 μm long, 197 μm wide. Sarcomere length: 2.13 μm.

Data analysis

The time course of tension development and the change in stiffness were fit to the sum of two exponential terms (Eq. 1), whereas the steady-state pCa-tension relation was fit by a modified Hill equation (Eq. 2):

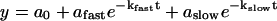(1)

and

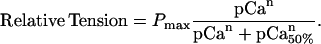(2)

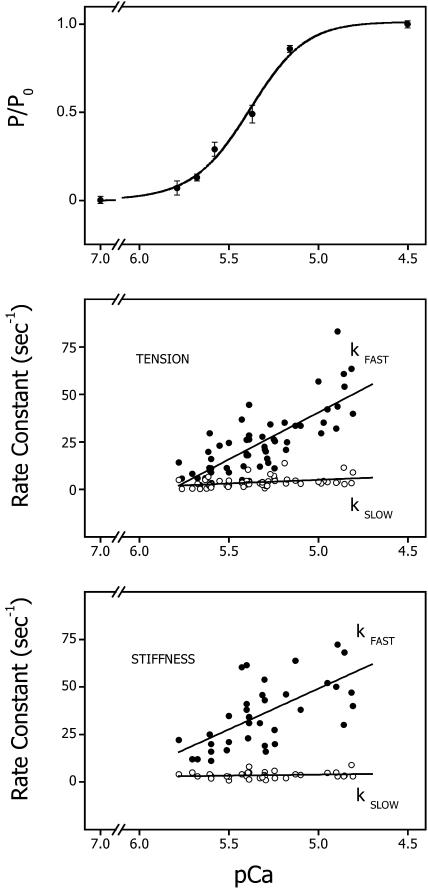
Both fitting procedures used the Levenberg-Marquardt (Press et al., 1988) routine of nonlinear least squares. When used, regression lines were calculated by the method of least squares. Data are expressed as mean ± the standard error of the mean (mean ± SE). In the case of the exponentials, the goodness of fit (χ²) was typically improved by going from one to two exponentials; thus, a biexponential was applied to all traces for consistency. Disparate rate constants were discerned for all but some of the lower activation levels (see Fig. 5).

FIGURE 5.

Steady-state tension and the observed rates for the rise in stiffness and tension plotted as a function of pCa. (Upper panel) The average pCa-tension relation for trabeculae used in this study. The data are expressed as means ± SE. The line is a fit by a modified Hill equation (see Eq. 2). The data are best fit with n = 2.76 and pCa_50% = 5.39. (Middle panel) The rate of the two components of the tension time course after activation by laser photolysis of NP-EGTA plotted as a function of the pCa produced by photolysis of NP-EGTA. The lines were fit by the method of least squares and are described by the following expression: y = 286 − 49x, r = 0.77 and y = 24 − 3.8x, r = 0.39, respectively, for k_fast and k_slow, from 58 determinations on 25 trabeculae. The free [Ca²⁺] was estimated from the pCa-tension relation for each trabecula as described in the text and Fig. 1. (Lower panel) The rate of the two components of the stiffness rise plotted as a function of the pCa produced by photolysis of NP-EGTA. The lines were fit by the method of least squares and are described by the following expression: y = 263 − 43x, r = 0.65 and y = 9 − 1x, r = 0.18, for k_fast and k_slow, respectively, from 37 determinations on 13 trabeculae.

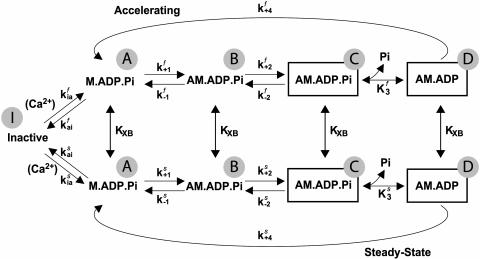
Prototypical biexponential tension and stiffness traces were generated from rate constant data averaged from multiple trials on multiple trabeculae (Fig. 5). The kinetic model shown in Scheme II was fitted to these traces using a Davidon-Fletcher-Powell algorithm, which adjusted selected parameters to achieve a best fit. The fitting and modeling routines were part of a data analysis program developed in-house using Borland Turbo C++ 3.0. The model is described in detail in the Appendix.

SCHEME II.

RESULTS

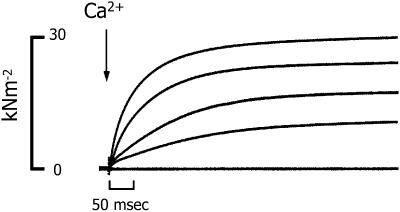
The Ca²⁺ dependence of the time course of stiffness and tension development was studied in skinned cardiac trabeculae, using laser photolysis of NP-EGTA to rapidly increase [Ca²⁺] within the contractile protein lattice. In Fig. 2 the tension time courses from a series of contractions evoked by NP-EGTA photolysis in a single trabeculae are superimposed. The free [Ca²⁺] produced was varied between pCa 5.9 and 4.8 by altering the laser energy and maintaining the total concentration of NP-EGTA and Ca²⁺ constant for each trabecula. The free [Ca²⁺] was estimated from the pCa-tension relation for each trabecula, as described in the methods section.

FIGURE 2.

Superimposed tension recordings of successive activations of a single trabecula by laser photolysis of NP-EGTA. The estimated free [Ca²⁺] used to initiate each contraction was pCa 4.79, 5.27, 5.40, and 5.44, respectively, changed by varying laser energy. For reference, the lowest tracing shows the tension recorded in relaxing solution (pCa > 8.0). Trabecula dimensions: 935 μm long, 172 μm wide. Sarcomere length: 2.20 μm.

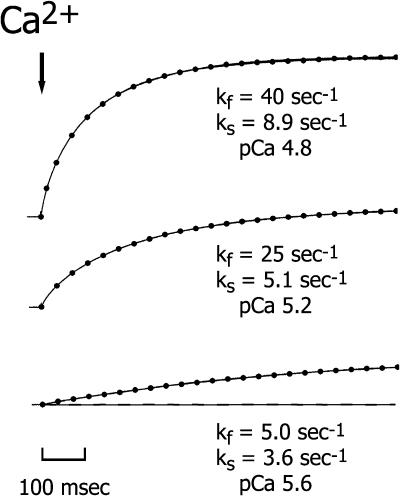
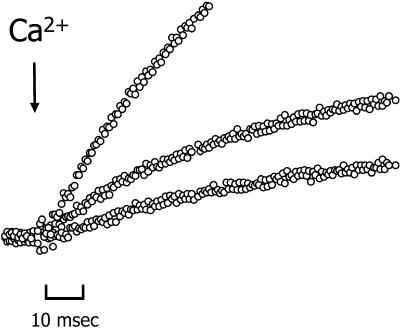
The time course of the rise in stiffness and tension was biexponential at all [Ca²⁺]. The data were fit to a double exponential expression (Eq. 1) to determine the rates and amplitudes of the two phases of the respective time courses. Fig. 3 illustrates the fit of the equation to the tension response of a skinned trabecula after a step increase in [Ca²⁺] from pCa > 6 to 4.8, 5.2, and 5.6, top, middle and bottom traces, respectively. In maximally activated contractions, P/P₀ > 0.9, the amplitude of the fast component of the tension rise (k_fast) averaged 21 ± 2% (mean ± SE, n = 11), with an average rate of 48 ± 6 s⁻¹, whereas the rate of the slower component (k_slow) was ∼8 times lower at 6.2 ± 1 s⁻¹. There was a brief lag (∼5 ms) after the laser pulse and before the rise in tension. A mechanical artifact resulting from the laser beam striking the preparation masked part of this early rise (typically 2–4 ms). However, there was no discernible dependence of the lag duration on [Ca²⁺] (see Fig. 4), and even at the lower [Ca²⁺] tension rise was consistently detected within 5 ms.

FIGURE 3.

Tension recordings from three contractions induced by different free [Ca²⁺] produced by NP-EGTA photolysis. The dots superimposed on the traces represent the fit of the recordings to a double exponential expression (Eq. 1). The estimated free [Ca²⁺] used to initiate each contraction are shown. The amplitude of the fast component of the tension rise was 26%, 20%, and 19% in the upper, middle, and lower panels, respectively. For reference, the dashed line in the lower panel represents pre-photolysis tension (∼2% of P_max). Trabecula dimensions: 918 μm long, 146 μm wide. Sarcomere length: 2.14 μm.

FIGURE 4.

Tension recordings superimposed on a rapid timescale of successive activations of a single trabecula by NP-EGTA photolysis. The estimated free [Ca²⁺] used to initiate each contraction was pCa 4.91, 5.40, and 5.55, respectively, changed by varying laser energy. Trabecula dimensions: 1224 μm long, 209 μm wide. Sarcomere length: 2.21 μm.

The rate of both the fast (k_fast) and slow (k_slow) components of the tension rise varied linearly with the log of photoreleased [Ca²⁺], as shown in the center panel of Fig. 5. The two rates varied approximately seven- and twofold, respectively, between pCa 5.8 and 5.0. The slope of the relationship between k_fast and k_slow and pCa was 50 and 4 s⁻¹ per pCa unit (p < 0.001 and p < 0.02, respectively; n = 61). A plot of the relative amplitude of these components as a function of [Ca²⁺] showed that they were Ca²⁺-independent (p > 0.9 for both k_fast and k_slow, data not shown). The composite pCa-tension relation from all the trabeculae used in these experiments is shown in the top panel of Fig. 5. The data are represented as means ± SE and are fit to a modified Hill equation (Eq. 2), giving values of n = 2.8 and pCa₅₀ = 5.4. The method of using each trabecula as a bioassay for estimating free [Ca²⁺] was limited to concentrations between approximately pCa 5.9 and 4.8, i.e., concentrations that developed force but did not saturate the level of developed force.

In the conditions used in this study (2 mM NP-EGTA, 1.7 mM total Ca²⁺), we estimated that at least 12% photolysis of NP-EGTA was required to step the free [Ca²⁺] from pCa > 6 to < 5, the concentration necessary for full activation of skinned cardiac trabeculae. Under these starting conditions NP-EGTA was not fully saturated with Ca²⁺. Because of the rebinding of photolytically released Ca²⁺ to free unphotolyzed NP-EGTA, the [Ca²⁺] was not “stepped” to a new higher concentration but instead the time course of Ca²⁺ release was transient, exhibiting a sharp rise and a slower decay to the final level. Estimates of the time course of the Ca²⁺ transient in solution studies using the fluorescent calcium indicator, calcium orange-5N, and computer simulations of the expected transient indicated that the steady-state level of Ca²⁺ is attained in under 3 ms (Ellis-Davies et al., 1996). The effect of this transient on the kinetics of activation of contraction is not clear. However, in the present experiments, the lower [Ca²⁺] released were achieved by reducing laser energy and thereby reducing the extent of NP-EGTA photolysis. Lower pulse energy should have resulted in a larger Ca²⁺ transient, as proportionately more of the Ca²⁺ released from the photolyzed Ca²⁺-loaded NP-EGTA would rebind to the unphotolyzed Ca²⁺-free NP-EGTA. However, neither the tension nor stiffness time course exhibited any rapid “spikes” within the initial 3 ms, even at the lowest free [Ca²⁺] produced, indicating the Ca²⁺ transients were too rapid to significantly alter the kinetics of activation. In addition, if the Ca²⁺ transient were responsible for k_fast, it would be difficult to explain the wide variation in k_fast with final [Ca²⁺] even though the Ca²⁺ transient varied much less, or why the amplitude of the fast component of tension rise was relatively constant at around 20% of the total tension response at all [Ca²⁺] even though the Ca²⁺ transient was proportionately larger at lower [Ca²⁺]. Thus the observed stiffness/tension time course probably reflected the intrinsic activation and cross-bridge kinetics of the preparation.

It was of interest to compare the time course of tension with that of stiffness. In the simplest interpretation of the work of Brenner and Eisenberg (1986), if calcium ions control the transition of cross-bridges from weakly to strongly attached conformations, then stiffness and tension should have the same time course. If, instead, cross-bridge formation and tension production occur in successive steps in the cross-bridge cycle, then the rise in stiffness should lead that of tension.

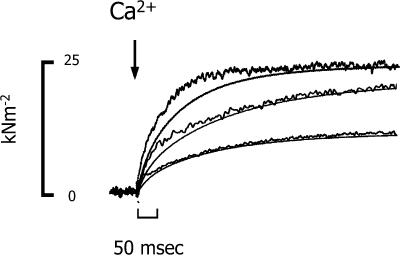
The time course of the change in the in-phase component of stiffness, a measure of the number of cross-bridge attachments, was monitored using a 1-kHz sinusoidal oscillation and demodulating the oscillation from the steady tension using either a lock-in amplifier or PC-based program that emulated a lock-in amplifier. The time course of stiffness, like that of tension, was biexponential. Fig. 6 shows the time course of stiffness and tension in three contractions of the same trabecula after the release of varying [Ca²⁺]. The initial rise in stiffness consistently increased with a slightly faster rate than tension at all [Ca²⁺]. There was a trend for stiffness to lead tension more at lower [Ca²⁺]. At full activation, pCa < 5.0, the rates of the fast and slow phases of the stiffness rise were 56 ± 7 and 4.1 ± 1 s⁻¹ (mean ± SE, n = 11). The relative amplitudes of the fast and slow components of the stiffness increase were similar to those of the tension time course, ∼25% and 75%, respectively, and Ca²⁺-independent (data not shown). The Ca²⁺ dependence of the two phases of the stiffness time course is shown in the bottom panel of Fig. 5. The fast component of the stiffness rise exhibited a Ca²⁺ dependence similar to the fast phase of the tension time course: 43 s⁻¹ per pCa unit (p < 0.001, n = 37). The rate of the slower component showed a slight but insignificant dependence on [Ca²⁺] (1 s⁻¹ per pCa unit, p < 0.3).

FIGURE 6.

The time course of the rise in tension and the in-phase component of stiffness in a trabecula after activation by NP-EGTA photolysis. To more easily compare the time of the change in tissue stiffness with the rise in tension, the stiffness recordings (noisier traces) were scaled to the peak tension for that activation. The final pCa produced on photolysis were 4.89, 5.17, and 5.39, respectively. Trabecula dimensions: 840 μm long, 208 μm wide. Sarcomere length: 2.16 μm.

DISCUSSION

The stiffness and tension time course was measured after a rapid increase in free [Ca²⁺] using laser photolysis of NP-EGTA within the contractile protein filament lattice of guinea pig skinned trabeculae. Both the stiffness and tension time courses were sensitive to varying [Ca²⁺] photolytically produced. At all [Ca²⁺], the rise in stiffness initially led that of tension by a few milliseconds but converged before steady tension was achieved. Both time courses exhibited biexponential behavior and with Ca²⁺-sensitive rates. The overall amplitude of the mechanical responses scaled with [Ca²⁺], whereas the relative amplitude of the rapid and slow components were independent of [Ca²⁺].

Stiffness-tension time course

As shown in Fig. 2, after a brief lag of ∼4 ms, NP-EGTA photolysis produced a rapid rise in stiffness and tension, both with a biexponential time course. The lag did not show a [Ca²⁺] dependence that would be expected if it arose from steps close to the Ca²⁺ binding step. Cheung and co-workers (Dong et al., 1996, 1997) reported that Ca²⁺ binding to isolated cardiac TnC or troponin is best described as a three-step process in which the initial bimolecular step is in rapid equilibrium with the Ca²⁺-bound complex, followed by two sequential first-order transitions. These transitions are believed to reflect helix reorientations that form the basis for Ca²⁺-induced interactions between TnC and TnI. Because we observed no [Ca²⁺]-dependent lag in the rise of tension and stiffness in fibers after a step [Ca²⁺] increase, these transitions must be too rapid to be rate limiting for cross-bridge formation or tension generation in situ. Elevated [Pi] has been shown to significantly increase the rate of tension rise after activation by NP-EGTA, which would not be expected if thin filament activation were limiting cross-bridge formation (Martin et al., 1995; Araujo and Walker, 1996). Our results are consistent with the rate limitation being within myosin kinetics rather than thin filament activation kinetics.

We propose instead that the onset of cross-bridge formation or strong binding in a pre-force state is controlled by a rapid equilibrium between [Ca²⁺] and the thin filament state, which controls the effective concentration of cross-bridge binding sites. The observed Ca²⁺-dependent rate of the stiffness and tension time course thus represents the flux of strong cross-bridge binding that is itself determined by myosin kinetics. A more in-depth discussion of an activation and cross-bridge mechanism that fits the majority of the observed characteristics of the Ca²⁺-dependent rise in stiffness and tension is provided later in the discussion of the model.

Until recently, the observed delay of force development relative to stiffness upon activation would be considered as evidence for a two-step mechanism of tension generation. The cross-bridge first attaches to the thin filament in a low force state followed by a second transition to a high force state. Thus, the earlier rise in stiffness over tension would indicate that Ca²⁺ regulation is mediated by controlling cross-bridge attachment, which is followed rapidly by force generation. This mechanism for force generation is supported by mechanical studies of fibers using ATPγS (Dantzig et al., 1988) and structural data from fiber studies using x-ray and fiber bifringence showing that myosin heads movement toward the thin filament precedes tension development (Kress et al., 1986; Irving, 1993). Evidence from electron microscopy of rapidly frozen fibers after activation by caged-Ca²⁺ (Lenart et al., 1996) also supports this view. Nevertheless, these studies do not prove that structural data and stiffness measurements detect the same attached cross-bridge state at the initiation of contraction.

Studies from several laboratories have shown that myofilament compliance, once thought to be negligible, may represent ∼50% of the fiber compliance (Huxley et al., 1994; Wakabayashi et al., 1994; Higuchi et al., 1995; Huxley and Tideswell, 1996). Thus, the lead of stiffness with respect to tension could be a complication of delayed tension increase resulting from sarcomeric shortening to extend the myofibrillar compliance, since filament sliding is thought to decrease tension more than cross-bridge number (Huxley, 1957). However the work of Cecchi et al. (1991) and, more recently, Hoskins et al. (2001) strengthens the correlation between structural data and stiffness by showing that intensity changes in the equatorial reflection from length-clamped intact single muscle fibers and stiffness led tension and, in addition, lattice expansion (thought to be another index of cross-bridge formation) and stiffness had similar time courses during the tetanus rise. These provide further support for the existence of an attached low force cross-bridge state before the force-generating transition.

Comparison with other studies

Previous studies using photolysis of caged-calcium to initiate contraction in skinned striated muscle universally report a Ca²⁺-dependent rate of tension development (Ashley et al., 1991; Araujo and Walker, 1994; Wahr and Rall, 1997; Palmer and Kentish, 1998). However, the reported shape of the tension time course varied. Studies by Ashley et al. (1991) and Wahr and Rall (1997) found a biexponential time course for frog skeletal muscle, whereas a monoexponential tension time course was reported for rabbit psoas, rat cardiomyocytes (Araujo and Walker, 1994), and rat and guinea pig trabeculae (Palmer and Kentish, 1998). The reasons for these differences are not known, particularly considering that the later studies by Palmer and Kentish were carried out on the same preparation using conditions similar to those in this study. Nevertheless, the slowing of the tension time course may represent a decrease in cross-bridge turnover during the rising phase of tension development and is consistent with results from earlier studies on fast and slow skeletal muscle using a real-time phosphate assay (He et al., 1997) or mechanical transients (Ford et al., 1986; Bagni et al., 1988; Josephson and Edman, 1998). The early rapid rates for cross-bridge binding and force generation are in accordance with the results from these later mechanical studies of skeletal muscle indicating that the rate for isometric tension recovery after a small quick length change (Ford et al., 1986; Bagni et al., 1988) or maximal shortening velocity (Josephson and Edman, 1998) is faster when applied during the rising phase of a tetanus than when applied on the plateau.

The maximal rate of the fast component of the stiffness and tension rise, k_fast, was 56 and 48 s⁻¹, respectively, whereas the rate of the slower component, k_slow, was around 6 s⁻¹, for both. The k_fast for stiffness and tension increased with pCa, 43 and 50 s⁻¹ per pCa unit, respectively, when the free [Ca²⁺] released was increased from ∼2 to 12 μM. k_slow for stiffness was not Ca²⁺-sensitive over the same range, whereas k_slow for tension was 4 s⁻¹ per pCa unit. In previous studies on skinned rat cardiomyocytes, Araujo and Walker (1994, 1996) reported that the apparent rate constant for tension development after caged calcium photolysis at 15°C, k_Ca increased linearly with Ca²⁺ nearly fivefold from 0.9 to 4 s⁻¹ between [Ca²⁺] producing 0.2 to 0.85 of P_max, compared to around eightfold (6.3 to 48 s⁻¹) for k_fast in these studies at 23°C. In a similar study of both rat and guinea pig skinned trabeculae at 22°C, Palmer and Kentish (1998) found a 14-fold (1 to 14 s⁻¹) increase in k_Ca in rat over a slightly broader range of [Ca²⁺] and only fivefold (0.5 to 2.6 s⁻¹) in guinea pig. The larger k_Ca near saturating [Ca²⁺] in the rat compared to guinea pig myocardium likely reflects the faster cross-bridge kinetics of rat cardiac myosin rather than differences in thin filament activation kinetics. However, it is difficult to reconcile why the value for k_Ca for guinea pig reported by Palmer and Kentish (1998) is ∼2 times slower than k_slow (6.2 s⁻¹) found in this study and 7.2 s⁻¹ reported by Stehle et al. (2002) for guinea pig myofibrils activated by rapid solution change at 23°C.

One of the main goals of this and similar studies is to describe the mechanism responsible for the Ca²⁺-dependence in the rate and extent of tension development in cardiac muscle. Some insights into the mechanism lie in determining both the step in the cross-bridge cycle that is regulated by thin filament activation and whether the rate of thin filament activation governs the stiffness/tension time course. As mentioned previously, the results showing a lead of stiffness over tension after Ca²⁺ activation along with those from a number of other laboratories using a variety of techniques indicate that Ca²⁺ regulation of striated muscle contraction is mediated by controlling cross-bridge attachment. An alternative hypothesis is that the rate of the tension generation step in the cross-bridge cycle or f_app, the rate of cross-bridge transition from a weakly attached low force state to a strongly attached high force state is controlled by Ca²⁺-induced changes in the thin filament (Brenner and Eisenberg, 1986). k_tr, the rate of tension redevelopment after a period of rapid shortening and a stretch back to initial length, is thought to measure f_app. All studies of fast and slow skeletal muscle (see, e.g., Metzger and Moss, 1990) and in most studies of cardiac muscle (see Introduction) have reported that k_tr is strongly Ca²⁺-sensitive. The results from k_tr are consistent with the hypothesis that Ca²⁺ regulation controls the rate of the force-generating step in the cycle. However, this conclusion is based predominantly on the assumption that k_tr measures only the force-generating transition and not attachment. f_app includes both the strong attachment and force-generating steps in the cross-bridge cycle, either of which could be Ca²⁺-sensitive and yield a Ca²⁺-sensitive f_app or k_tr.

Studies using caged-Pi have probed the force-generating steps of the cross-bridge cycle in skinned fast (Millar and Homsher, 1990; Dantzig et al., 1992; Walker et al., 1992) and slow (Millar and Homsher, 1992) skeletal and cardiac muscle (Araujo and Walker, 1996). These studies have concluded that force generation is a two-step mechanism involving an isomerization of AM.ADP.Pi state from a low to a high force state that is stabilized by a fast equilibrium step involving Pi release to form a second high force state, AM.ADP. The rate of the decrease in force induced by a sudden increase in [Pi], k_Pi, is a direct measure of this isomerization rate or the force-producing step in the cross-bridge cycle. As mentioned previously, studies of both skeletal and cardiac muscle have reported k_Pi to be either slightly or not affected by [Ca²⁺], indicating that the force-generating step in the cycle is not directly controlled by Ca²⁺. These results, along with those from studies mentioned above showing a strong Ca²⁺ dependence of k_tr, and still others showing that k_Pi is two to three times faster than k_tr, indicate that k_tr predominantly reflects the rate of a cross-bridge transition before tension generation. Together these findings are consistent with a model of Ca²⁺ regulation in which control is mediated by altering the rate of strong cross-bridge binding, which is followed by a rapid transition into a force-generating state.

Does thin filament activation or myosin kinetics limit cross-bridge formation? To date it has been difficult to measure directly the kinetics of thin filament activation in situ. In studies of the structural changes using time-resolved x-ray diffraction during activation of intact frog muscle, Kress et al. (1986) found that the position of tropomyosin changed before cross-bridges moved toward the thin filament. Baylor et al. (1983) concluded that in frog skeletal fibers at 16°C, the Ca²⁺ transient reaches its peak around 10 ms after stimulation, and Ca²⁺-troponin binding would saturate around 14 ms after stimulation. This Ca²⁺-TnC binding time course correlates well with a t_1/2 of 8 ms for tropomyosin movement reported by Kress et al. (1986) at a similar temperature and implies that the thin filament structural changes result from a rapid Ca²⁺ binding equilibrium that is rapid compared to cross-bridge formation.

In some of the trials in the present study, the free [Ca²⁺] before photolysis was sufficiently high to induce partial activation, in a few cases as high as 15% of maximal. In these cases, the level of Ca²⁺-loaded NP-EGTA before photolysis and thus the size of the step in free [Ca²⁺] would be greater. Nevertheless, the rate of the stiffness or tension rise saturated at all [Ca²⁺] that produced maximal tension. In a study comparing k_tr and k_Ca in skinned trabeculae from rat and guinea pig, Palmer and Kentish (1998) reported that in a given species, the maximal k_tr was similar to that of k_Ca. A similar finding was reported by Stehle et al. (2002) using rapid solution changes to activate guinea pig cardiac myofibrils. Because k_tr is measured under constant Ca²⁺ activation, bypassing any direct effect on the rate at which Ca²⁺ turns on the thin filament regulatory proteins, the similarity of k_Ca and k_tr suggests that the maximal Ca²⁺-activated rate of force development is limited by the rate of strong cross-bridge binding rather than by the rate at which the thin filament is activated by Ca²⁺ binding to TnC. The finding that Pi increased the rate of tension development after caged-Ca²⁺ photolysis in skinned trabeculae (Martin et al., 1995) and in cardiac myofibrils using rapid solution changes (Stehle et al., 2002) also supports this conclusion.

Is thin filament activation rate limiting for cross-bridge formation at subsaturating [Ca²⁺]? Biochemical studies of isolated cardiac TnC and troponin suggest that Ca²⁺-binding kinetics are sufficiently slow to limit strong cross-bridge binding (Dong et al., 1996, 1997), but it is not known whether this is the case within the intact contractile apparatus. In both skinned rat and guinea pig cardiac trabeculae, k_Ca and k_tr were reported to have similar Ca²⁺ sensitivities at activation levels producing 60% of maximal tension or greater, suggesting that over this range of [Ca²⁺], thin filament activation rate was not limiting for cross-bridge formation (Palmer and Kentish, 1998). As the activation levels were lowered further, k_tr remained relatively constant while k_Ca declined (Palmer and Kentish, 1998). However, Wolff et al. (1995) had reported previously that k_tr decreased linearly with relative tension down to activation levels producing 18% of maximal tension in skinned rat trabeculae with sarcomere length control and using a slack/release protocol that resulted in lower residual tension before the redevelopment phase. These results indicate that even at low levels of thin filament activation, cross-bridge binding and not thin filament kinetics determines the rate of tension rise. This premise is supported by the results from a study by Brenner and Chalovich (1999) in which a thin filament activation state at varying [Ca²⁺] was directly probed by using a fluorescent tag on TnI during a k_tr protocol. The authors concluded that equilibration among different states of the thin filament with [Ca²⁺] is rapid, and, as a result, k_tr was not rate limited by changes in the thin filament activation state that may have been induced by the isotonic contraction before tension redevelopment.

In our model described below, Ca²⁺-TnC binding and thin filament activation kinetics are too fast to limit cross-bridge formation and thus are more closely described by a steric blocking model of activation in which Ca²⁺ control of force generation is mediated by altering the apparent rate of strong cross-bridge binding. In terms of the three-state structural model of activation (Vibert et al., 1997), full switching on of the thin filament occurs stepwise, first requiring the movement of tropomyosin caused by Ca²⁺ binding to troponin, followed by a further movement induced by myosin binding to actin. Geeves and co-workers first introduced a three-step model from kinetic and equilibrium-binding studies of S1 binding to pyrene-labeled regulated actin filaments (see McKillop and Geeves, 1993). The present results would imply that the transition from the blocked (or B) state to the Closed (or C) or Ca²⁺-induced state is controlled by a rapid Ca²⁺-TnC equilibrium, whereas the next transition from the C to the M (or myosin-induced) state is dictated by the speed of myosin attachment. The force-generating transition quickly follows this cross-bridge formation step. Given that k_Pi is Ca²⁺-insensitive, only the B to C transition must be Ca²⁺-dependent. This is in general agreement with the findings of McKillop and Geeves (1993) in which the first transition (B to C) in thin filament states was found to be more Ca²⁺-sensitive than the final transition into the fully on state.

Thus, the apparent Ca²⁺ dependence of the rise in stiffness/ tension results from the flux of myosin binding, and the level or the state of the thin filament rather than the rate of its activation. Accordingly, the observed rate of tension development is not limited by the rate of structural changes in troponin or other components of the thin filament regulatory system. An implication of such a mechanism is that the tension time course is governed principally by myosin speed and is affected by conditions that influence cross-bridge kinetics such as [Pi] (Martin et al., 1995; Tesi et al., 2000), lattice spacing (Kawai and Schulman, 1985), and myosin light chain phosphorylation (Sweeney and Stull, 1990).

CONCLUSION

The results of the present study indicate that the rate and extent of both the increase in stiffness and tension in skinned cardiac trabeculae activated by laser photolysis of caged Ca²⁺ (NP-EGTA) is sensitive to the [Ca²⁺] released. The time course of the change in stiffness initially led that of tension at all [Ca²⁺]. These results are consistent with a mechanism of Ca²⁺ activation in which Ca²⁺ binding to TnC is in a rapid equilibrium with the level or state of thin filament activation. The level of activation controls the flux of cross-bridges into strongly attached low force states that are determined by the speed of myosin which, in turn, dictates the time course of the rise in stiffness and tension.

APPENDIX. MODEL DESCRIPTION

Model overview

The aim of the modeling was to find a kinetic scheme of Ca²⁺activation and cross-bridge cycling with the minimal number of steps that could accommodate several findings. Briefly, these include that the time courses of both stiffness and tension were biexponential and the rates for both phases were Ca²⁺-dependent. The amplitudes of the two phases relative to each other were Ca²⁺-independent. The rates for the fast phase were significantly faster than estimates of k_Pi from other studies (Martin and Barsotti, 1996), indicating that cross-bridge kinetics were more rapid during the initial rise in tension than later. Finally, k_Pi has been reported in other studies as minimally Ca²⁺-sensitive or Ca²⁺-insensitive. The proposed scheme is based on well-established cross-bridge states and includes a feedback mechanism in which cross-bridges enhance thin filament activation and slow their kinetics.

In this model, Ca²⁺ regulation is represented as a Ca²⁺-dependent, rapid equilibrium between inactive and active states of each regulatory unit. A regulatory unit is modeled as a single cross-bridge binding site. Because the contractile lattice constrains myosin to interact only with nearby, active regulatory units, the ratio of active myosin heads to active regulatory units is assumed to be constant. The effect of Ca²⁺ regulation is, therefore, to control the population of actively cycling myosin heads, which in this model is described as a transition from “Inactive”, a state that does not bind actin, to M.ADP.Pi states that are able to form cross-bridges. An alternative mechanism would be to employ direct control of the rate constants at the cross-bridge formation step. However, such a mechanism would eliminate the distinction between detached, cycling heads, i.e., those near active regulatory units, and detached heads near inactive regulatory units.

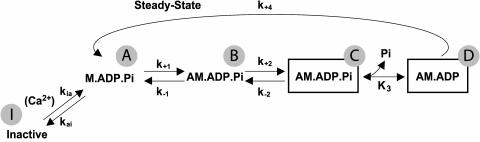
A four-state model (see Scheme I) is used to describe the cross-bridge biomechanical cycle. Heads in the M.ADP.Pi state bind to thin filament in a low force conformation, AM.ADP.Pi. Force is generated by the isomerization of this state to a Pi-bound, high force state, which is illustrated by the box surrounding, AM.ADP.Pi in Scheme I. The subsequent Pi-release step results in another high force state, AM.ADP. This two-step, force-generating mechanism is consistent with that proposed from studies of striated muscle using rapid jumps in [Pi] to alter isometric tension (e.g., Dantzig et al., 1992) and probing the effects of Pi on force generation by sinusoidal length oscillations (Kawai and Halvorson, 1991).

SCHEME I.

The rates of both cross-bridge binding and force generation are independent of thin filament activation kinetics. The attachment step, however, is “throttled” by the Ca²⁺-controlled rapid equilibrium that precedes it, with the apparent rate of attachment increasing as the equilibrium shifts toward the active state, saturating at maximal activation. To fit the biexponential stiffness and tension transients that follow activation by caged-Ca²⁺ photolysis, additional steps are required to be Ca²⁺-dependent, e.g., k₂ and/or K₃. However, such a scheme fails to fit several observations from other studies on the same and other muscle preparations. If either k₂ or K₃ are permitted to vary with [Ca²⁺], the model in Scheme I predicts that k_Pi will be highly Ca²⁺-dependent, inconsistent with results of previous studies on fast and slow skeletal and cardiac muscle. A more accurate model must reconcile seemingly divergent results: k_Ca is Ca²⁺-dependent, suggesting a Ca²⁺-controlled force-regenerating step, whereas k_Pi is Ca²⁺-insensitive, suggesting that the force-generating step is not Ca²⁺ controlled. In addition, we have found previously (Martin and Barsotti, 1996) that the apparent forward step of force isomerization, k_bc, deduced from caged-Pi experiments during steady-state contraction was 15 s⁻¹ and thus too slow to account for k_fast of 48 s⁻¹ at saturating [Ca²⁺] as described above.

The results suggest that initial cross-bridge kinetics are rapid, slowing toward their steady-state values during the stiffness/tension rise. We chose to model this behavior using two pathways as shown in Scheme II, where the upper and lower pathways represent the initial and final (steady state) cross-bridge kinetics. k_fast and k_slow reflect the different kinetics in the two pathways, and, to fit the data, the shift to the lower path should occur around 20% of the total tension rise at any pCa. The equilibrium between the pathways is thus described by a function, K_XB, that shifts in favor of the lower or slow path as cross-bridges accumulate. This shift lumps together cooperative effects of cross-bridges on both the thin filament and neighboring myosin heads. Such effects could include enhancement of thin filament activation (reviewed in Gordon et al., 2000) and strain imposed on cross-bridges when the two heads of the same myosin are bound simultaneously (Schmitz et al., 1996; Chakrabarty et al., 2002). As the fraction of strongly attached cross-bridges increases, it is presumed that each successive head is increasingly unable to bind to its nearest (i.e., most kinetically favorable) binding site. Such competitive interaction with neighboring heads likely decreases rate constants in the pathway, e.g., the weak-to-strong binding transition, tension generation, etc., while the equilibrium is maintained in favor of attachment as a result of cross-bridge-enhanced thin filament activation. This is similar conceptually to the myosin-induced C to M transition in the three-state model of thin filament activation mentioned previously. Although this model does not explicitly deal with effects of cross-bridge strain, strain dependence of rate constants could be implicit in the slowing of kinetics that occurs as strained cross-bridges accumulate.

Model parameters, listed in Table 1, were assigned according to prior work or by fitting to our results, i.e., stiffness/tension rise after activation with photolytic release of Ca²⁺. The rate constants of the forward and reverse force-generating transition, k₊₂ and k₋₂, were attained from caged-Pi experiments during steady-state contraction and here assigned values of 15 and 45 s⁻¹ for the steady-state or slow branch of the model. Dissociation constant K₃ was assigned a value of 4 mM from those same experiments and assumed to be identical for both branches. All other parameters were assigned by best fit. The fitting indicated that the shift toward the slow pathway begins as the ratio of attached to detached heads approaches 10% and is nearly complete at 30%. The fitting also yielded positive cooperativity upon the switch to the lower pathway where the equilibria K_ia and K₁ favor regulatory unit activation and cross-bridge formation.

TABLE 1.

Results from fitting Scheme II

Path	Kia	k1 (M−1 s−1)	k−1 (s−1)	K1 (μM)	k2 (s−1)	k−2 (s−1)	K3 (mM)	k5 (s−1)
Fast	0–0.42	1.1 × 106	280	260	360	330	4*	4.10
Slow	0–1000	3.9 × 104	3	77	15*	45*	4*	0.47

Rate constants were assigned (*) or fitted as described in the discussion. The only Ca²⁺-dependent parameter was K_ia. K_ia at individual [Ca²⁺] are listed in Table 2. n (see Eq. 3) was set to 7 whereas h was permitted to vary.

Model details

In the model, the equilibrium, K_XB, between upper and lower pathways of Scheme II is controlled by the fraction, x, of strongly bound cross-bridges as shown by the relations

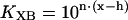(3)

and

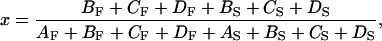(4)

where n is a coefficient reflecting the “steepness” of the slope, h is the value of x for which K_XB evaluates to 1, i.e., the “threshold for crossover,” and subscripts F and S indicate states in the fast or slow pathways. In fitting the model, n was set to 7 so that the crossover from upper to lower pathway occurred over a 30% change in x, while h was allowed to vary. The fitted value for h was 0.1. Tension is modeled as the sum of cross-bridges in states C and D in both pathways, whereas stiffness is the sum of cross-bridges in states B, C, and D. The stiffness contribution of bound state B was weighted as two thirds of that of the C and D states. This weighting was found to yield a reasonable lead of stiffness over tension after jumps in [Ca²⁺] as well as a decrease in stiffness and tension after jumps in [Pi] (data not shown).

Fitting

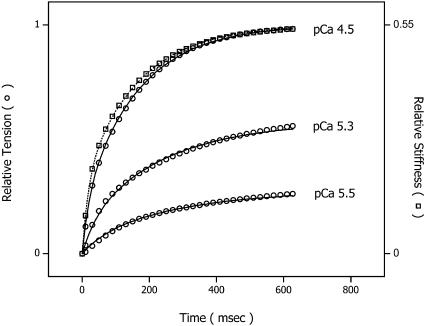
Fig. 7 shows a series of simulations using the above model after the release of three different [Ca²⁺]. The model simulations of stiffness and tension are represented as open squares and open circles, respectively. Both are superimposed on biexponential prototypical tension traces (solid lines) and a stiffness trace (dotted line at pCa 4.5) simulated from aggregate data shown in Fig. 5. The final tension ranged from full activation (top trace) to 25% P_max (bottom trace). For clarity, only the stiffness time course at maximal activation is shown. As illustrated, the model accurately predicts the Ca²⁺-sensitivity of both the magnitude and rate of the stiffness change and tension development without evoking direct Ca²⁺ modulation of force-producing steps.

FIGURE 7.

Series simulations of stiffness and tension time courses after the release of three different [Ca²⁺] using the above model. The stiffness and tension simulations are represented as open squares and open circles, respectively. Both are superimposed on biexponential prototypical tension traces (solid lines) and a stiffness trace (dotted line at pCa 4.5) simulated from aggregate data shown in Fig. 5. The final tension ranged from full activation (top trace) to 25% P_max (bottom trace). For clarity, only the stiffness time course at maximal activation is shown. The maximal stiffness amplitude is 55% of that measured in rigor.

The model was also tested for Ca²⁺-dependence of k_Pi and k_tr. In the case of k_Pi, the numerical simulation was first allowed to reach steady state, then the medium Pi was stepped to a final concentration 2 or 4 mM, emulating the experimental protocol. Exponentials were fit to the simulated transients, and the resultant values for k_Pi are listed in Table 2. Over the range of [Ca²⁺] simulated, k_Pi at 2 or 4 mM final [Pi] was insensitive to calcium similar to previous studies of skeletal (Millar and Homsher, 1990, 1992) and cardiac muscle (Martin et al., 2003) but slightly different from cardiac studies that reported a twofold increase in k_Pi over this range of [Ca²⁺] (Araujo and Walker, 1996).

TABLE 2.

Predictions from model simulations at varying pCa

	Fitted parameters		Predictions
Condition pCa	Kia fast	Kia slow	P/Pmax (%)	kPi 2 mM (s−1)	kPi 4 mM (s−1)	ktr (s−1)	kslow (s−1)
4.5	0.42	1000	100	30	38	6.0	6.10
5.3	0.20	1.0	50	30	37	2.7	4.21
5.5	0.10	0.39	25	31	40	2.4	3.45

Unitless equilibrium constants K_ia were obtained by fitting the model to the data. Rate constants k_Pi and k_tr were obtained by fitting exponentials to model simulations as described in the model discussion. Rate constants k_slow were obtained as described in methods and are provided for reference.

To simulate k_tr, k₄ was increased to 28 s⁻¹ in both fast and slow branches, which decreased steady-state tension to 30% of the isometric value to approximate the tension level observed immediately after restretch in studies of k_tr in skinned cardiac tissue and the corresponding distribution of biochemical states. Beginning from this condition, 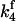and 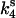were returned to their isometric values (see Table 1) to simulate the post-restretch recovery to isometric steady state. At all three [Ca²⁺], the simulated recovery transients were biexponential, the rapid phase comprising ∼15% of the total recovery amplitude. If the rate of the slow phase is designated k_tr, then at pCa 4.5, the simulated k_tr agrees with k_slow reported here (6.0 vs. 6.1 s⁻¹, respectively; see Table 2) and with k_tr values reported from guinea pig cardiac myofibrils, 6.8 s⁻¹ under similar conditions (Stehle et al., 2002). These estimates are faster than the 2.7 s⁻¹ reported in a previous study of guinea pig trabeculae (Palmer and Kentish, 1998). In addition, the simulations indicate that k_tr was less calcium-sensitive above pCa 5.3 than below, consistent with results from some skinned cardiac muscle studies (e.g., Palmer and Kentish, 1998). When taken together, these simulations indicate that even at submaximal activation levels, k_tr is determined primarily by myosin kinetics and not by reactivation of the thin filament by strong cross-bridge binding during tension redevelopment. A similar conclusion was reached in studies of rabbit skeletal muscle fibers by Brenner and Chalovich (1999).

Comparison with other models

Our model of thin filament activation is similar to the three-state model proposed by McKillop and Geeves (1993) and current structural models of thin filament activation (Vibert et al., 1997; Craig and Lehman, 2001). Our so-called Inactive state corresponds to McKillop and Geeves' blocked or B state, and the thin filament state in our upper and lower cycling pathways may correspond to the Ca-induced, C state and cross-bridge-induced, M state. In McKillop and Geeves' model, cross-bridges form at a regulatory unit that is in the C state, thereby inducing the regulatory unit into the M state. The M state must be attained before cross-bridges produce force. In our model, the Ca²⁺-induced state allows cross-bridge formation and cycling with rapid kinetics (upper pathway) and when cross-bridge number exceeds 10%, the myosin-induced M state is achieved and shifts the equilibrium in favor of further cross-bridge formation by slowing AM.ADP.Pi detachment back to M.ADP.Pi. Alternatively, there may be four states of the regulatory unit: two non-force–bearing states, B and C, and two force-bearing M states, with both fast and slow kinetics.

In our model, thin filament activation is modeled as a rapid Ca²⁺-binding equilibrium controlling the conversion of a regulatory unit from an Inactive to Active state that allows myosin binding. It is similar to earlier models (Landesberg and Sideman, 1994; Hancock et al., 1997; Brenner and Chalovich, 1999) in that transitions between thin filament states are not rate limiting for tension production. In these models, the time course of the change in stiffness and tension is determined by the flux of myosin heads from detached or weakly attached into strongly attached states. This differs from other models in which the force redevelopment rate is limited by relatively slow, cross-bridge–induced changes in thin filament activation or by slow Ca²⁺-binding kinetics (Millar and Homsher, 1990; Swartz and Moss, 1992; Campbell, 1997; Regnier et al., 1998; Razumova et al., 2000).

The level of activation in this model is cooperative and enhanced by strong cross-bridge binding. When this exceeds 10%, the kinetics shift from those described by the upper to the lower pathway in Scheme II in which cross-bridge kinetics are slower and the activation level (I to A transition) shifts to favor further cross-bridge binding (see Table 2). In other models of cardiac muscle activation, the dominant cooperative mechanism is the dependence of Ca²⁺-troponin C affinity on the number of force-generating cross-bridges (Landesberg and Sideman, 1994; Hancock et al., 1997). These models simulate the Ca²⁺-dependence of k_tr well, exhibiting a curvilinear relation with relatively smaller changes in k_tr at low [Ca²⁺] than at [Ca²⁺] resulting in around 50% maximal tension or greater. However, the relation between k_Ca and relative tension is more linear (see Fig. 5) than these models predict. Our model accurately simulates the dependence of both k_Ca (Fig. 7) and k_tr on relative tension (Table 2).

In summary, the model describes the Ca²⁺-dependence of rates and amplitudes for both the stiffness and tension time courses of guinea pig trabeculae, while maintaining only a marginal effect of Ca²⁺ on k_Pi. In addition, the model explains apparently contradictory results: at maximal activation and 23°C, the fast component of k_Ca is faster than k_Pi.