Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Mar;86(3):1820–1828. doi: 10.1016/S0006-3495(04)74249-6

BDNF Boosts Spike Fidelity in Chaotic Neural Oscillations

Shigeyoshi Fujisawa 1, Maki K Yamada 1, Nobuyoshi Nishiyama 1, Norio Matsuki 1, Yuji Ikegaya 1
PMCID: PMC1304016  PMID: 14990508

Abstract

Oscillatory activity and its nonlinear dynamics are of fundamental importance for information processing in the central nervous system. Here we show that in aperiodic oscillations, brain-derived neurotrophic factor (BDNF), a member of the neurotrophin family, enhances the accuracy of action potentials in terms of spike reliability and temporal precision. Cultured hippocampal neurons displayed irregular oscillations of membrane potential in response to sinusoidal 20-Hz somatic current injection, yielding wobbly orbits in the phase space, i.e., a strange attractor. Brief application of BDNF suppressed this unpredictable dynamics and stabilized membrane potential fluctuations, leading to rhythmical firing. Even in complex oscillations induced by external stimuli of 40 Hz (γ) on a 5-Hz (θ) carrier, BDNF-treated neurons generated more precisely timed spikes, i.e., phase-locked firing, coupled with θ-phase precession. These phenomena were sensitive to K252a, an inhibitor of tyrosine receptor kinases and appeared attributable to BDNF-evoked Na+ current. The data are the first indication of pharmacological control of endogenous chaos. BDNF diminishes the ambiguity of spike time jitter and thereby might assure neural encoding, such as spike timing-dependent synaptic plasticity.

INTRODUCTION

Central neurons fire temporally irregular spikes, as exemplified by Poisson-like histograms of interspike intervals. The patterns of activity are seemingly random and erratic, but experimental and theoretical works have revealed that neurons possess the regime of deterministic chaos, a nonlinear dynamic system with a few degrees of freedom (Elbert et al., 1994). Chaotic instability is important in executing activity adaptation and state transitions in response to environmental changes, and consequently creates a rich repertoire of responses (Rabinovich and Abarbanel, 1998). Indeed, neurons collectively give rise to oscillatory patterns, the frequencies and temporal dynamics of which may be associated with distinct behavioral states (Salinas and Sejnowski, 2001).

Recent evidence is also accumulating that external sensory stimuli or internal top-down signals lead to spike synchronization among different neurons (deCharms and Merzenich, 1996; Alonso et al., 1996; Riehle et al., 1997), suggesting that under certain states, individual neurons in vivo can produce action potentials with high temporal accuracy. Likewise, the existence of extremely narrow time windows for bidirectional regulation of synaptic strength (Markram et al., 1997; Bi and Poo, 1998) implies that neurons are capable of transmitting signals with millisecond fidelity. If the activity of individual neurons were governed merely by chance, these high-degree organizations could never occur. Neuronal chaos is, hence, thought to represent a preliminary state for order (Elbert et al., 1994; Rabinovich and Abarbanel, 1998). Little is known, however, about the mechanisms by which neurons transit between chaos and order or about the regulatory factors for this state switching.

Brain-derived neurotrophic factor (BDNF), a member of the neurotrophin family, has long been implicated in modulating membrane excitability (Kafitz et al., 1999; Blum et al., 2002), synaptic transmission (Kang and Schuman, 1995; Tanaka et al., 1997; Boulanger and Poo, 1999), and neuroplasticity (Thoenen, 1995; Figurov et al., 1996; Kovalchuk et al., 2002). We therefore hypothesized that BDNF regulates spike fidelity in the ambiguity of neuronal chaos. In this work, we report that cultured hippocampal neurons exhibit chaotic kinetics of membrane potential responses and drift toward a more reliable state after brief exposure to BDNF.

METHODS

Materials

Human recombinant BDNF was a gift from Sumitomo Pharmaceuticals (Osaka, Japan). d,l-2-Amino-5-phosphonopentanoic acid (AP5), 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), and picrotoxin were purchased from Sigma (St. Louis, MO). K252a was obtained from Kyowa Hakko (Tokyo, Japan). Tetrodotoxin was from Wako (Osaka, Japan).

Culture preparation

Cultured hippocampal neurons were prepared as described previously (Yamada et al., 2002), with some modifications. Briefly, the brains were isolated from embryonic day 18 (E18) Wistar rats, and the hippocampi were dissected out and treated with 0.25% trypsin (Difco Laboratories, Detroit, MI) and 0.01% deoxyribonuclease I (Sigma) at 37°C for 30 min. Neurons were plated at ∼20,000 cells/cm2 on polyethylenimine (Sigma) coated 13-mm-diameter coverslips in 35-mm-diameter dishes. The plating medium was Neurobasal medium (Life Technologies, Gaithersburg, MD) supplemented with 10% fetal bovine serum (Cell Culture Technologies, Cleveland, OH) with glutamine, penicillin, and streptomycin. Twelve hours after plating, the medium was changed to serum-free Neurobasal medium with 2% B27 supplement (Life Technologies). Electrophysiological recordings were performed after 8–12 days in culture.

Electrophysiology

A whole-cell recording technique was used with amphotericin B perforated patch configuration (Tanaka et al., 1997). Micropipettes (4–7 MΩ) were made from glass capillaries (Narishige, Tokyo, Japan). The pipettes were tip filled with internal solution and then back filled with internal solution containing 1 μg/ml amphotericin B (Sigma). The internal solution consisted of (in mM): 136.5 KMeSO4, 17.5 KCl, 9 NaCl, 1 MgCl2, 10 HEPES, 0.2 EGTA (pH 7.2). The external bath solution consisted of (in mM): 150 NaCl, 5 KCl, 1 MgCl2, 2 CaCl2, 10 glucose, 10 HEPES (pH 7.3 at 24°C), containing 500 μg/ml bovine serum albumin. Recordings were carried out with an Axopatch 200B amplifier (Axon Instruments, Foster City, CA). Signals were low-pass filtered at 1 kHz, digitalized at 10 kHz, and analyzed with a pCLAMP 8.0 software (Axon Instruments). All drugs were bath applied with the perfusion solution.

Analysis for chaotic profiles

To define whether or not the voltage responses were chaotic, we calculated Lyapunov exponent, which represents the degree to which the neighboring trajectories diverge exponentially on the subject of the sensitivity to the initial conditions (Wolf et al., 1985). The formula for the Lyapunov exponent λ of the trajectory computed at N time points is

graphic file with name M1.gif (1)

where τ is time iteration and di(t) is the distance between the original trajectory and a neighboring i trajectory at time t. Post hoc analyses were performed using the custom-written software Igor Pro (Wavemetrics, Lake Oswego, OR).

Mathematical modeling of cellular excitability

We formulated and used a single compartment (lumped neuron) model with Hodgkin-Huxley type Na+ and K+ conductances for oscillation and spike generation (Hodgkin and Huxley, 1952). In addition, we assumed the existence of new voltage-insensitive Na conductance gNa_VI as BDNF-evoked Na+ current. The membrane current i was expressed at the membrane potential V as follows:

graphic file with name M2.gif

where m is the sodium activation, h the sodium inactivation, n the potassium activation; ENa, EK, EL are the reversal potentials for sodium, potassium, and leakage current components, respectively; Inline graphic, Inline graphic, Inline graphic are the maximal ionic conductance through sodium, potassium, and leakage current components, respectively (Dayan and Abbott, 2001). In the above equations, the values of Inline graphic, Inline graphic, Inline graphic and gNa_VI were initially fixed at 120, 36, 0.3, and 0.01 mS/cm2, respectively, and ENa, EK, EL were fixed at 50, −77 and −54 mV, respectively. Using varying gNa_VI values, we examined numerical solutions of the Hodgkin-Huxley equations with the sinusoidal stimulation current. Analysis was performed using the custom-written software Matlab (MathWorks, Natick, MA).

RESULTS

Hippocampal neurons drifts between periodic and chaotic states

Using the perforated-patch current-clamp recording technique, we assessed the responses of membrane potential of cultured hippocampal neurons to external current oscillators. We injected somatic current with a cyclic sinusoidal function of A × sin (2π × f × t), where A, f, and t denote amplitude (pA), frequency (Hz), and time (s), respectively. Although the sinusoidal pattern of stimulation is quite artificial, this simplified method has often revealed an important basis of neural firing properties and thus is widely used as a potent model for natural synchronous oscillations. We examined the effects of various f values on membrane potential responses (A = 25 pA).

Neurons spontaneously displayed irregular firing without current injection (Fig. 1 A). They demonstrated different states of oscillations depending on varying frequencies of the driving functions (Fig. 1, B–F). In the range of 1–10 Hz, neurons generated action potentials that were tightly locked to specific phase angles of the forcing cycle, the numbers of spikes being 6, 3, 2, and 1 per cycle at sinusoidal 1, 2, 4, and 10 Hz, respectively (Fig. 1, B–E). These results indicate that action potentials were efficiently entrained to the driving oscillations. At 20 Hz, however, the responses resulted in a more complicated structure, which differed from the periodic waveforms at 1–10 Hz and appeared lawless (Fig. 1 F). This ambiguous behavior was still observed after pharmacological blockade of excitatory/inhibitory synaptic transmission (Fig. 2 C) but did not occur in the presence of 1 μM tetrodotoxin (N = 2, data not shown). Thus, the aperiodicity was not due to synaptic events but attributable to the activity of voltage-sensitive Na+ channels.

FIGURE 1.

FIGURE 1

Open in a new tab

Frequency-dependent transition between periodic and chaotic oscillations. Left panels indicate representative traces of membrane potential (top) in response to sinusoidal somatic current injection (bottom) at frequencies of 1 (B), 2 (C), 4 (D), 10 (E), and 20 Hz (F) with an amplitude of 25 pA. Zero hertz (A) indicates no current injection (free run). The responses were analyzed by reconstructing the phase spaces of V versus dV/dt (middle) and stroboscopic return maps obtained from Poincaré cross sections at sinusoidal phase 144°, at which the Lyapunov exponent of the 20-Hz oscillations rendered the maximal value (right). The return map for 0 Hz was reconstructed by a 164-ms separation. The neuron displayed harmonic spikes with 6:1, 3:1, 2:1, and 1:1 entrainments onto exterior 1-Hz, 2-Hz, 4-Hz, and 10-Hz oscillators, respectively, whereas at 20 Hz, it responded chaotically.

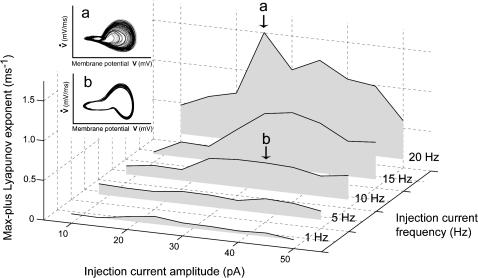
FIGURE 2.

FIGURE 2

Open in a new tab

Frequency- and amplitude-dependent transition between periodic and chaotic oscillations. The max-plus Lyapunov exponents of membrane potential in response to sinusoidal somatic current injection are plotted against both frequency (1, 5, 10, 15, and 20 Hz) and amplitude (10–50 pA). The insets show the phase portraits of membrane potential versus its temporal derivative (a, 25 pA at 20 Hz; b, 35 pA at 10 Hz).

The voltage responses to 20-Hz current were smaller than those to lower frequency (∼62%). In general, the response amplitude reduces as a function of frequency; the gain G follows the next equation (Koch, 1999):

graphic file with name M9.gif

In this experiment, the Cm value was 30.1 pF, and the Rm value was 420 MΩ. Therefore, G(f) is ∼60%, consistent with our experimental data.

To quantitatively evaluate these oscillatory states, we plotted the membrane potential V versus its derivative dV/dt. In the phase-locking responses at 1–10 Hz, the attractor was asymptotically a stable closed curve, i.e., a limit cycle (Fig. 1, B–E). In contrast, the trajectories of the 20-Hz responses filled up a portion of the phase space because of their instability, depicting a so-called strange attractor (Fig. 1 F). To address whether or not the membrane response is deterministic chaos, we constructed a first-return map, a logistic transfer function Vi versus Vi+1, where Vi (i = 1, 2…) is the sequential series of membrane potential sampled every period T (= 1/f). The map represents mutual correlations of responses in the neighboring periodic cycles; periodic oscillations converge into one focus of cross points because all return values are equivalent per cycle, while random noise fills the space because of no correlation between successive return trials. The periodic responses at 1–10 Hz produced a cluster around a stable fixed point on the diagonal line (Fig. 1, B–E). The strobomap of the 20-Hz oscillations revealed a noninvertible function that consisted of two branches (Fig. 1 F), the characteristic trajectory of which signifies that voltage responses gradually closed up to the diagonal breakpoint and spiraled away after several iterations, indicative of a repetitive folding/stretching process. Therefore, the apparently irregular responses at 20 Hz do not in fact result from noise or stochastic behavior but rather conform to deterministic chaos.

The emergence of chaos depends on both the amplitude and frequency of the driving oscillations. To quantify the degree of chaos, we calculated the largest Lyapunov exponent, which represents the degree to which the neighboring trajectories diverge exponentially on the subject of the sensitivity to the initial conditions. If the oscillation is completely periodic, the largest Lyapunov exponent is zero, and if the response is chaotic, it shows a positive value. At lower frequency (<15 Hz), the Lyapunov exponents were small and kept constant independent of the current amplitude (Fig. 2). The reason why the exponents were not zero was due to noise. At 15 and 20 Hz, however, the Lyapunov exponents became higher, and reached the maximum at an optimal current (∼35 pA at 15 Hz, and 25 pA at 20 Hz).

BDNF enhances spike reliability and precision

We sought to determine how BDNF modulates chaotic regimes. Neurons were stimulated with sinusoidal 20-Hz current injection with a 25-pA amplitude for 25 s. They were then treated with 50 ng/ml BDNF for 5–10 min and again stimulated with the same current injection in the continuous presence of BDNF. BDNF slightly increased the membrane conductance by 1.57 ± 1.07 μS/cm2, the maximal changes being 5.46 μS/cm2. The effect emerged >1 min after the bath perfusion. Consistent with this, BDNF induced a small change in the resting membrane potential by up to 2.70 mV, however, on average, the change was not significant (0.44 ± 0.45 mV; mean ± SE of six neurons). This apparent discrepancy is probably due to the problem of incomplete “space clamp” (Rall and Segev, 1985; Koch, 1999). Indeed, BDNF-evoked depolarization is found at dendrites (Kovalchuk et al., 2002). Alternatively, there could be compensatory mechanisms by which membrane potential can counteract an accidental, small fluctuation in conductance. Interestingly, BDNF-treated neurons displayed distinct oscillatory responses to the same pattern of current injection; the waveforms of membrane potential now became more stable and displayed action potentials more reproducibly (Fig. 3, A and B). Their trajectories of V versus dV/dt resembled a limit cycle, suggesting that BDNF reduces chaotic dynamics and enhances the reliability of spike events.

FIGURE 3.

FIGURE 3

Open in a new tab

BDNF reduces chaotic neural activity. (A and B) Representative waveforms (left top) of membrane potential in response to sinusoidal current injection (20 Hz, 25 pA, left bottom), and the corresponding stroboscopic portraits of membrane potential versus its temporal derivative (right) immediately before (A) and 5 min after 50 ng/ml BDNF application (B). (C) Average max-plus Lyapunov exponents in control (open bars) and BDNF-treated neurons (solid bars) in the absence (N = 8) and presence of 20 μM CNQX, 50 μM AP5, and 20 μM picrotoxin (PTX) (N = 9) or 200 nM K252a (N = 4). In each experiment, the driving current was adjusted to the amplitude that produced the largest chaotic response before drug application (usually 20–40 pA). *P < 0.05 versus control; t-test. Data are mean ± SE of N cases.

Fig. 3 C summarizes the effects of BDNF on the largest Lyapunov exponents. BDNF significantly decreased the Lyapunov exponents by ∼50%. This action was prevented by 200 nM K252a, an inhibitor of tyrosine receptor kinases (Fig. 3 C), which suggests that BDNF-induced TrkB activation mediates the modulation of chaos. The BDNF-TrkB system is reported to alter synaptic activity (Kang and Schuman, 1995; Tanaka et al., 1997; Boulanger and Poo, 1999), but the effect observed here was insensitive to a cocktail of channel receptor inhibitors, consisting of the non-NMDA (N-methyl-d-aspartate) receptor antagonist CNQX, the NMDA receptor antagonist AP5, and the γ-aminobutyric acid type A (GABAA) receptor antagonist picrotoxin (Fig. 3 C). Therefore, BDNF-induced chaos stabilization is not synaptically driven.

In this series of experiments, we were aware that BDNF-treated neurons were apt to fire at more advanced phases relative to individual oscillation cycles. To analyze this phenomenon in detail, we introduced another protocol of oscillatory current injection, in which sinusoidal 5-Hz (20 pA) and 40-Hz (10 pA) were superimposed (Fig. 4), because hippocampal neurons generate electroencephalographic θ-(around 5 Hz) and γ-(∼40 Hz) bands in vivo (Bragin et al., 1995) and in vitro (Fellous and Sejnowski, 2000), and their spike timing reliably shifts forward along the θ-cycle phase during spatial behavior of the animals (O'Keefe and Recce, 1993). This phase precession may play a role in cognitive processing (Lisman, 1999; Harris et al., 2002). In addition, spike timing in vivo is preferentially locked to γ-quanta, and thus, γ-oscillations are likely to synchronize spikes (Fries et al., 2001a,b; Csicsvari et al., 2003).

FIGURE 4.

FIGURE 4

Open in a new tab

BDNF narrows the time window of spike events and shifts spike timing relative to θ-phases. Synchronized oscillations of membrane potential (left top) in response to complex current consisting of a combination of sinusoidal θ-like (5 Hz, 20 pA) and γ-like (40 Hz, 10 pA) rhythm (left bottom) immediately before (A) and 5 min after treatment with 50 ng/ml BDNF (B). The number of spikes was normalized to the total number for 25 s and plotted against the phase of a 5-Hz sinusoid (right). In this neuron, the average phases of spike events were 114.2 ± 28.9° in control and 78.5 ± 13.3° in BDNF (mean ± SE, P < 0.01, Student's t-test), which indicates that BDNF induced forward phase precession in spike timing. The CV values of the spike timing in phase were 28.3% in control and 19.2% in BDNF (P < 0.01, F-test), which means that BDNF-treated neurons fired with more precise timing. See text for data of the other neurons.

When the combinatorial θ/γ-rhythm current was injected, neurons generated one action potential per θ-cycle, but its timing in each θ-phase varied from cycle to cycle and quantally jumped across γ-cycles (Fig. 4 A). After application of 50 ng/ml BDNF for 5–10 min, spikes were more tightly locked to a particular γ-cycle (Fig. 4 B). In five of eight neurons, BDNF significantly reduced the coefficient of variation (CV) of spike time jitter (P < 0.05: paired t-test), which indicates that BDNF decreases spike time variability. Furthermore, BDNF-treated neurons fired action potentials at earlier θ-phases, as compared with control neurons; the average advancement was 8.67 ± 3.02° in θ (P < 0.05: paired t-test, mean ± SE of eight neurons). In the presence of K252a, BDNF did not induce a phase shift; the average advance was 0.40 ± 1.26° (P > 0.9, N = 7).

To further illustrate how BDNF enhances the reliability of spike timing, we injected fluctuating current with white noise in the presence of CNQX, AP5, and picrotoxin. These patterns of waveform are designed to imitate physiological synaptic noises and have been used to evaluate the stability and precision of spike generation (Mainen and Sejnowski, 1995; Nowak et al., 1997). Spikes were weakly locked in our Gaussian white noise (μs = 50 pA, σs = 10 pA, τs = 3 ms; see also Mainen and Sejnowski (1995)) (Fig. 5 A). Their firing patterns became more stereotyped after application of 50 ng/ml BDNF (Fig. 5 B). In three of five neurons, BDNF significantly reduced the mean CV of spike time (CVBDNF/CVcontrol: 0.62 ± 0.66*, 0.70 ± 0.19*, 0.82 ± 0.14*, 0.87 ± 0.35, 1.08 ± 0.37; mean ± SD, *P < 0.05: paired t-test). No significant effect was observed in the presence of 200 nM K252a (CVBDNF/CVcontrol: 0.75 ± 0.53, 0.78 ± 0.45, 1.01 ± 0.34, 1.18 ± 0.55). Thus, BDNF tightened firing timing even if synaptic inputs fluctuate ambiguously.

FIGURE 5.

FIGURE 5

Open in a new tab

BDNF immobilizes spike patterns in random aperiodic drive. Reliability of firing pattern (top subpanels) evoked by repeated stimulation with Gaussian white noise current (bottom subpanels; μs = 50 pA, σs = 10 pA, τs = 3 ms) immediately before (A) and 5 min after treatment with 50 ng/ml BDNF (B). The middle subpanels indicate eight superimposed voltage traces. In this neuron, the average CV of spike timing was 72.8 ± 28.4 ms (mean ± SD of eight successive trials) in control and 32.4 ± 15.6 ms in BDNF (P < 0.05, t-test), which means that BDNF-treated neurons fired with more precise timing. See text for data of the other neurons.

NaV1.9-like conductance mimics the effect of BDNF in a simple model neuron

Blum et al. (2002) has recently indicated that BDNF evokes membrane depolarization through rapid activation of NaV1.9, a tetrodotoxin-resistant member of the family of voltage-gated Na+ channels. We thus hypothesized that the BDNF effect is attributable to recruitment of Na+ conductance. To address this possibility, we used a mathematical neuron model based on the Hodgkin-Huxley theory (Hodgkin and Huxley, 1952). Because the Hodgkin-Huxley model neuron responds to an exterior oscillator faster than a realistic neuron, we used a 150-Hz stimulus to induce chaos. This model neuron exhibited chaotic behavior in response to a sinusoidal 150-Hz oscillator, as evidenced by a strange attractor in the phase space and the positive value of Lyapunov exponents (Fig. 6 A, and see also Aihara et al. (1984)).

FIGURE 6.

FIGURE 6

Open in a new tab

Increasing NaV1.9-like conductance induces chaos stabilization and phase precession in a Hodgkin-Huxley model neuron. (A and B) Voltage-insensitive Na+ conductance (gNa_VI) reduces chaotic activities. The phase portraits indicate membrane potential versus its temporal derivative in response to sinusoidal current injection (150 Hz, 50.4 μA/cm2) before (A) and after addition of 0.01 mS/cm2 gNa_VI (B). (C–H) Summary of the effects of gNa_VI (C and D), Inline graphic (E and F), and Inline graphic (G and H) on the largest Lyapunov exponents (C, E, and G) and firing phase (D, F, and H). In the simulation of phase advancement (D, F, and H), we used stimulating current consisting of a combination of sinusoidal 5-Hz (2.5 μA/cm2) and 40-Hz (0.05 μA/cm2) cycles, and the spike phases in the 5-Hz cycle are plotted against changes in each conductance.

The conductance of BDNF-elicited NaV1.9 current is almost constant in the physiological ranges positive to the resting membrane potential, whereas it gradually decreases at membrane voltages below −65 mV (Blum et al., 2002). To mimic the BDNF effect with simplification, we incorporated voltage-insensitive “DC-like” Na+ conductance (gNa_VI) into the Hodgkin-Huxley neuron. When ΔgNa_VI was set to 10 μS/cm2, the attractor depicted a stable orbit (Fig. 6 B). Computer simulation by varying gNa_VI revealed that the critical point for transition between chaos and periodic oscillations was ∼6.3 μS/cm2; above this value, the Lyapunov exponents were zero (Fig. 6 C).We next examined the effect of this Na+ conductance on spike timing. We applied various gNa_VI values to the oscillating neuron in response to combinatorial 5-Hz (θ) and 40-Hz (γ) current. Increasing gNa_VI led to phase advancement of spikes in a quantal step manner (Fig. 6 D). Each step interval corresponded to the γ-cycle wavelength, i.e., 45° of θ, indicating that spikes were entrained to individual γ-cycles and their timing advanced at these intervals. We also assessed the impacts of changes in voltage-sensitive Na+ conductance (Inline graphic) and K+ conductance (Inline graphic) on chaotic firing. Unlike gNa_VI, surprisingly, increasing Inline graphic did not eliminate the chaotic properties (Fig. 6 E) whereas it induced the phase advance of spikes (Fig. 6 F). On the other hand, a decrease in Inline graphic was capable of increasing the spike reliability (Fig. 6 G) and shifting the firing phase (Fig. 6 H), both of which may resemble the effect of gNa_VI.

DISCUSSION

Neurons undergo complex transitions between diverse states. Irregular firing under resting conditions is probably due to synaptic noise and spontaneous self-sustained fluctuations. This unstable state is capable of drifting rapidly toward a well-defined state in response to external stimuli. The biophysical laws of synaptic plasticity require precise timing of spikes over millisecond timescales (Markram et al., 1997; Bi and Poo, 1998). It is hence critical to understand the regulatory system responsible for state transitions and spike precision. In the present study, we confirmed that neurons display a dynamic switch between periodic and aperiodic oscillations, depending on external sinusoidal oscillators, and have shown for the first time that BDNF enhances the accuracy of spike timing. BDNF has recently emerged as a candidate molecule mediating learning and memory. A rapid and selective increase in BDNF mRNA occurs during memory formation (Tokuyama et al., 2000; Mizuno et al., 2000), raising the possibility that BDNF/TrkB signaling may be involved in memory acquisition and consolidation (Tyler et al., 2002; Minichiello et al., 1999; Linnarsson et al., 1997). Physiological and anatomical evidence suggests that BDNF modulates activity-dependent neuroplasticity, linking neural activity with functional and structural modification of synaptic connection (Thoenen, 1995; McAllister et al., 1999; Poo, 2001). In addition, we have described here that BDNF decreases irregularity of firing patterns and enhances temporal precision of spikes, suggesting that BDNF does modulate outputs as well as inputs of neurons. With respect to temporal coding in neural representation (Singer, 1993), of particular importance is the finding that BDNF can alter spike timing even when the same input pattern of oscillation was presented; the data denote that BDNF can affect the read-out algorithm. It is our impression that the cellular mechanism by which BDNF causes the precise timing of action potentials is the stabilization of nonlinear fluctuations of membrane potential via enhancing the membrane conductance. Kafitz et al. (1999) indicated that BDNF induces inward Na+ current (probably as large as 500 μS/cm2 of conductance), but we found no evidence for such a large Na+ current. Under our conditions, BDNF-evoked changes in membrane conductance were up to only 5.46 μS/cm2. However, computational simulation revealed that adding small gNa_VI (<10 μS/cm2) was enough to eliminate chaotic behavior and elicit θ-phase precession. This may be supported by a recent in vitro study showing that increasing amounts of current injection, coupled with θ-oscillations, result in phase advancement (Magee, 2001). Therefore, changes in gNa_VI alone can account for the effects of BDNF. Of course, this notion does not rule out a possible involvement of other mechanisms relevant to the BDNF-TrkB signaling. Indeed, our data suggest that a decrease in Inline graphic can also imitate BDNF's effects. However, there has so far been no evidence that the acute application of BDNF actually modulates Inline graphic. More importantly, the action of Inline graphic was not evident until ΔInline graphic reached as large as ∼1 mS/cm2. Our empirical data did not indicate such a large increase in membrane conductance. Taken together, the addition of gNa_VI is the most likely explanation for BDNF-induced chaos stabilization and phase precession. Because gNa_VI is a voltage-insensitive and time-independent component, the increase in gNa_VI is, conceptionally, regarded as an increase in ion-selective “leak” conductance, yielding a rise in the reversal potential. This alteration in the membrane properties is possible to cause voltage-sensitive Na+ channels to work more reliably by changing their kinetics of activation and inactivation (Keynes, 1992). In our experiments, BNDF induced only slight depolarization in the somata, but it is possible that larger changes in the membrane potential occurred at peripheral sites, e.g., distal dendrites (Kovalchuk et al., 2002). Such local phenomena, if any, might be inaccessible by whole-cell recording because of inadequate space clamp (Rall and Segev, 1985; Koch, 1999).

Finally, elucidating chaos in biological systems is important in medical science; chaos control techniques are expected to bring about new diagnostic tools and therapies for certain types of diseases, including cardiac arrhythmias (Garfinkel et al., 1992; Poon and Merrill, 1997) and epilepsy (Schiff et al., 1994). In diverse research fields such as chemistry (Petrov et al., 1993), laser physics (Roy et al., 1992), electronic circuits (Hunt, 1991), mechanical systems (Ditto et al., 1990) as well as biological sciences (Garfinkel et al., 1992; Schiff et al., 1994), it has been demonstrated that artificial “oscillatory” stimulation can induce periodic pacing in the chaotic regime. In this respect, it is intriguing to find that in the present study, a simple “nonoscillatory” stimulus is sufficient to stabilize chaos. Thus, our data may describe a new strategy for treating chaos. In addition, this work provides the first evidence for pharmacological stabilization of chaos. Pharmacological approach for probing and controlling chaos would be of clinical benefit because of its convenience and accessibility.

Acknowledgments

We thank T. Yasui (University of Tokyo) for critical reading of an earlier version of the manuscript.

This work was supported in part by Grant-in-Aid for Science Research from the Ministry of Education, Culture, Sports, Science and Technology of Japan.

References

  1. Aihara, K., G. Matsumoto, and Y. Ikegaya. 1984. Periodic and non-periodic responses of a periodically forced Hodgkin-Huxley oscillator. J. Theor. Biol. 109:249–269. [DOI] [PubMed] [Google Scholar]
  2. Alonso, J. M., W. M. Usrey, and R. C. Reid. 1996. Precisely correlated firing in cells of the lateral geniculate nucleus. Nature. 383:815–819. [DOI] [PubMed] [Google Scholar]
  3. Bi, G. Q., and M. M. Poo. 1998. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18:10464–10472. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Blum, R., K. W. Kafitz, and A. Konnerth. 2002. Neurotrophin-evoked depolarization requires the sodium channel Na(V)1.9. Nature. 419:687–693. [DOI] [PubMed] [Google Scholar]
  5. Boulanger, L., and M. Poo. 1999. Gating of BDNF-induced synaptic potentiation by cAMP. Science. 284:1982–1984. [DOI] [PubMed] [Google Scholar]
  6. Bragin, A., G. Jando, Z. Nadasdy, J. Hetke, K. Wise, and G. Buzsáki. 1995. Gamma (40–100 Hz) oscillation in the hippocampus of the behaving rat. J. Neurosci. 15:47–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Csicsvari, J., B. Jamieson, K. D. Wise, and G. Buzsáki. 2003. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 37:311–322. [DOI] [PubMed] [Google Scholar]
  8. Dayan, P., and L. F. Abbott. 2001. Theoretical Neuroscience. MIT Press, Cambridge, MA.
  9. deCharms, R. C., and M. M. Merzenich. 1996. Primary cortical representation of sounds by the coordination of action-potential timing. Nature. 381:610–613. [DOI] [PubMed] [Google Scholar]
  10. Ditto, W. L., S. N. Rauseo, and M. L. Spano. 1990. Experimental control of chaos. Phys. Rev. Lett. 65:3211–3214. [DOI] [PubMed] [Google Scholar]
  11. Elbert, T., W. J. Ray, Z. J. Kowalik, J. E. Skinner, K. E. Graf, and N. Birbaumer. 1994. Chaos and physiology—deterministic chaos in excitable cell assemblies. Physiol. Rev. 74:1–47. [DOI] [PubMed] [Google Scholar]
  12. Fellous, J. M., and T. J. Sejnowski. 2000. Cholinergic induction of oscillations in the hippocampal slice in the slow (0.5–2 Hz), theta (5–12 Hz), and gamma (35–70 Hz) bands. Hippocampus. 10:187–197. [DOI] [PubMed] [Google Scholar]
  13. Figurov, A., L. D. Pozzo-Miller, P. Olafsson, T. Wang, and B. Lu. 1996. Regulation of synaptic responses to high-frequency stimulation and LTP by neurotrophins in the hippocampus. Nature. 381:706–709. [DOI] [PubMed] [Google Scholar]
  14. Fries, P., S. Neuenschwander, A. K. Engel, R. Goebel, and W. Singer. 2001a. Rapid feature selective neuronal synchronization through correlated latency shifting. Nat. Neurosci. 4:194–200. [DOI] [PubMed] [Google Scholar]
  15. Fries, P., J. H. Reynolds, A. E. Rorie, and R. Desimone. 2001b. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 291:1560–1563. [DOI] [PubMed] [Google Scholar]
  16. Garfinkel, A., M. L. Spano, W. L. Ditto, and J. N. Weiss. 1992. Controlling cardiac chaos. Science. 257:1230–1235. [DOI] [PubMed] [Google Scholar]
  17. Harris, K. D., D. A. Henze, H. Hirase, X. Leinekugel, G. Dragoi, A. Czurko, and G. Buzsáki. 2002. Spike train dynamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature. 417:738–741. [DOI] [PubMed] [Google Scholar]
  18. Hodgkin, A. L., and A. F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hunt, E. R. 1991. Stabilizing high-period orbits in a chaotic system: the diode resonator. Phys. Rev. Lett. 67:1953–1955. [DOI] [PubMed] [Google Scholar]
  20. Kafitz, K. W., C. R. Rose, H. Thoenen, and A. Konnerth. 1999. Neurotrophin-evoked rapid excitation through TrkB receptors. Nature. 401:918–921. [DOI] [PubMed] [Google Scholar]
  21. Kang, H., and E. M. Schuman. 1995. Long-lasting neurotrophin-induced enhancement of synaptic transmission in the adult hippocampus. Science. 267:1658–1662. [DOI] [PubMed] [Google Scholar]
  22. Keynes, R. D. 1992. A new look at the mechanism of activation and inactivation of voltage-gated ion channels. Proc. R. Soc. Lond. B Biol. Sci. 249:107–112. [DOI] [PubMed] [Google Scholar]
  23. Koch, C. 1999. Biophysics of Computation. Oxford University Press, New York, NY.
  24. Kovalchuk, Y., E. Hanse, K. W. Kafitz, and A. Konnerth. 2002. Postsynaptic induction of BDNF-mediated long-term potentiation. Science. 295:1729–1734. [DOI] [PubMed] [Google Scholar]
  25. Linnarsson, S., A. Bjorklund, and P. Ernfors. 1997. Learning deficit in BDNF mutant mice. Eur. J. Neurosci. 9:2581–2587. [DOI] [PubMed] [Google Scholar]
  26. Lisman, J. E. 1999. Relating hippocampal circuitry to function: recall of memory sequences by reciprocal dentate-CA3 interactions. Neuron. 22:233–242. [DOI] [PubMed] [Google Scholar]
  27. Magee, J. C. 2001. Dendritic mechanisms of phase precession in hippocampal CA1 pyramidal neurons. J. Neurophysiol. 86:528–532. [DOI] [PubMed] [Google Scholar]
  28. Mainen, Z. F., and T. J. Sejnowski. 1995. Reliability of spike timing in neocortical neurons. Science. 268:1503–1506. [DOI] [PubMed] [Google Scholar]
  29. Markram, H., J. Lubke, M. Frotscher, and B. Sakmann. 1997. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 275:213–215. [DOI] [PubMed] [Google Scholar]
  30. McAllister, A. K., L. C. Katz, and D. C. Lo. 1999. Neurotrophins and synaptic plasticity. Annu. Rev. Neurosci. 22:295–318. [DOI] [PubMed] [Google Scholar]
  31. Minichiello, L., M. Korte, D. Wolfer, R. Kuhn, K. Unsicker, V. Cestari, C. Rossi-Arnaud, H. P. Lipp, T. Bonhoeffer, and R. Klein. 1999. Essential role for TrkB receptors in hippocampus-mediated learning. Neuron. 24:401–414. [DOI] [PubMed] [Google Scholar]
  32. Mizuno, M., K. Yamada, A. Olariu, H. Nawa, and T. Nabeshima. 2000. Involvement of brain-derived neurotrophic factor in spatial memory formation and maintenance in a radial arm maze test in rats. J. Neurosci. 20:7116–7121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nowak, L. G., M. V. Sanchez Vives, and D. A. McCormick. 1997. Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb. Cortex. 7:487–501. [DOI] [PubMed] [Google Scholar]
  34. O'Keefe, J., and M. L. Recce. 1993. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 3:317–330. [DOI] [PubMed] [Google Scholar]
  35. Petrov, V., V. Gaspar, J. Masere, and K. Showalter. 1993. Controlling chaos in the Belousov-Zhabotinsky reaction. Nature. 361:240–243. [Google Scholar]
  36. Poo, M. M. 2001. Neurotrophins as synaptic modulators. Nat. Rev. Neurosci. 2:24–32. [DOI] [PubMed] [Google Scholar]
  37. Poon, C. S., and C. K. Merrill. 1997. Decrease of cardiac chaos in congestive heart failure. Nature. 389:492–495. [DOI] [PubMed] [Google Scholar]
  38. Rabinovich, M. I., and H. D. I. Abarbanel. 1998. The role of chaos in neural systems. Neuroscience. 87:5–14. [DOI] [PubMed] [Google Scholar]
  39. Rall, W., and I. Segev. 1985. Space clamp problems when voltage clamping branched neuron with intracellular microelectrodes. In Voltage and Patch Clamping with Microelectrodes. T. G. Smith, H. Lecar, S. J. Redman, and P. W. Gage, editors. 191–215.
  40. Riehle, A., S. Grun, M. Diesmann, and A. Aertsen. 1997. Spike synchronization and rate modulation differentially involved in motor cortical function. Science. 278:1950–1953. [DOI] [PubMed] [Google Scholar]
  41. Roy, R., T. W. Murphy, Jr., T. D. Maier, Z. Gills, and E. R. Hunt. 1992. Dynamical control of a chaotic laser: experimental stabilization of a globally coupled system. Phys. Rev. Lett. 68:1259–1262. [DOI] [PubMed] [Google Scholar]
  42. Salinas, E., and T. J. Sejnowski. 2001. Correlated neuronal activity and the flow of neural information. Nat. Rev. Neurosci. 2:539–550. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schiff, S. J., K. Jerger, D. H. Duong, T. Chang, M. L. Spano, and W. L. Ditto. 1994. Controlling chaos in the brain. Nature. 370:615–620. [DOI] [PubMed] [Google Scholar]
  44. Singer, W. 1993. Synchronization of cortical activity and its putative role in information processing and learning. Annu. Rev. Physiol. 55:349–374. [DOI] [PubMed] [Google Scholar]
  45. Tanaka, T., H. Saito, and N. Matsuki. 1997. Inhibition of GABAA synaptic responses by brain-derived neurotrophic factor (BDNF) in rat hippocampus. J. Neurosci. 17:2959–2966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Thoenen, H. 1995. Neurotrophins and neuronal plasticity. Science. 270:593–598. [DOI] [PubMed] [Google Scholar]
  47. Tokuyama, W., H. Okuno, T. Hashimoto, Y. X. Li, and Y. Miyashita. 2000. BDNF upregulation during declarative memory formation in monkey inferior temporal cortex. Nat. Neurosci. 3:1134–1142. [DOI] [PubMed] [Google Scholar]
  48. Tyler, W. J., M. Alonso, C. R. Bramham, and L. D. Pozzo-Miller. 2002. From acquisition to consolidation: on the role of brain-derived neurotrophic factor signaling in hippocampal-dependent learning. Learn. Mem. 9:224–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Yamada, M. K., K. Nakanishi, S. Ohba, T. Nakamura, Y. Ikegaya, N. Nishiyama, and N. Matsuki. 2002. Brain-derived neurotrophic factor promotes the maturation of GABAergic mechanisms in cultured hippocampal neurons. J. Neurosci. 22:7580–7585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wolf, A., J. B. Swift, H. L. Swinney, and J. A. Vastano. 1985. Determining Lyapunov exponents from a time series. Physica. 16D:285–317. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES