Abstract
Extracellular local field potentials are usually modeled as arising from a set of current sources embedded in a homogeneous extracellular medium. Although this formalism can successfully model several properties of extracellular local field potentials, it does not account for their frequency-dependent attenuation with distance, a property essential to correctly model extracellular spikes. Here we derive expressions for the extracellular potential that include this frequency-dependent attenuation. We first show that, if the extracellular conductivity is nonhomogeneous, there is induction of nonhomogeneous charge densities that may result in a low-pass filter. We next derive a simplified model consisting of a punctual (or spherical) current source with spherically symmetric conductivity/permittivity gradients around the source. We analyze the effect of different radial profiles of conductivity and permittivity on the frequency-filtering behavior of this model. We show that this simple model generally displays low-pass filtering behavior, in which fast electrical events (such as Na+-mediated action potentials) attenuate very steeply with distance, whereas slower (K+-mediated) events propagate over larger distances in extracellular space, in qualitative agreement with experimental observations. This simple model can be used to obtain frequency-dependent extracellular field potentials without taking into account explicitly the complex folding of extracellular space.
INTRODUCTION
Extracellular potentials, such as local field potentials (LFPs) or the electroencephalogram (EEG), are routinely measured in electrophysiological experiments. The fact that action potentials have a limited participation to the genesis of the EEG or LFPs was noted from early studies. Bremer (1938, 1949) proposed that the EEG is generated by nonpropagating potentials, based on the mismatch of time course between EEG waves and action potentials. Eccles (1951) proposed that LFP and EEG activities are generated by summated postsynaptic potentials arising from the synchronized excitation of cortical neurons. Intracellular recordings from cortical neurons later demonstrated a close correspondence between EEG/LFP activity and synaptic potentials (Klee et al., 1965; Creutzfeldt et al., 1966a,b). The current view is that EEG and LFPs are generated by synchronized synaptic currents arising on cortical neurons, possibly through the formation of dipoles (Nunez, 1981; Niedermeyer and Lopes da Silva, 1998).
The fact that action potentials do not participate to EEG-related activities indicate strong frequency-filtering properties of cortical tissue. High frequencies (>≈100 Hz), such as that produced by action potentials, are subject to a severe attenuation, and therefore are visible only for electrodes immediately adjacent to the recorded cell. On the other hand, low-frequency events, such as synaptic potentials, attenuate less with distance. These events can therefore propagate over large distances in extracellular space and be recordable as far as on the surface of the scalp, where they can participate in the genesis of the EEG. This frequency-dependent behavior is also seen routinely in extracellular unit recordings: the amplitude of extracellularly recorded spikes is very sensitive to the position of the electrode, but slow events show much less sensitivity to the position. In other words, an extracellular electrode records slow events that originate from a large number of neighboring neurons, whereas the action potentials are recorded only for the cell(s) immediately adjacent to the electrode. This fundamental property allows us to resolve single units from extracellular recordings.
However, little is known about the physical basis of the frequency-dependent attenuation of extracellular potentials in cortex. By contrast to intracellular events, for which biophysical mechanisms have been remarkably well characterized during the last 50 years (reviewed in Koch (1999)), comparatively little has been done to investigate the biophysical mechanisms underlying the genesis of extracellular field potentials (see review by Nunez (1981)). The reason is that LFPs result from complex interactions involving many factors, such as the spatial distribution of current sources, the spatial distribution of positive and negative electric charges (forming dipoles), their time evolution (dynamics), as well as the conductive and permittivity properties of the extracellular medium. One of the simplest and widely used model of LFP activity considers current sources embedded in a homogeneous extracellular medium (Nunez, 1981; Koch and Segev, 1998). Although this formalism has been successful in many instances (Rall and Shepherd, 1968; Klee and Rall, 1977; Protopapas et al., 1998; Destexhe, 1998), it does not account for the frequency-dependent attenuation and therefore is inadequate for modeling extracellular field potentials including spike activity.
In this article, we would like to investigate possible physical grounds for the frequency-filtering properties of LFPs. We start from first principles (Maxwell equations) and consider different conditions of current sources and extracellular media. We delineate the cases leading to frequency-filtering properties consistent with physiological data. We show that the assumption of a resistive homogeneous extracellular medium cannot account for the frequency-dependent attenuation. It is necessary to take into account the inhomogeneous structure of the extracellular medium (in both permittivity and conductivity) to account for frequency-dependent attenuation. We next analyze a simplified representation of current sources in nonhomogeneous media, and provide a simplified model that could be applied to simulate extracellular field potentials without using complex representations of extracellular space. We terminate by showing a concrete example of the genesis of extracellular LFPs from a conductance-based spiking neuron model.
MATERIAL AND METHODS
We will first develop a general formalism to express the temporal variations of extracellular potential, as well as a simple model in which most of the calculations can be done analytically (see “General theory” section; see also Appendices 1 and 2 for details). We will next explore this simplified model numerically to illustrate its frequency-filtering behavior (“Numerical simulations” section), in which we have performed two computations. i), Calculate the impedance: the impedance is given by an integral, which was evaluated numerically by standard numerical integration routines; and ii), convert time-dependent functions into frequency spectra. These conversions were done via Fourier transformation (as well as its reverse transformation), which were carried out in C using standard numerical routines (Press et al., 1986).
To test this formalism, we also considered a simple biophysical model of a spiking neuron containing voltage-dependent and synaptic conductances (last part of “Numerical simulations” section). A single-compartment neuron was constructed and included conductance-based models of voltage-dependent conductances and synaptic conductances. This model was described by the following membrane equation:
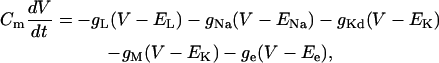 |
(1) |
where Cm = 1 μF/cm2 is the specific membrane capacitance, gL = 4.52 × 10−5 S/cm2 and EL = −70 mV are the leak conductance and reversal potential. 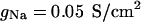 and
and 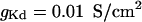 are the voltage-dependent Na+ and K+ conductances responsible for action potentials and were described by a modified version of the Hodgkin and Huxley (1952) model.
are the voltage-dependent Na+ and K+ conductances responsible for action potentials and were described by a modified version of the Hodgkin and Huxley (1952) model. 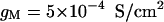 is a slow voltage-dependent K+ conductance responsible for spike-frequency adaptation.
is a slow voltage-dependent K+ conductance responsible for spike-frequency adaptation. 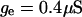 is a fast glutamatergic (excitatory) synaptic conductance. The voltage-dependent conductances were described by conventional Hodgkin-Huxley type models adapted for modeling neocortical neurons, and the synaptic conductance was described by a first-order kinetic model of neurotransmitter binding to postsynaptic receptors. These models and their kinetic parameters were described in detail in a previous publication (Destexhe and Paré, 1999). All numerical simulations were performed using the NEURON simulation environment (Hines and Carnevale, 1997).
is a fast glutamatergic (excitatory) synaptic conductance. The voltage-dependent conductances were described by conventional Hodgkin-Huxley type models adapted for modeling neocortical neurons, and the synaptic conductance was described by a first-order kinetic model of neurotransmitter binding to postsynaptic receptors. These models and their kinetic parameters were described in detail in a previous publication (Destexhe and Paré, 1999). All numerical simulations were performed using the NEURON simulation environment (Hines and Carnevale, 1997).
GENERAL THEORY
In this section, we outline the main features of the model starting from first principles (Maxwell equations). We will consider a number of different special cases and derive a simplified model with radial (spherical) symmetry. In the “Numerical simulations” section, we will investigate numerically the behavior of this simplified model.
In Maxwell's theory, the electric properties of a conductive medium are determined by two parameters, conductivity σ and permittivity ɛ. Although conductivity quantifies the local relation between the electric field and the current, permittivity characterizes the response of the system in terms of separation of opposite charges (polarization) in the presence of an electric field. Maxwell's theory of electromagnetism allows one to compute electric and magnetic fields or potentials, for a given distribution of charges and electric currents. Because charges move very slowly in biological media, the effects of magnetic fields are very small compared to that of the electric field and will be neglected here.
One of Maxwell's equations is Gauss' law:
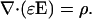 |
(2) |
Here E denotes the electric field, D = ɛE is the called displacement, and ρ is the charge density of the extracellular medium, also allowed to vary slowly in time.
The continuity equation relates the current density j to the charge density ρ:
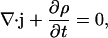 |
(3) |
which states a balance between the electric flux into some volume and the change of the total charge in this volume. In other words, no charge will get lost.
Finally, combining Ohm's law
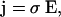 |
(4) |
and Eq. 3 we have for scalar conductivity
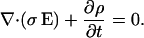 |
(5) |
In the following, we will assume that electric currents are distributed on the surface of the membrane (ionic currents), and that these currents are allowed to vary in time. Also, we have E = −∇V because the magnetic field is negligible.
Below, we successively consider different cases of increasing complexity, starting with a homogeneous extracellular medium, then going over to nonhomogeneous media.
Homogeneous extracellular media
Consider a membrane embedded in a homogeneous extracellular medium, with conductivity σ and permittivity ɛ being held constant in space and time. As shown in Appendix 3, using the assumption σ = σ0 = const., ɛ = ɛ0 = const., we get for each spectral component
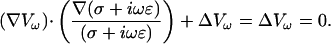 |
(6) |
Hence we find
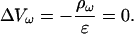 |
(7) |
Using the inverse Fourier transform, this yields
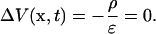 |
(8) |
One observes that the charge density ρ vanishes at the exterior of the sources. The solution depends on the geometry considered, its symmetries and boundary conditions. Moreover, the field is necessarily independent of frequency because the same equation is valid for all frequencies. Therefore, homogeneous media cannot display frequency-dependent properties.
Nonhomogeneous extracellular media
To account for frequency-dependent attenuation, we need to consider more realistic cases. A possible source of frequency-dependent attenuation is the presence of inhomogeneities in the conductivity and permittivity of the extracellular medium. We consider here different cases of spatial inhomogeneities of conductivity.
Stationary currents in spherically symmetric nonhomogeneous media
Before investigating the general case, let us first consider the case of a static spherical current source embedded in a medium where the conductivity σ conserves spherical symmetry, but varies as a function of distance r (as above we assume that σ does not depend on time). We also continue to assume that permittivity ɛ is homogeneous. If the total current flowing through the sphere of radius R is denoted by I, then the radial dependence of the current density is given by
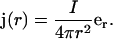 |
(9) |
In this case, the charge density ρ is nonzero and is given by
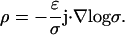 |
(10) |
Then Ohm's law implies for the spherically symmetric electric field
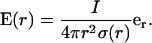 |
(11) |
The spherically symmetric electric potential is obtained by integrating the electric field, giving
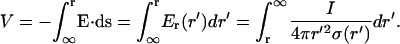 |
(12) |
Details of the calculation can be found in Appendix 1. If a constant conductivity is taken, this equation leads to the following expression:
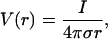 |
(13) |
which is widely used to model extracellular field potentials (Nunez, 1981; Koch and Segev, 1998).
Equation 12 shows that the potential may decrease or even increase, depending on the spatial variations of σ. An important consequence is that such net charge creates its own electric field (so-called secondary field), which will be analyzed in more detail below. What is the physical origin of this nonzero net charge? The current density behaves like J ∝ 1/r2, (Eq. 9), and the electric field like E ∝ 1/(σ(r)r2), (Eq. 11). Consequently, there will be accumulations of charges in some regions of lower conductivity, similar to traffic jams. Consider a more realistic case in which the conductivity of the extracellular space is constant on average, but displays spatial fluctuations around this average. This could correspond for example to different processes and obstacles in the extracellular medium. In this case, the electric field, going like 1/r2on average, fluctuates locally. This creates local areas of positive and negative charge, i.e., electric dipoles. Those dipoles also create a secondary electric field. However, to account for frequency dependence, time-varying current sources must necessarily be considered, in which case the situation is more complex. We will show below that in this case, the frequency response will be determined by the ratio σ/ɛ.
Time-varying currents in nonhomogeneous media
Let us now consider the general case where both ɛ and σ are nonhomogeneous in space, but constant in time. We assume that the current source is allowed to vary in time. The continuity equation implies that the charge density is also time dependent. Ohm's law implies that the electric field has a time dependence as well, and so will also the extracellular potential. Due to the inhomogeneity of ɛ, the extracellular potential does no longer satisfy Poisson's equation. To study the frequency dependence of the extracellular potential, we perform a Fourier transform of the electric field, the potential, and likewise of the charge density ρ.
ρω, the component of frequency ω of the temporal Fourier transform of the charge density ρ, satisfies
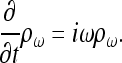 |
(14) |
This equation expresses the differential law of charge conservation for a given Fourier component. Now we consider the Gauss' law (Eq. 2), the law of charge conservation in differential form (Eq. 5), and carry out the Fourier transform with respect to time. Taking into account Eq. 14 yields
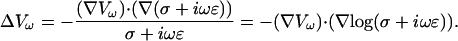 |
(15) |
For details, see Appendix 2.
This equation is general and applies to any particular symmetries (under the assumption of scalar conductivity). We consider below a series of special cases, as well as special symmetries.
Special cases
As a first special case, consider Eq. 15 when permittivity is constant. Then Ohm's law (Eq. 4) implies
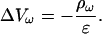 |
(16) |
Constant permittivity also implies 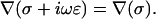 Hence Eq. 15 takes the form
Hence Eq. 15 takes the form
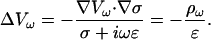 |
(17) |
We therefore observe the occurrence of a (complex) phase difference between the induced charge density ρ/ɛ and the current density j (recall: −∇Vω = Eω = jω/σ). This effect depends on the frequency ω of the Fourier component. Such phenomenon is well known from electric circuits of the resistance-capacitance (RC) type, where in general a phase difference between potential and current is observed. In particular, if the potential vanishes at some time t, the electric charge density will not immediately go to zero.
Equation 17 shows that for high enough frequency the induced charge density goes to zero. On the other hand, for low-frequency phenomena, the charge density will carry out large fluctuations and will be sensitive to spatial fluctuations of conductivity. This has important consequences for interpreting LFP activity (see “Frequency-filtering properties of nonhomogeneous media” section).
As another special case, consider Eq. 15 when the conductivity is constant. The law of charge conservation in differential form Eq. 5 then becomes
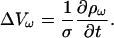 |
(18) |
Constant conductivity also implies 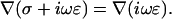 Hence Eq. 15 takes the form
Hence Eq. 15 takes the form
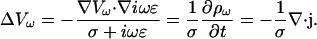 |
(19) |
This means in the limit of low frequencies that there are no current sinks or sources.
A third noteworthy special case is when both permittivity and conductivity are nonhomogeneous, but have a fixed ratio:
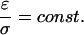 |
(20) |
Under those circumstances one obtains
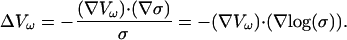 |
(21) |
All frequency dependence cancels out; the potential becomes frequency independent. This result shows that variations of conductivity are not sufficient to determine frequency-filtering properties, but the physically meaningful quantity is the ratio ɛ/σ, which must vary to yield frequency-dependent properties, as we will see below.
Frequency-filtering properties of nonhomogeneous media
We now analyze the frequency-filtering properties of Eq. 15. Consider this equation in two limit cases: i), ω ≪ σ/ɛ (low frequency limit); in this case, log(σ + iωɛ) ≈ log(σ), the solution becomes independent of the permittivity ɛ and is determined only by the conductivity σ and ii), ω ≫ σ/ɛ (high frequency limit); in this case, log(σ + iωɛ) ≈ log(iωɛ), and permittivity only determines the solution. These two cases will be considered in more detail below. The critical frequency around which this transition will occur depends on the relative values of σ and ɛ, and one can define the following critical frequency fcr
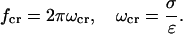 |
(22) |
As an example, consider the value of average resistivity ρres (inverse of conductivity σ) measured in rabbit cerebral cortex (Ranck, 1963), giving ρres = 3 Ωm. Taking the permittivity of salt water (ɛ = 7 × 10−10 F/m), gives a critical frequency of fcr of ∼1010 Hz. Thus, this analysis shows that the behavior will be similar for low and high frequency limits. However, if one evaluates 2πσ/ɛ for a resting membrane (closed ion channels; 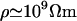 and
and 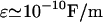 ), one finds for the critical frequency a value in the range between 0 and 100 Hz. The phenomenon of induced charges will be likely to play a role in the frequency range of synaptic inputs in cerebral cortex (0–40 Hz). On the other hand, higher frequencies (>100 Hz)—such as action potentials—are likely to cause negligible variations in charge density.
), one finds for the critical frequency a value in the range between 0 and 100 Hz. The phenomenon of induced charges will be likely to play a role in the frequency range of synaptic inputs in cerebral cortex (0–40 Hz). On the other hand, higher frequencies (>100 Hz)—such as action potentials—are likely to cause negligible variations in charge density.
Further, we can compare Eq. 15 to cases where there is no frequency dependence (i.e., Laplace Eq. 8). At the limit of high frequencies, the left term of Eq. 15 vanishes and this equation becomes equivalent to Eq. 8, showing that for high frequencies, one recovers the same behavior as for a homogeneous medium. To have a low-pass filter, similar to what is observed from extracellular recordings, one must have a situation in which the attenuation of the potential at low frequencies must be less than for homogeneous media. Inspection of the left term of Eq. 15 shows that the attenuation can be either less or more pronounced, resulting in low- or high-pass filters. The type of filter will depend on the behavior of the gradients of conductivity and permittivity. This behavior will be analyzed numerically in more detail later (see “Numerical simulations” section).
Time-varying currents in spherically symmetric nonhomogeneous media
To calculate the extracellular potential V generated by time-varying currents in nonhomogeneous media, Eq. 15 must be integrated by incorporating details about the particular geometry of current sources and extracellular properties. A general method for solving this problem is, e.g., finite-element analysis, which allows us to explicitly incorporate the complex shape and composition of extracellular space around neurons. However, this approach requires us to integrate complex morphological data and appropriate simulation tools. We defer this to a future study. To have a model of LFPs applicable to standard neuron models, we follow here a simpler approach, based on the following simplification: we consider that the variations of conductivity and permittivity have a radial symmetry in the vicinity of the current sources. This simplification allows us to obtain simpler expressions of the extracellular potential, still displaying frequency dependence, and apply this formalism using standard simulation tools.
Consider Eq. 15 for the case of a spherically symmetric system. Then the potential obeys
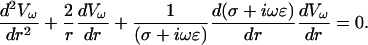 |
(23) |
Integrating this equation gives the following relation between two points r1 and r2 in the extracellular space,
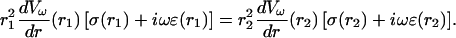 |
(24) |
This can be verified by differentiating this equation with respect to r, which then yields Eq. 23. Integrating Eq. 24 once more yields (assuming the extracellular potential vanishes at large distances, Vω(∞) = 0)
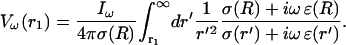 |
(25) |
This will be the main equation forming the basis of our simplified model of LFP. In the numerical part (“Numerical simulations” section), we will solve this equation for different spatial profiles of σ and ɛ. To this end, it is useful to define the impedance:
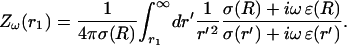 |
(26) |
Then Eq. 25 becomes
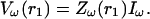 |
(27) |
The impedance is therefore the “filter” applied to theω-frequency component of the current source, to yield the corresponding frequency component of the extracellular potential. In the next section, we will examine the frequency-filtering properties of different extracellular media by calculating numerically the impedance for different cases of spatial inhomogeneities of conductivity and permittivity.
NUMERICAL SIMULATIONS
In this section, we use the expressions of the extracellular potential obtained above. In particular we analyze the behavior of the extracellular potential generated by a current source in a spherically symmetric nonhomogeneous medium (Eq. 25), and its associated impedance (Eq. 26). We investigated the frequency-filtering properties obtained for different cases of increasing complexity of the radial profile of σ and ɛ. The goal is to determine the conditions of spatial variations of conductivity and permittivity for which the frequency-filtering properties are consistent with physiological data. We terminate by an application of this model to calculating the LFP generated by a conductance-based spiking neuron model.
Parameters
Precise experimental data on the variations of permittivity ɛ and conductivity σ in the extracellular medium have not been measured so far. However, averaged values of these parameters are available from macroscopic measurements. A value for σ, averaged over large extracellular distances, σav, was measured by Ranck (1963) and was between 0.28 S/m and 0.43 S/m, for 5 Hz and 5 kHz, respectively. The macroscopic frequency dependence of conductivity seems therefore relatively weak. However, the situation is different microscopically. As reviewed in Nunez (1981), the conductivity of the cerebro-spinal fluid (CSF) is 1.56 S/m whereas the typical conductivity of membranes is from 10−9 to 3.5 × 10−9 S/m. This value was obtained from the resting (leak) membrane conductance of cortical neurons, typically around 4.5 × 10−5 S/cm2, multiplied by the thickness of the membrane (2–8 nm; Peters et al., 1991). Other types of membranes, such as myelinated or unmyelinated fibers, and glial cells, have different membrane conductances, which are in the range of 0.1–10−6 S/cm2 (Hille, 2001). At microscopic scales, there is therefore ∼9 orders of magnitude variations of conductivity.
Permittivity variations are not so dramatic. Fluids have higher permittivity, for example it is about 7 × 10−10 F/m for sea water. Membranes have a permittivity of from 10−11 to 8 × 10−11 F/m. The latter value was derived from the specific capacitance of membranes, C = 1 μF/cm2 (Johnston and Wu, 1997), and assuming a membrane thickness of 2–8 nm (Peters et al., 1991). Because those variations are small compared to the variations of conductivity, it is a good approximation to consider the permittivity as a constant. In the following, we will use the reference value of ɛ = 10−10 F/m.
In the following we will use normalized values for conductivity σ(r)/σ(R) and permittivity ɛ(r)/σ(R). Because the membrane is always surrounded by extracellular fluid, the conductivity at the source is σ(R) = 1.56 S/m. Based on the values estimated above, we use in simulations the values for the normalized conductivity σ(r)/σ(R) included between large values (equal to unity) and a low value of 2 × 10−9. Similarly, the normalized (constant) value of permittivity will be ɛ(r)/σ(R) = 6 × 10−11 s. We have verified that no qualitative change results from variations of these parameters.
Frequency-filtering properties of spherically symmetric media
We calculated numerically the impedance (Eq. 26) for different cases of spatial variations of conductivity and permittivity. In all cases we assumed a current source with spherical geometry, characterized by radius R, and that σ and ɛ vary according to a radial (spherical) symmetry around this current source (see scheme in Fig. 1 A). For each case, we represented the normalized impedance
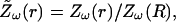 |
(28) |
which allows better comparison between the different cases. Because the value of impedance does not depend on the absolute value of permittivity and conductivity (dividing σ and ɛ by a constant factor does not change Zω(r) in Eq. 26), we used the normalized conductivity σ(r)/σ(R) and the normalized permittivity ɛ(r)/σ(R) defined above. It is also convenient to represent all distances in units of R, although we also considered absolute values of distances (see below).
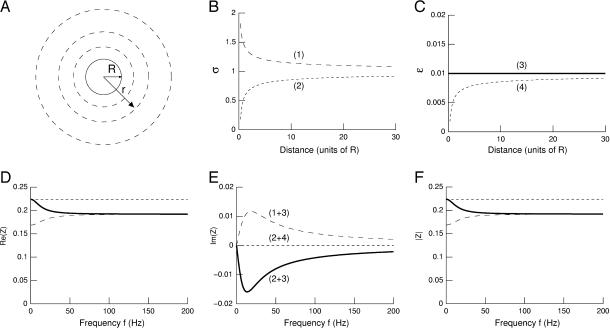
FIGURE 1.
Radial variations of conductivity and permittivity can induce frequency-filtering properties. (A) Scheme of the current source in radial symmetry. The current source is assumed to be spherical (solid line; radius R). The conductivity and permittivity vary in radial symmetry according to the distance r from the center of the source. (B) Conductivity σ versus radial distance r. Two cases are shown: (1) 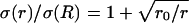 and (2)
and (2) 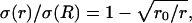 where r0 = 0.2025 R (R = 1 here). (C) Permittivity ɛ versus radial distance r. The two curves shown are: (3) ɛ(r)/σ(R) = 0.01 and (4)
where r0 = 0.2025 R (R = 1 here). (C) Permittivity ɛ versus radial distance r. The two curves shown are: (3) ɛ(r)/σ(R) = 0.01 and (4) 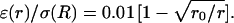 (D–F) Real part (D), imaginary part (E), and norm (F) of the impedance
(D–F) Real part (D), imaginary part (E), and norm (F) of the impedance 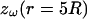 versus frequency f. Combining the profiles (1) and (3) in B and C leads to a high-pass filter (long-dashed line), whereas (2+3) gives low-pass characteristics (solid line). The combination (2+4) is such that
versus frequency f. Combining the profiles (1) and (3) in B and C leads to a high-pass filter (long-dashed line), whereas (2+3) gives low-pass characteristics (solid line). The combination (2+4) is such that 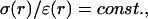 in which case there is no frequency dependence (short-dashed line).
in which case there is no frequency dependence (short-dashed line).
We first investigated a simple case of smooth variations of those parameters, to illustrate the different types of frequency filtering that can be obtained in this model. The profiles of conductivity and permittivity are shown in Fig. 1, B and C. These curves tend to be the same asymptotic value for large distances. The corresponding impedance is shown as a function of frequency f in Fig. 1, D–F (see Appendix 3 for details of the method). When the ratio σ/ɛ is kept constant (Fig. 1, D–F, short-dashed line), there is no frequency dependence as analyzed above in the “Special cases” section. In the case of a decreasing conductivity with distance combined with constant permittivity, one has a high-pass filter (Fig. 1, D–F, long-dashed line). By contrast, a low-pass filter is observed if an increasing conductivity with distance is combined with a constant permittivity (Fig. 1, D–F, solid line). Thus, there is a clear frequency-dependent behavior when σ and/or ɛ vary as function of distance r, if the ratio σ/ɛ is not constant. This also shows that low- and high-pass filters are both possible, depending on the exact form of the function σ(r) and ɛ(r). The impedance can also have a nonzero imaginary part, which means that beyond resistivity, the medium also has capacitive properties. In this case, there will be a phase difference between the potential and the current.
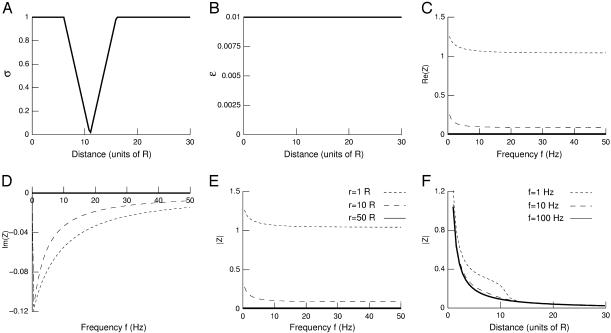
We next considered a case characterized by a localized drop of conductivity (Fig. 2 A) while permittivity was kept constant (Fig. 2 B). The resulting impedance measured at different distances from the source is shown in Fig. 2, C–E, as a function of frequency f. In this case, for distances around the conductivity drop, there is a moderate frequency dependence with low-pass characteristics (Fig. 2, C–E, short-dashed and long-dashed lines). However, for larger distances, the imaginary part is zero and there is no frequency dependence (Fig. 2, C–E, solid lines). This is explained by the fact that for large distances σ(r) = σ(R) and ɛ(r) = ɛ(R). This behavior can also be seen in the attenuation of the different frequency components illustrated in Fig. 2 F. There is a different attenuation only for distances around the region where conductivity varies.
FIGURE 2.
Frequency-filtering properties obtained by a localized drop in conductivity. (A) Profile of conductivity versus distance. The conductivity was described by 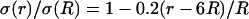 for
for 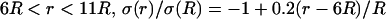 for
for 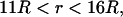 and
and 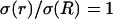 otherwise. (B) Profile of permittivity.
otherwise. (B) Profile of permittivity. 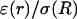 was constant and equal to 0.01. (C–E) Real part (C), imaginary part (D), and norm (E) of the impedance as a function of frequency f.
was constant and equal to 0.01. (C–E) Real part (C), imaginary part (D), and norm (E) of the impedance as a function of frequency f. 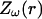 is shown for different distances r away from the source. (F) Attenuation of the impedance norm
is shown for different distances r away from the source. (F) Attenuation of the impedance norm 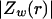 with distance. The different curves correspond to three different frequencies.
with distance. The different curves correspond to three different frequencies.
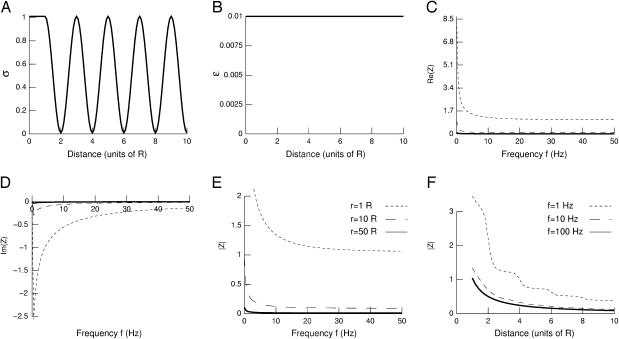
Because the extracellular space is composed of alternating fluids and membranes (Peters et al., 1991), which have high and low conductivity, respectively, we have next considered the situation where conductivity fluctuates periodically with distance (Fig. 3). Considering a cosine function of conductivity (Fig. 3 A) with constant permittivity (Fig. 3 B) leads to a rather strong frequency-dependent attenuation (Fig. 3, C–E) with low-pass characteristics. There was a strong attenuation with distance for all frequencies (Fig. 3 F). Very similar results were obtained with other periodic functions (for example by replacing cos by sin in the function used in Fig. 3 A), different oscillation periods, or even for damped oscillations of conductivity (not shown).
FIGURE 3.
Frequency-filtering properties obtained from a periodically varying conductivity. (A) Oscillatory profile of conductivity versus distance 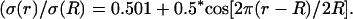 (B) Profile of permittivity
(B) Profile of permittivity 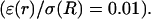 (C–E) Real part (C), imaginary part (D), and norm (E) of the impedance Zω(r) versus frequency f. The different curves are taken at different distances r outside of the current source. (F) Attenuation of the impedance norm
(C–E) Real part (C), imaginary part (D), and norm (E) of the impedance Zω(r) versus frequency f. The different curves are taken at different distances r outside of the current source. (F) Attenuation of the impedance norm  with distance. The different curves indicate the attenuation obtained at different frequencies.
with distance. The different curves indicate the attenuation obtained at different frequencies.
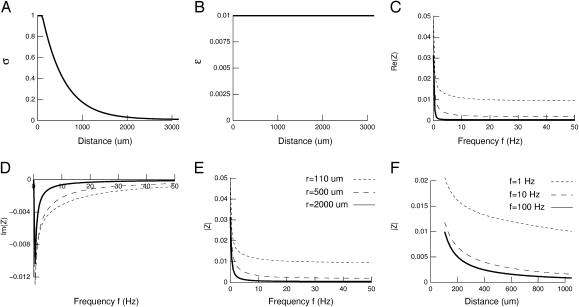
It could be argued that although fluids and membranes alternate in extracellular space, there is an efficient diffusion of ions only in the extracellular fluid around the membrane. For larger distances, diffusion becomes increasingly difficult because of the increased probability of meeting obstacles. In this case, conductivity would be highest around the source and progressively decrease to an “average” conductivity level for larger distances. This situation is illustrated in Fig. 4. We have considered that the conductivity is highest at the source, then decreases exponentially with distance with a space constant λ (Fig. 4 A; note that in this case, real distances were used). Permittivity was constant (Fig. 4 B). The resulting impedance displayed pronounced frequency-filtering properties with low-pass characteristics (Fig. 4,C–E). In particular, the attenuation with distance revealed strong differences between low and high frequencies of the spectrum (Fig. 4 F). Similar results can be obtained with other decreasing functions of connectivity (not shown).
FIGURE 4.
Frequency-filtering properties obtained with exponential decrease of conductivity. (A) Profile of conductivity. 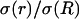 decays exponentially according to
decays exponentially according to 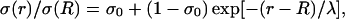 with a space constant
with a space constant 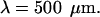 (B) Profile of permittivity.
(B) Profile of permittivity. 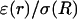 was constant (0.01). (C–E) Real part (C), imaginary part (D), and norm (E) of the impedance Zω(r) versus frequency f. The different curves show the impedance calculated at different distances r. (F) Attenuation of the impedance norm
was constant (0.01). (C–E) Real part (C), imaginary part (D), and norm (E) of the impedance Zω(r) versus frequency f. The different curves show the impedance calculated at different distances r. (F) Attenuation of the impedance norm 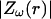 with distance. The different curves indicate the attenuation obtained at different frequencies.
with distance. The different curves indicate the attenuation obtained at different frequencies.
The above examples show that there can be a strong frequency-filtering behavior, with low-pass characteristics as observed in experiments. However, although these examples show a more effective filtering for high frequencies, it still remains to be shown that the high frequencies attenuate more steeply with distance compared to low frequencies. To this end, we define the quantity:
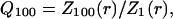 |
(29) |
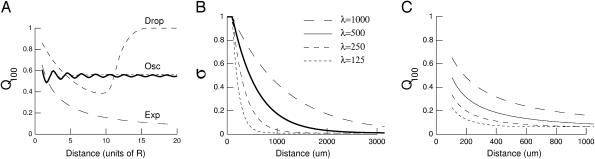
where Z1 and Z100 are the impedances computed at 1 Hz and 100 Hz, respectively. This ratio quantifies the differential filtering of fast and slow frequencies as a function of distance r. Fig. 5 A displays the Q100 values obtained for some of the examples considered above. In the case of a localized drop of conductivity (Fig. 5 A, Drop), there was an effect of distance for r < 16R, then the Q100 remained equal to unity for further distances. This behavior is in agreement with the impedance shown in Fig. 2, in which case there was no frequency filtering for r > 16R. For oscillatory conductivities (Fig. 5 A, Osc), the Q100 was always <1, consistent with the low-pass frequency-filtering behavior observed in Fig. 3. However, the Q100 oscillated around a value of 0.6 and did not further decrease with distance. Thus, in this case, although there was a clear low-pass filtering behavior, all frequencies still contribute by the same relative amount to the extracellular potential, regardless of distance. On the other hand, with exponential decay of conductivity, the Q100 monotonically decreased with distance (Fig. 5 A, Exp). Thus, this case shows both low-pass filtering behavior (Fig. 4) and a stronger attenuation of high frequencies compared to low frequencies (Fig. 5 A, Exp), which is in qualitative agreement with experiments. Analyzing exponentially decaying conductivities of different space constants (Fig. 5 B) revealed that the various patterns of distance dependence approximately followed the pattern of conductivity (Fig. 5 C). This type of conductivity profile is relatively simple and plausible, and will be the one considered in the biophysical model investigated below.
FIGURE 5.
Distance dependence of frequency-filtering properties. (A) Ratio of impedance at fast and slow frequencies (Q100) represented as a function of distance r (units of R). The Q100 ratios are represented for different profiles of conductivity. Drop, localized drop of conductivity (short-dashed line; same parameters as in Fig. 2). Osc, oscillatory profile of conductivity (solid line; same parameters as in Fig. 3; the dotted line indicates a damped cosine oscillation). Exp, exponential decrease of conductivity (long-dashed line; same parameters as in Fig. 4 except 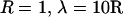 ). (B) Profiles of conductivity with exponential decay (same parameters as in Fig. 4; space constants λ indicated in μm). (C) Q100 ratios obtained for the conductivity profiles shown in B.
). (B) Profiles of conductivity with exponential decay (same parameters as in Fig. 4; space constants λ indicated in μm). (C) Q100 ratios obtained for the conductivity profiles shown in B.
Biophysical model of the frequency-filtering properties of local field potentials
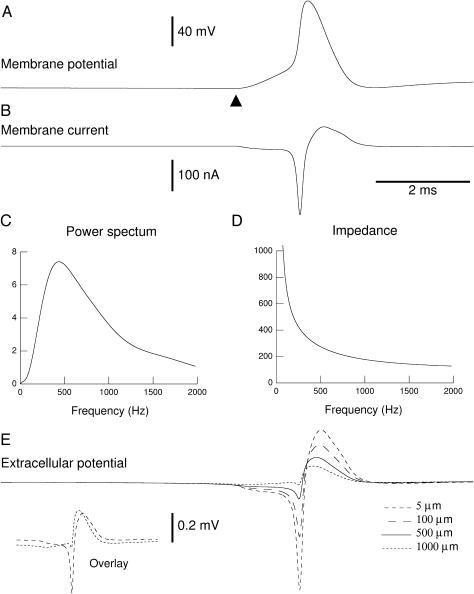
We have applied the above formalism to model the frequency dependence of the extracellular field potentials stemming from a conductance-based spiking neuron model. The details about the model are given in the Material and Methods section, whereas the details of the calculation of the extracellular LFP (general for any current source) is given in Appendix 3. The profile of conductivity and permittivity used is that of Fig. 4. We calculated the total membrane current generated by a single-compartment model of an adapting cortical neuron, containing voltage-dependent Na+ and K+ conductances for generating action potentials and a slow voltage-dependent K+ conductance responsible for spike-frequency adaptation. The model also contained a fast glutamatergic excitatory synaptic conductance, which was adjusted to evoke a postsynaptic potential just above threshold, to evoke a single action potential (Fig. 6 A). The total membrane current (Fig. 6 B) was calculated and stored to calculate its Fourier transform (power spectral density shown in Fig. 6 C). The impedance of the extracellular medium (Fig. 6 D) was calculated using absolute values of the parameters (Eq. 26).
FIGURE 6.
Frequency-filtered extracellular field potentials in a conductance-based model. (A) Membrane potential of a single-compartment model containing voltage-dependent Na+ and K+ conductances and a glutamatergic synaptic conductance. The glutamatergic synapse was stimulated at t = 5 ms (▴) and evoked an action potential. (B) Total membrane current generated by this model. Negative currents correspond to Na+ and glutamatergic conductances (inward currents), whereas positive currents correspond to K+ conductances (outward currents). (C) Power spectrum of the total current shown in B. (D) Impedance at 500 μm from the current source assuming a radial profile of conductivity and permittivity (as in Fig. 4). (E) Extracellular potential calculated at various distances from the source (5, 100, 500, and 1000 μm). The frequency filtering properties can be seen by comparing the negative and positive deflections of the extracellular potential. The fast negative deflection almost disappeared at 1000 μm whereas the slow positive deflection was still present. The inset in E (Overlay) shows the traces at 5 and 1000 μm overlaid.
This model was used to calculate the field potentials at different radial distances assuming the neuron was a spherical source (radius of 105 μm). The extracellular potential is indicated for 5, 100, 500, and 1000 μm away from the source (see Fig. 6 E) and strong frequency-filtering properties are apparent: the fast negative deflection of extracellular voltage showed a steep attenuation and almost disappeared at 1000 μm (although it had the highest amplitude at 5 μm). In contrast, the slow positive deflection of the extracellular potential showed less attenuation with distance and became dominant at large distances (500 and 1000 μm in the example of Fig. 6 E). This is best seen from the overlaid traces (see Fig. 6 E, inset), showing the marked difference in fast and slow components in the field potentials recorded at 5 and 1000 μm.
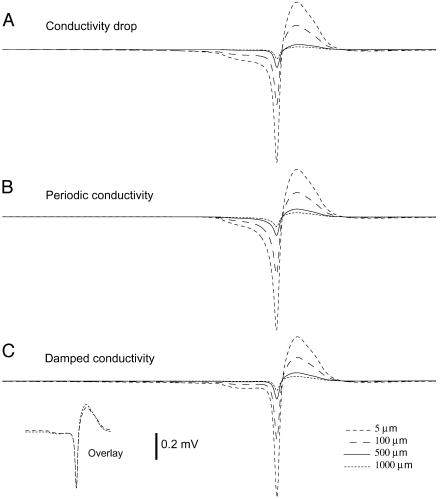
Thus, this example illustrates that the approach provided here can lead to a relatively simple model to calculate local field potentials with frequency-filtering properties. The exact profiles of filtering and attenuation depend on the exact shape of the gradients of conductivity/permittivity as well as on the spherical symmetry inherent to this model. This is illustrated in Fig. 7 for the other radial profiles of conductivity considered earlier (drop, periodic, and damped conductivity). This figure shows that for these particular profiles, the attenuation of fast and slow deflections is similar (the global shape of the LFP remains similar although attenuated in amplitude; see almost perfect overlay in the inset of Fig. 7 C). There is therefore a negligible frequency-dependent attenuation in those cases. This is in agreement with the quasi-absence of frequency-dependent attenuation evidenced in the quantitative analysis of Fig. 5 (see above). In contrast, Fig. 6 E shows that a radial model with exponentially decaying conductivity replicates the experimental observation that only slow frequencies propagate through large extracellular distances.
FIGURE 7.
Frequency-filtered extracellular field potentials for different radial profiles of conductivity. The extracellular potential was calculated from a conductance-based spiking neuron model (identical to that of Fig. 6) and was shown at various distances from the source (5, 100, 500, and 1000 μm) for different profile of conductivity. (A) Localized drop in conductivity (same profile as in Fig. 2 A, with drop starting at r = 120 μm and ending at r = 280 μm). (B) Same simulation using a periodic conductivity profile (profile as in Fig. 3 A with same extremal values as in Fig. 6 and a period of 2 μm). (C) Same simulation using damped oscillations of conductivity (same parameters as in B, with a space constant of λ = 500 μm). In all cases, the attenuation of the fast negative deflection was similar to the slow positive deflection, in contrast with Fig. 6 E. The inset in C (Overlay) shows the traces at 5 and 1000 μm overlaid, which are almost superimposable (compare with inset in Fig. 6 E).
DISCUSSION
In this article, we have provided a model of extracellular field potentials in nonhomogeneous media. We discuss here the validity of this model, how it relates to previous studies, and what perspectives are provided.
The theoretical analysis outlined in the “General theory” section shows that inhomogeneities of extracellular space (with respect to conductivity and/or permittivity) is a possible cause for frequency filtering. In general, nonhomogeneous extracellular media will differently affect the attenuation of the various frequency components of the current sources. The physical basis of such differential filtering is the ratio between conductivity and permittivity, which respective gradients will determine if extracellular media act as high-pass or low-pass filters. The composition of extracellular space is made from the alternance of fluids and membranes (Peters et al., 1991). Only ∼6% of the extracellular space is devoted to interstitial space (extracellular fluid), whereas the core of the volume is made by axons (34%), neuronal dendrites (35%), spines (14%), and glial cells (11%; see details in Braitenberg and Schüz (1998)). Because these media have very different conductivity and permittivity, one may expect the extracellular space to be electrically highly nonhomogeneous. The structural composition of extracellular space is thus very likely to be a main determinant of the frequency-filtering properties of LFPs. In addition, the conductivity of the extracellular fluid directly beneath the membrane depends on the ionic concentrations present. It turns out that the extracellular ionic concentrations may vary in time, in an activity-dependent manner (reviewed in Amzica (2002)). Therefore, it is also likely that there is an activity-dependent contribution to the filtering properties of the extracellular medium. Here, we did not consider such time-dependent variations of conductivity, but this type of contribution is certainly worth being considered by future theoretical work.
To correctly simulate the frequency-filtering behavior due to extracellular inhomogeneity, the extracellular potential should be calculated by a model incorporating details about the three-dimensional composition of the extracellular medium. Such type of simulations should use methods such as finite-element analysis. However, the complexity of this type of analysis, and of the data it requires, makes such simulations inaccessible to standard models. In addition, this requires orders of magnitude differences in computational power needs. For these reasons, we have considered the option of generating a simplified model under some approximation. We assumed that the geometry of extracellular inhomogeneities is spheric around the current source. In this condition, one can obtain relatively simple expressions of the extracellular potential such as Eq. 25. Not only this expression is amenable to theoretical analysis, but it is also sufficiently simple to be applied to current neuron models that do not have an explicit representation of extracellular space.
This method relies on a number of approximations, which will necessarily impact on the degree of realism provided by the model. A first approximation was to consider the genesis of extracellular potentials from a set of independent and punctual current sources, as in other simplified models of field potentials (Nunez, 1981; Destexhe, 1998; Koch and Segev, 1998). This approximation contrasts with the current sources and sinks (dipoles) underlying the genesis of field potentials by neurons (Nunez, 1981) and more realistic distributions should be considered in future extensions of this work. A second approximation was to consider that the profiles of conductivity and permittivity variations follow a radial symmetry around the current source. This approach therefore considers only the average “mean-field” variations around the source, and cannot incorporate the local variations of conductivity arising from different types of membranes. Electron microscopic reconstructions of the cortical neuropil (Peters et al., 1991) show that cerebral cortical tissue consists of a three-dimensional aggregate of randomly distributed cell types (neurons, glial cells, axons, myelin, blood vessels). Because each of these elements may have very different conductivity (Hille, 2001), more accurate average profiles of conductivity could be obtained by calculating the radial variations of conductivity and permittivity by averaging the profiles of σ and ɛ in all directions emanating from neuronal membranes using three-dimensional reconstructions of the neuropil. In this case, the particular conductivity of the different types of membranes could be incorporated, presumably leading to more accurate representations compared to the heuristic profiles assumed here. Another direction would be to measure experimentally those profiles, but such data are not currently available. Nevertheless, the heuristic profiles of conductivity and permittivity used here can give frequency-filtering properties in good qualitative agreement with experiments.
This approach is, however, not appropriate to investigate more quantitative problems, such as the precise localization of current sources from LFP activity, in which case quantitative models such as finite element analysis would be necessary. Intermediate approaches also exist, such as bidomain models, which have been successfully used for modeling extracellular potentials in several tissues (Basser and Roth, 2000; Miller and Henriquez, 1990). The bidomain approach consists of a different approximation to simulate the electrical behavior of media composed of elements of different conductivities. In this case, the medium is approximated by two spatially uniform “domains” of conductivity, each described by its own set of Laplace (or Poisson) equations, and the two sets of equations are coupled together. This approximation greatly simplifies the boundary conditions, which can be very complex for media such as the cerebral cortex. A comparison between the different approaches (finite-element analysis, bidomain models, and the present approach) would be needed to evaluate the advantages and pitfalls of each approximation.
These results lead to several interesting perspectives for future work or extensions. First, as mentioned above, the simplified model could be enhanced by comparison with a more realistic model, for example based on three-dimensional reconstructions of extracellular space. The simplified model could be adjusted so that it fits as closely as possible the behavior of the more realistic model, yielding more optimal expressions of the radial profiles of conductivity and permittivity. A second possible direction is the “reverse” problem of estimating neuronal activity based on LFP measurements. By using data on the spatial and temporal variations of multisite LFPs and multiunit activity, it should be possible to estimate what are the respective contributions of the natural frequency-filtering properties of extracellular space and the spatial coherence of neuronal sources in the different frequency components. For example, it was shown that a consistent relation between LFP and cell firing extends to large cortical distances (>7 mm) for slow waves but not for fast oscillations in the gamma (20–60 Hz) frequency range (Destexhe et al., 1999). A model of LFP is needed to evaluate whether this effect is really due to differences in the coherence of neuronal firing (as the single-unit data indicates), or if a large part could be explained by the low-pass filtering properties of the extracellular medium. A combination of experimental recordings and computational models will be needed to understand how neuronal activity translates into extracellular field potentials and vice versa.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
H.K. has been supported by the National Science and Engineering Research Council (NSERC, Canada). A.D. has been supported by the Medical Research Council (MRC, Canada), the Centre National de la Recherche Scientifique (CNRS, France), and the Human Frontier Science Program (HFSP). Supplementary information is available at http://cns.iaf.cnrs-gif.fr
APPENDIX 1: EXTRACELLULAR POTENTIAL IN NONHOMOGENEOUS MEDIA WITH SPHERICAL SYMMETRY
This Appendix refers to the “Stationary currents in apherically symmetric nonhomogeneous media” section: Recall σ = σ(r), ɛ = const. Then Gauss' law becomes
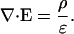 |
(30) |
The law of charge conservation becomes
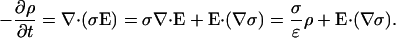 |
(31) |
Using Ohm's law and assuming σ ≠ 0, this becomes
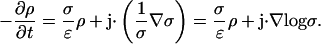 |
(32) |
We make the assumption that the current density j is stationary, i.e., it does not explicitly depend on time. Also, by assumption σ and ɛ are time independent. Hence denoting 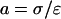 and
and 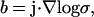 Eq. 32 takes the form
Eq. 32 takes the form
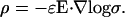 |
(33) |
It shows that the net charge density is different from zero.
Electric field for spherical current source
At the radius r = R, the electric field is given by the current
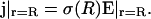 |
(34) |
The total current passing through a sphere (surface S, radius r) is given by
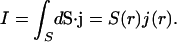 |
(35) |
Thus the current density as function of radius r behaves as
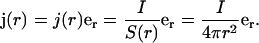 |
(36) |
Ohm's law implies for the electric field
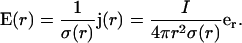 |
(37) |
Electric potential
Because the electric field is radially symmetric, so is also the potential, which obeys
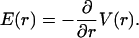 |
(38) |
Its solution is obtained from Eq. 37,
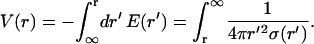 |
(39) |
An independent check of this solution can be obtained by considering the law of charge conservation.
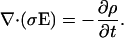 |
(40) |
Because of the time-independent charge density, this is equivalent at
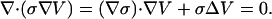 |
(41) |
APPENDIX 2: FOURIER COMPONENT OF THE EXTRACELLULAR FIELD POTENTIAL
This Appendix refers to the “Time-varying currents in nonhomogeneous media” section: Starting from Gauss' law
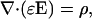 |
(42) |
the inhomogeneity of ɛ implies
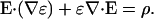 |
(43) |
Then the electric potential obeys
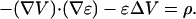 |
(44) |
We recall that the potential V and the charge density ρ are time dependent, whereas the permittivity ɛ is not. We define the Fourier transform of time-dependent function f(t) via
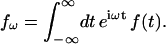 |
(45) |
Now we perform a Fourier transform with respect to time of the potential V and the charge density ρ to obtain an equation for the Fourier components at frequency ω,
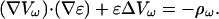 |
(46) |
Similarly, starting from the differential form of the law of charge conservation,
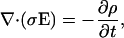 |
(47) |
from the Fourier transform of ρ follows that a component at frequency ω satisfies
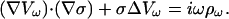 |
(48) |
Combining Eqs. 46 and 48 yields
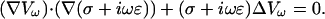 |
(49) |
APPENDIX 3: METHOD TO CALCULATE THE EXTRACELLULAR FIELD POTENTIAL FROM POINT CURRENT SOURCES
-
Compute the Fourier component ω of the impedance
where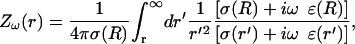
(50) 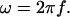 This expression incorporates the values of the conductivity σ(r) and permittivity ɛ(r) as a function of the distance r. It is also assumed that
This expression incorporates the values of the conductivity σ(r) and permittivity ɛ(r) as a function of the distance r. It is also assumed that 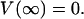
This quantity is computed for each frequency component ω of the spectrum, and for each extracellular distance r considered. It can be precalculated and stored in a matrix (Z[f][r]).
For each current source, compute the (complex) Fourier transform of the total membrane current, which we call here Iω.
- For each current source, compute the Fourier component ω of the extracellular potential:
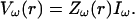
(51) For each current source, compute the extracellular potential by applying the (complex) inverse Fourier transform to Eq. 51.
Finally, combine the contributions from all current sources to yield the extracellular potential at a given position x in the extracellular space.
References
- Amzica, F. 2002. In vivo electrophysiological evidences for cortical neuron-glia interactions during slow (<1 Hz) and paroxysmal sleep oscillations. J. Physiol. (Paris). 96:209–219. [DOI] [PubMed] [Google Scholar]
- Basser, P. J., and B. J. Roth. 2000. New currents in electrical stimulation of excitable tissues. Annu. Rev. Biomed. Eng. 2:377–397. [DOI] [PubMed] [Google Scholar]
- Braitenberg, V., and A. Schüz. 1998. Cortex: statistics and geometry of neuronal connectivity, 2nd ed. Springer-Verlag, Berlin, Germany.
- Bremer, F. 1938. L'activité électrique de l'écorce cérébrale. Actualités Scientifiques et Industrielles. 658:3–46. [Google Scholar]
- Bremer, F. 1949. Considérations sur l'origine et la nature des “ondes” cérébrales. Electroencephalogr. Clin. Neurophysiol. 1:177–193. [PubMed] [Google Scholar]
- Creutzfeldt, O., S. Watanabe, and H. D. Lux. 1966a. Relation between EEG phenomena and potentials of single cortical cells. I. Evoked responses after thalamic and epicortical stimulation. Electroencephalogr. Clin. Neurophysiol. 20:1–18. [DOI] [PubMed] [Google Scholar]
- Creutzfeldt, O., S. Watanabe, and H. D. Lux. 1966b. Relation between EEG phenomena and potentials of single cortical cells. II. Spontaneous and convulsoid activity. Electroencephalogr. Clin. Neurophysiol. 20:19–37. [DOI] [PubMed] [Google Scholar]
- Destexhe, A. 1998. Spike-and-wave oscillations based on the properties of GABAB receptors. J. Neurosci. 18:9099–9111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe, A., D. Contreras, and M. Steriade. 1999. Spatiotemporal analysis of local field potentials and unit discharges in cat cerebral cortex during natural wake and sleep states. J. Neurosci. 19:4595–4608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe, A., and D. Paré. 1999. Impact of network activity on the integrative properties of neocortical pyramidal neurons in vivo. J. Neurophysiol. 81:1531–1547. [DOI] [PubMed] [Google Scholar]
- Eccles, J. C. 1951. Interpretation of action potentials evoked in the cerebral cortex. J. Neurophysiol. 3:449–464. [DOI] [PubMed] [Google Scholar]
- Hille, B. 2001. Ion Channels and Excitable Membranes, 3rd ed. Sinauer, Sunderland, MA.
- Hines, M. L., and N. T. Carnevale. 1997. The NEURON simulation environment. Neural Comput. 9:1179–1209. [DOI] [PubMed] [Google Scholar]
- Hodgkin, A. L., and A. F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, D., and S. Wu. 1997. Cellular Neurophysiology. MIT Press, Cambridge, MA.
- Klee, M. R., K. Offenloch, and J. Tigges. 1965. Cross-correlation analysis of electroencephalographic potentials and slow membrane transients. Science. 147:519–521. [DOI] [PubMed] [Google Scholar]
- Klee, M., and W. Rall. 1977. Computed potentials of cortically arranged populations of neurons. J. Neurophysiol. 40:647–666. [DOI] [PubMed] [Google Scholar]
- Koch, C. 1999. Biophysics of Computation. Oxford University Press, Oxford, UK.
- Koch, C., and I. Segev. 1998. Methods in Neuronal Modeling, 2nd ed. C. Koch and I. Segev, editors. MIT Press, Cambridge, MA.
- Miller, C. E., and C. S. Henriquez. 1990. Finite element analysis of bioelectric phenomena. Crit. Rev. Biomed. Eng. 18:207–233. [PubMed] [Google Scholar]
- Niedermeyer, E., and F. Lopes da Silva. editors. 1998. Electroencephalography, 4th ed. Williams and Wilkins, Baltimore, MD.
- Nunez, P. L. 1981. Electric Fields of the Brain: The Neurophysics of EEG. Oxford University Press, Oxford, UK.
- Peters, A., S. L. Palay, and H. F. Webster. 1991. The Fine Structure of the Nervous System. Oxford University Press, Oxford, UK.
- Press. W. H., H. P. Flannery, S. A. Teukolsky, and W. T. Vetterling. 1986. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
- Protopapas, A. D., M. Vanier, and J. Bower. 1998. Simulating large-scale networks of neurons. In Methods in Neuronal Modeling, 2nd ed. C. Koch and I. Segev, editors. MIT Press, Cambridge, MA. 461–498.
- Rall, W., and G. M. Shepherd. 1968. Theoretical reconstruction of field potentials and dendrodendritic synaptic interactions in olfactory bulb. J. Neurophysiol. 31:884–915. [DOI] [PubMed] [Google Scholar]
- Ranck, J. B., Jr. 1963. Specific impedance of rabbit cerebral cortex. Exp. Neurol. 7:144–152. [DOI] [PubMed] [Google Scholar]