First Principles Predictions of the Structure and Function of G-Protein-Coupled Receptors: Validation for Bovine Rhodopsin

Abstract

G-protein-coupled receptors (GPCRs) are involved in cell communication processes and with mediating such senses as vision, smell, taste, and pain. They constitute a prominent superfamily of drug targets, but an atomic-level structure is available for only one GPCR, bovine rhodopsin, making it difficult to use structure-based methods to design receptor-specific drugs. We have developed the MembStruk first principles computational method for predicting the three-dimensional structure of GPCRs. In this article we validate the MembStruk procedure by comparing its predictions with the high-resolution crystal structure of bovine rhodopsin. The crystal structure of bovine rhodopsin has the second extracellular (EC-II) loop closed over the transmembrane regions by making a disulfide linkage between Cys-110 and Cys-187, but we speculate that opening this loop may play a role in the activation process of the receptor through the cysteine linkage with helix 3. Consequently we predicted two structures for bovine rhodopsin from the primary sequence (with no input from the crystal structure)—one with the EC-II loop closed as in the crystal structure, and the other with the EC-II loop open. The MembStruk-predicted structure of bovine rhodopsin with the closed EC-II loop deviates from the crystal by 2.84 Å coordinate root mean-square (CRMS) in the transmembrane region main-chain atoms. The predicted three-dimensional structures for other GPCRs can be validated only by predicting binding sites and energies for various ligands. For such predictions we developed the HierDock first principles computational method. We validate HierDock by predicting the binding site of 11-cis-retinal in the crystal structure of bovine rhodopsin. Scanning the whole protein without using any prior knowledge of the binding site, we find that the best scoring conformation in rhodopsin is 1.1 Å CRMS from the crystal structure for the ligand atoms. This predicted conformation has the carbonyl O only 2.82 Å from the N of Lys-296. Making this Schiff base bond and minimizing leads to a final conformation only 0.62 Å CRMS from the crystal structure. We also used HierDock to predict the binding site of 11-cis-retinal in the MembStruk-predicted structure of bovine rhodopsin (closed loop). Scanning the whole protein structure leads to a structure in which the carbonyl O is only 2.85 Å from the N of Lys-296. Making this Schiff base bond and minimizing leads to a final conformation only 2.92 Å CRMS from the crystal structure. The good agreement of the ab initio-predicted protein structures and ligand binding site with experiment validates the use of the MembStruk and HierDock first principles' methods. Since these methods are generic and applicable to any GPCR, they should be useful in predicting the structures of other GPCRs and the binding site of ligands to these proteins.

INTRODUCTION

Integral membrane proteins comprise 20–30% of genes (Wallin and von Heijne, 1998) in humans and other forms of life, playing an important role in processes as diverse as ion translocation, electron transfer, and transduction of extracellular signals. One of the most important classes of transmembrane (TM) proteins is the G-protein-coupled receptor (GPCR) superfamily which, upon activation by extracellular signals, initiates an intracellular chemical signal cascade to transduce, propagate, and amplify these signals. GPCRs are involved in cell communication processes and in mediating such senses as vision, smell, taste, and pain. The extracellular signals inciting this transduction are usually chemical, but for the opsin family, it is visible light (electromagnetic radiation). Malfunctions in GPCRs play a role in such diseases as ulcers, allergies, migraine, anxiety, psychosis, nocturnal heartburn, hypertension, asthma, prostatic hypertrophy, congestive heart failure, Parkinson's, schizophrenia, and glaucoma (Wilson and Bergsma, 2000). Indeed, although they comprise ∼3–4% (Schöneberg et al., 2002) of the human genome, the GPCR superfamily represents one of the most important families of drug targets.

Within a class of GPCRs (for example, adrenergic receptors) there are often several subtypes (for example, nine for adrenergic receptors) all responding to the same endogenous ligand (epinephrine and norepinephrine for adrenergic receptors), but having very different functions in various cells. In addition, many different types of GPCRs are similar enough that they are affected by the antagonists or agonists for other types (e.g., among adrenergic, dopamine, serotonin, and histamine receptors), leading often to undesirable side effects. This makes it difficult to develop drugs to a particular subtype without side effects resulting from cross-reactivity to other subtypes. To design such subtype-specific drugs it is essential to use structure-based methods, but this has not been possible because there is no atomic-level structure available for any human GPCR. Consequently design of subtype-specific drugs for GPCR targets is a very tedious empirical process, often leading to drugs with undesirable side effects. The difficulty in obtaining three-dimensional structures for GPCRs is obtaining high-quality crystals of these membrane-bound proteins sufficient to obtain high-resolution x-ray diffraction data, and the difficulty of using NMR to determine structure on such membrane-bound systems. Hence we conclude that to aid the structure-based drug design for GPCR targets, it is essential to develop theoretical methods adequate to predict the three-dimensional structures of GPCRs from first principles. For globular proteins there have been significant advances in predicting the three-dimensional structures by using sequence homologies to families of known structures (Marti-Renom et al., 2000); however, this is not practical for GPCRs, inasmuch as a high-resolution crystal structure is available for only one GPCR, bovine rhodopsin—which has low homology (<35%) to most GPCRs of pharmacological interest.

Consequently we have been developing the MembStruk method for ab initio or first principles prediction of three-dimensional structure for GPCRs from primary sequence without using homology. MembStruk is based on the organizing principle provided by knowing that a GPCR has a single chain with seven helical TM domains threading through the membrane—which we find provides sufficient structural information (when combined with atomistic simulations such as molecular dynamics and Monte Carlo) for us to deduce three-dimensional structures for GPCRs that are adequate for prediction of the binding site and relative binding energy of agonists and antagonists. We have been applying MembStruk to several GPCRs, where the validation has been based on the comparison of the predicted binding site to experimental binding and mutation data. In this article we describe the details of the MembStruk method and validate the accuracy of the predictions by comparing with the only high-resolution crystal structure available for a GPCR, bovine rhodopsin.

Because the function of a GPCR is to signal to the interior of the cell in the presence of a particular ligand bound to the extracellular surface, it is most relevant to determine the three-dimensional structure for the conformation of the protein involved in activating G-protein. It is widely thought that there are two distinct conformations of GPCRs: one active and one inactive, in equilibrium, even in the absence of ligands (Melia et al., 1997; Strange 1998; Schöneberg et al., 2002). This equilibrium is shifted when a ligand binds to the GPCR. Thus it would be valuable to know four structures of the protein—the apo-protein in both the active and inactive forms and the ligand-bound form in both the active and inactive forms—so that one could study the process of GPCR activation. Even for bovine rhodopsin, there is crystal structure data for only one of these four (the ligand-bound inactive form). We postulate in this article a model of activation involving the second extracellular (EC-II) loop and TM3 in which the structure is assumed 1), to be in the active form when the EC-II loop is open and 2), to be in the inactive form when the EC-II loop is closed.

It is the closed conformation that is observed in the rhodopsin crystal structure (Palczewski et al., 2000; Okada, et al., 2001). In this article we report the MembStruk-predicted structures for all four structures, although comparison can be made directly to experiment only for the closed-loop-with-ligand case.

Except for bovine rhodopsin the only experimental validation for the accuracy of predicted GPCR structures must rest on predicting the binding sites and energies for various ligands and how they are modified by various mutations. To make such predictions from first principles, we developed the HierDock method, which we validate here by predicting the binding site of retinal in bovine rhodopsin both for the experimental three-dimensional structure and for the predicted structures (open and closed loop).

The first report on MembStruk and HierDock (Floriano et al., 2000; Vaidehi et al., 2002) focused on olfactory receptors, where ligand-binding data was available for 24 simple organic molecules to 14 different olfactory receptors (Malnic et al., 1999). More recently these methods have been applied to predict the structures and functions for GPCRs of such diverse subfamilies as β1- and β2-adrenergic receptor, dopamine D2 receptor, endothelial differentiation gene 6, and sweet gustatory and olfactory receptors (Vaidehi et al., 2002 ; Freddolino et al., 2004; Kalani et al., 2004; Floriano et al., 2004a). The HierDock technique has also been validated for globular proteins where the crystal structures are available (Wang et al., 2002; Datta et al., 2002, 2003; Kekenes-Huskey et al., 2003; Floriano et al., 2004b). We find that the predicted structures of the adrenergic and dopamine receptors lead to binding sites for the endogenous ligands in excellent agreement with the plentiful mutation and binding experiments. Similarly, the predicted binding sites and affinities for endothelial differentiation gene 6, the mouse I7 and rat I7 olfactory receptors, and the human sweet receptor are consistent with the available experimental binding data.

However, a quantitative assessment of the accuracy of these structure and function prediction methods can be made only for bovine rhodopsin, for which there is a high-resolution experimental crystal structure available with ligand attached to the protein. Thus this article provides a detailed study of rhodopsin to validate the various steps involved in our procedures for prediction of the three-dimensional structures of GPCRs (MembStruk) and for the prediction of the binding site and the binding energy of the retinal ligand to bovine rhodopsin (HierDock).

Computational Methods gives the details of the MembStruk and HierDock protocols, followed by Results and Discussion, which describes the results of structure and function prediction for bovine rhodopsin. These results are also discussed in the Summary and in the Conclusions section.

COMPUTATIONAL METHODS

Force fields (FF)

All calculations for the protein used the DREIDING force field (FF) (Mayo et al., 1990) with charges from CHARMM22 (MacKerell et al., 1998) unless specified otherwise. The nonbond interactions were calculated using the cell multipole method (Ding et al., 1992) in MPSim (Lim et al., 1997).

The ligands were described with the DREIDING FF (Mayo et al., 1990) using charges from quantum mechanics calculations on the isolated ligand; electrostatic potential charges calculated using Jaguar, Ver. 4.0 (Schrodinger, Portland, Oregon). For the lipids we used the DREIDING FF with QEq charges (Rappé and Goddard, 1991). Some calculations were done in the vacuum (e.g., final optimization of receptor structure to approximate the low dielectric membrane environment). For structural optimization in the solvent (water) we used the analytical volume Generalized-Born (Zamanakos, 2002) approximation to Poisson-Boltzmann continuum solvation.

We use the DREIDING FF due to its generic applicability to all molecules constructed from main group elements (particularly all organics), inasmuch as we will use our methods to predict the binding site and energy for a diverse set of ligands of interest to pharmacology. Indeed, we find below that the minimized structure for bovine rhodopsin deviates from the crystal structure by only 0.29 Å coordinate root mean-square error. The DREIDING FF with CHARMM22 charges has been validated for molecular dynamics simulations and binding energy calculations for many proteins (Brameld and Goddard, 1999; Datta et al., 2003, 2002; Wang et al., 2002; Kekenes-Huskey et al., 2003; Floriano et al., 2004b) with similar accuracy.

Validation of the force fields

The crystal structure of bovine rhodopsin (resolution, 2.80 Å) was downloaded from the protein structure database (PDB entry 1F88). The Hg ions, sugars, and waters were deleted from this structure. This crystal structure is missing 10 complete residues in loop regions and the side-chain atoms for 15 additional residues. We added the missing residues and side chains using WHATIF (Vriend, 1990). Then we added hydrogens to all the residues using the PolyGraf software. We then fixed the TM helices and minimized (using conjugate gradients) the structure of the loop region to a root mean-square force of 0.1 kcal/mol per Å. The potential energy of the entire structure of rhodopsin was then minimized (using conjugate gradients) to a root mean-square force of 0.1 kcal/mol per Å . This minimized structure deviates from the x-ray crystal structure by 0.29 Å coordinate root mean-square (CRMS) error over all atoms in the crystal structure. This is within the resolution of the crystal structure, validating the accuracy of the FF and the charges. This FF-minimized crystal structure is denoted as Ret(x)/closed(xray).

The MembStruk protocol for predicting structure of GPCRs

MembStruk uses the hydrophobic profile of multisequence alignment of GPCRs to assign the helical TM regions. This is combined with a series of steps of a Monte Carlo-like systematic search algorithm to optimize the rotation and translational orientation of the TM helices. This search algorithm allows the structure to get over barriers and make the conformational search more comprehensive. This is followed by molecular dynamics (MD) calculations at a variety of coarse-grain to fine-grain levels in explicit lipid bilayer.

MembStruk was first described in Floriano et al. (2000). This method (now labeled as MembStruk1.0), was improved to include energy optimization to determine the rotation of helices in the seven-helical TM bundle in Vaidehi et al. (2002) (now referred to as MembStruk2.0). In this article we have modified MembStruk (now denoted as MembStruk3.5) to also include optimization of the helix translations along their axes and rotational optimization using hydrophobic moment of the helices. The MembStruk3.5 procedure for predicting structures of GPCRs consists of the following steps:

1. Prediction of TM regions from analysis of the primary sequence.

2. Assembly and coarse-grain optimization of the seven-helix TM bundle.

3. Optimization of individual helices.

4. Rigid-body dynamics of the helical bundle in a lipid bilayer.

5. Addition of interhelical loops and optimization of the full structure.

Henceforth in this article any reference to MembStruk always indicates MembStruk3.5 unless specifically referenced otherwise. We will next discuss some of the details of these steps in MembStruk. We should emphasize here that these steps are all automated into a single MembStruk procedure. Thus the sequence is fed to MembStruk and the result at the end is a final three-dimensional structure for the protein in the lipid bilayer. Of course we also examine the various intermediate results generated in this procedure to allow us to detect problems, to gain insight into the validity of the various criteria, and to provide hints on improvements to make in the methods.

Step 1: Prediction of TM regions (TM2ndS)

Prediction of the TM helical regions for GPCRs from the sequence rests on the assumption that the outer regions of the TM helices (in contact with the hydrophobic tails of the lipids) should be hydrophobic, and that this character should be largest near the center of the membrane (Donnelly, 1993; Eisenberg et al., 1984). The TM2ndS method uses this concept to generate a hydrophobic profile.

Step 1a: Sequence alignment

The first part of Step 1 for TM2ndS uses the SeqHyd hydrophobic profile algorithm, which is based on peak signal analysis of the hydrophobic profile. We first tested the use of the Prift hydrophobicity scale (Cornette et al., 1987), but we found that the hydrophobicity index value for Arg was opposite that expected for a charged residue, leading to obviously incorrect assignments. We then switched to the use of the Eisenberg hydrophobicity scale (Eisenberg et al., 1982), which is based on sound thermodynamic arguments. This scale has a range from −1.76 to 0.73 and works well for Arg and other residues to give consistent TM predictions for the many systems we have investigated. The Eisenberg scale has been used in all published MembStruk results (1.0 onward). SeqHyd requires a multiple sequence alignment using sequences related to bovine rhodopsin. This is constructed by using an NCBI Blast search (Altschul et al., 1990, 1997) on bovine rhodopsin (primary accession number P02699) to obtain protein sequences with bit scores >200 but not identical (to avoid numerical bias in later calculations) to bovine rhodopsin (E-value < e⁻¹⁰⁰). We prefer an ensemble of sequences providing a uniform distribution of sequence identities from 35 to <100%. For bovine rhodopsin, this leads to the 43 sequences in Table S1 of the Supplemental Material. These 43 sequences plus bovine rhodopsin were used in ClustalW (Thompson et al., 1994) to generate a pairwise multiple sequence alignment. This sequence alignment included sequences with identities to the bovine rhodopsin sequence as low as 40%. In general we might include sequences with higher nonzero E-values, but including too low a homology might lead to additional alignment problems.

Step 1b: Average consensus hydrophobicity and initial TM assignment

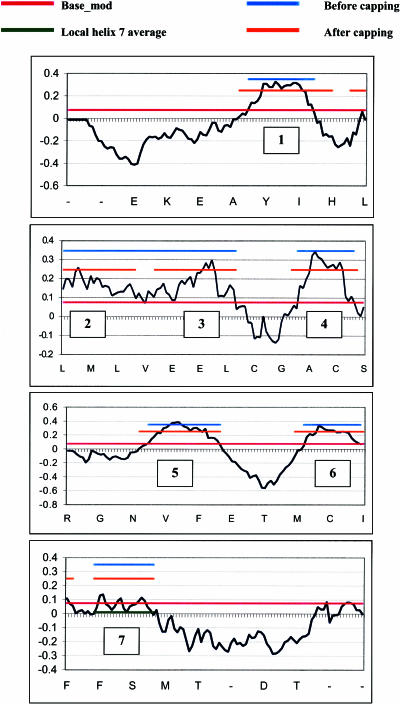
The second part of Step 1 of TM2ndS is to calculate the consensus hydrophobicity for every residue position in the alignment. This consensus hydrophobicity is the average hydrophobicity (using the Eisenberg hydrophobicity scale) of all the amino acids in that position over all the sequences in the multiple sequence alignment. Then, we calculate the average hydrophobicity over a window size (WS) of residues around every residue position, using WS ranging from 12 to 20. This average value of hydrophobicity at each sequence position is plotted to yield the hydrophobic profile, as shown in Fig. 1 for WS = 14. The baseline for this profile serves as the threshold value for determining the TM regions and is calculated as follows.

FIGURE 1.

Hydrophobicity profile from TM2ndS for bovine rhodopsin at window size of WS = 14. The pink line (at 0.07) is the base_mod (described in Step 1, average consensus hydrophobicity and initial TM assignment) used as the baseline in identifying hydrophobic regions. The predicted TM domains are indicated by the orange lines (after capping). The blue lines show the predictions before helix capping. Each tick mark indicates the sequence number for the alignment based on bovine rhodopsin (100 residues per panel). The residues at every fifth position are indicated below each panel. The partition of helix 7 into two parts results from the hydrophilic residues near its center.

First, we obtain the global average hydrophobicity value over all residues in the protein but excluding the amino terminus region (34 residues) and the carboxyl terminus region (42 residues). This global average is 0.041 for bovine rhodopsin. If the baseline thus obtained does not resolve the expected seven peaks, then TM2ndS automatically changes the baselines over a range of 0.05 from the global average (thus −0.009 to 0.091 for bovine rhodopsin). The baseline closest to the average that yields the seven peaks is used for TM region prediction. This modified baseline (base_mod) is shown as the pink line in Fig. 1. It provides the basis for the accurate determination of the TM regions in the sequence. This final baseline may be interpreted physically as a ΔG = 0 value above which residues are thermodynamically stable in the transmembrane and below which they are not. This baseline is unique to the particular protein to which it is being applied, with its individual environmental factors (water clusters, ions, hydrophobic or hydrophilic ligand or interhelical interactions, membrane composition) that may change the relative stability of any particular residue.

Below WS = 12 the fluctuations in hydrophobicity (noise) are too large to be useful. The lowest WS that yields seven peaks (with peak length >10 and <50, and peak area >0.8) is denoted as WS_min. The peaks ranges for WS_min are used as input for the helix-capping module discussed in the next section.

Fig. 1 shows that assigning the TM region to helix 7 is a problem because it has a shorter length and a lower intensity peak hydrophobicity compared with all the other helices. This has been observed for other GPCRs (Vaidehi et al., 2002). The low intensity of helix 7 arises because it has fewer highly hydrophobic residues (Ile, Phe, Val, and Leu) and because it has a consecutive stretch of hydrophilic residues (e.g., KTSAVYN). These short stretches of hydrophilic residues (including Lys-296) are involved in the recognition of the aldehyde group of 11-cis-retinal in rhodopsin. For such cases, we use the local average of the hydrophobicity (from minimum to minimum around this peak) as the baseline for assigning the TM predictions. TM2ndS automatically applies this additional criteria when the peak length is <23, the peak area is <0.8, and the local average >0.5 less than the base_mod. For bovine rhodopsin only TM7 satisfies this criterion and the local average (0.011) is shown by the red line in Fig. 1. Thus, this local average is automatically applied for proteins where the residues are relatively hydrophilic but in which the helix might still be stable because of local environmental factors (mentioned above) that stabilize these residues.

Step 1c: Helix capping in TM2ndS

It is possible that the actual length of the helix would extend past the membrane surface. Thus, we carry out a step aimed at capping each helix at the top and bottom of the TM domain. This capping step is based on properties of known helix breaker residues, but we restrict the procedure so as not to extend the predicted TM helical region more than six residues. We consider the potential helix breakers (Donnelly et al., 1994) as P and G; positively charged residues as R, H, and K; and negatively charged residues as E and D.

TM2ndS first searches up to four residues from the edge going inwards from the initial TM prediction obtained from the previous section for a helix breaker. If it finds one, then the TM helix edges are kept at the initial values. However, if no helix breaker is found, then the TM helical region is extended until a breaker is found, but with the restriction that the helix not be extended more than six residues on either side. The shortest helical assignment allowed is 21, corresponding to the shortest known helical TM region. This lower size limit prevents incorporation of narrow noise peaks into TM helical predictions.

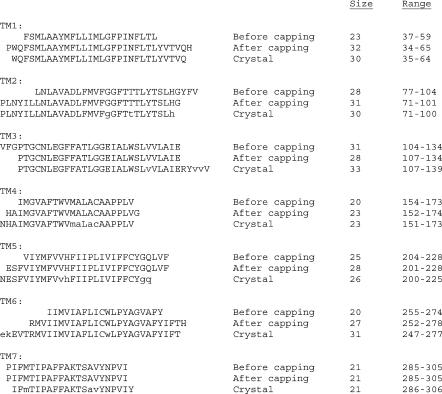
We have used this TM2ndS algorithm for predicting the structure for ∼10 very different GPCR classes (Vaidehi et al., 2002). In each case the predicted binding site and binding energy agrees well with available experimental data, providing some validation of the TM helical region prediction. However, only for bovine rhodopsin can we make precise comparisons to an experimental structure. Fig. 2 compares the predictions of TM helical regions for bovine rhodopsin to the TM helical regions as assigned in the crystal structure (Palczewski et al., 2000). To determine which residues have an α-helical conformation, we analyzed the φ−ψ angles using PROCHECK (Laskowski et al., 1993) and considered the experimental structure to be in an α-helix if −37 < φ < −77 and −27 < ψ < −67. This led to slightly shorter helices than quoted in the crystal structure article. Thus the lowercase letters in Fig. 2 indicate residues which are outside the above range but quoted as helices in the experimental article. The results are as follows.

FIGURE 2.

The transmembrane helical predictions (labeled as after capping) from TM2ndS compared with helix ranges from the bovine rhodopsin x-ray crystal structure. The predictions before TM2ndS capping are also shown. Those residues in the crystal structure that fall outside the range of α-helicity (using analysis described in Step 1c, Helix Capping in TM2ndS) are indicated in lowercase letters.

For TM1 our prediction adds P at the start and H at the end. In our final structure the (ϕ, ψ) for this P is (not-applicable [N-terminus], −43.6) and for this H is (−54.3, −32.4), whereas the values obtained in the crystal structure are (−44.3, −24.9) and (−72.5, 69.5), respectively. Since P and possibly H might be expected to break the helix, we are considering modifying our procedure to exclude such terminal P or H in the helix.

For TM2 our prediction adds HG at the end. In our final structure the (ϕ, ψ) for this H and G are (−73.6, −80.9) and (−55.0, 148.8), whereas the values obtained in the crystal structure are (−74.2, 0.5) and (66.1, 9.0), respectively. The crystal structure article considered the H as part of the helix. Since HG could be expected to break the helix, we are considering modifying our procedure to exclude the terminal HG in the helix. In fact, the HG angles in our final structure fall outside our criteria for α-helicity as a result of the MembStruk optimization of the structure.

For TM3 our predictions miss the RYVVV assigned in the crystal structure to the helix. Since the first and second V do not have (ϕ, ψ) in the usual range for α-helices, we consider that the VVV should be excluded. However, the polar character of RY leads TM2ndS to miss assigning them as part of the helix. The crystallographic (ϕ, ψ) values for R and Y residues are (−55.5, −63.8) and (−44.6, −56.3), whereas the values obtained in our final structure are (76.7, −51.4) and (−62.9, 119.2). It should be pointed out that the B-factors on the cytoplasmic end of the rhodopsin crystal structure are high in this region of the helix (PDB entry 1F88). This indicates that the helix is probably fluxional even when the receptor is not activated. Consequently caution should be used when comparing our predictions with the crystal structure at this end. Also, because the helices are translated to align hydrophobic centers in a later step of the procedure, this uncertainty in TM helical prediction may only lead to local errors in atomic structure.

For TM4 our prediction adds G at the end and misses N at the start. The crystallographic (ϕ, ψ) for these N and G residues are (−43.5, −59.6) and (169.8, 5.4), whereas the values obtained in our final structure are (−93.9, 119.6) and (112.5, −118.4). Thus the predictions are fine even though the G and N were misassigned. We are considering modifying our procedure to exclude a terminal G.

Compared to the crystal structure assignment, our prediction for TM5 adds LVF at the end and misses N at the start. In addition the GQ at the end terminus in the crystal structure assignment have (ϕ, ψ) outside the range for α-helices. Thus we consider that the terminal GQLVF in the TM2ndS predictions are in error, the largest error of any of the predictions. The crystallographic (ϕ, ψ) for these N and LVF residues are (−69.3, −51.1), (−48.2, −36.7), (−39.6, −27.1), and (−58.0, −26.5), whereas the values obtained in our final structure are (−109.9, −162.4), (−55.1, −47.8), (−63.4, −59.0), and (−81.5, 59.3). The rhodopsin crystal structure has high B-factors for the intracellular end of TM5 (just as for helix 3), suggesting caution in making comparisons.

For TM6 our prediction adds H at the end and misses EVT at the start. The crystallographic (ϕ, ψ) values for these EVT and H residues are (−57.6, −53.0), (−54.1, −55.7), (−56.3, −52.3), and (−81.3, 48.8), whereas the values obtained in our final structure are (−74.4, 72.3), (−73.1, 130.8), (−16.9, −53.0), and (7.1, 87.7). Thus the predictions are fine despite the misassignments. We are considering modifying our procedure to exclude a terminal H. In fact, the H angles in our final structure fall outside our criteria for α-helicity as a result of the MembStruk optimization of the structure.

For TM7 our prediction adds P at the start and misses Y at the end. The crystallographic (ϕ, ψ) for the P and Y residues are (−30.2, −48.1) and (−46.0, −55.0), whereas the value for P obtained in our final structure is (−43.6, −23.2). Since the current MembStruk protocol does not model the structures of the C- and N-termini, we did include the Y in our structure. Thus the predictions are fine despite the misassignments. We are considering modifying our procedure to exclude a terminal P, but it is not obvious that a modified method would automatically include the Y. In fact, the P angles in our final structure fall outside our criteria for α-helicity as a result of the MembStruk optimization of the structure.

Overall, we consider that the predictions agree sufficiently well with the crystal structure to be useful in building them into the assembly. In addition, we can see several improvements in the capping procedure of TM2ndS that could have decreased the errors in predicting which residues near the ends are considered to be helix breakers for capping the TM helices. However, this article is meant to validate the procedure we have been applying to many systems and we did not want to change the procedure on the basis of our only independent validation.

Step 2: Assembly and optimization of the seven-helical TM bundle

Having predicted the seven TM helix domains using TM2ndS, we next build them into the seven-helical TM bundle. This involves two steps: 1), assembly and optimization of the relative translation and 2), rotation of the helices.

Step 2a: Assembly of the seven TM helices into a bundle

Canonical right-handed α-helices are built for each helix using extended side-chain conformations. Then the helical axes are oriented in space according to the 7.5 Å electron density map of frog rhodopsin (Schertler, 1998). This 7.5 Å electron density map gives only the rough relative orientations of the helical axes, with no data on atomic positions. This serves as the starting point for optimization of the helices in the helical bundle. It should be emphasized here that no information as to helical translations or rotations was used. Since this electron density map showed no retinal present, it is not clear whether this form of rhodopsin is active or inactive. This same information has been used to build structures of ∼10 other GPCR classes (Vaidehi et al., 2002). In each case the predictions of binding site and binding energy agrees well with available experimental data, providing some validation for this general approach of constructing the TM bundle of GPCRs. However, for bovine rhodopsin we can make much more precise comparisons to the experimental structures, as reported below.

Step 2b: Optimization of the relative translation of the helices in the bundle

The translational and rotational orientation of each helix in the TM bundle is critical to the nature and conformation of the binding site in the GPCR. We do not use homology methods to predict these quantities because many GPCRs have very remote sequence homology to rhodopsin (ranging down to 10%) making it quite risky to base a three-dimensional structure on homology modeling using the rhodopsin crystal structure as template. Also we do not use atomistic molecular dynamics and molecular mechanics methods to optimize the structure, because the large barriers between various favorable positions can trap the conformation in local minima making such approaches ineffective in repositioning the helices. Instead, we developed methods to optimize the initial packing by translating and rotating the helices over a grid of positions and by using various properties of the amino acids in the sequence to suggest initial starting points. This Monte Carlo-like systematic conformational search algorithm for rotational and translational orientation of the helices allows the system to surmount barriers in the conformational space.

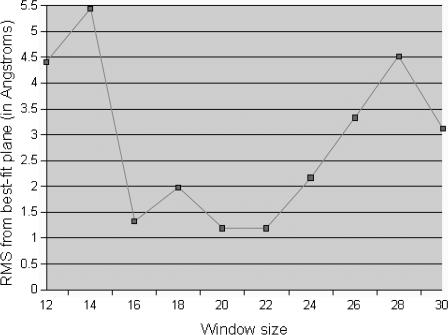
Our general principle in repositioning the helices is that the outer surface of the TM bundle (at least the middle regions) should be hydrophobic to have stabilizing interactions with the hydrophobic chains of the lipid. We imagine a midpoint plane through the lipid bilayer corresponding to the contact of the hydrophobic chains, which we denote as the lipid midpoint plane (LMP). We then assume that the hydrophobic regions of the TM bundle will position themselves such that the middle of their maximum hydrophobicity lies in this plane. We tested this concept for the crystal structure of bovine rhodopsin as follows. We determined the hydrophobic center (HC) for each helix as the maximum of the peak of hydrophobicity from the profiles generated with various window sizes (since we go an integer number of residues in each direction, window size is always even). Our criterion for the best-fit to experiment is that these seven positions when applied to the crystal structure would all lie in a single plane that could be taken as the LMP.

As shown in Fig. 3, the deviation of the calculated hydrophobic centers from lying in a single plane in the rhodopsin crystal structure is a minimum for WS 20 and 22. Thus Get_Centers calculates the overall hydrophobic center of each TM helix based on the average of centers obtained for a range of window sizes near 20. Get_Centers determines this range of window sizes as follows. First, each hydrophobic center (HC) is calculated for WS = 20. Then, the HCs are calculated for WS 12–30 (excluding WS = 20). For each helix Get_Centers determines the window sizes that yield HC less than five residues from the HC calculated at WS = 20. For example, consider helix 1 in Table 1. Here HC = 18 for WS = 20. For windows sizes 12, 14, 16, 18, 22, 24, 26, 28, and 30 we find HC = 15, 13, 20, 18, 17, 18, 15, 16, and 13. For WS 16, 18, 22, and 24 the HC are less than five from the value at WS = 20. Thus we consider that the hydrophobic center calculation is stable within this regime of window sizes. The HC calculated for WS 16, 18, 22, and 24 for the helices 2–7 are also less than five residues from the centers at WS = 20. Thus, Get_Centers averages the HC for window sizes 16, 18, 22, and 24 and then it averages these values with the HC at WS = 20 for each TM helix. Get_Centers takes these values (last column of Table 1) as the final TM helix centers. We find that for bovine rhodopsin, these seven HCs deviate by a root mean-square of 1.04 Å from a common plane.

FIGURE 3.

The RMS deviation for various window sizes (WS) of the central residues predicted from TM2ndS for bovine rhodopsin compared to the best-fit plane to the crystal structure minimized without ligand, Apo/closed(xtal). This suggests that the best WS is 16–22.

TABLE 1.

Window size
Helix number	12	14	16	18	20	22	24	26	28	30	HC
1	15	13	20	18	18	17	18	15	16	13	18.2
2	20	12	12	14	15	15	14	22	19	20	14.0
3	19	20	17	18	15	16	15	12	11	12	16.2
4	9	9	10	15	12	13	13	12	11	17	12.6
5	15	19	13	12	14	16	16	17	16	15	14.2
6	8	9	11	11	13	14	14	15	16	17	12.6
7	19	4	17	15	14	14	13	12	11	10	14.6

The last column shows the positions of the hydrophobic center (HC) predicted for each TM by TM2ndS for various window sizes. The first row (in boldface) has the window sizes chosen to calculate this hydrophobic center (underlined). Here position 1 corresponds to the first residue in the capped sequence in Fig. 2.

Step 2c: Optimization of the rotational orientation

Once the helices are aligned along their helical axes according to the calculated hydrophobic centers, the rotational orientation of the helices is optimized using either or both of the following steps.

• Orienting the net hydrophobic moment of each helix to point toward the membrane (phobic orientation): In this procedure (denoted as CoarseRot-H), the helical face with the maximum hydrophobic moment is calculated for the middle section of each helix, denoted as the hydrophobic midregion (HMR). The face is the sector angle obtained as follows. 1), The central point of the sector angle is the intersection point of the helical axis (the active helix that is being rotated) with the common helical plane (LMP) and 2), the other two points forming the arc, are the nearest projections (on the LMP) of the C_α vectors of the two adjacent helices. The calculation of the hydrophobic moment vector is restricted to this face angle. This allows the predicted hydrophobic moment to be insensitive to cases in which the interior of the helix is uncharacteristically hydrophilic (because of ligand or water interactions within the bundle). Currently we choose HMR to be the middle 15 residues of each helix straddling the predicted hydrophobic center and exhibiting large hydrophobicity. This hydrophobic moment is projected onto the common helical plane (LMP) and oriented exactly opposite to the direction toward the geometric center of the TM barrel (GCB). This criterion is most appropriate for the six helices (excluding TM3) having significant contacts with the lipid membrane. The LMP is the plane that most closely intersects the hydrophobic centers as described in Step 2b. The GCB is calculated as the center of mass of the positions of the α-carbons for each residue in the HMR for each helix summed over all seven. This procedure is called phobic orientation.

• Optimization of the rotational orientation using energy minimization techniques (RotMin): In this procedure, each of the seven TMs is optimized through a range of rotations and translations one at a time (the active TM) while the other six helices are reoptimized in response. After each rotation of the main chain (kept rigid) of each helix, the side-chain positions of all residues for all seven helices in the TMR are optimized (currently using SCWRL; Bower et al., 1997). The potential energy of the active helix is then minimized (for up to 80 steps of conjugate gradients minimization until an RMS force of 0.5 kcal/mol per Å is achieved) in the field of all other helices (whose atoms are kept fixed). This procedure is carried out for a grid of rotation angles (typically every 5° for a range of ±50°) for the active helix to determine the optimum rotation for the active helix. Then we keep the active helix fixed in its optimum rotated conformation and allow each of the other six helices to be rotated and optimized. Here the procedure for each of the six helices one by one is 1), rotate the main chain; 2), SCWRL the side chains; and 3), minimize the potential energy of all atoms in the helix. The optimization of these six helices is done iteratively until the entire grid of rotation angles is searched. This method is most important for TM3, which is near the center of the GPCR TM barrel and not particularly amphipathic (it has several charged residues leading to a small hydrophobic moment). This procedure is called RotMin.

For bovine rhodopsin, we used phobic orientation for placing the hydrophobic moments away from the GCB for all seven helices. Subsequently rotations were optimized using RotMin for helices 3 and 5 using small rotation angles of ±2.5°, ±5.0°, and ±8.0°. This optimizes the only salt bridge in the TM region (between residues His-211 and Glu-122). Coarse-grain rotation optimization combining both the energy optimization and hydrophobic moments is expected to provide better optimized TM helices than either one alone.

Step 3: Optimizing the individual helices

The optimization of the rotational and translational orientation of the helices described in the above steps is performed initially on canonical helices (we also apply them again to the helices after their optimizations described in Step 3). To obtain a valid description of the backbone conformation for each residue in the helix, including the opportunity of G, P, and charged residues to cause a break in a helix, the helices built from the Step 2 were optimized separately. In this procedure, we first use SCWRL for side-chain placement, then carry out molecular dynamics (MD) (either Cartesian or torsional MD called NEIMO; Jain et al., 1993; Mathiowetz et al., 1994; Vaidehi et al., 1996) simulations at 300 K for 500 ps, then choose the structure with the lowest total potential energy in the last 250 ps and minimize it using conjugate gradients.

This optimization step is important to correctly predict the bends and distortions that occur in the helix due to helix breakers such as proline and the two glycines. The MD also carries out an initial optimization of the side-chain conformations, which is later further optimized within the bundle using Monte Carlo side-chain replacement methods. This procedure allows each helix to optimize in the field due to the other helices in the optimized TM bundle from Step 2.

Step 4: Addition of lipid bilayer and fine-grain reoptimization of the TM bundle

To the final structure from Step 3 MembStruk adds two layers of explicit lipid bilayers. This consists of 52 molecules of dilauroylphosphatidylcholine lipid around the TM bundle of seven helices. This was done by inserting the TM bundle into a layer of optimized bilayer molecules in which a hole was built for the helix assembly and eliminating lipids with bad contacts (atoms closer than 10 Å). Then we used the quaternion-based rigid-body molecular dynamics (RB-MD) in MPSim (Lim et al., 1997) to carry out RB-MD for 50 ps (or until the potential and kinetic energies of the system stabilized). In this RB-MD step the helices and the lipid bilayer molecules were treated as rigid bodies and we used 1-fs time steps at 300 K. This RB-MD step is important to optimize the positions of the lipid molecules with respect to the TM bundle and to optimize the vertical helical translations, relative helical angles, and rotations of the individual helices in explicit lipid bilayers.

Step 5: loop building

Following the RB-MD, we added loops to the helices using the WHATIF software (Vriend, 1990). After the addition of loops, we used SCWRL (Bower et al., 1997) to add the side chains for all the residues. The loop conformations were optimized by conjugate gradient minimization of the loop conformations while keeping the TM helices fixed. This step also allows the general option of forming selected disulfide linkages (e.g., between the cysteines in the EC-II loop, which are conserved across many GPCRs, and the N-terminal edge of TM3 or EC3). In the case of bovine rhodopsin, the alignment of the 44 sequences from Step 1, Sequence Alignment, indicates only one pair of fully conserved cysteines on the same side of the membrane (extracellular side). The disulfide bond was formed and optimized with equilibrium distances lowered in decrements of 2 Å until the bond distance was itself 2 Å. Then the loop was optimized with the default equilibrium disulfide bond distance of 2.07 Å. Annealing MD was then used to optimize the EC-II loop at this stage. This involved 71 cycles, in each of which the loop atoms were heated from 50 K to 600 K and back to 50 K over a period of 4.6 ps. During this process the rest of the atoms were kept fixed for the first 330 ps and then the side chains within the cavity of the protein in the vicinity of the EC-II loop were allowed to move for 100 ps to allow accommodation of the loop. Subsequently a full-atom conjugate gradient minimization of the protein was performed in vacuum using MPSim (Lim et al., 1997). This leads to the final MembStruk-predicted structure for bovine rhodopsin.

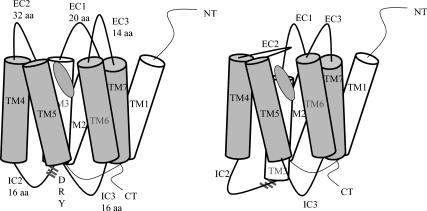
The crystal structure for the retinal/rhodopsin complex has a well-defined β-sheet structure for EC-II, which we speculate to be involved as a mobile gate for entry of 11-cis-retinal on the extracellular side of rhodopsin. Such a gating mechanism is illustrated in Fig. 4, in which the helix 3 coupled to this loop by a cysteine bond is the gatekeeper which responds to signaling structural substates of rhodopsin as follows:

• When rhodopsin binds 11-cis-retinal, the ground state conformation of the receptor is stabilized, thus shifting helix 3 toward the intracellular side (forming the D(E)RY-associated salt bridges at that end) and closing the EC-II loop. In fact, 11-cis-retinal has been shown to be an inverse agonist for G-protein signaling (Okada et al., 2001).

• In response to absorption of a photon, the 11-cis-retinal isomerizes to the all-trans conformation, inducing helix 3 to shift toward the extracellular side. This induction of helix 3 movement may be direct or indirect. It may be due to a direct clash of helix 3 with all-trans-retinal. This is consistent with the result of a cross-linking experiment in which the ionone ring of retinal interacts with Ala-269 when the receptor is activated (Borhan et al., 2000). This may occur because the trans-retinal clashes with helix 3 of the ground state rhodopsin crystal structure (Bourne and Meng, 2000). The induction of helix 3 movement may also occur indirectly in the following way: 11-cis-retinal as observed in the crystal structure interacts with aromatic side chains Trp-265 and Tyr-268 on helix 6. But all-trans-retinal does not have this stabilizing interaction with helix 6, which should decrease the energy barrier for helix 6 rotation (this has been observed in preliminary MD calculation we carried out, and in reports in the literature; Saam et al., 2002).

• This motion (of helix 3 or helix 6) breaks the DRY-associated salt bridges (Greasley et al., 2002) at the intracellular side. Helix 3 may have fewer constraints to movement, but since it is coupled by a disulfide linkage to the EC-II loop, movement on helix 3 would likely cause an opening of the EC-II loop to allow Schiff base reversion and exit of the free all-trans-retinal ligand. The breaking of this DRY salt bridge would also allow hinge motion (Altenbach et al., 2001a,b) of helix 6 to expand the molecular surface at the cytoplasmic end for G-protein binding. This model is consistent with the experimental mutations studies in which the disulfide has been shown to be important for ligand binding and receptor activation (Schöneberg et al., 2002).

FIGURE 4.

Schematic for a possible signaling mechanism in rhodopsin. Note that the movement of helix 3 (caused by interaction with the trans-isomer of retinal) exposes the DRY sequence to G-protein activation and as a result closes the EC-II loop to maintain the ligand inside the bundle sequence.

Building the loops without the constraint of coupling these cysteines leads to an open EC-II loop very different from the crystal structure of bovine rhodopsin. It is likely that both the open loop and closed loop structures play an important role in GPCRs, and indeed general observations of GPCRs suggests two distinct forms, one of which leads to activation of G-protein and one of which does not. We consider that one of these is likely the closed form and the other the open form. It seems likely that the ligand might not be able to diffuse into the active site when the loop is closed, and hence for most GPCRs (other than bovine rhodopsin) we visualize the process of activation as 1), the GPCR with the open form of EC-II loop can bind selectively to the appropriate ligand; 2), binding of the ligand favors closing of the EC-II loop; and 3), after closure of the loop, G-protein activation may begin.

Thus we have built two structures for bovine rhodopsin (here, MS denotes that the structure was predicted using MembStruk): Apo/closed(MS) has the cysteine coupling observed in the crystal and is the structure we compare to experiment after binding the retinal; and Apo/open(MS) is built without a constraint, forming what we believe would be the configuration which binds initially to the ligand.

Function prediction for GPCRs

Since there are no experimental structures available for any human GPCR, the only validation available for the accuracy of predicted structures for human GPCRs is to predict the ligand binding sites and the ligand binding energies. The accuracy in the predicted binding site can then be judged from site-directed mutagenesis experiments on the residues predicted to control selectivity. An even tougher test is to compare binding affinity of ligands to each other and to mutated proteins. For many GPCRs of pharmaceutical interest there is ample experimental data on ligand binding constants as well as agonist and antagonist inhibition constants for many GPCRs (for a compilation of this literature, see http://www.gpcr.org).

To carry out such function validations for the predicted structures, it is essential to have reliable and efficient procedures for predicting binding site and binding affinities. Since the ligand binding site is completely unknown for most GPCRs, we must scan the entire protein to identify likely binding sites and conformation of each ligand, and then we must reliably rank the relative binding energies of the various ligands in these sites. To do this we employ the HierDock procedure, which has been tested and validated for predicting ligand binding sites and ligand binding energies for many globular and membrane-bound proteins (Vaidehi et al., 2002; Kekenes-Huskey et al., 2003; Floriano et al., 2004b; Datta et al., 2003, 2002). These studies show that the multistep hierarchical procedure in HierDock ranging from coarse-grain docking to fine-grain MD optimization leads to efficient and accurate predictions for ligand binding in proteins.

The HierDock method was first described in Floriano et al. (2000), which we label as HierDock1.0. The method was improved in Vaidehi et al. (2002), which we label as HierDock2.0. In this article we present an improved version that we label as HierDock2.5. The various steps involved in this current procedure are as follows:

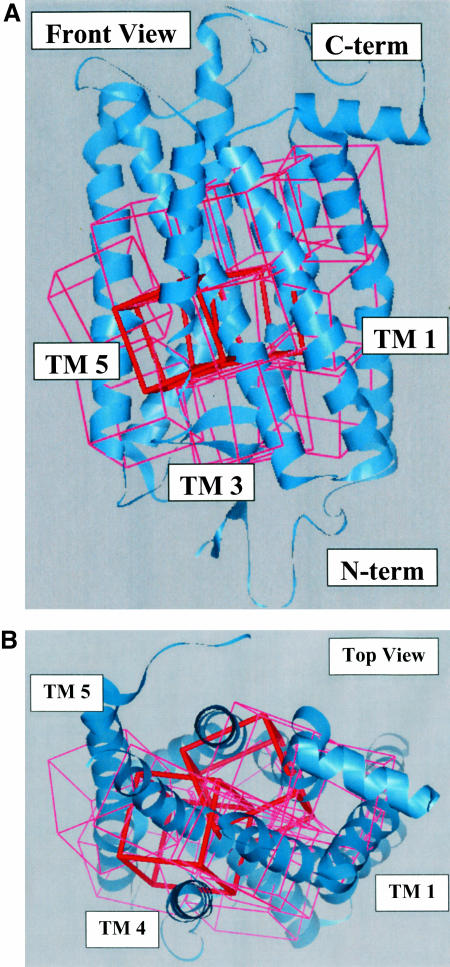
1. Sphere generation: We assume no knowledge of the ligand binding site in GPCRs and hence the entire molecular surface of the receptor is scanned to predict the energetically preferred ligand binding sites. The negative of the molecular surface of the protein was used to define potential binding regions within the receptor over which the various ligand conformations are to be sampled. The void regions are mapped with spheres generated over the whole receptor using the Sphgen program in DOCK 4.0. No assumptions were made on the nature or the location of the binding site in these receptors. For bovine rhodopsin this led to a total of 7474 spheres, which was partitioned into 13 overlapping docking regions each with a volume of 10 ų as shown in Fig. 5. We excluded from docking regions in contact with the membrane or near the intracellular region likely to be involved in binding to the G-protein. No assumptions were made on the nature or the location of the binding site in these regions.

2. Coarse-grain sampling: To locate the most favorable ligand binding site(s), we used DOCK 4.0 (Ewing and Kuntz, 1997) to generate a set of conformations for binding 11-cis-retinal (a ligand known to bind to bovine rhodopsin) to each of the 13 regions. For this docking step we used a bump filter of 10, a non-distance-dependent dielectric constant of 1.0, and a cutoff of 10 Å for energy evaluation. The ligands were docked as nonflexible molecules to generate and score 100 conformations of the ligand in each of the 13 regions. We then rejected any ligand conformation with <90% of the surface area buried into the protein and ranked the remainder by the ligand-protein interaction energy using DREIDING FF. The best binding energy conformation among the 13 regions was chosen as the putative binding region. Other conformations with binding energies within 100 kcal/mol of the best conformation were also chosen as possible binding regions.

3. Construction of putative binding region using a more refined sampling of ligand-protein interactions: A set of overlapping boxes were used to enclose the volume corresponding to the putative binding region (or regions) determined in Step 2, which is now to be used for a new sampling of ligand-protein conformations similar to Step 2.

4. Coarse-grain sampling of putative binding regions: To locate the most favorable ligand binding site(s), we again used DOCK 4.0 to generate a set of conformations for binding 11-cis-retinal (a ligand known to bind to bovine rhodopsin) to the putative binding region. We again used a bump filter of 10, a non-distance-dependent dielectric constant of 1.0, and a cutoff of 10 Å for energy evaluation. The ligands were docked as nonflexible molecules to generate and score 1000 conformations. We selected the 10% (i.e., 100) with best DOCK 4.0 score for further analysis.

5. Ligand-only minimization: The 100 best conformations selected from Step 4 were conjugate-gradient-minimized, keeping the protein fixed but all atoms of the ligand movable. Minimized ligand conformations that satisfied the buried surface area cutoff criterion of 75% were kept for the next step.

6. Ligand-protein full minimization: The ligand/protein conformations from Step 5 were further energy-minimized with all atoms (protein, lipid, and ligand) movable using conjugate gradients. The structure with the binding energy calculated by Eq. 1 was selected as

   (1)

   Here the energy of the ligand in water is calculated using DREIDING FF and analytical volume Generalized-Born continuum solvation method. Since a substantial part of the complex is in contact with the membrane environment, we did not solvate the complex.

7. Side-chain optimization: Using the best binding conformation from Step 6, the side-chain conformations for all the residues within 5 Å of the bound 11-cis-retinal conformation were optimized using the SCREAM side-chain optimization program (V. W. T. Kam, N. Vaidehi, and W. A. Goddard 3rd, unpublished). The resulting ligand-protein structure was finally optimized by conjugate gradient minimization allowing all atoms to relax.

8. Iterative HierDock (optional): The protein from Step 7 (optimized with ligand bound) was saved. Steps 4–6 were repeated again to obtain the best possible conformation for the ligand within the protein (with side chains optimized in the presence of the ligand). This step was performed for bovine rhodopsin.

FIGURE 5.

The 13 regions shown as boxes used in scanning the entire protein for the 11-cis-retinal putative binding site. The two boxes chosen as binding sites by HierDock are shown in red. (A) Front view with N-terminus at the bottom. (B) Top view obtained by rotating by 90° around the horizontal axis in A so that the N-terminus is out of view. These two orientations are used for all structures shown in this article.

RESULTS AND DISCUSSION

We first present the results for the validation of the HierDock protocol on the crystal structure of bovine rhodopsin, followed by results on structure and function prediction for bovine rhodopsin. To clarify our notation we summarize it here.

Ret(xtal)/closed(xtal) is obtained from the crystal structure by minimizing using the DREIDING FF. It deviates from the crystal structure by 0.29 Å CRMS. It has retinal bound as in the crystal structure and has the closed form of the EC-II loop. The retinal conformations differ by 0.22 Å CRMS. This further validates the FF. Since they differ so little, the retinal in the nonminimized crystal structure, Ret(xtal-noFF), is used as the reference structure for the HierDock validation step.

Apo/closed(xtal) is obtained from Ret(xtal)/closed(xtal) by removing the retinal and adding the proton to Lys-296. It was minimized without ligand. It deviates from the crystal structure by 0.74 Å CRMS. It is likely that this is a lower bound on the change in structure upon removal of the retinal. For a more complete optimization, we would use MD.

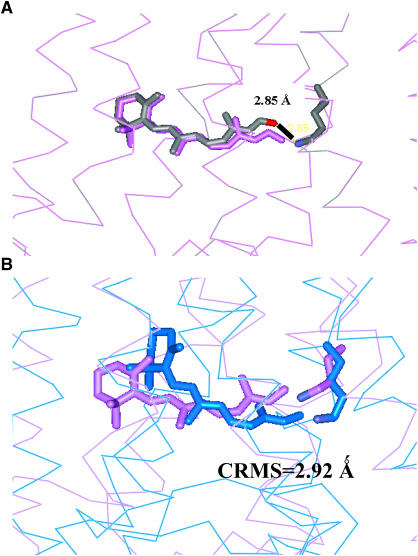
Ret(HD)/closed(xtal) is the predicted structure for 11-cis-retinal obtained by applying HierDock to Apo/closed(xtal) and then forming the Schiff base linkage to Lys-296 and minimizing. The Ret(HD) deviates from Ret(xtal) by 0.62 Å CRMS. To distinguish the error in ligand conformation due to the HierDock procedure from that due to MembStruk, the structure Ret(HD)/closed(xtal) will serve as the reference structure to compare to the predicted ligand conformations in the MembStruk structures.

Apo/closed(MS) is the MembStruk-predicted structure of the closed form, without the retinal. The TM bundle for this structure deviates by 2.84 Å CRMS main-chain atoms from Apo/closed(xtal) (4.04 Å CRMS for all TM atoms, excluding H).

Ret(HD)/closed(MS) is the predicted structure for 11-cis-retinal in the Apo/closed(MS) rhodopsin structure, obtained by applying HierDock to Apo/closed(MS) and then forming the Schiff base linkage to Lys-296 and minimizing the energy. The Ret(HD) deviates from Ret(HD)/closed(xtal) by 2.92 Å CRMS.

Apo/open(MS) is the MembStruk-predicted structure of bovine rhodopsin without the retinal. There are no experiments with which to compare. This structure differs in the TM region from Apo/closed(MS) by 0.11 Å.

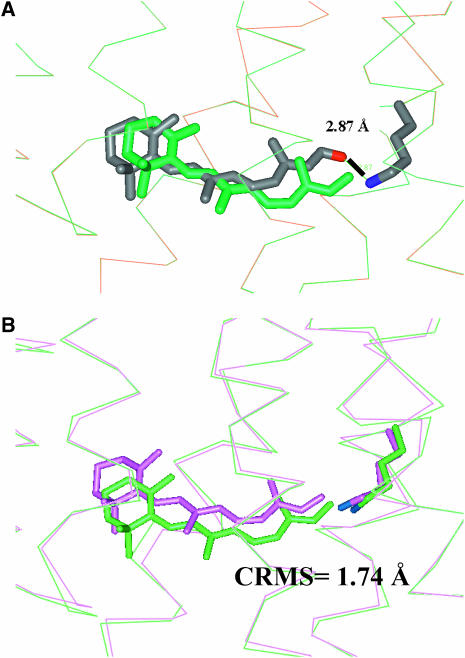
Ret(HD)/open(MS) is the predicted structure for 11-cis-retinal in rhodopsin obtained by applying HierDock to Apo/open(MS) and then forming the Schiff base linkage to Lys-296 and minimizing. There are no experiments with which to compare. The retinal differs from that in Ret(HD)/closed(MS) by 1.74 Å.

Validation for function prediction HierDock protocol for 11-cis-retinal on bovine rhodopsin

Bovine rhodopsin (a member of the opsin family) is the only GPCR to be crystallized in its entirety at a high resolution (2.8 Å). Thus we used this system as a test to validate the HierDock protocol for predicting the binding sites of GPCRs.

To test HierDock, we used the Apo/closed(xtal) structure with the retinal removed and minimized. First we did a complete HierDock scan as outlined above to predict the binding of 11-cis-retinal to bovine rhodopsin. The crystal structure of rhodopsin has the 11-cis-retinal covalently bound to Lys-296 (between the aldehyde of 11-cis-retinal and the N of the Lys), but for docking we cannot have a covalent bond to the crystal. Thus we docked the full 11-cis-retinal ligand (containing a full aldehyde group) and considered the Lys-296 to be protonated.

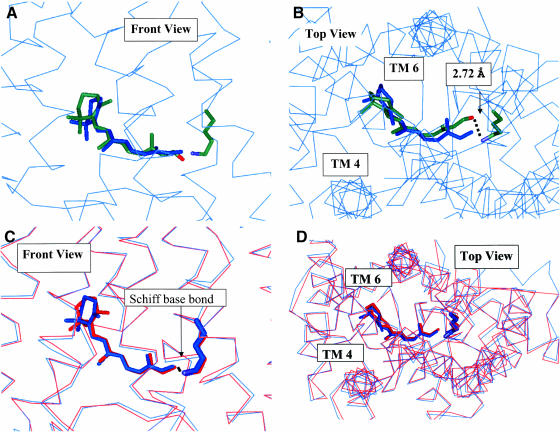
We applied Steps 1–2 of the HierDock described above for all 13 overlapping regions for Step 2 shown in Fig. 5. The initial scan of the entire rhodopsin (Steps 1 and 2 in Function Prediction for GPCRs) gave two good binding regions shown as the red boxes in Fig. 5. The data for this scanning step are shown in Table 2. The final optimized best binding structure for the retinal/rhodopsin complex from Step 6 of HierDock deviates by 1.11 Å CRMS from the ligand in the crystal structure as seen in Fig. 6, A and B. The binding site (defined as the seven residues that contribute at least 1 kcal/mol to the bonding) of this ligand is shown in Fig. 9 B. Lys-296 has hydrophilic interactions whereas the other side chains have van der Waals interactions. This docked structure has the retinal O 2.72 Å from the N of Lys-296. In addition, the retinal O and the closest H of the protonated Lys-296 N are just 2.35 Å apart, close enough to form an H-bond (likely an intermediate step before Schiff base formation). We then coupled these two units to form the covalent CN bond to Lys-296 while eliminating the H₂O. After minimizing the full ligand-protein structure, we find that the predicted structure for 11-cis-retinal bonded to the protein deviates from the crystal structure by only 0.62 Å CRMS as shown in Fig. 6, C and D. Most of this discrepancy results because the FF-minimized structure of the retinal has the ionone ring in a chair conformation which was retained in our docking procedure, whereas the crystal structure has the ionone ring in a half-chair conformation (which we calculate to be 2 kcal/mol higher in energy than the chair conformation within the minimized complex). This retinal/protein complex minimized with the DREIDING FF, denoted Ret(HD)/closed(xtal), serves as the reference structure for comparing the predicted structures in later sections. We consider that these results validate the HierDock protocol for a GPCR.

TABLE 2.

Box	Top 5% after coarse-grain ranking
1	2596, 2941, 2991, 3011, 4281
2	4440, 4621, 4625, 5509, 5513
3	2338, 2375, 2409, 2566, 2571
4	5844, 5961, 6006, 6244, 6278
5	None passed buried surface criteria
6	102, 118, 131, 136, 208
7	1366, 1370, 1374, 1374, 1379
8	No conformations generated from DOCK
9	12026
10	82, 139, 153, 377, 380
11	2348, 2348, 2566, 2843, 2843
12	No conformations generated from DOCK
13	551, 734, 931, 1110, 1226

Results from the coarse-grain docking step of HierDock to predict the binding site(s) in Apo/closed(xray). The energies of the top 5% after ranking (level 2 of HierDock) are shown for each box. Among all boxes, the best coarse-grain score is underlined. The scores within 100 kcal/mol of the top score are shown in bold.

FIGURE 6.

(A–D) Validation of HierDock. (A) Front view of the 11-cis-retinal conformation determined by HierDock for Ret(HD)/closed(xray) (colored by element ) compared to the published crystal structure (green). The CRMS difference in the ligand structures is 1.1 Å. (B) Top view of A. This shows that predicted position of the retinal aldehyde oxygen is 2.8 Å from the N of Lys-296, which is short enough for an H-bond. (C) Top view showing the result of making the Schiff base bond of 11-cis-retinal to Lys-296 in A and minimizing the resulting structure (blue), compared with the crystallographic ligand structure (red). The CRMS difference between these ligand structures is 0.62 Å. (D) Top view of C.

FIGURE 9.

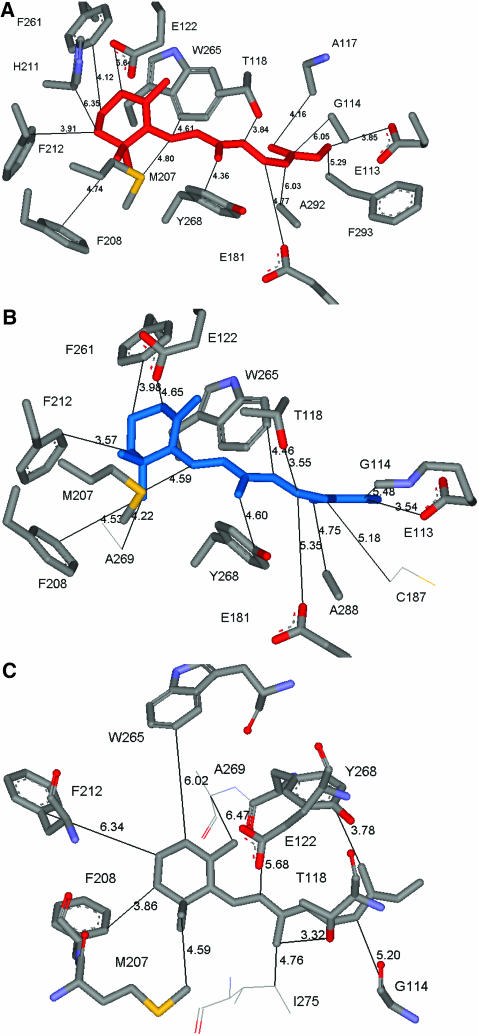
(A–D) Comparison of predicted binding sites for retinal (those residues within 5 Å of retinal that interact strongly with the ligand (contributions to binding >1 kcal/mol) before Schiff base bond formation in the three rhodopsin structures. (A) All three structures and ligand conformations are shown. The colors blue, gray, and orange correspond respectively to those structures analyzed in B–D. (B) NoSB-Ret(HD)/closed(xtal) structure. Here we see that seven residues bind more strongly than 1 kcal/mol. (C) NoSB-Ret(HD)/closed(MS). Here we see that five of the seven residues in B are predicted (only Phe-208 and Hsp-211, both rather weakly bound). We also find three additional residues (Phe-212, Ile-275, and Ala-117) that do not bind with 1 kcal/mol in B. (D) NoSB-Ret(HD)/open(MS). Here we see that six of the seven residues in C bind more strongly than 1 kcal/mol. We also find four additional residues that do not bind with 1 kcal/mol in B. This difference results from the shift in the retinal binding site upon closure of the EC-II loop. The side chains in common with the NoSB-Ret(HD)/closed(xtal) structure (in B) or with NoSB-Ret(HD)/closed(MS) (in C) within the binding site around the 11-cis-retinal are labeled with larger type.

In addition, we used HierDock to determine the binding site and best scoring ligand conformation for all-trans-retinal, with the binding energy calculated using Eq. 1 above. The binding energy for 11-cis-retinal was −1 kcal/mol whereas that for all-trans-retinal was ∼31 kcal/mol, a difference of 32 kcal/mol. This compares well with the experimental result that the retinal ligand/protein complex stores 34.7 ± 2.2 kcal/mol upon isomerization in the protein (Okada et al., 2001). This stored energy might be used to induce rigid-body helical motions needed for receptor activation and G-protein binding. This excellent agreement is probably fortuitous, inasmuch as we have not carried out full optimizations of the all-trans configuration, but it may be partly because cis- and trans-retinal are neutral isomers of each other with similar solvation energies.

Structure prediction of rhodopsin using MembStruk

We used MembStruk3.5 as detailed in The MembStruk Protocol for Predicting Structure of GPCRs to predict the structure of bovine rhodopsin using only the protein sequence. For the apo-rhodopsin we predicted two structures, one with the open EC-II loop and one with closed EC-II loop. These represent two different states of rhodopsin likely to play a role in activation of G-protein. The crystal structure of rhodopsin has a closed EC-II loop with the 11-cis-retinal bound to it. To validate this predicted structure, we should compare to the crystal structure for apo-rhodopsin (without a bound 11-cis-retinal). However, this crystal structure for the apo protein is not available. Thus instead we will compare the predicted structure to the minimized crystal structure of bovine rhodopsin after removing the 11-cis-retinal. In making these comparisons, we predicted two structures for apo-rhodopsin: 1), the open form, where no restrictions were made on the structure of EC-II loop, i.e., Apo/open(MS); and 2), the closed form, where we assumed that EC-II makes the same cysteine linkage as observed in the crystal structure, i.e., Apo/closed(MS).

The predicted TM domains are compared to the rhodopsin crystal structure in Fig. 2 and discussed in Step 1, Helix Capping in TM2ndS.

After optimization of the helices using MD (300 K for 500 ps), most helices yield the same bends as in the crystal. Thus helices 2 and 6 undergo significant bending (due to Pro-267 in helix 6 and due to Gly-89 and Gly-90 in helix 2), which is consistent with spin-labeling electron paramagnetic resonance experiments (Farrens et al., 1996). In addition, we find that helix 7 bends near the two prolines, which has also been shown by spin-labeling experiments (Altenbach et al., 2001a,b). We find that helix 1 undergoes significant bending due to a Gly/Pro combination, but this has not yet been studied experimentally. Such bending at hinge sites may be important for expanding the molecular surface needed at the cytoplasmic side to allow G-protein binding. We find similar hinge-bending with MD when the trans-isomer is bound to the helix assembly.

After assembling the optimized helices again into a bundle, we carried out RotMin on helices 3 and 5, the only helix pair with a potential salt bridge. The resulting seven-helix bundle was then inserted into a lipid bilayer, and optimized using rigid-body molecular dynamics as described in Step 4 of The MembStruk Protocol for Predicting Structure of GPCRs. This step leads to optimization of the vertical helical positions, relative helical angles, and rotations of the individual helices within a lipid environment. The CRMS difference before and after this rigid body MD is 1.10 Å for all atoms and 0.98 Å for main-chain atoms. This is consistent with the changes during this optimization step for other GPCRs (Vaidehi et al., 2002).

After adding the intracellular and extracellular loops, optimizing the side chains, and then optimizing the structure in vacuum with the TM helical region fixed (to eliminate bad contacts in the loop region), we then optimized the entire structure allowing all bonds and angles to change. These ab initio predictions of the structure were carried out for both the open and closed forms of the EC-II loop in apo-rhodopsin leading to the Apo/open(MS) and Apo/closed(MS) structures, where MS denotes a MembStruk-derived structure, and open or closed denotes the open or closed form of the EC-II loop. Although the crystal structure has the 11-cis-retinal bound, we will compare the predicted apo-rhodopsin structures to the minimized apo-protein of the crystal structure, Apo/closed(xray).

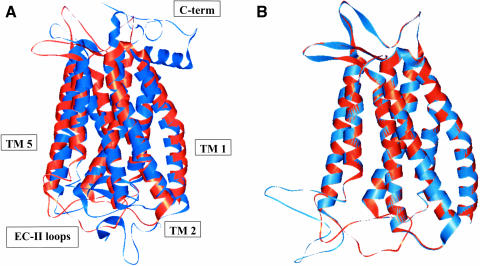
Comparing Apo/closed(MS) to Apo/closed(xray) we find a CRMS difference of 2.85 Å in the main-chain atoms and 4.04 Å for all the atoms in the TM helical region. These structures are compared graphically in Fig. 7 A. Comparing all residues including loops (but ignoring the residues not present or complete in the x-ray structure), the predicted structure differs from the crystal structure by 6.80 Å in the main chain and 7.80 Å CRMS for all atoms. The major contribution to this CRMS is the low-resolution loop region, which is likely to be quite fluxional and may be very different between crystal and solution. Specifically, the predicted topology and φ−ψ angles of the EC-II loop are consistent with that of a β-sheet. However, the specific twist of this β-sheet in the x-ray structure was not predicted well. Although this may be partly due to packing effects in the crystal structure, we consider that our prediction of the general topology of the EC-II loop to act as a “plug” to restrict retinal binding is adequate but that specific interactions with retinal may not be predicted well. In the function prediction results discussed below in the subsection called Apo/Closed(MS), we find that there are no specific favorable interactions between the ligand and the EC-II loop before Schiff base bond formation in the crystal structure (Fig. 9 B). Thus the EC-II may function initially primarily as an unspecific “plug” to disfavor certain ligand conformations. After Schiff base bond formation, the ligand is then stabilized by Glu-181 in the EC-II loop (Fig. 10 A). Thus accurate prediction of the atomic structure of the EC-II loop remains an important challenge.

FIGURE 7.

(A) Comparison of the predicted structure (orange) Apo/closed(MS) with the experimental structure (blue) Apo/closed(xray). They differ in the TM helical region by CRMS = 2.84 Å. (B) Comparison of the predicted Apo/closed(MS) structure (orange) with the predicted Apo/open(MS) structure (blue). They differ in the TM helical region by 0.11 Å.

FIGURE 10.

(A–C) Comparison of predicted binding sites of retinal with Schiff base bond formed. We considered residues within a 5 Å shell of the ligand (excluding the Lys-296 to which the retinal is bound) and determined those that contribute at least 1 kcal/mol of stabilization energy for the three rhodopsin structures. (A) Ret(xtal)/closed(xtal) structure. Here we see that 15 residues bind more strongly than 1 kcal/mol. (B) Ret(HD)/closed(xtal). Here we see that 12 of the 15 residues in A are predicted to bind strongly (Ala-117 and His-211 still contribute positively to bonding but are now rather weakly bound, at <1 kcal/mol). We find two additional residues (Cys-187 and Ala-269) that did not bind with 1 kcal/mol in A. (C) Ret(HD)/closed(MS). Here we find 8 of the 15 residues in A still bind strongly. We also find two additional residues (Ile-275 and Ala-269) that did not bind with 1 kcal/mol in A. A larger type is used to label the side chains in common with the Ret(xtal)/closed(xtal) structure within the binding site around the 11-cis-retinal.

We find that Apo/open(MS) deviates from Apo/closed(MS) by a CRMS difference of 0.11 Å in the main-chain atoms and 0.68 Å for all the atoms in the TM helical region. These structures are compared graphically in Fig. 7 C. This small difference in CRMS in the transmembrane region suggests that we need to carry out long timescale molecular dynamics for the helices to accommodate the EC-II loop conformational change. Comparing all residues, the predicted structure differs from the crystal structure by 4.74 Å in the main chain and 5.0 Å CRMS for all atoms. There is no experimental structure Apo/open(xray) with which to compare Apo/open(MS).

HierDock function prediction for Apo_rhod (MS) structures

Except for bovine rhodopsin, essentially all applications of HierDock to GPCRs must use predicted structures rather than experimental structures. The question here is that, given the errors in predicting the GPCR structure (2.8 Å CRMS in the TM helical region), can we hope to get accurate predictions in the binding site and binding energy? We will now test how well HierDock determines the binding site of 11-cis-retinal to the predicted rhodopsin structures Apo/open(MS) and Apo/closed(MS).

Here we repeated the full process described in Function Prediction for GPCRs. The void space for both the Apo/open(MS) and Apo/closed(MS) structures were partitioned into fourteen 7 Å × 7 Å × 7 Å boxes and scanned for the putative binding site of 11-cis-retinal (using the same ab initio FF-optimized ligand structure as in Validation for Function Prediction HierDock Protocol for 11-cis-retinal on Bovine Rhodopsin). Again the molecule includes the aldehyde group (no assumed formation of the Schiff base).

Apo/closed(MS)

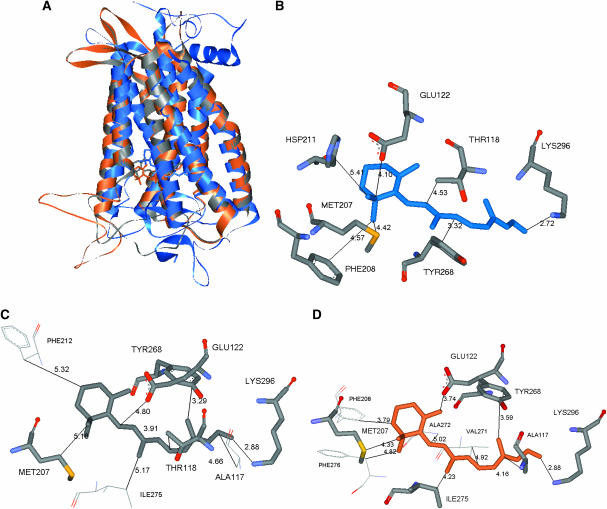
Scanning the entire Apo/closed(MS) receptor to find the binding site and binding energy for 11-cis-retinal used the steps described in Computational Methods. The best scoring conformation for 11-cis-retinal and its associated binding site, denoted as NoSB-Ret(HD)/closed(MS), are shown in Fig. 9 C. Here NoSB indicates the structure without the Schiff base covalent bond between the aldehyde group of 11-cis-retinal and Lys-296. This conformation (no covalent attachment) differs from Ret(HD)/closed(xtal) by 3.2 Å CRMS. We should emphasize that the Apo/closed(MS) structure was constructed purely from ab initio predictions with MembStruk, with no input from the x-ray crystal structure. Thus nowhere did we assume a lysine covalent bond with retinal in any of the docking procedures. Yet, the predicted structure identifies which Lys can bond to the retinal, with 2.85 Å between the predicted position of the retinal oxygen and the predicted position of the Lys-296 nitrogen.

Then starting with NoSB-Ret(HD)/closed(MS), we formed this Schiff's base bond (eliminating H₂O), and optimized the full ligand-protein complex with conjugate gradient minimization to obtain the Ret(HD)/closed(MS) structure. This differs from Ret(HD)/closed(xtal) by 2.92 Å CRMS. These structures are compared in Fig. 8, A and B.

FIGURE 8.

MembStruk validation using the closed EC-II loop. (A) The HierDock-predicted conformation of 11-cis-retinal (colored by element) in the MembStruk-predicted Apo/closed(MS) structure, denoted NoSB-Ret(HD)/closed(MS). Note that the aldehyde oxygen is 2.85 Å from the N of Lys-296. (B) The retinal structure after forming this Schiff base bond of 11-cis-retinal to Lys-296 and optimizing to form Ret(HD)/closed(MS) (violet). Ret(HD)/closed(xtal) (blue). These ligand structures were found to differ by 2.9 Å CRMS.

A second criterion for validity of the predicted binding site is to identify the residues interacting most strongly with the ligand, which can be used to predict mutational studies for validation and to design antagonists or agonists. Considering the binding site to be all residues within 5.0 Å of the ligand leads to 30 residues for Ret(xtal)/closed(xtal). For Ret(HD)/closed(MS) we find 26 residues (26 in common with Ret(x)/closed(xtal)) and for Ret(HD)/closed(xtal) we find 23 residues (15 in common with Ret(x)/closed(xtal)) in the binding site. More important is to establish which of these residues is responsible for ligand stabilization. Thus we calculated the interactions of all amino acid residues within 5 Å of the ligand and kept those that have a more favorable interaction than −1 kcal/mol interaction energy with the ligand. For Ret(xtal)/closed(xtal) this leads to the 15 residues shown in Fig. 10 A. For Ret(HD)/closed(MS) we find 10 residues (8 in common with Ret(x)/closed(xtal)) shown in Fig. 10 B and for Ret(HD)/closed(xtal) we find 14 residues (12 of which in common with Ret(x)/closed(xtal)) shown in Fig. 10 C. The interaction energies of the residues are shown in Table S2. The side chains identified as important include Trp-265 and Tyr-268, which have been implicated (Lin and Sakmar, 1996) to modulate the absorption frequency of 11-cis-retinal.

To provide an idea of how the retinal binds before Schiff base bond formation, we also considered the binding site as all residues within 5.0 Å of the ligand before bond formation that have a more favorable interaction than −1 kcal/mol interaction energy with the ligand. For NoSB-Ret(HD)/closed(xtal) this leads to the seven residues shown in Fig. 9 B. For NoSB-Ret(HD)/closed(MS) we find eight (six in common with NoSB-Ret(HD)/closed(xtal)) shown in Fig. 9 C. The interaction energies of the residues are shown in Table S1. Of the top interacting residues (three residues) in NoSB-Ret(HD)/closed(xtal), two (Tyr-268 and Lys-296) are also shown to rank among the top three in NoSB-Ret(HD)/closed(MS). The residue which was missed (Thr-118) ranked lower in NoSB-Ret(HD)/closed(MS) because it is actually closer to the retinal (in comparison with the NoSB-Ret(HD)/closed(xtal) structure), with distances as low as 2.8 Å (whereas an optimal van der Waals distance is ∼3.4 Å) to the polyene chain of retinal.

We conclude that the MembStruk-predicted structure is useful for predicting binding sites sufficiently well to direct mutation studies to elucidate the precise site.

Apo/open(MS)

We scanned the entire Apo/open(MS) receptor to find the binding site and binding energy for 11-cis-retinal using the steps described in Computational Methods. The best scoring conformation for 11-cis-retinal and its associated binding site, denoted as NoSB-Ret(HD)/open(MS), are shown in Fig. 9 D. The predicted structure identifies which Lys can bond to the retinal, with 2.87 Å between the predicted position of the retinal oxygen and the predicted position of the Lys-296 nitrogen.

Then starting with NoSB-Ret(HD)/open(MS), we formed this Schiff base bond (eliminating H₂O), and optimized the full ligand-protein complex with conjugate gradient minimization to obtain the Ret(HD)/open(MS) structure, This is no experimental structure with which to compare, but this structure differs from Ret(HD)/closed(MS) by 1.7 Å CRMS. These structures are compared in Fig. 11, A and B.

FIGURE 11.

MembStruk validation using the open EC-II loop. (A) The HierDock-predicted conformation (colored by element) of 11-cis-retinal in the MembStruk-predicted structure to form the NoSB-Ret(HD)/open(MS) structure. Note that the aldehyde oxygen is 2.87 Å from the N of Lys-296, which is short enough to form a hydrogen bond. (B) The Ret(HD)/open(MS) structure after forming the Schiff base bond (green), compared with the structure (violet) of 11-cis-retinal in Ret(HD)/closed(MS). These ligand structures differ by 1.7 Å CRMS. The EC-II loop may function to position the retinal ligand into its final conformation as found in the rhodopsin crystal structure.

A second criterion for validity of the predicted binding site is in identifying those residues close to the ligand to consider for mutational studies and drug design. Considering the binding site of NoSB-Ret(HD)/open(MS) as all residues within 5.0 Å of the ligand, the amino acid residues which interact with <−1 kcal/mol interaction energy with the ligand (10 residues) are shown in Fig. 9 D. Of these, six residues are also shown to interact with the ligand in the NoSB-Ret(HD)/closed(MS) structure discussed in the subsection called Apo/Closed(MS). We also find four additional residues (Phe-276, Phe-208, Val-271, and Ala-272) that do not bind with 1 kcal/mol in the NoSB-Ret(HD)/closed(MS) structure. This difference results from the shift in the retinal binding site upon opening of the EC-II loop. Thus, we consider that the retinal bound to the open-loop structure is partially stabilized by van der Waals interactions.

Exploring the signaling mechanism

Using MembStruk we predicted the two structures Apo/open(MS) with the EC-II in an open conformation and Apo/closed(MS) with it closed. The crystal structure of rhodopsin has the closed configuration in which EC-II has a well-defined β-sheet structure with the 11-cis-retinal bound. We speculate that changes in the structure of this loop are involved in activation of G-protein and in the entry of 11-cis-retinal on the extracellular side of rhodopsin. The idea is illustrated in Fig. 4, in which the helix 3 coupled to this loop by a cysteine bond is the gatekeeper which responds to signaling structural substates of rhodopsin as follows.

Starting with the inactive form Ret/closed with 11-cis-retinal covalently linked to the rhodopsin, the response to visible light causes the 11-cis-retinal to isomerize to all-trans-retinal, which in turn causes changes in the conformation (Altenbach et al., 2001a,b, 1996; Farrens et al., 1996) near the retinal that eventually leads to a structure in which the all-trans-retinal is covalently linked to the open form with a structure resembling the trans-Ret(HD)/open(MS) structure from our calculations.

The transformation from closed to open in Step 1 is caused by conformational changes responsible for activation (perhaps by the direct interaction of the trans-isomer with helix 3, to induce helix 3 to shift toward the extracellular side, breaking the DRY-associated salt bridges at the intracellular side).

Other processes hydrolyze off the trans-retinal to form a structure similar to Apo/open(MS) and then other processes reattach 11-cis-retinal to form a structure similar to Ret(HD)/open(MS).

The Ret(HD)/open(MS) relaxes eventually to form Ret(HD)/closed(MS), the inactive form. In this process the EC-II loop closes, perhaps caused by the helix 3 shifting toward the intracellular side, reforming the DRY-associated salt bridges at that end with the final result that the EC-II closes to form a structure similar to the inactive form.

Thus by using MembStruk and HierDock we have generated a total of six structures (summarized later) for ligand/protein complexes that can now be used to explore all the processes involving ligand binding and GPCR activation. The experiment provided just one of these six structures, but the validation with experiment allows us to have greater confidence in those five for which experimental structures are not available.

COMPARISON TO OTHER METHODS

There have been attempts to model the structure of GPCRs using homology modeling methods with either the bacteriorhodopsin or bovine rhodopsin crystal structure as template (Strader et al., 1994). Since there is only one known structure, these homology applications lead to transmembrane regions very similar to the bovine rhodopsin template structure. Moreover, many important GPCR targets have only low homology to bovine rhodopsin, making the models particularly unreliable (Archer et al., 2003). Thus the sequence identity of bovine rhodopsin to dopamine D2 receptor is 17%, to serotonin H1A 14%, and to G2A 13%, whereas good structures from homology models generally require >45% sequence identity.

GPCR structures have also been modeled using the properties of conserved residues in multiple sequence alignments followed by optimization of the structure using distance restraint to maximize the hydrogen bonds (Lomize et al., 1999). Distance restraints from various experiments were also used to predict the structure of bacteriorhodopsin (Herzyk and Hubbard, 1995). Comparing the TM helical region of their predicted structure to a bundle of ideal helices (i.e., not bent) superimposed on the bacteriorhodopsin electron cryomicroscopy structure, they reported a CRMS of 1.87 Å in the C-alphas.

Shacham et al. (2001) claim to have predicted the structure of bovine rhodopsin using an approach based on specificity of protein-protein interaction and protein-membrane interaction and the amphipathic nature of the helices. However, they have not yet provided any details of their method or of predictions on other GPCRs.

SUMMARY

Using MembStruk we predicted the three-dimensional structure of bovine rhodopsin protein interacting with 11-cis-retinal using only primary sequence information. This led to the following structures.

Apo/closed(MS) is the MembStruk-predicted structure of the closed form, without the retinal. The transmembrane assembly for this structure deviates from Apo/closed(xtal) by 2.84 Å CRMS for the main-chain atoms (4.04 Å CRMS for all transmembrane atoms, excluding H). Starting with the crystal structure and minimizing using the DREIDING FF leads to a structure that deviates from the crystal by 0.29 Å CRMS, indicating that the FF leads to a good description. Thus most of the 2.8 Å CRMS error is due to the MembStruk process.

Ret(HD)/closed(MS) is the predicted structure for 11-cis-retinal obtained by applying HierDock to Apo/closed(MS). This leads to close contact (2.8 Å) between the carbonyl of the retinal and the N of Lys-296. Forming the Schiff base linkage and minimizing leads to the Ret(HD) structure that deviates from Ret(HD)/closed(xtal) by 2.92 Å CRMS. Carrying out the same HierDock process for the minimized crystal structure leads to a predicted structure for 11-cis-retinal that deviates from Ret(xtal) by 0.62 Å CRMS. This indicates that it is, in fact, errors in the predicted protein structure that are responsible for the errors in ligand prediction.

Trans-Ret(HD)/closed(MS) is the predicted structure for all-trans-retinal obtained by converting 11-cis-retinal to all-trans and allowing the protein to respond. There is no experimental structure with which to compare.

Apo/open(MS) is the MembStruk-predicted structure of the open form without the retinal. There are no experiments with which to compare. This structure differs in the TM region from Apo/closed(MS) by 0.11 Å.

NoSB-Ret(HD)/open(MS) is the predicted structure for 11-cis-retinal obtained by applying HierDock to Apo/open(MS). There is no experimental structure with which to compare.

Ret(HD)/open(MS) is formed from NoSB-Ret(HD)/open(MS) by forming the Schiff base linkage to Lys-296 and minimizing. There are no experiments with which to compare. The retinal differs from that in Ret(HD)/closed(MS) by 1.74 Å.

The validation with experiment is sufficiently good that we can now start to explore the mechanisms by carrying out long timescale molecular dynamics and Monte Carlo calculations on these various forms to learn more about the mechanism of activation. Comparisons of the structures and energetics for these systems provide information that might be useful for understanding the mechanisms of binding and activation in rhodopsin in particular and GPCRs in general.

We have noted above several steps for which we anticipate substantial improvements and we are continuing to improve the methods. For example the individual optimization of the helices can be performed under a more constrained environment by performing torsional dynamics of each helix in the presence of other helices or by performing torsional dynamics of all helices simultaneously. For improved accuracy in predicting the structures and for predicting the ligand binding energy, we also intend to take into account the differential solvent dielectric environment between membrane and the hydrophilic and interfacial dielectric constants (Spassov et al., 2002).

CONCLUSIONS

These applications of TM2ndS, MembStruk, and HierDock to bovine rhodopsin validate these techniques for predicting both the structure of membrane-bound proteins and the binding site of ligands to these proteins. The predictions from such studies can be used to design experiments to test details of the structures that might lead to improved structures. This could lead to structures more accurate than any of these techniques individually. The HierDock and MembStruk techniques validated here should also be useful for applications to other GPCRs, particularly for targeting agonists and antagonists against specific subtypes.

In addition, these studies open the door to examination of the mechanism for activation (structural and energy changes) of signaling. Obtaining independent structures for each of the major steps involved in binding and activation (e.g., the six structures discussed for retinal-rhodopsin) provides the basis for computational studies and for experiments that should provide a basis for detailed examination of each step.

SUPPLEMENTAL MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.