A Nonlinear Discrete Dynamical Model for Transcriptional Regulation: Construction and Properties

Abstract

Transcriptional regulation is a fundamental mechanism of living cells, which allows them to determine their actions and properties, by selectively choosing which proteins to express and by dynamically controlling the amounts of those proteins. In this article, we revisit the problem of mathematically modeling transcriptional regulation. First, we adopt a biologically motivated continuous model for gene transcription and mRNA translation, based on first-order rate equations, coupled with a set of nonlinear equations that model cis-regulation. Then, we view the processes of transcription and translation as being discrete, which, together with the need to use computational techniques for large-scale analysis and simulation, motivates us to model transcriptional regulation by means of a nonlinear discrete dynamical system. Classical arguments from chemical kinetics allow us to specify the nonlinearities underlying cis-regulation and to include both activators and repressors as well as the notion of regulatory modules in our formulation. We show that the steady-state behavior of the proposed discrete dynamical system is identical to that of the continuous model. We discuss several aspects of our model, related to homeostatic and epigenetic regulation as well as to Boolean networks, and elaborate on their significance. Simulations of transcriptional regulation of a hypothetical metabolic pathway illustrate several properties of our model, and demonstrate that a nonlinear discrete dynamical system may be effectively used to model transcriptional regulation in a biologically relevant way.

INTRODUCTION

An emerging theme in modern biology is the development of accurate experimental techniques for monitoring cellular behavior (e.g., see Schena et al., 1996; Brown and Botstein, 1999; Turner and Varshavsky, 2000; Zhu et al., 2001; Baldi and Hatfield, 2002). Although current techniques are mostly used to identify molecular markers for certain types of disease (e.g., cancer; see Golub et al., 1999; Bittner et al., 2000; Kobayashi et al., 2003b), it is the monitoring and modeling of cellular behavior that could mostly benefit from them.

An important cellular process under investigation is transcriptional regulation. Understanding the biological mechanisms underlying transcriptional regulation may lead to significant advances in cell biology, drug development, and medicine. It is becoming increasingly clear that, to enrich our knowledge about transcriptional regulation and understand the role it plays in cellular function, we need to construct a sufficiently predictive mathematical model for such a process, derived from basic biological principles. Moreover, experimental and computational techniques should be developed to estimate the underlying structure of the model and its parameters. Model simplicity, via reasonable biological assumptions and approximations, is important, due to limited biological knowledge of the mechanisms underlying transcriptional regulation, and difficulties of current technologies in measuring underlying parameters. If the model is sufficiently predictive, we may use it as a computational tool (even in the absence of exact parameter values) to simulate biological scenarios (e.g., steady-state analysis, mutation effects, knock-out studies, perturbation effects, homeostatic and epigenetic regulation, etc.), and generate hypotheses pertaining to the mechanisms underlying transcriptional regulation and control. This plan seems to be easier, faster, and cheaper to implement in silice (i.e., on a digital computer by simulation) than in vivo or in vitro.

There have been considerable efforts to build models for transcriptional regulation (e.g., see Thomas and D'Ari, 1990; Kauffman, 1993; Smolen et al., 2000; Gibson and Mjolsness, 2001; Hasty et al., 2001a; Savageau, 2001; de Jong, 2002; Shmulevich et al., 2002; for reviews of such models and several references). Most models can be categorized as being “qualitative” or “quantitative.” The former models emphasize structural information sharing among genes and lack detailed quantitative description of transcriptional regulation. The later models focus on a quantitative description of transcriptional regulation and are often more biologically oriented than qualitative models. The Boolean network (Kauffman, 1993) is a good example of a qualitative model, whereas, transcriptional regulation models based on ordinary differential equations (ODEs) (Chen et al., 1999) are typical examples of quantitative models.

Typically, a qualitative model (like a Boolean network) is a “coarse” approximation of transcriptional regulation. It may provide some insights into the underlying mechanisms of transcriptional regulation, but it may also lead to biologically erroneous conclusions (e.g., see Hatzimanikatis and Lee, 1999). However, qualitative models may be used to predict steady-state behavior of transcriptional regulation. This is a useful property, because cells are often observed at steady state.

Cells may often transition to different states, due to environmental perturbations or genetic instability, which may result in differentiation during development, irreversible adjustments, or disease. Therefore, it is important to design transcriptional regulation models that sufficiently predict transient as well as steady-state behavior. It is believed that ODE-based models can accomplish this goal (e.g., see Hammond, 1993; Elowitz and Leibler, 2000; Gardner et al., 2000; Yildirim and Mackey, 2003). Models based on ODEs are considered to be more detailed than qualitative models, but require structural knowledge of the transcriptional machinery and of several biological parameters (e.g., identification of promoters, regulatory regions, transcription factors, mRNA decay rates, etc.). This knowledge is not currently available for most organisms, and it is thought to be the main disadvantage of ODE-based models. However, several current efforts are geared toward determining the structure of the transcriptional machinery and estimating its parameters (e.g., see Hammond, 1993; Endy et al., 1997; Arkin et al., 1998; Tavazoie et al., 1999; Akutsu et al., 2000b; Gardner et al., 2000; Turner and Varshavsky, 2000; Lee et al., 2002; Ronen et al., 2002; Wang et al., 2002). For these reasons, ODE-based models are becoming increasingly attractive as models for transcriptional regulation.

An attractive feature of a Boolean network is that it dynamically relates the state of transcriptional regulation at time t to its state at time t − Δt, for some Δt > 0. The state of transcriptional regulation is summarized by binary-valued variables, which are dynamically related from t − Δt to t by means of Boolean functions. In this formulation, the analysis and simulation of transcriptional regulation employs theoretical and computational tools from discrete dynamical systems theory (e.g., see Sandefur, 1993), specialized to the Boolean case.

On the other hand, ODE-based models represent transcriptional regulation by a (usually large) system of nonlinear ODEs. According to this formulation, the state of the system is summarized by real-valued variables, with regulatory interactions taking the form of differential and nonlinear functional relationships. Due to the size and nonlinear structure of the system, it is not in general possible to develop mathematical techniques for its analysis. In this case, analysis is done by means of numerical techniques and computer simulations. In particular, the system may be solved by a numerical technique, like a Runge-Kutta or a predictor-corrector method (e.g., see Meir et al., 2002). Although these methods lead to general analysis and simulation techniques for transcriptional regulation, they may not be efficient, and direct biological interpretation of the various terms in the resulting equations may not be possible.

As noted in Meir et al. (2002), instead of using general techniques, it may be more preferable to derive a numerical approach to transcriptional regulation by exploiting the specific nature of the problem at hand. In this article, we investigate the possibility of doing so, by replacing an ODE-based model for transcriptional regulation with a nonlinear discrete dynamical system that is “biologically transparent,” in the sense that the resulting equations preserve the biological relevance and structure of the original model. This allows us to construct a biologically relevant quantitative model for transcriptional regulation that, like the Boolean network, enjoys attractive dynamical properties and is amenable to efficient simulation and analysis.

The system proposed in this article is directly obtained from a well-known model of transcriptional regulation based on ODEs. The ODE-based model is derived for a large population of cells by applying simple arguments of chemical kinetics on the processes of transcription and translation. It is required that the cell population is large, because the derivation of the ODE-based model relies on the Boltzmann distribution of statistical mechanics, which specifies how energy is distributed in a large population of identical molecules at statistical equilibrium. Because the ODE-based model is central to our work, we show in the next section how this model is derived from first principles. The purpose of our discussion is to clarify the limitations of modeling transcriptional regulation by means of ODEs, and to establish terminology and notation.

In the third section, we show how to model transcriptional regulation by means of a discrete dynamical system. We view the processes of transcription and translation as being discrete, and replace the actual transcriptional machinery with one for which the speeds of transcription and translation, as well as the delays in cis-regulation, are constant and equal to their mean values. We refer to this as an “average” transcriptional machinery. Therefore, the discrete dynamical system derived in this section models an “average” behavior of transcriptional regulation. The system is obtained by discretizing the ODE-based model discussed in the previous section. The discretization step is taken to be the time δt that it takes the RNA polymerase II to read one nucleotide. Moreover, we assume that, for each t = δt, 2δt, …, both the fraction of DNA templates committed to the transcription of a given gene and the mRNA concentration associated with that gene, remain constant within the time interval [t − δt, t). The resulting dynamical system is referred to as a discrete transcriptional regulatory system. It is specified by means of parameters that characterize transcription, translation, and degradation, by functionals that characterize cis-regulation, and by time delays.

In the fourth section, we discuss the steady-state behavior of the discrete model under consideration. Our discussion is motivated by the fact that the steady-state behavior of a model for transcriptional regulation may be used to characterize the cell's phenotype, and focuses on three results. The first result shows that, at steady state, the mRNA concentration vector of the discrete model “decouples” from the steady-state protein concentration vector, in the sense that one vector can be derived as a solution of a system of (nonlinear in general) equations without knowledge of the other vector. The second result shows that there is a one-to-one correspondence between the steady-state mRNA concentration vector and the steady-state protein concentration vector. This suggests that, at steady state, mRNA expression data may be used to characterize protein activity, provided that a sufficiently good estimate of the steady-state mRNA concentration vector can be inferred from such data (this also requires that the model parameters associated with translation are known). The final result shows that the discrete model has the same steady-state behavior as the associated ODE-based model. This result, together with several computational advantages underlying the discrete model, indicates that it may be more preferable to use the proposed discrete dynamical system as a model for transcriptional regulation, than the original ODE-based model.

In the next section, and by using classical arguments from chemical kinetics, we specify the nonlinearities underlying cis-regulation and include both activators and repressors as well as the notion of regulatory modules in our formulation. The derivation is based on the assumption that regulatory proteins are free to bind at several distinct sites in a promoter's regulatory region, and on the assumption that different proteins do not interact with each other or affect each other's binding affinity. Moreover, the inclusion of repressor proteins in the formulation focuses on a specific repression mechanism by which, when a repressor protein binds on a DNA template, it either blocks the recruitment of the transcription initiation complex on the promoter or prevents the release of RNA polymerase II. Finally, we show how to model cis-regulation organized in a modular fashion. According to this organization, transcriptional activity of a given gene may be controlled by a set of distinct modules, with each module asserting its own transcriptional control, independently of other modules.

In the sixth section, we discuss several properties of the proposed discrete model, related to homeostatic and epigenetic regulation as well as to Boolean networks, and elaborate on their significance. In particular, the structure of the discrete model under consideration predicts a specific response of transcriptional regulation to changes in the cellular environment, and suggests that mRNA and protein degradation, together with the rates of mRNA and protein synthesis, may play an important role in homeostatic regulation. We show that the functional form of cis-regulation is scale-invariant. This property implies that an increase (decrease) in the rates of translation, accompanied by a proportional decrease (increase) in the affinity constants underlying the binding of proteins on a promoter's regulatory region, does not change the steady-state mRNA concentration but proportionally increases (decreases) the steady-state protein concentration. It also implies that an increase (decrease) in the rates of transcription, accompanied by a proportional decrease (increase) in the affinity constants, proportionally increases (decreases) both the steady-state mRNA and protein concentrations. These properties suggest that the rates of transcription and translation, together with the affinity constants, may play an important role in epigenetic regulation. We also discuss the problem of specifying the underlying parameters, we briefly remark on the appropriateness of the Hill function as a model for cis-regulation, and introduce a parameter that provides a trade-off between model accuracy and computational efficiency. Finally, we provide a mathematical argument that indicates a limitation of using a Boolean network as a model for transcriptional regulation.

In the seventh section, we present simulations, based on transcriptional regulation of a hypothetical metabolic pathway, that illustrate several aspects of the proposed discrete model. By varying the parameters of the model, and observing how these changes affect mRNA and protein activity, we demonstrate that the nonlinear discrete dynamical system proposed in this article may effectively be used to model transcriptional regulation in a biologically relevant way.

Finally, in the last section, we summarize our conclusions.

We believe that the main contribution of this work is to show that, by using available biological information pertaining to the processes of transcription, translation, and cis-regulation, we can derive a nonlinear discrete dynamical system that may serve as a promising and testable model for transcriptional regulation. Our theoretical discussions and simulations indicate that the proposed model is capable of sufficiently predicting basic biological function and producing biologically relevant responses. Finally, the discrete dynamical nature of the proposed model makes it very attractive for large-scale computational analysis and simulation studies of transcriptional regulation.

REVIEW OF A CONTINUOUS MODEL

To model transcriptional regulation, we consider a large population 𝒞 of genetically identical cells that express the same set of G (distinct) genes, and denote those genes by 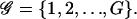We take the population to be large because the derivation of the continuous model discussed here (as well as the model for cis-regulation discussed later in this article) uses the Boltzmann distribution of statistical mechanics. The Boltzmann distribution specifies how energy is distributed in a large population of identical molecules (DNA templates, mRNAs, and regulatory proteins in our case) at statistical equilibrium. We view transcriptional regulation as a complex system of interacting genes and regulatory proteins (transcription factors), whose state at time t is summarized by the G × 1 vectors r(t) and p(t), given by

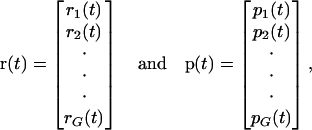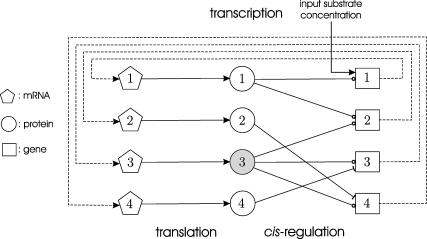
where r_i(t) and p_i(t) are the concentrations in 𝒞, at time t, of the mRNAs and regulatory proteins produced by the i^th gene (measured in mol/L or molarity M; the concentrations considered in this article are with respect to the total cellular volume in 𝒞). We consider systems that are “complete,” in the sense that p consists of all proteins that regulate transcription of the mRNAs in r. For ease of presentation, we focus on a transcriptional machinery that is “isolated,” in the sense that it is not subject to external inputs. If necessary, our formulation can be modified to consider those cases as well (see the example depicted in Fig. 5).

FIGURE 5.

An example of a tRS of a hypothetical metabolic pathway that consists of four genes. In this figure, ⊸ denotes an activator, whereas, ⊣ denotes a repressor.

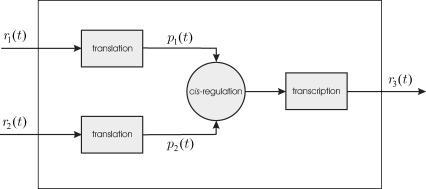
Given a target gene, we need to mathematically describe how its expression level (i.e., the mRNA concentration produced by this gene) is regulated by the expression levels of other genes. Fig. 1 depicts a block diagram of a model for transcriptional regulation, in which a target gene 3 is directly regulated by two other genes, 1 and 2. By “direct regulation” we mean that changes in the expression levels of genes 1 and 2 may produce a change in the expression level of gene 3 with no mediation from other genes. According to this model, the mRNAs transcribed from genes 1 and 2, with respective concentrations r₁(t) and r₂(t), at time t, are translated into two regulatory proteins whose concentrations are p₁(t) and p₂(t). These proteins bind to the control region of gene 3 and regulate the recruitment of general transcription factors and RNA polymerase II (for eukaryotic cells) to the gene's promoter. This step is referred to as cis-regulation. After the general transcription factors and RNA polymerase II have been assembled and positioned on the promoter, the RNA polymerase II initiates transcription of gene 3, whose mRNA concentration at time t is r₃(t).

FIGURE 1.

Block diagram of a model for transcriptional regulation. The target gene 3 is directly regulated by two genes 1 and 2. Transcriptional regulation involves three steps: translation, cis-regulation, and transcription.

In the diagram depicted in Fig. 1, we have assumed that mRNAs and proteins do not decay, and that the tasks of translation, cis-regulation, and transcription are completed instantaneously. It is a well-known fact however that mRNAs and proteins are subject to degradation and that the time required to complete transcription and translation is not negligible. Transcription is subject to a time delay for completing RNA chain elongation, whereas, translation is subject to a time delay for completing the elongation phase of protein synthesis. Moreover, and for controlling the assembly of the transcription initiation complex (i.e., the general transcription factors and RNA polymerase II) at the promoter, appreciable time is required for the transport of proteins to the nucleus, for the binding of these proteins to the appropriate DNA regulatory sequences, and for recruiting the general transcription factors at the promoter. These effects can be accounted for, by assuming that translation, cis-regulation, and transcription are subject to time delays τ_p,i, τ_c,i, and τ_r,i, respectively, for i ∈ 𝒢. In general, these delays depend on the particular genes under consideration.

To obtain a model for transcriptional regulation, we need to mathematically describe the three steps of translation, transcription, and cis-regulation. To derive a mathematical model for translation, we adopt the following notation: T, absolute temperature (in degrees Kelvin, K); R, gas constant (1.9872 cal mol⁻¹ K⁻¹); U_tr,i, activation energy of translation of the i^th mRNA (in cal/mol); U_dg,i, activation energy of degradation of the i^th regulatory protein (in cal/mol); r_i(t | U > U_tr,i), concentration, at time t, of i^th mRNA molecules in 𝒞 with energy greater than the activation energy U_tr,i; p_i(t | U > U_dg,i), concentration, at time t, of i^th regulatory protein molecules in 𝒞 with energy greater than the activation energy U_dg,i.

The activation energy depends on the specific aspects of the underlying chemical reaction. By using standard arguments from chemical kinetics (e.g., see Moore and Pearson, 1981; Chapter 5 and Espenson, 1995; Chapter 7), we take the rate of protein synthesis (per second) during translation to be proportional to the concentration of mRNAs with energy >U_tr, with proportionality constant α_tr. Similarly, we take the rate of protein degradation (per second) to be proportional to the concentration of proteins with energy >U_dg, with proportionality constant α_dg.

By focusing on the macroscopic behavior of translation during the time interval [t, t + Δt], for some Δt > 0, we can write:

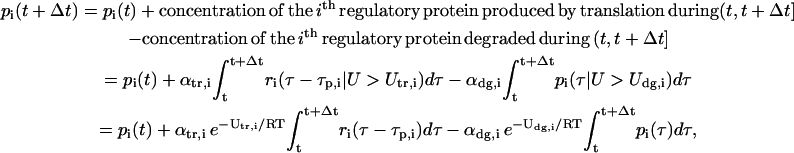(1)

for 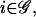where α_tr,i and α_dg,i are the proportionality constants (measured in s⁻¹) associated with the two reactions of mRNA translation and protein degradation, respectively. To obtain Eq. 1, we use a fundamental result of statistical mechanics, which states that, in a large population of identical molecules at statistical equilibrium with concentration η, the concentration η(U) of molecules with kinetic energy U is given by the Boltzmann distribution

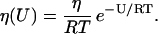This leads to

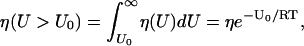(2)

where η(U > U₀) denotes the concentration of molecules in the population with kinetic energy greater than some threshold U₀. From Eq. 1, we obtain

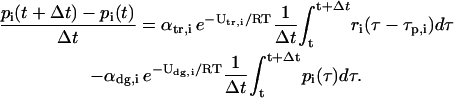(3)

By taking limits, as 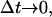on both sides of Eq. 3, and by setting

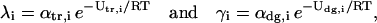(4)

we obtain the following system of rate equations:

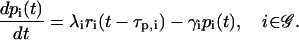(5)

These first-order ODEs imply that the rate of change in the concentration of the i^th regulatory protein at time t is proportional to the expression level r_i(t − τ_p,i) of gene i at time t − τ_p,i. Moreover, it implies that this protein degrades at a rate 0 < γ_i < ∞ (in s⁻¹), which is proportional to its concentration. In Eq. 5, 0 < λ_i < ∞ (in s⁻¹) is the rate of translation; i.e., the proteins synthesized per second from a mol of mRNA.

By following similar arguments, we can show that transcription can be modeled by the following system of rate equations:

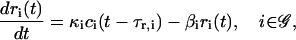(6)

where 0 ≤ c_i(t) ≤ 1 is the fraction, at time t, of DNA templates in 𝒞 that are committed to the transcription of gene i, and 0 < κ_i < ∞ is the transcription rate of gene i; i.e., the concentration of mRNAs synthesized per second when all DNA templates in 𝒞 are committed to the transcription of gene i (in M s⁻¹). We say that a DNA template is “committed” to the transcription of a gene, if it has successfully recruited the transcription initiation complex and has anchored it at the promoter of that gene. Note that a DNA template that is committed to transcription may not necessarily lead to transcription initiation. For this to happen, the energy of the committed DNA template should be greater than the activation energy of transcription initiation. The first-order ODEs in Eq. 6 imply that the rate of change in mRNA concentration produced from gene i at time t is proportional to the fraction c_i(t − τ_r,i) of DNA templates committed to the transcription of gene i at time t − τ_r,i. Moreover, they imply that these molecules degrade at a rate 0 < β_i < ∞ (in s⁻¹), which is proportional to their concentration.

In general, the cis-regulation of a target gene i may be modeled by the following equations:

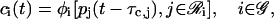(7)

where φ_i[·] is a (nonlinear) function, which is specific to the target gene under consideration, and 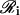is the set of all genes in 𝒢 that produce proteins, which regulate the transcription of the i^th gene. We refer to φ_i[·] as the cis-regulatory function of gene i. Moreover, we refer to 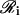as the regulatory set of gene i and to the genes in 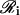as the regulating genes of gene i. We call the collection 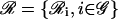of all regulatory sets a transcriptional regulatory network (tRN). In Eq. 7, we assume that transcription is controlled by the protein products, at times t − τ_c,j, 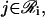obtained by translating the regulating genes of the target gene i.

We note here that several variations of the model governed by Eqs. 5–7 have been proposed in the literature (e.g., see Hargrove and Schmidt, 1989; Mjolsness et al., 1991; Mestl et al., 1995; Endy et al., 1997; Wolf and Eeckman, 1998; Chen et al., 1999; Hatzimanikatis and Lee, 1999; Akutsu et al., 2000b; Cherry and Adler, 2000; von Dassow et al., 2000; Elowitz and Leibler, 2000; Gardner et al. 2000; Hasty et al., 2000; Voit, 2000; Smolen et al., 2000; Gibson and Mjolsness, 2001; Mjolsness, 2001, Vohradský, 2001; Wahde and Hertz, 2001; de Jong, 2002; Yildirim and Mackey, 2003, and the references therein). A limitation of Eqs. 5–7 is that they only apply to a large population cells. Moreover, these equations are derived by employing a macroscopic view of the chemical reactions underlying translation, cis-regulation, and transcription. The resulting ODE-based model oversimplifies the complex structure of a cell's transcriptional activity, by ignoring several factors affecting such activity. For example, Eq. 5 ignores the effects of mRNA transport from the nucleus to the cytoplasm and mRNA localization in the cytoplasm, whereas Eq. 6 does not take into account the mechanisms of RNA processing. Eq. 7 oversimplifies transcriptional control by ignoring, for example, complex interactions, inside the cis-regulatory mechanisms, among regulatory proteins, general transcription factors, RNA polymerase II, chromatin remodeling complexes and DNA, and by ignoring the role that protein-DNA complexes play in transcriptional regulation. Finally, the model does not consider how protein folding affects transcriptional regulation and ignores several biochemical interactions among proteins and interactions between different biological and signaling pathways. Nevertheless, the ODE-based model governed by Eqs. 5–7 provides a “first-order” approximation of transcriptional activity that leads to a mathematically tractable model for transcriptional regulation.

To conclude this section, note that, by solving Eqs. 5 and 6 with respect to p_i(t) and r_i(t), we obtain

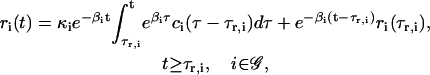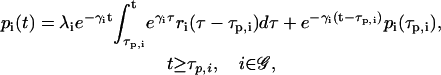which in turn result in

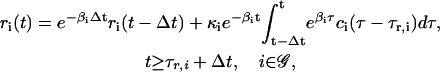(8)

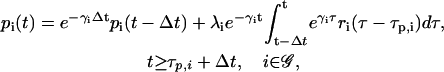(9)

for some Δt > 0. According to Eq. 8, the concentration r_i(t) of the i^th mRNA present in the cytoplasm at time t equals the concentration 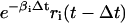of the mRNA that survives degradation during the time interval [t − Δt, t), plus the concentration 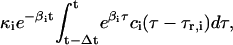of the new mRNA that is synthesized by transcription and survives degradation during the same interval. According to Eq. 9, the concentration p_i(t) of the i^th protein present in the cytoplasm at time t equals the concentration 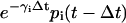of the protein that survives degradation during the time interval [t − Δt, t), plus the concentration 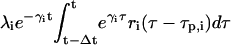of the new protein that is synthesized by translation and survives degradation during the same interval.

A DISCRETE MODEL

The previous ODE-based model provides a continuous description of transcriptional regulation. However, the processes of transcription and translation may be thought as being discrete. During transcription, the RNA polymerase II moves along the DNA in a stepwise fashion and extends the growing RNA chain by adding one nucleotide at a time (see Alberts et al., 2002, pp. 302–304). Similarly, during translation, a ribosome moves along an mRNA transcript by sequentially processing groups of three nucleotides (codons), and extends the growing polypeptide chain by adding one amino acid at a time (see Alberts et al., 2002, pp. 342–344). These observations, together with the need for solving Eqs. 5–7 using computational techniques, motivates us to derive a discrete model for transcriptional regulation.

The motion of RNA polymerase II along a DNA molecule may not be smooth (see Alberts et al., 2002, p. 313); its speed may depend on time, the particular gene transcribed, and other factors. Moreover, ribosomes may translate with different speeds at individual codons (e.g., see Sørensen and Pedersen, 1991), whereas, for each 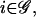the cis-regulation delay τ_c,i may fluctuate. To avoid complications, we replace the actual transcriptional machinery with one for which the speeds of transcription and translation, v_r and v_p, and the cis-regulation delays 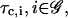are all constants, taken to be equal to their mean values. We refer to this machinery as an “average” transcriptional machinery. This implies that the discrete dynamical system to be derived in this section will model an “average” transcriptional activity. Because the transcription speed is constant, the transcription delay, τ_r,i, will be an integer multiple of the time δt that takes the RNA polymerase II to read one nucleotide. For eukaryotic cells, we may take the average transcription speed v_r ≅ 20 nucleotides/s (see Alberts et al., 2002, p. 304), in which case δt ≅ 0.05 s, whereas, we may take the average translation speed v_p ≅ 2 codons/s (see Alberts et al., 2002, p. 343). For this value of v_p, the translation delay, τ_p,i, is also an integer multiple of δt. Finally, we assume that the “average” transcriptional machinery is also characterized by cis-regulation delays τ_c,i, i ∈ 𝒢, which are integer multiples of δt as well.

For each 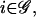we make the following two assumptions: 1) for each t = δt, 2δt, …, the fraction c_i of DNA fragments committed to the transcription of gene i remains constant in the time interval [t − δt, t); and 2) for each t = δt, 2δt, …, the mRNA concentration r_i remains constant in the time interval [t − δt, t).

In view of the small value of δt, as compared to the large timescale of transcription (recall that δt ≅ 0.05 s in eukaryotic cells, as compared to the duration of a typical transcription reaction, which ranges from minutes to hours), we may shift all transcription commitments within the interval (t − δt, t), for t = δt, 2δt, …, to time t, with negligible effects on transcription. Therefore, we may approximately assume that no new DNA templates commit to transcription within the time interval (t − δt, t), which explains assumption 1. On the other hand, and due to the fact that the transcription delay τ_r,i is an integer multiple of δt, new mRNAs are synthesized only at integer multiples of δt. This, together with the previous observation, implies that new mRNAs are synthesized only at times t = δt, 2δt, …. Moreover, experimental evidence suggests that mRNA half-lives are much larger than δt (e.g., see Wang et al., 2002, and compare the value δt ≅ 0.05 s for eukaryotic cells with the mRNA half-lives in yeast, which range from ∼3 min to >90 min). In view of these observations, and assumption 1, we may conclude that assumption 2 is a reasonable assumption as well.

We can now employ the previous two assumptions to show that, by using δt as a basic discretization step and by replacing the actual transcriptional machinery with an “average” one, Eqs. 5–7 can be transformed into a discrete dynamical system that can effectively simulate transcriptional regulation in an iterative fashion. From assumptions 1 and 2, we have that

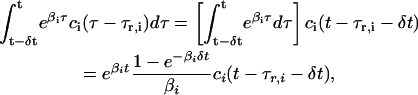and

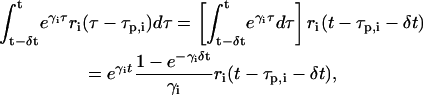for i ∈ 𝒢, which, together with Eqs. 8 and 9, with Δt = δt, result in

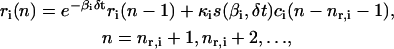(10)

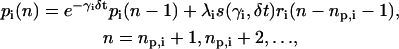(11)

where one iteration corresponds to the time step δt, n_r,i = τ_r,i/δt, n_p,i = τ_p,i/δt, and

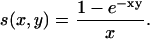(12)

Moreover, from Eq. 7, we have that

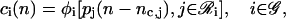(13)

where n_c,j = τ_c,j/δt.

According to Eq. 10, the concentration r_i(n) of the i^th mRNA present in the cytoplasm at step n equals the concentration 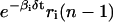of the mRNA that survives degradation from step n − 1 to step n, plus the concentration κ_is(β_i, δt)c_i(n − n_r,i − 1) of the new mRNA that is synthesized by transcription and survives degradation between these two steps. According to Eq. 11, the concentration p_i(n) of the i^th protein present in the cytoplasm at step n equals the concentration 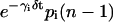of the protein that survives degradation from step n − 1 to step n plus the concentration λ_is(γ_i, δt)r_i(n − n_p,i − 1) of the new protein that is synthesized by translation and survives degradation between these two steps.

In the following, and to ease notation, we take the time delays τ_p,i, τ_c,i, and τ_r,i to be independent of i. In this case, Eqs. 10, 11, and 13 can be written in the following compact form:

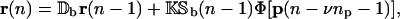(14)

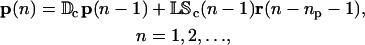(15)

where ν = (τ_r + τ_c)/τ_p. In Eqs. 14 and 15, D_b, D_c, K, and L are G × G diagonal matrices, given by

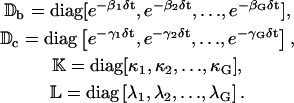Moreover, S_b(n) and S_c(n) are G × G diagonal matrices, given by

where

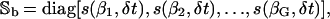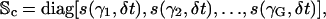and

Finally, Φ[p(n − νn_p − 1)] is an G × 1 vector-valued functional whose i^th element is 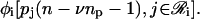We refer to Φ[·] as the cis-regulatory functional.

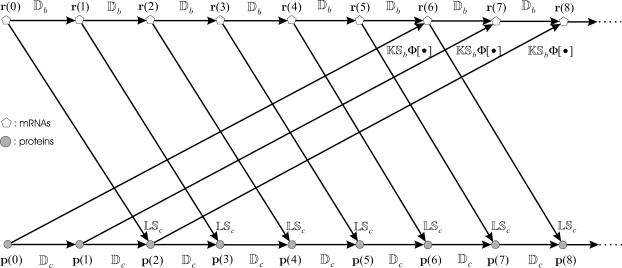
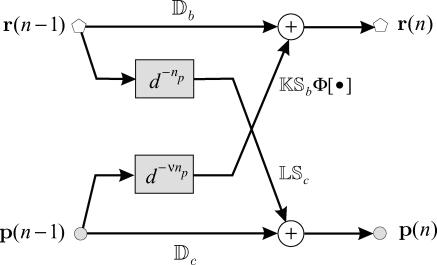
The iterations suggested by Eqs. 14 and 15 are depicted in Fig. 2, when τ_p = δt, τ_c = 3δt, and τ_r = 2δt. These iterations are initialized with an mRNA concentration vector r(0) and a protein concentration vector p(0). This implies that the fate of gene expression is determined by the initial concentrations of mRNAs and proteins. Matrices D_b and D_c model mRNA and protein degradation, respectively, whereas, matrices K and L model the rate of transcription and translation, respectively. For 0 ≤ n ≤ τ_p/δt = n_p only degradation is present. Translation of mRNAs to proteins takes place for n ≥ τ_p/δt + 1 = n_p + 1, whereas, transcription takes place for n ≥ (τ_c + τ_r)/δt + 1 = νn_p + 1. Note that the flow graph depicted in Fig. 2 has a modular structure; it consists of individual stages, with the n^th stage being the (nonlinear in general) multi-input/multi-output system depicted in Fig. 3 (for n ≥ νn_p + 1), where d denotes delay, such that d^−mx(n) = x(n − m).

FIGURE 2.

Iterative implementation of transcriptional regulation governed by Eqs. 14 and 15, when τ_p = δt, τ_c = 3δt, and τ_r = 2δt. The implementation is initialized with an mRNA concentration vector r(0) and a protein concentration vector p(0). Matrices D_b and D_c model mRNA and protein degradation, respectively, whereas, matrices K and L model the rate of transcription and translation, respectively. For 0 ≤ n ≤ τ_p/δt = 1 only degradation is present. Translation of mRNAs to proteins takes place for n ≥ τ_p/δt + 1 = n_p + 1 = 2, whereas, transcription takes place for n ≥ (τ_c + τ_r)/δt + 1 = νn_p + 1 = 6.

FIGURE 3.

The n^th stage (for n ≥ νn_p + 1) of the flow graph depicted in Fig. 2.

The model suggested by Eqs. 10–13 requires knowledge of the cis-regulatory functionals 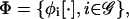the degradation parameters 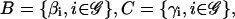the transcription and translation rates 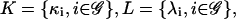and the delays 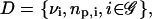where ν_i = (τ_r,i + τ_c,i)/τ_p,i. We refer to the collection 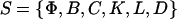as a (discrete) transcriptional regulatory system (tRS).

STEADY-STATE BEHAVIOR

An important issue associated with a tRS is whether or not the iterations suggested by Eqs. 10–13 converge to a steady state and, if they do, to characterize that state. In most cases, and in the absence of external control, for a tRS to be biologically plausible, it is required that the mRNA and protein concentration vectors r(n) and p(n) converge, as 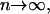to a steady-state mRNA concentration vector and a steady-state protein concentration vector 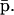In this case,

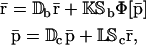(16)

from which we have that

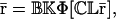(17)

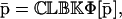(18)

where

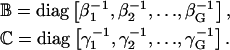This shows that is a fixed-point attractor of the functional Ψ_r[·], given by

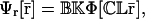(19)

whereas, 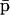is a fixed-point attractor of the functional Ψ_p[·], given by

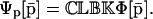(20)

We refer to Ψ_r[·] as the “genomic regulatory functional” and to Ψ_p[·] as the “proteomic regulatory functional” because the first functional can be used to determine the steady-state mRNA concentration vector, whereas, the second functional can be used to determine the steady-state protein vector.

The fixed-point attractors and 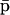may be used to characterize the cell's phenotype. This is based on the assumption that cells may be differentiated by the concentrations of regulatory proteins synthesized at steady state (or, equivalently, by the concentrations of the corresponding mRNAs), which give each cell type its unique characteristics; e.g., see Kauffman (1993) (Chapter 12) and Alberts et al. (2002) (pp. 375–376). It is believed that the transcriptional regulatory machinery of a given organism is hardwired in its DNA. This implies that regulation of transcription is controlled by the same mechanisms, irrespective of cell type. We may however view cell differentiation as being achieved by transcriptional regulation, which guides the tRS to reach steady-state mRNA and protein concentration values and 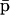that uniquely characterize the cell type. In this case, the driving force of cell differentiation is said to be “epigenetic” regulation.

An implication of Eqs. 17 and 18 is that, at steady state, the mRNA concentration vector “decouples” from the protein concentration vector 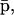in the sense that can be obtained as a solution of the system of (nonlinear in general) Eq. 17, without knowledge of 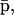whereas, can be obtained as a solution of the system of (nonlinear in general) Eq. 18, without knowledge of 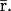It is however important to keep in mind that, despite this “decoupling,” computation of the steady-state mRNA concentration vector (and the steady-state protein concentration vector 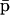) requires knowledge of the transcription parameters B, K, Φ and the translation parameters C, L, because Eq. 17 (and Eq. 18) depends on those parameters. Note also that there is a one-to-one correspondence between the fixed-point attractors of the genomic and proteomic regulatory functionals, because (recall Eq. 16)

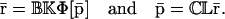(21)

The second equation above implies that, at steady state, 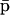may be determined from 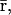provided that the underlying translation parameters C, L are known. This observation suggests that mRNA expression data, obtained by means of microarray gene expression profiling, may be used to characterize protein activity at steady state, provided that the translation parameters C, L are known, and a sufficiently good estimate of the steady state mRNA concentration vector can be inferred from such data.

Because Eqs. 10–13 have been obtained by discretizing Eqs. 5–7, it is of interest to investigate how the steady-state behavior of the discrete tRS is related to the steady-state behavior of the continuous tRS. From Eqs. 10–12, we can show that

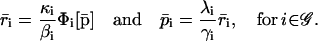(22)

On the other hand, if 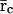and 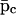are the steady states of Eqs. 5 and 6, then (by setting the derivatives in Eqs. 5 and 6 equal to zero), we obtain

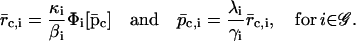(23)

Eqs. 22 and 23 verify that the discrete tRS has the same steady states as the continuous tRS, and show that the steady-state behavior of the discrete tRS is identical to that of the continuous tRS.

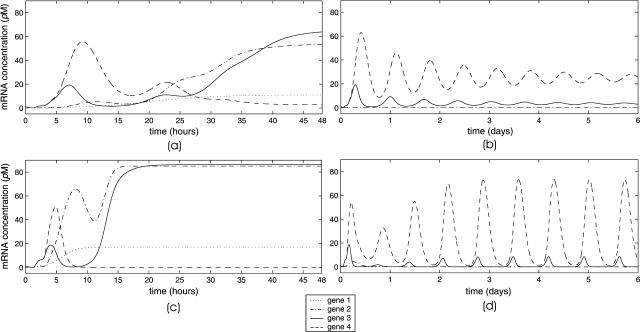
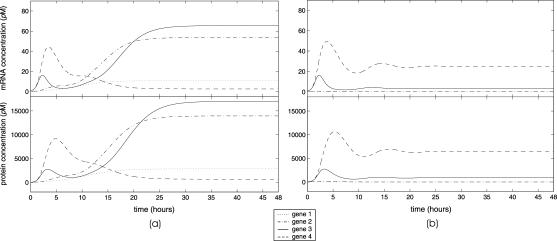
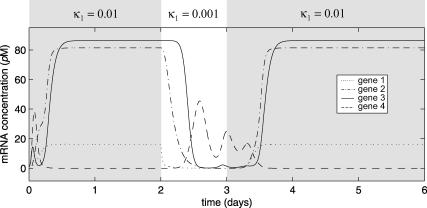
Besides fixed-point attractors, the tRS may be subject to limit-cycle attractors, which lead to oscillatory behavior. A tRS with limit-cycle attractors may be useful for modeling periodic cellular behavior, such as cell cycle control or circadian rhythms; see Kauffman (1993) (Chapter 12), and Elowitz and Leibler (2000); Smolen et al. (2000); Goldbeter et al. (2001); Hasty et al. (2001a,b); Tyson et al. (2001). In this article, we do not consider limit-cycle attractors (however, see Fig. 11 d).

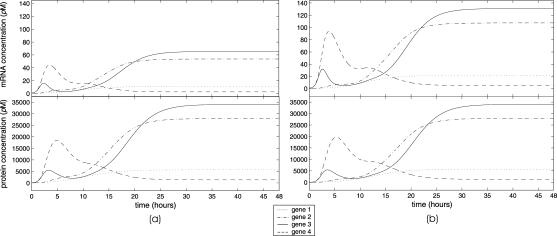
FIGURE 11.

Evolutions of mRNA concentrations of the tRS depicted in Fig. 5, when τ_r = 2000 s, τ_p = 200 s, τ_c = 2400 s, and: (a) κ₁ = 0.01 pM s⁻¹ and λ = 0.05 s⁻¹, (b) κ₁ = 0.001 pM s⁻¹ and λ = 0.05 s⁻¹, (c) κ₁ = 0.01 pM s⁻¹ and λ = 0.2 s⁻¹, (d) κ₁ = 0.001 pM s⁻¹ and λ = 0.2 s⁻¹.

A MODEL FOR cis-REGULATION

The cis-regulatory functions φ_i[·] in Eq. 7 are at the core of a tRS, because these functions specify how proteins regulate transcription. In this section, we derive a form for these functions by using simple arguments from chemical kinetics (see also Hill, 1985; Wang et al., 1999). Keep in mind however that the resulting model oversimplifies cis-regulation, because cis-regulation is controlled by rather complicated biochemical interactions (e.g., see Holstege et al., 1998).

To model cis-regulation, we consider again a large population 𝒞 of cells, and assume at the moment that the promoter of a given target gene is controlled by two regulatory proteins P₁ and P₂, with concentrations p₁ and p₂, respectively. Moreover, we assume that protein P₁ is free to bind at anyone of S₁ distinct sites of the promoter's regulatory region, whereas, protein P₂ is free to bind at anyone of S₂ distinct sites, with the binding sites of P₁ being different than that of P₂. Let D[s₁, s₂] be a DNA template with s₁ out of the S₁ sites being occupied by P₁ and s₂ out of the S₂ sites being occupied by P₂. The binding of proteins P₁ and P₂ at the promoter's regulatory region can be described by means of the following reversible reactions:

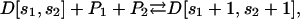(24)

for 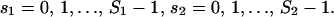If we assume that P₁ and P₂ do not interact with each other or affect each other's binding activity, then Eq. 24 can be sequentially written as

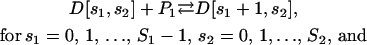(25)

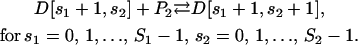(26)

In the following, d[s₁, s₂] denotes the concentration of DNA templates in 𝒞 with s₁ out of the S₁ sites being occupied by P₁ and s₂ out of the S₂ sites being occupied by P₂. Moreover, U_bd,i denotes the activation energy (in cal/mol) for a regulatory protein P_i to bind on a DNA template, whereas, U_ds,i denotes the activation energy (in cal/mol) for P_i to dissociate itself from the template.

At equilibrium, the concentration of free regulatory proteins P₁ that bind (per second) on DNA templates D[s₁, s₂] to produce DNA templates D[s₁ + 1, s₂] by means of the forward reaction in Eq. 25 must equal the concentration of regulatory proteins P₁ freed (per second) by the backward reaction. By using molecular collision theory (e.g., see Moore and Pearson, 1981, Chapter 4), it can be shown that the first concentration is proportional to the concentration of those proteins P₁ with kinetic energy >U_bd,1 times the concentration of sites available for P₁ to bind to, with proportionality constant α_bd,1 (measured in M⁻¹s⁻¹). Because each DNA template D[s₁, s₂] has S₁ − s₁ sites available for P₁ to bind to, the concentration of available binding sites for P₁ is (S₁ − s₁)d[s₁, s₂]. In this case, the concentration of free regulatory proteins P₁ that bind (per second) on DNA templates D[s₁, s₂] to produce DNA templates D[s₁ + 1, s₂] by means of the forward reaction in Eq. 25, is given by

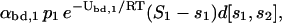where we have used Eq. 2.

On the other hand, the concentration of regulatory proteins P₁ freed (per second) by the backward reaction in Eq. 25 is proportional to the concentration of bound P₁ molecules on the DNA template D[s₁ + 1, s₂] with kinetic energy >U_ds,1, with proportionality constant α_ds,1 (measured in s⁻¹). Because each DNA template D[s₁ + 1, s₂] contains s₁ + 1 bound P₁ molecules, this concentration is given by

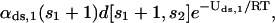where we have used again Eq. 2. Therefore, at equilibrium, we have that

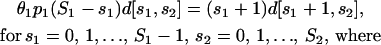(27)

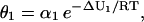(28)

with α₁ = α_bd,1/α_ds,1 and ΔU₁ = U_bd,1 − U_ds,1 being the binding free energy. The parameter θ₁ (measured in M⁻¹) is characteristic to the binding sites and is referred to as “affinity constant.” At equilibrium, and when U_bd,1 = U_ds,1, the values of p₁ (S₁ − s₁) d[s₁, s₂] and (s₁ + 1) d[s₁ + 1, s₂] must be equal; therefore, α₁ = 1 M⁻¹. In addition, because U_bd,1 ≤ U_ds,1, we have that 1 ≤ θ₁ ≤ ∞.

A similar argument applies to Eq. 26 and leads to

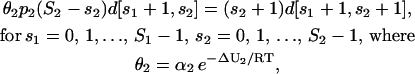(29)

with ΔU₂ = U_bd,2 − U_ds,2 and α₂ = 1 M⁻¹.

From Eqs. 27 and 29, it can be shown that

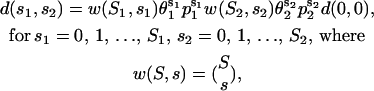(30)

are the so-called Binomial coefficients. If we ignore additional processes underlying cis-regulation (see Wang et al., 1999 for such processes) and assume that, for transcription to be initiated, it is necessary (but not sufficient) that a DNA template is bound by at least one P₁ protein or one P₂ protein, then the fraction c of DNA templates in 𝒞 committed to the transcription of the target gene will be given by

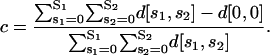(31)

The previous assumption agrees with the fact that transcription in eukaryotic cells can be initiated only in the presence of activator proteins (e.g., see Alberts et al., 2002, pp. 312–313). Eq. 31, together with Eq. 30, leads to

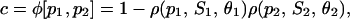where

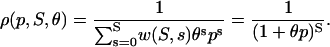(32)

Our discussion so far has been based on the assumption that regulatory proteins activate transcription; i.e., binding of regulatory proteins on a DNA template recruits the transcription initiation complex and initiates transcription. However, cis-regulation may also be controlled by regulatory proteins that repress transcription. Although eukaryotic genes employ several mechanisms for repressing transcription, we only consider here the mechanism by which a repressor protein binds on the DNA template, and either blocks the recruitment of the transcription initiation complex to the promoter, or prevents the release of the RNA polymerase II (see Alberts et al., 2002, pp. 405–406). This implies that, once a repressor protein binds on a DNA template, transcription cannot be initiated by that template, and leads to a simple model for the repression of transcription. Keep in mind however that, if necessary, it may be possible to derive models for other repression mechanisms as well.

If we assume that the previous protein P₂ is a repressor, then the repression mechanism under consideration implies that transcription may be initiated only if a DNA template is free of protein P₂ and there is at least one activator protein P₁ bound to it. Then, the fraction c of DNA templates committed to the transcription of the target gene will be given by

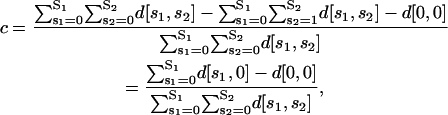which leads to

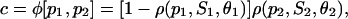as opposed to Eq. 31. In general, if the promoter of a given target gene is controlled by activators P₁, P₂,…, P_k and repressors P_k+1, P_k+2,…, P_J, it can be shown that

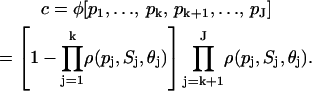(33)

It is believed that the organization of cis-regulation is modular; see Davidson (2001) (Chapter 1), Alberts et al. (2002) (pp. 408–413), Arnone and Davidson (1997), and Bolouri and Davidson (2002). This means that the regulatory region of a target gene may be partitioned into several entities (modules), with each entity being associated with different sets of regulatory proteins, which may assert a different type of control on transcription. This modular structure allows a gene to express itself under different conditions and different contexts.

We now derive a model for modular cis-regulation. For the purpose of our discussion below, we define a module as being that section of the regulatory region of a target gene, together with the associated regulatory proteins, which, at a given time, controls the promoter of that gene. For simplicity, we assume at the moment that the promoter of a given target gene is controlled by either one of two distinct modules, mod 1 and mod 2. We assume that a regulatory protein P₁ may bind at anyone of S₁ distinct sites of mod 1, whereas, a regulatory protein P₂ may bind at anyone of S₂ distinct sites of mod 2. For i = 1, 2, let d_i[s_i] be the concentration of all DNA templates in 𝒞, with s_i out of the S_i sites of mod i being occupied by protein P_i. If we assume that transcription is initiated by mod i, and if c_i is the fraction of the DNA templates committed to the transcription of the target gene due to the binding of P_i on mod i, then

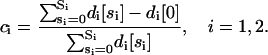(34)

If we now assume that, at a given time, transcription in the cell population 𝒞 may be initiated by either one of the two modules being occupied by at least one regulatory protein, then the fraction c of the DNA templates committed to the transcription of the target gene will be given by

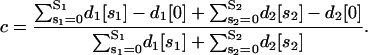(35)

From Eqs. 34 and 35, we obtain

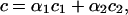where

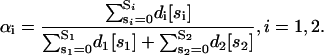Therefore, we can model modular cis-regulation as a weighted summation of separately asserted cis-regulations by each module. Note that α₁ + α₂ = 1.

The previous discussion can be generalized to include several modules and regulatory proteins. If we assume that the promoter of a target gene i is controlled by M_i modules, we can model transcriptional regulation by means of the following equation (recall Eq. 7):

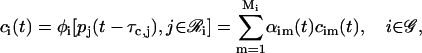(36)

where

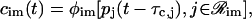(37)

for m = 1, 2, …, M_i, i ∈ 𝒢, and α_im(t), m = 1, 2, …, M_i, are nonnegative weights such that

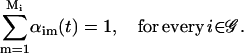In Eq. 36, 0 ≤ α_im(t) ≤ 1 quantifies the contribution of the m^th module to the transcriptional regulation of the i^th gene at time t, whereas, in Eq. 37, ℛ_im is the set of all genes in 𝒢 that produce the regulatory proteins associated with this module. Note that

According to Eq. 33, a general form for the cis-regulatory function φ_im[·] is given by

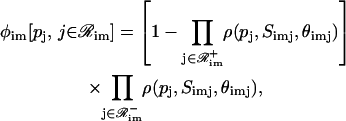(38)

for some 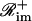and 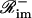such that ℛ_im⁺∩ℛ_im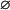⁻= and 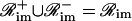. In Eq. 38, S_imj and θ_imj are the number of binding sites and the affinity constants, respectively, associated with the j^th protein that controls the m^th module of the i^th promoter. Note that, when 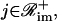the j^th protein acts as an activator, whereas, when 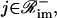the j^th protein acts as a repressor. It is assumed here that, if ℛ_im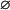⁺=, then 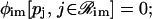i.e., transcription is not initiated if the associated regulatory region does not contain binding sites for activator proteins, in accordance with the fact that transcription in eukaryotic cells cannot be initiated in the absence of activator proteins.

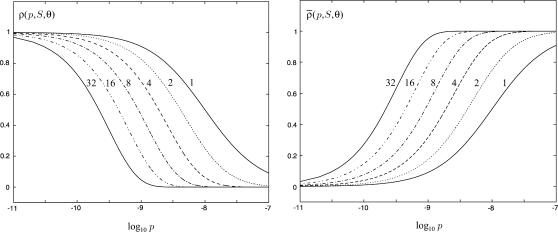
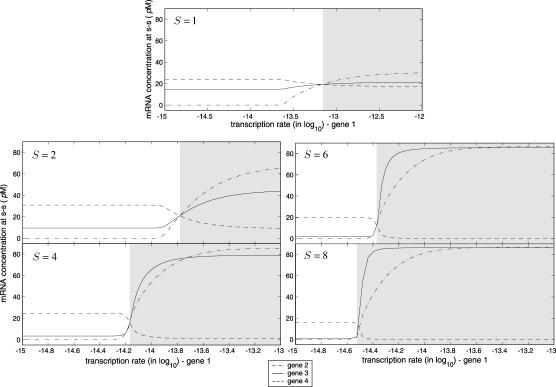
The choice in Eq. 38 is a simplified format for the cis-regulatory function of eukaryotic genes and agrees with the belief that activators and repressors work synergistically so that their joint effect is multiplicative; e.g., see Alberts et al. (2002) (p. 405); Herschlag and Johnson (1993); Savageau (2001). The basic ingredient of this model is the function ρ(p, S, θ), p ≥ 0, given by Eq. 32. For given values of S and θ, the functions ρ(p, S, θ) and 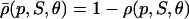model the fraction of DNA templates in 𝒞 committed to the transcription of a target gene, whose transcription is respectively controlled by a repressor or an activator protein that binds at S distinct sites of the control region with affinity constant θ. Fig. 4 depicts ρ(p, S, θ) and 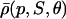as a function of log₁₀p, for several values of S and for θ = 10⁸ M⁻¹. As the protein concentration p increases, ρ monotonically decreases, whereas, 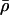monotonically increases. This implies that the rate of transcription monotonically decreases as a function of repressor concentration, whereas, it monotonically increases as a function of activator concentration. For a given protein concentration, ρ decreases as a function of S (or remains constant at saturating points), whereas, 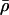increases as a function of S (or remains constant at saturating points). This implies that the number of regulatory binding sites influence transcription, with more sites resulting in lower transcription rates for the case of repression, and higher transcription rates for the case of activation. Note also that the higher the number of regulatory binding sites, the lower the protein concentration required to produce appreciable repression or activation. Finally, if we interchange p with θ, Fig. 4 suggests that stronger binding affinity produces lower transcription rates for a repressor and higher transcription rates for an activator. These observations have been shown to be consistent with experimental biological evidence (e.g., see Wang et al., 1999 and the references therein), and support the use of Eq. 38 as a plausible choice for cis-regulation. Finally, note that 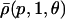is the well-known Michaelis-Menten function of enzyme kinetics.

FIGURE 4.

The functions ρ(p, S, θ) and 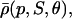plotted in terms of log₁₀ p, for S = 1, 2, 4, 8, 16, 32 and θ = 10⁸ M⁻¹.

Although we believe that the general trends we have described in this section are true, they may oversimplify cis-regulation. An explanatory model for cis-regulation may need to be placed in a combinatorial setting. For example, two proteins with weak individual DNA bindings at contiguous sites, for example, may have a strong inter-protein binding tendency, and thus remain bound on the DNA as a complex, achieving locational accuracy by essentially achieving more binding interactions with the DNA as a complex than as singletons. This combinatorial structure substantially complicates mathematical modeling of cis-regulation. We have therefore chosen in this article not to consider the role that protein-DNA complexes play in transcriptional regulation.

REMARKS

Homeostatic regulation

The form of the genomic regulatory functional Ψ_r[·] in Eq. 19 suggests a specific response of transcriptional regulation to changes in the cellular environment. To retain the same level of steady-state mRNA concentration, the tRS may compensate for changes in the underlying parameters by keeping Ψ_r fixed. In this case, the tRS may compensate for changes in the rates of transcription by appropriate changes in mRNA degradation (and vice versa), so that the product BK remains constant. Moreover, it may compensate for changes in the rates of translation by appropriate changes in protein degradation (and vice versa), so that the product CL remains constant. On the other hand, to retain the same level of steady-state protein concentration, the tRS may compensate for changes in the underlying parameters by keeping Ψ_p fixed. The form of the proteomic regulatory functional Ψ_p[·] in Eq. 20 suggests that, for the tRS to retain the same level of steady-state protein concentration, it may adjust the rates of transcription, the rates of translation, or mRNA and protein degradations so that the product CLBK remains constant. Equations 19 and 20 also suggest that changes in the rates of transcription and translation (or in mRNA and protein degradation) that leave the product LK (or the product CB) invariant, have no effect on the steady-state protein concentration (because such changes do not affect Ψ_p), but may affect the steady-state mRNA concentration (because such changes may affect Ψ_r). These remarks predict that mRNA and protein degradation, together with the rates of mRNA and protein synthesis, may play an important role in a transcriptional regulation that maintains the levels of mRNA and protein concentrations at or near fixed values (known as homeostatic regulation; see also Hargrove and Schmidt, 1989; Carrier and Keasling, 1997; Grunberg-Manago, 1999; Wang et al., 2002).

Epigenetic regulation

The function φ_im[·] in Eq. 38 results in a cis-regulatory functional Φ[·] that is scale-invariant, in the sense that its value does not change if p_j is multiplied by a constant a and the associated affinity constant θ_imj is divided by a. This is a direct consequence of the fact that (see Eq. 32) ρ(ap, S, θ/a) = ρ(p, S, θ), for a constant a.

This scaling property has some specific implications on regulation. It can be seen from Eqs. 17 and 18 that, if a tRS with parameters {κ_i}, {λ_i}, and {θ_imj} converges to 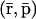at steady state, then the same tRS with parameters {κ_i}, {a_iλ_i}, and {θ_imj/a_i} may converge to 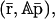where A = diag[a₁, a₂, …, a_G]. This implies that an increase (decrease) in the rates of translation, accompanied by a proportional decrease (increase) in the affinity constants, does not change the steady-state mRNA concentration but proportionally increases (decreases) the steady-state protein concentration. It can also be seen that the tRS with parameters {a_iκ_i}, {λ_i}, and {θ_imj/a_i} may converge to 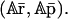This implies that an increase (decrease) in the rates of transcription, accompanied by a proportional decrease (increase) in the affinity constants, proportionally increases (decreases) both the steady-state mRNA and protein concentrations. These remarks predict that the rates of transcription and translation, together with the affinity constants, may play an important role in a type of transcriptional regulation that changes the state of the tRS from one level of steady-state mRNA and protein concentrations to another (known as epigenetic regulation; see also Hargrove and Schmidt, 1989).

Parameters

To employ a tRS as an accurate predictor of transcriptional regulation, we need to specify the model parameters. Some parameters may be determined directly from available a priori biological knowledge. For example, if the sizes of the genes composing a tRS and the sizes of the associated mRNA products are known, then the discretization step δt and the time delays τ_r,i and τ_p,i may be estimated. As we mentioned before, during transcription, the RNA polymerase II may be thought of moving stepwise along the DNA, so that the growing RNA chain is extended one nucleotide at a time. Let v_r be the average transcription speed of the RNA polymerase, measured in transcribed nucleotides per second (recall that, for eukaryotic cells, v_r ≅ 20 nucleotides/s), and let the size of the regulatory gene i of a given genome be G_i nucleotides. Then,

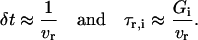On the other hand, during translation, ribosomes may be thought of adding amino acids to a polypeptide chain in a stepwise fashion, with an average speed v_p, measured in translated codons per second (recall that, for eukaryotic cells, v_p ≅ 2 codons/s). If the size of the mRNA sequence required to encode the i^th protein is R_i nucleotides, then

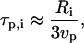because each amino acid is produced from a codon that contains three nucleotides.

Most parameters of a tRS, like the degradation parameters β, γ, the rates of transcription and translation κ, λ, and, most importantly, the cis-regulatory functional Φ[·], are not known a priori. These parameters need to be estimated by means of carefully designed in vivo or in vitro experiments and computational analysis of genomic data (e.g., see Hammond, 1993; Iyer and Struhl, 1996; Arkin et al., 1997, 1998; Endy et al., 1997; Liang et al., 1998; Lorsch and Herschlag, 1999; Tavazoie et al., 1999; Akutsu et al., 2000a,b; Gardner et al., 2000; Turner and Varshavsky, 2000; Voit 2000; Wahde and Hertz, 2001; Caselle et al., 2002; Lee et al., 2002; Ronen et al., 2002; Wang et al. 2002; Yeung et al. 2002; Yildirim and Mackey, 2003, for emerging estimation techniques). This problem is key to one of the most exciting areas of modern biology, which is attracting collaborative efforts between biologists, statisticians, electrical engineers, and computer scientists, and promises to revolutionize biological research (e.g., see Hartwell et al., 1999; VanBogelen et al., 1999; D'haeseleer et al., 2000; Smolen et al., 2000; Endy and Brent, 2001; Hasty et al., 2001b; Somogyi et al., 2001; de Jong, 2002; Michelson, 2002, and the references therein). In the absence of quantitative knowledge for model parameters, the tRS governed by Eqs. 10–13 can be used as a qualitative tool that may provide valuable insights on the behavior and properties of transcriptional regulation (e.g., by means of steady-state analysis, perturbation analysis, computational knock-out studies, and hypothesis testing, as well as by studying the effects that parameters have on the system's dynamic behavior and steady state). Some insights, obtained by means of the tRS proposed in this article, are discussed in the next section.

Implementation

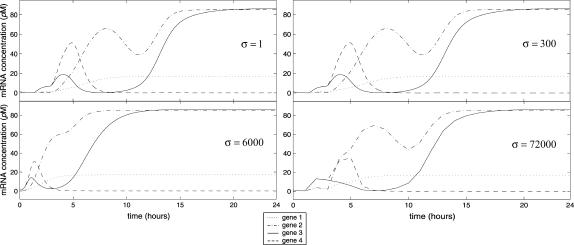
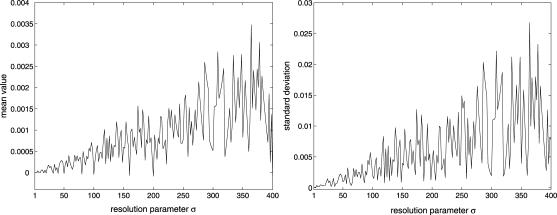
The discrete dynamical system governed by Eqs. 10–13 has been obtained by setting Δt = δt in Eqs. 8 and 9, and by considering assumptions 1 and 2. In view of the fact that the timescales of transcription, translation, and mRNA and protein degradation may be large, assumptions 1 and 2 may be still satisfied if we replace δt with a larger time step Δt = σδt, for some σ > 1, so that all time delays are integer multiples of Δt. In this case, the discrete model will be still governed by Eqs. 10–13, but with δt being replaced by Δt = σδt. The iterations required to simulate transcriptional regulation within a given time interval when Δt = σδt will be less than the iterations required when Δt = δt, reduced by a factor of σ. Parameter σ controls the “resolution” of the discrete model under consideration, and provides a trade-off between simulation accuracy and computational complexity. Clearly, smaller values of σ produce better accuracy but poor computational efficiency, whereas, larger values of σ may reduce accuracy but improve computational efficiency. Note that the steady-state behavior of the model does not depend on σ. Therefore, if the discrete dynamical system converges, it will converge to the same steady-state mRNA and protein concentration vectors, regardless of the particular value of σ.

The Hill function

Instead of ρ(p, S, θ) and 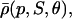repression and activation are frequently modeled by means of functions

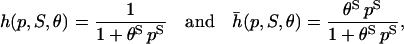(39)

respectively, where 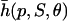is known as the Hill function (e.g., see Cherry and Adler, 2000; Elowitz and Leibler, 2000; Gardner et al., 2000; von Dassow et al., 2000; Ronen et al., 2002; Yildirim and Mackey, 2003). Note that h(p, 1, θ) = ρ(p, 1, θ) and 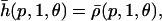but these functions are different for S > 1. It can be shown (e.g., see Hill, 1985, pp. 64–66) that the functions in Eq. 39 are only appropriate in the limiting case when the only possible binding configurations at a gene's control region are either all sites to be empty or all to be occupied (a condition known as extreme cooperativity). In view of the fact that cis-regulation may not be subject to extreme cooperativity, the use of Eq. 39 for modeling cis-regulation may be limited.

A note of caution

We want to point out here that there have been efforts to build tRSs by means of a functional Ψ[·] that relates the mRNA concentration vector r(n) at step n to the mRNA concentration vector r(n − 1) at step n − 1, by means of the following iterative equation (e.g., see Kauffman, 1993; Weaver et al., 1999; Wahde and Hertz, 2001; Baldi and Hatfield, 2002; de Jong, 2002; Shmulevich et al., 2002; Liebermeister, 2002):

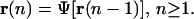(40)

If we take Ψ[·] to be the genomic regulatory functional Ψ_r[·] in Eq. 19, then the tRS governed by Eq. 40 will enjoy the same mRNA steady-state behavior (in terms of fixed-point attractors) as the tRS governed by Eqs. 14 and 15. In general however the transient behavior of these two systems will be different. As a matter of fact, the iterations suggested by Eqs. 14 and 15 imply that the value of the mRNA concentration vector r(n) cannot be inferred from knowing only its value at step n − 1. This can be seen by considering the case when n_p = ν = 0 (no time delays). This implies that

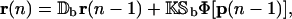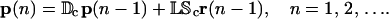From these equations, we have that

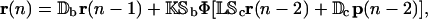which shows that r(n) depends on r(n − 1) and r(n − 2), as well as on p(n − 2). Therefore, transient transcriptional behavior is governed by a tRS whose state at step n requires mRNA concentration at steps n − 1 and n − 2 as well as protein concentration at step n − 2 (see also the related discussion in Hargrove and Schmidt, 1989; Chen et al., 1999; Hatzimanikatis and Lee, 1999). This is different from what Eq. 40 suggests. We therefore conclude that the regulatory system governed by Eq. 40 may only be appropriate for studying steady-state behavior (in terms of fixed-point attractors) and should not be used to study transient transcriptional behavior.

Boolean networks

Boolean networks are attractive models for transcriptional regulation for two main reasons: they are much simpler than the model discussed in this article, and seem to be compatible with the limited nature of gene expression data obtained by current microarray technologies. A Boolean network is based on the premise that the status of a target gene can be represented by a binary variable that takes value 1 if the target gene is active (ON) or 0 if the target gene is inactive (OFF), and that this provides enough information for the status of transcriptional regulation. A Boolean network model relates a binary mRNA concentration vector r_b(n) at step n to a binary mRNA concentration vector r_b(n − 1) at step n − 1, by means of the following iteration

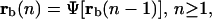for some functional Ψ[·]. In view of our previous discussion, this type of Boolean network may be useful for modeling transcriptional regulation at steady state.

To derive a Boolean network model that qualitatively reproduces the steady-state behavior of the discrete dynamical system discussed in this article (and, therefore, the behavior of the corresponding ODE-based model), we need to find a threshold operator H[·] and a functional Ψ[·] so that a binary mRNA concentration vector 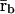is a fixed-point attractor of Ψ[·] if and only if 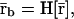for a fixed-point attractor of the genomic regulatory functional Ψ_r[·]. We assume that the threshold operator H[·] is such that H[r] = r_b, where, for i ∈ 𝒢, r_b,i = ∞, if r_i is larger than a given threshold value h_i (in which case, gene i is thought to be ON), and r_b,i = 0, if r_i is smaller than the threshold value h_i (in which case, gene i is thought to be OFF), and take Ψ[·] = HΨ_r[·]. Clearly, H[·] should be chosen such that:

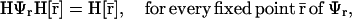(41)

in which case, every fixed-point attractor of Ψ_r[·] will lead to a fixed-point attractor 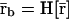of Ψ[·]. However, given the genomic regulatory functional Ψ_r[·], we may not be able to find the threshold values 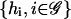so that Eq. 41 is satisfied. Moreover, it may not be true that every fixed-point attractor of Ψ[·] will correspond to a fixed-point attractor of Ψ_r[·]. Finally, limit-cycle attractors of the Boolean network may not correspond to limit-cycle attractors of the discrete tRS discussed in this article, and vice versa (see also the discussion in Glass and Kauffman, 1973; Bagley and Glass, 1996). These problems should be seriously considered when a Boolean network is used in place of a discrete tRS (for what might happen if we carelessly do so, see Hatzimanikatis and Lee, 1999).

AN EXAMPLE

We now present an example of a tRS that consists of four genes, and use this example to illustrate several properties of the proposed model. A graphical representation of the system is depicted in Fig. 5, where ⊸ denotes an activator and ⊣ denotes a repressor. We assume that the tRS regulates a hypothetical pathway, which metabolizes an input substrate to an output product. This is done by means of enzymes whose transcriptional control is regulated by the protein produced from gene 3. Moreover, we assume that the effect of higher input substrate concentration is to increase the transcription rate κ₁, whereas, the effect of lower substrate concentration is to reduce κ₁. Unless otherwise specified, the parameters associated with this example are taken to be gene independent. These parameters are summarized in Table 1.

TABLE 1.

Parameter values used in simulations

		Figure
Parameter	Value	6	7	8	9	10	11	12
Initial mRNA concentration	ri(0) = 1.25 pM, i = 1, 2, 3, 4	•	•	•	•	•	•	•
Initial protein concentration	pi(0) = 2.08 pM, i = 1, 2, 3, 4	•	•	•	•	•	•	•
Affinity constant	θ = 108 M−1	•		•	•	(b)	•	•
	θ = 5 × 107 M−1		•
	106 M−1 ≤ θ ≤ 1010 M−1					(a)
Number of binding sites	S = 1			•
	S = 2			•
	S = 4	•	•	•		•	•	•
	S = 6			•
	S = 8			•	•
mRNA half-life	ρ = 1200 s	•	•	•	•	•	•	•
Protein half-life	π = 3600 s	•	•	•	•	•	•	•
Transcription rate: gene 1	κ1 = 0.02 pM s−1		(b)
	κ1 = 0.01 pM s−1	(a)	(a)		•	•	(a,c)	•
	κ1 = 0.001 pM s−1	(b)			•		(b,d)
	0.001 pM s−1 ≤ κ1 ≤ 1 pM s−1			•
Transcription rate: genes 2–4	κ2 = κ3 = κ4 = 0.10 pM s−1		(b)
	κ2 = κ3 = κ4 = 0.05 pM s−1	•	(a)	•	•	•	•	•
Translation rate	λ = 0.05 s−1	•	(b)	•	•	•	(a,b)
	λ = 0.10 s−1		(a)
	λ = 0.20 s−1						(c,d)	•
Time delays	τr = τc = τp = 0 s	•	•	•	•	•
	τr = 2000 s, τc = 200 s, τp = 2400 s						•	•

We assume that each cis-regulator is controlled by one module with four binding sites, and set S = 4, θ = 10⁸ M⁻¹, κ₂ = κ₃ = κ₄ = 0.05 pM s⁻¹, and λ = 0.05 s⁻¹. The value of the affinity constant θ corresponds to a binding free energy of ΔU = −11.35 kcal/mol at temperature T = 310.15 K (or 37°C). The values of the transcription rates κ₂, κ₃, and κ₄ correspond to a transcriptional machinery that, on the average, produces one mRNA molecule every 8 s. This value turns out to be typical for yeast cells (Iyer and Struhl, 1996). We also assume that, on the average, the volume of each cell in 𝒞 equals to 4 pL (Alberts et al., 2002; Table 2–4). The translation rate λ is taken to be 10-fold larger than the rate of 0.3/min for translation initiation observed in vitro using a semipurified rabbit reticulocyte system (Lorsch and Herschlag, 1999).

The degradation parameters β and γ are specified by means of the mRNA and protein half-life parameters ρ and π, respectively, which satisfy

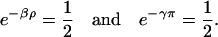In this case,

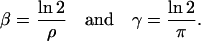We set ρ = 1200 s (20 min) and π = 3600 s (1 h). For clarity of presentation, we set all time delays equal to zero, in which case n_p = ν = 0. Nonzero time delays complicate the evolutions of mRNA and protein concentrations and make simple descriptions of system behavior rather difficult. Simulation results that include “realistic” nonzero time delays are provided at the end of this section (see Figs. 11 and 12). Due to zero delays, mRNA and protein concentrations reach steady-state values faster than it is biologically expected. The simulations are initialized with mRNA and protein concentrations given by r_i(0) = 1.25 pM and p_i(0) = 2.08 pM, for i = 1, 2, 3, 4. To obtain these values, we assume that, initially, each gene contributes, on the average, three mRNA and five protein molecules to a cell in 𝒞.

FIGURE 12.

Evolutions of mRNA concentrations of the tRS depicted in Fig. 5, when τ_r = 2000 s, τ_p = 200 s, τ_c = 2400 s, κ₁ = 0.01 pM s⁻¹, λ = 0.2 s⁻¹, and for four values of σ.

Fig. 6 a depicts typical evolutions of mRNA and protein concentrations. We assume that the transcription rate of gene 1 is given by κ₁ = 0.01 pM s⁻¹. The protein produced by gene 1 enhances transcription of gene 2, which produces enough protein to repress the transcription of gene 4. This results in protein 4 eventually reaching a state of low concentration, which releases the repression of gene 3. Gene 3 is now free to autoregulate, as well as to actively regulate gene 2. The mRNA and protein concentrations of these genes eventually reach appreciable steady-state values. The overall tRS converges to a “high” steady-state 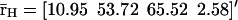and 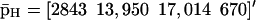(in pM). Computer simulations indicate that this state is stable, in the sense that, eventually, the tRS drives any perturbation to steady-state concentrations back to their nominal values.

FIGURE 6.

Evolutions of mRNA and protein concentrations of the tRS depicted in Fig. 5. The transcription rate for gene 1 is: (a) κ₁ = 0.01 pM s⁻¹, and (b) κ₁ = 0.001 pM s⁻¹.

On the other hand, a 10-fold reduction in the transcription rate of gene 1 results in the evolution depicted in Fig. 6 b. In this case, gene 1 cannot sustain its own transcription by autoregulation and eventually reaches a state of zero mRNA and protein concentrations. In turn, the concentration of protein 3 cannot sufficiently increase the expression level of gene 2, to produce enough proteins to repress gene 4, which also reaches a state of zero mRNA and protein concentrations. Because gene 3 is being repressed by gene 4, it gradually produces low mRNA and protein concentrations. The overall tRS converges to a “low” steady-state 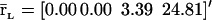and 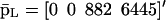(in pM). Computer simulations indicate that this state is stable as well.

Fig. 7 a depicts the evolutions of mRNA and protein concentrations when λ = 0.10 s⁻¹ and θ = 5 × 10⁷ M⁻¹. This amounts to a twofold increase in the rate of translation and a twofold decrease in the affinity constant. In this case, the steady state mRNA and protein concentration vectors are given by 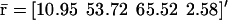and 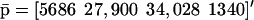(in pM), respectively. As we have discussed earlier, this change does not affect the steady-state mRNA concentration values, but produces steady-state protein concentration values that are two times larger than the ones depicted in Fig. 6 a. On the other hand, Fig. 7 b depicts the evolutions of mRNA and protein concentrations when κ₁ = 0.02 pM s⁻¹, κ₂ = κ₃ = κ₄ = 0.10 pM s⁻¹, and θ = 5 × 10⁷ M⁻¹. This amounts to a twofold increase in the rate of transcription and a twofold decrease in the affinity constant. In this case, the steady-state mRNA and protein concentration vectors are given by 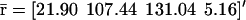and 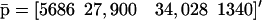(in pM), respectively. This change produces steady-state mRNA and protein concentration values that are two times larger than the ones depicted in Fig. 6 a.

FIGURE 7.

Evolutions of mRNA and protein concentrations of the tRS depicted in Fig. 5 for the case of: (a) a twofold increase in the rate of translation and a twofold decrease in the affinity constant, and (b) a twofold increase in the rate of transcription and a twofold decrease in the affinity constant.

The results depicted in Fig. 7 (and, more generally, our discussion about the scaling properties of a tRS) indicate that quantitative steady-state mRNA data alone, like data obtained by DNA chip technologies, may not be sufficient for predicting steady-state protein concentrations (see also Hatzimanikatis and Lee, 1999). It is suggested by Figs. 6 a and 7 a that the same steady-state mRNA concentrations may be associated with substantially different steady-state protein concentrations. Moreover, it is suggested by Fig. 7 that different steady-state mRNA concentrations may be associated with the same steady-state protein concentrations. These observations agree with biological evidence (e.g., see Gygi et al., 1999), and suggest that additional information is needed to predict steady-state protein concentrations from steady-state mRNA concentrations. As a matter of fact, Eq. 21 suggests a precise solution to this problem: to obtain 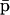from we need to know the value of the product CL (see Hargrove and Schmidt, 1989, for a similar observation).

Due to the fact that the protein concentration p_i(n) at step n is calculated from the protein concentration 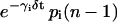at step n − 1 by adding the amount λ_is(γ_i, δt)r_i(ℏ − n_p,i − 1), which is a linear function of the mRNA concentration r_i(n − n_p,i − 1) at step n − n_p,i − 1 (recall Eq. 11), the protein evolutions depicted in Figs. 6 and 7 are very similar to the corresponding mRNA evolutions. For this reason, and in the rest of the article, we only depict mRNA evolutions.

Fig. 8 depicts steady-state (after 48 h) mRNA concentrations for genes 2, 3, and 4, as a function of the transcription rate κ₁ of gene 1, and for S = 1, 2, 4, 6, 8. As expected, for small values of κ₁ (i.e., for low input substrate concentrations), the tRS reaches a “low” steady state (i.e., low mRNA and protein concentrations for gene 3), whereas, for large values of κ₁, the tRS reaches a “high” steady state (i.e., high mRNA and protein concentrations for gene 3). The transition from the “low” to the “high” steady state is sharper for larger values of S (i.e., when more binding sites are available in the regulatory region). Moreover, larger values of S result in smaller “low” steady-state mRNA and protein concentrations for gene 3 and larger “high” steady-state concentrations. When S = 1 (i.e., when the Michaelis-Menten function is used to model cis-regulation), the transition between the “low” and “high” steady-state concentrations is slow. Moreover, the difference between the “low” and “high” mRNA and protein concentrations for gene 3 is very small. This indicates that the Michaelis-Menten function may not be appropriate for modeling cis-regulation, when the input substrate is expected to trigger gene expression in an all-or-none fashion (see also Cherry and Adler, 2000, for a similar remark).

FIGURE 8.

Steady-state mRNA concentrations of the tRS depicted in Fig. 5, as a function of the transcription rate κ₁ of gene 1, for S = 1, 2, 4, 6, 8.

For larger values of S, the transition from the “low” to the “high” steady state is sharper, whereas, the difference between these two states is larger. Moreover, the value of κ₁ at which this transition occurs decreases as S increases. This is a consequence of the fact that lower protein concentration is required to produce appreciable repression or activation when more binding sites are available in the regulatory region. It is clear from Fig. 8 that, when S = 8, small variations in the value of κ₁ around the critical value κ_1,c ≅ 10^−2.5 pM s⁻¹ (i.e., small variations in input substrate concentrations around a critical value) may produce sharp and fast changes in mRNA and protein concentrations for gene 3 (i.e., may produce sharp changes in the transcriptional control of the metabolic enzymes). In this case, the tRS under consideration may abruptly switch from the “low” to the “high” steady state (and vice versa). Note however that the tRS is robust for values of κ₁ that are not in the transition region, in the sense that changes in κ₁ produce no changes in steady-state values. Insensitivity of steady-state behavior on certain parameter values is an essential biological property of a tRS, which is related to its robustness (e.g., see the discussion in Kitano, 2002).

Clearly, for large values of S, the tRS under consideration acts as a switch, controlled by the particular value of κ₁: for κ₁ < κ_1,c, the tRS reaches the “low”steady state, whereas, for κ₁ > κ_1,c, it reaches the “high” steady state. This is illustrated in Fig. 9, which also indicates that the tRS under consideration is robust, in the sense that the system can effectively cope with environmental changes. This is another essential biological property (e.g., see the discussion in Kitano, 2002) illustrated by our example. Temporary changes in external conditions may cause temporary changes in mRNA or protein concentrations. As soon as the external influences disappear, effective transcriptional regulation causes mRNA and protein concentrations to return back to their nominal steady-state values (see also Fig. 10 b).

FIGURE 9.

Illustration of the switching behavior of the tRS depicted in Fig. 5, for S = 8. The tRS switches between the “high” and the “low” steady states as a function of the transcription rate κ₁ of gene 1.

FIGURE 10.

(a) Steady-state mRNA concentrations of the tRS depicted in Fig. 5, as a function of the affinity constant. (b) At the normal temperature of 37°C, the tRS approaches the “high” steady state. However, a heat induction at 40°C during a 24-h period results in the tRS to switch to a “lower” steady state. When the temperature reverses back to normal, the tRS stably switches back to the “high” steady state.

Fig. 10 a depicts the steady state (after 48 h) mRNA concentrations as a function of the affinity constant θ. This result indicates that, at large values of the affinity constant, gene 3 promotes activation (or repression) of enzymatic activity in the metabolic pathway under consideration, whereas, at small values of the affinity constant, gene 3 inhibits activation (or repression) of such activity. From Eq. 28, and for α₁ = 1, ΔU₁ ≤ 0, it is clear that the affinity constant monotonically increases as the temperature decreases. It is therefore expected that, at low temperatures, gene 3 will promote activation (or repression) of enzymatic activity in the metabolic pathway, whereas, at high temperatures, gene 3 will inhibit such activity. However, this may not be true, because parameters β, γ, κ, and λ depend on temperature as well (e.g., recall Eq. 4). Fig. 10 b illustrates how changes in temperature may affect transcriptional regulation. At the normal temperature of 37°C, the tRS under consideration reaches the “high” steady state, whereas, at a temperature of 40°C, the tRS switches to a “higher” steady state. To obtain this result, we consider a 15% decrease in the value of the affinity constant θ, and assume a 20% increase in the values of κ and λ, and no change in the values of β and γ (we assume zero activation energies for mRNA and protein degradation). Fig. 10 b also indicates that the metabolic pathway under consideration is robust to heat induction: the underlying tRS can effectively cope with a temporary increase in temperature, by reversing the mRNA and protein concentrations back to their nominal steady-state values after the temperature returns back to its previous value.

In a real situation, nonzero time delays should be specified. It has been recently shown by Kobayashi et al. (2003a) that, under certain conditions (which are satisfied by the model presented in this article), the steady-state behavior of a tRS with only positive feedback loops (i.e., loops that contain activators and possibly an even number of repressors) does not depend on time delays. However, this is not true when the tRS contains negative feedback loops, in which case time delays may directly affect steady-state behavior. It turns out that the feedback loops of the tRS depicted in Fig. 5 are all positive except one. The loop

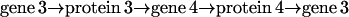involves an activator and a repressor and, therefore, it is a negative feedback loop. Hence, the steady-state behavior of the tRS depicted in Fig. 5 may depend on the time delays.

Fig. 11 depicts typical evolutions of mRNA concentrations of the tRS under consideration, when the time delays are taken to be nonzero and gene independent. We assume that the size of an average gene is ∼40,000 nucleotides, which implies that τ_r = 2000 s (we take v_r = 20 nucleotides/s). We also assume that the same average gene is transcribed to an mRNA of ∼1200 nucleotides long, which is then translated to a protein composed of 400 amino acids. This implies that τ_p = 200 s (we take v_p = 2 codons/s). Finally, we assume that the cis-regulation delay τ_c is, on the average, ∼20% larger than the transcription delay τ_r, in which case τ_c = 2400 s. By comparing the first row of Fig. 11 with Fig. 6, it is clear that it takes longer for the tRS to reach steady state in the case of nonzero time delays. As a matter of fact, for the evolution depicted in Fig. 11 a, it takes ∼72 h to reach steady state, as compared to ∼48 h for the evolution depicted in Fig. 6 a, whereas, for the evolution depicted in Fig. 11 b, it takes more than six days to reach steady state, as compared to ∼24 h for the evolution depicted in Fig. 6 b. Moreover, the evolutions are more complicated in the case of nonzero delays, although the same steady state is reached in both cases, because time delays do not affect the steady-state behavior of the tRS under consideration, as it is clear from Eqs. 17 and 18.

The situation changes if the rate of translation is increased to a value λ = 0.2 s⁻¹. The second row of Fig. 11 depicts typical evolutions of mRNA concentrations for this case. When κ₁ = 0.01 pM s⁻¹, the tRS converges to a steady-state mRNA and protein concentration vector after ∼24 h. However, a 10-fold reduction in the value of κ₁ results in a tRS that converges to a stable limit-cycle attractor. This is illustrated in Fig. 11 d. Although genes 1 and 2 shut off, genes 3 and 4 initiate a self-sustained oscillation whose cycle is completed in ∼16 h at steady state. This corroborates the fact that a tRS with at least one negative feedback loop may effectively be used to model gene-expression “clocks” (e.g., see Smolen et al., 2000).

We conclude this section with a brief discussion on how the time step Δt, used in the implementation of the discrete dynamical system, affects simulation accuracy and computational efficiency. As we have discussed before, Δt = σδt, where δt = 0.05 s and σ > 1 is a resolution parameter that provides a trade-off between simulation accuracy and computational efficiency. Larger values of σ lead to a more efficient implementation of the tRS at the expense of simulation accuracy. However, due to the slow timescales of transcription, translation, and degradation, as compared to the value of δt, large values of σ can be afforded, without compromising simulation accuracy. This is illustrated in Fig. 12, which depicts four evolutions of mRNA concentrations, obtained by using the same parameters as the ones used in Fig. 11 c, when σ = 1, 300, 6000, 72,000. These values correspond to Δt = 0.05 s, 15 s, 5 min, and 1 h, as well as to 1,728,000, 5760, 288, and 24 iterations, respectively. Note that, as σ increases, simulation accuracy decreases. The results obtained with σ = 6000 or 72,000 are clearly not acceptable, although they may provide a coarse approximation of mRNA evolution. Moreover, these results converge to the desired steady state, because the steady-state behavior of the tRS under consideration does not depend on σ, as it is clear from Eqs. 17 and 18. However, the evolutions obtained with σ = 300 are very close to the ones obtained with σ = 1.

If we assume that the relative errors, of approximating, at each time point, the evolutions of mRNA concentrations obtained when σ = 1 with the evolutions obtained when σ > 1, are statistically independent and identically distributed random variables, then we can estimate their mean value and standard deviation by standard empirical formulas. Fig. 13 depicts such estimates for the example depicted in Fig. 12, as a function of 1 ≤ σ ≤ 400. These results indicate that the number of iterations required for simulating the discrete dynamical model under consideration can be dramatically reduced with only a small compromise in simulation accuracy. For example, and according to Fig. 13, at any time point, the relative error of approximating the mRNA concentration depicted in Fig. 12 when σ = 1 with the one obtained when σ = 300, will on the average be equal to 5 × 10⁻⁴, with a standard deviation of ∼10⁻³. However, with σ = 300, the iterations required for simulating transcriptional regulation are 300 times fewer than the iterations required when σ = 1.

FIGURE 13.

The mean value and the standard deviation of the relative error in approximating, at each time point, the evolutions of mRNA concentrations obtained when σ = 1, with the evolutions obtained when 1 ≤ σ ≤ 400, as a function of σ.

CONCLUSION

In this article, we have considered the problem of modeling transcriptional regulation in a large population of cells. We have adopted a standard model for transcriptional regulation, based on ordinary differential equations that model transcription and translation, coupled with nonlinear equations that model cis-regulation. Simple arguments from chemical kinetics have led us to derive a model for cis-regulation that encompasses both activators and repressors, as well as the notion of regulatory modules. The need to use computational techniques for the analysis and simulation of transcriptional regulation has motivated us to derive a discrete model. Derivation of such a model is possible under certain assumptions and leads to a nonlinear discrete dynamical system, which is easy to implement and can be used to simulate transcriptional regulation in an iterative fashion. Moreover, the steady-state behavior of the proposed discrete dynamical system is identical to that of the continuous model.

We have discussed several mathematical properties of our model and have elaborated on their biological significance. Model implementation requires knowledge of several parameters, which are directly related to the biochemical mechanisms of transcription, translation, and cis-regulation. We have briefly discussed the problem of determining such parameters. We have adopted a hypothetical metabolic pathway, which we use to illustrate several properties of our model and show that a nonlinear dynamical system may effectively be used to quantitatively model transcriptional regulation in a biologically relevant way.

We have derived the proposed model for the case of transcriptional regulation in a large population of cells. However, it is also desirable to describe transcriptional regulation in a single cell, to take into account uncertainties about parameter values, and characterize modeling errors introduced by exemplifying transcriptional regulation. This entails development of a model by means of probabilistic techniques that effectively deals with uncertainty, for which the model presented in this article may serve as an “average” model. Construction of such a model for transcriptional regulation is currently under investigation.