Abstract
Flow dialysis has found widespread use in determining the dissociation constant (KD) of a protein-ligand interaction or the amount of available binding sites (E0). This method has the potency to measure both these parameters in a single experiment and in this article a method to measure simultaneously the KD and E0 is presented, together with an extensive error analysis of the method. The flow-dialysis technique is experimentally simple to perform. However, a number of practical aspects of this method can have a large impact on the outcome of KD and E0. We have investigated all sources of significant systematic and random errors, using the interaction between mannitol and its transporter from Escherichia coli as a model. Monte Carlo simulations were found to be an excellent tool to assess the impact of these errors on the binding parameters and to define the experimental conditions that allow their most accurate estimation.
INTRODUCTION
The strength and stoichiometry of protein-ligand interactions are important parameters for understanding the biological properties of proteins. The strength of the protein-ligand interaction, usually expressed as the dissociation constant KD, is a measure for the free energy associated with this interaction. Understanding of the protein-ligand interaction at the molecular level can be obtained by investigating the impact of changes in buffer composition, pH, or temperature, or by studying the effects of changes in substrate structure or mutations in the protein on the interaction. Investigations of allosteric mechanisms, enzyme inhibition, or competitive ligand interactions all rely on accurate estimation of both the dissociation constant (KD) and the stoichiometry of this interaction, the number of binding sites present (E0).
A number of experimental approaches is available to study protein-ligand interactions. When the protein and the ligand have sufficiently different sizes, various separation techniques, e.g., size-exclusion chromatography or equilibrium dialysis, can be employed to measure separately the concentrations of bound and unbound ligand. In equilibrium dialysis, the actual concentrations of interacting species are measured after equilibrium has been established between two compartments separated by a semipermeable membrane. This is a relatively slow technique, making this approach less suitable when one of the components is labile, or for high-throughput screening programs.
The actual chemical equilibrium between ligand and protein is usually reached within minutes or seconds. This led Colowick and Womack to develop a rapid method for measuring binding of ligand molecules that are able to diffuse across a semipermeable membrane: the flow-dialysis technique (Colowick and Womack, 1969; Womack and Colowick, 1973). The system consists of an upper chamber containing the protein-ligand system under investigation, and a lower chamber, separated from the upper chamber via a semipermeable dialysis membrane, through which a mobile phase flows. At a given flow rate, the concentration of ligand measured in the mobile phase is proportional to the concentration of free ligand in the upper chamber. This technique has found widespread use ever since (André and Linse; 2002; England and Hervé, 1992; Hellingwerf and Konings, 1980; Lolkema et al., 1990, 1992; Lolkema and Robillard, 1990; Porumb, 1994; Westerhoff et al., 1989).
Usually, a relatively small amount of radioactive ligand is added to a large pool of potential binding sites at protein concentrations that cause practically all ligand to be bound. By adding unlabeled ligand, the bound labeled ligand is replaced with the unlabeled ligand and appears in the mobile phase. At the end, an excess of unlabeled ligand is added to chase all labeled ligand from the binding sites. The radioactivity measured in the mobile phase then corresponds to all the radioactive ligand being unbound, as in an experiment without protein. Evaluation of the concentration of the labeled ligand in the mobile phase during such a titration yields the binding parameters (KD and E0).
In this article we present a different approach to obtain KD and E0 using flow dialysis. Cumulative amounts of radioactively labeled ligand are added to a fixed amount of binding sites in the regime of ligand concentrations from below the dissociation constant to near saturation. This approach enabled us to accurately determine both the KD and E0 with one sample in a single experiment within ∼30 min.
Several reports in the literature have indicated that improper analysis of the obtained data (e.g., ignoring background signal, overlooking nonspecific binding, a nonlinear relationship between a measured signal and the concentration of bound or free ligand, or the presence of partially inactivated components) and the use of inappropriate mathematical procedures to evaluate the data can cause severe bias in the obtained ligand binding parameters (Fuchs and Gessner, 2001; Larsson, 1997; Rovati et al., 1988; Schumacher and Von Tscharner, 1994). Thus, although flow dialysis is experimentally a simple and fast technique, accurate determination of the protein-ligand parameters necessitates a thorough evaluation of the experimental procedure. The use of a semipermeable membrane necessarily entails a certain leak of the labeled ligand (typically 0.5–1.0%/min). Preliminary work in our group indicated that leakage of ligand at such rates during a flow dialysis experiment has a significant impact on the apparent binding parameters, so this effect has to be properly corrected for. An extensive error analysis of the flow-dialysis experiment is presented, including Monte Carlo simulations to evaluate the effects of the relevant systematic and nonsystematic errors, and to define the experimental conditions that allow accurate estimation of the important binding parameters.
EXPERIMENTAL METHODS
Chemicals
D-[1-3H(N)]Mannitol (17.0 Ci/mmol) was purchased from NEN Research Products (Boston, MA). D-[1-14C]Mannitol (59.0 mCi/mmol) was purchased from Amersham Biosciences (Uppsala, Sweden). Radioactivity measurements were performed using Emulsifier Scintillator Plus obtained from Packard (Groningen, The Netherlands). dPEG was obtained from Kwant High Vacuum Oil Recycling and Synthesis (Bedum, The Netherlands).
Cell growth and isolation of ISO membrane vesicles
Plasmids harboring the wild-type mtlA gene or the mutant mtlA-G196D gene were transformed and subsequently grown in bacterial strain Escherichia coli LGS322 as described (Boer et al., 1995). LGS322, not transformed, and thus not expressing the mtlA gene, was used in control experiments (LGSminus). ISO membrane vesicles were prepared essentially as described (Broos et al., 1999). The vesicles were washed once with 25 mM Tris-HCl, pH 7.6, 1 mM dithiotreitol, and 1 mM NaN3, and quickly frozen in small aliquots in liquid nitrogen for storage at −80°C. Vesicles used for experiments were placed at 37°C for quick thawing and directly placed on ice until further use.
The flow dialysis system
The system as described by Lolkema et al. (1990) was used and a schematic representation is shown in Fig. 1. It consists of a dialysis cell with a 1.2 mL cylindrical upper compartment containing the enzyme solution. It is separated by a dialysis membrane (ServaPor, SERVA Electrophoresis, Heidelberg, Germany), molecular mass cutoff 14,000 Da) from the lower part: a spiral groove with a volume of 20 ± 1 μL engraved in a solid support (Feldmann, 1978).
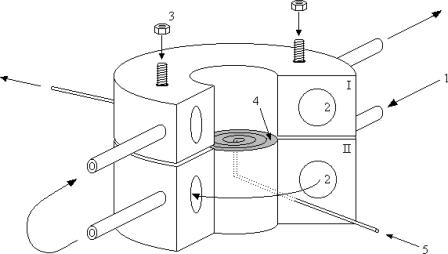
FIGURE 1.
Schematic representation of the flow dialysis cell. (1) Inlet of water from water bath at specific temperature. (2) Channels through the system for thermostatic use. (3) Upper part is fastened to the lower part to seal the contents of the lower spiral groove from the upper sample chamber. (4) The dialysis membrane (shaded) is stretched over the spiral groove and extends somewhat between the two domes. (5) Inlet of flow-through buffer (mobile phase) reaches the membrane in the middle and follows the spiral groove to the exit.
The mobile phase has a flow rate of 230 μL/min and is connected to a fraction collector via 30 cm tubing with an inner diameter of 0.5 mm, corresponding with 60 μL. A Teflon-coated magnetic bar (7 × 2 mm) stirs the upper compartment. The whole system was thermostated at 25 ± 0.1°C. All experiments were performed in 25 mM Tris-HCl, pH 7.6, 5 mM dithiotreitol, and 5 mM MgCl2 with 0.25% dPEG, unless stated otherwise. The upper compartment usually contained between 50 nM and 25 μM of binding sites, in 300–500 μL of the above buffer solution. The experiment was started after the protein solution had been equilibrated for 10 min at 25°C.
A typical flow dialysis experiment
A control experiment is carried out to estimate the rate of diffusion of the labeled ligand across the membrane (the leak rate) and the dead time of the system. In the control experiment, the upper compartment is filled with buffer solution and samples are collected for 20 min after the flow is started. After the first sample (six droplets) is collected, a known concentration of radioactive ligand (25–100% of the total concentration used in the experiment with protein) is introduced in the upper compartment. Sampling is continued during the next 9–10 min, after which a second addition of the same amount of radioactive ligand is made. The radioactivity of the collected samples was measured after addition of 2.0 mL of scintillation fluid. The background radioactivity (as determined from the first collected sample) was subtracted from all samples. A plot of the CPMs in the collected samples against the time yields two values for the leak rate (LR, %/min), and two values for the multiplication factor β, relating measured radioactivity and concentration of free ligand in the upper compartment. These values are averaged and used as such.
For each flow-dialysis experiment, a new dialysis membrane was used. The titration experiment with protein consists of 9 or 10 cycles of addition of radioactive ligand, equilibration, and sampling, each cycle taking exactly 3 min. The experiment is started by mixing all components and applying the sample with protein to the upper chamber. At t = 0′, a certain amount of radioactive ligand is applied to the upper chamber; 1 min after the addition of radioactive ligand, when the binding equilibrium already has been reached (Lolkema et al., 1990), the radioactivity in the mobile phase is measured by collecting, during 1.5 min, five samples of six droplets each for radioactivity counting. This cycle is repeated 9–10 times. Fig. 2 shows the precise time schedule employed during the titration cycles.
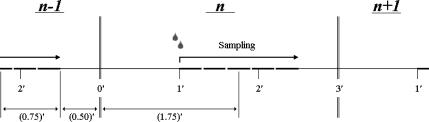
FIGURE 2.
Schematic representation of the time regime for leak (ΔSleak) determination. Relevant equation (Eq. 5): 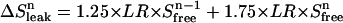 . The leak at each point n consists of two components. The first component (1.25′, in minutes) is the leak from the previous addition (n − 1) from halfway sampling until the end of sampling (0.75′) plus the remaining time until the next addition at point n (0.50′). The second component starts from the point of addition of a new amount of substrate at point n and lasts until halfway the sampling during n (1.75′).
. The leak at each point n consists of two components. The first component (1.25′, in minutes) is the leak from the previous addition (n − 1) from halfway sampling until the end of sampling (0.75′) plus the remaining time until the next addition at point n (0.50′). The second component starts from the point of addition of a new amount of substrate at point n and lasts until halfway the sampling during n (1.75′).
Theoretical background
Table 1 shows a glossary of symbols and definitions used in this article. For the equilibrium between a single ligand-binding, noncooperative enzyme (E) with ligand (S),
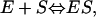 |
(1) |
the concentration of unbound ligand (Sfree) as a function of the total ligand (Stot) and total protein (Etot) concentrations can be written as follows:
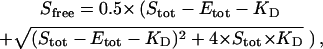 |
(2) |
with the equilibrium constant KD defined as:
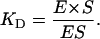 |
(3) |
In the upper compartment containing the protein, the total amount of ligand present at each cycle n (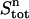 ) is given by
) is given by
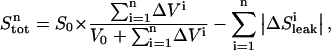 |
(4) |
in which ΔVi is the volume of added ligand at step i, V0 the initial volume in the upper compartment, and S0 the concentration of ligand in the stock solution. 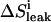 is the drop in the ligand concentration due to leak through the membrane at step i. In our system, the leak rate LR is small (usually <1%/min) and therefore the leak can be treated as a zero-order process. This makes it legitimate to average the five fractions during the same cycle. The time between halfway the sample collection of the previous titration cycle (n − 1) and halfway the sampling of cycle n is used to calculate the leak correction for cycle n. In our titration schedule (Fig. 2), these points are 1.25 min before and 1.75 min after the start point of cycle n, respectively, resulting in the following expression for the drop in the total ligand concentration due to leakage:
is the drop in the ligand concentration due to leak through the membrane at step i. In our system, the leak rate LR is small (usually <1%/min) and therefore the leak can be treated as a zero-order process. This makes it legitimate to average the five fractions during the same cycle. The time between halfway the sample collection of the previous titration cycle (n − 1) and halfway the sampling of cycle n is used to calculate the leak correction for cycle n. In our titration schedule (Fig. 2), these points are 1.25 min before and 1.75 min after the start point of cycle n, respectively, resulting in the following expression for the drop in the total ligand concentration due to leakage:
 |
(5) |
The total protein concentration at each point n ( ) is only dependent on the dilution caused by the addition of S, according to:
) is only dependent on the dilution caused by the addition of S, according to:
 |
(6) |
TABLE 1.
Glossary of symbols and definitions
| Symbol | Definition |
|---|---|
| V0 | Initial volume of protein solution in the flow chamber |
| ΔVi | Volume added at addition i |
 |
Standard error in ΔVi |
| S0 | Ligand concentration in stock solution |
| E0 | Initial concentration of binding sites in upper compartment |
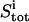 |
Total concentration of ligand at titration point i |
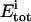 |
Total concentration of binding sites at titration point i |
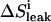 |
Correction for leak of ligand at sampling point i |
| Ci | Signal measured in samples after addition i |
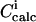 |
Calculated signal after addition i |
| KD | Dissociation constant |
| LR | Leak rate (%/min) |
| β | Ratio between CPM and free ligand concentration |
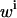 |
Weight of data point i |
Equations 2, 4, and 6 then yield a value for 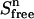 at each titration point. Multiplying
at each titration point. Multiplying 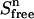 with β gives the signal
with β gives the signal 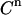 (CPMs measured after n additions):
(CPMs measured after n additions):
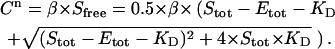 |
(7) |
Summarizing the procedure thus far, the raw data (i.e., total added volume 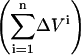 from the ligand stock solution and the radioactivity counted in the mobile phase at each titration step n) are used to calculate (Eqs. 4 and 5) the total ligand concentration
from the ligand stock solution and the radioactivity counted in the mobile phase at each titration step n) are used to calculate (Eqs. 4 and 5) the total ligand concentration 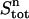 (corrected for the ongoing leak through the semipermeable membrane) and the concentration of free ligand (
(corrected for the ongoing leak through the semipermeable membrane) and the concentration of free ligand (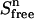 ). For this we use the values for β and the leak rate obtained from the control experiment. This leaves only the values of KD and E0 (and sometimes β, see below) to be determined by fitting the experimental data (
). For this we use the values for β and the leak rate obtained from the control experiment. This leaves only the values of KD and E0 (and sometimes β, see below) to be determined by fitting the experimental data (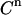 ) to Eq. 7. For this, any mathematical software package able to perform nonlinear least-squares minimization can be used. We chose the Levenberg-Marquardt algorithm.
) to Eq. 7. For this, any mathematical software package able to perform nonlinear least-squares minimization can be used. We chose the Levenberg-Marquardt algorithm.
However, since weight factors cannot be assumed to be the same for each titration point, they have to be calculated separately for each titration point, as will be shown below. Also, because the number of titration points is not enough to estimate the confidence intervals for the fitting parameters from the spread in the experimental values, we chose to implement a Monte Carlo approach to this end. All routines used were written in the software package Mathematica 4.1 (available on request).
The error function that has to be minimized is defined as:
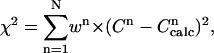 |
(8) |
with the weight wn of each data point taken as the inverse of the variance of the signal measured during cycle n:
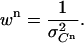 |
(9) |
The variance in the signal measured during cycle n is calculated as follows. The standard deviation in the total ligand concentration after n additions (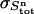 ) is dominated by the accumulated errors in the added volumes
) is dominated by the accumulated errors in the added volumes 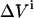 :
:
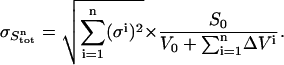 |
(10) |
The absolute error (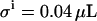 ) in pipetting was determined experimentally by weighing. Equation 10 yields the standard deviation of the total ligand concentration. Variations in the ligand concentration directly influence the signal C. Therefore, the first derivative of the signal C with respect to the total ligand concentration (Eq. 7) is used to evaluate the effect of variations in the total ligand concentration on the signal
) in pipetting was determined experimentally by weighing. Equation 10 yields the standard deviation of the total ligand concentration. Variations in the ligand concentration directly influence the signal C. Therefore, the first derivative of the signal C with respect to the total ligand concentration (Eq. 7) is used to evaluate the effect of variations in the total ligand concentration on the signal  :
:
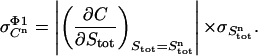 |
(11) |
This derivative is calculated numerically by incrementing Stot with a very small amount and calculating the quotient ΔCn/ΔStot.
The standard deviation in the signal due to counting uncertainties is given by:
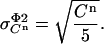 |
(12) |
The factor 5 arises from the averaging of the five samples collected per cycle. Being independent, these two contributions to the standard deviation in the measured signal 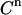 can be squared and summed to yield the total variance (
can be squared and summed to yield the total variance (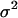 ):
):
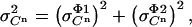 |
(13) |
which is used to determine the weight of each data point according to Eq. 9.
The impact of each error source on both the KD and E0 can be investigated by a MC simulation, offering the possibility to optimize an experimental setup. The Monte Carlo computer simulations generate many virtual data sets as follows. For each addition, a value for 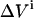 is taken at random from a normal distribution around the actual value used in the experiment, with a standard deviation equal to
is taken at random from a normal distribution around the actual value used in the experiment, with a standard deviation equal to 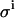 (e.g., 0.04 μL). Equations 4–7 are then used to calculate the corresponding signal. For the parameters LR and β, the experimental values are taken as such. For the parameters KD and E0, the values are used that yielded the best fit of Eq. 7 to the real experimental data. The counting error in the calculated signal is incorporated by replacing the calculated value for
(e.g., 0.04 μL). Equations 4–7 are then used to calculate the corresponding signal. For the parameters LR and β, the experimental values are taken as such. For the parameters KD and E0, the values are used that yielded the best fit of Eq. 7 to the real experimental data. The counting error in the calculated signal is incorporated by replacing the calculated value for 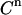 by a value taken at random from a normal distribution around
by a value taken at random from a normal distribution around 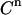 with a standard deviation equal to
with a standard deviation equal to 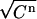 . This approximates the expected Poisson distribution very well. These virtual data sets are subsequently analyzed exactly as the real experimental data sets, and the observed variation in the best-fit parameters is taken to be an accurate representation of the real variation to be expected in experimentally obtained binding parameters. Apart from the nonsystematic errors mentioned, also the effects of systematic errors (use of incorrect weights for the data points, incorrect choice of the parameters LR or β) could be investigated with these virtual data sets, as will be shown below.
. This approximates the expected Poisson distribution very well. These virtual data sets are subsequently analyzed exactly as the real experimental data sets, and the observed variation in the best-fit parameters is taken to be an accurate representation of the real variation to be expected in experimentally obtained binding parameters. Apart from the nonsystematic errors mentioned, also the effects of systematic errors (use of incorrect weights for the data points, incorrect choice of the parameters LR or β) could be investigated with these virtual data sets, as will be shown below.
RESULTS
The enzyme we used to evaluate the method is the mannitol transporter from E. coli, EIImtl. It resides in the inner membrane and exhibits high-affinity mannitol binding in the nanomolar regime. Mutating the enzyme, by replacing glycine 196 for an aspartate (EII-G196D), results in mannitol binding with an affinity in the micromolar regime (Boer et al., 1995). For both enzymes, flow dialysis experiments are presented, including the control experiments, the fitting procedure, the impact of ligand leak on the apparent binding parameters (KD and E0), and the calculation of weight factors for the individual data points. The confidence limits of the binding parameters are determined by Monte Carlo computer simulations, taking the most important random errors into account.
High-affinity mannitol binding
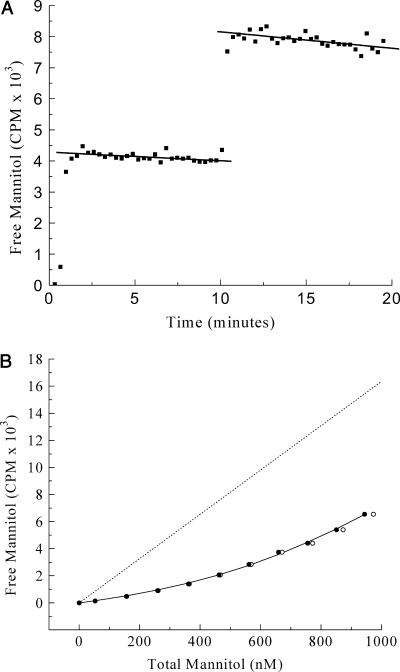
Fig. 3 shows the results of a binding experiment, executed as described in the Experimental Methods section, using wild-type EIImtl and [3H]mannitol. From the control experiment (Fig. 3 A), a value of 0.63%/min was calculated for the LR and a value of 16.34 CPM/nM for the factor β, which relates the radioactivity measured in the mobile phase with the concentration of unbound mannitol in the upper compartment.
FIGURE 3.
High-affinity mannitol binding to wild-type EIImtl. (A) Control experiment. Two additions, each 5 μL of 20.0 μM [3H]mannitol to 380 μL buffer in the dialysis cell. Solid lines represent linear fits. (B) Mannitol titration curve with additions of 1 × 1.0 μL and 9 × 2.0 μL of 20.0 μM [3H]mannitol. Dotted line was drawn using the β-value obtained from Fig. 3 A. (○) Uncorrected data; (•) data points corrected for leakage (see text).
ISO E. coli membrane vesicles, containing an amplified level of EIImtl, were used as the source of EIImtl for the titration shown in Fig. 3 B at a total membrane protein concentration of ∼1 mg/mL. The buffer used included the detergent dPEG, which efficiently solubilizes the vesicles, thus preventing any buildup of mannitol inside the vesicles and making all binding sites available. The enzyme was stable under these conditions, and solubilization by dPEG only marginally affected the binding characteristics (Lolkema et al., 1993). Fitting of these data using Eq. 7, not corrected for mannitol leakage (open circles in Fig. 3 B), yielded a KD of 205 nM and an E0 of 909 nM.
The correction for mannitol leakage has a significant effect on the binding parameters. Values for KD and E0 of 179 nM and 828 nM, respectively, were obtained when a leak rate of 0.63%/min was used in Eq. 5 for the leak correction (solid circles in Fig. 3 B).
The use of proper weight factors for the individual data points further improved the reliability of the obtained parameters. First the data were fitted with equal weights for each point. The best-fit values for the fitting parameters KD and E0 were then used to calculate improved weights (Eqs. 9–13) and improved values for KD and E0. This process was repeated until stable values for KD and E0 were obtained, resulting in a KD of 155 ± 23 nM and an E0 of 780 ± 46 nM, respectively (see Fig. 3 B, solid circles, connected). The weight factors employed varied from 5.4 × 10−3 for the first to 3.9 × 10−5 for the last titration point, emphasizing their importance for a correct analysis.
Low-affinity mannitol binding
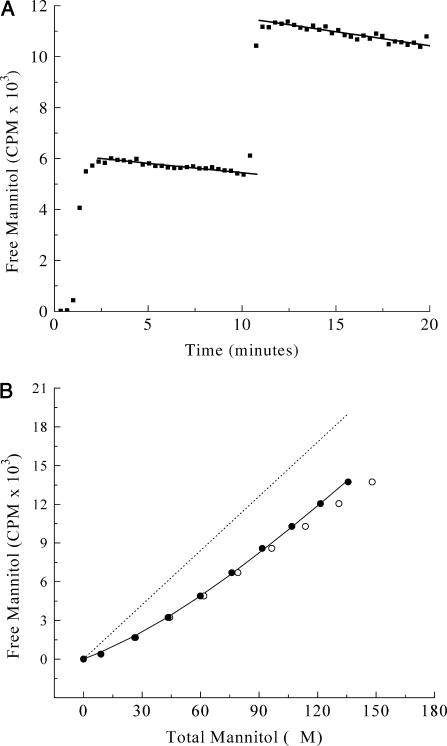
Low-affinity mannitol binding was investigated with mutant EII-G196D. This mutant shows mannitol binding affinity in the micromolar regime (Boer et al., 1995). The control experiment (Fig. 4 A) was performed with a 3.39 mM [14C]mannitol stock. From both mannitol leak decays, the LR and β-values were determined and averaged. This resulted in an LR of 1.03%/min and a β-value of 0.140 CPM/nM.
FIGURE 4.
Low-affinity mannitol binding to EII-G196D. (A) Control experiment. Two additions, each 5 μL of 3.39 mM [14C]mannitol to 380 μL buffer in the dialysis cell. Solid lines represent linear fits. (B) Mannitol titration curve with additions of 1 × 1.0 μL and 8 × 2.0 μL of 3.39 mM [14C]mannitol. Dotted line was drawn using the β-value obtained from Fig. 4 A. (○) Uncorrected data; (•) data points corrected for leakage (see text).
For the binding experiment with the EII-G196D protein (Fig. 4 B), a similar titration scheme as for high affinity binding was used. To vesicles, ∼20 mg/ml total membrane protein, 5 mM MgCl2, and 1.0% dPEG were added, and the mixture was incubated at 25°C for 10 min. The 20-fold higher concentration of vesicles used in this experiment had no effect on the leak rate or β-value. This was established by using E. coli vesicles not containing EIImtl (LGSminus strain, see Experimental Methods). Fitting of the raw data resulted in a KD of 88 μM and an E0 of 95 μM (Fig. 4 B, open circles). Correction for mannitol leak as described for the high affinity experiments on wild-type EIImtl resulted in a KD of 37 μM and an E0 of 52 μM. Complete analysis, including proper weight factors for the data points, resulted in a KD of 25 ± 6 μM and an E0 of 46 ± 8 μM (Fig. 4 B, solid circles). The standard deviations reported in this and the previous section were calculated from the quality of the fit and are not very reliable due to the small number of titration points. A better procedure for estimating the reliability of the binding parameters will be given below.
Monte Carlo simulations
Accuracy of the procedure
For an accurate determination of both the dissociation constant and the number of available binding sites in a single experiment, it is important to choose the amount of protein and the ligand concentration range so that both parameters can be optimally determined. Since the flow-dialysis procedure relies on the determination of the fraction of the total added ligand that is freely diffusible across the membrane, it is crucial that during a titration a significant fraction of the total added ligand is actually bound. In addition, as in any binding experiment, a high degree of saturation of the binding sites (>80%) must be realized. This leads to the following two important requirements for a good flow-dialysis experiment:
The total added ligand concentration must be varied from 0 to n times the total concentration of binding sites, with n in the range of 2–5.
The free ligand concentration must vary during a titration from 0 to k times the relevant KD, with k at least 4 (to reach 80% saturation).
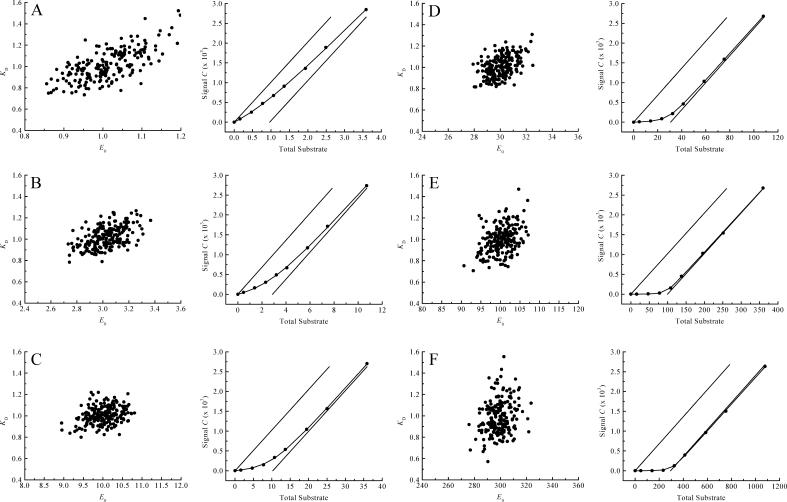
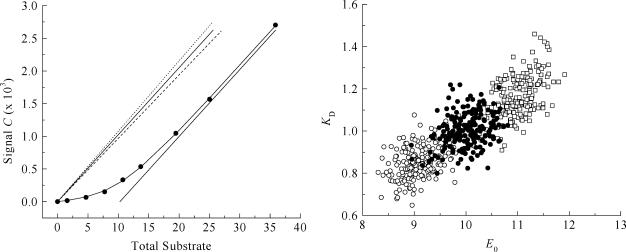
To establish quantitatively how the choice of conditions affects the accuracy of binding experiments, we carried out a large number of Monte Carlo simulations of such experiments. For these calculations we chose KD = 1, and E0 in the range 1–300. Each simulated titration consists of eight additions of ligand from a stock solution (relative volume increments 1, 2, 2, 2, 2, 4, 4, and 8 μL, with a standard deviation of σi = 0.08 μL) to an initial volume of 380 μL in the upper compartment. The concentration of the stock solution was chosen such that an excess of n = 3.7 of total added ligand over the binding sites was reached at the end of the titration. For each addition the total concentrations of ligand and binding sites were calculated (Eqs. 2 and 4), and from these the expected signal (Eq. 7). The β-value was chosen inversely proportional to the concentration of ligand in the stock solution to ensure that in every titration the signal reached similar values. Fig. 5, A–F, show some typical (virtual) binding experiments and the resulting distributions of binding parameters obtained from 200 of such virtual data sets, for a range of E0 values between 1 and 300. Fig. 6 shows the obtained accuracy for both parameters under the different conditions (solid symbols: squares for the KD, circles for E0). Clearly, the optimal range for E0 is between 3 and 30, if both KD and E0 need to be determined. Since we did not specify the concentration units in these calculations we can extrapolate this to other values for the KD by multiplying all concentrations with the actual KD value of the system under study. So, for our high affinity binding experiments (KD = ∼150 nM), the optimal range for E0 is between 3 and 30 × 150 nM. For the low-affinity (KD = 25 μM) experiments, the concentration of binding sites should be chosen between 3 and 30 × 25 μM for optimal accuracy.
FIGURE 5.
Monte Carlo simulations at different E0/KD ratios to evaluate the accuracy of the flow dialysis procedure. Each simulated titration consists of eight additions (relative additions: 1, 2, 2, 2, 2, 4, 4, and 8 μL to 380 μL initial volume) of substrate with  . For every E0/KD ratio, 200 virtual data sets were generated and fitted. Typical example titration curves of one of the virtual data sets together with the scatter plots are shown (E0/KD ratios for A, B, C, D, E, and F, are 1, 3, 10, 30, 100, and 300, respectively). The solid lines in these titration graphs represent the value of β, relating the signal C with the concentration of free ligand. Note that all concentration units are arbitrary and can be scaled at will.
. For every E0/KD ratio, 200 virtual data sets were generated and fitted. Typical example titration curves of one of the virtual data sets together with the scatter plots are shown (E0/KD ratios for A, B, C, D, E, and F, are 1, 3, 10, 30, 100, and 300, respectively). The solid lines in these titration graphs represent the value of β, relating the signal C with the concentration of free ligand. Note that all concentration units are arbitrary and can be scaled at will.
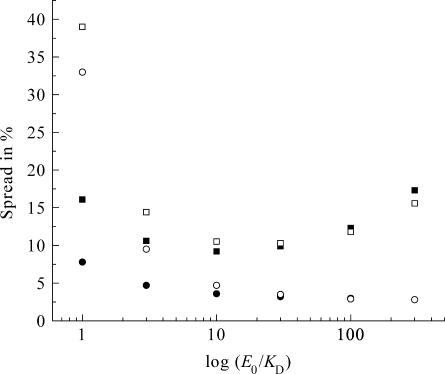
FIGURE 6.
Accuracy for both the KD and E0 at different conditions. Experimental conditions are as stated in the legend of Fig. 5. Squares represent the spread (%) in KD, circles the spread in E0: solid for two-parameter fitting (KD and E0), open for three-parameter fitting (KD, E0, and β).
Nonsystematic errors
To investigate the impact of the pipetting error 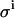 , we used values for the KD and E0 of 1 and 10, respectively, to generate 200 virtual data sets, as described in the Experimental Methods section, mimicking the conditions and procedures of real binding experiments. Four different values for the pipetting error
, we used values for the KD and E0 of 1 and 10, respectively, to generate 200 virtual data sets, as described in the Experimental Methods section, mimicking the conditions and procedures of real binding experiments. Four different values for the pipetting error 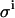 were used. These simulated data sets were analyzed exactly as described for the real data, each data set yielding best-fit values for the model parameters KD and E0. Table 2 shows the resulting uncertainties in the values found for KD and E0.
were used. These simulated data sets were analyzed exactly as described for the real data, each data set yielding best-fit values for the model parameters KD and E0. Table 2 shows the resulting uncertainties in the values found for KD and E0.
TABLE 2.
The impact of different pipetting errors 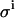 on the accuracy of the parameters KD and E0
on the accuracy of the parameters KD and E0
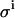 (μL) (μL) |
σKD (%) | σE0 (%) |
|---|---|---|
| 0.00 | 5.6 | 1.2 |
| 0.04 | 6.6 | 2.1 |
| 0.08 | 9.4 | 3.5 |
| 0.12 | 12 | 5.1 |
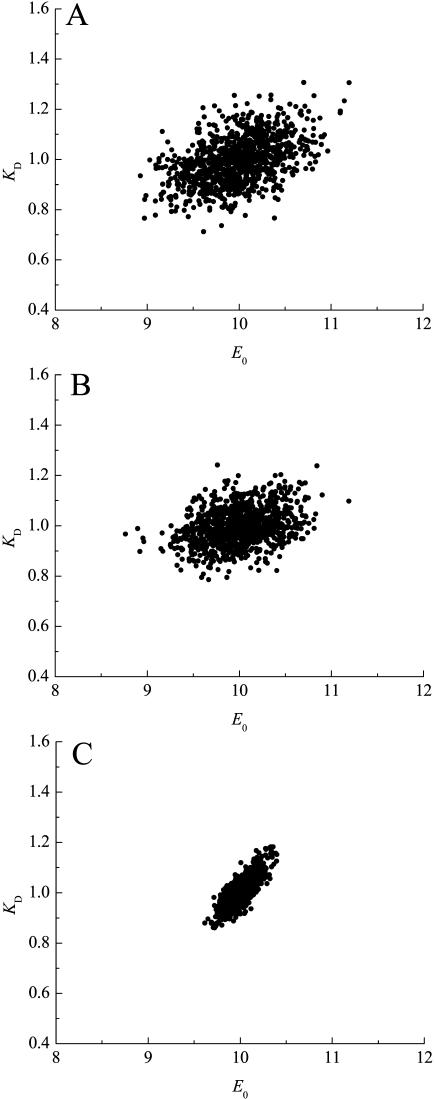
Next, we investigated the relative importance of the two sources of random errors, in pipetting and in counting. Fig. 7 A shows a spread of KD and E0 from 1000 virtual data sets simulated, where 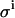 was set to 0.08 μL. Calculations including only the pipetting error are shown in Fig. 7 B. Calculations including only the counting error are shown in Fig. 7 C. These figures demonstrate that the pipetting error was the most important source of error in our experimental setup.
was set to 0.08 μL. Calculations including only the pipetting error are shown in Fig. 7 B. Calculations including only the counting error are shown in Fig. 7 C. These figures demonstrate that the pipetting error was the most important source of error in our experimental setup.
FIGURE 7.
Effect of the value for the leak rate (LR) and β on the spread of the parameters KD and E0. (A) Spread of KD and E0 from 1000 virtual data sets, with 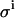 set to 0.08 μL; σKD (%) = 8.1, and σE0 (%) = 3.5. (B)
set to 0.08 μL; σKD (%) = 8.1, and σE0 (%) = 3.5. (B) 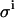 set to 0.08 μL, and β increased 1000 times; σKD (%) = 7.2, and σE0 (%) = 3.4. (C)
set to 0.08 μL, and β increased 1000 times; σKD (%) = 7.2, and σE0 (%) = 3.4. (C) 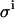 set to 0.0 μL; σKD (%) = 5.5, and σE0 (%) = 1.2.
set to 0.0 μL; σKD (%) = 5.5, and σE0 (%) = 1.2.
For the high-affinity data set with wild-type EIImtl, the standard deviations based on Monte Carlo simulations were 156 ± 6 nM for the KD and 784 ± 14 nM for E0. For the low-affinity data set on EII-G196D, these values were 25 ± 2 μM and 46 ± 1 μM.
Systematic errors
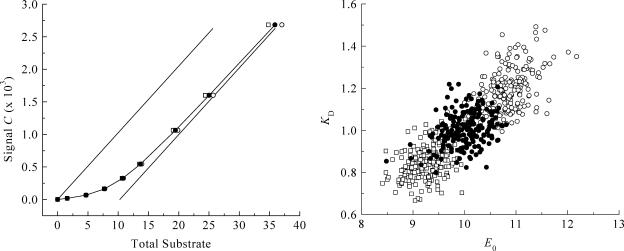
The effect of improper leak correction. To investigate the importance of leak correction (Eq. 5), we used the same Monte Carlo procedure to generate 200 virtual data sets under a range of conditions (E0/KD between 1 and 300), with LR equal to 0.6%/min. Analysis was done without leak correction (LR = 0%/min) or with a two-times overestimated value (LR = 1.2% min). The results are shown in Table 3, with an example of the titration curve and scatter plot obtained at E0/KD = 10 (Fig. 8). The use of incorrect leak rates results in a similar systematic trend at all E0/KD ratios. In addition, it leads to larger uncertainties in the parameters KD and E0: up to 17% for the KD, and 9% for E0 (see Table 3).
TABLE 3.
The impact of the correction for different leak rates (LR) at different E0/KD ratios
|
LR = 0.0%/min*
|
LR = 0.6%/min†
|
LR = 1.2%/min‡
|
||||
|---|---|---|---|---|---|---|
| E0/KD | KD (σKD in %) | E0 (σE0 in %) | KD (σKD in %) | E0 (σE0 in %) | KD (σKD in %) | E0 (σE0 in %) |
| 1 | 1.4 (16) | 1.3 (8) | 1.0 (16) | 1.0 (7) | 0.7 (16) | 0.7 (9) |
| 3 | 1.2 (11) | 3.4 (5) | 1.0 (10) | 3.0 (5) | 0.8 (11) | 2.6 (5) |
| 10 | 1.2 (9) | 10.9 (3) | 1.0 (8) | 10.0 (4) | 0.8 (10) | 9.3 (4) |
| 30 | 1.2 (10) | 31.6 (3) | 1.0 (10) | 30.1 (3) | 0.9 (10) | 28.6 (3) |
| 100 | 1.2 (11) | 104 (3) | 1.0 (11) | 100 (3) | 0.8 (11) | 96.4 (3) |
| 300 | 1.3 (17) | 311 (3) | 1.0 (16) | 299 (3) | 0.8 (17) | 220 (3) |
No leak correction.
Correct leak rate.
Twice the correct leak rate.
FIGURE 8.
Effect of improper leak correction. Monte Carlo simulations and example titration curve at an E0/KD ratio of 10, with 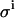 set to 0.08 μL. (○) LR = 0.0%/min; σKD (%) = 10.0, σE0 (%) = 8.8. (•) LR = 0.6%/min; σKD (%) = 3.4, σE0 (%) = 8.1. (□) LR = 1.2%/min; σKD (%) = 9.5, σE0 (%) = 3.6.
set to 0.08 μL. (○) LR = 0.0%/min; σKD (%) = 10.0, σE0 (%) = 8.8. (•) LR = 0.6%/min; σKD (%) = 3.4, σE0 (%) = 8.1. (□) LR = 1.2%/min; σKD (%) = 9.5, σE0 (%) = 3.6.
The effect of an improper β-value. To investigate the importance of the parameter β, which relates the measured radioactivity with the concentration of free ligand in the upper compartment, we used the same Monte Carlo procedure. Virtual data sets, generated as described above with a given β-value, were analyzed with β-values equal to 0.95 or 1.05 times the value used for the simulations (the “true” value). An example of the titration curve and scatter plot obtained at E0/KD = 10 is shown in Fig. 9. Errors of this magnitude in β lead to significant errors in the binding parameters at E0/KD ratios <3 and >30. Moreover, the quality of the fits under these conditions was significantly worse, especially at the higher E0/KD ratios, where the χ2 values were almost 50% higher (data not shown). This approach can be useful for recognizing such a systematic error. Under these conditions, one may decide to use β as the third parameter in a three-parameter fitting procedure, as will be discussed below.
FIGURE 9.
Effect of improper β-value. Monte Carlo simulations and example titration curve at an E0/KD ratio of 10, with 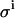 set to 0.08 μL. Open circles and dashed line, 0.95 × β; σKD (%) = 8.7, σE0 (%) = 3.7; solid circles and solid line, 1.00 × β; σKD (%) = 8.1, σE0 (%) = 3.5; open squares and dotted line: 1.05 × β; σKD (%) = 8.7, σE0 (%) = 3.2.
set to 0.08 μL. Open circles and dashed line, 0.95 × β; σKD (%) = 8.7, σE0 (%) = 3.7; solid circles and solid line, 1.00 × β; σKD (%) = 8.1, σE0 (%) = 3.5; open squares and dotted line: 1.05 × β; σKD (%) = 8.7, σE0 (%) = 3.2.
The effect of improper weight factors. The importance of correct weight factors in Eq. 8 is illustrated by repeating the above calculations and analyzing the resulting virtual data sets with equal weight factors for all data points. Neglecting the weight of the individual data points has a significant impact on the accuracy of the binding parameters, especially the KD (see Table 4). The effect can be explained by noting that correct weight factors emphasize the first titration points relative to the last points, where pipetting errors have accumulated and the uncertainty in the calculated radioactivity counts has increased. Hence, the use of equal weight factors for all data points overrates the last titration points.
TABLE 4.
The impact of improper correction for the weights of the data points at different E0/KD ratios
| E0/KD ratio | σKD (%) | σE0 (%) |
|---|---|---|
| 1 | 16 | 8 |
| 3 | 13 | 5 |
| 10 | 13 | 4 |
| 30 | 20 | 4 |
| 100 | 37 | 3 |
| 300 | 71 | 3 |
Three-parameter fit. The value for β in a flow dialysis experiment can in principle be extracted from the raw data, together with the KD and E0. We investigated this possibility to treat not only the binding parameters KD and E0 as fit parameters in our nonlinear least-squares regression procedure, but also the parameter β. Again we generated 1000 virtual data sets, and implemented a three-parameter fitting routine. Fig. 6 presents the obtained accuracy for KD and E0 at different E0/KD ratios (open symbols: squares for the KD, circles for E0). The optimal range for E0 values is narrower than when two parameters are fitted (solid symbols in Fig. 6).
At E0/KD ratios <10, the spread in β was more than 7%, whereas at the higher E0/KD ratios, this spread was minimal (data not shown). We concluded that accurate results could only be obtained in the regime where saturation of the binding sites at the end of the titration was virtually complete and sufficient information for a proper estimation of β is present in the data. Interestingly, when incorrect leak rates were used for the analysis, the routine compensated for this systematic error by adjusting the value for β, such that the relevant binding parameters KD and E0 were still estimated correctly (data not shown).
DISCUSSION
The attractive features of flow dialysis to evaluate protein-ligand interactions, compared to other experimental approaches include i), the relatively short time needed to estimate KD and E0; ii), the simple setup/equipment that can be easily constructed in a workshop; and iii), the flexibility in detection mode, e.g., scintillation counting or optical spectroscopy, depending on the type of label used in the ligand. In principle, any binding event can be studied provided that the protein or other macromolecular species can be separated from the ligand by a semipermeable membrane.
Commonly, the standard deviations of the best-fit binding parameters are estimated from the curvature of the χ2-function near its minimum. When only a small number of data points is available, these standard deviations can fluctuate significantly from one (virtual) binding experiment to the next, and the MC simulation procedure was found to be much more reliable. In addition, the MC simulations can be used to investigate where further improvements of the system can be worthwhile.
The differences in the leak rates observed in the high-affinity and low-affinity mannitol binding experiments is caused most likely by the use of two different batches of semipermeable membranes. This further emphasizes the importance of the control experiments, since the value for LR (and hence β) can be dependent on the membrane batch used.
The three-parameter fitting procedure was initially built to see if it was possible to obtain all parameters (KD, E0, and β) within a single experiment. In this case, a control experiment would not be needed, provided the leak rate is known for a given experimental setup. Here we show that at low E0/KD ratios, the saturation level is too low to make a proper estimation of E0 (see Fig. 6). The regime at which three parameters can be fitted properly with eight (averaged) data points is more restricted than when only two parameters must be fitted: for two-parameter fitting, the range is optimal at E0/KD ratios between 3 and 30, whereas for three-parameter fitting this range is narrowed down to E0/KD ratios between 10 and 30. Clearly, at the lower ratios the data points do not hold enough information to accurately determine β.
In conclusion, in this article a thorough evaluation of the accuracy of the flow-dialysis method is presented. Guidelines to optimize the experiment are given and the impact of all possible error sources that influence the KD and E0 parameters have been investigated. The use of these guidelines ensures an accurate and reliable measurement of both the KD and E0 in a single measurement.
Acknowledgments
This work was supported by the Netherlands Foundation for Chemical Research with financial aid from the Netherlands Organization for the Advancement of Scientific Research.
Abbreviations used: CPM, counts per minute; dPEG, decylpoly(ethylene glycol) 300; EIImtl, enzyme IImtl from Escherichia coli; ISO, inside-out; LR, leak rate; MC, Monte Carlo; mtl, mannitol.
References
- André, I., and S. Linse. 2002. Measurements of Ca2+-binding constants of proteins and presentation of the CaLigator software. Anal. Biochem. 305:195–205. [DOI] [PubMed] [Google Scholar]
- Boer, H., R. H. Ten Hoeve-Duurkens, J. S. Lolkema, and G. T. Robillard. 1995. Phosphorylation site mutants of the mannitol transport protein enzyme IImtl of Escherichia coli: studies on the interaction between the mannitol translocating C-domain and the phosphorylation site on the energy coupling B-domain. Biochemistry. 34:3239–3247. [DOI] [PubMed] [Google Scholar]
- Broos, J., F. Ter Veld, and G. T. Robillard. 1999. Membrane protein-ligand interactions in Escherichia coli vesicles and living cells monitored via a biosynthetically incorporated tryptophan analogue. Biochemistry. 38:9798–9803. [DOI] [PubMed] [Google Scholar]
- Colowick, S. P., and F. C. Womack. 1969. Binding of diffusible molecules by macromolecules: rapid measurement by rate of dialysis. J. Biol. Chem. 244:774–777. [PubMed] [Google Scholar]
- England, P., and G. Hervé. 1992. Synergistic inhibition of Escherichia coli aspartate transcarbamylase by CTP and UTP: binding studies using continuous-flow dialysis. Biochemistry. 31:9725–9732. [DOI] [PubMed] [Google Scholar]
- Feldmann, K. 1978. New devices for flow dialysis and ultrafiltration for the study of protein-ligand interactions. Anal. Biochem. 88:225–235. [DOI] [PubMed] [Google Scholar]
- Fuchs, H., and R. Gessner. 2001. The result of equilibrium-constant calculations strongly depends on the evaluation method used and on the type of experimental errors. Biochem. J. 359:411–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellingwerf, K. J., and W. N. Konings. 1980. Kinetic and steady-state investigations of solute accumulation in bacterial membranes by continuously monitoring the radioactivity in the effluent of flow-dialysis experiments. Eur. J. Biochem. 106:431–437. [DOI] [PubMed] [Google Scholar]
- Larsson, Å. 1997. Regression analysis if simulated radio-ligand equilibrium experiments using seven different mathematical models. J. Immunol. Methods. 206:135–142. [DOI] [PubMed] [Google Scholar]
- Lolkema, J. S., and G. T. Robillard. 1990. Subunit structure and activity of the mannitol-specific enzyme II of the Escherichia coli phosphoenolpyruvate-dependent phosphotransferase system solubilized in detergent. Biochemistry. 29:10120–10125. [DOI] [PubMed] [Google Scholar]
- Lolkema, J. S., D. Swaving-Dijkstra, and G. T. Robillard. 1992. Mechanics of solute translocation catalyzed by enzyme IImtl of the phosphoenolpyruvate-dependent phosphotransferase system of Escherichia coli. Biochemistry. 31:5514–5521. [DOI] [PubMed] [Google Scholar]
- Lolkema, J. S., D. Swaving-Dijkstra, R. H. Ten Hoeve-Duurkens, and G. T. Robillard. 1990. The membrane-bound domain of the phosphotransferase enzyme IImtl of Escherichia coli constitutes a mannitol translocation unit. Biochemistry. 29:10659–10663. [DOI] [PubMed] [Google Scholar]
- Lolkema, J. S., E. S. Wartna, and G. T. Robillard. 1993. Binding of the substrate analogue perseitol to phosphorylated and unphosphorylated enzyme IImtl of the phosphoenolpyruvate-dependent phosphotransferase system of Escherichia coli. Biochemistry. 32:5848–5854. [DOI] [PubMed] [Google Scholar]
- Porumb, T. 1994. Determination of calcium-binding constants by flow dialysis. Anal. Biochem. 220:227–237. [DOI] [PubMed] [Google Scholar]
- Rovati, G. E., D. Rodbard, and P. J. Munson. 1988. DESIGN: computerized optimization of experimental design for estimating Kd and Bmax in ligand binding experiments. Anal. Biochem. 174:636–649. [DOI] [PubMed] [Google Scholar]
- Schumacher, C., and V. von Tscharner. 1994. Practical instructions for radioactively labeled ligand receptor binding studies. Anal. Biochem. 222:262–269. [DOI] [PubMed] [Google Scholar]
- Westerhoff, H. V., A. H. C. A. Wiechmann, K. Van Dam, and K. J. Hellingwerf. 1989. On the evaluation of data from flow-dialysis experiments. J. Biochem. Biophys. Methods. 18:53–64. [DOI] [PubMed] [Google Scholar]
- Womack, F. C., and S. P. Colowick. 1973. Rapid measurement of binding of ligands by rate of dialysis. Methods Enzymol. 27:464–471. [DOI] [PubMed] [Google Scholar]