Theoretical Investigations on Azotobacter vinelandii Ferredoxin I: Effects of Electron Transfer on Protein Dynamics

Abstract

Structural, energetic, and dynamical studies of Azotobacter vinelandii ferredoxin I are presented for native and mutant forms. The protein contains two iron-sulfur clusters, one of which ([3Fe-4S]) is believed to play a central role in the electron-coupled proton transfer. Different charge sets for the [3Fe-4S] cluster in its reduced and oxidized state are calculated with broken symmetry ab initio density functional theory methods and used in molecular dynamics (MD) simulations. The validity of the ab initio calculations is assessed by comparing partially optimized structures of the [3Fe-4S] clusters with x-ray structures. Possible proton transfer pathways between the protein and the iron-sulfur cluster are examined by both MD simulations and ab initio calculations. The MD simulations identify three main-chain hydrogen atoms—HN(13), HN(14), and HN(16)—that are within H-bonding distance of the [3Fe-4S] cluster throughout the MD simulations. They could thus play a role in the proton transfer from the protein to the iron-sulfur cluster. By contrast, the HD2(15) atom of the Asp-15 is seldom close enough to the [3Fe-4S] cluster to transfer a proton. Poisson-Boltzmann calculations indicate that there is a low, but nonzero probability, that Asp-15 is protonated at pH 7; this is a requirement for it to serve as a proton donor. Ab initio calculations with a fragment model for the protein find similar behavior for the transfer of a proton from the OH of the protonated side chain and the main-chain NH of Asp-15. The existence of a stable salt bridge between Asp-15 and Lys-84 in the D15E mutant, versus its absence in the wild-type, has been suggested as the cause of the difference in the rate of proton transfer. Extensive MD simulations were done to test this idea; the results do not support the proposal. The present findings, together with the available data, serve as the basis for an alternative proposal for the mechanism of the coupled electron-proton transfer reaction in ferredoxin I.

INTRODUCTION

Proteins containing iron-sulfur clusters play important roles in biological systems. Examples include the transcription factor fumarate nitrate reduction protein, which requires an iron-sulfur cluster for its regulatory function (production of ammonia) to switch from aerobic to anaerobic metabolism (Khoroshilova et al., 1997) or aconitase where iron-sulfur centers are involved in regulatory control such as cluster degradation, conversion, or redox processes (Beinert et al., 1996). The iron-sulfur clusters in such systems are important both as structure-determining entities because of their interactions with protein ligands and as the reactive centers because of their electronic properties. The clusters can accept, release, shift, and store electrons; one example is the [NiFe]-hydrogenase of desulfovibrio gigas where three aligned iron-sulfur clusters appear to define the pathway for electron transport toward the outside of the protein (Volbeda et al., 1995). Iron-sulfur clusters can also bind and activate substrates such as in the binding of citrate to the Fe₄S₄ cluster of aconitase (Beinert et al., 1996). Additional interesting functions include the regulatory functions of Fe-S-containing protein in connection with binding of dioxygen, 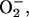and NO (Johnson, 1998; Hentze and Kühn, 1996).

In certain systems of biological relevance electron transfer is coupled to proton transfer. For example, in the bacterial photosynthetic reaction center, electron and proton transfer reactions convert light into chemical energy. In such reactions, the transfer of a proton is coupled to a change of the electronic structure of the proton acceptor. Coupled electron-proton transfer processes have been studied experimentally (Malmström, 1993) and theoretically (Cukier and Nocera, 1998; Hammes-Schiffer, 2001). One reason for the interest in this area is the importance of the proton transfer itself, which is involved in energy transduction (such as in the bacterial photosynthetic reaction center) and in structural rearrangement of proteins. Coupling proton transfer to the electronic structure of the surrounding protein matrix or a solvent complicates the processes considerably. Approaches that have been investigated include a dielectric formalism to treat solvent effects with two adiabatic electronic potential energy curves (Cukier, 1996; Cukier and Nocera, 1998), multistate continuum theory (Soudackov and Hammes-Schiffer, 2000), and the nonadiabatic instanton approach (Jang and Cao, 2001). Whereas the last has only been applied to models, the other two have been used in studies with a realistic representation of the system of interest (Cukier, 1996; Iordanova and Hammes-Schiffer, 2002). The two approaches differ mainly in the way that the solvent is taken into account. Cukier treats solvent coordinates in an adiabatic fashion (Cukier, 1996) and the method of Hammes-Schiffer takes solvent coordinates into account explicitly (Soudackov and Hammes-Schiffer, 2000).

Before treating such a complex reaction for a realistic system at a detailed (e.g., quantum mechanical) level it is essential to investigate its structural properties and the nuclear dynamics involved. For such a study it is important to use a system for which the necessary data are available. Recently, the coupled electron-proton transfer involving a [3Fe-4S] cluster in the Azotobacter vinelandii protein ferredoxin I (FdI) has been investigated in some detail, and a series of high-resolution x-ray structures for the native and mutant proteins were determined (Chen et al., 2000). The main conclusions from the experimental investigations, together with preliminary molecular dynamics (MD) simulations, concerned the role of the Asp-15 residue. The authors suggest that Asp-15 serves as the proton relay, i.e., the proton is accepted by the residue Asp-15 from the solvent and transported toward the iron-sulfur cluster [3Fe-4S] by rapid movements of the residue (Chen et al., 2000). This conclusion was based primarily on site-directed mutagenesis and pK_a studies of the native and mutant proteins; e.g., it was found that the wild-type (Asp-15) FdI had a faster rate (by two orders of magnitude) compared to the D15N and D15E mutants (Asp-15→Asn-15 and Asp-15→Glu-15, respectively; Chen et al., 2000). Cherepanov and Mulkidjanian (2001) have reported molecular dynamics simulations on wild-type ferredoxin I (PDB code 7FD1) and the Asp-15→Glu-15 mutant (PDB code 1D3W). For each system they analyzed one 1.25-ns trajectory and estimated the free energy along a progress coordinate (Cherepanov and Mulkidjanian, 2001). Their MD simulations indicated that there are two conformational substates (with and without a salt bridge between Lys-84 and Asp-15) for the wild-type FdI but only one substate with a salt bridge for the less active D15E mutant. They concluded from this that the presence of the salt bridge was directly responsible for the lowering of the transfer rate in the mutant. However, one trajectory is likely not to be sufficient for a firm conclusion.

Given these experimental and simulation studies, we investigate a number of unresolved questions concerning the coupled electron-proton transfer in ferredoxin I. In the present work, we use molecular dynamics simulations for an investigation of the structural, dynamic, and functional properties for FdI and some of its mutants. The necessary information about charge distributions, equilibrium geometries, and the energetics of smaller subsystems were derived from ab initio electronic structure calculations. The questions we address here concern mainly the possible proton donors around the [3Fe-4S] cluster, the sensitivity of the results to different charge distributions on the [3Fe-4S] cluster, and the effect of mutations on the dynamics of the proteins. We also determine the stability of the proposed salt bridge between Asp-15 and Lys-84 in the native protein and the D15E mutant by estimating the free energy along a chosen reaction coordinate. Since the role of a water molecule in the active site was already described in some detail (Meuwly and Karplus, 2003), we quote results from that study only where necessary in this work.

The article is organized as follows. After describing the methods in the next section, the x-ray and theoretical structures of the wild-type (PDB codes 7FD1, oxidized crystal; and 7FDR, reduced crystal; Schipke et al., 1999) and the three mutant proteins (D15N, PDB code 1FDD; D15E, PDB code 1D3W; and T14C, PDB code 1A6L) are explored. Ab initio structures and energetics of isolated and complexed Fe-S clusters are presented in Results, along with titration curves for the native and the T14C mutant. Hydrogen atoms around the [3Fe-4S] cluster that could serve as proton donors are identified and the stability of the salt bridge between residues 15 and 84 is investigated for the native and D15E mutants. In the Concluding Discussion, the results are discussed and conclusions are presented.

THEORETICAL METHODS

Ab initio electronic structure calculations

Electronic structure calculations are used to investigate the charge distributions and minimum energy structures of [3Fe-4S] clusters under different conditions (see below). The charges are needed for the MD simulations. All calculations were carried out using the Gaussian98 suite of programs (Frisch et al., 1998). The calculations started with a UHF/3-21G^* description and improved basis sets were used to refine the results. Finally, all calculations for the structures and the charges were carried out at the UB3LYP/6-31G^** level. The SCF density was converged to better than 10⁻⁵ E_h throughout. The oxidation states of the iron-sulfur clusters considered are [3Fe-4S]⁰ (S = 2) and [3Fe-4S]⁺ (S = 1/2) (Kent et al., 1980; Johnson, 1998). In all calculations broken symmetry wave functions are used (Noodleman et al., 1988). They are straightforward to calculate but are not true eigenfunctions of 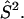The wavefunction for [3Fe-4S]⁺ (S = 1/2) contains one low-spin iron (Fe^II), which gives rise to a mixed spin state. In both cases considerable spin contamination is present. (For a detailed discussion, see Huynh et al., 1980 and Noodleman et al., 1988.) One possible consequence of the mixed spin state is that the geometry of the oxidized cluster is not very reliable. However, the resulting wave functions can be used for the estimates of the partial charges, which is the main purpose of the present considerations. Atomic charges were calculated based on several possible partition schemes: Mulliken charges, charges based on the analysis of natural bond orbitals (NBO) (Reed et al., 1985), and charges fitted to the electrostatic potential (ESP) (Singh and Kollman, 1984; Besler et al., 1990). In Meuwly and Karplus (2003) it was shown that the present approach gives satisfactory agreement with comparable calculations by Noodleman et al. (1988), Mouesca et al. (1994), and Li et al. (1998) on [2Fe-2S]^2−/3− (SCH₃)₄.

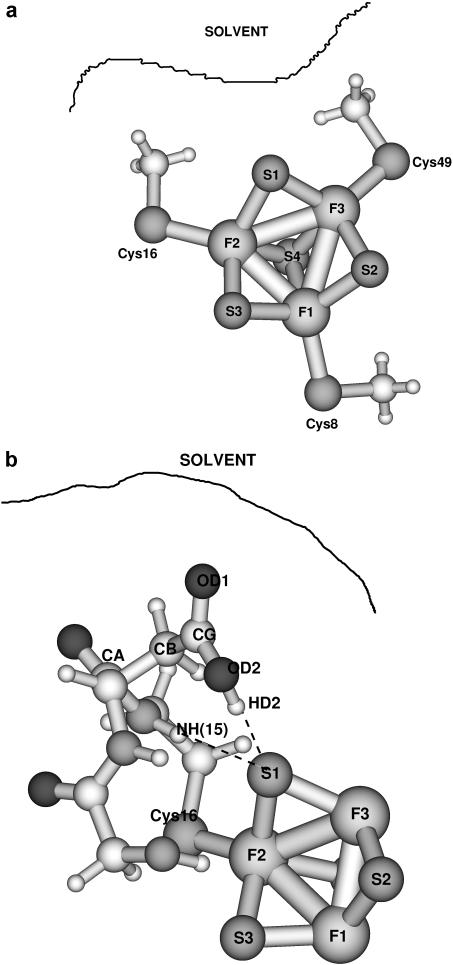
Calculations were carried out for five systems: [3Fe-4S]^0/+, [3Fe-4S]^0/+ (SCH₃)₃ (shown in Fig. 1 a), and the model system shown in Fig. 1 b. This model system is composed of the [3Fe-4S]⁰ cluster, the Asp-15 residue and part of the neighboring Thr-14 and Cys-16 residues. It provides a means of taking into account the immediate protein environment in the quantum mechanical calculations. In all cases, the x-ray structure of 7FDR was used as the starting geometry and in the geometry optimizations the dihedral angles in the [3Fe-4S] cluster and the protein environment were kept fixed; for the [3Fe-4S] (SCH₃)₃ systems the S-Fe bond lengths between cysteine-S atoms and the cluster-Fe atoms were also kept fixed. Only atom distances and valence angles within the [3Fe-4S] cluster were allowed to vary in the optimizations. The bare clusters are used primarily for calculating atomic charges for the MD simulations whereas the thiolate-complexed [3Fe-4S] (SCH₃)₃ are much closer to geometric mimics of protein active sites. Use of the bare clusters avoids the need to redistribute the charge of the SCH₃ groups in determining partial charges for the cluster. Related systems have been investigated previously by calculations on [2Fe-2S] and [4Fe-4S] clusters (Mouesca et al., 1994; Li et al., 1998; Torres et al., 2003), whereas Zhou and co-workers have synthesized a cuboidal Fe₃S₄ cluster (Zhou et al., 1996).

FIGURE 1.

(a) Model system [3Fe-4S]^0/+ 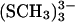for the investigation of the charges on the [3Fe-4S] cluster. The organic sulfur atoms have been placed at the positions of the Cys-S-atoms from 7FDR with their appropriate labelings. The numbering of the atoms is the one used in the text. (b) Model system for the calculation of intermolecular interactions between Asp-15 and an iron-sulfur cluster [3Fe-4S]. The labeling of the atoms (CA, CB, CG, OD1, OD2, and HD2) is the one used later. In both cases the solvent is indicated schematically.

In the studies of the proteins (see below), different states and preparations of the systems are described by a three-letter code. It labels the reduction state of the cluster (R for reduced, O for oxidized), the protonation state of the carboxylate of Asp-15 (P for protonated, and U for unprotonated), and the charge set used (M for Mulliken, N for NBO, and E for ESP charges).

Molecular dynamics simulations and preparation of the systems

All molecular dynamics simulations were carried out using the CHARMM program (Brooks et al., 1983). The minimizations were done using 1500 steps of Newton-Raphson minimization. They were carried out in vacuo, with a distance-dependent dielectric of strength 2 (ɛ(r) = 2r), and in explicit water (see below). In all calculations nonbonded terms were damped using a switch function for van der Waals terms and a shifted function for electrostatics at 12 Å. The stochastic boundary method was used to increase computational efficiency (Brooks and Karplus, 1983, 1989). Simulations of the different systems considered were carried out using Langevin dynamics with friction coefficients of 62 kcal/mol for water molecules and mass-scaled friction coefficients (up to 250 kcal/mol) for heavy atoms in the buffer region with a radius of 16 Å and defined around the center of mass of the [3Fe-4S] cluster. In all trajectory calculations that used SHAKE to constrain the hydrogen-bond lengths the time step was 1 fs (Van Gunsteren and Berendsen, 1977). The total simulation time for each run was 250 ps unless otherwise stated. For most results five different trajectories were calculated. They were started from initial conditions generated toward the end of the equilibration stage, namely at 65, 67.5, 70, 72.5, and 75 ps. Several Langevin dynamics simulations were carried out without SHAKE in which case the time step was reduced to 0.1 fs and the total simulation time was 50 ps. Umbrella-sampling (Bartels and Karplus, 1997) was used to investigate rotational barriers for the carboxylic group of the Asp-15 residue. The orientational angle of the COOH group was changed in increments of 10° between 0° and 360°. Each of the 10 runs consisted of eight iterations with 500 molecular dynamics steps for equilibration, followed by 5000 steps during which the statistics were acquired. As in Bartels and Karplus (1997), the umbrella potential is represented with 12 trigonometric functions. Because the 10 individual umbrella-sampling runs started from different initial conditions the estimated free energy profiles can vary considerably. Variances between 1 kcal/mol and 3 kcal/mol were found.

For the structural calculations and the MD simulations it is necessary to provide charges on the atoms of the [3Fe-4S] cluster. In addition, force-field parameters have to be provided for the S-Fe bonds and the S-Fe-S and Fe-S-Fe angles. For the angular terms the same parameters were used as by Banci and co-workers (Banci et al., 1992), namely k = 55 kcal/mol/Å and θ_eq = 109.5° and θ_eq = 75° for the equilibrium angles of the S-Fe-S and Fe-S-Fe valence angles, respectively. For the Fe-S bond an equilibrium value of 2.35 Å was chosen in accordance with the x-ray and ab initio structures and the force constant was k = 250 kcal/mol/Å. This value is close to the force constant calculated for Fe-S at the B3LYP/6-31G^** level. Also, such a force constant is typical in the CHARMM22 force field for Fe-X interactions where X is N, C, and O.

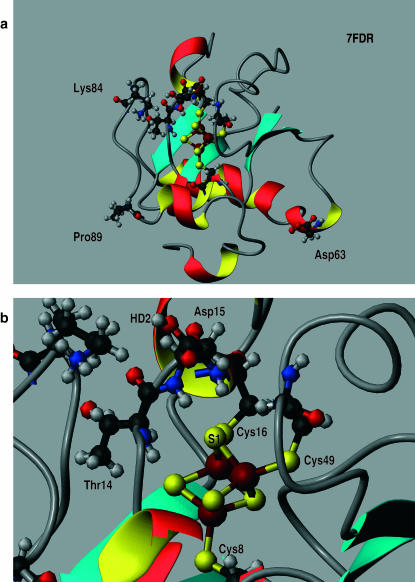
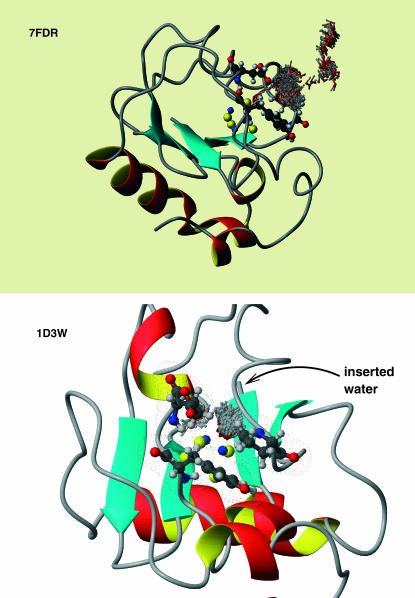
The crystal structures of 7FD1 (oxidized wild-type), 7FDR (reduced wild-type), and 1FDD (D15N) from the Protein Data Bank (PDB) were used to set up the systems (Schipke et al., 1999; Stout et al., 1998; Shen et al., 1993). The proteins consist of 856 heavy atoms. All x-ray water molecules were removed. An overview of 7FDR shown in Fig. 2, a and b, gives a detailed view of the region around the [3Fe-4S] cluster. Hydrogen atoms were added by using the method of Brünger and Karplus (1988). Subsequently, the structures were partially minimized with constraints on the side-chain atoms (50 kcal/mol) and the backbone and iron-sulfur-cluster atoms (100 kcal/mol). Three layers of solvent water were added from an equilibrated sphere of 20 Å radius around the [3Fe-4S] cluster; the center of the sphere was the center of mass of the [3Fe-4S] cluster. For the equilibration of the water the protein atoms were fixed and the water molecules were equilibrated using Langevin dynamics (Brooks and Karplus, 1983). Then 75 ps of equilibration Langevin dynamics were run, for the entire system at a temperature of 300 K, before the production runs.

FIGURE 2.

(a) Overview of 7FDR. Residues 14, 15, 63, 84, and 89 are represented as ball-and-stick models. Likewise, the [3Fe-4S] cluster along with the cysteines bound to it (8, 16, and 49) are represented as ball-and-stick. (b) Enlarged view of the site of interest together with a number of key residues for the present study. The [3Fe-4S] cluster is bound to Cys-8, Cys-16, and Cys-49.

Calculation of titration curves

The calculation of the average protonation state as a function of pH particularly for the Asp-15 residue is of importance in itself and is needed to choose the initial conditions from which to start the MD simulations (see above). To this end the procedure proposed by Schaefer and co-workers was used (Schaefer et al., 1997). The linearized finite-difference Poisson-Boltzmann method is used to calculate the electrostatic free energy and the titration curves of the residues are obtained by explicitly summing over all terms of the partition function. The ionic strength was 145 mmol which is the physiological value. 7FD1 contains 37 titratable sites. Since a calculation using an exact summation over all realizations is very time-consuming (it involves 9 × 2³⁴ terms) residues further away than 20 Å from Asp-15 were not considered as titratable residues; they were given standard CHARMM22 charges for pH 7. The validity of this approach was verified by introducing some of the omitted titratable groups into the calculation and checking for any differences in pK_a that arose. In every case 28 titratable groups were retained; this leads to a total of 9 × 2²⁵ terms.

The Asp-15 residue was assumed to be a three-state system, including either of the two oxygen atoms (OD1 and OD2) as proton acceptors and the unprotonated state. The standard 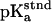of both states was taken to be 3.7 so that the intrinsic 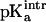of Asp-15 is 4.0, the value from experiment in solution. In all calculations the [3Fe-4S] clusters were modeled as a five-state system (unprotonated and one proton at each sulfur atom).

RESULTS

Structural data

The structures of the isolated [3Fe-4S] cluster and a model [3Fe-4S] (SCH₃)₃ cluster obtained by ab initio calculations are presented here. The results provide information about the influence of the presence of negative charges (through the SCH₃ group) on the geometry of the [3Fe-4S] cluster. The optimized structures from ab initio and force-field calculations and temperature-averaged structures are also compared. The role of nearby protein side chains for proton transfer is described in Exploration of Proton Transfer Mechanisms by Simulations.

Nuclear charges for the bare [3Fe-4S] clusters

In addition to the standard force field for the protein and water molecules in the CHARMM program a consistent set of atomic charges for [3Fe-4S]^0/+ is required for the MD simulations. They were determined at the UB3LYP/6-31G^** level. Two structures for the cluster were used to assess the variability of the charges with the structure of the cluster. One was the minimum energy structure of the isolated [3Fe-4S]⁺ with UHF and the 3-21G^* basis set and the other one was the experimentally determined structure in the protein; as to the latter, it was found that the structures of [3Fe-4S]⁰ and [3Fe-4S]⁺ are very similar (see below) (Schipke et al., 1999). The geometry and the atom labeling are shown in Fig. 1. The calculated and experimentally determined structures differ primarily in the S-Fe and Fe-Fe bond lengths, which are 2.28 Å and 2.68 Å on average in the x-ray structure and 2.46 Å and 2.94 Å on average in the UHF/3-21G^* geometry. Charges based on the UHF/3-21G^* structure are reported for illustrative purposes only; all MD simulations were carried out using the charges calculated for the x-ray structure. Mulliken charges, NBO charges (Reed et al., 1985), and charges fitted to the electrostatic potential (ESP) (Singh and Kollman 1984; Besler et al., 1990) are reported in Table 1. As already observed previously the atomic charges are substantially different from the nominal charges of +3 and −2 for Fe and S atoms, respectively (Banci et al., 1992). Despite the relatively large changes in bond lengths (≈0.4 Å) between the experimental and the UHF/3-21G^* geometry (see above), the nuclear charges vary only by ∼0.1 e between the two structures.

TABLE 1.

Atomic charges using B3LYP/6-31G^** for different models for the [3Fe-4S]^0/+ clusters

Model	S4	S	Fe
[3Fe-4S]0
Mulliken/UHF geometry	−0.630	−0.590	0.800
Mulliken/Exp geometry	−0.510	−0.480	0.650
NBO/UHF geometry	−1.100	−0.980	1.350
NBO/Exp geometry	−1.000	−0.920	1.250
ESP/Exp geometry	−0.700	−0.630	0.863
[3Fe-4S]+
Mulliken/UHF geometry	−0.560	−0.330	0.850
Mulliken/Exp geometry	−0.360	−0.250	0.700
NBO/UHF geometry	−0.980	−0.590	1.250
NBO/Exp geometry	−0.830	−0.640	1.250
ESP/Exp geometry	−0.538	−0.398	0.910

S4 signifies the threefold coordinate inorganic sulphur. All charges are given in units of e.

Geometrical parameters of the [3Fe-4S] (SCH₃)₃ clusters

The bare, gas phase [3Fe-4S] clusters are not good structural models for the protein-bound iron-sulfur clusters (Mouesca et al., 1994; Li et al., 1998; Zhou et al., 1996). To gain more insight into the validity of the UB3LYP/6-31G^** method on which the charges are based, optimized structures of the model systems [3Fe-4S] 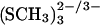were investigated; the latter are closer to the protein-bound clusters in terms of the local charge environment, as well as to a model system. Zhou and co-workers have synthesized a cuboidal Fe₃S₄ cluster in a nonprotein environment (1,3,5-tris((4,6-dimethyl-3-mercaptophenyl)thio)-2,4,6-tris(p-tolythio)benzene) and obtained an x-ray structure for [3Fe-4S]⁰ (Zhou et al., 1996); their structural results are also given in Table 2. The structures of [3Fe-4S]^0/+ clusters in A. vinelandii have been determined in two different crystals by x-ray crystallography (PDB codes 6FD1, 7FD1 for oxidized [3Fe-4S]⁺; and 6FDR, 7FDR for reduced [3Fe-4S]⁰). From the analysis it was concluded that the structures of [3Fe-4S]⁺ and [3Fe-4S]⁰ are the same within experimental error (≈±0.02 Å for Fe-S bonds; Schipke et al., 1999). In all ab initio geometry optimizations the bond lengths and the valence angles were optimized, whereas the dihedral angles were fixed at the values from x-ray crystallography. Bond lengths and angles of (SCH₃)⁻ with respect to the cluster were fixed at the x-ray values in 6FD1(for [3Fe-4S]⁰), and 6FDR (for [3Fe-4S]⁺). The (SCH₃)⁻ ligand is a model for the cysteine residues Cys-8, Cys-16, and Cys-49, in the protein environment. In Table 2 the bond lengths at the UB3LYP/6-31G^** level are reported together with data from the literature. Results are given as average distances of the S-Fe and Fe-Fe bonds. In the following only the average distances are discussed. The S4-Fe distances refer to the threefold-coordinated sulfur atom in [3Fe-4S]. In general, bringing the cluster into a protein environment leads to an elongation of all bonds. The effect on the averaged distances is between 0.05 Å (for S₄-Fe) and 0.2 Å (for Fe-Fe distances). We also note that each (SCH₃)⁻ substituted cluster had a charge of −2 and −3, which in itself is likely to lead to an expansion. Recently, the structures of various oxidation states of the [4Fe-4S] clusters have been investigated using the local density approximation with the parameterization of Vosko, Wilk, and Nusair and nonlocal corrections for exchange and correlation together with an uncontracted triple-ζ Slater-type basis set augmented by polarization functions (Torres et al., 2003). It was found that geometries and electronic properties of these clusters are well described by density functional theory using broken symmetry wavefunctions, which were also used here. The differences between experimentally measured and calculated bond lengths found there are between 0.01 Å and 0.07 Å for Fe-Fe distances (0.1 Å and 0.15 Å here) and below 0.01 Å up to 0.1 Å for Fe-S distances (0.02 Å to 0.11 Å here). These calculations were carried out with symmetry constraints which was not done here. This may explain in part some of the differences between experimental and calculated data observed in the present case, in particular for the Fe-Fe distances. Also, the [3Fe-4S] clusters are more open and flexible compared to the [4Fe-4S] cluster due to the “missing” Fe atom. This is considered further below where the clusters are investigated at finite temperature. In line with the observations in Torres et al. (2003), an expansion of the core is found upon reduction of the cluster.

TABLE 2.

Averaged distances (in Å) from ab initio calculations of the free clusters and [3Fe-4S] (SCH₃)₃^2−/3− compared to experimental values

	[3Fe-4S]0 Free	[3Fe-4S]+ Free	[3Fe-4S]0	[3Fe-4S]+	[3Fe-4S]0 X-ray in 6FD1*	[3Fe-4S]+ X-ray in 6FDR*	[3Fe-4S]0 X-ray in nonprotein†
[S4-Fe]	2.35	2.30	2.40	2.33	2.29	2.31	2.30
[S-Fe]	2.22	2.19	2.32	2.24	2.25	2.25	2.26
[Fe-Fe]	2.61	2.65	2.83	2.80	2.68	2.68	2.70

^*Schipke et al. (1999).

^†Zhou et al. (1996).

Structures of isolated and protein-bound [3Fe-4S] clusters at finite temperature

To assess the influence of the protein environment on the average structure of the cluster, trajectories were run for the isolated [3Fe-4S]^0/+ cluster and for 7FDR at 100 K; 100 K was used because the crystal data correspond to that temperature. In all calculations the same force-field parameters (force constants for intermolecular bonds and valence angles) were used for reduced and oxidized [3Fe-4S]; the only difference between the two were the atomic charges of the clusters.

For the isolated clusters, MD simulations were carried out as follows. After heating [3Fe-4S]^0/+ to 100 K for 5 ps and equilibrating for 25 ps, production runs 50 ps in length were analyzed for the S-Fe and Fe-Fe distances. It is found that the averaged nonbonded Fe-Fe distance is ∼2.70 Å (for oxidized [3Fe-4S]) and 2.65 Å (for reduced [3Fe-4S]), slightly larger than the values found in the ab initio calculations (see Table 2). For comparison, optimization of the isolated [3Fe-4S] clusters using the molecular mechanics force field yields 2.69 Å and 2.65 Å, respectively. The Fe-Fe distances for the oxidized cluster are larger by 0.04 Å (for both structural optimizations with the force field and the thermally averaged motion) than for the reduced cluster, whereas the bonded S-Fe distances are quite similar for both clusters.

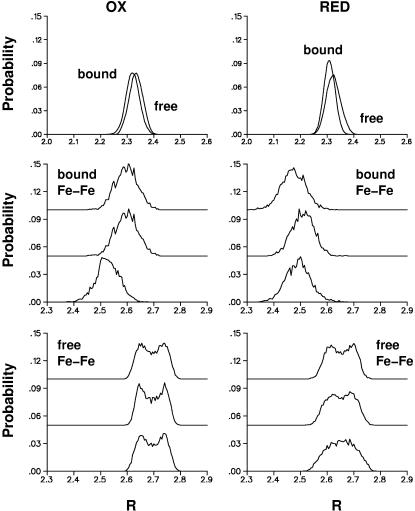
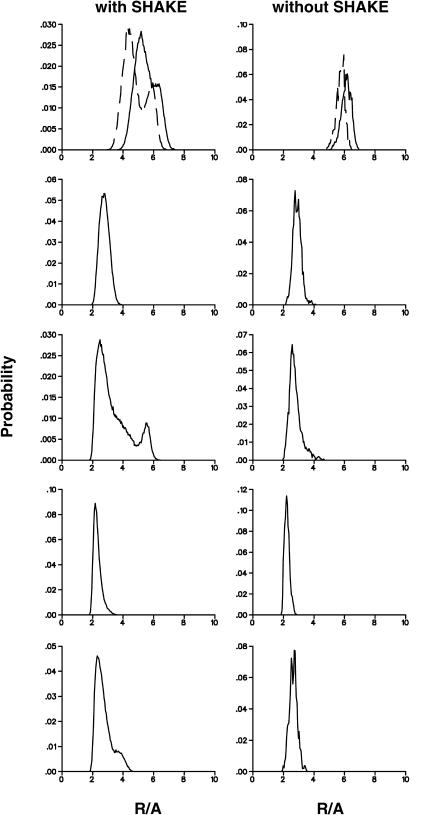
To investigate the effect of the protein environment on the structure of the [3Fe-4S] clusters the minimized structure of 7FDR was equilibrated at 100 K for 75 ps. Subsequently a molecular dynamics trajectory was run for 100 ps and the time-averaged S-Fe and Fe-Fe distances were calculated as before. Fig. 3 shows distribution functions of the various distances. The S-Fe distances within the [3Fe-4S] cluster are very similar to those in the free [3Fe-4S] cluster (Fig. 3, top panels) for both reduced and oxidized [3Fe-4S]. However, the thermally averaged nonbonded Fe-Fe distances are considerably shortened (0.1 Å for oxidized and 0.13 Å for reduced [3Fe-4S]) compared to the free cluster (see Fig. 3, middle and lower panels). Thus, the protein leads to a compression of the [3Fe-4S] cluster through nonbonded (van der Waals and electrostatic) interactions, in particular for the Fe-Fe distances. This finding also establishes that the [3Fe-4S] is quite deformable.

FIGURE 3.

Probability distributions for the three individual Fe-Fe distances for the free (bottom panel) and protein-bound (middle panel) [3Fe-4S]^0/+ clusters; the protein structure used was 7FDR. The thermal average of all nine Fe-S distances is shown in the top panels for the free and protein-bound clusters. Probability distribution functions for [3Fe-4S]⁺ are displayed on the left, and for the [3Fe-4S]⁰ on the right.

One possibility for comparing the results of the MD simulations with experimental data is to consider the widths of the probability distribution functions of the bond lengths. In the simulations they are ≤0.05 Å for Fe-S bonds and ≈0.1 Å for nonbonded Fe-Fe distances (see Fig. 3). Related quantities can be derived from the isotropic thermal parameters U_iso. They are converted into variances of bond lengths using 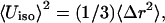where Δr is the radius of the thermal sphere (Stout and Jensen, 1989). Using the values given in Zhou et al. (1996) for (1,3,5-tris((4,6-dimethyl-3-mercaptophenyl)thio)-2,4,6-tris(p-tolythio)benzene), this yields Δr ≈ 0.1 Å and thus the width of the probability distribution function of a particular bond length can be at most ±0.2 Å. This width originates from both the thermal distribution and the uncertainty of the experiment. All calculations described so far indicate that effects of the protein on the change in the structure of the cluster upon oxidation or reduction are small. Mainly the unbound Fe-Fe distances appear to be altered; the variance in these distances is of the order of 0.15 Å, which is also the difference in the geometries between the free clusters and the clusters connected to the (SCH₃) groups in the ab initio calculations (Table 2).

Structures of native and mutant ferredoxin I

X-ray structures of the native FdI in the reduced and oxidized form of the [3Fe-4S] cluster have been determined. Before discussing structures obtained from calculations, it is useful to consider the x-ray structures of 6FD1, 7FD1, 6FDR, and 7FDR (Chen et al., 2000; Schipke et al., 1999). Stout and co-workers found that the differences between the oxidized and reduced structures (e.g., 6FD1 vs. 6FDR) are similar to the differences between the two oxidized (6FD1 vs. 7FD1) and the two reduced structures, respectively (Stout et al., 1998). For example, the six pairwise least-squares superpositions of the four x-ray structures give root-mean square deviations of 0.18 Å to 0.42 Å for all atoms and from 0.09 Å to 0.12 Å for main-chain N, C_α, C, and O atoms (Schipke et al., 1999). These variations give an indication of the uncertainty in the crystal data and suggest that the changes with the ionization state are small.

To gain an overview of the influence of different charge sets and the conditions used (see Theoretical Methods for definitions) the structure of 7FDR (with a reduced [3Fe-4S] cluster) was optimized using the adoptive Newton-Raphson algorithm with a variety of parameter sets. The results are collected in Tables 3–5. For each realization of the system (see Ab Initio Electronic Structure Calculations, in Theoretical Methods), the distances and angles important for the proton transfer are reported. In Table 3 these geometrical parameters are presented for the system that was minimized in vacuo (ɛ = 1) with 1000 steps of Newton-Raphson optimization. In the last three columns of Table 3 the geometrical parameters are given for the optimization carried out with a distance-dependent dielectric constant, ɛ(r) = 2r (such calculations are referred to with an additional 2 in the three-letter symbol). All optimizations that use a protonated Asp-15 lead to better agreement between the x-ray structures and the calculated structures; e.g., there is near-quantitative agreement for the OD2(15)–NZ(84), N(15)–S1, and N(14)–S3 distances and the angle S1-OD2(15)-NZ(84) is in much better agreement with experiment than for unprotonated Asp-15. The differences between RPM, RPN, and RPE are quite small despite the considerably different charge sets (see Table 1). Table 4 collects the root-mean square deviations (RMSD) for each of the optimizations with respect to the x-ray structure. RMSD values for the heavy atoms and main-chain atoms are comparable to the pairwise least-squares fits mentioned above (Schipke et al., 1999). Performing the optimizations with a distant-dependent dielectric has a favorable effect on the agreement between the x-ray and theoretical structures; i.e., the calculations with a distant-dependent dielectric reduce the RMSD values by up to 50%.

TABLE 3.

Important intermolecular distances for 7FDR (reduced) under various conditions

Distance (Å)	X-ray*	RPM	RUM	OPM	OUM	RPN	RUN	OPN	OUN	RPE	RPM2	RPN2	RPE2
OD2(15)–S1	4.71	5.22	4.56	5.23	3.96	5.25	4.49	5.23	3.46	5.16	4.95	4.98	4.96
OD2(15)–NZ(84)	4.55	5.08	2.81	5.17	3.36	5.12	2.84	5.20	3.79	5.13	4.50	4.51	4.50
NZ(84)–S1	7.53	7.15	6.63	7.34	6.76	7.07	6.63	7.35	6.82	7.10	6.93	6.86	6.92
N(14)–S3	3.15	2.96	3.04	3.06	3.08	2.96	3.03	3.07	3.06	3.00	3.10	3.12	3.09
N(15)–S1	3.27	3.33	3.61	3.60	3.76	3.36	3.64	3.64	3.72	3.41	3.10	3.35	3.32
S1–OD2(15)–NZ(84)	99	88	126	90	135	88	128	90	133	89	94	92	94

In all cases the structure has been optimized without explicit water molecules for 1000 steps of Newton-Raphson minimization. R and O refer to reduced and oxidized [3Fe-4S], P and U to protonated and unprotonated Asp-15, and M and N to Mulliken and NBO charges, respectively. The additional label 2 in the last three columns indicates that these calculations were carried out in distance-dependent dielectric ɛ(r) = 2r.

^*Schipke et al. (1999).

TABLE 5.

Important intermolecular distances in 7FDR (reduced) after solvation and 1500 steps of Newton-Raphson

Distance (Å)	X-ray*	RPM	RPN	RPE
OD2(15)–S1	4.71	4.88	4.82	5.15
OD2(15)–NZ(84)	4.55	4.67	4.47	4.75
NZ(84)–S1	7.53	7.02	7.18	7.12
N(14)–S3	3.15	3.06	2.91	3.11
N(15)–S1	3.27	3.09	3.11	3.76
S1–OD2(15)–NZ(84)	99	95	101	92

^*Schipke et al. (1999).

TABLE 4.

Overall quality of the optimizations; RMSD values for different regions of 7FDR and clusters after 1000 steps of Newton-Raphson minimization; values in Å

RMSD	RPM	RUM	OPM	OUM	RPN	RUN	OPN	OUN	RPE	RPM2	RPN2	RPE2
Heavy atoms	0.4338	0.4384	0.4451	0.4453	0.4332	0.4468	0.4405	0.4426	0.4329	0.2739	0.2750	0.2741
Protein backbone	0.2115	0.2140	0.2255	0.2239	0.2119	0.2121	0.2222	0.2209	0.2119	0.1537	0.1545	0.1540
Protein heavy	0.4382	0.4429	0.4498	0.4499	0.4375	0.4410	0.4452	0.4472	0.4375	0.2762	0.2771	0.2763
Protein sidechain	0.5307	0.5363	0.5425	0.5432	0.5296	0.5342	0.5373	0.5403	0.5297	0.3290	0.3301	0.3292
All FeS cluster atoms	0.1942	0.1933	0.1973	0.1909	0.2065	0.2079	0.1858	0.1823	0.1650	0.1303	0.1361	0.1300
Fe of FeS clusters	0.1463	0.1435	0.1571	0.1448	0.1516	0.1511	0.1402	0.1350	0.1226	0.0935	0.0975	0.0936
S of FeS clusters	0.2280	0.2281	0.2267	0.2235	0.2446	0.2472	0.2181	0.2154	0.1947	0.1556	0.1625	0.1550

After solvating the systems in explicit water (see Molecular Dynamics Simulations and Preparation of the Systems) the structures of the protein with reduced [3Fe-4S] and protonated Asp-15 were again minimized. This was done for the three charge sets (M, N, and E) using 1500 steps of Newton-Raphson minimization. The resulting geometrical parameters are displayed in Table 5. The charge sets give reasonable agreement with the experimental structure. All geometrical parameters are influenced by the explicit description of the solvent. For example, the OD2(15)-NZ(84) distance decreases by ≈0.5 Å when explicit water molecules are included. Other prominent changes concern the OD2(15)-S1 and the N(15)-S1 bonds, which contract upon solvation of the protein in explicit water (see Tables 3 and 5).

For 7FD1, which contains the oxidized [3Fe-4S] cluster, the same set of calculations was carried out. The results are collected in Table 6. In particular, it was of interest to determine whether the salt bridge between OD2(15)–NZ(84) is formed because this is of central concern in elucidating possible reaction mechanisms proposed in previous work. The in vacuo optimizations (ɛ = 1) results shown in Table 6 indicate that structures with unprotonated Asp-15 (letter codes XUY; see Molecular Dynamics Simulations and Preparation of the Systems) form a very strong salt bridge. However, the OD2(15)-NZ(84) distance is considerably smaller (by up to 20%) than the experimental value (3.56 Å), whereas with a protonated Asp-15 it is too long by up to 1.1 Å. Use of a distant-dependent dielectric (ɛ(r) = 2r) corrects the latter disagreement. For the unprotonated Asp-15 the salt bridge is still too short. For the other geometrical parameters in Table 6 there is better agreement between the structure with protonated Asp-15 and experiment. Finally, structural optimizations for 7FD1 in explicit water were carried out for protonated and unprotonated Asp-15 and oxidized [3Fe-4S]. The geometrical parameters (not shown) change compared to the calculations with a distant-dependent dielectric as was described for 7FDR (see above).

TABLE 6.

Important intermolecular distances for 7FD1 (oxidized) under various conditions

Distance (Å)	X-ray*	RPM	RUM	OPM	OUM	RPN	RUN	OPN	OUN	OPM2	OUM2	OPN2	OUN2
OD2(15)–S1	4.67	4.44	4.52	4.50	4.36	4.44	4.48	4.44	4.22	4.50	4.51	4.51	4.54
OD2(15)–NZ(84)	3.56	4.63	2.75	4.65	2.88	4.67	2.77	4.72	2.95	4.09	2.71	4.06	2.70
NZ(84)–S1	7.21	7.18	6.73	7.44	6.86	7.21	6.74	7.44	6.80	7.31	6.62	7.22	6.63
N(14)–S3	3.30	2.98	3.05	3.12	3.10	2.98	3.03	3.09	3.04	3.13	3.15	3.03	3.11
N(15)–S1	3.46	3.38	3.73	3.80	3.87	3.41	3.75	3.82	3.84	3.46	3.51	3.31	3.47
S1–OD2(15)–NZ(84)	122	105	135	109	142	105	135	109	143	117	132	116	131

In all cases the structure has been optimized without explicit water molecules for 1000 steps of Newton-Raphson. R and O refer to reduced and oxidized [3Fe-4S], P and U to protonated and unprotonated Asp-15, and M and N to Mulliken and NBO charges, respectively.

^*Schipke et al. (1999).

For 1FDD (D15N mutant) only the oxidation state of the [3Fe-4S] cluster and the charge set used can be varied. The optimizations were carried out in the same way as for the wild-type proteins (see above and Molecular Dynamics Simulations and Preparation of the Systems). Table 7 compares the bond lengths that were considered for the two wild-type proteins. The x-ray structure and the calculations agree to within 0.2 Å for the NZ(84) and S1 distance. The hydrogen bond N(14)-S3 is predicted slightly too short whereas N(15)-S1 is overestimated by ∼0.2 Å. If the optimizations are carried out with a distant-dependent dielectric (ɛ(r) = 2r) the former is unaffected, whereas the latter contracts by ∼0.3 Å. Overall, experiment and theory are in satisfactory agreement.

TABLE 7.

Important intermolecular distances for 1FDD under various conditions

Distance (Å)	X-ray*	RM	OM	RN	ON	RE	RM2	OM2	RN2	ON2	RE2
NZ(84)–S1	7.43	7.10	7.30	7.04	7.27	7.08	7.12	7.18	7.08	7.16	7.11
N(14)–S3	3.36	3.08	3.20	3.02	3.14	3.06	3.10	3.14	3.05	3.10	3.08
N(15)–S1	3.52	3.75	3.86	3.72	3.90	3.74	3.41	3.48	3.34	3.44	3.39

In all cases the structure has been optimized without explicit water molecules for 1000 steps of Newton-Raphson.

^*Schipke et al. (1999).

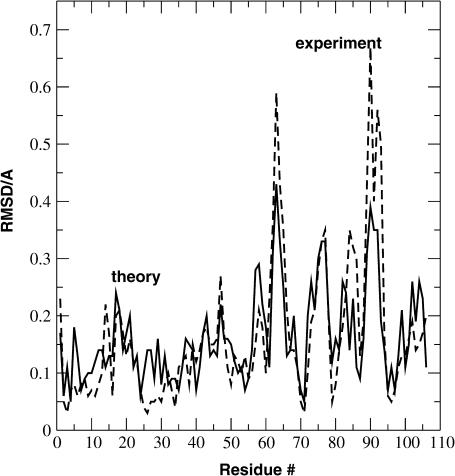
Until now the immediate environment of the [3Fe-4S] cluster was discussed. It is also possible to compare experimental and theoretical structures of the entire protein. This is done in Fig. 4. It shows the RMSD of all backbone atoms between 7FD1 and 1FDD for the experimental (Schipke et al., 1999; Chen et al., 2000) and the theoretical structure as a function of the residue number. The structures were optimized for 1000 steps of Newton-Raphson minimization with ɛ(r) = 2r. The characteristic peaks at residues Asp-63 and at Pro-89 to Asp-93 (see Fig. 2 for an overview) are reasonably well reproduced by the theoretical structures. The differences between the x-ray structures for 1FDD and 7FD1 are well preserved by the optimizations using the calculated charge sets and the CHARMM22 force field.

FIGURE 4.

Root mean-square deviation between experimental (dashed) 7FD1/1FDD and theoretically (solid) predicted structures as a function of the residue number. The theoretical calculations were done with the OPE parameter.

Titration curves for native and mutant FdI

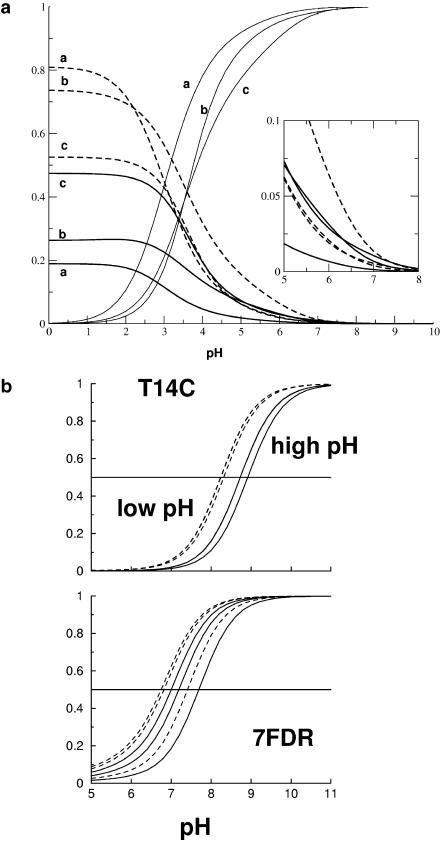
Titration curves for 7FDR were calculated for three different protein structures taken toward the end of the equilibration run at 65 (a), 70 (b), and 75 (c) ps (see Molecular Dynamics Simulations and Preparation of the Systems). For Asp-15, the orientation of the carboxylic acid between structures a and c differs by 90°. In a, one oxygen atom (OD1; see Fig. 1) is completely solvent-exposed (pK_a = 3.9), whereas the other oxygen atom (OD2) points toward the interior of the protein; in c, both oxygen atoms are solvent-exposed but far away from the cluster. The results of the titration calculations for Asp-15 are shown in Fig. 5 a. It shows that the pK_a values vary between 3.5 and 4.0, depending upon the structure (a, b, or c). As shown in the inset of Fig. 5, at pH 7 the carboxylate still has some probability of being protonated. It is reasonable, therefore, to assume that the Asp-15 can serve as a proton acceptor and donor, even though it has a normal pK_a for an aspartic acid. This is a prerequisite for proton transfer from the solvent via Asp-15 to the [3Fe-4S]⁰ cluster (Chen et al., 2000).

FIGURE 5.

(Upper panel) Titration curve for Asp-15 in 7FDR; 28 of the 36 protonatable groups were retained in the calculations (see text). The curves are calculated for structures taken at 65 ps (a), 70 ps (b), and 75 (c) ps of the equilibration run. Dashed lines are the deprotonation curves of OD1, the dotted lines for OD2, and the solid line gives the protonation curve of the protein (see Fig. 1 for numbering). The curves are labeled according to the structure (a–c) for which they were calculated. The inset shows a magnification of the region at ∼pH 7. (Lower panel) Titration curves for [3Fe-4S]^0/+ in the native FdI (below) and the mutant T14C (above). Dashed lines are for low pH solvent, solid lines for high pH solvent. The horizontal line allows us to determine the approximate pK_cluster from the intersection with each curve.

For the [3Fe-4S]^0/+ cluster, experimental data exist for the shift in pK_a in different mutants and in high- and low-pH solvent (pH 8.55 and 4.59 for native Fd1, respectively; Hirst et al., 1998). The pK_a of the [3Fe-4S]⁰ cluster in the native protein was estimated from the behavior of the proton transfer at different pH to be 7.8 when Asp-15 is ionized (high pH solvent) and 6.5 when Asp-15 is protonated (low pH solvent; Chen et al., 2000; Hirst et al., 1998).

Titration curves for the [3Fe-4S]^0/+ cluster in native 7FDR were calculated. To our knowledge, there is no experimental value for the gas phase or solution 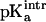of the free [3Fe-4S]⁰ cluster. We estimated this value by using the experimental pK_a for [3Fe-4S]⁰ and comparing it with the protein contribution obtained by the Poisson-Boltzmann calculations. The structure of 7FDR (with Asp-15 ionized, i.e., high-pH solvent) after 75 ps of equilibration dynamics was used and a range of values for 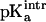between 6.5 and 7.5 with an interval of 0.1 were examined. For each of these values the corresponding pK_a was calculated. For 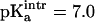the value of pK_a = 7.8 estimated from experiment (Chen et al., 2000) was obtained. Using 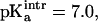titration curves for [3Fe-4S]⁰ were calculated for the three structures (a–c, see above) in high- and low-pH solvent (equivalent to ionized and protonated Asp-15). The results are given in the lower panel of Fig. 5 b; it shows that the pK_a values in high pH solvent range from 7 to 7.8 (experimental value: 7.8 ± 0.1) whereas they span 6.6–7.4 in low pH solvent (experimental value: 6.5 ± 0.1). In all cases the difference in pK_a for a given structure between unprotonated and protonated Asp-15 is 0.4. The correct trend of pK_a changes as a function of pH is obtained, although the magnitude of the change is smaller than the experimental estimate. In the experiment a range of protein structures contribute to the measured values of the pK_a values due to fluctuations at finite temperature; i.e., the experiment samples a distribution of structures which give rise to the observed pK_a values and not only one single x-ray structure. We note also that the experimental pK_a values were determined indirectly from the pH dependence of the proton transfer rates (Hirst et al., 1998).

To study the effect of a mutation on the pK_a values the T14C mutant was chosen because it has the largest change in pK_a compared to native FdI (Chen et al., 2000). The structure of T14C was prepared by a procedure analogous to that used for 7FDR (see Calculation of Titration Curves) and the structures after 65, 70, and 75 ps were again used for calculating the titration curves. In a high pH solvent (Asp-15 ionized) a pK_a of 8.6 to 8.8 was calculated whereas in low pH solvent (Asp-15 protonated) it was between 8.1 and 8.2. Again, the correct sign for the pH dependence is obtained whereas the magnitude is smaller than that inferred from experiment: pK_a = 8.4 high pH solvent and pK_a = 7.1 low pH solvent (Chen et al., 2000).

Exploration of proton transfer mechanisms by simulations

The molecular dynamics simulations are aimed at investigating various aspects of the coupled electron-proton transfer in A. vinelandii FdI. The questions we address here are:

• 1) What influence do different charge distributions on the [3Fe-4S] cluster have on the structure and dynamics?

• 2) Which protons in the neighborhood of the [3Fe-4S] cluster can serve as possible proton donors?

• 3) What changes around the active site are induced by mutations?

• 4) Can a water molecule enter and exit from the active site (around the [3Fe-4S] cluster) and be stabilized by it and could it serve as a possible proton donor?

One aspect of question 3, effect of mutations on the structures, was already treated in the last section; in particular, the observed changes in the overall structure of the proteins upon mutations are reproduced by structural minimizations. The remaining questions will be addressed here. Simulations for the proteins 7FDR, 7FD1, and 1D3W were carried out with the different realizations characterized by the three-letter symbols introduced in Molecular Dynamics Simulations and Preparation of the Systems.

To put the calculations in perspective it is useful to recall the putative overall reaction mechanism inferred from the experimental observations (Chen et al., 2000). Starting from the oxidized [3Fe-4S]⁺ cluster electron transfer leads to reduction ([3Fe-4S]⁰). Next, a proton is transferred from the environment and H⁺–[3Fe-4S]⁰ is formed which, after release of the proton, can oxidize back to [3Fe-4S]⁺. The calculations presented here aim particularly at investigating various aspects of the proton transfer to [3Fe-4S]⁰. For example, if Asp-15 is the source of the proton for [3Fe-4S]⁰, an important process is the delivery of a proton from the solvent to Asp-15, which requires a rotation of the carboxylic group to move the proton close enough to S1 of [3Fe-4S]⁰. Further, for the observed rate (1300 s⁻¹) the proton on Asp-15 (which has a low probability of being there) must spend sufficient time close to S1 of [3Fe-4S]⁰ to provide a high probability for proton transfer.

Possible hydrogen atom donors to [3Fe-4S]

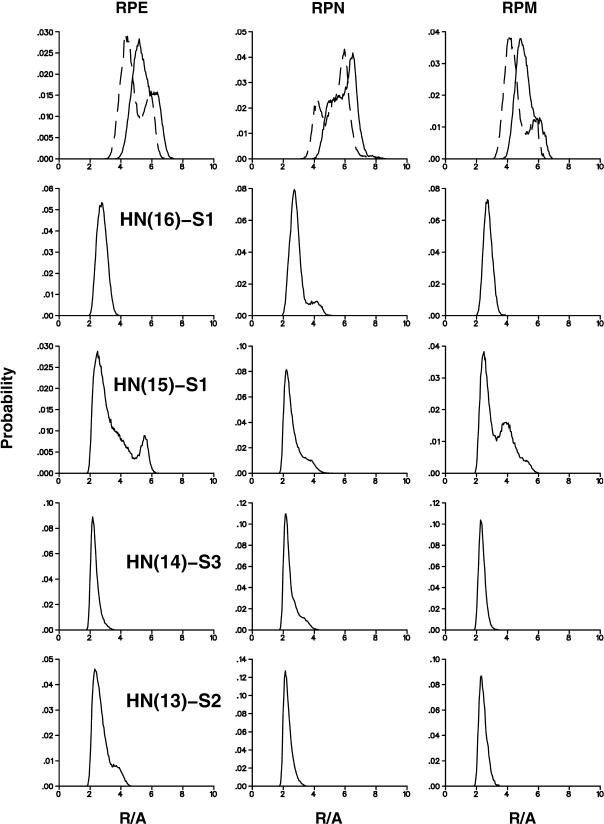
In the following, the distribution functions of hydrogen atoms around the [3Fe-4S] cluster are examined. Fig. 2 shows that there are a number of hydrogen atoms in the neighborhood of the [3Fe-4S] cluster which could, in principle, serve as proton donors. The most obvious candidate for proton transfer to [3Fe-4S]⁰ is HD2(Asp-15), as was suggested based on the experimental analysis and some MD simulations. However, there are several other protons in the surroundings. They include HN(Tyr13), HN(Thr14), HN(Asp-15), and HN(Cys-16). In the following the distribution functions for the distances of HD2(15)–S1, OD2(15)–S1, HN(16)–S1, HN(15)–S1, HN(14)–S3, and HN(13)–S2 are evaluated. Transfer from main-chain NH atoms would normally be expected to require protonation (i.e., 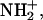but see below); we use the simulations for the neutral system here. The OD2(15)-S1 distance is considered (see Fig. 1), in addition to the corresponding HD2(15) distance to provide direct comparison with Chen et al. (2000). All distribution functions are averages over five independent trajectories, each 250 ps in length, as described in Molecular Dynamics Simulations and Preparation of the Systems. To check the sensitivity of the results to the charge distribution on the [3Fe-4S] cluster, the distribution functions were calculated for all three charge sets (M, N, and E; see Ab Initio Electronic Structure Calculations for nomenclature).

The density profiles for the five hydrogen-sulfur distances and the oxygen-sulfur distance are shown in Fig. 6 for the three charge distributions of the cluster. The profiles indicate that hydrogen atoms other than HD2(15) (see Fig. 1 for the numbering) can approach [3Fe-4S] more closely and thus could serve as possible proton donors. In particular, HN(15)–S1 and HN(14)–S3 have a rather pronounced peak ∼2 Å in all simulations. As can be seen the profiles are quite similar despite the rather different charges (see Table 1). This is in line with the results from the minimizations and the scan of the potential energy surface for rotating Asp-15; i.e., the precise charges used are of little importance for the average dynamics of the system (Meuwly and Karplus, 2003).

FIGURE 6.

Average of distance distributions in 7FDR. All averages are taken over five independent runs, each 250 ps in length. The top panel shows distribution functions for the HD2(15)-S1 (dashed) and OD2(15)-S1 (solid) distances. From left to right the systems RPE, RPN, and RPM are shown. R (in Å) stands collectively for the respective distance.

Because proton transfer intrinsically involves considerable proton motion, it is important to determine what influence constraining the bond lengths involving the hydrogen atoms have on the results. A molecular dynamics simulation for 7FDR (RPN) with and without SHAKE (i.e., with constrained and unconstrained hydrogen heavy atom bonds), was performed. The time step for the two otherwise identical simulations was 0.1 fs. Fig. 7 shows the distribution functions for both the unconstrained and constrained runs. Overall, the distribution functions are very similar. Thus, treating the hydrogen bonds with SHAKE appears to be satisfactory.

FIGURE 7.

Distance distributions with (left) and without (right) SHAKE in 7FDR/RPE. Both simulations are identical, apart from the fact that one uses SHAKE whereas the other does not. The same distances as in Fig. 6 are shown.

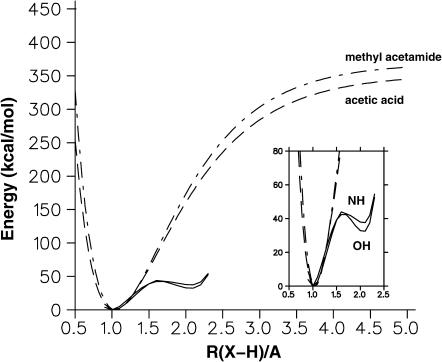
Since the potential energy parameters in the CHARMM22 program are not designed to treat proton transfer (i.e., no bond-breaking/bond-making is possible) we carried out ab initio calculations for a model system to examine the proton transfer from HN(15) and OD2(15), respectively, to the [3Fe-4S] cluster. The system used consisted of a small part (Thr-14, Asp-15, and Cys-16) of the protein and [3Fe-4S]; see Fig. 1. For these calculations no structural optimizations were carried out; i.e., all bond lengths, valences, and dihedral angles were kept fixed except for the position of the proton itself. Also, this was a gas phase calculation (no solvent effects included) so that it is of interest only for comparative purposes. For the calculation of the proton transfer curves (see Fig. 8) from the protein to the [3Fe-4S] cluster the OD2(15) was brought to within 3.5 Å of S1, which is the same distance as N(15)–S1. The hydrogen atoms HD2(15) and NH(15) were placed along the hydrogen bond OD2(15)–S1 and N(15)–S1 (optimal hydrogen bonding). In this geometry the hydrogen atoms were moved between r_X–S1 = 0.8 Å and 2.3 Å with step size 0.1 Å, where X is either OD2(15) or N(15). In both cases, a double minimum potential with a barrier height of 42 kcal/mol (OD2(15)–HD2(15)–S1) and 44 kcal/mol (N(15)–NH(15)–S1), respectively, was found. The secondary minimum (X–H-S1) has a depth of 10 kcal/mol (OD2(15)–HD2(15)–S1) and 7 kcal/mol (N(15)–NH(15)–S1), respectively. This shows that in the gas phase the proton is almost equally likely to come from the Asp side chain as from the main-chain nitrogen atom whereas the overall reaction is highly endothermic in both cases. Thus, solvation effects due to the protein and the surrounding water must play a significant role. The pK_a values are 3.9 for Asp and ≈10 for main-chain NH. A possibility is that the NH is protonated first (to give 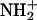) as in acid-catalyzed hydrogen exchange. We note that it has been found that a neutral His does give up a proton to form His⁻ in certain enzymatic reactions (Bash et al., 1991). For comparison the gas phase deprotonation energies of methyl acetamide (CH₃CONHCH₃→CH₃CON⁻CH₃ + H⁺) and of acetic acid (CH₃CO₂H→CH₃CO₂⁻ + H⁺) were calculated in their respective optimized geometries at the B3LYP/6-31G^** level. The calculated deprotonation energies are 369 kcal/mol and 352 kcal/mol, which compares favorably with 361.8 ± 2.2 kcal/mol and 348.1 ± 2.2 kcal/mol from experiment (Decouzon et al., 1990; Taft and Topsom, 1987; Hunter and Lias, 1998). For comparison, Fig. 8 also shows energies calculated from scanning the N-H (methyl acetamide) and O-H (acetic acid) distance between 0.6 Å and 1.5 Å. The energies are fitted to Morse curves that yield the calculated deprotonation energies.

FIGURE 8.

Proton abstraction potential along the N-NH(15) and OD2-HD2(15) bonds for the Thr¹⁴-Asp¹⁵-Cys¹⁶ structure with the [3Fe-4S]⁺ cluster (see Fig. 1 b). No structural optimizations are carried out along the path. For both cases a double well potential with similar forward (protein-H→S) and slightly different reverse (SH→protein) barriers is observed. For comparison the deprotonation curves from methyl acetamide (CH₃COOH) and the peptide group CH₃CONHCH₃ to their respective ions are also shown. The inset shows an enlargement of the energy range relevant to proton abstraction from the protein fragment to the [3Fe-4S]⁰ cluster.

Rotational motion of the carboxylic acid

If Asp-15 is the proton transfer agent, it must accept the proton from the solvent and transport it to [3Fe-4S]. This is likely to involve rotation of COOH around CB-CG (see Fig. 2 b). Our calculations concerning the rotation have been previously described in some detail (Meuwly and Karplus, 2003). Here, we only present the results. Minimum energy curves for rotating the COOH-group of Asp-15 have a barrier for rotation between 25 and 30 kcal/mol (with and without surrounding water molecules) if the COOH is in its anti-conformation (see Fig. 1 b)). For the syn-conformation, the barrier is reduced by ∼5 kcal/mol. However, for proton transfer from the carboxyl group the hydrogen atom can approach the sulfur atom more closely in the anti-conformation as indicated in Fig. 1 b). These results are almost independent of the atomic charge set used for the [3Fe-4S] cluster. Umbrella-sampling techniques were used to estimate the free energy differences for the rotation and the potential of mean force was calculated for rotation around the dihedral angle (CA-CB-DG-OD2; see Fig. 1 b). The barrier for rotation reduces by a factor of 3 to 8 kcal/mol but the overall shape of the rotational potential is little changed. Thus, the rotational motion is an activated process with a time constant of the order of μs (Meuwly and Karplus, 2003).

Comparison of wild-type and mutant ferredoxin I

The experimental work established that proton transfer in the D15E (Asp→Glu, PDB code 1D3W) mutant is considerably retarded (by two orders of magnitude) compared to native A. vinelandii (7FD1) (Chen et al., 2000). On the basis of this work it was suggested that the carboxylate of Asp-15 plays an important role in 7FD1 and, more specifically that it acts as the proton relay from the solvent to the cluster. For the native 7FD1 it was found in a single 1.25-ns trajectory (Cherepanov and Mulkidjanian, 2001) that the salt bridge between N(Lys-84) and O(Asp-15) frequently breaks and is restored during MD simulations. The simulations apparently also showed that the longer side chain of Glu-15 forms a stronger salt bridge than Asp-15 with Lys-84 through simulations of the D15E mutant (1D3W). It was concluded that “Glu-15 is effectively immobilized and cannot serve as a mobile proton carrier” (Cherepanov and Mulkidjanian, 2001), whereas Asp-15 in native 7FD1 is able to do so.

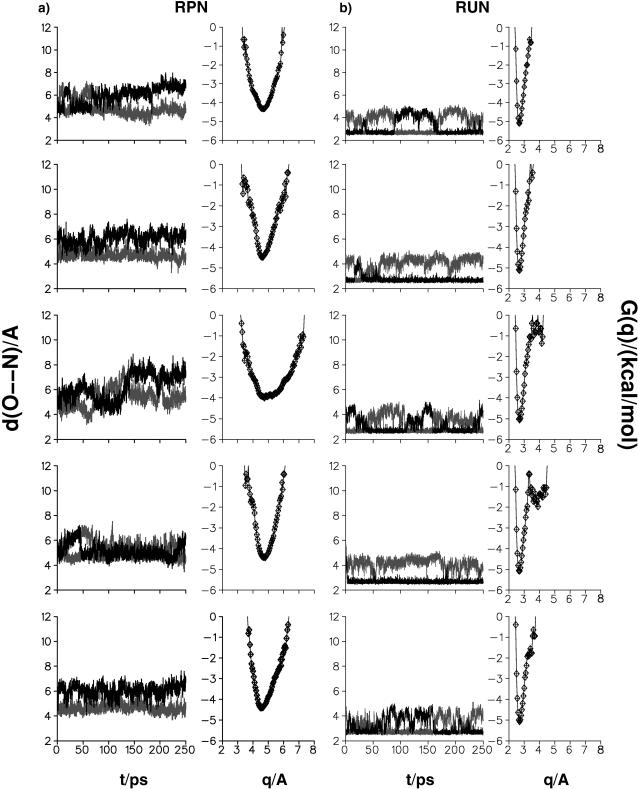
The above suggestion is sufficiently interesting that we decided to explore it in more detail by molecular dynamics simulations with the present parameterization and charges. In the following, NBO charges were employed throughout (see Ab Initio Electronic Structure Calculations); i.e., we used RUN (unprotonated Asp-15) and RPN (protonated Asp-15) realizations for 7FD1, and RUN for 1D3W. Five simulations with varying initial conditions, each 250 ps in length, were calculated and analyzed for each of the three systems. For 7FD1(RPN) no close N(Lys-84)–O(Asp-15) approach is observed; i.e., no salt bridge is formed (Fig. 9 a), as expected. However, in the case of 7FD1(RUN) (Fig. 9 b) the five runs reveal strong salt bridges which are interrupted only by rotation of the carboxyl group; i.e., when the binding partner to N(Lys-84) changes from OD1(Asp-15) to OD2(Asp-15) in a transition that takes on the order of μs (see Exploration of Proton Transfer Mechanisms by Simulations). For 1D3W (see Fig. 10) two out of five trajectories were very similar to those in Cherepanov and Mulkidjanian (2001). However, the remaining trajectories showed completely different behavior. In addition to the stable salt bridge between Glu-15 and Lys-84 (the result found by Cherepanov and Mulkidjanian, 2001) the N(Lys-84)–O(Glu-15) bridge is broken and restored for periods of several tens of ps and in one case the salt bridge was broken for almost 200 ps. This is shown in Fig. 10.

FIGURE 9.

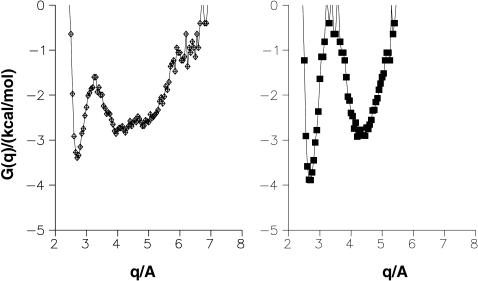
Time history for the salt bridge in 7FD1 for protonated and unprotonated Asp. In a, the two O(15)–NZ(84) distances (usually larger than 4 Å) for RPN show that the salt bridge does not form and the G(q) has a single, wide minimum. For the unprotonated Asp (right panels) the salt bridge is never broken; the distances also show that the carboxyl group rotates during the simulation.

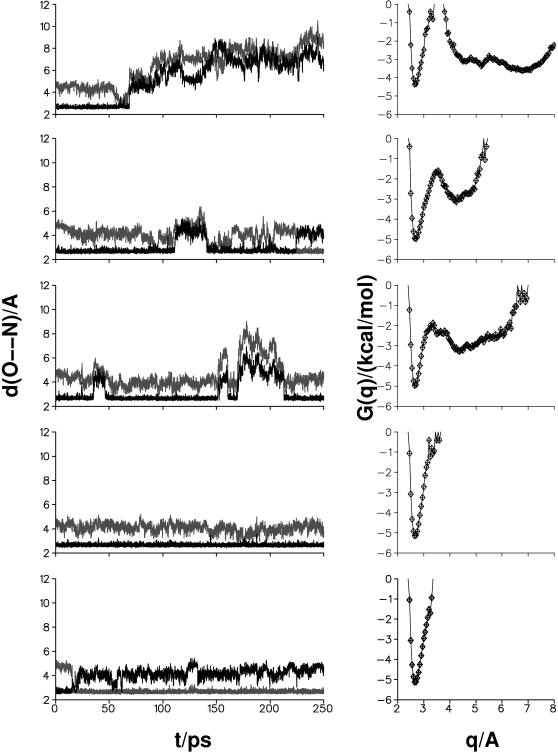
FIGURE 10.

Formation and stability of the salt bridge between Asp-15 and Lys-84 for the mutant D15E. Two runs (lower two traces) show a stable salt bridge throughout, and the next two runs show the breaking and reforming of the salt bridge, whereas in the remaining trace, the salt bridge does not reform. G(q) curves associated with the time histories are shown to the right of each time history.

From the time history of the N(Lys-84)–O(Asp-15) and N(Lys-84)–O(Glu-15) distances the free energy profile (or potential of mean force) can be estimated according to −G(q) = kT log P(q) + G₀, where G₀ is a constant, P(q) is the distribution function of the time history for the coordinate q in question, k is the Boltzmann constant, and T is the temperature. From the OD1(15)–NZ(84) and OD2(15)–NZ(84) distances the coordinate q was determined by choosing the shorter of the two distances along each trajectory (see also Cherepanov and Mulkidjanian, 2001). In Figs. 9 and 10 the G(q) curves are shown together with the time histories of the two O–N coordinates discussed above. The G(q) in Fig. 9 a confirms that the salt bridge is never formed in the present simulations for 7FD1(RPN). In some cases, similar free energy profiles to those reported in Cherepanov and Mulkidjanian (2001) are observed for the native 7FD1(RUN) protein (see Fig. 9 b, right panels) and the 1D3W mutant (see Fig. 10). However, the destruction of the salt bridge N(Lys-84)–O(Glu-15) is found for 1D3W (see Fig. 10).

The reported rupture of the salt bridge for the unprotonated wild-type protein 7FD1(RUN) appears to be more the exception than the rule as shown in Fig. 9 b. Because of this apparent disagreement with the results from Cherepanov and Mulkidjanian (2001), five additional runs, each 500 ps in length and with varying initial conditions, were analyzed for RUN. In two cases the disruption of the salt bridge N(Lys-84)–O(Asp-15) was found as was observed in Cherepanov and Mulkidjanian (2001). The corresponding G(q) profiles are shown in Fig. 11. For the remaining three runs the salt bridge was again stable over the entire length of the trajectory.

FIGURE 11.

G(q) for 7FD1(RUN) for trajectories where the salt bridge N(Lys-84)–O(Asp-15) breaks and restores during dynamics. See also right-hand column of Fig. 9 for comparison.

These results suggest that formation and/or destruction of the salt bridge between Asp-15 and Lys-84 is not directly involved in the difference in the primary mechanism of the proton transfer between 7FD1 and 1D3W. It is, however, possible (and likely) that the salt bridge plays a role in opening and closing the access (e.g., for water, see next section) to the active site. In summary, we find that for the native, unprotonated 7FD1 the salt bridge is more stable than previously assumed (see Fig. 9 b), whereas for the mutant D15E it is less stable than previously assumed (Fig. 10). This will have important consequences for the proposed reaction mechanism which was believed to proceed exclusively via salt bridge formation between Asp-15 and Lys-84 in 7FD1 (Chen et al., 2000; Cherepanov and Mulkidjanian, 2001). An alternative reaction mechanism based on these findings is presented in the Concluding Discussion.

Simulations with water in the active site

The x-ray structures (Chen et al., 2000) and an NMR study of a related protein (ferredoxin from Bacillus schlegelii; Aono et al., 1998) do not report any water nearby the [3Fe-4S] cluster (the “active region”). Nevertheless, it is of interest to consider the effect of water molecules in the immediate vicinity of [3Fe-4S]. It is known that if interior waters are mobile, they may not be visible in x-ray structures (Ernst et al., 1995; Clore et al., 1990; Chandrasekhar et al., 1992); i.e., in many cases, the number of water molecules that are observed is smaller than that required to fill the available space in a cavity as indicated by simulations. In a previous publication this question has been treated in some detail for the native 7FDR and the mutant 1D3W (Meuwly and Karplus, 2003). Here, we summarize the salient points that are necessary to justify possible alternative reaction mechanisms which can be proposed if water plays a role, as described in Meuwly and Karplus (2003).

If a water molecule is brought to within 2 Å of a sulfur atom of the [3Fe-4S] cluster, MD simulations show that the water molecule is stable within the cavity. From time to time it forms hydrogen bonds with the available sulfur atoms. Within the cavity the water molecule is mobile and performs strongly hindered rotations. This is due to the hydrogen bond between the water-hydrogen and the sulfur atom, as well as collisions between the water molecule and surrounding atoms of the polypeptide chain. The different trajectories for water in the active site of the native protein (7FD1) showed that in the majority of cases (four out of five) the water escaped from the active site on a timescale between 15 ps and 150 ps. In one case the water molecule remained within the cavity. Identical simulations for the Asp-15→Glu-15 mutant D15E (PDB code 1D3W) revealed a different behavior of the water molecule within the active site. In two out of five cases the water molecule was literally trapped within the cavity and in only one case the water left the region around the [3Fe-4S] cluster. In the two other cases the water molecule performed hindered rotations in the active site around the [3Fe-4S] cluster. This implies that it is less probable for a water molecule to diffuse out of the cavity in the D15E mutant than for the native 7FDR protein.

CONCLUDING DISCUSSION

This study concerned the proton transfer from the solvent and the surrounding protein to a buried [3Fe-4S] cluster in ferredoxin I from a mechanistic point of view. The analysis provides insight concerning the possible mechanisms that should be investigated with more elaborate techniques. The actual proton transfer process, which would require quantum mechanical techniques, was not treated. This is left to the future.

Experimental studies have established that proton transfer in the A. vinelandii ferredoxin I mutant D15E (Asp→Glu, PDB code 1D3W) is retarded by two orders of magnitude compared to that in the wild-type (7FD1) (Chen et al., 2000). Based on this result, it was suggested that the carboxylate of Asp-15 in 7FD1 acts as the proton relay from the solvent to the cluster. The calculations reported here investigate this proposal in more detail and consider alternative possibilities.

The questions asked are:

• 1) What influence do different charge distributions on the [3Fe-4S] clusters have on the structure and dynamics?

• 2) Which protons around the [3Fe-4S] cluster can serve as possible proton donors?

• 3) What detectable changes around the active site using MD simulations are induced by mutations at Asp-15?

• 4) Is water stabilized in the active region (around the [3Fe-4S] cluster) and could it play a role in the proton transfer reaction?

Question 1

Atomic charges for a molecular dynamics force field on the [3Fe-4S] cluster were determined by ab initio calculations by different methods. These charges differ sufficiently (by up to a factor of two) so that they could have an effect on the static and dynamic properties of the system. However, the low energy configurations, rotational barriers for the carboxyl group and the average dynamics appear to be largely insensitive to the particular charge distribution. The validity of the ESP charges was tested in pK_a calculations for the native protein and a mutants. They showed the experimentally observed trends.

Question 2

The probability density profiles provide evidence that hydrogen atoms other than HD2 of Asp-15 approach the sulfur atoms of the [3Fe-4S] cluster (see e.g., Fig. 6) to within hydrogen-bonding distance. For example, HN(15)–S1 and HN(14)–S3 can be as close as 2 Å, which is much closer than any of the approaches of HD2(Asp-15) to S1, the closest sulfur atom of [3Fe-4S]. In the gas phase, ab initio calculations have shown that the forward barrier for proton transfer from the main-chain NH to the closest S atom of the [3Fe-4S] cluster is comparable to the barrier for proton transfer from the hydrogen atom of the carboxyl group. However, the pK_a of the Asp is much lower than that of a main-chain NH so that proton abstraction from the NH might first require proton transfer from the solvent to form 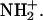Detailed solvation calculations are necessary to resolve this question.

Questions 3 and 4

From the RMSD values between the structures of the native and the mutant 1FDD protein, changes at position 15 along the polypeptide chain appear to have a larger influence on more distant parts in the protein than on the immediate environment. The largest differences occur at residues Pro-61 and Asp-90. These residues are ∼16 Å and 20 Å, respectively, from position 15. The significance of this result has yet to be explored. In the molecular dynamics runs the differences between the native protein and the 1D3W mutant are most clearly seen in the stability of the salt bridge between OD2(15) and NZ(84), and the behavior of a water molecule that was inserted into the active site. Contrary to what was previously found (Cherepanov and Mulkidjanian, 2001) the salt bridge in the native protein is surprisingly stable, whereas the salt bridge in the 1D3W does break for short or more extended periods of time. Water is stabilized around the active site for both the native protein and the 1D3W mutant. The mutant differs insofar as the water molecule appears to be less likely to escape from the active site than in the case of the native protein, as already noted in our previous work (Meuwly and Karplus, 2003). This finding has further implications for a revised reaction mechanism (see below). It has been suggested that an entatic effect due to the protein enhances the proton coupled electron transfer. The fact that the calculations indicate that the effects of the protein on the change in the structure of the cluster upon oxidation or reduction are small does not support this suggestion (Schipke et al., 1999). However, to fully investigate the role of an entatic effect would require a more detailed analysis; see, for example, the study of Roos and co-workers of blue copper protein (Olsson et al., 1998).

The role that buried water molecules can play in influencing the structure, dynamics, and function in proteins has been well established (Meyer, 1992; Fischer and Verma, 1999). A water molecule around the [3Fe-4S] cluster shows high mobility which could make it invisible to x-ray crystallography (Fig. 12). Nevertheless, the hydrogen atoms of the water molecule approach the [3Fe-4S] cluster to hydrogen-bonding distance and so could serve as a proton bridge (Meuwly and Karplus, 2003). The MD simulations of 7FD1 RPN (see Table 3 for definition) show that water can be stabilized in the active region for several tens of ps before leaving the cluster pocket. Interestingly, the exit of the water from the pocket is in every case coupled to considerable motion of Asp-15 and Pro-50 (Meuwly and Karplus, 2003). The water molecule tends to escape when Asp-15 and Pro-50 start to move apart (see Fig. 12). This effect is seen in all four simulations on 7FD1 RPN where the water escapes the active site. Similar fluctuations in the Asp-15 to Pro-50 distance occur in runs where the water molecule is not in the active site. For all runs without initial occupation of the cavity by water, no water was observed to enter over the timescale of the simulations.

FIGURE 12.

The 7FD1(RPN) protein and 500 snapshots of water positions superimposed from a 250-ps run (above). The first frame of the protein was taken and the water molecules were inserted into the figure. It is shown which part of the available space the water molecule explores in the resting frame of the protein. In the lower frame the same illustration as above is shown for D15E. In addition the van der Waals surface of residues Glu-15 and Pro-50 are indicated (dotted). The surface shows that there is no space for the water to escape.

From the simulations of the wild-type protein with and without Asp protonated and with and without water around the [3Fe-4S] cluster, the following reaction mechanism is proposed: initially, Asp-15 is unprotonated which leads to a very stable salt bridge between Lys-84 and Asp-15 (see Fig. 9 b). Residues Asp-15 and Pro-50 are moving sufficiently to open and close a cleft which leads toward the [3Fe-4S] cluster. Solvent water can penetrate into the “active region” (the zone around [3Fe-4S]) and protonate Asp-15. The salt bridge between N(Lys-84) and O(Asp-15) now breaks (see Fig. 9 a). This is manifest in the simulations. After rotation of Asp-15, such that the hydrogen atom is pointing toward the [3Fe-4S] cluster and the enclosed water molecule, proton transfer from COOH to water can occur. This leads to H₃O⁺ in the active site. From there, the proton could be transferred directly onto [3Fe-4S] or to the main chain to form 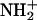before proton transfer to the cluster. At the same time, the salt bridge N(Lys-84)–O(Asp-15) is reestablished because Asp-15 is deprotonated. This in turn opens the cleft. The region between residues Asp-15 and Pro-50 can open up again and the water molecule is able to leave the active site. This is possible, as shown by simulations of the wild-type protein with unprotonated Asp-15 with water around the active site (Meuwly and Karplus, 2003).

The fact that for the 1D3W mutant water is less frequently observed to leave the active site than for the native protein could be a partial explanation for the slower reaction rate observed for 1D3W. Because water leaves the active site less frequently it is also less probable for the water molecule to diffuse into the active site. This suggests that the electron-coupled proton transfer reaction is not only gated by the salt bridge between residues 15 and 84 but also by the probability of water entering the active site.

In summary we have investigated the conditions under which proton transfer from the environment to the buried [3Fe-4S] cluster appears possible. First, charges for the reduced and oxidized [3Fe-4S] cluster were calculated at the B3LYP/6-31G^** level and tested in energy minimizations of the protein. The theoretical setup (charges on [3Fe-4S], force constants, boundary conditions, and treatment of solvent) was validated through different comparisons with experimental observables. The subsequent MD simulations showed that other hydrogen atoms than the one attached to Asp-15 spend time close to the [3Fe-4S] cluster. The energetic requirements to bring the proton from the outside toward the [3Fe-4S] cluster were also investigated. It was found that the required rotation of the carboxylic acid is possible. Finally, the dynamics of water molecules around the [3Fe-4S] cluster was considered. It was found (Meuwly and Karplus, 2003) that water molecules can escape (and therefore enter) the cavity in the case of native 7FD1. However, for the D15E mutant, there appears to be the possibility that water is “locked” on the timescale of the simulations (1 ns) and thus entrance of exterior water molecules into the protein is less likely. This latter finding may provide an explanation for the experimentally observed decrease in the reaction rate between native 7FD1 and certain mutants.