A Statistical-Thermodynamic Model of Viral Budding

Abstract

We present a simple statistical thermodynamic model for budding of viral nucleocapsids at the cell membrane. The membrane is modeled as a flexible lipid bilayer embedding linker (spike) proteins, which serve to anchor and thus wrap the membrane around the viral capsids. The free energy of a single bud is expressed as a sum of the bending energy of its membrane coat, the spike-mediated capsid-membrane adhesion energy, and the line energy associated with the bud's rim, all depending on the extent of wrapping (i.e., bud size), and density of spikes in the curved membrane. This self-energy is incorporated into a simple free energy functional for the many-bud system, allowing for different spike densities, and hence entropy, in the curved (budding) and planar membrane regions, as well as for the configurational entropy of the polydisperse bud population. The equilibrium spike densities in the coexisting, curved and planar, membrane regions are calculated as a function of the membrane bending energy and the spike-mediated adhesion energy, for different spike and nucleocapsid concentrations in the membrane plane, as well as for several values of the bud's rim energy. We show that complete budding (full wrapping of nucleocapsids) can only take place if the adhesion energy exceeds a certain, critical, bending free energy. Whenever budding takes place, the spike density in the mature virions is saturated, i.e., all spike adhesion sites are occupied. The rim energy plays an important role in determining the size distribution of buds. The fraction of fully wrapped buds increases as this energy increases, resulting eventually in an all-or-nothing mechanism, whereby nucleocapsids at the plasma membrane are either fully enveloped or completely naked (just touching the membrane). We also find that at low concentrations all capsids arriving at the membrane get tightly and fully enveloped. Beyond a certain concentration, corresponding approximately to a stoichiometric spike/capsid ratio, newly arriving capsids cannot be fully wrapped; i.e., the budding yield decreases.

INTRODUCTION

Viruses are submicroscopic infective agents, consisting of a small genome (one or several strands of RNA or DNA) and a protective coat, which in the simplest case is assembled from many identical copies of just one viral capsid protein (Levy et al., 1994; Goff, 2001; Knipe and Howley, 2001). Since these minimal blueprints cannot actively reproduce themselves, viruses prey on the biochemical machinery of living cells for their own propagation (usually to their host's demise), and they can be classified as to the kind of cells they infect. In the following we will be concerned with the late stage of the replication cycle of enveloped animal viruses. Their name derives from the fact that they infect animal (including human) cells, and their nucleoprotein capsid is additionally enveloped by a lipid bilayer. Embedded in this bilayer are viral proteins (often called spikes) which play a crucial role in both the virus' initial entry into and its final exit from the host cell.

Most animal viruses enter their host cells via active cell processes (Sieczkarski and Whittaker, 2002). One common example is receptor-mediated endocytosis, in which the binding of a viral spike protein to some specific receptor protein on the outer cell membrane triggers the internalization of the virus inside an endosome. Lowering the endosomal pH causes fusion of the viral membrane with the endosome membrane and the release of the virus genome into the cytoplasm. The subsequent translation and replication of the viral genome by the cellular machinery ultimately leads to the generation of many new nucleoprotein capsids which, however, still have to leave the cell and which are not yet covered by a lipid membrane. These remaining two tasks are solved simultaneously in a process termed budding (Garoff et al., 1998), when the viral nucleoprotein capsid becomes wrapped at a cellular membrane—often, but not exclusively, the plasma membrane. Hence, the viral particles not only obtain their final coating, but also either leave the cell or at least enter the secretory pathway.

The above scenario poses a critical difficulty: inasmuch as the presence of spike proteins is crucial for the virus to be infective (no spikes, no trigger for endocytosis), the budding mechanism must ensure that enough spikes are incorporated into the bilayer coat during envelopment. Even though the viral genome will direct the cellular machinery to synthesize the spike proteins and deposit them in the membrane at which budding will ensue, this by itself does not imply that enough of them will actually end up in the viral coat—unless they are severely overexpressed in the membrane, which appears not very economical.

Thirty years ago Garoff and Simons (1974) proposed a solution to this puzzle which rests on the simple idea that the spike proteins also mediate the adhesion between the nucleoprotein capsid and the lipid membrane. This automatically guarantees that after budding the mature virion contains spikes, because otherwise it would not have been able to bud in the first place. Even though it was subsequently realized that this simple model does not hold for all enveloped viruses (for a review, see Garoff et al., 1998), it is by now clearly established as the maturation route for hepadnaviruses and alphaviruses. The extensively studied model system in the latter case is the Semliki Forest virus (SFV). This is a tightly enveloped, roughly spherical, animal virus of ∼70 nm in diameter, containing one molecule of linear positive-sense single-stranded RNA (∼10⁴ nucleotides), enclosed inside a capsid of icosahedral symmetry (T = 4) and ∼40-nm diameter. The virus is covered with 80 spikes, each consisting of a trimer of glycoproteins, which dock at specific binding sites of the capsid and thereby also reflect the T = 4 icosahedral symmetry. SFV buds at the plasma membrane (see Strauss and Strauss, 1994, for a general review on alphaviruses).

The intuitively appealing budding model outlined above poses a number of questions which deserve both qualitative and quantitative understanding. For instance: The model ensures that spikes will be present in budded virions, but why is it that actual virions are basically fully covered with spikes, that is, why are no spikes missing? Is there a certain minimum concentration of spikes in the membrane required before budding can commence? What happens if several capsids compete for spikes? How are spikes drawn to the budding site? And is there a way to adjust the production of spikes and capsids such as to maximize the overall production of mature virions?

Another important question pertaining to the above budding model is whether the gradual enveloping of a membrane-bound nucleocapsid is driven by thermal curvature fluctuations of the lipid membrane, or perhaps by some other mechanism. This issue has been studied theoretically by Lerner et al. (1993) using a detailed model for the time between successive membrane wrapping steps (corresponding to the addition of a spike-mediated adhesion site). These authors concluded that a nonzero membrane spontaneous curvature (Helfrich, 1973) may be necessary to ensure complete membrane wrapping within the experimentally observed budding times of ∼10–20 min. We shall briefly return to this issue in the closing section of this article.

The membrane bending energy is evidently important in determining the dynamical characteristics of bud formation, from the moment a nucleocapsid has arrived at the cytoplasmic surface of the cell membrane until its release, coated by a lipid-spike membrane, into the intercellular space. Furthermore, energetically, the formation of a stable bud requires that the bending energy should be counterbalanced by the spike-mediated adhesion between the nucleocapsid and the lipid membrane, which provides the driving force for viral budding. In the present article, based on this notion, we develop a simple theoretical model for the budding scenario proposed by Garoff and Simons. The model takes into account that two mechanisms oppose the enveloping of the nucleocapsid by the lipid-spike membrane. First, as already emphasized, wrapping the membrane around the capsid involves an elastic bending energy penalty; and second, efficient capsid-membrane binding requires accumulation of spike proteins in these membrane regions. That is, spike proteins must diffuse from the surrounding planar bilayer into the curved budding regions (Nardi et al., 1998), rendering the spike distribution nonuniform, which involves a demixing entropy penalty. Another important factor which we take into account is the line energy (Lipowsky, 1993; Kumar et al., 2001) associated with the saddle-like rim connecting the immature bud to the embedding planar membrane. Whether or not budding occurs depends upon a delicate balance of all these energetic and entropic contributions, which determine the spike populations in different membrane regions and the size distribution of the budding virions. Our aim is to study this balance within a statistical-thermodynamic scheme that will enable us to address several of the questions put forward above in qualitative and quantitative terms.

THEORETICAL MODEL

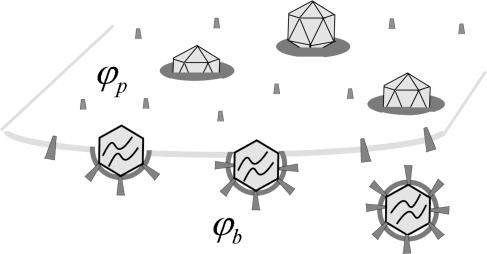
Viral budding is a dynamical many-particle process, whereby nucleocapsids arrive at one side of the plasma membrane and are released, enveloped by a membrane coat, at the other side. The number of capsids attached to the membrane surface, their size (i.e., wrapping stage) distribution, and the average density of spikes in their coating membranes, depend on the time elapsed since the moment of infection, the size and shape of the infected cell, and a variety of other (fluctuating) variables. Electron micrographs of virally infected cells generally reveal a population of bud sizes at different stages of maturation, as very schematically illustrated in Fig. 1. The goal of the model presented in the next section is to quantify the principal characteristics of this bud population. Underlying this model is the assumption that the time required for viral bud maturation (many minutes usually) is long enough to allow spike diffusion and equilibration between the curved (budding) and planar membrane regions. Consequently, the distribution of bud sizes and spike densities in a membrane containing given numbers of spike linker proteins (L) and adsorbed viral nucleocapsids (N), can be treated using equilibrium statistical thermodynamics. In reality, both L and N are time-dependent quantities, dictated by the time history of the infected cell. Our model does not describe the temporal evolution of these (supposedly slowly varying) quantities but, rather, the momentary bud population corresponding to given L and N.

FIGURE 1.

A schematic representation of the budding process. Naked nucleocapsids arrive at the cytoplasmic leaflet of the cell membrane, where linker glycoproteins (i.e., spikes) help to anchor and envelope them by the membrane. The spike concentration in the curved membrane around the partially wrapped buds (ϕ_b) is generally different from that in the planar regions (ϕ_p).

Free energy

Suppose N viral nucleocapsids have adsorbed onto a cell membrane embedding L linker proteins (spikes). The capsids are wrapped to different extents by the adsorbing membrane, resulting in a polydisperse two-dimensional solution of buds, with the lipid-spike membrane serving as the embedding solvent. Let Ma denote the total membrane area, where a is the cross sectional area per spike, at maximal membrane coverage. (Of course, even at full coverage, the spikes are embedded in the lipid matrix.) From the definition of a it follows that the maximal number of membrane adhesion sites (equivalently, spikes) on the capsid's surface is K = 4πR²/a, where R is the radius of the membrane-coated viral capsid. This limit is achieved when the capsid is fully wrapped by a lipid membrane saturated with spikes. In the numerical calculations presented in the next section we shall use K = 80, as for SFV, corresponding to a ≈ 192 nm² for R ≈ 35 nm. Hereafter, we shall use a as our unit of area, and 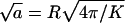(≈14 nm) as our unit of length. All energies will be measured in units of the thermal energy k_BT, with k_B denoting Boltzmann's constant and T the temperature.

Let n_k denote the number of capsids wrapped around by a membrane section of area k, which varies between k = 0 and k = K. The former value corresponds to a free capsid which has arrived at the membrane and is ready to wrap (we may think of it as being loosely associated with the membrane without involvement of spikes), whereas the latter value corresponds to a capsid which is fully enveloped by the membrane. Thus,

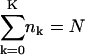(1)

and

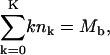(2)

where M_b is the total (curved) membrane area associated with budding capsids and M_p = M − M_b is the total area of the planar regions. Assuming that the membrane is tightly attached to the (spherical) capsids, the membrane curvature in all buds is the same, except for the existence of a small circular rim at the point where the membrane detaches from the capsid and where the curvature is not spherical but rather toroidal. We shall use κ to denote the membrane bending energy in the bud phase, and ε for the binding energy between a spike protein and the capsid. Clearly then, the energy of the composite (spike-and-capsid-dressed) membrane is lowered by spike diffusion into the curved budding regions. Yet, this segregation of spikes between planar and curved regions is entropically unfavorable. Furthermore, spike diffusion into the budding domains is correlated (though not trivially) with an increase of the overall curved area and hence also increases the total membrane bending energy. The equilibrium densities of spikes in the planar and curved regions are thus governed by the balance of these free energy contributions, as well as additional factors mentioned below.

We shall use ϕ_p = L_p/M_p to denote the spike density in the planar membrane and ϕ_b = (L − L_p)/M_b ≡ L_b/M_b for the (average) spike density in the budding regions (see Fig. 1). Our goal is to calculate ϕ_p, ϕ_b and the bud size distribution, {n_k}, as a function of the average spike density, φ = L/M, and capsid density, c = N/M. To this end we need an expression for F(L_b, {n_k}; L, M, N) = −ln Q(L_b, {n_k}; L, M, N), the free energy corresponding to a given distribution of bud sizes {n_k}, and a given partition {L_b, L_p}, of the L spikes between the curved and planar regions, with Q(L_b, {n_k}; L, M, N) denoting the canonical partition function of a system with given L_b, {n_k}, L, M, N, and T. The equilibrium values of ϕ_p, ϕ_b, and the equilibrium bud size distribution 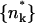will be determined by minimizing F(L_b, {n_k}; L, M, N) with respect to L_b and {n_k}, or another set of K independent variables. (Note that L_b and {n_k}, together with L, M, and N, define the system completely, including ϕ_p, ϕ_b, etc.)

The free energy, F(L_b, {n_k}; L, M, N) = F(L_b, {n_k}), should account for the spike entropy in the planar and budding membrane regions, the spike-capsid binding energy, the membrane bending energy in the bud phase, the line energy associated with the bud rims (see e.g., Lipowsky, 1993; Kumar et al., 2001), and the configurational entropy of the buds in the membrane plane. Using k_BT as our unit of energy, all these contributions are accounted for by the (approximate) free energy functional,

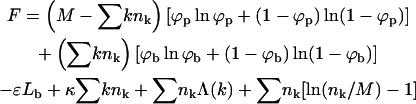(3)

with

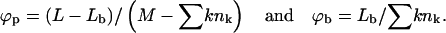The first term in Eq. 3 represents the configurational entropy of the L_p spikes embedded in the planar parts of the membrane, expressed in terms of a two-dimensional lattice gas model. The rest of the spike linkers (L_b in number) are distributed among the curved budding regions (hereafter also called the bud phase). The second term in Eq. 3 accounts for the entropy associated with all possible partitionings of the L_b (indistinguishable) spikes among the M_b sites of the curved regions. Note that we do not, a priori, assign a particular number of spikes (say, 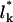) to a bud of size k. In fact, by allowing for all possible distributions of the L_b spikes among all buds, we also account for all fluctuations around the average l_k. (The average spike density 〈l_k〉/k = ϕ_{b, k} ≡ ϕ_b is independent of k, because the spikes' chemical potential in all buds, μ_b, must be the same everywhere in the membrane, including in the various k-buds; see below.) The next three terms in Eq. 3 are energetic: −L_bε = −M_bϕ_bε is the total spike-capsid binding energy. 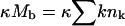is the total membrane curvature energy in the budding regions. For a lipid bilayer characterized by a bending modulus k_c and a spontaneous curvature c₀, the bending energy per unit area around a bud of radius R is κ = (1/2)k_c(2/R − c₀)² (Helfrich, 1973). The spontaneous curvature of cell membranes is usually nonzero, because their two constituent leaflets are generally of different compositions. Similarly, nonzero spontaneous curvature can also be induced by asymmetric membrane proteins. For the simplest case of vanishing spontaneous curvature (c₀ = 0) and a typical bending modulus of k_c = 20 k_BT (Sackmann, 1995) we find κ = 2π (using K = 4πR² = 80), which we will frequently use as a characteristic value. However, one should keep in mind that for a given bending modulus k_c, the bending energy per unit area, κ, may actually be smaller (if c₀ > 0) or larger (c₀ < 0) than the value implied by c₀ = 0. The third energetic term, the sum 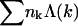, is the total line energy of the rim, with Λ(k) denoting the line energy of a k-bud (see below). Finally, the last term in Eq. 3 accounts for the configurational entropy of the polydisperse two-dimensional bud mixture, treated here as a multicomponent ideal gas. More elaborate models, taking into account excluded area effects and other interactions between buds are possible, but not warranted here.

The equilibrium state of the system can now be found by minimizing F with respect to L_b and {n_k}; the latter minimization should obey the conservation condition of the total number of spikes, Eq. 1. From ∂F/∂L_b = 0 we obtain

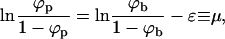(4)

expressing the equality of the spike's chemical potential (μ) in the planar and curved regions. Recall that ln [ϕ_p/(1 − ϕ_p)] is the chemical potential of a noninteracting lattice gas of density ϕ_p (Hill, 1960). Similarly, ln [ϕ_b/(1 − ϕ_b)] − ε is the chemical potential of a noninteracting lattice gas of particles with lower (−ε) ground-state energy.

Minimizing F with respect to all n_k, subject to Eq. 1, we find

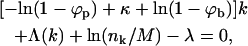(5)

with λ denoting the Lagrange multiplier conjugate to Eq. 1. Hence, the normalized bud size distribution is given by

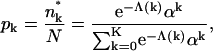(6)

where we have used Eq. 1 to eliminate λ and defined

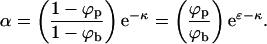(7)

To evaluate the p_k values (for known ε, κ, Λ(k), L, M, and N) we need ϕ_p and ϕ_b. From Eq. 4 we obtain one equation relating these two variables. Another one is provided by the spike conservation condition between the two phases (i.e., the lever rule):

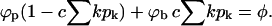(8)

In general, since Λ(k) is not a simple function of k, the evaluation of ϕ_p and ϕ_b, and hence of 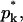is only possible numerically. In all the calculations presented in the next section, the line energy associated with a k-bud will be modeled as being proportional to the length, ℒ(k), of its rim, with a constant line energy per unit length γ. Simple geometry then yields

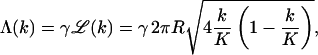(9)

where R is the radius of the capsid. Note that 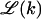vanishes for k = 0 and k = K, and is maximal (2πR) when the membrane coats one capsid hemisphere (k = K/2).

The saddle-like curvature of the lipid-protein membrane at the bud's rim is different from both the simple spherical shape of the membrane around the bud, and the planar geometry of the surrounding membrane. If the membrane is under nonzero lateral tension (which is the case for all cell membranes; Morris and Homann, 2001), this rim will contribute an additional bending energy (Deserno and Bickel, 2003). Its dependence on k is not as simple as assumed in Eq. 9, but the general features of large energies near the equator (k ≈ K/2) and small values at the poles (small or large degrees of wrapping) are identical. Another contribution to γ may arise from the possibly different lipid-protein compositions across the boundary separating the curved and planar membrane regions. In addition to the difference in the density of spike proteins these two regions may also differ in lipid composition and the content of other proteins. In fact, some studies suggest that the chemical composition of various viral membranes, e.g., certain retroviruses, is different from that of the host plasma membrane, resembling the composition of lipid rafts (Chazal and Gerlier, 2003). It is less clear whether raft-like composition is also typical of alphaviruses; yet, it has been shown that increased concentrations of cholesterol (which is also abundant in membrane rafts) are vital for their efficient budding (Lu and Kielian, 2000).

Changes in curvature and composition at the bud rim are most likely coupled to each other, because different lipid species involve different spontaneous curvatures. If this were the boundary between ordinary phase-separated (planar) domains of different compositions, then γ would be on the order of 1 k_BT per molecular diameter (see e.g., Riviere et al., 1995). Most recently, the coupling between curvature and composition has been clearly demonstrated in mixed lipid vesicles, revealing line energies on the order of 1 k_BT per nm (Baumgart et al., 2003). The origin of the line energy in (say, binary) lipid membranes is the nonideal mixing of the lipid species. In our problem, assuming that the lipids in the planar (bud-free) membrane are randomly mixed, the chemical contribution to γ should be smaller. (The difference in composition is enhanced by the different curvatures.) In the absence of detailed information pertaining to the line energy between the budding and planar membrane regions, we shall treat γ as a variable, ranging between zero and 1 k_BT per unit length, .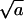

The final stage of the budding process, i.e., the pinching-off of the fully wrapped bud and its release into the intercellular space, involves an energy barrier associated with the fusion and scission of the lipid-protein membrane of the bud's narrow neck. This process is most likely mediated by special scission proteins, e.g., TSG101 in the case of HIV (Garrus et al., 2001; Freed, 2003). Our theoretical model is meant to account only for those stages of the budding process preceding the final scission of the bud. That is, the process leading to the formation of a nearly mature, almost fully wrapped (narrow neck) bud; assuming that its formation leads to irreversible pinching-off of the viral particle. In our model calculations we shall assume that this irreversible pinching-off is the fate of all buds for which k ≥ 0.9K. (The value 0.9 is quite arbitrary, but its precise value is immaterial for our purposes.) The concentration of these buds, c_w, would be proportional to the rate of budding, if this were a steady-state process.

Macroscopic phase approximation

Before turning to the numerical results for the bud size distribution, let us briefly come back to Eq. 5 and consider a limiting case of considerable interest; hereafter referred to as the macroscopic (bud) phase approximation. The key idea is to neglect the fact that the total curved membrane area is split up between N buds and rather think of it as one single phase which coexists with the planar membrane phase. We can then neglect the configurational entropy of the individual buds, i.e., the last term in Eq. 3. (The same would hold if the bud distribution in the membrane plane were frozen. Similarly, if all buds were of the same size, this configurational term would only depend on c and hence cannot influence the amount of wrapping at any given c.) Furthermore, if all buds were indeed forming one continuous phase the line energy would identically vanish. Thus, within the macroscopic phase approximation we shall also ignore the line energy term in Eq. 3; corresponding formally to Λ(k) = 0 for all k. Eq. 5 thus reduces to [−ln(1 − ϕ_p) + κ + ln(1 − ϕ_b)]k − λ = 0, which can only be fulfilled (for all k) if λ = 0 and

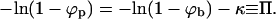(10)

This last equation could also be derived from the free energy functional corresponding to the macroscopic phase approximation, namely, the free energy obtained from Eq. 3 upon deleting the two last (bud entropy and line energy) terms. That is,

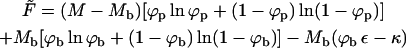(11)

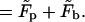(12)

This expression may be interpreted as the free energy of a system of total area M, divided into two macroscopic regions: a planar phase of area M_p and a bud phase of total area M_b. 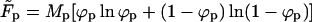is the free energy of the planar phase, involving only the configurational entropy of the spikes. Similarly, 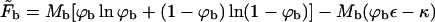is the free energy of the bud phase, which, in addition to the spike configurational entropy, accounts also for the spike-mediated membrane-nucleocapsid adhesion energy and the membrane bending energy. Note that 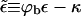may be interpreted as the effective adhesion energy per unit area in the bud phase.

Minimizing 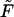with respect to L_b (at constant M_b) we find again, as expected, Eq. 4 for the equality of the spikes chemical potential in the two phases. Eq. 10 follows from the minimization of 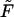with respect to M_b; recall that 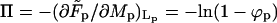is the familiar expression for the pressure of an ideal lattice gas (Hill, 1960), in our case the two-dimensional gas of spikes in the planar membrane. Similarly, −ln(1 − ϕ_b) = Π + κ should be interpreted as the pressure in the budding region. It is larger than Π (by κ) because of the bending energy penalty associated with increasing the area of the bud phase. Note that Eq. 10 is analogous to Laplace's equation for the pressure difference across a curved surface (Rowlinson and Widom, 2002), with κ playing the analog role to that of the surface tension. Note finally that if we reinsert the two equilibrium conditions, Eqs. 4 and 10, back into the free energy Eq. 11, we regain the familiar thermodynamic relation 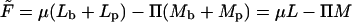, between the Helmholtz (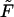) and Gibbs (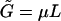) free energies; in this case the free energies of a two-dimensional system of area M containing L spikes at pressure Π.

Equations 4 and 10, expressing the equality of chemical potentials and pressures of the spike gas in the p and b phases, dictate the spike densities (ϕ_p and ϕ_b) in two (hypothetical) macroscopic coexisting phases. Solving these equations we obtain

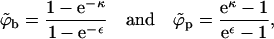(13)

with the tilde reminding us that these equations are only valid in the macroscopic phase approximation.

From Eq. 13 it follows that phase coexistence is only possible if ε ≥ κ ≥ 0. Physically, this is a consequence of the fact that for ε ≤ κ the energy of the p phase is lower than that of the b phase, 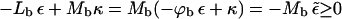, even if the buds are densely covered by spikes; i.e., negative effective adhesion energy 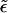even for ϕ_b = 1. Under these circumstances there is no thermodynamic driving force for phase separation (and hence spike density segregation). Thus, ε = κ marks a critical value for the adhesion energy, below which budding cannot take place. Note that ε = κ implies 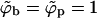, whereas for ε > κ we must have 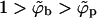. This rather unusual spike-condensation scenario implied by Eq. 11 is not an ordinary two-dimensional phase separation of the kind encountered, say, in an interacting lattice gas (where a −ϕ² term drives the transition). In fact, for a given M_b, Eq. 11 is completely analogous to the free energy of, e.g., a bulk solution (the p phase) of spikes, embedding an adsorbing surface (the b phase) onto which the spikes adsorb. Our system is slightly more complicated because the area of the adsorbing surface is not a constant.

One interesting and immediate prediction of Eq. 13, pertaining to the case where coexistence is possible, i.e., ε ≥ κ, is that for most lipid membranes (where, typically, κ ≥ 3), the spike density in the curved membrane regions coating the buds is nearly saturated (ϕ_b → 1).

RESULTS AND DISCUSSION

The numerical results presented in this section focus on the following issues:

1. The partitioning of spike proteins between budding and planar membrane domains—i.e., the equilibrium densities, ϕ_b, ϕ_p—as a function of the adhesion energy, ε, the (normalized) membrane bending energy, κ, and the line energy at the bud's rim, γ.

2. The distribution of bud sizes, {p_k}, for several choices of ε, κ, and γ.

3. The concentration of mature (fully wrapped; k ≥ 0.9 K) nucleocapsids, c_w, as a function of the total concentration of capsids in the membrane, c, and the average spike density, φ.

Largely due to the lack of detailed information pertaining to all the relevant physical constants and parameters in our model (e.g., c, ε, and φ), our calculations are not intended to mimic any particular system. Whenever possible, however, our choice of physical constants was guided by data corresponding to alphaviruses. Thus, in all calculations we have used K = 80 for the number of available spike binding sites per nucleocapsid (Garoff et al., 1998). In most calculations ε, κ, and γ are treated as variables. Some calculations require specific values for these material constants, which were chosen as follows: For the bending energy per unit area, κ = 2π (corresponding to k_c = 20 for lipid membranes of zero spontaneous curvature, but to softer or harder membranes if c₀ is positive or negative, respectively). The spike-capsid adhesion energy is not known. However, following the suggestion that aromatic residues in the capsid protein create a hydrophobic docking pocket for the side chain of the spike glycoprotein (Skoging et al., 1996), and assuming that the corresponding binding energy is comparable to typical antibody-antigen interactions (for which the dissociation constant K_d is on the order of 10⁻¹⁰M), then ε ≈ 20 (Nelson and Cox, 2004), which is the typical adhesion energy used in some of the calculations. (Recall that both ε and κ are measured in units of k_BT.) For γ we have examined several values in the range 0–1 (in units of k_BT per unit length, ).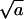

In some of the calculations below the capsid density, c is treated as a variable. As a specific representative value in many of the calculations we have used c = 0.005. Note that this is actually a rather large two-dimensional capsid concentration—inasmuch as c is the number of capsids per unit membrane area, a, which is much smaller than the capsid's surface area. More specifically, the capsid's surface area is 4πR²/a = K = 80, so that its projection on the membrane plane is πR² = 20. Thus, just for comparison, the maximal value of c, corresponding to the hypothetical limit where all capsids are unwrapped and densely packed in the membrane plane is 0.045 (that is, (1/20) × 0.91, with 0.91 marking the maximal projected area fraction of spheres in two dimensions). Another limit, also hypothetical but of interest for the choice of c, corresponds to the case where all capsids attached to the membrane are fully enveloped by the lipid-spike coat and, furthermore, densely packed against each other within the membrane plane. The total membrane area per bud is now 4πR² + πR²/0.91, with the second term accounting for the planar membrane area per bud. For K = 80 this yields c ≈ 0.01. Thus, anticipating a distribution of different bud sizes our default choice, c = 0.005, amounts to a rather crowded though not closely packed population of capsids at the cell surface.

No quantitative data are available for φ. Based on partial experimental information, φ appears to vary in the range 0.01–0.1 (Briggs et al., 2003; Quinn et al., 1984). From the rate of spike synthesis (∼10⁵ spikes/cell per min), cell surface area (∼3000 μm² ≈ 15 × 10⁶ a), and protein dwell time (∼15 min), one can estimate that φ ≈ 0.1, assuming that all spikes arrive at the plasma membrane (Briggs et al., 2003). Some of the calculations presented below were carried as a function of φ for its entire range, [0,1] . Others were performed for selected values of φ. All bud size distributions were derived by solving for α using the expression for the optimal bud size distribution (Eq. 6), the chemical potential equality (Eq. 4), and the conservation condition (Eq. 8).

Spike partitioning

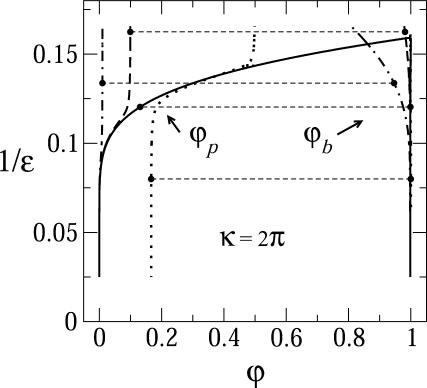
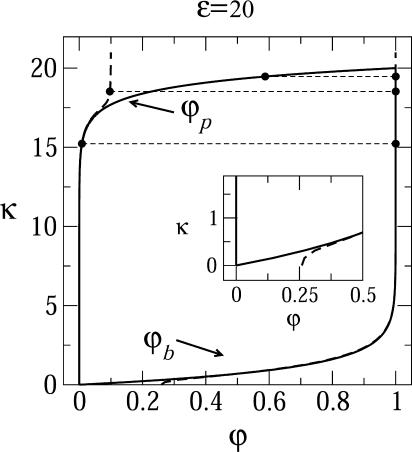
Fig. 2 shows the equilibrium densities of spikes in the budding (ϕ_b) and planar (ϕ_p) membrane regions in the (ϕ, 1/ε) plane, for a given bending rigidity κ = 2π. (Plotting 1/ε is suggested by the fact that for a given strength of the adhesion energy, this quantity is proportional to T. For a given T it is of course inversely proportional to the interaction strength. Phase diagrams are often plotted in terms of this effective temperature.) Similarly, Fig. 3 shows the corresponding phase diagram in the (ϕ, κ) plane for a given spike adhesion energy, ε = 20. (Recall from Eq. 10 that κ is somewhat analogous to excess pressure.) In both figures, one set of data corresponds to the macroscopic phase approximation in which the curved and planar membrane regions are treated as macroscopic phases, ignoring finite (bud) size effects and line energy contributions. These results (shown by the solid curves in Figs. 2 and 3) are ordinary phase diagrams, as obtained by solving the coexistence conditions, Eqs. 4 and 10, which yield 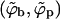, as given by Eq. 13. Consistent with the discussion in the previous section, both figures reveal that spike phase separation can only take place if ε is larger than κ (1/ε < 1/2π in Fig. 2). Otherwise, the membrane bending energy overcomes the adhesion energy and prohibits budding. In the two-phase region, coexisting densities are connected by horizontal tie lines, such as the light dashed lines in the figures. As usual, the relative proportions of material in the two phases is dictated by the lever rule, Eq. 8.

FIGURE 2.

Equilibrium spike densities in the budding (ϕ_b) and planar (ϕ_p) membrane regions. This (ϕ, 1/ε) diagram was calculated for κ = 2π, and γ = 0. The solid curve is a phase diagram describing the coexisting spike densities 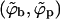when all budding regions are treated as one macroscopic phase, in equilibrium with a planar membrane phase. The pairs of dash-dotted, dashed, and dotted curves are the coexisting spike densities calculated for a system of discrete buds where φ = 0.01, 0.1, and 0.5, respectively; in all cases, c = 0.005. The horizontal dashed lines are representative tie lines, connecting pairs of coexisting spike densities.

FIGURE 3.

Phase diagram in the (ϕ; κ) plane for ε = 20, and γ = 0. The solid curves describe the coexisting spike densities 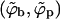when all budding regions are treated as one macroscopic phase. The dashed curves describe the results for a system of discrete buds of two-dimensional density c = 0.005, in a membrane with spike density φ = 0.1. Shown are a few tie lines (light dashed horizontal lines). The inset magnifies the behavior in the low κ regime.

As we have mentioned above, a noteworthy prediction of the macroscopic phase approximation is that whenever phase separation takes place, the spike density in the budding virions is essentially saturated, i.e., 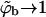, which is in line with the experimentally observed stoichiometric ratio between the number of available adhesion sites on the capsid and the number of spike trimers in the virion (Mancini et al., 2000).

Also shown in Figs. 2 and 3 are the coexisting spike densities when the discreteness of the virions and hence the entropy of their polydisperse size distribution are taken into account. For these calculations, which utilize Eqs. 4 and 6–8, we must specify the capsid concentration c and the average spike density φ. In Fig. 2 we show the coexisting densities for c = 0.005 and φ = 0.01, 0.1 and 0.5. (φ = 0.5 is rather hypothetical and mainly used to emphasize the role of the buds' finite size.) The numerical results shown here are all for γ = 0, yet it should be noted that very similar coexisting densities (ϕ_b, ϕ_p) are obtained for nonzero line energies. The value of γ is more important in its effect on the size distribution of buds, as discussed below.

From Eq. 4 it follows that for every (positive) value of ε the spike density in the budding regions, ϕ_b, should be higher than that in the planar ones, ϕ_p. Note, however, that unlike in the coexistence of two macroscopic phases, whose densities are independent of the average density, φ, and whose relative proportions are governed by the lever rule, in a system containing discrete buds, ϕ_p and ϕ_b may depend on both φ and c. Noting that 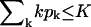, it follows from Eq. 8 that ϕ_p ≥ (φ − ϕ_bcK), which for c = 0.005 and K = 80, as in Fig. 2, implies ϕ_p ≥ φ − 0.4. Clearly, this lower bound is only relevant for very high values of φ, as shown in Fig. 2 for φ = 0.5. Actually, for this high value of φ and for large ε we expect all buds to be fully wrapped 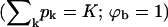, so that ϕ_p = (φ − cK)/(1 − cK) = 0.1667, consistent with the result in Fig. 2 for c = 0.005, K = 80, φ = 0.5, and in marked contrast to the value ϕ_p ≈ 0 found in the macroscopic phase approximation. This difference is a direct consequence of the large value of cK. For relatively large c, e.g., c = 0.005, a nonzero lower bound on ϕ_p is only relevant for unreasonably large (e.g., φ = 0.5) average spike density. For smaller values of c the lower bound on ϕ_p may be realized for more realistic, lower, values of φ.

In Fig. 2 we see that, for φ = 0.01 and 0.1 and large ε, the coexisting densities calculated for a system of finite-size buds are very similar to those obtained in the macroscopic phase approximation: 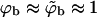and 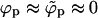. This behavior persists as long as 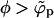, with the coexisting densities (ϕ_b, ϕ_p) following closely their macroscopic phase analogs. However, as 1/ε increases (and correspondingly also 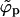) a point will be reached where 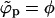. Since ϕ_p cannot exceed φ beyond this point (unlike 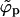), ϕ_p → φ as 1/ε keeps increasing. In this regime, ϕ_b must decrease, as follows from Eq. 4. There is no critical point in a system of finite-size buds, and from Fig. 2 it follows that the spike density in the budding regions is still much larger than in the planar membrane, even for ε < κ (and hence 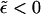). It should be stressed, however, that this (mathematically correct) result does not convey any information regarding the number and extent of membrane-wrapped capsids. This information can only be provided by the bud size distributions, as discussed below. In fact, due to the configurational entropy of the finite bud phase, the membrane contains an exponentially small fraction of small buds; however, as we shall see below, no bud maturation is possible when ε < κ.

Fig. 3 shows the phase diagram in the (ϕ, κ) plane, for ε = 20. The results corresponding to the macroscopic bud phase approximation are shown by the solid curves, which bound (above and below) the two-phase region. As usual, coexisting densities are connected by horizontal tie lines. The dashed curves in this figure describe the results for finite size buds, embedded in a membrane where c = 0.005 and φ = 0.1. The figure shows that in the limit κ → 0, both 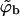and 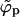must vanish, as follows from Eqs. 10 and 4; the first requiring 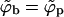for κ = 0 and the second showing that for nonzero ε this can only be fulfilled if both densities vanish. The bottom right corner of the diagram (small κ and nonzero φ) is a one-phase region where only the curved, budding phase exists. Indeed, for low κ and nonzero φ, the spikes-rich bud phase is of much lower energy (chemical potential) as compared to the planar membrane.

As κ increases, the gap between the coexisting densities widens rapidly, with ϕ_b → 1 (saturation) and ϕ_p ≈ 0, reflecting the strong preference for the budding phase for ε > κ. Again, a critical point, beyond which no phase separation can take place is reached when κ = ε, and the critical density is φ = 1. Above the coexistence line we again find only the planar phase.

As we found for Fig. 2, within the two-phase region the coexisting densities in a system of discrete buds are generally similar to those obtained in the macroscopic (bud) phase approximation. Differences appear when κ becomes comparable or larger than ε. As already remarked with respect to Fig. 2, once κ gets larger than ε, no buds are formed, as will become apparent after discussing the bud size distributions. Differences between the finite and macroscopic bud systems appear also in the low κ limit. In the finite-bud system, when κ = 0, buds bearing a finite spike density coexist with a planar, spike-free, membrane.

Bud size distribution

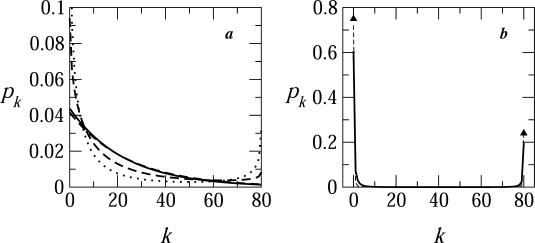
In Fig. 4 we show several distributions of bud sizes, corresponding to different choices of γ, as obtained by solving Eqs. 4 and 6–8, with a line energy modeled according to Eq. 9 in all cases for c = 0.005, ε = 20, κ = 2π, and φ = 0.1. For γ = 0 the size distribution is rather broad, with the probability of finding a bud of size k decreasing monotonically with k (solid curve in Fig. 4 a). If no line tension penalty is involved, the size distribution of the buds is primarily determined by the last, mixing entropy, term in Eq. 3, which favors a random distribution of the available spikes among the various buds, and hence a broad (exponential) distribution of bud sizes. Consequently, the fraction of nearly fully wrapped buds is necessarily small. For nonzero γ we expect an increase in the populations of the two extreme bud sizes; the nearly fully wrapped (k ≈ K) capsids on the one hand, and totally naked nucleocapsids (k ≈ 0) on the other. This is, of course, a consequence of the fact that the circumference of the bud is maximal at its equator (k = K/2), and minimal near the poles (k = 0, K).

FIGURE 4.

The distribution of bud sizes in a system where φ = 0.1, c = 0.005, ε = 20, and κ = 2π. The solid, dashed, and dotted lines in a correspond to γ = 0, 0.1, and 0.2. The solid curve in b is for γ = 0.6. For larger values of γ, the size distribution is strictly bimodal, with peaks k = 0 and k = K, as shown by the triangles for γ = 1.

Indeed, as γ increases, the size distribution becomes bimodal—i.e., in addition to the maximum at k = 0, a second maximum emerges at k = K, with a concomitant depletion of intermediate size capsids. For γ ≥ 0.5, the size distribution is sharply bimodal, with peaks at k = 0 and k = K. In other words, budding becomes an all-or-nothing process, whereby nucleocapsids arriving at the membrane either become fully wrapped by a membrane, or remain naked; no partially wrapped capsids are stably attached to the membrane. For the conditions corresponding to Fig. 4 (namely, ε significantly larger than κ) the spike density in the fully enveloped buds is essentially saturated, ϕ_b ≈ 1 (whereas 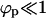). Thus, for large γ (≥ 0.6 in Fig. 4 b), the number of fully wrapped capsids, n_K, is dictated by the total number of spikes embedded in the membrane, L. Since each essentially fully enveloped nucleocapsid engages K spikes, it follows that n_K ≈ L/K, and hence the fraction p_K of these capsids in the system is p_K ≈ φ/cK. For large γ the high-k-peak is essentially confined to k = K, thus p_K is almost the same as the fraction of essentially wrapped capsids introduced above, 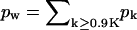. Consistent with the results in Fig. 4 b we find that indeed p_w ∼ φ/cK = 0.1/(0.005 × 80) = 0.25.

Pictorially then, when nucleocapsids arrive at a membrane characterized by a large value of γ, they get fully enveloped by membrane coats, recruiting spike proteins to ensure tight membrane-capsid binding. Once all spike proteins are engaged in bud coats, newly arriving nucleocapsids necessarily remain naked. Similar qualitative behavior is found for other values of c and φ. The dependence of the fraction of fully enveloped buds on these and other variables is discussed below.

An instructive analogy may be drawn between the behavior of a membrane-bud system of large γ and a self-assembling micellar solution. The all-or-nothing scenario characterizing this case, where the only buds possible are the fully wrapped ones, is completely analogous to the aggregation mechanism of surfactants in solution, forming monodisperse (typically spherical) micelles of size K; all smaller sizes involve much larger formation free energies and therefore do not form. The formation free energy of the micelle, per molecule, is simply our 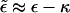, and ϕ_p (which is indeed extremely small, yet nonzero) is the analog of the concentration of monomeric surfactant in solution, usually referred to as the critical micellar concentration; see, for example, Israelachvili (1992) and Ben-Shaul and Gelbart (1994).

Mature buds

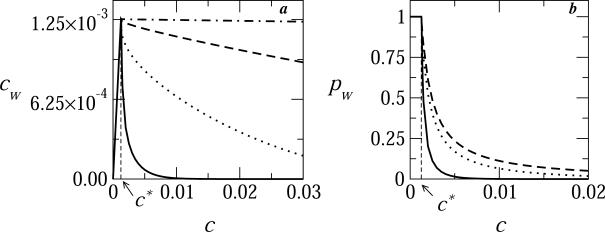
Fig. 5 describes the concentration, c_w = p_wc, and the fraction p_w of mature virions, i.e., nearly or fully enveloped capsids (k ≥ 0.9K), as a function of the bud density in the membrane plane, c. The different curves correspond to different values of γ, all for φ = 0.1, κ = 2π, and ε = 20. We know already that for these values of ε and κ the spike density in bud membranes is nearly saturated, ϕ_b ≈ 1. For small values of c, that is c < c^* where c^* = φ/K (here c^* = 0.1/80 = 0.00125), there should be enough spikes to fully envelope all the nucleocapsids arriving at the membrane, so that c_w = c, consistent with the low c behavior in Fig. 5. However, since the number of spikes in the membrane is not unlimited, as soon as c increases beyond c^*, the bud size distribution is bound to change, since the total curved (budding) membrane area is distributed among a larger number of buds. For large γ, as noted in analyzing Fig. 4, {p_k} is bimodal with peaks at k = 0 and k = K, and hence an increase in c beyond c^* = φ/K hardly affects c_w, and hence c_w/c = p_w is inversely proportional to c. On the other hand, when γ is small (e.g., γ = 0 in Fig. 5) both the absolute number and the fraction of fully wrapped buds decreases with c, indicating that efficient viral budding requires a nearly stoichiometric ratio of spikes to capsids, φ/c = K. If, as our model assumes, c and φ are indeed slowly varying quantities, then c_w could be interpreted as being (proportional to) the momentary budding rate.

FIGURE 5.

The concentration (a) and fraction (b) of essentially fully wrapped viral capsids (k ≥ 0.9 K) as a function of the two-dimensional concentration of nucleocapsids at the membrane plane, for a system with ε = 20, κ = 2π, φ = 0.1, and γ = 0 (solid curve), γ = 0.3 (dotted curve), γ = 0.5 (dashed curve), and γ = 1 (dot-dashed curve). c^* = φ/K is the optimum (i.e., stoichiometric) value of the capsid concentration for efficient budding (here c^* = 0.1/80 = 0.00125).

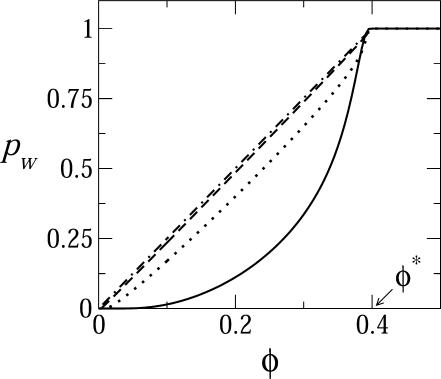
In Fig. 6 we show the fraction of mature buds as a function of the average spike concentration in the membrane. For the two curves describing the behavior of a system with nonzero γ, p_w increases linearly with φ, saturating at the threshold spike concentration φ = φ^* = cK, above which there are always enough spikes to fully wrap all nucleocapsids arriving at the membrane. This is the behavior expected for a bimodal (k = 0 or K) distribution of bud sizes, as we found to be the case for these values of γ. The nonlinear increase of p_w with φ for γ = 0 is a consequence of the highly polydisperse size distribution of buds in this case (see Fig. 4).

FIGURE 6.

The two-dimensional fraction p_w of essentially fully wrapped capsids (k ≥ 0.9 K) as a function of the average spike density in the membrane plane, for a system with ε = 20, κ = 2π, and c = 0.005, and γ = 0 (solid curve), γ = 0.3 (dotted curve), γ = 0.5 (dashed curve), and γ = 1 (dot-dashed curve). φ^* = cK is the stoichiometric value of the spike concentration for optimum budding (here φ^* = 80 × 0.005 = 0.4).

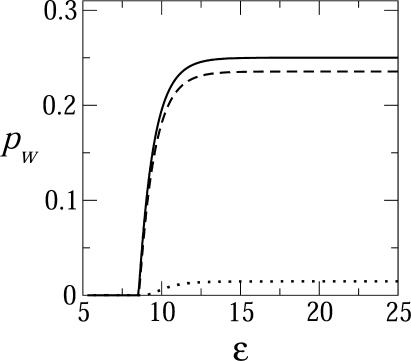
Finally, in Fig. 7 we show how p_w depends on the spike-mediated adhesion energy. These calculations confirm that budding cannot take place unless the adhesion energy counterbalances the membrane bending energy penalty. For large γ, once ε exceeds the κ threshold, the budding fraction increases rapidly, and saturates when all available spikes have been consumed. For very small values of γ (here represented by γ = 0), the threshold behavior is more moderate, reflecting the broad distribution of bud sizes and the relatively small fraction of fully wrapped buds.

FIGURE 7.

The two-dimensional fraction, p_w, of essentially fully wrapped capsids (k ≥ 0.9 K) as a function of the spike adhesion energy, ε, for a system with κ = 2π, c = 0.005, and φ = 0.1, and γ = 0 (dotted curve), γ = 0.5 (dashed curve), and γ = 1 (solid curve).

SUMMARY AND CONCLUSIONS

In this article we have cast the budding scenario proposed by Garoff and Simons (1974) into a statistical thermodynamic model, which has enabled us to address in both qualitative and quantitative terms a variety of questions raised by this scenario. One of our first results is the fact that, for essentially all biologically meaningful values of the membrane elastic constant and the spike binding strength, the spike density on wrapped capsids is saturated. In other words, if budding takes place, all binding sites on the capsid will be occupied. This is a nontrivial result of our calculation in the sense that it is not a necessary consequence of the mechanism of spike-assisted budding alone. The underlying reason for this is rather that entropic terms involved with the spikes are basically outweighed by energetic ones for the interaction strengths present in nature. Intermediate densities, which are entropically favorable, do not occur, because a vast coexistence region spans almost the entire range between φ = 0 and φ = 1. If one looks at the hypothetical case of extremely flexible membranes and likewise extremely weakly adhering spikes, entropy becomes significant and the coexistence regions in Figs. 2 and 3 contract toward the line ϕ ε − κ = 0. The naive argument that all adhesion binding sites will start to become occupied by spikes once the gain in binding energy can pay for the bending energy penalty is thus not too far off, but this finding could only be confirmed a posteriori.

Beyond that, our calculations yield of course more than an asymptotic attachment density of ϕ_b ≈ 1. In particular, the opposite side of the coexistence region, describing the planar membrane phase, depends strongly on ε, and ϕ_p covers a wide density range (see Fig. 2). In the macroscopic phase approximation, ϕ_p, ε, and κ are linked by a very simple equation, Eq. 13, which provides a useful link between these important but difficult to measure quantities. In fact, it turns out that under all interesting conditions the coexistence lines of the macroscopic phase approximation describe the preferred densities in the planar regions and on the capsids for any given average spike density quite well. For weak binding, ε < κ, the density ϕ_p in the planar region essentially (i.e., up to an exponentially small correction) coincides with the average density, φ, as one would expect; thus dictating ϕ_b by Eq. 4 (which generally implies 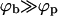; see Fig. 2). Since, the bud entropy term favors the existence of buds, some (small) buds should form even in the ε < κ regime. However, the fraction (M_b/M) of the membrane area occupied by these buds (as confirmed by calculations not reported here) is negligibly small and bud maturation is obviously impossible.

Once the adhesion strength gets large enough such that the average density φ finally exceeds the macroscopic coexistence density 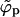, the spike density ϕ_p in the planar region departs from φ, joins into the macroscopic coexistence line 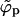, and thereby begins to decrease. When this happens, the bud phase finally acquires a macroscopic number of spikes and budding becomes possible. Upon further increasing, ε, spikes are continuously shifted from the p phase to the b phase. However, in the discrete case there exists one more limitation which the macroscopic phase approximation does not know about—namely, that the total number of capsids per area (and thus the amount of occupiable binding sites) is finite. It may thus happen that all spikes have been transferred into the b phase before the p phase is emptied. If this occurs, ϕ_p can no longer follow 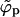(which approaches 0 as ε → ∞), and instead saturates at a finite density. This is evidently favored if the spike concentration is high, but also if the capsid concentration is low.

The above scenario is also nicely reflected by our studies of the bud size distribution. For instance, Fig. 7 illustrates that wrapping will only commence once ε exceeds the critical threshold κ, even though a bud phase existed before. Perhaps an even more interesting insight from the analysis of the bud size distribution is that the line energy associated with the bud rims, although acting as an additional penalty toward wrapping, nevertheless promotes the production of more mature virions, as has been clearly demonstrated by Fig. 7. It has been pointed out previously (Deserno and Gelbart, 2002; Deserno and Bickel, 2003) that a line energy suppresses partially wrapped states and can therefore also shift the wrapping balance toward full envelopment. The same effect is at work in the present situation, only with the subtle additional feature that the bud size distribution comes along with an entropy, which is thereby also reduced.

The line energy thereby helps to increase the efficiency of budding. Indeed, Fig. 5 shows that the budding rate increases, and that the maximum in c_w as a function of c, which is most strongly pronounced for γ = 0, is broadened. This again follows because capsids are not wasted in partially wrapped states. However, one should not overlook that the fraction of budding virions nevertheless starts to decrease beyond the stoichiometric point, which is therefore the optimum point at which the virus should operate (i.e., without either wasting spikes or capsids). It would be interesting to test this optimality prediction experimentally.

Let us finally address what is still missing in our model. One important point, which has been put forward by Lerner et al. (1993), touches upon the discreteness of spike binding. What we have treated as a smooth energy landscape (i.e., the total wrapped area simply gets multiplied by the effective adhesion strength 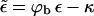) is, in fact, a sequence of energy barriers which have to be overcome when proceeding from a capsid with l bound spikes to a capsid with l + 1 bound spikes. The key observation is that between l and l + 1 one has to pay the bending price in advance before finally being compensated by one more unit of binding energy. Taking into account the role of membrane curvature fluctuations, Lerner and co-workers estimate that on reasonable experimental timescales (∼10–20 min) efficient budding from membranes of zero spontaneous curvature may only take place if the membrane bending modulus is rather small (≤7 k_BT). They therefore suggest that budding could possibly occur from precurved membrane regions, where c₀ > 0, thereby reducing the membrane bending energy barriers. Lerner and co-workers further suggest that the wedge-shaped spike proteins could possibly be the origin of the nonzero spontaneous curvature. It should be noted that such estimates of the membrane bending rigidity based on calculated budding rates may be quite sensitive to the details of the kinetic model. Yet, these estimates do not affect our model in which, as we have stressed, all effects due to the membrane bending energy are embodied in κ, including the possibility of a nonzero spontaneous curvature.

Perhaps the most crucial approximation in our model is the use of equilibrium statistical thermodynamics to calculate the bud size distribution. Spike diffusion within the membrane plane is, most likely, fast enough to equilibrate the spike densities between the curved budding regions and the embedding planar membrane. What is not clear, and requires further theoretical modeling, is whether the bud size distribution is indeed equilibrated. Nevertheless, even though preliminary, our analysis provides many quantitative and thus testable predictions, which we expect to apply at least in certain limiting cases.

After completion of this manuscript we received a preprint from Drs. Damien van Effenterre and Didier Roux, entitled Adhesion of Colloids on a Cell Surface in Competition for Mobile Receptors, which will appear in Europhysics Letters. They estimate mean-field equilibrium values for the surface concentration of adsorbed colloids, and the average number of ligand-receptor bonds per colloid, as a function of bulk colloid concentration. While the effects of curvature, line energy, and bud size distribution (and hence capsid wrapping) effects are neglected, they also find that there is an optimal ratio between colloids and linkers for adhesion by the membrane. (Note added in proof: Meanwhile, this article has been published, van Effenterre and Roux, 2003).