Abstract
We study a physical model for the formation of bud-like invaginations on fluid lipid membranes under tension, and apply this model to caveolae formation. We demonstrate that budding can be driven by membrane-bound proteins, provided that they exert asymmetric forces on the membrane that give rise to bending moments. In particular, caveolae formation does not necessarily require forces to be applied by the cytoskeleton. Our theoretical model is able to explain several features observed experimentally in caveolae, where proteins in the caveolin family are known to play a crucial role in the formation of caveolae buds. These include 1), the formation of caveolae buds with sizes in the 100-nm range and 2), that certain N- and C-termini deletion mutants result in vesicles that are an order-of-magnitude larger. Finally, we discuss the possible origin of the morphological striations that are observed on the surfaces of the caveolae.
INTRODUCTION
It has long been understood that invaginations form spontaneously on cell membranes (Alberts et al., 1994). These invaginations, which eventually separate from the membrane as mature, membrane-bound vesicles, play an essential role in cellular trafficking and signaling (Stahlhut et al., 2000; Lisanti et al., 1994). The mechanism by which such invagination is controlled is still far from fully understood, although it is now widely accepted that certain membrane-bound proteins, including clathrin and caveolin, play an important role. The formation of clathrin-coated pits is thought to be driven by the controlled geometric aggregation of clathrin into rigid scaffolding, which forces the membrane to curve (Takei and Haucke, 2001; Mashl and Bruinsma, 1998). The mechanism for formation of the second most common class of membrane invaginations, known as caveolae, is less well understood. Caveolae, which are less morphologically distinct than clathrin-coated pits, resemble Ω-shaped invaginations with a typical size of ∼100 nm (Rothberg et al., 1992; Schlegel et al., 1998; Westermann et al., 1999). They are present at high concentrations on primary adipocytes, fibroblasts, muscle cells, and pulmonary type 1 cells as well as endothelial cells, and perform a variety of functions ranging from signal transduction to intracellular transport (Gilbert et al., 1999; Schlegel and Lisanti, 2001). A “striated coat” can be seen on the cytoplasmic side of the caveolae membrane. It is believed to reflect the organization of a recently discovered class of membrane-bound proteins, called caveolins, which are crucial to the formation of caveolae (Lisanti et al., 1994).
The protein caveolin has a hairpin structure, with a short membrane-spanning sequence, flanked by two hydrophilic termini, both found on the cytoplasmic side of the cell membrane: a 101-amino-acid polypeptide N-terminus tail (polymer), and a shorter (44 a-a) C-terminal, which is strongly attached to the membrane (Schlegel and Lisanti, 2001). These caveolin molecules are typically found in small aggregates of 15–17 molecules (Schlegel et al., 1998; Sargiacomo et al., 1995), the aggregation being driven by residues of the N-terminal located close to the membrane. Furthermore, it is believed (Schlegel and Lisanti, 2001) that there exist some specific C-terminal to C-terminal attractions, which are responsible for the organization of the protein aggregates at the surface of the caveolae membrane. Mutational analysis of caveolin-induced vesicle formation have been recently performed (Li et al., 1998) and is discussed in relation with our theory in the Conclusions section.
Caveolae are now thought to influence cell physiology in many ways, including growth and cell division, adhesion, and hormonal response (Fielding and Fielding, 2000). These invaginations have been associated with the formation of lipid rafts (Kurzchalia and Parton, 1999)—glycosphingolipid- and cholesterol-enriched microdomains within the plasma membrane of eukaryotic cells. Their ability to perform many different tasks might be achieved by their involvement in reporting change in membrane composition by signal transduction to the nucleus. It may also be connected to their regulation of signal traffic in response to extracellular stimuli, including mechanical stress (Park et al., 2000).
From a physical point of view, spontaneous vesicle formation has been observed in vitro by adding amphiphilic polymers to various lipid systems (Lasic et al., 2001). It can be viewed as an example of the so-called curvature instability of fluid membranes containing inclusions, predicted to occur for inclusions that locally influence the membrane curvature (Leibler, 1986; Leibler and Andelman, 1987). There have been physical studies of the inclusion-induced budding of vesicles (Kim and Sung, 1999; Seifert, 1993; Jülicher and Lipowsky, 1996) and works on the effect of single (Lipowsky, 1997; Hiergeist et al., 1996) and distributed (Nicolas, 2002) polymers grafted on membranes.
Many theoretical studies have also been devoted to understanding physical coupling between integral membrane proteins and biological membranes. Such couplings include local disruption of the bilayer molecular structure in the vicinity of the protein (hydrophobic mismatch, local membrane tilt), and the behavior of foreign bodies in a fluctuating environment (for reviews, see Goulian, 1996 and Mouritsen and Andersen, 1998).
Our aim is to study the effect of small inclusions, such as proteins, that affect the shape of the cell membrane. We assume that this “foreign” object exerts a force on the membrane, which may be due either to entropic effects, similar in origin to the pressure exerted by a gas onto the walls of its container, or to specific mechanochemical forces. Throughout we will attempt to compare our rather general theory with the specific phenomenon of caveolin-mediated formation of caveolae. The fact that membrane-bound objects exert a force on the membrane arises naturally from theories that describe polymers grafted to surfaces. These have been extensively developed over the last decade or so, based on early ideas due to de Gennes (1991) and others. The forces exerted by membrane-bound inclusions, as well as their interactions, have been calculated in certain ideal situations (e.g., idealized polymers on a tensionless membrane; Bickel et al., 2001; Breidenich et al., 2000). In what follows, we will analyzed arbitrary force distributions, which allow for the description of specific inclusions, such as the caveolin aggregates. We also focus on tension-bearing membranes, a situation that we believe more closely approximates the plasma membrane of the cell.
Our physical description of caveolae formation in cell membranes involves the segregation of the caveolin proteins into strongly curved membrane patches. This segregation is driven by the protein's predilection for a curved surface—itself a consequence of the forces it exerts on the membrane.
Our model is based on the mechanical response of fluid membranes to local forces applied by membrane-bound proteins (Membrane Response to an Arbitrary Force Distribution, below). The force distribution which can result from the particular structure of oligomers of the membrane protein caveolin is discussed in Models for Membrane-Bound Proteins. Physical theories for the several levels of protein self-organization at the cell membrane (the formation of the protein oligomers, and the formation of membrane invagination) are presented in Bud Structure and Morphology, followed by Results for Various Force Distributions. We then briefly comment on possible physical mechanisms for the peculiar protein arrangement (stripe formation) at the bud surface (Microphase Separation at the Bud Surface). The Conclusions section discusses topics such as the possible function of caveolae as membrane mechanosensors, the influence of the membrane composition, and the effect of mutation of the protein caveolin. The main mathematical symbols used in this text are listed in Table 1.
TABLE 1.
Table of symbols used in the text
| Symbol | Denomination (and Dimensions) | Numerical value |
|---|---|---|
| Membrane | ||
| κ | Bending modulus (energy) | 20 kBT |
| γ | Surface tension (energy/area) | 10−4 N/m |
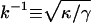
|
Decay length | 30 nm |
| Proteins | ||
| E0 | Energy scale for applied force | 10 kBT |
| a, b | Size of the oligomer core and corona | 2 nm, 5 nm |
| s1 = πb2 | Oligomer surface area | 75 nm2 |
| Drr | Force distribution second moment (energy × length) | 100 kBT × nm |
| V(r) | Oligomers interaction potential (energy) | see text |
| B2 | Oligomers second virial coefficient (area) | 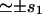 |
| Buds | ||
| ℰp,b,ep,b | Aggregate total and per particle energies | |
| μ, φ | Oligomer chemical potential and surface fraction | |
| Rmin = 4κs1/Drr | Radius of a closed packed bud (φ = 1) | 60 nm |
MEMBRANE RESPONSE TO AN ARBITRARY FORCE DISTRIBUTION
The deformation energy of a membrane involves its surface tension γ and bending rigidity κ. Cells commonly adjust their surface tension to a set value via a mechanism known as surface-area-regulation (Morris and Homann, 2001). Hence membrane phenomena over sufficiently long timescales effectively occur at constant surface tension. It is also known that the composition of biological membranes exhibits spatial variations. Caveolar membranes, for instance, show a high cholesterol content (Fielding and Fielding, 2000), the precise biochemical role of which is not yet entirely clear. From a physical point of view, it is known that cholesterol increases the local rigidity of the membrane (Evans and Rawicz, 1990; Song and Waugh, 1993). Local variations of membrane rigidity are not included in the following model, but some (limited) information on the impact of cholesterol on caveolae at the physical level can be obtained by examining the effect on uniform changes in κ across the whole membrane. It has also being suggested that the chiral nature of cholesterol may play a role in the process of bud formation (Sarasij and Rao, 2002).
Initially, we restrict our analysis to a membrane that is weakly deformed by the presence of the inclusions. We proceed by writing down the free energy of an infinite planar fluid membrane as a standard expansion in powers and gradients of the membrane displacement u(r) from its flat (unperturbed) position (Safran, 1994). This is modified to include the leading order term arising from the coupling to u of the applied pressure distribution f(r), which will arise from the action of inclusion(s). (No net force acts on the membrane, inasmuch as no net force can be exerted by an object that is not externally attached—i.e., to the cytoskeleton. For more details see Evans et al., 2003.) More details on the mathematical analysis involved in the derivation of Eqs. 2 and 4, below, can be found in Evans et al. (2003).
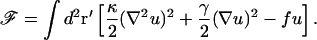 |
(1) |
Typically values for phospholipid bilayers are κ ≈ 20 kBT (Evans and Rawicz, 1990). (It is usually helpful to compare energies to the energy available from thermal fluctuations kBT, where kB is the Boltzmann constant and T the temperature.) The surface tension is reported to be in the range γ ≈ 10−2−10−1 pN/nm (Sheetz and Dai, 1996). The interplay of surface tension and bending rigidity defines a characteristic lengthscale 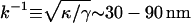 .
.
Minimization of this energy results in the equilibrium membrane displacement u(r), and is reported in more detail elsewhere (Evans et al., 2003). We find 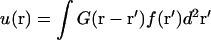 with the Green's function (the response to a point force) given by
with the Green's function (the response to a point force) given by
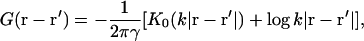 |
(2) |
where K0 is a modified Bessel function (Abramowitz and Stegun, 1984), which decreases exponentially over a size k−1. The membrane displacement is discussed further in Models for Membrane-Bound Proteins.
Overlap of displacements due to neighboring inclusions lead to membrane-mediated interactions between them. The interaction potential Φ(r) between two similar inclusions separated by a vector r is obtained by inserting the total force distribution f(r′) + f(r′ + r) into Eq. 1 and identifying the r-dependence of the resulting energy (see Evans et al., 2003, for the general theory). The interaction energy per inclusion (interaction potential) reduces to
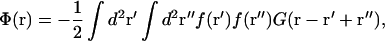 |
(3) |
where G(r) is the real-space Green's function given by Eq. 2.
If the inclusions have a circular symmetry (f(r′) = f(r′)) and do not overlap (r > 2b where b is the spatial extent of the force), we have been able to determine the interaction potential exactly in an analytic form
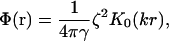 |
(4) |
where 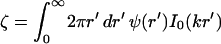 characterizes the strength of the interaction (I0 is another modified Bessel function; Abramowitz and Stegun, 1984). The interaction is everywhere repulsive in the regime of validity r > 2b.
characterizes the strength of the interaction (I0 is another modified Bessel function; Abramowitz and Stegun, 1984). The interaction is everywhere repulsive in the regime of validity r > 2b.
MODELS FOR MEMBRANE-BOUND PROTEINS
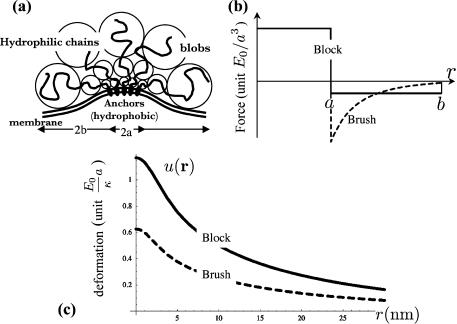
Up to this point, we have been able to avoid making any but a few rather general assumptions about the form of the force exerted by the membrane inclusions. We will now proceed to consider some specific models for the force distribution. We do this both to make possible the later quantitative comparison with experiments and to demonstrate how such forces are expected to arise on general physical grounds. The force distributions and the subsequent membrane deformations (from Eq. 2) are shown in Fig. 1.
FIGURE 1.
(a) Sketch of the blob model for the anchored protein aggregate and (b) force distribution for the two models used in the article: brush distribution (dashed, corresponding to a) and block distribution (solid). The membrane is pushed down by the corona of grafted polymers out to r = b = 5 nm and is pulled upwards by the anchored core inside r′ = a = 2 nm. (c) The corresponding membrane deformation u(r) in unit (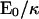 )a for k−1 = 30 nm. The brush distribution has a weaker effect on the membrane because the force is mostly concentrated near its center (r = 0). For aggregates residing on the cytoplasmic face of the membrane, including caveolin homo-oligomers, the cell interior would be above the membrane.
)a for k−1 = 30 nm. The brush distribution has a weaker effect on the membrane because the force is mostly concentrated near its center (r = 0). For aggregates residing on the cytoplasmic face of the membrane, including caveolin homo-oligomers, the cell interior would be above the membrane.
Random coil polymers
In this section we treat caveolin proteins as flexible, linear polymer chains in the random coil configuration, anchored to the membrane. The idealized picture enables us to extract an analytic estimate of the force distribution. In the language of polymer physics (de Gennes, 1991), the caveolin homo-oligomer can be viewed as a brush of 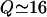 polymer chains, grafted by one end to a small patch of membrane of radius a. The flexible chains on average arrange themselves radially to form a hemisphere of radius b (Fig. 1 a). Thus for radial distances a < r < b one finds a corona of randomly coiled polymer chains with a chain density that is larger near the core and smallest on the outskirts of the distribution.
polymer chains, grafted by one end to a small patch of membrane of radius a. The flexible chains on average arrange themselves radially to form a hemisphere of radius b (Fig. 1 a). Thus for radial distances a < r < b one finds a corona of randomly coiled polymer chains with a chain density that is larger near the core and smallest on the outskirts of the distribution.
A central concept in the theory of polymer physics is the existence of a correlation length or blob size ξ(r) (de Gennes, 1991), which is roughly the distance between interchain contacts in the corona of the caveolin brush (viewed as a semidilute polymer solution). Each chain can then be thought of as a string of correlation blobs extending radially outwards, with small values of ξ corresponding to large densities of monomers. The classical Daoud-Cotton model (Daoud and Cotton, 1982) takes advantage of the fact that the surface area of a hemisphere of radius r is approximately filled by Q close-packed blobs, to deduce the scaling of the correlation length, 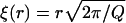 . It can be shown (de Gennes, 1991) that the work done in generating each blob is kBT, independent of the blob size. Thus we may write the pressure in this region as the energy per blob divided by the volume of a blob,
. It can be shown (de Gennes, 1991) that the work done in generating each blob is kBT, independent of the blob size. Thus we may write the pressure in this region as the energy per blob divided by the volume of a blob,
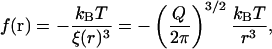 |
(5) |
which is a result that is valid for a < r < b, and which is consistent with more detailed calculations (Bickel et al., 2001; Breidenich et al., 2000). The physical origin of this pressure can be understood as simply due to the exchange of momentum due to collisions of the polymer chains with the membrane. It is therefore purely entropic in origin, as evidenced by the overall kBT energy scale. For r > b the pressure is zero since the chains have finite length (in fact, it is exponentially small; Bickel et al., 2001; Breidenich et al., 2000). The pressure in the core binding region is assumed constant and must involve a total force equal and opposite to that applied by the corona, as
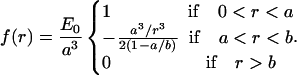 |
(6) |
Note that the strength of the force is characterized by the energy scale, E0 = f(r = 0)a3. For the Q-chain oligomer, it is E0 = 2 kBT(Q/2π)3/2(1 − a/b) ∼ 4 kBT.
Block distribution
We believe that the polymer brush model captures some of the fundamental properties of a collection of large hydrophilic proteins anchored to a biomembrane, namely: 1), a downward pressure exerted by the cytosolic portion of the proteins, combined with 2), an upward pull from the anchors (the hydrophobic region of the proteins). However, it employs rather strong assumptions (random coil configuration, absence of internal structure, and large size of the polymer chains) which are certainly not satisfied for the protein caveolin. The simplest example of a general force distribution that satisfies the criteria above is a block distribution, for which the force exerted by the hydrophobic anchors (between 0 < r < a) and the hydrophilic sections (a < r < b) are both constant: E0/a3 = fr<a = (1 − b2/a2)fa<r<b. The membrane deformation for such distribution is larger than for the brush distribution for the same strength, as characterized by the energy E0, since the force is not concentrated near the center of the distribution (Fig. 1 c).
BUD STRUCTURE AND MORPHOLOGY
Caveolae formation involves a hierarchy of self-organization, ranging from the nanometric scale (oligomers of ∼15 particles and size ∼5 nm) up to buds of radius ∼100 nm. We review briefly the theoretical framework of thermal self-organization (Safran 1994), and give insights on the caveolin homo-oligomer formation, which we view essentially as a micellization in two dimensions. We then describe in some detail the formation of caveolae buds.
Consider a solution of particles of average surface fraction 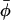 , that can exist either as isolated entities or in larger aggregates (homo-oligomers) of p particles and of energy ℰp = pep. The concentration Cp of p-sized aggregates follows a Boltzmann law (Safran 1994):
, that can exist either as isolated entities or in larger aggregates (homo-oligomers) of p particles and of energy ℰp = pep. The concentration Cp of p-sized aggregates follows a Boltzmann law (Safran 1994): 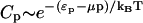 , where μ is the chemical potential of the particles, usually fixed by the average concentration
, where μ is the chemical potential of the particles, usually fixed by the average concentration  . There is an energetic tendency to form aggregates if the energy per particle ep is (at least in some regime) a decreasing function of the aggregation number p. It overcomes the entropic dispersive effect beyond a critical value of
. There is an energetic tendency to form aggregates if the energy per particle ep is (at least in some regime) a decreasing function of the aggregation number p. It overcomes the entropic dispersive effect beyond a critical value of  (the critical aggregation concentration), usually defined as the concentration at which the density of aggregates is equal to the density of isolated particles. At the critical aggregation concentration and above the average size p* of the aggregates is the one that minimizes the energy per protein in the aggregate. The root mean-squared deviation Δp from the average depends upon the steepness of the energy variation around that minimum. Expressed in the form of equation, these conditions yield (for
(the critical aggregation concentration), usually defined as the concentration at which the density of aggregates is equal to the density of isolated particles. At the critical aggregation concentration and above the average size p* of the aggregates is the one that minimizes the energy per protein in the aggregate. The root mean-squared deviation Δp from the average depends upon the steepness of the energy variation around that minimum. Expressed in the form of equation, these conditions yield (for 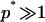 ):
):
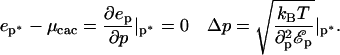 |
(7) |
The driving force for homo-oligomerization is an attractive interaction between specific motives on the N-terminal of the protein (Sargiacomo et al., 1995). We proceed by assuming that all proteins in the interior of the oligomer experience a mutual attraction, and contribute to the oligomer energy ℰp via a negative linear term −μ′p. Proteins in the outskirts of the oligomer on average experience less attraction, as they have less neighbors. They increase the energy ℰp by a factor 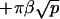 , where β is the energy loss (per protein) for being on the outskirts (the equivalent of the surface tension of a liquid). Bringing proteins together also leads to steric and/or entropic repulsion (crowding). For a polymer brush, for instance, the latter contribution to ℰp is +αp3/2 (see Eq. 5). Solving Eq. 7 with
, where β is the energy loss (per protein) for being on the outskirts (the equivalent of the surface tension of a liquid). Bringing proteins together also leads to steric and/or entropic repulsion (crowding). For a polymer brush, for instance, the latter contribution to ℰp is +αp3/2 (see Eq. 5). Solving Eq. 7 with 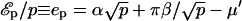 , the experimental observation (oligomers containing 14–16 proteins; Sargiacomo et al., 1995) are consistent with α = 2 kBT and β = 10 kBT. Both numbers are physically reasonable: the frustration α which results in bringing many proteins close to one another might be expected to be approximately of the order of kBT per protein, and the calculated energy loss β for proteins on the outskirts of the oligomers is approximately of the order of hydrogen bond energy (10 kBT) per protein. Although quite crude, this model provides a thermodynamic description for the first level of self-organization in caveolar membranes, which is able to reproduce the experimental observation on caveolin oligomerization, namely
, the experimental observation (oligomers containing 14–16 proteins; Sargiacomo et al., 1995) are consistent with α = 2 kBT and β = 10 kBT. Both numbers are physically reasonable: the frustration α which results in bringing many proteins close to one another might be expected to be approximately of the order of kBT per protein, and the calculated energy loss β for proteins on the outskirts of the oligomers is approximately of the order of hydrogen bond energy (10 kBT) per protein. Although quite crude, this model provides a thermodynamic description for the first level of self-organization in caveolar membranes, which is able to reproduce the experimental observation on caveolin oligomerization, namely 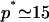 and
and 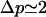 .
.
The formation of the caveolae themselves can be described more accurately, as we will now show. Inasmuch as caveolae involve a large number of oligomers, a precise description at the molecular level seems less crucial. We model the Ω-shaped invagination by a closed sphere of radius R. Thus we neglect the small caveolae “neck,” where the quasispherical bud joins onto the quasiplanar membrane. This is one of the core simplifications of our approach, which is valid provided that the neck geometry is substantially controlled by specific proteins (such as dynamin) and is rather independent of the caveolae radius. There is experimental evidence (Oh et al., 1998) to show that the composition of the caveolae neck is indeed very different from the composition of the caveolae themselves (this is a generic feature of large membrane invaginations).
Following these assumptions the neck energy has little influence upon the equilibrium features that we discuss below (radius, composition, critical budding concentration), but enters the thermodynamic theory as an addition to the energy barrier to be overcome to reach the equilibrium state. This does not impose any additional limitations on our work, inasmuch as we are interested in calculating the equilibrium bud conformation, and do not discuss how this equilibrium is reached.
The bending moments exerted by the protein oligomers, which are all on the cytoplasmic side of the membrane, drives the bud formation, expected to occur above a critical budding concentration (cbc) of oligomers (see Fig. 2). For small concentration φ < φcbc (Fig. 2 a), the membrane is uniformly covered by oligomers and remains almost flat. Buds start forming as the concentration increases, and outnumber isolated oligomers at the cbc (Fig. 2 b). If the concentration is increased further (Fig. 2 c), then the concentration of isolated oligomers, and the bud size, remain almost constant (φ1 = φcbc), whereas the number of buds increases.
FIGURE 2.
Sketch of bud formation upon increase of oligomer concentration. (a) Below the critical budding concentration (cbc), the membrane is uniformly covered by isolated oligomers. (b) At the cbc, buds have formed and outnumber isolated inclusions. (c) Above the cbc, the size and shape of the buds remains the same, and their number increases with the concentration.
The free energy per membrane inclusion in the bud eb (Eq. 8 below) contains several contributions. Energy is gained if the membrane curves to accommodate the deformation imprinted by the caveolin oligomer. A membrane curving away from the caveolin aggregate is favored (first term, right-hand side of Eq. 8). In the limit of small curvature, the energy reduction per oligomer is of ∼−Drr/R (Eq. 9). On the other hand, bud formation costs an energy that depends on the bending rigidity and surface tension (second and third terms, RHS of Eq. 8), and leads to higher local oligomer concentration, modifying the pair interaction energy (fourth term, RHS of Eq. 8). This interaction is characterized by the second virial coefficient B2 (Eq. 9), and involves the interaction potential V(r) (see Results for Various Force Distributions). The last term in the RHS of Eq. 8 is the mixing entropy of a gas of membrane inclusions on a lattice,
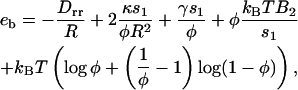 |
(8) |
where s1 = πb2 is the oligomer area, and with
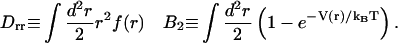 |
(9) |
Minimizing this energy with respect to R gives the optimal bud radius R* = Rmin/φ, where Rmin ≡ 4κs1/Drr corresponds to the minimal radius of a bud densely packed with caveolin. Further energy minimization leads to the optimal amount of protein φ* recruited in the bud, defined by
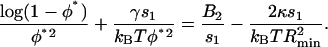 |
(10) |
This equation has a clear physical meaning. The protein coupling to the membrane curvature effectively reduces the second virial coefficient by an amount 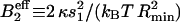 , which indicates an attraction between oligomers (Leibler, 1986).
, which indicates an attraction between oligomers (Leibler, 1986).
The optimal concentration of Eq. 10 corresponds to an energy minimum 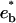 . At the cbc (Eq. 7), it is equal to the oligomer chemical potential:
. At the cbc (Eq. 7), it is equal to the oligomer chemical potential:  . The latter can be related to the concentration φ1 of isolated oligomer via μ = log(φ1/(1 − φ1)) + 2B2φ1, which is the chemical potential of a gas on a lattice with pair interaction. The equation defining the critical budding concentration is
. The latter can be related to the concentration φ1 of isolated oligomer via μ = log(φ1/(1 − φ1)) + 2B2φ1, which is the chemical potential of a gas on a lattice with pair interaction. The equation defining the critical budding concentration is
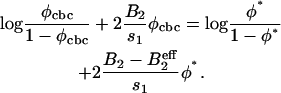 |
(11) |
The mean variation of the radius ΔR2 ≡ 〈R2〉 − R*2 can be approximately calculated by using a steepest descent method to calculate moments of the bud size distribution (Eq. 7). We find 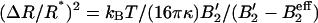 , where B′2 ≡ B2 + s1/(2φ*(1 − φ*)) > 0 includes both the interaction between brushlets and the entropic contribution (note that if B′2 < 0, the inclusions spontaneously demix on the flat membrane). The mean radius variation shows the signature of the membrane curvature instability mentioned earlier (Leibler, 1986). If the coupling between membrane and inclusion is sufficiently strong:
, where B′2 ≡ B2 + s1/(2φ*(1 − φ*)) > 0 includes both the interaction between brushlets and the entropic contribution (note that if B′2 < 0, the inclusions spontaneously demix on the flat membrane). The mean radius variation shows the signature of the membrane curvature instability mentioned earlier (Leibler, 1986). If the coupling between membrane and inclusion is sufficiently strong: 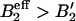 , or
, or 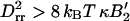 , then small fluctuations of any lengthscale are unstable and the mean variation of radius becomes large. The actual dispersion in bud size depends on how close we are to the instability. It is ∼6% for the parameters used below. Note that variations in shape that conserve the mean curvature of the membrane should be larger, as they only cost a fraction of the energy penalty corresponding to variation of the bud global size. From electron micrographs of caveolar membranes, the projected radius variation is ∼20% (Rothberg et al., 1992; see also Fig. 13.48 in Alberts et al., 1994).
, then small fluctuations of any lengthscale are unstable and the mean variation of radius becomes large. The actual dispersion in bud size depends on how close we are to the instability. It is ∼6% for the parameters used below. Note that variations in shape that conserve the mean curvature of the membrane should be larger, as they only cost a fraction of the energy penalty corresponding to variation of the bud global size. From electron micrographs of caveolar membranes, the projected radius variation is ∼20% (Rothberg et al., 1992; see also Fig. 13.48 in Alberts et al., 1994).
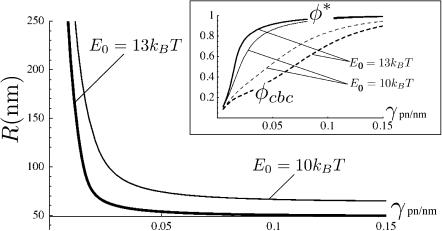
Numerical calculation of the bud radius and protein concentration in the membrane is shown in Fig. 3 upon variation of the surface tension for different values of the coupling strength (for an attractive energy Eatt = 0.5 kBT, see Results for Various Force Distributions). A strong variation in bud size is observed for small surface tension. At larger tension, the radius is almost insensitive to γ. Bud formation is, however, less favorable, as can be seen from the increase of the cbc. Our model also predicts the existence of a critical point (P. Sens and M. S. Turner, unpublished results), hence a possible coexistence of buds of different radius, connected to the curvature instability studied by Leibler (1986). We will not discuss this further here, as it is probably not relevant to the problem of caveolae formation.
FIGURE 3.
Variation of the caveolae preferred radius R* (in nm) with the surface tension for a short-range attraction of Eatt = 0.5 kBT between brushlets (see Results for Various Force Distributions). Two values of the coupling strength E0 are displayed: E0 = 10 kBT (thin line) and E0 = 13 kBT (thick line). The inset shows the variation of the bud composition φ* (solid) and critical budding concentration (dashed) for the two coupling strengths. The other parameters are a = 2 nm, b = 5 nm, and κ = 20 kBT.
We have derived the bud morphology as a function of two variables that depend on the actual shape of the force distribution, B2 and Drr. To make quantitative prediction, we study below two “extreme” force distributions.
RESULTS FOR VARIOUS FORCE DISTRIBUTIONS
In this section we discuss the results above for the polymer brush model and the block model. The force distributions involve three parameters. The lengthscales a and b can be measured experimentally: 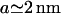 and
and 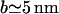 . The energy scale of the force E0 can be calculated for the brush model, and will be estimated for the block model (Eq. 6). We present results for the minimal radius Rmin (connected to the force moment Drr) and the membrane-mediated interaction Φ(r). The excluded volume B2 involves the full interaction potential and is discussed at the end of this section.
. The energy scale of the force E0 can be calculated for the brush model, and will be estimated for the block model (Eq. 6). We present results for the minimal radius Rmin (connected to the force moment Drr) and the membrane-mediated interaction Φ(r). The excluded volume B2 involves the full interaction potential and is discussed at the end of this section.
The calculation results in a unified description of the force distribution via the energy scale E0 and the ratio of size of the protein aggregate over deformation range ka (for ka ≪ 1). The bud radius is Rmin/b = ακ/E0, with
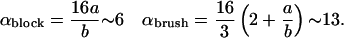 |
(12) |
The oligomer-oligomer interaction is given by Eq. 4, and involves the force moment ζ = −β(ka)2E0/a, with
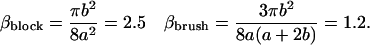 |
(13) |
Brush distribution
For ideal Gaussian chains, the energy scale given by Eq. 6 is 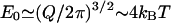 . Most of the force is concentrated near the center of the distribution, and has a small effect on the membrane. Fig. 1 shows that the deformation is quite small (∼0.4 nm). However, collective effects lead to the formation of fairly small buds of minimum bud radius
. Most of the force is concentrated near the center of the distribution, and has a small effect on the membrane. Fig. 1 shows that the deformation is quite small (∼0.4 nm). However, collective effects lead to the formation of fairly small buds of minimum bud radius 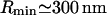 (much larger, however, than the caveolae). The membrane-mediated interaction between protein aggregates is very small, of ∼10−3 kBT.
(much larger, however, than the caveolae). The membrane-mediated interaction between protein aggregates is very small, of ∼10−3 kBT.
Block distribution
The block distribution is probably more relevant to the case of stiff, short proteins such as caveolin. We choose the strength of the force so that each protein contributes to the kBT of energy as 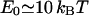 , which imposes a displacement u(r = 0) = 2 nm (Fig. 1). The corresponding minimum bud radius,
, which imposes a displacement u(r = 0) = 2 nm (Fig. 1). The corresponding minimum bud radius, 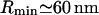 , is comparable to the radius of caveolae. Radius variation with surface tension is shown in Fig. 3. The interaction potential is Φ(r) = 0.02 K0(kr) kBT. We believe that, although small, this repulsive interaction might be responsible for the remarkable phase behavior of the proteins at the surface of the buds (see Microphase Separation at the Bud Surface).
, is comparable to the radius of caveolae. Radius variation with surface tension is shown in Fig. 3. The interaction potential is Φ(r) = 0.02 K0(kr) kBT. We believe that, although small, this repulsive interaction might be responsible for the remarkable phase behavior of the proteins at the surface of the buds (see Microphase Separation at the Bud Surface).
Second virial coefficient and critical budding concentration
The virial coefficient B2 defined by Eq. 9 involves the interaction potential V(r) describing the membrane-mediated physical interaction of Eq. 4. The hard-core repulsion, by which two oligomers cannot occupy the same patch of membrane, is taken into account via the lattice gas entropy of mixing included in Eq. 8. Moreover, we have experimental evidence (Schlegel and Lisanti, 2001, 2000) that there exists short-range specific attractions between the protein side chains (C-termini). To describe this attraction, we adopt the exponentially short-range form Vatt = −Eatte−(r−b)/b, where Eatt ∼ kBT is the strength of the attraction, in range the size of the b-oligomer. The short-range attraction acts to increase the oligomer density inside the invagination. The resulting buds are crowded with proteins φ ∼ 0.8, and are quite small, with a radius ∼R = 70 nm (see Fig. 3).
MICROPHASE SEPARATION AT THE BUD SURFACE
One peculiar feature of the caveolae is their striated texture, believed to correspond to alignment of protein oligomers at the surface of these “gnarly buds” (Rothberg et al., 1992; see also Fig. 13.48 in Alberts et al., 1994). This finding is particularly striking, inasmuch as it is not trivial to understand how radially symmetrical oligomers may organize themselves into nonsymmetrical phases. We argue that the stripe phase might be a signature of the membrane mediated repulsion between protein aggregates (see Evans et al., 2003, for a complete derivation of the results below). Molecular dissection of the caveolin protein has shown that the oligomers interact attractively via the third distal region of their C-termini (Schlegel and Lisanti, 2000). This attraction may lead to gas/liquid phase separation of the caveolin oligomers, which results in dense membrane patches (the liquid) coexisting with less dense regions (the gas). Our situation is more complex, as we have shown the existence of an additional, membrane-mediated, longer-range repulsion between oligomers. It has been recently argued at the light of computer simulation (Sear et al., 1999; Sear and Gelbart, 1999) that under this long-range repulsion, the gas and liquid phases are broken into microdomains (circles at small concentration, and stripes for higher concentration). This is because large aggregates are costly, due to the long-range repulsion, whereas small aggregates (circles or stripes) are favored by the short-range attraction. A simple theory with exponentially decreasing interactions of range λa (attractive) ≪λr (repulsive), and strength Ea and Er shows (Evans et al., 2003) that periodic arrays of dense and dilute regions are expected for strong enough repulsion 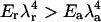 . For oligomers,
. For oligomers, 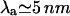 , λr ∼ 50 nm, and
, λr ∼ 50 nm, and 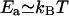 . A repulsive interaction as low as 10−2 kBT between protein oligomers can indeed produce a well-ordered phase. For these parameters, the structure size is approximately a few oligomer diameters, which compares well with the experimental observations.
. A repulsive interaction as low as 10−2 kBT between protein oligomers can indeed produce a well-ordered phase. For these parameters, the structure size is approximately a few oligomer diameters, which compares well with the experimental observations.
CONCLUSIONS
Caveolae are an important and much studied example of bud-like invaginations formed by the concentration of membrane proteins on cellular membranes. Much is known about the various actors responsible for the formation of these “buds,” but a global understanding of the process is currently lacking. Such an understanding should include general concepts of thermodynamics and membrane physics. Based on this idea, we have constructed a theory for the formation of caveolae that incorporates the structural specificity of the membrane protein caveolin. Our results sustain comparison with experimental data for caveolae.
Proteins in the caveolin family are known to play a crucial role in the formation of caveola, by forming homo-oligomers that concentrate in the buds. We argue that asymmetrically anchored membrane proteins (or protein oligomers for caveolin) can apply forces to the membrane. We examined several models for the origin and magnitude of these forces, which may be purely entropic in origin or may result from stronger interactions. Such forces act to exert bending moments on the membrane and drive the formation of bud-like structures, for which we are able to make theoretical predictions. Our model correctly reproduces the size of the buds (of ∼100 nm), and provides a physical explanation for the origin of the morphological striations observed on their surface.
Our results also shed light on several experimental observations concerning the function of caveolae and the result of caveolin mutation. It has recently been suggested that caveolae-like domains play a critical role in the mechanosensing and/or mechanosignal transduction of the extracellular signal-regulated kinase pathway (Park et al., 2000). We predict that although the membrane tension has little effect on the size of the buds (caveolae indeed have a similar structure in different kinds of cells, which possibly bear different tensions), the amount of caveolin protein required to observe bud formation does increase strongly with surface tension. Increasing the tension (either via a shear stress or by direct cell manipulation) may result in the disappearance of the buds if the available protein amount is insufficient. This is a testable prediction, as the tension of cell membranes is affected by direct cell manipulations such as micropipette experiments (Sheetz and Dai, 1996).
We have also described how the control of the morphology of caveolae can be achieved in a number of ways, including by the level of cholesterol in a membrane. High cholesterol content in membrane is known to result in higher membrane rigidity, driving an increase in the bud radius. The existence of lipid rafts is often related to the formation of caveolae. The influence these ordered membrane domains have on the physical properties of the membrane is currently not known, but modifications of the membrane mechanical properties by rafts can easily be included in our model. The formation of rafts could also promote the aggregation of caveolin in caveolar domains, without qualitatively affecting the physical picture that emerges from our model.
Finally, our theory also provides a framework for the understanding of caveolae formation in mutant caveolin systems (Li et al., 1998). Mutants which lack the self-attractive segment of the N-termini (responsible for the formation of the homo-oligomers) are still competent to drive vesicle formation, but result in much larger buds R ∼ 1 μm. This is consistent with the fact that the force exerted by isolated proteins should be ∼10 times smaller than the force exerted by oligomers resulting in a 10-fold increase of the bud radius. Mutants which lack the mutually attractive C-terminus result in similarly larger buds. Within our theory, this mutation results in a weaker oligomer-oligomer attraction, hence in a lower density of caveolin in caveolae and therefore larger buds. However, our theory predicts that oligomer attraction should not strongly influence the bud size. A natural conclusion would be that the C-termini contribute, either directly or indirectly, to the force exerted on the membrane, and that this force is reduced in mutants.
Acknowledgments
We gratefully acknowledge insightful discussions with A. Johner, G. Rowland, and R. Ball.
M.S.T. acknowledges the support of the Royal Society (United Kingdom) in the form of a University Research Fellowship.
References
- Abramowitz, M., and I. A. Stegun. 1984. Pocketbook of Mathematical Functions. Verlag Harri Deutsch, Frankfurt, Germany.
- Alberts, B., D. Bray, J. Lewis, M. Raff, K. Roberts, and J. Watson. 1994. Molecular Biology of the Cell. Garland, New York.
- Bickel, T., C. Jeppesen, and C. M. Marques. 2001. Local entropic effects of polymers grafted to soft interfaces. Eur. Phys. J. E. 4:33–43. [Google Scholar]
- Breidenich, M., R. R. Netz, and R. Lipowsky. 2000. The shape of polymer-decorated membranes. Europhys. Lett. 49:431–437. [Google Scholar]
- Daoud, M., and J. P. Cotton. 1982. Star-shaped polymers. J. Phys. I (Fr.). 43:531–538. [Google Scholar]
- de Gennes, P. G. 1991. Scaling Concepts in Polymer Physics. Cornell University Press, Ithaca, NY .
- Evans, A., M. S. Turner, and P. Sens. 2003. Interactions between proteins bound to biomembranes. Phys. Rev. E. 67:041907. [DOI] [PubMed] [Google Scholar]
- Evans, E., and W. Rawicz. 1990. Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 64:2094–2097. [DOI] [PubMed] [Google Scholar]
- Fielding, C. J., and P. E. Fielding. 2000. Cholesterol and caveolae: structural and functional relationships. Biochim. Biophys. Acta. 1529:210–222. [DOI] [PubMed] [Google Scholar]
- Gilbert, A., J. P. Paccaud, M. Foti, G. Porcheron, J. Balz, and J. L. Carpentier. 1999. Direct demonstration of the endocytic function of caveolae by a cell-free assay. J. Cell Sci. 112:1101–1110. [DOI] [PubMed] [Google Scholar]
- Goulian, M. 1996. Inclusions in membranes. Curr. Opin. Colloid Int. 1:358–361. [Google Scholar]
- Hiergeist, C., V. A. Indrani, and R. Lipowsky. 1996. Membranes with anchored polymers at the adsorption transition. Europhys. Lett. 36:491–496. [Google Scholar]
- Jülicher, F., and R. Lipowsky. 1996. Shape transformations of vesicles with intramembrane domains. Phys. Rev. E. 53:2670–2683. [DOI] [PubMed] [Google Scholar]
- Kim, Y. W., and W. Sung. 1999. Vesicular budding induced by a long and flexible polymer. Europhys. Lett. 47:292–297. [Google Scholar]
- Kurzchalia, T. V., and R. G. Parton. 1999. Membrane microdomains and caveolae. Curr. Opin. Cell Biol. 11:424–431. [DOI] [PubMed] [Google Scholar]
- Lasic, D. D., R. Joannic, B. C. Keller, P. M. Frederik, and L. Auvray. 2001. Spontaneous vesiculation. Adv. Colloid Interface Sci. 89–90:337–349. [DOI] [PubMed] [Google Scholar]
- Li, S., F. Galbiati, D. Volonté, M. Sargiacomo, J. A. Engelman, K. Das, P. E. Scherer, and M. P. Lisanti. 1998. Mutational analysis of caveolin-induced vesicle formation. Expression of caveolin-1 recruits caveolin-2 to caveolae membranes. FEBS Lett. 434:127–134. [DOI] [PubMed] [Google Scholar]
- Leibler, S. 1986. Curvature instability in membranes. J. Phys. I (Fr.). 47:507–516. [Google Scholar]
- Leibler, S., and D. Andelman. 1987. Ordered and curved meso-structures in membranes and amphiphilic films. J. Phys. I (Fr.). 48:2013–2018. [Google Scholar]
- Lipowsky, R. 1997. Flexible membranes with anchored polymers. Colloids Surf. A. 128:255–264. [Google Scholar]
- Lisanti, M. P., P. E. Scherer, J. Vidugiriene, Z. L. Tang, A. Hermanowskivosatka, Y. H. Tu, R. F. Cook, and M. Sargiacomo. 1994. Characterization of caveolin-rich membrane domains isolated from an endothelial-rich source: implications for human disease. J. Cell Biol. 126:111–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mashl, R. J., and R. F. Bruinsma. 1998. Spontaneous curvature theory of clathrin-coated membranes. Biophys. J. 74:2862–2875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris, C. E., and U. Homann. 2001. Cell surface area regulation and membrane tension. J. Membr. Biol. 179:79–102. [DOI] [PubMed] [Google Scholar]
- Mouritsen, O. G., and O. S. Andersen. 1998. In Search of a New Biomembrane Model. Biologiske Skrifter, Copenhagen, Denmark.
- Nicolas, A. 2002. Polymères greffés sur une membrane: quelques aspects théoriques. PhD thesis, Université J. Fourier, Grenoble, France.
- Oh, P., D. P. McIntosh, and J. E. Schnitzer. 1998. Dynamin at the neck of caveolae mediates their budding to form transport vesicles by GTP-driven fission from the plasma membrane of endothelium. J. Cell Biol. 141:101–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park, H., Y. M. Go, R. Darji, J. W. Choi, M. P. Lisanti, M. C. Maland, and H. Jo. 2000. Caveolin-1 regulates shear stress-dependent activation of extracellular signal-regulated kinase. Am. J. Physiol. Heart Circ. Physiol. 278:1285–1293. [DOI] [PubMed] [Google Scholar]
- Rothberg, K. G., J. E. Heuser, W. C. Donzell, Y. S. Ying, J. R. Glenney, and R. G. Anderson. 1992. Caveolin, a protein component of caveolae membrane coats. Cell. 68:673–682. [DOI] [PubMed] [Google Scholar]
- Safran, S. A. 1994. Statistical Thermodynamics of Surfaces, Interfaces and Membranes. Perseus, Cambridge, MA.
- Sarasij, R., and M. Rao. 2002. Tilt texture domains on a membrane and chirality induced budding. Phys. Rev. Lett. 88:088101. [DOI] [PubMed] [Google Scholar]
- Sargiacomo, M., P. E. Scherer, Z. L. Tang, E. Kübler, K. S. Song, M. C. Sanders, and M. P. Lisanti. 1995. Oligomeric structure of caveolin: implications for caveolae membrane organization. Proc. Natl. Acad. Sci. USA. 92:9407–9411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlegel, A., D. Volonté, J. A. Engelman, F. Galbiati, P. Mehta, X. L. Zhang, P. E. Scherer, and M. P. Lisanti. 1998. Crowded little caves: structure and function of caveolae. Cell. Signal. 10:457–463. [DOI] [PubMed] [Google Scholar]
- Schlegel, A., and M. P. Lisanti. 2000. A molecular dissection of caveolin-1 membrane attachment and oligomerization. Two separate regions of the caveolin-1 C-terminal domain mediate membrane binding and oligomer/oligomer interactions in vivo. J. Biol. Chem. 275:21605–21617. [DOI] [PubMed] [Google Scholar]
- Schlegel, A., and M. P. Lisanti. 2001. Caveolae and their coat proteins, the caveolins: from electron microscopic novelty to biological launching pad. J. Cell Physiol. 186:329–337. [DOI] [PubMed] [Google Scholar]
- Sear, R. P., S. W. Chung, G. Markovich, W. M. Gelbart, and J. R. Heath. 1999. Spontaneous patterning of quantum dots at the air-water interface. Phys. Rev. E. 59:R6255–R6258. [DOI] [PubMed] [Google Scholar]
- Sear, R. P., and W. M. Gelbart. 1999. Microphase separation versus the vapor-liquid transition in systems of spherical particles. J. Chem. Phys. 110:4582–4588. [Google Scholar]
- Seifert, U. 1993. Curvature-induced lateral phase segregation in two-component vesicles. Phys. Rev. Lett. 70:1335–1338. [DOI] [PubMed] [Google Scholar]
- Sheetz, M. P., and J. W. Dai. 1996. Modulation of membrane dynamics and cell motility by membrane tension. Trends Cell Biol. 6:85–89. [DOI] [PubMed] [Google Scholar]
- Song, J., and R. E. Waugh. 1993. Bending rigidity of SOPC membranes containing cholesterol. Biophys. J. 64:1967–1970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahlhut, M., K. Sandvig, and B. van Deurs. 2000. Caveolae: uniform structures with multiple functions in signaling, cell growth, and cancer. Exp. Cell Res. 261:111–118. [DOI] [PubMed] [Google Scholar]
- Takei, K., and V. Haucke. 2001. Clathrin-mediated endocytosis: membrane factors pull the trigger. Trends Cell Biol. 11:385–391. [DOI] [PubMed] [Google Scholar]
- Westermann, M., H. Leutbecher, and H. W. Meyer. 1999. Membrane structure of caveolae and isolated caveolin-rich vesicles. Histochem. Cell Biol. 111:71–81. [DOI] [PubMed] [Google Scholar]