A Transient Diffusion Model Yields Unitary Gap Junctional Permeabilities from Images of Cell-to-Cell Fluorescent Dye Transfer Between Xenopus Oocytes

Abstract

As ubiquitous conduits for intercellular transport and communication, gap junctional pores have been the subject of numerous investigations aimed at elucidating the molecular mechanisms underlying permeability and selectivity. Dye transfer studies provide a broadly useful means of detecting coupling and assessing these properties. However, given evidence for selective permeability of gap junctions and some anomalous correlations between junctional electrical conductance and dye permeability by passive diffusion, the need exists to give such studies a more quantitative basis. This article develops a detailed diffusion model describing experiments (reported separately) involving transport of fluorescent dye from a “donor” region to an “acceptor” region within a pair of Xenopus oocytes coupled by gap junctions. Analysis of transport within a single oocyte is used to determine the diffusion and binding characteristics of the cellular cytoplasm. Subsequent double-cell calculations then yield the intercellular junction permeability, which is translated into a single-channel permeability using concomitant measurements of intercellular conductance, and known single-channel conductances of gap junctions made up of specific connexins, to count channels. The preceding strategy, combined with use of a graded size series of Alexa dyes, permits a determination of absolute values of gap junctional permeability as a function of dye size and connexin type. Interpretation of the results in terms of pore theory suggests significant levels of dye-pore affinity consistent with the expected order of magnitude of typical (e.g., van der Waals) intermolecular attractions.

GLOSSARY

Primary symbols introduced in the text

A_mem

Area of intercellular membrane

A_pore

Cross-sectional area of gap junctional pore

(AP)_pore

A_pore × P_pore

A_Hamaker

Hamaker constant for permeant-pore van der Waals interaction

a

Stokes-Einstein equivalent radius of dye permeant

BG

Optical correction accounting for background fluorescence intensity

b

Bound dye concentration

c

Free dye concentration

D_aq

Bulk aqueous diffusion coefficient of dye permeant

D_cyt

Cytoplasmic diffusion coefficient of dye permeant

D_pore

In-pore diffusion coefficient of dye permeant

(ΔV)_j

Voltage drop actually occurring across gap junctions

(ΔV)_total

Total voltage drop occurring across oocyte pair

Radial distance of any point on oocyte surface from origin

G_obs

Macroscopically observable intercellular electrical conductance

h_e

Dimensionless hydrodynamic coefficient giving pore access resistance

I_j

Current between coupled oocytes

Equilibrium constant for dye binding to cytoplasm

k_cyt

Rate constant (s⁻¹) for dye binding to cytoplasm

K_pore

Pore partition coefficient of dye permeant

Factor in K_pore accounting for permeant-pore affinity

kT

Boltzmann's constant multiplied by absolute temperature

L

Characteristic length = 1 mm

ℓ_pore

Length of gap junctional pore

N_pore

Number of open gap junctions between oocytes

n

Normal vector on cellular membrane

P_junc

Permeability (mm/s) of intercellular membrane

P_pore

Unitary permeability (mm/s) of gap junction

R_pore

Mean radius of gap junctional pore

r

Radial distance from origin in spherical coordinates

t

Elapsed time after dye injection

(x,y,z)

Cartesian position coordinates within oocyte

x

Position vector within oocyte

Greek symbols

α

Normalization constant for assumed initial Gaussian distribution of dye

β

Sum of all nonmembrane electrical resistances

γ_pore

Unitary channel conductance

λ

Ratio a/R_pore of permeant/pore radii

Ω

Subset of space occupied by oocyte

σ

Standard deviation for assumed initial Gaussian distribution of dye

θ, φ

Polar and azimuthal angles in spherical coordinates

ξ

Fractional distance from origin to oocyte surface

Subscripts and other affixes

_double

Refers to double-cell experiment

_single

Refers to single-cell experiment

_spot

Refers to epicenter of dye injection

₊

Distinguishes acceptor oocyte above the plane z = 0

₋

Distinguishes donor oocyte below the plane z = 0

∧

Distinguishes dimensionless variables

INTRODUCTION

Gap junctions are intercellular pores, considerably larger than ion-specific channels, that directly connect the interiors of neighboring cells (Edelson, 1990; Kumar and Gilula, 1996; Simon and Goodenough, 1998; Yeager et al., 1998; Harris, 2001). They are formed when two hemichannels (half-pores, connexons), each comprising six connexin subunits (of which >20 types are currently known; Harris, 2001; Eiberger et al., 2001), dock in the intercellular medium. Such pores represent key features of multicellular organisms because they provide the only documented means for the direct exchange of small metabolites between cells. As such, they have been implicated in a multitude of normal physiological and disease processes including electrical synchronization of heart beat, homeostasis, tumor suppression, and direction of early developmental processes (Edelson, 1990; Lo, 1996). Most cells express multiple connexin types, which may associate to form hemichannels that are either homomeric (comprising only one type) or heteromeric (comprising multiple types). Complete gap junctions may also be either homotypic (if the two constituent hemichannels are identical) or heterotypic (if they are not).

Although gap junctions were once often regarded simply as indiscriminate aqueous conduits between cells, a growing body of evidence in the literature indicates that they exhibit significant selectivity based on a complex interplay of physicochemical factors (Flagg-Newton et al., 1979; Brink and Dewey, 1980; Brink and Ramanan, 1985; Traub et al., 1994; Elfgang et al., 1995; Veenstra et al., 1995; Veenstra, 1996; Cao et al., 1998; Nicholson et al., 2000; Gong and Nicholson, 2001; Harris, 2001). Permselectivity features of connexins are not restricted to simple size or charge discrimination, and are likely to significantly influence their function in biological systems. This fact is graphically illustrated in recent studies of Goldberg et al. (1999, 2002), where the rates of transmission of specific endogenous metabolites through gap junctions composed of different connexins expressed in C6 glioma cell monolayers were compared. The surprising conclusion from this comparison was that two connexins (i.e., Cx43 and Cx32), which form channels with similar dye permeability, showed as much as 300-fold differences in permeability to ATP, and lower levels of relative selectivity for other metabolites including ADP, AMP, glutamate, and glutathione. Bevans and Harris (1999) also observed a dramatic shift in selectivity between cAMP and cGMP in reconstituted hemichannels when the connexin composition (ratio of Cx32/Cx26 subunits) was changed. Clearly, quantitative descriptions of gap junctional selectivity for a variety of compounds varying in different physical parameters will be needed if one is to ultimately elucidate the underlying molecular mechanisms and develop generalizable rules for the permeability features of a given connexin.

An important avenue toward this end is provided by experiments in which dye is introduced into one member of a pair (Veenstra et al., 1995; Cao et al., 1998; Valiunas et al., 2002), a chain (Simpson et al., 1977; Schwarzmann et al., 1981; Brink and Ramanan, 1985; Zimmerman and Rose, 1985), or a monolayer (Flagg-Newton et al., 1979; Schwarzmann et al., 1981; Safranyos and Caveney, 1985; Steinberg et al., 1994; Traub et al., 1994; Elfgang et al., 1995; Goldberg et al., 1995; Cao et al., 1998) of cells, and observed to spread linearly or radially into the neighboring cell(s) as a function of time. The ultimate goal of such experiments is to deduce absolute, or at least relative, values of unitary (single-pore) junctional permeabilities P_pore of various channel types to probes of varying size, shape, charge, and other physicochemical properties. This microscopic parameter quantifies the diffusive flow ℱ (moles/time) of dye through a single channel according to the relation

(1)

in which A_pore denotes the cross-sectional area of the channel opening and (c₋ − c₊) denotes the concentration driving force across the channel (Hille, 1992, pp. 296–298, 337–341; Nitsche, 1999, p. 480). We refer to the product A_poreP_pore, representing the constant of proportionality between concentration difference and resulting molecular flow, simply as (AP)_pore, because the two factors usually appear together.

There generally exist two complications in the translation of observed dye transfer rates into unitary junctional area-times-permeability factors (AP)_pore. The first is the fact that the intercellular membrane permeability P_junc is not directly indicative of (AP)_pore, because it represents the collective outcome of many unitary channel transport processes proceeding in parallel, as described by the equation

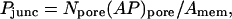(2)

with N_pore the number of open channels between coupled cells and A_mem the coupled membrane area. Thus, a given membrane permeability may in principle derive from a large number of channels of low permeability, or a small number of channels of high permeability. This potential ambiguity is obviated by studies (Steinberg et al., 1994; Traub et al., 1994; Veenstra et al., 1995; Cao et al., 1998; Valiunas et al., 2002) in which dye transfer measurements are accompanied by intercellular electrical conductance measurements, so that the total number of channels can be counted if their unitary conductance is known.

A second, more serious complication arises from the fact that observed dye transfer rates represent the net outcome of the membrane resistance actually sought, and a mass transfer resistance associated with diffusion through cellular cytoplasm to and from the membrane. If the cells employed are sufficiently small, or if the membrane has sufficiently low permeability, then the cytoplasm is effectively well mixed and the dye transfer rate is directly indicative of the (rate-limiting) value of P_junc. This parameter can then be deduced from a data analysis scheme in which individual cells are treated as coupled, well-mixed compartments (Zimmerman and Rose, 1985; Cao et al., 1998; Valiunas et al., 2002). Generally, however, a diffusion model is needed to analyze data and deconvolute membrane from cytoplasmic transport effects. Ample precedent for such diffusion models exists, as has been reviewed recently (Nitsche, 1999). The study of fluorescent dye transfer between septate giant axons of the earthworm by Brink and Ramanan (1985) exemplifies a rigorous analysis of this type. These authors determined values of P_junc and the cytoplasmic diffusivity D_cyt for three dyes, and found that transfer of dichlorofluorescein (but not carboxyfluorescein) was accompanied by a significant cytoplasmic diffusion resistance. A decrease of the apparent transport coefficients for Lucifer Yellow with time was indicative of significant dye binding to components of the cytoplasm. Similar and more complex models of diffusion within single cells (e.g., Horowitz et al., 1970; Kargacin and Fay, 1991) and cell aggregates (e.g., Ramanan and Brink, 1990; Christ et al., 1994) exist.

Apparently the only determination to date of absolute values of junctional permeability on a per-channel basis has been reported recently by Valiunas et al. (2002). Their combined measurements of fluorescence intensity and conductance yielded unitary transfer rates for Lucifer Yellow (LY) in HeLa cells coupled by junctions comprising rat Cx43 and Cx40 connexins. The smallness of their system tends to minimize the physical factors discussed above.

This article addresses a new series of experiments (Weber et al., 2004) based on a novel system in which passage of fluorescent dye from a “donor” Xenopus oocyte to a coupled “acceptor” oocyte is quantified by digital video images (Nicholson et al., 2000), with concurrent measurement of the electrical conductance between the same cell pair. The specific purpose is to develop the modeling infrastructure needed to deduce unitary gap junctional permeabilities from raw data in the form of the ratio of acceptor-cell/donor-cell fluorescence intensities as a function of time. Equations describing the transient, three-dimensional cytoplasmic and transmembrane diffusion process are formulated and then solved using a finite difference technique. A separate single-cell version of the model, fitted to data for uncoupled oocytes, is used to deduce values of the cytoplasmic diffusivity D_cyt, as well as two parameters characterizing binding to the cytoplasm, which figure in the full double-cell model. The theory ultimately yields curves for the acceptor/donor concentration ratio that fit the raw data well, and lead to self-consistent values of (AP)_pore. The efficacy of the approach is demonstrated with reference to passage of three Alexa-series dyes through gap junction channels composed of a number of connexin types. The outcome is a set of results for (AP)_pore at a level of quantitation surpassing previous more-qualitative analyses in the literature. These results demonstrate both dye and connexin dependencies of channel permeability. Derived unitary permeability data are found to be consistent with a microscopic model embodying an interplay between hindered diffusion and a permeant-pore affinity factor, the latter making the pore energetically favorable for the dye, thereby increasing in-pore concentration and flux levels. Valiunas et al. (2002) noted that the flux values they measured for LY were below those one would expect for efficient propagation of labile signals in multicellular networks. The values measured here for the Alexa-series dyes, however, are more consistent with what one might expect for propagation of such signals.

SUMMARY OF EXPERIMENTS ANALYZED

Fig. 1 gives a schematic representation of the experimental setup considered here (Weber et al., 2004). Two Xenopus oocytes are immersed in medium within a well created by pushing the end of a plastic microfuge tube into a layer of agar at the bottom of a petri dish. A relatively small (41.4 nl) bolus of 10 mM fluorescent dye solution (Alexa 350, Alexa 488, or Alexa 594 in the experiments analyzed here, Molecular Probes, eugene, OR) is introduced by micropipette at a prescribed injection spot x_spot within one of these cells. Fluorescence intensity is averaged over two square imaging boxes, respectively positioned to reflect dye concentrations within “donor” and “acceptor” regions, at a number of discrete time points.

FIGURE 1.

Experimental setup (Weber et al., 2004) as seen from the side.

The experiments considered (Weber et al., 2004) are of two types. For any particular dye, single-cell experiments aim to quantify the cytoplasmic diffusivity D_cyt, and the binding (forward) rate coefficient k_cyt and equilibrium constant 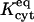for any reversible binding to elements of the cytoplasm, without the complication of intercellular transfer. Although oocyte pairs are still employed to maintain a geometry identical to that of subsequent double-cell experiments, no connexins are expressed, making the intercellular membrane between the coupled cells effectively impermeable. The point of injection x_spot = x_spot,single lies at one side of one of the oocytes. The donor and acceptor imaging windows (0.43 × 0.43 mm) are positioned at opposite sides of this injected oocyte to quantify the equilibration process as dye spreads across it by diffusion and binds to the cytoplasm, in principle eventually settling down to a spatially uniform distribution.

Double-cell experiments, in which given connexins are expressed, address the junctional permeability of the intercellular membrane. The point of injection x_spot = x_spot,double lies near the center of one oocyte, and dye diffuses to the other oocyte through the intercellular membrane, whose permeability is the only remaining unknown parameter to be determined by data fitting. Donor and acceptor imaging windows (0.86 × 0.86 mm) are centered on the injected cell and its neighbor, respectively, to track this process.

Typical raw data recorded from the imaging system are shown in Fig. 2 (Weber et al., 2004), which presents snapshots of the dye distribution at selected times after injection in cases of (A) single-cell and (B) double-cell experiments. Fluorescence intensity is encoded in terms of hue; it increases in the order of: black (zero) → violet → blue → green → yellow → red → white (highest). These images show clearly the spreading of dye across the cellular cytoplasm (A and B) and through the intercellular membrane (B). They also give a feel for the inhomogeneity of the cellular cytoplasm, and the possible variability from experiment to experiment.

FIGURE 2.

Representative images of intracellular diffusion (A) and intercellular transfer (B) of Alexa488, viewed from the oocyte vegetal pole (Weber et al., 2004). Fluorescence intensity (indicating concentration) is encoded in terms of hue, increasing in the order of: black (zero) → violet → blue → green → yellow → red → white (highest). Specific times are as marked beside each snapshot. (A) Single-cell case. Dye diffuses from left to right (with lateral spreading) within one oocyte in the absence of junctional permeability. (B) Double-cell case. Dye diffuses from left to right within and between oocytes coupled by Cx32/Cx32 channels.

The data ultimately fitted with the model (see Figs. 5 and 6 below) comprise the ratio of average fluorescence intensities measured in the acceptor and donor boxes as a function of time, derived by automated image analysis of the preceding type of raw data.

FIGURE 5.

Fits of the computed single-cell acceptor-box/donor-box ratio (Eq. 22) as a function of time (solid curves) to corresponding fluorescence intensity data (points) for (A) Alexa 350, (B) Alexa 488, and (C) Alexa 594. Calculations are based on the refined mesh. Parameter values are marked beside each computed curve. D_cyt is the cytoplasmic diffusivity; k_cyt and K_cyt^eq are the forward rate constant and equilibrium constant, respectively, for dye binding to the cytoplasm; and BG accounts for background signal resulting from any initially uniformly distributed dye, as well as autofluorescence and/or light refraction. For each dye, the parameter values listed in Table 1 represent averages of the values belonging to the individual curves (see text). The dashed curve in B represents a calculation in which binding of dye to the cytoplasm has been artificially suppressed by setting k_cyt = 0 (the value of K_cyt^eq is then immaterial). Its divergence from the experimental data demonstrates the importance of including binding in the model. Similar no-binding curves yield the same conclusion for the other dyes, but they are omitted in A and C to avoid clutter. Execution times required to generate these curves with one of our two Fortran codes, compiled with an Absoft Pro Fortran 7.0 F77 compiler (Absoft, Rochester Hills, MI) and run on an 850-MHz Pentium III notebook PC, range from ∼6 h (upper curve in A) to 16 h (solid curve in B).

FIGURE 6.

Examples of fits of the computed double-cell acceptor-box/donor-box ratio (Eq. 22) as a function of time (solid curves) to corresponding fluorescence intensity data (points). Calculations are based on the coarse mesh. The key adjustable parameter is the (dimensionless) intercellular membrane permeability 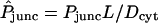, marked for each curve. BG accounts for background signal resulting from autofluorescence and/or light refraction. (A) Alexa 350 in Cx37/Cx43 heterotypic channels. (B) Alexa 488 in Cx26/Cx26 homotypic channels. The execution time required to generate each calculated curve is ∼7 min for A and 12 min for B (see computer specifications given in Fig. 5 legend).

FORMULATION OF THE MODEL AND METHODS OF CALCULATION

Quantitative analysis of the preceding experiments is carried out within the framework of a comprehensive computational model of intra- and intercellular dye diffusion, comprising a number of elements needed to deconvolute intercellular membrane permeability from cytoplasmic diffusion and binding. The analysis ultimately yields absolute values of permeability on a per-channel basis.

Geometry

As shown in Fig. 3, the shapes of the two oocytes are idealized in terms of identical truncated (intersecting) ellipsoidal surfaces with prescribed semiaxes and positions chosen to match dimensions measured from a number of images of the system. The two ellipsoids intersect along an ellipse representing the perimeter of the planar intercellular membrane, comprising the apposed, junctionally coupled portions of the two cellular membranes at z = 0. According to the coordinate system used here, the direction up in the laboratory is equivalent to the −y direction. A view from the bottom (Fig. 2)—looking up at the oocytes through the petri dish—corresponds to the view employed experimentally with the inverted microscope. This represents a view from the positive y axis, and reveals the half-length (1.06 mm) and width (1.33 mm) of the cell pair, as well as the width of the intercellular membrane (0.78 mm). A side view (Fig. 1) corresponds to a view along the x axis and reveals the thickness of the oocytes (1.14 mm). The cell receiving the initial injection of dye (at a prescribed point x_spot) is taken to be the “−” cell below the plane z = 0, so that diffusion occurs primarily in the +z direction. In a single-cell experiment (with x_spot = x_spot,single) the dye stays inside this “−” cell, whereas in a double-cell experiment (with x_spot = x_spot,double) dye enters the “+” cell through the intercellular membrane. According to the assumed truncated ellipsoidal shape, the volume V_cell of each oocyte is ≅ 0.90 mm³ and the area A_mem of the intercellular membrane is ≅ 0.41 mm². Also represented in Fig. 3, B–E, are the imaging boxes and optical paths.

FIGURE 3.

Quantitative perspective views of the model geometry. (A) Cutaway view of oocytes contained in the agar well. (B and C) Cutaway representations of (B) single-cell and (C) double-cell cases, including imaging boxes and epicenters of dye injection. (D and E) Representations of optical paths defined by the imaging boxes for (D) single-cell and (E) double-cell cases.

It is convenient later to work with position vectors, coordinates, and length parameters made dimensionless using a characteristic length L = 1 mm, which are distinguished by the “∧” affix. Thus, for instance, , , etc. Required for subsequent analysis is a representation of the “+” and “−” oocyte surfaces in spherical coordinates based at the origin (which coincides with the center of the elliptical intercellular membrane). (Polar and azimuthal angles θ and φ are measured from the positive z and x axes, respectively, as in the usual definition of spherical coordinates; see Bird et al., 2002, p. 826.) On these surfaces, the (dimensionless) radial distance varies with θ and φ as given by a function defined in Appendix A. The regions of space occupied by these respective oocytes are denoted by

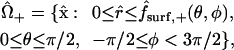(3)

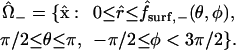(4)

The intercellular membrane at 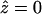is denoted by and corresponds to the coordinate value θ = π/2. The uncoupled cellular membranes are the surfaces given by 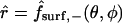for π/2 ≤ θ ≤ π and 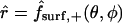for 0 ≤ θ ≤ π/2, respectively denoted by 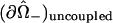and .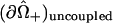

Governing transport equations

Theoretical analysis focuses on the concentrations c₋ and c₊ of freely diffusing dye within the “−” and “+” oocytes, which are functions of position x = (x, y, z) and time t, and are defined over the respective spatial domains Ω₋ and Ω₊ for all t ≥ 0. Also considered are populations of dye molecules bound to the cytoplasm, for which the corresponding concentration fields are denoted by the symbols b₋ and b₊.

A number of physicochemical parameters enter the model and determine the predicted outcome of a dye transfer experiment. Individual cells are characterized by a diffusivity D_cyt (mm²/s) of dye within the cytoplasm, as well as a forward rate constant k_cyt (s⁻¹) and equilibrium constant K_cyt^eq (dimensionless) for reversible binding of dye to the cytoplasm. The latter two parameters appear in rate expressions of the form

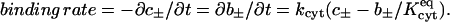(5)

The intercellular membrane is characterized by a permeability P_junc having the dimensions of a velocity (mm/s). This parameter represents the proportionality between the concentration difference across the membrane and the resulting flux through it, as expressed by a relation of the form

(6)

Values of the preceding parameters are presented later (see Table 1 and Figs. 5 and 6 below).

TABLE 1.

Dye properties, and model parameters characterizing the cellular cytoplasm in terms of a reasonable fit to the single-cell data (Fig. 5), for each dye

Symbol (if assigned)	Definition of parameter	Value for Alexa 350	Value for Alexa 488	Value for Alexa 594
	Molecular weight (excl. Na+ counterion)	326.31	547.50	735.81
Daq	Diffusivity in bulk water at 25°C	5.7 × 10−4 mm2/s	4.3 × 10−4 mm2/s	3.7 × 10−4 mm2/s
a	Stokes-Einstein equivalent radius	4.3 Å	5.7 Å	6.6 Å
	Net charge	−1	−2	−2
Dcyt	Diffusivity in cytoplasm	1.85 × 10−4 mm2/s	3.8 × 10−4 mm2/s	2.4 × 10−4 mm2/s
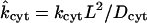	Dimensionless forward rate coefficient for binding to cytoplasm	6.6	3.5	2.97
kcyt	Dimensional forward rate coefficient for binding to cytoplasm	1.22 × 10−3 s−1	1.33 × 10−3 s−1	7.12 × 10−4 s−1
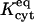	Equilibrium constant for binding to cytoplasm	5.75	10	6.1

In the cases of Alexa 350 and Alexa 594, for which two experimental curves were measured and fitted, the model parameters listed represent average values derived as described in the text.

In the transport equations that follow, time is made dimensionless using the characteristic length L = 1 mm and the diffusivity D_cyt of dye in the cytoplasm (yet to be determined) as . All dye concentrations are made dimensionless using a characteristic value c₀ (defined in the next subsection), and are regarded as functions of dimensionless position and time. Thus, we deal with 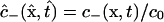, , 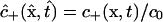etc.

The time-dependent intracellular diffusion and binding process is governed by the dimensionless equations (compare to Bird et al., 2002, Chap. 19; Cussler, 1997, pp. 319–320; Deen, 1998, pp. 54–56)

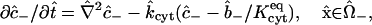(7)

(8)

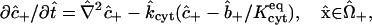(9)

(10)

in which 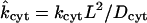is a dimensionless binding rate coefficient. Dye transfer through the intercellular membrane is described by the equation

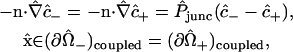(11)

in which the unit normal vector n points in the +z direction (from the “−” cell to the “+” cell), and denotes a dimensionless membrane permeability.

The images recorded from the experimental system show essentially no leakage for the dyes Alexa 488 and Alexa 594. Although some such leakage into the external solution is evident for Alexa 350, the concentrations involved are small compared with the observed intracellular concentrations. Therefore, although our model allows for an arbitrary permeability of the uncoupled portions of the two cellular membranes, actual calculations are performed with this permeability set to zero. The additional boundary conditions effectively imposed are thus

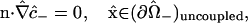(12)

(13)

Characterization of dye injections and initial conditions

For all dye diffusion studies, injections by micropipette introduced 41.4 nl (0.0414 mm³) of a 10 mM dye solution into one oocyte, amounting to 4.14 × 10⁻¹⁰ mol of dye (Weber et al., 2004). The characteristic concentration c₀ is specifically defined in terms of this mole number as c₀ = (4.14 × 10⁻¹⁰ mol of injected dye)/L³ = 4.14 × 10⁻¹⁰ mol/mm³ = 0.414 mM.

The injected volume is small but finite (roughly one-twentieth of the cell volume), and the insertion and removal of the pipette undoubtedly causes some mixing of the cellular contents. Therefore, the injection process produces an initial dye distribution within the “−” cell that is highly concentrated around the point of injection, but is not a perfectly sharp Dirac delta distribution. We model it using a multivariate Gaussian (normal) distribution,

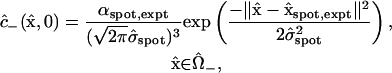(14)

in which the standard deviation 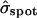(≅ 0.21) is set by the reasonable order-of-magnitude criterion that the volume of injected dye equal the volume of a sphere with radius equal to the standard deviation, 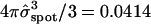. The position vector 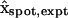represents the epicenter of the injection, which differs between single- and double-cell experiments, distinguished by the subscript expt (either single or double). The coordinates assumed in the model are and , based on a separate series of injections (mimicking those in the actual dye transfer experiments) specifically aimed at locating the epicenters (Weber, 2003). These points are marked by tiny spheres in Fig. 3. The factor α_{spot, expt} is a normalization factor computed such that the Gaussian distribution is normalized (has unit volume integral) over the injected (“−”) cell. Its numerical values turn out to be α_{spot, single} ≅ 1.68 and α_{spot, double} ≅ 1.11 for single- and double-cell cases, respectively. (The Gaussian distribution without the factor α_{spot, expt} is normalized over all space.)

The remaining initial conditions reflect the facts that, at the instant of injection, no dye has diffused into the “+” cell, and binding has not had a chance to occur:

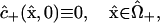(15)

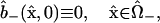(16)

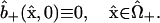(17)

Finite difference solution

Equations 7–17 collectively constitute a coupled set of initial boundary value problems to be solved for the position and time dependencies of the intracellular concentrations 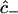, , , 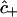and 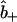. Given the location of the injection spot on the yz plane, the solution of these equations must be symmetric around this plane, so that attention can be restricted to the interval −π/2 ≤ φ ≤ π/2. Our approach to their solution involves a new radial coordinate representing the fractional distance from the origin to the cell surface in each direction defined by the polar and azimuthal angles θ and φ, namely

(18)

within the “+” and “−” oocytes, respectively. Thus, the (uncoupled membrane) surfaces of the oocytes correspond to the coordinate value ξ = 1. Within each, the triple of coordinates (ξ, θ, φ) defines a coordinate system which is nonorthogonal, but has the attractive feature that the oocyte domain is given by one of the simple expressions

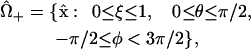(19)

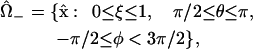(20)

making it directly amenable to finite difference discretization without any complexity in the generation of a spatial mesh. The standard formula for the Laplacian operator 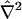in spherical coordinates (Bird et al., 2002, p. 836) adopts a rather lengthy form in terms of first and second derivatives with respect to ξ, θ, and φ, given in Appendix A, which also provides explicit expressions for the normal derivatives appearing in the boundary conditions (Eqs. 11–13), as well as other requisite properties of our coordinate system.

The intervals 0 ≤ ξ ≤ 1, 0 ≤ θ ≤ π, and −π/2 ≤ φ ≤ π/2 are respectively divided into N_r, 2N_θ, and 2N_φ subdivisions. Fig. 4 shows the resulting spatial discretization (at the cross section y = 0) for (Fig. 4 A) a coarse mesh with N_r = N_θ = N_φ = 6 and (Fig. 4 B) a more refined mesh with N_r = N_θ = N_φ = 12. Discrete values of the dye concentrations , , , and are defined on either of these meshes at each time (i, j, and k, respectively, indexing the values of ξ, θ, and φ).

FIGURE 4.

Spatial discretization at the cross section y = 0 corresponding to two meshes used in the finite difference calculations. (A) Coarse mesh with N_r = N_θ = N_φ = 6. (B) Refined mesh with N_r = N_θ = N_φ = 12.

To start, all concentration values at the nodes of the computational mesh are assigned initial values according to Eqs. 14–17. The normalization constant α_spot,expt for the Gaussian initial distribution 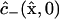is computed by approximating the required volume integral using Simpson's rule. For interior nodes (nodes for which θ ≠ π/2 and ξ < 1), the right-hand side of Eq. 7 or 9 is computed using second-order (three-point) central difference approximations for all derivatives appearing in 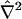(Appendix A, Eq. 36), and Euler's method with a prescribed time step is used to advance the nodal concentration values in time. Symmetry conditions are incorporated into the process of imposing the differential equation at nodes for which φ = −π/2 or π/2. For nodes at the physical boundaries (intercellular membrane, θ = π/2, and uncoupled cellular membranes, ξ = 1), the boundary conditions (Eqs. 11–13) are applied to compute concentration values consistent with the updated interior values, using asymmetric (one-sided) formulas for normal derivatives. All nodal values of the bound dye concentrations are updated according to Eqs. 8 and 10 by Euler's method using the complete set of current values and . Further details of the procedure are given by Chang (2003).

The preceding calculation (including optical computations discussed in the next subsection) was coded in Fortran and run on several PCs. For reference, timing data for runs on a PC are included in the captions of Figs. 5 and 6 below. Execution time increases very rapidly with increasing degree of mesh refinement, because of the increasing number of nodes, and—further—a concomitantly decreasing time step 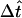needed to maintain numerical stability (determined empirically, and surprisingly small). Fitting of cytoplasmic properties to single-cell data (Fig. 5 below) was carried out using the refined mesh (N_r = N_θ = N_φ = 12, see Fig. 4 B; ), because here it is especially important to resolve intracellular concentration gradients accurately as dye diffuses from one side of the oocyte to the other. Fitting of the intercellular membrane permeability to double-cell data (Fig. 6 below) was performed using the coarse mesh (N_r = N_θ = N_φ = 6, see Fig. 4 A; 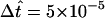), because here the intracellular diffusion process is less critical, especially when the intercellular membrane controls the rate of dye transfer.

Optical analysis of the model

Consider a given donor or acceptor imaging box marked, say, in the xz plane (Fig. 3, B and C). Of special relevance is the subset of the cytoplasm comprising all points whose projections in the +y or −y directions (which are respectively downwards or upwards in the laboratory) onto the x,z plane fall inside the box (see optical paths marked in Fig. 3, D and E). We assume that the average fluorescence intensity measured from such a box is proportional to the total amount of dye (mobile and bound) contained in this subset, i.e., visible through the window defined by the imaging box. At any time, this quantity (divided by the box area, and made dimensionless with c₀L) is given by an integral of the form

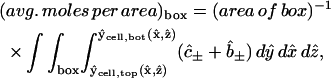(21)

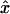where box stands for either the (dimensionless) donor or acceptor box. The symbols and denote functions, defined in Appendix A, giving the coordinates of the upper and lower oocyte surfaces, respectively, in terms of and 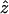. Numerical approximation of the nested integrals in Eq. 21 is effected using Simpson's rule. Required values of the intracellular concentrations are interpolated from the nodal values 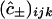and defined on the finite difference mesh using a three-dimensional extension of two-dimensional bilinear interpolation.

At any time, the calculated quantity directly comparable with the measured acceptor-box/donor-box fluorescence intensity ratio is

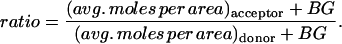(22)

The adjustable parameter BG represents an additive correction accounting for the fact that the cellular cytoplasm, agar, and/or petri dish can contribute a background signal additional to the fluorescence intensity deriving from injected dye. This phenomenon may be due to autofluorescence and/or light refraction. The parameter BG also serves to account approximately for any spatially uniform contribution to the initial distribution of dye in the single-cell experiments, caused by possible mixing of the cellular contents during the injection process.

Counting of channels

Equation 2 makes it possible to determine the unitary channel area-times-permeability factor, (AP)_pore, from the membrane permeability P_junc, provided one has the ability to count open channels between oocytes. Toward this end, dye transfer measurements were accompanied by measurements of the macroscopically observable intercellular electrical conductance G_obs (Weber et al., 2004), defined as

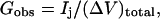(23)

where I_j denotes the current passing between cells as measured by the dual cell voltage-clamp, and (ΔV)_total denotes the total cell-to-cell voltage drop. The conductance G_obs yields the number of open channels N_pore with knowledge of the unitary channel conductance γ_pore. However, G_obs is not simply equal to N_poreγ_pore owing to sources of electrical resistance other than the membrane channels (e.g., cytoplasmic resistance), which cause (ΔV)_total to exceed the voltage drop (ΔV)_j actually occurring across the intercellular membrane.

Sophisticated models exist for dual voltage-clamp measurement of electrical conductance between cells, addressing junctional access resistance and other factors (e.g., Wilders and Jongsma, 1992; Van Rijen et al., 1998). For present purposes, an estimate was obtained experimentally for the relation between the fraction (ΔV)_j/(ΔV)_total of the total voltage drop occurring across the intercellular membrane, and G_obs, as described by Weber et al. (2004) and presented in their Fig. 5 E. A simple cell-pair conductance model was then developed to support an empirical correlation of these data (Appendix B). It leads to the equations

(24)

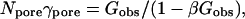(25)

where β is a parameter representing the sum of all nonmembrane resistances, which act in series with the channel-derived membrane resistance. Using the value β ≅ 12,800 S⁻¹ in units of reciprocal siemens or ohms (S⁻¹ = Ω), this type of relation provides a reasonable description of the data (Weber et al., 2004, their Fig. 5 E). With this fitted value of β, Eq. 25 allows the number of open channels N_pore to be estimated from the measured intercellular conductance G_obs. Further discussion of the parameter β is provided in Appendix B.

RESULTS

The ultimate outcome of the diffusion model is a prediction of the observable acceptor-box/donor-box ratio given by Eq. 22 as a function of time. Parameter values are determined by trial-and-error adjustment to obtain reasonable fits of the computed curves to the experimental data.

Analysis of single-cell experiments—characterization of cytoplasmic diffusion and binding

Our first step is to ascertain values of the model parameters characterizing the cellular cytoplasm (Table 1). This determination is made by fitting of the measured curves showing acceptor-box/donor-box fluorescence intensity ratio as a function of time in the single-cell experiments (Weber et al., 2004), in which dye diffuses across the cytoplasm of only one (the “−”) oocyte. The apparent starting point of each data set is matched by adjusting BG. The initial rapid rise of a calculated curve is controlled by the cytoplasmic diffusivity D_cyt. With a given value of D_cyt, the shape of the “shoulder” (i.e., the region of high curvature between the initial rapid rise and the later leveling off) depends mainly upon k_cyt. Given D_cyt and k_cyt, the choice of K_cyt^eq then determines the calculated acceptor/donor level at longer times. Judicious use of these facts expedites the fitting process. As a general philosophy we use the minimum K_cyt^eq consistent with the data. Fig. 5 compares the computed and measured curves. In cases where two experimental curves were measured and fitted (for Alexa 350 and Alexa 594, represented in parts A and C), the values of D_cyt, k_cyt, and K_cyt^eq listed in Table 1 represent averages of the respective values belonging to the individual curves. The dimensionless binding rate coefficient 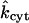is computed by making the average k_cyt dimensionless using the average D_cyt. Alexa 488 differs from the other two dyes in the respect that all three data sets exhibit a steeper initial rise and a more abrupt leveling off, indicative of a higher D_cyt for this dye. They are fitted collectively by the single theoretical curve shown in part B. The model parameter showing the greatest variability among fits to different data sets for a given dye (and therefore the greatest uncertainty) is K_cyt^eq. For Alexa 594 the two fitted values of K_cyt^eq differ by a factor of ∼5, owing to significant differences between the measured acceptor/donor levels at longer times (see Fig. 5 C).

Included for reference in Table 1 are values of the bulk aqueous diffusivity D_aq of each dye at 25°C, estimated from the molecular structure using the Wilke-Chang correlation, together with Schroeder's rule as a predictor of the molar volume (Poling et al., 2001, pp. 4.33–4.35, 11.21–11.23). The Stokes-Einstein equivalent radius a follows from D_aq according to the formula a = kT/(6πμD_aq) (Deen, 1987; Poling et al., 2001, p. 11.21).

Analysis of double-cell experiments—determination of intercellular membrane and unitary channel permeability

For a double-cell experiment the parameter to be determined is the apparent macroscopic permeability of the intercellular membrane (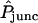 in dimensionless form), which depends upon the unitary channel permeability and the degree of intercellular coupling (i.e., number of functional channels); see Eq. 2. For all combinations of dye and type of connexin expressed in the oocytes, this parameter was fitted by trial and error to each of a number of measured curves giving the acceptor-box/donor-box fluorescence intensity ratio as a function of time (Weber et al., 2004), producing values in the range 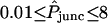. Data sets were screened to ensure that they conformed to pre-established criteria. Initial junctional conductance had to be between 5 and 50 μS to obtain sufficient signal while avoiding artifacts from cytoplasmic bridges, and was not allowed to increase more than twofold over the 6-h duration of the experiment. Fig. 6 shows examples of fits of the model to the data. Some data sets contained more scatter or other nonidealities, as detailed by Chang (2003), but the model could offer a reasonable representation of all the data. In all, 189 double-cell data sets were analyzed.

Aside from 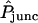, one (and sometimes two) parameters varied between double-cell experiments. The estimated starting point of each curve was matched approximately by adjusting the background parameter BG appearing in Eq. 22. For a minority (approximately one-quarter) of data sets, K_cyt^eq was reduced (usually by a factor of 2 or 4) because the observed high rate of cell-to-cell dye transfer (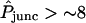) was consistent with a lower degree of cytoplasmic binding. The implied variability in 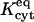agreed with that already observed in fitting the single-cell data (which showed variations in by a factor of ∼5).

In double-cell control experiments, the preparatory step of injection with connexin RNA and antisense oligonucleotide to endogenous Xenopus Cx38 was replaced by an injection of antisense oligonucleotide alone (so that no channels would be expressed in the cellular membrane). A small fluorescence intensity sometimes observed in the acceptor imaging box represents a background likely to arise from refraction or optical imperfections in the system, or some residual endogenous channel formation. As an order-of-magnitude check on the possible effects of such imperfections, they may be characterized in terms of an “equivalent” degree of intercellular membrane permeability that would give rise to the same rate of change of the acceptor/donor. The conclusion of this analysis (Chang, 2003) is that values of 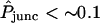(which arise for data sets showing low dye transfer rates) might not be significant as they fall under the possible level of optical noise in the system. This threshold value of applies to Alexa350; the average noise level seems to be lower for the other two dyes.

For each experimental curve to which a value of was fitted, N_pore was estimated from the measured intercellular conductance using Eq. 25 together with the known unitary channel conductance. Table 2 lists unitary conductances for the channel types considered. It agrees well with a recent approximate tabulation of unitary conductances “in 120–150 mM salt” (Harris, 2001, p. 383), and is roughly applicable to currents carried by the natural cytoplasmic medium. The final result of our analysis is the quantity A_memP_junc/N_pore = (AP)_pore (compare to Eq. 2). It represents the effective constant of proportionality between a macroscopic dye concentration difference across the intercellular membrane, and the resulting molecular flow (moles/time), reckoned on a per-channel basis. Fig. 7 shows the variation of (AP)_pore with unitary channel conductance for each dye. Because of variations over more than an order of magnitude, we report mean values (with error bars indicating mean ± SE) of the logarithm of (AP)_pore. For each combination of dye and channel type, the logarithm of the ratio of membrane permeability to channel number was averaged over all data sets analyzed.

TABLE 2.

Unitary conductances γ_pore of channels

Type of channel	Unitary conductance γpore (pS)	Reference for unitary conductance
mCx45/mCx45	32*	Moreno et al. (1995), Veenstra et al. (1994)
rCx32/rCx32	55	Bukauskas et al. (1995a), Suchyna et al. (1999)
rCx26/rCx32	90†	Suchyna et al. (1999)
rCx43/rCx43	90‡	Veenstra et al. (1995)
rCx26/rCx26	135	Bukauskas et al. (1995a), Suchyna et al. (1999)
mCx37/rCx43	140§
mCx40/mCx40	198	Bukauskas et al. (1995b)
mCx37/mCx37	315	Traub et al. (1998)

Species designations are m for mouse and r for rat. Although the internal pipette solutions used to measure the reported conductance values vary, their correspondence with the natural cytoplasmic medium is a reasonable approximation.

^*Data exist for channels comprising chick, rat, and human connexin protein; the measured unitary conductance is 32 pS for all three species. Given the apparent consistency among species, we use this value as an estimate for the mouse Cx45/Cx45 channels actually studied.

^†Heterotypic Cx26/Cx32 channels exhibit current-rectifying behavior, i.e., a nonlinear current-voltage characteristic. Value listed is approximate conductance at zero voltage.

^‡Value listed is for nonphosphorylated channel.

^§Value listed is not a measured value, but rather an estimate based on the assumption that the constituent hemichannels act as resistances in series, each resistance being one-half the resistance of the corresponding complete homotypic channel. Evidence for the efficacy of this estimate is furnished by the case of heterotypic Cx26/Cx32 channels (for which conductance data are available as listed), in which case the same calculation yields an error of only −13%.

FIGURE 7.

Correlations of (AP)_pore with γ_pore for (A) Alexa 350, (B) Alexa 488, and (C) Alexa 594. The points with error bars represent the mean ± SE of log₁₀[(AP)_pore].

The approximate practical upper and lower limits on 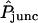(8 and 0.1, respectively) discussed above indicate that the oocyte system is capable of determining intercellular membrane permeabilities over a range spanning roughly two orders of magnitude. They are translated approximately into corresponding limits on (AP)_pore in Appendix C. The conclusion is that values of (AP)_pore exceeding the order of 1.4 × 10⁻⁹ mm³/s (log₁₀[(AP)_pore/(mm³/s)] − 8.9) are probably not reliably indicated. In this regime the dye transfer rate is limited by intracellular diffusion and does not reflect the (high) membrane permeability. Noise in the system may be characterized in terms of an equivalent permeability, and renders possibly insignificant values of (AP)_pore below the order of 1.8 × 10⁻¹¹ mm³/s (log₁₀[(AP)_pore/(mm³/s)] − 10.7).

DISCUSSION

The final derived data (Fig. 7) are discussed in detail in Weber et al. (2004) in terms of functional comparisons between different gap junctions. Here we focus on what our analysis and the results say about the physics of the intercellular transfer process.

Factors affecting the macroscopically observable rate of dye transfer

Xenopus oocytes furnish a good system for the quantification of dye transfer rates (Nicholson et al., 2000; Weber et al., 2004). However, they present the challenge that the desired junctional permeability is convoluted with a number of other obscuring physical factors. It is worthwhile to recap the effects these factors have on our derived values of (AP)_pore.

The most important nonjunctional phenomenon influencing intercellular transfer seems to be binding of dye to components of the cytoplasm. We assume reversible binding because all attempts at describing the data with an irreversible binding model failed. The fitted values of 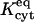, ranging from ∼6 to 10 (Table 1), indicate that the bound state is strongly preferred for all three dyes (because they significantly exceed unity). The characteristic binding times 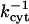are on the order of 10–20 min. Although the precise microscopic origin of the binding process remains to be clearly defined, this type of gradual phenomenon has been indicated in other dye transfer studies (Brink and Ramanan, 1985). It is worth noting that the levels of the acceptor/donor curves in Fig. 5 (significantly below unity) after one-half hour represent a transient phenomenon. Because of the reversibility of binding, these curves would ultimately reach values around unity after a much longer elapsed time, i.e., the final equilibrium state is a spatially uniform distribution of dye.

An analysis not explicitly accounting for binding would erroneously ascribe the consequent slowness of dye transfer to lower apparent values of intercellular membrane (and unitary channel) permeability. The double-cell experiments alone provide no means of deconvoluting the effects of intercellular membrane (and ultimately junctional) diffusional resistance, and binding. The single-cell data (Fig. 5) provide the independent information needed to characterize the latter, and hence achieve the deconvolution. Two illustrative calculations performed to test the effects of binding indicate that, for cases of moderate and high membrane permeability, ignoring binding would decrease the derived values of (AP)_pore by factors of ∼10 and 60, respectively. We could fit the double-cell data in this way, but to do so would be to ignore the very strong and consistent evidence for a significant degree of binding embodied in Fig. 5.

Because of the O(1 mm) path length across an oocyte, the role played by cytoplasmic diffusional resistance is also significant. Its quantitative importance is made clear by values of the dimensionless parameter 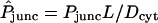, representing the ratio of intercellular membrane to cytoplasmic permeabilities, found to be around unity or greater in many cases (see, e.g., labels on curves in Fig. 6). Mobilities of dye molecules are noticeably lower in cytoplasm than in bulk water. Values of D_cyt range from ∼30 to 90% of the corresponding values of D_aq (Table 1), reflecting hindered mobility in the cytoplasmic milieu. They describe the initial rise of the curves in Fig. 5, before onset of the gradual binding process. At longer times, binding further (and dramatically) slows intracellular movement of dye. Theoretically, once sufficient time has passed for binding equilibrium to be achieved (t ≫ 10–20 min), free and bound molecules would move collectively in a hypothetical infinite cytoplasmic medium with an apparent diffusivity 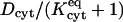(Cussler, 1997, pp. 32–34). Altogether, the reduction in mobility within cytoplasm relative to bulk water observed here is consistent with the reduction seen for a variety of molecular permeants and cell types—typically by a factor of roughly 2–5, with further retardation if binding occurs (Mastro and Keith, 1984, p.185s; Nitsche, 1999, pp. 484–485).

The measurement of intercellular conductance concomitantly with dye transfer is key to counting channels, thereby enabling the deduction of unitary permeabilities from intercellular membrane permeabilities. Our procedure specifically accounts for the phenomenon that the voltage drop (ΔV)_j actually occurring across the membrane is generally only a fraction of the total observed intercellular voltage drop (ΔV)_total, owing to apparently significant nonmembrane (e.g., cytoplasmic) electrical resistances. This phenomenon is addressed quantitatively by our conductance model (see Eqs. 24 and 25, and Appendix B). If we would ignore it (i.e., assume that the observed intercellular conductance G_obs is simply proportional to N_pore), then we would underestimate the number of channels. Derived values of (AP)_pore would come out higher than the correct values, typically by a factor of ∼2.

Magnitude and dye/channel size-dependence of unitary permeability

Examination of Fig. 7, A–C, indicates that the derived unitary area-times-permeability factors lie between ∼10⁻¹¹ and 10⁻⁹ mm³/s, and, broadly speaking, exhibit an overall decrease with increasing dye molecular weight progressing from Alexa 350 (MW = 326.31, excluding sodium ion) to Alexa 594 (MW = 735.81), a trend which accords with intuition. Examination of each individual part (A, B, or C) of this figure indicates that significant variations exist among channels (distinguished by their unitary conductances on the abscissa), and that—if any broad trend were to be identified—it would be an overall decrease in permeability with increasing channel conductance. Insofar as channel conductance is an indicator of average pore radius, this trend seems anomalous, because bigger pores might be expected to be easier to traverse by diffusion. Anomalies in the correlation of dye permeability with channel conductance are well known, and speak for physics more complex than simply hindered diffusion through a featureless aqueous pore (e.g., Veenstra et al., 1995; see Harris, 2001, p. 396).

To assess the magnitudes and trends of the derived unitary permeabilities, it is instructive to apply pore diffusion theory to these data. Following ample precedent (Levitt, 1975, 1985, 1991; Dwyer et al., 1980; Zimmerman and Rose, 1985; Hille, 1992; Beblo and Veenstra, 1997; Wang and Veenstra, 1997; Valiunas et al., 2002), for order-of-magnitude purposes we idealize channels as circular cylindrical pores and dye permeants as hard spheres. A reasonable estimate of the pore length ℓ_pore is 160 Å (Veenstra et al., 1995; compare to Wilders and Jongsma, 1992). Dye molecules are characterized in terms of their Stokes-Einstein equivalent radii (Table 1). The unitary pore area-times-permeability factor is given by

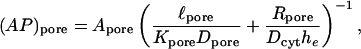(26)

in which 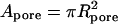is the pore cross-sectional area. The partition coefficient comes from a well-known formula (Pappenheimer et al., 1951; Renkin, 1954; Dwyer et al., 1980; Levitt, 1985; Deen, 1987) expressing the fact that only a fraction of the pore cross section is accessible to the permeant center owing to its finite size (steric exclusion),

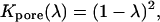(27)

where λ = a/R_pore is the ratio of permeant (a) to pore (R_pore) radii. The mean in-pore diffusivity is approximated using the equation

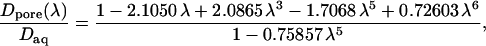(28)

derived by Haberman and Sayre (1958), which is very commonly used to describe hindered diffusion in biological pores and channels generally (Levitt, 1975, 1985, 1991; Dwyer et al., 1980) and gap junctions in particular (Beblo and Veenstra, 1997; Wang and Veenstra, 1997; Valiunas et al., 2002; compare to Zimmerman and Rose, 1985). It is based on continuum hydrodynamic theory, which may be applied only approximately to small pores. Technically, D_pore is the axial diffusivity averaged over all radial positions, whereas this equation gives the diffusivity for translation along the pore axis. As reviewed by Deen (1987), the centerline diffusivity is in fact a good approximation to the radial average. Equation 26 includes a term for the pore access resistance at both ends of the pore, quantified by a dimensionless hydrodynamic function, h_e, calculated rigorously by Keh (1986). His numerical values of h_e, calculated in the range 0 ≤ λ ≤ 0.6, are well approximated by a simple formula that we have fitted for use here, namely

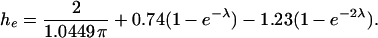(29)

The first term, an exact result due to Kelman (1965) expressed in Keh's (1986) notation, is usually approximated as 2/π (Hall, 1975; Hille, 1992, p. 296; Veenstra, 1996). We use the cytoplasmic diffusivity D_cyt in conjunction with h_e in Eq. 26 because the access process is dominated by diffusion to and from the pore mouth through the cytoplasmic medium (as opposed to water in the pore).

Fig. 8 A shows the dependence of (AP)_pore upon pore radius R_pore predicted by Eqs. 26–29 for Alexa 350 (Stokes-Einstein radius a = 4.3 Å). The levels of permeability corresponding to the data points in Fig. 7 A are represented as horizontal dotted lines for each connexin tested. It is seen that, to match the data, classical pore diffusion theory requires pore radii ranging from ∼18 to 40 Å. Such radii are much larger than all published estimates of channel size made on the basis of unitary channel conductance (e.g., Veenstra, 1996; Beblo and Veenstra, 1997; Wang and Veenstra, 1997) and passive diffusion of molecular size probes (e.g., Flagg-Newton et al., 1979; Schwarzmann et al., 1981; Gong and Nicholson, 2001; see Harris, 2001, pp. 391–396), as well as direct structural determinations (e.g., Yeager et al., 1998; Unger et al., 1999; see Harris, 2001, pp. 335–338), all of which suggest diameters < 20 Å (i.e., radii < 10 Å).

FIGURE 8.

Illustrative calculation showing the dependence of (AP)_pore upon R_pore for Alexa350 (Stokes-Einstein equivalent radius = 4.3 Å) as predicted by the pore theory embodied in Eqs. 26–30. Horizontal dotted lines represent levels of permeability for each connexin tested, corresponding to the data points in Fig. 7 A. (The highest, second highest, and lowest dotted lines correspond to Cx45, Cx40, and Cx37 channels, respectively. The remaining channels exhibit intermediate levels of permeability that differ negligibly from each other.) (A) Theory without van der Waals affinity. Pore access resistance is accounted for. (B) Theory with van der Waals affinity factor calculated as described in Appendix D. The Hamaker constant has been set to 6 × 10⁻²⁰ J. The lowest and highest (solid) curves correspond to calculations with and without the pore access resistance, respectively. The intermediate (dashed) curve gives the geometric mean of these two results.

Energetic interactions between the dye permeant and pore, not included in the above formulation, are likely to exist, and constitute potentially important factors affecting pore permeability. Any attractive interactions would make the pore environment energetically favorable, thereby elevating in-pore concentrations relative to cytoplasm, and concomitantly increasing the permeant flux for a given pore radius. Equivalently, relative to the no-interaction case, a given level of flux would occur with a smaller pore size. Thus, attractive interactions might explain the general trend for permeability to increase with decreasing conductance indicated by Fig. 7, and also high absolute values of permeability.

As an illustrative step toward considering the possible effects of permeant-pore attraction, we present here a calculation of (AP)_pore allowing for van der Waals interaction. Our reasons for selecting this example are that the van der Waals interaction is ubiquitous, and can also be estimated rigorously from the assumed pore model. In this regard it is worth noting that recent work elucidating the pore-lining amino acid residues in Cx32 channels has shown them to be largely hydrophobic (Skerrett et al., 2002), which suggests that, at least within the membrane spanning region of the pore, electrostatic interactions may play a reduced role. Calculations could in principle be carried out for electrostatic interactions (compare to Smith and Deen, 1980, 1983; Jordan et al., 1989; Levitt, 1991). However, they would require very specific assumptions about the distribution of charges facing the pore interior as a function of axial position. While they may exist at the pore mouth (see below) or in the part of the pore spanning the extracellular gap between cells, there are currently no structural data to confirm this or map their positions.

The primary effect of van der Waals (or any other attractive) interaction in Eq. 26 is to increase K_pore because of the energetic favorability of the in-pore environment relative to the cytoplasm outside. This effect may be represented in the form of an extra affinity factor 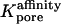appearing in a modified form of Eq. 27, namely

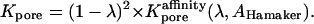(30)

The calculation of 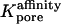is summarized in Appendix D, which also indicates typical orders of magnitude of the Hamaker constant A_Hamaker, the key parameter quantifying the strength of the van der Waals attraction. Fig. 8 B shows the predicted dependence of (AP)_pore on R_pore for Alexa350 allowing for the additional effects of permeant-pore van der Waals attraction, based on a reasonable choice of A_Hamaker (6 × 10⁻²⁰ J; see Appendix D), as well as short-range repulsion. The lowest and highest (solid) curves are based on Eq. 26 with and without the pore access resistance term, respectively. Because the permeant-pore attraction would tend to reduce the access resistance, the actual permeability must be intermediate between the results for these two limiting cases. Presented as a guide to the eye, the dashed curve represents the geometric mean of the two calculated values of (AP)_pore at each pore radius. Notably, this curve suggests that the measured permeabilities of most of the channels studied here are consistent with a pore radius < 10 Å (i.e., diameter < 20 Å)—a value compatible with other measured gap junction pore diameters mentioned above.

The introduction of permeant-pore affinity adds considerable intrigue to the microscopic picture. Although a given level of permeability can be matched by an unrealistically large value of R_pore, as in the no-interaction case (compare to Fig. 8 A), it can also be matched by a much smaller value of R_pore. The underlying physical reason is that, with a snug fit in a small pore, the pore wall is close to the permeant surface on all sides, and the resulting energetic interaction is very strongly favorable. For instance, the energy of attraction in a pore with R_pore = 10 Å varies from −1.6 to −5.5 kT progressing outward from the centerline to the maximum allowable radius. This effect may be so strong that dye flux actually increases with decreasing R_pore, over a certain range of radii, despite the concomitant decrease in pore cross-sectional area and solute mobility. This phenomenon is clearly evident in Fig. 8 B, and also explains the general trend of increasing permeability with decreasing γ_pore for a given dye. A corollary of this statement is that one could see elevated permeability as probe size increases for a given channel, i.e., a tighter fit elevates in-pore concentration levels (and hence flux) because of the more energetically favorable environment (in the form of higher attraction of the probe to the pore walls). This effect can be so strong that it dominates over the increased level of hindrance. For example, Alexa 488 shows slightly higher flux through Cx43 channels than Alexa 350. With Alexa 594 in Cx43 channels one reaches a permeant size where mobility must be very strongly impeded at a constriction somewhere along the pore. Thus the permeability to this dye is again lower.

Calculations not shown suggest that electrostatic interactions could give rise to energies of similar magnitudes (compare to Harris, 2001, p. 384). They will be open to similar quantitative assessment once sufficient definitive information becomes available about magnitudes and locations of charges in the pore lining.

Overall, considering both their high absolute values and correlation with unitary electrical conductance (Fig. 7), our derived data on unitary channel permeability strongly suggest the existence of permeant-pore affinity factors if these data are to be explained in terms of reasonable pore radii. Identification of these factors, which might constitutes the net outcome of several intermolecular forces, constitutes an important subject for future experimental and theoretical investigation. It is worth emphasizing that the term affinity as used here refers to an energetically favorable environment in the pore, which elevates in-pore concentrations relative to the bulk (cytoplasmic) solutions outside, and thereby the permeant flux. It does not imply the existence of binding sites that immobilize the dye permeant, or an attraction to the wall so strong that ultrahigh friction preludes its axial diffusion. Permeabilities of the pores themselves may be so high (possibly due to affinity factors as suggested here) that the rate of dye diffusion might be affected significantly or even limited by the pore access resistance (see the three curves shown in Fig. 8 B quantifying the effects of varying degrees of access resistance).

Comparison with the results of Valiunas et al. (2002)

It is worthwhile to compare our findings with the only other reported determination of absolute values of dye passage rates on a per-channel basis for gap junctions (Valiunas et al., 2002). Their results can be cast in the form of the pore area-times-permeability factor, because the concentration difference driving transjunctional diffusion is also reported. Analysis of the specific typical 15-min experiment represented in their Fig. 2 yields the value log₁₀[(AP)_pore/(mm³/s)] ≅ −11.6 for rat Cx43 channels. This value for Lucifer Yellow (LY) is significantly below those found for the series of Alexa dyes considered here (log₁₀[(AP)_pore/(mm³/s)] ranging from −9.37 to −9.95 in the same type of channel). Valiunas et al.'s dye transfer rates for Cx40 channels are even lower. These authors specifically comment that their permeation rates imply a surprisingly ineffective gap junctional pathway for intercellular transfer of messenger and metabolite molecules, although our current results would suggest a much greater level of effectiveness.

Any physical phenomena slowing dye transfer would be lumped into the low apparent junctional permeability reported by Valiunas et al. Cytoplasmic diffusional resistance is not a factor given the small size of HeLa cells and, further, perfusion of the donor cell in their experimental Method 1. Brink and Ramanan (1985) reported very noticeable cytoplasmic binding of LY in earthworm septate median giant axons, although it seemed to occur gradually (over the timescale of hours). The extent to which binding might be responsible for low transfer rates of LY in Valiunas et al.'s experiments is unclear, as the passive perfusion afforded by a whole cell patch is unlikely to displace dye bound near the membrane. However, it probably would not change their conclusions by an order of magnitude. Thus, differences between our results and theirs may come down to the difference in dye permeants and possible differences in the state of the channel.

Although LY has a smaller molecular weight than our intermediate Alexa 488 dye, its conjugated three-ring system is more rigid than that of the Alexa probes, so it is difficult to compare their effective diameters. The distributions of surface charge, although anionic for all of these dyes, also differ significantly. Thus, structural differences between dye probes could be responsible for the observed differences in permeability. This possibility is supported by new preliminary data (A. Verma, University at Buffalo, unpublished observations), for which initial assessments suggest somewhat lower LY permeability through Cx43 channels relative to Alexa 488 in the same oocyte system considered here.

In addition, it is worth noting that mammalian cells often cause phosphorylation of Cx43 (Musil and Goodenough, 1991), whereas oocytes do not (Zhou et al., 1999). This could clearly affect the access resistance to the pore. Consistent with this, phosphorylation of Cx43 by PKC has been associated with a 30% decrease in unitary conductance from 90 to 60 pS (Moreno et al., 1994). Calculations not shown suggest that if such changes occur as an electrostatic effect of the ring of negative charges introduced by the phosphate groups at the channel mouth, then these charges would have to be positioned relatively close to the pore mouth to affect conductance, given the salt shielding that could occur in cytoplasm. The implied electrostatic barrier at each end of the pore for an anionic dye permeant (larger than a small ion) could then dramatically reduce the rate of dye transfer. The implication is that Valiunas et al.'s low permeability may also derive in part from a pore entrance effect present in their system and absent in ours.

Resolution of absolute (as opposed to relative) values of junctional permeability has the potential for revealing much about the microscopic physical mechanisms of pore diffusion and entrance effects. Valiunas et al.'s (2002) analysis and our work underscore the importance of focusing on absolute values.

APPENDIX A: MATHEMATICAL DETAILS RELATING TO THE MODEL GEOMETRY AND THE COORDINATE SYSTEM BASED ON EQ. 18

The semiaxes (ℓ_x ≅ 0.66 mm, ℓ_y ≅ 0.57 mm, ℓ_z ≅ 0.59 mm) and centers (x_0, ± = (0, 0, ± z₀) with z₀ ≅ 0.47 mm) of the ellipsoids representing the oocytes are computed to match four key dimensions measured from a number of images of the system, namely the half-length, width, and thickness of the oocyte pair, and the width of the intercellular (common, coupled) portions of the cellular membranes seen from the bottom. The major (x) and minor (y) semiaxes of the elliptical intercellular membrane at z = 0 formed by the intersection of these ellipsoids are ≅ 0.39 mm and ≅ 0.33 mm, respectively.

With reference to Eqs. 3, 4, and 18, the function 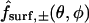specifying the dimensionless radial distance on the surface of the “+” or “−” oocyte in terms of θ and φ is given explicitly by the set of formulas

(31)

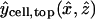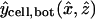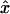The functions and appearing in Eq. 21 specify the coordinates of the upper and lower oocyte surfaces, respectively, in terms of and 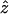. They are given explicitly by

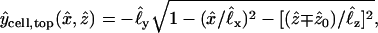(32)

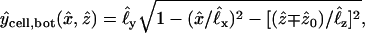(33)

in which the upper (−) signs apply to the “+” oocyte and the lower (+) signs apply to the “−” oocyte. These formulas are equivalent to Eq. 31 (and are more transparently indicative of the assumed ellipsoidal shapes).

The relations

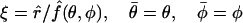(34)

(compare to Eq. 18) define the 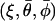coordinate system employed in our analysis, which is nonorthogonal (compare to Bird et al., 1987, pp. 597ff). Here and in subsequent equations the symbol 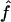is used as shorthand for 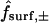. Application of the chain rule of differentiation (Bird et al., 2002, p. 826) yields the following expressions for partial derivatives with respect to 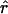, θ, and φ in terms of partial derivatives with respect to ξ, , and :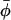

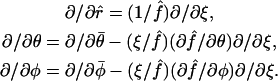(35)

These expressions serve to rewrite the standard formula for the Laplacian operator in spherical coordinates (Bird et al., 2002, p. 836) in terms of first and second derivatives with respect to ξ, , and :

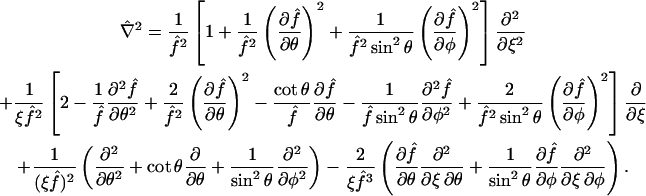(36)

In this as in subsequent formulas, we make the notational change , . In Eq. 11, the normal derivative on the intercellular membrane (at or θ = π/2) is

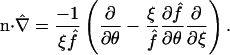(37)

In Eqs. 12 and 13, the corresponding derivative on the uncoupled membrane surfaces (given by 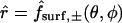or ξ = 1) is

(38)

The differential element of volume, used in the computation of the normalization factors α_spot,single and α_spot,double, is given by

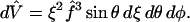(39)

APPENDIX B: SIMPLE CELL-PAIR CONDUCTANCE MODEL UNDERLYING EQS. 24 AND 25

Fig. 9 depicts a simple, effectively one-dimensional electrical model of the cell pair, accounting for resistances in series across the intercellular membrane junctions and the bulk cytoplasms, as well as a possible additional resistance within each cell. These three types of electrical resistances (), and corresponding voltage drops (ΔV), are identified by the descriptive subscripts j, cyt, and other, respectively. A likely important contributor to is the junctional access resistance, addressed in detail by Wilders and Jongsma (1992). These authors found that the voltage drop (ΔV)_j/(ΔV)′ (in the notation of Fig. 9) equals 0.91 for an isolated channel, and drops to 0.56 (i.e., is significantly less than unity) for a junctional plaque comprising 1951 channels, owing to interactions between them.

FIGURE 9.

Schematic circuit diagram for simple resistances-in-series model of cell-to-cell voltage drop.

Consideration of the resistivity of the cytoplasm (Wilders and Jongsma, 1992, p. 946; compare to Hille, 1992, p. 8), as well as the approximate length and width of the electrical path, yields the estimate for the total cytoplasmic electrical resistance. Insofar as the difference between this estimate and the fitted value β ≅ 12,800 Ω might be significant, it suggests a substantial value of 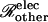, likely attributable to junctional access resistance. Fig. 9 furnishes an approximate basis for addressing this factor. According to it, the total intercellular voltage drop is given by

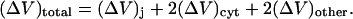(40)

Conservation of charge at steady state dictates that three expressions for the intercellular current be equal:

(41)

At least two analyses of these two equations are possible (Chang, 2003). If the channel access resistances act independently, then 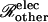should vary with the number of channels as . In the other extreme of N_pore-dependence, 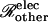might be regarded as a constant, independent of N_pore, representing an average parameter or else possibly reflecting a kind of saturation effect. Among these two possible assumptions we choose the latter, because the former denies interactions between channels, which were clearly demonstrated by Wilders and Jongsma (1992). With the latter assumption ( 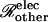= constant, independent of N_pore), straightforward manipulations of Eqs. 23, 40, and 41 then yield Eqs. 24 and 25 in the main text, together with the explicit expression

(42)

for the parameter β, representing the sum of all nonmembrane resistances, which act in series with the channel-derived membrane resistance .

Our tentative conclusion is as follows. If our estimate is too low, then bulk cytoplasmic resistance may actually exist at a level (of order 12,800 Ω) sufficient to explain the substantial decrease in (ΔV)_j/(ΔV)_total with increasing G_obs (Weber et al., 2004, their Fig. 5 E). On the other hand, if bulk cytoplasmic resistance is insufficient to account for this decrease (as we suspect), then the substantial value 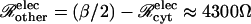implies a substantial voltage drop (ΔV)_other, qualitatively consistent with an interaction between channel access resistances (Wilders and Jongsma, 1992).

APPENDIX C: APPROXIMATE RELATION BETWEEN DIMENSIONLESS MEMBRANE PERMEABILITY AND DIMENSIONAL UNITARY CHANNEL PERMEABILITY

The average of the three cytoplasmic diffusivities listed in Table 1 is 2.7 × 10⁻⁴ mm²/s. This average D_cyt may be used to convert 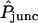into its dimensional equivalent 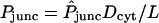(with L = 1 mm). Typical values of the intercellular conductance G_obs and unitary channel conductance γ_pore are 40 μS and 135 pS, respectively, from which it follows that N_pore typically equals 6.1 × 10⁵ pores in the intercellular membrane according to Eq. 25. With these inputs, together with the intercellular membrane area A_mem = 0.41 mm², Eq. 2 yields the approximate relation

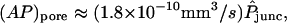(43)

which implies the values (AP)_pore ≈ 1.4 × 10⁻⁹ mm³/s and 1.8 × 10⁻¹¹ mm³/s, corresponding to and 0.1, respectively.

APPENDIX D: CALCULATION OF INTERACTION ENERGY AND PARTITION COEFFICIENT FOR VAN DER WAALS INTERACTION BETWEEN DYE PERMEANT AND PORE

The key parameter quantifying the strength of van der Waals attraction is the Hamaker constant A_Hamaker. It is defined as π²n_permeantn_poreC, where C is the parameter quantifying the −C(distance)⁻⁶ energy of the dispersion interaction between any pair of atoms in the permeant and pore, and n_permeant and n_pore represent the number densities of atoms in these two material bodies (Israelachvili, 1992, p. 176; see also Hiemenz, 1986, pp. 620, 647). Typical values of A_Hamaker for organic molecules interacting across vacuum lie in the range from 4 to 7 in units of 10⁻²⁰ J (van Oss, 1994, p. 157; Israelachvili, 1992, pp. 178, 186–187). Interposition of water between the interacting surfaces (instead of vacuum) typically reduces A_Hamaker threefold to tenfold, and the presence of dissolved ions further reduces its value (Hiemenz, 1986, pp. 653–655; Russel et al., 1989, pp. 146–155; Israelachvili, 1992, 188–192). However, in the confined permeant-pore gap, these effects may be only partially operative.

An estimate of the van der Waals energy Ψ_vdW can be obtained using the well-established “microscopic theory,” involving pairwise addition (integration) of contributions from all elements of volume in the permeant molecule and surrounding pore (Hiemenz, 1986, pp. 644–649; Russel et al., 1989, pp. 130–135; Israelachvili, 1992, pp. 155–158, 176–178; Papadopoulos and Kuo, 1990; Bhattacharjee and Sharma, 1995). The energy depends upon the radial coordinate r of the permeant (distance of its center from the pore axis), and may be regarded as a function of either r or its dimensionless equivalent η ≡ r/R_pore. Following a derivation essentially identical to that of Bhattacharjee and Sharma (1995), Ψ_vdW can be written in the form

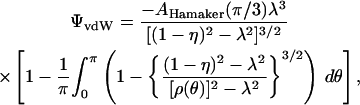(44)

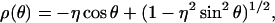where λ = a/R_pore as defined in the main text. The integral is approximated numerically using Simpson's rule.

The energy Ψ_vdW diverges at configurations corresponding to dye-pore contact (r = R_pore − a or η = 1 − λ). In reality, such contact is prevented by an additional interaction, namely, the strong, short-range Born repulsion (Israelachvili, 1992, p. 109; Bhattacharjee and Sharma, 1995). As do the latter authors, we account approximately for this phenomenon without modifying Eq. 44 by introducing an effective minimum separation distance h_repul between the spherical dye and cylindrical pore surfaces, generally accepted to be 1.57 ± 0.09 Å (van Oss, 1994, pp. 14, 154–160; Bhattacharjee and Sharma, 1995).

The single-pore partition coefficient is the radial average of a Boltzmann factor based upon the permeant-pore interaction energy (Deen, 1987), here Ψ_vdW(r):

(45)

This equation may be recast in the form

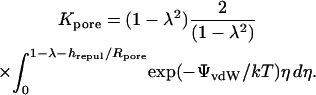(46)

As written, the first factor quantifies purely geometrical exclusion based on the permeant radius a (compare to Eq. 27), and the second factor is precisely the affinity factor 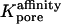introduced in Eq. 30, for which the integral is approximated numerically using Simpson's rule.

Our best estimates of effective Hamaker constants, obtained by rough fitting of the pore theory to the observed values of (AP)_pore, are 6, 3, and 2 in units of 10⁻²⁰ J, respectively, for Alexa 350, Alexa 488, and Alexa 594. These values are in line with the typical order of magnitude cited above. The apparent decrease in effective A_Hamaker with increasing dye molecular weight (MW) accords with intuition. Assuming roughly constant chemical composition and density among dyes, A_Hamaker should be constant and the mean molecular radius should follow a MW^1/3 scaling law. Because of the importance of diffusion, however, our analysis is based on Stokes-Einstein equivalent radii, which increase more rapidly than MW^1/3 in the progression Alexa 350 → Alexa 488 → Alexa 594 (see Table 1). This fact implies a concomitant decrease in effective material properties like density and Hamaker constant.

In principle, the van der Waals (or any other) permeant-pore interaction biases the average implicit in D_pore, giving greater relative weight to radial positions nearer to the pore wall. However, it is very clear from experiments (Ilic et al., 1992) and rigorous hydrodynamic calculations (Lewellen, 1982; Ilic et al., 1992; Tullock et al., 1992) for the sphere-cylinder geometry that variations in solute mobility with radial position exist but are not dramatic. For instance, for the case λ = 0.5 the variation is <∼20% (see Ilic et al., 1992, their Fig. 3; Tullock et al., 1992, their Fig. 13) excepting very small sphere-wall gaps, which would be precluded here by the phenomenon of short-range permeant-pore repulsion. Lewellen (1982) has commented specifically on the surprising weakness of this radial dependence. Therefore, the centerline formula (Eq. 28) can still be applied as a good approximation in the presence of permeant-pore energetic interactions.