The External K⁺ Concentration and Mutations in the Outer Pore Mouth Affect the Inhibition of Kv1.5 Current by Ni²⁺

Abstract

By examining the consequences both of changes of [K⁺]_o and of point mutations in the outer pore mouth, our goal was to determine if the mechanism of the block of Kv1.5 ionic currents by external Ni²⁺ is similar to that for proton block. Ni²⁺ block is inhibited by increasing [K⁺]_o, by mutating a histidine residue in the pore turret (H463Q) or by mutating a residue near the pore mouth (R487V) that is the homolog of Shaker T449. Aside from a slight rightward shift of the Q-V curve, Ni²⁺ had no effect on gating currents. We propose that, as with H_o⁺, Ni²⁺ binding to H463 facilitates an outer pore inactivation process that is antagonized by K_o⁺ and that requires R487. However, whereas H_o⁺ substantially accelerates inactivation of residual currents, Ni²⁺ is much less potent, indicating incomplete overlap of the profiles of these two metal ions. Analyses with Co²⁺ and Mn²⁺, together with previous results, indicate that for the first-row transition metals the rank order for the inhibition of Kv1.5 in 0 mM K_o⁺ is Zn²⁺ (K_D ∼ 0.07 mM) ≥ Ni²⁺ (K_D ∼ 0.15 mM) > Co²⁺ (K_D ∼ 1.4 mM) > Mn²⁺ (K_D > 10 mM).

INTRODUCTION

Kv1.5 (KCNA5) channels, which are expressed in cardiac myocytes (Fedida et al., 1993; Tamkun et al., 1991) and in smooth muscle cells of airways, the intestine, and the vasculature (Adda et al., 1996; Clement-Chomienne et al., 1999), are members of a major structural class of K⁺ channels in which the α-subunit consists of six transmembrane (TM) segments with a pore-forming or P-region positioned between transmembrane segment five (S5) and segment six (S6). A characteristic feature of the 6TM-1P subunit is the charge-bearing segment four (S4) domain whose movement upon membrane depolarization (Baker et al., 1998; Larsson et al., 1996) is linked to the opening of the activation gate, which is believed to comprise the cytoplasmic ends of the four S6 regions in the tetrameric channel assembly. Macroscopic currents through Kv1.5 channels resemble delayed rectifier currents. Thus, with a strong sustained depolarization, channel activation is rapid and voltage-dependent whereas inactivation is voltage-independent and occurs on a timescale of seconds.

Kv1.5 channels exhibit only outer pore (P/C-type) inactivation (Fedida et al., 1999) and in this regard are different from Shaker channels, which also show inner pore (N-type) inactivation (Hoshi et al., 1991). The term C-type inactivation was coined to describe the slow inactivation process in Shaker that was uncovered when ball-and-chain or N-type inactivation was removed (ShakerIR) by deletion of the cytoplasmic N-terminal residues 6–46. C-type inactivation is coupled to channel activation and is believed to involve a conformational change in the outer pore mouth that extends to the selectivity filter delimited by the highly conserved GYG sequence. Because C-type inactivated ShakerIR (Starkus et al., 1997) and Kv1.5 (Wang et al., 2000a) channels are able to conduct Na⁺ ions, the current view is that the conformational change at the outer pore mouth involves an incomplete constriction rather than a complete collapse. An important consequence of C-type inactivation is a leftward shift of the gating charge versus voltage relationship, or Q-V curve, and charge immobilization (Fedida et al. 1996, Olcese et al., 1997).

In ShakerIR channels the residue at position 463 in the S6 segment was the first shown to influence the rate of C-type inactivation (Hoshi et al., 1991). Subsequently, point mutations of the threonine residue (T449) in the outer pore mouth were shown to dramatically accelerate (T449E, T449A, T449K) or slow (T449Y, T449V) C-type inactivation (Lopez-Barneo et al., 1993). In Kv1.5 channels the residue homologous to T449 is R487 and it has been shown that inactivation is substantially slowed in Kv1.5 R487V when Na⁺ is the charge carrier but not when K⁺ is the permeant ion (Fedida et al., 1999; Wang et al., 2000a).

The finding that ShakerIR/Kv1.5 channels with the pore mutation W434F/W472F were Na⁺- but not K⁺-conductive and showed wild-type gating charge behavior, including gating charge immobilization after channel inactivation (Chen et al., 1997; Olcese et al., 1997), was one of the first indications of the complexity of outer pore inactivation. To account for the properties of the ShakerIR W434F nonconducting mutant it was proposed that there was also a so-called P-type inactivation process that prevented K⁺ conduction but that was different from C-type inactivation in that it did not affect gating charge movement (Olcese et al., 1997; Yang et al., 1997). Restoration of ionic current in the double mutant Shaker W434F, T449Y supports the hypothesis that enhanced inactivation accounts for the ShakerIR W434F conductance loss (Yang et al., 2002).

An intriguing divergence in the structure-function relationships of Kv1.5 and ShakerIR is seen in the response to extracellular acidification. In Kv1.5 external protons cause, in addition to a rightward shift of the g-V curve that is often referred to as the gating shift, a concentration-dependent decrease of the maximum macroscopic conductance (g_max) as well as an acceleration of the inactivation rate of residual currents (Steidl and Yool, 1999; Kehl et al., 2002). In contrast, in ShakerIR channels increasing [H⁺]_o does not reduce g_max but the gating shift and the speeding of inactivation are observed (Perez-Cornejo, 1999; Starkus et al., 2003). A number of lines of evidence now support the view that protonation of a histidine residue (H463), the equivalent of Shaker F425, in the pore turret (S5-P linker) plays an important role in the proton-induced conductance loss/block in Kv1.5. Thus, in the Kv1.5 H463Q mutant there is a large rightward shift of the concentration dependence of the H_o⁺ block (Kehl et al., 2002). The finding that the H_o⁺ block is antagonized by K_o⁺ and is also reduced in the R487V mutant (Jäger and Grissmer, 2001; Kehl et al., 2002) has suggested that the protonation of H463 facilitates an inactivation process requiring R487. An alternative explanation involving direct pore block by protons has been ruled out on the basis of single channel recordings (Kwan et al., 2003) and the finding that the Na⁺ current through inactivated Kv1.5 channels is maintained after extracellular acidification (Zhang et al., 2003).

Additional support for a crucial role of H463 in the H_o⁺-induced decrease of g_max is provided by reports showing that divalent cations known to bind to histidine residues also affect Kv1.5 currents. Harrison et al. (1993) first reported that extracellular Zn²⁺ blocks Kv1.5 currents and, as with the H_o⁺ block, this effect of Zn²⁺ is inhibited either by increasing K_o⁺ or by mutating H463 and/or R487 (Kehl et al., 2002). Ni²⁺ is also a histidine ligand and although it too has been reported to block Kv1.5 currents expressed in Chinese hamster ovary (CHO) cells (Perchenet and Clement-Chomienne, 2001), the mechanism of, and the molecular determinants for, the block have not been resolved. To test the hypothesis that the mechanistic basis for the Ni²⁺ block is essentially the same as that outlined above for Zn²⁺ and H_o⁺, we set out in this study to address the following questions. Is the block of Kv1.5 by Ni²⁺ antagonized by increasing [K⁺]_o? Does Ni²⁺ speed the inactivation rate of residual Kv1.5 currents? Is the effect of Ni²⁺ affected either by mutating H463, a putative Ni²⁺ coordination site, or by mutating R487, a site implicated in the regulation of outer pore inactivation? Are gating currents affected by Ni²⁺? And finally, is the blocking effect of Ni²⁺ replicated by other divalent cations such as Co²⁺, Cd²⁺, and Mn²⁺?

MATERIAL AND METHODS

Cell preparation

As described previously (Wang et al., 2000a), wild-type (wt) and mutant human Kv1.5 channels, henceforth referred to simply as Kv1.5 channels, were studied in a human embryonic kidney cell line (HEK293) (Wang et al., 2000b). Cells were dissociated for passage by using trypsin-EDTA and were maintained in minimum essential medium (MEM), 10% fetal bovine serum, penicillin-streptomycin, and 0.5 mg ml⁻¹ gentamicin in an atmosphere of 5% CO₂ in air. All tissue culture supplies were obtained from Invitrogen (Burlington, Ontario, Canada).

Point mutations of the wt Kv1.5 α-subunit in the plasmid expression vector pcDNA3 were made using the Quikchange Kit (Stratagene, La Jolla, CA) to convert the histidine (H) residue at position 463 to glutamine (Q) (H463Q) or the arginine (R) at position 487 to valine (R487V). Stable transfections of HEK293 cells were made using 0.8 μg of Kv1.5 H463Q or Kv1.5 R487V cDNA and 2 μL of Lipofectamine 2000 (Invitrogen, Carlsbad, CA). Geneticin (0.5 mg/mL) was added 48 h after transfection. Because Shaker-related channels such as Kv1.5 are homotetramers (MacKinnon, 1991) a given point mutation will exist in each of the four subunits of the channel assembly.

Recording solutions

The standard bathing solution contained, in mM, 140 NaCl, 3.5 KCl, 10 Hepes, 2 CaCl₂, 1 MgCl₂, and 5 glucose and its pH was adjusted to 7.4 with NaOH. Hepes was replaced by Mes when the pH of the extracellular solution was <6.8 in the experiments directly comparing the proton block and the Ni²⁺ block. Where the effect of the external concentration of potassium ([K⁺]_o) on the divalent metal cation block was examined, a nominally K⁺-free solution was made by substituting NaCl for KCl and, for [K⁺]_o >3.5 mM, NaCl was replaced by KCl. The standard patch pipette solution for recording K⁺ currents contained 130 KCl, 4.75 CaCl₂ (pCa²⁺ = 7.3), 1.38 MgCl₂, 10 EGTA, and 10 Hepes and was adjusted to pH 7.4 with KOH. Solutions of divalent metal ions were made by dilution of 0.1–1-M stock solutions of the chloride salt in distilled water. At pH 7.4 the concentration of Ni²⁺ that can be used was limited to 10 mM or less by virtue of the solubility product for Ni(OH)₂ (∼2 × 10⁻¹⁶).

Mouse fibroblasts expressing Kv1.5 channels at a low density were used to record unitary currents from outside-out patches. The inside face of the patch was exposed to standard patch pipette solution and the outside face was exposed to standard bath solution either with or without added Ni²⁺.

For gating current recordings the bath solution contained, in mM, 140 NMGCl, 1 MgCl₂, 10 Hepes, 2 CaCl₂, and 10 glucose and the pH was adjusted to 7.4 with HCl. The patch pipette solution contained 140 NMGCl, 1 MgCl₂, 10 Hepes, and 10 EGTA and was adjusted to pH 7.2 with HCl. Chemicals were purchased from Sigma Aldrich Chemical (Mississauga, Ontario, Canada).

Signal recording and data analysis

Macroscopic currents were recorded at room temperature (20–22°C) using the patch-clamp technique primarily in the whole-cell configuration. In some of the cell lines expressing mutant Kv1.5 channels at a high level, i.e., the H463Q and some of the R487V mutants, the large amplitude of the whole-cell currents necessitated recording macroscopic currents from outside-out patches. Voltage clamp experiments were done with an EPC-7 patch-clamp amplifier and Pulse+PulseFit software (HEKA Electronik, Lambrecht, Germany). Patch electrodes were made from thin-walled borosilicate glass (World Precision Instruments, Sarasota, FL) and had a resistance of 1.0–2.5 MΩ measured in the bath with standard internal and external solutions. Typically, 80% series resistance compensation was used and an on-line P/N method, for which the holding potential was −100 mV and the scaling factor was 0.25, was used to subtract the leak current as well as any uncompensated capacitive currents. Current signals filtered at 3 kHz (−3 dB, 8-pole Bessel) were digitized (16 bit) at a sampling interval of 100 μs (10 kHz). Voltages have been corrected for the liquid junction potentials.

In an experiment, a section of glass coverslip with cells attached to it was placed in the recording chamber (0.5 ml vol) and was continuously perfused with bathing solution. After recording currents in the control solution the inflow was switched to the test solution and once 5–6 ml had been flushed through the bath the treated responses were recorded. Recovery currents were taken after flushing the bath with 5–6 ml of control solution. If the recovery currents were not within ±15% of the pretreatment amplitudes the data for that cell were discarded. By this criterion most cells showed recovery.

To quantify the effect of Ni²⁺ and other metal cations on Kv1.5, tail currents were recorded at −40 or −50 mV after depolarizing prepulses of differing magnitude. Peak tail current amplitudes were obtained by fitting a polynomial function and taking the fitted value for the maximum current. After normalization of tail currents either to the maximum current of the control or the treated response, data points were fitted to a single Boltzmann function:

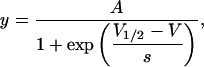(1)

where, when y is the current normalized with respect to the control response, A is the proportion of the control g_max. When y is the current normalized with respect to the maximal treated current, A is the best fit value for the normalized maximal response and ideally has a value of unity. V_1/2 is the half-activation potential or midpoint of the activation curve, V is the voltage during the prepulse, and s is the slope factor, in mV, reflecting the steepness of the voltage dependence of gating.

To quantify gating charge movement during activation, charge-voltage (Q_on-V) curves were generated by time integration of on-gating currents as described previously (Chen et al., 1997). Activation gating in Kv1.5 is best fit by the sum of two Boltzmann functions where the larger component, known as Q₂, represents ∼80% of the total charge movement (Hesketh and Fedida, 1999). However, for simplicity, Q-V data obtained at pH 7.4 and 5.4 were fitted to Eq. 1 where y is the charge moved, A is the maximal charge (Q_max), and V is the voltage at which the on-gating charge (Q_on) is evoked. V_1/2 represents the midpoint of the Q-V curve and s reflects the steepness of the voltage dependence of charge movement.

Concentration-response data were fitted to the Hill equation:

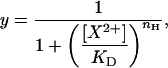(2)

where y is the proportion of the control g_max, K_D is the equilibrium dissociation constant for the test cation (X²⁺), and n_H is the Hill coefficient reflecting the number of test cations binding per channel.

Microscopic currents were low-pass filtered at 3 kHz (8-pole Bessel), sampled at 10 kHz and digitally filtered at 1 kHz for the data analysis using TAC and TACFit (Bruxton, Seattle, WA). Leak and uncompensated capacitive currents were subtracted using a template generated from blank sweeps. Half-amplitude threshold analysis was used to idealize single channel recordings for the generation of dwell-time histograms.

Data are expressed as the mean ± SE except for the values obtained by nonlinear least-squares fitting routines (Igor, Wavemetrics, Lake Oswego, OR) which are expressed as the mean ± SD. The paired-sample t-test was used to compare the inactivation rates of residual currents in Ni²⁺ and H_o⁺. A P-value of 0.05 or less was considered significant.

RESULTS

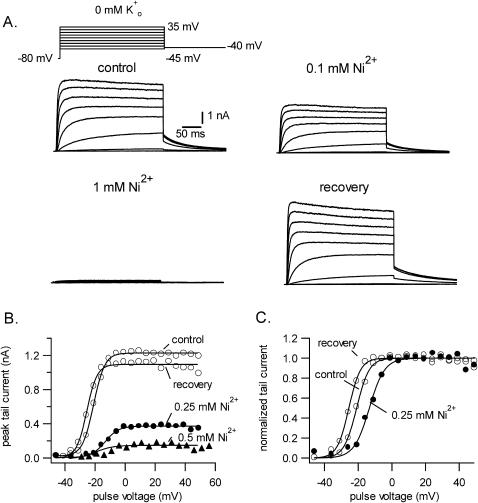
Shown in Fig. 1 A are traces confirming the block of Kv1.5 currents by external Ni²⁺. From a holding potential of −80 mV and with 0 mM K_o⁺, currents were evoked by a family of 300 ms depolarizations from −45 to +35 mV with a cycle length of 5 s. Tail currents were recorded at −40 mV. After obtaining the control responses, the perfusate was switched to a test bathing solution containing 0.1 mM Ni²⁺ and then to one containing 1 mM Ni²⁺. Complete recovery was obtained after returning to Ni²⁺-free solution. As noted previously (Perchenet and Clement-Chomienne, 2001), and in contrast to the effects with Zn²⁺ (Zhang et al., 2001a), with Ni²⁺ there was neither a significant change of the activation kinetics nor an obvious effect on the decay of residual pulse currents. The effect of Ni²⁺ on the current behavior during longer depolarizing pulses is examined below (Fig. 4).

FIGURE 1.

Ni²⁺ block of Kv1.5 currents in 0 mM K_o⁺. (A) Control currents evoked by a family of 300-ms depolarizations from −45 to +35 mV, here shown in 10-mV increments, from a holding potential of −80 mV. Tail currents were recorded at −40 mV. Perfusion of solution containing 0.1 mM Ni²⁺ and then 1 mM Ni²⁺ caused a concentration-dependent inhibition of the current. Recovery traces illustrate the complete reversal of the Ni²⁺ block. (B and C). Ni²⁺ decreases g_max and shifts the g-V curve slightly rightward. (B) Peak tail current at −40 mV after a 300-ms depolarization to the voltage indicated on the x axis. Note the absence of any voltage dependence of the inhibition between 0 and 50 mV. (C) The g-V relationship derived by normalizing tail currents with respect to the maximum tail current shows that Ni²⁺ caused a 10-mV shift of the half-activation voltage. Current tails in 0.5 mM Ni²⁺ were too small to be unequivocally analyzed.

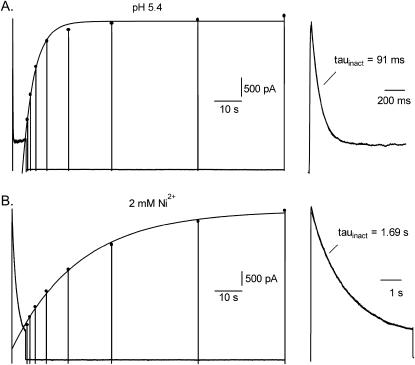
FIGURE 4.

A comparison of the residual current behavior, done in 3.5 mM K_o⁺ with a concentration of H_o⁺ (A) or Ni²⁺ (B) estimated to block 80–95% of the channels, reveals divergent effects on inactivation. From a holding potential of −80 mV, the voltage protocol consisted of a 5-s step to 50 mV followed by 50-ms steps at variable intervals to 50 mV to monitor recovery from inactivation. Current during the 5-s pulse is shown expanded on the right side of the figure. (A) At pH 5.4 the inactivation of current during the 5-s pulse is well fitted by a single exponential with a time constant of 91 ms. Peak currents, marked by the filled circles, that were evoked by the 50-ms test pulses were fitted to a single exponential with a time constant of 4.3 s. (B) In the same cell after switching to solution containing 2 mM Ni²⁺ at pH 7.4, inactivation was ≈20 times slower (τ_inact = 1.69 s) and recovery from inactivation was ≈5 times slower (τ_recovery = 24.8 s) than at pH 5.4.

Increasing [K⁺]_o causes a rightward shift of the concentration dependence of the Ni²⁺ block

To quantify the block by Ni²⁺, g-V curves were constructed from peak tail currents as described in the Methods section. Fig. 1 B plots the peak tail current amplitude versus the pulse voltage for the same cell in 0 mM K_o⁺ without Ni²⁺ and with 0.25 or 0.5 mM Ni²⁺. In this cell 0.25 mM and 0.5 mM Ni²⁺ decreased the maximum tail current, and by extension the maximum conductance (g_max), by ∼70% and 90%, respectively. To more clearly illustrate the effect of Ni²⁺ on the midpoint (V_1/2) of the g-V curve, the currents in panel B were normalized with respect to the maximum current for the same treatment group and are presented in panel C. It is evident that Ni²⁺ caused a rightward shift of the g-V curve and this is assumed to reflect a change of surface charge due to screening and/or binding to the channel. With 0.25 mM Ni²⁺ the shift of V_1/2 determined from the best fit of the g-V data to the Boltzmann function was 10.6 ± 0.9 mV (n = 4). The gating shift with 0.5 mM Ni²⁺ was not determined because the standard deviation in the fitted values for V_1/2 was quite large.

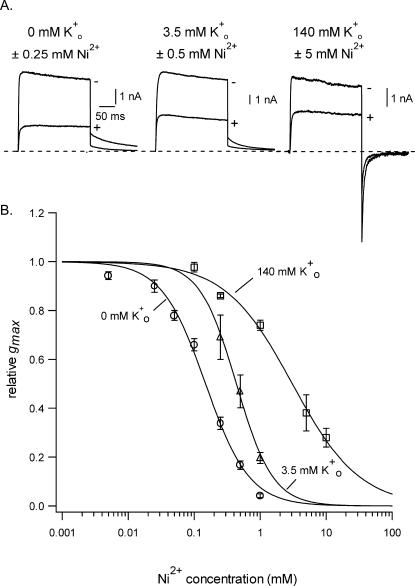
Fig. 2 shows the concentration-response relationship for the block of Kv1.5 by Ni²⁺ and the influence of [K⁺]_o thereon. Panel A illustrates representative current traces from three different cells in 0 mM (left), 3.5 mM (middle), and 140 mM (right) K_o⁺. In the absence of Ni²⁺ (−Ni²⁺) the current in each of the K_o⁺ concentrations had a similarly slow rate of decay. The inward tail current recorded at −40 mV in 140 mM K_o⁺ is due to the shift of E_K to ∼0 mV. To produce a similar degree of block in the three different experiments it was necessary to increase the Ni²⁺ concentration to offset the effect of increasing [K⁺]_o. Note that in each example the Ni²⁺ block was not associated with an acceleration of pulse current decay. The latter observation, together with the fact that the tail current decay was not slowed, as best seen with the traces in 140 mM K_o⁺, supports the conclusion that a block of the open channel occurring with intermediate-to-slow kinetics (vis à vis the activation rate) is not involved. For the graph in Fig. 2 B the g_max relative to the control value has been plotted against the concentration of Ni²⁺ for experiments in which [K⁺]_o was 0 mM (open circles), 3.5 mM (open triangles), or 140 mM (open squares). The solid lines overlaying the three data sets represent the best fit to Eq. 2. With 0 mM K_o⁺ the K_D for the Ni²⁺ block was 0.15 ± 0.01 mM and n_H was 1.3 ± 0.1. Increasing [K⁺]_o to 3.5 mM increased the K_D to 0.44 ± 0.02 mM and n_H was 1.6 ± 0.2. With 140 mM K_o⁺ the K_D was 3.1 ± 0.3 mM and n_H was 0.9 ± 0.1. These results clearly demonstrate that, as with the block by H_o⁺ and Zn²⁺, the block of Kv1.5 by Ni²⁺ is antagonized by increasing [K⁺]_o.

FIGURE 2.

Increasing [K⁺]_o changes the concentration dependence of the block of Kv1.5 by Ni²⁺. (A) Representative traces obtained from three different cells showing, superimposed, the currents evoked in the K_o⁺ concentrations indicated either without (−) or with (+) the Ni²⁺ concentration indicated. The voltage protocol consisted of a 300-ms step from −80 mV to 50 mV followed by a step to −40 mV. Increasing [K⁺]_o necessitates a higher concentration of Ni²⁺ to produce roughly the same degree of block. The time calibration is the same for the three sets of traces. (B) The concentration-response relationship for Ni²⁺ in 0, 3.5, and 140 mM K_o⁺ shows that increasing [K⁺]_o from nominally K⁺-free to 3.5 mM shifted the K_D from 0.15 ± 0.01 mM to 0.44 ± 0.02 mM. Increasing K_o⁺ to 140 mM shifted the K_D for the Ni²⁺ block to 3.1 ± 0.3 mM. Each point represents the mean ± SE of measurements from three to seven cells.

The time courses of the onset and the offset of the Ni²⁺ block are similar

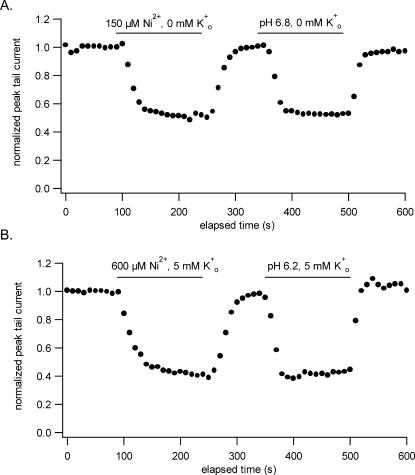
Using a fast solution application system, Perchenet and Clement-Chomienne (2001) noted that the offset of the Ni²⁺ block was rapid but that the onset was comparatively much slower. They found, with test pulses delivered at 15-s intervals and using 1 mM Ni²⁺ and 5 mM K_o⁺, that steady-state block was reached only after 5–7 min. Because a similar phenomenon is not seen with H_o⁺ or Zn²⁺, we felt it was important to characterize the time dependence of the Ni²⁺ block and did so by comparing the time course of the current inhibition by Ni²⁺ with that by H_o⁺. Graphs summarizing the outcome of this comparison are shown in Fig. 3. For each graph, the peak tail current, measured at −40 mV after a 300-ms pulse to 50 mV applied at 10-s intervals, was plotted against the elapsed time. In Fig. 3 A, Ni²⁺ and H_o⁺ were applied for the duration indicated by the horizontal bar at concentrations of 150 μM and 0.16 μM (pH 6.8) (Kehl et al., 2002), respectively, and in 0 mM K_o⁺ to cause roughly 50% block of the current at the steady state. In four such experiments we consistently found that the time courses for the onset and offset of the block by Ni²⁺ and H_o⁺ were similar. Because the failure to uncover any asymmetry in the on- and off-time courses might be attributed to the absence of K_o⁺, experiments were also done with 5 mM K_o⁺ which necessitated using higher concentrations of Ni²⁺ and H_o⁺ to compensate for the effect of K_o⁺ on the block. Fig. 3 B shows that the outcome was still the same: after switching from the control to the test perfusate the relaxation to the steady state was complete in less than a minute, a time frame that appears to reflect primarily the dynamics of solution exchange in the bath and is much shorter than the onset noted by Perchenet and Clement-Chomienne (2001).

FIGURE 3.

A comparison of the time course of the onset and offset of the inhibition of Kv1.5 by Ni²⁺ and H_o⁺. Concentrations of Ni²⁺ or H_o⁺ producing ∼50% steady-state inhibition with 0 mM K_o⁺ (A) and, in a different cell, with 5 mM K_o⁺ (B) were used. Peak tail currents measured at −40 mV after a 300-ms depolarization to 50 mV applied at a 10-s interval are plotted against the elapsed time. The horizontal bar indicates the duration of each application. The results do not reveal any obvious asymmetry in the onset versus the offset of the block either with or without K_o⁺. As with H_o⁺, the time course for the development or reversal of the Ni²⁺ block was similar and in both cases is presumed to reflect the time course of solution exchange in the bath.

Ni²⁺ block is associated with a slight acceleration of inactivation of residual currents

In addition to blocking Kv1.5 currents, extracellular acidification accelerates the rate of inactivation of residual currents (Kehl et al., 2002; Steidl and Yool, 1999) and this was the motivation for determining if there was a similar association between block and inactivation with Ni²⁺. Our approach to addressing this question was to use cells expressing Kv1.5 channels at a very high density so that despite the reduction of g_max by 80–95% the residual currents were virtually unfettered by endogenous HEK currents and could therefore be unambiguously analyzed. The voltage protocol consisted of a 5-s step from −80–50 mV followed by brief depolarizations to 50 mV to track recovery from inactivation (Fedida et al., 1999). An interval of 120 s between the 5-s pulses was used to permit complete recovery from inactivation in the experiments with Ni²⁺. Initially, these experiments were done with 0 mM K_o⁺ but the interpretation of the data was confounded by a very slowly rising phase of current with a time constant of 1–1.5 s in 1 mM Ni²⁺ and 200–300 ms at pH 5.9, which followed a normally activating component of current (not shown). This slow component was not observed with 3.5 mM K_o⁺, consequently this was the [K⁺]_o used when comparing the effects on inactivation of concentrations of H_o⁺ and Ni²⁺ that reduce g_max by 80–95% (Fig. 2 and Kehl et al., 2002). Results representative of those obtained in five experiments with 2 mM Ni²⁺ and five experiments with pH 5.4 are shown in Fig. 4, A and B, where the effects of H_o⁺ and Ni²⁺, respectively, were tested on the same cell. At pH 5.4 the inactivation of the residual current during the 5-s pulse was well fitted by a single exponential with a time constant of 91 ms and the steady-state current was ∼25% of the peak amplitude. At pH 5.4 the mean inactivation time constant (τ_inact) at 50 mV was 101 ± 3 ms (n = 5 cells). In Fig. 4 A recovery from inactivation, tested by 50 ms depolarizations delivered from 0.5 s up to 96 s after the 5-s depolarization, was fitted to a single exponential with a time constant of 4.3 s. The mean τ_recovery at pH 5.4 was 4.2 ± 0.1 s. In contrast, currents recorded after switching from pH 5.4 solution to perfusate containing 2 mM Ni²⁺ at pH 7.4 (Fig. 4 B) showed much slower inactivation as well as slower recovery from inactivation: τ_inact = 1.69 s and τ_recovery = 24.8 s. In the five cells tested with 2 mM Ni²⁺ the mean value for τ_inact and τ_recovery was 1.71 ± 0.07 s and 23.5 ± 2.1 s, respectively. Because of their very large amplitude, currents in Ni²⁺-free medium at pH 7.4 could not be recorded from these cells, however, the best fit to a single exponential of the current decay during 7–10 s depolarizations to 60 mV at pH 7.4 in Kv1.5 is typically of the order of 2–3 s (Kehl et al., 2002) and the τ_recovery measured at −80 mV in 5 mM K_o⁺ and using a similar voltage protocol is 1.1 s (Fedida et al., 1999).

The K_D for the Ni²⁺ block is increased in the H463Q and R487V mutants

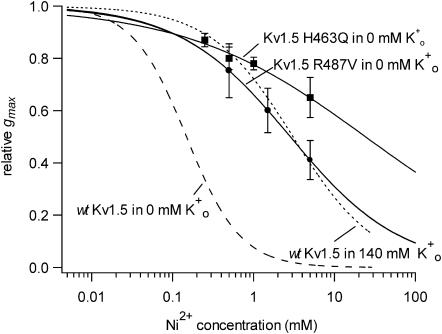
We next examined the effect of Ni²⁺ in Kv1.5 channels in which either a putative Ni²⁺ binding site in the S5-P linker (turret) was mutated to a glutamine residue (H463Q) or the residue analogous to Shaker T449 was changed from arginine to valine (R487V). To circumvent the potential problem of changes of the K_o⁺-dependence of the block relief, the analysis of the effect of Ni²⁺ on currents from these mutated channels was done with 0 mM K_o⁺. Concentration-response curves for the Ni²⁺ block of currents from Kv1.5 H463Q (filled squares) and Kv1.5 R487V (filled circles) are shown superimposed in Fig. 5. As with the block by H_o⁺ and Zn²⁺ (Kehl et al., 2002), the concentration dependence for the block by Ni²⁺ was shifted substantially to the right by either mutation. In Kv1.5 R487V the K_D was estimated to be 2.8 ± 0.004 mM or roughly 20-fold higher than in wt Kv1.5. With Kv1.5 H463Q the concentration dependence of the block was much more shallow (n_H ∼ 0.4) than in wt Kv1.5 and the K_D was estimated by extrapolation to be 24 ± 8 mM, which is from 100- to 200-fold higher than in wt Kv1.5.

FIGURE 5.

Ni²⁺ sensitivity is reduced in Kv1.5 H463Q and Kv1.5 R487V. Experiments with the mutant channels were done with 0 mM K_o⁺ to preclude a change of the K_o⁺ binding as the basis for the change of the sensitivity to Ni²⁺. Because Ni²⁺ is known to bind to histidine (H) residues, a mutant was constructed in which glutamine (Q) was substituted for H463, a residue in the S5-P linker that forms part of the outer pore vestibule. Kv1.5 H463Q (▪) was from 100- to 200-fold less sensitive to Ni²⁺ (K_D = 24 ± 8 mM; n_H = 0.4 ± 0.04) compared to the wt Kv1.5 responses (dashed line taken from Fig. 2) measured in the same recording condition, i.e., 0 mM K_o⁺. In another mutant construct, the arginine (R) residue near the entrance to the pore mouth that has been implicated, by alignment with Shaker T449, in the outer pore inactivation mechanism, was mutated to valine. The sensitivity of Kv1.5 R487V currents (•) to Ni²⁺ was ∼20-fold less (K_D = 2.8 ± 0.004 mM; n_H = 0.7 ± 0.001) than that measured under the same recording conditions in wt Kv1.5. The dotted line, which was taken from Fig. 2, represents the line fitted to the block of wt Kv1.5 in 140 mM K_o⁺.

Ni²⁺ decreases channel availability

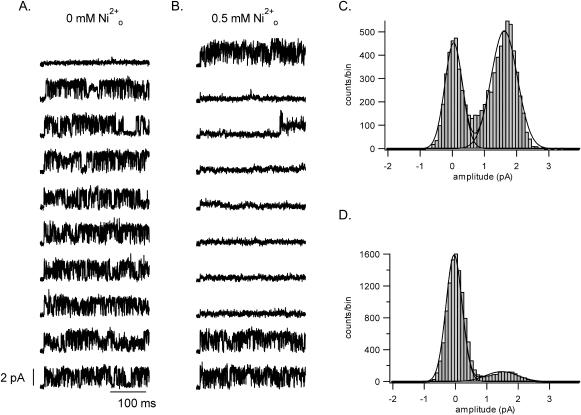
Macroscopic current amplitude (I) is, in general, the product of the number of channels available (N), the single channel current (i), and the channel open probability (P_o)(I = NP_oi). To gain a clearer insight into which of these variables was affected by Ni²⁺ ions, recordings were made from outside-out patches containing a single channel. Fig. 6 A shows representative, consecutive control sweeps evoked by a 300-ms depolarization from −80 mV to 100 mV applied at a frequency of 0.1 Hz. As reported previously (Chen and Fedida, 1998), channel openings occurred in bursts of varying duration and within bursts channel closings were frequent but brief. With seconds-long pulses (not shown) we observed closed states with longer mean dwell times, which are assumed to reflect a multistep inactivation pathway. Double-Gaussian fits to the control all-points amplitude histogram (e.g., Fig. 6 C) indicates an open channel current (i) of 1.7 ± 0.1 pA (n = 8 patches). After switching to medium with 0.5 mM Ni²⁺, which is the K_D for the block in 3.5 mM K_o⁺ (Fig. 2), there was no significant change of the single-channel current (e.g., Fig. 6 D; 1.6 ± 0.1 pA, n = 6 patches), and the P_o in sweeps containing channel activity was also not significantly affected (P_o,-Ni = 0.64 ± 0.06 versus P_o,+Ni = 0.61 ± 0.06). There were, however, many more blank sweeps in the presence of the Ni²⁺ (Fig. 6 B). Channel availability (N), defined as the number of sweeps with channel activity divided by the total number of sweeps, decreased significantly from the control value of 0.90 ± 0.06 (n = 6 patches) to 0.43 ± 0.14 (n = 6 patches) in Ni²⁺.

FIGURE 6.

Ni²⁺ effects at the single channel level. (A) Shown here are 10 representative and consecutive control sweeps in a one-channel, outside-out patch that were evoked by a 300-ms pulse from −80 mV to 100 mV applied at 0.1 Hz and with [K⁺]_i = 140 mM and [K⁺]_o = 3.5 mM. Data were digitally filtered at 1 kHz. (B) From the same patch as in A, 10 consecutive sweeps evoked with the same voltage protocol but with 0.5 mM Ni²⁺ in the external perfusate. The main effect of Ni²⁺ is to reduce channel availability. Representative all-point amplitude histograms from a different one-channel patch in control and 0.5 mM Ni²⁺-containing perfusate are shown in panels C and D, respectively. A double-Gaussian fit to data gave a mean current in each case of 1.6 pA.

Ni²⁺ causes a rightward shift of the Q_on-V curve but does not affect Q_max

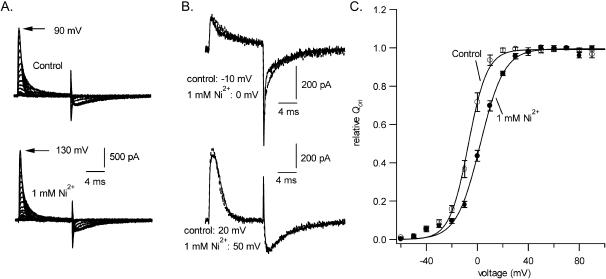
A possible explanation for the current block by Ni²⁺ is that one or more transitions in the gating pathway is prevented. To address that possibility, gating currents were recorded in an HEK293 cell line expressing Kv1.5 W472F channels. The W472F mutation produces channels that are not K⁺ conductive, but that have normal gating currents. Fig. 7 A shows gating current traces in control solution and in 1 mM Ni²⁺. On-gating currents were evoked by 12-ms pulses between −60 and 130 mV from a holding potential of −100 mV. In the control traces, charge movement was first evident at ∼−50 mV and the peak amplitude and decay rate increased as the intensity of the depolarization increased. After depolarizations up to −10 mV the off-gating current at −100 mV was rapid (e.g., Fig. 7 B, upper traces) but after stronger depolarizations there was a clear rising phase to the off-gating current and the peak current was substantially smaller and occurred much later (e.g., Fig. 7 B, lower traces) than was the case following steps to −10 mV or less. This pronounced change of off-gating current after stronger depolarizations has been attributed at least in part to a weakly voltage-dependent transition in the return pathway between the open and closed states (Perozo et al., 1993). To construct the charge-voltage (Q-V) curves shown in Fig. 7 C, on-gating currents were integrated and Q_on was normalized with respect to the control maximal charge movement (Q_max). Although charge movement is better fitted by a double-Boltzmann function to account for a smaller component of charge movement with depolarizations up to −20 mV (Hesketh and Fedida, 1999), the data of Fig. 7 C were fitted to a single Boltzmann function.

FIGURE 7.

To determine if the conductance loss caused by Ni²⁺ was due to an inhibition of transitions in the activation pathway, the effect of 1 mM Ni²⁺ on gating charge movement in Kv1.5 W472F, a nonconducting mutant, was examined. Internal and external permeant ions were replaced by NMG⁺ to prevent ionic currents through endogenous HEK293 channels. The family of traces in the top of panel A shows control on-gating currents evoked between −60 and 90 mV from a holding potential of −100 mV and off-gating currents at −100 mV; the lower traces of panel A show the gating currents in 1 mM Ni²⁺. Control and treated traces, taken at the voltages indicated to account for the gating shift, have been superimposed in B to show that the kinetics of the on- and off-gating currents are not substantially affected by Ni²⁺. (C) The Q_on-V curve constructed from six cells by integrating the on-gating currents and normalizing with respect to the control Q_max confirms that, although Ni²⁺ caused an ∼10-mV rightward shift of the V_1/2, the Q_max did not decrease. Fitting to a Boltzmann function gave control and treated V_1/2 values of −6.8 ± 1.2 mV and 2.2 ± 0.8 mV, respectively, and values of 7.0 ± 1.4 mV and 9.2 ± 1.2 mV for s.

In six experiments of the type illustrated in Fig. 7, the control V_1/2 and s were −6.8 ± 1.2 mV and 7.0 ± 1.4 mV. After switching to 1 mM Ni²⁺ V_1/2was 2.2 ± 0.8 mV and s was 9.2 ± 1.2 mV. The difference in V_1/2 between 1 mM Ni²⁺ and control medium was 9.0 ± 3.0 mV. Aside from this gating shift, the gating current was essentially unaffected by 1 mM Ni²⁺. In contrast to the situation with 1 mM Zn²⁺ where Q_max decreased by ∼15% (Zhang et al., 2001b), Q_max was unchanged by 1 mM Ni²⁺.

Co²⁺ and Cd ²⁺, but not Mn²⁺, block Kv1.5

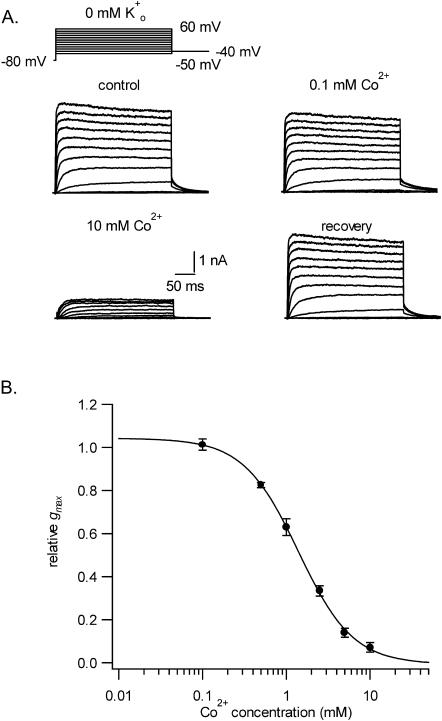
Other divalent transition metals that can bind to histidine include Cu²⁺, Fe²⁺, Co²⁺, Cd²⁺, and Mn²⁺. Because a precipitate formed with Cu²⁺ and Fe²⁺, only the effects of Co²⁺, Cd²⁺, and Mn²⁺ could be compared to those of Ni²⁺. The experimental protocol was the same as that described for Fig. 1 and was confined to tests with a 0-mM K_o⁺ solution. Fig. 8 A shows a representative example of the effect of Co²⁺ on currents evoked by the voltage protocol illustrated above the control responses. Switching from the control solution to one containing 0.1 mM Co²⁺ had no significant effect on the current but 10 mM Co²⁺ decreased the peak tail current after a +60-mV pulse by >90%. Virtually complete recovery occurred after returning to the control solution. Fitting of g-V curves (not shown) to Eq. 1 revealed that V_1/2 shifted by 11.4 ± 0.9 mV with 1 mM Co²⁺ and by 25.3 ± 1.3 mV with 10 mM Co²⁺. Neither concentration of Co²⁺ significantly affected the slope factor of the g-V curve (not shown). A fit of the Hill equation to the concentration-response data for Co²⁺ (Fig. 8 B) gave an estimate for n_H of 1.3 ± 0.1 and a K_D (1.4 ± 0.1 mM) that was roughly 10 times larger than that for Ni²⁺ under the same recording conditions.

FIGURE 8.

also causes a concentration-dependent block of Kv1.5 currents but is an order of magnitude less potent than Ni²⁺. Shown in panel A are control and treated current traces evoked in 0 mM K_o⁺ with the voltage protocol indicated above the control responses. In contrast to the ∼35% block of the current with 0.1 mM Ni²⁺ (see Fig. 2), 0.1 mM Co²⁺ had no effect. However, with 10 mM Co²⁺ the maximum peak tail current amplitude decreased by ∼90%. As with Ni²⁺, the block by Co²⁺ was completely reversible. (B) Concentration-response data obtained in 0 mM K_o⁺, with each point representing the mean ± SE of measurements in three to eight cells, were fitted to Eq. 2, which gave a K_D of 1.4 ± 0.1 mM and an n_H of 1.3 ± 0.1.

The effects of Cd²⁺ are not illustrated but closely resembled those of Co²⁺. The K_D was 1.5 ± 0.4 mM and the n_H was 1.3 ± 0.3. In 1 mM Cd²⁺ the V_1/2 for the g-V relationship was shifted rightward by 19.5 ± 1.2 mV.

Of the divalent cations we tested for an ability to block Kv1.5, Mn²⁺ proved to be the least effective. At 10 mM, the highest concentration used, g_max was 73 ± 3% of the control value. The midpoint of the g-V relationship was shifted rightward by 21.5 ± 0.7 mV (n = 3).

Co²⁺ and Zn²⁺ mimic the effect of Ni²⁺ on Kv1.5 inactivation

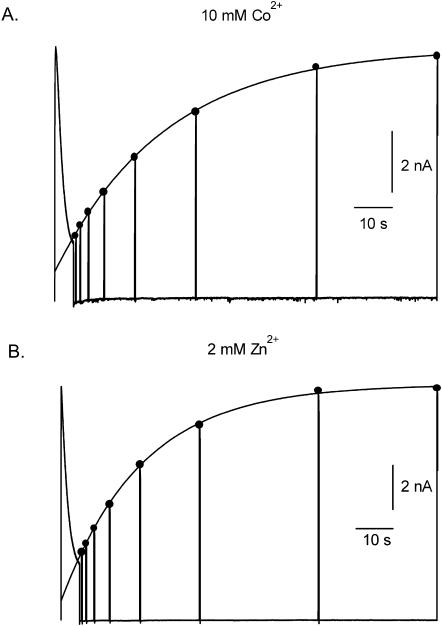
Fig. 9 A illustrates representative results of the effect of 10 mM Co²⁺ on inactivation and recovery from inactivation using a voltage protocol identical to that described for Fig. 4. Again, a slowly rising phase of current seen in 10 mM Co²⁺, K_o⁺-free medium (not shown) necessitated recording with 3.5 mM K_o⁺. In 10 mM Co²⁺ both the onset of and recovery from inactivation was comparable to that seen with 2 mM Ni²⁺ (Fig. 4). In the four cells studied with 10 mM Co²⁺, τ_inact and τ_recovery were 1.3 ± 0.1 s and 24.6 ± 1.7 s, respectively. As noted above, Zn²⁺ also causes a concentration and K_o⁺-dependent inhibition of Kv1.5 currents and for that reason its effects on inactivation were also examined (Fig. 9 B). Using a Zn²⁺ concentration of 2 mM, which is estimated to reduce g_max by 80–90% in 3.5 K_o⁺, τ_inact was 1.64 ± 0.3 s and τ_recovery was 27.7 ± 2.1 s (n = 5 cells). Thus, a feature that is shared by Ni²⁺, Co²⁺, and Zn²⁺ is an ability to substantially slow recovery from inactivation and to modestly accelerate inactivation. In this regard at least these divalent cations are clearly distinct from extracellular protons that, by comparison, accelerate inactivation to a far greater extent (τ_inact ≈ 100 ms at pH 5.4) and slow recovery from inactivation much less (τ_recovery ≈ 4 s at pH 5.4).

FIGURE 9.

Co²⁺ and Zn²⁺ mimic the effect of Ni²⁺ on macroscopic inactivation. (A) Using a voltage protocol identical to that described for Fig. 4, the τ_inact with 10 m M Co²⁺ in 3.5 mM K_o⁺ was well fitted by a single exponential with a time constant of 1.6 s. The fit of an exponential function to the peak currents evoked by 50-ms test pulses after the 5-s pulse to 50 mV gave a τ_recovery of 21.8 s. (B) With 2 mM Zn²⁺ in 3.5 mM K_o⁺, τ_inact was 1.86 s and τ_recovery was 29.3 s. Because Zn²⁺ slowed the activation rate the duration of test pulses used to monitor recovery was increased to 200 ms. These data indicate a clear difference in the effect on Kv1.5 inactivation of divalent cations versus external protons (Fig. 4 A).

DISCUSSION

As reported previously (Perchenet and Clement-Chomienne, 2001), external Ni²⁺ ions were shown to reversibly block human Kv1.5 currents (Fig. 1). We have also shown here that Ni²⁺ block is affected by [K⁺]_o (Fig. 2). Thus, with 0 mM K_o⁺ the K_D for the Ni²⁺ block is ∼150 μM whereas with 3.5 mM K_o⁺ the K_D increases to 400 μM. The latter value is consistent with the K_D of 570 μM obtained with 5 mM K_o⁺ in CHO cells (Perchenet and Clement-Chomienne, 2001). Increasing K_o⁺ to 140 mM increased the K_D to ∼3 mM. The n_H of 1.2–1.6 derived from concentration-response data in 0–5 mM K_o⁺ (see also Perchenet and Clement-Chomienne, 2001)) suggests that the block requires the binding of at least two Ni²⁺ ions. In the study with Kv1.5 expressed in CHO cells the Ni²⁺ block was shown, regardless of the pulse frequency, to develop slowly over a 2–5 min period (Perchenet and Clement-Chomienne, 2001) despite the use of a fast drug application system. These data were interpreted to reflect a large disparity in the association and dissociation rate constants for Ni²⁺ binding to the closed state of the channel. Although we agree that the Ni²⁺ block can occur from the closed state, we found no evidence for a slow development of that block (Fig. 3).

One possible interpretation of the inhibition of the Ni²⁺ block by K_o⁺ is that it reflects an interaction in the channel pore either by competition for the same binding site or by an electrostatic effect between separate Ni²⁺ and K⁺ binding sites. However, as noted with the block by Zn²⁺ and H_o⁺ (Kehl et al., 2002), the block by Ni²⁺ shows no voltage dependence over a range of voltages where the open probability is maximal (Perchenet and Clement-Chomienne, 2001). This observation supports the conclusion that the Ni²⁺ binding site is at least not in a region of the pore that is within the electric field and, by extension, that Ni²⁺ is not blocking by occlusion of the pore. The fact that Kv1.5 currents are blocked by H_o⁺, Zn²⁺, and Cd²⁺, whereas Shaker channels are not, also suggests a binding site external to the pore (e.g., in the turret) because in Kv1.5 and Shaker there is complete homology from the N-terminal end of the pore helix to the GYG pore signature sequence.

As is the case with the block of Kv1.5 by H_o⁺ and Zn²⁺, the sensitivity of Kv1.5 channels to Ni²⁺ is greatly affected (Fig. 5) either by mutating H463 in the pore turret or by mutating R487, a residue in the outer pore mouth that has been shown in Shaker channels to play a pivotal role in P/C-type inactivation. These results with the 463Q and 487V mutant channels, as well as the sensitivity of the Ni²⁺ block to K_o⁺ and the outcome of other substitutions at position 463 (see below), are consistent with a model in which the binding of Ni²⁺ to one or more H463 residues in the pore turret facilitates an inactivation process that involves the outer pore mouth. Although this model is the same as that proposed for the H_o⁺ and Zn²⁺ block of Kv1.5, there is not complete overlap of the effects of these three metal cations. For example, the inactivation rate of the residual currents is markedly different with the divalent cations (Ni²⁺, Co²⁺, Zn²⁺) compared to H_o⁺ (Figs. 4 and 9). Thus, for example, using concentrations that produce a similar degree of block in 3.5 mM K_o⁺, the residual currents inactivated roughly 20 times faster with H_o⁺ (pH 5.4) than with Ni²⁺ (Fig. 4). Additionally, the shift of the midpoint of the g-V curve and the Q_on-V curve by Ni²⁺ was also much less than with either H_o⁺ or Zn²⁺. Finally, the dramatic slowing of the activation rate observed with Zn²⁺ (Zhang et al., 2001a) is not seen with either Ni²⁺ or H_o⁺. It seems unlikely, though we cannot disprove, that these differences are due solely to the nature of ligand coordination by the histidine residues in the turret. Particularly in the case of H_o⁺, the involvement of additional binding sites seems likely. This is suggested by the fact that although ShakerIR channels are largely resistant to the conductance collapse in low pH, acidification does accelerate current inactivation (Perez-Cornejo, 1999; Starkus et al., 2003). Furthermore, we and others have shown that manipulations that reduce the block of Kv1.5 by metal cations do not affect the gating shift (Kehl et al., 2002; Trapani and Korn, 2003).

From the data in Fig. 5 it is also apparent that neither of the outer pore mutations completely prevents current inhibition by Ni²⁺. Currents through the Kv1.5 H463Q construct decreased by ∼30% in 5 mM Ni²⁺ and, as with the Zn²⁺ block of this mutant channel (Kehl et al., 2002), the n_H fitted to the concentration dependence of this block was quite small (∼0.5) suggesting the involvement of a binding site and mechanism of action that is different. In the case of the R487V mutant, the K_D and the n_H for the Ni²⁺ block with 0 mM K_o⁺ are similar to that estimated for wt Kv1.5 in 140 mM K_o⁺. Paradoxically, neither of these manipulations, increasing [K⁺]_o or mutating R487, substantially affects the inactivation rate of macroscopic currents carried by K⁺ during sustained depolarizations (Fedida et al., 1999). Although the latter observations might be construed as evidence against an involvement of outer pore inactivation in the Ni²⁺ block, that is to say neither manipulation can be shown directly to affect the current decay rate, an alternative explanation is that these manipulations inhibit an outer pore inactivation process occurring from a closed state but are much less effective against inactivation from the open state. In this connection, a K_o⁺-sensitive (K_D ∼ 0.8–10 mM) inactivation process occurring from a closed state has been suggested to account for the decline of the macroscopic conductance seen in fast-inactivating ShakerIR T449 mutants when the [K⁺]_o is decreased (Lopez-Barneo et al., 1993) and there is evidence in ShakerIR supporting, not exclusively, “multiple, independent pathways of which C-type is only one” (Yang et al., 1997).

As with some of the T449 mutations in Shaker, there are mutations of Kv1.5 H463 that can dramatically affect outer pore inactivation. For example, mutants in which glycine (G) (Kehl et al., 2002) or arginine (R) (Eduljee et al., 2003) is substituted for H463 display rapidly inactivating currents (τ_inact = 35–75 ms) and, again as in the Shaker T449X mutants, these rapidly inactivating mutants show a collapse of the macroscopic conductance in 0 mM K_o⁺. Furthermore, in the H463G mutant the conductance collapse in 0 mM K_o⁺ is prevented by the R487V mutation (Trapani and Korn, 2003). The outcome of these H463G and H463R mutations is significant because it shows directly that the physicochemical properties of the residue at this position can dramatically affect the time course of open- (and closed-?) state inactivation and thus offers additional support for the proposition that noncovalent chemical modification of H463 by the binding of Ni²⁺, in addition to other metal cations, can affect inactivation.

Another significant property of the H463G mutant is that K_o⁺ affects the g_max with a K_D of ∼1 mM (Eduljee et al., 2003). This low millimolar K_D is comparable not only to that estimated for the fast-inactivating ShakerIR mutants (Lopez-Barneo et al., 1993) but to that obtained for the relief by K_o⁺ of the H_o⁺ and Zn²⁺ block (Kehl et al., 2002; Zhang et al., 2001a). A detailed study of the K_o⁺-dependence of the Ni²⁺ block was not undertaken here. However, using the K_D of the Ni²⁺ block in zero and 3.5 mM K_o⁺, and assuming, for simplicity, a competitive interaction, the K_D for the relief of the block by K_o⁺ is calculated to be ∼1.5 mM. A consistent pattern that emerges from these studies, whether it is the spontaneously occurring conductance collapse in ShakerIR and Kv1.5 mutant channels or the metal ion-induced block/conductance collapse in wt Kv1.5, is that inhibition of the conductance loss occurs with low millimolar K_o⁺ concentrations and that this inhibition occurs in the absence of a change of the inactivation rate measured during depolarizing pulses. This implies that there is an outer pore inactivation process, perhaps that occurring from the closed state, that is much more sensitive to K_o⁺ and, we suggest, given that its inactivation rate is not distinguishable from wt Kv1.5 channels, that in Kv1.5 the R487V mutation selectively affects this same inactivation process. With the fast-inactivating ShakerIR mutants, Lopez-Barneo et al. (1993) remarked that the tendency for the conductance to collapse (inactivate from the closed state?) in 0 mM K_o⁺ is associated with fast current inactivation. This correlation also applies to Kv1.5 H463G where the inactivation rate is some 20-fold faster than in wt Kv1.5 channels but it is much less evident with the Ni²⁺, Co²⁺, and Zn²⁺ block where the inactivation rate of residual currents is only approximately twofold faster than in controls (Figs. 4 and 9).

Particularly in view of the low concentrations of K_o⁺ needed to relieve the metal cation block, a question that inevitably arises is whether the external K⁺ binding site can also be populated by outward K⁺ flux through the open channel. Though it has not been studied for Ni²⁺ block, our recent finding (Zhang et al., 2003) of virtually identical K_Ds for the block by H_o⁺ of outward K⁺ or Na⁺ currents argues against a contribution of outward K⁺ currents in the block relief. One explanation for this apparent absence of an effect of K⁺ efflux through the open pore is that K⁺ ions at the outer pore mouth rapidly equilibrate with the external solution. Alternatively, if Ni²⁺-bound channels are inactivating from a closed state, or if the open time is very brief (Zhang et al., 2003), there would be no opportunity for block relief by outward K⁺ currents.

A comparison of currents from one channel outside-out patches (Fig. 6) before and after the application of 0.5 mM Ni²⁺ showed: 1), that open channel current (i) at 100 mV did not change; 2), that the open probability (P_o) during 300-ms sweeps containing channel activity was not changed; and 3), channel availability (N) decreased from a value of ≈0.9 in the control to ≈0.4 during treatment. Although a detailed analysis and comparison of open- and closed-time behaviors have not yet been done, these preliminary data are consistent with a model in which Ni²⁺ binding facilitates a reversible transition from an available to an unavailable (closed-state inactivated?) state.

Gating current analyses (Fig. 7) showed that, as with H_o⁺ (Kehl et al., 2002), Ni²⁺ did not affect Q_max. This finding rules out the possibility that the prevention of one or more of the transitions in the activation pathway accounts for the Ni²⁺-induced decrease of g_max. Ni²⁺ treatment also caused an ∼10 mV shift of the Q_on-V curve but this was much less than the 50–60 mV shift seen with H_o⁺ or Zn²⁺ (Kehl et al., 2002; Zhang et al., 2001b). As noted above, it is not clear if this disparity in the gating shift reflects differences in ligand coordination with H463 residues or if the larger shift with H_o⁺ and Zn²⁺ reflects interactions with additional binding sites.

Transition metal ions that have now been shown to block Kv1.5 currents are Zn²⁺, Cd²⁺, Ni²⁺, and Co²⁺ (Fig. 8). For the first-row transition metals the rank order for the inhibition of Kv1.5 in 0 mM K_o⁺ is Zn²⁺ (K_D ∼ 0.07 mM) ≥ Ni²⁺ (K_D ∼ 0.15 mM) > Co²⁺ (K_D ∼ 1.4 mM) > Mn²⁺ (K_D > 10 mM) and, as such, is in accord with the Irving-Williams order (Glusker, 1991). Zn²⁺, Ni²⁺, and Co²⁺, which are intermediate Lewis acids, are known to bind to the thiolate side group of cysteine and the imidazole nitrogen of the histidine. Zn²⁺ is also able to bind to carboxylate and carbonyl oxygen atoms. Cd²⁺, a second-row transition metal, is a soft Lewis acid and typically has a higher affinity for a soft base such as the thiolate ion. Preliminary work with the H463C mutant shows a sensitivity to block by Cd²⁺ that is greater than for wt Kv1.5.

In Ca_v2.3 (α1E) channels, external Ni²⁺ causes, in addition to a rightward shift of the g-V curve, a reduction of the slope conductance with an estimated K_I of 300 μM (Zamponi et al., 1996). The blocking reaction appears to be bimolecular and is also affected by the type of permeant ion (e.g., Ca²⁺ versus Ba²⁺). It was suggested that the Ni²⁺ block of Ca_V2.3 reflected changes of permeation due to direct occlusion of the pore in addition to a possible change of the permeant ion concentration at the pore mouth. In voltage-gated K⁺ channels, divalent cations have proved to be useful probes of gating and permeation. However, whereas Zn²⁺ and Cd²⁺ have been studied in some detail (e.g., Gilly and Armstrong, 1982; Spires and Begenisich, 1994), Ni²⁺ has been used somewhat sparingly. In HERG K⁺ channels, external Ni²⁺, as well as Cd²⁺, Co²⁺, and Mn²⁺, increased the maximum current amplitude, an effect that was imputed to an alteration of inactivation gating (Paquette et al., 1998). Interestingly, in HERG channels mutations at a number of sites in the S5-P linker can dramatically alter inactivation (Liu et al., 2002), a finding that underscores the findings with Kv1.5 that, either by substitution through point mutation, or by chemical modification through ligand binding, residues in this region can profoundly influence the rate and extent of one or more inactivation processes occurring at the outer pore mouth.