Abstract
We report the combined use of steady-state fluorescence resonance energy transfer (FRET) experiments and molecular dynamics (MD) simulations to investigate conformational distributions of the prion protein (PrP) repeat system. FRET was used for the first time to probe the distance, as a function of temperature and pH, between a donor Trp residue and an acceptor dansyl group attached to the N-terminus in seven model peptides containing one to three repeats of the second decarepeat of PrP from marsupial possum (PHPGGSNWGQ)nG, and one and two human PrP consensus octarepeats (PHGGGWGQ)nG. In multirepeat peptides, single-Trp mutants were made by replacing other Trp(s) with Phe. As previous work has shown PrP repeats do not adopt a single preferred stable conformation, the FRET values are averages reflecting heterogeneity in the donor-acceptor distances. The T-dependence of the conformational distributions, and derived average dansyl-Trp distances, were obtained directly from MD simulation of the marsupial dansyl-PHPGGSNWGQG peptide. The results show excellent agreement between the FRET and MD T-dependent distances, and demonstrate the remarkable sensitivity and reproducibility of the FRET method in this first-time use for a set of disordered peptides. Based on the results, we propose a model involving cation-π or π-π His-Trp interactions to explain the T- (5–85°C) and pH- (6.0, 7.2) dependencies on distance, with HW i, i + 4 or WH i, i + 4 separations in sequence being more stable than HW i, i + 6 or WH i, i + 6 separations. The model has peptides adopting loosely folded conformations, with dansyl-Trp distances very much less than estimates for fully extended conformations, for example, ∼16 vs. 33, ∼21 vs. 69, and ∼22 vs. 106 Å for 1–3 decarepeats, and ∼14 vs. 25 and ∼19 vs. 54 Å for 1–2 octarepeats, respectively. The study demonstrates the usefulness of combining FRET with MD, a combination reported only once previously. Initial “mapping” of the conformational distribution of flexible peptides by simulation can assist in designing and interpreting experiments using steady-state intensity methods, and indicating how time-resolved or anisotropy methods might be used.
INTRODUCTION
Low-complexity sequence in proteins is now recognized to be a significant proportion of coding sequence (∼10%) but its structure and functions have been little studied (Wootton, 1994; Wright and Dyson, 1999). Generally, such regions are conformationally disordered; they may form ordered structure only when associated with ligands or in a different environment (e.g., membrane). Methods to study such structures and interactions are not well established, and in only a few ideal cases where the disordered peptide is a small part of the protein have the ordered or folded states in liganded complexes been structurally resolved by high-resolution (x-ray, NMR) methods. For x-ray crystallographic studies, crystallization is a particular problem, whereas application of NMR methods to repetitive sequence is impeded by lack of unique nuclear Overhauser enhancements (NOE), which makes assignments ambiguous.
Consequently, a number of lower resolution experimental methods have been used to study “structure” in these peptides. These operate at several levels to probe the presence of both local H-bonded structure, such as β-strands and α-helices, as well as longer-range conformational structure. Methods such as vibrational or electronic spectroscopy (FTIR, Raman, circular dichroism) can be used to probe local structure, and, in some cases, NMR can also be used to probe local and longer-range structure. Fluorescence resonance energy transfer (FRET) is another method for probing longer-range structure (Wu and Brand, 1994). Interaction with ligands can also be detected and characterized structurally by these methods, as well as others such as fluorescence titration spectrophotometry, equilibium dialysis (ED), and electron paramagnetic resonance (EPR).
In general, it is necessary to apply several different such techniques to build up models of conformational and other properties of disordered peptides. From the mid-1990s, this approach has been applied to the tandem-repeat region of prion protein (PrP) using fluorescence titration, mass spectrometry, circular dichroism (CD), FTIR, Raman, NMR, x-ray crystallography, EPR, and ED, to study structure of peptide both free and when bound to copper ions (Hornshaw et al., 1995; Miura et al., 1996, 1999; Brown et al., 1997; Smith et al., 1997; Stockel et al., 1998; Viles et al., 1999; Aronoff-Spencer et al., 2000; Bonomo et al., 2000; Whittal et al., 2000; Yoshida et al., 2000; Jackson et al., 2001; Kramer et al., 2001; Gustiananda et al., 2002; Burns et al., 2002, 2003; Luczkowski et al., 2002; Garnett and Viles, 2003). This active literature encompassing many laboratories is likely the most comprehensive current set of studies on a disordered peptide system. However, inconsistencies in the reported results among both methods and authors indicate that integration of this suite of methods to define the properties of a disordered peptide system is not straightforward.
Understanding the biochemical and biophysical properties of PrP is important because of its association with the fatal neurodegenerative disorders such as Creutzfeldt-Jakob disease in humans and bovine spongiform encephalopathy in animals (Prusiner, 1998). PrP is an unusual protein, for which an alternative conformer (PrPSc) accumulates as amyloid plaques in diseased brains. As shown by NMR structures (Zahn et al., 2000), mammalian protein divides into two main parts, a C-terminal folded domain of ∼100 residues, which undergoes a conformational change in the generation of PrPSc, and an N-terminal flexibly disordered region of also ∼100 residues, which includes five octapeptide repeats in the middle. The normal function of PrP is still debatable, but several findings suggest a role in copper metabolism (Brown et al., 1997; Pauly and Harris, 1998; Brown, 1999) associated with binding to the N-terminal region, primarily to the octapeptide repeats (Qin et al., 2002; Burns et al., 2003). Another possible function is indicated by recent findings of binding of glycosaminoglycans, especially heparan sulfate (Warner et al., 2002), to the basic regions enclosing the repeat region, which is facilitated by copper-bound repeats (Gonzalez-Iglesias et al., 2002). Although the region including the repeats is not essential for mediating pathogenesis, it modulates the extent of these events and of disease presentation (Flechsig et al., 2000).
The results of NMR structural analysis showing the complete N-terminal region of PrP to be flexibly disordered (Zahn et al., 2000), have been confirmed by application of a range of low-resolution techniques, including CD (Hornshaw et al., 1995; Viles et al., 1999; Bonomo et al., 2000; Whittal et al., 2000), FTIR (Gustiananda et al., 2002), and Raman (Miura et al., 1996, 1999) spectroscopies, which show lack of formal H-bonded structure and suggest random coil. However, another CD study reports the presence of nonrandom structure similar to the poly-l-proline type II left-handed helix (Smith et al., 1997), whereas a recent NMR study suggests certain residues within the repeats adopt loop and β-turn structure (Yoshida et al., 2000). It is clear, however, that the repeats do not adopt a single fixed conformation. These low-resolution methods show development of more folded structure on binding of copper ions, although the binding properties (mode, strength, stoichiometry) appear very dependent on peptide details (model or authentic sequence, number of repeat units, extent of inclusion of proximal and distal N-terminal regions or whole protein). Consequently, several models of the structure of copper complexes of the repeat region have been reported (Stockel et al., 1998; Miura et al., 1999; Viles et al., 1999; Aronoff-Spencer et al., 2000; Bonomo et al., 2000; Jackson et al., 2001; Burns et al., 2002; Luczkowski et al., 2002).
FRET is another method in the low-resolution structural repertoire, which is both sensitive and versatile, and is increasingly used as it offers a different “window” for illuminating aspects of protein structure, namely through-space residue distance. The proximity of two points of interest in the protein molecule can be measured by labeling them with different chromophores; the donor is excited initially and transfers energy to the acceptor. The donor must have fluorescent properties, whereas the acceptor does not necessarily fluoresce. If energy transfer from the donor to the acceptor occurs, the fluorescence of the donor (both intensity and lifetime) decreases, whereas the fluorescence of the acceptor, if it fluoresces, increases. The distance between donor and acceptor can be obtained by employing the Förster equation, which relates the efficiency of transfer with distance (for reviews, see Stryer, 1978; Wu and Brand, 1994; dos Remedios and Moens, 1995; Selvin, 1995). In this work we have used FRET to probe the average distance in model PrP-repeat peptides, between donor tryptophan (Trp) and the N-terminal residue to which an acceptor dansyl group has been added. FRET has not previously been applied to the PrP-repeat system.
As already mentioned, existing evidence suggests PrP-repeat peptides do not adopt a single preferred stable conformation, and, thus, heterogeneity in the donor-acceptor distance is expected. This heterogeneity cannot be detected from steady-state intensity measurements using a standard fluorimeter, as employed in this work. Although, in principle, such information on the distribution of distances between chromophores can be obtained from fluorescence decay (time resolved) or fluorescence anisotropy decay experiments (Wu and Brand, 1994), to our knowledge, these methods have been applied only to protein systems with a small number of alternative conformations, or to small highly flexible peptides that adopt a more restricted range of conformations under certain conditions, such as in TFE or in the presence of ligands: galanin in TFE (Kulinski et al., 1997), RNase s-peptide in TFE (Maliwal et al., 1993), melittin in complex with calmodulin, troponin and phospholipids (Lakowicz et al., 1994), and bradykinin in TFE (de Souza et al., 2000). Consequently, we have performed an MD simulation on one PrP-repeat peptide, to obtain conformational distributions and an independent estimate of the distance between Trp and the dansyl group. We use the MD results to assist in the interpretation of the experimental FRET data. There is only one other report in the literature for combined use of FRET and simulation, for study of a 10-residue MAP-kinase substrate, in nonphosphorylated and phosphorylated states, at the N-terminus of tyrosine hydroxylase (Stultz et al., 2002). For the MD simulation, we have used the replica exchange (REMD) method (Sugita and Okamoto, 1999), which improves sampling and has the additional advantage of directly providing results at different temperatures for comparison with experiment.
In summary, in this work we explore use of FRET in determining the average conformational extension of disordered PrP-repeat peptides of different length and sequence, as probed by the Trp-dansyl distance and as a function of pH and temperature, and compare the results with those from MD simulations. The MD simulations are further analyzed to characterize the conformational distributions. Peptide systems used are the second decarepeat of a PrP from marsupial possum (Dans-PHPGGSNWGQG), and the human PrP consensus octarepeat (Dans-PHGGGWGQG). For multirepeat peptides, mutants were made containing a single Trp residue by replacing other Trp(s) with Phe.
MATERIALS AND METHODS
Peptide synthesis and labeling
Peptides were synthesized chemically using the 9-fluorenylmethyloxycarbonyl (FMOC) method on Applied Biosystems 430A (Foster City, CA) and Rainen Symphony/Multiplex peptide synthesizers, supplied by the Biomolecular Resource Facility at the John Curtin School of Medical Research, Australian National University. As required, the N- or C-terminus, or both, were protected by acetylation or amidation, respectively. For dansylated peptides, the dansyl group was attached to the imino (Pro) end of the peptide while the peptide was still attached to the resin, using two methods: reaction of deprotected resin with dansyl chloride (Sigma-Aldrich, St. Louis, MO) (Stryer and Haughland, 1967), or direct addition of FMOC-dansyl-Pro (Fluka, Buchs, Switzerland), instead of FMOC-Pro, to the amino group of His in the peptide synthesis. In the first method, ∼0.5 g of deprotected resin was removed from the reaction vessel and reacted for 1 h with 250 mg dansyl chloride (large excess) in methylene chloride containing triethylamine (1:1 equivalent of peptide), and then washed thoroughly with methylene chloride. In both methods, the dansylated peptide was released from the resin by stirring for 1.5 h with TFA containing 0.25% water and 0.25% triisopropylsilane (Sigma-Aldrich). After filtering off the resin, the crude peptide was precipitated with ether and purified by high-performance liquid chromatography (solvents water and acetonitrile, both containing 1% TFA; 5–40% gradient of acetonitrile over 30 min).
Stock solutions (1 ml) of peptides of concentration ∼3 mM were prepared in distilled water. The concentrations were determined on a sample diluted 50-fold into sodium phosphate buffer (25 mM Na2HPO4, 75 mM NaCl, pH 8.0) by measuring the optical absorption on a Cary 1 Bio ultraviolet-visible spectrophotometer using a 1-cm path length cuvette. The concentrations of the nondansylated peptides were calculated based on the Trp absorption maximum at 280 nm (A280) and extinction coefficient (ɛ280) of 5500 M−1cm−1 (Pace and Schmid, 1997). The concentrations of the dansylated peptides and the degree of labeling were determined based on the dansyl absorption maximum at 331 nm (A331) and extinction coefficient (ɛ331) of 4000 M−1cm−1, and a correction factor for absorption by dansyl at 280 nm of 0.386 (Haughland, 2001). Hence, the peptide and dansyl concentrations are:
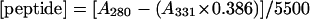 |
(1) |
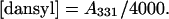 |
(2) |
The degree of labeling (DOL) was calculated using the formula
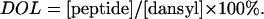 |
(3) |
The degree of labeling for all dansylated peptides was 100%.
Peptide samples for each set of experiments were diluted into degassed buffers to give concentrations of 4 or 5 μM, and the concentrations were rechecked spectrophotometrically as above. Aliquots were stored in sealed Eppendorf tubes at 4°C. For the experiments, the sealed tubes were equilibrated in a water bath at the desired temperature, then quickly added to the sample cell and the fluorescence spectra taken immediately. Universal buffer (multicomponent buffer, 25 mM citric acid, 25 mM KH2PO4, 25 mM sodium tetraborate, 25 mM Tris, 25 mM KCl) (Perrin and Dempsey, 1974) adjusted to desired pH values (pH 3.0, 5.0, 6.5, 7.2, and 9.5) was used.
Fluorescence measurements
We employed a steady-state method, in which the fluorescence emission intensity of peptide in a 5-mm path length quartz cuvette with maximum volume of 0.5 mL was measured using a Perkin Elmer LS 50B spectrofluorimeter (Wellesley, MA). Measurements were made to monitor the intrinsic fluorescence of the Trp residue in the nondansylated peptide, and in the dansylated peptide undergoing FRET from Trp to dansyl. Duplicate measurements were taken unless otherwise indicated.
As Trp residues are capable of undergoing homotransfer, i.e., an energy transfer process between Trp groups, this process is prevented by exciting Trp at 295 nm rather than at 280 nm (Weber and Shinitzky, 1970). However, in these experiments, there is only one Trp residue per peptide and initial experiments indicated the FRET distance does not differ between measurements with excitation at 280 and 295 nm. As the fluorescence emission intensity is significantly higher, and, hence, provides greater sensitivity, for excitation at 280 nm rather than at 295 nm, we used 280-nm excitation, with band slit width 5 nm. Emission spectra were obtained between 300 and 550 nm, and emission intensity at 350 nm (Trp emission maximum) and 535 nm (dansyl emission maximum) was recorded. The temperature was set constant at 25°C by means of a circulating water bath, except where the effect of temperature was investigated when it was varied (5, 15, 40, 55, 70, 85°C).
Calculation of donor-acceptor apparent distance
Experimental data were analyzed using the Förster equation (Förster, 1948), which relates energy transfer efficiency (E) with distance (R) between donor and acceptor pairs:
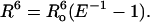 |
(4) |
Where Ro, the Förster distance (in Å) at which the transfer efficiency is 50% and specific for a particular donor-acceptor pair, is defined as:
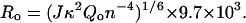 |
(5) |
The value of Ro depends on J, the spectral overlap integral, κ2, the orientation factor for a dipole-dipole interaction, n, the refractive index of the medium between the donor and acceptor, and Qo, the quantum yield of fluorescence of the energy donor in the absence of acceptor.
The value of κ2 cannot be directly measured and is the major uncertainty in the calculation of distance. Its value depends on the relative orientations of the donor and acceptor dipoles; it is 0 if all angles are perpendicular and 4 if both transition moments are in line with the separation vector. Provided that both donor and acceptor can undergo unrestricted isotropic motion and rotate freely, κ2 assumes a numerical value of 2/3. dos Remedios and Moens (1995) argue that the assumption of a value of 2/3 for κ2 appears to be valid for small peptides and small proteins. The Trp and dansyl groups should have considerable motional freedom as they are attached to the rest of the peptide molecule via covalent single bonds. Assuming κ2 = 2/3 for the Trp and dansyl pair, Ro is 21 Å (Dunn et al., 1981); this value was used in the calculation of distances.
As the presence of an energy acceptor in the vicinity of an excited energy donor provides an additional mode for the deexcitation process, from donor quenching, E is calculated from the equation:
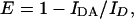 |
(6) |
where IDA is the fluorescence intensity of the donor in the presence of acceptor and ID is the fluorescence intensity of the donor only.
Molecular dynamics simulations
MD simulations were performed to provide an independent estimate of distance between the Trp and dansyl groups for comparison with the experimental results. The test system was dansylated Msp-1. The initial peptide structure was generated with the aid of the model building options in the InsightII program (Accelrys, San Diego, CA). This structure was energy minimized before adding solvent molecules, and the system consisting of solvent and peptide was then MD equilibrated for 80 ps.
The replica-exchange molecular dynamics (REMD) simulation technique (Sugita and Okamoto, 1999) was used to sample effectively the conformational space of the peptide in solution. The REMD simulations were performed using 24 parallel trajectories (replicas) on a Compaq AlphaServer using the standard message-passing interface (MPI) protocol. The temperatures at which the 24 trajectories were run were distributed exponentially from a minimum value of 280 K to a maximum value of 620 K. After the initial MD equilibration phase of 80 ps, the 24 replicas were run for a total of 3 ns of REMD. Exchanges between replicas with neighboring temperatures were attempted every 0.2 ps according to the usual Metropolis criteria. The REMD simulations yield the canonical ensemble at each of the 24 temperatures between 280 and 620 K. Coordinates for analysis were collected every 0.1 ps (720,000 “snapshot” peptide structures in total).
The 80-ps equilibration and the REMD simulations were carried out using a time step of 0.002 ps with the application of SHAKE (Ryckaert et al., 1977) for constraining covalent bond lengths and with the hydrogen masses set to 3 amu. The AMBER force-field parameters (Cornell et al., 1996) were used for the peptide. Atomic charges for the dansyl fragment were obtained from the PM3 electrostatic potential (Cummins and Gready, 1994). The peptide was solvated in a spherical shell (20-Å radius) of 978 TIP3P (Jorgensen et al., 1983) water molecules. The bulk solvent effects were simulated by applying tethering potentials to all 978 water molecules and half-harmonic restraining potentials to the water molecules at the spherical boundary region (Cummins and Gready, 1996). The nonbonded interaction lists were updated every 25 time steps (0.05 ps), with 20 and 10 Å residue-based cutoffs for the calculation of the electrostatic and van der Waals interactions, respectively. The initial energy minimization and equilibration, and the REMD simulations, were performed using the computer program Molecular Orbital Programs for Simulations (MOPS) (Cummins, 1996).
Analysis of MD simulation data
For ease of comparison with experiment, the 24 simulation temperatures translate to the range 7–34°C: (7, 16, 27, 37, 48, 59, 71, 83, 96, 109, 122, 136, 150, 165, 181, 197, 213, 230, 248, 266, 285, 305, 325, 347). The distance for each snapshot coordinate set was calculated between the midpoints of the bridging bonds of the naphthalene (dansyl) and the indole (tryptophan) rings. The length of the fully extended chain of the peptides was estimated in the following way. The length of the peptide backbone between successive residues is 3.63 Å (Creighton, 1983). In Msp, for example, with seven peptide bonds separating the N-terminal and the Trp-8 residue, the total backbone length is 25.41 Å when the peptide is fully extended. After addition of the lengths of the dansyl group and the Trp side chain, the total distance between the centers of the dansyl group attached to the N-terminus and the indole group of Trp-8 in the fully extended peptide chain is ∼32.6 Å (see Table 4 for full list). For Msp, this value in fact corresponds to the largest distance between the midpoints of the bridging bonds of the naphthalene and the indole rings obtained for a single snapshot and high temperature (see Fig. 9).
TABLE 4.
Measured FRET distances, and their differences, in Å, for all peptide pairs at pH 6.0 and pH 7.2 at temperatures 25°C and 85°C, together with estimated distances for fully extended forms (in bold)
| Peptide | FRET distance | Δ Distance from Msp1capNC | Δ Distance from Msp2F18capNC | Δ Distance from Msp2F8capNC | |
|---|---|---|---|---|---|
| Msp1capNC Extended form: 32.6 Å | |||||
| pH 6.0 | 25°C | 15.45 ± 0.29 | – | – | – |
| 85°C | 17.24 ± 0.17 | – | – | – | |
| pH 7.2 | 25°C | 15.64 ± 0.08 | – | – | – |
| 85°C | 18.42 ± 0.14 | – | – | – | |
| Msp2F18capNC Extended form: 32.6 Å | 0.0 Å | ||||
| pH 6.0 | 25°C | na | na | – | – |
| 85°C | na | na | – | – | |
| pH 7.2 | 25°C | 16.12* | 0.48 | – | – |
| 85°C | 17.66 ± 0.13 | −0.76 | – | – | |
| Msp2F8capNC Extended form: 68.9 Å | 36.3 Å | 36.3 Å | |||
| pH 6.0 | 25°C | na | na | na | – |
| 85°C | na | na | na | – | |
| pH 7.2 | 25°C | 21.61 ± 0.32 | 5.97 | 5.49 | – |
| 85°C | 23.30 ± 0.19 | 4.88 | 5.64 | – | |
| Msp3F8,F18capNC Extended form: 105.2 Å | 72.6 Å | 72.6 Å | 36.3 Å | ||
| pH 6.0 | 25°C | 22.91 ± 0.11 | 7.46 | na | na |
| 85°C | 24.54 ± 0.83 | 7.30 | na | na | |
| pH 7.2 | 25°C | 22.34 ± 0.14 | 6.70 | 6.22 | 0.73 |
| 85°C | 24.71 ± 0.41 | 6.29 | 7.05 | 1.41 | |
| Δ Distance from Hu1capNC | Δ Distance from Hu2F14capNC | ||||
| Hu1capNC Extended form: 25.3 Å | |||||
| pH 6.0 | 25°C | 14.52 ± 0.05 | – | – | – |
| 85°C | 15.91 ± 0.11 | – | – | – | |
| pH 7.2 | 25°C | 14.36 ± 0.11 | – | – | – |
| 85°C | 16.26 ± 0.27 | – | – | – | |
| Hu2F14capNC Extended form: 25.3 Å | 0.0 Å | ||||
| pH 6.0 | 25°C | na | na | – | – |
| 85°C | na | na | – | – | |
| pH 7.2 | 25°C | 14.89 ± 0.22 | 0.53 | – | – |
| 85°C | 16.42 ± 0.08 | 0.16 | – | – | |
| Hu2F6capNC Extended form: 54.4 Å | 29.1 Å | 29.1 Å | |||
| pH 6.0 | 25°C | na | na | na | – |
| 85°C | na | na | na | – | |
| pH 7.2 | 25°C | 18.64 ± 0.17 | 4.28 | 3.75 | – |
| 85°C | 20.42 ± 0.19 | 4.16 | 4.00 | – | |
Inconsistent duplicate value (see Fig. 4) not used.
FIGURE 9.
Distributions of dansyl-Trp distances for DansMsp1capC at various temperatures calculated from the REMD data over simulation time 2–3 ns (10,000 coordinate sets per temperature). Bars are drawn for 0.2-Å intervals. Distance, x axis; number of occurrences of distance, y axis.
Direct calculation of κ2 from the MD data
The MD data provide a means for direct calculation of κ2 (Eq. 5). For each snapshot, κ2 was calculated according to:
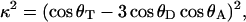 |
(7) |
where θT is the angle between the donor emission (Trp excited state) and acceptor absorption (dansyl ground state) transition moments and θD and θA are the angles between the donor-acceptor connection line (the vector representing the displacement between the midpoint of the bridging bond of the naphthalene ring from that of the indole ring) and the donor emission and acceptor absorption transition moments, respectively (van der Meer, 2002). The transition moments of the Trp excited state and the dansyl ground state were calculated by Dr. Jeff Reimers, University of Sydney, using time-dependent density functional theory (TDDFT) (Bauernschmitt and Ahlrichs, 1996) with the Gaussian 98 package (Frisch et al., 1998); B3LYP/6-31+G* (ground state) and CIS/6-31+G* (excited (π,π*) state) (Foresman et al., 1992) optimized geometries were used. Full details of these calculations and the MD analysis are reported separately (J. R. Liggins, P. L. Cummins, J. R. Reimers, Z. Cai, and J. E. Gready, unpublished).
RESULTS
Spectral overlap between Trp and dansyl
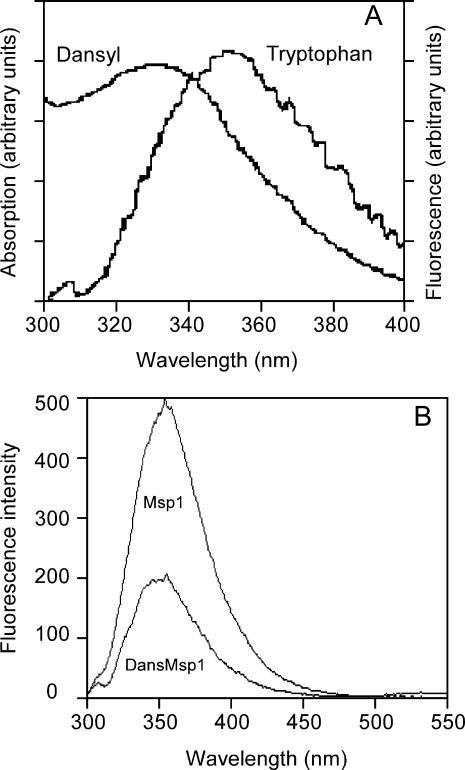
As shown in Fig. 1 A, the emission spectrum of Trp appreciably overlaps the absorption spectrum of dansyl bound to a representative Msp peptide. Such effective overlap is necessary for efficient FRET, as illustrated in Fig. 1 B for dansylated and nondansylated forms of an Msp peptide. The λmax value for Trp emission of 355 nm indicates Trp is highly exposed to solvent as 355 nm is the emission maximum for aqueous Trp amino acid (Schmid, 1997). The significant decrease in Trp emission intensity for the dansylated peptide indicates substantial energy transfer. The similarity of the λmax values and general spectral shape for the dansylated and nondansylated forms suggests that introduction of the dansyl group does not change the environment around Trp, i.e., it is still highly exposed to solvent. This result also provides some confidence that attachment of the dansyl group to the N-terminus of Msp peptides does not perturb their structure greatly.
FIGURE 1.
Sample spectra for the FRET experiments. (A) Spectral overlap between the Trp emission spectrum λmax 355 nm (λex 280 nm) and the absorption spectrum of dansyl with λmax 331 nm, in the DansMsp1capC peptide. (B) Typical data from FRET experiments showing Trp emission (λex 280 nm) for 5 μM Msp1 reference spectrum and 5 μM DansMsp1 spectrum. The small long wavelength band at 500–550 nm with maximum at 535 nm is emission from dansyl that also arises from the resonance energy transfer.
CD spectra of dansylated peptide
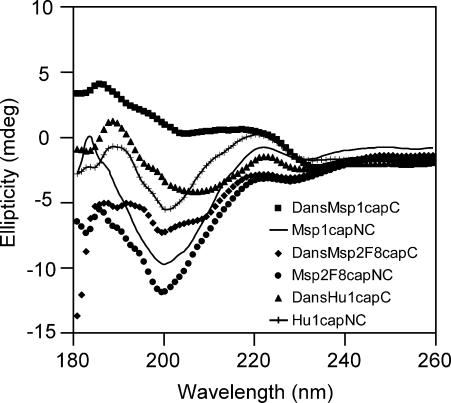
A further check for possible perturbation was made by running CD spectra of dansylated and nondansylated forms of two Msp peptides and one Hu peptide, as shown in Fig. 2. The spectra of the nondansylated peptides (Msp1capNC, Msp2F8capNC, and Hu1capNC) show characteristics of disordered structure, with a strong negative band around 200 nm, and a small maximum around 220 nm accompanied by a very weak negative band near 230 nm (Johnson, 1990; Woody, 1995). Although spectral changes are apparent for the dansylated forms, the spectra do not resemble those of any category of secondary structure other than random coil/disordered polypeptide. This evaluation, however, needs to keep in mind that aromatic rings, including in some cases the aromatic side chains of peptides, can contribute to the CD spectrum in the far-ultraviolet region (Woody and Durker, 1996). Stella et al. (2002) have reported the tendency of the naphthalene ring in the dansyl group to affect the CD spectrum of peptides in the region of 190–250 nm.
FIGURE 2.
CD spectra of dansylated (200 μM for DansMsp1capC and DansHu1capC, 100 μM DansMsp2F8capC) and nondansylated peptides (200 μM for Msp1capNC and Hu1capNC, 100 μM Msp2F8capNC) in water at pH 5 and 25°C, cell path length 1 mm.
Peptide sets for FRET experiments
Based on the above indications from CD and the Trp emission spectra that there is little structural perturbation upon dansyl attachment, we used a number of pairs of dansylated and nondansylated peptides to measure FRET distances between Trp and the N-terminal residue of several marsupial and human PrP repeat peptides (see Table 1). This pair of probes has previously been used to measure the distance between Trp and the N-terminal residue of small disordered peptides (19 residues) (Lakowicz et al., 1994).
TABLE 1.
Peptide pairs used for measuring FRET distances
| Distance between | Peptide with donor Trp (W) only | Peptide with donor Trp (W) and acceptor (Dansyl) | Size |
|---|---|---|---|
| W8 and dansyl in Msp1 | Msp1 | DansMsp1 | 11 |
| NH-PHPGGSNWGQG-COOH | Dansyl-PHPGGSNWGQG-COOH | ||
| W8 and dansyl in Msp1capN | Msp1CapN | DansMsp1 | 11 |
| AcN-PHPGGSNWGQG-COOH | Dansyl-PHPGGSNWGQG-COOH | ||
| W8 and dansyl in Msp1capNC | Msp1CapNC | DansMsp1CapC | 11 |
| AcN-PHPGGSNWGQG-CONH2 | Dansyl-PHPGGSNWGQG-CONH2 | ||
| W8 and dansyl in Msp2F18capNC | Msp2F18CapNC | DansMsp2F18CapC | 21 |
| AcN-PHPGGSNWGQPHPGGSNFGQG-CONH2 | Dansyl-PHPGGSNWGQPHPGGSNFGQG-CONH2 | ||
| W18 and dansyl in Msp2F8capNC | Msp2F8CapNC | DansMsp2F8CapNC | 21 |
| AcN-PHPGGSNFGQPHPGGSNWGQG-CONH2 | Dansyl-PHPGGSNFGQPHPGGSNWGQG-CONH2 | ||
| W28 and dansyl in Msp3F8,F18capNC | Msp3F8,F18capNC | DansMsp3F8,F18capC | 31 |
| AcN-(PHPGGSNFGQ)2PHPGGSNWGQG-CONH2 | Dansyl-(PHPGGSNFGQ)2PHPGGSNWGQG-CONH2 | ||
| W6 and dansyl in Hu1capNC | Hu1CapNC | DansHu1CapC | 9 |
| AcN-PHGGGWGQG-CONH2 | Dansyl-PHGGGWGQG- CONH2 | ||
| W6 and dansyl in Hu2F14capNC | Hu2F14capNC | DansHu2F14capC | 17 |
| AcN-PHGGGWGQPHGGGFGQG-CONH2 | Dansyl-PHGGGWGQPHGGGFGQG-CONH2 | ||
| W14 and dansyl in Hu2F6capNC | Hu2F6capNC | DansHu2F6capC | 17 |
| AcN-PHGGGFGQPHGGGWGQG-CONH2 | Dansyl-PHGGGFGQPHGGGWGQG-CONH2 |
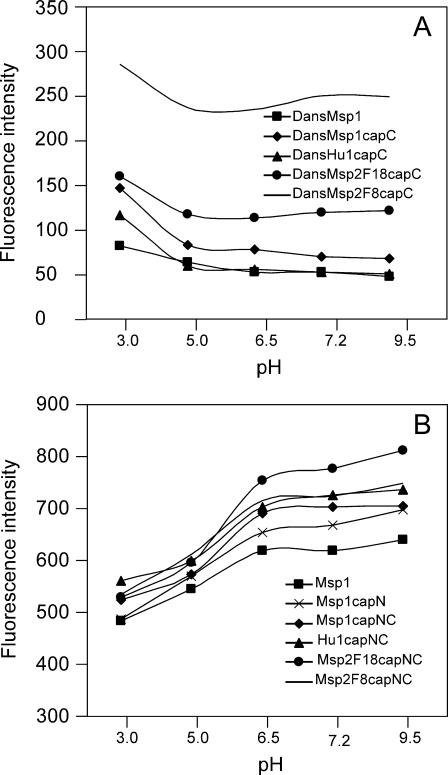
pH Dependence of Trp emission intensity of dansylated and nondansylated peptides
As shown in Fig. 3, the fluorescence intensity (λex 280 nm, λem 335 nm) of dansylated and nondansylated peptides was pH dependent within the 3–9.5 range, indicating effects from protonation and deprotonation of some groups. The intensity of dansylated peptide is highest at pH 3, but falls to roughly constant from pH 5 (Fig. 3 A). The pattern for nondansylated peptide is the reverse; it is lowest at pH 3 and rises until it is roughly constant from pH 6.5 (Fig. 3 B).
FIGURE 3.
Effect of pH on the fluorescence emission intensity of dansylated and nondansylated peptides. Peptide concentrations were 5 μM in universal buffer. Solutions were excited at 280 nm with slit width 5 nm; emission intensity was monitored at 355 nm; temperature 25°C. (A) Dansylated peptides. (B) Nondansylated peptides.
Trp fluorescence arises from the indole ring of its side chain, and the decrease in intensity at lower pH has been ascribed to a loss of aromaticity in the indole cationic form (Pesce et al., 1971), which has a pKa ∼ 6.5; this ionization explains the pH dependence of nondansylated peptides in Fig. 3 B. The different pH dependence of the dansylated peptides in Fig. 3 A is due to compounding emission at 335 nm from protonated dansyl, which has a pKa ∼ 4 for the dimethylamino substituent (Lagunoff and Ottolenghi, 1966). Thus, although the neutral dansyl group emits at 535 nm when excited at 285 nm, its protonated form has strong emission at both 535 and 330 nm (Lagunoff and Ottolenghi, 1966). Due to this complication at low pH, the FRET measurements were restricted to the pH range 6.0–9.5.
pH dependence of FRET distances
The pH dependence of the FRET distances at pHs 6.5, 7.2, and 9.5 at 25°C was measured for the peptide sets 1–5 and 7 in Table 1. This includes the Msp-1 set of uncapped, N-terminally capped, and N- and C-terminally capped forms, Msp2F18capNC and Msp2F8capNC, and Hu1capNC. Results for the calculated FRET distances between Trp-8 and dansyl for the Msp-1 set are shown in Table 2. These were obtained from duplicate measurements of the Trp emission intensities for both dansylated and relevant nondansylated forms at 335 nm (λex 280 nm), calculating the energy transfer efficiencies using Eq. 6, and, hence, calculating the distance using Eq. 4, assuming Ro is 21 Å (Dunn et al., 1981) (see Methods).
TABLE 2.
FRET distance (R) measured at 25°C between W8 and dansyl in Msp1, Msp1CapN, and Msp1CapNC, and their protonation states based on pKa values for α-carboxyl (3.5–4.3), α-amino (6.8–7.9), and imidazole side chain of His (6.2) (Creighton, 1983)
| Msp1
|
Msp1capN
|
Msp1capNC
|
||||
|---|---|---|---|---|---|---|
| pH | Protonation state | R (Å) | Protonation state | R (Å) | Protonation state | R (Å) |
| 6.5 | 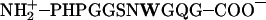 |
15.15 ± 0.26 | AcN–PHPGGSNWGQG–COO– | 14.67 ± 0.29 | AcN–PHPGGSNWGQG–CONH2 | 14.90 ± 0.24 |
| 7.2 | NH–PHPGGSNWGQG–COO– | 15.47 ± 0.36 | AcN–PHPGGSNWGQG–COO– | 15.01 ± 0.40 | AcN–PHPGGSNWGQG–CONH2 | 14.91 ± 0.19 |
| 9.5 | NH–PHPGGSNWGQG–COO– | 14.83 ± 0.13 | AcN–PHPGGSNWGQG–COO– | 14.35 ± 0.09 | AcN–PHPGGSNWGQG–CONH2 | 14.52 ± 0.07 |
Noting that the basic peptide model has the N-terminus capped in the reference peptide, as a control for dansyl, then the Msp results are the atypical set. Within the error limits, the results for the Msp-1 set in which the reference peptide has free Pro at the N-terminus show slightly longer FRET distances; this effect may be due not only to ionization but to a hydrophobic effect from capN acetylation. There appears to be little effect from having the C-terminus either free or amidated. Although there is some evidence for the distances for the Msp-1 set in Table 2 and the short Hu1capNC peptide in Table 3 to be lower at pH 9.5 than at pH 6.5 or 7.2, this effect diminishes for the longer peptides in Table 3, and for Msp2F18capNC and Msp2F8capNC. Distances at pHs 6.5 and 7.2 are very similar for the N- and C-capped peptides. In general, these results show little effect from pH variation.
TABLE 3.
FRET distances (in Å) measured at 25°C between the dansyl group and W8 in Msp1CapNC and Msp2F18CapNC, W18 in Msp2F8CapNC, and W6 in Hu1CapNC
| pH | Hu1CapNC | Msp1CapNC | Msp2F18CapNC | Msp2F8CapNC |
|---|---|---|---|---|
| 6.5 | 14.22 ± 0.07 | 14.90 ± 0.24 | 16.26 ± 0.25 | 19.44 ± 0.24 |
| 7.2 | 14.19 ± 0.37 | 14.91 ± 0.19 | 16.04 ± 0.01 | 19.45 ± 0.02 |
| 9.5 | 13.54 ± 0.09 | 14.52 ± 0.07 | 15.84 ± 0.10 | 19.33 ± 0.14 |
The results in Table 3 begin to show the variability in the FRET distances as a function of distance in sequence space between the donor and acceptor, as well as a modulating effect from total peptide length. Thus, at pH 7.2, the distance for the shortest peptide Hu1capNC where the FRET measurement is between Trp-6 and dansyl is 14.2 Å, which is ∼0.7 Å shorter than that for Msp1capNC of 14.9 Å where the measurement is between Trp-8 and dansyl. Although the sequence distance for the Msp2F18capNC peptide, i.e., Trp-8 to dansyl is the same as in the Msp1capNC peptide, the results show a FRET distance of ∼16 Å that is ∼1.1 Å longer than in Msp1capNC. For the Msp2F8capNC peptide where FRET measures the distance between Trp-18 and dansyl, i.e., ten residues more in sequence length than for Msp2F18capNC, the FRET distance of 19.5 Å is longer by only ∼3.5 Å.
In general, the experimental FRET distances between Trp and dansyl are much lower than their theoretical distances in a fully extended peptide chain (Table 4). Thus, the distances for Msp1capNC (15.5–18.4 Å, depending on T and pH) and Hu1capNC (14.4–16.3 Å) peptides, compared with the fully extended distances (32.6 and 25.3 Å, respectively) indicate the peptides are somewhat compacted. This effect is greatly amplified for the longer peptides. Thus, for example for Msp3F8,F18capNC with estimated extended distance 105.2 Å, the FRET distances range from 22.3 to 24.7 Å; these are only 6.3–7.5 and 0.7–1.4 Å longer than those for Msp1capNC and Msp2F8capNC with extended distances 32.6 and 68.9 Å, respectively. Similarly for Hu2F6capNC with extended distance 54.4 Å, the FRET distances range from 18.6 to 20.4 Å; these are only 4.2–4.3 and 3.8–4.0 Å longer than those for Hu1capNC and Hu2F14capNC with the same extended distance of 25.3 Å. A model for the loose folding is presented in Discussion.
Temperature dependence of FRET distances at pH 7.2
Experiments were carried out to investigate the effect of temperature on the structure of the peptides. Preliminary experiments for the Msp1capNC and Msp3F8,18capNC systems at 25, 40, 55, and 70°C at pHs 6.5, 7.2, and 9.5 were done to check for pH dependence of the FRET distances at other temperatures. As these showed little pH dependence (results not shown), the initial T-dependence studies were restricted to pH 7.2.
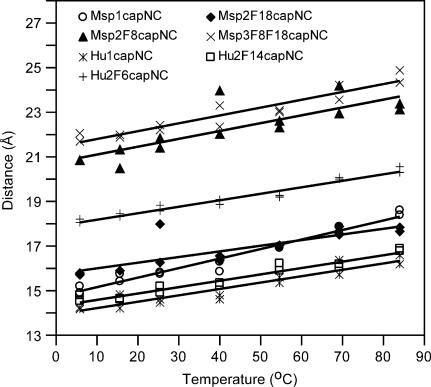
The results of duplicate experiments at temperatures 5, 15, 25, 40, 55, 70, and 85°C for the four marsupial and three human N- and C-capped peptides in Table 1 are shown in Fig. 4. The tendency for the FRET distance in peptides with the same distance in sequence space between Trp and dansyl to be longer when they are attached to longer peptides is also observed in these results. Thus, FRET distances of Trp6-dansyl in Hu1capNC < Trp6-dansyl in Hu2F14capNC < Trp8-dansyl in Msp1capNC < Trp8-dansyl in Msp2F18capNC < Trp14-dansyl in Hu2F6capNC < Trp18-dansyl in Msp2F8capNC < Trp28-dansyl in Msp3F8,F18capNC. However, interestingly, at 60°C, the FRET distance between Trp8-dansyl in Msp1capNC starts to exceed that between Trp8-dansyl in Msp2F18capNC.
FIGURE 4.
Temperature dependence of FRET distances at pH 7.2. Calculated distances from duplicate measurements are plotted for temperatures 5, 15, 25, 40, 55, 70, and 85°C, for four Msp and three Hu peptide pairs. Lines of best fit are drawn. The slopes of the lines in Å/°C are: Msp1capNC 0.043 ± 0.002; Msp2F18capNC 0.025 ± 0.005; Msp2F8capNC 0.036 ± 0.007; Msp3F8,F18capNC 0.035 ± 0.003; Hu1capNC 0.029 ± 0.003; Hu2F14capNC 0.029 ± 0.002; and Hu2F6capNC 0.029 ± 0.002.
Fig. 4 also shows that the FRET distances increase regularly with increasing temperature, indicating that the macroscopic average of the peptide conformation becomes more extended. However, at the highest temperature studied (85°C), the structures are still much less than fully extended. This suggests that intramolecular interactions continue to hold the structure of the peptides together, so that it still does not collapse at the high temperature.
Fig. 4 shows small but interesting trends in the rate of increase of distance with temperature; the slopes are given in the caption. As the slope reflects the stability of the loosely folded structure of the peptides, the results indicate Msp2F18capNC is the most stable, followed by the set of three Hu peptides, then Msp2F8capNC and Msp3F8,F18capNC, with Msp1capNC being the least stable. A proposed model to explain these trends is briefly outlined below and presented more fully in Discussion.
A factor that can stabilize a folded structure in PrP-repeat peptides is the interaction between Trp and His residues. This interaction has previously been observed in both the NOE data and NMR structure calculations of human octarepeat peptides; these indicated that the β-proton of His is in close proximity to the aromatic ring of Trp, which is four residues distant (Yoshida et al., 2000). Interaction of His and Trp has mainly been explained by cation-π interaction or π-π interaction (Gallivan and Dougherty, 1999), depending on the protonation state of the His residue. Such interactions have been reported to produce elevated pKa values for His in proteins and peptides (Loewenthal et al., 1992; Fernandez-Recio et al., 1997). Thus, it is possible that His-Trp cation-π interaction(s) stabilizes folded structure in PrP-repeat peptides, even at pH 7.2. If such interactions contribute to the structure remaining loosely folded at the highest temperature studied (85°C), then it is possible that this stabilization might be enhanced at lower pH at which His is completely protonated.
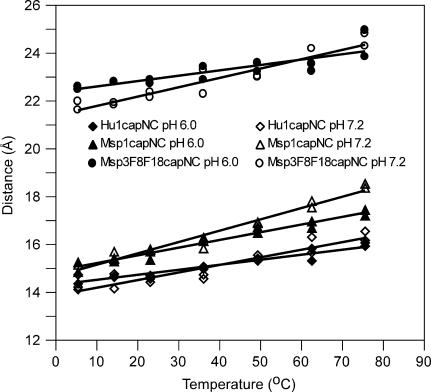
Consequently, although, as noted above, the preliminary T-dependence results at a restricted T range (25–70°C) showed little pH effect at 6.5 or 9.5 compared with 7.2, we tested for a stabilization effect from protonated His by performing T-dependence experiments at pH 6.0 for three representative peptides, Hu1capNC, Msp1capNC, and Msp3F8,F18capNC. A pH lower than 6 was not possible for reasons discussed previously (Fig. 3). Results of duplicate experiments at temperatures between 5 and 85°C are shown in Fig. 5, together with the corresponding results at pH 7.2. Of interest here are the relative slopes for the pH 6.0 and 7.2 results, not the absolute values of the distances at the lower temperature whose variation is likely due to procedural factors only (concentration effects from new solutions). The results clearly show lower slopes for all three peptides at pH 6.0 compared with 7.2: 0.019 vs. 0.029 for Hu1capNC, 0.029 vs. 0.043 for Msp1capNC, and 0.020 vs. 0.035 for Msp3F8,F18capNC. Thus, the results are consistent with the hypothesis that His-Trp cation-π interaction(s) stabilizes the loosely folded structure in PrP-repeat peptides. Experiments to determine the apparent pKa value of His are needed to clarify whether the pKa value is elevated.
FIGURE 5.
Temperature dependence of FRET distances at pH 6.0. Calculated distances from duplicate measurements are plotted for temperatures 5, 15, 25, 40, 55, 70, and 85°C, for Hu1capNC, Msp1capNC and Msp3F8,18capNC. Lines of best fit are drawn. The slopes of the lines in Å/°C are: Hu1capNC 0.019 ± 0.007; Msp1capNC 0.029 ± 0.002; Msp3F8,F18capNC 0.020 ± 0.005. For reference, data for pH 7.2 from Fig. 4 are also shown.
Comparison of simulated FRET efficiencies and Förster distances
To compare the experimental and simulated results, the FRET efficiency (E) of the donor (Trp)/acceptor (dansyl) pair was calculated from values of κ2 (Eq. 7) and the Trp-dansyl distance r obtained from the REMD simulations as:
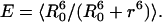 |
(8) |
Equation 8 is a variation of Eq. 4, whereas R0 is defined in Eq. 5. The average was taken over all 10,000 coordinate sets generated between 2 ns and 3 ns for each temperature. r is the distance for each coordinate set calculated between the midpoints of the bridging bonds of the naphthalene (dansyl) and the indole (tryptophan) rings. As detailed in Methods, the value of R0 obtained from Eq. 5 when κ2 is assumed to be 2/3 is 21 Å for the Trp/dansyl pair (Dunn et al., 1981). If κ2 is not assumed to be 2/3 but calculated directly from Eq. 7 using the simulation data, then R0 can be obtained by dividing 21 Å by (2/3)1/6 and then multiplying by (κ2)1/6, i.e.,
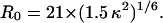 |
(9) |
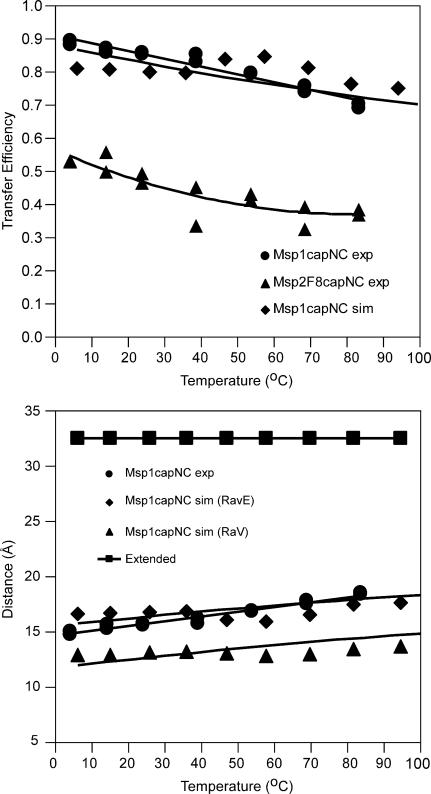
For a simulation temperature corresponding to, for example, 27°C, an average value of E of 0.80 is calculated by this procedure, which is in close agreement with the experimentally obtained value of 0.85 at 25°C obtained using Eq. 6. The general good agreement of the simulated and experimental efficiencies as a function of temperature for Msp-1 is shown in Fig. 6 top. To highlight this agreement, the experimental FRET efficiencies of the Msp2F8capNC peptide are shown for comparison.
FIGURE 6.
Comparison of the temperature dependence of the experimental FRET efficiencies and distances with results calculated from the REMD simulation for DansMsp1capC, using 10,000 coordinate sets between 2 and 3 ns for each temperature (range 7–97°C). (Top) FRET efficiencies E calculated from Eq. 6 (experimental: •, linear fit) and Eqs. 7–9 (simulated: ♦, polynomial fit). For reference, the experimental efficiencies for Msp2F8capNC are shown (▴, polynomial fit). (Bottom) FRET distances R and RavE calculated from Eq. 4 using E values from A. (experimental: •, linear fit; simulated: ▴, polynomial fit). For refererence, also shown are Rav values (⋄, polynomial fit) calculated directly as the 6th root of the average value of r6, where r is the distance for each coordinate set between dansyl and Trp (see text for details). For scale, the estimated distance (see Methods) for the fully extended peptide (32.6 Å) is shown.
The experimental Förster distance R is obtained from Eq. 4 using the experimentally calculated FRET efficiency E (Eq. 6), where R0 is 21 Å assuming κ2 is 2/3. The most informative way to compare the simulation with experiment is to calculate a value of R (RavE) using Eq. 4, with the average simulated value of E obtained from Eq. 8 and R0 from Eq. 9. As shown in Fig. 6 bottom, the RavE values calculated from the REMD simulation data for DansMsp1 are in remarkably close agreement with the experimental results for Msp1capNC/DansMsp1capC over the measured temperature range (5–85°C), both in terms of absolute values and rates of increase with temperature. The agreement is particularly striking when one compares both the simulated and experimental values with the value for a fully extended polypeptide chain, i.e., 32.6 Å.
For comparison, the average values of R (Rav) were also calculated directly as the 6th root of the average value of r6. Again, the average is over all 10,000 coordinate sets generated between 2 ns and 3 ns for each temperature (see Fig. 6 bottom). Over this time period the average calculated value of κ2 was not 2/3, and the Rav values are somewhat smaller than the experimental values. For example at 27°C, Rav is 13.0 Å, whereas at 25°C the experimental R value is 15.6 Å (Table 4).
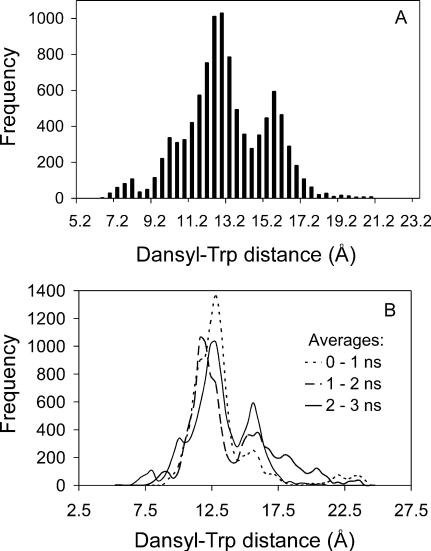
Analysis of conformational distributions from the simulation at 27°C
The distribution of distances between dansyl and Trp was calculated for each coordinate set generated by the REMD simulation at 27°C between 2 and 3 ns (a total of 10,000 coordinate sets); the distance was measured, as above, between the midpoints of the bridging bonds of the naphthalene and the indole rings. The result is shown in Fig. 7 A. A major group of fairly compact conformations with an average distance of ∼11.9 Å is apparent, as well as a significant minor group of slightly less compact conformations with average distance ∼15.4 Å. There are also two minor groups of conformations: one very compact with an average distance ∼7.8 Å and the other much looser with average distance ∼19.6 Å. If the analysis is performed over the 0–1-and 1–2-ns time periods, similar profiles (Fig. 7 B) are obtained although it is apparent the conformational distribution is variable over simulation time.
FIGURE 7.
Distribution of dansyl-Trp distances for DansMsp1capC calculated from the REMD data at 27°C (300 K). (A) Over simulation time 2–3 ns (10,000 coordinate sets). Bars are drawn for 0.4-Å intervals. (B) Over time periods 0–1, 1–2, and 2–3 ns (10,000 coordinate sets each).
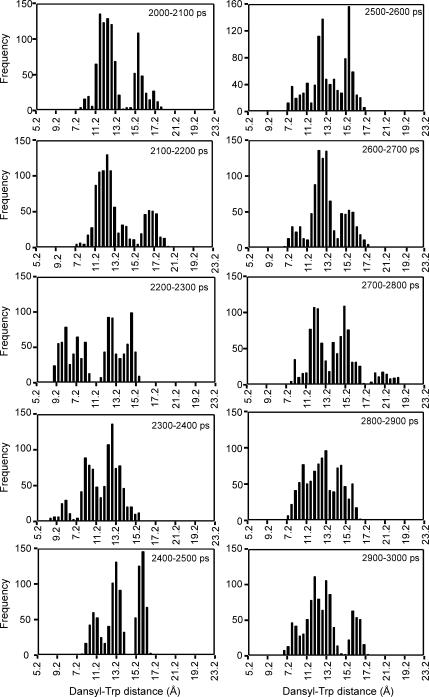
To examine the timescale of this variation, the distance data between 2 and 3 ns in Fig. 7 A have been split into 10 batches of 100 ps (1,000 snapshots) in Fig. 8. This shows some quite rapid conformational changes between some successive 100-ps periods. For example, a minor group of slightly extended conformations centered at ∼17.2 Å is prominent between 2100 and 2200 ps but disappears between 2200 and 2300 ps. A group of conformations centered at ∼15.2 Å is prominent between 2700 and 2800 ps and between 2800 and 2900 ps but disappears between 2900 and 3000 ps. A minor group of compact conformations centered at ∼8.6 Å is absent between 2100 and 2200 ps, is prominent between 2200 and 2300 ps, is still present but less prominent between 2300 and 2400 ps, but disappears between 2400 and 2500 ps.
FIGURE 8.
Distributions of dansyl-Trp distances for DansMsp1capC calculated from the REMD simulation data at 27°C (300 K) for batches of 100 ps (1,000 coordinate sets each) within the 2–3-ns time period. Bars are drawn for 0.4-Å intervals. Distance, x axis; number of occurrences of distance, y axis.
Analysis of conformational distributions from the simulation as a function of temperature
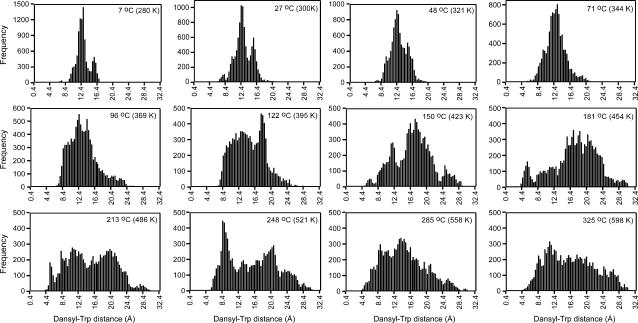
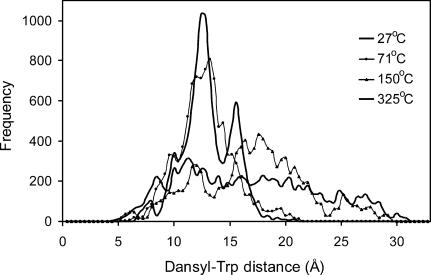
The effect of temperature on the distribution of distances has been calculated for each coordinate set generated between 2 and 3 ns at various temperatures between 7 and 325°C (10,000 coordinate sets for each T); these are presented in Fig. 9 (Fig. 7 A is the second panel). It can be seen that, although at biophysical temperatures there are dominant conformations and these are fairly compact, at higher temperatures the conformational spread becomes broad, accessing both very compact conformations at 4.4 Å and near fully extended conformations at >30 Å at the highest simulation temperature (325°C). The overlay in Fig. 10 shows these trends for selected temperatures. A striking feature of Figs. 9 and 10 is that the minor group of slightly less compact conformations with an average distance of ∼15.4 Å is very prominent at all the low temperatures, disappearing into the general mass of loosely extended conformations at temperatures >71°C.
FIGURE 10.
Overlay of distributions of dansyl-Trp distances at various temperatures (27, 71, 150, 325°C) for DansMsp1capC calculated from the REMD data over simulation time 2–3 ns (10,000 coordinate sets each), plotted at 0.4-Å intervals.
DISCUSSION
FRET experiments
We have found Trp-dansyl FRET to be an efficient system to investigate conformational properties of PrP-repeat peptides. The method has excellent sensitivity as the initial Trp intensity is high because Trp is solvent exposed and not undergoing thermal deexcitation, as it would be if buried in a protein. However, a major source of error is determination of concentration. Experience with two experimenters and repeat experiments show that small differences in concentration between dansylated and nondansylated samples may give variation in calculated FRET distances of >0.5 Å; this error is not apparent in duplicate samples taken from the same diluted stock. An example of possible discrepancies are the FRET distances for Msp1CapNC at pH 7.2 and 25°C in Tables 3 and 4 (14.9 vs. 15.6 Å).
Another potential source of error is the effect of dansyl attachment on both the Trp environment and on the structure of the peptide. The FRET method requires separate measurements of Trp emission intensity for nondansylated and dansylated pairs of peptides. As Trp intensity is very sensitive to the environment around the Trp residue, the method requires that this environment is unchanged in the dansylated peptide so that its intrinsic intensity is the same as in the reference nondansylated form. If this is not the case then the measured intensity decrease due to the resonance energy transfer to dansyl would contain other contributions and lead to errors in estimation of the Trp to dansyl distance from use of the Förster equation. Most applications of FRET involve folded proteins for which disturbance of the protein structure from dansylation is readily detectable, or can be minimized by optimum design of donor and acceptor positions if a high-resolution structure is available. For peptides lacking formal structure, such as studied here, there is no guidance in the literature on the effect of dansylation. We used CD to check for an effect. The CD spectra for the nondansylated form showed characteristic features of disordered structure. Although some spectral changes were apparent for the dansylated forms, the spectra are not consistent with any secondary structure category and resemble, most, random coil disordered polypeptide. Hence, we have assumed that dansylation did not cause structural changes that would invalidate application of the FRET method. However, even if the effect of dansylation perturbation was nonnegligible we note that the major interest in the current work is not the absolute FRET distances, but their trends among the peptides and as a function of temperature and pH; it does not seem reasonable that these would be differentially affected by dansylation, invalidating the comparisons. We also note that it is possible to address this issue directly by separate simulations of dansylated and nondansylated peptides, and we plan to do such checks in further work.
Initial protocol experiments showed that the usable pH range is >∼6 for FRET measurements using the Trp-dansyl donor-acceptor pair, with excitation at 280 nm and monitoring emission at 335 nm. Complicating emission from dansyl at 335 nm arising from the protonated form of dansyl restricts use at lower pHs. Initial results for selected peptides showed negligible dependence of the FRET distances on pH in the range 6–9.5, or from amidation of the peptide C-terminus, but that the distances for peptide with a free imino-Pro N-terminus (Msp) are slightly longer than those with N-acetylated peptide. Consequently we conducted the initial T-dependence experiments using the full set of seven N- and C-capped peptides at pH 7.2.
Comparison of the average FRET values at 25°C with estimates of the Trp-dansyl distances for a fully extended conformation (Table 4), showed that the measured average peptide conformation is much more compact and that this effect is much amplified for the longer peptides. For example, for Msp1capNC with seven peptide backbone groups separating the N-terminal and Trp-8 residues the measured distance at pH 7.2 is 15.6 Å compared with the extended estimate of 32.6 Å, whereas for Msp2F8capNC (17 intervening residues) and Msp3F8, F18capNC (27 intervening residues) the distances are 21.6 and 68.9 Å, and 22.3 and 105.2 Å, respectively. Although this result is not unexpected, it is worthwhile stressing as a notion persists for more extended conformations in disordered peptides, and the N-terminal region of PrP is so drawn in schematics in the NMR structure papers (e.g., Zahn et al., 2000).
The FRET distances for all four marsupial and three human peptides at pH 7.2 over the measured range 5–85°C, showed small but interesting trends in the rate of increase of average distance with temperature, which is implied in the slope of the lines. The slope reflects the stability of the loosely folded structures of the peptides. For all peptides, the FRET distance, and, hence, degree of compaction, increases slowly with temperature, but even at 85°C the largest percentage increase (Msp1capNC) is only 24%, i.e., the average structure is still not near fully extended. In terms of structural stability the slope results indicate Msp2F18capNC is the most stable, followed by the set of three Hu peptides, then Msp2F8capNC and Msp3F8,F18capNC, with Msp1capNC being the least stable. We note that although Trp fluorescence is itself T-dependent, the FRET method does not depend on absolute fluorescence intensity but the ratio of intensities of dansylated and nondansylated peptide; hence, this intrinsic T-dependent effect should largely cancel and not confound the real effect we propose here of T-dependent stabilities.
Our initial interpretation of these T-dependent trends on the basis of the model presented below, encouraged us to extend the T-dependent studies to pH 6.0, at which His would be protonated, for a representative subset of three peptides, Msp1capNC, Hu1capNC, and Msp3F8, F18capNC. These show consistently lower slopes, and demonstrate the remarkable sensitivity of the FRET method to measuring distances in this designed set of disordered peptides. Although time and peptide cost prevented further studies, it would be interesting to extend the peptides set. For example, to complete the Msp-3 set, i.e., with Msp3F18,28capNC and Msp3F8,28capNC, to compare with the Msp1capNC and Msp2F18capNC results with eight and 18 residue (including dansyl “residue”) separations, respectively. Similarly it would be interesting to extend peptide lengths, for example, to the Msp4 or Hu3 series.
As interactions between Trp and His in the form of cation-π or π-π interactions, depending on the protonation state of His, are recognized as an important noncovalent binding interaction in structural biology (Gallivan and Dougherty, 1999), we suspected that such interactions were involved in stabilizing the loosely folded structure of the PrP-repeat peptides, even at the highest temperature studied (85°C). The cation-π interaction has been shown to contribute significantly to maintaining the stability of thermophilic proteins (Gromiha, 2002; Gromiha et al., 2002), and to result in an elevated pKa for one His of 7.75 in barnase (Loewenthal et al., 1992). Changes in pKa values of His engaged in cation-π interactions with Trp also stabilized α-helical structure in model Ala-based peptides (Fernandez-Recio et al., 1997). Thus, it is possible that this cation-π interaction stabilizes folded structure in PrP-repeat peptides, even at pH 7.2. Results of T-dependence experiments performed for three representative peptides at pH 6.0, at which His is expected to be mostly protonated, support this idea in showing lower relative slopes for each peptide at the lower pH. We note a possible confounding effect in interpretation of these experiments, namely that His quenches Trp fluorescence in a strongly distance-dependent manner; as the FRET method depends on the ratio of intensities of dansylated and nondansylated peptide, the His quenching effect should again largely cancel, as for the T-dependence of quenching.
As this set of peptides contains an interesting distribution of His and Trp residues separated by variable distances in the sequence, we then sought to interpret the slopes for each peptide in terms of the hypothesis of cation-π interaction for His and Trp. Table 5 shows that peptides where Trp is four residues distant from His generally have smaller slopes than peptides where Trp is six residues distant from His. The interaction of His and Trp in a separation of WH i,i + 4 or HW i,i + 4 was reported to be the most stabilizing in α-helical peptides (Fernandez-Recio et al., 1997). The WH i,i + 4 geometry was also proposed as a stabilizer for the loop structure in Hu-PrP octarepeat peptide (Yoshida et al., 2000); NOE data and NMR structure calculations indicated close proximity of the β-proton of His to the aromatic ring of Trp.
TABLE 5.
Temperature dependence of the FRET distances, and the geometry of the possible cation-π interactions in Msp and Hu PrP-repeat peptides
| Peptide | Sequence | Slope (Å/°C) pH 6.0 | Slope (Å/°C) pH 7.2 | Geometry |
|---|---|---|---|---|
| Msp1capNC | PHPGGSNWGQG | 0.029 ± 0.002 | 0.043 ± 0.002 | HW i,i + 6 |
| Msp2F8capNC | PHPGGSNFGQPHPGGSNWGQG | – | 0.036 ± 0.007 | HF i,i + 6; FH i,i + 4; HW i,i + 6 |
| Msp3F8,F18capNC | (PHPGGSNFGQ)2PHPGGSNWGQG | 0.020 ± 0.005 | 0.035 ± 0.003 | HF i,i + 6; FH i,i + 4; HF i,i + 6; FH i,i + 4; HW i,i + 6 |
| Hu2F6capNC | PHGGGFGQPHGGGWGQG | – | 0.029 ± 0.002 | HF i,i + 4; FH i,i + 4; HW i,i + 4 |
| Hu1capNC | PHGGGWGQG | 0.019 ± 0.007 | 0.029 ± 0.003 | HW i,i + 4 |
| Hu2F14capNC | PHGGGWGQPHGGGFGQG | – | 0.029 ± 0.002 | HW i,i + 4; WH i,i + 4; HF i,i + 4 |
| Msp2F18capNC | PHPGGSNWGQPHPGGSNFGQG | – | 0.025 ± 0.005 | HW i,i + 6; WH i,i + 4; HF i,i + 6 |
The possible cation-π interaction with geometry of HW i,i + 4 or WH i,i + 4 is presented in the four bottom rows.
For the di- and trirepeat peptides a possible confounding effect may arise from the substitution of Phe for Trp; His-Phe cation-π or π-π interactions are conceivable although the literature suggests that the Trp residue is the most likely of the aromatics to be involved in a cation-π interaction (Gallivan and Dougherty, 1999). Thus, replacement of Trp with Phe would result in a decrease of the stabilizing cation-π interactions in the longer mutant peptides relative to wild-type ones. Table 5 shows that the presence of Phe either four or six residues distant from His does not seem to influence the slopes.
Overall, the data suggest that in the wild-type Msp peptide, the structure of multidecarepeat peptide would be more stable than that of single-decarepeat peptide because in multidecarepeats there is at least one cation-π interaction with geometry of WH i,i + 4. For the same reason, the folded structure in Hu octarepeat peptides is predicted to be more stable than that in Msp decarepeat peptides.
FRET experiments and copper binding
As we and others have shown that Cu2+ ions bind to PrP-repeat peptides and induce more defined and compact structure (Hornshaw et al., 1995; Miura et al., 1996; Viles et al., 1999; Bonomo et al., 2000; Whittal et al., 2000; Gustiananda et al., 2002), comparative FRET studies to investigate the effect of copper binding would be useful. Unfortunately, the dansyl-Trp donor-acceptor system is not suitable as binding of Cu2+ ions to human PrP-repeat peptides changes the environment of Trp, and leads to substantial quenching of Trp fluorescence. In fact, this effect has been used in fluorescence titration experiments to determine dissociation constants for copper (Hornshaw et al., 1995; Stockel et al., 1998; Jackson et al., 2001; Kramer et al., 2001). An additional problem for the Msp peptides is that their mode for binding copper differs from that for the human and other mammalian PrP repeats; this requires the HGGG sequence that is not present in the marsupial sequence (HPGG). Under experimental conditions suitable for FRET, i.e., dilute solutions, copper binding to the Msp peptides involves a free α-imino PrP group at the N-terminus. Binding would, thus, be disrupted by N-terminal dansylation, as it is by N-capping (M. Gustiananda P. I. Harris, and J. E. Gready, unpublished). Although it may be possible to design other donor-acceptor systems for attachment to the N- and C-termini of mammalian PrP-repeat peptides that do not disrupt the conformational distribution much compared with the reference nonmodified peptide, the donor would need to have long wavelength excitation that does not excite Trp. Attachment of donor and/or acceptor groups within the repeat or multirepeat peptides that would not disturb the conformational distribution does not seem realistic.
MD simulations
Förster-analogous distances (RavE) calculated from the REMD simulation data for DansMsp1 using Eqs. 8 and 9 are in remarkably close agreement with the experimental results for Msp1capNC/DansMsp1capC over the measured temperature range (5–85°C), both in terms of absolute values and rate of increase with temperature (Fig. 6). The agreement is particularly striking when one compares the simulated and experimental values with the value for the fully extended polypeptide chain, and with experimental data for peptides that measure the distances for other dansyl-Trp sequence separations. RavE distances provide the best measure for comparison with the experimental distance as they correct for the assumed value of κ2 of 2/3 used in defining the Ro value as 21 Å, which scales the experimental distances in Eq. 4.
The second comparison method we used, in which Förster-analogous distances, Rav, were calculated simply as the 6th root of the average value of r6, for r measured directly for each snapshot coordinate set, give values lower than experiment (Fig. 6). The discrepancy may arise from a number of factors, including the κ2 assumption of 2/3 being unfounded for this peptide system or the conformational distribution in the simulation not being converged. To investigate further, we have extended the simulation time to some tens of nanoseconds, and have also undertaken parallel simulations to test aspects of the REMD protocols. Detailed analysis of the convergence of both the κ2 value (calculated directly from Eq. 7) and the conformational distribution, as a function of temperature, will be reported separately (J. R. Liggins, P. L. Cummins, J. R. Reimers, Z. Cai, and J. E. Gready, unpublished). However, for reference we note that extended simulation data out to 22 ns for the current MD protocol, which was necessary to ensure adequate sampling of the dansyl and Trp ring rotations, show good agreement of the calculated κ2 value with 2/3, except at the lowest temperatures.
Analysis of the MD data shows that the peptide does not adopt a single preferred structure, and consequently displays large heterogeneity in Trp-dansyl donor-acceptor distance. This agrees with our CD data, indicating that PrP repeats either from marsupial or human do not adopt an ordered structure, and also with much literature data reporting PrP repeats as random coil. The distribution of distances generated by the REMD simulation at 27°C between 2 and 3 ns indicates a predominant group of fairly compact conformations with average distance ∼11.9 Å and a minor group with average distance ∼15.4 Å. Analysis of the data between 2 and 3 ns in 100-ps batches shows the timescale of the distribution variation is quite rapid. Although analysis over the 0–1 and 1–2 ns time periods shows similar profiles it is clear the conformational distribution is variable over simulation time; as discussed above, this dependence is being investigated further. The effect of temperature on the distance distribution between 2 and 3 ns between 7 and 325°C shows the conformational spread becomes broad at temperatures above the biophysical range, accessing both very compact conformations at 4.4 Å and near fully extended conformations at >30 Å at 325°C. But a notable feature is that the minor group of conformations with an average distance ∼15.4 Å is very prominent at temperatures up to 71°C.
It is useful to check the effect of different averaging over these heterogeneous distributions, as it will be apparent that an average value of r calculated as the 6th root of 〈r6〉, which mimics the experimental FRET average, will be larger than the actual mean distance 〈r〉. It is clear from Fig. 10 that the difference will be larger for higher temperatures where the distribution is much broader, i.e., where the effect of the r6 weighting will be more prominent. From the MD simulation data for the 2–3-ps time period we calculate differences between the 6th root of 〈r6〉 and 〈r〉 of 0.9 and 4.3 Å, at 27°C and 325°C, respectively. The potential differences in these averages are, thus, of importance in interpreting FRET distances for heterogeneous distributions, such as disordered peptides. As discussed below, sampling beyond the 3-ns simulation time reported here may broaden the distributions at the lower temperatures, so that the effect of weighting toward higher distances may become more significant.
The MD simulations we report are our first attempt to represent conformational distributions of these disordered peptides, a computational problem that has not been addressed in the literature. We are currently assessing questions of optimal simulation time and best protocols, to cross-validate the behavior we found here. For example, the current simulations performed on peptide in a spherical drop of water at constant temperatures could produce artifacts resulting from changes in solvent density for longer simulation times. Therefore, merely extending the current simulations is not an adequate test of convergence of the conformational distributions, although it should be adequate to sample ring rotations as we report above for κ2 calculations. Consequently, we are also performing simulations for the canonical (NTV) ensemble in which the density of the system remains fixed, as well as varying the type of boundary condition (box or spherical) used in the simulations to see what effect this has on the peptide conformations. For purposes of comparison with experiment we are confident the current MD results are valid, but we plan to undertake more extensive conformational analysis from extended simulations with modified protocols with a view to directly testing our His-Trp interaction model. Thus, we plan to use PCA and other methods to extract clusters of related semifolded structures, noting that more than one conformational cluster may be able to satisfy FRET and His-Trp distances and that cluster distribution evolves with simulation time (cf. Fig. 8).
The MD analysis indicates that the FRET distance calculated from steady-state intensity measurements, as we used, will be very much a dynamical average. Although, in principle, fluorescence decay (time resolved) or fluorescence anisotropy decay experiments can be used to detect a large distribution of distances between chromophores (Wu and Brand, 1994), these experiments appear to have been done so far only for protein and peptide systems with a small number of alternative conformations (Maliwal et al., 1993; Lakowicz et al., 1994; Kulinski et al., 1997; de Souza et al., 2000). Such distance distributions reflect the populations of peptide conformations that coexist in equilibrium during the fluorescence lifetime. It would be interesting to examine the PrP repeat-peptide system with these fluorescence decay methods, and to correlate the results with the MD conformational distributions. In particular, if the minor group of conformations with an average distance of ∼15.4 Å turns out to be a stable feature of longer timescale MD simulations up to 71°C, it would be interesting to see if decay methods could detect and differentiate these from the major group at shorter distance (∼11.9 Å).
CONCLUSIONS
The results show FRET measurements to be a simple yet potentially powerful method to study long-range conformational behavior in disordered peptides, a difficult area for experimental investigation. The FRET results are both sensitive to experimental conditions, such as temperature and pH, but also well reproducible. The study also demonstrates the usefulness of combining FRET experiments with MD simulations, a combination reported only once previously. Initial “mapping” of the conformational distribution of flexible peptides by simulation can assist in designing and interpreting experiments using steady-state intensity methods, as in this work. However, the simulations also suggest how time resolved or anisotropy methods might be used to study the conformational distribution, and could be even more useful in planning and analyzing these more complex and expensive experiments.
Acknowledgments
We thank Dr. Jeff Reimers, University of Sydney, for doing the time-dependent density functional theory (TDDFT) calculations.
The work was supported by Australian National University IAS block grant funding to J.E.G., and by generous grants of computing time on the APAC Compaq SC supercomputer at ANU.
References
- Aronoff-Spencer, E., C. S. Burns, N. I. Avdievich, G. J. Gerfen, J. Peisach, W. E. Antholine, H. L. Ball, F. Cohen, S. B. Prusiner, and G. L. Millhauser. 2000. Identification of the Cu(2+) binding sites in the N-terminal domain of the prion protein by EPR and CD spectroscopy. Biochemistry. 39:13760–13771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauernschmitt, R., and R. Ahlrichs. 1996. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 256:454–464. [Google Scholar]
- Bonomo, R. P., G. Imperllizzeri, G. Pappalardo, E. Rizzarelli, and G. Tabbi. 2000. Copper(II) binding modes in the prion octapeptide PHGGGWGQ: a spectroscopic and voltammetric study. Chem. 6:4195–4202. [DOI] [PubMed] [Google Scholar]
- Brown, D. R. 1999. Prion protein expression aids cellular uptake and veratridine-induced release of copper. J. Neurosci. Res. 58:717–725. [PubMed] [Google Scholar]
- Brown, D. R., K. Qin, J. W. Herms, A. Madlung, J. Manson, R. Strome, P. E. Fraser, T. Kruck, A. von Bohlen, W. Schulz-Schaeffer, A. Giese, D. Westaway, and H. Kretzschmar. 1997. The cellular prion protein binds copper in vivo. Nature. 390:684–687. [DOI] [PubMed] [Google Scholar]
- Burns, C. S., E. Aronoff-Spencer, C. M. Dunham, P. Lario, N. I. Avdievich, W. E. Antholine, M. M. Olmstead, A. Vrielink, G. J. Gerfen, J. Peisach, W. G. Scott, and G. L. Millhauser. 2002. Molecular features of the copper binding sites in the octarepeat domain of the prion protein. Biochemistry. 41:3991–4001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns, C. S., E. Aronoff-Spencer, G. Legname, S. B. Prusiner, W. E. Antholine, G. J. Gerfen, J. Peisach, and G. L. Millhauser. 2003. Copper coordination in the full-length, recombinant prion protein. Biochemistry. 42:6794–6803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1996. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- Creighton, T. E. 1983. Proteins: Structures and Molecular Principles. W. H. Freeman, New York.
- Cummins, P. L., and J. E. Gready. 1994. The electrostatic potential in the semiempirical molecular orbital approximation. Chem. Phys. Lett. 225:11–17. [Google Scholar]
- Cummins, P. L., and J. E. Gready. 1996. Solvent effects in active-site molecular dynamics simulations on the binding of 8-methyl-N5-deazapterin and 8-methyl-pterin to dihydrofolate reductase. J. Comput. Chem. 17:1598–1611. [Google Scholar]
- Cummins, P. L. 1996. Molecular Orbital Programs for Simulations (MOPS), Australian National University, Canberra, Australia.
- de Souza, E. S., I. Y. Hirata, L. Juliano, and A. S. Ito. 2000. End-to-end distance distribution in bradykinin observed by Förster resonance energy transfer. Biochim. Biophys. Acta. 1474:251–261. [DOI] [PubMed] [Google Scholar]
- dos Remedios, C. G., and P. D. Moens. 1995. Fluorescence resonance energy transfer spectroscopy is a reliable “ruler” for measuring structural changes in proteins. Dispelling the problem of the unknown orientation factor. J. Struct. Biol. 115:175–185. [DOI] [PubMed] [Google Scholar]
- Dunn, B. M., C. Pham, L. Raney, D. Abayasekara, W. Gillespie, and A. Hsu. 1981. Interaction of alpha-dansylated peptide inhibitors with porcine pepsin: detection of complex formation by fluorescence energy transfer and chromatography and evidence for a two-step binding scheme. Biochemistry. 20:7206–7211. [DOI] [PubMed] [Google Scholar]
- Fernandez-Recio, J., A. Vazquez, C. Civera, P. Sevilla, and J. Sancho. 1997. The tryptophan/histidine interaction in alpha-helices. J. Mol. Biol. 267:184–197. [DOI] [PubMed] [Google Scholar]
- Flechsig, E., D. Shmerling, I. Hegyi, A. J. Raeber, M. Fischer, A. Cozzio, C. von Mering, A. Aguzzi, and C. Weissmann. 2000. Prion protein devoid of the octapeptide repeat region restores susceptibility to scrapie in PrP knockout mice. Neuron. 27:399–408. [DOI] [PubMed] [Google Scholar]
- Foresman, J. B., M. Head-Gordon, J. A. Pople, and M. J. Frisch. 1992. Toward a systematic molecular orbital theory for excited states. J. Phys. Chem. 96:135–149. [Google Scholar]
- Förster, T. 1948. Intermolecular energy migration and fluorescence. Ann. Phys. 2:55–75. [Google Scholar]
- Frisch, M. J., G. W. Truck, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle, and J. A. Pople. 1998. Gaussian 98, Rev. A7. Gaussian, Inc., Pittsburgh, PA.
- Gallivan, J. P., and D. A. Dougherty. 1999. Cation-pi interactions in structural biology. Proc. Natl. Acad. Sci. USA. 96:9459–9464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garnett, A. P., and J. H. Viles. 2003. Copper binding to the octarepeats of the prion protein. Affinity, specificity, folding and co-operativity; insights from circular dichroism. J. Biol. Chem. 278:6795–6802. [DOI] [PubMed] [Google Scholar]
- Gonzalez-Iglesias, R., M. A. Pajares, C. Ocal, J. C. Espinosa, B. Oesch, and M. Gasset. 2002. Prion protein interaction with glycosaminoglycan occurs with the formation of oligomeric complexes stabilized by Cu(II) bridges. J. Mol. Biol. 319:527–540. [DOI] [PubMed] [Google Scholar]
- Gromiha, M. M. 2002. Influence of cation-π interactions in mesophilic and thermophilic proteins. J. Liq. Chromatography Rel. Technol. 25:3141–3149. [Google Scholar]
- Gromiha, M. M., S. Thomas, and C. Santhosh. 2002. Role of cation-π interactions to the stability of thermophilic proteins. Prep. Biochem. Biotechnol. 32:355–362. [DOI] [PubMed] [Google Scholar]
- Gustiananda, M., P. I. Haris, P. J. Milburn, and J. E. Gready. 2002. Copper-induced conformational change in a marsupial prion protein repeat peptide probed using FTIR spectroscopy. FEBS Lett. 512:38–42. [DOI] [PubMed] [Google Scholar]
- Haughland, R. P. 2001. Handbook of Fluorescent Probes and Research Products, 8th. Ed. Molecular Probes, Inc., Eugene, OR.
- Hornshaw, M. P., J. R. McDermott, J. M. Candy, and J. H. Lakey. 1995. Copper binding to the N-terminal tandem repeat region of mammalian and avian prion protein: structural studies using synthetic peptides. Biochem. Biophys. Res. Commun. 214:993–999. [DOI] [PubMed] [Google Scholar]
- Jackson, G. S., I. Murray, L. L. Hosszu, N. Gibbs, J. P. Waltho, A. R. Clarke, and J. Collinge. 2001. Location and properties of metal-binding sites on the human prion protein. Proc. Natl. Acad. Sci. USA. 98:8531–8535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, W. C., Jr. 1990. Protein secondary structure and circular dichroism: a practical guide. Proteins. 7:205–214. [DOI] [PubMed] [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kramer, M. L., H. D. Kratzin, B. Schmidt, A. Romer, O. Windl, S. Liemann, S. Hornemann, and H. Kretzschmar. 2001. Prion protein binds copper within the physiological concentration range. J. Biol. Chem. 276:16711–16719. [DOI] [PubMed] [Google Scholar]
- Kulinski, T., A. B. Wennerberg, R. Rigler, S. W. Provencher, M. Pooga, U. Langel, and T. Bartfai. 1997. Conformational analysis of galanin using end to end distance distribution observed by Förster resonance energy transfer. Eur. Biophys. J. 26:145–154. [DOI] [PubMed] [Google Scholar]
- Lagunoff, D., and P. Ottolenghi. 1966. Effect of pH on the fluorescence of dimethylaminonaphthalenesulphonate (DNS) and several derivatives. C. R. Trav. Lab. Carlsberg. 35:63–83. [PubMed] [Google Scholar]
- Lakowicz, J. R., I. Gryczynski, G. Laczko, W. Wiczk, and M. L. Johnson. 1994. Distribution of distances between the tryptophan and the N-terminal residue of melittin in its complex with calmodulin, troponin C, and phospholipids. Protein Sci. 3:628–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenthal, R., J. Sancho, and A. R. Fersht. 1992. Histidine-aromatic interactions in barnase. Elevation of histidine pKa and contribution to protein stability. J. Mol. Biol. 224:759–770. [DOI] [PubMed] [Google Scholar]
- Luczkowski, M., H. Kozlowski, M. Stawikowski, K. Rolka, E. Gaggelli, D. Valensin, and G. Valensin. 2002. Is the monomeric prion octapeptide repeat PHGGGWGQ a specific ligand for Cu2+ ions? J. Chem. Soc. Dalton Trans. 2269–2274.
- Maliwal, B. P., J. R. Lakowicz, G. Kupryszewski, and P. Rekowski. 1993. Fluorescence study of conformational flexibility of RNase s-peptide: distance-distribution, end-to-end diffusion, and anisotropy decays. Biochemistry. 32:12337–12345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miura, T., A. Hori-i, and H. Takeuchi. 1996. Metal-dependent alpha-helix formation promoted by the glycine-rich octapeptide region of prion protein. FEBS Lett. 396:248–252. [DOI] [PubMed] [Google Scholar]
- Miura, T., A. Hori-i, H. Mototani, and H. Takeuchi. 1999. Raman spectroscopic study on the copper(II) binding mode of prion octapeptide and its pH dependence. Biochemistry. 38:11560–11569. [DOI] [PubMed] [Google Scholar]
- Pace, C. N., and F. X. Schmid. 1997. How to determine the molar absorbance coefficient of a protein. In Protein Structure: A Practical Approach. T. E. Creighton, editor. IRL Press, Oxford, UK. 253–259.
- Pauly, P. C., and D. A. Harris. 1998. Copper stimulates endocytosis of the prion protein. J. Biol. Chem. 273:33107–33110. [DOI] [PubMed] [Google Scholar]
- Perrin, D. D., and B. Dempsey. 1974. Buffers for pH and Metal Ion Control. Chapman and Hall, London, UK.
- Pesce, A. J., C.-G. Rosen, and T. L. Pasby. 1971. Fluorescence Spectroscopy: An Introduction for Biology and Medicine. Marcel Dekker Inc., New York.
- Prusiner, S. B. 1998. Prions. Proc. Natl. Acad. Sci. USA. 95:13363–13383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, K. F., Y. Yang, P. Mastrangelo, and D. Westaway. 2002. Mapping Cu(II) binding sites in prion proteins by diethyl pyrocarbonate modification and matrix-assisted laser desorption ionization-time of flight (MALDI-TOF) mass spectrometric footprinting. J. Biol. Chem. 277:1981–1990. [DOI] [PubMed] [Google Scholar]
- Ryckaert, J.-P., G. Ciccoti, and H. J. C. Berendsen. 1977. Numerical integration of Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- Schmid, F. X. 1997. Optical spectroscopy to characterize protein conformation and conformational changes. In Protein Structure: A Practical Approach. T. E. Creighton, editor. IRL Press, Oxford, UK. 261–297.
- Selvin, P. R. 1995. Fluorescence resonance energy transfer. Methods Enzymol. 246:300–334. [DOI] [PubMed] [Google Scholar]
- Smith, C. J., A. F. Drake, B. A. Banfield, G. B. Bloomberg, M. S. Palmer, A. R. Clarke, and J. Collinge. 1997. Conformational properties of the prion octa-repeat and hydrophobic sequences. FEBS Lett. 405:378–384. [DOI] [PubMed] [Google Scholar]
- Stella, L., M. Venanzi, M. Carafa, E. Maccaroni, M. E. Straccamore, G. Zanotti, A. Palleschi, and B. Pispisa. 2002. Structural features of model glycopeptides in solution and in membrane phase: a spectroscopic and molecular mechanics investigation. Biopolymers. 64:44–56. [DOI] [PubMed] [Google Scholar]
- Stockel, J., J. Safar, A. C. Wallace, F. E. Cohen, and S. B. Prusiner. 1998. Prion protein selectively binds copper(II) ions. Biochemistry. 37:7185–7193. [DOI] [PubMed] [Google Scholar]
- Stultz, C. M., A. D. Levin, and E. R. Edelman. 2002. Phosphorylation-induced conformational changes in a MAP-kinase substrate: implications for tyrosine hydroxylase activation. J. Biol. Chem. 277:47653–47661. [DOI] [PubMed] [Google Scholar]
- Stryer, L. 1978. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 47:819–846. [DOI] [PubMed] [Google Scholar]
- Stryer, L., and R. P. Haughland. 1967. Energy transfer: a spectroscopic ruler. Proc. Natl. Acad. Sci. USA. 58:719–726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita, Y., and Y. Okamoto. 1999. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 314:141–151. [Google Scholar]
- van der Meer, B. W. 2002. Kappa-squared: from nuisance to new sense. Rev. Mol. Biotechnol. 82:181–196. [DOI] [PubMed] [Google Scholar]
- Viles, J. H., F. E. Cohen, S. B. Prusiner, D. B. Goodin, P. E. Wright, and H. J. Dyson. 1999. Copper binding to the prion protein: structural implications of four identical cooperative binding sites. Proc. Natl. Acad. Sci. USA. 96:2042–2047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warner, R. G., C. Hundt, S. Weiss, and J. E. Turnbull. 2002. Identification of the heparan sulfate binding sites in the cellular prion protein. J. Biol. Chem. 277:18421–18430. [DOI] [PubMed] [Google Scholar]
- Weber, G., and M. Shinitzky. 1970. Failure of energy transfer between identical aromatic molecules on the excitation at the long wavelength edge of absortion spectrum. Proc. Natl. Acad. Sci. USA. 65:823–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittal, R. M., H. L. Ball, F. E. Cohen, A. L. Burlingame, S. B. Prusiner, and M. A. Baldwin. 2000. Copper binding to octarepeat peptides of the prion protein monitored by mass spectrometry. Protein Sci. 9:332–343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woody, R. W. 1995. Circular dichroism. Methods Enzymol. 246:34–71. [DOI] [PubMed] [Google Scholar]
- Woody, R. W., and A. K. Durker. 1996. Aromatic and cystine side-chain circular dichroism in proteins. In Circular Dichroism and the Conformational Analysis of Biomolecules. G. D. Fasman, editor. Plenum Press, New York. 109–157.
- Wootton, J. C. 1994. Sequences with ‘unusual’ amino acid compositions. Curr. Opin. Struct. Biol. 4:413–421. [Google Scholar]
- Wright, P. E., and H. J. Dyson. 1999. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol. 293:321–331. [DOI] [PubMed] [Google Scholar]
- Wu, P., and L. Brand. 1994. Resonance energy transfer: methods and applications. Anal. Biochem. 218:1–13. [DOI] [PubMed] [Google Scholar]
- Yoshida, H., N. Matsushima, Y. Kumaki, M. Nakata, and K. Hikichi. 2000. NMR studies of model peptides of PHGGGWGQ repeats within the N-terminus of prion proteins: a loop conformation with histidine and tryptophan in close proximity. J. Biochem. 128:271–281. [DOI] [PubMed] [Google Scholar]
- Zahn, R., A. Liu, T. Luhrs, R. Riek, C. von Schroetter, F. Lopez Garcia, M. Billeter, L. Calzolai, G. Wider, and K. Wuthrich. 2000. NMR solution structure of the human prion protein. Proc. Natl. Acad. Sci. USA. 97:145–150. [DOI] [PMC free article] [PubMed] [Google Scholar]