Spontaneously Formed Monodisperse Biomimetic Unilamellar Vesicles: The Effect of Charge, Dilution, and Time

Abstract

Using small-angle neutron scattering and dynamic light scattering, we have constructed partial structural phase diagrams of lipid mixtures composed of the phosphatidylcholines dimyristoyl and dihexanoyl doped with calcium ions (Ca²⁺) and/or the negatively charged lipid, dimyristoyl phosphatidylglycerol (DMPG). For dilute solutions (lipid concentration ≤1 wt %), spontaneously forming unilamellar vesicles (ULVs) were found, and their polydispersity was determined to be ∼20%. The stability of the Ca²⁺- or DMPG-doped ULVs was monitored over a period of 4 days and their structural parameters (e.g., average outer radius, 〈R_o〉) were found to be insensitive to the lipid concentration (C_lp). However, doping the dimyristoyl/dihexanoyl system with both Ca²⁺ and DMPG resulted in ULVs whose 〈R_o〉 was found to be C_lp dependent. The 〈R_o〉 of DMPG-doped ULVs remained unchanged over an extended period of time (at least 4 days), a good indication of their stability.

INTRODUCTION

Spontaneously formed unilamellar vesicles (ULVs) have great potential for application as vehicles for drug delivery (Gregoriadis, 1995; Lee, 2002) and gene therapy (Maurer et al., 1999). However, ULVs obtained by filtration or sonication are usually unstable and polydisperse. Over the last decade or so, spontaneously forming ULVs have been observed in many cationic-anionic surfactant mixtures (Kaler et al., 1989, 1992; Murthy et al., 1991; Yatcilla et al., 1996; Villeneuve et al., 1999; Bergstrom et al., 1999; Bergstrom and Pedersen, 2000) and cationic surfactant systems (Viseu et al., 2000). Although some of them are believed to be thermodynamically stable, with low polydispersities, issues concerning biocompatibility and biodegradability must be considered for biologically relevant applications.

Phospholipids share many of the characteristics exhibited by surfactants. However, unlike surfactant systems, phospholipids are the main constituents of cell membranes, making them a promising group of materials suitable for engineering biocompatible systems. In the past, spontaneously formed ULVs were found in phospholipid mixtures composed of long- and short-chain lipids (Gabriel and Roberts, 1984; Ollivon et al., 2000). However, their stability, as a function of total lipid concentration, (C_lp), and polydispersity were seldom studied. Other approaches used in obtaining monodispersed ULVs were either through micelle-to-vesicle transitions induced by a temperature jump (Andelman et al., 1994; Lesieur et al., 2000; Nieh et al., 2001, 2002) or through a simple dilution of the system (Schurtenberger et al., 1984, 1985; Egelhaaf and Schurtenberger, 1999). Regardless of the method, the average vesicle radius, 〈R_o〉, has always been found to vary as a function of C_lp, an indication that ULVs were sensitive to their external environment. Two exceptions that we are aware of are an indirect measurement of a surfactant mixture composed of sodium dodecyl sulfate and didodecyldimethyl ammonium bromide reported by Marques et al. (1998) and a surfactant aqueous mixture of sodium oleate/octanol (Gradzielski et al., 1999).

Several theories of spontaneous ULV formation have been developed over the past few decades. Since the formation of ULVs from a symmetric bilayer (same chemical composition in both the outer and inner bilayer leaflets) costs energy (Israelachvili, 1992), entropy gain has usually been thought of as the main reason for the formation of stable vesicular structures. Safran et al. (1990, 1991) have shown that vesicles can be more stable than lamellar structures in the limit of large bending rigidity, k_b, if the attractive interactions between the two surfactants in a mixture are sufficiently strong. On the other hand, Bergstrom (1996, 2001) and Bergstrom and Eriksson (1996, 1998) have studied the stability of ULV in surfactant mixtures taking into account a variety of contributions to the system's total energy including geometrical packing, electrostatics, headgroup interactions, chain conformation, and mixing. Yuet and Blankschtein (1996a,b) have determined the size distribution of ULVs in surfactant mixtures based on a detailed molecular-thermodynamic model. Another study that has attempted to simultaneously tackle the theoretical and experimental issues was carried out by Oberdisse et al. (1996), Oberdisse and Porte (1997), and Oberdisse (1998) using the so-called “vesicle cell model” (VCM) to investigate the effect of charge density (ρ), dilution, salinity, and k_b on the size of the ULVs. Despite all of the above-mentioned studies, there is still no clear understanding of the factors affecting the vesicle size distribution in a given experimental situation. In addition, it has been shown that, at least in some cases, ULVs are not equilibrium structures, but are kinetically trapped (Marques, 2000; Leng et al., 2003).

In the last few years, there has been a great deal of scientific activity in a system forming bilayered micelles or so-called “bicelles” (Sanders and Landis, 1995; Katsaras et al., 1997). Although bicelles are commonly produced using a variety of surfactants (Sanders and Prestegard, 1990; Chung and Prestegard, 1993; Sanders and Landis, 1995), recently a number of groups have produced biomimetic bicelles composed of long- (e.g., the phosphatidylcholine (PC) dimyristoyl (DMPC)) and short-chain (e.g., dihexanoyl (DHPC)) phospholipids doped with either paramagnetic ions, charged lipids/surfactants, or both (Prosser et al., 1996, 1998; Losonczi and Prestegard, 1998). Most recently, Nieh et al. (2001, 2002) have shown that the bilayer charge density plays an important role in determining the structures produced by these mixtures. For example, in the dilute regime (i.e., lipid concentration <0.01 g/ml) bicelles were found in DMPC/DHPC mixtures doped with the negatively charged lipid, dimyristoyl phosphatidylglycerol (DMPG) (DMPC/DMPG = 15). However, monodispersed ULVs were observed when the mixtures were doped with the lanthanide trivalent cation, thulium (Tm³⁺), or with a combination of DMPG and Tm³⁺. In nondoped systems (i.e., no net surface charge), multilamellar vesicles (MLVs) were routinely observed. One can seemingly thus produce monodispersed ULVs by merely adjusting the charge density of these mixtures.

Here we report on a series of small-angle neutron scattering (SANS) and dynamic light scattering (DLS) experiments, where the morphology of the lipid mixtures was monitored as a function of ρ, C_lp, and temperature. The charge density of the membranes was introduced through doping with the negatively charged lipid, DMPG, and the salt, CaCl₂, either individually or in combination. In this study, instead of the previously used trivalent cation, Tm³⁺, we have used the physiologically relevant divalent cation, Ca²⁺, which is known to have a strong binding affinity for phosphatidylcholine headgroups (Gennis, 1989). Throughout the experiment, the molar ratio of long- (DMPC or DMPC + DMPG) to short-chain (DHPC) lipid remained constant at 3.2, whereas the bilayer surface charge was controlled by varying the amounts of DMPG and/or Ca²⁺. SANS and DLS were used to probe the size and polydispersity of the ULVs. We find that some of our experimental results do not agree with the predictions of the vesicular cell model (Oberdisse et al., 1996; Oberdisse and Porte, 1997; Oberdisse, 1998). More importantly, as determined by SANS, the size of DMPG-doped ULVs was found not to change over a period of at least 4 days. In some cases, the ULV size was surprisingly found to be independent of C_lp, implying potential for the practical use (e.g., drug delivery) of this system.

MATERIALS AND METHODS

Sample preparation

DMPC, DHPC, and DMPG were purchased from Avanti Polar Lipids (Alabaster, AL); calcium chloride (CaCl₂) was obtained from Sigma (St. Louis, MO). All chemicals were used without further purification. Before use, the solvent, deuterium oxide (99.9%, Cambridge Isotope, Andover, MA), was filtered through a 0.1 μm filter.

Solutions of DMPC/DHPC (molar ratio = 3.2/1) and of DMPC/DMPG/DHPC (molar ratio = 2.67/0.53/1) in D₂O were prepared with a C_lp of 20 wt % by vortexing and temperature cycling the mixtures from 10°C to 50°C. These solutions were then diluted to a C_lp of 2 wt %. Mixing appropriate amounts of the 2 wt % solutions yielded DMPC/DMPG molar ratios ranging from 305 to 11. Subsequently, each 2 wt % DMPC/DMPG mixture was diluted to its final C_lp of between 1.0 and 0.25 wt %.

The Ca²⁺-doped solutions were produced by adding small amounts of CaCl₂ solution (20 wt % in filtered D₂O) to the 2 wt % DMPC/DHPC solution resulting in DMPC/Ca²⁺ mixtures whose molar ratios ranged from 1 to 50. The new solutions were subsequently diluted to yield a C_lp of 1.0, 0.5, and 0.25 wt %. The same procedure was employed for preparing solutions doped with both DMPG and Ca²⁺, using two of the 2 wt % DMPC/DHPC/DMPG solutions (DMPC/DMPG = 10 and DMPC/DMPG = 155) to start with. Solutions of five different DMPC/DMPG/Ca²⁺ molar ratios were made, ranging from DMPG-rich to Ca²⁺-rich. Most samples were prepared and refrigerated for a period of at least 1 month before experimentation. However, some samples were placed in an oven, at 45°C, for periods of up to 14 days.

Small-angle neutron scattering

For a solution of nearly identical scattering objects, the intensity of scattered radiation I(Q), as a function of the scattering vector, Q (Q = 4πsin(θ/2)/λ, where λ is the wavelength of the neutron and θ the scattering angle), can be interpreted in terms of a form factor, F(Q), and a structure factor, S(Q). F(Q) characterizes the scattering length density of a scattering object, whereas S(Q) describes the arrangement of the collection of objects in the solution. The measured scattered intensity is given by

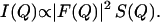SANS experiments were performed using the high resolution NG7 30m SANS instrument at the NIST Center for Neutron Research located at the National Institute of Standards and Technology (Glinka et al., 1998); 8 Å neutrons (Δλ/λ = 11%) and two sample-to-detector distances (15.3 and 1.2 m) were employed to carry out all of the SANS experiments described herein. With a horizontal detector offset of 20 cm, the effective Q range covered was between 0.002 and 0.32 Å⁻¹. After correcting for ambient background and empty cell scattering, the two-dimensional raw data were circularly averaged yielding a one-dimensional intensity distribution, I(Q), which was put on an absolute scale (cross section per unit volume) using the incident neutron flux. From the high-Q scattering intensity plateau of the reduced data, the incoherent scattering from hydrogen was obtained and subtracted from the corresponding data.

An analytical expression for the structure factor, S_MSA(Q), has been obtained by Hayter and Penfold (1981) by solving the Ornstein-Zernike equation in the mean spherical approximation (MSA), which accounts for the repulsive electrostatic interactions between macroions. This expression was used in fitting the data from all ULVs and strongly charged bicelle systems. In the case of dilute and weakly charged bicelles, the structure factor is expected to be unity, and was thus not considered. S_MSA(Q) was determined from the total lipid concentration, the dielectric constant of the solvent, the surface charge density of the lipid aggregates, and the ionic strength of the solution. In the case of samples containing DMPG, the surface charge of the object can be calculated with the assumption of complete dissociation of the Na⁺ counterions. However, in the case of samples with Ca²⁺, the surface charge is not known, and as such becomes a variable parameter, since the amount of Ca²⁺ ions bound to the lipids in the membrane can, in principle, vary with the experimental conditions. In these cases, both the surface charge density and ionic strength were not fixed a priori, but were determined from the best fits to the data.

The form factor of a core shell disk (CSD) model, convoluted with the instrumental resolution, was used to represent the scattering from a bicelle (Nieh et al., 2001, 2002). Bilayer thickness was derived from the center-to-center distance between the two hydrophilic regions (which represent the lipid headgroups) sandwiching the hydrophobic region (consisting of two acyl chain regions) of a single bilayer. The scattering length densities of 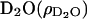and the hydrophobic region of the bilayer (ρ_phobic) were calculated to be 6.38 × 10⁻⁶ and −4.3 × 10⁻⁷ Å⁻², respectively, whereas that of the hydrophilic part of the lipid (ρ_philic = 3.2 × 10⁻⁶ Å⁻²) was obtained from the best fit to the data, as previously indicated by Nieh et al. (2001, 2002). The value of the bilayer thickness was found to vary within the limits of 50 ± 5 Å, which is consistent with the total thickness of gel phase DMPC bilayers (Hung and Chen, 2000). The only parameter allowed to vary without any constraints was the radius of the bicelles.

The ULV form factor was based on a core shell sphere (CSS) model, where the bilayer is approximated as a single layer of constant scattering length density (ρ_lipid = 3.2 × 10⁻⁷ Å⁻²). In reality, the scattering length density across the bilayer is not uniform due to the differences in the composition of the headgroup and chain regions. However, the above model with a constant value of ρ_lipid (the single-well profile), which reduces the number of fitting parameters as well as simplifies the calculation, is found to be sufficient to describe the experimental data. The total radius of the vesicle was taken to be the inner radius of the sphere plus the bilayer thickness. As in the case of bicelles, the radius was not constrained, whereas the thickness was restricted to lie between 25 and 45 Å.

Dynamic light scattering

For a dilute solution of spherical noninteracting particles, where each particle, i, of radius R_i undergoes Brownian motion, the Stokes-Einstein equation describes the relationship between R_i and the diffusion coefficient, D_i,

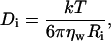(1)

where k, T, and η_w are the Boltzmann constant, absolute temperature, and the viscosity, in our case, of D₂O, respectively. For nonspherical particles (e.g., disks, cylinders, etc.), an equivalent hydrodynamic radius, R_Hi is used to replace R_i in Eq. 1. In the DLS measurement, the time-dependant intensity autocorrelation function, G(τ), is obtained, and is given by

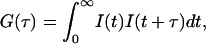(2)

where τ is the time delay. From the Siegert relation, G(τ) can be expressed in terms of the field autocorrelation function, g(τ) as

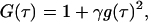(3)

where γ is the instrumental coherence factor. g(τ) represents the time decay of the position autocorrelation function of the particles and in a polydisperse system can be written as

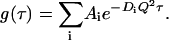(4)

In this expression, Q is the scattering vector and A_i represents the light-scattering amplitude of the particle i with diffusion coefficient D_i.

Cumulant analysis methods and regularization methods such as CONTIN are usually employed in analyzing the experimental data to obtain the diffusion coefficient (Santos and Castanho, 1996). Cumulant analysis is usually applied to systems having a monomodal and sometimes bimodal size distribution so that the characteristic function g(τ) of the size probability distribution is expanded as a series of cumulants. At small τ, the first cumulant can be expressed in the form of D_effQ², where D_eff is the effective diffusion coefficient.

For analysis methods such as CONTIN, the aim is to solve Eq. 4 through eigenvalue decomposition combined with regularization, a smoothing technique. The size distribution function can then be resolved in terms of the eigenvalues, D_i (or R_Hi), and the average hydrodynamic radius, R_H, is obtained by normalizing it to the scattered intensity of the particles (z-average), but not by their volume (Pencer et al., 2001). We mostly used cumulant analysis to interpret our data from monodisperse samples, whereas CONTIN sometimes was used for samples with bimodal size distributions to understand possible structures in the system. In some cases, the size distribution function obtained from the CONTIN analysis has three or more maxima. Currently, we do not know whether these distributions are reliable or if they are artifacts due to strong interparticle interactions.

DLS was performed on a DynaPro/MS-X (Protein Solutions, Charlottesville, VA), which was designed to measure the scattering intensity at a fixed scattering angle (θ) of 90°, containing 256 channels covering shift times of between 1 and 10⁵ μs. The instrument was equipped with a power-adjustable laser source having a λ of 782.8 nm and a temperature-controlled sample cell. λ in the solution is inversely proportional to its refractive index, n_s, and hence Q is linearly proportional to n_s. Since the solutions are dilute (<2 wt %), we may take n_s to be the same as that of D₂O, which according to Bertie and Lan (1995) is 1.325 for λ = 782.8 nm at 25°C. Further, n_s is weakly dependent on temperature; n_s of H₂O at 10°C and 50°C for a similar wavelength (λ = 706.52 nm) differ by ∼0.3% (Lide, 1990), which yields a difference of only ∼0.6% in R_H. We were unable to find any measurement of the refractive index of D₂O for λ = 782.8 nm in the temperature range of interest reported in the literature. Hence, we have taken n_s to be a constant in our analysis. The resultant error on R_H should be negligible, since the temperature dependence of the D₂O n_s can be expected to be similar to that of H₂O. On the other hand, the significant temperature dependence of D₂O viscosity, η_w (Cho et al., 1999), was taken into account when calculating R_H.

The intensity overflow limit for the detector was ∼7 × 10⁶ counts/s. The intensity time correlation function was at first obtained by averaging over a period of acquisition times, usually ∼10 s, as a function of τ. The normalized G(τ), 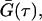was then obtained from the average of 30 or more acquisitions. Before experimentation, the DLS setup was tested using standard polystyrene microbead solutions demonstrating that a precise R_H value could be obtained for samples with particle size between 1 nm and 1 μm with an error of ±2%. Due to multiple scattering, DLS was not carried out on turbid samples.

RESULTS AND DISCUSSION

Nondoped solutions

For DMPC/DHPC systems, we have previously observed the formation of MLVs at low lipid concentrations (≤0.01 g/mL, ≈1 wt %) and over a temperature range between 10°C and 45°C (Nieh et al., 2002). Note that the gel-to-L_α phase transition of pure DMPC multibilayers occurs at T_M = 23°C. Bicelles were observed at higher lipid concentrations (≥5 wt %) and T ≈ 10°C. In the case of ULVs and the much smaller bicelles, a transparent solution is normally observed. However, some solutions were found to be rather turbid and could not be studied using DLS. The turbidity of these samples indicates the presence of large aggregates in the system, probably MLVs. These samples are denoted as dispersions in Tables 1–3.

TABLE 1.

Summary of DLS results from Ca²⁺-doped samples at various temperatures, dopant compositions, and total lipid concentrations

		Temperature (°C)
		<TM						>TM
		10		15		25		35		45
DMPC/Ca2+	Clp wt %	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)
50	2	B/U*	71/1612	B/U	70/2083	Disp†		Disp		Disp
	1	ULV	491	ULV	499	Disp		Disp		Disp
	0.5	Disp		Disp		Disp		Disp		Disp
	0.25	Disp		Disp		Disp		Disp		Disp
20	2	Bic	77	Bic	78	Disp		Disp		Disp
	1	ULV	530	ULV	524	Disp		Disp		Disp
	0.5	Disp		Disp		Disp		Disp		Disp
	0.25	Disp		Disp		Disp		Disp		Disp
10	2	Bic	90	Bic	88	Disp		Disp		Disp
	1	ULV	335	ULV	318	ULV	306	ULV	573	ULV	601
	0.5	Disp		Disp		Disp		Disp		Disp
	0.25	Disp		Disp		Disp		ULV	918	ULV	918
5	2	Bic	82	Bic	70	Disp		Disp		Disp
	1	ULV	303	ULV	298	ULV	401	ULV	399	ULV	413
	0.5	ULV	831	ULV	841	ULV	888	ULV	873	ULV	902
	0.25	ULV	537	ULV	535	ULV	598	ULV	612	ULV	633
2	2	Bic	97	Bic	96	Disp		Disp		Disp
	1	MM‡		MM		MM		ULV	398	ULV	375
	0.5	Disp		Disp		Disp		Disp		Disp
	0.25	ULV	504	ULV	462	ULV	475	ULV	474	ULV	512
1	2	Bic	95	Bic	97	Disp		Disp		Disp
	1	MM		MM		MM		ULV	432	ULV	447
	0.5	Disp		Disp		Disp		Disp		Disp
	0.25	ULV	427	ULV	443	ULV	458	ULV	479	ULV	493

^*B/U, bimodal distribution obtained through CONTIN analysis.

^†Disp, dispersions.

^‡MM, samples for which CONTIN analysis gives multimodal size distributions.

TABLE 3.

Summary of DLS results from both Ca²⁺- and DMPG-doped samples at various temperatures, dopant compositions, and total concentrations

			Temperature (°C)
			<TM				>TM
DMPC ratios			10		15		25		35		45
DMPG	Ca2+	Clp wt %	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)
155	50	All	Disp*		Disp		Disp		Disp		Disp
155	2	2	Bic	103	Bic	102	ULV	368	MM		MM
		1	MM†		MM		MM		MM		MM
		0.5	Disp		Disp		Disp		MM		MM
		0.25	ULV	460	ULV	469	ULV	514	ULV	522	ULV	526
10	50	2	Bic	61	Bic	67	Bic	91	ULV	288	ULV	335
		1	MM		MM		MM		MM		MM
		0.5	MM		MM		MM		MM		MM
		0.25	MM		MM		MM		MM		MM
10	5	All	Disp		Disp		Disp		Disp		Disp
10	2	All	Disp		Disp		Disp		Disp		Disp

^*Disp, dispersions.

^†MM, samples for which CONTIN analysis gives multimodal size distributions.

Ca²⁺-doped solutions

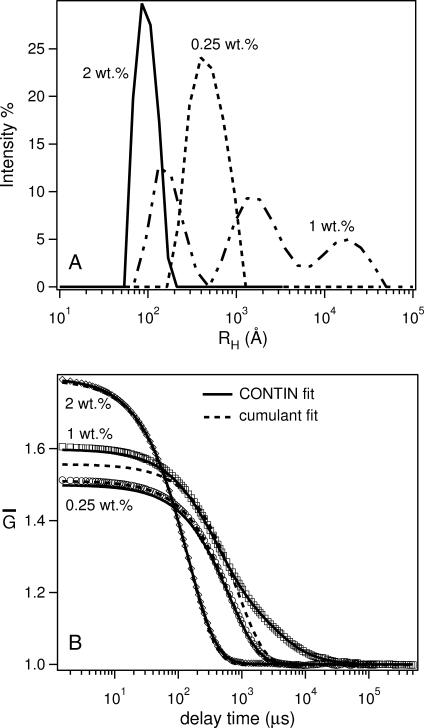
Table 1 is a summary of the phase behavior of the Ca²⁺-doped system, as measured by DLS. Generally speaking, R_H of bicelles is in the range of 100 Å, whereas that of ULVs varied from 300 Å to >1000 Å. Fig. 1 A shows the size distribution function for the 2:1 DMPC/Ca²⁺ mixture at three different lipid concentrations. Depending on C_lp, 2:1 DMPC/Ca²⁺ can either form bicelles (2 wt %), ULVs (0.25 wt %), or some other structures giving rise to multimodal size distributions (1 wt %). For an exponentially decaying correlation function, shown in Fig. 1 B, both cumulant (dotted curves) and CONTIN analyses give good fits to the experimental data (solid curves). However, for C_lp = 1 wt %, the cumulant method proved to be inadequate, since the decay of the autocorrelation function is not a single exponential. Although the CONTIN method produces a more consistent fit to the experimental data, the size distribution function (Fig. 1 A) is characterized by three peaks (multimodal distribution), making it, at present, difficult to determine the precise structures. As mentioned previously, the system might indeed contain aggregates with various structures or the distribution obtained is an artifact due to strong interparticle interactions. The structure of these systems can only be determined through SANS.

FIGURE 1.

(A) R_H distribution function obtained from CONTIN analysis of the normalized autocorrelation function 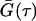(B) for 2:1 DMPC/Ca²⁺ samples at various concentrations (C_lp = 2, 0.5, and 0.25 wt %) and 15°C. A single modal distribution with R_H ∼ 100 Å is found for 2 wt % samples, representing bicelles, whereas R_H of ∼450 Å for the C_lp = 0.25 wt % mixture is indicative of ULVs. However, the trimodal distribution function for C_lp = 1 wt % samples either represents the coexistence of heterogeneous structures or is an artifact due to strong interparticle interactions. (B) 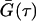for 2:1 DMPC/Ca²⁺ samples. Cumulant fits are depicted by dotted curves, whereas CONTIN fits are represented by solid curves. The 1 wt % sample exhibits a multimodal distribution (A) and could not be adequately described by the cumulant fit.

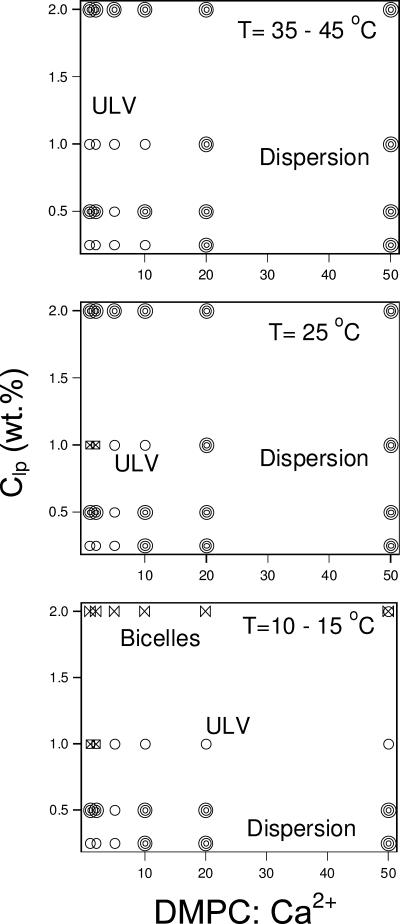
A partial phase diagram of the Ca²⁺-doped system is shown in Fig. 2. In the next section we discuss the effect of T, C_lp, and salt composition (DMPC/Ca²⁺) on the various structural parameters of this system.

FIGURE 2.

Structural phase diagram of Ca²⁺-doped samples as a function of T, C_lp, and the amount of Ca²⁺ dopant based on DLS results listed in Table 1. The phases represented by different symbols are: ULVs (circles); dispersion (multicircles); bicelles (bow ties); coexistence of bicelles and ULVs (circle + bow tie); and samples exhibiting multimodal (squares with cross inside).

T < T_M

Weakly doped systems (DMPC/Ca²⁺ ≥ 10). Table 1 shows that weakly doped systems (DMPC/Ca²⁺ ≥ 10:1) contain monodisperse bicelles at the highest concentration (2 wt %), the only exception being the sample with the lowest Ca²⁺ concentration (DMPC/Ca²⁺ = 50:1), which is made up of a combination of bicelles and large ULVs. As these samples are diluted, the opaqueness of the samples increases, probably indicating the formation of a dispersion.

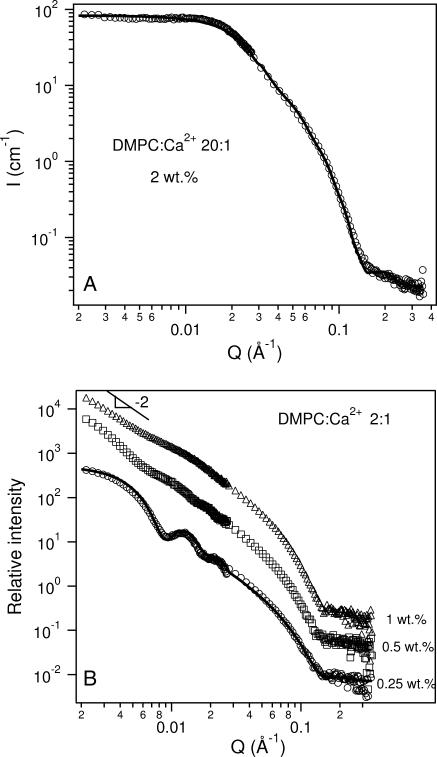
The SANS data for solutions of DMPC/Ca²⁺ = 20, presented in Fig. 3 A, are representative of the bicellar phase. From the best fit to the data, the bilayer thickness and the bicellar radius were found to be ∼50 and ∼110 Å (Table 4), respectively. This value of the bilayer thickness is consistent with the thickness of gel phase DMPC bilayers (Hung and Chen, 2000).

FIGURE 3.

(A) SANS data for a 2 wt % sample of 20:1 DMPC/Ca²⁺ at 10°C. The best fit using a core shell disk (CSD) model (solid curve) shows good agreement with the data and is representative of bicelles. The fit parameters are listed in Table 4. (B) SANS data for 2:1 DMPC/Ca²⁺ samples at 10°C for C_lp values between 0.25 wt % and 1 wt %. Monodisperse ULVs are observed in the 0.25 wt % sample and the solid curve is the best fit using a core shell spherical (CSS) model. The fit parameters are shown in Table 5. For 1 wt % and 0.5 wt % samples, SANS data indicate a mixture of structures with the low-Q intensity exhibiting a Q⁻² dependence, indicative of large-sized particles. To better visualize the data, and fits to the data, they have been multiplied by arbitrary rescaling factors.

TABLE 4.

Best-fit parameters from SANS data of 2 wt % bicelle solutions at 10°C doped either with Ca²⁺ or DMPG

Dopant	〈Rbic〉 (Å)	Bilayer Thickness (Å)	Charge (e/bicelle)
Ca2+ 20:1	106 ± 4	50 ± 2	–
Ca2+ 2:1	106 ± 4	50 ± 2	–
DMPG 305:1	113 ± 5	50 ± 2	–
DMPG 205:1	117 ± 4	50 ± 1	–
DMPG 155:1	117 ± 5	50 ± 2	–
DMPG 65:1	104 ± 3	43 ± 2	19 ± 2
DMPG 35:1	99 ± 3	44 ± 2	32 ± 3

A transition from bicelles to ULVs was found in solutions with DMPC/Ca²⁺ molar ratios ≥10 as the sample was diluted to 1 wt %. Further dilution (concentration ≤0.5 wt %) resulted in the sample becoming opaque (Struppe and Vold, 1998), with DMPC precipitating out of solution as a result of DHPC demixing from DMPC. In the ULV regime (1 wt %), R_H decreased with increasing amounts of Ca²⁺. This observation does not follow the prediction of the VCM put forth by Oberdisse and Porte (1997) that predicts an increase in the vesicular size with increasing salt concentration. As VCM does not take into account the association of salts with the surface of the membrane, the decreasing ULV size may possibly be explained by the fact that Ca²⁺ ions bind with DMPC, imparting a charge density to the ULVs. As a result of this charge, the ULVs become smaller with increased surface charge density, which is predicted by VCM.

Moderately doped systems (DMPC/Ca²⁺ = 5). Samples with DMPC/Ca²⁺ = 5 start off as bicelles, at high lipid concentrations, but are dominated by the presence of ULVs at lower lipid concentrations. This lipid/salt ratio is unique in its ability to form stable ULVs. Going from 1.0 wt % to 0.5 wt %, R_H increased from 310 Å to 870 Å. However, diluting the system further to 0.25 wt % resulted in R_H of 550 Å. One possible explanation for this variation in R_H is that upon dilution, the total lipid concentration, ionic strength of the solution, and the charge density on the ULV surface all change simultaneously. VCM predicts that a decrease of the former two parameters would result in a slow decrease in vesicular size. On the other hand, a decrease in charge density would dramatically increase the vesicular size. As a result, vesicular size is directly dependent on whichever of these parameters dominates. It is possible that the dissociation of Ca²⁺ ions from the lipids might overwhelm both the dilution and salinity effects resulting in a substantial change in R_H in the concentration range between 1 wt % and 0.5 wt %, whereas the dilution and salt effects may dominate when C_lp changes from 0.5 wt % to 0.25 wt %.

Highly doped samples (DMPC/Ca²⁺ ≤ 2). Unlike the weakly doped samples, the phase sequence for highly doped systems upon dilution is as follows: bicelle → unknown aggregates → ULV. The bicelles seen at the highest lipid concentrations are very similar to those observed at other doping ratios. However, the size distribution function for 1 wt % solutions at 15°C, obtained from CONTIN analysis (Fig. 1 B), shows a trimodal distribution of R_H. As mentioned previously, this method is better suited for systems exhibiting either unimodal or bimodal distributions of R_H. As such, the trimodal distribution obtained might not truly reflect the structure of this solution. For solutions at 0.5 wt %, a stable could not be obtained as the intensity was close to the count rate limit of the instrument, and hence the size of the aggregates is not known. The most dilute samples (0.25 wt %) yielded monodispersed ULVs with R_H ∼ 450 Å.

The presence of ULVs in the most dilute sample was verified from SANS data (Fig. 3 B shows that for DMPC/Ca²⁺ 2:1). Table 5 shows that the vesicular shell thickness (one bilayer thick) is ∼38 Å, smaller than the thickness observed in bicelles, possibly resulting from higher intermixing levels of DMPC and DHPC taking place in ULVs. Note that the average outer radius of the vesicles, R_ves, is 340 Å (Table 5), smaller than the 500 Å radius obtained from DLS (Table 1). This may be explained by the fact that R_ves from the SANS model was obtained on the basis of the volume average (Hayter, 1985), whereas, as mentioned previously, the R_H from DLS measurements is derived based on the intensity average (z-average) (Pencer et al., 2001). For C_lp = 0.5 wt %, SANS data (Fig. 3 B) contain weak oscillations along the scattering curve, indicative of reasonably monodisperse ULVs. At low Q, the scattering data of 0.5 wt % and 1 wt % samples exhibit a slope of ∼−2. This is characteristic of objects with a large and reasonably flat surface, possibly large ULVs, MLVs, or extended lamellae.

TABLE 5.

Best-fit parameters from SANS data of ULV solutions at various temperatures, times, lipid concentrations, and dopants

T (°C)	Dopant ratio	Clp wt %	Time	〈Rves〉 (Å)	Bilayer Thickness (Å)	Polydispersity
10	Ca2+ 2:1	0.25	–	339 ± 10	37 ± 2	0.16 ± 0.02
	DMPG 155:1	0.5	–	330 ± 10	39 ± 2	0.18 ± 0.03
		0.25	–	319 ± 15	40 ± 3	0.19 ± 0.02
45	Ca2+ 2:1	1	5 h	386 ± 20	31 ± 2	0.24 ± 0.02
			4 days	425 ± 5	33 ± 3	0.18 ± 0.02
			2 weeks	510 ± 25	30 ± 3	0.28 ± 0.04
		0.25	–	388 ± 15	33 ± 2	0.17 ± 0.02
	DMPG 155:1	1	–	378 ± 15	31 ± 3	0.23 ± 0.01
		0.5	3 h	381 ± 10	34 ± 2	0.16 ± 0.02
			4 days	382 ± 15	34 ± 2	0.15 ± 0.02
			2 weeks	332 ± 10	32 ± 3	0.19 ± 0.02
		0.25	–	363 ± 20	33 ± 2	0.22 ± 0.03
	DMPG:Ca2+	1	–	415 ± 5	33 ± 2	0.11 ± 0.02
	155:2:1	0.25	–	267 ± 20	32 ± 2	0.22 ± 0.03

Thus for Ca²⁺-doped mixtures at T ≤ T_M (Fig. 2), we can summarize the results as follows: a), For C_lp ≥ 2 wt %, bicelles are the predominant or only morphology present in all solutions studied. b), For 0.5 wt % ≤ C_lp ≤ 1 wt %, further doping the DMPC/DHPC with Ca²⁺ to a lipid/salt ratio of 5:1 has the effect of transforming a dispersion (possibly MLVs) into ULVs as a result of Ca²⁺ ions binding with lipid molecules and thus increasing the charge density of the bilayers. However, strongly doped mixtures with the same C_lp form a variety of structures. c), For C_lp = 0.25 wt %, not only do ULVs form upon increasing Ca²⁺ concentration, but they are also stable at the highest Ca²⁺ concentration. d), At constant C_lp, increasing the Ca²⁺ concentration yields ULVs with a smaller R_H.

T > T_M

We have previously reported, over a similar range of concentrations, but at temperatures greater than T_M, the transformation of bicellar mixtures into MLVs, or ULVs (Nieh et al., 2001, 2002, 2003). One can explain the structural transitions by considering the following scenarios. One is the decrease in bilayer rigidity above T_M, which can in principle favor the formation of ULVs (Israelachvili, 1992). Another is the phase separation of DHPC and DMPC resulting in the formation of DMPC MLVs and DHPC micelles. Finally, an unbinding of individual bilayers from the MLVs may be taking place, producing ULVs (Mutz and Helfrich, 1989). All of them, to a greater or lesser extent, may play a role in the resultant morphologies. For the phase diagram at T > T_m (Fig. 2), the phase transitions tentatively attributed to the above-mentioned factors will be discussed in detail.

Weakly doped systems (DMPC/Ca²⁺ ≥ 10). Nearly all of the weakly doped mixtures became turbid and exceeded the maximal intensity limit for DLS at elevated T. This is possibly indicative of MLV formation due to the demixing of DMPC and DHPC (Struppe and Vold, 1998). However, at a DMPC/Ca²⁺ ratio of 10:1, dilution caused the formation of a dispersion at intermediate concentrations between two ULV phases. Of note is that the size of the most dilute ULVs (0.25 wt %) is ∼900 Å, in contrast to ∼300–600 Å for samples at a higher concentration (1 wt %). Suffice it to say that more studies are needed to unravel the details of these transitions. Also, as the temperature increases from 25°C, we observe the formation of ULVs from the dispersion, possibly due to the unbinding of MLVs in this most dilute sample, instead of the expected demixing of the two lipids (Struppe and Vold, 1998).

Moderately doped systems (DMPC/Ca²⁺ = 5). For moderately doped systems (DMPC/Ca²⁺ 5:1) and T > T_M, ULVs dominate the phase diagram, although the highest lipid concentration now gives rise to a dispersion (possibly MLVs) rather than bicelles. Further, the ULV radii are similar for T > T_M and T < T_M. However, the size of ULVs shows a maximum at a concentration of 0.5 wt % (Table 1).

Strongly doped systems (DMPC/Ca²⁺ ≤ 2). When the temperature is raised above the main transition, DLS studies show that highly Ca²⁺-doped samples at 1 wt % form ULVs, whereas at lower temperatures they contain unresolved structures. R_H of very dilute samples shows a weak temperature dependence (Table 1), such that at 45°C dilute ULVs are larger than those formed at higher concentrations. This is most noticeable in the DMPC/Ca²⁺ 2:1 sample, where at 45°C, R_H is 535 Å for 0.25 wt % and 394 Å for 1 wt %. However, R_ves as determined by SANS (Table 5) indicates that these ULVs are in fact of similar size, and that only over time does the radius increase. This may be due to long-range electrostatic interactions between the ULVs, which can lead to lower values of the hydrodynamic radius, R_H, as measured by DLS (Philipse and Vrij, 1988; Riese et al., 2000). Also, the DLS studies could not be carried out on samples of C_lp = 0.5 wt %, as in the case of T < T_M, since the scattering intensity exceeded the limit of the instrument.

In summary, above the DMPC main transition temperature (T_M > ∼23°C), a dispersion (presumably MLVs) predominates in weakly charged systems. For moderately and heavily doped samples, ULVs are observed at C_lp of 1 and 0.25 wt %. Also, structures that cannot be resolved by DLS, and unexpectedly large ULVs are found in 0.5 wt % samples with DMPC/Ca²⁺ ≤ 10, at low and high temperatures, respectively.

DMPG-doped solutions

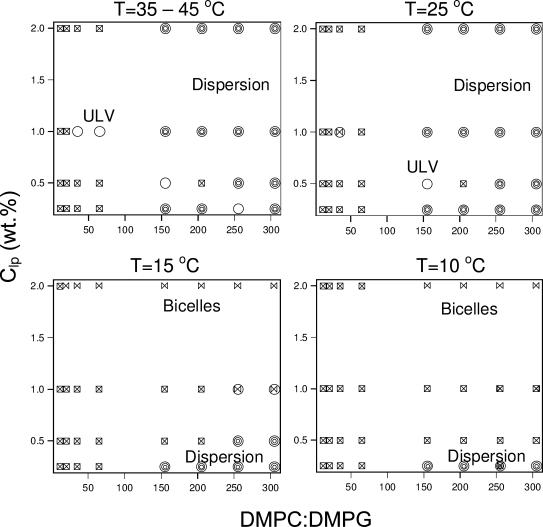
Unlike Ca²⁺ ions, DMPG lipid molecules integrate with the DMPC/DHPC bilayer and impart a higher charge density for the same molar dopant ratio. Further, the charge imparted to the bilayer is independent of dilution. The various structures determined from DLS measurements of DMPG-doped mixtures are shown in Fig. 4 and are summarized in Table 2.

FIGURE 4.

Structural phase diagram for DMPG-doped samples as a function of T, C_lp, and the amount of DMPG dopant, based on DLS results shown in Table 2. The phases represented by the symbols are: ULVs (circles); dispersion (multicircles); bicelles (bow ties); coexistence of bicelles and ULVs (circle + bow tie); and multimodal size distribution from CONTIN analysis (squares with cross inside).

TABLE 2.

Summary of DLS results from DMPG-doped samples at various temperatures, dopant compositions, and total concentrations

		Temperature (°C)
		<TM						>TM
		10		15		25		35		45
DMPC/DMPG	Clp wt %	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)	Type	RH (Å)
305	2	Bic	92	Bic	93	Disp*		Disp		Disp
	1	MM†		B/ULV‡	101/2404	Disp		Disp		Disp
	0.5	MM		MM		Disp		Disp		Disp
	0.25	Disp		Disp		Disp		Disp		Disp
255	2	Bic	82	Bic	84	Disp		Disp		Disp
	1	MM		B/ULV	130/1203	Disp		Disp		Disp
	0.5	MM		MM		ULV	424	Disp		Disp
	0.25	MM		MM		MM		ULV	772	ULV	831
205	2	Bic	99	Bic	83	Disp		Disp		Disp
	1	MM		MM		Disp		Disp		Disp
	0.5	MM		MM		MM		MM		MM
	0.25	Disp		Disp		Disp		Disp		Disp
155	2	Bic	70	Bic	70	Disp		Disp		Disp
	1	MM		MM		Disp		Disp		Disp
	0.5	MM		MM		ULV	387	ULV	320	ULV	324
	0.25	Disp		Disp		Disp		Disp		Disp
65	2	MM		Bic	44§	MM		MM		MM
	1	MM		MM		MM		ULV	302	ULV	297
	0.5	MM		MM		MM		MM		MM
	0.25	MM		MM		MM		MM		MM
35	2	MM		Bic	30§	MM		MM		MM
	1	MM		MM		B/U‡	94/1550	ULV	177	ULV	179
	0.5	MM		MM		MM		MM		MM
	0.25	MM		MM		MM		MM		MM
20	2	MM		Bic	19§	MM		MM		MM
	1 → 0.25	MM		MM		MM		MM		MM
11	All	MM		MM		MM		MM		MM

^*Disp, dispersions.

^†MM, samples for which CONTIN analysis gives multimodal size distributions.

^‡B/U, bimodal distribution obtained through CONTIN analysis.

^§Single exponential decay of DLS measurement was obtained at 20°C instead of 15°C.

T < T_M

Weakly doped systems (DMPC/DMPG ≥ 255). We take weakly DMPG-doped samples to be composed of DMPC/DMPG ratios ≥ 255. After doping with DMPG, all of the 2 wt % mixtures became transparent at low T, and R_H values indicate the presence of monodispersed bicelles for all samples at temperatures between 10°C and 15°C. Diluting these samples results in either a bicelle → ULV → dispersion transition or a bicelle → dispersion transition.

Moderately doped systems (205 ≥ DMPC/DMPG ≥ 155). Systems with DMPC/DMPG ratios between 155:1 and 205:1 exhibit a similar phase behavior as the above-mentioned weakly doped systems. At the highest lipid concentrations, bicelles are formed, whereas the most dilute samples form a dispersion. As mentioned previously, this dispersion probably occurs due to phase separation. The SANS data (Fig. 5), collected 2 weeks after the DLS studies, show the presence of ULVs for C_lp = 0.25 and 0.5 wt % for a DMPC/DMPG ratio of 155:1 and T = 10°C. No Bragg peak (at Q ∼ 0.1 Å⁻¹) is observed, implying that there are no MLVs in the solution. However, the turbidity of the sample decreased over the 2-week interval, and hence it is possible that MLVs initially present in the solution had transformed into ULVs by the time the SANS studies were carried out.

FIGURE 5.

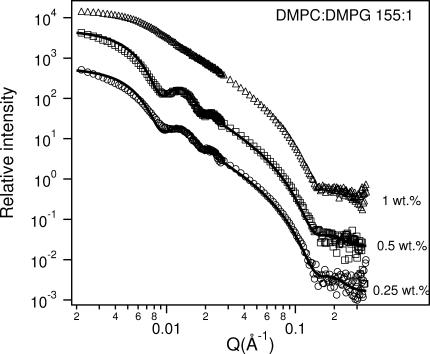
SANS data from 155:1 DMPC/DMPG samples for various C_lp at 10°C . With the exception of the 1 wt % sample, ULVs are observed. The best-fit parameters for ULVs are shown in Table 5. To better visualize the data and the fits to the data, they have been multiplied by arbitrary rescaling factors.

Of note is that for a C_lp = 2 wt %, the bicelles have radii of ∼90 Å (Table 2), the only exception again being the sample with a DMPC/DMPG ratio of 155:1, whose R_H was determined to be ∼70 Å. A possible reason for this exceptional behavior is discussed later.

Strongly doped systems (65 ≥ DMPC/DMPG). DLS measurements indicated multimodal distributions for nearly all concentrations and ratios studied. Moreover, the samples were transparent, indicative of the presence of small structures such as bicelles or ULVs. The complex size distributions make DLS results difficult to interpret. However, previous SANS measurements on this system indicate the formation of bicelles, whose size is independent of concentration (Nieh et al., 2002).

The complex multimodal size distribution is the result of a nonexponential decay of the field autocorrelation function observed at the high τ regime. In the case of Ca²⁺-doped samples exhibiting this behavior, SANS shows an unresolved structure, which is reflected in the uncertainty of the measured R_H (e.g., Fig. 1 B, 1 wt % 2:1 at 10°C). On the other hand, SANS data of DMPG-doped systems, where nonexponential decay of the autocorrelation function is found, clearly show the existence of bicelles. The uncertainty in the DLS data most probably stems from the presence of complex interparticle interactions, as shown by Nägele and Baur (1997), who have proposed the “dynamic cage effect” to explain this type of behavior. Unlike Ca²⁺-doped mixtures, the only water-soluble ions in DMPG-doped samples are Na⁺ ions dissociating from the DMPG lipid molecules themselves. As a result, these solutions are of low ionic strengths. We therefore suspect that the DLS data are affected by the strong interparticle interactions in these systems, and give rise to the nonexponential decay of the intensity autocorrelation functions, which could then be interpreted as a population of larger particles. However, currently, we are unable to unambiguously determine whether or not the nonexponential decay seen for long relaxation times results from the presence of particles of different sizes or from long-range interactions between particles of one size.

Stable bicelles were measured only for dilute samples near T_M. The R_H of these bicelles is considerably reduced compared with the weakly doped systems indicating that the effective diffusion coefficient, D_eff, derived from the cumulant analysis becomes larger with increasing charge density. The same phenomenon has been reported by other groups (Philipse and Vrij, 1988; Riese et al., 2000), who described the strong Q-dependence of D_eff for charged particles in an extremely low ionic strength solution (i.e., large Debye screening length). For such a system, the structure factor, S(Q), has a peak centered at Q_max resulting from the positional correlations between the particles. The effective diffusion coefficient in such a case is dependent on Q, and can be approximated as D_eff ∼ D_o/S(Q), where D_o is the diffusion coefficient in the absence of interparticle interactions. The Q-dependence of D_eff means that its value could be much larger than that for a neutral particle of the same size, as the value of Q in DLS is much smaller than the Q_max of the system, so that S(Q), due to the repulsive interparticle interactions, is ≪1.

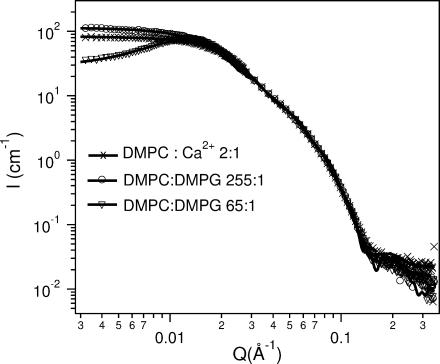
SANS data presented in Fig. 6 are consistent with the conclusions derived from the DLS studies. An intensity peak was observed in the vicinity of Q_max = 0.013–0.014 Å⁻¹, indicative of strong interparticle interactions due to electrostatic repulsion. Note that D_eff from DLS was measured at Q = 0.0011 Å⁻¹, an order of magnitude smaller than the Q_max determined by SANS. As a consequence, a smaller R_H (i.e., larger D_eff, Table 2) is expected when Q ≪ Q_max. To verify that the variance of R_H is mainly the result of strong interparticle interactions, the bicellar size was determined from SANS data. The best fits shown in Table 4 closely agree with the corresponding SANS data (Fig. 5).

FIGURE 6.

SANS data for 2 wt % samples of molar ratio 255:1 DMPC/DMPG (circles) and 65:1 (triangles) at 10°C. The crosses are the 2:1 DMPC/Ca²⁺ data at 10°C. For all three samples the high-Q data collapse onto each other indicating that all three samples have morphologies with the same bilayer thickness. Curves corresponding to the symbols are the best fits. The 255:1 DMPC/DMPG and the 2:1 DMPC/Ca²⁺ samples are best described by the core shell disk (CSD). On the other hand, because of the strong electrostatic interactions, the 65:1 DMPC/DMPG mixture is best fitted using a combination of the CSD model and MSA structure factor. The best-fit parameters for all three systems are shown in Table 4.

In summary, the low ionic strength of the solutions results in strong interparticle interactions, and as such, DLS cannot conclusively determine the structures present in DMPG-doped solutions. However, judging from the SANS data, bicelles generally exist at the highest concentrations (2 wt %). Moreover, SANS data indicate the presence of relatively monodisperse ULVs at 10°C for samples with DMPC/DMPG, 155:1 and C_lp = 0.25 wt % and 0.5 wt %.

T > T_M

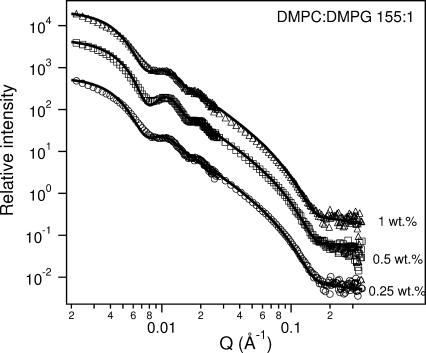
Weakly and moderately doped systems (DMPC/DMPG ≥ 155). Above the phase transition temperature, the amount of charge in the weakly doped samples is not enough to prevent the formation of a dispersion (presumably MLVs). However, in some cases, dilution results in the formation of ULVs (DMPC/DMPG = 255, 0.5 wt % at 25°C and 0.25 wt % at 35°C and 45°C). This is also generally true for moderately doped samples, although at 0.5 wt %, non-MLV, weakly turbid samples were observed. For a DMPC/DMPG ratio of 205:1, DLS shows a multimodal size distribution. However, at a ratio of 155:1 only ULVs are formed. The R_H for the 0.5 wt % preparation is characteristic of a sample that is reasonably monodisperse throughout the temperature range from 25°C to 45°C. In Figs. 5 and 7, we present SANS data at 10°C and 45°C for DMPC/DMPG mixtures with a molar ratio of 155:1 and several values of C_lp. ULVs are observed at both temperatures for C_lp = 0.25 wt % and 0.5 wt %, whereas ULVs are only seen for the 1 wt % mixture at 45°C. Further analysis based on the CSS model and MSA structure factor reveals detailed structural information of the ULVs, and are summarized in Table 5. The R_ves values are invariant upon dilution, but increase from ∼320 Å to ∼380 Å as T increases from 10°C to 45°C (Table 5). The bilayer thickness obtained from fitting the data (Table 5) is smaller at higher T (∼32 Å, whereas bilayer thickness is ∼38 Å at low T), and is consistent with the fact that the melted DMPC acyl chains are more flexible in the high-T L_α phase, compared to their “stretched-out” state at low T.

FIGURE 7.

SANS data for various C_lp 155:1 DMPC/DMPG samples at 45°C. ULVs are observed in all cases. The best-fit parameters for ULVs are shown in Table 5. To better visualize the data and the fits to the data, they have been multiplied by arbitrary rescaling factors.

Strongly doped samples (65 ≥ DMPC/DMPG). Highly doped DMPG samples exhibit complex behavior both above and below the main transition temperature. Particle interactions in such strongly charged systems overwhelm the propensity of DMPC to form MLVs, although it is difficult to say with any certainty whether the dominant structures are bicelles or ULVs. For two molar ratios of DMPC/DMPG (65:1 and 35:1) and a C_lp of 1 wt %, the samples exhibit practically a single modal distribution (i.e., presence of one dominant structure) at higher T, possibly as a result of ULV formation.

In summary, there are two major differences between the DMPG-doped systems at T > T_M and those at T < T_M. The first is that at T > T_M and for the highest lipid concentration (2 wt %), the bicelles become unstable and transform into a dispersion (possibly MLVs) or a mixture of heterogeneous structures. The second difference is that the range of DMPC/DMPG molar ratios giving rise to ULVs is extended (i.e., between 35:1 and 155:1).

Both Ca²⁺- and DMPG-doped solutions

Solutions doped with either high or low concentrations of both Ca²⁺ and DMPG have a translucent appearance, regardless of temperature. This can be attributed either to Ca²⁺-induced aggregation of ULVs, or to the formation of MLVs due to the demixing of DMPC and DHPC. To remain transparent, a solution has to contain a high concentration of either DMPG or Ca²⁺, not both. This observation is consistent with the observation by Kaler et al. (1992), who reported that ULV formation is not favored when both positive-and negative-charged surfactant species are present in equal quantities.

At T < T_M, R_H values for mixtures of DMPC/DMPG = 155 and DMPC/Ca²⁺ = 2 indicate the presence of monodisperse particles. For the highest C_lp bicelles of R_H ∼ 100 Å were observed, whereas the lowest C_lp formed ULVs with R_H ∼ 480 Å. However, a multimodal distribution was found for intermediate concentrations, whereas the intensity exceeded the DLS instrumental limit for the sample of 0.5 wt % (Table 3). For T > 35°C, all of the samples with C_lp ≤ 1 wt % formed ULVs. ULVs in the 0.25 wt % sample were especially stable over the entire temperature range studied (10°C ≤ T ≤ 45°C).

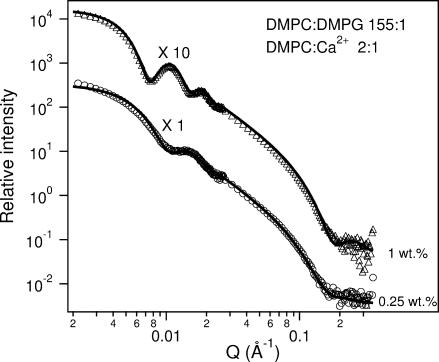
Fig. 8 contains the SANS results for the 1 wt % and 0.25 wt % mixtures at 45°C and their best fits using the CSS + MSA model. Note that unlike the singly doped systems (e.g., either Ca²⁺ or DMPG), upon dilution the first SANS peak shifts toward higher Q values indicating that R_ves decreases dramatically with decreasing C_lp (Table 5). Such behavior is consistent with our previous results (Nieh et al., 2001) as well as the prediction by VCM (Oberdisse and Porte, 1997). On the other hand, DLS data (Table 3) shows no clear trend as a function of C_lp. This conflict between the DLS results and the SANS data (Table 5) as a function of C_lp is possibly due to the strong interparticle interactions affecting the value of R_H, which was calculated using the Stokes-Einstein formula. Finally, DLS results for samples with molar ratios of DMPC/DMPG = 10 and DMPC/Ca²⁺ = 50, at 2 wt % and higher dilutions, although not opaque, show multimodal size distributions, indicating the presence of a variety of structures.

FIGURE 8.

SANS data for various C_lp samples doped with both DMPG and Ca²⁺ (DMPC/DMPG 155:1 and DMPC/Ca²⁺ 2:1) at 45°C. The triangles and circles represent 1 wt % and 0.25 wt % samples, respectively. Solid curves are the best fits using the CSS model combined with the MSA structure factor. The fits are in very good agreement with the data indicating that both of these samples form ULVs. Of note is that the peak positions in the curves are different, and reflect the fact that the ULVs differ in size. The best-fit parameters are presented in Table 5. Both the data and the best fits are multiplied by arbitrary rescaling factors for better viewing.

Concentration effect and time evolution of the ULV

Although the spontaneous formation of ULVs has been previously reported (see Introduction), as predicted by VCM, their size has always been found to be concentration-dependent (Schurtenberger et al., 1985; Kaler et al., 1989; Oberdisse and Porte, 1997; Egelhaaf and Schurtenberger, 1999; Bergstrom and Pedersen, 2000). Our experimental data from samples doped with both Ca²⁺ and DMPG are consistent with these observations. However, in striking contrast are the samples that are doped with either Ca²⁺ or DMPG. Both of these mixtures contain monodisperse ULVs whose size is invariant as a function of lipid concentration (e.g., DMPC/Ca²⁺ = 2, at 45°C, and DMPC/DMPG = 155, 1–0.25 wt % at both 10°C and 45°C). The importance of interparticle interactions can be deduced from the values of the intervesicular distance and the Debye length. The intervesicular distance (d_ves) can be estimated as

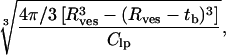resulting in a value of ∼1700 Å for the 1 wt % solution at a DMPC/DMPG molar ratio of 155, using R_ves = 378 Å and t_b = 31 Å (Table 5). The Debye length for this system is ∼375 Å, which is comparable to (d_ves – 2 R_ves), the typical separation between the surfaces of two neighboring vesicles. Hence, strong intervesicular interactions are present at these concentrations. It is interesting that despite these strong interactions, the ULV size remains invariant upon dilution.

Helfrich (1973) derived the curvature energy, F, for a membrane to be 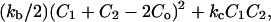where k_b and k_c are the bending and the Gaussian curvature moduli, respectively, whereas C₁ and C₂ are the two principal curvatures (for spherical vesicles C₁ = C₂ = 1/R_ves) and C_o is the spontaneous curvature. Winterhalter and Helfrich (1992) also found that imparting a charge to the system results in a larger, effective k_b while at the same time lowering the effective k_c. This contribution lowers the free energy and favors the formation of vesicles. However, it is not clear if this mechanism can account for the observed insensitivity of the vesicle size to dilution.

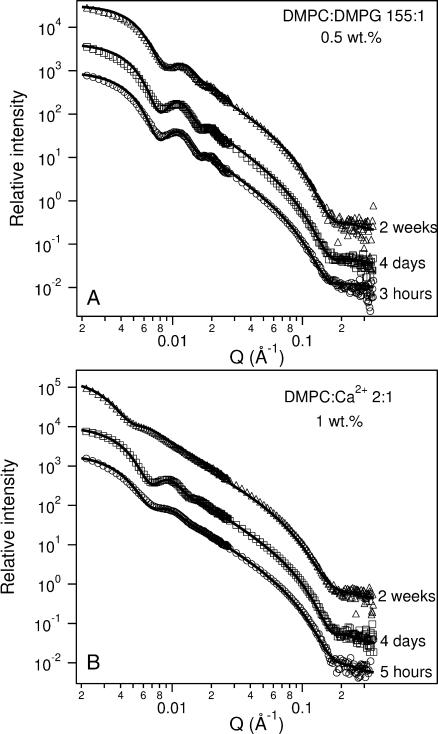
To the best of our knowledge, in the only report of ULV size as a function of time, Yatcilla et al. (1996) reported that ULVs composed of cetyltrimethyl ammonium bromide (CTAB) and sodium octyl sulfate rapidly increased in size after initial formation, and only attained equilibrium size after an extended period of time. However, our SANS result for the sample with DMPC/DMPG = 155 (C_lp = 0.5 wt %) demonstrates that these ULVs are stable and monodisperse over a period of 4 days at 45°C (Fig. 9 A). However, R_ves does get slightly smaller (332 ± 10 Å) and polydispersity increases after 2 weeks at 45°C from 0.16 ± 0.02 to 0.19 ± 0.02, indicating either a very slow equilibration of the ULVs or a gradual degradation of the lipids at these relatively high temperatures.

FIGURE 9.

SANS data of ULV time dependence for (A) 0.5 wt % 155:1 DMPC/DMPG and (B) 1 wt % 2:1 DMPC/Ca²⁺ incubated at 45°C. DMPG-doped ULVs remain unchanged, both in size and polydispersity, over a period of 4 days. However, both the size and the polydispersity of Ca²⁺-doped ULVs are found to vary with time. The best-fit parameters are shown in Table 5. To better distinguish between the data and the best fits, arbitrary rescaling factors have been used.

Analysis of Ca²⁺-doped ULVs (Fig. 9 B), on the other hand, indicates a result much similar to that reported by Yatcilla et al. (1996) where, after 4 days, R_ves increased from 386 Å to 425 Å and finally, after 2 weeks of incubation at 45°C, to 510 Å (Table 5). Polydispersity decreased after 4 days and then increased after 2 weeks. For this mixture, it seems that the ULVs are continuously fusing and forming larger ULVs with time. From the DMPG- and Ca²⁺-doped systems data, we speculate that the time dependence of the Ca²⁺-doped ULV size may be related to the fact that the bilayer charge density varies with time as Ca²⁺ ions desorb. On the other hand, since the hydrophobic portion of DMPG molecules is always embedded in the membrane, the surface charge density is essentially fixed for DMPG-doped ULVs.

Effect of temperature on the stable ULVs

As mentioned previously and summarized in Table 5, for samples with DMPC/DMPG = 155 and DMPC/Ca²⁺ = 2, the values for R_ves obtained from SANS are larger above T_M than below. This observation is unexpected since the bending modulus, k_b, of the membrane increases as the phase goes from L_α to gel, and therefore, so does the bending free energy (Helfrich, 1973) for the membrane of same curvature (i.e., 1/R_ves for the vesicular case). Yuet and Blankschtein (1996b) have proposed a theoretical model in which they calculate the total free energy of surfactant mixtures at a molecular level, and find that smaller ULVs can be obtained upon increasing the asymmetry of hydrophobic tail length between the two surfactants. Since the asymmetry between long- and short-chain PCs increases when DMPC is in the gel phase, this trend is in agreement with our observations. However, it should be pointed out that the above theory considers bilayers in the L_α phase, and may not be applicable to the present situation. More recently, Jung et al. (2001) have studied the formation of ULVs made up of “stiff” and “flexible” surfactants, CTAB/ sodium octyl sulfate and CTAB/sodium perfluorooctanoate, respectively. The stiffer mixture was found to give rise to smaller and more monodisperse ULVs. This trend is again in agreement with what we observe, although the fact that these experiments were carried out in the L_α phase makes a direct comparison somewhat more difficult.

Another possibility is that ULVs formed in the L_α phase, are trapped in the gel phase. From the structural parameters, we find the change in the ULV size across the transition to correspond to ∼10% decrease in the bilayer volume, which is of the same order of magnitude as the change in the density across the gel → L_α phase transition.

CONCLUSIONS

The structure and particle size of charge-doped DMPC/DHPC mixtures at low lipid concentrations (≤2 wt %) have been examined as a function of charge density, salt concentration, temperature, lipid concentration, and time. The primary findings are as follows:

1. Contrary to almost all previously published experimental results, SANS data show an invariant R_ves value for monodisperse ULVs doped either with DMPG (DMPC/DMPG = 155) or Ca²⁺ ions (DMPC/Ca²⁺ = 2). The invariance of R_ves over a wide range of lipid concentrations and temperatures reflects the high stability of the present ULVs. These properties (monodispersity, invariant R_ves and temporal stability) are qualities that may be appealing for drug delivery and other controlled release applications.

2. The vesicle cell model proposed by Oberdisse and Porte (1997) can, to some extent, explain the trend of R_ves as a function of surface charge density. However, this theory does not predict the observed independence of R_ves on C_lp in both of the singly doped systems.

3. The increase of R_ves with increasing T in 155:1 DMPC/DMPG mixtures and in some Ca²⁺-doped samples might be attributed to the changes in the bilayer rigidity. It is also conceivable that the ULVs, formed in the L_α phase, are trapped in the much more rigid gel phase. More studies are required to understand this behavior.