Scaling and Mean-Field Theories Applied to Polymer Brushes

Analysis of the osmotic pressures of aqueous poly(ethylene glycol) solutions indicates a power-law behavior in the range of volume fractions from 0.08–0.12 to 0.33 or higher, for polymers with average molecular masses in the range 1500–4000 Da. The exponent of the power law is closer to a value of 2, which is predicted by mean-field theory, than to the value of 5/4, which is predicted by scaling theory for a good solvent. The latter value is attained by long polymers, with molecular masses 8000–20,000 Da. Quantitative predictions of the repulsive pressure between grafted polymer brushes requires a further scaling factor, additional to that relating bulk osmotic pressure and polymer volume fraction, in both scaling and mean-field theories.

Recently, Hansen et al. (2003) established the validity of scaling theory applied to lipid-grafted polymer brushes. The criterion used was that the effective monomer concentration of polymer in the brush should equal that at which the osmotic pressure, Π_f, of the corresponding free poly(ethylene glycol) (PEG) polymer in bulk solution conforms to that for a very long polymer, PEG:20,000. With the latter, the dependence of Π_f on volume fraction, φ_f, of free polymer is that predicted by scaling theory for a good solvent, viz., 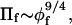over a wide range of φ_f in the semidilute regime. This criterion is achieved in polymer brushes only for relatively long PEG polymers at relatively high grafting densities, e.g., PEG:5000 lipid at a mol fraction of X₅₀₀₀ ≅ 0.07–0.1, or PEG:2000 lipid at a mol fraction X₂₀₀₀ ≅ 0.23 (Hansen et al., 2003). These contents of PEG lipid exceed those at which micellization is initiated in unsupported liposomal membranes (Montesano et al., 2001), and those that are used routinely in the steric stabilization of liposomes for drug delivery (Lasic and Needham, 1995).

It is therefore of considerable practical interest to inquire as to whether, with less restrictive criteria, scaling-theory behavior could still be fulfilled in polymer brushes. The requirement of convergence to universal behavior, independent of molecular weight, used by Hansen et al. (2003) ensures a fortiori that scaling theory holds. Nevertheless, it is possible that the characteristic power-law dependence of Π_f on volume fraction of free polymer might be achieved with smaller polymers before strict conformity to the osmotic pressure of the very long polymers is reached. An associated consideration is the extent to which mean-field theory might apply to the polymer brush. It is likely that criteria for the latter may be less restrictive than for scaling theory, because uniform monomer density throughout the brush is not required by mean-field theory of stretched polymers (Pincus, 1991; Milner et al., 1988). In addition to scaling theory, mean-field theory also has been used extensively for interpreting data on polymer-lipid brushes (Hristova and Needham, 1994; Marsh et al., 2003; Netz and Andelman, 2003). For free polymers in bulk solution, the dependence of osmotic pressure on polymer volume fraction predicted by mean-field theory is 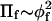in the semidilute regime, which differs significantly from that for scaling theory (De Gennes, 1979). The mean-field prediction corresponds to dominance of the second-order term in a virial expansion, for the semidilute regime.

In the above connection, it is worthwhile to review the predictions of scaling theory over the entire range of polymer concentration. At very low mol fractions, the osmotic pressure of the dilute polymer will obey the ideal “gas” law: 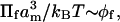with exponent one. At higher volume fractions, the more general version of scaling theory is (Grosberg and Khokhlov, 1994):

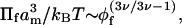(1)

where v is the exponent associated with the Flory radius of the polymer, 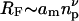, with n_p being the degree of polymerization. For a good solvent: v = 3/5, which leads to the familiar scaling theory exponent of 9/4 in Eq. 1, for the semidilute regime. For an ideal solvent, however, which gives rise to effective Gaussian behavior, the Flory exponent is v = 1/2, and the exponent of the osmotic pressure in Eq. 1 becomes 3. The latter may apply in the so-called melt regime at very high volume fractions, where correlation effects vanish and give way to effective Gaussian behavior, via the Edwards mechanism (Grosberg and Khokhlov, 1994; Netz and Andelman, 2003). With increasing volume fraction of polymer, therefore, scaling theory predicts a crossover from the dilute regime, for which the exponent of the osmotic pressure is one, to the semidilute regime where the exponent of the osmotic pressure is 9/4 for good solvents. Hence, it is possible that an osmotic pressure coefficient of 2, as predicted by mean-field theory, could represent a part of the crossover region between the dilute and semidilute regimes. By the same token, of course, a 9/4 power law might be viewed as part of the crossover between the semidilute and melt regimes. The distinction between crossover and semidilute behavior can only be decided experimentally. In what follows, we characterize the semidilute regime as a sustained region in which the dependence of osmotic pressure on polymer volume fraction is characterized by a single exponent, considerably greater than unity, up to at least moderately high concentrations. A further requirement is that the transition to the dilute regime, at low volume fractions, should take place relatively abruptly, i.e., over a considerably shorter interval.

Table 1 gives the exponent, m_f, of the power-law dependence of Π_f on φ_f for aqueous solutions of poly(ethylene glycol) (PEG) polymers of different lengths at room temperature. Values of m_f are obtained from linear regression of the logarithmic expression:

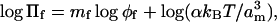(2)

to osmotic pressure data from Rand (2002), and from Reid and Rand (1997a,b) where not duplicated on the website. In Eq. 2 and above, a_m is the effective size of the monomer unit, α is the proportionality constant introduced by Hansen et al. (2003), k_B is Boltzmann's constant, and T is the absolute temperature. Values of the volume fraction, φ_f, were obtained from the weight fraction, w, of polymer according to the definition of the latter by Reid and Rand (1997a):

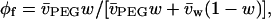(3)

where 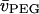and 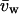are the partial specific volumes of PEG and water, respectively. A value of 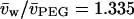was obtained from the densitometric data of Hasse et al. (1995) for PEG:4000 at 20°C. The latter corresponds to a monomer size of 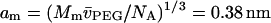, where M_m = 44.06 and N_A is Avogadro's number (cf., Evans et al., 1996).

TABLE 1.

Exponent, m_f, in the dependence of osmotic pressure on volume fraction, φ_f, of free poly(ethylene glycol) of various molecular weights (mol wt) in aqueous solution

Mol wt	mf	φf	(b3/b2) × φf*
1000	1.79 ± 0.04	0.08–0.43	0.0
1500	1.91 ± 0.07	0.12–0.53	0.1–0.5
2000	1.98 ± 0.05	0.08–0.33	0.4–1.5
3000	2.09 ± 0.06	0.08–0.29	0.4–2.0
4000	1.93 ± 0.05	0.08–0.29	0.0
6000	2.14 ± 0.08	0.08–0.29	0.3–1.2
8000	2.27 ± 0.07	0.08–0.29	0.4–1.4
10,000	2.27 ± 0.11	0.08–0.29	0.5–1.8
20,000	2.21 ± 0.03	0.02–0.40	0.1–1.2

Osmotic pressure, Π_f, from the listings by Rand (2002) and from Reid and Rand (1997a,b), where they are not duplicated on the website. Exponent is obtained by linear regression with: 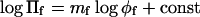. The range of φ_f-values used is indicated.

^*Ratio of third to second virial terms in Eq. 4 over the range of φ_f from which m_f is determined. Virial coefficients b₂ and b₃ were obtained from constrained fits of Eq. 4 truncated to the third term, over the full experimental range of φ_f.

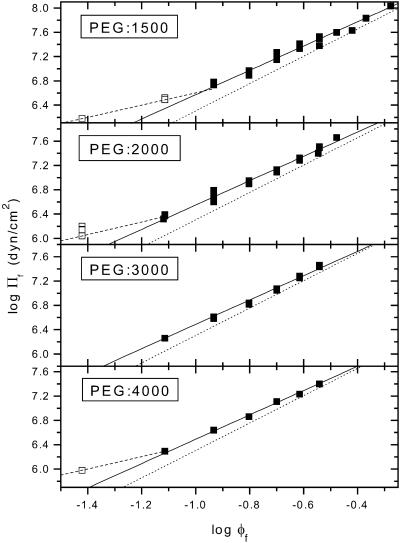
The results of Table 1 indicate a scaling-law behavior (m_f = 9/4) for the longer polymers, PEG:8000–PEG:20,000. However, for the shorter polymers, PEG:1500–PEG:4000, the power law corresponds better to that expected from mean-field theory (m_f = 2), and PEG:6000 exhibits intermediate behavior. Values of m_f significantly below two are obtained for PEG:1000 and yet-shorter polymers. Representative data for PEG:1500–PEG:4000 are shown in Fig. 1. In this case, the solid-line fits are with a fixed value of m_f = 2 (cf. Table 1). The dependence on φ_f for PEG in this size range differs systematically from that for the very long polymer PEG:20,000. A fit to the data for the latter with a fixed value of m_f = 9/4 (cf., Table 1) is indicated by the dotted lines in Fig. 1. As seen from Fig. 1 and Table 1, a characteristic m_f = 2 power-law behavior is displayed by PEG:2000–PEG:4000 from φ_f = 0.08 onwards, and from φ_f = 0.12 onwards for PEG:1500. For PEG:2000, this is a factor of two lower than the stricter criterion used by Hansen et al. (2003), and is comparable to the critical volume fraction for overlap: 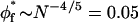for a polymer of length N = 45 monomers.

FIGURE 1.

Dependence of osmotic pressure, Π_f, of aqueous solutions of poly(ethylene glycol)s on volume fraction, φ_f, of free polymer. Data from Rand (2002), and from Reid and Rand (1997a,b), where they are not duplicated on the website. Molecular weight of the PEG is indicated. Solid lines are linear fits to the solid symbols, with fixed slope m_f = 2. Dotted lines are linear fits to data for PEG:20000 over the range φ_f = 0.02–0.40, with fixed slope of m_f = 9/4. Dashed lines represent a slope of m_f = 1 for the data at lowest volume fraction (open symbols).

From Fig. 1, it is clear that the osmotic pressure of the shorter polymers PEG:1500–PEG:4000 approximates to that of PEG:20,000, only at higher values of φ_f than those at which linearity (i.e., power-law behavior with m_f = 2) is attained. In this connection, it is significant that the pressure between bilayers containing 10 mol % PEG:5000 lipid is well described by scaling theory (Hansen et al., 2003). Whereas, on the other hand, the pressure between less dense brushes formed by 4.5 mol % PEG:2000 lipid is better described by mean-field theory (Efremova et al., 2000). In Fig. 1, the osmotic pressure is consistent with an exponent 2, up to the highest volume fractions for which measurements were made. This represents a considerable range of polymer concentrations. Only at the lowest volume fractions are there deviations from this constant power law. Then there is a relatively abrupt transition toward a region in which the exponent becomes ∼1. This crossover region is much narrower than the region of constant slope with m_f = 2. The latter is therefore identified with the semidilute regime.

An alternative means of analyzing osmotic pressure data from the free polymer is to use a virial expansion (see, e.g., Cohen and Highsmith, 1997):

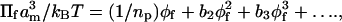(4)

where n_p (monomers) is the polymer length, and b₂, b₃ are the second and third virial coefficients, respectively. Estimates of b₂ and b₃ can be obtained from fitting Π_f/φ_f as a function of φ_f with a second-order polynomial, under the constraint that the first term, 1/n_p, is fixed by the polymer molecular weight. The final column of Table 1 gives the ratio of the third to second virial terms in the osmotic pressure expansion, over the ranges of φ_f for which the logarithmic fits were made according to Eq. 2. For PEG:1000 and PEG:4000, inclusion of the third virial term in Eq. 4 does not improve the fit. Additionally, the second virial term dominates for PEG:1500. These results are consistent with the predictions of mean-field theory. However, for the intermediate-length polymers PEG:2000 and PEG:3000, the third virial term can be appreciable. For the longer polymers, PEG:8000–PEG:20,000, which conform to the predictions of scaling theory, the osmotic pressure also can be described adequately by a virial expansion that is limited to the first three terms (Cohen and Highsmith, 1997). In the latter cases, the third virial term is also appreciable. Consequently, the virial expansion is not especially useful for comparing the performance of the mean-field and scaling theories. Below it will be seen that entirely equivalent treatments of the mean-field and scaling approaches predict a power-law dependence, as given by Eq. 2, in both cases.

A further aspect of the use of data from bulk solutions of the free polymer is worthy of consideration. This is the question of transferability of the scaling factor α for the osmotic pressure in Eq. 2 from bulk solution to the polymer brush. Hansen et al. (2003) tacitly assumed that the value of α from polymer osmotic pressure measurements should be taken over quantitatively in interpreting measurements of bilayer-bilayer interactions in the presence of grafted polymer brushes. A consistent comparison of the two types of measurement requires tracking of multiplicative constants that normally are neglected. In terms of volume fraction, φ, the free energy of the grafted polymer chain is given from scaling theory by (Alexander, 1977):

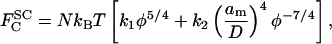(5)

where N is the number of monomers per polymer chain and D is the average distance between grafting sites. Here k₁ and k₂ are constants representing the relative strengths of the osmotic and stretching contributions, respectively, to the free energy. For a free polymer, only the first term enters. It is convenient for what follows to write k₁ = (4/5)α and k₁/k₂ = (7/5)λ³; the reason for doing this, as will be seen later, is that α becomes directly the scaling factor for the osmotic pressure and λ the scaling factor for the natural length of the polymer brush. The pressure in the polymer brush is given by: , which then leads to:

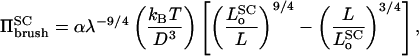(6)

where L is the length of the polymer brush, and 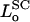is the equilibrium value of L when Π_brush = 0. The change of variable from φ to L is made by invoking the relation 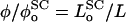(Hansen et al., 2003), where the equilibrium monomer volume fraction of the unstressed brush is , obtained from the condition: ∂F_c/∂φ = 0. The length of the unstressed polymer brush is therefore:

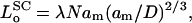(7)

where λ is the explicit multiplicative constant for scaling theory. From Eq. 6, putting the second (i.e., stretching) term equal to zero, the osmotic pressure of the free polymer is given by:

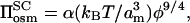(8)

which defines α as fully consistent with Eq. 2. Thus, in general, two multiplicative constants are required to describe the pressure, Π_brush, in the polymer brush: that for the bulk osmotic pressure, α, and that for the equilibrium length of the polymer brush, λ. Comparing Eq. 8 with Eq. 6, it is seen that only in the case that λ = 1 are the multiplicative factors for bulk osmotic pressure and pressure in the polymer brush equal. This, of course, depends on the value of a_m used to obtain λ in Eq. 7, but demonstrates that there is not a strict requirement for equality of the two multiplicative factors.

A comparable calculation using mean-field theory leads to the following relations. The polymer free energy per chain is given by (see, e.g., De Gennes, 1979):

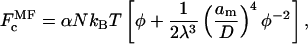(9)

where, in this case, the multiplicative terms scaling the osmotic and stretching contributions to the free energy are given respectively by: k₁ = α and k₂/k₁ = 1/2λ³. The osmotic pressure of the free polymer is correspondingly given by:

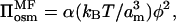(10)

consistent with Eq. 2. Note that Eq. 10 is derived in exactly the same manner, i.e., on the same level, as is Eq. 8, which is the corresponding asymptotic form for scaling theory. The equilibrium length of the unstressed brush in mean-field theory is given by:

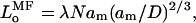(11)

where λ is defined in Eq. 9, in order that Eq. 11 corresponds with the equivalent expression (viz., Eq. 7) in scaling theory. The pressure in the brush according to mean-field theory then becomes:

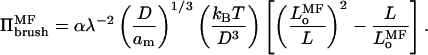(12)

The relation of the multiplicative constant for Π_brush to that for the equilibrium length L_o therefore differs from that in scaling theory. The fact that the multiplicative factors may differ between bulk osmotic pressure and pressure in the polymer brush further lessens the constraints that must be met to achieve semidilute behavior in the polymer brush.

In conclusion, there is reason to believe that the criteria for semidilute behavior in a good solvent introduced by Hansen et al. (2003) may apply to a less restricted range of polymer brushes that are of direct experimental interest. Additionally to the above considerations, it further seems likely that semidilute behavior will be achieved more readily for grafted polymers than for those free in solution. This is exemplified by the critical overlap condition 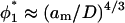for the grafted polymer, which, unlike that for free polymer 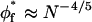, is independent of polymer length.