Pulling-Speed-Dependent Force-Extension Profiles for Semiflexible Chains

Abstract

We present theory and simulations to describe nonequilibrium stretching of semiflexible chains that serve as models of DNA molecules. Using a self-consistent dynamical variational approach, we calculate the force-extension curves for worm-like chains as a function of the pulling speed, v₀. Due to nonequilibrium effects the stretching force, which increases with v₀, shows nonmonotonic variations as the persistence length increases. To complement the theoretical calculations we also present Langevin simulation results for extensible worm-like chain models for the dynamics of stretching. The theoretical force-extension predictions compare well with the simulation results. The simulations show that, at high enough pulling speeds, the propagation of tension along the chain conformations transverse to the applied force occurs by the Brochard-Wyart's stem-flower mechanism. The predicted nonequilibrium effects can only be observed in double-stranded DNA at large (∼100 μm/s) pulling speeds.

INTRODUCTION

The ability to manipulate single molecules using optical tweezers and atomic force microscopy under equilibrium conditions has provided a detailed understanding of the elasticity of biopolymers such as DNA, actin, and microtubules (Smith et al., 1992; Bensimon et al., 1995; Mackintosh et al., 1995; Bar-Zvi et al., 1995; Finer et al., 1994). To a first approximation these molecules are adequately described as semiflexible polymers chains (Smith et al., 1992; Bensimon et al., 1995; Mackintosh et al., 1995) which are usually modeled as either freely jointed chains or worm-like chains (WLCs). At sufficiently high ionic strength, experimentally measured force (f)-extension (z) curves (f, z) for both single- and double-stranded DNA molecules can be quantitatively described using the WLC model (Marko and Siggia, 1995). However, there are significant counterion-dependent deviations from the WLC predictions for the (f, z) curves at low ionic strengths and at low values of f (Baumann et al., 1997). In an earlier article we showed that, by taking into account chain conformational fluctuations, one can quantitatively describe the measured experimental (f, z) results for DNA for monovalent counterions (Lee and Thirumalai, 1999). These studies show that the equilibrium response of DNA to tension is reasonably well understood, and that the WLC model is adequate in describing DNA elasticity, especially at high salt concentration.

A WLC in the presence of tension can be mapped onto a Schrödinger equation for a dipole confined to a unit sphere subject to an electric field (Fixman and Kovac, 1973). The numerical solution of the resulting equation and a simple extrapolation formula (Marko and Siggia, 1995),

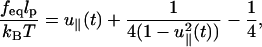(1)

provides nearly exact fits to the experimental data (Marko and Siggia, 1995) thus showing that elasticity of DNA can be fit by the WLC model. In Eq. 1, l_p is the persistence length and u_‖ is the relative extension of the chain with respect to the contour length L, i.e., u_‖ = z/L. The static (f, z) curve has also been obtained (Ha and Thirumalai, 1997) using a field theory in which the constraint u²(s) = 1 is replaced by a global constraint 〈u²(s)〉 = 1. Thus, the WLC model serves as a reasonable model for describing the single molecule force-extension profiles of DNA.

In recent years pulling experiments have been used to measure, at the single molecule level, the interaction forces between biological molecules. In addition, a number of experiments have shown that denaturation of proteins and RNA by force can be used to probe the underlying energy landscape (Zhuang and Rief, 2003). In most of these cases the pulling speeds are so large that unfolding and dissociation of complexes take place under nonequilibrium conditions. More importantly, the full utility of the single molecule experiments is realized only when they are combined with detailed molecular dynamics simulations (Rief and Grubmüller, 2002; Heymann and Grubmüller, 2001; Bayas et al., 2002; Isralewitz et al., 2001). Indeed, such simulations, which utilize large pulling speeds to observe unfolding events in a relatively short time, have played an important role in constructing the unfolding (or unbinding) energy landscape. Thus, understanding nonequilibrium effects due to mechanical stretching of biological molecules and complexes is not only important for describing their function but also is needed for interpreting computer simulation results.

Whereas most of the theories for DNA describe the static force-extension relation (Marko and Siggia, 1995; Ha and Thirumalai, 1997; Cizeau and Viovy, 1997), measurements are made by stretching the molecules at a constant pulling speed v₀ (Rief et al., 1999). Although for DNA currently available experimental (f, z) curves have been measured at near-equilibrium (see below), it is useful to ascertain if measurable nonequilibrium effects can be predicted. If nonequilibrium effects prevail then the influence of energy dissipation, which is proportional to the drift velocity V(s) of monomers and their size (d(s)), should be taken into account in describing the (f, z) curves. Thus, the dynamical response of filaments of semiflexible molecules subject to external forces becomes relevant. Theoretical studies of the dynamics of WLC molecules (Seifert et al., 1996; Brochard-Wyart et al., 1999; Everaers et al., 1999; Morse, 1998) and simulations (Cheon et al., 2002; Noguchi and Yoshikawa, 2000) have recently been reported. Seifert et al. (1996), who considered the propagation of suddenly applied tension to a thermally excited semiflexible chain, found that the applied tension propagates only subdiffusively for a semiflexible chain. More recently, Brochard-Wyart et al. (1999) have considered the dynamics of taut DNA molecules and treated a variety of transient regimes. They showed that, in general, the relaxation in the longitudinal direction (parallel to the applied force) is much faster than in the transverse direction. When the tension is suddenly applied at one end of the chain by pulling at a given speed, the nonuniform tension profile increases from the fixed end in proportion to the drift velocity of the monomers. The longitudinal profile of the chain ρ(z) depends on the local tension f(z). The conformation of the chain in this limit is described by the stem-flower model (Brochard-Wyart, 1995).

In this article, we first provide a theoretical framework for interpreting experiments and computer simulations that could probe the pulling-speed dependence of force-extension profiles for WLC models. We consider the regime in which the tension propagation is fast compared to the relaxation of the chain. In this limit, the longitudinal profile of the chain can be approximated as a uniform cylinder. To anticipate the distinct time regimes it is useful to characterize the relaxation times for the WLC under tension. Consider a WLC chain whose equilibrium size is 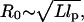where L is the contour length and l_p is the persistence length. The chain is rod-like on a length scale smaller than l_p, but on a larger scale (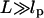) chain flexibility becomes important. On applying a force f < f_c = k_BT/R₀, the chain conformation is unperturbed. The dissipative force at the pulling speed v₀ is f_D ∼ η₀R₀v₀ where η₀ is the solvent viscosity. Distortion of the chain conformation occurs only when the force exceeds f_c. The characteristic pulling speed v₀ at f_c = f_D is

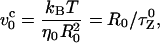(2)

where 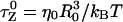is the Zimm relaxation time for weak perturbations (Brochard-Wyart et al., 1999). Significant nonequilibrium effects can be discerned only when the pulling speed exceeds 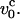The value of 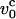at water viscosity η ∼1 cP for typical parameters for DNA (L ∼ 10 μm, l_p ∼ 50 nm), is 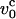∼ 800 μm/s. The typical pulling speeds used in experiments, i.e., v₀ (1–10)μm/s, are at least two orders-of-magnitude smaller than 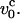Therefore, for all practical purposes the current experiments only probe the equilibrium response of DNA (except in cases when the strands melt) to force. However, nonequilibrium response considered here may be observed in force-extension profiles of longer DNA molecules.

Consider a WLC chain at equilibrium under tension with f = k_BT/ρ_f where ρ_f is the transverse size of the chain. As described by Brochard-Wyart (1995), nonuniform profiles (trumpets and stem-flower profiles) manifest themselves when the pulling speed reaches 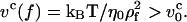The chain relaxation time under tension is 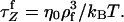Below the threshold pulling speed, the chain conformation can be approximated as a uniform cylinder.

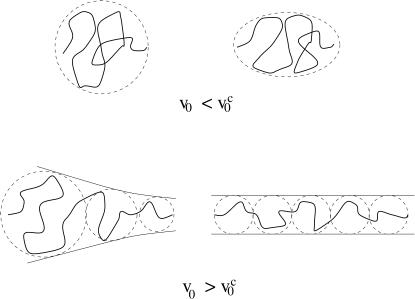
If the chain is pulled at constant pulling speed 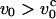the relaxation time for the chain is longer than the time for the tension propagation. The nonuniform tension along the contour leads to the transient trumpet-like chain conformation (see Fig. 1). As time progresses, further stretching results in smaller transverse fluctuations. When the smallest transverse size matches ρ with the pulling speed v₀ = k_BT/η₀ρ², the transverse size of the chain becomes stationary. As a result, the chain envelope can be approximated again as a uniform cylinder.

FIGURE 1.

Schematic sketch of the envelope of chain conformations as a function of the pulling speeds. (Top) Weak deformation of the chain at pulling speeds 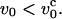The right-hand side gives a sketch of the stationary deformation induced by pulling. (Bottom) Nonuniform longitudinal profiles when v₀ > 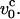The trumpet-like profile gives rise to a steady-state cylindrical profile upon stretching at constant pulling speeds.

The contour length of the typical DNA molecule is considerably large compared to its persistence length. Our aim here is to construct force-extension curves for L ≥ l_p. Therefore we concentrate on the extension of the chain on large scale only and treat the dynamical influence of local (rod-like) structure self-consistently. We estimate the total dissipation under the assumption that the force acting on each monomer is uniform along the chain.

In this article we first calculate the force extension of a worm-like chain subject to a time-dependent force. We use a dynamical mean field approach that effectively replaces the local constraint 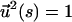by a global constraint 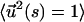for all times. The static version of this method has been used successfully to compute the static force-extension curves (Ha and Thirumalai, 1997). The theory, which assumes that the tension propagates uniformly along the chain, is only valid when the pulling speed is not significantly larger than 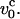We find highly nonmonotonic variations in the (f, z) curves at a given value of v₀ as l_p changes. This is very different from the corresponding equilibrium stretching situation. To access the validity of the approximations and to obtain a microscopic picture of the dynamics of tension propagation, we also present Langevin simulation results for an extensible WLC that is subject to a time-dependent stretching force. In the strong pulling limit our simulations also validate the stem-flower model which was proposed to describe the fate of polymers in strong flows.

THEORY

We consider a semiflexible chain made of N monomers with Kuhn length b (L = Nb). The effective partition function describing the chain under uniform tension is (Marko and Siggia, 1995),

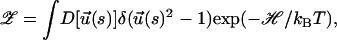(3)

where

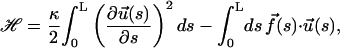(4)

and where κ, the bending rigidity of the semiflexible chain, is related to l_p as l_p = κ/k_BT.

To obtain insights into the pulling speed dependence on the (f, z) profiles we use a tractable mean field representation of the WLC. The basic idea is to replace the constraint 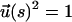by the global constraint 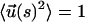where 〈..〉 is an average over the distribution in Eq. 3. With this, we can rewrite the free energy as

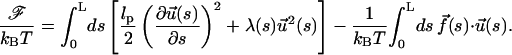(5)

The variable λ(s) is the undetermined Lagrange multiplier that enforces the global constraint and is a function of the applied stress. From now on we use the dimensionless persistence length 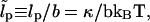and the dimensionless force 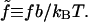Length is measured in units of b.

Following our earlier work (Lee and Thirumalai, 1999; Ha and Thirumalai, 1997) we evaluate the integral over λ(s) by the stationary phase approach. In terms of q, the Fourier variable conjugate to s, the saddle point condition is

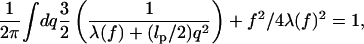(6)

which, in the thermodynamic limit (L → ∞), reduces to

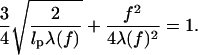(7)

The average elongation z_e = 〈z〉 is related to λ as follows,

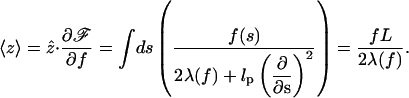(8)

Here we generalize the mean field approach to probe dynamics of WLC under tension. Consider a WLC chain in equilibrium at a force f_o. At t = 0, the chain is pulled in the 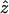direction at a constant speed v₀ so that z(t + Δt) = z(t) + v₀Δt. In a relatively short time we expect the chain to orient itself in the direction of the force. This occurs when DNA is subject to forces >1 pN.

Upon application of force, we assume that the tension propagation is fast enough so that the variation due to this stretch occurs uniformly through the contour of the chain. It has been argued that even at large pulling speeds, comparable to those used in simulations, the propagation of applied tension is rapid (Evans and Ritchie, 1997). Using this assumption we write the tangential vector in the z direction as u_‖(s, t) ≡ u_‖(t) = z(t)/N, and its time derivative du_‖(t)/dt = v₀/N where Nl_p = L. We introduce the time-dependent mean field variable λ(t) to enforce the nonequilibrium global constraint 〈u²(t)〉 = 1. We assume that λ(s, t) ≡ λ(t) is only a function of t and is independent of s. If the propagation of tension is fast enough then this approximation is expected to be valid. Here we justify this approximation by making comparisons with simulations.

In terms of the Fourier transformed variable q (which becomes continuous in the N → ∞ limit) the free energy functional given in Eq. 4 becomes

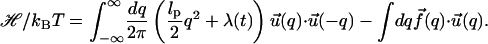(9)

Balancing the transverse force 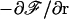and the viscous drag 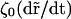(ζ₀ is the monomer friction coefficient that is proportional to η₀) we obtain the equation of motion. Since 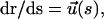we obtain

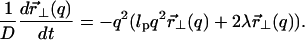(10)

With the stationary approximation, the force is constant along the contour of the chain, i.e., 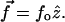Upon taking derivatives on both sides of the above equation with respect to s, the equation of motion for 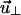becomes

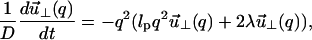(11)

where D = k_BT/ζ₀ is the monomer diffusion constant. In this description (Rouse Model) the hydrodynamic screening length is effectively the size of the monomers. We measure time in units of t₀ ≡ b²/D.

The equal time dynamical structure factor S(q, t) is

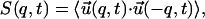(12)

where 〈…〉 indicates the average over both the initial condition and the thermal noise. We decompose S(q, t) into two components, S_‖ and S_⊥, where S_‖ and S_⊥ are the parallel and perpendicular components of S(q, t), respectively,

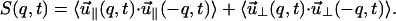(13)

The time evolution of the dynamic structure factor S_⊥(q, t) can be written as (Langer, 1992)

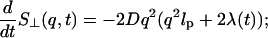(14)

thus,

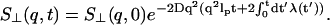(15)

We impose the global constraint in the form of a sum-rule

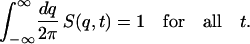(16)

The mean elongation 〈z(t)〉/N can be evaluated using Eq. 8. Assuming a λ(t) that satisfies Eq. 8 exists, the sum-rule (Eq. 16) can be expressed as

(17)

The components of the initial equal time dynamical structure factors S(q, 0) in the perpendicular direction are given as

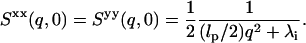(18)

Integrating Eq. 17 over q, we obtain

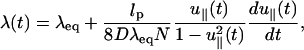(19)

where λ_eq is the equilibrium value that satisfies Eq. 8 at t = 0. Note that λ(t), which is a function of the pulling speed v₀=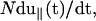 is related to the transverse component of the time-dependent force f^tr(t) by (from Eq. 8),

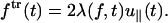(20)

This is the additional drag force due to the dissipation of the transverse mode. Because the transverse and the longitudinal modes are coupled (〈u²〉 = 1), the dissipation in the transverse mode results in a net force in the longitudinal direction. Inserting Eq. 19 into Eq. 20 results in the expression for the transverse component of the time-dependent force f^tr(t),

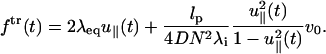(21)

The force-extension relation consists of two parts: the first term corresponds to the static contribution and the second term is the dynamic contribution. If the system was in equilibrium at t = 0 with small force f_o ≈ 0 (Ha and Thirumalai, 1997) we may approximate λ_eq ≈ 1/l_p. Then, the pulling-speed-dependent force-extension relation is written as

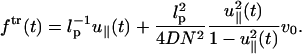(22)

Note that the first term of the right-hand side is identical to the first term in the static calculation (see Eq. 1). The second term on the right-hand side of Eq. 21 is proportional to the product of the pulling speed and the inverse of the diffusion coefficient (1/D), which is related to the energy dissipation. The effective friction depends on the geometric factor 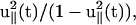which reaches a maximum at large extensions. Furthermore, this relation depends on the history of the chain, i.e., the choice of initial conformation at the starting point of the pulling. If the system was in equilibrium with constant force at t = 0, the choice of λ_eq should satisfy Eq. 7 with finite force f ≠ 0. If the chain is released from the extended conformation (i.e., 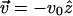) where the equilibrium force is f ≥ 2/l_p, then λ_eq should be chosen as λ_eq ≈ f/2 ≈ l_p. This could lead to hysteresis in the force-extension curve.

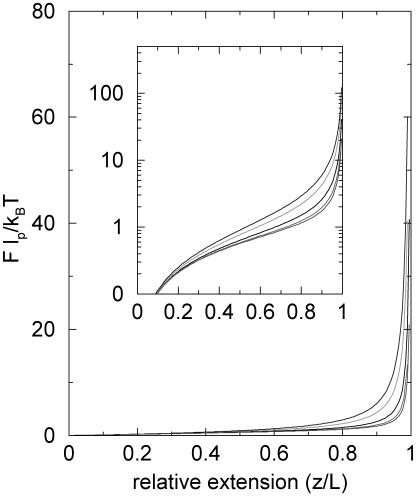
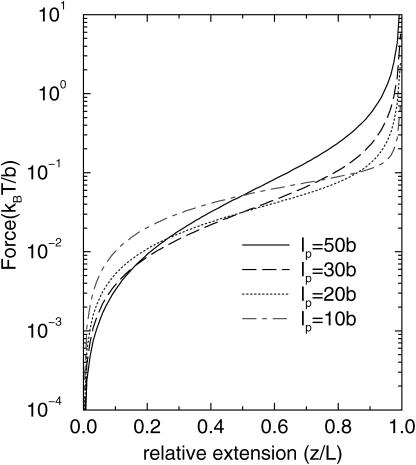
We have numerically solved the self-consistent dynamical equations to obtain the pulling-speed-dependent (f^tr, z) curves (see Fig. 2). In our theory the longitudinal elastic constant (see Eq. 26 below) k_b is infinite. From Fig. 2 we note that the force required to stretch the WLC to given extension increases as v₀ increases. In Fig. 3, we plot the l_p dependence of force extensions at the fixed pulling speed v₀ = 1b/t₀. The flexible chain requires larger force at small extension. As the extension becomes comparable to the contour length, the stiffer chain (larger l_p) requires larger force. This crossover stems from the fact that the excess stored length in the case of flexible chain should be released at small extension whereas the transverse fluctuation of the semiflexible chain remains until z becomes large. The nonmonotonic dependence in (f^tr, z) as a function of l_p is a nonequilibrium effect and cannot be observed if the WLC is stretched under equilibrium conditions (see Eq.(1)).

FIGURE 2.

Theoretically determined dynamical (f^tr, z) curves for a WLC at various pulling speeds. The values of the pulling speeds change from v₀ = (0.5, 1, 2, 3)b/t₀ from bottom to top. The persistence length l_p = 20b and N = 100. The inset is in linear-log scale.

FIGURE 3.

Dynamical (f^tr, z) curves for a WLC chain for varying values of the persistence length l_p (10, 20, 30, 50)b. The pulling speed is v₀ = 1b/t₀.

The total drag force is the sum of the drag from the transverse mode and the longitudinal mode. The longitudinal displacement (i.e., extension along the applied force) is determined by the dynamics at finite pulling speed rather than by diffusive motion which has been considered elsewhere (Brochard-Wyart et al., 1999; Seifert et al., 1996; Everaers et al., 1999). The drag force arising from the motion in the direction of the pulling is

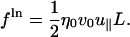(23)

Thus, the total drag force is

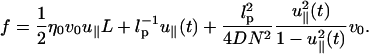(24)

SIMULATIONS

We have performed Langevin simulations of an extensible worm-like chain model (EWLC) that is subject to nonequilibrium stretching force. We undertook these simulations for the following reasons:

1. The theory described above has a number of approximations. Although the effect of replacing u²(s) = 1 by the global constraint 〈u²(s)〉 = 1 is correct for equilibrium stretching (Ha and Thirumalai, 1997), its validity when pulling under nonequilibrium conditions is not clear. Moreover, the neglect of variations in the longitudinal profiles of the chain, which is especially important at high pulling speeds, requires scrutiny. The simulations allow us to access the effects of these assumptions on the predicted results.

2. It has been pointed out by Brochard-Wyart (1995) that there are several distinct mechanisms for tension propagation in flexible polymers. Similarly, Seifert et al. (1996) have identified various timescales in the way the applied force propagates across the semiflexible filaments. To obtain additional insights into the microscopic mechanism underlying tension propagation as a function of the pulling speeds we have performed a series of simulations by assuming that the chain dynamics can be described by the Langevin equation. We use an extensible WLC (EWLC) model to mimic the possibility of stretching the chain beyond L by connecting the beads of WLC by a spring with large but finite longitudinal elastic constant (see below).

The dynamics of stretching is obtained by integrating the Langevin equation

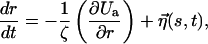(25)

where the friction coefficient ζ = k_BT/D and the value of D in water at 300 K is D ∼ 10⁻⁶ cm²/s. The thermal noise η(s, t) is assumed to be Gaussian with zero mean, and the correlation is given by 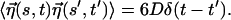The equations of motion are integrated with step size δt = 2.5 × 10⁻⁴t₀.

We consider a stiff chain consisting of 100 monomers. The monomers are connected by a molecular spring with a longitudinal elastic constant k_b that allows for fluctuations around the equilibrium bond length b.

The energy function for a given chain conformation of the EWLC is

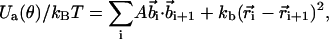(26)

where 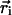is the position of i^th monomer, 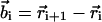is the bond vector, and k_b is the molecular spring constant. The strength of the angular potential A determines the stiffness of the chain. We determined the persistence length l_p using the formula for the fixed-bond-angle model of the worm-like chain,

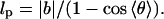(27)

where 〈θ〉 is average angle between the adjacent bonds. For A = 20, the persistence length l_p = (19 ± 2)|b| for the two values of k_b (see below) considered. If this is equated to l_p = ∼53 nm for the λ-phage DNA (Smith et al., 1992) then the bond length 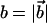is ∼2.8 nm.

The contour length of the simulated chain (N = 100) corresponds to 280 nm, which is comparable to the length of the ssDNA, L = 300 nm, used in experiments of Rief et al. (1999). To make qualitative comparisons with AFM experiments (Rief et al., 1999), the terminal of the EWLC is pulled along the z axis with the force

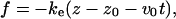(28)

where z is the end-to-end distance (extension in the z direction), z₀ is the end-to-end distance of the chain in the absence of force, v₀ is the pulling speed, and k_e is the spring constant of the cantilever in the pulling experiments. We use k_e = 5 k_BT/|b|² = 2.64 pN/nm. In our simulations pulling speeds vary from (0.1–2)b/t₀ which correspond to (3.6 × 10⁴ − 7.2 × 10⁵)μm/s. This is ∼5 orders-of-magnitude faster than experimental values (Rief et al., 1997, 1999) and is typical of the pulling speeds used in simulations. Most of the simulations were done with k_b = 2 × 10³ k_BT/|b|² ≈ 10³ pN/nm, which mimics the actual DNA molecule spring constant of 800 pN per Kuhn length. With this model, we allow for internal stretch of the backbones at large values of f.

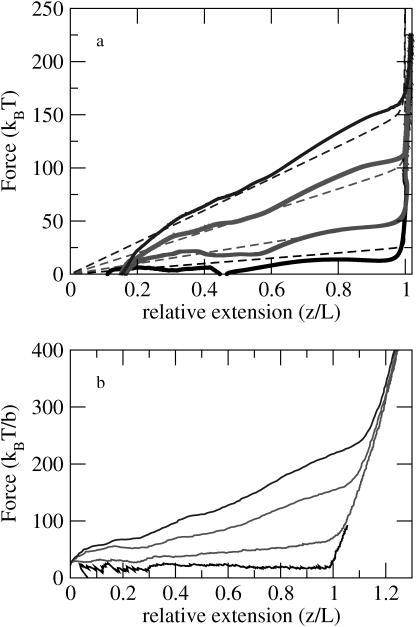
To access the validity of the theory we have obtained the (f, z) curves at different pulling speeds (Fig. 4, top) using Langevin simulations. Because the theory is only valid when k_b is infinite we chose a sufficiently large value of k_b (= 10,000 k_BT/|b|²) for which stable integration of the Langevin equations are possible. The results in Fig. 4, top, show that, at all the pulling speeds, the theory and simulations are in good agreement. This justifies the assumptions made in obtaining the nonequilibrium force-extension curves. The comparison between theory and simulations also shows that the present theory can be used to interpret future simulations of nonequilibrium stretching of WLC.

FIGURE 4.

(Top) Comparison of the theoretical and simulation results for the force-extension curves at various pulling speeds. The dashed lines are the theoretical results and the thick lines represent simulation results. The simulations were performed for the EWLC chain with k_b = 10,000 k_BT/|b|². A large k_b was chosen for better comparison with the theory in which it is assumed that k_b is infinite. The pulling speeds change from v₀ = (0.5, 1, 2, 3)b/t₀ from the bottom to the top curve. (Bottom) Plots of the dynamical force-extension curves for the EWLC at various pulling speeds. The persistence length l_p = 20b and N = 100. The molecular spring constant is 2000 k_BT/b², which corresponds to the slope at large values of z/L. The pulling speeds change from v₀ = (0.5, 1, 2, 3)b/t₀ from the bottom to the top curve.

In Fig. 4, bottom, we present the force-extension curves obtained from simulations at various pulling speeds for the chain with k_b = 2000 k_BT/|b|² which is a realistic value for DNA. Each curve is an average of force-extension over 20 different initial conformations of which the end-to-end vectors are oriented in the direction of pulling. The slope of the (f, z) plots at large extensions (z/L > 1) reflects the overall stretching of the chain. In accord with the theoretical predictions (Fig. 2), we find that as the pulling velocity increases, the force required to extend the chain increases. For v₀ ≤ 1b/t₀, tension is uniform along the chain resulting in a longitudinal profile that is also uniform along the z-direction. Therefore, the approximation that the applied tension is uniform along the chain, which was made in our theory, is valid. Coil-to-rod transition occurs in the (f, z) curves over a narrow extension range when L > L₀ (Fig. 4). The transition point appears at larger extension when the pulling speed is larger, reflecting that a part of the chain is straightened and more stretched than the corresponding contour length, although entropy still prevails in the conformation of the other part.

We also computed, using Langevin simulations, chain extension at constant force. The equilibrium extension is obtained by averaging over 10⁴t₀. The initial conformations for the simulations are prepared from both the overstretched chain conformation (L > L₀) and relaxed conformation. The static equilibrium force at a given extension is smaller than what is found under nonequilibrium conditions. Coil-to-rod transition also occurs at smaller forces (data not shown).

An important aspect of the simulations is that one can directly obtain a microscopic picture of the dynamics of tension propagation. When the pulling speed is large v₀ > 1b/t₀, the tension along the chain is no longer uniform and the profile, ρ(z) ∼ k_BT/ζv(z), is determined by the local z-dependent drift velocity v(z). If one end is pulled at a constant speed v₀ whereas the other end is fixed, the local drift velocity of the chain scales linearly with the distance from the fixed end. If the local force is larger than k_BT/l_p, entropic contribution is suppressed, which results in the segment being locally stretched. We observe that the end of the chain that is close to the pulling terminus is straightened whereas the part close to the fixed end remains closer to the initial coil-like conformation. The rod-like part (stem) grows as the extension increases. These features are shown in the serious of snapshots in Fig. 5. This limit, which is observed at high pulling speed in our simulations, corresponds to the stem-flower model (Brochard-Wyart, 1995).

FIGURE 5.

Snapshots of the EWLC from simulations done at the pulling speed v₀ = 3b/t₀. The extension of each figure corresponds to z = 11.02, 33.85, 46.48, 59.11, and 103.89, respectively. The contour length is L = 100. All lengths are measured in units of b.

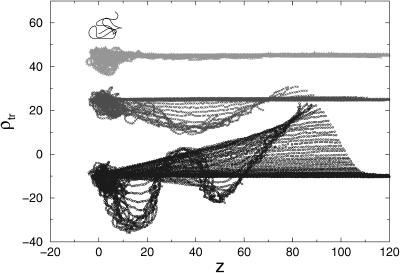
The stem-flower mode of tension propagation is more dramatically shown in Fig. 6 in which we produce a two-dimensional projection of the monomer coordinates at various pulling speeds. Each curve in this figure represents the positions of the monomers (the y axis represents locations transverse to the force direction and the x axis denotes the coordinates (z) parallel to f). All the snapshots are taken at equal time intervals. At lower pulling speeds (for example, v₀ = 1b/t₀, which is the second profile from the bottom) the conformations of the chain in the transverse direction spread out. On the other hand, at larger pulling speeds, the fluctuations in the transverse direction are localized. At the highest pulling speed, v₀ = 3b/t₀, the diffusive motion is strongly suppressed. This regime most clearly exhibits the stem-flower profile anticipated by Brochard-Wyart (1995) in the context of coil-to-stretch transition in polymers subject to elongational flow.

FIGURE 6.

Two-dimensional projection of the chain conformations at various pulling speeds. The y axis represents the coordinates transverse to the pulling direction and the x axis is the extension in the direction of force. The uppermost figure corresponds to a chain at equilibrium. The subsequent profiles represent the chain deformations at pulling speeds v₀ = (2.0, 1.0, 0.5)b/t₀ from top to bottom. At each pulling speed the conformations represent the dynamics of the evolution of the chain deformation. The stem-flower model for chain stretching is evident at high pulling speeds.

CONCLUSIONS

We have presented a theory to describe the pulling-speed-dependent elastic response of WLC when it is stretched from one end. Using a self-consistent dynamical variational approach, we have calculated quantitative estimations for the force extension of worm-like chains subject to a time dependent force. As expected, the measured forces at finite pulling speeds are larger than the static stretching force f_eq. The theoretical force-extension estimation also predicts that at small forces (extensions), the larger the l_p, the bigger the dissipation. Therefore, larger force is required at a given extension. When the extension is comparable to the contour length, dissipative forces are larger for larger values of l_p. The competition between the viscous force and the stretching force, both of which depend on l_p, gives rise to nonmonotonic variations in the (f, z) curves as l_p is altered. This prediction, which is a purely nonequilibrium effect, is amenable to experimental test.

To complement the theoretical predictions we performed Langevin simulations for extensible WLC, which show that at pulling speeds v₀ ≤ b/t₀, the uniform cylinder approximation for the transverse envelope is valid. For larger pulling speeds, the transient behavior of WLC is well described by the previously described physical picture (Brochard-Wyart et al., 1999; Seifert et al., 1996). In particular, the stem-flower tension propagation mechanism at high pulling speeds is confirmed in our simulations. A direct comparison between our theoretical predictions and simulations for large value of the longitudinal spring constant (see Fig. 4, bottom) shows excellent agreement. The favorable agreement between theory and simulations justifies the use of dynamic self-consistent theories to probe nonequilibrium response of semiflexible macromolecules, such as DNA, to force.

In this article hydrodynamic interactions have been neglected. If the hydrodynamic interactions are not fully screened, the major friction comes from the largest dimension of the moving element, i.e., the size in the axial direction R_z. The friction that the moving object experiences is η₀R_z rather than ∼η₀Nb. For a rod-like element, the largest dimension is approximately the length of the chain when the extension is comparable to the contour length. The total friction is proportional to the length of the chain ∼L (with logarithmic corrections) if the object is moving in the direction of the force. If one end of the chain is fixed then hydrodynamic friction from the rotational mode (∼L³) will play a role in the dissipation mechanism. These considerations suggest that, in the limit of high pulling speeds, hydrodynamic interactions can significantly affect the force-extension profiles. Numerical simulations, along the lines used previously (Dunweg, 1993; Abrams et al., 2002), would be needed to examine the role of hydrodynamic interactions.