Size Effects on Diffusion Processes within Agarose Gels

Abstract

To investigate diffusion processes in agarose gel, nanoparticles with sizes in the range between 1 and 140 nm have been tested by means of fluorescence correlation spectroscopy. Understanding the diffusion properties in agarose gels is interesting, because such gels are good models for microbial biofilms and cells cytoplasm. The fluorescence correlation spectroscopy technique is very useful for such investigations due to its high sensitivity and selectivity, its excellent spatial resolution compared to the pore size of the gel, and its ability to probe a wide range of sizes of diffusing nanoparticles. The largest hydrodynamic radius (R_c) of trapped particles that displayed local mobility was estimated to be 70 nm for a 1.5% agarose gel. The results showed that diffusion of particles in agarose gel is anomalous, with a diverging fractal dimension of diffusion when the large particles become entrapped in the pores of the gel. The latter situation occurs when the reduced size (R_A/R_c) of the diffusing particle, A, is >0.4. Variations of the fractal exponent of diffusion (d_w) with the reduced particle size were in agreement with three-dimensional Monte Carlo simulations in porous media. Nonetheless, a systematic offset of d_w was observed in real systems and was attributed to weak nonelastic interactions between the diffusing particles and polymer fibers, which was not considered in the Monte Carlo simulations.

INTRODUCTION

Diffusion properties in random media such as soils (Sahimi, 1993), gels (Starchev et al., 1997; Pluen et al., 1999) bacterial cytoplasm (Berland et al., 1995; Schwille et al., 1999a), membranes (Saffman and Delbrück, 1975; Peters and Cherry, 1982; Ghosh and Webb, 1988) and channels (Wei et al., 2000) are subject to considerable theoretical and experimental interest. Diffusion in gels is an important component in many biological (Ottenbrite and Huang, 1996), pharmaceutical (De Rossi et al., 1991), and environmental applications (Buffle, 1988). The hindered diffusion of solutes in gels has been modeled (Amsden, 1998) and is well-documented for agarose gels (Johnson et al., 1996; Pluen et al., 1999). Agarose gel is the preferred chromatographic medium used for separating biological molecules of molecular mass >250 kDa, for which minimal nonspecific binding and retention of the biological activity is required.

In most real systems, disorder may exist over a finite range of distances. In this range, the diffusion process cannot be described by the classical Fick's law and hence is usually referred to as anomalous diffusion (Harder et al., 1987; Havlin, 1989). At larger distances than this window range, the effect of disorder on diffusion may be very small due to statistical effects which cancel each other. In a porous crystal, there is a single or few correlation lengths, ξ. In a fractal medium there is no correlation length and diffusion should appear to be identical, but anomalous, at all time- and length-scales, because independently of its size a diffusing probe experiences the same average obstruction (Bunde and Havlin, 1991). In a real disordered system, there is a finite continuous distribution of ξ such that the diffusion process appears normal outside the range of ξ, and anomalous within it (Saxton, 1994). In addition, when considering real-size diffusing particles, a third diffusion process, trapped diffusion, may be observed and is related to the excluded structures' volume and pore connectivity (Kerstein, 1985).

Structure and transport in agarose gels have been widely studied with respect to gel electrophoresis. Recently the agarose gel structure has been characterized as fractal (Krueger et al., 1994; Manno and Palma, 1997). Nevertheless, to the best of our knowledge, the relationship between the fractal structure exponent and the diffusing particle size has never been fully studied, mainly due to a lack of techniques that allow for determination of the particle behavior over a large size range. For such gels formed by entanglement, it is possible to define a correlation length as an average distance between entanglement points. In case of elastic-interactions between solutes and gel fibers, the mobility of the tracer should be affected by the relative ratio of the size of the particle to the average correlation length of the network. The interest in studying the particle size dependence of diffusion is that particles with smaller sizes can penetrate into smaller holes in the gel. In this manner the gel structure can be probed at different scales by using particles with various sizes. An independence of the diffusion process on the size of particles would mean that the gel structure is scale-invariant, at least in the observed size range. The topological structure of pores in polyacrylamide gels has been investigated by light-scattering (Suzuki and Nishio, 1992; Joosten et al., 1991, 1990) by analyzing the diffusion of latex beads within the gel. But this technique is only sensitive to particles with sizes comparable to those of the largest pores. Netz and Dorfmüller (1995) have also examined the diffusion processes by means of a three-dimensional Monte Carlo (MC) simulation of hard spheres in random porous media built to approximate the topology of polyacrylamide gels. They have shown evidence for each of the three types of diffusion processes mentioned above and an independence of the fractal exponent of diffusion, d_w, (see Eq. 2) on the polymer fraction.

In general, a major limitation with respect to detailed studies of the diffusion of colloids and macromolecules in gels is the lack of appropriate experimental techniques. Pulse-field-gradient spin-echo nuclear magnetic resonance (Abragam, 1964) has been used to study the diffusion of myoglobin in agarose and λ-carrageenan gels (Hirota et al., 2000). Photon correlation spectroscopy is not suitable, because of the strong background scattering and the large amount of diffusing particles required, which in turn may strongly perturb the gel structure. Diffusing wave spectroscopy (Urban et al., 2000; Pine et al., 1988) extends the range of application of traditional light-scattering techniques to systems which exhibit strong multiple scattering. Unfortunately it is not selective and the size range of probes that can diffuse remains small. Single particle tracking (Ghosh and Webb, 1988; Starchev et al., 1997; So et al. 1998) can be used, but only in a limited length range (0.2–15 μm), due to the low resolution of optical microscopy. In addition, the technique is time-consuming and the reproducibility is poor. Methods based on fluorescence detection such as fluorescence recovery after photobleaching (FRAP) and fluorescence correlation spectroscopy (FCS) have advantages because very local measurements can be made in addition to measurements in very dilute solutions. FRAP (Vaz et al., 1982) has been used to study the diffusion of dextran, DNA, proteins, and latex beads in agarose gels (Pluen et al., 1999). In that case, it was shown that globular proteins and latex particles have a very similar diffusive behavior in agarose gels. Nonetheless FCS should be better suited for such studies due to its high selectivity and sensitivity and its capability of performing nonperturbing diffusion measurements at selected three-dimensional positions, with a high spatial resolution (micrometer). FCS was first introduced by Madge et al. (1974) and it has been recently developed further thanks to the use of confocal optics (Rigler et al., 1993). This method is highly selective since only the fluorescently labeled diffusing particles are observed. It can be used with compounds in a size range of 1–150 nm and hence gel pore size can be investigated. It has been used, in particular, for biochemical investigations of anomalous diffusion in cell cytoplasm and membranes (Berland et al., 1995; Schwille et al., 1999a). Qian et al. (1992) studied the diffusion of fluorescent beads in actin gel and found a large broadening of the autocorrelation function. Guiot et al. (2002) has investigated the diffusion of latex particles and dextrans in microbial biofilms by FCS and fitted their data with an anomalous diffusion model. FCS is a very sensitive technique since even a single fluorescent molecule can be reliably detected. Generally FCS needs lower fluorophore concentration, uses a lower laser power than FRAP, and is thus more appropriate for nondestructive measurements.

In this study, we have investigated the diffusion properties of solutes with varying sizes, at infinite dilution, in agarose gel, by means of FCS. The sizes of solutes vary from ∼50 times less to two times more than the average pore size. We interpret the data with anomalous diffusion equations. The results have been compared with three-dimensional Monte Carlo simulations of hard spheres in porous media, which approximate the topology of real polymer gels to be validated.

THEORETICAL BACKGROUND

Diffusion within fractal networks of pores

Fractal networks such as percolating clusters are usually characterized by a power law distribution of the hole size in space (Havlin, 1989),

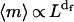(1)

where 〈m〉 is the ensemble average of the number of empty holes in the space volume characterized by a linear size L. The exponent d_f is so-called mass fractal dimension by analogy with the mass fractal dimensions of colloidal aggregates. In the general case of fractals, d_f is a fractional number smaller than the dimension of space of interest. The independence of d_f on scale is also referred to as self-similarity and is an important property of rigorous fractals.

The diffusion behavior of a particle within a medium can be characterized by its mean-square displacements 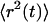vs. time, t, which is written (Havlin and Ben-Avraham, 1987) as

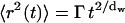(2)

where Γ is the transport coefficient and d_w is defined as the fractal dimension of diffusion. When d_w = 2, the diffusion process is normal and

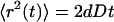(3)

where d is the dimensionality of space and D is the diffusion coefficient. When d_w ≠ 2, because of the obstructions sensed by the particles, diffusion is considered to be anomalous (Harder et al., 1987; Havlin, 1989). Anomalous diffusion, however, is not necessarily caused by a fractal matrix, but can also be due to nonelastic interactions between the network and the diffusing particles (Saxton, 1996). Anomalous diffusion is different from trapped diffusion where the particles are permanently trapped in holes without issue. In such cases, when t → ∞ the mean-square displacements tend to a constant value. In the case of anomalous diffusion, combining Eqs. 2 and 3 show that D depends on the timescale of the measurement (Saxton, 2001)

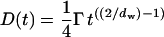(4)

So this parameter is not suitable to characterize the diffusing medium; d_w is better.

Fluorescence correlation spectroscopy

The FCS technique is based on the quantification of fluctuations in the intensity of emitted light from a small number of particles located in a micrometric confocal volume (SV). The transverse radius of the SV is usually ∼300 nm and its half-height is approximately five times longer as fixed by the confocal optics. The profile intensity is assumed to be Gaussian in the transversal direction. This assumption is valid for small detector aperture and/or overfilled back-aperture (Hess and Webb, 2002).

Using the previous assumption, the normalized autocorrelation function of the fluorescence intensity fluctuations due to the free diffusion of a single species can be described by a hyperbolic function (Aragon and Pecora, 1976),

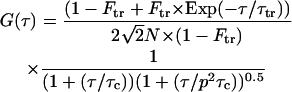(5)

where F_tr is the triplet fraction, τ_tr is the triplet time, τ is the delay time, τ_c is the characteristic mean time that fluorescent particles spend in the SV, p is the ratio between longitudinal and transverse radius of the SV (p = ω_z/ω_xy), and N is the mean number of particles in the SV. In case of large detector aperture, the confocal volume is non-Gaussian and the experimental autocorrelation curve cannot be adequately fitted using Eq. 5. Some indications of such trouble are given by a diverging structure parameter, additional diffusing species, …. In a fully isotropic microenvironment around the confocal volume, and for particle radius <ω_xy/10, the diffusion coefficient (D) of particles is given by

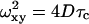(6)

where ω_xy is the transverse radius of the SV. For larger particles, with radius up to ω_xy/2, a correction can be applied as explained by Starchev et al. (1998). Values of p are obtained from calibration of the apparatus with R6G, which has a diffusion coefficient of 2.8 × 10⁻⁶ cm² s⁻¹ in water (Madge et al., 1974).

In gels, Eq. 6 is only applicable to calculate D from measured τ_c when the particle size is much smaller than the pore size. Therefore the more general equation holds,

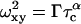(7)

with 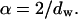Indeed, the shape of the FCS-autocorrelation function in fractal media is broader than in free solution because of heterogeneous obstructions to diffusion (Sengupta et al., 2003). In such a case, the diffusion time of a particle will depend on its surrounding microenvironment, leading to broader curve of the autocorrelation function than would be observed in solution. Thus the autocorrelation function resembles those observed for diffusion in a polydisperse particles suspension.

Schwille et al. (1999b) has introduced a more general equation for the autocorrelation function for the case of anomalous diffusion in disordered media (Bouchaud and Georges, 1990) where the term 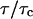(Eq. 5) is replaced by 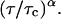The authors assumed an anomalous model because the classical Eq. 5 failed to fit the autocorrelation function of a single species diffusing through the membrane and cell cytoplasm.

EXPERIMENTAL SECTION

Starting materials and general procedures

Diffusing particles

Rhodamine 6G (R6G, Sigma 99%), Rhodamine 123 (R123, Acros Organics, Noisy-Le-Grand, France, puriss), and Nile Blue (NB, Acros) were of analytical grade. Humic acids (Suwannee River humic acid, HA) were obtained from the International Humic Acid Substances Society (St. Paul, MN). Three fluorescent proteins (Alexa-488-labeled codfish parvalbumin, Texas-Red labeled chicken ovalbumin, and R-phycoerythrin) were obtained from Molecular Probes (Eugene, OR). Ovalbumin was purified further on a G-100 gel column. The ionic strength (μ) was adjusted with NaCl (BDH AnalaR). Ultrapure water (>18 MΩ cm) was used for preparing all solutions. Starburst (PAMAM) amine- or carboxylate-terminated dendrimers were obtained from Sigma-Aldrich (St. Louis, MO) and covalently labeled with Rhodamine B (D₄R_B) or Rhodamine 123 (D_4.5R₁₂₃), respectively, in a phosphate buffer at pH = 6, by using EDC (Templeton et al., 1999), then separated from the free dye with a G-100 gel column. β-cyclodextrin modified pink fluorescent microspheres (48 ± 5 nm) were purchased from Duke Scientific (Palo Alto, CA). Carboxylate-modified latex beads (40 ± 4 nm, 60 ± 6 nm, 80 ± 8 nm, 100 ± 10 nm, 140 ± 10 nm) were obtained from Bangs Laboratories (Fishers, IN). Ludox-HS30 Silica beads (12 ± 2 nm) were obtained from Sigma-Aldrich. These latter nonfluorescent particles were labeled respectively by adsorption of R6G and R123. Stock solutions of HTO (DuPont NEN Research Products, Boston, MA) and ¹⁰⁹Cd (Pharmacia Biotech, Pfizer, New York, NY; in 0.1 M HCl) were diluted 10× and 200×, respectively, with water to obtain suitable activities for spiking during diffusion experiments. M(NO₃)_x salts (M = Tl⁺, Cd²⁺, Cu²⁺, Pb²⁺) were obtained from Merck (Whitehouse Station, NJ; puriss).

Labeling of the latex beads was performed by adsorption of R6G: 10 μl of the original suspension (10% w/w) of latex beads was diluted to 0.5 ml with Milli-Q water (Millipore, Billerica, MA) and mixed with 0.5 ml R6G (10⁻⁶ M for 30 nm, 3 × 10⁻⁷ M for 60 nm, and 4 × 10⁻⁸ M for 100-nm latex particles). The obtained solutions were sonicated for 2 min, and then filtered (Millipore filter Ø = 200 nm).

Solid samples of lyophilized proteins were dissolved and sonicated for 2 min, filtered (Millipore filter Ø = 200 nm), and then diluted in the range 10⁻⁷–10⁻⁸ M for FCS measurements in the case of parvalbumin and R-phycoerythrin. These samples were monodisperse and one-component. The commercial Texas-Red-labeled ovalbumin needs to be purified from free dye. This has been done over a Sephadex G-100 gel column (Amersham Biosciences, London, UK).

All experiments were prepared as follows: Fresh mother suspensions were prepared each time by sonicating the material for several minutes, filtering, then checking them by FCS in saline water at the desired ionic strength. During these first sets of FCS measurements in solution, the fraction of the mother solution was adjusted to get an optimal FCS signal (both in water solution and in gel, knowing that the fluorescence intensity is lowered by ∼20% in 1.5% agarose gel as compared to the water solution, due to light-scattering). Another FCS cell was then prepared with two holes (one for the solute in gel and the other for the solute in the corresponding buffered solution without agarose). For a given solute, the hot gel suspension of tracer and the corresponding suspension of tracer in buffered solution (made at room temperature) were both prepared within a couple of minutes. The mother suspension used to make the two solutions (roughly 10–50 μL for a total volume of 2 mL) was then preheated to 60°C for 3 min to avoid any local gelling when the suspension was added to the hot gel solution. The hot gel suspension of fluorescent tracers was left 15 min more inside the oven to ensure good mixing before being deposited in a hole of the FCS cell. Outside the oven, in quasi-adiabatic conditions, it was then left to cool slowly for the next hour on the microscope and finally studied. During this period, a calibration was made and the water suspensions were measured before the corresponding gel suspensions. All the structure parameters p, obtained during the calibration processes using Eq. 5, were in the range 5–10; residues between calculated and experimental autocorrelation functions were small and statistical.

Agarose gels

Purified agarose (LGL, molecular biology grade, lot #8041) obtained from Biofinex (Praroman, Switzerland) was used without further purification. Agarose gels were prepared by adding the desired volume of phosphate buffer (5 × 10⁻³ M or 0.01 M, pH = 7.0) to a given amount of agarose powder before heating the mixture to between 90 and 100°C until complete dissolution of the polymer. Solutions were covered and heated at 60°C for 60 min, then completed with hot water to keep the polymer fraction constant. Fluorescent particles were introduced into the hot, clear solution, which was transferred into a FCS cell and left to cool to its gelling temperature (below 37°C).

Measurement of diffusion times and fractal exponents by FCS

Diffusion times of particles within the gel were measured by fluorescence correlation spectroscopy (FCS; ConfoCor Axiovert 135 TV; Carl Zeiss International, Zurich, Switzerland), except for metal ions and tritiated water (HTO). For these latter tracers, diffusion coefficients in the agarose gel were determined (Fatin-Rouge et al., 2003) using a diaphragm diffusion cell made of two plastic compartments (source and receiving) connected by a gel window. For FCS measurements, the setup was with a 50-μm pinhole. The objective in water immersion was 40× and the microscope inverted. Fluorophores in the gel samples were excited with an Ar⁺ (488 or 514 nm) or an He/Ne laser (545 nm) and fluorescence intensity was measured with an avalanche photodiode (SPCM-200PQ). Variations of the fluorescence intensity in the confocal volume (∼1 μm³) are attributed to the translational diffusion of the fluorescent particles. Artifacts from non-Gaussian confocal volume have been minimized as checked in calibration and buffer solutions. Although this condition may be altered in gel, we have verified that it is of minor importance here compared to the effects of the particle size on the autocorrelation function. The objective of this work was to use only a one-component system, since it is clear that polydispersity can mask the anomalous diffusion behavior. So generally, autocorrelation functions were analyzed using the modified Eq. 5 for anomalous diffusion. Two-component systems were present only in the case of latex particles fluorescently labeled with adsorbed dye. In the other cases, the binding was covalent, and if needed, free label was removed using a Sephadex chromatographic column before use. The use of two-component systems (free dye and labeled particle) has been avoided as far as possible here to test the validity of the fractal approach in FCS. In the case of a coexistence of free dye with noncovalently R6G-labeled latex beads, fluctuations of intensity were analyzed using the following equation (Schwille et al., 1999a) for a two-component model,

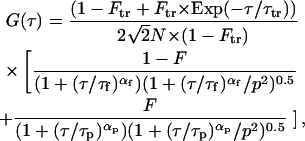(8)

where F is the fraction of the fluorescently labeled particles, and τ_f and α_f are the diffusion time of the free label (R6G) and the corresponding anomalous exponent, respectively. The diffusion times τ_f and α_f were fixed to the values obtained from diffusion of the dye alone in the gel by fitting G(τ) with F = 0 in Eq. 8. The value τ_p is the diffusion time of the noncovalently labeled particles and α_p is their corresponding anomalous exponent. In Eq. 8, the quantum yields of the free and adsorbed dyes are equal, as experimentally observed, within 30% deviation, by adding latex beads to R6G solutions under typical labeling conditions and no correction of brightness has been applied. Therefore, for R6G-labeled latex beads, G(τ) has been fitted with a two-component model. The fractions of free R6G in the buffered solutions, as calculated from FCS data, were low (<10%). In the case of diffusion within the gel, the calculated fraction of free dye—R6G_free/(R6G_free + R6G_adsorb)—increased 2–4 times as compared to diffusion in water, probably as a result of a non-negligible immobilized fraction of latex beads in small pores (see Fig. 1 and the following section).

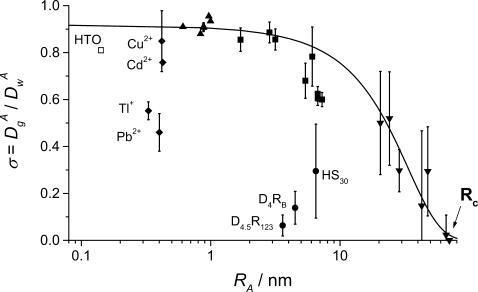
FIGURE 1.

The value σ (μ ≥ 10⁻²) as a function of the hydrodynamic radius R_A for HTO, □; trace metals, ♦ R6G, NB, R123, HA, ▴; proteins, ▪; latex beads, ▾; Ludox-HS30 silica (HS₃₀); and NH₂- or CO₂H-dendrimers, • (D₄R_B and D_4.5R₁₂₃, respectively). The line shows the compounds displaying only steric interactions with the gel.

Each reported α-value is the mean of at least 20 measurements that were obtained at 10 different places in the same sample of gel to check its homogeneity and to ensure representative values for α. Acquisition times in the range of 20–200 s were used to improve the signal/noise ratio. Mathematical analyses were performed on the averaged FCS autocorrelation functions. The experiments were conducted twice for all tracer sizes to check reproducibility. For all the control buffered solutions, α ≡ 1.0 within small deviations.

RESULTS AND DISCUSSION

Diffusivity: pore-size analysis and interactions with matrix

The reduced diffusion coefficient, σ, of a particle A within a porous material is a key parameter in characterizing the material porosity,

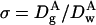(9)

where 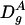and 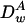are, respectively, the diffusion coefficient of particle A in the gel and in water.

The value σ is still ≤1 and is lowered by sterical, chemical, and electrical interactions with polymer fibers. It was shown earlier (Fatin-Rouge et al., 2003) that the latter interactions can be cancelled if the ionic strength, μ, is >5 × 10⁻³–10⁻² for a 1.5% agarose gel.

Many models have been proposed to describe diffusion through gels (Masaro and Zhu, 1999), generally by considering hydrodynamic interactions only. In those cases σ is expressed as a function of the polymer fraction (φ), solute size, etc., to get average parameters that describe the porous matrix.

Although confocal techniques are very useful to measure diffusivity, in porous media they can only provide an estimation of this parameter when the size of diffusing particles is not small compared to pore sizes. Indeed, Eq. 6 is not valid when diffusion is anomalous or is not isotropic in all space dimensions. Rigorously, the time-dependent diffusion coefficients, 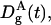should be calculated using Eqs. 4 and 7. Nevertheless, as a first step, 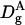values can be estimated by Eq. 6. So, the corresponding variations of σ versus the hydrodynamic radius of the particle A, R_A, are qualitative (see Fig. 1), but they allow 1), an estimation of an average pore size of the matrix; 2), a determination of the minimum size of trapped particles, R_c (which in turn gives an estimation of the largest pore size); and 3), importantly here, they allow the detection of specific interactions between diffusing particles and polymer fibers that would induce a misinterpretation of anomalous diffusion.

For agarose gels, it has been observed previously (Fatin-Rouge et al., unpublished) that while the correlation length of the polymer's pores, ξ, is fairly independent of the ionic strength (for μ ranging from 0 to 1), it will depend to a large extent on the cooling rate during gelification. For a 1.5% agarose gel, ξ = 77 ± 11 nm, but this value can be as small as 50 nm in case of very fast cooling. The cooling rate has been carefully reproduced here to ensure that the samples had the same morphological characteristics. The pore-size distributions obey the Weibull second-order distribution function which depends on the average pore radius only, and can describe many random networks made of rigid chains (Amsden, 1998).

In these experiments, the rather large ionic strength in concert with the quasi-infinite dilution of the diffusing particles has suppressed electrical interactions between particles and gel fibers (Fatin-Rouge et al., 2003). Diffusing particles can be separated into two groups (Fig. 1): a first group of compounds that includes organic dyes, proteins, and latex beads, providing the upper values of σ and showing small or negligible interactions with fibers. The absence of interactions might be due to hydrophobic properties of these compounds. The second group of compounds is composed of more hydrophilic compounds: HTO, silica (HS₃₀), NH₂-, or CO₂H-dendrimers (D₄R_B and D_4.5R₁₂₃, respectively), which exhibit an affinity for the agarose network. From the first group of particles, R_c is estimated to be 70 nm for a 1.5% agarose gel (see Fig. 1). Based on the fact that σ varies little with R_A up to R_A = 7 nm (see Fig. 1), Eq. 11 in Fatin-Rouge et al. (2003) can be used to estimate an average pore radius of R_p = ∼37 ± 2 nm. This latter value is in good agreement with ξ (ξ = 77 ± 11 nm), which is usually considered as a good approximation for the mean pore diameter.

Validity of FCS correlation function for anomalous diffusion in porous matrices

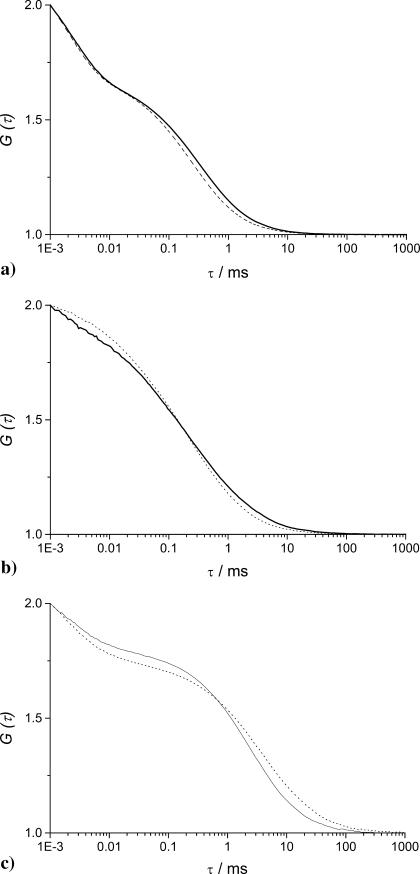
When restricted diffusion occurs, the FCS autocorrelation curves of a single diffusing species display a typical broadening along the time axis as shown in Fig. 2. In Fig. 2, a and b, while the experimental autocorrelation functions in gel and in buffered solution are normalized both in amplitude and time, the curves are clearly different. In Fig. 2 c, the apparent increase of correlation times of the diffusing particles comes from the restricted diffusion within the porous medium, inside the confocal volume and its surroundings. Because of this effect the autocorrelation functions failed to be fitted with the classical Eq. 5 describing uniform diffusion (see χ² values given in legend of Fig. 2). So, Eq. 5 modified with the anomalous exponent α has been used to take into account the fractal character of the diffusing medium. The two-component analysis (Eq. 8) has been used for nonfluorescent latex particles only, which were labeled by adsorption of R6G. The validity of the anomalous model for analyzing the FCS correlation functions obtained for diffusion in agarose gels is tested below by comparing experimental results with those from three-dimensional Monte Carlo simulations of the diffusion of hard spheres in randomly built porous media, which approximate the topology of real polymer gels (Netz and Dorfmüller, 1995). They have fully characterized their porous media and, although the average pore size they have determined is lower than what we have obtained for agarose gels (Fatin-Rouge et al., unpublished), the pore-size distribution functions are quite close. Accordingly, the reduced correlation length ξ*, which is ξ/2R_C, has been introduced in an effort of comparison with the results obtained by Netz and Dorfmüller (1995), because it should be similar for all the porous media that follow close distribution laws.

FIGURE 2.

Normalized FCS autocorrelation functions of diffusing particles within a 1.5% agarose gel (full lines) and in water (dashed lines). The χ² values corresponding to anomalous (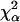) and normal (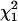) diffusion models for tracer diffusion within agarose gel are given. (a) Parvalbumin: p = 6.55,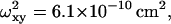 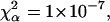and 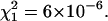(b) R-Phycoerythrin: p = 5.44,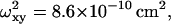 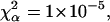and 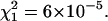(c) 50-nm latex microspheres: p = 5.64,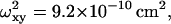 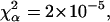and 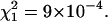Phosphate buffer 5 mM; pH = 7.0; T = 20.0°C.

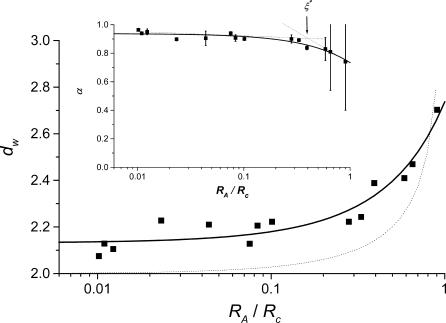
For free diffusion in solution, α = 1. Variations of the fractal exponent, α, with the reduced hydrodynamic radius of particles, R_A/R_c, are presented in Fig. 3 and Table 1. Only the compounds that do not display a significant chemical interaction were considered (see line in Fig. 1). Two domains are found: 1), a domain where α is quasiconstant and less than unity (α = 0.93 ± 0.04) for R_A/R_c = 0.01 to 0.4 and 2), a domain corresponding to R_A/R_c ≥ 0.4, where α decreases when R_A/R_c increases. The reduced correlation length of the porous medium, which has been estimated as ξ* = 0.4, is the intercept of the tangent lines to the curve, as shown in the insert of Fig. 3. The value ξ* can be seen as a limit between two diffusion domains. The value obtained from Monte Carlo simulations, ξ* ∼ 0.6, is slightly larger for the randomly built porous media (Netz and Dorfmüller, 1995). This difference can be explained by the differences in pore-size distributions between our agarose gels and the modeled porous media. For FCS measurements, the deviations in Figs. 1 and 3 reflect that the size of the tracer is a probe of local heterogeneity: small dyes like rhodamines see the gel as homogeneous, and then deviations increase with the diffusing particle size; but there is a critical size comparable with the mean pore size where the diffusion behavior changes dramatically and is very position-dependent because the tracer can meet very different situations, such as hindered diffusion in pore larger than its size or trapped diffusion in a pore of similar size. The variability increases as the ratio 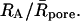This phenomenon has been observed in Monte Carlo simulations of tracer diffusion in porous networks as reported by Netz and Dorfmüller (1995). In the first domain, the fact that α < 1 suggests the possibility of a special diffusion process that is different from normal diffusion. In an infinite self-similar matrix it is expected that α will be independent of the probe-particle size, since all probes should experience the similar obstructive pathways because fractals have no correlation length. The invariance of α for R_A < 30 nm suggests, therefore, that anomalous diffusion occurs at the scale < 60 nm. The decrease of α at R_A/R_c ≥ 0.4 (Fig. 3) suggests a transition from anomalous to trapped diffusion for a particle with 30 nm < R_A < R_c. The resulting value ξ ∼ 60 nm (estimated from Fig. 3 insert, as 0.4 × 2R_c) is comparable to 77 ± 11 nm obtained from neutron-scattering experiments (Fatin-Rouge et al., unpublished). The appearance of trapped diffusion depends on R_A/R_c since small particles can travel in a connected network of pores, whereas the larger ones are quickly trapped. Small particles may also experience fiber bundles as porous media whereas larger ones do not. In our conditions of sample preparation, connectivity decreased markedly when the particle-reduced radius was >0.4.

FIGURE 3.

Plot of the fractal dimension of diffusion d_w as a function of reduced particle size. Full line is simulated with the empirical Eq. 10. Dotted line simulates results obtained from MC simulations of bead diffusion in fractal polyacrylamide networks (Netz and Dorfmüller, 1995). Insert is a plot of the fractal exponent α-dependence on reduced particle size. The reduced correlation length of agarose pores has been estimated as the intercept of tangent dotted lines (arrow). Phosphate-buffered solutions; pH = 7.0; μ ≥ 10⁻²; T = 20.0°C.

TABLE 1.

Value of the exponent α as a function of particles' hydrodynamic radii in a 1.5% agarose gel

Particle	RA/nm	α
R6G*	0.74	0.964(1)
R123*	0.80	0.940(2)
Humic acid*	0.90	0.95(2)
Parvalbumin†	1.70	0.898(2)
—*	3.20	0.905(50)
Ovalbumin*	5.50	0.94(1)
R-Phycoerythrin†	6.10	0.907(22)
—*	7.40	0.90(1)
Latex beads*	20.5	0.90(3)
—	24.1	0.892(4)
—	28.7	0.837(13)
—	42.8	0.83(8)
—	47.7	0.81(27)
–	66.1	0.74(34)

pH = 7.0 (phosphate); T = 20°C.

^*μ = 0.01.

^†μ = 0.1.

The validity of introducing a fractal exponent in the analytical formula of the FCS correlation function is supported (Fig. 3) by the similarity in the experimental change of d_w with R_A/R_c and the values obtained from Monte Carlo simulations (Netz and Dorfmüller, 1995). The experimental and theoretical curves of d_w versus the reduced hydrodynamic radius of particles are very similar, although experimental values of d_w tended to 2.1, whereas Monte Carlo simulated values were found to converge to 2.

Both Monte Carlo simulations (Netz and Dorfmüller, 1995) and the present study show that d_w varies little for R_A/R_c ≤ 0.4–0.6, depending on the specificity of the pore-size distributions, and then increases quickly at larger values. As reported for simulations (Netz and Dorfmüller, 1995), at these larger values of R_A/R_c, deviations become large (see Fig. 3), because the tracer size is similar to the average pore diameter and then diffusion is hindered or trapped. In any case, the experimental variations of d_w vs. R_A/R_c presented in Fig. 3 can be well described by a simple empirical function (see Fig. 3, solid line),

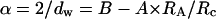(10)

where A and B are simple parameters and are equal to 0.20 ± 0.02 and 0.938 ± 0.007, respectively.

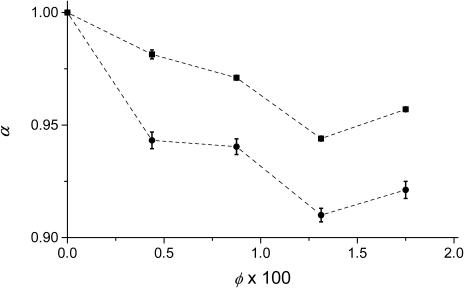
To have a better understanding of the observed offset in real experiments, we have analyzed the diffusion of particles in agarose gels with various fiber fractions, φ. The variations of α vs. φ is presented in Fig. 4. The value d_w is predicted to be fairly independent of φ in the MC simulations where only hard-sphere potentials between particles and fibers are considered (Netz and Dorfmüller, 1995). The experimental behavior of d_w vs. φ could be the result of an increasing nonspecific interaction of the diffusing particles with the gel fibers or an increasing deviation from a nearly Gaussian confocal volume. Such nonspecific interactions may be due to attractive van der Waals interactions not considered in the MC simulations. To more realistically describe diffusion through the gels, it may be necessary to introduce a more realistic potential in further MC studies.

FIGURE 4.

Plot of the fractal exponent α-dependence on volume fraction of agarose. R6G, ▪; Parvalbumin, •. Phosphate-buffered solutions; pH = 7.0; μ ≥ 10⁻²; T = 20.0°C.

CONCLUSION

In real heterogeneous porous media, the anomalous diffusion of particles occurs on a limited range of length- or timescales, because their structure is only fractal over a limited size scale. FCS has been shown to be very useful in giving information about the diffusion processes of particles with sizes ranging from much less to greater than ξ-value, the average pore size of the gel. The validity of the mathematical expression of the FCS autocorrelation function for diffusion in fractal media has been confirmed by the good agreement of our experimental results with previous three-dimensional Monte Carlo simulations of diffusion within gels. A systematic offset of the fractal exponent of diffusion d_w, as compared to simulations, has been observed in agarose gel, which could be related to nonspecific van der Waals interactions between diffusing particles and the polymer network.

Two diffusion processes have been observed for a reduced hydrodynamic radius of diffusing particle. At R_A/R_c < ξ* = 0.4, which is a reduced correlation length, the diffusion is anomalous. Above this value, the connectivity of the pores decreases rapidly and diffusion of particles becomes entrapped. This suggests that the particle diffusion process can only be described as anomalous over a limited range of lengths, because connectivity depends on the reduced particle size.

APPENDIX: GLOSSARY

d_f

Mass fractal dimension

d_w

Fractal exponent of diffusion

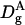
Diffusion coefficient of particle A within the gel

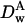
Diffusion coefficient of particle A in water

F

Fraction of the fluorescently labeled particles

F_tr

Triplet fraction

L

Linear size

〈m〉

Ensemble average of the number of empty holes

N

Mean number of particles in the confocal volume

p

FCS structure parameter of the confocal volume

R_A

Hydrodynamic radius of diffusing particle

R_c

Critical radius, i.e., the minimum size of completely trapped particles within the gel

R_p

Average pore radius of a porous material

SV

FCS sample volume

α

Anomalous exponent

φ

Volume fraction of fibers in the gel

μ

Ionic strength (/M)

σ

Reduced diffusion coefficient in a porous medium

τ

Delay time

τ_c

Diffusion time

τ_f, τ_p

Diffusion times of the free label and the noncovalently labeled particles, respectively

τ_tr

Triplet time

ξ

Correlation length or network mesh size

ξ*

Reduced correlation length

ω_z, ω_xy

Longitudinal and transverse radii of the SV, respectively

Γ

Transport coefficient