Gating of the Large Mechanosensitive Channel In Situ: Estimation of the Spatial Scale of the Transition from Channel Population Responses

Abstract

Physical expansion associated with the opening of a tension-sensitive channel has the same meaning as gating charge for a voltage-gated channel. Despite increasing evidence for the open-state conformation of MscL, the energetic description of its complex gating remains incomplete. The previously estimated in-plane expansion of MscL is considerably smaller than predicted by molecular models. To resolve this discrepancy, we conducted a systematic study of currents and dose-response curves for wild-type MscL in Escherichia coli giant spheroplasts. Using the all-point histogram method and calibrating tension against the threshold for the small mechanosensitive channel (MscS) in each patch, we found that the distribution of channels among the subconducting states is significantly less dependent on tension than the distribution between the closed and conducting states. At −20 mV, all substates together occupy ∼30% of the open time and reduce the mean integral current by ∼6%, essentially independent of tension or P_o. This is consistent with the gating scheme in which the major rate-limiting step is the transition between the closed state and a low-conducting substate, and validates both the use of the integral current as a measure of P_o, and treatment of dose-response curves in the two-state approximation. The apparent energy and area differences between the states ΔE and ΔA, extracted from 29 independent dose-response curves, varied in a linearly correlated manner whereas the midpoint tension stayed at ∼10.4 mN/m. Statistical modeling suggests slight variability of gating parameters among channels in each patch, causing a strong reduction and correlated spread of apparent ΔE and ΔA. The slope of initial parts of activation curves, with a few channels being active, gave estimates of ΔE = 51 ± 13 kT and ΔA = 20.4 ± 4.8 nm², the latter being consistent with structural models of MscL, which predict ΔA = 23 nm².

INTRODUCTION

MscL, a large-conductance mechanosensitive channel, first isolated from Escherichia coli (Sukharev et al., 1994), is a fast-acting pressure-release valve that prevents osmotic rupture of a bacterial cell when tension in the cytoplasmic membrane approaches the lytic limit (Levina et al., 1999; Booth and Louis, 1999). MscL is especially attractive from the biophysical point of view as an example of a transmembrane protein that dramatically changes its conformation in a tension-dependent manner. The solution of the crystal structure of MscL homolog from Mycobacterium tuberculosis (TbMscL) (Chang et al., 1998) had opened numerous possibilities for detailed studies of its gating mechanism.

The TbMscL structure, solved to a 3.5 Å resolution, revealed a tightly packed assembly of five identical subunits, each bearing two transmembrane helices, and was interpreted as a closed state. An atomic-scale homology model of closed E. coli MscL (EcoMscL) has been built and several hypothetical open conformations proposed (Sukharev et al., 2001b). Based on the previous kinetic analysis (Sukharev et al., 1999), the opening of MscL was modeled as a two-step process, with the first transition from the closed to a pre-expanded intermediate low-conducting state followed by a transition to the fully open state (Sukharev et al., 2001a,b). To model a pre-expanded nonconducting or low-conducting state, the N-terminal segments (unresolved in the crystal structure) were invoked and presented as a short helical bundle that can occlude the pore while the barrel is expanded. Further expansion of the barrel was proposed to separate the N-terminal bundle (cytoplasmic gate), resulting in full opening. Structural modeling (Sukharev et al., 2001b) and molecular dynamic simulations (Gullingsrud and Schulten, 2003; Colombo et al., 2003; Kong et al., 2002) suggested that the expansion of the barrel must be achieved through an outward movement of transmembrane helices associated with substantial tilting. The models of the EcoMscL in the closed and open (expanded) states were supported by cysteine cross-linking experiments in situ, as well as with patch-clamp experiments on cysteine mutants (Sukharev et al., 2001a; Betanzos et al., 2002). A similar character of the conformational transition was independently concluded from electron paramagnetic resonance studies of EcoMscL reconstituted in liposomes (Perozo et al., 2002). The open conformation depicts a pore of ∼9–10 nm² in cross section to satisfy the 3.2-nS conductance, and predicts a large-scale conformational rearrangement of the transmembrane part of the protein accompanied with a 40° tilting of helices and large in-plane expansion (Betanzos et al., 2002).

The amount of in-plane expansion for a mechanosensitive tension-gated channel has the same fundamental meaning as the gating charge for a voltage-gated channel and defines the sensitivity to the stimulus. The cloning of V-gated channels, sequencing, and determination of the number of charged residues in voltage-sensor domains went in parallel with extensive experimental measurements of gating charges, as reviewed in Bezanilla (2000). Relating the amount of expansion for mechanogated channels with discrete conformations predicted by modeling and other methods appears to be a problem of the same significance. As the stereochemical aspect of MscL opening is becoming better understood, the thermodynamic description remains not only incomplete, but also inconsistent with the atomic model predictions. A previous thermodynamic treatment of multichannel recordings made in liposomes in the framework of the two-state model (Sukharev et al., 1999) estimated the intrinsic energy of MscL transition as 19 kT and the in-plane expansion as 6.5 nm², the latter being too small to accommodate the highly conductive pore. The dose-response curves recorded in situ from giant spheroplasts in preliminary trials have estimated ΔA as 10–15 nm², which is larger than in liposomes, but still half of what the structural models predict. It seemed important to find what caused this apparent systematic discrepancy and to estimate the true values for ΔA and ΔE. It should be noted that experimentation with mechanosensitive channels is less straightforward than with V-gated channels, because membrane tension, which is the main thermodynamic parameter driving the transition, is not easily determined from the pipette pressure.

In this article we conduct a systematic study of single-channel traces and dose-response curves for MscL in patches excised from giant spheroplasts. We utilize the activation pressure of MscS as a reference point to assess the tension acting on MscL. By analyzing occupancies of major subconducting states as a function of tension we validate the use of the integral current recorded from multichannel patches as a measure of P_o and the two-state model for gross thermodynamic description of MscL gating. We also modify the kinetic scheme of MscL in accordance with the dependencies of subconducting states on tension and voltage. We estimate ΔA and ΔE from large data sets and show that when the channel population in the patch is nonuniform, the observed values may be substantially lower than true parameters. By measuring the limiting slope of dose-response curves we find a more realistic value for ΔA that better corresponds to the model predictions.

MATERIALS AND METHODS

Spheroplast preparation

Giant spheroplasts were prepared essentially as described previously (Martinac et al., 1987). Escherichia coli pB104 mscL-, recA- cells harboring the p5-2-2b vector with mscL under the control of a lac-inducible promoter (Blount et al., 1996a) were used for all preparations. Overnight cultures grown in Luria-Bertani medium in the presence of 100 μM ampicillin (255 rpm, 37°C) were diluted 1:100 into the same medium and incubated for 3 h to an OD₆₀₀ of 0.4–0.8. This culture was then diluted 1:10 into (modified) Luria-Bertani medium containing 100 μM ampicillin and additional 60 μg/ml cephalexin (Sigma Chemical, St. Louis, MO), an antibiotic that blocks cell septation. The culture was incubated with shaking for 1.5 h at 37°C, until filamentous cells reached 50–150 μm in length. The mscL gene was induced by 1 mM isopropyl-b-d-thiogalactopyranoside (IPTG) (Research Products International, Mt. Prospect, IL) 30 min before harvesting. The filaments were gently spun down and converted into giant spheroplasts by 0.2 mg/ml lysozyme and 5 mM EDTA, at room temperature. After full induction by IPTG, 40–70 channels were observed in each patch. To decrease the number of expressed channels, the induction by IPTG was omitted, while bacteria were grown in (modified) Luria-Bertani medium or in the glucose-containing SOB medium. Noninduced cells typically exhibited 3–7 channels per patch.

Electrical recording

The standard patch-clamp technique (Hamill et al., 1981) was used to record MscL single-channel current in inside-out patches excised from giant spheroplasts. Patch electrodes were pulled from borosilicate capillaries (100 μL disposable pipettes; Fisher Scientific, Pittsburg, PA) on a Sutter P-97 micropipette puller (Sutter Instruments, Novato, CA) and were used without fire-polishing. All pipettes had bubble numbers near 4.5 in 95% ethanol, corresponding to a resistance ∼5 MΩ in the symmetrical recording solution containing (in mM): 200 KCl, 90 MgCl₂, 10 CaCl₂, and 5 HEPES-KOH, pH 6. The bath solution was the same plus 0.3 M sucrose added to increase the osmotic stability of the spheroplasts. The currents were recorded using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) under the holding potential between −20 and −60mV, at room temperature. Currents filtered at 10 kHz by the built-in lowpass Bessel filter of the amplifier and an external 8-pole Bessel filter (Model 3381 filter, Krohn-Hite, Avon, MA) were digitized at 25 kHz with a Digidata 1322A data acquisition system and pCLAMP8 software (Axon Instruments).To better resolve short subconducting states, in some experiments patch electrodes were coated with dental wax (Kerr, Romulus, MI). Currents in such instances were filtered at 30 kHz and sampled at 100 kHz. Suction was applied to the patch-clamp pipette by a screw-driven syringe and measured with a digital pressure gauge (PM015D, World Precision Instruments, Sarasota, FL).

Data analysis

To identify the substates, continuous traces (typically 5-min long) were recorded at constant pipette pressures in the range of open probabilities (P_o) between 0.01 and 0.08. After baseline correction that removed drift and some obvious MscS fluctuations, probability density histograms were calculated and fitted by the sum of Gaussian functions, representing the closed and open states and a variety of subconductance levels using HISTAN, a software custom-written in Matlab. Five “long” recordings from two independent spheroplast preparations were subjected to current amplitude analysis. In patches where nonadapted MscS was present, the baseline itself was subjected to amplitude analysis to estimate the amount of interference that MscS activities potentially bring to MscL histograms (see Results).

To record dose-response curves, the suction applied to the pipette interior was first increased relatively quickly with the rate of ∼60 mm Hg/s, passing the MscS activation point, until we observed first MscL openings. Then the pressure was changed in smaller increments of ∼10 mm Hg and kept constant for ∼5 s between the steps. The open probability (P_o) was calculated for each pressure step as the mean integral current divided by the maximum current which could be attained at saturating pressures. For multichannel patches, the maximal conductance (and the total number of channels) was estimated by extrapolating partial activation curves. This could be done with a >5% accuracy after reaching ∼80% of saturation. Most of the traces used for analysis displayed >95% current saturation as assessed by the sigmoidal fitting procedure (see Appendix 2 for analysis of fitting errors). The integral conductance G normalized to the inferred maximal G_max conductance produces effective open probability P_o^eff that includes contributions from all subconducting states. In addition to measurements of P_o^eff, the recordings were analyzed using the amplitude threshold detection technique. In this method, traces containing <6 channels were idealized and transitions were scored when the current crossed the threshold line (set at 0.1 of full conductance) between the levels representing the closed and fully open states. From idealized traces, the closed and open state durations for the channels were measured, P_o was calculated, and the gating parameters were extracted as described below. Both methods gave similar results and the potential discrepancies are estimated in the Discussion.

Because MscL is activated by tension but not directly by pressure, the pressure gradients (p) across the patch were converted to tensions (γ) by the Laplace's law, γ = pr/2, where r is the radius of patch curvature. Without imaging, the patch curvature is not generally known. Therefore we used the activation threshold of the ever-present small conductance mechanosensitive channel (MscS) as a reference point. Previous studies (Cui and Adler, 1996; Sukharev, 2002) have suggested that the midpoint for MscS activation by membrane tension (γ_1/2^MscS) is 5.5 ± 0.1 dyn/cm. By scoring the pressure at which half of MscS channels become active (p_1/2^MscS) in each record, we converted the pressure gradient scale into the tension scale using the formula: γ = (p/p_1/2^MscS) × 5.5 dyn/cm, where γ is the tension at a given p pressure across the patch. Such a conversion implies that the radius of curvature of the patch is independent of pressure in the given range. Based on observations of liposome patches (Sukharev et al., 1999), the membrane is essentially flat at a zero pressure, and becomes spherical under a gradient. As the pressure increases, the curvature of liposome patches saturates and remains stable at tensions >4–5 dyn/cm, which is likely to be true for spheroplast patches as well.

The dose-response curves for MscL were fitted with the two-state Boltzmann-type model,

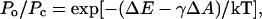(1)

where P_o and P_c are the open and closed state probabilities, ΔE is the energy difference between the states in an unstressed membrane, ΔA is the in-plane protein area change upon the gating transition, γ is the membrane tension, and kT has the conventional meaning (Howard and Hudspeth, 1988; Sachs, 1992; Sukharev et al., 1999).

Protein area calculations

The molecular models of the closed and the open states that satisfy the 3.2-nS unitary conductance—conformations 2 and conformation 11, respectively—were taken from Sukharev et al. (2001b). PDBAN, the program for analysis of cross-sectional areas was custom-written in Matlab. Solvent-accessible surfaces were created from PDB coordinates using the surface of a rolling spherical probe. For the outer protein surface, which is in contact with lipid, the probe radius was chosen as 4 Å; for the inner water-accessible surface it was 1.4 Å. The cross sections of the solvent-accessible surfaces normal to the pore axis were generated and the areas were calculated. The areas of two protein slices located at the positions ±12 Å from the midplane of the membrane, i.e., near the hydrophobic core boundaries, were averaged, and the numbers taken as in-plane cross-sectional areas for a particular conformation.

Statistical modeling of the tension response of a mixed channel population

The amount of channel expansion ΔA_o = 23.3 nm² was estimated from molecular models, and the corresponding energy of the transition, ΔE_o = 58.9 kT was calculated using Eq. 1 and the condition of γ_1/2 = 10.4 dyn/cm determined in experiments (see Results). These values were taken as the initial single-channel parameters for simulations. Sets of normally distributed random numbers ΔE_i and ΔA_i with different standard deviations were generated using the randn function of Matlab. The standard deviations were varied, between 1 and 20 kT for ΔE (∼58.9 kT), and between 0.5 and 3.5 nm² for ΔA (∼23.3 nm²). Pairs with a fixed ΔE and random ΔA, random ΔE, and fixed ΔA, or both random parameters, modeled individual channels in a population. P_o/P (γ) curves for each channel were generated using Eq. 1 and then superimposed to simulate the dose-response curves of the entire channel population in the patch. Fitting of the population dose-response curves in the range of P_o/P_c from 0.01 to 100 (measurable in a typical experiment) to the two-state model yielded apparent parameters, ΔE_app, ΔA_app, which were then plotted as a function of standard deviation of the corresponding parameter. Based on the average numbers of channels per patch typically observed in uninduced or IPTG-induced spheroplasts, we repeated such simulations for 5- and 50-channel populations to determine at what standard deviations of true ΔE and ΔA the distributions of ΔE_app and ΔA_app would resemble the experimentally observed scatter (see also Appendix 1).

RESULTS

Pressure-current responses of spheroplast patches and the tension scale

Current traces from two representative patches with 52 and five MscL channels are shown in Fig. 1, A and B, respectively. Both recordings were made in spheroplasts in inside-out configuration at −20 mV (pipette positive). The total number of channels per patch was 50 ± 5 (n = 11) in induced cells and 5 ± 2 (n = 20) in noninduced spheroplasts. The later number of channels illustrates the leakage of the vector promoter. This minimal level of expression, combined with possible clustering of channels, did not permit reproducible recordings from true single-channel patches.

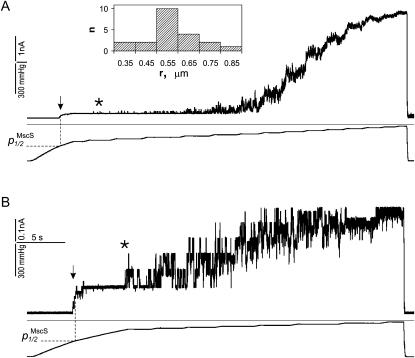
FIGURE 1.

Activation of MscL by transbilayer pressure gradients. (A) Patch-clamp recordings of channels at −20 mV (pipette positive) from spheroplasts expressing the wild-type MscL after induction with IPTG (1 mM, 30 min). A total of 52 channels were observed at the pressure close to saturating. (B) MscL activities recorded without IPTG induction. Five channels are observed in this particular experiment. The pressure traces measured in mm Hg are shown below each current trace. The points of half-maximal activation of MscS and first openings of MscL are indicated by arrows and asterisks, respectively. Using pressure that elicits half-maximal activation of MscS, p_1/2^MscS (which corresponds to tension of 5.5 dyn/cm), the pressure scale was converted into the scale of tensions. Inset represents the distribution of radii of curvature (r) calculated from the law of Laplace in 21 patches sampled with standard 5 MOhm pipettes.

Before MscL activation, the small mechanosensitive channel, i.e., MscS (Martinac et al., 1987; Sukharev et al., 1993), endogenous to the strain, always activated at a lower suction (arrow), exhibiting the unitary current of ∼25 pA, under given ionic conditions (see Materials and Methods). MscL exhibits first openings (∼75 pA, asterisk) at suction ∼1.5–1.6 times higher than that required to open MscS, consistent with previous observations (Blount et al., 1996b). MscL activities increase with pressure and in both instances reach saturation. At a pressure application rate of 50–60 mm Hg/s, as shown in the trace, MscS channels activate in an almost threshold-like manner and the steep onset marks the midpoint of its activation by pressure (p_1/2^MscS), which corresponds to the tension of γ_1/2^MscS = 5.5 dyn/cm, as reported previously (Cui and Adler, 1996; Sukharev, 2002). Assuming that the patch is a hemispherical cup and its radius of curvature (r) does not change in this range of pressures, the relation γ/γ_1/2^MscS = p/p_1/2^MscS can be derived from the law of Laplace: γ = pr/2. Thus, determination of p_1/2^MscS allows us to present activation curves measured in different pressure ranges in a unified tension scale and treat them statistically.

Having p_1/2^MscS one can also estimate r for a given size of pipettes, which provides information about patch geometry. In 21 independent trials, p_1/2^MscS was determined as 148 ± 29 mm Hg. Based on this data, the law of Laplace produces r = 0.58 ± 0.12 μm, with the actual distribution illustrated in Fig. 1 A (inset). Assuming that patches are hemispherical caps delineated by ∼60° angle relative to the axis of the pipette (Sukharev et al., 1999), their areas can be estimated as 1.1 ± 0.46 μm² (n = 21).

The structure of subconducting states

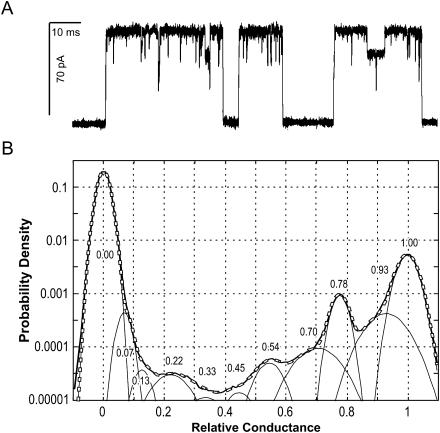
To address the question of whether the mean current would be an adequate measure of open probability of MscL at each pressure step, we analyzed the occupancies of subconducting states under different conditions. Fig. 2 A shows the fragment of a typical MscL trace recorded at −20 mV. The openings activated by moderate suction display short-lived substates seen as downward flickers from the fully open state (<0.5-ms long) and distinct long-lived subconductance levels (>2 ms). The short-lived substates are visited predominantly from the open state. Transitions to similar short substates are also observed from the long-lived substates. A typical all-point amplitude histogram constructed from a 5-min long continuous recording is presented in Fig. 2 B. A reasonably good fit of the experimental histogram by a sum of nine Gaussian curves indicates several discernable peaks with amplitudes of 0.22, 0.54, and 0.78 relative to the amplitude of the fully open state. The fit also suggests the presence of less prominent and more scattered intermediate levels centered near 0.7 and 0.93. The accuracy of fitting also required two low-populated peaks positioned near 0.33 and 0.45, and two more peaks with amplitudes of 0.07 and 0.13; however, their closeness to the highly populated closed state reduces the confidence of their exact position and occupancy. The prominent peak at 0.78 represents the long-lived subconducting state (L_0.78) visited predominantly from the fully open state. L_0.78 is kinetically different from short-lived substates S_0.22, S_0.45, S_0.70, and S_0.93. Its occupancy relative to the fully open state varied from patch to patch and had a tendency to increase with tension (see below). The occupancies of all other subconducting states varied in different trials with average standard deviation of ±26% relative to the mean (n = 8), whereas positions of the peaks were reproducible with the accuracy of 2%.

FIGURE 2.

Representative single channel currents of MscL recorded in a 30-kHz bandwidth from an inside-out patch at −20 mV (A). A 0.15-s fragment of a 5-min trace is shown with openings as upward deflections. The all-point amplitude histogram (B) compiled of 120 bins (solid envelope curve) includes the entire 5-min data set. It was fitted by a sum of 11 Gaussian distributions (dashed line). The peak positions shown by numbers represent amplitudes of subconducting states relative to the amplitude of the fully open state.

It should be noted that usually one (rarely two) active MscS channels were present in the patch during MscL recording. At pressures that activate MscL, these non-inactivated MscS channels were fully open displaying infrequent and short downward deflections. Amplitude histograms of traces containing one MscS (no active MscL) showed two peaks with positions at −0.08 and −0.29 (scaled by the amplitude of open MscL) and occupancies of 0.004 and 0.0003, respectively. This estimates the potential contamination of MscL histograms with MscS activities, which is very small and does not interfere with low-occupancy substates of MscL.

The total occupancies were remarkably reproducible (for a set of eight traces recorded at low P_o), being 0.26 ± 0.09 for all substates and 0.74 ± 0.09 for the fully open state, together making 0.93 ± 0.02 of the current expected for an ideal open channel without substates. The long-lived substate of 0.54 relative amplitude (L_0.54) appeared in approximately one-third of patches and its occupancy positively correlated with the occupancy of L_0.78. The short substates S_0.22, S_0.45, S_0.70, and S_0.93 are visited not only from the fully open state, but also show up as brief (10–40 μs) intermediate stair-like levels observed during opening or closing transitions (not shown). These levels correspond to the amplitudes of short substates (0.28, 0.71, and 0.90) previously reported in liposome-reconstituted patches (Sukharev et al., 1999). Because the fragments of liposome recordings were much shorter than those used in the present work, the substate with the relative amplitude near 0.45 was unaccounted for in the previous analysis. The substate L_0.78 was not considered previously either (Sukharev et al., 1999), as it seemed to represent not an intermediate, but an alternative open state (see Discussion).

Effect of voltage on subconducting states

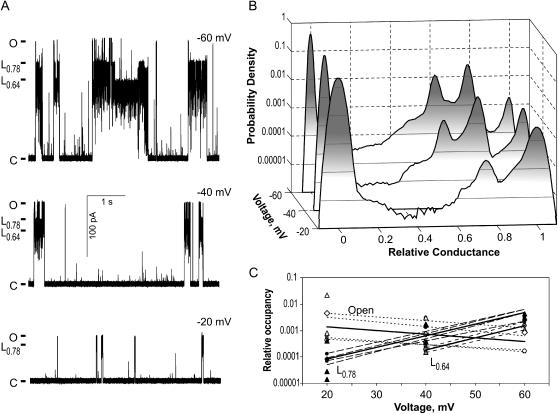
Hyperpolarizations beyond −40 mV substantially increased the occupancy of the long-lived subconducting states of MscL, consistent with observations by other groups (B. Martinac, personal communication). In this type of experiment, the combined action of negative pressure of 200–300 mm Hg and voltage compromised the stability of patches, which precluded steady recordings at voltages more negative than 60 mV. Fragments of the continuous trace recorded at constant pressure of 207 mm Hg and three different voltages (−20, −40, and −60 mV) are presented in Fig. 3 A. The pressure was initially chosen such that at −20 mV the openings were infrequent. As the voltage increased, the frequency of openings did not change substantially, but the dwell time in conducting states increased due to switching to the long-lived substates. The expanded traces recorded at −40 mV showed that the preferential sequence of transitions is such that the two long-lived substates are visited sequentially and exclusively from the fully open state. To close, the channel has to make a brief return to the fully open state. At −60 mV, however, closing transitions from intermediate conducting states were scored, or the brief full openings before closures in these instances were too short to be resolved (not shown).

FIGURE 3.

Long-lived subconducting states of MscL are voltage-dependent. (A) Representative fragments of a continuous MscL trace recorded under constant 207 mm Hg suction at −20 (bottom), −40 (middle), and −60 mV (top). (B) All-point amplitude histograms generated from 1-min fragments of the continuous trace recorded at a constant tension and three different voltages. The occupancies of the long-lived substates with the relative conductances of 0.78 and 0.64 increase at more negative membrane potentials. (C) Occupancies of the fully open state (open symbols) and the two long-lived substates L_0.78 (solid symbols) and L_0.64 (shaded symbols), normalized relative to the occupancy of the closed state. The solid lines represent the mean probability slopes for four independent data sets. The transferred net charges (q_ik) resulted from transitions between any two states i and k and were calculated from the ratios of probabilities by fitting with equation p_k/p_i = [p_k(0)/p_i(0)] × exp(−q_ik ΔV/kT), where p_i(0) and p_k(0) are the probabilities of specified states at 0 voltage. An outward movement of 0.8 e and inward movement of 3.5 e across the entire field were associated with C→O and O→L_0.78 transitions, respectively.

As seen from all-point histograms (Fig. 3 B), the occupancies of the two long-lived substates, L_0.78 and a new one with the relative amplitude of 0.64 (L_0.64), simultaneously increased with the voltage, whereas the occupancy of the fully open state slightly decreased. The results of Gaussian fitting of four sets of traces are presented in Fig. 3 C as logarithm of probability (relative to P_c) versus voltage. The slope of P_o decrease suggests that 0.8 ± 0.2 positive elementary charge needs to be transferred from inside to the outside as the channel opens (C→O). The occupancy of L_0.78 increases with the slope that corresponds to the transfer of 3.5 ± 0.2 positive elementary charges from the extracellular to the intracellular side of the membrane accompanying the O→L_0.78 transition. The occupancies of the two long-lived substates change in parallel, thus their ratio remains practically constant.

Effect of tension on subconducting states

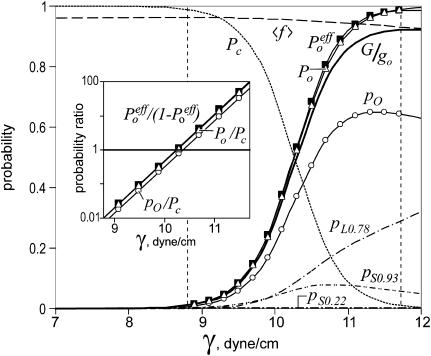
To analyze how the occupancy of individual substates changes with tension, a number of traces containing 3–5 channels were recorded in the range of open probabilities between 0.02 and 0.85. Amplitude histograms for one-channel fragments recorded at constant tensions were generated and compiled as a smooth three-dimensional diagram (see Fig. 4 A and its legend for details). The surface represents the probability density for conducting states with amplitudes between 0.1 and 1.1, as a function of tension. The ridge on the far right edge represents the fully open state, whereas the lower ridge next to it corresponds to the prominent L_0.78. The elevated point in the corner closest to the viewer indicates the presence of low-conducting substates, which gradually disappear as tension increases. Because the patches contained different number of channels, the baseline was excluded from the statistics and the ridge corresponding to the closed state is not shown. The total probability of conducting states between 0.1 and 1.1 at each tension was normalized to be unity. The inset above shows the actual open probability (calculated from the integral current of the entire channel population) plotted against tension in the same scale. It is evident from the diagram that whereas P_o changes by more than two orders of magnitude in the given range of tensions, the shape of the landscape remains essentially the same and the relative occupancies of major subconducting states do not change substantially.

FIGURE 4.

Relative occupancies of the MscL conductive substates as a function of applied tension. (A) The three-dimensional amplitude histogram representing the probability of a single MscL channel to be in a particular conductive state at different tensions is compiled from 10 independent traces. The x axis indicates the magnitude of applied tension, γ, relative to the midpoint tension for MscL activation, γ_1/2; the y axis shows the relative conductance of ion channel normalized to the conductance of the fully open state. The z axis displays the probability density in a logarithmic scale. The inset above is the plot of open probability (P_o) versus γ/γ_1/2, which represents a simultaneous fit of 10 dose-response curves with Eq. 1. (B) Occupancies of conductive states derived from amplitude histograms, as that in Fig. 2, recorded at different tensions (see Materials and Methods). Only the relative occupancies of S_0.22 (♦), L_0.78 (•), and S_0.93 (▴) versus tension are presented. The combined relative occupancy of all nine substates together (▵) as well as occupancies of the fully open state (▪) remained practically constant over the range of tensions relative to the total occupancy of all conducting states taken as unity. The □ represents the effective amplitude of the integral current A_IC, which is the sum of all substate occupancies multiplied by the corresponding amplitudes over the total probability of being open (see Appendix 2).

Fig. 4 B represents the numerical data obtained from Gaussian fits of eight averaged amplitude histograms (cross sections of the above surface at different tensions). The occupancy of short subconducting states S_0.22 (♦) and S_0.93, (▴) slowly decrease, whereas the occupancy of the long-lived L_0.78 (•) increases. The slopes of the tension dependencies indicate relatively small, but measurable differences in in-plane areas occupied by the substates. The areas of S₀₂₂ and S_0.93 are estimated to be smaller than that of the fully open state by 3.4 and 1.9 nm², respectively. The increase of L_0.78 occupancy with tension suggests that this conformation of the channel is wider by ∼1.8 nm² than the open state. Correspondingly, the effective area changes for C→S₀₂₂, C→S_0.93 and C→L_0.78 transitions would represent 74%, 85%, and 114% of the apparent area change for the entire closed to open (C→O) transition (12.8 nm², in its uncorrected form as deduced from multichannel dose-response curves, see below).

As a result of opposite tendencies for the short- and long-lived substates, the combined occupancy of all subconducting states remains practically constant (▵) relative to that of the fully open state (▪), as well as relative to the total occupancy of all conducting states (□). The numbers show that all subconducting states occupy ∼26% of the time the channel conducts above the threshold of 0.1 and reduce the mean current by ∼6% relative to the level of the fully open state, essentially independent of tension and P_o (for estimations of the accuracy of such approximation, see Discussion). This is consistent with the model which includes one dominant tension-dependent transition (C→S₀₂₂) and with previous observations (Sukharev et al., 1999) that once MscL makes a transition from the closed state to the low conducting substate, it quickly becomes distributed between the fully open state and a group of upper substates with shallow dependencies on tension.

Dose-response curves

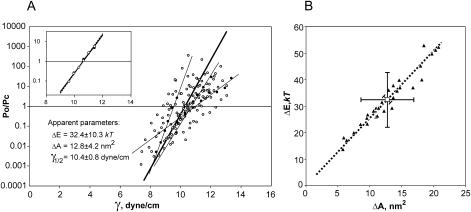
We analyzed 29 dose-response curves from patches with a few or multiple MscL channels, obtained with or without induction, respectively. The combined data are presented as log (P_o/P_c) versus tension in Fig. 5 A. Scaling of tensions was done for each dose-response curve individually using MscS as an internal gauge. Before fitting and statistical treatment, we compared the open probabilities estimated from the same traces with two different methods. As illustrated by the inset to Fig. 5, the P_o/P_c values obtained from a five-channel patch are the same when measured from the integral current (○) or using the threshold method (•); the difference in parameters ΔE and ΔA estimated from the fits was <1%. Note that the amplitude threshold technique can be easily applied when the number of MscL channels in the patch is <5; smearing of levels in recordings containing more channels, however, makes the threshold assignment difficult. Assessment of P_o from integral current, in contrast, is insensitive to the number of channels in the patch. For uniformity, the entire data set presented in Fig. 5 was obtained using the integral current only.

FIGURE 5.

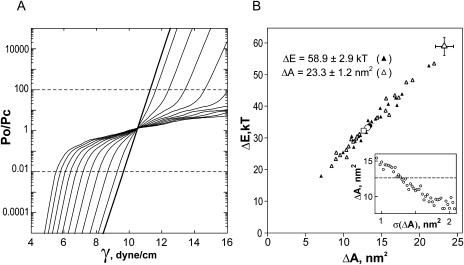
Dose-response curves and apparent gating parameters of MscL. (A) Twenty-nine independent curves (10 from induced and 19 from uninduced patches) plotted as P_o/P_c ratio versus membrane tension and fitted to the two-state model. Apparent parameters ΔE, ΔA, and γ_1/2 were extracted from each fit, averaged, and presented as the mean ± SD. The thick solid line represents the curve with the average parameters. Thin solid lines are examples of individual curves with varying slopes. (Inset) P_o/P_c versus tension plots obtained from the same trace with five active channels. ○ represent P_o obtained from the integral current; • show P_o determined using the amplitude threshold (0.1) detection technique. (B) Energies of MscL gating transition (ΔE) plotted against apparent protein area changes (ΔA) calculated from individual traces. Vertical, horizontal, and diagonal error bars represent standard deviations of ΔE, ΔA, and γ_1/2 = ΔE/ΔA, respectively, around their mean values. Dotted line is the linear fit passing through the origin. Pirson's correlation coefficient of ΔE and ΔA values is 0.98.

Each curve presented in Fig. 5 A was fitted by the two-state model yielding a pair of parameters, ΔE and ΔA. The thick solid line represents the effective dose-response curve recreated with the mean values across the data set, ΔE = 32.4 kT and ΔA = 12.8 nm². The individual curves (three examples are shown by thin lines), however, displayed different slopes; as a result, the scatter of parameters was quite large, being ±10.3 kT for ΔE and ±4.2 nm² for ΔA (standard deviations). The minimum observed values of ΔE and ΔA were 13.7 kT and 5.8 nm², whereas the maximum values were 52.2 kT and 20.8 nm², respectively. The point of intersection with the x axis, representing the tension midpoint (γ_1/2) for each curve was more consistent, with the mean position at 10.40 ± 0.8 dyn/cm. When ΔE and ΔA from each experiment were plotted against each other (Fig. 5 B), the two parameters were linearly correlated (Pirson's correlation coefficient, R = 0.98) with a slope of 10.4 dyn/cm. This reflects the fact that different activation curves have different slopes, but intersect with the x axis close to the same point of 10.4 dyn/cm. As dictated by Eq. 1 (see Materials and Methods), the tension γ_1/2 that causes equipartitioning of the channel between the closed and open states is equal to the ΔE/ΔA ratio.

Intrinsic gating parameters and statistical modeling of population response

To explain the correlated variation of ΔE and ΔA we analyzed several potential sources of systematic and random errors and their effects on the combined population response. We were unable to reproduce this linear correlation by introducing a systematic deviation of gating parameters in Eq. 1 uniformly for all channels in a patch. Indeed, an error in pressure-to-tension conversion (due to the accuracy of p_1/2^MscS determination, for instance) changes only effective ΔA and γ_1/2, whereas ΔE should stay constant. Conversely, if, for instance, applied pressure had an uncontrolled offset from trial to trial, then we would observe a variation of the midpoint position (γ_1/2), which would convert into a variation of ΔE, but not ΔA. Simultaneous random variations of ΔA and ΔE from patch to patch are not expected to correlate.

We inferred that a large scatter in the slope of the activation curves, and a much smaller scatter of γ_1/2 may be specifically due to heterogeneity of channel population in each patch. Indeed, if the midpoint positions of activation curves for individual channels in the patch are scattered around the mean, the midpoint of the curve measured on the entire population should not deviate much from that mean. However, because some channels activate earlier, and some later on tension, the smearing of the resultant curve is expected to decrease the slope. Since we never observed any significant deviation of MscL unitary conductance from 3.2 nS, we presumed that the channel conformation in the open state is rather uniform and the protein expansion between the states, ΔA, is most likely to be the same across the channel population. The local tension, however, may vary due to a local mechanical inhomogeneity of the membrane, and the term γΔA is expected to vary. Because only the product contributes to the free energy (Eq. 1), the variation of γ would be equivalent to variation of ΔA. The intrinsic energy of the gating transition (ΔE) of the channel may also be sensitive to the lipid or protein microenvironment in the membrane in which a particular channel resides. The scatter of ΔE and/or ΔA among channels in the population is predicted to reduce the apparent slope of the combined activation curve, and this reduction would be more pronounced when standard deviations of ΔE and/or ΔA increase.

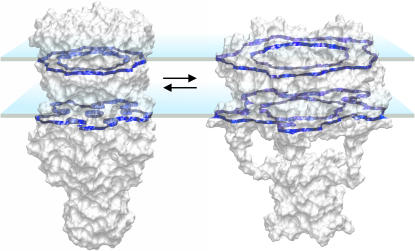
To choose realistic initial parameters, ΔE_o and ΔA_o, reflecting the intrinsic behavior of channels (unperturbed by the surroundings), we analyzed previously developed molecular models of MscL. The open conformation 11 (as in Sukharev et al., 2001b) with helical tilts of 72° (M1) and cross-sectional pore area of 10 nm² gave the closest prediction of the channel conductance (A. Anishkin, unpublished calculations). This conformation is compared with the closed MscL in Fig. 6, where both models are shown with their solvent-accessible surfaces and the in-plane cross sections. The mean cross-sectional areas of the open and closed conformations were computed as 40.8 and 17.5 nm², respectively. The difference of 23.3 nm² was taken as the initial parameter ΔA_o. The energy of the transition, satisfying this area change, and the midpoint tension of 10.4 dyn/cm in Eq. 1 is 58.9 kT, which was taken as the initial ΔE_o.

FIGURE 6.

The models of the E. coli MscL in the open and closed conformations shown with solvent-accessible surfaces. The positions of the transmembrane helices forming the barrel correspond to conformations 2 (closed) and 11 (open) from Sukharev et al. (2001b), whereas the bundle-like arrangement of the C-terminal segments in the open state is taken from Anishkin et al. (2003). The cross-section planes are positioned approximately at the boundaries of the hydrophobic core of the membrane (±12.5 A along the z axis). The average cross-sectional areas of the modeled closed and open states are 17.5 and 40.8 nm², respectively, predicting the transition-related area change of 23.3 nm².

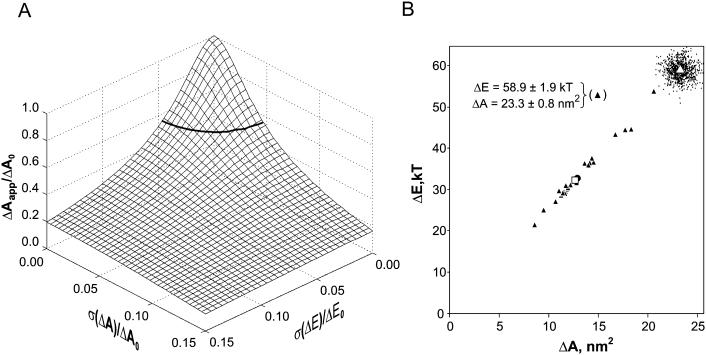
The details of simulations are presented in the Appendix 1. In summary, introduction of a scatter in either ΔE or ΔA reduced the slope of the middle part of activation curves. Simultaneous variations of both ΔE and ΔA further reduced the slope of the population response. Fig. 7 A illustrates how the apparent gating parameters should depend on widths of the ΔE and ΔA distributions. The solid line girding the surface at the level of 0.55 assigns the possible combinations of σ(ΔE) and σ(ΔA) that would produce the mean apparent parameters observed in the experiment (ΔE = 32.4 kT, ΔA = 12.8 nm²) from the initial parameters predicted by the model.

FIGURE 7.

Simulated tension responses of nonuniform channel populations. Intrinsic gating parameters based on the atomic models ΔE_o = 58.9 kT and ΔA_o = 23.3 nm² were randomized with variable standard deviations. The combined dose-response curves for 100 channel populations were then computed and fit with Eq. 1 to obtain apparent parameters ΔA_app and ΔE_app. (A) A three-dimensional representation of ΔA_app/ΔA_o as a function of relative σ(ΔA) and σ(ΔE). The surface illustrates that a 5% scatter of either parameter reduces ΔA_app to approximately one-half. (B) Simulated results for 15 populations of 50 channels and 15 populations of five channels in which both ΔE and ΔA were simultaneously varied around their mean values (cloud of small dots). Pairs of ΔE and ΔA are shown with ▴. The • in the center of the scatter shows mean values for ΔA_app and ΔE_app. The □ (overlapping with the circle) represents the mean parameters observed in the experiment (same as in Fig. 5). The values of standard deviations that closely reproduce the experimental scatter are denoted in B. See Appendix 1 for details of simulations.

We found that the course of the combined response curve is sensitive not only to the standard deviation, but also to the particular distribution of channel parameters around the mean, resulting in a large variation of the slope of the fitting line from trial to trial. Larger deviations of apparent parameters are expected in smaller channel populations. We attempted to reproduce the experimentally observed data set by simulating 15 populations of 50 channels and 15 populations of five channels (as in induced or uninduced patches). The final round of simulations included simultaneous random variations of both ΔE and ΔA. The results are presented in Fig. 7 B where the entire population of simulated channels is shown as a cloud of small dots around the point representing the mean parameters. The apparent parameters determined from population fits are represented as triangles scattered along the diagonal. The simulations readily reproduce the linearly correlated pairs of apparent ΔA and ΔE with the width of the scatter and the mean close to the experimentally observed values (compare Fig. 7 B with Fig. 5 B). Results presented in Fig. 7 (and Fig. A1, see Appendix 1) illustrate that the effective total deviation of parameters characterized by the square root of the sum of the two squared standard deviations σ(ΔE) and σ(ΔA) should be ∼5%, to accurately reproduce the experimentally observed parameters from the modeling predictions.

Estimation of gating parameters from multichannel traces

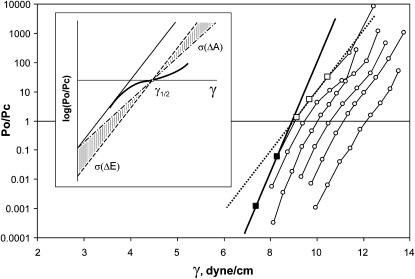
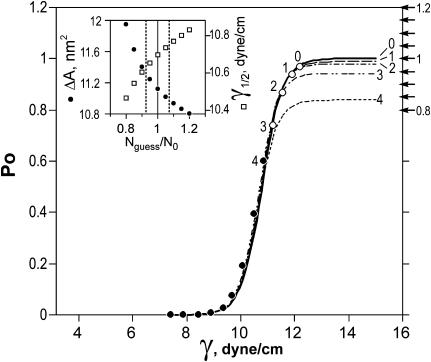
The above analysis shows that true thermodynamic parameters of gating could be readily estimated from single-channel traces. As mentioned above, those recordings were practically impossible to obtain due to the substantial leakage of the promoter and possible clustering of channels. From the simulated dose-response curves (Fig. A1, Appendix 1) one can see that the slope of the population response significantly deviates only in the middle, whereas the leftmost and rightmost parts of the curves have a slope close to that of an ideally uniform population, reflecting only the subpopulations of channels that activate very early or very late on tension. For this reason, we analyzed the slopes of leftmost parts of multichannel activation curves, i.e., the regions where only one or two channels were active. Examples of such curves are represented in Fig. 8. Like the simulated ones, these dose-response curves exhibit visible inflections. Fitting of the middle part of the left curve (dashed line) gives the estimation of ΔA of ∼12 nm², whereas fitting the two initial points representing a subpopulation of early channels only (solid line) produces the slope of 22 nm². One needs to remember that, although the initial slope gives a better estimation of ΔA, the intersection of the solid line with the x axis represents the midpoint only for the early channels. The correct midpoint position for the channel population in the patch can be obtained by fitting the entire curve. The inset in Fig. 8 illustrates two ways of treating such dose-response curves. In the scenario where only ΔE varies (σ(ΔE) > 0, ΔA = const), activation curves for individual channels are translated up and down relative to the mean position); therefore, a line passing through the whole-population midpoint with the slope estimated from two initial points would be a representation of the dose-response curve for the mean channel. If only ΔA varies, activation curves for individual channels will be pivoting around the common intercept with the vertical axis (σ(ΔA) > 0, ΔE = const), crossing the horizontal axis at different points. In this case, a line connecting the population midpoint with the common intercept would represent mean parameters of the channel. The lower slope of the line implies that in the case of variable ΔA the estimations of both ΔE and ΔA are slightly lower compared to the situation of variable ΔE. In reality, both ΔE and ΔA may vary, and the resultant curve may lie anywhere in the shaded area between the two lines. The initial slope of eight independently measured curves with visible inflections yielded ΔA = 20.4 ± 4.8 nm², highly consistent with molecular models. With the midpoint for the entire population γ_1/2 = 10.4 ± 0.8 dyn/cm, the upper limits for ΔE and ΔA were estimated as 52.5 kT and 20.43 nm² (as if ΔE is variable), whereas the lower limits corresponding to variation in ΔA were estimated as 50.9 kT and 19.8 nm², respectively. After averaging, ΔE = 51.7(±13) kT, and ΔA = 20.1(±4.8) nm² can be taken as a realistic experimental estimation of gross parameters of MscL gating.

FIGURE 8.

Examples of experimental activation curves of wild-type MscL exhibiting different degrees of slope variation. The curves display a noticeable S-like shape with a steeper slope at the ends, and more shallow dependence near γ_1/2. The inflection was more pronounced in patches with smaller number of channels (3–7). Linear fit of initial points (solid line) defines the limiting slope, which gives higher estimates for ΔE and ΔA than the fit of the middle region (denoted by line). The inset illustrates procedure of reconstruction of the mean single-channel activation curve for channel populations of ΔA. The inflected spline line represents the population dose-response curve. The fit of the initial region is shown by solid line. A parallel translation of this line to the population midpoint (γ_1/2) yields the mean for a population with varying ΔE only (dashed line). Rotating the initial fitting line around the vertical axis intercept, such that it crosses the horizontal axis at γ_1/2, yields the mean curve for a population with varying ΔA (dot-dashed line). The hatched area represents possible intermediate line positions for populations in which ΔE and ΔA may vary simultaneously.

DISCUSSION

Previous analysis of MscL gating has been done on purified channels reconstituted in asolectin liposomes (Sukharev et al., 1999). Patch-clamp recording was combined with video imaging to evaluate the curvatures of patches in a range of pressure gradients. Single-channel traces recorded in liposome patches were initially idealized with an amplitude threshold criterion. The open and closed time distributions were essentially monoexponential and the rate constants were fit with a two-state model reasonably satisfying the scheme with one closed and one open state (Sukharev et al., 1999). P_o curves plotted against membrane tension gave the midpoint of MscL activation (γ_1/2) of 11.8 dyn/cm, and ΔA estimated from the steepness of the curves by the two-state model was 6.5 nm². This area change was suspiciously small for a molecule predicted to form a large conducting pore of 3-nm diameter. Previously we attempted to explain the small apparent ΔA by modeling MscL gating as transitions between two unequal harmonic wells representing a soft closed state and a stiff open state (Sukharev and Markin, 2001). The model described well experiments in liposomes, but gave unrealistic parameter estimates from data obtained in native membranes. The possible heterogeneity of channels in native or reconstituted populations was not considered at that time.

Liposome patches are large enough for imaging, but during continuous recordings are mechanically unstable, having a tendency to slide up the pipette under pressure (Sukharev et al., 1999). Here we presented an analysis of MscL activity recorded from smaller patches in spheroplasts. Instead of video imaging (which is inaccurate due to small patch size), we used MscS as an internal tension gauge (Fig. 1). A steep activation of MscS at ∼5.5 dyn/cm in both liposomes (Sukharev, 2002) and spheroplasts (Cui and Adler, 1996) made this channel a good standard for two reasons. First, MscS appears to exhibit a more consistent behavior in spheroplasts and liposomes, whereas MscL exhibits a time-dependent decrease in activity in liposomes (Hase et al., 1995). For this reason the midpoint of 11.8 dyn/cm determined in liposomes may be a slight overestimation compared to that in the native membrane. Second, if we were using γ_1/2 of MscL as a reference point, we would have to measure the entire activation curve for every patch, which is not feasible. To our advantage, MscS activates at lower tensions than MscL, thus it automatically gauges the entire range of stimuli, including those situations where MscL was activated to low P_o. The established procedure of recording and treatment allows us to present disparate P_o-pressure curves in unified tension scale without patch imaging, as well as compare different MscL mutants in other studies. The accuracy of pressure-to-tension conversion is estimated as ∼±8% (see Appendix 2). The midpoint of MscL activation determined from 29 independent traces as 10.4 ± 0.8 dyn/cm (Fig. 5 A), is a key parameter, which now permits thermodynamic analysis of MscL function in the native membrane. MscS, present in the majority of patches, also allowed us to assess the radius of curvature for each patch and its variability (Fig. 1, inset), which usually remains out of sight in most channel studies.

Previous time-resolved recordings revealed complex channel behavior involving transitions between several subconducting states. How applicable, then, is a simple two-state model to MscL characterization? The multistate analysis, however, showed that only the first transition from the closed to the low-conducting substate is strongly tension-dependent (Sukharev et al., 1999). Thus, the presence of a single dominant tension-dependent step in the linear kinetic scheme suggested that a two-state model is still a reasonable approximation for overall thermodynamic description. Indeed, if beyond the single tension-dependent step the channel is distributed between several conducting states in a tension-independent manner, the kinetic description becomes simpler, and the total occupancy of conducting states may be reasonably characterized by the integral current. The analysis of substate occupancies of MscL and integral currents in native membranes presented above supports these notions. Ideally, the calculations of occupancies and areas related to each subtransition and the entire C→O transition could be done from single-channel traces, in which there is no ambiguity as to which conducting state belongs to what channel. This was not feasible and the substate analysis as well as recordings of dose-response curves had to be done on multichannel populations.

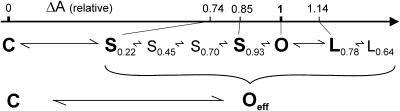
Out of the nine subconducting states detected by Gaussian fits of amplitude histograms (Fig. 2), the three most prominent were characterized in more detail. The occupancies of short-lived substates S_0.22 and S_0.93 are near 10⁻³ and 10⁻¹ relative to the occupancy of the fully open state (O), and decrease with tension (Fig. 4 B). This is consistent with the notion that S_0.22 and S_0.93 are intermediate states characterized by smaller area changes, constituting of ∼74 and 85% of ΔA for the fully open state. In contrast, the occupancy of the long-lived substate L_0.78 increases with tension (Fig. 4). The dependencies of the L_0.78 occupancy on tension and voltage (Figs. 3 and 4) show that the O→L_0.78 transition is associated with ∼14% additional protein expansion and an equivalent of an inward transfer of 3.5 positive charges across the transmembrane field. The occupancy of the second long-lived state L_0.64, which is visited from L_0.78, increases with voltage in proportion with the occupancy of L_0.78, suggesting no additional charge transfer during the latter transition (Fig. 3). The fact that the long-lived substates are visited exclusively from the fully open state places L_0.78 and L_0.64 beyond the open state in the kinetic scheme aligned with the coordinate representing the cross-sectional area of the protein (Fig. 9).

FIGURE 9.

The kinetic scheme of MscL aligned with the reaction coordinate representing the protein in-plane area change. The main tension-dependent transition from C to S_0.22 is associated with the largest area increase. The long-lived subconducting states (L_0.78 and L_0.64) are characterized with larger in-plane areas than the open state (O). Uncorrected estimates of area and energy differences between the major states are presented in Table 1. According to the data presented in Fig. 8, the corrected area and energy changes between the closed (C) and fully open (O) states are ∼20.1 nm² and 52 kT. Correspondingly, the distances from the closed state to other substates can be rescaled as 14.8 nm² (49 kT) for S_0.22, 17.0 nm² (47 kT) for S_0.93, and 22.9 nm² (61 kT) for L_0.78.

Having the conductances and effective areas for the major conducting states, we can predict the behavior of the integral current as a function of tension using the approach similar to one previously described for voltage-gated channels (Sigg and Bezanilla, 1997). The numerical simulation below will illustrate the similarity between the parameters ascribed to the fully open conformation and the effective gating parameters estimated in the two-state approximation.

We first define how the measured integral current depends on the probabilities and conductances of individual states. Suppose each of the i^th conducting states is characterized by its probability, p_i, and conductance, g_i, which can also be denoted through the fractional conductance f_i = g_i/g_O, where g_O is the conductance of the fully open state. The area differences, ΔA_i, and intrinsic energies in the absence of tension, ΔE_i, are measured for each conducting state relative to those of the closed state (C). The probability of being in any of the conductive states, i.e., nonweighted (by conductance) open probability, can be presented as the sum

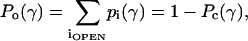where P_c(γ) is the probability of any nonconducting state, on the assumption that MscL has only one closed state (C), P_c(γ) = p_C(γ). The probabilities of individual states can be calculated according to Boltzmann, with the free energies written as ΔE_i–ΔA_iγ, which include the work of externally applied tension,

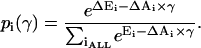To account for contributions of substates in the total current, we use their probabilities and fractional conductances. The time-averaged fractional conductance of the channel can then be expressed as

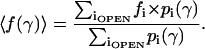The difference of the total fractional conductance from unity 1 − 〈f(γ)〉 therefore represents the reduction of the time-averaged conductance of a multistate channel (observed as integral current) from that of an ideal channel that displays only a fully open state. The integral conductance at a given tension can be written as

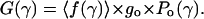In the following numerical simulation we approximated the system with a five-state model C ↔ S_0.22 ↔ S_0.93 ↔ O ↔ L_0.78 with the parameters for each state listed in Table 1. The calculated occupancies of each substate, p_i(γ),〈f(γ)〉, and the effective channel conductance, G(γ), are shown in Fig. 10. The computed G(γ) dependence was then treated as an experimental curve. It was fitted with a sigmoidal curve to find G_max and calculate the effective conductance-weighted open probability P_o^eff = G(γ)/G_max, the same as values measured in the experiments. As seen from the plot, P_o, P_o^eff, and G(γ)/g_O increase in proportion; however, G(γ)/g_O does not saturate, but asymptotically approaches 〈f(γ)〉. The probabilities for intermediate states S_0.22 and S_0.93 behave non-monotonously and the probability for the fully open state (p_O) starts declining at high tensions as the occupancy of the long-lived substate L_0.78 increases. Note that, in determination P_o^eff, we divided G(γ) by G_max (assessed as an asymptote from the sigmoidal fit in the experimental range of tensions), but not by G(∞), because the latter starts declining at very high tensions due to the larger presence of L_0.78.

TABLE 1.

Fractional conductances and uncorrected energy and area parameters for selected substates

Conducting state	C	S0.22	L0.78	S0.93	O	Po	Poeff
Fractional conductance	0	0.22	0.78	0.93	1	1	〈f(γ)〉
ΔA, nm2	0	9.3	14.4	10.7	12.67	12.68	12.80
ΔE, kT	0	31.0	38.4	29.3	32.50	32.17	32.41

The occupancies of S_0.22, S_0.93, L_0.78, and O at different tensions were estimated from cross sections of the cumulative amplitude histogram (Fig. 4 B). The areas (ΔA) and energies (ΔE) for each substate relative to the fully open state were calculated from probability ratios by Eq. 1. The probability of the fully open state, in turn, was estimated from the integral conductance as presented in Fig. 5 A. The parameters for individual states were used in the five-state model to calculate the total conductance G, P_o, and P_o^eff, from which the gross energy and area parameters were then re-estimated. The parameters ΔA and ΔE for the fully open state included in the model and the effective parameters estimated from nonweighted P_o or weighted P_o^eff open probabilities (two right columns) are practically indistinguishable. See Discussion.

FIGURE 10.

Probabilities of different states (p_i), open probabilities (P_o), and the average fractional conductance (P_c) computed with a five-state MscL model. The parameters for individual states used in the model are given in Table 1. The effective open probability P_o^eff weighted by substate conductances was calculated from the integral conductance presented as G/g_O . The fitting of the weighted (P_o^eff) and nonweighted (P_o) open probabilities (inset) gave slopes and energies almost identical to the parameters of the fully open state included in the model. See Discussion.

Using the two-state fitting procedure with Eq. 1 (see Materials and Methods) we extracted effective gating parameters from the simulated multistate dose-response curve P_o^eff(γ) and compared them with parameters determined from the nonweighted P_o(γ) curve as well as with parameters for the fully open state (O) initially included in the model. The results of fitting in semilogarithmic scale are shown in Fig. 10 (inset). All obtained areas and energies (see Table 1) are very close and the error introduced by the presence of substates (compare parameters for O with those in the column for P_o^eff) is <2%. The use of nonweighted open probability, as would be measured by a threshold technique, is also justified as the P_o(γ) curve gives essentially the same result. The difference between P_o^eff(γ) and P_o(γ) is negligible because one can be obtained from the other by introducing the factor 〈f(γ)〉/〈f〉_max ≈ 1, where 〈f〉_max = G_max/g_O. Note that 〈f(γ)〉 is essentially constant and changes only from 0.97 to 0.93 in the experimental range of tensions (8.5–11.7 dyn/cm) where the P_o/P_c ratio changes from 0.01 to 100. This independence of the parameter 〈f  〉 to tension is due to a serendipitous mutual compensation of different substate contributions. As a result, the effective area and energy parameters determined from either the integral current or P_o (Fig. 10, inset, and Table 1) closely reflect the properties of the fully open state (O).

Consistent with the modeling, which took into account only three prominent substates, the experimentally observed 〈f(γ)〉 stays at the level of 0.94 ± 0.016 in the range of P_o between 0.02 and 0.85 (Fig. 4 B). This follows from the fact that channels spend 68% of their time in the fully open state, and two major substates—S_0.93 and L_0.78 (occupying 29% out of 32% belonging to all substates) have comparable conductances but opposite tension dependencies (Fig. 4 B). The S_0.22 substate has low conductance, but its contribution is negligibly small due to very low occupancy. With a practically constant total substate contribution, the experimental activation curves calculated by the threshold technique and from the integral current are very similar (Fig. 5 A, inset).

Thus, simple two-state formalism can be applied safely to characterize gross parameters for wild-type MscL. This rule, however, may not hold for certain MscL mutants (A. Anishkin, C.-S. Chiang, and S. Sukharev, unpublished results) or other mechanosensitive channels in which the occupancies of prominent substates substantially change with tension (Yao et al., 2001).

In the two-state approximation, the average expansion and energy of the C→O transition estimated from 29 independent curves were 12.8 ± 4.2 nm² and 32 ± 10.3 kT. These effective parameters measured on populations, as was mentioned above, may not reflect the intrinsic parameters for individual channels. The energies and areas were found to be linearly correlated, but at the same time strongly scattered. The inference that this distribution of parameters is a consequence of nonuniformity of the channel populations was well supported by statistical simulations. The results illustrate that a relatively small (∼5%) deviation of either ΔE or ΔA around their mean values would result in a dramatic (≥50%) decrease of the average slope of dose-response curves leading to a corresponding underestimation of apparent ΔE and ΔA parameters. We should note that a similar underestimation of the Hill coefficient caused by population heterogeneity has been reported for cAMP-gated channels (Ruiz et al., 1999). A strong sensitivity of the composite dose-response curve not only to the standard deviation, but also to the particular distributions of individual channel parameters in the patch (within the deviation interval), results in a substantial spread of the apparent ΔE and ΔA parameters from patch to patch. A much narrower scatter of the midpoint position, γ_1/2, reflects a symmetrical character of distributions of the actual ΔE and ΔA in channel populations, centered around the median, which reproduces well from trial to trial. So far, the simulated dose-response curves and extracted parameters (Fig. 7 B) closely resemble the distribution and linear correlation of ΔE and ΔA observed experimentally (Fig. 5 B).

These conclusions explain the relationships between the observed and predicted ΔA and ΔE values. ΔA predicted from the atomic-scale models is in the range of 23 nm², which, implies ΔE = 59 kT (to satisfy ΔE/ΔA = γ_1/2 = 10.4 dyn/cm). A dispersion of either ΔE by 3 kT or ΔA by 1 nm² around these mean parameters would reproduce the experimental data set with an average apparent ΔE of 32 kT and ΔA of 12 nm². The data also suggest that smearing of the activation curves leads not only to reduction of the gross gating parameters that reflect the C→O transition, but may also result in a proportional reduction of the parameters for the subtransitions. For instance, the protein expansion during the O→L_0.78 transition estimated as 1.7 nm² under conditions that produce ΔA = 12 nm² for the entire C→O transition, in reality should be twice as large (see Fig. 9 and legend).

On the other hand, the analysis of only the leftmost regions of inflected experimental activation curves, which is reminiscent of the limiting slope method used for multistate voltage-gated channels (Almers, 1978; Sigg and Bezanilla, 1997), allows us to overcome smearing of activation curves (Fig. 8). It yields ΔE = 51 kT and ΔA = 20.4 nm², which appear to be reasonable experimental estimations of the true gating parameters. The areas and energies for the substates rescaled according to the corrected gross parameters are listed in the legend to Fig. 9. These values should help in the relating of the substates to modeled intermediate conformations, and prompt further studies of physical interactions contributing to the total energy of gating transition in MscL.

Why are channel populations nonuniform? The deviations of gating parameters within channel populations can be ascribed to heterogeneity of the native membrane, creating a slightly different physical environment for each channel. Indeed, a 5% deviation in ΔA or ΔE producing a dramatic reduction of the slope of simulated dose-response curves is equivalent to a 5% deviation in tension experienced by individual channels, a value not unrealistically large. A physical reason for heterogeneity may be formation of clusters, in which channels are subjected to different tensions depending on the actual position in the cluster, or variations of local protein/lipid environment in the native membrane. Does this functional heterogeneity have any biological meaning for a cell? Probably, because in this case a biochemically uniform population of channels would automatically generate a more graded permeability changes in response to a varied osmotic challenge.

In conclusion, the analysis of MscL gating in spheroplasts is consistent with the kinetic scheme in which the major tension-sensitive step is the transition from the closed to the short low-conducting substate. This substate represents a highly pre-expanded conformation characterized by a relative area only 25% smaller than of that of the fully open state with essentially the same intrinsic energy. In contrast to the short-lived substates, the long-lived substates do not appear to be intermediates, but rather alternative open states stabilized by negative voltages. The distribution of channels among the subconducting states is considerably less dependent on tension than the distribution between the closed and conducting states. This validates the use of integral current as a means for estimating P_o, and the two-state approximation for gross thermodynamic treatment. The midpoint of the dose-response curves measured on multichannel patches appears to accurately reflect the average midpoint across the population. Since a small heterogeneity of the population is capable of severely reducing the apparent ΔE and ΔA parameters, the slope can be evaluated using only the initial, leftmost regions of activation curves. The total protein expansion obtained in this fashion reasonably corresponds to that predicted from structural models of MscL.

APPENDIX 1

Simulated responses of nonuniform channel populations

Sets of 100 random numbers, with given standard deviations (σ(ΔE) or σ(ΔA)) around initial parameters ΔE_o = 58.9 kT and ΔA_o = 23.3 nm², were generated to simulate nonuniform populations of channels. Dose-response curves were generated for each channel according to Eq. 1 and summed up to simulate the tension response of the population. For σ(ΔA) = 0 (no scatter), the population response is a straight line as seen from Fig. A1, A. As σ(ΔA) increases, the curves become increasingly inflected exhibiting lower slope in the middle. A similar tendency was observed when a scatter between 0 and 20 kT was introduced to the ΔE parameter, resulting in a set of symmetrical curves relative to the midpoint (not shown). Simultaneous variations of both ΔE and ΔA further reduced the slope of the middle part of curves. The simulated dose-response curves were fitted with a linear function in log(P_o/P_c) − γ coordinates in the range of P_o/P_c between 0.01 and 100, typically measurable in experiments. The apparent area change (ΔA_app), determined from the fit, decreases dramatically with standard deviations σ(ΔE) and σ(ΔA), as shown by the three-dimensional graph in Fig. 7 A. One may see that a relative scatter (σ(ΔE)/ΔE_o or σ(ΔA)/ΔA_o) of only ∼0.05 reduces the measurable protein expansion to a half. The girdle around the surface at the level of 0.55 assigns the possible combinations of σ(ΔE) and σ(ΔA) that would effectively reduce the intrinsic parameters predicted by the structural model to match the apparent parameters observed in the experiment (ΔE = 32.4 kT, ΔA = 12.8 nm²).

FIGURE A1.

Statistical simulations of tension responses of nonuniform channel populations. (A) Simulated population dose-response curves with fixed ΔE_o = 58.9 kT and ΔA scattered ∼ΔA_o = 23.3 nm² with standard deviations σ(ΔA) varying from 0 to 10 nm² (100 channels). (B) Simulated results (pairs of ΔA_app and ΔE_app) for 15 populations of 50 channels and 15 populations of five channels obtained either with varied ΔE and constant ΔA (▴), or varied ΔA and constant ΔE (▵). The inset shows the dependence of the mean ΔA_app on standard deviation σ(ΔA); the dashed line marks the experimental ΔA. The parameters and standard deviations denoted in B produce the mean ΔE_app and ΔA_app shown by ○ and • in the middle of each scatter. The □ represents the parameters observed in the experiment (same as in Fig. 5). The same populations as in B were simulated with both ΔE and ΔA parameters randomized around their mean values, which is illustrated in Fig. 7 B.

The course of the combined response curve is very sensitive not only to the standard deviation, but also to the particular distribution of channel parameters around the mean, resulting in a large variation of the slope of the fitting line from trial to trial. We attempted to reproduce the experimentally observed data set by simulating 15 populations of 50 channels and 15 populations of five channels (as in induced or uninduced patches). In the first round, we varied ΔE ∼58.9 kT, while keeping ΔA constant at 23.3 nm²; in the second set of simulations ΔA was varied with constant ΔE. The data are presented in Fig. A1, B, with ▴ and ▵, respectively. The point representing the initial parameters is in the upper right corner with the corresponding standard deviation bars, whereas the mean apparent parameters are denoted by • and ○ near the middle of the scatter. The inset in Fig. A1, B, shows that with the given initial ΔE_o and ΔA_o, the experimental data set can be accurately reproduced only with σ(ΔA) between 1.1 and 1.3 nm². The simulations, therefore, can be used to assess the degree of non-homogeneity of protein environment in the membrane with a relatively good precision. The third round of simulations included simultaneous random variations of both ΔE and ΔA. The results are presented in Fig. 7 B with the population of simulated channels shown as a cloud of small dots around the point representing the mean, whereas the “apparent” parameters are represented as ▴. Results presented in Figs. 7 and A1 illustrate that the effective deviation of parameters (σ(ΔE) or σ(ΔA)) should be ∼0.05, to reproduce the mean parameters ΔA and ΔE and the scatter observed in experiments (Fig. 5) from the modeling predictions.

As a factor before γ in Eq. 1, the spatial parameter ΔA defines the slope of the dose-response curve on tension. The reciprocal parameter, kT/ΔA, is the width of the curve, defining the range of tensions over which the P_o/P_c ratio changes e-fold. The steeper the activation curve (and the smaller the width), the more sensitive the apparent ΔA would be to the scatter of the midpoint positions for individual channels. The simulations suggested the following rule of thumb: when the scatter of individual curves in the population (i.e., standard deviation of their midpoints around the mean position) is equal to the width of activation curves, the apparent slope of the population response will be reduced twice, relative to the slope of an individual curve. Another simple rule that emerged from the two-state simulations was that no matter what the actual ΔA, a dispersion σ(ΔE) of ∼3 kT will always produce an approximately twofold reduction of the slope of the population response.

APPENDIX 2

Analysis of errors

Errors of pressure-to-tension conversion

The first question is related to the accuracy of pressure to tension conversion using the half-activation pressure for MscS. Based on imaging of liposome patches, the tension for half-activation of MscS (γ_1/2^MscS) was determined to be 5.5 ± 0.1 dyn/cm (Sukharev, 2002). On the assumption of constant curvature of patches at these tensions, we expect tension to be proportional to the pressure. If there was a systematic error in determination of p_1/2^MscS or γ_1/2^MscS, this would change the parameter ΔA for MscL, proportionally, without changing ΔE (see Eq. 1 and inset to Fig. 8). In addition, a random error may come from inconsistency of MscS activation from patch to patch. The latter introduces a random deviation into the conversion procedure (σ_c), which can be estimated from the analysis of variance of γ_1/2 for MscL measured on multichannel patches. Although ΔE (and correspondingly γ_1/2) for individual MscL channels is predicted to be scattered (±5%) in each patch, the mean γ_1/2 should be well reproducible due to a large number (∼50) of channels in each patch and likely symmetrical distribution. From statistical simulations of 50-channel populations above we concluded that the intrinsic deviation of the mean γ_1/2 from patch to patch (σ_i) is expected to be ∼±0.17 dyn/cm or 1.7% of the mean. The actual standard deviation of γ_1/2 observed in experiments, σ_eff, was ±0.8 dyn/cm or 7.7%. Using the relationship σ_eff² = σ_c² + σ_i² we estimate the accuracy of conversion as ±7.5%, which includes potential variation among MscS channels and other procedural parameters such as the rate of pressure application. Although approximate, the conversion procedure seems to be practical.

Errors from fitting of incomplete dose-response curves

It has been noted in Materials and Methods that the determination of maximal number of active channels in the patch included an extrapolation procedure. In the first approximation the values of total patch conductance (G) were plotted as a function of γ and fitted with the sigmoidal function G = G_max/[1+ exp((γ_1/2–γ)/α)] to estimate G_max. The ratio G/G_max was taken as P_o^eff. For curves that reached 90% of saturation this was sufficient for G_max estimation with a 5% accuracy. To better account for the low P_o range, where the dependence of P_o is expected to be close to exponential, the ratio of P_o/(1–P_o) was plotted versus γ in semilogarithmic coordinates and fit with a straight line. G_max was then varied to minimize the deviation of the log[P_o/(1–P_o)] from linearity. The contribution of the first half of activation curve always appears to be more reliable because the patches are more stable at lower tensions (no drift) and a baseline correction is feasible. The accuracy of the latter procedure is illustrated in Fig. A2. The dose-response curve is created from the trace presented in Fig. 1 A. The last point (numbered as 0) corresponds to 96% saturation according to the Boltzmann fit. By truncating the curve at point 4 (60% saturation) and fitting the remainder, we underestimate G_max by ∼19%. By taking into account points 3 (76%), 2 (85%), and 1 (93%), we underestimate G_max by 5, 3, and 1%, respectively. In the next simulation we utilized the lower portion of the curve (black dots), and deliberately introduced deviations in G_max from the best fit to see how sensitive the estimated gating parameters are to the error. The G_max levels to which the curves were extrapolated are shown by arrows on the right side of Fig. A1 C, and the extracted area and γ_1/2 parameters are presented in the inset. A 20% underestimation of G_max results in ∼2% underestimation of γ_1/2, and 8% overestimation of ΔA. A 20% overestimation of G_max leads to the errors of 1% and 4% in determination of γ_1/2 and ΔA, respectively. Because for most of our dose-response curves the error in G_max was <7%, both parameters were measured with the accuracy of 1–4%, which is significantly less than the experimentally observed scatter.

FIGURE A2.

Illustration of the accuracy of the dose-response curve-fitting procedure. The P_o data from the trace presented in Fig. 1 A was truncated at different points (1–4), then fit with sigmoidal curves. Deviations of estimated G_max values from G_max determined from fitting the entire curve were assessed (see text). The upper limit of the fitting curve was then constrained to different levels deviating from the true G_max by as much as 20% both ways (the discrete levels are indicated by arrows on the right side of the graph). Variations of ΔA and γ_1/2 values obtained after introducing the errors in G_max are presented in the inset. See Appendix 2.