Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 May;86(5):2883–2895. doi: 10.1016/S0006-3495(04)74340-4

Water Dynamics and Dewetting Transitions in the Small Mechanosensitive Channel MscS

Andriy Anishkin 1, Sergei Sukharev 1
PMCID: PMC1304157  PMID: 15111405

Abstract

The dynamics of confined water in capillaries and nanotubes suggests that gating of ion channels may involve not only changes of the pore geometry, but also transitions between water-filled and empty states in certain locations. The recently solved heptameric structure of the small mechanosensitive channel of Escherichia coli, MscS, has revealed a relatively wide (7–15 Å) yet highly hydrophobic transmembrane pore. Continuum estimations based on the properties of pore surface suggest low conductance and a thermodynamic possibility of dewetting. To test the predictions we performed molecular dynamics simulations of MscS filled with flexible TIP3P water. Irrespective to the initial conditions, several independent 6-ns simulations converged to the same stable state with the pore water-filled in the wider part, but predominantly empty in the narrow hydrophobic part, displaying intermittent vapor-liquid transitions. The polar gain-of-function substitution L109S in the constriction resulted in a stable hydration of the entire pore. Steered passages of Cl− ions through the narrow part of the pore consistently produced partial ion dehydration and required a force of 200–400 pN to overcome an estimated barrier of 10–20 kcal/mole, implying negligibly low conductance. We conclude that the crystal structure of MscS does not represent an open state. We infer that MscS gate, which is similar to that of the nicotinic ACh receptor, involves a vapor-lock mechanism where limited changes of geometry or surface polarity can locally switch the regime between water-filled (conducting) and empty (nonconducting) states.

INTRODUCTION

Ion channels conduct ions across the membranes, generally by providing a polar or aqueous environment inside protein cavities. Before and after passing a narrow selectivity filter lined by specific groups that replace water, the ions remain dissolved in water even deep inside the channel proteins. The recent crystallographic data revealed water-filled central cavities in potassium channels (Jiang et al., 2002a,b). The gating process in these channels has been inferred as pinching off the water channel connecting the central cavity with the cytoplasmic compartment by four pore-lining α-helices (Jiang et al., 2002a, 2003; Kelly and Gross, 2003). The closed conformation of the bacterial mechanosensitive channel MscL is also characterized by a narrow constriction (4 Å in diameter) lined by conserved valines contributed from each subunit (Chang et al., 1998). The opening of MscL was inferred as an iris-like expansion producing a wide water-filled pore (Sukharev et al., 2001; Betanzos et al., 2002; Perozo et al., 2002; Gullingsrud and Schulten, 2003). The residues forming narrow regions of closed pores in gated channels are consistently hydrophobic, and substitutions with polar or charged residues in narrow gate regions result in easily opened or constitutively open channels, often at a subconducting state (Labarca et al., 1995; Ou et al., 1998; Yoshimura et al., 1999; Sukhareva et al., 2003). Presently, there is little information about water distribution in constricted regions of closed channels, apart from several molecular dynamic simulations, suggesting that such narrow hydrophobic parts are likely to be dehydrated (Berneche and Roux, 2000; Biggin et al., 2001; Gullingsrud and Schulten, 2003). An interesting problem was presented several years ago by the structures of the nicotinic ACh receptor in the closed and open states (Unwin, 1995). Although obtained at low resolution, the structures suggested that the gating transition causes limited changes of the pore geometry while dramatically changing the conductance. A slight widening of the recently refined pore constriction (Miyazawa et al., 2003) was proposed to be accompanied by a significant change of the surface polarity. The question of whether only the Born repulsion from the walls (Parsegian, 1969) prevents ions from entering the hydrophobic pore, or something more dramatic such as a cooperative dewetting transition that plugs the channel (Beckstein et al., 2001), vividly persists and deserves steadfast attention.

Previous experimental and computational studies of water in capillaries, narrow slits, and nanopores showed that confined water may be substantially different from the bulk water. Subject to capillary condensation (Evans, 1990), liquid water may be compacted near the polar wall (Brovchenko et al., 2000), or destabilized by a hydrophobic surface promoting evaporation (Lum et al., 1999). Dewetting transitions in hydrophobic capillaries are initiated by formation of a vapor-like phase between the wall and the fluid resulting in metastable dynamic liquid plugs that coexist with the vapor phase (Monette et al., 1992). The behavior of water simulated in cylindrical nanotubes depends on the internal diameter of the tube and interactions with the surface (Hummer et al., 2001). Arranged as hexagonal structures inside the tube, water can form ice at room temperature (Mashl et al., 2003), although under other circumstances confined water was found as fluid, as in the bulk (Allen et al., 2002). Recent simulations of water in model channels by the Sansom group (Beckstein et al., 2001; Beckstein and Sansom, 2003) showed that the stability of liquid phase inside a hydrophobic nanopore critically depends on the pore geometry and polarity of the wall. The presence of one or two polar atoms in the pore lining was shown to be sufficient to switch the regime to a fully hydrated state. Simulated liquid-vapor oscillations in hydrophobic channels resembled cycles of capillary evaporation and condensation, in which the mean equilibrium occupancy of the pore by water was governed predominantly by the rate of evaporation (Beckstein and Sansom, 2003).

In the present work we describe the results of molecular dynamics simulations of water inside the mechanosensitive channel, MscS. The crystal structure of MscS has been recently solved by the Rees group (Bass et al., 2002) revealing a relatively wide pore (7–15 Å between the solvent-accessible surfaces) formed by seven identical helices. Because the pore in most parts can sterically accommodate an ion with its hydration shell, the conformation was deemed open. The highly hydrophobic character of pore-exposed residues, however, raised questions about the stability of fluid water inside the pore and the energetics of ion permeation. To address these questions, we conducted equilibrium MD simulations of water in MscS as well as steered simulations of ion permeation through the narrow part of the pore. The water dynamics showed clear dewetting transitions in the pore, consistent with continuum estimations of free energies of different states of hydration based on the character of pore lining and geometry. Steered simulations of ion passage through the pore suggested a substantial barrier for ion permeation. The simulations also predicted that the primary effect of hydrophilic gain-of-function substitutions in the pore lining is stabilization of the hydrated state of the pore.

METHODS

MD simulation

The MscS crystal structure coordinates (PDB entry 1MXM, Bass et al., 2002) were taken as the initial conformation for MD simulations. The channel was reoriented to have its symmetry axis coinciding with the z axis of the simulation cell. Hydrogens were added using PSFGEN, part of the NAMD package (Kale et al., 1999).

We limited the simulated part of the protein to the pore-forming region only. The first set of simulations was conducted with a larger protein fragment containing 574 residues (27–38, 79–127, 137–140, 151–153, and 162–175 of each monomer, 8260 protein atoms, Fig. 1 a), surrounding the pore. The protein fragment was embedded into a 40 Å-thick octane slab (523 molecules) imitating the hydrocarbon core of the membrane, which was positioned at the level of the highest hydrophobicity of the outer channel surface, between the levels of tyrosines Y27 and Y75. This system was hydrated with 15,507 water molecules making 68,492 atoms in total. Three variants of this system were simulated: octane-embedded WT channel with water only; octane-embedded WT channel with water and 53 sodium and 60 chloride ions (making 200 mM NaCl); and L109S mutant channel in the latter configuration. Simulations started with water-filled pore if not stated otherwise.

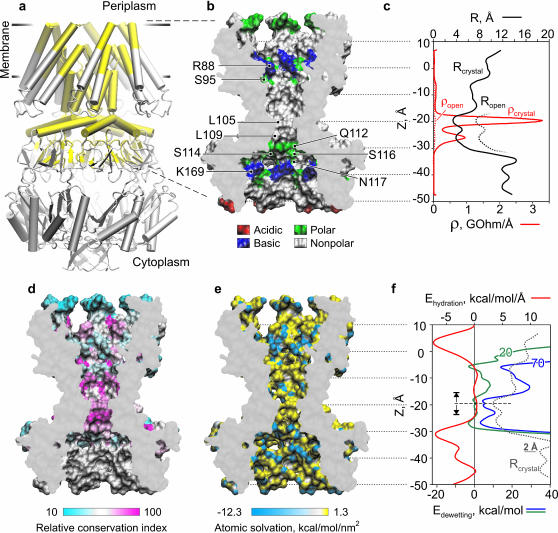
FIGURE 1.

FIGURE 1

Open in a new tab

Properties of MscS pore: radius, resistance, surface polarity, hydration energy, and evolutionary conservancy. (a) Crystal structure of E. coli MscS (Bass et al., 2002) in a schematic representation. The pore region considered for continuum estimations and then included in MD simulations is highlighted yellow. (b) The cross section of the central pore region with its solvent-accessible surface (probe R = 1.4 Å) is colored according to the residue type: acidic (red), basic (blue), polar (green), and nonpolar (white). Positions of residues defining the polarity are indicated. (c) Effective pore radius R (black solid line) and specific resistance ρ (red solid line) as functions of z coordinate. A hypothetical widening of the constriction and the corresponding drop of resistance are shown by dotted lines. (d) The pore region is colored according to the relative conservation index for the YggB family (data from Pivetti et al., 2003). (e) The surface of the pore is colored according to the atomic solvation energies with hydrophilic atoms shown in blue. (f) Hydration energy (red) and free energies of dewetting calculated with the surface tension parameter σ = 70 (blue) and 20 mJ/m2 (green). The initiation of the vapor phase formation was inferred in the narrowest part of the pore (dashed line).

In the second set, a smaller fragment of MscS (308 residues from A79 to V122) was embedded into a hexagonal water box. Simulations were initiated in four different water-filled configurations: empty pore with dry central part and extracellular vestibule; pore with water-filled vestibules but dry nonpolar central part; pore with dry constriction; and pore completely filled with water—bringing 9575–9800 water molecules into the system (32,911–33,586 atoms in total).

All simulations were performed using NAMD2 program (Theoretical Biophysics Group and National Institutes of Health Resource for Macromolecular Modeling and Bioinformatics, Beckman Institute, University of Illinois at Urbana-Champaign, Urbana, IL) with CHARMM22 force field in a flexible hexagonal periodic box as an NPT ensemble at 310 K and 1 atm pressure (Langevin piston method). The flexible TIP3P water model (Jorgensen et al., 1983) was used. Electrostatics was calculated using the particle mesh Ewald (PME) method with a grid spacing of ∼1 Å. In two additional simulations the electrostatic cutoff method was used instead of PME to assess the effect of long-range electrostatic interactions. The cutoff threshold in these instances was set at 10 Å with switching started at 8.5 Å.

In all simulations the backbone atoms were harmonically restrained with a soft spring constant (kf = 1 kcal/mol/Å2) at the positions found in the crystal structure, which was necessary to prevent drift from the initial conformation as the protein subunits were no longer continuous polypeptides. All side chains remained unrestrained. Bad contacts were removed by energy minimization of the complete systems. The systems were then equilibrated at 1 atm and 310 K for 0.1 ns, during which the protein/octane boundary and small distortions of the protein stabilized. Other program settings were as in Anishkin et al. (2003). Results were analyzed with PDBAN software custom written in MatLab, and visualized using VMD (Humphrey et al., 1996). Time-dependent trajectories were plotted using Microsoft Excel.

Steered molecular dynamic (SMD) simulations

SMD simulations were performed to visualize the permeation of ions through the MscS pore and to assess the energetics of this process. In these simulations a chloride ion was harmonically attached to the steering plane with a spring constant of 1 kcal/mol/Å2. The plane was moved between the initial and end positions in opposite pore vestibules, separated by 38 Å, within 1 ns. The distance thus covered by the ion was comparable to the average distance (∼35 Å) a chloride ion travels in 1 ns in the bulk as a result of free diffusion (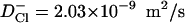Inline graphic). During simulations, the position of the ion and the applied force were recorded every 100 fs. For estimation of the potential of the mean force, both the position and force were averaged with the running frame of 50 ps (Fig. 6), which permitted us to separate the steered movement from the thermal noise. SMD simulations were started with the system initially pre-equilibrated for at least 4 ns and performed in the absence of voltage or concentration gradients. Because the ion was moved between two positions of similar equilibrium occupancies, the energies of the ion in the starting and final positions were assumed to be equal. The total energy cost of the complete steered transition was ascribed to the irreversible work against the friction force. The mean friction coefficient for each individual trajectory was assumed to be constant, and the friction force proportional to the average velocity of steered movement (Gullingsrud et al., 1999),

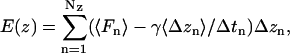graphic file with name M2.gif
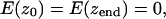graphic file with name M3.gif

where NZ is the number of the recorded SMD steps before the position z, and 〈Δzn〉 (averaged over 50-ps time frame) is the shift in z direction for the corresponding step. Because the trajectories varied and the microenvironments for ion movement were different in each run (see Fig. 6 a), the mean friction coefficient was independently adjusted for each trace to equate the total energy cost to zero. The average values for the friction coefficient, γ, inside the channel were 0.89 ± 0.32 and 0.74 ± 0.09 pN × ns/Å for WT MscS and the fully hydrated L109S mutant, respectively. The dispersion of the friction coefficient simply reflects variations in total energy dissipated and a somewhat irreversible character of steered ion motion.

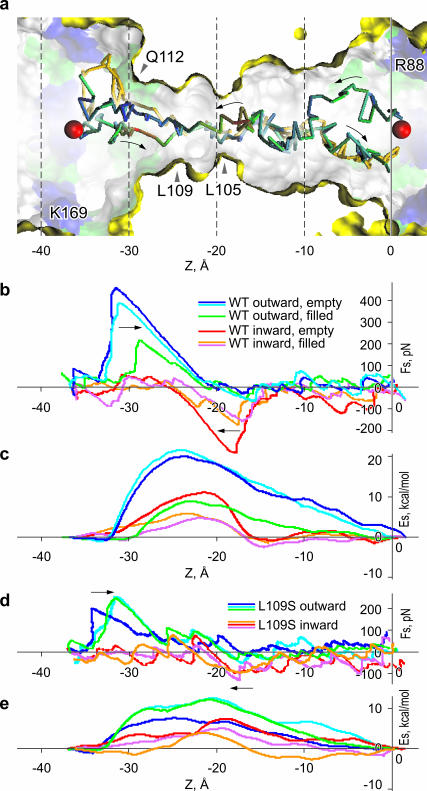
FIGURE 6.

FIGURE 6

Open in a new tab

Steered movement of Cl− ion through WT and L109S MscS pores. (a) The initial points for the outward (from left to right) and inward movements through the constriction are shown by red spheres. The ion was harmonically restrained to a plane which was moved with a velocity of 38 Å/ns along the z axis. In the course of transition, the ion was free to move in x and y directions. Three trajectories, two outward and one inward, are shown. Two of the trajectories are color-coded according to the force applied to the ion (red being the highest). The key residues are denoted. (b) The steering force (smoothed with a 50-ps running frame) as a function of z coordinate for three independent transitions in each direction. The state of the pore (water-filled or empty) at the moment of ion's entry into the constriction for each trace is shown in the legend. (c) The potential energy of the ion inside the pore calculated as the difference of total work produced by the steering force and the friction losses (see Methods). The force (d) and the energy (e) profiles for the steered movement of Cl− through the permanently hydrated L109S MscS pore.

Water density maps

Probability density distributions of the occurrence of water oxygens in space were calculated using a volumetric grid with a 0.5 Å step. The densities were normalized relative to the bulk water outside the pore. Two-dimensional maps represent 2 Å slices along the pore axis, averaged for the last 5.5 ns of WT MscS simulation, or last 3.5 ns for GOF MscS with 1-ps time step.

Hydrogen bonding maps

Hydrogen bonds were defined by the geometric criteria: the donor-acceptor distance <3.5 Å, and the angle between the donor-hydrogen and hydrogen-acceptor lines <30°. H-bonds were scored and averaged for entire simulations after initial equilibration for 0.5 ns. The number of bonds was mapped onto a volumetric grid with a 0.5 Å step. Two-dimensional maps represent 2 Å slices along the pore axis through the center of the pore. The numbers reflect an average state of H-bonding only for the frames, when water was present in the particular location.

Hydration energy profile and energy of pore dewetting

The calculations of the hydration energy profiles were performed for 10 frames, separated by 50 ps, of the last 0.5 ns of the WT MscS simulation in the presence of ions. For each conformation, the hydration energy per atom was calculated using the GETAREA web-based software (Fraczkiewicz and Braun, 2002) with the probe radius of 1.4 Å and atomic solvation parameters taken from Wesson and Eisenberg (1992). A custom-written algorithm permitted us to select the atoms on the outer and inner surfaces of the protein separately. The selected atoms on each surface were grouped in 1 Å slices along the z axis normal to the membrane plane. Hydration energies for all atoms in each slice were summed up, which produced the hydration energy density along the axis. The initial profile was smoothed on the assumption of Gaussian distribution of the z coordinate for each atom with root mean-square deviation = 2.5 Å. The dewetting process was modeled as a breakdown of water column in the narrowest part of the pore, and moving the two water boundaries apart. Variations of the free energy of dehydration for each compartment separately (presented in the continuum form by Eq. 1; see Results) were calculated as

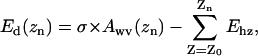graphic file with name M4.gif

where σ is surface tension of water, Awv(z) is the area of water-vapor interface (approximated with the cross-sectional area of the pore in a given location z), and Ehz is the hydration energy of all pore-facing atoms in a given slice.

Mean pore cross section and radius calculations

Solvent-accessible surfaces (SAS) were created for 10 snapshots (every 50 ps during the last 0.5 ns) of the WT MscS simulated in the presence of salt. VDW radii from the CHARMM22 parameters set and a spherical probe of a 1.4 Å radius were used. A set of cross sections normal to the pore axis was created for the SAS with a step of 0.5 Å. Average pore radii were calculated as described in the next section. All the calculations were done using PDBAN software custom written in MatLab.

Pore conductance calculations

The conductance of the channel (G) was calculated using Hille equation (Hille, 2001), taking into account the access resistances and the resistance of the pore itself in a solution of given bulk conductivity g:

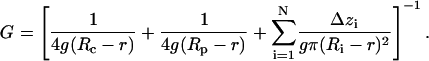graphic file with name M5.gif

The effective radius of the pore (Ri) in a given location along the channel axis (zi) was defined as a radius of the circle equal in area to the corresponding cross section of the inner solvent-accessible pore surface. Channel pore was represented as a set of N cylindrical slices of thickness Δzi = 0.5 Å with radii Ri. The effective ion-accessible pore area was determined with a probe of 2.83 Å in radius, which approximates a generic ion (R = 1.43 Å, the average between radii of Na+ and Cl−) coated with half of its hydration shell (r = 1.4 Å). Access resistances were determined from the effective radii of the cytoplasmic (Rc) and periplasmic (Rp) pore entrances. The resistance of the cytoplasmic domains of MscS below the level of side openings was not included in calculations.

RESULTS

The pore surface of MscS: continuum estimations of conductance and hydration energy

The heptameric crystal structure of MscS is shown in Fig. 1 a. Only the membrane-spanning region, comprising parts of TM1, TM2, the entire TM3 lining most of the pore and a part of the cytoplasmic vestibule (highlighted yellow), was taken into consideration. To our advantage, the TM3 helices were resolved particularly well in the original structure (based on the β-temperature factors), reducing the ambiguities of side chain orientation. The region is magnified and presented as water-accessible surface in Fig. 1 b where pore-exposed side chains are color-coded according to their charge and polarity. The pore can be divided into four characteristic regions: 1), the wide (effective surface-to-surface radius R = 8–10 Å, Fig. 1 c) extracellular vestibule lined with polar serines 95 and positively charged arginines 88; 2), the central nonpolar region (R = 7–8 Å); 3), the hydrophobic constriction (R = 3.5–4.5 Å) lined by rings of leucines 105 and 109; and 4), the wide and polar intracellular vestibule with positive lysines 169. The entire pore is sterically accessible to water. In the assumption of uniform filling of the pore with electrolyte of ∼30 mS/cm bulk conductivity used in patch-clamp experiments (Martinac et al., 1987; Sukharev, 2002), we estimated the pore conductance using the Hille equation (Hille, 2001). The resistance was calculated for individual half-Ångstrom slices (plotted as smooth line in Fig. 1 c) and then integrated along the pore length yielding the total pore resistance of 14.3 GOhm, corresponding to a 70-pS conductance (see Methods for details), which is much smaller than the previous estimation using HOLE (Bass et al., 2002) and known conductance of the open MscS (Martinac et al., 1987). The constricted region (Fig. 1 c), as seen from the plot, contributes most of the resistance. In theory, an increase of the radius of the constriction by 4 Å, as shown in Fig. 1 c (dotted line), would increase the conductance to ∼1 nS, corresponding to the open-channel value measured in most experiments. This method of conductance estimation was also tested for the known structure of α-hemolysin (Song et al., 1996) with similar pore dimensions (r ≈ 9 Å, 50 Å long), yielding 104 pS (in a solution with 13 mS/cm conductivity), which is close to the experimental value of 108 pS (Merzlyak et al., 1999).

For more detailed visualization of the pore interior we mapped the surface (Fig. 1 e) according to solvation parameters for individual atoms (Wesson and Eisenberg, 1992). A few partially exposed polar (blue) atoms in the central nonpolar cavity belong to the backbone of TM3. No polar atoms are exposed in the constriction. Conspicuously, the most hydrophobic area of the channel is also the most conserved region among the twelve members of Eco-MscS (YggB) subfamily, based on the sequence alignment (Pivetti et al., 2003) (Fig. 1 d). Using Wesson-Eisenberg solvation energies and water-exposed areas for each atom (Fraczkiewicz and Braun, 2002) we reconstructed the hydration energy density profile along the pore (Fig. 1 f, red line). The profile indicates that the entire nonpolar region 20 Å-long is characterized by slightly positive hydration energy. It is flanked by two deep minima corresponding to the wider polar vestibules.

We estimated the energy cost of pore dewetting by introducing an imaginary break in the narrowest part of water column and then moving the two boundaries apart. Variations of free energies in the lower and upper water compartments were defined as the sum of the protein dehydration energy and the energy for creation of new water/vapor interface,

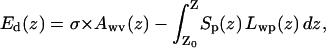graphic file with name M6.gif (1)

where σ is surface tension of water, Awv(z) is the area of water-vacuum interface (approximated with the cross-sectional area of the pore in a given location z), Sp(z) is the protein hydration energy per square Ångstrom, and Lwp(z) is the perimeter of the pore cross section. Plotted in Fig. 1 f, the free energy curves (calculated with the parameter σ = 70 and 20 mJ/m2) show three characteristic minima, two of them flank the hydrophobic constriction and the third coincides with the boundary between the nonpolar part and the outer vestibule. The positions of these minima suggest the limits of the dehydrated area if an interruption of the continuous liquid phase inside the pore occurs. With the bulk-like tension (σ = 70 mJ/m2) the two lower minima would be preferentially occupied, favoring the empty state of the constriction by ∼3 kcal/mole. The assumption that confined water has lower tension due to compromised hydrogen-bond network (σ = ∼20 mJ/m2) diminishes both the barrier and the energy in the third minimum, permitting stable dewetting of the entire nonpolar region. These three states—the water-filled state, the state with vapor-plugged constriction, and the state with completely dehydrated nonpolar part of the pore—were observed in different molecular dynamic simulations presented below.

MD simulations of water in WT and L109S MscS pores

A cross section of the simulation cell, which contains the transmembrane region of WT MscS (574 residues), 15,507 molecules of water, and 53 Na+ and 60 Cl− ions is shown on Fig. 2 a in the end of a 6-ns simulation. Only the backbone of the protein was softly restrained, whereas the side chains were free to move. During the equilibration period, the protein-octane boundary adjustments and a small relaxation of distal parts of the protein backbone were observed. The analysis of displacements of the softly restrained backbone indicated that the packing of TM3 domains forming the pore was stable, consistent with the lower temperature factor in that region of the crystal structure.

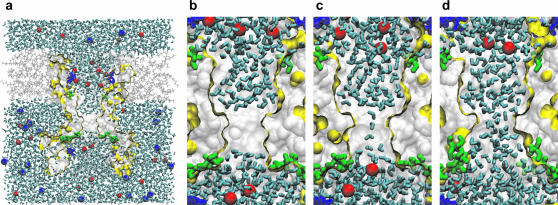
FIGURE 2.

FIGURE 2

Open in a new tab

Water dynamics in wild-type and gain-of-function MscS channels. (a) A cross section through the simulation box with the protein (yellow boundary), water (cyan sticks), octane (gray lines), sodium (blue VDW sphere), and chloride (red VDW sphere) ions. Basic (blue) and polar (green) residues facing the pore lumen are shown as sticks. Snapshots of the pore region in the vapor-plugged (b) and partially water-filled (c) states of WT MscS, and of the stably hydrated L109S gain-of-function mutant (d).

The simulation was initiated with the pore completely filled with water; but soon, within the first 100 ps, water left the constriction. In the course of the following 6 ns, the pore constriction was found in one of two typical states: the most probable empty (vapor-plugged) state (Fig. 2 b), or the partially filled state with a single string of water (Fig. 2 c) connecting the two bulk reservoirs. Rarely, a double string of water molecules was also observed (not shown). Although the water-accessible space in the constriction region was able to accommodate 4–5 water molecules in one layer across the channel, the observed single- and double-string states occupied between 25% and 50% of the available space. The strings oscillated creating a variety of central or wall-attached configurations, while never wetting the full surface. All water molecules in the string were H-bonded, with the dipoles oriented uniformly either up or down. The orientation (as observed in the absence of external electric field) was random and appeared to result from instantaneous configurations of molecules in the beginning of every new filling cycle.

The plot of the occupancy of the constriction region with water vs. time (Fig. 3a ) demonstrates repeated switching between empty (∼83% of the time) and filled states. The results of the same simulation are also represented as a plot of z coordinates of water oxygens (Fig. 3 b). At the boundaries of the vapor plug, water fluctuates substantially, making 50-ps-long excursions (∼4–5 Å) from both sides. The filling transitions occurred usually as a result of two big fluctuations occurring simultaneously on both ends of the vapor plug. There was no apparent correlation between the presence of water in the pore and the conformations of side chains of leucines 105 or 109 lining the constriction. The average z coordinates and radial positions for terminal carbons of L109 are presented as a function of time in Fig. 3 c.

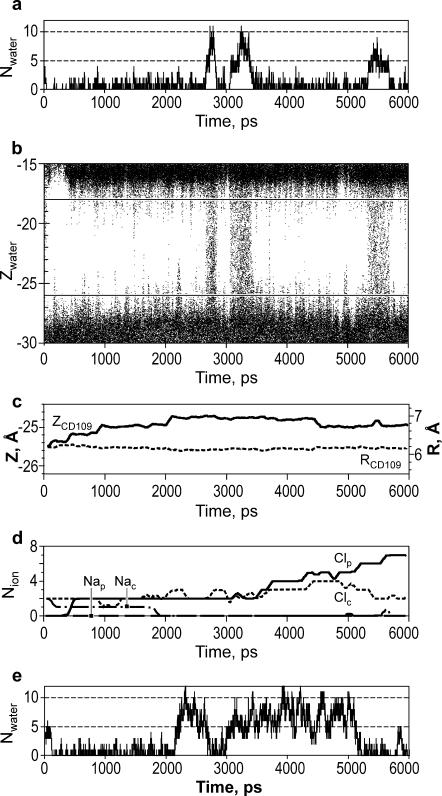
FIGURE 3.

FIGURE 3

Open in a new tab

Water occupancy of MscS pore during 6-ns simulations as a function of time. (a) The number of water molecules found in the narrowest pore region of WT MscS simulated in the presence of salt. (b) The z positions of water molecules in the pore region. Each point represents the position of a water oxygen at a given time step. Horizontal lines in b delineate the central region (−26 Å > z > −18 Å) where the water molecules were scored. (c) The average z coordinates of the terminal carbons of all seven L109 side chains (solid line) and their average distance from the axis of the pore (dashed line). 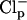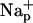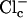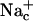(d) The average number of chloride and sodium ions in the periplasmic (Inline graphic and Inline graphic) and in the cytoplasmic (Inline graphic and Inline graphic) halves of the pore. (e) The pore occupancy by water presented as in a for the simulation of WT MscS without ions.

Equilibrium state is independent of initial configuration

We performed a set of four simulations (6 ns each) beginning with: the channel completely filled with water; or mostly filled with dehydrated constriction only; or with only vestibules filled; or with empty channel including hydrophilic outer vestibule. A smaller channel segment was simulated (A79 to V122) to speed up the process. Independent of the initial state, all simulations converged to the water-filled channel with the predominantly empty constriction, displaying periodic filling transitions, similar to the behavior of the larger channel segment in previous simulations. For the starting conditions with completely empty or partially filled channel, wetting of the wider nonpolar region of the pore presented considerable kinetic barrier which occurred at the boundary with the extracellular vestibule, as predicted by free energy minima calculated in continuum approximation (Fig. 1 f). In both sets, the larger and smaller simulated pore fragments demonstrated periodic dewetting of the hydrophobic constriction with the upper water boundary located at the level of residue A102 (Fig. 2 b).

Simulations with electrolyte versus pure water

As expected, in the presence of 150 mM NaCl, chloride ions accumulated during the simulation near positive charges of arginines and lysines in the channel vestibules (Fig. 2, b and c, and Fig. 3 d). This was accompanied by a decrease in local concentration of sodium ions. No clear correlation was observed between the number of chloride ions present in the channel vestibule and the probability of water-filled state of the constriction. Chloride ions were rarely observed in the nonpolar channel region, and never in the hydrophobic constriction.

When simulated in the absence of ions, the water in pore showed a qualitatively similar periodic behavior to that in the presence of salt, but higher total probability of water-occupied state (∼50% of the time, Fig. 3 e). Fluctuations between single- and double-string modes with a period of ∼250 ps were observed during the longer occupancy period. The results suggest that the physiological concentration of salt may shift the equilibrium toward the empty pore state. This behavior is consistent with the well-known effect of surface tension increase in concentrated salt solutions. Indeed, the local concentration of Cl− ions attracted by positive charges of R88 to the outer vestibule reached 3 M in the end of simulation.

Computation of electrostatics with a cutoff effects the state of pore hydration

The role of the long-range electrostatic interactions was indirectly estimated by repeating the simulations (with the larger protein fragment) with the cutoff method of electrostatics calculation instead of the particle mesh Ewald (PME). Other simulation conditions were the same as in the first set. Simulations were initiated with the pore completely filled with water. The removal of the long-range electrostatic interactions had lead to a complete emptying of both the constriction and the wider nonpolar part of the pore. After retracting to the upper vestibule (to the position predicted by the third free energy minimum, Fig. 1 f) during the first 150–200 ps of simulation, liquid water was never observed in the entire nonpolar pore region again in two independent 6-ns simulations conducted with or without salt.

Gain-of-function mutation stabilizes the water-filled state of the pore

In the contrast to WT MscS, the gain-of-function mutant L109S, with wider and significantly more hydrophilic constriction region, was stably hydrated for all 4 ns of the simulation, with either the PME or cutoff methods of electrostatics calculation. Water filled completely all solvent-accessible space (Fig. 2 d).

Water in MscS: maps of density and hydrogen bonding

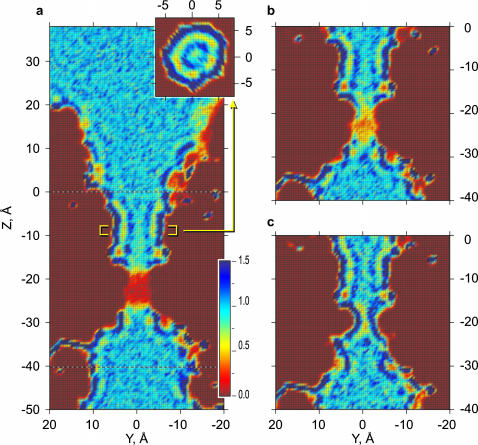
Water density maps (Fig. 4) were computed as the probability to see the oxygen of a water molecule in a particular grid location and normalized to the density of bulk water. In the pore vestibules, the water density distribution is similar to that in the bulk, with a slightly denser layer near the pore surface. In the nonpolar region, the layering of water is pronounced in all simulations of WT MscS with salt (Fig. 4 a), with pure water (Fig. 4 b), or in the L109S GOF mutant channel (Fig. 4 c). The cross section normal to the pore axis (Fig. 4 a, inset) shows that water in this confined region is organized as two concentric cylinders without a clear sevenfold symmetry despite the heptameric organization of the pore. The pattern of water density follows the contour of the cavity, which is round and uniformly hydrophobic in this region. In other cross sections, the sevenfold symmetry is more pronounced near polar atoms, especially near the exposed backbone of G101 (not shown).

FIGURE 4.

FIGURE 4

Open in a new tab

Water densities in wild-type and L109S gain-of-function MscS pores. The probability of the occurrence of water oxygens was calculated using a three-dimensional volumetric grid and normalized to the density of bulk water outside the pore. The maps represent 2 Å slices along the pore axis, averaged for the last 5.5 ns of WT MscS simulation with (a) and without (b) salt, and for 3.5 ns of L109S (c) in the presence of salt. Inset in a shows the density in the slice across the wider nonpolar region where water is organized as two concentric cylindrical layers.

In the hydrophobic constriction of WT MscS, the time-averaged water density is significantly decreased; in simulations with pure water it is ∼0.35 of bulk density (Fig. 4 b), and ∼0.12 in the presence of salt (Fig. 4 a). This reflects both the preference to the empty state and the absence of complete wetting during filling periods. The pore constriction of L109S GOF MscS, in contrast, shows a higher density of water with characteristic layering, reflecting stable hydration of the region with water distributed as a single tubular layer.

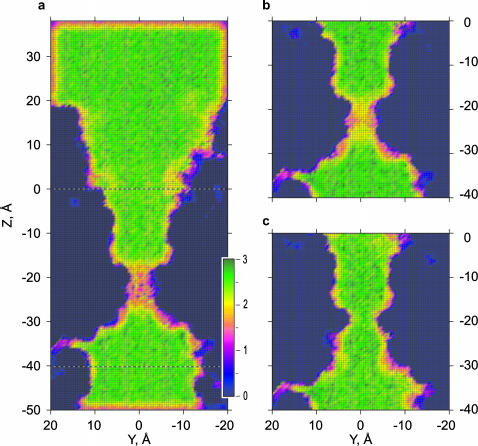
The average number of hydrogen bonds per one water molecule was defined by the geometric criteria (see Methods). Because H-bonds were scored only when water oxygen was present in the corresponding cell of the grid, the average number of bonds presented on the maps is independent of the average occupancy in a particular location. It can be seen from the maps (Fig. 5) that in the vestibules, as well as in the wider nonpolar region, the average number of hydrogen bonds (2.53) is close to that in the bulk phase (2.52). In the hydrophobic constriction, water bonding is significantly decreased, yielding, in average, 1.69 and 1.89 bonds in WT MscS in the presence or absence of salt, respectively (Fig. 5, a and b). For the GOF L109S mutant, water does not show any significant loss of H-bonds in the modified constriction region, being able to find the same number of neighbors as in the bulk. The bonding to protein atoms was not included in these computations.

FIGURE 5.

FIGURE 5

Open in a new tab

Densities of hydrogen bonding in WT and GOF MscS. Hydrogen bonds defined by the geometric criteria (see Methods) were counted and averaged for entire simulations as in Fig. 4. The maps represent 2 Å slices along the pore axis through the center of the pore. (a) WT MscS simulated with 200 mM NaCl and (b) without ions. (c) L109S gain-of-function mutant simulated in the presence of salt, showing bulk-like density of H-bonds throughout the pore.

Steered ion movement through the channel

In an attempt to visualize the process of ion passage through the narrow pore region and roughly estimate the energetics of permeation, a set of steered (SMD) simulations was performed. Cl− was chosen as a permeant ion because open MscS has a weak anionic preference (Martinac et al., 1987; Sukharev, 2002). The start and end points for the steered movement were located in two opposite vestibules, at z = −37 Å and z = +1 Å on the pore axis inside the rings of positively charged residues, where maximal concentrations of Cl− were observed in previous simulations. The ion was softly attached to the steering plane which was translated between these points during 1 ns. This passage time was similar to the diffusion time of a Cl− ion across a comparable distance in the bulk, illustrating that the steering velocity was not unreasonably high. At the start, the ion was positioned on the pore axis, but in the course of transition the ion was free to move along x and y coordinates. Three 1-ns runs in each direction for the WT and L109S channels were performed. Sample trajectories through the WT channel, two in the outward direction, and one inward, are shown in Fig. 6 a. Two trajectories (one for each direction) are colored according to the force required to pull the ion (red is the highest absolute value of force). Trajectories of ions softly restrained to the plane exhibited large random variations, especially in the vestibules, resembling trajectories of unrestrained diffusional motion in the bulk. When the pore constriction was in a dehydrated state, the ion had a tendency to diffuse in the direction of the channel wall and hang near the partial positive charges of Q112.

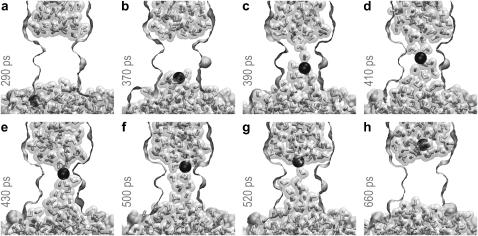
Steering of the ion into a dehydrated pore led to a depletion of the ion hydration shell and a temporary partial filling of the constriction, as illustrated in Fig. 7. In the bulk, a Cl− ion coordinated water with the maxima of radial density for oxygens at 3.1 and 5.2 Å, and minima at 3.8 and 6.1 Å, defining the first and the second hydration shells of 7.5 and 23.3 water molecules in average. The highest loss of hydration shell around the ion (approximately one-half) was observed when the ion was just entering the constriction (Fig. 7, a and b). A partial dehydration required maximal force and led to the steepest rise of energy (Fig. 6, b and c). The maximum of energy (∼20 kcal/mole) was consistently observed near the middle of the constriction, between the rings of conserved leucines, where the second shell was stripped down to 5.9 molecules. At this point the ion had typically grabbed onto the string of water from the opposite side and its further motion proceeded down-hill. By this time, the ion restored its first hydration shell to ∼5.5 water molecules, still having 35% of the second shell. In the constriction, a water-free space around the ion was always observed either equatorially (Fig. 7, d and e) or on one side (Fig. 7, c and f). The pore surface was never fully hydrated even in the presence of the ion in the middle of the pore. Upon passing the ring of leucines 105, the ion completely restored its first hydration shell, and restored the second to ∼90%, whereas water in the constriction thinned to a single string and then retracted (Fig. 7 h). After passing the constriction, the ion is actively expelled from the pore, as seen from a short stretch of trajectory characterized with a slightly negative force, signifying movement ahead of the steering plane. Further path to the end point required essentially no force.

FIGURE 7.

FIGURE 7

Open in a new tab

Sequential snapshots of the steered ion movement through a vapor-plugged MscS pore. The ion experiences the highest resistance when it enters the constriction and at the same time loses a part of the hydration shell (a and b). The ion regains its complete hydration shell only after exiting the constriction (g and h), which is accompanied by a small acceleration (see Fig. 6 and text). The presence of ion in the middle of the pore (c–f) does not result in the complete hydration of the wall.

A similar sequence was observed when the ion was steered in the opposite direction; the maximum force was again applied when entering the constriction, and the ion experienced expulsion from the channel while exiting on the other side. As seen from Fig. 6 b, the passing of ion through a partially hydrated pore required half the force to enter the pore and the energy barrier was also lower by ∼5 kcal/mole, although located at approximately the same position. The structure of the partial hydration shell in this case was similar to that shown in Fig. 7, c–g. The difference in forces and energy profiles observed for the passages in two opposite directions may be attributed to a nonequilibrium character of movement of a steered ion, and a simplified method of accounting for friction. More sampling and a slower steering would be required for an accurate reconstruction of the potential of the mean force inside the pore (Gullingsrud et al., 1999; Jensen et al., 2002).

The permanently hydrated pore on the L109 gain-of-function mutant poses fewer impediments for permeation as seen from the profiles of force and energy for three simulations in each direction (Fig. 6, d and e). The maximum force, as previously, is required for entering the constriction from either side. The tip of the energy barrier is now located near L105, and the second, smaller maximum appears at the cytoplasmic entrance to the constriction, near Q112. The profiles for the movement in each direction are more consistent from run to run; however, simulations under more equilibrium conditions will be required to clarify the reason for the observed hysteresis.

DISCUSSION

Recent advances in membrane protein crystallography provide foundations for quantitative descriptions of ion conduction and selectivity in channels (Berneche and Roux, 2001; Im and Roux, 2002), and for realistic models of gating (Jiang et al., 2002b, 2003; Sukharev et al., 2001). When the functional state (open or closed) of a channel resolved under specific crystallization conditions is not evident, computation of conduction rates may help in such assessments. Based on crystallographic dimensions of the pore and inferred distribution of charges, potential profiles can be reconstructed, but this requires assumptions on the dielectric properties of different compartments, friction coefficients along the permeation path, and usually imply uniform filling of all accessible space inside the pore with water (see Nonner et al., 1999, and references therein). The previous studies (Beckstein and Sansom, 2003) and the results above, however, indicate that the latter may not be universally applicable, and the state of the solvent in certain types of pores should be taken into consideration.

The simulations of the hydrated MscS pore presented above have been performed with a number of simplifications. Only the pore-forming fragments of the protein (Fig. 1 a) were included, and the dielectric environment of the membrane hydrocarbon was imitated by an octane slab. By using these approximations we avoided the problem of an excessively large simulation cell and uncertainties in the lipid packing around the channel that we could have faced with explicit lipids. The stability of the system was ensured by harmonic backbone restraints. A cautious approach raises questions of whether such restraints distort the observed dynamics of water in the pore. Based on results of previous studies (Chiu et al., 1991; Smith and Sansom, 1998), we conclude that in our system this is highly unlikely because 1), the restraints were relatively soft and energy-conserving; 2), the side chains facing the pore were unrestrained; and 3), the lining of the relatively wide pore contains mostly nonpolar atoms that weakly interact with water.

Although MscS appears to be stereochemically open (Bass et al., 2002), the observed dynamics of water in the narrow hydrophobic (and most conserved) part of the pore exhibits typical dewetting transitions. The average density of water in this location was consistently below 0.12 relative to that of the bulk. Even when the fluid phase was continuous across the pore forming a string, most of the solvent-accessible volume in the constriction was filled with vapor. Frequent transitions between the preferential vapor-plugged and intermittent water-filled states suggest that the system is somewhere near its critical point. We realize that the critical regime of water strongly depends on the parameters of the force field used in the simulation; see, for example, Hummer et al. (2001). Even switching the electrostatics computation method from PME to cutoff changes the hydration equilibrium in the wider nonpolar part of the pore. Nevertheless, detailed pictures of qualitatively different water behavior, bulk vs. nonbulk, observed in this work allow us to make a number of predictions regarding the role of water in channel gating and functional state of MscS in particular.

The discrete two-state behavior of water in most of our simulations is very similar to what was observed previously in simulations of model hydrophobic channels (Allen et al., 2002; Beckstein et al., 2001; Beckstein and Sansom, 2003) and in carbon nanotubes with decreased water-wall interactions (Hummer et al., 2001). Although at this point we have not been able to vary the width of the pore independently of other parameters, the difference in hydration between the narrow and wider nonpolar regions of the pore, as well as the effect of L109S substitution, all indicate critical dependences on the radius and hydrophilicity of the lining. The packing of water in different parts of the pore illustrated by density maps (Figs. 4 and 5) supports the previous notion (Beckstein and Sansom, 2003) that two concentric layers of water molecules is probably the minimal amount of water that remains stable in a nonpolar environment and retains its bulk-like density and number of hydrogen bonds. The emptying of the wider nonpolar region of the pore in the cutoff simulations should be considered not as a simple computational artifact, but more as an indication that under certain conditions (narrower conformation, for instance) this part of the channel may also be in a dehydrated state. The positions of water/vapor boundaries for all observed dewetting transitions are in good agreement with the polarity of the surface, and thermodynamic minima calculated in continuum approximation form the atomic pore structure (Fig. 1 f).

The constriction of MscS (R = 3.5 Å) is too narrow to accommodate two cylindrical layers of water. Lined with two separate rings of leucines along the 10 Å span, the constriction resembles a rippled superhydrophobic surface (Nakajima et al., 2001). The atomic density of extended hydrocarbon chains is relatively low, compared to denser surfaces of nanotubes (Hummer et al., 2001; Mashl et al., 2003), and therefore offers only weak van der Waals interactions with the solvent. Although we found no direct correlation between the conformation of L105 side chains and the hydration state of the pore, the thermal motion of side chains might exert additional destabilizing effect on liquid water in the pore confinement, as opposed to the stabilizing effect of rigid walls on water structure inside carbon nanotubes (Hummer et al., 2001).

The hydrophobic constriction of the L109S mutant channel is wider, shorter, and effectively more hydrophilic, which allows for a stable accommodation of one cylindrical layer of water. The expression of this gain-of-function mutant was shown to suppress the growth of bacterial cells (Miller et al., 2003a). The toxicity may be either because the setpoint for L109S channel activation is inappropriately low, as for MscL gain-of-function mutants (Ou et al., 1998), or because the permanently hydrated channel confers a proton leakage. It should be noted that the proton transport is usually tightly controlled by organisms. The leakage via proton wire was eliminated in the structural design of aquaporins by the orientational interruption of the hydrogen-bonded water chain (de Groot and Grubmuller, 2001; Tajkhorshid et al., 2002) and the electrostatic barrier in the middle of the pathway (de Groot et al., 2003). On the other hand, proton channels are specially engaged in the cellular locations where high rates of proton transport are required (DeCoursey et al., 2003). It seems that ion channels in the closed conformation should not pass protons, either; therefore, a continuous internal water pathway should be interrupted.

The results above strongly suggest that the structure of the pore region represents a state with extremely low ionic conductance. The simplest macroscopic estimation of the conductance for MscS pore uniformly filled with electrolyte using the Hille equation yields 70 pS. When an ion was steered through the pore, an uncompensated loss of the second hydration shell and at least one-third of the first hydration shell was consistently observed. As a result, the estimated permeation barrier in the (partially hydrated) constriction is as high as 10 kcal/mole (17 kT). Given that the conductance of two channel vestibules is in the order of 10−9 S, a barrier of 17 kT in the middle of the channel would reduce the total conductance to ∼10−16 S. The more probable dehydrated (vapor-plugged) state of the constriction poses an even larger impediment (34 kT), making it nonconductive. For the L109S channel, which is permanently hydrated and poses a lower barrier for permeation (∼5 kcal/mole), the estimated conductance would still be in the order of 1 pS, i.e., three orders-of-magnitude lower than the actual conductance of open MscS (Martinac et al., 1987).

If MscS in the crystal conformation does not conduct ions, then can we make any prediction regarding the open state? As shown in Fig. 1 c, a hypothetical widening of the constriction makes the nonpolar part of the pore roughly cylindrical with the radius of 8–9 Å. Such a pore would accommodate at least four water molecules across the lumen, which ensures its bulk-like density and H-bonding, and provides full hydration for an ion. This would be consistent with the experimentally observed linear dependence of unitary conductance with the bulk conductivity of the surrounding electrolyte (Sukharev, 2002), suggesting a bulk-like environment inside the pore, with only slight preference to anions. According to estimations by Hille equation, such a pore would conduct at ∼1 ns. At this stage, however, it is difficult predict the directions of tension-driven helical movements that would eliminate the constriction.

If the crystal structure of MscS is not the open state, then what functional state does it represent? The tight packing and limited mobility (low β-factor) of the TM3 helices are more consistent with the unperturbed (resting) state of the pore. One should remember that MscS is not a simple binary channel. It readily opens in response to a tension onset, but when subjected to sustained tension, especially in the native membrane, it tends to adapt with time (Levina et al., 1999). The adapted state is nonconducting (and therefore should be called inactivated or desensitized) and long-lived. The possibility that the crystal structure is the inactivated state of the channel should be considered. Indeed, the TM1 and TM2 helices are oriented in the crystals at an unusual 30° to the pore axis, as if the protein is in an expanded open-like state. Such an expanded state may be stable in the detergent in the absence of lateral pressure of lipids. However, the TM3 helices could have collapsed back to a more stable closed-like state, favoring dewetting of the pore. Whether or not TM3 helices could be packed more tightly to achieve a “true” resting state in which the entire nonpolar part of the pore is dehydrated remains to be clarified. The cross-linking study of Miller et al. (2003b) suggests that, in the native resting state, MscS may have a more compact conformation than in the crystals. Alternatively, dewetting, which is sensitive to long-range electrostatic interactions, may result from the change in the dielectric properties of the space around the pore when TM1 and TM2 helices replace some water by moving closer to TM3 in the absence of tension.

A scenario in which two separate parts of the pore are engaged in opening and in inactivation gating transitions resembles the hypothetical sequence of events during the opening and desensitization of the nicotinic ACh receptor (Auerbach and Akk, 1998). Indeed, in many respects the constriction of MscS pore is similar to the gate region of the nicotinic ACh receptor (Miyazawa et al., 2003), where two hydrophobic girdles are formed near the side chains of α-L251 and α-V255 positioned in rank at a distance of one helical turn. A pseudo-fivefold symmetrical structure of nAChR has a water-accessible opening slightly smaller (R = 3 Å) than that of MscS built with a sevenfold symmetry. Apparently, it also does not permit passage of an ion with its full first hydration shell. The entire nonpolar region of nAChR pore is actually extended due to the presence of α-V259 above the constriction. By analogy with MscS, it seems highly probable that the hydrophobic mechanism of nAChR gating also involves switching between hydrated and vapor-filled states of the pore (Beckstein and Sansom, 2003). Our preliminary simulations of the AChR pore indicate a strong tendency for gate dewetting (A. Anishkin, unpublished). Substitutions of leucines at positions equivalent to α-L251 with serines in four nAChR subunits make the channel progressively more sensitive to agonists (Labarca et al., 1995), which is analogous to the effects of many gain-of-function mutations in MscL (Yoshimura et al., 1999), rendering these channels more sensitive to membrane tension. Polar or charged substitutions within the gate of Kv channels also produce left shifts of activation curves and a small constitutive conductance (Sukhareva et al., 2003). The relationship between pore hydration and stability of the closed state(s) in channels must be studied in detail.

In conclusion, the reported MD simulations of the small mechanosensitive channel MscS strongly suggest that the crystal structure does not represent the open state. The pore region is likely to be in the vapor-plugged desensitized or closed state. The stably dehydrated state of hydrophobic constrictions may be a common property of channels with electrically tight gates. This gating mechanism reduces the closed-state ion and proton leakage to essentially zero by utilizing the propensity of water to cooperative dewetting transitions.

Acknowledgments

The authors thank John Weeks and Indira Shrivastava for critical reading of the manuscript, and Bob Eisenberg and Mark Sansom for stimulating discussions.

The work was supported by grants from the National Aeronautics and Space Administration and the National Institutes of Health to S.S.

References

  1. Allen, R., S. Melchionna, and J. P. Hansen. 2002. Intermittent permeation of cylindrical nanopores by water. Phys. Rev. Lett. 89:175502. [DOI] [PubMed] [Google Scholar]
  2. Anishkin, A., V. Gendel, N. A. Sharifi, C. S. Chiang, L. Shirinian, H. R. Guy, and S. Sukharev. 2003. On the conformation of the COOH-terminal domain of the large mechanosensitive channel MscL. J. Gen. Physiol. 121:227–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Auerbach, A., and G. Akk. 1998. Desensitization of mouse nicotinic acetylcholine receptor channels. A two-gate mechanism. J. Gen. Physiol. 112:181–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bass, R. B., P. Strop, M. Barclay, and D. C. Rees. 2002. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 298:1582–1587. [DOI] [PubMed] [Google Scholar]
  5. Beckstein, O., P. C. Biggin, and M. S. P. Sansom. 2001. A hydrophobic gating mechanism for nanopores. J. Phys. Chem. B. 105:12902–12905. [Google Scholar]
  6. Beckstein, O., and M. S. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Berneche, S., and B. Roux. 2000. Molecular dynamics of the KcsA K+ channel in a bilayer membrane. Biophys. J. 78:2900–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Berneche, S., and B. Roux. 2001. Energetics of ion conduction through the K+ channel. Nature. 414:73–77. [DOI] [PubMed] [Google Scholar]
  9. Betanzos, M., C. S. Chiang, H. R. Guy, and S. Sukharev. 2002. A large iris-like expansion of a mechanosensitive channel protein induced by membrane tension. Nat. Struct. Biol. 9:704–710. [DOI] [PubMed] [Google Scholar]
  10. Biggin, P. C., G. R. Smith, I. Shrivastava, S. Choe, and M. S. Sansom. 2001. Potassium and sodium ions in a potassium channel studied by molecular dynamics simulations. Biochim. Biophys. Acta. 1510:1–9. [DOI] [PubMed] [Google Scholar]
  11. Brovchenko, I., D. Paschek, and A. Geiger. 2000. Gibbs ensemble simulation of water in spherical cavities. J. Chem. Phys. 113:5026–5036. [Google Scholar]
  12. Chang, G., R. H. Spencer, A. T. Lee, M. T. Barclay, and D. C. Rees. 1998. Structure of the MscL homolog from Mycobacterium tuberculosis: a gated mechanosensitive ion channel. Science. 282:2220–2226. [DOI] [PubMed] [Google Scholar]
  13. Chiu, S. W., E. Jakobsson, S. Subramaniam, and J. A. McCammon. 1991. Time-correlation analysis of simulated water motion in flexible and rigid gramicidin channels. Biophys. J. 60:273–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. de Groot, B. L., T. Frigato, V. Helms, and H. Grubmuller. 2003. The mechanism of proton exclusion in the aquaporin-1 water channel. J. Mol. Biol. 333:279–293. [DOI] [PubMed] [Google Scholar]
  15. de Groot, B. L., and H. Grubmuller. 2001. Water permeation across biological membranes: mechanism and dynamics of aquaporin-1 and GlpF. Science. 294:2353–2357. [DOI] [PubMed] [Google Scholar]
  16. DeCoursey, T. E., D. Morgan, and V. V. Cherny. 2003. The voltage dependence of NADPH oxidase reveals why phagocytes need proton channels. Nature. 422:531–534. [DOI] [PubMed] [Google Scholar]
  17. Evans, R. 1990. Fluids adsorbed in narrow pores—phase-equilibria and structure. J. Phys. Cond. Matt. 2:8989–9007. [Google Scholar]
  18. Fraczkiewicz, R., and W. Braun. 2002. Exact and efficient analytical calculation of the accessible surface areas and their gradients for macromolecules. J. Comp. Chem. 19:319–333. [Google Scholar]
  19. Gullingsrud, J., R. Braun, and K. Schulten. 1999. Reconstituting potentials of mean force through time series analysis of steered molecular dynamics simulations. J. Comp. Phys. 151:190–211. [Google Scholar]
  20. Gullingsrud, J., and K. Schulten. 2003. Gating of MscL studied by steered molecular dynamics. Biophys. J. 85:2087–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hille, B. 2001. Ion Channels of Excitable Membranes. Sinauer, Sunderland, MA.
  22. Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
  23. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  24. Im, W., and B. Roux. 2002. Ion permeation and selectivity of OmpF porin: a theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 322:851–869. [DOI] [PubMed] [Google Scholar]
  25. Jensen, M. O., S. Park, E. Tajkhorshid, and K. Schulten. 2002. Energetics of glycerol conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. USA. 99:6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jiang, Y., A. Lee, J. Chen, M. Cadene, B. T. Chait, and R. MacKinnon. 2002a. Crystal structure and mechanism of a calcium-gated potassium channel. Nature. 417:515–522. [DOI] [PubMed] [Google Scholar]
  27. Jiang, Y., A. Lee, J. Chen, M. Cadene, B. T. Chait, and R. MacKinnon. 2002b. The open pore conformation of potassium channels. Nature. 417:523–526. [DOI] [PubMed] [Google Scholar]
  28. Jiang, Y., V. Ruta, J. Chen, A. Lee, and R. MacKinnon. 2003. The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 423:42–48. [DOI] [PubMed] [Google Scholar]
  29. Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  30. Kale, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
  31. Kelly, B. L., and A. Gross. 2003. Potassium channel gating observed with site-directed mass tagging. Nat. Struct. Biol. 10:280–284. [DOI] [PubMed] [Google Scholar]
  32. Labarca, C., M. W. Nowak, H. Zhang, L. Tang, P. Deshpande, and H. A. Lester. 1995. Channel gating governed symmetrically by conserved leucine residues in the M2 domain of nicotinic receptors. Nature. 376:514–516. [DOI] [PubMed] [Google Scholar]
  33. Levina, N., S. Totemeyer, N. R. Stokes, P. Louis, M. A. Jones, and I. R. Booth. 1999. Protection of Escherichia coli cells against extreme turgor by activation of MscS and MscL mechanosensitive channels: identification of genes required for MscS activity. EMBO J. 18:1730–1737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lum, K., D. Chandler, and J. D. Weeks. 1999. Hydrophobicity at small and large length scales. J. Phys. Chem. B. 103:4570–4577. [Google Scholar]
  35. Martinac, B., M. Buechner, A. H. Delcour, J. Adler, and C. Kung. 1987. Pressure-sensitive ion channel in Escherichia coli. Proc. Natl. Acad. Sci. USA. 84:2297–2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mashl, R. J., S. Joseph, N. R. Aluru, and E. Jakobsson. 2003. Anomalously immobilized water: a new water phase induced by confinement in nanotubes. Nano Lett. 3:589–592. [Google Scholar]
  37. Merzlyak, P. G., L. N. Yuldasheva, C. G. Rodrigues, C. M. Carneiro, O. V. Krasilnikov, and S. M. Bezrukov. 1999. Polymeric nonelectrolytes to probe pore geometry: application to the alpha-toxin transmembrane channel. Biophys. J. 77:3023–3033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Miller, S., W. Bartlett, S. Chandrasekaran, S. Simpson, M. Edwards, and I. R. Booth. 2003a. Domain organization of the MscS mechanosensitive channel of Escherichia coli. EMBO J. 22:36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Miller, S., M. D. Edwards, C. Ozdemir, and I. R. Booth. 2003b. The closed structure of the MscS mechanosensitive channel. Cross-linking of single cysteine mutants. J. Biol. Chem. 278:32246–32250. [DOI] [PubMed] [Google Scholar]
  40. Miyazawa, A., Y. Fujiyoshi, and N. Unwin. 2003. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 424:949–955. [DOI] [PubMed] [Google Scholar]
  41. Monette, L., A. J. Liu, and G. S. Grest. 1992. Wetting and domain-growth kinetics in confined geometries. Phys. Rev. A. 46:7664–7679. [DOI] [PubMed] [Google Scholar]
  42. Nakajima, A., K. Hashimoto, and T. Watanabe. 2001. Recent studies on super-hydrophobic films. Monatsh. Chem. 132:31–41. [Google Scholar]
  43. Nonner, W., D. P. Chen, and B. Eisenberg. 1999. Progress and prospects in permeation. J. Gen. Physiol. 113:773–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ou, X., P. Blount, R. J. Hoffman, and C. Kung. 1998. One face of a transmembrane helix is crucial in mechanosensitive channel gating. Proc. Natl. Acad. Sci. USA. 95:11471–11475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Parsegian, A. 1969. Energy of an ion crossing a low dielectric membrane: solutions to four relevant electrostatic problems. Nature. 221:844–846. [DOI] [PubMed] [Google Scholar]
  46. Perozo, E., D. M. Cortes, P. Sompornpisut, A. Kloda, and B. Martinac. 2002. Open channel structure of MscL and the gating mechanism of mechanosensitive channels. Nature. 418:942–948. [DOI] [PubMed] [Google Scholar]
  47. Pivetti, C. D., M. R. Yen, S. Miller, W. Busch, Y. H. Tseng, I. R. Booth, and M. H. Saier, Jr. 2003. Two families of mechanosensitive channel proteins. Microbiol. Mol. Biol. Rev. 67:66–85 (table.). [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Smith, G. R., and M. S. Sansom. 1998. Dynamic properties of Na+ ions in models of ion channels: a molecular dynamics study. Biophys. J. 75:2767–2782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Song, L., M. R. Hobaugh, C. Shustak, S. Cheley, H. Bayley, and J. E. Gouaux. 1996. Structure of staphylococcal alpha-hemolysin, a heptameric transmembrane pore. Science. 274:1859–1866. [DOI] [PubMed] [Google Scholar]
  50. Sukharev, S. 2002. Purification of the small mechanosensitive channel of Escherichia coli (MscS): the subunit structure, conduction, and gating characteristics in liposomes. Biophys. J. 83:290–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Sukharev, S., M. Betanzos, C. S. Chiang, and H. R. Guy. 2001. The gating mechanism of the large mechanosensitive channel MscL. Nature. 409:720–724. [DOI] [PubMed] [Google Scholar]
  52. Sukhareva, M., D. H. Hackos, and K. J. Swartz. 2003. Constitutive activation of the Shaker Kv channel. J. Gen. Physiol. 122:541–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tajkhorshid, E., P. Nollert, M. O. Jensen, L. J. Miercke, J. O'Connell, R. M. Stroud, and K. Schulten. 2002. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 296:525–530. [DOI] [PubMed] [Google Scholar]
  54. Unwin, N. 1995. Acetylcholine receptor channel imaged in the open state. Nature. 373:37–43. [DOI] [PubMed] [Google Scholar]
  55. Wesson, L., and D. Eisenberg. 1992. Atomic solvation parameters applied to molecular dynamics of proteins in solution. Protein Sci. 1:227–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Yoshimura, K., A. Batiza, M. Schroeder, P. Blount, and C. Kung. 1999. Hydrophilicity of a single residue within MscL correlates with increased channel mechanosensitivity. Biophys. J. 77:1960–1972. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES